Detecting and Correcting for Paleomagnetic Inclination Shallowing of Sedimentary Rocks: A Review

Introduction

One of the outstanding problems in understanding paleomagnetic records of sedimentary rocks is inclination shallowing, i.e., the recording of magnetic remanence inclination that is shallower than that of the ambient field in which sedimentary rocks were magnetized. Recognition of non-ideal paleomagnetic recording in sedimentary rocks raises concern because our knowledge of the spatial-temporal behavior of the geomagnetic field is largely based on paleomagnetic records from sedimentary rocks due to their widespread occurrence and ability to record geomagnetic field variations relatively continuously. Recognition of inclination shallowing in sedimentary rocks has led to efforts to investigate processes that can cause this problem since it was first discovered 60 years ago (King, 1955). Laboratory re-deposition experiments and modeling work have shown that inclination shallowing could occur during sediment deposition and can be related to factors such as particle shape, viscosity, pH, and current shear (e.g., Griffiths et al., 1960; Verosub et al., 1979; Tauxe et al., 2006). Paleomagnetic studies of recent sediments and ancient sedimentary rocks have demonstrated that inclination shallowing could also take place after deposition and is associated with sediment compaction (Deamer and Kodama, 1990; Kodama, 1997). The degree of inclination shallowing can be described by the empirical formula (King, 1955):

$\begin{array}{ll}f=\text{ tan }(I_o)∕\text{tan }(I_f)& \left(1\right)\hfill \end{array}$

where f is the flattening factor, I_o is the observed, shallowed inclination and I_f is the inclination of the ambient field. The flattening factor f ranges from 1.0 (no inclination shallowing) to 0 (total inclination shallowing).

While our knowledge of the acquisition mechanism of depositional remanent magnetization (DRM) and post-depositional remanent magnetization (pDRM) continues to advance via modern, more sophisticated laboratory re-deposition experiments and novel modeling work (Katari and Tauxe, 2000; Jezek et al., 2012; Spassov and Valet, 2012; Roberts et al., 2013), examining the reliability of paleomagnetic records from sedimentary rocks is of paramount importance before these data are used to test tectonic models and to examine geomagnetic field behavior. Not all sedimentary paleomagnetic records are plagued by inclination shallowing, but many have been significantly biased by this phenomenon (Kodama, 2012). Hence, it is critical to detect and correct for shallowing to ensure the reliability of paleomagnetic data from sedimentary rocks.

To detect inclination shallowing in sedimentary rocks, one straightforward approach is to compare paleomagnetic data from sedimentary rocks with those from coeval igneous rocks, provided that the contemporaneous age of both types of rocks can be assured and a sufficient number of igneous cooling units are sampled to adequately average secular variation. These requirements can be satisfied in some sections where multiple basalt layers are sandwiched between sedimentary layers (Gilder et al., 2003; Li et al., 2013). However, in reality, such conditions are rare and are not commonly present in a sedimentary section of interest. For situations like this, two means of detecting and correcting for inclination shallowing are widely used, the magnetic anisotropy-based approach (Jackson et al., 1991; Kodama, 1997) and the elongation/inclination (E–I) technique (Tauxe and Kent, 2004). While numerous studies have used these two approaches, it is important to note that both approaches are based on certain assumptions and, thus, each has its intrinsic limitations. In this brief review, we comparatively assess these two approaches by highlighting their basic assumptions and associated limitations. Our analysis cautions against blind use of these techniques and emphasizes that the combined use of different types of magnetic anisotropy data could provide stronger evidence for inclination shallowing and offer new insights into detecting and correcting for inclination shallowing.

The Elongation/Inclination (E–I) Approach

The E–I approach takes advantage of the characteristic directional distributions of paleomagnetic directions due to geomagnetic secular variation. Tauxe and Kent (2004) constructed a statistical model of geomagnetic paleosecular variation (PSV), i.e., TK03.GAD, to quantify directional distributions. The TK03.GAD model was configured to fit the paleomagnetic directional data from lava flows erupted over the past 5 Myr and accounts for the latitudinal dependence of virtual geomagnetic pole (VGP) scatter S(λ). This model is designed to have a circular distribution of VGPs and thus predicts an elongated distribution of magnetic directions along the magnetic meridian. The degree of elongation, E, decreases with increasing latitude, and therefore increasing inclination, I. Thus, an E–I curve is created from this model. Deviations of the E–I relationship of observed paleomagnetic directions from the expected E–I curve could indicate the existence of inclination flattening. Specifically, an elongated distribution of directions along the perpendicular to the meridian, i.e., E–W in the horizontal plane, is considered diagnostic of inclination shallowing. Once inclination shallowing is recognized, the degree of shallowing can be quantified utilizing the model's E–I curve. Because the flattening factor, f, ranges from 1.0 to 0, varying the f factor leads to different E–I pairs. Once an E–I pair matches the E–I curve of the model, an optimum f value is found and the corrected inclination I_f is obtained by correcting the data using the obtained f value (Tauxe and Kent, 2004).

One obvious advantage of the E–I approach is that it is relatively easy to use and no additional rock magnetic measurements are required (see Section The Magnetic Anisotropy-Based Approach). Only the E–I data analysis is necessary for standard paleomagnetic data. This approach has been widely used since its introduction.

While it is easy to use and often provides reasonable interpretations, the intrinsic limitations associated with the assumptions are noteworthy. First, the TK03.GAD model is based on fitting paleomagnetic data from the past 5 Myr and it assumes that the geomagnetic field behaved similarly throughout geological time. To test whether the model is valid further back in time, Tauxe et al. (2008) analyzed paleomagnetic data from large igneous provinces (LIPs) with ages back to the Cretaceous and found that the E–I pairs of these data agree with the model's prediction. Paleomagnetic data from ~1.1 Ga lava flows also appear to agree with the model (Tauxe and Kodama, 2009). So far, the model has not been tested with data from the Paleozoic and Neoproterozoic. Furthermore, the previously mentioned LIP data are mainly from middle-high latitudes and data from middle-low latitudes are lacking. It will be important to test the model with data from mid-low latitudes where the elongation feature of magnetic directions is most pronounced as predicted by the model. Second, a large dataset (n > 100) is needed to represent a sufficiently long period of time so that directional distributions caused by PSV are adequately sampled. For sedimentary rocks, the time period recorded by a sample is a function of sediment accumulation rate (SAR; Kodama, 2012). SARs in pelagic or hemipelagic settings are usually about 1.0–10.0 cm/kyr or less. A typical paleomagnetic specimen of 2.2 cm thickness would average 220–2200 years or more, which suggests that PSV has been smoothed even in one specimen. This is in sharp contrast to the spot reading of the geomagnetic field from lava flows over the past 5 Myr on which the PSV model is based. Therefore, the E–I method is not suitable for sedimentary rocks with slow SARs. While the dataset should be large enough to adequately sample PSV, the duration sampled should not be so long that the results are affected by plate motion (Tauxe and Kodama, 2009). Third, local tectonics need to be taken into account. Relative vertical-axis rotations between sampling sites can lead to an apparent E–W elongation, which is not related to inclination shallowing. Kodama (2012) pointed out that the E–I method led to an over-correction of inclination shallowing in Oligocene–Miocene redbeds from coastal California (Hillhouse, 2010), where the over-correction was attributed to unrecognized vertical-axis rotations. Fourth, the TK03.GAD model assumes hemispheric symmetry of the geomagnetic field. Asymmetrical field behavior at high latitudes may persist and the model can only predict field behavior at high latitudes of the northern hemisphere (N.H.) reasonably well (Cromwell et al., 2013), which would thus limit its use to N.H. data only. Finally, Linder and Gilder (2012) recently stated that circular VGP distributions, as required by the TK03.GAD model, are based on paleomagnetic directions derived from a wide distribution of site longitudes. However, because paleomagnetic studies are usually from one or two localities, they argue that a Fisherian distribution of directions and the associated precision parameter, k, should be used for a paleomagnetic study instead. No details are given as to how k can be used for E–I corrections. Nonetheless, while the E–I approach is relatively easy to use, its assumptions and intrinsic limitations should be kept in mind, and uninformed use of the approach may lead to over- or under-corrections.

The Magnetic Anisotropy-Based Approach

Magnetic anisotropy, or magnetic fabric, is described by a second-rank tensor that is graphically represented by an ellipsoid (Tarling and Hrouda, 1993). Magnetic anisotropy can thus be characterized by the shape and orientation of the principal axes (K_max, K_int, K_min) of the ellipsoid. During deposition and post-depositional compaction, bedding-parallel flattening can cause shallower inclinations than that of the ambient field and the development of an oblate fabric, which is characterized by K_min perpendicular to bedding with K_int and K_max lying within the bedding plane (Tarling and Hrouda, 1993). The presence of oblate fabrics is commonly taken as evidence for inclination shallowing (Kodama, 1997).

Jackson et al. (1991) developed a theoretical model for correcting inclination shallowing that links the flattening factor f to magnetic anisotropy:

$\begin{array}{ll}f=\frac{{\text{K}}_{\text{min}}\left(\text{a}+2\right)-1}{{\text{K}}_{\text{max}}\left(\text{a}+2\right)-1}& \left(2\right)\hfill \end{array}$

where K_max and K_min are the normalized maximum and minimum axes of the bulk magnetic anisotropy, and a is the anisotropy of individual magnetic particles. For remanence-carrying hematite grains, Tan and Kodama (2003) modified Equation (2) as follows:

$\begin{array}{ll}f=\frac{{\text{K}}_{\text{min}}\left(2\text{a}+1\right)-1}{{\text{K}}_{\text{max}}\left(2\text{a}+1\right)-1}& \left(3\right)\hfill \end{array}$

assuming that hematite occurs as platelets with the remanence confined to the basal plane of the particle. The advantage of this approach is that inclination shallowing is directly linked to evidence for shallowing, i.e., magnetic anisotropy. In this approach, it is assumed that the initial magnetic anisotropy at deposition is nearly isotropic or negligible and that magnetic particles initially align faithfully with the ambient field. Also, the degree of inclination shallowing corresponds to the degree of magnetic anisotropy development. This assumption appears to be supported by field data. For instance, laminated rocks have been shown to have a stronger foliation and shallower inclinations than mass-flow faces in an extensional basin on the Iberian margin (Garcés et al., 1996). Also, well-foliated Cretaceous marine sedimentary rocks from Baja California have shallower inclinations than non-foliated samples (Vaughn et al., 2005). Besides these end-member scenarios, development of magnetic anisotropy was found to generally correspond to the degree of inclination shallowing in a Quaternary marine succession that is undergoing compaction on the northern slope of the South China Sea (Li et al., 2014).

In Equations (2) and (3), inclination shallowing is a function of both bulk magnetic anisotropy and individual particle anisotropy (Figure 1). Therefore, in addition to standard paleomagnetic data acquisition, detailed laboratory rock magnetic experiments are needed to determine the bulk magnetic remanence anisotropy and the individual particle anisotropy.

FIGURE 1

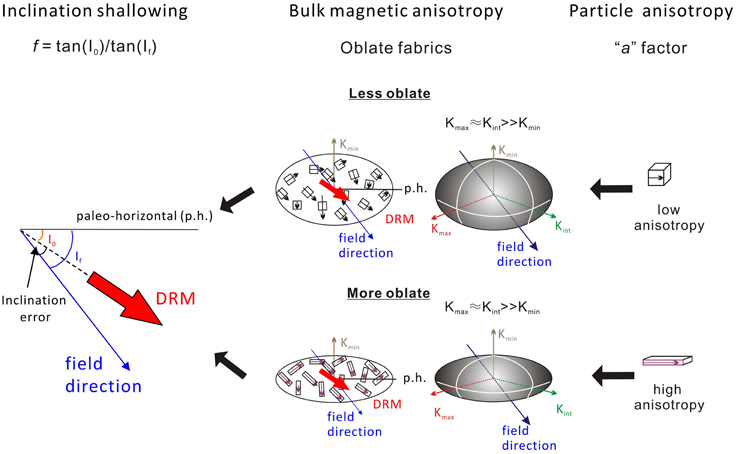
Figure 1. Schematic diagram that indicates how inclination shallowing is a function of both bulk anisotropy and individual particle anisotropy “a” factor.

Determining Bulk Magnetic Anisotropy

Anisotropy of magnetic susceptibility (AMS) is perhaps the most widely measured bulk magnetic anisotropy in paleomagnetic studies. However, AMS is carried by all types of magnetic minerals in a rock, i.e., diamagnetic, paramagnetic, and ferrimagnetic minerals. For inclination shallowing corrections, the bulk magnetic anisotropy used must be the remanence anisotropy, i.e., the anisotropy of only the remanence-carrying grains. If the remanence is carried by magnetite, the remanence-carrying magnetite grains are identified by the coercivity range over which the characteristic remanent magnetization (ChRM) was isolated by alternating field (AF) demagnetization. The bulk anisotropy of these grains can be determined by measuring, in theory, three orthogonal partial anhysteretic remanent magnetizations (pARM). In practice, redundant measurements (e.g., nine orientations in McCabe et al., 1985) are necessary to accurately define a second-rank tensor. Between each step of pARM acquisition and measurement, the sample is demagnetized at a peak AF high enough to remove the previously applied pARM. The measurements are then used to compute the anisotropy of anhysteretic remanence (AAR), i.e., the bulk remanence anisotropy of the sample.

If the remanence resides in hematite, remanence-carrying grains are identified by the unblocking temperature ranges over which the ChRM was isolated. Bulk magnetic anisotropy of these grains can be determined by measuring isothermal remanent magnetization (IRM) acquired with an applied direct current (DC) field high enough to magnetize the coercivity component that carries the ChRM (Tan and Kodama, 2002; Tan et al., 2003, 2007). For example, Tan et al. (2003) used a DC field of 1.2 T applied along nine orientations, following McCabe et al. (1985), for the Cretaceous Kapusaliang Formation redbeds of central Asia. Thermal demagnetization at 680°C was performed between each step of IRM acquisition and measurement, and the nine orientation IRMs were then used to determine the bulk magnetic anisotropy of isothermal remanence (AIR). Alternatively, samples can be given partial thermal remanent magnetizations (pTRM) along nine orientations using the unblocking temperature range determined by thermal demagnetization of the ChRM and the bulk magnetic anisotropy can be determined by the anisotropy of thermal remanence, i.e., ATR (Tan and Kodama, 2002; Schmidt and Williams, 2013). Repeated heating can cause transformation of mineral phases and changes in the magnetic grain size distribution of samples. Also, AIR determination for IRMs acquired at a low field following the approach of McCabe et al. (1985) can be severely undermined by the effects of magnetic history on IRM acquisition (Tauxe et al., 1990; Mitra et al., 2011). To overcome these issues, high-field IRM (hf-IRM) can be alternatively used to measure the bulk remanence anisotropy (Kodama and Dekkers, 2004). The applied field is strong enough to saturate all hematite grains along each orientation, therefore, there is no need to demagnetize the samples between each hf-IRM orientation to remove the influence from the previously applied IRM. For instance, a hf-IRM can be imparted at an applied field of 5 T along nine orientations and measured accordingly (Bilardello and Kodama, 2009). Regardless of the type of remanent magnetization used to determine the bulk anisotropy, all of these techniques require labor-intensive laboratory experiments. Simplified procedures have, therefore, been proposed. One procedure involves imparting and measuring the remanent magnetization along only three orthogonal directions, two within and the other perpendicular to the bedding plane (Tan and Kodama, 2002; Tan et al., 2003; Schmidt et al., 2009). Alternatively, multiple subsamples collected along three orthogonal directions can be treated separately (Bilardello, 2015). Another procedure involves imparting an IRM at 45° to the bedding plane to quantify the anisotropy (Hodych and Buchan, 1994). These simplified treatments essentially estimate the bulk anisotropy based on partial anisotropy measurements. The partial bulk anisotropy needs to be compared with one determined from a complete second-rank tensor to ensure that they are equivalent. Also, for the multiple subsample approach, a non-uniform distribution of magnetic particles could bias bulk anisotropy determination.

Determining Individual Particle Anisotropy a

Individual particle anisotropy a can be determined by redeposition-compaction experiments, direct measurement of magnetic mineral extracts, or a curve fitting technique (Kodama, 1997, 2009). Redeposition-compaction experiments are conducted in a known field to mimic deposition and natural post-depositional processes. Compacted samples are treated as if they were natural samples so that their ChRM and bulk anisotropy can be measured. Since the ambient field at which the experiments were conducted is known, particle anisotropy “a” can be determined by joint use of Equations (1) and (2). For magnetic extracts, magnetic particles are dispersed in epoxy that is exposed to a static magnetic field to align the particles along the field as the epoxy solidifies. The remanent magnetization along the hard- and easy-axis are measured and particle anisotropy is defined by the ratio of the easy-axis component over the hard-axis component. Both redeposition-compaction experiments and direct measurements of magnetic extracts involve a significant amount of laboratory work. To simplify the procedure, Kodama (2009) developed a curve-fitting approach that involves least-squares fitting of bulk anisotropy data to a theoretical correction curve to find the effective particle anisotropy.

The advantage of the anisotropy-based method is that it focuses directly on the magnetic grains that carry the shallowed inclination. The disadvantage is that it requires intensive laboratory rock magnetic experiments. Many of these experiments need specialized instruments that are not commonly available in paleomagnetism laboratories, thus limiting their use. In addition, there are two main challenges in using this method. One is isolating bulk anisotropy of ChRM-carrying grains and the other is determining individual particle anisotropy. Rocks often contain different types of minerals with different grain sizes. Isolating the anisotropy of ChRM-carrying grains can be challenging because it can be masked by the anisotropies of co-existing magnetic minerals that do not carry a ChRM. Combined use of different treatments can help to isolate contributions from different magnetic mineral fractions. For example, AF demagnetization at 100 mT and thermal demagnetization at 125°C have been combined with the nine position anisotropy measurement to eliminate the influence of magnetite and goethite on ChRMs carried by hematite (Bilardello and Kodama, 2010). Monitoring AMS during stepwise chemical demagnetization allows determination of bulk magnetic anisotropy of pigmentary hematite by subtraction of AMS between two demagnetization steps and isolation of bulk magnetic anisotropy of detrital hematite grains (Tan and Kodama, 2002; Tan et al., 2003). The other challenge is that it is difficult to accurately determine the individual particle anisotropy a factor.

Outlook

Comparative studies of the E–I and anisotropy-based approaches yield generally consistent results (e.g., Tauxe et al., 2008), which demonstrate the effectiveness of both approaches for correcting shallow inclinations. However, either of these approaches should not be used without full appreciation of their underlying assumptions and intrinsic limitations. The E–I approach is easy to use, which presents both opportunities and dangers, such as inadequate sampling of PSV or local vertical axis rotations. The anisotropy-based approach involves intensive laboratory rock magnetic experiments, thus making it less desirable, but magnetic anisotropy provides direct evidence for the inclination shallowing. Use and comparison of both techniques would be valuable for robust inclination shallowing correction in sedimentary rocks.

Author Contributions

All authors listed, have made substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Bin Wen for help with crafting the figure. We thank Editor Andrew Roberts and Reviewers Mike Jackson and Lisa Tauxe for their insightful comments that helped improve the manuscript. We gratefully acknowledge fruitful discussion with Xiaodong Tan. Y.-X. Li is supported by the National Natural Science Foundation of China (41274071, 41230208). K. P. Kodama is supported by NSF EAR-1322002.

References

Bilardello, D., and Kodama, K. P. (2009). Measuring remanence anisotropy of hematite in red beds: anisotropy of high-field isothermal remanence magnetization (hf-AIR). Geophys. J. Int. 178, 1260–1272. doi: 10.1111/j.1365-246X.2009.04231.x

CrossRef Full Text | Google Scholar

Bilardello, D., and Kodama, K. P. (2010). A new inclination shallowing correction of the Mauch Chunk Formation of Pennsylvania, based on high-field AIR results: implications for the Carboniferous North American APW path and Pangea reconstructions. Earth Planet. Sci. Lett. 299, 218–227. doi: 10.1016/j.epsl.2010.09.002

CrossRef Full Text | Google Scholar

Bilardello, D. (2015). Isolating the anisotropy of the characteristic remanence-carrying hematite grains: a first multispecimen approach. Geophys. J. Int. 202, 695–712. doi: 10.1093/gji/ggv171

CrossRef Full Text | Google Scholar

Cromwell, G., Tauxe, L., Staudigel, H., Constable, C. G., Koppers, A. A. P., and Pedersen, R.-B. (2013). In search of long-term hemispheric asymmetry in the geomagnetic field: results from high northern latitudes. Geochem. Geophys. Geosyst. 14, 3234–3249. doi: 10.1002/ggge.20174

CrossRef Full Text | Google Scholar

Deamer, G. A., and Kodama, K. P. (1990). Compaction-induced inclination shallowing in synthetic and natural clay-rich sediments. J. Geophys. Res. 95, 4511–4529. doi: 10.1029/JB095iB04p04511

CrossRef Full Text | Google Scholar

Garcés, M., Parés, J. M., and Cabrera, L. (1996). Further evidence for inclination shallowing in red beds. Geophys. Res. Lett. 23, 2065–2068. doi: 10.1029/96gl02060

CrossRef Full Text | Google Scholar

Gilder, S. A., Chen, Y., Cogné, J. P., Tan, X., Courtillot, V., Sun, D., et al. (2003). Paleomagnetism of Upper Jurassic to Lower Cretaceous volcanic and sedimentary rocks from the western Tarim Basin and implications for inclination shallowing and absolute dating of the M-0 (ISEA?) chron. Earth Planet. Sci. Lett. 206, 587–600. doi: 10.1016/S0012-821X(02)01074-9

CrossRef Full Text | Google Scholar

Griffiths, D. H., King, R. F., Rees, A. I., and Wright, A. E. (1960). Remanent magnetism of some recent varved sediments. Proc. R. Soc. A 256, 359–383. doi: 10.1098/rspa.1960.0113

CrossRef Full Text | Google Scholar

Hillhouse, J. W. (2010). Clockwise rotation and implications for northward drift of the western Transverse Ranges from paleomagnetism of the Piuma Member, Sespe Formation, near Malibu, California. Geochem. Geophys. Geosyst. 11, Q07005. doi: 10.1029/2010GC003047

CrossRef Full Text | Google Scholar

Hodych, J. P., and Buchan, K. L. (1994). Early Silurian palaeolatitude of the Springdale Group red beds of central Newfoundland: a palaeomagnetic determination with a remanence anisotropy test for inclination error. Geophys. J. Int. 117, 640–652. doi: 10.1111/j.1365-246X.1994.tb02459.x

CrossRef Full Text | Google Scholar

Jackson, M. J., Banerjee, S. K., Marvin, J. A., Lu, R., and Gruber, W. (1991). Detrital remanence inclination errors and anhysteretic remanence anisotropy: quantitative model and experimental results. Geophys. J. Int. 104, 95–103. doi: 10.1111/j.1365-246X.1991.tb02496.x

CrossRef Full Text | Google Scholar

Jezek, J., Gilder, S. A., and Bilardello, D. (2012). Numerical simulation of inclination shallowing by rolling and slipping of spherical particles. Comput. Geosci. 49, 270–277. doi: 10.1016/j.cageo.2012.06.013

CrossRef Full Text | Google Scholar

Katari, K., and Tauxe, L. (2000). Effects of pH and salinity on the intensity of magnetization in redeposited sediments. Earth Planet. Sci. Lett. 181, 489–496. doi: 10.1016/S0012-821X(00)00226-0

CrossRef Full Text | Google Scholar

King, R. F. (1955). Remanent magnetism of artificially deposited sediments. Monthly Notices Roy. Astron. Soc. Geophys. Suppl. 7, 115–134. doi: 10.1111/j.1365-246X.1955.tb06558.x

CrossRef Full Text | Google Scholar

Kodama, K. P. (1997). A successful rock magnetic technique for correcting paleomagnetic inclination shallowing: case study of the Nacimiento Formation, New Mexico. J. Geophys. Res. 102, 5193–5206. doi: 10.1029/96JB03833

CrossRef Full Text | Google Scholar

Kodama, K. P. (2009). Simplification of the anisotropy-based inclination correction technique for magnetite- and haematite-bearing rocks: a case study for the Carboniferous Glenshaw and Mauch Chunk Formations, North America. Geophys. J. Int. 176, 467–477. doi: 10.1111/j.1365-246X.2008.04013.x

CrossRef Full Text | Google Scholar

Kodama, K. P. (2012). Paleomagnetism of Sedimentary Rocks: Process and Interpretation. Oxford: Wiley-Blackwell.

Google Scholar

Kodama, K. P., and Dekkers, M. J. (2004). Magnetic anisotropy as an aid to identifying CRM and DRM in red sedimentary rocks. Stud. Geophys. Geod. 48, 747–766. doi: 10.1023/B:SGEG.0000045481.47203.33

CrossRef Full Text | Google Scholar

Li, Y. X., Shu, L. S., Wen, B., Yang, Z. Y., and Ali, J. R. (2013). Magnetic inclination shallowing problem and the issue of Eurasia's rigidity: insights following a paleomagnetic study of Upper Cretaceous basalts and redbeds from SE China. Geophys. J. Int. 194, 1374–1389. doi: 10.1093/gji/ggt181

CrossRef Full Text | Google Scholar

Li, Y. X., Wang, S. P., Fu, S. Y., and Jiao, W. J. (2014). Recognizing the threshold magnetic anisotropy for inclination shallowing: implications for correcting inclination errors of sedimentary rocks. Front. Earth Sci. 2:8. doi: 10.3389/feart.2014.00008

CrossRef Full Text | Google Scholar

Linder, J., and Gilder, S. A. (2012). Latitude dependency of the geomagnetic secular variation S parameter: a mathematical artifact. Geophys. Res. Lett. 39, L02308. doi: 10.1029/2011GL050330

CrossRef Full Text | Google Scholar

McCabe, C., Jackson, M., and Ellwood, B. B. (1985). Magnetic anisotropy in the Trenton limestone: results of a new technique, anisotropy of anhysteretic susceptibility. Geophys. Res. Lett. 12, 333–336. doi: 10.1029/GL012i006p00333

CrossRef Full Text | Google Scholar

Mitra, R., Taxue, L., and Gee, J. S. (2011). Detecting uniaxial single domain grains with a modified IRM technique. Geophys. J. Int. 187, 1250–1258. doi: 10.1111/j.1365-246X.2011.05224.x

CrossRef Full Text | Google Scholar

Roberts, A. P., Florindo, F., Chang, L., Heslop, D., Jovane, L., and Larrasoaña, J. C. (2013). Magnetic properties of pelagic marine carbonates. Earth Sci. Rev. 127, 111–139. doi: 10.1016/j.earscirev.2013.09.009

CrossRef Full Text | Google Scholar

Schmidt, P. W., and Williams, G. E. (2013). Anisotropy of thermoremanent magnetization of Cryogenian glaciogenic and Ediacaran redbeds, South Australia: neoproterozoic apparent or true polar wander? Global Planet. Change 110, 289–301. doi: 10.1016/j.gloplacha.2012.11.008

CrossRef Full Text | Google Scholar

Schmidt, P. W., Williams, G. E., and McWilliams, M. O. (2009). Palaeomagnetism and magnetic anisotropy of late Neoproterozoic strata, South Australia: implications for the palaeolatitude of the late Cryogenian glaciation, cap carbonate and the Ediacaran system. Precamb. Res. 174, 35–52. doi: 10.1016/j.precamres.2009.06.002

CrossRef Full Text | Google Scholar

Spassov, S., and Valet, J. P. (2012). Detrital magnetizations from redeposition experiments of different natural sediments. Earth Planet. Sci. Lett. 351, 147–157. doi: 10.1016/j.epsl.2012.07.016

CrossRef Full Text | Google Scholar

Tan, X., and Kodama, K. P. (2002). Magnetic anisotropy and paleomagnetic inclination shallowing in red beds: evidence from the Mississippian Mauch Chunk Formation, Pennsylvania. J. Geophys. Res. 107, 2311. doi: 10.1029/2001jb001636

CrossRef Full Text | Google Scholar

Tan, X., and Kodama, K. P. (2003). An analytical solution for correcting palaeomagnetic inclination error. Geophys. J. Int. 152, 228–236. doi: 10.1046/j.1365-246X.2003.01848.x

CrossRef Full Text | Google Scholar

Tan, X., Kodama, K. P., Chen, H., Fang, D., Sun, D., and Li, Y. (2003). Paleomagnetism and magnetic anisotropy of Cretaceous red beds from the Tarim basin, northwest China: evidence for a rock magnetic cause of anomalously shallow paleomagnetic inclinations from central Asia. J. Geophys. Res. 108, 2107. doi: 10.1029/2001jb001608

CrossRef Full Text | Google Scholar

Tan, X., Kodama, K. P., Gilder, S., and Courtillot, V. (2007). Rock magnetic evidence for inclination shallowing in the Passaic Formation red beds from the Newark basin and a systematic bias of the Late Triassic apparent polar wander path for North America. Earth Planet. Sci. Lett. 254, 345–357. doi: 10.1016/j.epsl.2006.11.043

CrossRef Full Text | Google Scholar

Tarling, D. H., and Hrouda, F. (1993). The Magnetic Anisotropy of Rocks. New York, NY: Chapman and Hall.

Google Scholar

Tauxe, L., and Kent, D. V. (2004). “A new statistical model for the geomagnetic field and the detection of shallow bias in paleomagnetic inclinations: was the ancient field dipolar?” in Timescales of the Internal Geomagnetic Field Geophysical Monograph, Vol. 145, eds J. E. T. Channell, D. V. Kent, W. Lowrie, and J. Meert (Washington, DC: American Geophysical Union), 101–116.

Tauxe, L., Kodama, K., and Kent, D. V. (2008). Testing corrections for paleomagnetic inclination error in sedimentary rocks: a comparative approach. Phys. Earth Planet. Inter. 169, 152–165. doi: 10.1016/j.pepi.2008.05.006

CrossRef Full Text | Google Scholar

Tauxe, L., and Kodama, K. P. (2009). Paleosecular variation models for ancient times: clues from Keweenawan lava flows. Phys. Earth Planet. Inter. 177, 31–45. doi: 10.1016/j.pepi.2009.07.006

CrossRef Full Text | Google Scholar

Tauxe, L., Steindorf, J. L., and Harris, A. (2006). Depositional remanent magnetization: toward an improved theoretical and experimental foundation. Earth Planet. Sci. Lett. 244, 515–529. doi: 10.1016/j.epsl.2006.02.003

CrossRef Full Text | Google Scholar

Tauxe, L., Constable, C., Stokking, L., and Badgley, C. (1990). Use of anisotropy to determine the origin of characteristic remanence in the Siwalik red beds of northern Pakistan. J. Geophys. Res. 95, 4391–4404. doi: 10.1029/jb095ib04p04391

CrossRef Full Text | Google Scholar

Vaughn, J., Kodama, K. P., and Smith, D. P. (2005). Correction of inclination shallowing and its tectonic implications: the Cretaceous Perforada Formation, Baja California. Earth Planet. Sci. Lett. 232, 71–82. doi: 10.1016/j.epsl.2004.11.026

CrossRef Full Text | Google Scholar

Verosub, K. L., Ensley, R. A., and Ulrick, J. S. (1979). The role of water content in the magnetization of sediments. Geophys. Res. Lett. 6, 226–228. doi: 10.1029/GL006i004p00226

CrossRef Full Text | Google Scholar