- Department Planets and Comets, Max Planck Institute for Solar System Research, Göttingen, Germany
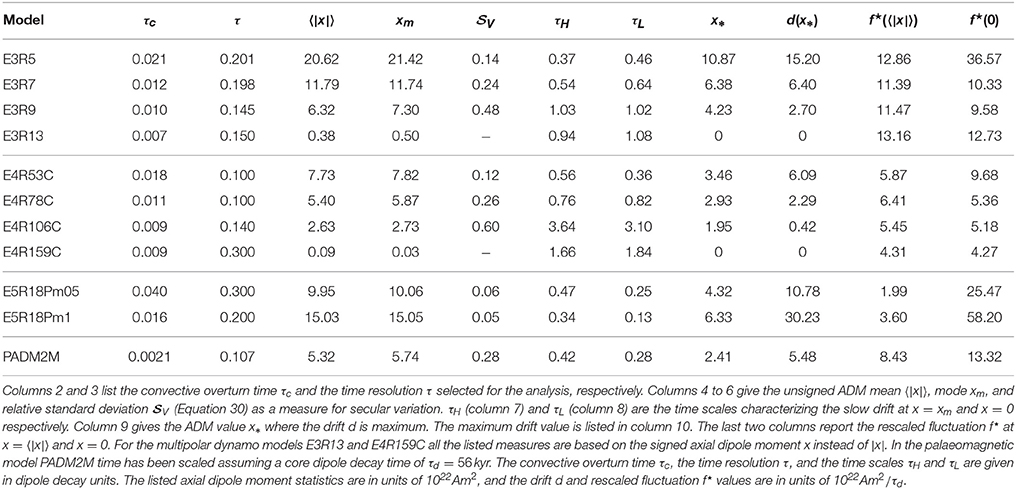
Earth's axial dipole field changes in a complex fashion on many different time scales ranging from less than a year to tens of million years. Documenting, analysing, and replicating this intricate signal is a challenge for data acquisition, theoretical interpretation, and dynamo modeling alike. Here we explore whether axial dipole variations can be described by the superposition of a slow deterministic drift and fast stochastic fluctuations, i.e. by a Langevin-type system. The drift term describes the time averaged behavior of the axial dipole variations, whereas the stochastic part mimics complex flow interactions. The statistical behavior of the system is described by a Fokker-Planck equation which allows useful predictions, including the average rates of dipole reversals and excursions. We analyze several numerical dynamo simulations, most of which have been integrated particularly long in time, and also the palaeomagnetic model PADM2M which covers the past 2Myr. The results show that the Langevin description provides a viable statistical model of the axial dipole variations on time scales longer than about 1kyr. For example, the axial dipole probability distribution and the average reversal rate are successfully predicted. The exception is PADM2M where the stochastic model reversal rate seems too low. The dependence of the drift on the axial dipole moment reveals the nonlinear interactions that establish the dynamo balance. A separate analysis of inductive and diffusive magnetic effects in three dynamo simulations suggests that the classical quadratic quenching of induction predicted by mean-field theory seems at work.
1. Introduction
Earth's internal magnetic field is produced in the liquid iron core in a complex highly nonlinear dynamo mechanism. Geomagnetic data provide a window into this process which can be exploited for clues on the internal dynamics. Information on shorter time scales of years to decades can rely on a combination of high quality satellite data and historical data. The respective models can describe the field up to spherical harmonic degree and order 14 beyond which the small scale crustal field starts to dominate (Jackson et al., 2000). Archaeomagnetic models cover a period up to about 10kyr ago with a spatial resolution equivalent to perhaps degree and order 4 and a temporal resolution of about 100yr (Korte et al., 2011; Pavón-Carrasco et al., 2014). On longer times scales, however, one mostly has to rely on palaeomagnetic data where resolving more than the dipole component is challenging and the dating is often problematic.
A combination of the different data sources reveals that dipole variations have a broad temporal power spectrum shaped by the nonlinear interaction between processes acting on different time scales (Constable and Johnson, 2005). Shorter time scales in the range of years are likely tied to wave phenomena (Gillet et al., 2010) while decadal to centennial variations reflect the convective flow dynamics (Christensen et al., 2012). Longer time scales are typically related to field reversals and excursions. Variations in the reversal rate over some 10Myr represent the longest time scale that likely reflects changes in the Earth's lower mantle structure (McFadden and Merrill, 1984; Biggin et al., 2012).
Statistical analyses attempt to extract essential information from the intricate but limited geomagnetic signal. Constable and Parker (1988) assume that the variations in the individual Gauss coefficients, that describe Earth's surface field, obey a so-called giant Gaussian process (GGP). The statistic of each coefficient is thus a Gaussian defined by mean and (co)variance. The advantage of this approach is that the time averaged field can be deduced without requiring exact dating. Palaeomagnetic records covering more than the last 5Myr can thus be exploited to reveal that a strong axial dipole moment indeed clearly dominates the time averaged field. But there are also hints for additional, much weaker and persistent non-axisymmetric (possibly also equatorially symmetric) contributions. We refer to Hulot and Bouligand (2005) for an overview of the different refinements to the GGP suggested over the years. This approach provides, however, little information on the internal dynamics beyond the standard deviation as a measure for the mean palaeomagnetic secular variation.
Statistical approaches have also proven useful when dealing with full 3D numerical dynamo simulations where the wealth and complexity of information is hard to interpret. Wicht and Meduri (submitted), referred to as WM16 in the following, analyzed the probability distribution of axial and equatorial dipole moments in several different numerical dynamo models. With the exception of the largest Ekman number cases which seem the most remote from Earth conditions, the results obey a simple statistical systematic. Both equatorial dipole moment contributions have a Gaussian distribution with zero mean and a variance that is nearly independent of the Rayleigh number Ra. The axial dipole moment (ADM) distribution, however, shows a much more interesting behavior. At relatively small Ra, where the dipole never reverses, the distribution is also Gaussian but with a non-zero mean. On increasing Ra the mean decreases until small ADMs become more likely. Reversals (and excursions) then start and the distribution resembles the superposition of three Gaussians, two high ADM ones with non-zero means of opposite sign and a smaller third with zero mean. When increasing Ra further, the high ADM Gaussians combine with the third: The dipole loses its dominant role and the field becomes multipolar.
WM16 suggest that the third Gaussian reflects a new weak dynamo state that facilitates reversals and excursions. The dynamo may enter this state once the dipole moment has decreased to at least 30% of its mean, a prerequisite for reversals and excursions that seems to agree with palaeomagnetic inferences (Channell et al., 2009). However, reversal and excursion durations are excessively long in the simulations thus leading to a too pronounced weak state Gaussian.
A more refined model that concentrates on the statistics of dipole moment variations was pioneered by Hoyng et al. (2001) and Schmitt et al. (2001). They suggest that the ADM dynamics can be described by the Langevin equation
This simple stochastic differential equation is used to describe a wealth of different physical processes where many smaller fast varying subsystems interact to yield a slower large scale dynamics (see, e.g., Friedrich et al., 2011). Since small scale eddies are thought to team up to maintain Earth's slowly varying dipole field, the Langevin equation may indeed offer a viable statistical model for variations in the axial dipole moment x(t). The slow deterministic large scale dynamics, called drift in the Langevin formalism, is described by the function d(x) while the fast small scale dynamics creates the stochastic fluctuations f(x)L(t) called diffusion. This latter expression refers to the application to Brownian motion where the stochastic action of many microscopic particles conspires to induce large scale diffusion. We will use the term fluctuation instead to avoid confusion with the magnetic diffusion. The fluctuation amplitude f(x) formulates the dependence on x, while the random noise L(t) has a vanishing time average and infinitely small correlation time (see Section 2.2).
ADM fluctuations can only be expected to be statistically uncorrelated on time scales longer than the typical time scale of convective motions. Hoyng et al. (2001) therefore suggest that only time scales beyond the convective overturn time τc of approximately 120yr for Earth obey the Langevin equation and simply use time resolutions τ > τc for analyzing the magnetic data. Drift and fluctuation functions are then related to the mean variation 〈〉 and root mean square (RMS) variation {} for a given discrete data set x(ti) (with ti + 1 = ti + τ) by
and
Details on the formalism are given in Section 2.2.
When a stochastic system starts at time t with a well-defined value x(t), it can assume different values at time t + τ with different probabilities. The dynamics can thus be expressed as an evolution of the associated time dependent probability distribution p(x, t) which is governed by the Fokker-Planck equation (FPE) for the Langevin system. Because of the wealth of applications, the Langevin equation (1) and the associated FPE have been extensively studied (see, e.g., Risken and Frank, 1996; Van Kampen, 2007; Friedrich et al., 2011) and lead to interesting analogies and testable predictions in the dynamo context.
For example, x can be thought of as the position of a stochastic particle in the potential U(x) defined by dU(x)∕dx = −d(x) and illustrated in Figure 1. The two minima in U(x), say at ±xm, are separated by a hump around x = 0 and reflect the bistable nature of a reversing dynamo. The drift d(x) models the mean force that drives the particle to ±xm while the random fluctuations f(x) allow the particle to leave the potential minima. When the fluctuations correlate sufficiently, the particle can cross the potential barrier and may undergo a “field reversal” (Schmitt et al., 2001).
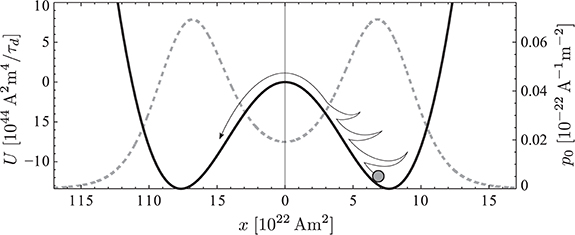
Figure 1. Drift potential U(x) (solid curve, left axis) and steady-state probability density function p0(x) (dashed curve, right axis) for the “particle-in-well” analog to reversing dynamos. The potential forces provide the deterministic slow drift while fast stochastic fluctuations enable the particle to cross the potential barrier that separates both polarities. p0 is the analytical solution of the stationary Fokker-Planck equation (Equation 27). The reversing dynamo model shown is E3R9. After Figure 2 in Schmitt et al. (2001).
The stationary solution p0(x) of the FPE provides a prediction of the ADM probability distribution that can be compared with the data. Figure 1 illustrates the bimodal p0(x) associated to the respective potential U(x). Deviations from a pair of Gaussian distributions like those reported by WM16 are more likely for small ADM values where the particular form of the potential well is decisive. The steady-state distribution p0(x) allows several other properties to be predicted, like the mean ADM 〈x〉 and its standard deviation σx as a measure for palaeosecular variation. The mean reversal waiting time 〈TR〉, i.e. the mean time between successive reversals, can be predicted from the mean first passage time of the potential well. Fokker-Planck theory also predicts a Poissonian occurrence of reversals and thus an Earth-like distribution of reversal waiting times (Schmitt et al., 2001).
Hoyng et al. (2001) developed a simple quenched αΩ mean-field dynamo with a stochastic contribution in the α-forcing that reproduces several important features of Earth's reversal behavior. For example, the normal secular variation is interspersed by relatively short stochastic reversals (and excursions) that obey an Earth-like statistic (Schmitt et al., 2001). Using a semi-analytical approach, Hoyng et al. (2001) confirm that the dynamics of their model is well described by the Fokker-Planck formalism and suggest that this could hold for all reversing dynamos including Earth. When adjusting the free parameters so that p0(x) reproduces the geomagnetic Sint-800 axial dipole distribution (Guyodo and Valet, 1999), the model also reproduces the palaeomagnetic σx value of about 0.3〈x〉. Reversal waiting times, however, are in the order of 1Myr and thus longer than the respective estimates suggested by palaeomagnetic data for the last 20Myr or so (Ogg, 2012).
The dependence of drift and fluctuation on the ADM provides clues on the feedback between dynamo and Navier-Stokes equations. The interpretation is complicated by the nonlinear nature of the feedback mechanism but the related problems have been addressed by mean-field theory (Krause and Rädler, 1980) which predicts a quadratic quenching of field production via Lorentz force effects on the flow. Hoyng et al. (2001) therefore suggest the form
where γ has the dimension of a growth rate and xn is a normalization factor. Brendel et al. (2007) analyze the palaeomagnetic Sint-2000 record that covers the last 2Myr (Valet et al., 2005). Though the lack of data for particularly small or large dipole moments is problematic, the quadratic quenching (4) seems to reasonably describe the drift d(x). For small ADM values the drift grows roughly linearly with a rate γ ≈ (1∕20)kyr−1. Surprisingly, however, the fluctuation f is almost independent of x and thus shows no obvious quenching (Brendel et al., 2007).
Kuipers et al. (2009) revert to fully self-consistent numerical dynamo simulations from Wicht et al. (2009) at an Ekman number of E = 10−3 and three different Rayleigh numbers which included reversing cases covering much longer timespans than Sint-2000. At least two of the three analyzed cases show a drift d reminiscent of quadratic quenching while f remains once more nearly independent of x.
Buffett et al. (2013) pick up on the idea of interpreting ADM variations with the Langevin model (1) and, in addition to Sint-2000, also analyze the newer PADM2M data set (Ziegler et al., 2011) which covers the same time frame. Their analysis largely confirms the results of Brendel et al. (2007), including a roughly constant f profile that seems to slightly increase toward lower ADMs. Rather than Equation (4), they use the linear relation ≈ − γ (x − 〈x〉) around the mean ADM 〈x〉. This also offers a decent fit of the drift for a decay rate of γ ≈ (1∕30)kyr−1 that is similar to the value inferred by Brendel et al. (2007). The respective decay times are within the range of τd = 25kyr to τd = 56kyr estimated for Earth's fundamental dipole mode. The upper value is based on the higher electrical conductivity of S∕m suggested by Pozzo et al. (2012) that we generally adopt here. Because of the similarity, Buffett et al. (2013) proposed that the drift around 〈x〉 reflects the Ohmic decay of additional magnetic modes that can be regarded as a disturbance of the mean state. Decay times shorter than τd could be explained by the fact that these additional modes have a more complex radial structure.
The mean reversal waiting time inferred by Buffett et al. (2013) from the analysis of the Fokker-Planck equation is roughly 1Myr for both Sint-2000 and PADM2M data sets which seems once more too long. Higher reversal rates would be promoted by either a lower drift potential well or larger fluctuation amplitudes around x = 0. Unfortunately, this crucial parameter region is only poorly constrained by the palaeomagnetic records which contain very few low ADM instances.
The situation is even worse for the dynamo simulations analyzed by Buffett et al. (2014). The use of more realistic parameters (E = 5 × 10−5 and magnetic Prandtl number Pm = 0.5) than in typical reversing dynamo simulations requires high spatial resolution and short time steps. To keep numerical costs at bay, the model was therefore only integrated for an equivalent of 0.83Myr and a relatively low Rayleigh number had to be chosen. Consequently, the simulation never showed any sign of reversals or excursions and the ADM varies only by about 10% around its mean. This severely restricts the usefulness of the dynamo model for the statistical analysis but the d and f profiles are at least compatible with their palaeomagnetic counterparts.
The scope of this paper is to apply the Langevin and Fokker-Planck formalisms to much longer dynamo simulations than previously analyzed. Models introduced by WM16 form the basis but are supplemented by runs in the parameter range explored by Buffett et al. (2014). The longer integration times help to cover the full ADM spectrum which is essential for reversing cases. By separately analyzing ADM variations due to magnetic field production and Ohmic decay, we clarify their distinct impact and better constrain the nonlinear feedback effects. The paper is organized as follows: We start by briefly introducing the analyzed dynamo models in Section 2.1 and describe the Langevin stochastic model and the methods applied for our analysis in Section 2.2. Section 3.1 discusses the reconstructed drift and fluctuation profiles of the Langevin equation for the numerical dynamo models and for the palaeomagnetic model PADM2M. Section 3.2 details the results of the statistical analysis. Section 4 discusses the relative contribution of magnetic field induction and diffusion to the reconstructed drift and fluctuation profiles in the numerical simulations. The paper closes with a discussion in Section 5.
2. Materials and Methods
2.1. Numerical Dynamo Models
We employ the MHD code MagIC (Wicht, 2002) for long, statistically relevant numerical integrations at different parameters. MagIC solves for convection (under the Boussinesq approximation) and magnetic field production in a rotating spherical shell using a pseudo-spectral numerical scheme with mixed implicit/explicit time stepping. Details on the mathematical formulation of the problem and the numerical implementation can be found in Wicht (2005) and Christensen and Wicht (2015). An updated version of the code is publicly available at https://github.com/magic-sph/magic. The code uses a dimensionless formulation that lumps the physical properties into five dimensionless parameters: the Ekman number E = ν∕Ωd2, the (modified) Rayleigh number Ra = goΔCd∕νΩ, the Prandtl number Pr = ν∕κ, the magnetic Prandtl number Pm = ν∕λ, and the aspect ratio a = ri∕ro. Physical properties are the kinematic viscosity ν, system rotation rate Ω, outer boundary reference gravity go, thermal diffusivity κ, magnetic diffusivity λ, outer boundary radius ro, and inner boundary radius ri. The shell thickness d = ro − ri serves as a reference length scale. The spherical shell, that represents the Earth's outer core, is bounded by an electrically insulating mantle at ro and a conducting inner core at ri which rotates according to viscous and Lorentz torques (Wicht, 2002). No-slip flow boundary conditions have been adopted in this work.
Two forms of convective driving are used. Thermal bottom driving is modeled using a fixed codensity jump ΔC across the shell. Compositional driving imposes a vanishing codensity flux at ro and a fixed codensity at ri. Homogeneously distributed internal sinks compensate the “light elements” entering the system at the inner boundary. This setup requires a modified Rayleigh number where the prescribed sinks instead of the imposed codensity jump define the codensity scale.
Most of the models analyzed here have been introduced by WM16 and use an Earth-like aspect ratio of a = 0.35 and a Prandtl number of Pr = 1. Table 1 lists the input model parameters and some time averaged properties. Four thermally driven cases at a relatively large Ekman number of E = 10−3 and a magnetic Prandtl number of Pm = 10 were integrated over extremely long timespans. They only differ in Rayleigh number and include two stable dipole dominated models, an Earth-like reversing model with several hundred reversals, and a multipolar case. The four chemically driven models at E = 3 × 10−4 cover the same fundamental regimes but could only be run for much shorter periods because of the larger numerical costs. The respective Earth-like reversing case at E = 3 × 10−4 covers only 20 reversals. We have added two additional models in the regime discussed by WM16 with a low Ekman number of E = 3 × 10−5, a relatively low Rayleigh number, and the two magnetic Prandtl numbers of Pm = 0.5 and Pm = 1. These latter models cover only a short period in time and never reverse. The model naming convention adopted by WM16 has been extended here to include Pm. In general ExRyPmz refers to a model with an Ekman number E whose unsigned exponent is x, supercriticality Ra∕Rac = y (with Rac the critical Rayleigh number for the onset of convection) and Pm = z. An additional C at the end of the model name refers to chemical convection mimicked by setting the buoyancy flux through the outer boundary to zero as discussed above. Other models use purely thermal driving with fixed lower and upper codensity condition and no internal buoyancy sinks/sources.
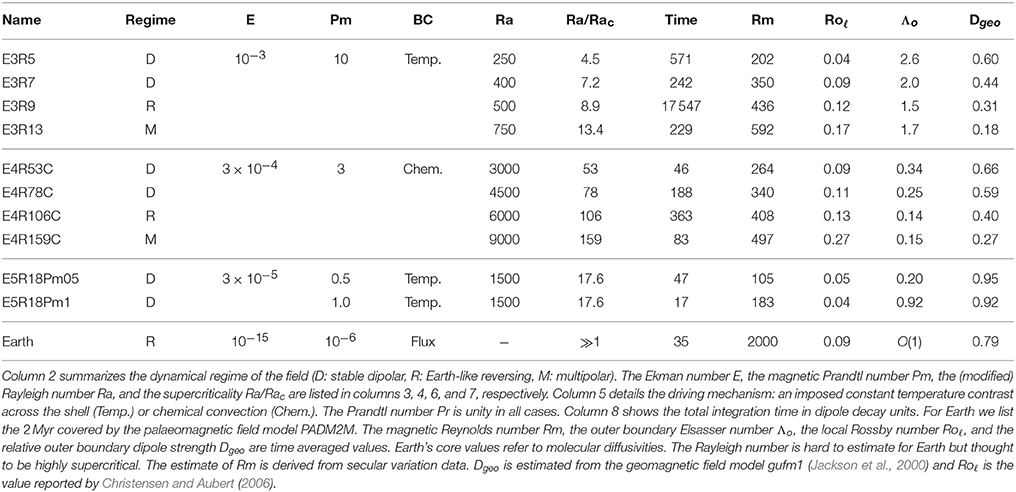
Table 1. List of input parameters and time averaged properties for the explored dynamo models and for Earth.
WM16 also explore compositionally driven cases at E = 10−3. Since the dynamics turned out to be very similar to the thermally driven cases at the same Ekman number, we refrain from analyzing these models here. Shorter sections of models E3R5, E3R9, and E3R13 have been analyzed by Kuipers et al. (2009).
The magnetic Reynolds number
where U is the RMS flow velocity in the fluid volume, is a measure for magnetic induction relative to diffusion. The local Rossby number
where the length scale ℓ is the typical convective flow scale introduced by Christensen and Aubert (2006), is a measure for the relative impact of inertia. Time averaged values of Rm and Roℓ are listed in columns nine and ten of Table 1. For Roℓ < 0.1 the dynamo is typically dipole dominated and remains stable, i.e. neither undergoes reversals nor excursions (models E3R5, E3R7, E4R53C, E4R78C, and the two cases at E = 3 × 10−5). Multipolar dynamos which reverse more or less continuously are characterized by Roℓ > 0.1 (models E3R13 and E4R159C). Dynamo models with Earth-like rare reversals where the axial dipole still dominates on time average and the reversals last much shorter than the stable polarity epochs are found at the transition (Wicht and Tilgner, 2010).
Column eleven in Table 1 shows the time averaged Elsasser number
where Bo is the total RMS field strength at the outer boundary, ρ the outer core density, and μ the magnetic permeability. Since the magnetic field is scaled with (μλρΩ)1∕2 here, the non-dimensional magnetic field amplitude at the outer boundary is identical to . The relative dipole strength Dgeo shown in the last column of Table 1 is the ratio of the RMS dipole field at the surface to Bo when considering only spherical harmonic contributions up to degree and order 11.
The time throughout this paper is scaled in the core dipole decay time
which amounts to τd = 56kyr for Earth when based on the electrical conductivity S∕m suggested by Pozzo et al. (2012). We will also refer to the magnetic diffusion time
and the typical time scale of convective motions, the so-called overturn time
which is roughly 120yr for Earth when estimated from secular magnetic field variations. The magnetic field is rescaled to dimensional units, for example the dipole moment, by assuming ρ = 1.1 × 104kgm−3, the magnetic permeability of vacuum for μ, and Ω = 7.29 × 10−5sec−1.
2.2. Langevin and Fokker-Planck Analysis
The Langevin equation
has a slow deterministic drift contribution d(x) supplemented by fast stochastic variations L(t) with amplitude f(x). The noise source L(t) is assumed to be Gaussian with a vanishing mean,
and an infinitely small correlation time so that
Here δ(τ) is the Dirac delta function and the angular brackets denote a time average. The factor 2 on the right hand side of the above expression is simply a common convention.
The evolution of the probability distribution p(x, t) for the Langevin stochastic process (Equation 11) is governed by the Fokker-Planck equation (Risken and Frank, 1996; Van Kampen, 2007)
The two functions D(x) and F(x) of the FPE are given by the first and second moments of x,
and
Both D and F can be directly calculated from a discrete time sequence of the ADM when compromising on the limit τ → 0 and are then simply related to the mean variation 〈〉 = τ − 1〈x(t + τ) − x(t)〉 and RMS variation {} = τ − 1(〈[x(t + τ) − x(t)]2〉)1∕2 already mentioned in Section 1. This highlights that D and F directly provide fundamental statistical information about the dynamo process even without embarking deeper into the Fokker-Planck theory.
An ambiguity in solving the above time averages over stochastic fluctuations in the limit τ → 0 motivates two different formalisms for connecting the FPE (14) with the Langevin equation (11), the so-called Itô and Stratonovich approximations (Risken and Frank, 1996; Friedrich et al., 2011). This distinction is of little practical interest for the finite τ used in data analysis. The discrete Langevin equation
with
and
then provides a particularly simple “working-model” that is consistent with the discrete data x(t). In the following we will mostly refer to the rescaled fluctuation amplitude
which allows a more direct comparison to the drift d(x).
Equation (17), often referred to as the Euler-Maruyama integration scheme for the Langevin equation (Maruyama, 1955), is the analog of a first-order Euler forward method for ordinary differential equations and can easily be forwarded in time to provide a simulated data set that can be compared with the input data x(t).
Constructing the drift and fluctuation profiles for the Langevin equation (or FPE) relies on binning the variations δx(τ) = x(t + τ) − x(t) according to x. The probability distribution of the unsigned axial dipole moment |x| tells us which interval we can cover with reasonable statistical confidence. Only absolute values need to concern us here since the dynamo equation is insensitive to the sign of x. The interval is then divided into bins of width Δx that represent a central value xi. The width reflects a compromise between the number of data within each bin and the fact that variations over the bin should be small.
After the discrete variations δxj(τ) have been calculated for each data point of the discrete time series xj = x(tj), mean and RMS are evaluated by averaging over the Ni data in each bin:
and
The relations
and
yield the discrete counterparts of the D and F (d and f) terms in the Fokker-Planck (Langevin) equation.
As discussed in Section 1, the Langevin description can only be expected to hold once τ exceeds the convective overturn time τc. This is confirmed by the fact that, for example, D and F become roughly independent of τ once τ > τc (Buffett and Matsui, 2015). Figure 2 illustrates the dependence of the binned Di and Fi on τ for models E3R9 and E5R18Pm05. The solid vertical line marks the convective overturn time in the respective models. In model E3R9, for example, a time resolution τ of at least five times τc ≈ 0.1τd guarantees that drift and fluctuation profiles become nearly independent of τ. Similar inferences also hold for the other cases explored here, though the worse statistics of the shorter runs complicates the choice of τ. For model E5R18Pm05, for example, variations in both profiles are particularly strong for the lowest and the highest ADM bins which include relatively few instances (Figure 2, middle panels). A time resolution τ of about seven times τc ≈ 0.04τd has been chosen for analyzing this model. Tests with the different models have shown that a larger number of entries per bin Ni is desirable to provide reliable profiles. The bin width Δx has therefore mostly been adjusted to guarantee . Bins with fewer entries have been excluded from the analysis.
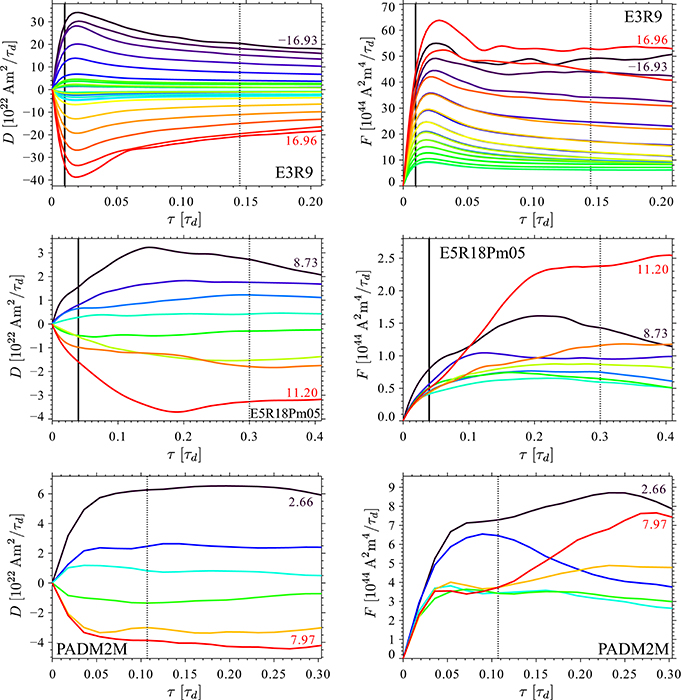
Figure 2. Dependence of the drift D and fluctuation F functions on the time resolution τ for models E3R9 (top panels), E5R18Pm05 (middle panels) and PADM2M (bottom panels). The colors indicate different axial dipole moment bins. In each panel the lowest and the highest bins are identified by the ADM value at the midpoint of the bin. The bin width Δx∕1022Am2 is 1.47, 0.35, and 1.06 for models E3R9, E5R18Pm05, and PADM2M, respectively. The solid and dotted vertical lines mark the convective overturn time and the selected time resolution, respectively. In the palaeomagnetic model PADM2M time has been rescaled using an Earth's core dipole decay time of τd = 56kyr.
The bottom panel of Figure 2 illustrates the drift and fluctuation profiles for the palaeomagnetic virtual axial dipole moment (VADM) from model PADM2M. This model covers the last 2Myr with a resolution of roughly 5–10 kyr. We nevertheless started with a 1kyr resolution calculated from the PADM2M cubic B-spline representation (Ziegler et al., 2011). The drift and fluctuation profiles only become independent of τ once τ exceeds about 4kyr which is considerably larger than Earth's overturn time. The reason is that τ has to be chosen at least as large as the effective resolution of the model to get rid of any correlations introduced by the model regularization (Buffett et al., 2013). We evaluate the drift and fluctuation for τ = 6kyr in the following. An even larger time resolution could be in order but would reduce the already low number of samples even further. To have a fair number of bins we already had to reduce the minimum number of entries per bin to and choose a relative large bin width Δx.
Since PADM2M covers only few reversals and excursions, instances of low VADM are rare and we could not constrain this particularly interesting region with sufficient confidence. Adding to this problem is the fact that local field in a palaeomagnetic record is interpreted as being caused by the virtual axial dipole moment. Contributions from the equatorial dipole and higher field harmonics can therefore make the VADM significantly larger than the ADM during reversals or excursions. Drift and fluctuation are obviously harder to constrain and the profiles remain relatively uncertain, in particular for VADM values x < 0.5〈x〉.
Once an appropriate binning scheme and time resolution τ have been selected, the required functions can be modeled by least-square-fitting power series expansions to the binned values, for example
and
The exponents reflect that the mean variation is an odd function while the RMS variation is even. Generally low truncation values of N = 3 or N = 4 and M = 2 suffice for an adequate description.
The steady-state probability density function (PDF) p0(x), solution of the stationary FPE, can then be calculated analytically
In the above expression denotes the normalizing constant. A comparison with the PDF of the data provides some means to verify the Langevin and Fokker-Planck approaches for a given data set. The mean 〈x〉 and standard deviation σx predicted by p0 provide measures to judge the similarity, at least when the PDF is simple enough.
Knowing p0 allows us to infer additional statistical properties of the system. For example, for a stochastic particle starting at x(t = 0) = x′ > 0 the mean time to leave the positive part of the drift potential (0 ≤ x < ∞) is given by Van Kampen (2007):
The mean escape time 〈Te〉 is also often referred to as the mean first passage time at x = 0. Hoyng et al. (2001) report that 〈Te〉 is nearly independent of x′ as long as x′ lies near the bottom of the potential well. According to standard theory (Risken and Frank, 1996; Van Kampen, 2007), the escape time statistic can be proven to be Poissonian which is intuitively plausible since the crossings of the potential barrier are rare events and the stochastic fluctuations are completely uncorrelated. Consequently, the PDF of Te is the exponential .
At the escape time Te, the stochastic particle will be located close to the top of the drift potential at x = 0 so that the fluctuations can easily yield a polarity change. The particle can then be expected to have an equal chance of falling in either potential trough. When the particle ends up in the same trough from where it started, the event is classified as a “grand excursion” rather than a reversal. WM16 introduced the term grand excursions for excursions during which the ADM ventures into the reverse polarity. Following this reasoning, the mean waiting time for a reversal is expected to be 〈TR〉 = 2〈Te〉 which can be shown to hold analytically (Hoyng et al., 2001; Van Kampen, 2007). Forwarding the discrete Langevin equation (17) allows us to calculate the probability distribution p(Te) and to estimate the mean escape time 〈Te〉 to verify the theoretical predictions discussed above.
3. Results
3.1. Drift and Fluctuation Profiles
Table 2 lists the selected time resolutions τ and some characteristic properties of the stochastic models for all the cases explored here. Figure 3 illustrates how drift and fluctuation profiles change when increasing the Rayleigh number for the E = 10−3 models. The polynomial expansions (Equations 25 and 26) permit to draw profiles for ADM values that are never reached in the simulations. This does not necessarily make sense in all cases but allows, for example, a tentative prediction of the reversal rate where no reversals have been observed. We will discuss this point further below.
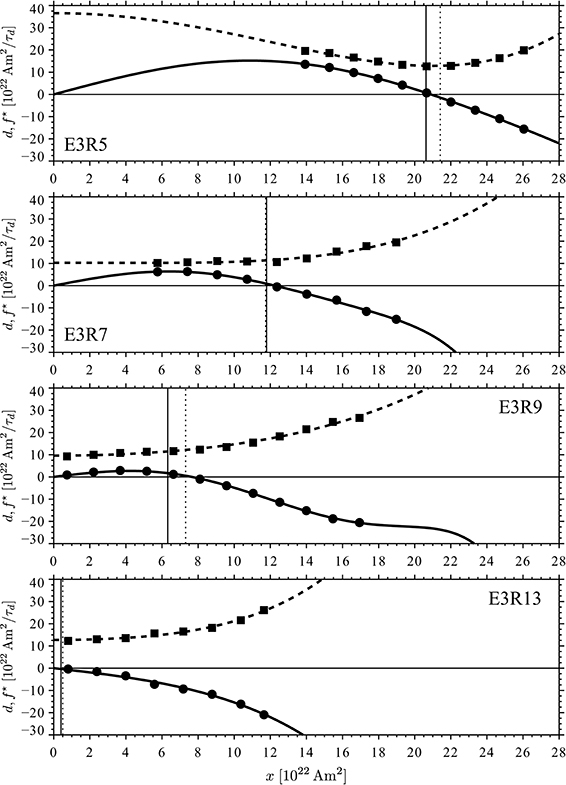
Figure 3. Drift d (circles) and rescaled fluctuation f⋆ (squares) as function of the axial dipole moment x for the four dynamo models at Ekman number E = 10−3. The curves are the respective low order polynomial fits based on Equations (25) and (26). The solid and dotted vertical lines mark, respectively, the mean and the mode of the (signed) unsigned axial dipole moment distribution in the (multipolar) stable dipolar and reversing models.
The ADM value xm where the drift (or mean variation) d becomes negative marks the point where the potential U(x) has a minimum and the probability distribution a maximum, i.e. xm is the mode of the ADM distribution (dotted vertical lines in Figure 3). The fact that xm does not coincide with the unsigned axial dipole moment mean 〈|x|〉 in case E3R9 highlights the asymmetric nature of the distribution in a reversing model (see WM16). Note that mean and mode in Table 2 are based on the signed ADM in the multipolar cases E3R13 and E4R159C but on the unsigned ADM in the other cases. For x > xm (x < xm) the slow negative (positive) drift drives the system back toward the mean. The fluctuation (or RMS variation) f⋆, always larger in amplitude than the drift, is instrumental in driving the system to other values that fill the ADM probability distribution.
Buffett et al. (2013) suggest that the drift decreases linearly around 〈x〉 and that seems to be also roughly true for the simulations explored here. The authors characterize the drift dynamics with the time scale τH defined by 〈〉 ≈ 〈x〉∕τH. We use the power series expansion (25) to yield:
This time scale provides an estimate for the slow relaxation time into either potential trough in U(x). The values listed in Table 2 demonstrate that τH increases with the Rayleigh number, ranging from 0.37τd for model E3R5 to about one τd for the reversing case E3R9.
In the non-reversing cases (top two panels of Figure 3), the drift d starts to level off for smaller ADM values and finally bends over to meet x = 0 in the reversing case (third panel). For small ADMs the drift increases roughly linearly and can be characterized by the growth time scale τL which is, like τH in Equation (29), defined by the drift derivative but now evaluated at x = 0. This time scale is overall quite similar to τH and also increases with Ra (see Table 2). Note, however, that τL is not directly supported by data for E3R5 and E3R7 where the ADM always remains relatively strong. The somewhat large value of τL ≈ τd for the reversing model E3R9 is consistent with the increased probability for low ADM values which WM16 explained with a distinct low dipole moment state.
As expected, both time scales τL and τH roughly coincide in the multipolar case E3R13 where the drift decreases monotonically (Figure 3, bottom panel). The negative drift slope at x = 0 means that the drift is always destructive while the fluctuations drive the ADM toward positive or negative values and thus play a key role in reversals that happen more or less continuously in this case.
The variation of the ADM value x* where the drift reaches its maximum reveals further interesting insights. Table 2 shows that the maximum drift value d(x*) decreases significantly with increasing Rayleigh number. This can be compared with the amplitude of the rescaled fluctuation f⋆ characterized by the values at x = 〈|x|〉 and x = 0 in Table 2. For the non-reversing model E3R7 the ratio of f⋆(〈|x|〉) to maximum drift is roughly 1.8 but increases to about 4.2 in the reversing case E3R9. Fluctuations thus have an easier time to overcome the restoring drift force and potentially lead to reversals.
In the particle-in-well analogy, x* represents the point where the drift potential U(x) changes curvature and its slope starts to become shallower. When Ra increases both x* and 〈|x|〉 decrease, but the former slower than the latter. This effectively means that the height of the drift potential well decreases and polarity changes can happen more easily.
The fluctuation f⋆ has a concave shape in the non-reversing case E3R5 (Figure 3, top panel) with a somewhat weaker slope on the lower ADM flank and a minimum around the mean ADM. In the other cases f⋆ monotonically increases with x and nearly doubles its value. Table 2 shows that the value f⋆(〈|x|〉) changes relatively mildly with Ra and is similar to the value at x = 0. The exception is the low Rayleigh number case E3R5 where the latter value is not directly supported by data.
The drift and fluctuation curves for the E = 3 × 10−4 models shown in Figure 4 are very similar to those just discussed. The drift profile shows clear steepening for large ADM values that is only evident for case E3R13 at the larger Ekman number. The dependence of the selected drift and fluctuation measures on the Rayleigh number also follows the trend discussed above (cf. Table 2). However, the characteristic drift time scales τH and τL are particularly large for the reversing case E4R106C and reach more than three dipole decay times. The particular parameter combination promotes a much slower drift than in all other cases.
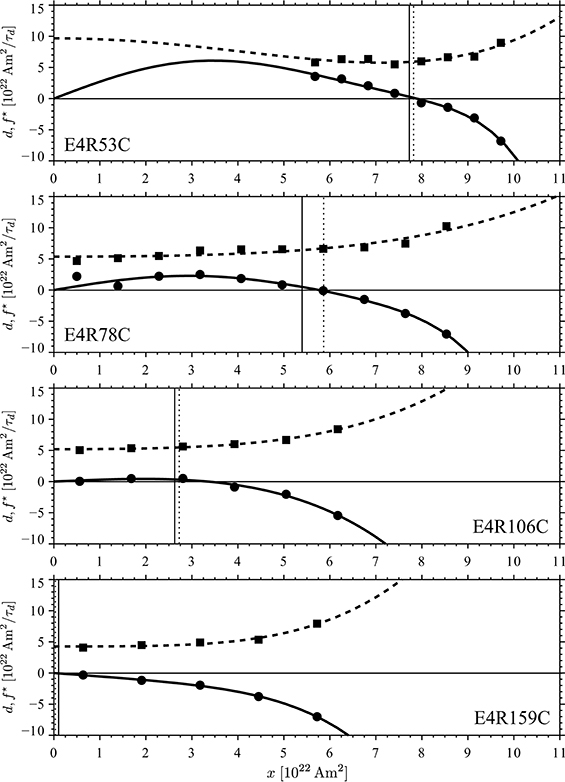
Figure 4. Same as Figure 3 but for the four dynamo models at Ekman number E = 3 × 10−4.
Finally, Figure 5 shows the remaining two models with the smallest Ekman number E = 3 × 10−5. Since the Rayleigh number is relatively small and the models have only been run for a comparatively short time, they sample only a limited ADM range. Little more can be said than that the linear drift and concave fluctuation curves are very similar to those discussed above. The difference in magnetic Prandtl number in these two low Ekman number cases has virtually no impact.
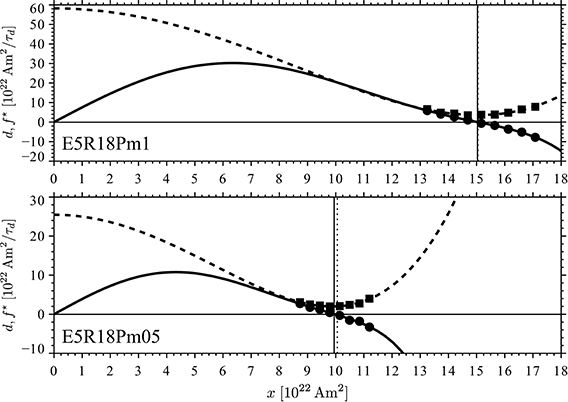
Figure 5. Same as Figure 3 but for the two dynamo models at Ekman number E = 3 × 10−5. The upper (lower) panel shows the case at magnetic Prandtl number Pm = 1 (Pm = 0.5).
Figure 6 presents the drift and fluctuation profiles for the palaeomagnetic model PADM2M. As already discussed in the previous section, the scarcity of low VADM instances makes it difficult to constrain the profiles below about 50% of the mean VADM. Drift and fluctuation profiles are similar to those for the numerical simulations. However, there is no sign that the drift d levels off toward lower ADM values as in the numerical cases. Overall, the drift data seem more or less consistent with a linear decrease, except perhaps for the lowest and the highest ADM bins. The fitted drift profile (solid curve in Figure 6) tries to meet individual points even though they are not well constrained and should not be over interpreted. The typical relaxation time toward the equilibrium state τH is about 0.42τd or 23kyr, in agreement with the value found by Buffett et al. (2013). The typical time for the palaeomagnetic axial dipole moment to leave the low field intensities is τL = 16kyr which is similar to the 20kyr suggested by Brendel et al. (2007) for Sint-2000 data. The fluctuation profile slightly rises toward lower ADM values, a behavior only found for the lower Rayleigh number simulations E3R5, E5R18Pm1, and E5R18Pm05.
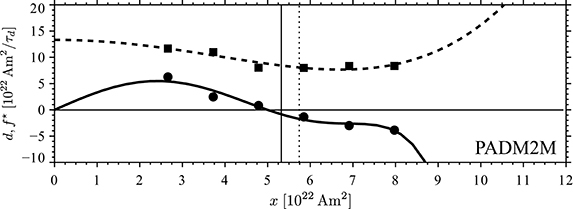
Figure 6. Same as Figure 3 but for the palaeomagnetic (virtual) axial dipole moment variations from model PADM2M. Time is rescaled using an Earth's core dipole decay time of τd = 56kyr.
3.2. Validation of the Stochastic Model
The stochastic model represented by the Langevin and Fokker-Planck equations should be validated against the original data, i.e. against the numerical simulation results and the palaeomagnetic model PADM2M. The validation presented here has two levels. In the first level we compare with integrations of the discrete Langevin equation (17). Hundreds of such realizations, each integrated as long as the original numerical dynamo model, provide a statistical ensemble that allows us to estimate the error for statistics based on the respective integration time. The ensemble mean, on the other hand, is equivalent to very long integrations that usually cannot be afforded in the full numerical dynamo simulation. The second level of validation consists in a comparison with the analytical predictions from the FPE discussed in Section 2.2. An agreement between the results from very long integrations of the Langevin equation and the FPE confirms that the latter indeed describes the statistical behavior of the former and that we have correctly linked the two differential equations.
Figure 7 visually compares part of the original axial dipole moment time series from model E3R9 (top left panel) with one realization of the respective stochastic model (bottom left panel) which was initialized with the same ADM as the numerical simulation. The two time series seem to show very similar temporal variations on different time scales. For example, longer stable polarity epochs are interspersed with abrupt reversals and excursions. Naturally, the stochastic model can only capture variations on time scales longer than τ.
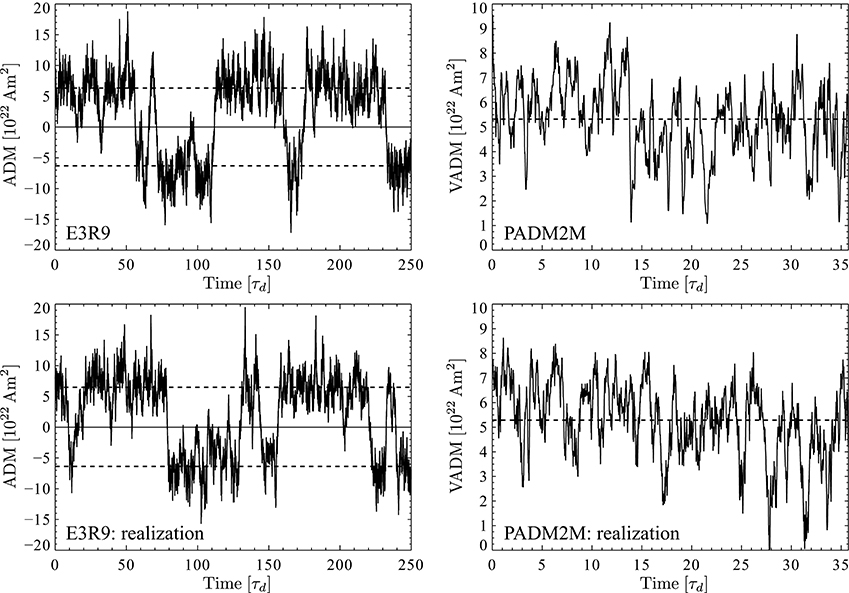
Figure 7. Axial dipole moment variations for the reversing dynamo model E3R9 and for the palaeomagnetic model PADM2M (top panels) with the respective realizations of the stochastic model (bottom panels). E3R9 is shown over an interval of 250 dipole decay times τd while PADM2M covers 2Myr or about 36τd. The horizontal dashed lines mark the unsigned axial dipole moment mean values. The stochastic realizations have been started with the same initial (V)ADM values of the original time series.
The unsigned ADM mean for model E3R9 is 〈|x|〉 = 6.32 × 1022Am2 with a standard deviation of . The ensemble average over 104 realizations integrated as long as the original numerical model (more than 17 thousand dipole decay times or about 950Myr for Earth) yields a mean of and a standard deviation of , in good agreement with the numerical simulation. The overbar indicates the ensemble average here. A comparison of column four in Table 2 and column two in Table 3 reveals similarly good agreement for all numerical models and for PADM2M, not only for the mean but also for the mode values xm. As expected, and are practically identical in the non-reversing cases while the ADM mean is systematically lower than the mode for the reversing models (and for PADM2M) due to the significant contribution of low axial dipole moment instances. The VADM time series obtained from a realization of the stochastic model (Figure 7, bottom right panel) seems also to capture the different temporal variations present in the original palaeomagnetic time series (Figure 7, top right panel).
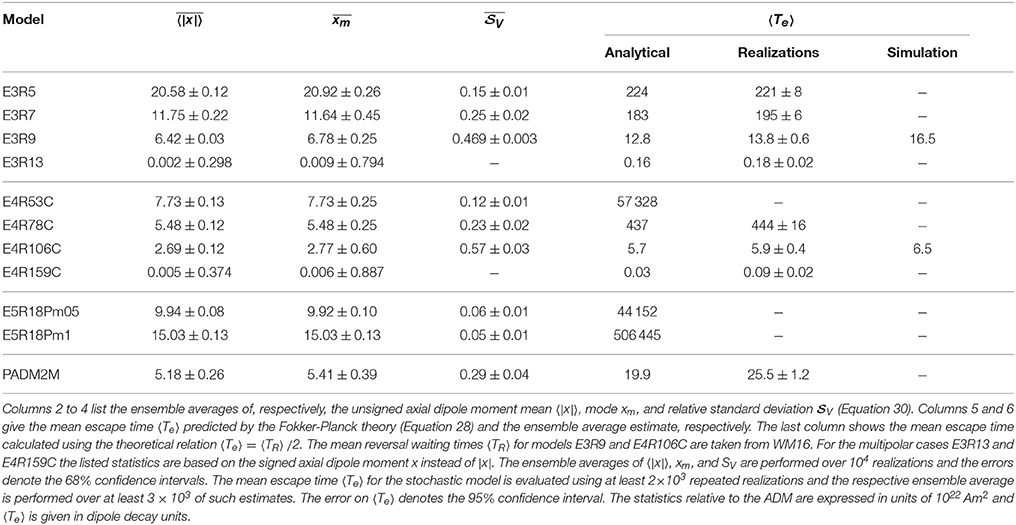
Table 3. Relevant statistical properties of the axial dipole moment inferred from numerical realizations of the stochastic model for all the cases explored.
Figure 8 illustrates the similarity of the various ADM distributions for the two reversing models E3R9 (top panel) and E4R106C (middle panel). The predicted steady-state distributions from the FPE p0 (thick light gray curves) agree nicely with the numerical simulations (open squares) and perfectly overlap long numerical realizations of the respective stochastic model (black curves). The very long simulation run for E3R9 provides a tight constraint and leads to very good agreement of all PDFs. The much shorter integration time for E4R106C, however, is also the reason for the PDF asymmetry. This asymmetry should ultimately vanish for longer integrations as shown by the stochastic realization.
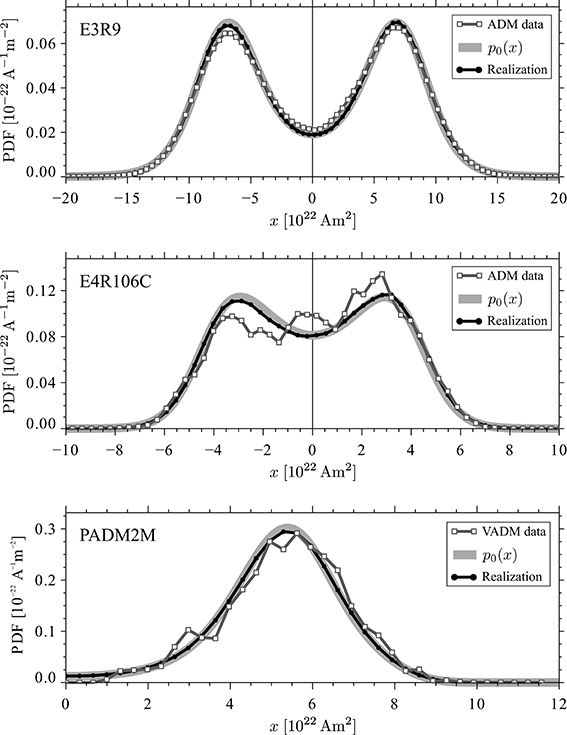
Figure 8. Comparison of axial dipole moment probability distributions for the reversing dynamo models E3R9 (top panel) and E4R106C (middle panel), and for the palaeomagnetic model PADM2M (bottom panel). The binned probability density function of the original (V)ADM data is shown with open squares. The thick light gray curve is the analytical steady-state solution of the Fokker-Planck equation p0(x) (Equation 27) and the black curve is the PDF obtained from a long (several tens of thousand dipole decay times) numerical integration of the stochastic model.
The good agreement of the VADM distribution from PADM2M with the simulated distribution suggests that the stochastic model successfully reproduces the variability of the palaeomagnetic time series (Figure 8, bottom panel). Once more, the predicted steady-state PDF p0 overlaps with the distribution from a long numerical realization as expected. Both distributions closely follow the original data PDF. Since PADM2M covers only the last 2Myr of palaeomagnetic variations, however, the confidence intervals on the estimates of the ADM mean and mode remain relatively large (see Table 3). A minor difference between p0 and the data PDF occurs for low dipole field intensities: The stochastic model predicts a small, but still non-zero probability whereas the data probability is vanishingly small. One reason for this discrepancy might be related to the few instances of low VADMs in the palaeomagnetic record. The left flank of the original VADM data distribution is only somewhat more populated than the right flank. While this slightly asymmetric profile might indicate the presence of a “weak dynamo state” as discussed by WM16, it is certainly much less pronounced than in model E3R9 or E4R106C. The latter model shows a particularly high probability for low field intensities, but choosing slightly lower Rayleigh numbers for the simulation should reduce this effect. The analytical steady-state distributions of non-reversing and multipolar dynamos show similarly good agreements with simulation data and stochastic model realizations but are not illustrated here.
The relative standard deviation
quantifies the variability of the unsigned axial dipole moment around its mean value and this provides a measure for the secular variation (SV). Ensemble averages of V are reported in Table 3 together with the estimated standard errors. In the E = 10−3 and E = 3 × 10−4 cases V increases with the Rayleigh number Ra as expected. The two models at E = 3 × 10−5 show a less pronounced SV of the order of 5% consistent with their highly dipolar character and the relatively small Rayleigh number. In PADM2M the relative standard deviation is , significantly smaller than both the reversing dynamo models analyzed here. In the limits of statistical errors, the SV ensemble averages are identical to the V values in the original numerical simulation (cf. Table 2). In the multipolar cases the measure V must be based on the signed ADM x but, since 〈x〉 vanishes in these models, it is not well-defined. The signed ADM standard deviation σx for the multipolar case E3R13 (E4R159C) is 3.50 × 1022Am2 (2.03 × 1022Am2). The ensemble average over 104 realizations yields a standard deviation of (3.43±0.15) × 1022Am2 ((1.98±0.16) × 1022Am2) which well agrees with the numerical simulation.
The stochastic model allows us to calculate the mean escape time 〈Te〉, i.e. the average time required by x to change sign or to cross the drift potential barrier in the particle-in-well paradigm. Once more, we can rely on numerical realizations of the stochastic process and on the analytical prediction (28) based on the FPE. Both values are listed in columns five and six of Table 3 for all the explored models. In addition we list values based on the mean reversal waiting times 〈TR〉 for models E3R9 and E4R106C provided by WM16, using the relation 〈Te〉 = 〈TR〉∕2 (see Section 2.2).
The reversing and multipolar models at E = 10−3 and E = 3 × 10−4 present ensemble averages of 〈Te〉 close to the respective analytical predictions. Though the escape time Te is not well constrained by the simulation data for stable dipolar dynamos, the fitted drift and fluctuation functions nevertheless yield a prediction. The analytical 〈Te〉 ranges from few hundred dipole decay times for the E = 10−3 cases to very large values for the highly dipolar models at E = 3 × 10−5. Since the stochastic realizations showed too few or no reversals for models E4R53C, E5R18Pm05, and E5R18Pm1 we could not list the respective estimates in Table 3. The 〈Te〉 values from the stochastic realizations match the analytical predictions for the stable dipolar models E4R78C and E3R5 in the limits of statistical errors. The ensemble average of 〈Te〉 is close to the predicted value for E3R7.
The average Earth's reversal rate is about 4Myr−1 when estimated from palaeomagnetic reversal chronologies for the last 20Myr or so (Biggin et al., 2012). During the last 2Myr either seven or five reversals are discussed depending on whether the Cobb Mountain event that occurred 1.2Myr ago is regarded as a subchron. This translates into rates of 3.5 or 2.5 Myr−1. The Fokker-Planck analysis, however, predicts a much smaller rate of only 0.45Myr−1. A possible explanation for the discrepancy is the poor coverage of low VADMs in the PADM2M data. Figure 6 shows that we fail to sufficiently constrain drift and fluctuation profiles for values below about 50% of the mean VADM in our analysis. Even for larger VADMs the size of the data sample is not at all at the level of the numerical simulations. Since the dynamics at small axial dipole moments is particularly important for determining the reversal likelihood, it seems conceivable that additional data may lead to more realistic predictions of the reversal rate. A smaller drift maximum d(x*) or larger fluctuations at small x values would both help.
Fokker-Planck theory also predicts that the escape times are exponentially distributed with a mean value 〈Te〉 given by Equation (28) and listed in Table 3. Figure 9 shows the binned PDF p(Te) for the reversing dynamo models and for PADM2M together with the predicted exponential distributions. The analytical predictions are in very good agreement with the numerical realizations. Once more, this demonstrates the validity of the Fokker-Planck description of the stochastic process.
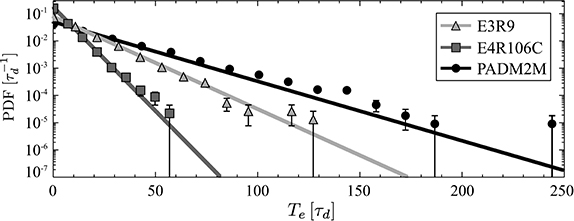
Figure 9. Probability density functions of the escape time Te obtained from 104 numerical realizations of the stochastic model for the reversing dynamo models E3R9 and E4R106C, and for the palaeomagnetic model PADM2M. The solid lines are the exponential PDFs predicted by the Fokker-Planck theory with 〈Te〉 the mean escape times (28) listed in Table 3. The error bars mark the estimated standard errors in each bin (mostly smaller than the symbol sizes themselves).
The stochastic model allows us to predict more than just the mean reversal waiting times. For example, we can access the mean waiting time 〈TW〉 for the axial dipole moment to reach any given value x when starting with the configuration x = xm. Since xm is the most likely ADM value, this is a relevant scenario. Small variations can be achieved by direct fluctuations and can therefore be rather fast. However, Figure 10 shows that the waiting time increases rapidly away from xm once several fluctuations have to team up to lead to more substantial variations. The combined fluctuations have to overcome the slow drift and the large 〈TW〉 values prove that this is quite difficult. The waiting times are generally longer than a simple dipole decay and larger for x > xm than for x < xm. The palaeomagnetic model PADM2M generally shows the longest mean waiting times and they are longer in model E3R9 than in E4R106C. The values at x = 0 are consistent with the predicted mean escape times 〈Te〉 listed in Table 3. Smaller reversal rates thus reflect a general tendency for a slower axial dipole decrease over a large range of dipole moments.
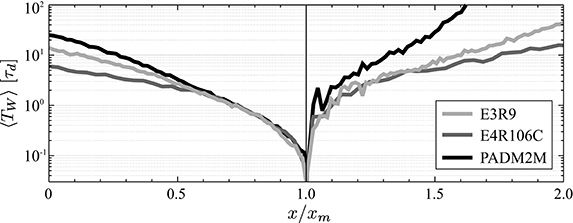
Figure 10. Mean waiting time 〈TW〉 as function of the axial dipole moment x for the reversing dynamo models E3R9 and E4R106C, and for the palaeomagnetic model PADM2M. The ADM is normalized with its mode xm (see Table 3). The averages are calculated over 104 realizations of the stochastic model started with x = xm.
The results shown in Figure 10 permit to estimate how much more likely a reversal (or grand excursion) becomes when the ADM has already decreased to a certain value. An ADM decrease to 50% requires two to three dipole decay times. For model E4R106C the event then still lies, on average, about four decay times or roughly 200kyr in the future. For PADM2M the next reversal or grand excursion will occur, on average, in 1Myr and the fact that the ADM is already half of its preferred value hardly matters.
4. Interior Dynamo Action
Changes in the axial dipole moment are either of inductive or diffusive origin. The ratio of magnetic field production to the Ohmic decay is often estimated by the magnetic Reynolds number Rm = Ud∕λ, where U is a characteristic flow velocity. Rm can also be interpreted as the ratio of the diffusive to the inductive or convective time scale. For the dynamo simulations explored here, Rm ranges from about 100 to about 500 and is perhaps 2000 for Earth. Induction can clearly happen on much faster time scales than Ohmic decay.
To explore the role of the two processes in the drift and fluctuation contributions discussed above, we have performed additional shorter runs for models E3R5, E3R9, and E3R13. During these simulations we stored the axial dipole contribution of magnetic field induction and diffusion within the spherical shell. No-slip boundary conditions force the flow and thus the induction to vanish at both boundaries. We therefore analyze the axial dipole variation just below the outer Ekman boundary layer which was identified by inspecting the radial kinetic energy profile.
The analysis of both contributions follows the scheme already outlined above. MagIC actually solves for inductive and diffusive changes of all spherical harmonics contributions to the radial magnetic field. Variations in the axial dipole contribution B10 of the radial field are directly related to variations in the axial dipole moment. For accessing induction and diffusion separately we integrate both contributions to the degree ℓ = 1 and order m = 0 harmonic dynamo equation over τ:
The superscripts (I) and (D) mark inductive and diffusive effects respectively. The square brackets with the subscript 10 refer to the axial dipole (ℓ = 1, m = 0) contributions and denotes the unit vector in the radial direction. Equation (31) provides the recipe for separating axial dipole field changes into Langevin (or Fokker-Planck) drift and fluctuation profiles for the inductive and diffusive contributions. For example, the two binned drift contributions are
and
The two induction and diffusion related fluctuation functions are
and
The angular brackets now refer to averages over the entries in B10 bins of width ΔB10.
Since the dipole field within the dynamo region is not a potential field, it cannot be expressed in terms of a dipole moment to facilitate a direct comparison with the ADM analysis presented in the previous sections. We therefore simply use non-dimensional values for time and B10, that are given in units of τd and (μλρΩ)1∕2 respectively, and compare relative variations and the general form of drift and fluctuation profiles.
The left panels in Figure 11 show the drift functions for models E3R5, E3R9, and E3R13. Included are results when using all available data in gray and for time resolutions of τ = 0.1 or τ = 0.05 in black. Results for all data cannot provide an appropriate Langevin model but nevertheless give an interesting reference. For time resolutions τ > τc the profiles are very similar to those for the ADM sequences of the respective models presented in Section 3.1. The absolute diffusive contribution (dashed curves) increases roughly proportional to B10 (or x) in all three cases. It depends only mildly on the time resolution because diffusion is a slow process. As expected, Ohmic decay acts destructively and exerts a simple linear drift toward B10 = 0. The diffusive effects level off for small B10 values in model E3R5 which also shows some other distinct properties that we will discuss below.
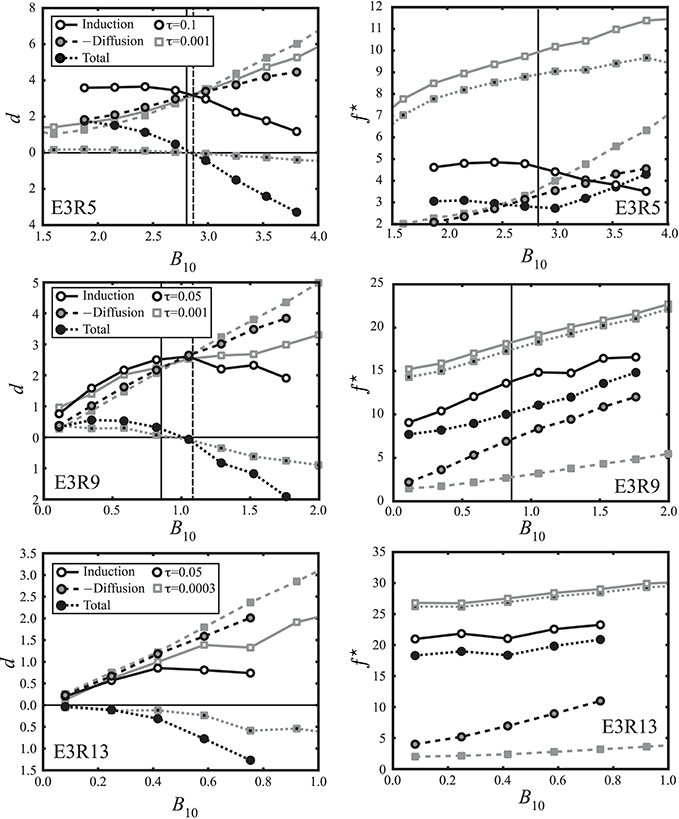
Figure 11. Axial dipole variations beneath the outer Ekman boundary layer in models E3R5 (top panels), E3R9 (middle panels) and E3R13 (bottom panels). The left panels show separate drift profiles for induction d(I) (solid lines with open symbols), negative diffusion −d(D) (dashed lines with gray filled symbols) and the total d (dotted lines with black filled symbols). Two different time resolutions τ have been used, the smallest available for the respective numerical data set (squares), and a value τ > τc when the Langevin and Fokker-Planck formalisms can be expected to hold (circles). The right column shows the respective rescaled fluctuation profiles f⋆. For E3R9 (E3R13) the black profiles have been amplified by a factor 3 (5). The solid (dashed) vertical line marks the axial dipole mean (mode). All values are given in dimensionless units.
The inductive contribution (solid curves in Figure 11, left panels) generally shows a more complex dependence on B10, on τ, and also on Ra. For small time resolutions τ < τc, this constructive term generally grows with increasing B10. The increase is roughly linear for model E3R5 but slightly levels off for larger dipole field intensities in models E3R9 and E3R13. Inductive and diffusive profiles cross at a value slightly larger than the mean axial dipole intensity 〈B10〉, with diffusion dominating for larger and induction for smaller values. This is equivalent to the point where the total drift (dotted curves) vanishes and defines the preferred B10 value and/or the minimum in the respective drift potential as discussed above. Solid and dashed vertical lines in the left panels of Figure 11 mark 〈B10〉 and the crossing point respectively.
When τ is increased beyond the overturn time, the d(I) profiles (solid black curves in Figure 11, left panels) assume a different form that remains roughly constant for yet larger τ in agreement with our discussion in Section 2.2. For model E3R5, the profile now decreases for larger B10 but still crosses the negative diffusive contributions. The decrease is likely a sign of magnetic flow quenching. The dominance of diffusive effects beyond and inductive effects below the preferred B10 value becomes much more pronounced once the faster fluctuations have been filtered out. The inductive profiles for E3R9 and E3R13 increase roughly linearly for small B10 values and seem to show quenching effects for larger field strengths, for case E3R9 more so than for E3R13. In the multipolar case E3R13 the induction profile remains always smaller than the diffusive one which explains the negative total drift toward B10 = 0.
Profiles of the fluctuation contributions f⋆(I) and f⋆(D) are shown in the right panels of Figure 11. Most profiles simply increase monotonically with B10 and, contrary to the drift, inductive effects clearly dominate. The exception is once more E3R5 at τ = 0.1, the only model where quenching seems to significantly impact the fluctuation. For larger B10 values, f⋆(I) decreases so significantly that diffusive effects start to dominate the rescaled fluctuation in this model. Note that the fluctuation amplitude, contrary to the drift, also strongly depends on τ.
We refrain from fitting analytical functions to the drift and fluctuation profiles and use the ratio
for estimating the respective time scales from the Langevin analysis. Using this definition for the total drift would bear the problem that the respective profile passes through zero at the preferred B10 value. We can, however, calculate the time scales that characterize purely inductive or purely diffusive mean or RMS variations, keeping in mind that they may not reflect the true variations which are generally a combination of both effects. For example, the resulting time scales for the mean variations d are defined as
and
Similar definitions hold for the RMS variations f⋆.
Figure 12 compares all four such time scales for mean and RMS variations and the selected τ values. As expected, time scales based on the RMS variations f⋆ (gray curves) are shorter than the respective scales based on the mean d (black curves). The differences remain smaller for diffusive contributions which have predominately one sign. Since the rescaled fluctuation profiles depend strongly on τ, however, the respective time scales are hard to constrain and decrease with τ.
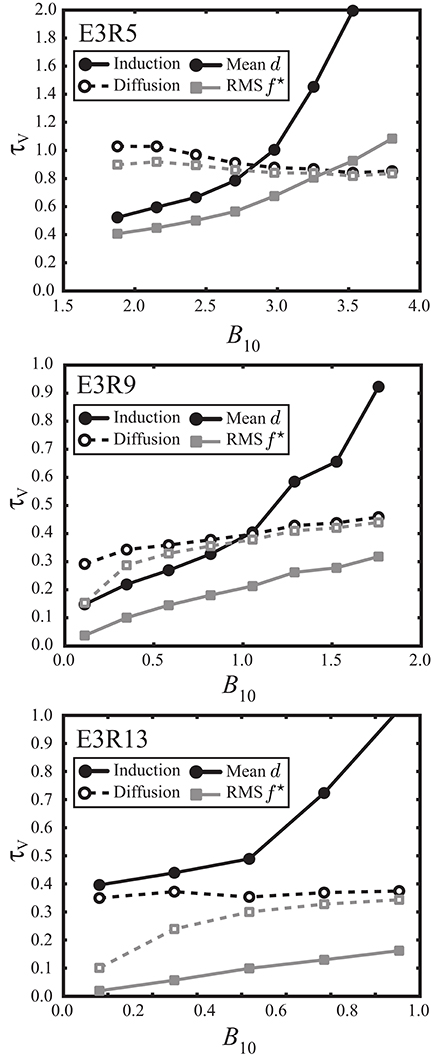
Figure 12. Time scales τV for the cases with τ > τc depicted in Figure 11 (see the text for more explanation). All quantities in dimensionless units.
The diffusive drift time scales (dashed black curves) remain close to one for dynamo E3R5 but decrease to roughly 0.4 for E3R9 and 0.35 for E3R13. This indicates that dipole contributions with a more complex internal radial structure than the fundamental decay mode contribute to the axial dipole, as suggested by Buffett et al. (2014). Inductive mean variations (solid black curves) are somewhat faster for lower B10 values but can reach much larger values when B10 increases. The shortest drift time scales are clearly associated to mean inductive variations which therefore dominate the B10 dynamics. These time scale estimates somewhat differ from those in Section 3.1 which were based on the total drift and thus on the difference between inductive and diffusive profiles.
We started this section with discussing the magnetic Reynolds number as a measure for the ratio of diffusive to inductive time scales. Our analysis allows us to calculate the ratio of these time scales based on, for example, the mean axial dipole variations d for τ > τc which reflect the long time scale dynamo balance. The respective magnetic Reynolds numbers decrease with B10 and cross unity where induction and diffusion profiles meet. Maximum values at low B10 only reach about two for models E3R5 and E3R9 but never exceed unity for E3R13. This is in strong contrast to the much larger values between Rm = 100 and 500 based on RMS flow velocities which may reflect local fast magnetic field fluctuations but not the balance that rules the slow axial dipole dynamics.
The decrease of inductive effects with increasing field strength offers interesting clues on the nonlinear feedback between flow and magnetic field that establishes the dynamo balance. Classical mean-field theory predicts a quadratic quenching of the so-called α-effect that parametrizes the production of axisymmetric field via the interaction of non-axisymmetric field and non-axisymmetric flow (Roberts, 1967; Krause and Rädler, 1980). The field induction then scales like
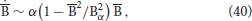
where is the axisymmetric field, α is a generic simplified scalar representing the strength of the interaction between non-axisymmetric field and flow, and Bα is a normalization factor. Following Brendel et al. (2007), we adapted the above expression to the analysis of axial dipole fluctuations considered here by assuming that the quenching only depends on the axial dipole field:
The variation at vanishing dipole field, , is an additional parameter only required when describing the fluctuation profile which remains non-zero at B10 = 0.
Figure 13 shows fits of the form (41) to the mean (black) and RMS (gray) induction profiles for model E3R9. While the agreement is not perfect, in particular for the mean induction d(I), the results nevertheless indicate that the quadratic quenching predicted by mean-field theory may indeed apply. The fitting parameters are (α = 3.27, Bα = 2.13) for d(I) and (α = 2.40, Bα = 3.00) for f⋆(I) which confirm the much weaker quenching of field fluctuations. Note, however, that fluctuations are more strongly quenched in model E3R5.
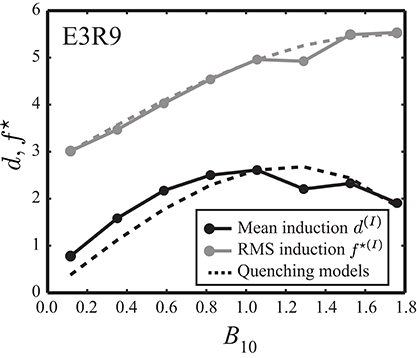
Figure 13. Quenching of mean axial dipole induction d(I) (black) and RMS induction f⋆(I) (gray) for the dynamo model E3R9 with τ > τc depicted in Figure 11. Dashed lines show the quadratic quenching models described in the text. All quantities in dimensionless units.
5. Discussion
Our analysis has confirmed that a stochastic Langevin model can describe the axial dipole moment variations in numerical dynamo simulations and in a palaeomagnetic field model. Separating the dynamics into a slow drift and faster stochastic fluctuations requires to exclude time scales where correlations of flow features still matter. On time scales longer than about a millennium, however, the stochastic model offers a viable description of the axial dipole field dynamics and provides useful prediction of, for example, its probability distribution (Hoyng et al., 2001; Buffett et al., 2013).
Fokker-Planck theory also allows us to predict the mean reversal rate which reasonably well agrees with the rates in the two reversing dynamo simulations explored here. For Earth, however, the stochastic model based on the palaeomagnetic PADM2M data predicts a rate about 10 times lower than the 4Myr−1 suggested by the marine magnetic anomaly record for the last 20Myr (Biggin et al., 2012; Ogg, 2012). A similar stochastic Langevin model for PADM2M by Buffett et al. (2013) suggests a mean reversal rate of about one reversal per Myr, which is roughly twice the value we predict but still four times lower than Earth's estimates. A possible reason for these discrepancies could be that the palaeomagnetic data are insufficient to constrain the stochastic model.
Figure 14 subsumes our results by comparing drift and fluctuation for the reversing dynamo model E3R9 and for PADM2M. At the lowest ADM where the palaeomagnetic data still allow us to roughly constrain the stochastic model, the drift is already significantly larger than for E3R9. This strong drift away from the polarity transition translates into the low reversal rate. Larger fluctuation amplitudes partly compensate this effect in the analysis of Buffett et al. (2013). Additional palaeomagnetic records, containing a larger fraction of low ADM instances, would help to better pin down the drift and fluctuation profiles. As discussed above, the fundamental problem that palaeomagnetic sequences provide virtual axial dipoles rather than the true axial dipole contribution can also become an issue when the ADM is so low that its signal is blurred by other field contributions.
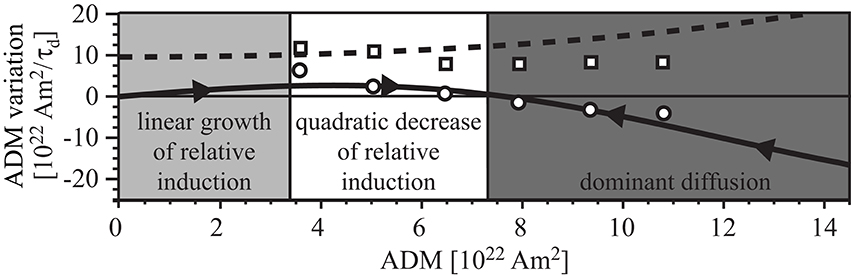
Figure 14. Drift d and rescaled fluctuation f⋆ for the reversing dynamo model E3R9 (solid and dashed curves respectively) and for the palaeomagnetic model PADM2M (open circles and squares respectively). Colored backgrounds separate the regimes for the different inductive and diffusive contributions found in the simulations.
Experiments with synthetic drift and fluctuation profiles could help to reconstruct the axial dipole moment variations at small field intensities leading to more realistic predictions of the reversal rate. Another problem are the slow changes of the Earth's reversal rate over time, for example due to variations in the lower mantle structure, and normal statistical fluctuations may also play a role (Biggin et al., 2012). After all, the last reversal occurred about 780 thousand years ago.
The secular variation, measured by the relative standard deviation V, is smaller in model PADM2M than in the two reversing dynamo models studied here. One possible reason is the coarse time resolution of the palaeomagnetic model. For the simulations we chose a time resolution τ of 15 times the convective overturn time while this factor has to be increased to about 60 for PADM2M. Perhaps more significant is the fact that the palaeomagnetic model is based on sedimentary data which are known to average out faster field variations due to the long locking time. It is therefore likely that the palaeomagnetic model misses extreme variations or averages them out. Both effects potentially lead to narrower distributions which could be tested for the numerical models, an analysis we plan to conduct in the future. Alternatively, a slight decrease in Rayleigh number may not only reduce the reversal rate but also lead to leaner probability distributions.
Following the ideas of Hoyng et al. (2001), we explored the drift and fluctuation profiles for clues on the nonlinear interaction between flow and magnetic field. An analysis of the axial dipole variations just below the outer Ekman boundary layer allowed separating inductive and diffusive contributions in the simulations. The results seem to confirm the classical picture also illustrated in Figure 14. For a very weak field, the mean field generation grows linearly with the field amplitude. The diffusion also increases linearly but the slope is slightly shallower, at least when the dynamo is not multipolar. The positive net slope results in a growing drift toward stronger axial dipole fields. At some intermediate field strengths, however, the mean induction become gradually less efficient likely due to Lorentz forces quenching the flow dynamics. The net slope then decreases until diffusive effects start to dominate where the total drift crosses the zero line. The crossing point establishes the ADM mode or most likely value xm.
Buffett et al. (2014) suggest that diffusive effects are responsible for the drift toward xm from both sides, i.e. also for x < xm. Our analysis confirms the more classical view that diffusion always acts destructively while any drift toward stronger fields is an inductive effect. The idea by Buffett et al. (2014) was motivated by the fact that the involved drift time scales are always very slow. We confirm that the drift is indeed never significantly faster than dipole decay but for a different reason: The drift (or mean axial dipole variation) reflects the slow fundamental induction-diffusion balance of the dynamo mechanism that is established via the nonlinear interaction between flow and magnetic field. The strong quenching effects evident in most drift profiles support this view and suggest that this fundamental aspect could actually be inferred from axial dipole moment observations.
The fluctuations (or RMS axial dipole variations) act on time scales at least a factor two faster. The much weaker quenching effects suggest that the fluctuations are too fast to establish a balance. Note, however, that the fluctuation time scale decreases with the temporal resolution τ and we have chosen relatively large τ values here. Fluctuation quenching is bound to become even smaller when τ is decreased further.
Is the idea of an additional weak field state in reversing dynamos, suggested by WM16, supported by the analysis presented here? As stated above, the modes xm of the unsigned ADM distribution are determined by the values where the drift crosses zero with a negative slope (or equivalently where the drift potential has a local minimum). A distinct weak dipole moment state would thus require the drift to assume a negative slope around x = 0, which is exactly the configuration we find for multipolar dynamos. For reversing dynamos, however, the slope is positive around x = 0 so that the net drift drives the system away from the origin toward xm. This suggests that Earth-like rare reversals are actually not interludes where the dynamo ventures into the multipolar state. Instead they are facilitated by the simple fact that the drift amplitude decreases toward x = 0 while the fluctuation amplitude remains large. Once the stochastic fluctuations have conspired to reduce the axial dipole moment sufficiently enough, any further fluctuation has an easy game to accomplish a polarity change. The likelihood for reaching weak dipole moments, on the other hand, is determined by a combination of different effects. For example, smaller mode values xm, shallower negative drift slopes around xm, a late turning point x* of the drift slope, or a small positive drift slope around x = 0 all increase the likelihood that the dynamo assumes weak ADM values and thus make reversals more likely. Further analysis should clarify the role of these different factors.
We have only started to analyze quenching effects and a more in depth comparison with predictions from mean-field theory would be certainly interesting. An extension of the internal induction and diffusion analysis to deeper depths, other field harmonics, and more dynamo cases could clarify how widely the simple picture we paint here actually applies. Unfortunately, it remains very difficult to include low Ekman number cases with E < 3 × 10−5 since the respective simulations are too computationally demanding.
Author Contributions
Both authors contributed equally to running and analyzing the numerical simulations. The publication charges are funded by the MPDL.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Biggin, A. J., Steinberger, B., Aubert, J., Suttie, N., Holme, R., Torsvik, T. H., et al. (2012). Possible links between long-term geomagnetic variations and whole-mantle convection processes. Nat. Geosci. 5, 526–533. doi: 10.1038/ngeo1521
Brendel, K., Kuipers, J., Barkema, G. T., and Hoyng, P. (2007). An analysis of the fluctuations of the geomagnetic dipole. Phys. Earth Planet. Inter. 162, 249–255. doi: 10.1016/j.pepi.2007.05.005
Buffett, B., and Matsui, H. (2015). A power spectrum for the geomagnetic dipole moment. Earth Planet. Sci. Lett. 411, 20–26. doi: 10.1016/j.epsl.2014.11.045
Buffett, B. A., King, E. M., and Matsui, H. (2014). A physical interpretation of stochastic models for fluctuations in the Earth's dipole field. Geophys. J. Int. 198, 597–608. doi: 10.1093/gji/ggu153
Buffett, B. A., Ziegler, L., and Constable, C. G. (2013). A stochastic model for palaeomagnetic field variations. Geophys. J. Int. 195, 86–97. doi: 10.1093/gji/ggt218
Channell, J. E. T., Xuan, C., and Hodell, D. A. (2009). Stacking paleointensity and oxygen isotope data for the last 1.5 Myr (PISO-1500). Earth Planet. Sci. Lett. 283, 14–23. doi: 10.1016/j.epsl.2009.03.012
Christensen, U., and Wicht, J. (2015). “Numerical dynamo simulations,” in Treatise on Geophysics, 2nd Edn., Chapter 10, Vol. 8, ed G. Schubert (Oxford: Elsevier), 245–277. doi: 10.1016/B978-0-444-53802-4.00145-7
Christensen, U. R., and Aubert, J. (2006). Scaling properties of convection-driven dynamos in rotating spherical shells and applications to planetary magnetic fields. Geophys. J. Int. 116, 97–114. doi: 10.1111/j.1365-246X.2006.03009.x
Christensen, U. R., Wardinski, I., and Lesur, V. (2012). Time scales of geomagnetic secular acceleration in satellite field models and geodynamo models. Geophys. J. Int. 190, 243–254. doi: 10.1111/j.1365-246X.2012.05508.x
Constable, C., and Johnson, C. (2005). A paleomagnetic power spectrum. Phys. Earth Planet. Inter. 153, 61–73. doi: 10.1016/j.pepi.2005.03.015
Constable, C., and Parker, R. (1988). Statistics of the geomagnetic secular variation for the past 5 m.y. J. Geophys. Res. 93, 11569–11581. doi: 10.1029/JB093iB10p11569
Friedrich, R., Peinke, J., Sahimi, M., and Reza Rahimi Tabar, M. (2011). Approaching complexity by stochastic methods: from biological systems to turbulence. Phys. Rep. 506, 87–162. doi: 10.1016/j.physrep.2011.05.003
Gillet, N., Jault, D., Canet, E., and Fournier, A. (2010). Fast torsional waves and strong magnetic fields within the Earth's core. Nature 465, 74–77. doi: 10.1038/nature09010
Guyodo, Y., and Valet, J.-P. (1999). Global changes in intensity of the Earth's magnetic field during the past 800kyr. Nature 399, 249–252. doi: 10.1038/20420
Hoyng, P., Ossendrijver, M. A. J. H., and Schmitt, D. (2001). The geodynamo as a bistable oscillator. Geophys. Astrophys. Fluid Dyn. 94, 263–314. doi: 10.1080/03091920108203410
Hulot, G., and Bouligand, C. (2005). Statistical paleomagnetic field modelling and symmetry considerations. Geophys. J. Int. 161, 591–602. doi: 10.1111/j.1365-246X.2005.02612.x
Jackson, A., Jonkers, A., and Walker, M. (2000). Four centuries of geomagnetic secular variation from historical records. Philos. Trans. R. Soc. Lond. A358, 957–990. doi: 10.1098/rsta.2000.0569
Korte, M., Constable, C., Donadini, F., and Holme, R. (2011). Reconstructing the Holocene geomagnetic field. Earth Planet. Sci. Lett. 312, 497–505. doi: 10.1016/j.epsl.2011.10.031
Krause, F., and Rädler, K.-H. (1980). Mean-Field Magnetohydrodynamics and Dynamo Theory. Oxford: Akademie-Verlag Berlin and Pergamon Press.
Kuipers, J., Hoyng, P., Wicht, J., and Barkema, G. (2009). Analysis of the variability of the axial dipole moment of a numerical geodynamo model. Phys. Earth Planet. Inter. 173, 228–232. doi: 10.1016/j.pepi.2008.12.001
Maruyama, G. (1955). Continuous Markov processes and stochastic equations. Rend. Circ. Mat. Palermo 4, 48–90. doi: 10.1007/BF02846028
McFadden, P. L., and Merrill, R. T. (1984). Lower mantle convection and geomagnetism. J. Geophys. Res. 89, 3354–3362. doi: 10.1029/JB089iB05p03354
Ogg, J. G. (2012). “Geomagnetic polarity time scale,” in Geologic Time Scale 2012, eds F. M. Gradstein, J. G. Ogg, M. Schmitz, and G. Ogg (Boston, MA: Elsevier), 85–113.
Pavón-Carrasco, F. J., Osete, M. L., Torta, J. M., and De Santis, A. (2014). A geomagnetic field model for the holocene based on archaeomagnetic and lava flow data. Earth Planet. Sci. Lett. 388, 98–109. doi: 10.1016/j.epsl.2013.11.046
Pozzo, M., Davies, C., Gubbins, D., and Alfè, D. (2012). Thermal and electrical conductivity of iron at Earth's core conditions. Nature 485, 355–358. doi: 10.1038/nature11031
Risken, H., and Frank, T. (1996). The Fokker-Planck Equation. Methods of Solution and Applications. Berlin; Heidelberg: Springer-Verlag.
Schmitt, D., Ossendrijver, M. A. J. H., and Hoyng, P. (2001). Magnetic field reversals and secular variation in a bistable geodynamo model. Phys. Earth Planet. Inter. 125, 119–124. doi: 10.1016/S0031-9201(01)00237-0
Valet, J.-P., Meynadier, L., and Guyodo, Y. (2005). Geomagnetic dipole strength and reversal rate over the past two million years. Nature 435, 802–805. doi: 10.1038/nature03674
Wicht, J. (2002). Inner-core conductivity in numerical dynamo simulations. Phys. Earth Planet. Inter. 132, 281–302. doi: 10.1016/S0031-9201(02)00078-X
Wicht, J. (2005). Palaeomagnetic interpretation of dynamo simulations. Geophys. J. Int. 162, 371–380. doi: 10.1111/j.1365-246X.2005.02665.x
Wicht, J., Stellmach, S., and Harder, H. (2009). “Numerical models of the geodynamo: from fundamental Cartesian models to 3d simulations of field reversals,” in Geomagnetic Field Variations - Space-Time Structure, Processes, and Effects on System Earth, Springer Monograph, eds K. Glassmeier, H. Soffel, and J. Negendank (Berlin; Heidelberg; New York: Springer), 107–158. doi: 10.1007/978-3-540-76939-2_4
Wicht, J., and Tilgner, A. (2010). Theory and modeling of planetary dynamos. Space Sci. Rev. 152, 501–542. doi: 10.1007/s11214-010-9638-y
Keywords: geodynamo, geomagnetic field, field reversals, numerical simulation, stochastic model, statistical analysis
Citation: Meduri DG and Wicht J (2016) A Simple Stochastic Model for Dipole Moment Fluctuations in Numerical Dynamo Simulations. Front. Earth Sci. 4:38. doi: 10.3389/feart.2016.00038
Received: 23 December 2015; Accepted: 24 March 2016;
Published: 22 April 2016.
Edited by:
Angelo De Santis, INGV / G. D'Annunzio University, ItalyReviewed by:
Maria Luisa Osete, Complutense University of Madrid, SpainBejo Duka, University of Tirana, Albania
Philip Livermore, University of Leeds, UK
Copyright © 2016 Meduri and Wicht. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Domenico G. Meduri, bWVkdXJpQG1wcy5tcGcuZGU=
 Domenico G. Meduri
Domenico G. Meduri Johannes Wicht
Johannes Wicht