- Department of Earth Sciences, University of Geneva, Geneva, Switzerland
Magma fluxes in the Earth's crust play an important role in regulating the relationship between the frequency and magnitude of volcanic eruptions, the chemical evolution of magmatic systems, and the distribution of geothermal energy and mineral resources on our planet. Therefore, quantifying magma productivity and the rate of magma transfer within the crust can provide valuable insights to characterize the long-term behavior of volcanic systems and to unveil the link between the physical and chemical evolution of magmatic systems and their potential to generate resources. We performed thermal modeling to compute the temperature evolution of crustal magmatic intrusions with different final volumes assembled over a variety of timescales (i.e., at different magma fluxes). Using these results, we calculated synthetic populations of zircon ages assuming the number of zircons crystallizing in a given time period is directly proportional to the volume of magma at temperature within the zircon crystallization range. The statistical analysis of the calculated populations of zircon ages shows that the mode, median, and standard deviation of the populations varies coherently as function of the rate of magma injection and final volume of the crustal intrusions. Therefore, the statistical properties of the population of zircon ages can add useful constraints to quantify the rate of magma injection and the final volume of magmatic intrusions. Here, we explore the effect of different ranges of zircon saturation temperature, intrusion geometry, and wall rock temperature on the calculated distributions of zircon ages. Additionally, we determine the effect of undersampling on the variability of mode, median, and standards deviation of calculated populations of zircon ages to estimate the minimum number of zircon analyses necessary to obtain meaningful estimates of magma flux and final intrusion volume.
Introduction
Magmatic systems are depicted as composed of regions of magma accumulation (magmatic reservoirs) distributed at different depths within the Earth's crust, connected by subvertical feeding structures (e.g., Hildreth and Moorbath, 1988; Annen et al., 2006; Caricchi et al., 2014). Field studies, petrography, petrology, geochemistry, and thermal modeling support this model and additionally provide evidences for the periodic transfer of magma to the shallower portions of magmatic systems (Hildreth, 1981; de Saint-Blanquat et al., 2001, 2011; Coleman et al., 2004; Glazner et al., 2004; Annen et al., 2006; Connolly et al., 2009; Schaltegger et al., 2009; Bouilhol et al., 2011; Paterson et al., 2011; Schoene et al., 2012; Solano et al., 2012, 2014; Havlin et al., 2013; Caricchi et al., 2014; Jagoutz, 2014). In periodically replenished magmatic reservoirs, the relative volume of magma and residual melt of various compositions change over hundreds of thousands to millions of years as a function of the average rate of magma injection, the thermal properties and chemistry of the wall rocks and the topology of the pertinent phase diagrams for magmas contained within the magmatic system (Spera and Bohrson, 2001; Annen et al., 2006; Glazner, 2007; Solano et al., 2012, 2014; Melekhova et al., 2013; Caricchi et al., 2014; Nandedkar et al., 2014; Caricchi and Blundy, 2015a). The rate of magma transfer between the different portions of a magmatic system plays a pivotal role in controlling the physical and chemical evolution of magmas from the mantle to the surface, creating an intrinsic link between temperature evolution, crystallization, and variation of residual melt composition (Crisp, 1984; Annen et al., 2006; White et al., 2006; Glazner, 2007; Stolper and Asimow, 2007; Annen, 2009; Caricchi et al., 2014; Caricchi and Blundy, 2015b). Therefore, determining magma fluxes within the Earth's crust would allow us to establish links between the geochemistry of magmas erupted at the surface and the temporal evolution of the chemical and physical properties of magmatic reservoirs at depth. However, as most of the magma produced in the mantle is actually not erupted at the surface but crystallizes at depth to form intrusions, the determination of magmatic fluxes is extremely challenging (Bacon and Lanphere, 2006; Lipman, 2007). Several approaches have been used to quantify such fluxes, including large scale geophysics (Crisp, 1984; White et al., 2006). The eruptive fluxes of various volcanoes and volcanic systems have been estimated but because the volume ratio of extruded vs. intrusive products is hard to determine, it is difficult to directly link magma eruption rates with magma flux in the crust (Marsh, 1981; Crisp, 1984; Bacon and Lanphere, 2006; Lipman, 2007; Salisbury et al., 2011; Caricchi et al., 2014; Lipman and Bachmann, 2015; Muir et al., 2015).
We recently developed a method that uses the distribution of precise U-Pb dates obtained from single grains of zircon to determine the rate of assembly and final volume of magmatic intrusion in the crust (Caricchi et al., 2014). The foundation of this method is that zircon crystallizes within a given range of temperature (Tzr; a function of magma composition and zirconium concentration; Hanchar and Watson, 2003; Miller et al., 2003; Boehnke et al., 2013) and its crystallization can be dated by radio-isotopic methods (e.g., Schaltegger et al., 2015). Under the assumption that the number of zircons crystallizing within a given time interval is proportional to the magma volume within Tzr, the distribution of dates of a population of zircons provides an image of the time-integrated evolution of temperature in a magmatic reservoir (Caricchi et al., 2014). To quantify the relationships between magma flux, final volume, and the characteristics of the resulting population of zircon ages, we performed thermal modeling. The results reveal that the mode, median and standard deviation of the calculated populations of zircon ages vary systematically as a function of magma flux and final volume of the intrusion. Therefore, the comparison between the synthetic age populations and those retrieved in natural magmatic systems can provide information on the final volume of the intrusion and the rate at which the pluton was accreted (Caricchi et al., 2014). The statistical characteristics of the calculated populations of zircon ages depends on the range of temperature at which zircon crystallizes, from the depth of emplacement (i.e., the temperature of the wall rocks), and the geometry of the intrusion (Caricchi et al., 2014). Here we present a detailed investigation of the effect of considering different ranges of zircon saturation temperature (700–750, 700–800, 700–850°C), as well as different intrusion geometries, and wall rock temperatures, on the mode, median, and standard deviation of the calculated zircon age distributions, which were not explored in Caricchi et al. (2014). Additionally, we assess the impact of undersampling to determine the minimum number of zircons required to apply the method we propose.
Methods
Thermal Modeling and Calculation of Synthetic Populations of Zircon Ages
We use heat conduction-advection theory to determine the distribution and evolution of temperature in a crust that experiences magma injection and cooling. The basic equation of heat conduction-advection theory is a mathematical statement of conservation of energy combined with Fourier's Law of heat conduction. For an axisymmetrical geometry, this equation can be written as:
where T is the temperature, t is the time, r is the horizontal distance relative to the symmetry axis, z is the depth, ur and uz are the solid velocities in the r and z directions, respectively, k is the thermal conductivity, ρ is the density, Cp is the specific heat per unit mass, L is the latent heat of fusion per unit mass and χc is the crystal fraction. The crystal fraction is assumed to vary with temperature according to
where
The velocities ur and uz depend on the intrusion geometry and magma injection rate. This formulation was selected to fit the variation of crystallinity with temperature observed for magma of granodioritic composition (Piwinskii and Wyllie, 1968). Most calculations were performed assuming outward inflating spherical magma chambers, though we tested sensitivity to the intrusion geometry by comparing these results with horizontally expanding cylinders and vertically accreting cylinders. The velocities ur and uz depend on the intrusion geometry and magma injection rate. During the intrusion phase, ur and uz are constant in time, whereas they are zero after intrusion has ceased. They are simply determined by providing the space for each newly intruded pulse. For example, for an outwardly inflating cylinder, the radial velocity for all points adjacent to the intrusion is simply ur = dr/dt where dr is the radius of the intruded pulse and dt is the time interval between pulses, while the vertical velocity (uz) is zero.
The initial temperature was assumed to be a constant geothermal gradient. For boundary conditions, the temperature was assumed to be constant on the upper (i.e., the surface) and lower (z = 30 km) boundaries. The right boundary was assumed to be zero horizontal heat flux. Magma injection was implemented by modifying the temperature (to the liquidus temperature) of nodes within the newly injected portion of the magma chamber. Parts of the r = 0 boundary not influenced by magma injection were assumed to have zero horizontal heat flux. Solutions to Equation (1) were obtained with the Petrov–Galerkin Finite Element Method on 4-node quadrilaterals. Unless specified otherwise, all calculations were performed with the following parameter values: initial geothermal gradient 30°C km−1, intrusion depth = 10 km, thermal conductivity 2.7 W m−1 K−1, heat capacity 1 kJ kg−1 °K−1, rock density 2700 kg m−3, latent heat of fusion 350 kJ kg−1, intrusion temperature 900°C.
Synthetic zircon-age distributions were calculated on the basis of the thermal calculations using the following procedure:
1) The final cooled pluton was divided into numerous discrete equal-volume cells.
2) The temperature evolution of each cell was tracked back in time from a cold state to the time when each cell was initially intruded. Note that the position of the cells change in time due to progressive intrusion.
3) Each constant volume cell was assumed to grow zircons at a constant rate when its temperature was within a specified zircon crystallization window Tzr (700–750, 700–800, and 700–850°C). The lower temperature was chosen to be close to the granitic water saturated minimum (Johannes and Holtz, 1996).
4) The total number of zircons in all cells within the pluton is tracked in time, giving the zircon-time distribution.
Zircon Dating
U-Pb age determinations on zircon may be carried out using high-precision, bulk dating techniques (chemical abrasion, isotope dilution, thermal ionization mass spectrometry; CA-ID-TIMS), or spatially resolved, spot analyses using an ion microprobe (secondary ion mass spectrometry; SIMS) or laser ablation linked to an inductively coupled plasma mass spectrometer (LA-ICP-MS). The three techniques differ largely in terms of sampled volumes and precisions; accuracy of the techniques depends on a well-calibrated tracer solution in the case of CA-ID-TIMS (Condon et al., 2015) or on external reference materials in the case of the two in-situ techniques. CA-ID-TIMS utilizes whole grains or parts of grains, inevitably mixing growth zones of different age, and achieves a typical precision and accuracy of 0.05–0.1% (2σ) in 206Pb/238U date (up to ~0.3% for 1 Ma old zircon; Wotzlaw et al., 2015), contrasting to the ca. 1–2% typical uncertainties for both SIMS and LA-ICP-MS (Schaltegger et al., 2015).
The geochronological method of choice to satisfy the preconditions of our model approach needs to be capable of resolving timescales of magmatic crystallization, which are commonly in the range of 104 to few 105 years for crustal plutons (e.g., Leuthold et al., 2012; Schoene et al., 2012; Broderick et al., 2015). This implies that in-situ U-Pb dating techniques do not provide sufficient age resolution in magmatic systems older than 15–30 Ma, because of the inherent 1–2% external uncertainty of these methods (Schaltegger et al., 2015).
We therefore required to use high-precision 206Pb/238U dates produced using CA-ID-TIMS techniques on entire or fragments of zircon grains. Any such date will provide time-averaged information, weighted for volume of the different zircon sectors and their U-content. We will show below that despite the lack of spatial resolution, the resulting dates provide an image of the time-integrated evolution of temperature in a magmatic reservoir and can be used to calculate fluxes and volumes using our method.
Results
The method we proposed in Caricchi et al. (2014) consists of using zircon age populations to retrieve information on magma fluxes and the final volume of the reservoir in which the zircon crystallized. The zircon age data are first transformed into a time sequence, posing time zero equal to the oldest zircon age. The population (in kilo-years) is then bootstrapped to obtain ranges of mode, median, and standard deviation. These three ranges are then plotted using contoured figures of mode, median, and standard deviation such as Figure 3 of Caricchi et al. (2014) and the area defined by the intercept of the three ranges provide estimates of magma flux and volume (see also Caricchi et al., 2014). In the following we present (i) the influence that various factors may have on the final results; (ii) a quantification of the minimum number of zircons required to obtain meaningful results using the approach we propose; (iii) discuss possible artifacts arising from the selection of the wrong analytical technique by applying our method to datasets of low precision data (iv) and shows an application of our method to published data for Mt. Capanne pluton (Elba island, Italy).
Thermal Modeling
Thermal modeling shows that the average temperature of a magmatic reservoir drops throughout the period of injection and once the injection of magma comes to an end, the rate of decrease of the average temperature increases (Figure 1). During magma injection, the average temperature tends to values that are directly proportional to the magma flux and inversely proportional to the duration of the intrusion. As expected, the duration of cooling once the injection of magma stops increases with increasing final volume of the intrusion (Figure 1).
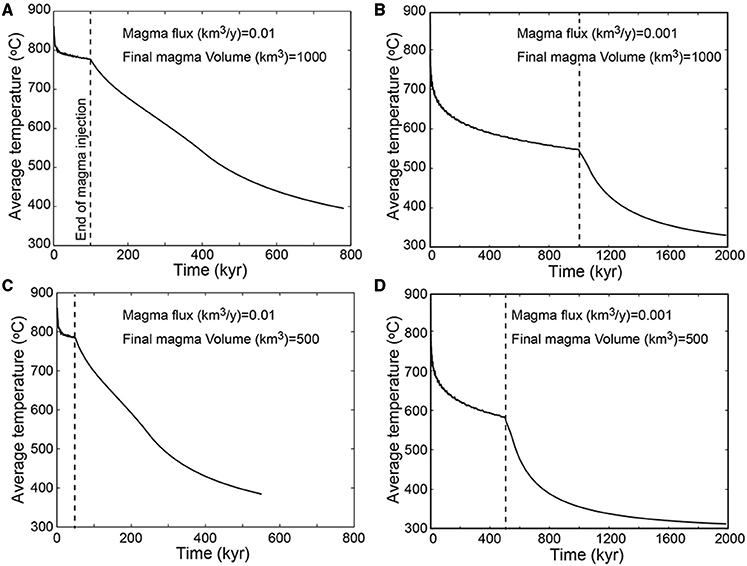
Figure 1. Temporal evolution of the average intrusion temperature for thermal models performed at injection fluxes of 0.01 and 0.001 km3/y for (A,C) and (B,D), respectively.
The average temperature of the intrusion drops even during magma injection because while the rate at which magma (and enthalpy) is supplied to the system remains constant in our models, the rate of heat release increase because the surface over which enthalpy is lost to the wall rocks increases (Marsh, 1981; Caricchi et al., 2014). Hence, during the assembly of a magmatic intrusion, the thermal structure of the reservoir evolves and the relative volumes of magma within different temperature ranges change in time (Figure 2). The flux of magma within the magmatic reservoir exerts a first order control on the relative volume of magma within different temperature ranges. As a consequence, magma fluxes also control the time span over which residual melts of various compositions are present (in different relative proportions) within a reservoir. While we will not dwell long on this aspect, such results indicate that the rate of magma input in subvolcanic reservoirs affects the long-term probability of magmas of different compositions to be sampled during volcanic eruptions (Melekhova et al., 2013; Caricchi and Blundy, 2015b). On the other hand, in magmatic systems that are assembled extremely rapidly and cool over time, the probability of magma with a given composition to be present within the magma reservoir is exclusively controlled by the topology of the phase diagram (Marsh, 1981).
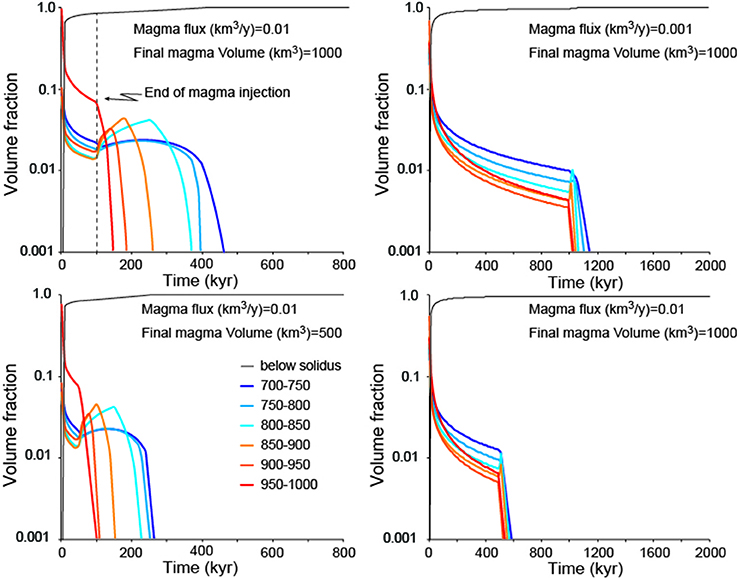
Figure 2. Temporal evolution of the volume fraction of magma within different temperature intervals (colored lines). The black line shows the fraction of magma at temperature lower than the solidus (700°C).
The thermal modeling results show that from the beginning of the injection event, magma cools through the range of zircon saturation temperature leading to the continuous crystallization of zircon (Figures 3, 4). The resulting distribution of synthetic zircon ages is directly linked to the rate of magma input and the final volume of intruded magma (Figure 4; Caricchi et al., 2014).
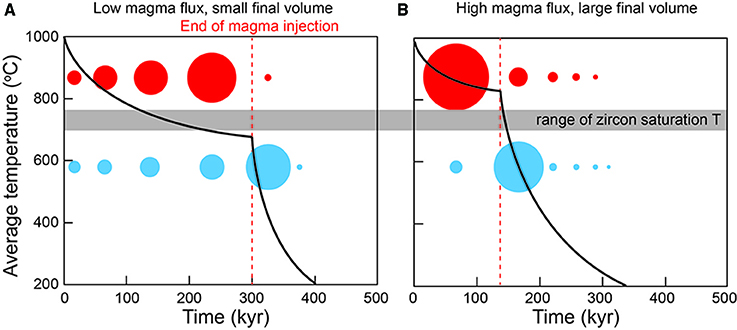
Figure 3. Schematic representation of the evolution of the relative volume of magma above (red circles) and below (light blue circles) the range of zircon saturation temperature in time. (A) Temporal evolution of volumes and temperature for a magmatic reservoir of small volume assembled at low average magma flux. (B) Temporal evolution of volumes and temperature for a magmatic reservoir of large volume assembled at high average magma flux. The black line shows the evolution in time of the average temperature of the intrusion.
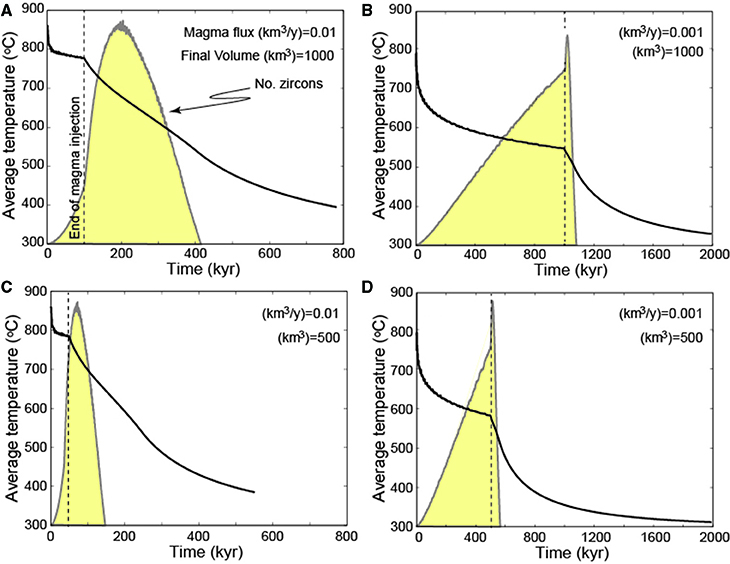
Figure 4. Combined temporal evolution of the average temperature of the intrusion and resulting population of zircon crystallization times. The shape of the zircon crystallization time population reflects the evolution in time of the relative volume of magma within the range of zircon saturation temperature. The modeled final volumes were 500 and 1000 km3 for (C,D) and (A,B), respectively.
Effect of Zircon Saturation Temperature
The range of zircon saturation temperature varies as function of magma chemistry (Hanchar and Watson, 2003; Miller et al., 2003; Boehnke et al., 2013) and this should be taken into account when applying the method we propose (Caricchi et al., 2014). For this reason we calculated synthetic zircon age populations for three ranges of temperature: 700–750, 700–800, and 700–850°C (Figures 5, 6; Table 1). The comparison shows that the difference in mode, median, and standard deviation for zircon age populations calculated considering the three different ranges of zircon saturation temperature at the same magma flux and final volume are very similar and only differ by 0.1–0.2 log units (Figures 5, 6). This is true for all models performed within the range of magma flux (10−4–10−1 km3/y) and final volume (30–10,000 km3) investigated here (Figure 6; Table 1). We also tested the effect of decreasing the solidus temperature and therefore the lower limit of Tzr from 700 to 680°C. The resulting synthetic population of zircon ages show a difference slightly lower than 0.1 log units in mode and median values. Such variations are small and do not produce any significant difference in the values of magma flux and volume. The wide range of zircon saturation temperature used in these tests indicates that our method can be applied to magmas of various compositions.
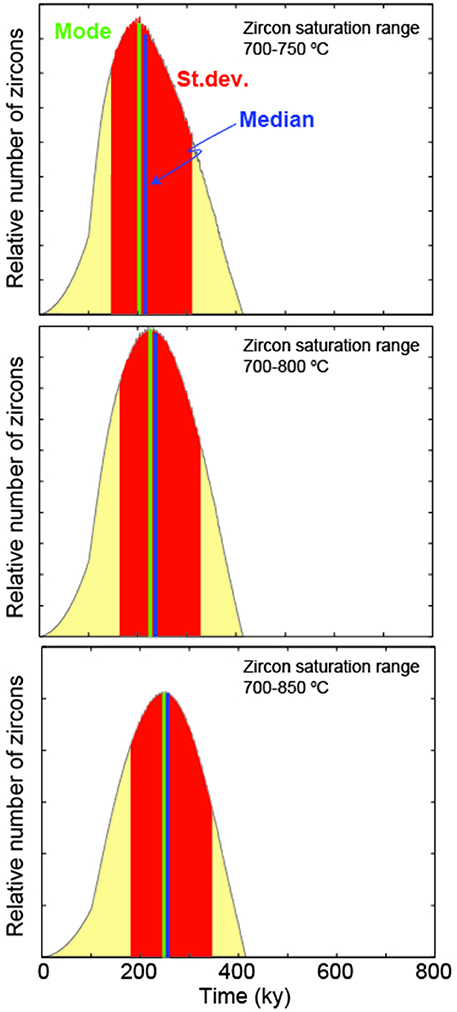
Figure 5. Mode, median, and standard deviation of population of zircon crystallization times obtained for a constant magma flux of 0.01 km3/y, final volume of 1000 km3, and different ranges of zircon saturation temperatures.
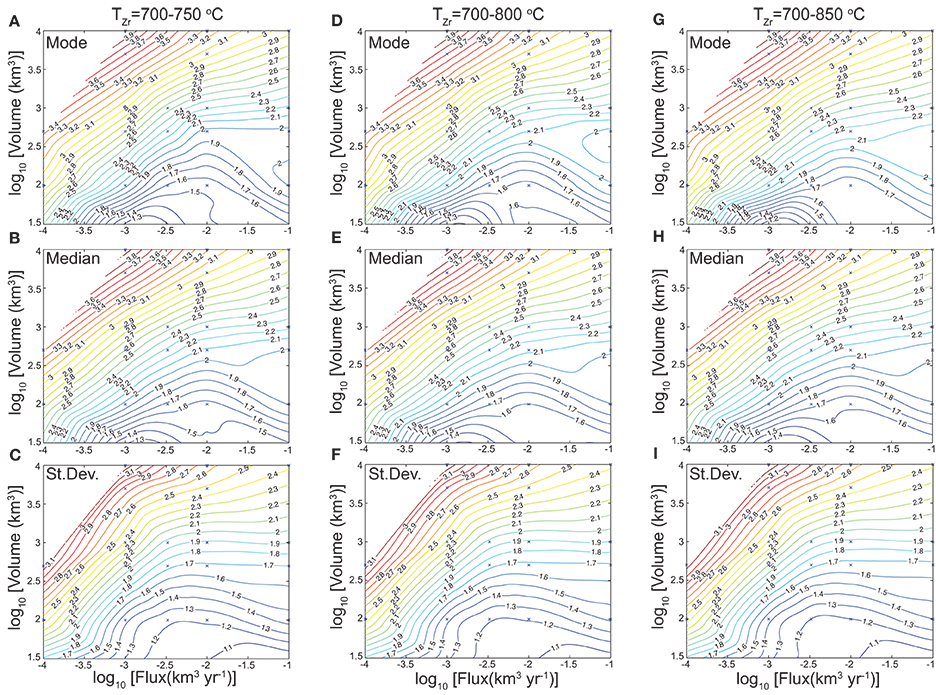
Figure 6. Contours of mode (A,D,G), median (B,E,H), and standard deviation (C,F,I) for zircon age spectra obtained from thermal modeling. The number within the contours shows the logarithmic values of the respective parameters in kilo-years. Values presented in (A–C) were obtained for a range of zircon crystallization temperature (Tzr) of 700–750°C, (D–F) for Tzr between 700 and 800°C, and (G–I) for Tzr between 700 and 850°C.
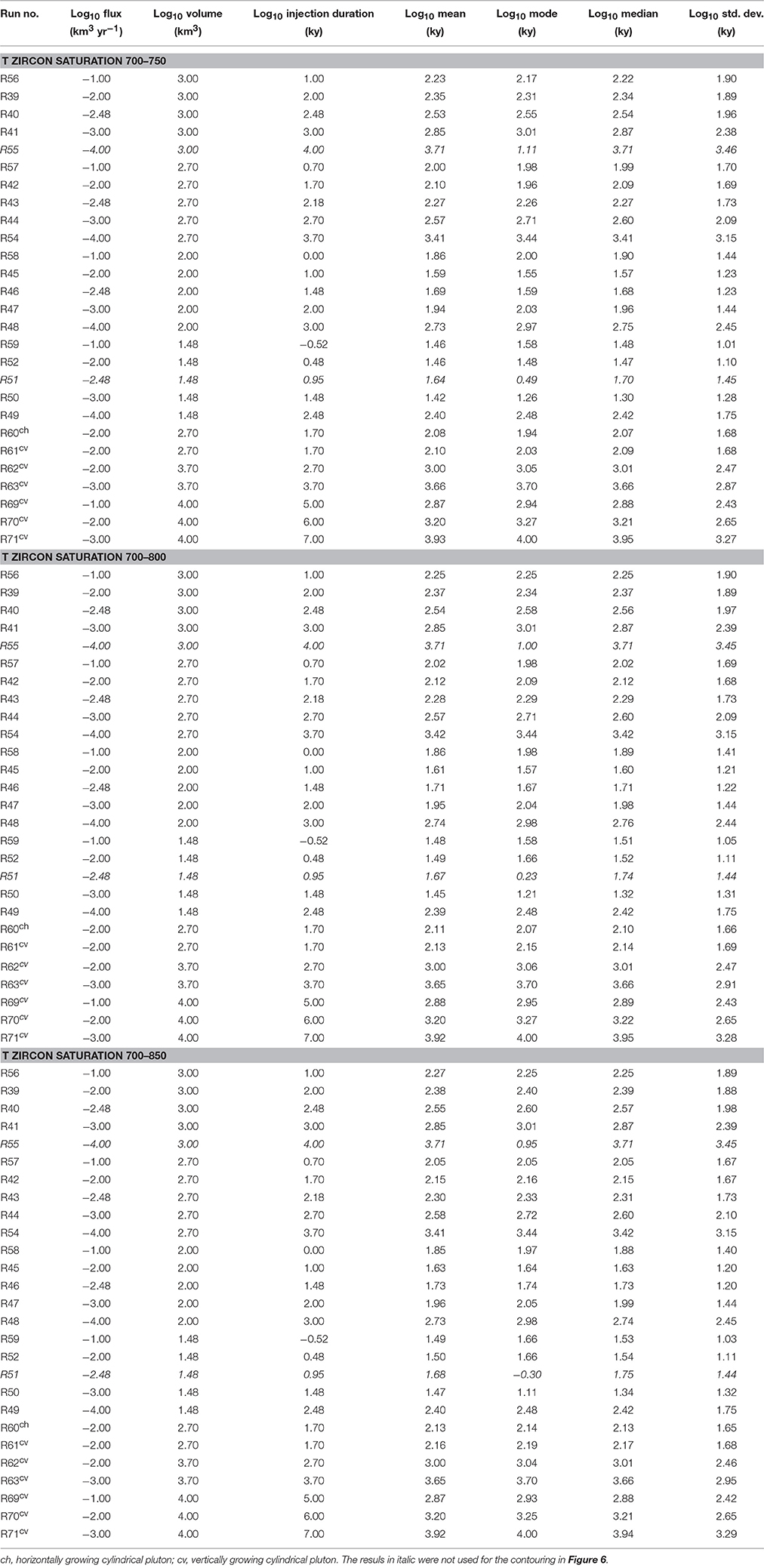
Table 1. Statistical parameters obtained for the different injected volumes, injection fluxes, and ranges of zircon saturation temperature.
Effect of Intrusion Geometry, Wall Rock Temperature, and Magma Injection Temperature
Thermal calculations were repeated for the same rate of magma input and final volume but different geometries of the intrusions (Table 1). The variability of mode, median, and standard deviation observed by changing intrusion geometry is always lower than 0.2 logarithmic units, and have, therefore, only a minor impact on the estimated values of magma flux and final volume obtained applying our method to natural populations of zircon ages (Caricchi et al., 2014). More complicated intrusion geometries can be envisaged, however, because of the intrinsic mechanical and thermal instabilities of irregular boundaries in magmatic systems, thermal anomalies tend to evolve rapidly to sub-spherical or cylindrical shapes over time (Gudmundsson, 2012; Paulatto et al., 2012). This implies that more complex geometry can potentially change some details of the zircon crystallization time population but not change significantly mode, median, and standard deviation of the population and therefore, not affect significantly the estimates obtained with our method.
Tests for magma injection temperature and temperature of the wall rocks were already performed in Caricchi et al. (2014) and show similarly limited effect on the synthetic populations of zircon crystallization times.
Number of Zircons Required
The calculated populations of zircon ages are obtained by considering all zircons that crystallized during the entire supersolidus history of the simulated intrusion. Clearly, the number of zircons analyzed in a geochronology study always represents a subsample of all zircons present in magmatic rocks. Therefore, it is important to address the effect of undersampling on mode, median, and standard deviation of a natural population of zircon ages on the final estimates of magma flux and volume of the intrusion. This allow us to estimate the minimum number of zircons required for the results obtained by our method to be meaningful. To test the impact of subsampling on the statistical parameters (i.e., mode, median, and standard deviation) required for the estimation of magma fluxes and volumes, we randomly sub-sampled two populations of ages with different characteristics. In the first example, we consider a normal distribution of zircon ages (no. 10,000) with a standard deviation of 10 ky and a median age of 100 ky (Figure 7). Three tests were performed in which each subsample consists of 10, 30, and 50 ages, respectively. For each subsample we calculated mode, median, and standard deviation and repeated the procedure 10,000 times. The spread in mode, median, and standard deviation obtained with this procedure is shown in Figure 7, where the red circle represents the mode, median, and standard deviation for the distribution shown in panel a. The results show that for a normal distribution that spans a relatively limited range of ages, already ten ages are sufficient to determine the mode, median, and standard deviation within a two-sigma value of about 0.2 logarithmic units (Figure 7), which, as shown in Figure 6, is sufficient to constrain magma fluxes and final volume of the magmatic reservoir. Clearly, increasing the number of analyzed zircons decreases the uncertainty on the mode, median, and standard deviation of the population of zircon ages. We considered another scenario in which the population of zircon age is positively skewed with mode, median, and standard deviation values of 50, 80, and 60 ky, respectively. In this case, bootstrapping shows that ranges of mode, median, and standard deviation become significantly tighter when 30–50 zircon age determinations are performed (Figure 8).
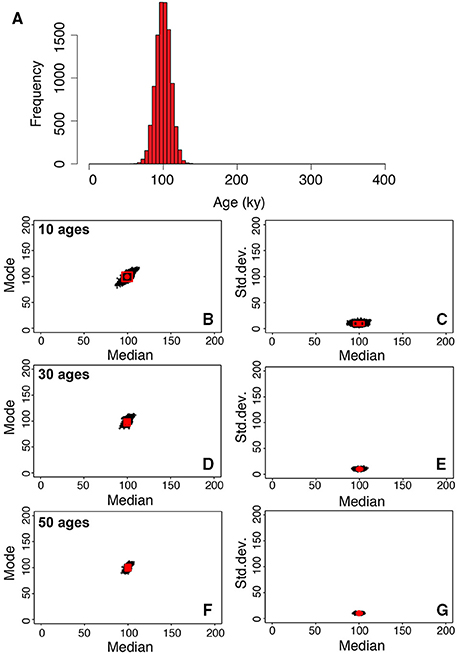
Figure 7. (A) Normal distribution of ages characterized by a modal and median values of 100 ky and a standard deviation of 10 ky. (B,D,F) Each black point in the panels shows the values of mode, median, and standard deviation obtained by bootstrapping of the population of zircon crystallization times represented in (A). Distributions of the values of mode and median obtained by sampling the distribution reported in (A), 10, 30, and 50, times respectively. The procedure has been repeated 10,000 times for each subsample of 10, 30, and 50 ages. (C,E,G) Distributions of the values of standard deviation and median obtained by sampling the distribution reported in (A), 10, 30, and 50 times, respectively. The red boxes provide the 95% confidence intervals for mode, median, and standard deviation.
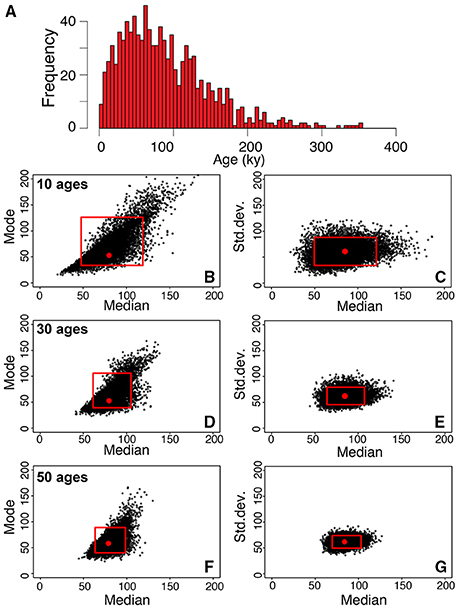
Figure 8. (A) Distribution of ages characterized by a mode of 50 ky, a median of 80 ky, and a standard deviation of 60 ky. (B,D,F) Each black point in the panels shows the values of mode, median, and standard deviation obtained by bootstrapping of the population of zircon crystallization times represented in (A). Distributions of the values of mode and median obtained by sampling the distribution reported in (A), 10, 30, and 50 times, respectively. The procedure has been repeated 10,000 times for each subsample of 10, 30, and 50 ages. (C,E,G). Distributions of the values of standard deviation and median obtained by sampling the distribution reported in (A), 10, 30, and 50 times, respectively. The red boxes provide the 95% confidence intervals for mode, median, and standard deviation.
In-situ Vs. Whole Zircon Techniques
The method proposed here has been developed for high-precision 206Pb/238U dates from entire zircon grains (CA-ID-TIMS) with the implicit assumption of the model that the mass of zircon that crystallizes within a given time period is proportional to the mass of magma within the range of zircon saturation temperature. The method can also be applied to zircon U-Pb dates determined via spot analysis, however, the age determinations from different zones of a zircon should be weighted using a quantitative volumetric model for concentrically grown zircon (e.g., Samperton et al., 2015), in order to reflect the mass of zircons of a particular age and its U concentration. For example, if a population is constituted of zircons with large rims and small cores of equal U concentration, performing one measurement for the rim and one for the core without weighting the ages would artificially increase the statistical weight of older ages. This would lead to a decrease of the values of mode and median (of the population of ages converted in times) and potentially result in an underestimate of the final volume of the magmatic reservoir (Figure 6). Because of the geometry of the contours in Figure 6 the estimates of magma flux would be less affected by not performing the weighting procedure. An additional aspect to consider is the analytical uncertainty on the U-Pb dates that is increased by a factor of 20–40 for in-situ vs. whole grain techniques (Schaltegger et al., 2015). Since we bin our dates for the averaged two-sigma error of individual analyses, larger errors would result in smoother age distributions with smaller ranges of mode, median and standard deviation obtained by bootstrapping. For a normal distribution of imprecise zircon ages with individual uncertainties exceeding the duration of the magmatic process we intend to characterize (Figure 7), our statistical values would be entirely defined by the analytical parameters of our U-Pb age determination. The resulting smaller range of mode, median, and standard deviation would provide tight constraints of magma flux and final volume, which, however, would be a direct measure of the internal reproducibility of the U-Pb dating procedure. For a skewed distribution as shown in Figure 8, our statistical values would be calculated from an arbitrary mixture of analytical variance with protracted duration of zircon crystallization and generate a pure artifact.
This implies that our method can be applied using CA-ID-TIMS 206Pb/238U dates with a state-of-the-art uncertainty of 0.05% up to a maximal age of about 500 Ma; beyond this age we may be able to use highest-precision 207Pb/206Pb dates of concordant zircon grains in rare cases (e.g., Zeh et al., 2015).
Application: Magmatism in Elba Island, Italy
A large dataset of high precision data (168 CA-ID-TIMS zircon age determinations) has been recently published by Barboni and Schoene (2014), Barboni et al. (2015) for a series of magmatic intrusions exposed in Elba island (Italy). We applied our method to these data to show an example of the procedure to follow and to validate our approach.
The largest number of analyses was performed for zircons included in megacrystals of orthoclase recovered from the S. Andrea facies of the Mt. Capanne pluton (94 age determinations; Barboni and Schoene, 2014). The Mt. Capanne pluton has been divided on the basis of field and geochemical analyses in three main facies, which from the structurally higher to the lower are identified in the literature as S. Andrea, S. Francesco, and S. Piero (Rocchi et al., 2010).
We first exclude ages that are older than the oldest measured age by more than the average two-sigma error of the measurements (Figure 9). Ages are transformed in “time” by subtracting to the oldest age the single ages, so that the oldest age corresponds to zero time (Figure 10). Ranges for mode, median, and standard deviation for each population (now transformed in time populations) are obtained by resampling each time distribution 1000 times (bootstrapping). Once the 95% confidence intervals for mode, median, and standard deviation of the populations are determined the contours shown in Figure 6 can be used to obtain estimates of the intrusion volume and the average magma flux at which the pluton was constructed (Figure 11; Table 2).
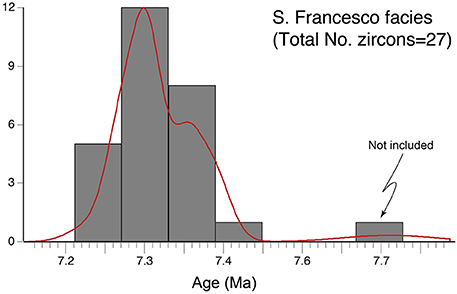
Figure 9. Distribution of zircon age population for the S. Francesco facies of the Mt. Capanne pluton from Barboni et al. (2015).
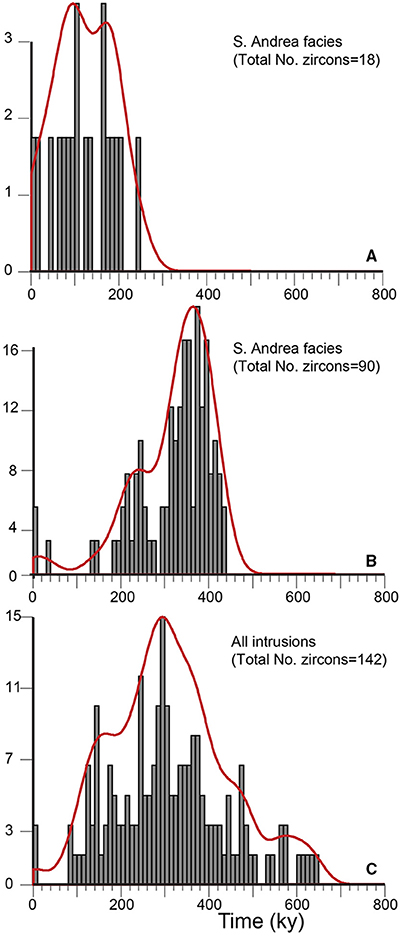
Figure 10. (A) Distribution of zircon crystallization times for the S. Andrea facies from Barboni et al. (2015). (B) Distribution of zircon crystallization times for the S. Andrea facies from Barboni and Schoene (2014). (C) Distribution of crystallization times reported by Barboni et al. (2015) for all intrusions of Elba Island.
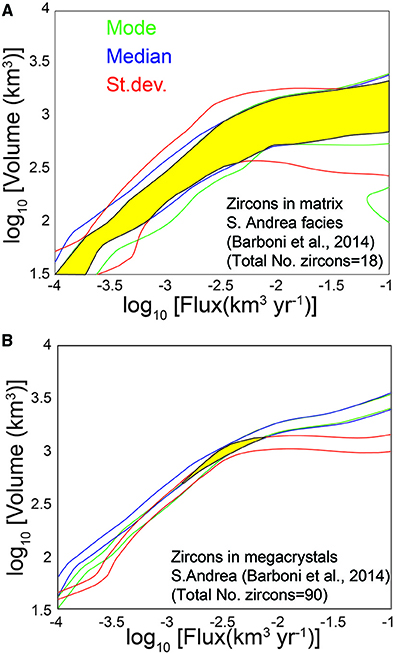
Figure 11. The lines represent the 95% confidence interval for mode, median, and standard deviation obtained by bootstrapping the populations of zircon crystallization times presented in Figure 10 (A,B), respectively. The colored areas provide the estimated volume and magma flux obtained applying the method presented in this contribution. Estimates were obtained by considering a zircon crystallization between 700 and 750°C. Using different zircon crystallization ranges would not change significantly the final estimates as contours in Figure 6 for different Tzr are very similar.

Table 2. Values obtained by the bootstrapping of the zircon age popualtions of Barboni et al. (2015).
Our calculations show that the 18 age determinations for the matrix of S. Andrea facies of the Mt. Capanne pluton (Barboni and Schoene, 2014) were not sufficient to obtain meaningful estimates of magma flux and volume of the intrusion (Figure 11A). This indicates that the real distribution of zircon ages is complex and 18 zircons ages are not sufficient to fully determine the relevant statistical parameters of the age distribution required for our analysis. On the other hand, our method provides tight constraints for magma flux (10−2.7–10−2 km3/y) and intrusive volume (300–1000 km3) when the 90 age determinations for zircons retrieved in megacrystals of orthoclase from (Barboni and Schoene, 2014) are used (Figure 11B). This suggests that in this case, 90 dates are sufficient to describe the distribution of zircon ages during the growth of the megacrystals. While we do not develop any geological interpretation for the significance of the population of zircon ages included in the megacrystals and retrieved from the matrix of the S. Andrea facies, we discuss these results on the basis of flux and total volume.
It is interesting to note that the volume estimates from zircons in the megacrystals from the Mt. Capanne intrusion, are significantly larger than the volumes of the different facies of the Mt. Capanne estimated from fieldwork (~250 km3; Farina et al., 2010; Figure 11B). This suggests that, in agreement with petrological and thermal modeling results (Farina et al., 2010; Barboni et al., 2015), the zircons crystallized at depth within a larger reservoir and only a limited number of zircons number crystallized at emplacement depth.
Discussion
An important issue regarding our method is the portion of the magmatic system about which zircon age populations provide information on volume and rate of assembly. Because we consider the age of a zircon to represent the time at which it crystallizes, our method provides information on the magmatic reservoir where most or all the zircons crystallize. For instance, if zircons dated in a pluton crystallized at depth (Schoene et al., 2012; Barboni et al., 2015), the method we propose will provide information on the magma fluxes and the volume of the reservoir at a deeper crustal level (Broderick et al., 2015). Importantly, if zircons are mobile within magmatic systems, zircon age populations could provide important information on the development and final volume of inaccessible portions of magmatic systems.
Several evidences exist for the mobility of zircons in magmatic systems: In one of our previous publications (Caricchi et al., 2014), we showed that the spread in zircon ages for specimens retrieved in porphyritic plugs associated with ore deposits is too large to be explained by in-situ crystallization of zircons at emplacement depth. These plugs are volumetrically small with respect to the volume of magma required to generate the ore deposits (Steinberger et al., 2013), and therefore would cool through zircon saturation temperature rapidly producing a limited spread in zircon ages (Caricchi et al., 2014). A spread in ages of 200–500 ky obtained from analyses of zircons separated from single hand specimens (Schaltegger et al., 2009; Schoene et al., 2012; Broderick et al., 2015), provide additional support for the mobility of zircons within magmatic systems, given that a hand-size parcel of magma cannot cool through the range of zircon crystallization temperature over half million year. Analyses of zircons in volcanic products also suggest that they are mobile and can be extracted from partially crystallized magmatic mushes before or during an eruption, as also shown for other minerals (Cooper and Wilson, 2014). For zircons retrieved in volcanic products, if evidences exist for re-heating above the zircon saturation temperature and rejuvenation (e.g., Bachmann and Bergantz, 2003) in the period preceding an eruption, our method will need to be applied with caution. Resorption or lack of zircon crystallization in the period preceding the eruption would produce a depletion of the younger portions of the zircon populations, which, in turn, would result in a decrease of the mode, median, and standard deviation recalculated following our approach (Bindeman and Simakin, 2014). Figure 6 shows how a decrease of the value of these parameters leads to an underestimation especially in the final volume of the magmatic reservoir. Such effect is evident when applying of our method to zircons retrieved from the products of the Fish Canyon Tuff for which pre-eruption re-heating was suggested (Wotzlaw et al., 2013; Caricchi et al., 2014). The results of our analysis show magma fluxes compatible with those expected for super eruptions while the estimated volume is even lower than the volume of erupted magma (see Figure 4 of Caricchi et al., 2014). Estimates of magma flux are less affected by this process because of the topology of the contours we obtained by computing the synthetic populations of zircon ages by thermal modeling.
Concluding Remarks
• We provide a model approach to use age distributions from high-precision 206Pb/238U dates for estimating volumes and fluxes of the magmatic system the zircons crystallized in. The dates must offer sufficient precision to resolve the duration of magmatic processes, otherwise applying our method will lead to statistical artifacts confounding analytical precision with age dispersion.
• The mobility of zircons within magmatic systems is essential for our method to provide information on the thermal evolution of magmatic systems. The existence of zircon crystals that crystallized over several hundred thousands of years in one hand-sample evidences that physical processes mingle zircon populations therefore increasing the probability of sampling zircon-age populations on a statistically representative basis.
• The computed volumes and fluxes represent the magma portion from which zircon crystallized, e.g., a magma storage area in the middle or lower crust, and do not necessarily represent the volume and flux of the shallower and potentially exposed part of a magmatic system.
• Estimating the intrusive fluxes and the final volume of the magmatic system associated with much smaller-volume, upper crustal mineralized intrusions will therefore yield quantitative information on the relationship between magma fluxes and volumes and total metal endowment of magmatic ore deposits (Chelle-Michou et al., 2015).
• Volume and flux estimates from volcanic rocks can be useful to estimate intrusive-extrusive ratios, but caution should be used when evidence for extensive zircon resorption exist.
• It is essential that multiple populations of zircons, which did not crystallize continuously within the same magmatic system, are not analyzed at the same time. The result would be an overestimate of the volume of the magmatic system, resulting from an increase of the values of the standard deviation (Figure 6).
The thermal modeling and statistical analysis performed in this contribution, shows that population of zircon ages reflect the thermal evolution of crustal magmatic intrusions. Because the temporal evolution of temperature in magmatic systems strongly depend on the rate at which enthalpy (i.e., magma) is supplied to the magma reservoirs and on its volume, population of zircon ages offer an opportunity to quantify magma fluxes in the Earth's crust.
Author Contributions
LC conceived the study, lead the research, and the writing of the manuscript. GS performed the numerical modeling and analyzed the data. All authors contributed to the development of the study and the writing of the manuscript.
Funding
This project has received support from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement No 677493 FEVER) and the Swiss National Science Foundation.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Annen, C. (2009). From plutons to magma chambers: thermal constraints on the accumulation of eruptible silicic magma in the upper crust. Earth Planet. Sci. Lett. 284, 409–416. doi: 10.1016/j.epsl.2009.05.006
Annen, C., Blundy, J. D., and Sparks, R. (2006). The genesis of intermediate and silicic magmas in deep crustal hot zones. J. Petrol. 47, 505–539. doi: 10.1093/petrology/egi084
Bachmann, O., and Bergantz, G. W. (2003). Rejuvenation of the fish canyon magma body: a window into the evolution of large-volume silicic magma systems. Geology 31, 789–792. doi: 10.1130/G19764.1
Bacon, C. R., and Lanphere, M. A. (2006). Eruptive history and geochronology of mount mazama and the Crater Lake region, Oregon. Geol. Soc. Am. Bull. 118, 1331–1359. doi: 10.1130/B25906.1
Barboni, M., Annen, C., and Schoene, B. (2015). Evaluating the construction and evolution of upper crustal magma reservoirs with coupled U/Pb zircon geochronology and thermal modeling: a case study from the Mt. Capanne pluton (Elba, Italy). Earth Planet. Sci. Lett. 432, 436–448. doi: 10.1016/j.epsl.2015.09.043
Barboni, M., and Schoene, B. (2014). Short eruption window revealed by absolute crystal growth rates in a granitic magma. Nat. Geosci. 7, 524–528. doi: 10.1038/ngeo2185
Bindeman, I. N., and Simakin, A. G. (2014). Rhyolites—hard to produce, but easy to recycle and sequester: Integrating microgeochemical observations and numerical models. Geosphere 10, 1–27. doi: 10.1130/GES00969.1
Boehnke, P., Watson, E. B., Trail, D., Harrison, T. M., and Schmitt, A. K. (2013). Zircon saturation re-revisited. Chem. Geol. 351, 324–334. doi: 10.1016/j.chemgeo.2013.05.028
Bouilhol, P., Connolly, J. A. D., and Burg, J. P. (2011). Geological evidence and modeling of melt migration by porosity waves in the sub-arc mantle of Kohistan (Pakistan). Geology 39, 1091–1094. doi: 10.1130/G32219.1
Broderick, C., Wotzlaw, J. F., Frick, D. A., Gerdes, A., Ulianov, A., Gunther, D., et al. (2015). Linking the thermal evolution and emplacement history of an upper-crustal pluton to its lower-crustal roots using zircon geochronology and geochemistry (southern Adamello batholith, N. Italy). Contrib. Mineral. Petrol. 170:28. doi: 10.1007/s00410-015-1184-x
Caricchi, L., and Blundy, J. (eds.). (2015a). “Experimental petrology of monotonous intermediate magmas,” in Chemical, Physical and Temporal Evolution of Magmatic Systems, (London: Geological Society), 105–130.
Caricchi, L., and Blundy, J. (eds.). (2015b). “The temporal evolution of chemical and physical properties of magmatic systems,” in Chemical, Physical and Temporal Evolution of Magmatic Systems, (London: Geological Society), 1–15.
Caricchi, L., Simpson, G., and Schaltegger, U. (2014). Zircons reveal magma fluxes in the Earth's crust. Nature 511, 457–461. doi: 10.1038/nature13532
Chelle-Michou, C., Chiaradia, M., and Béguelin, P. (2015). Petrological evolution of the magmatic suite associated with the coroccohuayco Cu (–Au–Fe) porphyry–skarn deposit, Peru. J. Petrol. 56, 1829–1862. doi: 10.1093/petrology/egv056
Coleman, D. S., Gray, W., and Glazner, A. F. (2004). Rethinking the emplacement and evolution of zoned plutons: geochronologic evidence for incremental assembly of the Tuolumne Intrusive Suite, California. Geology 32, 433. doi: 10.1130/g20220.1
Condon, D. J., Schoene, B., McLean, N. M., Bowring, S. A., and Parrish, R. R. (2015). Metrology and traceability of U-Pb isotope dilution geochronology (EARTHTIME Tracer Calibration Part I). Geochim. Cosmochim. Acta 164, 464–480. doi: 10.1016/j.gca.2015.05.026
Connolly, J. A. D., Schmidt, M. W., Solferino, G., and Bagdassarov, N. (2009). Permeability of asthenospheric mantle and melt extraction rates at mid-ocean ridges. Nature 462, 209–212. doi: 10.1038/nature08517
Cooper, G. F., and Wilson, C. J. N. (2014). Development, mobilisation and eruption of a large crystal-rich rhyolite: the ongatiti ignimbrite, New Zealand. Lithos 198, 38–57. doi: 10.1016/j.lithos.2014.03.014
Crisp, J. A. (1984). Rates of magma emplacement and volcanic output. J. Volcanol. Geother. Res. 20, 177–211. doi: 10.1016/0377-0273(84)90039-8
de Saint-Blanquat, M., Horsman, E., Habert, G., Morgan, S., Vanderhaeghe, O., Law, R., et al. (2011). Multiscale magmatic cyclicity, duration of pluton construction, and the paradoxical relationship between tectonism and plutonism in continental arcs. Tectonophysics 500, 20–33. doi: 10.1016/j.tecto.2009.12.009
de Saint-Blanquat, M., Law, R. D., Bouchez, J. L., and Morgan, S. S. (2001). Internal structure and emplacement of the papoose flat pluton: an integrated structural, petrographic, and magnetic susceptibility study. Geol. Soc. Am. Bull. 113, 976–995. doi: 10.1130/0016-7606(2001)113%3C0976:ISAEOT%3E2.0.CO;2
Farina, F., Dini, A., Innocenti, F., Rocchi, S., and Westerman, D. S. (2010). Rapid incremental assembly of the Monte Capanne pluton (Elba Island, Tuscany) by downward stacking of magma sheets. Geol. Soc. Am. Bull. 122, 1463–1479. doi: 10.1130/B30112.1
Glazner, A. F. (2007). Thermal limitations on incorporation of wall rock into magma. Geology 35, 319–322. doi: 10.1130/G23134A.1
Glazner, A. F., Bartley, J. M., Coleman, D. S., Gray, W., and Taylor, R. Z. (2004). Are plutons assembled over millions of years by amalgamation from small magma chambers? GSA Today 14, 4–11. doi: 10.1130/1052-5173(2004)014%3C0004:APAOMO%3E2.0.CO;2
Gudmundsson, A. (2012). Magma chambers: formation, local stresses, excess pressures, and compartments. J. Volcanol. Geother. Res. 237–238. 19–41. doi: 10.1016/j.jvolgeores.2012.05.015
Hanchar, J. M., and Watson, E. B. (2003). Zircon saturation thermometry. Rev. Mineral. Geochemist. 53, 89–112. doi: 10.2113/0530089
Havlin, C., Parmentier, E. M., and Hirth, G. (2013). Dike propagation driven by melt accumulation at the lithosphere-asthenosphere boundary. Earth Planet. Sci. Lett. 376, 20–28. doi: 10.1016/j.epsl.2013.06.010
Hildreth, W. (1981). Gradients in silicic magma chambers: implications for lithospheric magmatism. J. Geophys. Res. 86, 10153–10192. doi: 10.1029/JB086iB11p10153
Hildreth, W., and Moorbath, S. (1988). Crustal contributions to arc magmatism in the Andes of central Chile. Contrib. Mineral. Petrol. 98, 455–489. doi: 10.1007/BF00372365
Jagoutz, O. (2014). Arc crustal differentiation mechanisms. Earth Planet. Sci. Lett. 396, 267–277. doi: 10.1016/j.epsl.2014.03.060
Johannes, W., and Holtz, F. (1996). Petrogenesis and Experimental Petrology of Granitic Rocks. Heidelberg: Springer.
Leuthold, J., Müntener, O., Baumgartner, L. P., Putlitz, B., Ovtcharova, M., and Schaltegger, U. (2012). Time resolved construction of a bimodal laccolith (Torres del Paine, Patagonia). Earth Planet. Sci. Lett. 325–326, 85–92. doi: 10.1016/j.epsl.2012.01.032
Lipman, P. W., and Bachmann, O. (2015). Connecting ignimbrite to batholith in the Southern Rocky Mountains: Integrated perspectives from geological, geophysical, and geochronological data. Geosphere 11, 705–743. doi: 10.1130/GES01091.1
Lipman, P. W. (2007). Incremental assembly and prolonged consolidation of Cordilleran magma chambers: evidence from the Southern Rocky Mountain volcanic field. Geosphere 3, 42. doi: 10.1130/GES00061.1
Marsh, B. D. (1981). On the crystallinity, probability of occurrence, and rheology of lava and magma. Contrib. Mineral. Petrol. 78, 85–98.
Melekhova, E., Annen, C., and Blundy, J. (2013). Compositional gaps in igneous rock suites controlled by magma system heat and water content. Nat. Geosci. 6, 1–5. doi: 10.1038/ngeo1781
Miller, C. F., McDowell, S. M., and Mapes, R. W. (2003). Hot and cold granites? Implications of zircon saturation temperatures and preservation of inheritance. Geology 31, 529–532. doi: 10.1130/0091-7613(2003)031<0529:HACGIO>2.0.CO;2
Muir, D. D., Barfod, D. N., Blundy, J. D., Rust, A. C., Sparks, R. S. J., and Clarke, K. M. (2015). “The temporal record of magmatism at Cerro Uturuncu, Bolivian Altiplano,” in Chemical, Physical and Temporal Evolution of Magmatic Systems, eds. L. Caricchi and J. D. Blundy (Geological Society of London), 57–84.
Nandedkar, R. H., Ulmer, P., and Müntener, O. (2014). Fractional crystallization of primitive, hydrous arc magmas: an experimental study at 0.7 GPa. Contrib. Mineral. Petrol. 167, 1015. doi: 10.1007/s00410-014-1015-5
Paterson, S. R., Okaya, D., Memeti, V., Economos, R., and Miller, R. B. (2011). Magma addition and flux calculations of incrementally constructed magma chambers in continental margin arcs: combined field, geochronologic, and thermal modeling studies. Geosphere 7, 1439–1468. doi: 10.1130/GES00696.1
Paulatto, M., Annen, C., Henstock, T. J. Kiddle, E., Minshull, T. A., Voight, R. S. J., et al. (2012). Magma chamber properties from integrated seismic tomography and thermal modeling at Montserrat. Geochem. Geophys. Geosyst. 13, Q01014. doi: 10.1029/2011gc003892
Piwinskii, A. J., and Wyllie, P. J. (1968). Experimental studies of igneous rock series—a zoned pluton in Wallowa batholith Oregon. J. Geol. 76, 205–234. doi: 10.1086/627323
Rocchi, S., Westerman, D. S., Dini, A., and Farina, F. (2010). Intrusive sheets and sheeted intrusions at Elba Island, Italy. Geosphere 6, 225–236. doi: 10.1130/GES00551.1
Salisbury, M. J., Jicha, B. R., de Silva, S. L., Singer, B. S., Jiménez, N. C., and Ort, M. H. (2011). 40Ar/39Ar chronostratigraphy of Altiplano-Puna volcanic complex ignimbrites reveals the development of a major magmatic province. Geol. Soc. Am. Bull. 123, 821–840. doi: 10.1130/B30280.1
Samperton, K. M., Schoene, B., Cottle, J. M., Keller, C. B., Crowley, J. L., and Schmitz, M. D. (2015). Magma emplacement, differentiation and cooling in the middle crust: integrated zircon geochronological-geochemical constraints from the Bergell Intrusion, Central Alps. Chem. Geol. 417, 322–340. doi: 10.1016/j.chemgeo.2015.10.024
Schaltegger, U., Brack, P., Ovtcharova, M., Peytcheva, I., Schoene, B., Stracke, A., et al. (2009). Zircon and titanite recording 1.5 million years of magma accretion, crystallization and initial cooling in a composite pluton (southern Adamello batholith, northern Italy). Earth Planet. Sci. Lett. 286, 208–218. doi: 10.1016/j.epsl.2009.06.028
Schaltegger, U., Schmitt, A. K., and Horstwood, M. S. A. (2015). U-Th-Pb zircon geochronology by ID-TIMS, SIMS, and laser ablation ICP-MS: recipes, interpretations, and opportunities. Chem. Geol. 402, 89–110. doi: 10.1016/j.chemgeo.2015.02.028
Schoene, B., Schaltegger, U., Brack, P., Latkoczy, C., Stracke, A., and Gunther, D. (2012). Rates of magma differentiation and emplacement in a ballooning pluton recorded by U–Pb TIMS-TEA, Adamello batholith, Italy. Earth Planet. Sci. Lett. 355–356, 162–173. doi: 10.1016/j.epsl.2012.08.019
Solano, J. M. S., Jackson, M. D., Sparks, R. S. J., and Blundy, J. (2014). Evolution of major and trace element composition during melt migration through crystalline mush: implications for chemical differentiation in the crust. Am. J. Sci. 314, 895–939. doi: 10.2475/05.2014.01
Solano, J. M. S., Jackson, M. D., Sparks, R. S. J., Blundy, J. D., and Annen, C. (2012). Melt segregation in deep crustal hot zones: a mechanism for chemical differentiation, crustal assimilation and the formation of evolved magmas. J. Petrol. 53, 1999–2026. doi: 10.1093/petrology/egs041
Spera, F. J., and Bohrson, W. A. (2001). Energy-constrained open-system magmatic processes I: General model and energy-constrained assimilation and fractional crystallization (EC-AFC) formulation. J. Petrol. 42, 999–1018. doi: 10.1093/petrology/42.5.999
Steinberger, I., Hinks, D., Driesner, T., and Heinrich, C. A. (2013). Source plutons driving porphyry copper ore formation: combining geomagnetic data, thermal constraints, and chemical mass balance to quantify the magma chamber beneath the bingham canyon deposit. Econ. Geol. 108, 605–624. doi: 10.2113/econgeo.108.4.605
Stolper, E., and Asimow, P. (2007). Insights into mantle melting from graphical analysis of one-component systems. Am. J. Sci. 307, 1051–1139. doi: 10.2475/08.2007.01
White, S. M., Crisp, J. A., and Spera, F. J. (2006). Long-term volumetric eruption rates and magma budgets. Geochem. Geophys. Geosyst. 7, Q03010. doi: 10.1029/2005GC001002
Wotzlaw, J.-F., Bindeman, I. N., Stern, R. A., D'Abzac, F.-X., and Schaltegger, U. (2015). Rapid heterogeneous assembly of multiple magma reservoirs prior to Yellowstone supereruptions. Sci. Rep. 5:14026. doi: 10.1038/srep14026
Wotzlaw, J.-F., Schaltegger, U., Frick, D. A., Dungan, M. A., Gerdes, A., and Günther, D. (2013). Tracking the evolution of large-volume silicic magma reservoirs from assembly to supereruption. Geology 41, 867–870. doi: 10.1130/G34366.1
Keywords: zircon geochronology, magma fluxes, intrusive-extrusive ratio, distribution of mineral resources, frequency and magnitude of volcanic eruptions
Citation: Caricchi L, Simpson G and Schaltegger U (2016) Estimates of Volume and Magma Input in Crustal Magmatic Systems from Zircon Geochronology: The Effect of Modeling Assumptions and System Variables. Front. Earth Sci. 4:48. doi: 10.3389/feart.2016.00048
Received: 15 February 2016; Accepted: 08 April 2016;
Published: 27 April 2016.
Edited by:
Rosa Anna Corsaro, Istituto Nazionale di Geofisica e Vulcanologia, ItalyReviewed by:
Georg Florian Zellmer, Massey University, New ZealandMaurizio Petrelli, University of Perugia, Italy, Italy
Copyright © 2016 Caricchi, Simpson and Schaltegger. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Luca Caricchi, bHVjYS5jYXJpY2NoaUB1bmlnZS5jaA==
 Luca Caricchi
Luca Caricchi Guy Simpson
Guy Simpson Urs Schaltegger
Urs Schaltegger