- 1Dipartimento DiSTeM, Università di Palermo, Palermo, Italy
- 2Istituto Nazionale di Geofisica e Vulcanologia, Palermo, Italy
- 3Fusion and Technology for Nuclear Safety and Security Department, ENEA, Frascati, Italy
- 4ENEA Guest, Frascati, Italy
- 5Department of Industrial Engineering, University of Rome “Tor Vergata”, Rome, Italy
- 6Vitrociset SpA, Roma, Italy
We report here on the results of a proof-of-concept study aimed at remotely sensing the volcanic CO2 flux using a Differential Adsorption lidar (DIAL-lidar). The observations we report on were conducted in June 2014 on Stromboli volcano, where our lidar (LIght Detection And Ranging) was used to scan the volcanic plume at ~3 km distance from the summit vents. The obtained results prove that a remotely operating lidar can resolve a volcanic CO2 signal of a few tens of ppm (in excess to background air) over km-long optical paths. We combine these results with independent estimates of plume transport speed (from processing of UV Camera images) to derive volcanic CO2 flux time-series of ≈16–33 min temporal resolution. Our lidar-based CO2 fluxes range from 1.8 ± 0.5 to 32.1 ± 8.0 kg/s, and constrain the daily averaged CO2 emissions from Stromboli at 8.3 ± 2.1 to 18.1 ± 4.5 kg/s (or 718–1565 tons/day). These inferred fluxes fall within the range of earlier observations at Stromboli. They also agree well with contemporaneous CO2 flux determinations (8.4–20.1 kg/s) obtained using a standard approach that combines Multi-GAS-based in-plume readings of the CO2/SO2 ratio (≈8) with UV-camera sensed SO2 fluxes (1.5–3.4 kg/s). We conclude that DIAL-lidars offer new prospects for safer (remote) instrumental observations of the volcanic CO2 flux.
Introduction
A major step forward in ground-based volcano monitoring has recently arisen from the advent of modern instrumental techniques and networks for volcanic gas observations (Galle et al., 2010; Oppenheimer et al., 2014; Saccorotti et al., 2014; Fischer and Chiodini, 2015). Such technical advances provide improved temporal resolution relative to traditional direct sampling techniques (Symonds et al., 1994; Giggenbach, 1996). As longer-term volcanic gas records increase in number and quality, full empirical evidence is finally emerging for increased CO2 flux emissions prior to eruption of mafic to intermediate volcanoes (Aiuppa, 2015). Precursory plume CO2 flux increases have been now detected at several volcanoes, including Etna (Aiuppa et al., 2008; Patanè et al., 2013), Kilauea (Poland et al., 2012), Redoubt (Werner et al., 2013), Turrialba (de Moor et al., 2016a), and Poas (de Moor et al., 2016b).
At Stromboli (in Italy), however, CO2 flux observations have been particularly valuable for interpreting, and eventually predicting, the volcano's behavior (Aiuppa et al., 2010a, 2011). On Stromboli, the “regular” mild strombolian activity is occasionally interrupted by larger-scale vulcanian-style explosions, locally referred as “major explosions” or (in the most extreme events) “paroxysms” (Rosi et al., 2006, 2013; Andronico and Pistolesi, 2010; Pistolesi et al., 2011; Pioli et al., 2014). These explosions, although short-lived (tens of seconds to a few minutes), represent a real hazard for local populations, tourists and volcanologists, since they produce fallout of coarse pyroclastic materials over wide dispersal areas (Rosi et al., 2013). In addition, such events are not anticipated by any detectable anomaly in the geophysical or volcanological record, perhaps because they originate deep in the crustal roots of the volcano's' plumbing system (Bertagnini et al., 2003; Métrich et al., 2005, 2010; Allard, 2010). Observational evidence suggests, however, that “major explosions” (Aiuppa et al., 2011) and “paroxysms” (Aiuppa et al., 2010a) are both systematically preceded by days/weeks of anomalous CO2-rich gas leakage from Stromboli's deep (8–10 km) magma storage zone (Aiuppa et al., 2010b). CO2 flux emissions from the open-vent crater plume have become, therefore, a unique monitoring tool for volcanic hazard assessment and mitigation on the volcano.
On Stromboli, as at other volcanoes, the volcanic gas CO2 flux is calculated from a combination of co-measured SO2 fluxes and plume CO2/SO2 ratios (Burton et al., 2013; Aiuppa, 2015). While the SO2 flux can remotely be sensed by UV spectroscopy (Oppenheimer, 2010; Oppenheimer et al., 2011), measuring the CO2/SO2 ratio requires in-situ direct sampling and/or measurements via Multi-GAS (Aiuppa et al., 2010a) or Fourier Transform Infra-Red Spectrometry (La Spina et al., 2013) in the vicinity of hazardous active vents. As such, implementation of novel techniques for the remote observation of the volcanic CO2 flux, from more distal (and safer) locations, remains highly desirable.
New prospects for ground-based remote detection of the volcanic CO2 flux have recently become available from the advent of a new lidar (Light Detection and Ranging) using the DIAL (Differential Absorption lidar) technique (Aiuppa et al., 2015; Fiorani et al., 2015, 2016). DIAL-lidars (Weitkamp, 2005; Fiorani, 2007) use backscattering of artificial light (laser) from atmospheric back-scatterers and/or from the volcanic plume itself, and are therefore potentially ideal for remote volcanic CO2 detection (Fiorani et al., 2013; Queißer et al., 2015, 2016). In previous work, we demonstrated the ability of our lidar to remotely resolve the volcanic CO2 flux from a relatively proximal measuring site (<200 m from the source vents) (Aiuppa et al., 2015). Here, we extend this work by reporting on a successful CO2 flux detection at Stromboli over a far longer optical path (~3 km distance from the vents). Results of this proof-of-concept experiment confirm lidars as promising tools for remote monitoring of the volcanic CO2 flux (Aiuppa et al., 2015; Queißer et al., 2016).
Materials and Methods
The Bridge Lidar
Our measurements on Stromboli (Figure 1) were obtained using the same DIAL-lidar described in Aiuppa et al. (2015) and Fiorani et al. (2015, 2016), and realized within the context of the FP7-ERC project Bridge (www.bridge.unipa.it). Only key information is reported here, and the reader is referred to previous studies for a detailed description of the instrument. In brief, the Bridge lidar (Figure 1D) uses a complex transmitter that integrates (i) an injection seeded Nd:YAG laser with (ii) a double grating dye laser. This transmitter is used to generate laser radiation at ~2010 nm, a region of the electromagnetic spectrum absorbed by atmospheric CO2, while showing minimal cross-sensitivity to H2O (Fiorani et al., 2013). At the ON and OFF wavelengths selected for this experiment, the differential cross section of CO2 is five orders of magnitude larger than that of H2O (Rothman et al., 2013). Considering a CO2 mixing ratio of 400 ppm, and with the upper and lower ranges of H2O mixing ratios used in atmospheric models (Berk et al., 2014), i.e., from 2.59% (tropics, sea level) to 0.141% (high latitude, winter, sea level), the respective CO2 absorption is 3 and 5 orders of magnitude larger than that of H2O. The 2.59% H2O mixing ratio is not far from the saturated water vapor pressure at standard atmospheric conditions. We conclude that, even in a condensing volcanic plume, H2O absorption is negligible compared to that of CO2.
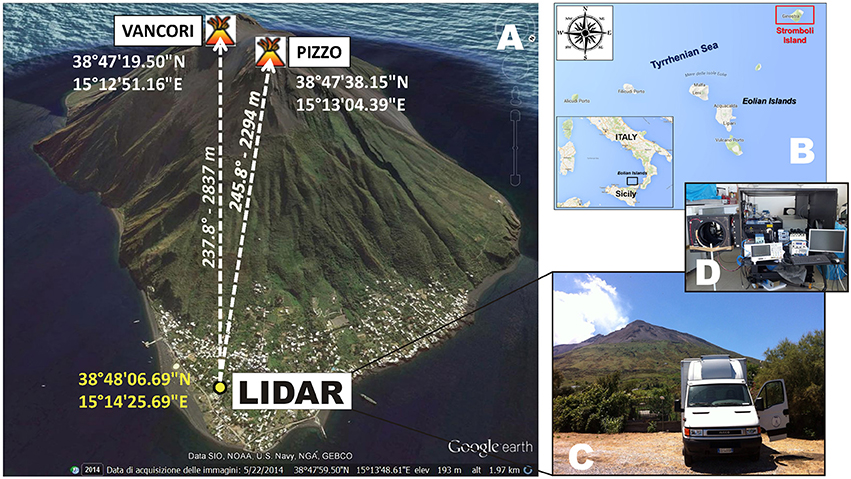
Figure 1. (A) Google Earth map of Stromboli volcano, showing positions of the measurement site (“LIDAR”) and of the Vancori and Pizzo peaks, see text; (B) Positioning of Stromboli relative to the mainland and the Aeolian archipelago; (C) the laboratory truck with the volcano summit in the background; (D) interior or the laboratory track.
A piezo-electric element is used to sequentially switch the wavelength of the transferred laser beam, from λON (2009.537 mm: maximum CO2 absorption) to λOFF (2008.484 nm: no CO2 absorption), at 10 Hz repetition rate. These closely spaced pairs of laser beams are sequentially transmitted into the atmosphere, where they are eventually scattered back by atmospheric back-scatterers (aerosols, water droplets, particles) in either the volcanic plume or the background atmosphere. During their atmospheric propagation, the laser beams are also reflected by any obstacle encountered along the optical path, e.g., in our specific case, the Pizzo and Vancori walls/rims in front of or behind the volcanic plume (see Figures 1, 2). The returned signal is captured by the lidar receiver (a Newtonian telescope, diameter: 310 mm), and then detected and amplified by an InGaAs PIN photodiode module, directly connected with the analog-to-digital converter (ADC).

Figure 2. Maps illustrating geometries of (A) Pizzo scans and (B) Vancori scans. In the horizontal Pizzo scan in (A), the Field Of View (FOV) of the lidar was sequentially rotated (at constant elevation) at heading angles ranging from 227° to 317° (the Pizzo morphological peak was intercepted at ~245.8°). In (B), the heading angle was kept constant at 237.8°, while the plume was vertically profiled at elevations of 16 to 21°. (C,D) are pseudo-color images, from processing of UV camera data, showing distribution of SO2 column amounts (in ppm m, see scale). The locations of Pizzo and Vancori are indicated in (C). During June 24–25, the UV camera images (see example in C) identified the plume as a nearly vertically rising band of peak SO2 column amount, north of the Pizzo area; on June 26–29, the plume was instead transported south-southeast of Pizzo by the prevailing north-northwesterly winds (see image D).
Field Operations
During our experiment, the DIAL-lidar operated from a small laboratory truck (Figure 1C), positioned in a fixed position at the base of the volcano in the Scari area, ~2–2.5 km from the degassing vents on the volcano's summit (Figures 1, 2). The lidar operated during June 24–29, 2015, including an initial instrumental setup phase. Stable weather conditions (temperature, 22–26 °C; no rainfall) persisted during the entire measurement window.
During operations, two large motorized elliptical mirrors (major axis: 450 mm) simultaneously aimed the laser beams and the telescope, allowing the laser beam of the lidar to scan the volcanic plume either horizontally (Figure 2A) or vertically (Figure 2B). In particular, during June 24–25, the volcanic plume was mainly dispersed northwards by gentle southerly winds. From our Scari observation point (Figure 2), the plume was seen to rise nearly vertically north of the Pizzo area (Figure 2C). The Line Of Sight (LOS) of the lidar was therefore pointed north of Pizzo and the horizontal scan mode was preferred (heading angles: 227–317°; Figure 2A). Vertical scans above the Pizzo area were also performed. For simplicity, we refer below to these June 24–25 measurements as the Pizzo scans (Figure 2A).
On June 26–29, the plume was instead transported south-southeast by the prevailing north-northwesterly winds (Figure 2D). Vertical scans were therefore preferred that were operated at constant heading angle (237.8°) and at elevation angles from 16 to 21° (Figure 2B). In such conditions, the Pizzo and Vancori peaks were intercepted at elevation angles of 16.98° and 17.78°, respectively, and the volcanic plume was in all cases encountered in the 2300–2700 m range. We hereafter refer to these scans as the Vancori scans (Figure 2B).
During each profile, 100 lidar returns, 50 at λON, 50 at λOFF, and interlaced (OFF after ON, OFF again and so on), were emitted at a 10 Hz rate, then co-added and averaged to increase the signal-to-noise ratio, reducing the signal sampling frequency to 0.1 Hz (temporal resolution of 10 s). The spatial resolution was about 5 m (corresponding to the rise time of the detector module due to its bandwidth). Plume scans, both horizontal and vertical, were retrieved combining about 50 profiles in <10 min. Typically, 10 scans at different elevations were repeated, obtaining a three-dimensional tomography of the volcanic plume.
A cell filled with standard CO2 gas was periodically used during operations, for check of wavelength accuracy, repeatability and stability. In brief, our calibration procedure involved measuring-by photoacoustic spectroscopy—the absorption of the CO2 gas cell as a function of wavelength. This calibration, limited to a small interval near the predicted λON, allowed identifying the wavelength at which cell absorption is maximum. The laser system was finally forced to transmit at this radiation. The CO2 absorption cross-section used in our calculations was based on HITRAN data (Rothman et al., 2013).
UV Camera
Concurrently with our lidar observations, a dual-UV camera system (Kantzas et al., 2010; Tamburello et al., 2012; Burton et al., 2014) was used to monitor the temporal variations of the SO2 flux and plume transport speed. A fully autonomous system, similar to that used in other recent work (D'Aleo et al., 2016), was mounted on the roof of the laboratory truck and operated every day from 6 am to 4 pm (Local Time). The UV camera system acquired sequential images of the plume at ~0.5 Hz using two JAI CM 140 GR cameras. Both cameras had 10-bit digitization and 1392 × 1040 pixels, using an Uka Optics UV lens with a ~37° field of view. Distinct band-pass filters, centerd at either 310 nm (where SO2 absorbs) or 330 nm (no SO2 absorption), were mounted on the back on the lenses of the two cameras. Each set of co-acquired images from the two UV cameras was processed using the methodology of Kantzas et al. (2010) and integrated into the Vulcamera software (Tamburello et al., 2011, 2012), to calculate an absorbance for each camera pixel. Absorbance was converted into an SO2 column amount from readings of a co-exposed Ocean optics USB2000+ UV Spectrometer, as outlined in Lübcke et al. (2013). Cameras and spectrometer were both controlled by a mini-pc Jetway. To calculate SO2 flux time-series, we used Vulcamera to derive temporal records of SO2 integrated column amounts (ICAs) along a plume cross-section, perpendicular to the plume transport direction. The obtained ICA time-series were then combined with high-temporal resolution (~1 Hz) records of plume transport speed. This latter was derived using an Optical Flow sub-routine using the Lukas/Kanade algorithm (Bruhn et al., 2005; Peters et al., 2015), integrated in Vulcamera. In our specific case, the Lucas-Kanade method was used to track movements of gas fronts (e.g., gas-rich and/or ash-free portions of the plume, having well distinct absorbance features) in consecutive UV camera frames, which allowed us quantifying plume transport speed at 0.5 Hz. We tested performance of this method by using artificial images with known particle velocities, and obtained errors in estimated velocities of <5%. Table 1 lists daily means (±1 SD: standard deviation) of both SO2 fluxes and plume transport speed (Vp) during our observational period.
Results
Characteristics of the DIAL-Lidar Signal
According to lidar theory (Fiorani, 2007), the optical power returned to the lidar receiver at any time t is produced by back-scattering of the laser beam by an atmospheric layer at distance R (range) from the source, where R = ct/2 and c is the speed of light. As such, the lidar offers range-resolved information on atmospheric structure and properties (aerosols, particles and gas molecules) along the laser beam, in the form of an intensity (I) vs. range plot (Figure 3).
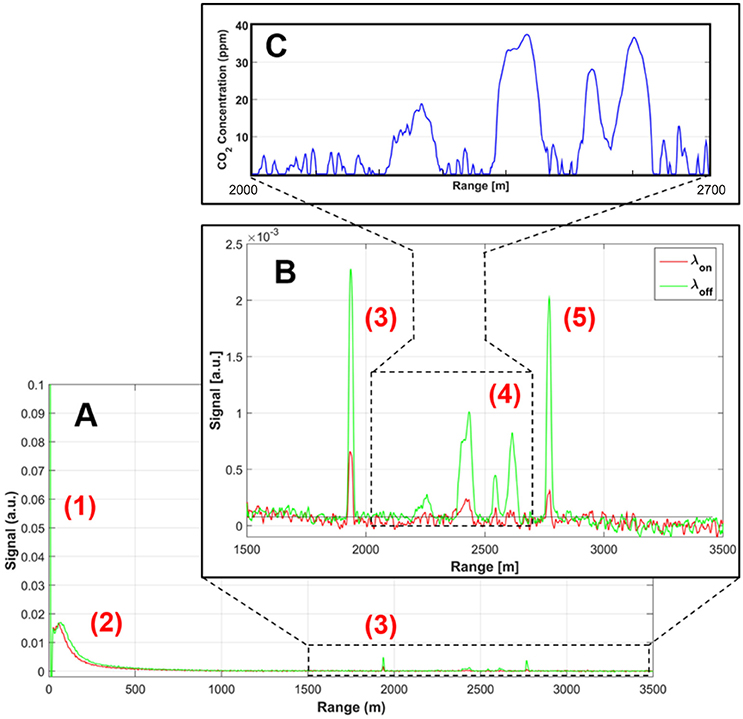
Figure 3. (A) Example of a lidar-based atmospheric profile, obtained at Stromboli during a typical Vancori scan, in the form of a range (distance) vs. signal intensity (arbitrary units, a.u.) plot. Peak (1) yields the pulse transmission zero-time (scattering, inside the laboratory truck, of some photons of the transmitted laser pulse); peak (2) is the returned signal from atmospheric back-scatterers along the laser optical path; peak (3) is the returned signal produced by reflection of the lidar beam by southeastern margin of the Pizzo morphological peak. (B) is a detail of (A), for ranges between 1500 and 3500 m. In this panel, peak (3) is as in (A); the series of peaks observed in the range interval 2300–2700 m (4) are due to back-scattering of the laser beam from the volcanic plume; peak (5) is produced by reflection of the laser beam by the Vancori peak; (C) a profile of in-plume excess CO2 concentrations, in the 2000–2700 m range interval, calculated from processing of the lidar signal in (B). See text for the procedure used.
Upon its atmospheric propagation, the beam intensity decreases approximately (a) exponentially, due to atmospheric extinction, according to the Lambert-Beer law; and (b) as 1/R2, because the solid angle subtended by the receiver is A/R2, where A is the telescope's effective area. The two processes are superimposed. As such, in order to better observe the atmospheric back-scattering, a “range corrected signal, S” is commonly used, being given by: S = ln(I R2) (see below). Since the system works in DIAL mode, each intensity profile is in fact acquired at two distinct wavelengths, λON–absorbed by CO2–and λOFF–not absorbed by CO2 (Figure 3). The two wavelengths are so close that atmospheric behavior, except from CO2 absorption, is practically identical. The measured intensity contrast between the co-emitted λON and λOFF signals allow range-resolved CO2 concentrations in the volcanic plume to be obtained.
An example of a lidar-based atmospheric profile, obtained at Stromboli during a typical Vancori scan, is illustrated in Figure 3. As described above, the lidar registered one such profile every 10 s, since 100 lidar returns acquired at 10 Hz were co-added and averaged to increase the signal-to-noise ratio. Each of the atmospheric profiles (e.g., Figure 3) acquired during the Vancori scan contains the following characteristic features:
1) at R ~0, a first strong intensity peak is recorded for both λON and λOFF (Figure 3A); this peak, which we refer to as I0, ON and I0, OFF, is due to scattering inside the laboratory truck of some photons of the transmitted laser pulse. This peak yields the pulse transmission zero-time, and its intensity is proportional to the transmitted energy (used for signal normalization),
2) for R between 0 and ~500 m, a weak signal is observed that is returned from atmospheric back-scatterers encountered by the laser beam along the optical path (Figure 3A); this signal, as explained before, attenuates with distance and vanishes at R ~500 m,
3) a IP, ON and IP, OFF peak at R ~1900 m (Figures 3A,B); this is produced by reflection of the lidar beam by the southeastern margin of the Pizzo morphological peak (see Figure 2),
4) a series of weak but resolvable peaks observed in the range interval 2300–2700 m (Figure 3B); in these peaks, the λON signal appears strongly attenuated relative to the co-acquired λOFF signal, a fact due to laser absorption by CO2 molecules in the volcanic plume,
5) a IV, ON and IV, OFF peak at R ~2800 m, which is produced by reflection of the laser beam by the Vancori peak (Figure 3B).
Atmospheric profiles obtained during the Pizzo scans of June 24–25 share similar characteristics, except that the Pizzo morphological peak is intercepted by the lidar beam at R ~2300 m, and the plume is encountered either before or after the Pizzo (Figure 4). The Vancori peak was obviously not encountered.
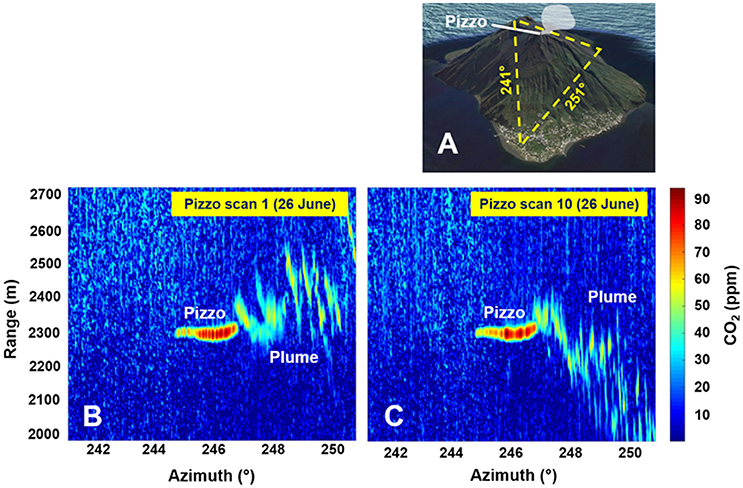
Figure 4. Example of two CO2 concentration maps (B,C) obtained during a Pizzo horizontal scan on June 26. Geometry of the scans and location of the plume are schematically shown in (A). The maps show the distribution of CO2 concentrations in the lidar's Field Of View (FOV), as a function of heading angle and range. Each map was obtained by interpolation of all CO2 concentration profiles (e.g., same as 3A), obtained during a given Pizzo scan. In the maps, the red colored horizontal bands identify the margin of the Pizzo peak (heading angle: 244–245°), while the volcanic plume is the band of peak CO2 concentration (up to 60 ppm) areas at heading angles of 245–250°.
Data Processing and Calculation of CO2 Concentrations
We processed each acquired atmospheric profile using a Matlab analysis routine, with the aim of calculating the CO2 concentrations in the atmospheric background and in the volcanic plume. The data processing routine consists of the following steps, all based on the Lambert-Beer law relation:
a) Initially, the CO2 concentration in the natural background atmosphere, C0, is calculated as:
where IP, ON (IP, OFF) stands for intensity of the ON (OFF) lidar signal [(3) in Figure 3A] caused by reflection of the laser beam off the surface of the Pizzo wall (RP = 2294 m); I0, ON (I0, OFF) is the intensity of the ON (OFF) lidar peak caused by laboratory scattering of the laser pulse [(1) in Figure 3A]; and Δσ is the CO2 differential absorption cross-section.
b) Secondly, ΔC, the average excess CO2 concentration in the volcanic plume cross-section between Pizzo and Vancori [(3,5) in Figure 3B], is derived from:
Where IV, ON (IV, OFF) is the peak intensity of the ON (OFF) lidar signal caused by reflection of the laser beam off the surface of the Vancori rock wall (at RV = 2837 m).
c) Thirdly, CCO2, i, the excess CO2 concentration corresponding to each i-th ADC channel of the lidar profile (Figure 3C) is calculated from:
where ΔR is the range interval corresponding to each ADC channel, and Ii, OFF and Ri are the OFF lidar signal and the range of the i-th ADC channel (the OFF signal has been chosen because its signal-to-noise ratio is higher). Figure 3C shows an example of in-plume excess CO2 concentration profile, obtained by applying the procedure above to the lidar profile of Figure 3B (in the 2100–2700 m range interval, where the volcanic plume was detected).
In-Plume CO2 Concentration Maps
A series of CO2 concentration profiles (one every 10 s), all similar to those shown in Figure 3C, were obtained as the volcanic plume was sequentially scanned by our DIAL-lidar, either horizontally or vertically, during the Pizzo/Vancori scans. By interpolating all CO2 concentration profiles obtained during a single scan, we obtained sequences of CO2 concentration maps, examples of which are shown in Figures 4, 5. Since a full scan of the plume was completed in ~1000–2000 s, each map is in fact obtained from the combination of ~50 to ~100 atmospheric profiles.
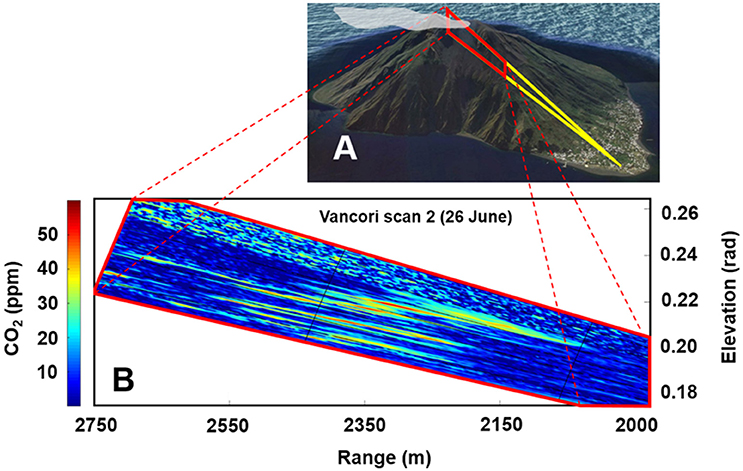
Figure 5. Example of a CO2 concentration map (B) obtained during a Vancori vertical scan on June 26. Geometry of the scan and location of the plume is schematically shown in (A). The map shows the distribution of CO2 concentrations in the lidar's FVO, as a function of range and elevation, and was obtained by interpolation of all CO2 concentration profiles (e.g., same as 3A) obtained during a given Vancori scan. In the map, the volcanic plume corresponds to the cluster of high CO2 concentrations (up to 60 ppmv) in the range interval 2200–2500 m and 0.2–0.22 rad (17–19.5°) elevations. The blue colored areas in the 2000–2000 m range correspond to near ambient (<10 ppm above background) CO2 concentrations.
The maps illustrate the 2D distribution of CO2 concentrations as a function of azimuth angle [°] (X axis) and range [m] (Y axis) for horizontal scans (Figure 4); or as a function of range [m] (X axis), and elevation angle [°] (Y axis) for the vertical scans (Figure 5). In both plots, the color scales (from blue to red) illustrate the level of CO2 concentrations (in [ppm]) in the investigated space.
Figures 4, 5 demonstrate the ability of our DIAL-lidar to resolve in-plume volcanic CO2 from the atmospheric background CO2 (blue colors). In the CO2 distribution maps, clusters of peak CO2 concentration areas (marked by red, orange and yellow colors) identify the geometry of the plume. The lidar-based plume locations are consistent with visual and UV observations of volcanic plume dispersion (Figure 2). In the Pizzo horizontal scans, the plume was intercepted north of the Pizzo peak (heading angle: 244–245°), and is identified in the maps of Figure 4 as a cluster of peak CO2 concentrations (up to 60 ppm above ambient air) at heading angles of 245–250°. The plume was detected over a relative wide range interval (R = 2000–2400 m), relative to the Pizzo peak (R ~2300 m). This is consistent with the slightly variable plume transport directions during our June 24–25 observation period that dispersed the plume either toward (Figure 4B) or away from (Figure 4A) the lidar observation point (R = 0). A few Pizzo vertical scans (not shown) confined the vertical extension of the plume to a diagonal band, extending from R = 2300 m and elevation ~19° (the Pizzo area) to R ~2700 m and ~20° elevation. Figure 5 is an example of a CO2 distribution map obtained during a vertical Vancori scan. The map exhibits a clear volcanic plume signal, as marked by a cluster of high CO2 concentrations (up to 60 ppm) in the range interval 2200–2500 m and 17–19.5° elevation. CO2 remained at background air levels for range distances <2000 and >2800 m.
CO2 Flux
The CO2 concentration maps served as basis for calculating the CO2 flux. To this aim, and by analogy with previous work (Aiuppa et al., 2015), we integrated the background-corrected (excess) CO2 concentrations over the entire plume cross-sectional area covered by each scan, and multiplied this integrated column amount by the plume transport speed. Mathematically, the CO2 flux (ΦCO2, in kg·s−1) was obtained from:
where vP is the plume transport speed (in [m/s]) obtained from processing of UV camera images (Table 1); NmolCO2−total is the total-plume CO2 molecular density (expressed in molecules m−1); and PMCO2 and NA are, respectively, the CO2 molecular weight and Avogadro's constant. The term NmolCO2−total was obtained by integrating the effective average excess CO2 concentrations ( [ppm]) over the entire plume cross section, according to:
where: Nh is the atmospheric number density (molecules m−3) at the crater's summit height, the term 10−6 converts into a dimensionless quantity, and Ai represents the i-th effective plume area, given by:
where ΔR is the spatial resolution of the lidar (1.5 m) and li is the i-th arc of circumference (Figure 6B):
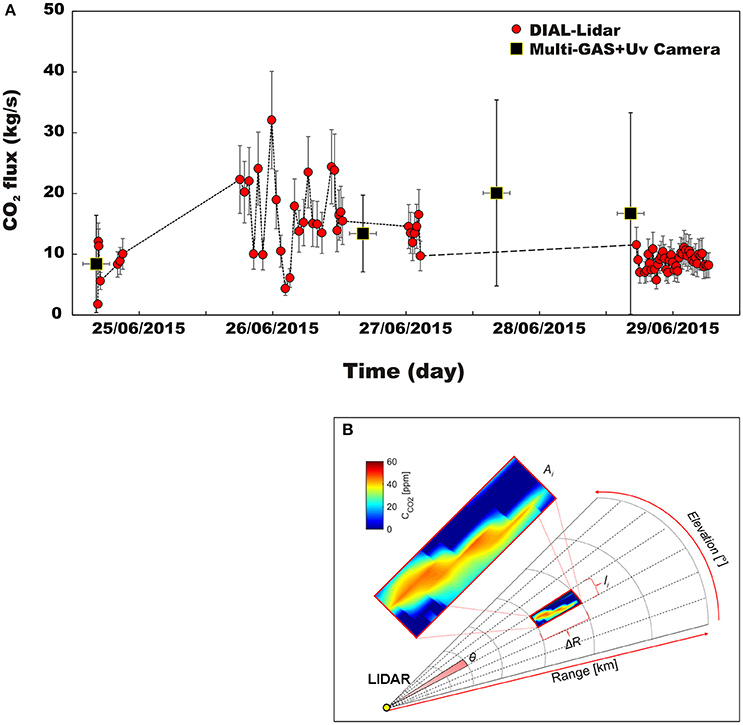
Figure 6. (A) Time-series of CO2 fluxes from Stromboli volcano on June 24–29, 2015. Our DIAL-lidar based fluxes (red circles) were obtained using the procedure detailed in the text. For comparison, independent CO2 flux estimates, obtained by multiplying the in-plume CO2/SO2 ratio (from Multi-GAS) by the SO2 flux (from UV Cameras), are also presented. The two independent time-series are consistent (within error, see also Table 1). (B) Schematic plot defining the parameters used in the CO2 flux calculation procedure (see text).
In relation (9), Ri is the i-th distance vector (in meters) and θ is the angular resolution of the system expressed in radians (ranging from 0.04° π/180 = 1.75 10−4 rad to 0.1° π/180 = 0.00175 rad) (Figure 6B).
Our obtained CO2 fluxes, shown in Figure 6A, range from 1.8 to 32.1 kg/s. The lidar-based CO2 flux time-series (Figure 6A) has maximum temporal resolution of 16–33 min (the time required to complete a full scan of the plume for our instrumental configuration). Temporal gaps in the dataset are caused by decreases in the signal-to-noise ratio (SNR) that prevent us from accurately detecting a clear CO2 excess. These SNR decreases are likely caused by reduction of the backscattering coefficient of the probed air parcel, reflecting temporal variations in condensation extent of the volcanic gas plume. Visual (and UV camera) observations confirmed that the plume was variably condensed during our measurement interval, possibly due to slight changes in atmospheric conditions.
We evaluate the overall uncertainty in our derived CO2 fluxes at ± 25% at 1s (see appendix).
Discussion
The scarcity of volcanic CO2 flux data in the geological literature (see Burton et al., 2013 for a recent review) is a direct consequence of the technical challenges in resolving the volcanic CO2 signal from the large atmospheric background (≈400 ppmv). In contrast to SO2, which is present at the part per billion level in the background atmosphere, allowing the volcanic flux to be routinely measured from ground and space using UV spectroscopy (Oppenheimer, 2010), remote sensing of volcanic CO2 has only been achieved during eruptions of mafic volcanoes. In such circumstances, magma/hot rocks can effectively be used as a light source for ground-based Fourier Transform Infra-Red (FTIR) spectrometers (Allard et al., 2005; Burton et al., 2007; Oppenheimer and Kyle, 2008). In contrast, measurement of the far more common “passive” CO2 emissions from quiescent volcanoes has required access to hazardous volcano's summit craters for direct sampling of fumaroles (Fischer and Chiodini, 2015) or in-situ measurement of plumes via either Multi-GAS instruments (Aiuppa, 2015) or active-FTIR (Burton et al., 2000; La Spina et al., 2013; Conde et al., 2014).
A major breakthrough has recently arisen from the possible application of lidars to remote volcanic CO2 sensing (Fiorani et al., 2013, 2015, 2016; Aiuppa et al., 2015; Queißer et al., 2015, 2016). Aiuppa et al. (2015) were the first to report on a DIAL-lidar-based remote measurement of the volcanic CO2 flux at Campi Flegrei volcano, but their observations were limited to short (<200 m) measurement distances. Here, we have extended this earlier work to demonstrate that DIAL-lidars can successfully detect volcanic CO2 at tens of ppmv above the atmospheric background over optical paths up to ≈3 km (Figures 4, 5). Similar results have recently been obtained at Campi Flegrei volcano by Queißer et al. (2016), suggesting that lidar may soon become an important operational tool in volcanic-gas research.
Our results constrain the CO2 flux at Stromboli during June 24–29, 2015 (Figure 6A). Averaging all successful results during each measurement day, we obtain daily averages of the CO2 flux between 8.3 ± 2.1 (June 24) and 18.1 ± 4.5 (June 25) kg/s, which correspond to cumulative daily outputs of 718 and 1565 tons, respectively. These results fall well in the range of previous CO2 measurements on Stromboli. Aiuppa et al. (2010a, 2011) found that the CO2 flux exhibits large temporal oscillations on Stromboli, from as low as 60 tons/day to as high as 11,000 tons/day, the highest values being observed in the days prior to paroxysmal and/or major explosions. The time-averaged CO2 flux from Stromboli has been evaluated at 550 tons/day (Aiuppa et al., 2011) and at 1040–1200 tons/day (Allard, 2010). Our lidar-based CO2 flux for the entire (June 24–29) measurement period is reasonably close, averaging at 1050 ± 250 tons/day (mean of 80 individual measurements).
Figure 6A offers further confirmation to the robustness of our results. In the figure, we compare our lidar-based CO2 fluxes with independent estimates, in which the CO2 flux was derived by multiplying the CO2/SO2 ratio of the plume by the SO2 flux. This latter approach has been used at volcanoes for years (Aiuppa, 2015), and at Stromboli involves use of two fully automated Multi-GAS instruments, operating on the volcano's summit to measure the in-plume CO2/SO2 ratio (Figure 2A; Aiuppa et al., 2009, 2010a,b; Calvari et al., 2014). This is combined with SO2 fluxes, delivered from either the FLAMES network of scanning UV spectrometers (Burton et al., 2009) or from UV camera observations (Tamburello et al., 2012), to obtain the CO2 flux.
Problems with this Multi-GAS + SO2 flux approach include issues of different temporal resolutions and poor temporal alignment of the two time-series. Successful Multi-GAS measurements of plume composition on Stromboli (Aiuppa et al., 2009, 2010b) are restricted to periods when the volcanic plume is dispersed by the local wind field into the Pizzo area, where the instruments are deployed (see Figure 2A). In addition, the Multi-GAS cannot operate continuously, but only during four equally spaced measurement cycles per day, each being 30 min long (Aiuppa et al., 2009). As such, the temporal resolution of the CO2/SO2 ratio time-series is 6 h at best. In contrast, the temporal resolution of UV spectrometers/cameras is higher, from ~10 to 20 min (Burton et al., 2009) to 0.5 s (Tamburello et al., 2012), but observations are intrinsically limited to daylight hours and to good meteorological conditions (no clouds).
Figure 7 exemplifies the issue related to misalignment between Multi-GAS and UV observations. In the June 26th example, the only successful Multi-GAS acquisition period (from 1600 to 1630 h local time) clearly did not overlap with the SO2 flux acquisition window (0900 to 1600 h local time). To overcome this problem, the common practice is to average out available Multi-GAS and UV spectroscopy data to obtain daily means of the CO2 flux (Aiuppa et al., 2010a). Owing to the large inter-daily variability of SO2 flux (e.g., Figure 7), however, large uncertainties are associated with these derived CO2 fluxes (see Table 1, and errors bars in Figure 6A).
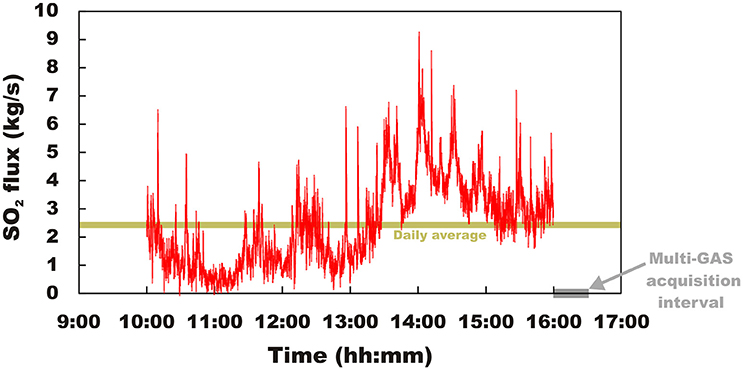
Figure 7. Temporal record of the volcanic SO2 flux from Stromboli on June 26 th, 2015, as derived from our UV camera observations. The figure exemplifies misalignment between Multi-GAS and SO2 flux time-series; plume CO2/SO2 ratios on June 26th were successfully measured only during the 1600–1630 local time Multi-GAS acquisition period, immediately after the end of the SO2 flux acquisition window (0900–1600 local time). Poor temporal alignment is a flaw in the technique of estimating the CO2 flux through a combination of Multi-GAS and UV camera records.
In spite of the issues above, we find overall consistency between the lidar-based and the traditional (Multi-GAS + UV spectroscopy-based) CO2 fluxes (Figure 6A). This provides mutual validation for both quantification approaches. Our lidar-based CO2 flux time-series (Figure 6A) are manifestly more continuous and of better temporal resolution (16–33 min). In addition, the lidar as with other remote sensing techniques is intrinsically safer. We caution, however, that further development is required before the lidar can become an operative tool for volcano monitoring. Improvements will need to occur in portability (the prototype weighs ~1100 kg), and reduced power requirement (6.5 kW) and costs (300 kUS $). In addition, the current measurement protocol is complex and thus requires great familiarity with the technique. Efforts are now being made to make the lidar more simple, user-friendly and fully automated, including development of an on-line remote control system and of a self-checking routine of the laser's wavelength settings. Electro-optics and laser/lidar private manufacturers need to be directly involved to transition the prototype into a more widely accessible, commercial instrument.
Conclusions
Our proof-of-concept study demonstrates the ability of DIAL-lidars to remotely (≈3 km distance) measure the volcanic CO2 flux. Our reported lidar-based CO2 fluxes at Stromboli volcano (1.8 ± 0.5 to 32.1 ± 8.0 kg/s) are in the same range as those obtained using standard techniques that require in-situ observations and are intrinsically more risky for operators. Our results, with those of Queißer et al. (2016), open new prospects for the use of lidars for instrumental remote monitoring of volcanic CO2 flux. Further work is warranted in order to standardize and widen potential applications of Lasers in volcanic gas studies.
Author Contributions
AA, LF, and SS conceived the idea. AA, LF, SS, GM, and MN conducted the lidar/UV camera experiment. SP and RD processed the data, with help from AA, LF, and SS. ML provided the Multi-GAS results. AA drafted the manuscript with help from all co-authors.
Funding
The research leading to these results has received funding from the European Research Council under the European Union's Seventh Framework Program (FP7/2007/2013)/ERC grant agreement n 305377 (PI, Aiuppa), and from the DECADE-DCO research initiative.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Società Enel Produzione spa is kindly acknowledged for logistical support and for kindly providing access to “Centrale ENEL di Stromboli” during the field campaign. The authors wish to thank the Comune di Lipari, Circoscrizione di Stromboli, for authorizing use of the lidar on Stromboli.
References
Aiuppa, A. (2015). “Volcanic gas monitoring,” in Volcanism and Global Environmental Change, eds A. Schmidt, K. E. Fristad, and L. T. Elkins-Tanton (Cambridge: Cambridge University Press), 81–96.
Aiuppa, A., Bertagnini, A., Métrich, N., Moretti, R., Di Muro, A., Liuzzo, M., et al. (2010b). A model of degassing for Stromboli volcano, earth planet. Sci. Lett. 295, 195–204. doi: 10.1016/j.epsl.2010.03.040
Aiuppa, A., Burton, M., Allard, P., Caltabiano, T., Giudice, G., Gurrieri, S., et al. (2011). First observational evidence for the CO2-driven origin of Stromboli's major explosions. Solid Earth 2, 135–142. doi: 10.5194/se-2-135-2011
Aiuppa, A., Burton, M., Caltabiano, T., Giudice, G., Guerrieri, S., Liuzzo, M., et al. (2010a). Unusually large magmatic CO2 gas emissions prior to a basaltic paroxysm. Geophys. Res. Lett. 37, L17303. doi: 10.1029/2010GL043837
Aiuppa, A., Federico, C., Giudice, G., Giuffrida, G., Guida, R., Gurrieri, S., et al. (2009). The 2007 eruption of Stromboli volcano: insights from real-time measurement of the volcanic gas plume CO2/SO2 ratio. J. Volcanol. Geotherm. Res. 182, 221–230. doi: 10.1016/j.jvolgeores.2008.09.013
Aiuppa, A., Fiorani, L., Santoro, S., Parracino, S., Nuvoli, M., Chiodini, G., et al. (2015). New ground-based lidar enables volcanic CO2 flux measurements. Sci. Rep. 5:13614. doi: 10.1038/srep13614
Aiuppa, A., Giudice, G., Gurrieri, S., Liuzzo, M., Burton, M., Caltabiano, T., et al. (2008). Total volatile flux from Mount Etna. Geophys. Res. Lett. 35, L24302. doi: 10.1029/2008gl035871
Allard, P. (2010). A CO2-rich gas trigger of explosive paroxysms at Stromboli basaltic volcano, Italy. J. Volcanol. Geoth. Res. 189, 363–374. doi: 10.1016/j.jvolgeores.2009.11.018
Allard, P., Burton, M. R., and Mure, F. (2005). Spectroscopic evidence for a lava fountain driven by previously accumulated magmatic gas. Nature 433, 407–410. doi: 10.1038/nature03246
Andronico, D., and Pistolesi, M. (2010). The November 2009 paroxysmal explosions at Stromboli. J. Volcanol. Geotherm. Res. 196, 120–125. doi: 10.1016/j.jvolgeores.2010.06.005
Berk, A., Conforti, P., Kennett, R., Perkins, T., Hawes, F., and van den Bosch, J. (2014). “MODTRAN6: a major upgrade of the MODTRAN radiative transfer code,” in Proceedings SPIE 9088, Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XX, 90880H (Baltimore, MD) (Accessed June 13, 2014).
Bertagnini, A., Métrich, N., Landi, P., and Rosi, M. (2003). Stromboli an open window on the deep feeding system of a steady state volcano. J. Geophys. Res. 108, 2336. doi: 10.1029/2002JB002146
Bruhn, A., Weickert, J., and Schnörr, C. (2005). Lucas/kanade meets horn/schunck: combining local and global optic flow methods international. J. Comput. Vis. 61, 211–231. doi: 10.1023/B:VISI.0000045324.43199.43
Burton, M., Allard, P., Murè, F., and La Spina, A. (2007). Depth of slug-driven strombolian explosive activity. Science 317, 227–230. doi: 10.1126/science.1141900
Burton, M. R., Caltabiano, T., Murè, F., and Randazzo, D. (2009). SO2 flux from Stromboli during the 2007 eruption: results from the FLAME network and traverse measurements. J. Volcanol. Geotherm. Res. 182, 214–220. doi: 10.1016/j.jvolgeores.2008.11.025
Burton, M. R., Oppenheimer, C., Horrocks, L. A., and Francis, P. W. (2000). Remote sensing of CO2 and H2O emission rates from Masaya Volcano, Nicaragua. Geology 28, 915–918. doi: 10.1130/0091-7613(2000)28<915:RSOCAH>2.0.CO;2
Burton, M. R., Prata, F., and Platt, U. (2014). Volcanological applications of SO2 cameras. J. Volcanol. Geotherm. Res. 300, 2–6. doi: 10.1016/j.jvolgeores.2014.09.008
Burton, M. R., Sawyer, G. M., and Granieri, D. (2013). Deep carbon emissions from volcanoes. Rev. Mineral. Geochem. 75, 323–354. doi: 10.2138/rmg.2013.75.11
Calvari, S., Bonaccorso, A., Madonia, P., Neri, M., Liuzzo, M., Salerno, G. G., et al. (2014). Major eruptive style changes induced by structural modifications of a shallow conduit system: the 2007-2012 Stromboli case. Bull. Volcanol. 76, 1–15. doi: 10.1007/s00445-014-0841-7
Conde, V., Robidoux, P., Avard, G., Galle, B., Aiuppa, A., Muñoz, A., et al. (2014). Measurements of SO2 and CO2 by combining DOAS, Multi-GAS and FTIR: study cases from Turrialba and Telica volcanoes. Int. J. Earth Sci. 103, 8, 2335–2347. doi: 10.1007/s00531-014-1040-7
D'Aleo, R., Bitetto, M., Delle Donne, D., Tamburello, G., Battaglia, A., Coltelli, M., et al. (2016). Spatially resolved SO2 flux emissions from Mt Etna. Geophys. Res. Lett. 43, 7511–7519. doi: 10.1002/2016GL069938
de Moor, J. M., Aiuppa, A., Avard, G., Wehrmann, H., Dunbar, N., Muller, C., et al. (2016a). Turmoil at Turrialba Volcano (Costa Rica): degassing and eruptive processes inferred from high-frequency gas monitoring. J. Geophys. Res. Solid Earth 121, 5761–5775. doi: 10.1002/2016JB013150
de Moor, J. M., Aiuppa, A., Pacheco, J., Avard, G., Kern, C., Liuzzo, M., et al. (2016b). Short-period volcanic gas precursors to phreatic eruptions: insights from Poás Volcano, Costa Rica. Earth Planet. Sci. Lett. 442, 218–227. doi: 10.1016/j.epsl.2016.02.056
Fiorani, L. (2007). “Environmental monitoring by laser radar,” in Lasers and Electro-optics Research at the Cutting Edge, ed S. B. Larkin (Hauppauge, NY: Nova Science Publishers), 119–171.
Fiorani, L., Santoro, S., Parracino, S., Nuvoli, M., Minopoli, C., Aiuppa, A., et al. (2015). Volcanic CO2 detection with a DFM/OPA-based lidar. Opt. Lett. 40, 1034–1036. doi: 10.1364/OL.40.001034
Fiorani, L., and Durieux, E. (2001). Comparison among error calculations in differential absorption lidar measurements. Opt. Laser Technol. 3, 371–377. doi: 10.1016/S0030-3992(01)00041-X
Fiorani, L., Saleh, W. R., Burton, M., Puiu, A., and Queißer, M. (2013). Spectroscopic considerations on DIAL measurement of carbon dioxide in volcanic emissions. J. Optoelectron. Adv. Mater. 15, 317–325.
Fiorani, L., Santoro, S., Parracino, S., Maio, G., Nuvoli, M., and Aiuppa, A. (2016). Early detection of volcanic hazard by lidar measurement of carbon dioxide. Nat. Hazards 83, 21. doi: 10.1007/s11069-016-2209-0
Fischer, T. P., and Chiodini, G. (2015). “Volcanic, magmatic and hydrothermal gas discharges,” in Encyclopaedia of Volcanoes, 2nd Edn, eds H. Sigurdsson, B. Houghton, S. McNutt, H. Rymer, and J. Stix (London: Academic Press; Elsevier), 779–797.
Galle, B., Johansson, M., Rivera, C., Zhang, Y., Lehmann, T., Platt, U., et al. (2010). Network for Observation of Volcanic and Atmospheric Change (NOVAC)-A global network for volcanic gas monitoring: network layout and instrument description. J. Geophys. Res. 115:D05304. doi: 10.1029/2009JD011823
Giggenbach, W. F. (1996). “Chemical composition of volcanic gases,” in Monitoring and Mitigation of Volcanic Hazards, ed R. Scarpa and R. J. Tilling (Heidelberg: Springer), 221–256.
Kantzas, E. P., McGonigle, A. J. S., Tamburello, G., Aiuppa, A., and Bryant, R. G. (2010). Protocols for UV camera volcanic SO2 measurements. J. Volcanol. Geotherm. Res. 94, 55–60. doi: 10.1016/j.jvolgeores.2010.05.003
La Spina, A., Burton, M. R., Harig, R., Mure, F., Rusch, P., Jordan, M., et al. (2013). New insights into volcanic processes at Stromboli from Cerberus, a remote-controlled open-path FTIR scanner system. J. Volcanol. Geotherm. Res. 249, 66–76. doi: 10.1016/j.jvolgeores.2012.09.004
Lübcke, P., Bobrowski, N., Illing, S., Kern, C., Alvarez Nieves, J. M., Vogel, L., et al. (2013). On the absolute calibration of SO2 cameras. Atmos. Meas. Tech. 6, 677–696. doi: 10.5194/amt-6-677-2013
Métrich, N., Bertagnini, A., and Di Muro, A. (2010). Conditions of magma storage, degassing and ascent at Stromboli: new insights into the volcano plumbing system with inferences on the eruptive dynamics. J. Petrol. 51, 603–626. doi: 10.1093/petrology/egp083
Métrich, N., Bertagnini, A., Landi, P., Rosi, M., and Belhadj, O. (2005). Triggering mechanism at the origin of paroxysms at Stromboli (Aeolian archipelago, Italy): the 5 April 2003 eruption. Geophys. Res. Lett. 32:L103056. doi: 10.1029/2004GL022257
Oppenheimer, C. (2010). Ultraviolet sensing of volcanic sulfur emissions, Elements 6, 87–92. doi: 10.2113/gselements.6.2.87
Oppenheimer, C., Fischer, T. P., and Scaillet, B. (2014). “Volcanic Degassing: Process and Impact,” in Treatise on Geochemistry, The Crust, 4, eds H. D. Holland and K. K. Turekian (Amsterdam: Elsevier), 111–179.
Oppenheimer, C., and Kyle, P. R. (2008). Probing the magma plumbing of Erebus volcano, Antarctica, by open-path FTIR spectroscopy of gas emissions. J. Volcanol. Geotherm. Res. 177, 743–754. doi: 10.1016/j.jvolgeores.2007.08.022
Oppenheimer, C., Scaillet, B., and Martin, R. S. (2011). Sulfur degassing from volcanoes: source conditions, surveillance, plume chemistry and earth system impacts. in Sulfur in magmas and melts: its importance for natural and technical processes. Rev. Miner. 73, 363–422. doi: 10.2138/rmg.2011.73.13
Patanè, D., Aiuppa, A., Aloisi, M., Behncke, B., Cannata, A., Coltelli, M., et al. (2013). Insights into magma and fluid transfer at Mount Etna by a multiparametric approach: a model of the events leading to the 2011 eruptive cycle. J. Geophys. Res. Solid Earth 118, 3519–3539. doi: 10.1002/jgrb.50248
Peters, N., Hoffmann, A., Barnie, T., Herzog, M., and Oppenheimer, C. (2015). Use of motion estimation algorithms for improved flux measurements using SO2 cameras. J. Volcanol. Geotherm. Res. 300, 58–69. doi: 10.1016/j.jvolgeores.2014.08.031
Pioli, L., Pistolesi, M., and Rosi, M. (2014). Transient explosions at open-vent volcanoes: the case of Stromboli (Italy). Geology 42, 863–866. doi: 10.1130/G35844.1
Pistolesi, M., Donne, D. D., Pioli, L., Rosi, M., and Ripepe, M. (2011). The 15 March 2007 explosive crisis at Stromboli volcano, Italy: Assessing physical parameters through a multidisciplinary approach. J. Geophys. Res. Solid Earth 116, B12206. doi: 10.1029/2011JB008527
Poland, M. P., Miklius, A., Sutton, J. A., and Thornber, C. R. (2012). A mantle-driven surge in magma supply to Kılauea Volcano during 2003-2007. Nat. Geosci. 5, 295–300. doi: 10.1038/ngeo1426
Queißer, M., Burton, M., and Fiorani, L. (2015). Differential absorption lidar for volcanic CO2 sensing tested in an unstable atmosphere. Opt. Express 23, 6634–6644. doi: 10.1364/OE.23.006634
Queißer, M., Granieri, D., and Burton, M. (2016). A new frontier in CO2 flux measurements using a highly portable DIAL laser system. Sci. Rep. 6:33834. doi: 10.1038/srep33834
Rosi, M., Bertagnini, A., Harris, A. J. L., Pioli, L., Pistolesi, M., and Ripepe, M. (2006). A case history of paroxysmal explosion at Stromboli: timing and dynamics of the April 5, 2003 event. Earth Planet. Sci. Lett. 243, 594–606. doi: 10.1016/j.epsl.2006.01.035
Rosi, M., Pistolesi, M., Bertagnini, A., Landi, P., Pompilio, M., and Di Roberto, A. (2013). Stromboli volcano, Aeolian Islands (Italy): present eruptive activity and hazards. Geol. Soc. Memoir 37, 473–490. doi: 10.1144/M37.14
Rothman, L. S., Gordon, I. E., Babikov, Y., Barbe, A., Chris Benner, D., Bernath, P. F., et al. (2013). The HITRAN2012 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 130, 4–50. doi: 10.1016/j.jqsrt.2013.07.002
Saccorotti, G., Iguchi, M., and Aiuppa, A. (2014). “In situ Volcano monitoring: present and future,” in Volcanic Hazards, Risks and Disasters, ed P. Papale (Amsterdam: Elsevier), 169–202.
Symonds, R. B., Rose, W. I., Bluth, G. J. S., and Gerlach, T. M. (1994). Volcanic-gas studies: methods, results and applications. Rev. Mineral. Geochem. 30, 1–66.
Tamburello, G., Aiuppa, A., Kantzas, E. P., McGonigle, A. J. S., and Ripepe, M. (2012). Passive vs. active degassing modes at an open-vent volcano (Stromboli, Italy). Earth Planet. Sci. Lett. 359, 106–116. doi: 10.1016/j.epsl.2012.09.050
Tamburello, G., Kantzas, E. P., McGonigle, A. J. S., and Aiuppa, A. (2011). Vulcamera: a program for measuring volcanic SO2 using UV cameras. Ann. Geophys. 54, 2. doi: 10.4401/ag-5181
Weitkamp, C. (ed.). (2005). “Lidar: range-resolved optical remote sensing of the atmosphere,” in Springer Series in Optical Sciences, Vol. 102. (New York, NY: Springer).
Werner, C., Kelly, P. J., Doukas, M., Lopez, T., Pfeffer, M., McGimsey, R., et al. (2013). Degassing of CO2, SO2, and H2S associated with the 2009 eruption of Redoubt Volcano, Alaska. J. Volcanol. Geotherm. Res. 259, 270–284. doi: 10.1016/j.jvolgeores.2012.04.012
Appendix–Uncertainty and Error Analysis
Our lidar-based CO2 fluxes are affected by the following error sources:
i. systematic error in CO2 concentration measurement,
ii. statistical error in CO2 concentration measurement,
iii. error in plume transport speed,
iv. error in identifying the integration area.
i. Systematic error of the CO2 concentration measurement-It is well known that the DIAL-lidar systematic error is dominated by imprecision in wavelength setting (Fiorani et al., 2015), leading to inaccuracy in differential absorption cross section and thus in gas concentration. To minimize this error, we implemented a photo-acoustic cell filled with pure CO2 at atmospheric pressure and temperature, close to the laser exit, in order to control the transmitted wavelength before each atmospheric measurement. This procedure allows us to set the ON/OFF wavelengths with better accuracy than the laser linewidth (Fiorani et al., 2016). Assuming that the error in the wavelength setting is ±0.02 cm−1 (half laser linewidth), in the wavelength region used in this study, the systematic error of the CO2 concentration measurement is 5.5%.
ii. Statistical error of the CO2 concentration measurement - The statistical error has been calculated by standard error propagation techniques from the standard deviation of the lidar signal at each ADC channel. As discussed in Fiorani and Durieux (2001), the statistical error of the lidar signal increases with range. As a consequence, the uncertainty associated with the derived CO2 concentrations also increases with range. In the distance range between Pizzo and Vancori, representing a mean measurement range, and at typical atmospheric and plume conditions encountered during this study, the statistical error of the CO2 concentration measurement was about 2%. The statistical error exceed 5% at 4 km (well beyond our measurement range).
iii. Error in plume transport speed - The standard deviation and the average value of the wind speed have been calculated for each measurement session, and the corresponding relative error was evaluated (by error propagation technique) at 3%.
iv. Error in identifying the integration area - The integration area in which an excess CO2 concentration is actually present is probably the most difficult parameter to retrieve accurately, and therefore represents the main error source in our calculated volcanic CO2 fluxes. The following procedure has been followed. For each CO2 concentration map (e.g., Figure 5), we initially measured: 1) A15, the area where the excess CO2 concentration was larger than 15 ppm; and 2) A25 the area where the excess CO2 concentration was larger than 25 ppm. Then, the average between A15 and A25 was taken as the best-estimated area, and their semi-difference as the error (~25%). The above thresholds have been chosen because below 15 ppm noise becomes significant, while above 25 ppm the plume area is reduced to its core. Use of a 15 ppm threshold likely underestimates the area (and thus the flux) of the order of magnitude of the measurement error, i.e., 10–20%.
Assuming that each error source is statistically independent, we can quadratically sum all the errors and obtain a cumulative error of ~ 25% (dominated by the area error).
Keywords: volcanic CO2, DIAL-lidar, Stromboli, remote sensing, CO2 flux
Citation: Aiuppa A, Fiorani L, Santoro S, Parracino S, D'Aleo R, Liuzzo M, Maio G and Nuvoli M (2017) New Advances in Dial-Lidar-Based Remote Sensing of the Volcanic CO2 Flux. Front. Earth Sci. 5:15. doi: 10.3389/feart.2017.00015
Received: 07 November 2016; Accepted: 06 February 2017;
Published: 21 February 2017.
Edited by:
John Stix, McGill University, CanadaReviewed by:
Jacob B. Lowenstern, United States Geological Survey, USAMarie Edmonds, University of Cambridge, UK
Copyright © 2017 Aiuppa, Fiorani, Santoro, Parracino, D'Aleo, Liuzzo, Maio and Nuvoli. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Alessandro Aiuppa, YWxlc3NhbmRyby5haXVwcGFAdW5pcGEuaXQ=
†Present Address: Giovanni Maio, ARES Consortium, Rome, Italy
 Alessandro Aiuppa
Alessandro Aiuppa Luca Fiorani3
Luca Fiorani3 Stefano Parracino
Stefano Parracino