- School of Earth Sciences, University of Bristol, Bristol, United Kingdom
Intrusions of magma induce thermal aureoles in the country rock. Analytical solutions predict that the thickness of an aureole is proportional to the thickness of the intrusion. However, in the field, thermal aureoles are often significantly thinner or wider than predicted by simple thermal models. Numerical models show that thermal aureoles are wider if the heat transfer in the magma is faster than in the country rock due to contrasts in thermal diffusivities or the effect of magma convection. Large thermal aureoles can also be caused by repeated injection close to the contact. Aureoles are thin when heat transfer in the country rock is faster than heat transfer within the magma or in case of incrementally, slowly emplaced magma. Absorption of latent heat due to metamorphic reactions or water volatilization also affects thermal aureoles but to a lesser extent. The way these parameters affect the thickness of a thermal aureole depends on the isotherm under consideration, hence on which metamorphic phase is used to draw the limit of the aureole. Thermal aureoles provide insight on the dynamics of intrusions emplacement. Although available examples are limited, asymmetric aureoles point to magma emplacement by over-accretion for mafic cases and by under-accretion for felsic cases, consistent with geochronological data.
Introduction
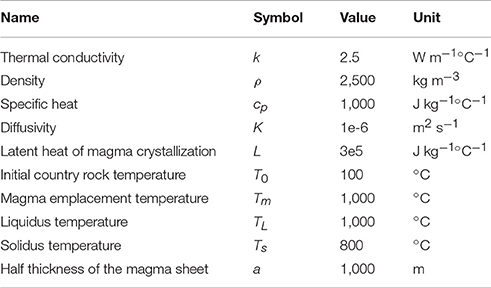
Contact metamorphic aureoles are due to the elevation in temperature in country rocks induced by the proximity of an igneous intrusion. Simple analytical models predict that the thickness of a thermal aureole, i.e., at what distance from the intrusion contact a metamorphic mineral appears that is characteristic of a certain temperature, is proportional to the thickness of the igneous intrusion. However, in reality, contact aureoles are often thinner, and sometimes wider than predicted. For example, the aureole associated with the several kilometers thick Manaslu leucogranite is only observed over a thickness of 100 m (Guillot et al., 1995). In contrast, andalusite registers the thermal impact of 5.5 km thick Western Adamello intrusion 1,700 m away from the contact (Floess and Baumgartner, 2015). A compilation of contact aureole thicknesses (Reverdatto et al., 1970; Barton et al., 1991) shows that for a given depth and intrusion composition, i.e., for a given initial country rock and magma temperature, aureole thicknesses relative to intrusion thicknesses vary significantly (Figure 1). Galushkin (1997) reports reduced thermal effects around a number of relatively small intrusions (from 1.3 to 20 m thick) and explains low temperatures by emplacement of the intrusion in a shell of cooler magmatic rocks but without explaining how this shell formed without transiting through high magmatic temperatures.
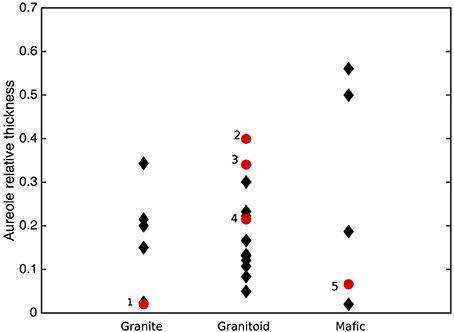
Figure 1. Compilation of thermal aureole relative thickness for different intrusion compositions. The aureole relative thickness is the aureole thickness divided by the intrusion thickness. Black diamonds are data from Reverdatto et al. (1970) for meso- or hypabyssal metamorphic facies that are amphibolite hornfels and muscovite hornfels. Red dots are for (1) the Manaslu (Guillot et al., 1995), (2) the Alta stock (Cook and Bowman, 1994), (3) the Western Adamello tonalite (Floess and Baumgartner, 2015), (4) the Cupsuctic (Bowers et al., 1990), (5) the Skaergaard (Bufe et al., 2014).
In the present paper, I briefly review the parameters controlling aureole thicknesses around tabular intrusions and explore a few mechanisms that can explain large variations in the thickness of aureoles. Tabular intrusions include sills, dykes, and laccoliths. Geophysical data and field observations show that plutons are also often tabular in shape (Cruden and McCaffrey, 2001). The intensity and extent of contact metamorphism depends on physical parameters, like thermal diffusivities or the temperature of the intruded magma, which are related to magma and country rocks compositions. Mechanisms that affect heat transfer include convection in the magma, hydrothermal circulation in the country rock, and, most importantly, the mechanism and timescale of magma emplacement.
Methods: Analytical and Numerical Computation of Heat Transfer from a Magma Intrusion to the Country Rock
In this paper, I model aureoles induced by conductive heat transfer by (i) an instantaneously emplaced single magma sheet and (ii) an incrementally emplaced magma body with a time interval between magma increments.
For an instantaneously emplaced magma sheet of thickness 2a, the temperatures T as a function of time t and distance to the sheet center x can be analytically calculated with the following equation (Furlong et al., 1991):
where T0 is the initial temperature of the rocks in which the magma is emplaced, ΔT is the temperature difference between T0 and the magma temperature Tm, and K is the thermal diffusivity.
The effect of the latent heat L released by crystallization of the magma can be accounted for by increasing ΔT as follows (Jaeger, 1964):
where cp is the specific heat of magma. However, Furlong et al. (1991) noted that this way of correcting ΔT overestimates the temperatures at the contact between magma and country rock.
Numerical simulation allows taking into account release of latent heat of crystallization, including the latent heat absorbed by metamorphic reactions, and modeling incrementally emplaced magma sheets. The temperature evolution is computed numerically according to the equation of heat flow:
or
where Q is:
where ρ is density, X is melt fraction, and k is thermal conductivity. Thermal conductivity relates to thermal diffusivity through K = k/ρcp.
Finite differences are used to solve for Q along a 1D grid (Figure 2) with dx, the distance between nodes and dt, the computation time steps:
Superscript p is for moment in time and subscript i is for nodes position in space.
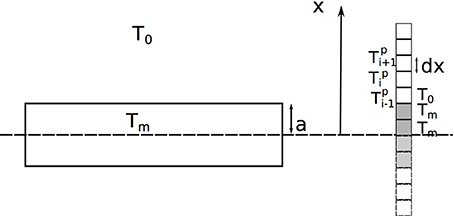
Figure 2. Model setup. Magma intrusions are sheets of half width a. Temperatures are calculated analytically in a one-dimensional half-space with Equation (1) or numerically with Equations (5–10). The system initial temperature is T0 and is perturbed by emplacement of magma with temperature Tm. dx is the dimension of the cell of the numerical grid.
Whittington et al. (2009) showed that k varies with temperature. In case of varying k, Equation (6) becomes (Hunt et al., 2006):
T is retrieved from Q using Equation (5). This requires knowing how melt fraction X varies with T. The relationship between T and X depends on rock composition and on pressure.
Here, I opted for a simple linear relationship between temperatures and melt fractions so that:
With Ts and Tl, the solidus and liquidus temperatures, respectively. The actual X-T relationships are not linear for most magmas. An accurate knowledge of the X-T relationship is important to precisely determine the melt fraction evolution over time. However, for the purpose of this contribution, which is to determine the thickness of thermal aureoles, the controlling parameters are the total heat content of the magma and not the exact evolution of melt fraction with time.
Equation (8) was also used when including latent heat of metamorphic reaction or water volatilization in the country rock. In this case, X is either the fraction of mineral that reacted or the portion of water volatilized, and Ts and Tl are the lower and upper temperatures bounding the reaction.
The simulation initial conditions are T = Tm and X = 1 at the j first nodes, with jdx = a, and T = T0 and X = 0 for all the other nodes. The boundary conditions are no heat flux through the boundary so that:
and
The simulation run over time, calculating temperatures at each time step dt. The simulation stops when temperatures have dropped everywhere below a threshold value that was chosen as T0 + (500 − T0)/2.
Because the thickness of thermal aureoles is recorded by the presence of metamorphic mineral phases, the geologically relevant parameter is the maximum temperature Tmax reached in the country rock as a function of distance from the intrusion contact.
The validity of the numerical code based on Equations (5–10) was tested by comparing the results with those obtained with the analytical solutions (1) and (2) for an instantaneously emplaced magma sheet. The values of the parameters used in the computations are reported in Table 1. If the latent heat is set to 0 and if the physical parameters are constant in time and space and the same for the magma and the country rock, the profile of Tmax obtained with the numerical simulation is identical to the profile of Tmax obtained using Equation (1). As noted by Furlong et al. (1991), if latent heat is included, the analytical solution (Equations 1, 2) over-estimates temperatures close to the contact (Figure 3).
Figure 3. Comparison of the maximum temperatures obtained numerically and analytically. If the latent heat is set to 0, the curves are superposed. If the latent heat is set to 300 kJ/kg, the maximum temperatures close to the contact obtained with Equations (1, 2) are higher than the temperatures obtained numerically.
For an incrementally growing body, regular emplacement of new magma increments is simulated by setting the first j cells to T = Tm and X = 1, with jdx corresponding to the thickness of a magma batch. To simulate the accommodation of the increment by displacement of the intrusion walls, the former values of the cells (before the increments) are transferred to the cells of position i + j. The time interval between two increments depends on the emplacement rate that is tested.
The computations, analytical and numerical, do not explicitly integrate heat transfer by convection. Convection is expected to enhance heat transfer within the magma for thick intrusions, or within the country rocks for permeable water-rich environments. The effect of convection can be approximated by an increase in the value of diffusivities, which is discussed later.
Results
Instantaneous Intrusion without Diffusivity Contrasts
The temperature evolution in the country rock after the instantaneous emplacement of a sheet-like magma intrusion depends on the thickness of the intrusion, the country rock initial temperature and composition, the magma emplacement temperature and latent heat of crystallization, and the thermal diffusivity (c.f. Equation 1). Thermal diffusivity controls the time that is needed for a given point to reach a maximum in temperature (Tmax) and the time it takes for temperatures to decay (Figure 4). In the absence of diffusivity contrasts between the intrusion and the country rock, the thermal diffusivity does not influence the height of the maximum in temperature. Thus, in the absence of spatial variations of diffusivities, profiles of Tmax are independent from the absolute value of thermal diffusivities and depend only on the magma and country rocks initial temperatures and on the intrusion thickness (Figure 5). Figure 6A shows that the distance to the contact of a given Tmax, i.e., the thickness of the contact aureole, is a linear function of the intrusion thickness. For a given initial temperature and rock type the relative thickness of the aureole l/a, with l the thickness of the aureole, is a constant (Figure 6B). This result is in stark contrast with the data compiled by Reverdatto et al. (1970) and Barton et al. (1991) that show large variations in the relative thickness of aureoles (Figure 1).
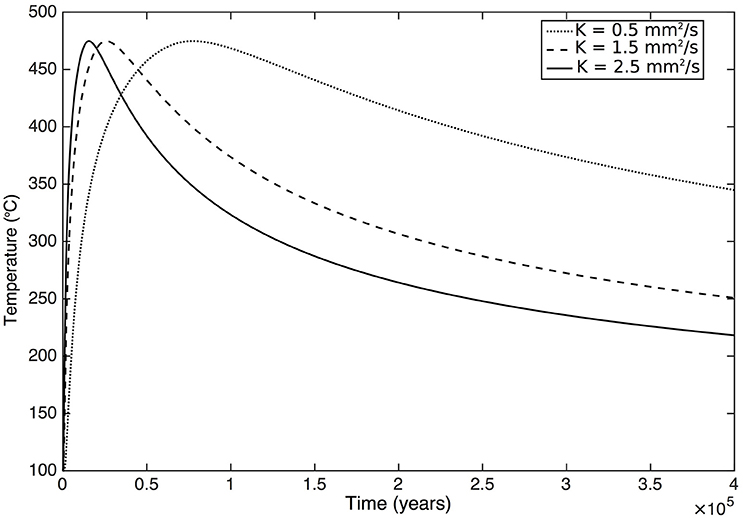
Figure 4. Evolution of temperatures over time at 525 m from the contact of a 2 km thick intrusion for different thermal diffusivities K. There is no spatial variation of diffusivities, which are identical in the magma and the country rock.
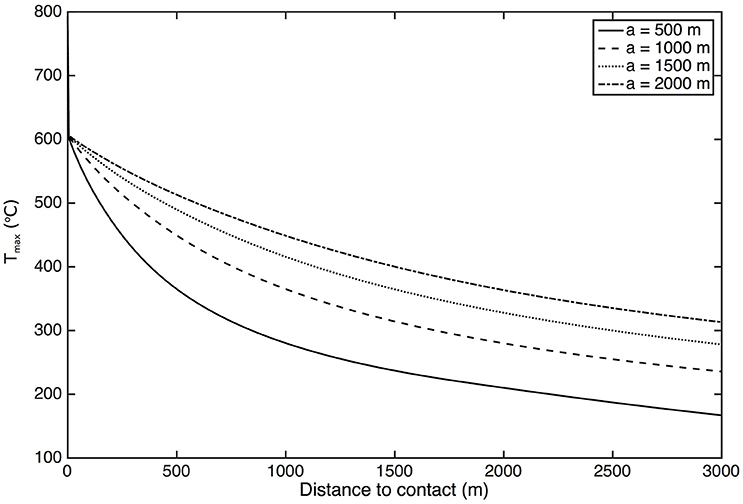
Figure 5. Maximum temperatures reached by the country rock as a function of distance from the intrusion contact for different intrusion half-thicknesses a, all other parameters being equal.
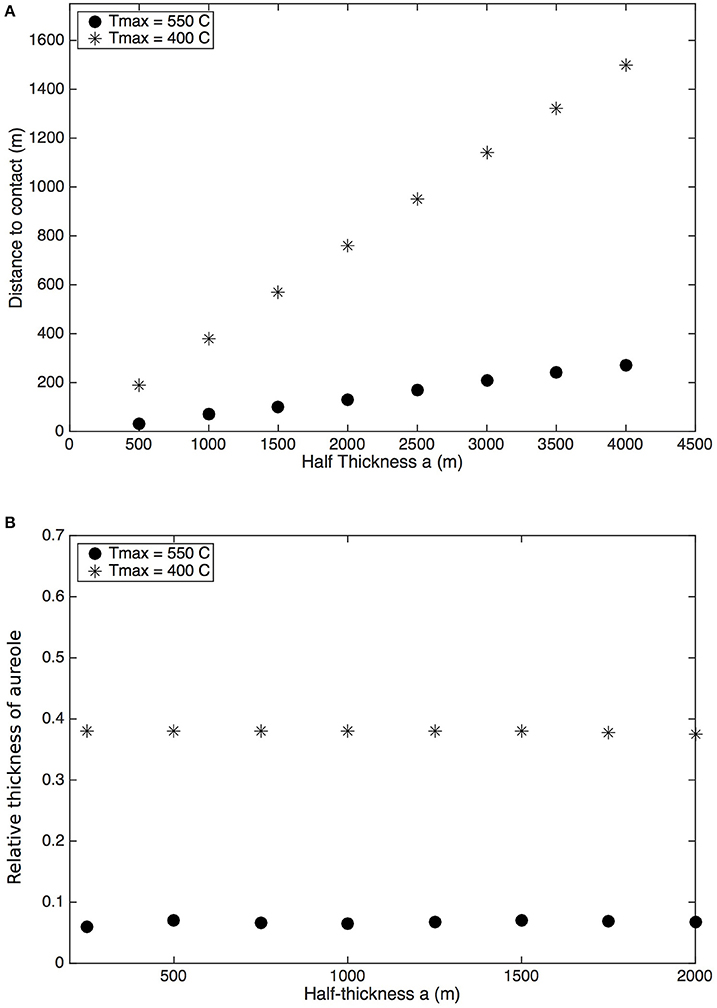
Figure 6. (A) Thickness of the thermal aureole expressed as the distance from the contact, where Tmax is 550°C, respectively 400°C, as a function of the intrusion thickness. (B) Relative thickness of the aureole expressed as the distance to the contact divided by the intrusion thickness.
Diffusivity Contrasts
For the simulation shown on Figures 7, 8, thermal diffusivity K was varied by varying thermal conductivity k and keeping ρ and cp constant. Although, Tmax is independent from diffusivity as long as diffusivity does not vary spatially, spatial variation of diffusivity, and in particular diffusivity contrasts between the intrusion and the country rock have a marked effect on Tmax profiles (Figures 7, 8). Nabelek et al. (2012) showed that in models where diffusivity is temperature-dependent and decreases with increasing temperatures (Whittington et al., 2009), Tmax in contact aureoles are lower than with a constant diffusivity of 10−6 m2/s. If the intrusion diffusivities are higher than the country rock diffusivities, the country rock acts as an insulating layer that slows down heat transfer from the intrusion. Heat builds up in the country rocks close to the contact resulting in elevated temperatures and larger aureoles. A similar effect has been described by Jaupart and Provost (1985), who showed how heat focusing at the boundary between a high conductivity granitic rock and a low conductivity sedimentary rock results in elevated temperatures and melting. In contrast, if the country rock diffusivity is higher than the intrusion diffusivity, heat is rapidly dissipated, temperatures in the country rocks remain relatively low, and the thermal aureole is relatively small. Figure 7 shows that a diffusivity contrast can reduce the aureole thickness to less than the definition of the numerical grid (10 m) or almost double it in comparison to an absence of contrast. The increase in aureole thickness is bounded and is more important when high temperatures are considered (Figure 8).
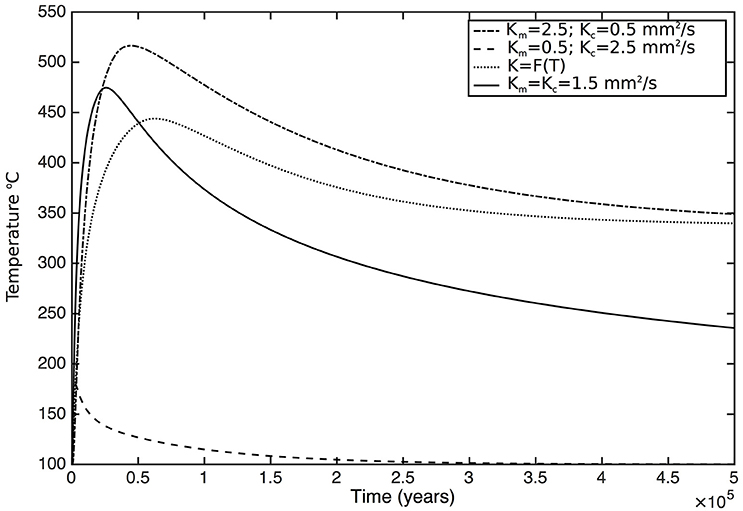
Figure 7. Evolution in time of temperatures at 525 m from the contact of a 2 km thick intrusion for different contrasts in diffusivities between the intrusion (Km) and the country rock (Kc) and for a temperature dependant conductivity [K = F(T); (Whittington et al., 2009)].
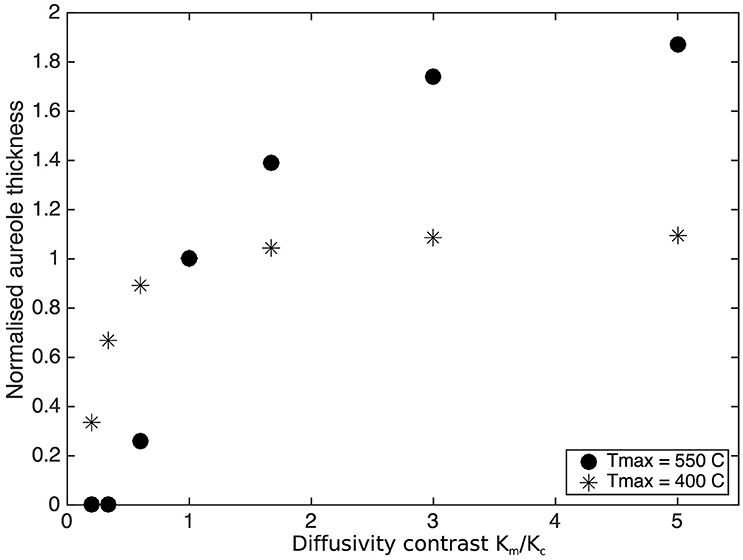
Figure 8. Thickness of the thermal aureole expressed as the distance from the contact, where Tmax is 550°C, respectively 400°C, as a function of diffusivity contrasts (= conductivity contrasts). Values for the distance from contact are normalized to the value without diffusivity contrast.
Water in the Country Rock
The presence of water in the country rock is expected to affect the value of temperatures in a contact aureole as metamorphic reactions and water volatilization absorb latent heat (Wang and Song, 2012). Water can be part of the crystal structure or be in rock pores. Emplacement of shallow intrusions in water-saturated sediments can result in the boiling of pore water. The overpressures due to fluid expansion causes fluidization textures or the formation of sediments dykes and pipes, and hydrothermal vents (e.g., Svensen et al., 2006).
To investigate the thermal impact of the presence of water in the country rock, I simulated the case where a sill of magma is emplaced in shallow water-saturated sediments. The water-filled porosity is 35%, the pressure is 0.1 kbar, corresponding to a depth of 400 m, and the initial country-rock temperature is 30°C. At this pressure, the water boiling point is 311°C and the latent heat absorbed by water volatilization is 1,317 kJ/kg (www.thermexcell.com). Figure 9 compares profiles in Tmax obtained for three different country rocks, all other parameters being equal: (1) a dry sediment; (2) a sediment with water locked in hydrous minerals and dehydration between 400 and 600°C absorbing 160 kJ/kg (Walther and Orville, 1982); (3) a water-saturated sediment as described above. The effect of heat being absorbed by water volatilization is to decrease temperatures and the thickness of aureoles. This effect is partly compensated by the effect of pore-water high specific heat (4,180 J/kg °C), which increases temperatures (Nabelek et al., 2012; Wang, 2012). As a result, peak temperatures are highest for dry sediments and lowest for water-saturated sediments (Figure 9). However, the effect of water in sediments on aureole thickness is relatively weak in comparison with the effect of diffusivity contrasts or incremental emplacement.
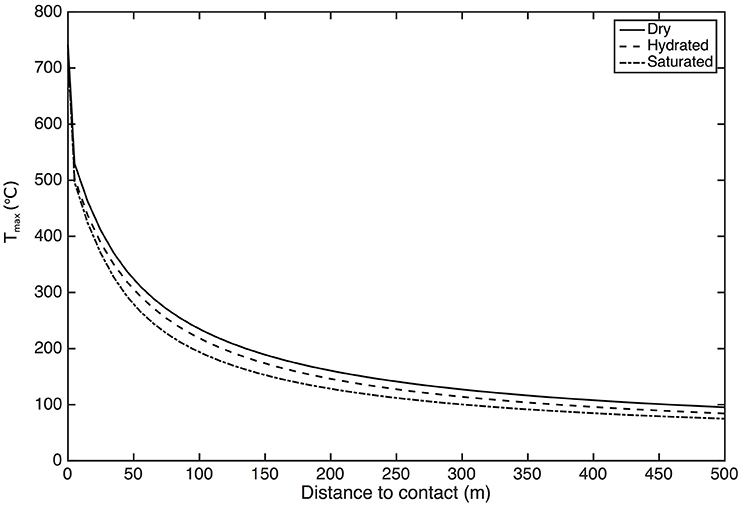
Figure 9. Maximum temperatures Tmax as a function of distance to the intrusion contact. Plain line: the country rock is dry and no latent heat is absorbed in the country rock when temperatures increase. Dashed line: the country rock contains hydrous minerals that dehydrate between 400 and 600°C, absorbing 160 kJ/kg. Dashed-dotted line: The country rock contains 35% pore water and devolatilizes at 311°C absorbing 1317 kJ/kg. The intrusion is 100 m thick and the initial country rock temperature is 30°C.
Incremental Emplacement
Incrementally emplaced intrusions grow by addition of smaller discrete magma batches. In this paper, I focus on sheet-like intrusions (horizontal or vertical) that grow by additions of thinner sheets. The temperature evolution within the growing intrusion and in the surrounding country rock is controlled by the intrusion emplacement rate. Emplacement rate is the thickness of the thinner sheets divided by the time interval between sheets (e.g., Michaut and Jaupart, 2006; Annen, 2009).
Dating of large (several kilometers thick) tabular bodies of granitoids commonly indicate that they grow top-down (Michel et al., 2008), i.e., that sheets under-accrete. Magma and heat are repeatedly advected at the floor contact. As a result, the top and bottom thermal aureoles are asymmetric and the thermal imprint on the country rock is more important at the floor than at the roof of the intrusion (Figure 10). If each magma increment is repeatedly injected in the middle of the body (intra-accretion) the two aureoles on each side of the body are symmetrical (Figure 11). The thickness of the aureole depends on the emplacement rate or, for a fixed thickness of the increments, on the recurrence time. On Figures 10, 11, the thickness of the aureole induced by an incrementally growing body is normalized by the thickness of the aureole induced by an instantaneously emplaced body of the same thickness and characteristics, and the recurrence time interval is non-dimensionalized by dividing it by the diffusion timescale of a single sill increment (a2/K). With short recurrence intervals (fast emplacement) the top and bottom aureoles are similar to the aureole induced by an instantaneously emplaced body. If emplacement is by under-accretion, the thickness of the top aureole keeps decreasing (Figure 10A) as the recurrence time interval increases, whereas the bottom aureole first increases, reaches a maximum, and then sharply decreases (Figure 10B). With long recurrence intervals (slow emplacement) both aureoles (Figure 10), as well as the aureole of an intra-accreting body (Figure 11), converge toward a thickness that corresponds to the aureoles thickness induced by the emplacement of a single increment. In other words, the thermal imprint of a large and slowly incrementally emplaced body reduces to the thermal imprints of one small single increment. The respective evolution of the top and bottom aureole is reversed in case of bottom-up growth (over-accretion). In case of intra-accretion, both contacts get further in time from the locus of magma injection and aureole thicknesses decrease sharply as the recurrence interval increases (Figure 11).
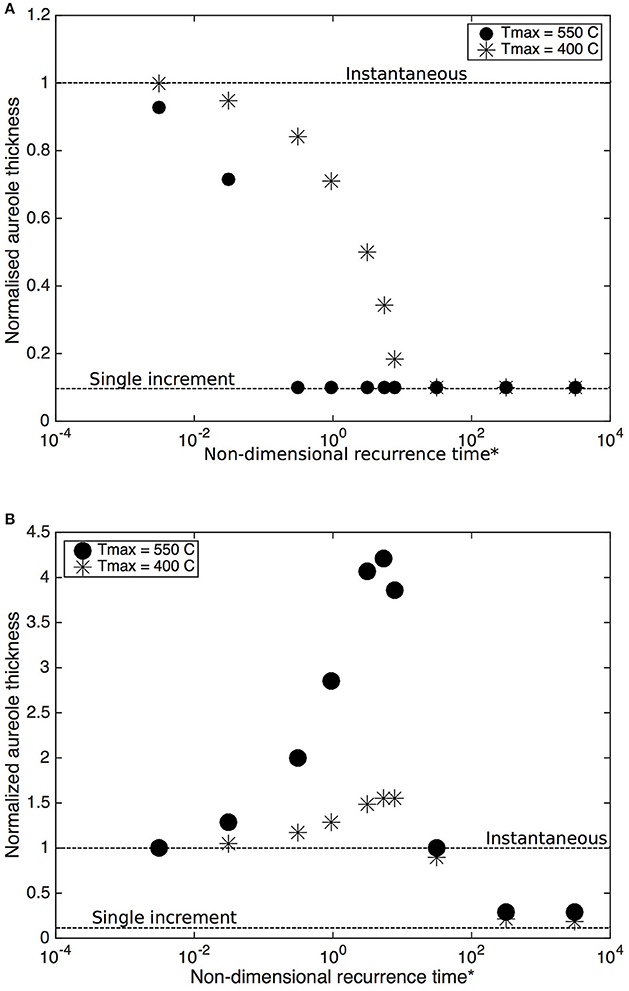
Figure 10. Aureole thickness induced by an incrementally growing magma body as a function of the time interval between magma increments. The magma body grows by under- or over-accretion of 10 sills. The aureole thickness is normalized by the value of the aureole thickness induced by the same body instantaneously emplaced (shown by the upper horizontal dashed line). The time interval between increments is normalized by the heat diffusion timescale through an increment (a2/K). As the time interval between sills becomes long relative to the heat diffusion timescale, the thickness tends toward the aureole thickness induced by a single sill (lower horizontal dashed line). (A) Aureole thickness at the contact that gets further away from new sills as the body grows, i.e., the top aureole in case of under-accretion. (B) Aureole thickness at the contact where sills are repeatedly injected, i.e., at the bottom aureole in case of under-accetion.
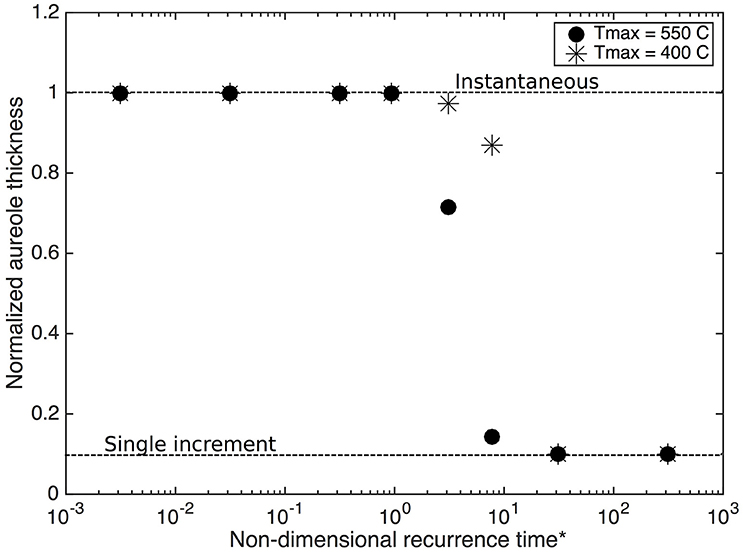
Figure 11. Same as Figure 10 for a magma body emplaced by sills intra-accretion. In this case the top and bottom aureoles are identical.
The increase in aureole thickness and the exact shape of the thickness-recurrence time relationship depend on the value of Tmax under consideration. An increase in thickness is more marked for high peak temperatures. For Tmax = 550°C, incremental emplacement can result in aureole thickness four times wider than in case of an instantaneously emplaced intrusion (Figure 10B).
Discussion and Conclusions
The thermal impact of a magma intrusion on the country rock depends on the difference in temperature between the magma and its surrounding and on the thickness of the intrusion. For a given background temperature, the thickness of a thermal aureole scales linearly with the thickness of the associated intrusion. Larger aureoles can be due to contrasts in diffusivity. Diffusivity is the ratio between thermal conductivity k and the volumetric heat capacity ρcp, and corresponds to the rate at which heat get transferred. Heat transfer within the magma that is large relative to heat transfer through the country rock corresponds to a small Biot number, a situation that has been shown to lead to high magma-country rock boundary temperatures (Carrigan, 1988). Heat is transferred more rapidly within the intrusion than through the country rock if the country rock is insulating or if the magma is convecting. The thermal conductivity of a rock is the sum of the conductivities of its minerals (Robertson, 1988). Porous rocks that are poor in quartz and contain water or air in pores are the most insulating (Robertson, 1988). They are most likely found at shallow depth. Thermal convection in magma is significantly accelerating heat transfer within the magma and has the same effect as high conductivities. For example, Joesten (1991) explains very high temperatures in the Christmas mountain contact aureole by magmatic convection. Convection is most important for large magma chambers and low viscosity magmas. The other factor that can explain large thermal aureoles is the incremental emplacement of magma. For a range magma injection recurrence intervals, the aureole at the contact where magma is repeatedly injected is increased. This effect has been reported by Floess and Baumgartner (2015) for the aureole of Western Adamello.
Thermal aureoles that are smaller than predicted by simple analytical models can be due to contrasts in apparent diffusivity, where heat transfer is slower within the magma than in the country rocks, corresponding to large Biot Number which has been shown to reduce the magma-country rock temperature (Carrigan, 1988). Low porosity, quartz-rich country rocks have high thermal conductivities. Heat transfer in the country rock can be enhanced by hydrothermal convection. Wang and Manga (2015) show that hydrothermal convection induces complexly-shaped thermal aureoles. Diffusivities decrease with temperatures (Robertson, 1988; Whittington et al., 2009). As a magma cools down and transfer heat to its surrounding, the magma diffusivity increases and the country rock diffusivity decreases. Nabelek et al. (2012) show that taking this effect into account in calculations decreases the thickness of thermal aureoles. Incremental emplacement of the magma intrusion can result in dramatically reduced thermal aureole if the time interval between magma batches is long. The limiting case is when the time interval between magma batches is so long that the country rock completely cool down between magma injection and the thickness of the thermal aureole is controlled by the thickness of one single batch.
In the absence of diffusivity contrasts between magmas and country rocks, the value of diffusivity does not affect maximum temperatures. However, it affects the time taken by the temperature to decay and for how long the rock stays at high temperature. Since metamorphic processes are time-dependent (Joesten, 1991; Nabelek et al., 2012; Mori et al., 2017), the aspect of the contact aureole could be affected by the value the thermal diffusivity even when the peak temperature is unaffected.
According to the calculations presented here, there is an upper limit to the thickness a thermal aureole can reach. In contrast, in theory, there is no limit on how small a thermal aureole can be. The thickness of an aureole is varying in different proportions for different isotherms (see also Floess and Baumgartner, 2015). Thus, when studying specific cases, speaking of the thickness of a thermal aureole in a general way can be misleading and it is important to specify what isotherm is being considered. In the field, which isotherm can be identified depends on what metamorphic minerals can form, hence on the composition of the rock.
A difficulty in applying models to thermal aureoles observed in nature it that the three-dimensional geometry of the associated intrusion is rarely clear in the field. The extension of the intrusion is often unknown and the roof and floor are rarely available for observation (Johnson et al., 2011). Only exceptionally do outcropping conditions allow for the simultaneous observation of the different sides of a pluton.
Bufe et al. (2014) fitted the thermal aureoles of the basaltic layered intrusion of Skaergaard (Greenland) with an instantaneously emplaced magma sphere 4 km in radius. In the field, the limit of the thermal aureole is determined by microcline becoming disordered sanidine and by quartz recrystallization, corresponding to an isograd of ~500°C. The edge of the aureole at the floor and lower wall of the intrusions is at 390 m from the contact. Bufe et al. (2014) note that the aureoles temperatures at this level are lower (about 100°C less) than the temperature at the intrusion roof and upper wall (Manning et al., 1993). The difference is attributed to heterogeneous release of latent heat of crystallization. An alternative explanation is an incremental emplacement of the intrusion from bottom to top, by over-accretion.
An example of an intrusion where the thermal aureole at the lateral wall was modeled is the quartz-monzonite Cupsuctic pluton in Maine, USA (Bowers et al., 1990). The distance between the biotite isograd (460°C) and the contact of the 6–8 km in diameter pluton range from a few hundred meters to about 1.5 km. Bowers et al. (1990) discuss the role of convection and conclude that hydrothermal convection affects the outer part of the aureole but not the inner part, and emphasize the importance of the pluton geometry in controlling the isograd contours shape. They successfully fit the isograds delimited by the appearance of Biotite at 460°C, Andalusite at 510°C, and Silimanite at 580°C, with a discoid, 4 km thick, instantaneously emplaced intrusion.
The granodioritic Alta stock in Utah, USA, investigated by Cook and Bowman (1994) is 2–3 km in diameter. The thermal aureole is delimited by an outer tremolite zone (410–450°C), an outer forsterite zone (490°C), and an inner forsterite zone (575°C). The aureole delimited by the outer tremolite zone reaches 1 km. Cook and Bowman (1994) failed to reproduce the aureole temperatures with a conductive model and an instantaneously emplaced stock. Their modeled temperatures are lower than the temperatures inferred from mineral assemblages. The authors preferred explanation for the discrepancy is that heat is advected by fluids, but they do not consider the possible effect of an incremental emplacement.
In contrast to the Alta stock and Cupsuctic pluton, the thermal aureole at the roof and floor of the Manaslu leucogranite (Centre Nepal) can be observed. According to a detailed analysis of the metamorphic assemblages and of the microstructures by Guillot et al. (1995), the temperature remained high at the base of the pluton, whereas the cooling was more rapid at the top. The top aureole is <100 m. These characteristics suggest an incremental emplacement of the pluton by under-accretion (Annen et al., 2006). The thickness of the Manaslu leucogranite plution is estimated to between 5 and 12 km (Guillot et al., 1995). The top aureole can be reproduced with numerical simulation if the leucogranite pluton results from the slow amalgamation of 10–100 m thick sills over more than 5 million years (Annen et al., 2006).
It is interesting to compare the thickness of the roof aureole of the Manaslu (<100 m) with the aureole in the roof of the Moosebokmeguntic igneous complex in the Northern Apalachian. Although, the Mooselookmeguntic granite to graniodioritic intrusions is only 2 km thick and much thinner than the Manaslu leucogranite, the aureole is much thicker with the isograd determined by the garnet zone exceeding 1 km (Johnson et al., 2011). The thermal aureole was fitted by Johnson et al. (2011) with a conductive model and instantaneous emplacement, which suggests that this intrusion might have been rapidly emplaced.
Modeling of the thermal aureole of the Western Adamello tonalite by Floess and Baumgartner (2015) indicates that the aureole is too thick to be accounted for by an instantaneous emplacement of the pluton. The Western Adamello tonalite is considered to be ~5 km-wide. The presence of andalousite at 1,700 m of the contact, of basement melting at 350 m of the contact, and of shale abundant melting and presence of orthopyroxene at 50 m of the contact, determine isograds of 525, 675, and 800°C, respectively. To fit the aureole, Floess and Baumgartner (2015) modeled the external zone of the Westen Adamello tonalite as a conduit by alternating periods of continuous magma flow with periods without flow.
Several asymmetric aureoles have been reported (Guillot et al., 1995; Alvarez-Valero et al., 2014; Bufe et al., 2014). Asymmetric aureoles can be explained by incremental emplacement (Figure 10) or by the presence of a fault on one side of the pluton along which the intrusion has been exhumed (Alvarez-Valero et al., 2014). Interestingly, higher temperatures at the roof than at the floor are reported for Skaeregaard mafic intrusion (Bufe et al., 2014) whereas the opposite is true for Manaslu leucogranite intrusion (Guillot et al., 1995). It suggests a magma emplacement by over-accretion for the mafic case and by under-accretion for the felsic case in good agreement with geochronological data that indicate ages that become younger toward the floor for incrementally-emplaced granite intrusions and toward the roof for mafic intrusions (Leuthold et al., 2012).
Understanding the emplacement dynamics of igneous bodies is critical because intrusion geometries and emplacement rates control the volumes of magma that are molten and the degrees of melting during and after emplacement (Hanson and Glazner, 1995; Yoshinobu et al., 1998; Glazner et al., 2004; Annen, 2009), thus they control the ability of a magma to convect, to differentiate, to mix, to be contaminated, and to erupt (Annen, 2011). The thickness of thermal aureoles provides insights on magma emplacement timescales (Annen et al., 2006; Floess and Baumgartner, 2015). As emphasized by Wang (2012), caution must be exerted when inverting results and trying to recover magma emplacement conditions from the characteristics of thermal aureoles as different sets of parameters can lead to similar results. Nevertheless, provided that the effect of physical parameters is correctly taken into account, the combination of field observation and numerical simulations is a powerful tool to understand magma emplacement dynamics.
Author Contributions
CA drafted the work, wrote and ran the numerical code, produced, analyzed, and interpreted the results, and wrote the text.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This paper benefited from stimulating discussions with Michel de Saint-Blanquat, Thierry Menand, and Jon Blundy. It also benefited from interactions with the participant of the 2010 LASI IV conference, where part of this work was presented. The reviewers and the editor are thanked for their constructive comments that helped improving the manuscript.
References
Alvarez-Valero, A. M., Jagoutz, O., Stanley, J., Manthei, C., El Maz, A., Moukadiri, A., et al. (2014). Crustal attenuation as a tracer for the emplacement of the Beni Bousera ultramafic massif (Betico-Rifean belt). Geol. Soc. Am. Bull. 126, 1614–1624. doi: 10.1130/B31040.1
Annen, C. (2009). From plutons to magma chambers: thermal constraints on the accumulation of eruptible silicic magma in the upper crust. Earth Planet. Sci. Lett. 284, 409–416. doi: 10.1016/j.epsl.2009.05.006
Annen, C. (2011). Implications of incremental emplacement of magma bodies for magma differentiation, thermal aureole dimensions and plutonism-volcanism relationships. Tectonophysics 500, 3–10. doi: 10.1016/j.tecto.2009.04.010
Annen, C., Scaillet, B., and Sparks, R. S. J. (2006). Thermal constraints on the emplacement rate of a large intrusive complex: the Manaslu Leucogranite, Nepal Himalaya. J. Petrol. 47, 71–95. doi: 10.1093/petrology/egi068
Barton, M. D., Staude, J. M., Snow, E. A., and Johnson, D. A. (1991). Aureole systematics. Rev. Mineral. 26, 723–847.
Bowers, J. R., Kerrick, D. M., and Furlong, K. P. (1990). Conduction model for the thermal evolution of the Cupsuptic aureole, Maine. Am. J. Sci. 290, 644–665. doi: 10.2475/ajs.290.6.644
Bufe, N. A., Holness, M. B., and Humphreys, M. C. S. (2014). Contact metamorphism of precambrian gneiss by the skaergaard intrusion. J. Petrol. 55, 1595–1617. doi: 10.1093/petrology/egu035
Carrigan, C. R. (1988). Biot number and thermos bottle effect: implications for magma-chamber convection. Geology 16, 771–774. doi: 10.1130/0091-7613(1988)016<0771:BNATBE>2.3.CO;2
Cook, S. J., and Bowman, J. R. (1994). Contact-metamorphism surrounding the Alta stock - thermal constraints and evidence of advective heat-transport from calcite plus dolomite geothermometry. Am. Mineral. 79, 513–525.
Cruden, A. R., and McCaffrey, K. J. W. (2001). Growth of plutons by floor subsidence: implications for rates of emplacement, intrusion spacing and melt-extraction mechanisms. Phys. Chem. Earth A 26, 303–315. doi: 10.1016/S1464-1895(01)00060-6
Floess, D., and Baumgartner, L. P. (2015). “Constraining magmatic fluxes through thermal modelling of contact metamorphism,” in Chemical, Physical and Temporal Evolution of Magmatic Systems, eds L. Caricchi and J. D. Blundy (London: Geological Society), 41–56.
Furlong, K. P., Hanson, R. B., and Bowers, J. R. (1991). “Modeling thermal regimes,” in Contact Metamorphism, ed D. M. Kerrick (Chelsea, MI: Mineralogical Society of America), 437–498.
Galushkin, Y. I. (1997). Thermal effects of igneous intrusions on maturity of organic matter: a possible mechanism of intrusion. Org. Geochem. 26, 645–658. doi: 10.1016/S0146-6380(97)00030-2
Glazner, A. F., Bartley, J. M., Coleman, D. S., Gray, W., and Taylor, Z. T. (2004). Are plutons assembled over millions of years by amalgamation from small magma chambers? GSA Today 14, 4–11. doi: 10.1130/1052-5173(2004)014<0004:APAOMO>2.0.CO;2
Guillot, S., Le Fort, P., Pêcher, A., Roy Barman, M., and Aprahamian, J. (1995). Contact metamorphism and depth of emplacement of the Manaslu granite (central Nepal). Implications for Himalayan orogenesis. Tectonophysics 241, 99–119. doi: 10.1016/0040-1951(94)00144-X
Hanson, R. B., and Glazner, A. F. (1995). Thermal requirements for extensional emplacement of granitoids. Geology 23, 213–216. doi: 10.1130/0091-7613(1995)023<0213<0213:TRFEEO>2.3.CO;2
Hunt, B. R., Lipsman, R. L., and Rosenberg, J. (2006). A Guide to Matlab for Beginners and Experienced Users. Cambridge: Cambridge University Press.
Jaeger, J. C. (1964). Thermal effects of intrusions. Rev. Geophys. 2, 443–466. doi: 10.1029/RG002i003p00443
Jaupart, C., and Provost, A. (1985). Heat focusing, granite genesis and inverted metamorphic gradients in continental collision zones. Earth Planet. Sci. Lett. 73, 385–397. doi: 10.1016/0012-821X(85)90086-X
Joesten, R. L. (1991). Kinetics of coarsening and diffusion-controlled mineral growth. Rev. Mineral. 26, 507–582.
Johnson, S. E., Jin, Z. H., Naus-Thijssen, F. M. J., and Koons, P. O. (2011). Coupled deformation and metamorphism in the roof of a tabular midcrustal igneous complex. GSA Bull. 123, 1016–1032. doi: 10.1130/B30269.1
Leuthold, J., Müntener, O., Baumgartner, L. P., Putlitz, B., Ovtcharova, M., and Schaltegger, U. (2012). Time resolved construction of a bimodal laccolith (Torres del Paine, Patagonia). Earth Planet. Sci. Lett. 325–326, 85–92. doi: 10.1016/j.epsl.2012.01.032
Manning, C. E., Ingebritsen, S. E., and Bird, D. K. (1993). Missing mineral zones in contact metamorphosed basalts. Am. J. Sci. 293, 894–938. doi: 10.2475/ajs.293.9.894
Michaut, C., and Jaupart, C. (2006). Ultra-rapid formation of large volumes of evolved magma. Earth Planet. Sci. Lett. 250, 38–52. doi: 10.1016/j.epsl.2006.07.019
Michel, J., Baumgartner, L. P., Putlitz, B., Schaltegger, U., and Ovtcharova, M. (2008). Incremental growth of the Patagonian Torres del Paine laccolith over 90 k.y. Geology 36, 459–462. doi: 10.1130/G24546A.1
Mori, H., Mori, N., Wallis, S., Westaway, R., and Annen, C. (2017). The importance of heating duration for Raman CM thermometry: evidence from contact metamorphism around the Great Whin Sill intrusion, UK. J. Metamorph. Geol. 35, 165–180. doi: 10.1111/jmg.12225
Nabelek, P. I., Hofmeister, A. M., and Whittington, A. G. (2012). The influence of temperature-dependent thermal diffusivity on the conductive cooling rates of plutons and temperature-time paths in contact aureoles. Earth Planet. Sci. Lett. 317–318, 157–164. doi: 10.1016/j.epsl.2011.11.009
Reverdatto, V. V., Sharapov, V. N., and Melamed, V. G. (1970). The controls and selected peculiarities of the origin of contact metamorphic zonation. Contrib. Mineral. Petrol. 29, 310–337. doi: 10.1007/BF00371278
Robertson, E. C. (1988). Thermal Properties of Rocks. Open File Report U.S. Geological Survey 88–441, 106.
Svensen, H., Jamtveit, B., Planke, S., and Chevallier, L. (2006). Structure and evolution of hydrothermal vent complexes in the Karoo Basin, South Africa. J. Geol. Soc. 163, 671–682. doi: 10.1144/1144-764905-037
Walther, J. V., and Orville, P. M. (1982). Volatile production and transport in regional metamorphism. Contrib. Mineral. Petrol. 79, 252–257. doi: 10.1007/BF00371516
Wang, D. (2012). Comparable study on the effect of errors and uncertainties of heat transfer models on quantitative evaluation of thermal alteration in contact metamorphic aureoles: thermophysical parameters, intrusion mechanism, pore-water volatilization and mathematical equations. Int. J. Coal Geol. 95, 12–19. doi: 10.1016/j.coal.2012.02.002
Wang, D. Y., and Manga, M. (2015). Organic matter maturation in the contact aureole of an igneous sill as a tracer of hydrothermal convection. J. Geophys. Res. Solid Earth 120, 4102–4112. doi: 10.1002/2015JB011877
Wang, D. Y., and Song, Y. C. (2012). Influence of different boiling points of pore water around an igneous sill on the thermal evolution of the contact aureole. Int. J. Coal Geol. 104, 1–8. doi: 10.1016/j.coal.2012.08.009
Whittington, A. G., Hofmeister, A. M., and Nabelek, P. I. (2009). Temperature-dependent thermal diffusivity of the Earth's crust and implications for magmatism. Nature 458, 319–321. doi: 10.1038/nature07818
Keywords: thermal aureole, contact metamorphism, magma intrusion, thermal diffusivity, incremental magma emplacement
Citation: Annen C (2017) Factors Affecting the Thickness of Thermal Aureoles. Front. Earth Sci. 5:82. doi: 10.3389/feart.2017.00082
Received: 04 August 2017; Accepted: 02 October 2017;
Published: 18 October 2017.
Edited by:
Georg F. Zellmer, Massey University, New ZealandReviewed by:
Takeshi Kuritani, Hokkaido University, JapanAntonio M. Álvarez-Valero, University of Salamanca, Spain
Mattia Pistone, University of Lausanne, Switzerland
Copyright © 2017 Annen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Catherine Annen, Y2F0aGVyaW5lLmFubmVuQGJyaXN0b2wuYWMudWs=
 Catherine Annen
Catherine Annen