Wind Tunnel Experiments: Influence of Erosion and Deposition on Wind-Packing of New Snow

1. Introduction

Wind-packed snow in the form of thin, hard crusts or thicker slabs is relevant in both alpine and polar areas. In mountainous terrain, wind slabs affect the avalanche danger and wind-packed snow in general affects how the snow cover interacts with the atmosphere. Especially at high latitudes, wind-packing affects the mass balance. Permanent deposition of snow often only occurs when the snow is packed and hardened by wind (Groot Zwaaftink et al., 2013). Yet, it is still not clear how these wind-hardened layers form. There are many qualitative descriptions of wind-packed snow, especially in polar literature (e.g., Schytt, 1958; Benson, 1967; Alley, 1988) and many different formation processes such as e.g., deposition of humidity onto the surface, fragmentation of snow crystals, or sintering have been proposed (e.g., Seligman, 1936; Schytt, 1958; Kotlyakov, 1966; Benson, 1967; Alley, 1988). Experimental evidence and quantitative information, however, are scarce.

In Sommer et al. (2017c), we presented a new wind tunnel specifically designed to study the formation of wind crusts. A SnowMicroPen (SMP) (Schneebeli and Johnson, 1998; Proksch et al., 2015) was used to measure changes in snow hardness. We showed that saltation is a necessary condition for wind-packing. No wind crust formed without drifting snow. However, saltation is not a sufficient condition. In many cases, wind with drifting snow did not lead to the formation of a crust or the resulting “crust” was still very soft. We suggested that spatial and temporal patterns of erosion and deposition may play a key role.

The available SMP data did not permit to test this hypothesis, however. Now, wind tunnel experiments were performed with an additional instrument, a Microsoft Kinect, allowing us to quantify erosion and deposition. Their influence on wind-packing is studied in this paper. The goal is to better understand why drifting snow forms a wind crust in some cases but not always.

In section 2, the wind tunnel and the main instruments are briefly introduced. The Kinect data acquisition and processing is described and the sensor is characterized with regard to its accuracy. Furthermore, the performed experiments and analyses are described. The combined SMP and Kinect results are presented in section 3. Discussion of the results and conclusions follow in sections 4 and 5.

2. Methods

2.1. Wind Tunnel and Main Instruments

The wind tunnel consists of a closed-circuit channel with an obround shape. This setup allows to simulate an infinite fetch. The two half-circles are separated by 1 m long straight sections. The overall length is 2.2 m and the width 1.2 m. The channel itself is 50 cm high and 20 cm wide (Figure 1A). An electric motor drives a model-aircraft propeller to create wind. The wind speed and other meteorological parameters are measured at the start of the main test section (Figure 1A). The wind tunnel and the instrumentation is described in detail in Sommer et al. (2017c).

FIGURE 1

Figure 1. (A) The Kinect mounted obliquely above the main test section of the wind tunnel. The modular support allowed us to find the best possible position and orientation of the Kinect in situ. Details of the Kinect sensor (B) and of the four reference targets attached to the windows of the main test section (C). The channel in (A) is 20 cm wide and 50 cm high. The straight section is 1 m long.

The SMP is the main instrument and is used to measure the hardness of snow on the ground. The SMP is a constant speed penetrometer measuring a profile of resisting force with a spatial resolution of 4 μm as the measuring tip is pushed into the snow. SMP measurements (SMPs) were acquired mostly in the main test section. The SMP can be positioned freely but most often SMP positions were chosen on a regular grid. In the cross-stream direction, SMPs were acquired in the center and 4 cm to each side. In the streamwise direction, the SMPs were 3 cm apart (see also Figure 3F).

In winter 2016/2017, a Microsoft Kinect 2.0 (or v2, Pagliari and Pinto, 2015) was installed as an additional instrument. The Kinect is a motion sensing input device for the Microsoft Xbox gaming console. It is basically a low-cost 3D scanner. The Kinect was installed above the main test section (Figure 1A) and it measures the evolution of snow depth in the entire straight section. The Kinect (Figure 1B) computes depth by measuring the phase shift of the emitted, modulated infrared light. The depth camera has a resolution of 512 × 424 pixels and a field of view of 70 × 60°. The sensor, including accuracy considerations and comparisons to the Kinect 1.0, is described in Lachat et al. (2015), Pagliari and Pinto (2015), and Yang et al. (2015). Pagliari and Pinto (2015) attest an accuracy of about 1.5 cm and a precision (repeatability) of about 1 mm to the depth camera at ranges up to 4 m. Yang et al. (2015) reported an accuracy of below 2 mm over most of the field of view at a range of 1 m. In the center of the field of view, the same accuracy was observed at distances up to 3 m.

The Kinect is mounted about 30 cm above the cover of the main test section at an oblique angle of about 17° (Figure 1A). Ideally, the Kinect would be embedded in the cover and look straight down at the surface. The sensor is mounted above the cover because the minimum distance it can resolve is 50 cm. Furthermore, the emitted infrared light is reflected off the Plexiglas cover and leads to a blind spot in the depth image. The oblique mounting angle moves this blind spot from the center to the edge of the field of view. The exact mounting angle is measured before each experiments by taking 100 depth images of a flat surface in the main test section. The cover of the test section with the Kinect on it has to be removed for SMP measurements between the wind periods. Therefore, it cannot be excluded that the Kinect is in a slightly different position for each wind period. Such misalignments were on the order of millimeters but still reduce the accuracy of the snow depth measurements. To correct these errors, four rectangular reference targets were installed in the main test section (Figure 1C). These fixed targets can be used to align the images of the different wind periods with each other. The eight corners of these targets pointing into the channel were used as reference points for the registration. During wind periods, depth images were acquired at a nominal rate of 5 Hz. The effective frame rate was only about 3.6 Hz on average due to the long (≈10 m) USB cable even though an active cable was used.

2.2. Experiments

All experiments started with fresh snow collected on trays outside the building during snowfalls. The filled trays are placed underneath the wind tunnel while it is lifted by a crane. The wind tunnel, which is open at the bottom, is then lowered into the snow cover. The experiments therefore start with a continuous cover of natural and almost undisturbed new snow. The initial snow was usually a few hours old and had a density between 30 kg/m³ and about 100 kg/m³. Grain sizes and shapes varied with the meteorological conditions during the snowfalls.

Experiments consisted of one or several wind periods, before and after which, SMP measurements were performed. A typical wind period was about 30 min long but there were some as long as several hours or as short as a few minutes. Averaged over all SMPs, the cumulative duration of wind periods before an SMP was almost 3 h. The median was 1 h and 15 min, the maximum almost 21 h and the minimum was <4 min. The wind speed was between 3 and 7 m/s in most wind periods. Higher wind speeds would be possible but were not practical due to the increasing centrifugal effects in the turns. The air temperature in the wind tunnel varied between −9 and 1°C.

Several experiments were performed with an obstacle in the test section. This allowed to force deposition of snow and to test the difference between wind-exposed and wind-sheltered deposition. Figure 2 shows the obstacle at the beginning of an experiment. A 6 × 6 × 18 cm rectangular block of wood was pressed halfway into the snow such that a triangular obstacle with a height of about 4 cm remained.

FIGURE 2

Figure 2. The obstacle in the test section at the beginning of an experiment. The obstacle is a block of wood with a square 6 × 6 cm cross section.

2.3. Data Processing

The SMP data processing is described in Sommer et al. (2017c). In short, each force profile is reduced to a representative number called “SMP hardness” by calculating the 90% quantile of the force signal in the topmost centimeter of snow. Section 3 shows results using the SMP hardness as well as the full SMP profile.

The Kinect depth images are processed in Matlab. After aligning all raw depth images (Figure 3A) to those of the first wind period to account for the variable Kinect position, they are transformed into 3D point clouds to simplify the further processing. The point clouds are rotated by the previously determined mounting angle (Figure 3B). The point clouds are then cropped to contain only the snow surface (Figure 3C). The corners are cut off because there, the four targets obstruct the view of the snow surface. Finally, the point clouds are filtered to remove isolated points, for example in SMP measurement holes (Figure 3D), and transformed back to depth images with a resolution of 2 mm per pixel (Figure 3E). Additionally, the average depth of each target is calculated at each time step and these target depths are saved for later use.

FIGURE 3

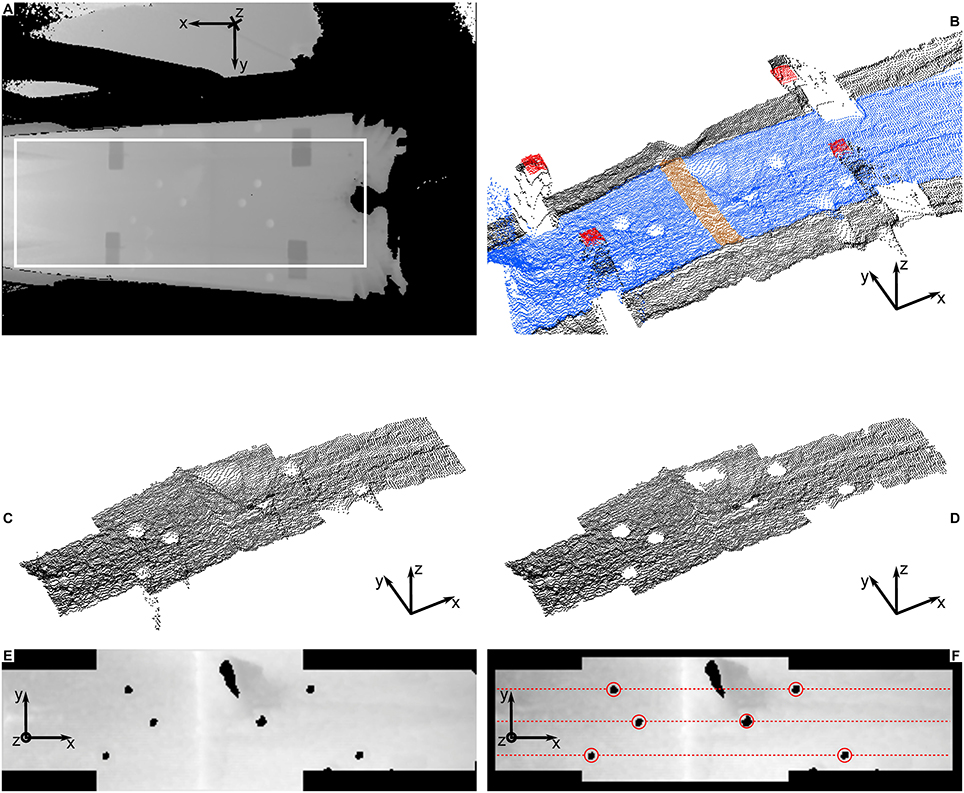
Figure 3. Processing steps of the Kinect data. The coordinate system in each sub-figure shows the same real-life directions: x is the streamwise direction, y is the cross-stream direction and z is the vertical. (A) Raw Kinect depth image. The four darker rectangles are the targets, the lighter circles are SMP holes. The black circular shape on the right is the reflection blind spot. The other black areas are too close to the sensor to be resolved. (B) Point cloud of the raw depth image inside of the white rectangle in (A). The targets are red, the snow surface is blue and an almost buried artificial obstacle is colored brown. (C) Point cloud cropped to contain only the snow surface and the obstacle. The four corners are cut away to remove the targets. (D) Filtered point cloud. Isolated points are removed. The SMP holes are now more clearly visible. There is also a measurement shadow just downstream of the obstacle. (E) Processed depth image. The SMP holes and the measurement shadow appear as black areas, as do the cut off corners. The obstacle is visible as a light, vertical line. (F) Processed and corrected depth image. The edges are cut away during the correction. The effect of the correction is most visible on the left. The red circles indicate the manually determined SMP positions. The dashed, red lines show the three lines on which all SMPs are acquired and where the Kinect profiles are calculated.

Some corrections are then applied to the processed depth images. The measured depth of the stationary targets usually varied by a few mm during experiments. These variations could be due to temperature variations of the Kinect's electronics. Furthermore, the measured depth always decreased by about 2 mm when a person was close to the window in the main test section. Apparently, the infrared signal measured by the Kinect is influenced by the body heat or the additional reflection. These errors were corrected using the target depths. The variations around the mean target depths was subtracted from the measured snow depth. The depth evolution was a little different for each target. Therefore, each pixel was corrected individually using a weighted average of the four targets based on the distances between the current pixel and the four targets. The accuracy and linearity of the Kinect were characterized by taking depth images of a flat surface in the main test section at nine different known heights above the floor (see also section 2.4). The height of the flat surface was increased by either 20 or 21 mm at each step. The characterization revealed a slight non-linearity of the measured depth that, in addition, depended on the position in the field of view. This non-linearity of the Kinect was corrected using the characterization images. The depth images of the flat surface were smoothed by applying a moving window filter that averaged the depths within radii of five pixels. A five pixel wide band was therefore discarded at each edge (Figure 3F). The smoothed images were used to fit a second-order correction for each remaining pixel. These corrections fit the nine measured heights of the flat surface to the corresponding true heights and were then applied to the processed depth images. Averaged over every pixel, the second-order correction for the depth D is $D_{new}=2.51·10^{-4}{D}_{old}^2+0.90D_{old}-20.15$. The fit is very good for every pixel. The adjusted R² is always higher than 0.999 and the Root Mean Squared Error is 0.6 mm on average and 1.8 mm for the worst pixel. The constant offset may seem like a large correction. It is due to the different coordinate systems used for the Kinect and to measure the real heights of the flat surface. The order of magnitude of this offset has no consequence because the Kinect is only used to measure depth changes.

The positions of the SMP measurements are determined manually in the processed and corrected depth images (Figure 3F). The SMP holes were clearly visible in most cases. The snow depth evolution can then be calculated at each SMP position. The depths within a radius of six pixels of the SMP position were averaged and a moving window filter with a width of 10 s was applied afterwards.

The processed and corrected depth images were also used to calculate snow depth profiles in the streamwise direction. Profiles were calculated at the three cross-stream positions that were also used for all SMPs (Figure 3F). The profiles were averaged over eight pixels in the cross-stream direction. The absolute depth measured by the Kinect depends on the position in the depth image. This is probably due to the Kinect's lens and is especially accentuated toward the edges of the field of view. This means that a flat surface in reality does not appear flat in the depth image. Therefore, relative snow depth profiles were calculated by subtracting the initial profiles. For experiments with an artificial obstacle in the main test section, the obstacle was not removed in the relative profiles. Figure 7 in the results section includes some examples of relative snow depth profiles.

2.4. Kinect Accuracy Assessment

During the Kinect characterization, two measurements were made at each height of the flat surface. The first measurements were used to fit the corrections. The second measurements were used to assess the accuracy of the Kinect with regard to snow depth changes. We use “height” and “height changes” here because the characterization was done without snow. Height refers to the distance between the floor and the flat surface. The accuracy was assessed on a 3 × 16 grid of positions in the main test section that were usually used for SMP measurements. As for the SMPs, the depths were averaged within a radius of six pixels of these positions. For every position, absolute and relative errors were then calculated. The errors were large at the three positions at the upstream edge of the field of view. This could be due to the reflection blind spot which is located there. These positions are therefore neglected here and no Kinect data from these positions is used in the results. The errors in the remaining 45 positions were quite similar.

Figure 4A shows the mean absolute errors as a function of the height change and the lower of the two heights and Figure 4B shows the mean absolute relative errors. The means were calculated using the remaining 45 positions. For the mean absolute errors, there is no significant trend with either height or height change. As a result, the mean absolute relative errors decrease with increasing height change. The overall averages of the mean absolute errors are 0.60 mm and 1.28%. The overall maximum absolute errors for any combination of position, height, and height change are 2.58 mm and 9.69%.

FIGURE 4

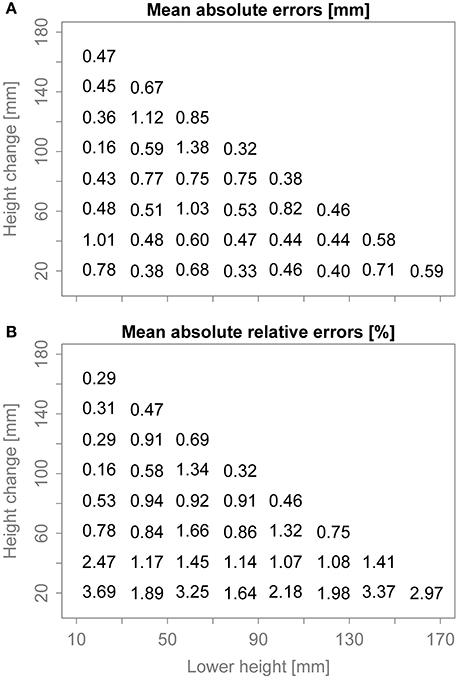
Figure 4. Mean absolute errors (A) and mean absolute relative errors (B) as functions of height change and the height of the bottom surface. Each number is the mean of the errors at the 45 remaining positions.

2.5. Dataset and Analyses

A total of 1,054 SMPs were acquired during 38 experiments in the winters 2015/16 and 2016/17. Six hundred and eighty eight SMPs were taken after wind periods with drifting snow. For 335 of those measurements, snow depth data from the Kinect is available. The following results are mostly based on this last group of SMPs. Only 27 measurements from the first winter, i.e., SMPs without Kinect data, are used here. For these measurements, we know from the log and by manual observation whether they were acquired after erosion or deposition, for example. This information is not available for most SMPs from the first winter and these data can therefore not be used here. The Kinect and SMP data, as well as the postprocessing scripts, are publicly available on Envidat (Sommer et al., 2017a,b).

In the next section, boxplots are used to compare groups of SMPs (e.g., erosion or deposition) and the Kruskal-Wallis test (Kruskal and Wallis, 1952) is used to determine whether they differ significantly. This is a non-parametric test and can therefore be used even if the data are not normally distributed or if the sample size is small. Scatterplots and correlation coefficients are used to show relationships between variables.

3. Results

3.1. Erosion and Deposition

Figure 5 compares SMPs that were taken at positions where snow was either eroded or deposited. The boxplots show the overall SMP hardness change between the initial and the current measurements. No measurable hardening occurs when snow is eroded. The median SMP hardness change of the “Erosion” group is 3 mN and the standard deviation is 2 mN. In the “Deposition” group, there are SMP hardness changes between 0 and 860 mN and the median of the group is 100 mN. A Kruskal-Wallis test confirms that the two groups are different at a significance level of α < 0.001.

FIGURE 5

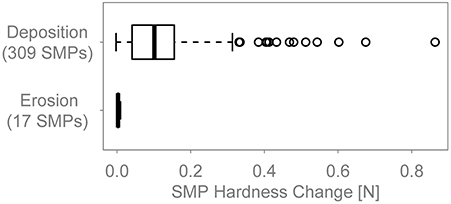
Figure 5. Boxplots comparing SMPs that were acquired in positions were snow was either deposited or eroded.

3.2. Obstacle Experiments

Figure 6 shows the boxplots comparing SMPs acquired on the windward or leeward side of the obstacle. The experiments with obstacle were split in two groups based on whether saltation started spontaneously or not. During experiments at warm temperatures and/or deliberate low wind speed, drifting snow did not start spontaneously and saltation could only be achieved and sustained by sieving snow into the wind tunnel (see Figure 1 in Sommer et al., 2017c). Furthermore, only SMPs that were acquired after a single wind period with drifting snow are shown in Figure 6. Both the windward and leeward side of the obstacle were usually filled up during the first wind period with drifting snow. The obstacle as such was therefore not effective anymore during subsequent drifting snow events and the corresponding SMPs cannot be analyzed with regard to wind-exposed and wind-sheltered deposition.

FIGURE 6

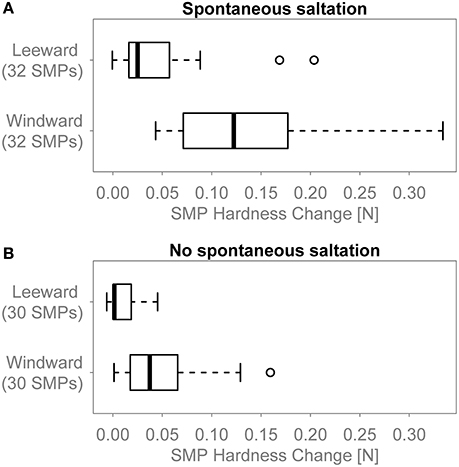
Figure 6. Boxplots comparing SMPs that were acquired either on the windward or the leeward side of the obstacle during experiments where (A) saltation started spontaneously or (B) saltation could only be achieved by sieving snow into the wind tunnel.

During the experiments with spontaneous saltation shown in Figure 6A, the median hardness change of the SMPs on the leeward side of the obstacle was 25 mN. The median of the “Windward” group is 120 mN. For the experiments with no spontaneous saltation (Figure 6B) the median SMP hardness change is 2 mN for the “Leeward” group and 37 mN for the “Windward” group. In both cases, the Kruskal-Wallis test confirms at a significance level of α < 0.001 that the SMP hardness change on the windward side is higher than on the leeward side. The hardness increase with spontaneous drifting is higher than without spontaneous drifting in leeward and windward locations. In fact, the “Leeward” group in Figure 6A shows comparable hardness changes as the “Windward” group in Figure 6B. If the experiments with and without spontaneous saltation are not separated, the difference between the windward and the leeward side is less clearly visible in the boxplots but a Kruskal-Wallis test still confirms that the SMP hardness increases more on the windward side at a significance level of α < 0.001.

3.3. Wind Exposure

The classification of SMPs in groups either windward or leeward of the obstacle is a very crude representation of wind-exposed and wind-sheltered deposition. For example, how wind-sheltered a position on the leeward side is depends on the distance to the obstacle and also on time as the surface evolves. As mentioned before, the leeward side becomes less wind-sheltered as snow is being deposited. We used the relative Kinect snow depth profiles to calculate the wind exposure parameter Sx (Winstral and Marks, 2002) for each SMP position as a function of time. Sx is the maximum upwind slope, i.e., the slope between the point of interest and the shelter-giving point which maximizes the upward angle. Positive Sx values mean the point of interest is wind-sheltered while wind-exposed points have negative Sx. We used a maximum search distance of 200 mm and also introduced a minimum distance of 5 mm to limit the influence of nearby features. Five millimeters is the diameter of the SMP measuring tip. Figure 7 shows some examples of shelter-giving points.

FIGURE 7

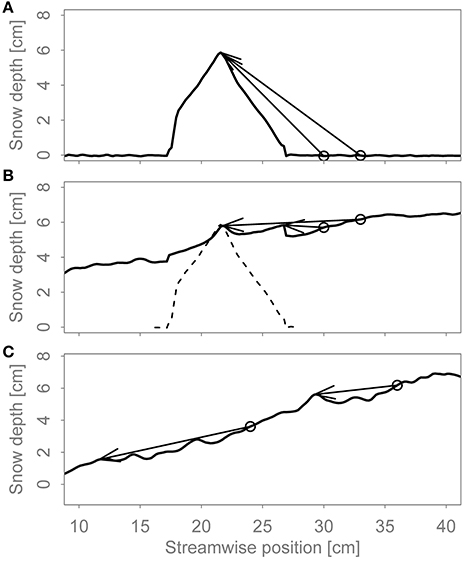
Figure 7. Relative Kinect snow depth profiles and arrows showing some examples of shelter-giving points. The circles show the SMP positions. The wind is from left to right. (A) Initial conditions of an experiment with an obstacle and two highly wind-sheltered SMP positions. (B) Same experiment as in (A) but after deposition of snow around the obstacle. The same SMP positions are now not wind-sheltered anymore. The dashed line outlines the obstacle. (C) Two examples of wind-exposed SMP positions during an experiment without an obstacle.

To analyze the effect of wind exposure or sheltering on wind-packing in more detail we want to correlate Sx with the penetration resistance or force measured by the SMP. While Sx is a function of time, the force is a function of penetration depth. Therefore, we need to map depth to time and vice-versa or, in other words, we need to know at what time each snow layer was deposited. The mapping for a given SMP is calculated on the basis of the Kinect snow depth data at this SMP position (Figure 8A). Only time periods with a monotonically increasing snow depth are kept. If there was erosion during the wind period, the mapping splits the wind period in several deposition periods. A moving window filter with a width of 1 mm and 50% overlap is then applied to the mapping. However, there is no averaging across gaps between deposition periods longer than 10 s and there must be at least 30 SMP sample points in each window. Filter windows that do not meet these requirements were removed. Furthermore, filter windows within 4.3 mm of the snow surface were also removed. 4.3 mm is the height of the conic part of the SMP measuring tip. Only starting at this depth, can the measuring tip be considered to be completely in the snow. For each remaining filter window, the Sx and force values within it are averaged (Figures 8A–C and the red line between them). These averages are then plotted against each other in a scatterplot (Figure 8D).

FIGURE 8

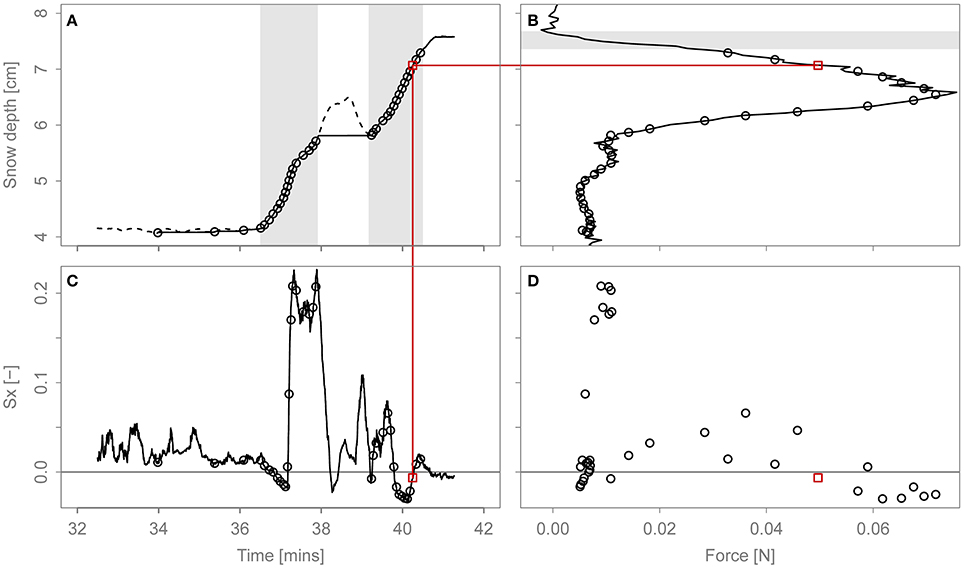
Figure 8. Correlating the SMP force with Sx. (A) Depth-time mapping. The dashed line is the underlying snow depth data. It can be seen how the mapping splits the wind period in distinct deposition periods. The two main deposition periods are highlighted. The circles show the remaining points after the moving window filter is applied to the mapping. (B) SMP force profile. The neglected part of the profile close to the snow surface is highlighted (C) Sx as a function of time. (D) Scatterplot of Sx against force. The red line across the sub-plots shows for one filter window how the mapping in (A) connects force (B) with Sx (C). The corresponding filter window is shown as a red square in all four sub-plots.

Figure 9 shows a scatterplot of Sx against the SMP force with data from 87 SMPs. Settling can make it difficult to match the Kinect snow depth data to the SMP force profile. However, it is relatively straightforward for SMPs where saltation occurred only during one of the preceding wind periods. These 87 SMPs acquired during experiments both with and without the obstacle are used here. The overall correlation coefficient of the 4,534 Sx and force pairs is −0.63. Practically no hardening occurs for Sx above 0.3. For Sx below 0.2, almost any force appears to be possible but the highest forces have mostly negative Sx. There are about ten points with Sx ≈ 0.2 and forces between 0.17 and 0.23 N that seem to contradict this. These points are all from a single SMP measurement. It is unclear whether this SMP measurement is reliable or if there was a problem with the mapping, for example. The influence of the moving filter width, which is 1 mm in Figure 9, was tested. As the width is increased, the number of points decreases but the shape of the point cloud stays the same and the correlation coefficient actually increases. For a filter width of 20 mm, there are 1,596 points and the correlation coefficient is −0.7.

FIGURE 9

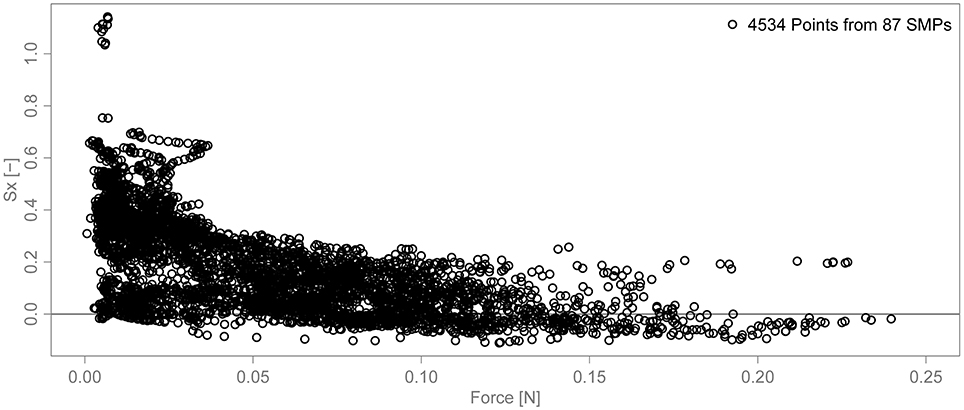
Figure 9. Scatterplot of Sx against the SMP force showing the effect of wind-exposure on wind-packing. The plot is the same as Figure 8D but shows 4,534 points from 87 SMPs.

3.4. Deposition Rate

The Kinect data can also be used to calculate the deposition (and erosion) rate at the SMP positions. The snow depth data is too noisy to use a numeric derivative. Instead, the average slope in a 15 s moving window was calculated. The same mapping (Figure 8A) is then used to correlate the SMP force to the deposition rate. Figure 10 shows the corresponding scatterplot. Based on Figure 9, only points with Sx < 0.2 are shown here. The correlation coefficient between the 2,983 point pairs is −0.40. All points with a hardness above 0.15 N have a deposition rate below about 0.2 mm/s and all points with a deposition rate above about 0.6 mm/s have a hardness below 0.1 N.

FIGURE 10

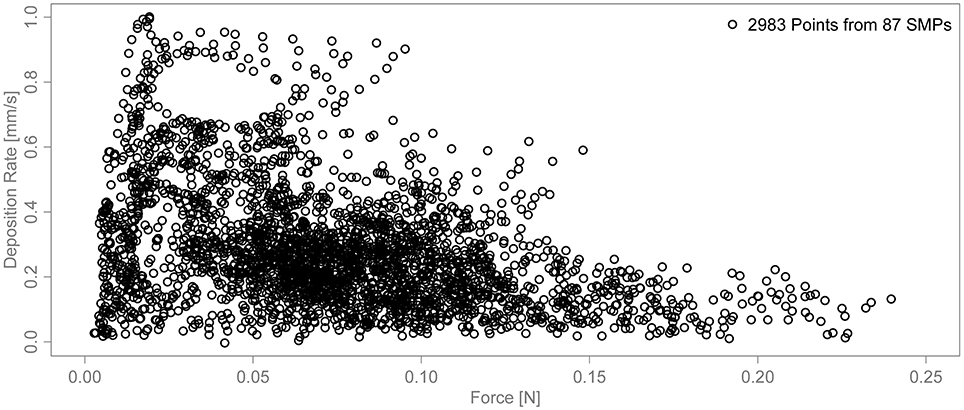
Figure 10. Scatterplot of the deposition rate against the SMP force. The plot shows the 2,983 points with Sx < 0.2 from the same 87 SMPs as in Figure 9.

A multilinear regression between the SMP force and Sx, deposition rate and their interaction results in an adjusted R² of 0.47. All three terms in the model are highly significant. Sx alone explains 40% of the variability.

4. Discussion

The raw Kinect data requires complex processing to become useful but after the different corrections, snow depth changes could be measured with an accuracy of <1 mm in most positions in the main test section (Figure 4). Therefore, the Kinect is well-adapted to quantify erosion and deposition in the wind tunnel. Even so, some problems remain. Settling makes it difficult to match SMP force profiles to the Kinect snow depth data if there was more than one wind period with drifting snow before the SMP was acquired. These SMPs had to be neglected in the current study. In many experiments, there was only one short wind period with drifting snow at the beginning of the experiment. Often, the wind was cut off as soon as the depositions in the test section buried the artificial obstacle and the subsequent measurement periods were either without drifting snow or even without wind. In these cases, the decrease of the snow depth measured by the Kinect after the first wind period is the settling and it can be corrected with a simple offset because the settling during the short period with drifting snow can be neglected. If saltation continues in subsequent wind periods, it is unclear how much of the snow depth change is due to erosion, deposition or settling. Maybe a simple model could be used to “reverse” the settling in these cases or the settling could be measured independently of the Kinect. It can be assumed that settling is mostly caused by the compaction of the undisturbed snow below the wind crust because the crust is usually a lot denser. Therefore, the depth evolution of the interface between the wind crust and the undisturbed snow would be a good indicator of settling except if an existing wind crust is completely eroded again.

During our experiments, no hardening occurred when snow was being eroded (Figure 5). There are only 17 SMPs in the “Erosion” group. Most likely, more measurements were made after erosion but this plot only contains those for which we were absolutely sure that there was only erosion before the SMP was acquired. The distribution of these 17 measurements is very narrow and the conclusion that saltation can only form wind crusts if no snow is eroded can therefore be made. Nevertheless, we cannot generally conclude that erosion never leads to hardening of the remaining snow. The 17 SMPs in Figure 5 measured the effect of erosion on new snow. The effect of erosion may be different on older, already wind-influenced snow. We acquired many SMPs were a wind crust was first deposited and then partly eroded again. These measurements could theoretically be used to study the effect of erosion on old snow. However, it is very difficult to differentiate between the effects of the initial deposition and the subsequent erosion. The SMPs before and after erosion were necessarily acquired at different positions. The spatial variability in our wind tunnel is too high to attribute hardness changes between those SMPs to erosion. Hardness changes between SMPs are only meaningful if the snow cover was homogeneous before the change occurred. We can test the effect of erosion on new snow because the initial snow cover is homogeneous. We would therefore need an equally homogeneous old snow cover. Maybe a slab of dense, homogeneous snow could be prepared in the cold lab and then be placed in the wind tunnel's test section or old snow could be sieved into the wind tunnel. In our opinion, the main factor determining whether erosion has a hardening effect on the remaining snow is the erosion rate. In the limiting case where saltation causes neither deposition nor erosion, i.e., the two are in equilibrium, it can be expected that the continuous impacts of particles at the surface will eventually harden the snow. Then, if snow is eroded only slowly, it is very likely that the remaining snow is still being hardened because most particles only impact on the surface without removing any snow. The main reason why erosion had no effect on new snow is probably because the snow was eroded too quickly. For older snow consisting of smaller, already wind-influenced particles, erosion may be slower and could have a hardening effect on the remaining snow. It is likely that the effect increases as the angle of impact becomes more perpendicular. This could be how the extremely hard windward edges of zastrugi are formed. The formation of zastrugi has been described in detail by e.g., Doumani (1967), Filhol and Sturm (2015), and Goodwin (1990). The potential hardening effect of erosion is not discussed, however.

We only observed wind crusts after snow had been deposited but not all depositions were hard (Figure 5). An important factor determining the hardness of a deposition of wind-blown snow is whether the snow was deposited in a wind-exposed or wind-sheltered area. Our results show that the snow is hardened more on the windward side than on the leeward side of an obstacle (Figure 6). However, the hardening on the windward side during experiments without spontaneous drifting (Figure 6B) is comparable to the hardening on the leeward side during experiments were saltation occurred spontaneously (Figure 6A). This suggests that environmental conditions such as wind speed, air temperature and the properties of the snow cover have an effect on wind crust formation as well. Furthermore, windward and leeward of an obstacle is a rather poor classification because the wind-exposure of a given position can change dramatically as snow is being deposited and eroded at and upwind of this position. The combination of Kinect and SMP data enables us to correlate the SMP force at a given penetration depth with the wind exposure parameter Sx at the corresponding time. This scatterplot of Sx against force (Figure 9) gives a more complete picture of the influence of wind-exposure on wind-packing than the windward/leeward boxplots in Figure 6. There appears to be a transition at Sx ≈ 0.25. No significant hardening occurs at Sx > 0.25 and below this value, any amount of hardening seems possible. The regime shift at Sx ≈ 0.25 is valid in the wind tunnel and it is unclear whether the same value is relevant in real terrain at the catchment scale. In such a case, digital elevation models typically have a resolution between one and several tens of meters and the elevation differences are much higher than in the wind tunnel. The settings to calculate Sx have to be adapted to the larger scale and this could lead to different values.

The variability in wind-exposed areas can be partly explained by the deposition rate (Figure 10). Deposition in wind-exposed areas only leads to significant hardening if the snow is deposited slowly enough. Rapidly deposited snow remains relatively soft. This could be observed on the windward side of the obstacle where snow was often deposited very quickly at the beginning of experiments. It appears that there is not enough time to harden the snow if it is deposited too quickly. However, there are also many points with a low deposition rate and a low SMP force. Slow deposition in a wind-exposed area is still not a sufficient condition to form a hard wind crust.

The parameters Sx and deposition rate explain roughly half of the observed variability of wind crust hardnesses. The remaining variability is difficult to explain with our data. There are small positive correlations between the SMP force and the density and temperature of the fresh snow. This shows that the initial conditions have an effect on the resulting wind crust. However, adding these two parameters to the multilinear regression increases the adjusted R² by only four percentage points to 51%. We attempted to add meteorological parameters such as wind speed, air temperature and air humidity to the linear model. No clear and robust trends could be found between the SMP force and those parameters. The main reason for that is probably the narrow range of meteorological conditions in the wind tunnel during the experiments. Another parameter that could be important is the saltation intensity or the drifting mass flux. So far, this was not measured in the wind tunnel but this could maybe be done with a particle counter. We would expect a positive correlation between the saltation intensity and the hardness. This could explain the differences in SMP hardness change between the experiments with and without spontaneous saltation (Figure 6). Another parameter that was not discussed so far is time. As described in section 2, the durations of wind periods varied a lot. However, at the time scale of hours there was no relationship between the hardness of snow and the duration of experiments.

Up to recently, no quantitative studies on wind-packing were available and which physical processes are at work was a matter of speculation (e.g., Seligman, 1936; Schytt, 1958; Kotlyakov, 1966; Benson, 1967; Alley, 1988). Sommer et al. (2017c) could show that saltation is necessary. This excludes some of the proposed processes and means that fragmentation of snow crystals in the saltation layer and subsequent sintering could be the dominating process. In this study, we now saw that the wind-exposure during deposition is important and observed wind crusts after only a few minutes of wind. This suggests that the impact of snow particles during deposition could be another important hardening process. Sintering, on the other hand, appears less important since we did not observe increasing hardnesses with increasing experiment duration. However, it is important to keep the relevant time scales in mind. While the fragmentation happens as the snow particles are still mobile and the hardening due to the impact momentum happens at the moment of deposition, sintering begins only afterwards. At the time scale of hours, it could be that the hardening due to sintering is masked by the hardening due to deposition. It is possible that at a time scale of days, the hardness would continue to increase due to sintering of the previously deposited snow.

Even if no quantitative statements can be made about the importance of the different processes based on our results, they could help to improve snow cover models such as Snowpack or Crocus (Vionnet et al., 2012; Groot Zwaaftink et al., 2013) or earth system models (van Kampenhout et al., 2017). Such models contain simple parameterizations to account for the hardening due to wind. With our results, it is not possible to replace the parametric model with a physical model of wind-packing but the necessary conditions that we found could be implemented.

Wind slabs deposited onto leeward slopes are a major avalanche danger (e.g., Schweizer, 2003). Our result, that snow deposited in wind-sheltered areas remains soft, does not contradict that. The observed, small hardness increase is enough to form a cohesive layer. The existence of such a cohesive slab is the main condition for the formation of a slab avalanche. The hardness of the overlying slab influences fracture initiation and propagation in the weak layer and therefore how easily an avalanche can be triggered. In fact, as the hardness of the slab increases, it becomes more difficult to initiate a fracture but once initiated, it propagates more easily (van Herwijnen and Jamieson, 2007). Our results suggest that soft wind slabs are prevalent shortly after drifting-snow events and that hard wind slabs may become more relevant as sintering hardens the deposited slab.

5. Conclusions

In this study, we looked at the effect of saltation on wind-packing through the combination of SMP and Kinect data. Several necessary conditions for the formation of a wind crust could be identified. There has to be deposition of snow in a wind-exposed area and the deposition rate has to be low. However, these conditions are not sufficient and about half of the observed hardness variability cannot be explained. Furthermore, the results do not allow quantitative statements about which physical processes are at work or how saltation affects old snow. More experimental work is necessary to answer these questions. Nevertheless, the fact that about half of the variability could be explained may allow for a rudimentary parametrization in larger-scale models.

Author Contributions

CS did the most of the research and wrote the manuscript. ML and CF conceived and supervised the project, provided guidance, helped with the analysis and revised the manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer MM and handling editor declared their shared affiliation.

Acknowledgments

We would like to thank Ken Mankoff for the idea of installing a Kinect in the wind tunnel and the SLF workshop and electronics lab for their help with the installation. Research reported in this publication was supported by the Swiss National Science Foundation under grant number 200021_149661. Finally, we thank the two reviewers for their constructive comments.

References

Alley, R. B. (1988). Concerning the deposition and diagenesis of strata in polar firn. J. Glaciol. 34, 283–290.

Google Scholar

Benson, C. S. (1967). Polar regions snow cover. Proc. Phys. Snow Ice 1, 1039–1063.

Google Scholar

Doumani, G. A. (1967). Surface structures in snow. Phys. Snow Ice 1, 1119–1136.

Google Scholar

Filhol, S., and Sturm, M. (2015). Snow bedforms: a review, new data, and a formation model. J. Geophys. Res. 120, 1645–1669. doi: 10.1002/2015JF003529

CrossRef Full Text | Google Scholar

Goodwin, I. D. (1990). Snow accumulation and surface topography in the katabatic zone of Eastern Wilkes Land, Antarctica. Antarc. Sci. 2, 235–242.

Google Scholar

Groot Zwaaftink, C. D., Cagnati, A., Crepaz, A., Fierz, C., Macelloni, G., Valt, M., et al. (2013). Event-driven deposition of snow on the Antarctic Plateau: analyzing field measurements with SNOWPACK. Cryosphere 7, 333–347. doi: 10.5194/tc-7-333-2013

CrossRef Full Text | Google Scholar

Kotlyakov, V. (1966). The Snow Cover of the Antarctic and Its Role in the Present Day Glaciation of the Continent. Jerusalem: IPST.

Google Scholar

Kruskal, W. H., and Wallis, W. A. (1952). Use of ranks in one-criterion variance analysis. J. Am. Stat. Assoc. 47, 583–621.

Google Scholar

Lachat, E., Macher, H., Mittet, M.-A., Landes, T., and Grussenmeyer, P. (2015). First experiences with Kinect V2 sensor for close range 3D modelling. Int. Arch. Photogr. Rem. Sens. Spat. Inform. Sci. XL-5/W4(5W4), 93–100. doi: 10.5194/isprsarchives-XL-5-W4-93-2015

CrossRef Full Text | Google Scholar

Pagliari, D., and Pinto, L. (2015). Calibration of Kinect for Xbox one and comparison between the two generations of microsoft sensors. Sensors 15, 27569–27589. doi: 10.3390/s151127569

PubMed Abstract | CrossRef Full Text | Google Scholar

Proksch, M., Löwe, H., and Schneebeli, M. (2015). Density, specific surface area, and correlation length of snow measured by high-resolution penetrometry. J. Geophys. Res. 120, 346–362. doi: 10.1002/2014JF003266

CrossRef Full Text | Google Scholar

Schneebeli, M., and Johnson, J. B. (1998). A constant-speed penetrometer for high-resolution snow stratigraphy. Ann. Glaciol. 26, 107–111.

Google Scholar

Schweizer, J. (2003). Snow avalanche formation. Rev. Geophys. 41:1016. doi: 10.1029/2002RG000123

CrossRef Full Text | Google Scholar

Schytt, V. (1958). Snow Studies at Maudheim. Oslo: Norsk Polarinstitutt.

Seligman, G. (1936). Snow Structure and Ski Fields: Being an Account of Snow and Ice Forms Met with in Nature, and a Study on Avalanches and Snowcraft. London: Macmillan.

Sommer, C. G., Lehning, M., and Fierz, C. (2017a). Wind Crust Formation: Microsoft Kinect Data. Davos: WSL Institute for Snow and Avalanche Research SLF.

Sommer, C. G., Lehning, M., and Fierz, C. (2017b). Wind Crust Formation: SnowMicroPen Data. Davos: WSL Institute for Snow and Avalanche Research SLF.

Sommer, C. G., Lehning, M., and Fierz, C. (2017c). Wind tunnel experiments: saltation is necessary for wind-packing. J. Glaciol. 63, 950–958. doi: 10.1017/jog.2017.53

CrossRef Full Text | Google Scholar

van Herwijnen, A., and Jamieson, B. (2007). Snowpack properties associated with fracture initiation and propagation resulting in skier-triggered dry snow slab avalanches. Cold Reg. Sci. Technol. 50, 13–22. doi: 10.1016/j.coldregions.2007.02.004

CrossRef Full Text | Google Scholar

van Kampenhout, L., Lenaerts, J. T. M., Lipscomb, W. H., Sacks, W. J., Lawrence, D. M., Slater, A. G., et al. (2017). Improving the representation of polar snow and firn in the community earth system model. J. Adv. Model. Earth Syst. 9, 2583–2600. doi: 10.1002/2017MS000988

CrossRef Full Text | Google Scholar

Vionnet, V., Brun, E., Morin, S., Boone, A., Faroux, S., Le Moigne, P., et al. (2012). The detailed snowpack scheme Crocus and its implementation in SURFEX v7.2. Geosci. Model Dev. 5, 773–791. doi: 10.5194/gmd-5-773-2012

CrossRef Full Text | Google Scholar

Winstral, A., and Marks, D. (2002). Simulating wind fields and snow redistribution using terrain-based parameters to model snow accumulation and melt over a semi-arid mountain catchment. Hydrol. Process. 16, 3585–3603. doi: 10.1002/hyp.1238

CrossRef Full Text | Google Scholar

Yang, L., Zhang, L., Dong, H., Alelaiwi, A., and Saddik, A. E. (2015). Evaluating and improving the depth accuracy of Kinect for windows v2. IEEE Sens. J. 15, 4275–4285. doi: 10.1109/JSEN.2015.2416651

CrossRef Full Text | Google Scholar