Modeling Winter Precipitation Over the Juneau Icefield, Alaska, Using a Linear Model of Orographic Precipitation

1. Introduction

Ongoing world-wide glacier mass loss has major implications for sea level, local water resources, and natural hazards. A glacier's mass budget is determined by the balance of snow accumulation and ablation. However, assessing and modeling snow accumulation in complex glacierized terrain remains challenging, since observations are prone to wind-induced undercatch and generally scarce (Sevruk et al., 2009), and precipitation (and associated snow accumulation) typically varies greatly at small spatial scales in such environments. Jarosch et al. (2012) summarized the precipitation downscaling methods employed in recent glacier mass balance modeling studies. Glacier mass balance models have often applied simple empirical, mostly elevation-dependent, relations to distribute point precipitation data across glacier surfaces (e.g., Hock and Holmgren, 2005; Radić et al., 2014) or directly used gridded coarse-scale climate data (e.g., Ziemen et al., 2016). Both approaches typically fail to resolve the complex precipitation patterns in glacierized mountainous terrain (Schuler et al., 2008; Jarosch et al., 2012).

The purpose of this study is to utilize an orographic precipitation model to provide fine resolution winter precipitation fields of the Juneau Icefield, one of the largest ice masses in North America, to be used for the improvement of mass balance modeling efforts in this region. The rugged and complex terrain of the Juneau Icefield area poses challenges for modeling the climate and glaciers in this region. Ziemen et al. (2016) was the first modeling study to make projections for the entire domain of Juneau Icefield using a physically-based ice flow model rather than simple scaling or empirical methods employed by previous regional projections of ice mass loss of Alaska (e.g., Radić and Hock, 2011; Huss and Hock, 2015). However, when attempting to calibrate model parameters for the reference period (1979–2013), Ziemen et al. (2016) were unable to match modeled results to observations. This was attributed to the 20 km grid cell resolution of the meteorological forcing being unable to resolve the precipitation gradients across the icefield caused by orographic effects. They addressed this problem by introducing new tuning parameters to adjust the pattern and amount of the precipitation input. While their method was effective given the limitations of the meteorological forcing, it is not an ideal solution because it lacks physical basis and is therefore not easily transferred spatially or temporally. A physically-based solution is needed.

The importance of orographic precipitation and the range of modeling approaches that have been developed to investigate the impacts of orographic precipitation on precipitation patterns is discussed extensively in the the literature. Roe (2005), Smith (2006), and Houze (2012) provide comprehensive reviews. Orographic precipitation processes strongly determine regional precipitation patterns in mountainous regions where the forced ascent of air masses over topography leads to condensation and increased precipitation on the windward side relative to the lee side of mountain ranges. At local scales, orographic precipitation processes force and combine with other dynamical and microphysical processes to shape complex precipitation patterns and resulting snow accumulation patterns in mountainous terrain (Zängl, 2007; Vionnet et al., 2017).

A range of physically-based orographic precipitation models exist and have evolved over time. Broadly, these models differ by the degree to which airflow dynamics and cloud microphysics are represented (Roe, 2005). The most complex approach is to use a regional climate model for dynamic downscaling of coarser scale gridded climate products to finer spatial resolution, but regional climate models are typically too computationally expensive to generate results at the resolutions necessary to resolve orographic precipitation effects (Roe, 2005; Gutmann et al., 2016), especially for large areas like the Juneau Icefield. The linear theory of orographic precipitation model (hereafter referred to as the LT model) (Smith and Barstad, 2004) utilizes linearized mountain wave airflow dynamics and characteristic delay timescales to represent cloud microphysics, making it physically-based yet computationally efficient. While the LT model includes many assumptions and is not able to represent nonlinear processes, it is highly adaptable and has been explored and applied in numerous mountainous regions (e.g., Smith et al., 2004; Barstad and Smith, 2005; Anders et al., 2007, 2008; Minder, 2010). However, it has only been used for direct glaciological applications in Iceland (Crochet et al., 2007; Jóhannesson et al., 2007), Norway (Schuler et al., 2008), Western Canada (Jarosch et al., 2012), and Patagonia (Weidemann et al., 2013).

Here, we apply the LT model to the Juneau Icefield to downscale coarse-scale 20 km resolution gridded winter precipitation fields from the Weather Research and Forecasting Model (WRF) to 1 km grid resolution for the period 1979–2013. We focus on the winter season due to its importance for glacier mass balance modeling. To assess uncertainties of the model, we perform sensitivity experiments varying adjustable parameter values within reasonable ranges, the underlying grid resolution, and the source of the meteorological forcing data. We determine that the normalized precipitation pattern derived from the LT model is robust for all experiments and an improvement from previous methods of precipitation downscaling for the Juneau Icefield region, but precipitation amounts vary greatly between experiments.

2. Study Site

The Juneau Icefield is located on the border between Alaska and Canada in the Coast Mountains (Figure 1) and covers an area of 4,149 km² (Kienholz et al., 2015). The icefield terrain ranges in elevation from sea level in the southwest, where the city of Juneau is located, to ~2,500 m a.s.l. The icefield is intimately connected to the ecosystems and communities of the area (O'Neel et al., 2015). Mass loss from the icefield will not only alter the geography and landscape of the immediate area, but will also impact physical and biological processes of downstream ecosystems as glacier runoff patterns change (Hood and Berner, 2009; O'Neel et al., 2015).

FIGURE 1

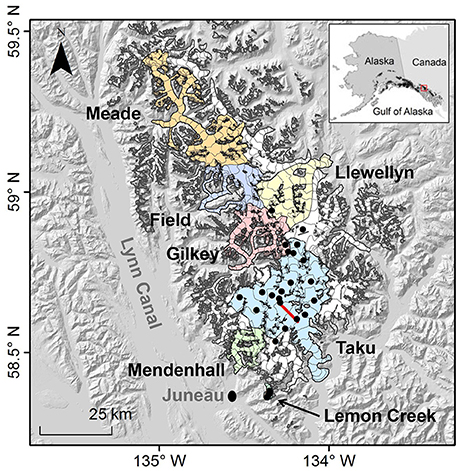
Figure 1. Location and topography of the Juneau Icefield. Major outlet glaciers are marked (Lemon Creek, Medenhall, Taku, Gilkey, Llewellyn, Field, and Meade Glaciers), as well as the location of the town of Juneau. The black dots show the location of net accumulation snow pit measurements taken by the Juneau Icefield Research Program (JIRP; Pelto et al., 2013) from 2003 to 2013 and used for model calibration. The red line on Taku Glacier shows the location of the transect of net accumulation observations taken in 1998, 2004, 2005, 2010, and 2011 (Pelto et al., 2013) used for model validation. Contour lines (gray) within the icefield area show topography at 100 m intervals. The glacier outlines are from Kienholz et al. (2015). The hillshaded topography is the SRTM DEM at 30 m resolution.

Due to topographic effects, the icefield is divided into a maritime southwestern portion that receives roughly 3–4 m w.e. of precipitation per year (Pelto et al., 2013) and a significantly drier eastern portion. The icefield is in the direct path of southwesterly storms that cross the Gulf of Alaska, transporting warm, moist air to southeast Alaska from the Pacific (Fleming et al., 2000; Simpson et al., 2002). When these moisture-laden air parcels encounter the steep terrain of the Coast Mountains, they are forced to ascend and air cools enough for water vapor to condense into cloud water, from which precipitation may form. While there are other processes that cause the uplift of air masses and precipitation events, the orographic lifting mechanism is always present and controls the average precipitation pattern of the region. As air masses continue over the mountain divide and descend on the eastern side, evaporation of cloud water occurs in the descending and warming air, thus creating the steep precipitation gradient apparent on the Juneau Icefield.

Based on the Randolph Glacier Inventory (RGI; Pfeffer et al., 2014) there are 162 individual glaciers making up the Juneau Icefield (Kienholz et al., 2015). Taku Glacier, Mendenhall Glacier, and Lemon Creek Glacier, in the southwest corner of the icefield (Figure 1), are the most widely studied glaciers of the icefield due to their proximity to Juneau (e.g., Motyka and Begét, 1996; Miller and Pelto, 1999; Motyka et al., 2003; Boyce et al., 2007; Truffer et al., 2009; Pelto, 2011). The largest outlet glacier is Taku Glacier, a former tidewater glacier with an area of 735 km² and a length of 60 km (Kienholz et al., 2015). Taku Glacier has displayed an interesting advance/retreat pattern in the last centuries, contrasting with regional glacier change trends, and is currently advancing. On the drier eastern side, Llewellyn Glacier is the second largest glacier of the icefield (450 km², 37.5 km long) and is one of the largest glaciers in British Columbia. Llewellyn Glacier has been receding rapidly, especially in the past two decades, and has lost the most area of all the outlet glaciers in the icefield (Beedle and Raup, 2008). Pelto (2017) shows that all major outlet glaciers, other than Taku, have experienced terminus recession during the period 1984–2013.

Ziemen et al. (2016) provide a review of specific mass balance rates for different time periods ranging from 1948 to 2010 for the entire Juneau Icefield and of Taku Glacier derived from both geodetic and glaciological methods. There is consensus that the icefield-wide specific mass balance rate was negative during all investigated periods. However, the specific mass balance rate of Taku Glacier was slightly positive during all periods of investigation, consistent with its current advance. Ziemen et al. (2016) projected a 58–68% volume loss of the icefield in 2099 compared to 2010.

3. Model Description

3.1. The Linear Theory Model (LT Model)

The LT model was introduced by Smith and Barstad (2004). Variations of the original model have since been used (Table 1), but the core equations and concepts have persisted. The following is an overview of the core model, which is addressed in full in Smith and Barstad (2004) with an evaluation of model skill discussed in Barstad and Smith (2005). More recent model variations will be presented in section 3.2.

TABLE 1

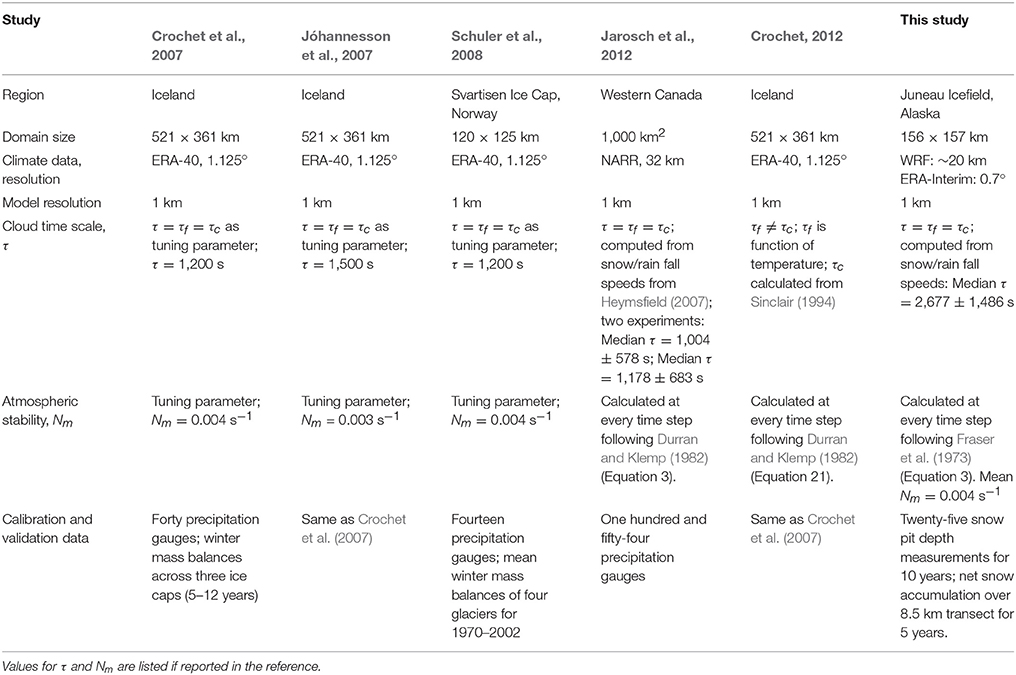
Table 1. Summary of characteristics of previous glaciological applications of the LT model and this study.

In the LT model, air masses are forced to ascend as they pass over a topographic barrier, causing condensation of water vapor to cloud water over the windward slope. The air masses are assumed to be saturated. Cloud water is advected downstream and converted into falling hydrometeors according to a time scale τ_c. The hydrometeors fall to the surface according to a time scale τ_f. As hydrometeors descend on the lee side of the topographic barrier, they evaporate or precipitate depending on atmospheric conditions. Thus, the spatial pattern and intensity of precipitation is determined by (1) the topography over which the air mass is uplifting, (2) microphysical processes that control the rate of condensation and hydrometeor formation and fallout, (3) atmospheric conditions (e.g., temperature, water vapor, and stability of the air column), and (4) airflow dynamics (vertical and horizontal velocity variations with altitude).

The model treats core aspects of non-linear orographic precipitation generation as linear processes. Linear mountain wave theory is used to solve for variations in vertical velocity of air masses with altitude. It assumes that the altitude of the topographic barrier is relatively small compared to vertical wavelength of mountain waves created by crossing the barrier in a stably stratified atmosphere. The cloud time scales, τ_c and τ_f, are used to represent linear approximations of cloud microphysics processes. These assumptions allow for the investigation of the major processes governing orographic precipitation with relatively simple and compact equations. Furthermore, the LT model requires only a limited number of inputs and has relatively low computational cost.

The LT model is based on two steady-state advection equations that describe cloud water (q_c) and hydrometeor (q_h) formation in a horizontal domain described by the coordinates x and y:

$\begin{array}{ll}\frac{D{q}_c}{Dt}\approx \text{U}·\nabla q_c=S(x,y)-\frac{q_c(x,y)}{{\tau }_c},& (1)\end{array}$

$\begin{array}{ll}\frac{D{q}_h}{Dt}\approx \text{U}·\nabla q_h=\frac{q_c(x,y)}{{\tau }_c}-\frac{q_h(x,y)}{{\tau }_f},& (2)\end{array}$

where q_c(x, y) and q_h(x, y) are the vertically integrated cloud water density and hydrometeor density respectively, and U = Ux + Vy is the advecting wind vector with northward and eastward components V and U. τ_c and τ_f generally range from 200 to 2,000 s (Smith and Barstad, 2004; Barstad and Smith, 2005; Crochet et al., 2007; Schuler et al., 2008) and their determination is discussed in section 3.2.2. S(x, y) is the vertically integrated (from z = 0 to z = ∞) condensation rate to cloud water as a response to uplift over terrain, referred to as the source term.

The amount of cloud water at a given time is determined by the balance of S(x, y) and the conversion rate of cloud water to hydrometeors, q_c(x, y). Similarly, the amount of hydrometeors at a given time is determined by the balance of the conversion rate of cloud water to hydrometeors, q_c(x, y), and the loss of hydrometeors due to fallout, q_h(x, y). The final term in Equation 2 $\frac{q_h(x,y)}{{\tau }_f}$ then corresponds to the precipitation rate, P(x, y).

By spectral decomposition and algebraic manipulation, the following transfer function at the core of the LT model is

$\begin{array}{ll}\widehat{P}(k,l)=\frac{C_{w}i\sigma ĥ(k,l)}{(1-im{H}_w)(1+i\sigma {\tau }_f)(1+i\sigma {\tau }_c)}.& (3)\end{array}$

$\widehat{P}(k,l)$ is the Fourier-transform of the distributed precipitation rate related to the Fourier-transform of terrain elevation ĥ(k, l), with k and l being the horizontal wave numbers. This relation depends on the uplift sensitivity factor, C_w, thickness of the moist layer, H_w, the intrinsic frequency, σ = Uk + Vl, and the conversion and fallout time scales, τ_c and τ_f. Terrain is the only gridded variable used in this calculation. The other variables are calculated from vertically averaged meteorological input data and then the resulting quantities are horizontally averaged over the model domain.

In Equation (3), the vertical wave number m controls the depth and tilt of the forced air uplift and is a function of the moist Brunt-Väisälä frequency, N_m, a quantity describing atmospheric stability, such that

$\begin{array}{ll}m={\left[\left(\frac{N_m^2-{\sigma }^2}{{\sigma }^2}\right)(k^2+l^2)\right]}^{\frac{1}{2}}.& (4)\end{array}$

$\widehat{P}(k,l)$ is transformed back into the x-y space domain and is added to the background precipitation, P_∞, that accounts for large-scale frontal and convective precipitation separate from orographic precipitation. Total precipitation, P_total, is then

$\begin{array}{ll}{P}_{\text{total}}(x,y)=max\left[{\displaystyle \int \int }\widehat{P}(k,l)e^{i(kx+yl)}dkdl+P_{\infty },0\right].& (5)\end{array}$

P_∞ is derived from the large-scale meteorological forcing by removing the inherent orographic effect from the large-scale precipitation. To this end, Equation (3) is applied to the coarse resolution terrain. Bilinear interpolation is used to distribute P_∞ to the finer resolution grid of $\widehat{P}(k,l)$. Equation (3) is formulated such that the solution can be negative. This represents leeside evaporation in the model as airflow descends. If the sum of the orographic precipitation and background precipitation is negative then the value is set to 0 (Equation 5).

3.2. Model Parameters

Although the LT model is physically-based, there are several free parameters that must be adjusted and tuned for the model results to match available observations. Early applications of the LT model required the optimization of the parameters N_m, τ_c, and τ_f that were assumed constant in time and space (Smith and Barstad, 2004; Barstad and Smith, 2005; Crochet et al., 2007; Jóhannesson et al., 2007; Schuler et al., 2008). Smith and Barstad (2004) show typical values for these parameters. Following Jarosch et al. (2012) and Crochet (2012), we implement parameterizations of N_m, τ_c, and τ_f that utilize physical constants, tuning parameters, and the input meteorological variables at every time step, so that N_m, τ_c, and τ_f vary in time, but our implementation differs from the studies listed in Table 1.

3.2.1. Atmospheric Stability, N_m

The calculation of N_m is not trivial and can be approximated with a variety of methods. The method employed in this model version follows Fraser et al. (1973), also used by Smith and Barstad (2004). While Durran and Klemp (1982) improved upon the Fraser et al. (1973) expression, they yield similar results for the range of atmospheric conditions in the Juneau Icefield region, thus we use the simpler Fraser et al. (1973) expression. N_m is calculated from

$\begin{array}{ll}{N}_m^2=\frac{g}{\overline{T}}({\Gamma }_m-{\Gamma }_e)& (6)\end{array}$

where g is gravitational acceleration and $\overline{T}$ is vertically averaged air temperature weighted by the moisture content at several pressure levels (Jarosch et al., 2012). Γ_e is the environmental lapse rate and Γ_m is the moist adiabatic lapse rate. Γ_m is calculated according to Stone and Carlson (1979) using vertically averaged values of atmospheric properties from the meteorological input data weighted by moisture content. This follows the convention that a positive lapse rate represents cooling with increasing elevation.

In summary, N_m is not a tuning parameter as in some previous studies, but is instead calculated from the vertical average of four pressure levels (1,000, 900, 800, and 750 hPa) of the coarse input climate data fields with the average weighted by moisture content allowing the most appropriate value to be used at every time step based on atmospheric conditions. N_m is calculated for every grid cell and the domain averaged value is used in the calculation of orographic precipitation. Barstad and Smith (2005) report that typical values of N_m range between 0 s⁻¹, representing an atmosphere with no stratification, and 0.01 s⁻¹ representing a stably stratified atmosphere. The assumptions of the LT model are violated when there is an unstable atmosphere (N_m < 0).

3.2.2. Cloud Time Scale, τ, and Hydrometeor Fall Speeds, υ_snow and υ_rain

While τ_f can be easily approximated by considering the height from which the hydrometeors are falling, a simple relation for τ_c is more difficult to formulate. There is no direct relationship between τ_c and τ_f, but according to previous authors, the model behavior is most sensitive to the total time scale of both processes, and the difference between these values is less important. For convenience, we adopted this approach and the time scales will subsequently be referred to as a singular τ. Following previous studies (Table 1), we set τ_c and τ_f to the same value ($\tau ={\tau }_c={\tau }_f=\frac{H_w}{\upsilon }$), where υ is the fall speed of the hydrometeors. H_w (Equation 3) and υ are both gridded quantities at the resolution of the course input climate data varying in space and time. H_w is calculated directly from input climate data grids at four pressure levels where vertically averaged values of Γ_m and air temperature, T, weighted by moisture content are used.

While the expression and general concept of τ is the same for all studies which calculate, rather than tune τ, recent studies have used different parameterizations of the fall speeds, υ, in their calculation of τ (Table 1). Jarosch et al. (2012) fully parameterized liquid hydrometeor fall speed in terms of physical constants and climate data based on Heymsfield (2007). Crochet (2012) calculated hydrometeor fall speeds as a function of atmospheric mixing ratios derived from the climate data and a free parameter, whose value was determined from Sinclair (1994). However, Crochet (2012) showed that further parameterization and increased model complexity did not significantly improve or alter LT model results. We do not have the appropriate data to validate a more complex approach so we used a more simple formulation.

We define the fall speed υ at each grid cell as a function of air temperature to account for the slower fall speed of snow (solid hydrometeors) as compared to that of rain (liquid hydrometeors). In contrast to previous implementations of the LT model, two bounding values were used to calculate υ where the lower bound is v_snow and the upper bound is υ_rain (Roth, 2016). These values were used as tuning parameters rather than tuning the value of τ. υ also relies on a transition temperature, T_mid, and a transition window, σ_T, representing a temperature range where a mixture of rain and snow is assumed. T_mid is generally between −1°C and 1°C. For values of $\overline{T}$ inside the bounds of $T_{\mathrm{\text{mid}}}\pm \frac{{\sigma }_T}{2}$, a linear transition between the bounding values of υ_snow and υ_rain was calculated. In this study, we used $T_{\mathrm{\text{mid}}}=0^{°}C$ and ${\sigma }_T=4^{°}C$.

Average snow fall speed is 1.0 m s⁻¹ for dry snow and 2.0 m s⁻¹ for wet snow based on empirical evidence (Locatelli and Hobbs, 1974; Yuter et al., 2006). Rain fall speeds can range from <2.0 to 9.0 m s⁻¹, but Yuter et al. (2006) showed that during a specific rain event hydrometeors exhibited a fall speed of 4.0 m s⁻¹ most often, and we adopted this value for υ_rain. We based our initial choice of υ_snow on literature values, and then tuned this parameter in the calibration procedure (see section 6.2). We performed a sensitivity analysis to evaluate the impact of υ_snow and υ_rain values on the resulting precipitation field.

At each time step, the domain average of τ was used to calculate precipitation across the domain in Equation (3). Thus, precipitation was calculated with a τ value that is constant across the domain but varies in time. We acknowledge this is a crude approximation for υ and τ. We use a simple precipitation partitioning scheme to account for the precipitation pattern differences resulting from different fall speeds without introducing more parameters. In reality, there is a spectrum of hydrometeor fall speeds at every elevation and hydrometeors vary in type as they are descending. Smith and Barstad (2004) neglected all of this in the original model. Typical fall speeds of solid and liquid hydrometeors are different enough to have a noticeable effect on the resulting precipitation fields. With a lower fall speed, representative of solid hydrometeors, the precipitation fields are smoothed because hydrometeors are transported over a longer horizontal distance before reaching the surface. With a high fall speed, representative of liquid hydrometeors, most of the hydrometeors fall out faster resulting in an unsmoothed precipitation field.

4. Data

4.1. Digital Elevation Models (DEMs)

The LT model was applied to a digital elevation model (DEM) of 1 km resolution derived from bilinear interpolation of a 30 m resolution DEM from the Shuttle Radar Topography Mission (SRTM) flown over the region in 2000 (USGS, 2004) (Figure 3F). The 1 km resolution captures the complex features relevant to the physics of the LT model, but it does smooth the terrain. The maximum elevation of the 1 km resolution DEM is 2,300 m a.s.l., while the highest peak in the Juneau Icefield region is ~2,500 m a.s.l.

We used regional-scale climate data from the WRF (Skamarock et al., 2008) (Figure 2) forced by global-scale ERA-Interim Reanalysis data as input to the LT model. Additionally, for a sensitivity analysis, we used the ERA-Interim Reanalysis climate data as direct input to the LT model. The assumed topographies associated with both datasets are drastically smoothed due to the coarse resolution. The ERA-Interim topography for the model domain, with ~100 km resolution for global climate applications, is depicted as a smooth ramp with maximum elevation of 1,150 m a.s.l. The model domain is represented by only eight grid points in the ERA-Interim dataset (Figure 3D). The WRF topography for the model domain, with ~20 km resolution, depicts a smooth increase and decrease in elevation with a maximum elevation of 1,600 m a.s.l and is represented by 70 grid points (Figure 3E).

FIGURE 2

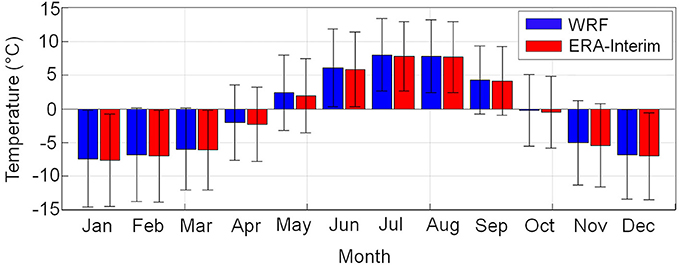
Figure 2. Monthly mean temperatures from the WRF dataset (blue) and ERA-Interim (red) averaged over the period 1979–2013. For both datasets, the temperature grids at every time step were vertically averaged over the four pressure levels used (1,000, 900, 800, 750 hPa) and then horizontally averaged over the entire model domain. The error bars represent the standard deviation over the modeling period for each month.

FIGURE 3

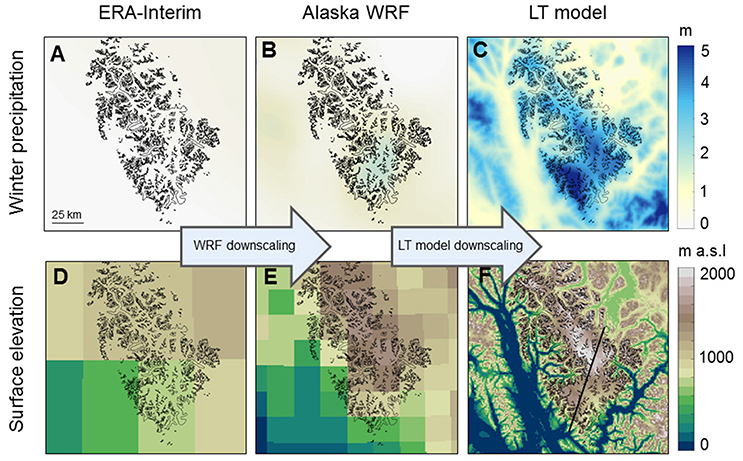
Figure 3. Modeled winter (October–March) precipitation (A–C) and corresponding digital elevation models (D–F) averaged over 1979–2013 from ERA-Interim, the WRF data from Bieniek et al. (2016), and the LT model. Grid cell resolutions are ~100 km, ~20 km, and 1 km, respectively. To facilitate direct comparison to the LT model results, the ERA-Interim and WRF precipitation fields have been interpolated to 1 km resolution. The outline of the Juneau Icefield is shown in black. Black dashed line in (F) indicates the location of the vertical cross section in Figure 9.

4.2. Meteorological Variables

The meteorological variables used as input by the LT model are air temperature, relative humidity, and horizontal wind components. These data were taken from Bieniek et al. (2016), who dynamically downscaled ERA-Interim Reanalysis variables using WRF. ERA-Interim Reanalysis climate data are a global gridded climate data from the European Centre for Medium-Range Weather Forecasts (ECMWF) and extend from 1979 to the present (Dee et al., 2011). The dataset describes the three-dimensional structure of the atmosphere for each time step. It is one of the best performing reanalysis datasets in terms of temperature and precipitation biases in the Alaska region (Lindsay et al., 2014; Lader et al., 2016). Bieniek et al. (2016) used WRF to downscale ERA-Interim to a ~20 km grid for Alaska. These data are the highest resolution data currently covering all of Alaska for the 1979–2015 period. This dataset will be referred to as the WRF data. Note that this is different from the climate input used by Ziemen et al. (2016), who used WRF to downscale output from a free-running global climate model rather than a reanalysis.

The meteorological variables were obtained on hourly time steps, but the LT model was run on 6-h time steps. We used the instantaneous values of each variable at 0:00, 6:00, 12:00, and 18:00 h for each day. We aimed to resolve the effect of different weather conditions and hence employed this relatively short time step. When applying the model at longer time scales, it is not straightforward to derive the required parameters like N_m or τ and a simple average may not be sufficient.

Variables were obtained from four different pressure levels (1,000, 900, 800, 750 hPa), which span an altitude range from sea level to roughly 3,000 m a.s.l. At each pressure level, specific humidity was converted to relative humidity following standard calculations. For every 6-h time step, the gridded fields of air temperature, relative humidity, and horizontal wind components were vertically averaged, weighted by the moisture content, and horizontally averaged over the model domain to calculate necessary variables and feed Equation (3).

4.3. Background Precipitation, P_∞

Hourly precipitation data from WRF were summed resulting in precipitation fields for every 6-h time step. These data were used to calculate the background precipitation that is unrelated to orographic effects, P_∞ (Equation 5). The WRF precipitation data include some orographic enhancement from the WRF topography that must be removed prior to applying the LT model to the finer resolution DEM to avoid double-counting of the orographic effect. We followed the procedure outlined by Schuler et al. (2008) and apply the LT model to the coarse WRF topography using the WRF meteorological variables. The resulting orographic precipitation was subtracted from the WRF precipitation data to yield P_∞. Negative precipitation values of P_∞ resulting from this scheme represent the effect of evaporation. P_∞ was interpolated using bilinear interpolation to the finer resolution grid and then added to the orographic precipitation calculated on the finer resolution grid (Equation 5) to yield P_total. P_total was simply bounded at 0 to avoid negative precipitation values.

4.4. Glaciological Data

We used data from The Juneau Icefield Research Program (JIRP; Pelto et al., 2013) to evaluate model results. JIRP has created an extensive annual mass balance dataset for Taku and Lemon Creek Glaciers. This record is the longest continuous glacier mass balance series in North America, starting in 1946 and continuing today. For each year net snow accumulation (in m water equivalent, w.e.) was derived from snow depth sounding and density measurements in snow pits at 25 fixed locations ranging in elevation from 950 m to 2,100 m a.s.l (Figure 1). We used the available data from 2003 to 2013 for model calibration. While the snow pit locations are concentrated on the windward (southwest) side of the icefield, there are eight sites located on the leeward (northeast) side of the icefield. Snow pit depth measurements were conducted in July and August and therefore represent net snow accumulation from an unknown date of the last summer surface to the date of the measurement.

JIRP also conducted net snow accumulation measurements along transects in the accumulation area of Taku glacier for 5 years to better determine the distribution of net snow accumulation. These data were collected at 60 points along a 8.5 km transect on Taku Glacier in late July of 1998, 2004, 2005, 2010, and 2011 by probing to the last summer surface at horizontal intervals of 200 m. The transect was positioned just above the transient snow line and ranged from 900 to 1,150 m a.s.l. (Figure 1). Three point measurements made within 25 m were averaged to determine the snowpack depth at each probing location. These data were converted to water equivalent using mean snow density observed in snow pits along the transect in three locations (Pelto et al., 2013) and were used to validate the LT model after calibration.

5. Model Application

The model was set up on an UTM Zone 8 grid at a resolution of 1 km and comprised a domain of 156 × 157 km (Figure 1), matching the domain used by Ziemen et al. (2016). Bilinear interpolation was used to interpolate the WRF climate grids in Polar Stereographic projection and the SRTM DEM in Alaska Albers Equal Area Projection to the model grid for input. The model was run at 6 h time steps starting 1 January 1979 until 31 December 2013. Model parameters with the following initial values were used: υ_snow = 1.0 m s⁻¹, υ_rain = 4.0 m s⁻¹, T_mid = 0°C, and σ_T = ±4°C. We used υ_snow = 1.0 m s⁻¹, the average fall speed of dry snow (Yuter et al., 2006) and υ_rain = 4.0 m s⁻¹ as this was the most observed rain fall speed by Yuter et al. (2006) (see section 3.2.2).

The LT model was only applied at a time step if relative humidity exceeds 90%. Forcing the model with meteorological variables from the WRF dataset resulted in the LT model being applied in 86% of the time steps. The precipitation fields from WRF, interpolated to 1 km resolution, were adopted in the remaining 14% of time steps. Within the time steps where the LT model was run, the atmosphere must be stable for the LT model equations to be valid. If a negative N_m value was calculated then the LT model was still applied, but with N_m = 0 s⁻¹. This occurred in 15% of the time steps.

6. Model Calibration and Validation

There were no precipitation gauge data available on the Juneau Icefield and only very few stations in the domain at elevations too low to assist in constraining model parameters or validating the model (Figure 1). Therefore, we used the available net snow accumulation measurements (section 4.4) as representations of seasonally aggregated precipitation to calibrate and validate the LT model parameters.

6.1. Deriving Net Snow Accumulation From LT Model Precipitation

The available net snow accumulation measurements could not be directly compared to the output of the LT model (total precipitation). First, some of the precipitation falls as rain. Second, the observations include mass loss due to melt and the redistribution of snow by wind. In particular, we expect that significant melt occurred by the time the measurements were performed in July and August, well after the onset of the melt season, as suggested by monthly mean air temperatures considerably exceeding 0°C (Figure 2). To compare model results to the available observations, we computed net snow accumulation from the modeled precipitation by extracting the snow portion of precipitation and then applying a standard temperature-index model to account for melt (see section 6.1 for details). Other ablation processes were considered to be negligible. We assumed that all melt water and rain water exits the snow or firn pack and is not retained (see section 9 for discussion).

We first extracted the snow portion of precipitation from total modeled precipitation at each time step and grid cell based on the calculated fall speed, which varied between the values of υ_snow and υ_rain depending on the vertically averaged air temperature. When υ = υ_snow all precipitation was assumed to fall as snow, while rain was assumed in case υ = υ_rain. For the transition temperature range $T_{\mathrm{\text{mid}}}\pm \frac{{\sigma }_T}{2}$, where υ_snow < υ < υ_snow, a mixture of snow and rain was assumed and the snow portion was computed from linear interpolation between 100 and 0% snow. While more sophisticated methods exist for partitioning snow and rain, this simple scheme is appropriate given the coarse spatial resolution of the vertically averaged air temperature data.

We assumed a start date of 1 October for the observations because the glaciological data refer to an unknown start date (stratigraphic time system). We derived modeled net snow accumulation for the period between 1 October of the previous year and each sites observation date and applied a temperature-index model for the same time period. These calculations were executed on the grid cells of the model domain that corresponded to the locations of the snow pit and probing transect observations.

To apply the temperature-index model, near surface air temperature was downscaled from the native climate data resolution to the LT model resolution using the standard atmosphere lapse rate Γ = 0.0065 K m⁻¹ to correct for elevation differences between the LT model and the climate model topography. Melt was calculated at every 6-h time step when air temperature exceeded 0°C using a degree-day factor, f_m. We applied a range of factors for snow whose values were based on Braithwaite (2008). He summarized and reported mean snow degree-day factors used in previous studies with 95% confidence intervals that range between 3.2 and 6.2 mm d⁻¹ K⁻¹. Braithwaite (2008) suggested that 4.1 ± 1.5 mm d⁻¹ K⁻¹ be used as a first-assumption degree-day factor for snow melt around the equilibrium line altitude for an unknown glacier. This closely matches the degree-day factor of 4.0 mm d⁻¹ K⁻¹ for snow used on the Juneau Icefield by Ziemen et al. (2016). Ablation assessments performed during JIRP indicate a degree-day factor close to the f_m = 3.2 mm d⁻¹ K⁻¹ shown in Figure 4.

FIGURE 4

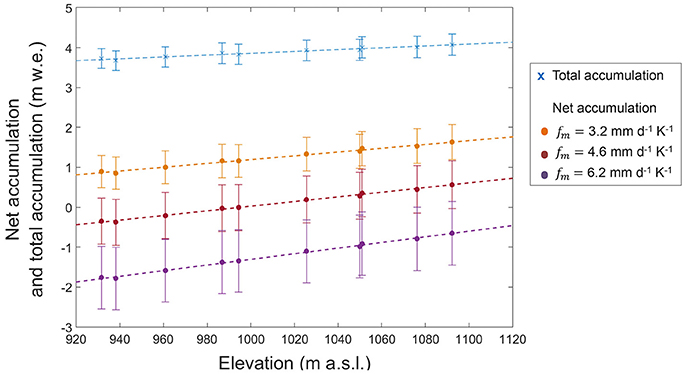
Figure 4. Modeled net accumulation (i.e., the balance between total snow accumulation and ablation) derived from the precipitation results of the LT model as a function of elevation. Dots refer to the averages over the 5 observation years and the error bars show ± one standard deviation. Modeled net accumulation was calculated over the period from 1 October of the previous year and the exact July observation date of each year using a temperature-index model and three different melt factors to account for melt. Modeled values refer to the grid cells in the model domain that match observation locations. Additionally, average modeled total snow accumulation (blue crosses) ± one standard deviation is shown demonstrating considerable melting during the period of the observations.

Initially, we used the degree-day factor of f_m = 4.1 mm d⁻¹ K⁻¹ suggested by Braithwaite (2008), with the units converted to match the 6-h time steps used in this study. It should be noted that applying the temperature-index model using 6 h time steps and four different temperature values per day results in a greater amount of melt calculated per day compared to using daily time steps and daily mean temperatures with the same degree-day factor.

Figure 4 shows that the temperature-index model generates substantial melt during the observation period. Total snow accumulation is reduced by approximately 3–3.5 m w.e when applying a degree-day factor of f_m = 4.1 mm d⁻¹ K⁻¹. This indicates that melt is a dominant process in this location before the time observations were made in late July, and hence the choice of melt factor can significantly alter the net snow accumulation derived from the LT model. To address this uncertainty we treated f_m as a parameter tuned in the calibration procedure.

6.2. Calibration Results

The net snow accumulation data from the snow pits were used for model calibration. In addition to f_m, we optimized the snow fall speed parameter, υ_snow, of the LT model. Rain fall speed has little effect on the winter precipitation and was assumed constant at υ_rain = 4 m s⁻¹. Other parameter values listed in section 5 were held constant. During calibration, each parameter was varied over a range of reasonable values and the best agreement between model results and observations was determined. Initially, υ_snow values ranged from 0.2 to 1.6 m s⁻¹ at steps of 0.2 m s⁻¹ and f_m values ranged from 2 to 7 mm K⁻¹ d⁻¹ at steps of 1 mm K⁻¹ d⁻¹. Best agreement was judged based on (a) minimizing the bias, (b) maximizing the coefficient of determination (r²) between modeled results and observations, and (c) minimizing the mean absolute error (MAE). We only considered parameter combinations that resulted in an absolute bias of <10 cm and chose the parameter set that maximized the r² value while also minimizing the MAE value as evaluated from Figure 5.

FIGURE 5

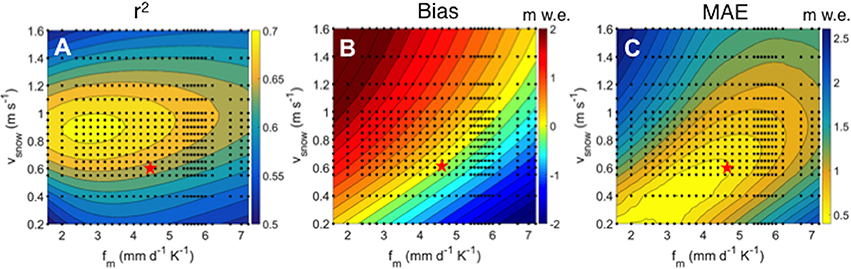
Figure 5. Model performance as a function of snow fall speed υ_snow and melt factor f_m, for three statistical criteria used to calibrate model parameters. (A) Coefficient of determination r² values (B) bias and (C) mean absolute error (MAE) calculated from the comparison of model results using a range of melt factors, f_m, and snow fall speed values, υ_snow, to the net accumulation snow pit observations. Actual model runs with the parameter combinations used are shown with black dots. Contours and colors show the statistical values interpolated over the whole range of parameter combinations. Note the different colorbars and values represented in each plot although yellow represents best performance for all three criteria. The red star represents the optimized parameter set that was chosen.

The parameter values obtained from this process were υ_snow = 0.60 m s⁻¹ and f_m = 4.6 mm K⁻¹ d⁻¹ with a bias of −0.03 m w.e., r² = 0.64, and MAE = 0.61 m w.e. Figure 6 shows a scatter plot of model results vs. snow pit observations for this optimized parameter set. We refer to this optimized parameter set as the reference run.

FIGURE 6

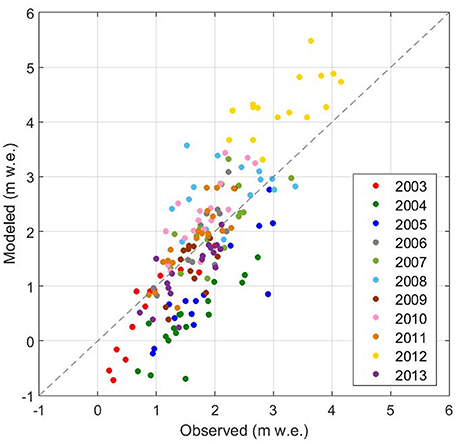
Figure 6. Modeled vs. observed net accumulation (m w.e.) from snow pit observations. Model results are from the optimized parameter set where υ_snow = 0.60 m s⁻¹ and f_m = 4.6 mm d⁻¹ K⁻¹. Snow pit observations are from 2003 to 2013 with the individual years shown in different colors. Modeled net accumulation was calculated over the period between 1 October of the previous year and the observation date of each year. The dashed black line represents perfect agreement between the observations and model results.

6.3. Model Validation

To validate the model and the calibrated parameters, we compared the modeled net snow accumulation of the reference run to the probing transect data (Figure 7). We calculated the averages of the observations and model results for the 20 points that had measurements available for all 5 years. While the model results and observations are weakly correlated when considering all data points (r² = 0.48), there is a much stronger correlation for the average of all the values (r² = 0.93). The amount of net accumulation along the transect for each individual year is overestimated (year 2010) or underestimated by the model (2004, 2005, and 2011). The model best matches the observations from 1998.

FIGURE 7

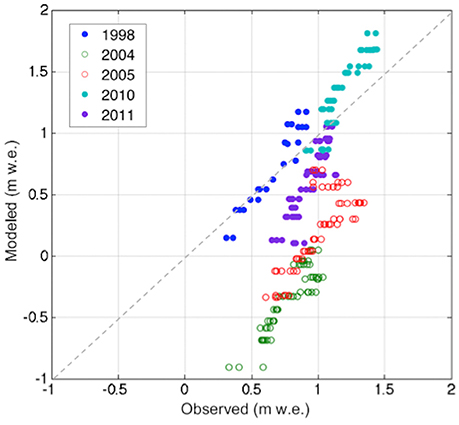
Figure 7. Modeled vs. observed net accumulation (m w.e.) along a transect on upper Taku Glacier (Figure 1) for 5 years. Model results are from the optimized parameter set where υ_snow = 0.60 m s⁻¹ and f_m = 4.6 mm degree⁻¹ day⁻¹. For all data points shown, r² = 0.48, bias = −0.48 m w.e., and MAE = 0.57 m w.e.. Modeled values are strongly underestimated in years 2004 and 2005 attributed to anomalously warm summer temperatures and associated higher uncertainties in the melt model (see text). Only considering the years 1998, 2010, and 2011 there is stronger agreement (r² = 0.70, MAE = 0.23 m w.e., and bias = −0.08 m w.e.). The number of observations varies from year to year. Modeled net accumulation was calculated over the period between 1 October of the previous year and the observation date of each year. Since the model resolution is 1 km, some model grid cells contain the location of multiple observation locations. The dashed gray line represents perfect agreement between the observations and model results.

The model shows the worst agreement for the years 2004 and 2005. For these years, summer temperatures were above average in the region, with 2004 being the warmest summer in the 1979–2013 time period. Arendt et al. (2013) found strongly negative annual mass balances for all glaciers in the Gulf of Alaska region in 2004 and 2005. The melt model used here to account for melt prior to the snow measurements in summer introduced large uncertainty to the modeled net accumulation in 2004 and 2005 when melt was a dominant process. In contrast, years 1998, 2010, and 2011 all had cooler than average summer temperatures, and hence errors in the melt calculation have less impact on the comparison between LT model results and measured snow accumulation. Only considering the years 1998, 2010, and 2011, the model results and observations show stronger agreement (r² = 0.70 with a bias of −0.08 m w.e.).

7. LT Model Results

7.1. Precipitation Pattern and Amount

The precipitation results of the LT model with the optimized υ_snow parameter are shown in Figure 3C. WRF and ERA-Interim precipitation data are shown for comparison. We assessed the amount and pattern of the total winter precipitation averaged over the entire model period (1979–2013) with the winter season being defined as October–March.

To facilitate analysis of differences in spatial pattern we followed the approach by Schuler et al. (2008) and derived a winter precipitation index for the Juneau Icefield from the optimized parameter set (Figure 8). The index was calculated for each icefield grid cell as the percentage of the local winter precipitation amount to the icefield-wide spatial winter precipitation mean, thus representing a measure of each grid cell's deviation from the icefield-wide mean. All values were averaged over the modeling period 1979–2013. Grid cell values larger than 100% indicate winter precipitation larger than the spatial mean and vice versa.

FIGURE 8

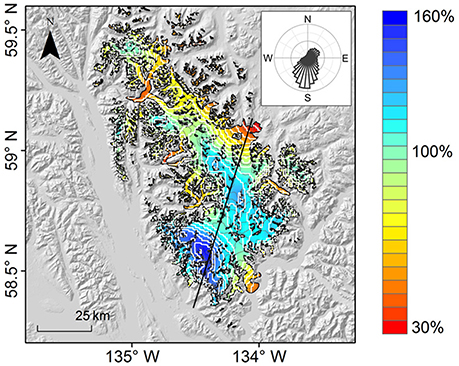
Figure 8. Winter precipitation index map for the Juneau Icefield calculated from the LT model run with optimized parameter set (υ_snow = 0.60 m s⁻¹ and f_m = 4.6 mm d⁻¹ K⁻¹). The precipitation index values represent the ratio of the local winter (October–March) precipitation at each grid cell averaged over 1979–2013 to the icefield-wide spatial mean averaged over the same period (3.4 m), expressed as a percentage. The precipitation index is also illustrated with white contours (at intervals of 10%). The black contour lines illustrate the topography (at intervals of 100 m). The black line indicates the location of the vertical cross section in Figure 9, which is in the direction of the dominant winter (October–March) wind direction as shown by the inset. Inset shows winter wind directions calculated from the horizontally and vertically averaged U and V wind vectors of WRF used as input into the LT model for all time steps over the period 1979–2013. Bins are in 10 degree increments and length of bins represents the percentage of time steps in each bin. The outer most circle is 4%.

The results of the LT model are encouraging and clearly show variability lacking in the coarse precipitation fields of the ERA-Interim and WRF datasets (Figure 3C). Results show two areas of maximum precipitation, in the southwest corner and in the center of the icefield, corresponding to topographic maxima that surround a local precipitation minimum in the upper area of Taku Glacier. The LT model solution reveals a complex spatial precipitation pattern superimposed on the large-scale orographic precipitation pattern across the icefield with generally higher precipitation amounts on the windward (southwest) side compared to the lee (northeast) side of the icefield. Low precipitation amounts falling below 40% of the icefield-wide mean (Figure 8) are found at the lowest elevations on Llewellyn Glacier in the east and Taku Glacier in the southeast, but also over large portions of the glacier tongues of major outlet glaciers draining to the west (Gilkey, Field, and Meade Glaciers, Figure 1). These glaciers occupy narrow valleys flanked by precipitous mountain walls thus effectively shadowing these glaciers from large precipitation amounts. Orographic enhancement is most pronounced in the southwest part of the icefield with winter precipitation up to double the icefield-wide mean (Figure 8). The overall pattern is more complex than the manually adjusted precipitation field used in Ziemen et al. (2016), where precipitation amounts from the WRF model were manually increased west of the ice divide and decreased east of the divide to match observations.

Figure 9 shows a vertical cross section of average winter precipitation for the optimized parameter set (υ_snow = 0.6 m s⁻¹) and the surface elevation of the 1 km DEM in the direction of the dominant winter (October–March) wind direction (Figure 8 inset). The area of maximum precipitation (between 10 and 30 km) does not correspond to the region of maximum elevation (between 50 and 70 km), as would be expected if precipitation was scaled linearly with elevation. Orographic lifting is more extreme for the area of high elevation in the south, and thus average winter precipitation is greater. The local precipitation maxima areas occur on the windward side of the two areas of maximum surface elevation. The local precipitation minimum is offset in the downwind direction from the local topographic minima at 35 km distance along the transect. Though Figure 9 provides a more detailed view of the LT model results in comparison to topography in the dominant wind direction, it should not be overinterpreted. The values of winter precipitation are the sum of LT model results at every time step with differing wind directions.

FIGURE 9

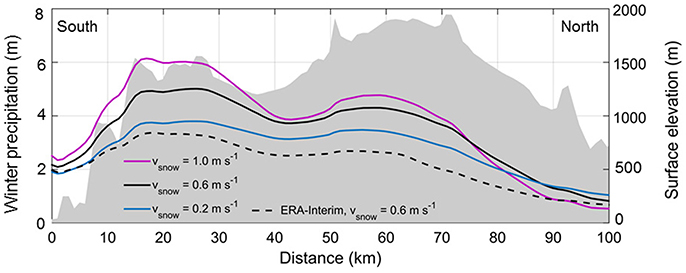
Figure 9. Vertical cross sections along the line shown in Figures 3, 8, 12 for surface elevation and modeled winter precipitation with three different υ_snow values. Results from LT model forced directly by ERA-Interim data are show (dashed line). The cross section is in the direction of the dominant winter (October–March) wind direction. Surface elevation is from the 1 km DEM in Figure 3F.

The icefield-wide spatial mean (excluding non-glacierized areas of the domain) of winter precipitation averaged over the modeling period (1979–2013) is 3.4 ± 1.1 m (the uncertainty range is within one standard deviation from all icefield grid cells) and the maximum value on the icefield is 5.8 m located in the southwestern branch of upper Taku Glacier. Due to the coarse resolution of both climate datasets, total winter precipitation amounts of the initial WRF and ERA-Interim datasets are considerably lower compared to the results from the LT model.

7.2. Cloud Time Scale τ

The median τ value for the 1979–2013 time period is 2,677 ± 1,486 s (the uncertainty range is ± median absolute deviation), and thus greater than all τ values used by other studies (Table 1). Figure 10A shows that τ has a pronounced seasonal pattern with considerably higher values in winter (roughly 3,700 s) than in summer (roughly 800 s) and relatively sharp transitions between summer and winter values. The latter is also apparent from the frequency distribution in Figure 10B. In winter, the lower bound of fall speeds, υ_snow, is used to calculate τ more often resulting in larger τ values for all winter months (October–March). Conversely, in summer, the upper bound of fall speeds is used to calculate τ more frequently resulting in smaller τ values. Summer τ values have much smaller standard deviations and the mean values show less variability in time compared to winter τ values. This is due to more homogenous fall speeds calculated across the model domain in summer, while during winter, it is not uncommon given the icefield's maritime environment that snow is modeled at higher elevations, while the precipitation is modeled to fall as rain at lower elevations.

FIGURE 10

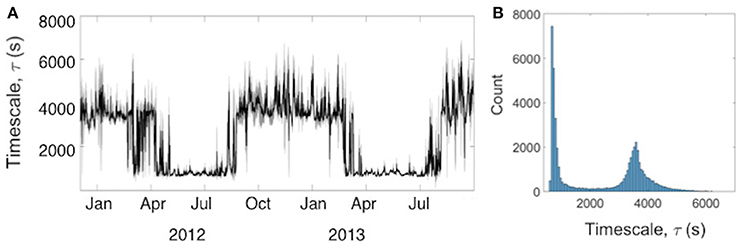
Figure 10. (A) Cloud time scale τ at every 6 h time step for the period 1 January 2012–31 December 2013 (black line). Values refer to the reference model run and represent spatial means over the entire model domain. The gray area represents the standard deviation of all grid cell values at every time step. (B) The corresponding frequency distribution of τ values in 50 s bins.

8. Uncertainty and Sensitivity Analysis

Sources of uncertainties include inaccuracies in the input data (meteorological forcing, topography), inadequacies in model physics, and the assumptions of the values of the free model parameters. Conventional error propagation analysis is not feasible since the validity of the inherent assumptions (normality, independence of parameters, etc.) can not be verified. Therefore, to assess uncertainties and the robustness of the LT model results, we conducted a series of sensitivity experiments. We varied the LT model parameters of snow fall speed, υ_snow, and rain fall speed, υ_rain, as well as the horizontal resolution of the underlying DEM, and the source of the input climate data. We ran the LT model at 5 km resolution in addition to the 1 km resolution of the reference run. In addition, we forced the LT model with ERA-Interim meteorological variables directly rather than the dataset downscaled using WRF to explore the necessity of using the computationally expensive WRF model. All other parameters were held constant.

For each sensitivity experiment, we calculated the mean winter precipitation pattern and the corresponding icefield-wide mean averaged over the 1979–2013 time period, as described in section 7.1.

The choice of domain size may also influence the LT model results due to the effect of domain-wide averaging on bulk values that characterize the lifted air mass. Hence, uncertainties in the spatial precipitation pattern are expected to increase as the model domain becomes larger.

8.1. Fall Speed Parameters, υ_snow and υ_rain

We focus on the fall speed parameters υ_snow and υ_rain because they are unique to the parameterization of the LT model used in this study. Holding all other model parameters constant, we ran the LT model for all parameter combinations from a range of υ_snow and υ_rain values. As there are no direct observations of hydrometeor fall speeds on the Juneau Icefield, reasonable ranges of υ_snow and υ_rain were determined from Yuter et al. (2006) where υ_snow values ranged from 0.2 to 2.0 m s⁻¹ and υ_rain values ranged from 3.0 to 5.0 m s⁻¹, using a step size of 0.2 m s⁻¹ to traverse each parameter range.

In general, higher fall speeds lead to greater amounts of precipitation within the modeling domain and higher precipitation maxima and stronger precipitation gradients, because the hydrometeors fall to the ground faster and less moisture is transported out of the domain. In contrast, lower fall speeds lead to advection of hydrometeors further across the icefield and out of the model domain as they fall from the moist layer causing lower precipitation efficiency and a weaker precipitation gradient across the icefield. Figure 11 shows the sensitivity of icefield-wide winter precipitation to the choice of υ_snow and υ_rain.

FIGURE 11

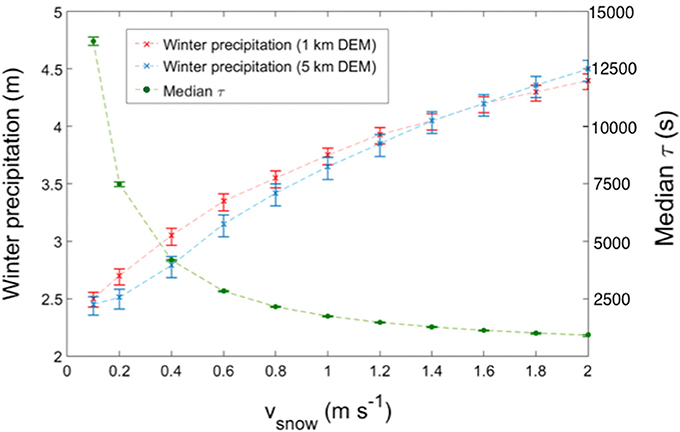
Figure 11. Winter precipitation and cloud time scale, τ as a function of snow fall speed, υ_snow. Winter precipitation refers to the icefield-wide spatial mean averaged over the months October–March for the period 1979–2013. Results are shown for the model runs using two different DEM resolutions (1 and 5 km). τ values represent the median of every time step's value where the LT model was applied. Note that τ does not vary with LT model resolution, as it is calculated from the meteorological input data. A rain fall speed of υ_rain = 4.0 m s⁻¹ is used for the calculations. For all three curves, the error bars represent the range of results due to varying υ_rain between 3.0 m s⁻¹ (lowest bar) and 5.0 m s⁻¹ (highest bar).

For all parameter combinations, the icefield-wide winter precipitation averaged over the period 1979–2013 ranges from 2.5 to 4.4 m. We find that the precipitation amount is more sensitive to υ_snow than υ_rain. Increasing υ_rain from 3.0 to 5.0 m s⁻¹ causes an increase in icefield-wide winter precipitation of only approximately 0.25 m, while a similarly sized increase of υ_snow from 0.2 to 2.0 m s⁻¹ produces approximately 2.0 m more winter precipitation. This not surprising since we only consider winter precipitation, where υ_rain is applied far less frequently than υ_snow.

Also shown in Figure 11 are median τ values for each combination of υ_snow and υ_snow. τ decreases exponentially as υ_snow increases and the resulting icefield-wide winter precipitation increases. This agrees with previous LT model sensitivity experiments by Smith and Barstad (2004) and Barstad and Smith (2005), where larger values of τ resulted in decreased orographic enhancement and vice versa.

Figure 12 shows the sensitivity of the spatial distribution of average winter precipitation to the choice of υ_snow, and Figure 9 shows vertical cross sections of these results. With increasing υ_snow values, precipitation index values are amplified meaning that locally the average winter precipitation values become increasingly larger than the spatial mean. Figure 9 shows that local precipitations gradients are steeper with increased υ_snow values. The sensitivity to υ_snow is not uniform along the vertical cross section. Windward regions and ridge tops show greater variation than leeside regions with changes in υ_snow values, consistent with the sensitivity analysis of Barstad and Smith (2005). Areas of high and low precipitation index occur in the same locations for each parameter combination indicating that the overall precipitation pattern is relatively insensitive to the choice of υ_snow in contrast to the amount of total precipitation.

FIGURE 12

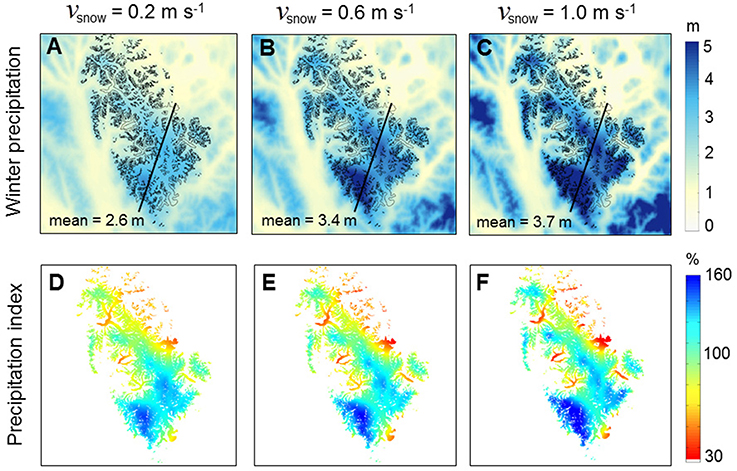
Figure 12. Modeled winter (October–March) precipitation (A–C) and precipitation index (D–F) averaged over the period 1979–2013 for three different values of υ_snow. The precipitation index values indicate local deviations from the spatial mean and are computed as the ratio of each grid cell's winter precipitation to the icefield-wide spatial mean of winter precipitation, expressed as a percentage. The means noted in (A–C) refer to the icefield-wide spatial mean.

8.2. Horizontal Resolution

The precipitation amount and pattern are also sensitive to the spatial resolution of the DEM to which the LT model is applied. This has been explored extensively by previous authors, a summary of which is provided by Crochet et al. (2007). Depending on the model used and the observations available to tune the model, previous studies have chosen DEMs with spatial resolutions between 1 and 5 km (Crochet et al., 2007). As the resolution decreases, the topography is smoothed resulting in lower elevation maximum. As a result, the model calculates less local precipitation because air masses experience less uplift within the model.

In addition to the 1 km DEM resolution used in the reference run, we ran the model using a 5 km DEM. In Figure 13 we compare the variation in model results introduced by the spatial resolution to the variation resulting from the υ_snow and υ_rain parameter choices.

FIGURE 13

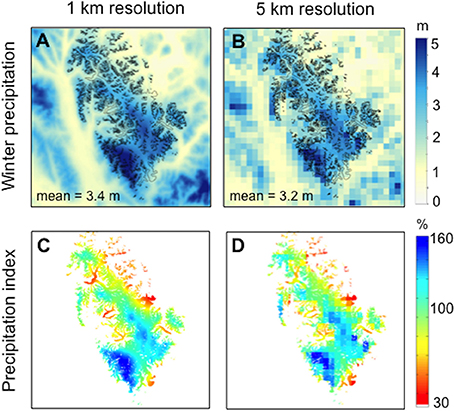
Figure 13. Modeled winter (October–March) precipitation (A,B) and precipitation index (C,D) averaged over the period 1979–2013 applying the LT model to the 1 km (A) and the 5 km (B) DEM. The precipitation index values indicate local deviations from the spatial mean and are computed as the ratio of each grid cell's time-averaged winter precipitation to the icefield-wide spatial winter precipitation mean, expressed as a percentage. The means noted in (A,B) refer to spatial means over all grid cells, whose center lies inside the icefield outline. Thus the total area over which the spatial average is taken varies between the two cases.

Consistent with previous studies (Crochet et al., 2007), the coarser resolution leads to a decrease in icefield-wide winter precipitation for most of the tested range of υ_snow values. For υ_snow <1.6 m s⁻¹, however, this is reversed, most likely due to artifacts, when averaging over all coarse-scale grid cells within the icefield boundary. The absolute differences between the results from the two DEM resolutions do not exceed 0.3 m for any of the tested combinations of υ_snow and υ_rain. Figure 11 also indicates that similar icefield-wide winter precipitation amounts can be obtained with different combinations of DEM resolution and choices of υ_snow. Figure 13 indicates that the pattern of winter precipitation is similar between the two experiments and the icefield-wide means differ by <5%.

Utilizing the LT model at 1 or 5 km resolutions does not imply that actual precipitation does not exhibit complex variations at much smaller scales. The assumptions of the LT model are not appropriate for modeling at smaller scales, where additionally processes and more complex airflow dynamics dominate the precipitation pattern.

8.3. Forcing the LT Model With ERA-Interim Reanalysis

While the downscaled regional WRF dataset is the currently best available climate dataset for Alaska, it is computationally expensive to produce. For future mass balance modeling efforts in Alaska, it may be more effective to directly force the LT model with a readily available global climate data product. We compared the results of the LT model forced by the WRF data (~20 km resolution) to those resulting from forcing the model directly by the ERA-Interim data (~100 km resolution). With this forcing, the DEM used to derive the ERA-Interim data was used to calculate background precipitation and the same meteorological variables previously described were used from the ERA-Interim data as input. Grid resolution (1 km) and all model parameters were identical to those of the reference run.

When forced with ERA-Interim data directly, the LT model produces less icefield-wide winter precipitation compared to the solution produced by the WRF input (2.3 ± 0.7 m instead of 3.4 ± 1.1 m.; uncertainty is ± one standard deviation over all icefield grid cells; Figure 14). As with the previous sensitivity experiments, the overall spatial pattern is similar. The ERA-Interim forcing generates systematically more precipitation on the eastern side and less precipitation on the southwestern side of the icefield, relative to the icefield-wide mean, compared to the reference run driven by WRF data. Figure 9 shows the vertical cross section of average winter precipitation results when forced by ERA-Interim directly (dashed black line) in comparison to the results produced by WRF input (solid black line).

FIGURE 14

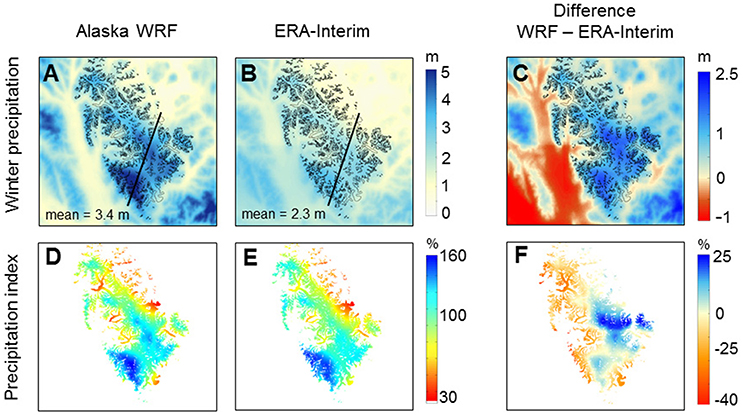
Figure 14. Modeled winter (October–March) precipitation (A,B) and precipitation index (D,E) averaged over the period 1979–2013 forcing the LT model with WRF (A,D) and ERA-Interim (B,E) data. The precipitation index values indicate local deviations from the spatial mean and are computed as the ratio of each grid cell's time-averaged winter precipitation to the icefield-wide spatial winter precipitation mean, expressed as a percentage. Difference maps with LT model results forced by ERA-Interim subtracted from those forced by WRF data are also shown for both variables (C,F).

The discrepancy between the total winter precipitation amounts of the two experiments can be explained by the vertical and horizontal averaging of the climate variables prior to applying the LT model. While the initial climate input is spatially variable in both the vertical (pressure levels) and horizontal directions, the LT model equations are solved using the domain's spatial means. These averaged quantities are slightly different for the two climate datasets due to the difference in resolution and underlying topography. In general, the finer resolution of the WRF grids and resulting less smoothed topography means that a larger range of values are represented in a given grid for any variable. This results in larger spatially averaged quantities compared to the average quantities calculated from the lower resolution ERA-Interim grids.

In addition, the number of time steps the LT model is applied differs between the two model runs. The WRF dataset leads to the application of the LT model in 86% of time steps compared to 79% for the ERA-Interim dataset. Due to the coarse resolution of both climate datasets, the precipitation fields of the climate datasets have considerably lower precipitation amounts compared to the LT model. Hence, when the LT model is applied less often, as in the ERA-Interim case, the average winter precipitation includes more time steps that are unaltered from the original ERA-Interim precipitation.

Despite the differences, the results from the WRF and ERA-Interim forcings both create precipitation fields that are consistent with what would be expected for the terrain and dominating airflow dynamics in this region. In both cases, the LT model generates a spatial precipitation variability that was previously unresolved in available climate data for the region. We cannot say whether forcing the LT model with the WRF or ERA-Interim dataset leads to more “realistic” precipitation fields due to the scarcity of total precipitation observations. However, these experiments indicate that the amount of winter precipitation calculated by the LT model is sensitive to the input climate dataset, in addition to DEM resolution and choice of υ_snow and υ_rain values. This indicates that similar LT model results can be achieved with either climate input dataset in conjunction with different combinations of DEM resolution, υ_snow, and υ_rain values.

9. Discussion

9.1. Precipitation Pattern and Amount

The LT model produces precipitation fields at a scale relevant for icefield-wide glacier mass balance modeling with a persistent general precipitation pattern regardless of parameter combination, horizontal resolution, and input data. The pattern reflects the finer spatial resolution of the topography used in the LT model in comparison to the coarse resolution topography used by WRF and ERA-Interim. However, validating the precipitation pattern produced by the LT model over the Juneau Icefield is hampered by the limited spatial extent of available observations covering only a small area with little elevation range. In addition, the transect on Taku Glacier is perpendicular to the large-scale precipitation gradient over the icefield rather than along the precipitation gradient.

While the precipitation pattern produced by the LT model is robust, the amount of precipitation is sensitive to the model parameters, horizontal resolution, and input data. The icefield-wide spatial mean of average winter precipitation varies between 2.5 and 4.4 m for reasonable choices of snow fall speed. The amount of winter precipitation from the LT model cannot be validated rigorously by the available observations. Direct winter precipitation measurements are lacking, and the limited mass balance observations were taken in late July, i.e., after substantial melt on the order of several meters had occurred. We accounted for this by using a temperature-index model to calculate melt. However, this introduces additional uncertainty as the melt factor is not well-constrained. Varying the melt factor within reasonable ranges suggested in the literature varied the modeled net accumulation considerably. Hence, there are too many degrees of freedom to constrain the total winter precipitation amounts with the available observations.

LT model results that under or overestimate total precipitation can be made to match the available net accumulation observations by optimizing the melt factor within the range of values suggested in the literature. Thus, the model may show good agreement to the observations but for the incorrect reasons. Furthermore, the assumed invariant lapse rate used to downscale the temperature field in the melt calculation is a large assumption and introduces uncertainty. We suspect the lapse rate is responsible for the modeled underestimation and overestimation of low and high observed net accumulation values, respectively in Figure 6, 7. A secondary source of uncertainty is the calculation of total snow accumulation input for melt model. We used a simple linear transition precipitation partitioning scheme. Harpold et al. (2017) outlines a range of more sophisticated methods and these could be employed in future work. Additional uncertainties are the neglect of processes other than melt. For example, we do not consider the process of refreezing of melt water or rain water within the snow or firn pack, for which only very little information exists (Pelto et al., 2013). It is possible that a more sophisticated melt model coupled with a more sophisticated precipitation partitioning model could better constrain the amount of melt and better match available observations, but the total precipitation from the LT model results would still need to be validated. Currently, the validation data do not exist to justify more complex approaches.

9.2. Informing Observation Network Design

Previous studies have used relatively dense networks of precipitation gauge or winter mass balance measurements to validate the LT model results. Observations on the Juneau Icefield are scarce. However, the results of the LT model can be used to inform where observations should occur in order to help constrain the free model parameters of the LT model and determine Juneau Icefield mass balance with a minimum number of observations. For example, measurement sites along steep precipitation gradients and at modeled local maxima (such as at the divide between Gilkey Glacier and Llewellyn Glacier) and local minima (such as on the upper main branch of Taku Glacier bounded by two local maxima) (Figure 1) would provide important data to constrain total precipitation amounts on the icefield. It should be noted that beginning in 2015, winter balance observations have been made on the icefield by the USGS and the results of this study could inform where more observation sites could be located.

9.3. Precipitation Index Map and Glacier Mass Balance Modeling Applications

Snow accumulation on glaciers often exhibits a persistent pattern from year-to-year and accumulation index maps have been used to describe this pattern for input in distributed mass balance and hydrological modeling (Schuler et al., 2007, 2008). Following the approach of Schuler et al. (2008) we derived a winter precipitation index map for the Juneau Icefield using the LT model (Figure 8). We considered total precipitation, not just snow accumulation, as the fraction of snow and rain could be dealt with in a more sophisticated mass balance modeling scheme. While there is a general tendency that the precipitation index increases with elevation, there are large areas of deviation. In these areas the orographic precipitation pattern would not be resolved if a simple elevation dependent approach was used to distribute precipitation. Such areas are easily identified in Figure 8, where elevation contours (black) and precipitation index contours (white) do not coincide.

The consistent pattern produced by the LT model and the uncertainty of the precipitation amount suggests that an accumulation index map may be a practical approach for further mass balance modeling of the Juneau Icefield. Functionally, this precipitation index map could be used in conjunction with a precipitation correction factor contained within the mass balance model scheme that would increase or decrease precipitation amount across the domain, while maintaining the pattern specified by the index map. The accumulation index map approach also decreases computational cost for interfacing the LT model with a mass balance model.

This approach is most applicable to icefield-wide and large outlet glacier (e.g., Taku Glacier, Llewellyn Glacier, and Meade Glacier) mass balance modeling studies. While the LT model results are an improvement to existing precipitation fields for the region, they should be considered a reasonable approximation of the general precipitation pattern and should be assessed within the context of the limitations and assumptions of the LT model. The subtle changes to local precipitation gradients with different LT model parameters will be more important to assess if utilizing these results in small glacier basin mass balance modeling. Small scale orographic effects and additional processes, which are superimposed on the general precipitation pattern, were not considered with this modeling approach and within the physics of the LT model. The Intermediate Complexity Atmospheric Model (ICAR) (Gutmann et al., 2016) may be an appropriate next step for improving precipitation downscaling in the Juneau Icefield region at finer scales applicable to mass balance modeling. Additionally, observations and modeling of smaller scale processes, such as preferential deposition and the seeder-feeder mechanism (e.g., Mott et al., 2014; Gerber et al., 2017; Vionnet et al., 2017), would increase our understanding of precipitation and snow accumulation patterns in the area. Regardless of model approach and resolution, the lack of observations for calibration and validation data will remain a significant challenge.

10. Conclusions

We assessed the ability of a LT model as a physically-based, intermediate complexity tool that can be used to downscale coarse gridded global or regional precipitation fields for the purposes of glacier mass balance modeling. The Juneau Icefield was used as a study site to address previous challenges of mass balance modeling related to the representation of orographic precipitation in the precipitation input data. In contrast to previous studies we computed the cloud time scale, τ, at each time step as a function of the fall speeds for snow and rain. τ values varied substantially between summer and winter indicating that assuming τ constant in time, as done in previous studies (Table 1), is problematic.

Modeled net snow accumulation derived from the LT model precipitation output agreed reasonably well with corresponding point observations across large parts of the ice cap although uncertainties remain with regard to the amount of melt that had occurred by the time of the measurements in July/August.

The LT model produced winter precipitation fields with the expected orographic precipitation pattern previously unresolved in existing gridded datasets for the area. These datasets also show considerably lower icefield-wide winter precipitation amounts than the LT model results due to strongly smoothed topography.

Sensitivity experiments varying the snow and rain fall speed, the horizontal resolution of the underlying DEM, and the climate input data indicate that the spatial pattern of winter precipitation persists in all experiments, while the amount of winter precipitation varied with these factors, and was most sensitive to the choice of snow fall speed. Hence ground observations are needed to constrain the LT model parameters so that total amounts of precipitation are reproduced accurately. Optimal model parameters will vary with grid resolution and source of climate input data. Nevertheless, when ground observations are scarce or lacking, the LT model can assist in designing and optimizing an observation network.

Based on the persistence of the precipitation pattern produced by the LT model, we suggest that the LT model has great potential to improve glacier mass balance modeling in regions with complex topography and orographic effects, and it should become a more widely used tool for downscaling precipitation input for these purposes.

Author Contributions

AR led the development of this study, prepared all datasets, performed all calculations and made all figures. She wrote the paper with major contributions from RH. RH initiated the study and contributed to the modeling strategy and interpretation of results. TS provided the original MATLAB code for the LT model, coded the new model developments and assisted with model application. PB provided the downscaled WRF data and assisted with the acquiring of ERA-Interim data. MP provided the mass balance data from the Juneau Icefield from the Juneau Icefield Research Program. AA assisted with the handling of the climate data files. All co-authors commented on the manuscript.

Funding

This work was initiated during AR's 4-month stay at the Geoscience Department of the University of Oslo supported by the Glaciology Exchange program (GlacioEx) funded by SIU (Norwegian Center for International Cooperation in Education). AR was additionally supported by the Resilience and Adaptation Program at the University of Alaska Fairbanks (UAF), the Alaska Center for Climate Assessment and Policy (ACCAP): Interactive Climate Science for Alaska (NOAA Award NA11OAR4310141) at UAF. PB was funded by grant/cooperative agreement G10AC00588 from the U.S. Geological Survey and the UAF Alaska Climate Science Center, RH by NASA grants NNX11AF41G and 80NSSC17K0566, and AA by NSF grant PLR-1644277. Part of the publication fee was paid by Alaska Center for Climate Assessment and Policy (ACCAP): Science, Decision-Support, and Capacity Building for Climate Resilience in Alaska (NOAA Award NA16OAR4310162) at UAF.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work includes content that first appeared in AR's M.S. thesis (Roth, 2016). This is the only medium this content has appeared in and its publication complies with the policy of the University of Alaska Fairbanks. We thank C. Kienholz, M.Truffer, and U.Bhatt, for their comments and support. C. Trainor and M. van Muelken provided support and organized funding opportunities. This work would not be possible without the students and staff of JIRP who have contributed to the invaluable dataset of Juneau Icefield observations for more than 40 years.

References

Anders, A. M., Roe, G. H., Durran, D. R., and Minder, J. R. (2007). Small-scale spatial gradients in climatological precipitation on the olympic Peninsula. J. Hydrometeorol. 8, 1068–1081. doi: 10.1175/JHM610.1

CrossRef Full Text | Google Scholar

Anders, A. M., Roe, G. H., Montgomery, D. R., and Hallet, B. (2008). Influence of precipitation phase on the form of mountain ranges. Geology 36, 479–482. doi: 10.1130/G24821A.1

CrossRef Full Text | Google Scholar

Arendt, A., Luthcke, S., Gardner, A., O'Neel, S., Hill, D., Moholdt, G., et al. (2013). Analysis of a GRACE global mascon solution for Gulf of Alaska glaciers. J. Glaciol. 59, 913–924. doi: 10.3189/2013JoG12J197

CrossRef Full Text | Google Scholar

Barstad, I., and Smith, R. B. (2005). Evaluation of an orographic precipitation model. J. Hydrometeorol. 6, 85–99. doi: 10.1175/JHM-404.1

CrossRef Full Text | Google Scholar

Beedle, M., and Raup, B. (2008). “A GLIMS inventory of the Juneau Icefield, Alaska,” in IGS: International Workshop on World Glacier Inventory (Lanzhou).

Bieniek, P., Bhatt, U. S., Walsh, J. E., Rupp, T. S., Zhang, J., Krieger, J. R., et al. (2016). Dynamical downscaling of ERA-Interim temperature and precipitation. J. Appl. Meteorol. Climatol. 55, 635–654. doi: 10.1175/JAMC-D-15-0153.1

CrossRef Full Text | Google Scholar

Boyce, E. S., Motyka, R. J., and Truffer, M. (2007). Flotation and retreat of a lake-calving terminus, Mendenhall Glacier, southeast Alaska, USA. J. Glaciol. 53, 211–224. doi: 10.3189/172756507782202928

CrossRef Full Text | Google Scholar

Braithwaite, R. J. (2008). Temperature and precipitation climate at the equilibrium-line altitude of glaciers expressed by the degree-day factor for melting snow. J. Glaciol. 54, 437–444. doi: 10.3189/002214308785836968

CrossRef Full Text | Google Scholar

Crochet, P. (2012). High Resolution Precipitation Mapping in Iceland by Dynamical Downscaling of ERA-40 with a Linear Model of Orographic Precipitation. Technical Report VI 2012-003, Iceland Meteorological Office, Reykjavik, Iceland. Available online at: http://en.vedur.is/about-imo/publications/2012/ (Accessed 8 May, 2015).

Crochet, P., Jóhannesson, T., Jónsson, T., Sigurdsson, O., Björnsson, H., Pálsson, F., et al. (2007). Estimating the spatial distribution of precipitation in Iceland using a linear model of orographic precipitation. J. Hydrometeorol. 8, 1285–1306. doi: 10.1175/2007JHM795.1

CrossRef Full Text | Google Scholar

Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., et al. (2011). The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 137, 553–597. doi: 10.1002/qj.828

CrossRef Full Text | Google Scholar

Durran, D. R., and Klemp, J. B. (1982). On the effects of moisture on the Brunt-Väisälä frequency. J. Atmos. Sci. 39, 2125–2158. doi: 10.1175/1520-0469(1982)039<2152:OTEOMO>2.0.CO;2

CrossRef Full Text | Google Scholar

Fleming, M. D., Stuart Chapin, F. III., Cramer, W., Huffords, G. L., and Serreze, M. C. (2000). Geographic patterns and dynamics of Alaskan climate interpolated from a sparse station record. Glob. Change Biol. 6, 49–58. doi: 10.1046/j.1365-2486.2000.06008.x

CrossRef Full Text | Google Scholar

Fraser, A. B., Easter, R. C., and Hobbs, P. V. (1973). A theoretical study of the flow of air and fallout of solid precipitation over mountainous terrain: Part I. Airflow model. J. Atmos. Sci. 30, 801–812. doi: 10.1175/1520-0469(1973)030<0801:ATSOTF>2.0.CO;2

CrossRef Full Text | Google Scholar

Gerber, F., Lehning, M., Hoch, S. W., and Mott, R. (2017). A close-ridge small-scale atmospheric flow field and its influence on snow accumulation. J. Geophys. Res. 122, 7737–7754. doi: 10.1002/2016JD026258

CrossRef Full Text | Google Scholar

Gutmann, E., Barstad, I., Clark, M., Arnold, J., and Rasmussen, R. (2016). The Intermediate Complexity Atmospheric Research Model (ICAR). J. Hydrometeorol. 17, 957–973. doi: 10.1175/JHM-D-15-0155.1

CrossRef Full Text | Google Scholar

Harpold, A. A., Kaplan, M. L., Zion Klos, P., Link, T., McNamara, J. P., Rajagopal, S., et al. (2017). Rain or snow: hydrologic processes, observations, prediction, and research needs. Hydrol. Earth Syst. Sci. 21, 1–22. doi: 10.5194/hess-21-1-2017

CrossRef Full Text | Google Scholar

Heymsfield, A. (2007). Refinements to ice particle mass dimensional and terminal velocity relationships for ice clouds. Part II: Evaluation and parameterizations of ensemble ice particle sedimentation velocities. J. Atmos. Sci. 64, 1068–1088. doi: 10.1175/JAS3900.1

CrossRef Full Text | Google Scholar

Hock, R., and Holmgren, B. (2005). A distributed surface energy-balance model for complex topography and its application to Storglaciären, Sweden. J. Glaciol. 51, 25–36. doi: 10.3189/172756505781829566

CrossRef Full Text | Google Scholar

Hood, E., and Berner, L. (2009). Effects of changing glacial coverage on the physical and biogeochemical properties of coastal streams in southeastern Alaska. J. Geophys. Res. 114, 1–10. doi: 10.1029/2009JG000971

CrossRef Full Text | Google Scholar

Houze, R. A. (2012). Orographic effects on precipitating clouds. Rev. Geophys. 50, 1–47. doi: 10.1029/2011RG000365

CrossRef Full Text | Google Scholar

Huss, M., and Hock, R. (2015). A new model for global glacier change and sea-level rise. Front. Earth Sci. 3:54. doi: 10.3389/feart.2015.00054

CrossRef Full Text | Google Scholar

Jarosch, A. H., Anslow, F. S., and Clarke, G. K. C. (2012). High-resolution precipitation and temperature downscaling for glacier models. Clim. Dyn. 38, 391–409. doi: 10.1007/s00382-010-0949-1

CrossRef Full Text | Google Scholar

Jóhannesson, T., Adalgeirsdóttir, G., Björnsson, H., and Crochet, P. (2007). Effect of Climate Change on Hydrology and Hydro-Resources in Iceland. Technical Report OS-2007/011, National Energy Authority–Hydrological Service, Reykjavík, Iceland.

Google Scholar

Kienholz, C., Herreid, S., Rich, J. L., Arendt, A., Hock, R., and Burgess, E. W. (2015). Derivation and analysis of a complete modern-date glacier inventory for Alaska and northwest Canada. J. Glaciol. 61, 403–420. doi: 10.3189/2015JoG14J230

CrossRef Full Text | Google Scholar

Lader, R., Bhatt, U. S., Walsh, J. E., Rupp, T. S., and Bieniek, P. A. (2016). Two-meter temperature and precipitation from atmospheric reanalysis evaluated for Alaska. J. Appl. Meteorol. Climatol. 55, 901–922. doi: 10.1175/JAMC-D-15-0162.1

CrossRef Full Text | Google Scholar

Lindsay, R., Wenshahan, M., Schweiger, A., and Zhang, J. (2014). Evaluation of seven different atmospheric reanalysis products in the arctic. J. Clim. 27, 2588–2606. doi: 10.1175/JCLI-D-13-00014.1

CrossRef Full Text | Google Scholar

Locatelli, J. D., and Hobbs, P. V. (1974). Fall speeds and masses of solid precipitation particles. J. Geophys. Res. 79, 2185–2197. doi: 10.1029/JC079i015p02185

CrossRef Full Text | Google Scholar

Miller, M. M., and Pelto, M. S. (1999). Mass balance measurements on the Lemon Creek Glacier, Juneau Icefield, Alaska 1953-1998. Geografiska Ann. Ser. A 81, 671–681.

Google Scholar

Minder, J. R. (2010). The sensitivity of mountain snowpack accumulation to climate warming. J. Clim. 23, 2634–2650. doi: 10.1175/2009JCLI3263.1

CrossRef Full Text | Google Scholar

Mott, R., Scipión, D., Schneebeli, M., Dawes, N., Berne, A., and Lehning, M. (2014). Orographic effects on snow deposition patterns in mountainous terrain. J. Geophys. Res. 119, 1419–1439. doi: 10.1002/2013JD019880

CrossRef Full Text | Google Scholar

Motyka, R. J., and Begét, J. E. (1996). Taku Glacier, Southeast Alaska , U.S.A.: late Holocene history of a tidewater glacier. Arctic Alpine Res. 28, 42–51.

Google Scholar

Motyka, R. J., O'Neel, S., Connor, C. L., and Echelmeyer, K. A. (2003). Twentieth century thinning of Mendenhall Glacier, Alaska, and its relationship to climate, lake calving, and glacier run-off. Glob. Planet. Change 35, 93–112. doi: 10.1016/S0921-8181(02)00138-8

CrossRef Full Text | Google Scholar

O'Neel, S., Hood, E., Bidlack, L., Fleming, S. W., Arimitsu, M. L., Arendt, A., et al. (2015). Icefield-to-Ocean linkages across the Northern Pacific Coastal Temperate Rainforest ecosystem. Bioscience 65, 499–512. doi: 10.1093/biosci/biv027

CrossRef Full Text | Google Scholar

Pelto, M. (2011). Utility of late summer transient snowline migration rate on Taku Glacier, Alaska. Cryosphere 5, 1127–1133. doi: 10.5194/tc-5-1127-2011

CrossRef Full Text | Google Scholar

Pelto, M. (2017). Chapter 3: Recent Climate Change Impacts on Mountain Glaciers. San Francisco, CA: John Wiley & Sons, Inc. doi: 10.1002/9781119068150.ch3

CrossRef Full Text

Pelto, M., Kavanaugh, J., and McNeil, C. (2013). Juneau Icefield mass balance program 1946-2011. Earth Syst. Sci. Data 5, 319–330. doi: 10.5194/essd-5-319-2013

CrossRef Full Text | Google Scholar

Pfeffer, W. T., Arendt, A. A., Bliss, A., Bolch, T., Cogley, J. G., Gardner, A. S., et al. (2014). The Randolph glacier inventory: a globally complete inventory of glaciers. J. Glaciol. 60, 537–552. doi: 10.3189/2014JoG13J176

CrossRef Full Text | Google Scholar

Radić, V., Bliss, A., Beedlow, A. C., Hock, R., Miles, E., and Cogley, J. G. (2014). Regional and global projections of twenty-first century glacier mass changes in response to climate scenarios from global climate models. Clim. Dyn. 42, 37–58. doi: 10.1007/s00382-013-1719-7

CrossRef Full Text | Google Scholar

Radić, V., and Hock, R. (2011). Regionally differentiated contribution of mountain glaciers and ice caps to future sea-level rise. Nat. Geosci. 4, 91–94. doi: 10.1038/ngeo1052

CrossRef Full Text | Google Scholar

Roe, G. H. (2005). Orographic precipitation. Ann. Rev. Earth Planet. Sci. 33, 645–671. doi: 10.1146/annurev.earth.33.092203.122541

CrossRef Full Text | Google Scholar

Roth, A. (2016). Applying a Model of Orographic Precipitation to Improve Mass Balance Modeling of the Juneau Icefield. Master's thesis, University of Alaska Fairbanks, Fairbanks, AK

Schuler, T. V., Crochet, P., Hock, R., Jackson, M., and Barstad, I. (2008). Distribution of snow accumulation on the Svartisen ice cap, Norway, assessed by a model of orographic precipitation. Hydrol. Process. 22, 3998–4008. doi: 10.1002/hyp.7073

CrossRef Full Text | Google Scholar

Schuler, T. V., Loe, E., Taurisano, A., Eiken, T., Hagen, J. O., and Kohler, J. (2007). Calibrating a surface mass-balance model for Austfonna ice cap, Svalbard. Ann. Glaciol. 46, 241–248. doi: 10.3189/172756407782871783

CrossRef Full Text | Google Scholar

Sevruk, B., Ondrás, M., and Chvíla, B. (2009). The WMO precipitation measurement intercomparisons. Atmos. Res. 92, 376–380. doi: 10.1016/j.atmosres.2009.01.016

CrossRef Full Text | Google Scholar

Simpson, J. J., Hufford, G. L., Fleming, M. D., Berg, J. S., and Ashton, J. B. (2002). Long-term climate patterns in Alaskan surface temperature and precipitation and their biological consequences. IEEE Trans. Geosci. Remote Sens. 40, 1164–1184. doi: 10.1109/TGRS.2002.1010902

CrossRef Full Text | Google Scholar

Sinclair, M. R. (1994). A diagnostic model for estimating orographic precipitation. J. Appl. Meteorol. 33, 1163–1175. doi: 10.1175/1520-0450(1994)033<1163:ADMFEO>2.0.CO;2

CrossRef Full Text | Google Scholar

Skamarock, W., Klemp, J., Dudhi, J., Gill, D., Barker, D., Duda, M., et al. (2008). A Description of the Advanced Research WRF Version 3. Technical Report NCAR/TN-475+STR, Mesoscale and Microscale Meteorology Division, National Center for Atmospheric Research, Boulder, CO. Available online at: http://www2.mmm.ucar.edu/wrf/users/docs/arw_v3.pdf (Accessed 5 June, 2015).

Google Scholar

Smith, R. B. (2006). “Progress on the theory of orographic precipitation,” in Tectonics, Climate, and Landscape Evolution, eds S. D. Willett, N. Hovius, M. T. Brandon, and D. M. Fisher (Boulder, CO: Geological Society of America), 1377–1391.

Smith, R. B., and Barstad, I. (2004). A linear theory of orographic precipitation. J. Atmos. Sci. 61, 1377–1391. doi: 10.1175/1520-0469(2004)061%3C1377:ALTOOP%3E2.0.CO;2

CrossRef Full Text | Google Scholar

Smith, R. B., Barstad, I., and Bonneau, L. (2004). Orographic precipitation and Oregon's climate transition. J. Atmos. Sci. 62, 177–191. doi: 10.1175/JAS-3376.1

CrossRef Full Text | Google Scholar

Stone, P. H., and Carlson, J. H. (1979). Atmospheric lapse rate regimes and their parameterization. J. Atmos. Sci. 36, 415–423.

Google Scholar

Truffer, M., Motyka, R. J., Hekkers, M., Howat, I. M., and King, M. (2009). Terminus dynamics at an advancing glacier: Taku Glacier, Alaska. J. Glaciol. 55, 1052–1060. doi: 10.3189/002214309790794887

CrossRef Full Text | Google Scholar

USGS (2004). Shuttle Radar Topography Mission, 1 Arc Second scene SRTM-149-445–SRTM-149-464, Unfilled Unfinished 2.0, February 2000.

Vionnet, V., Martin, E., Masson, V., Lac, C., Naaim Bouvet, F., and Guyomarc'h, G. (2017). High-resolution large eddy simulation of snow accumulation in Alpine Terrain. J. Geophys. Res. 122, 11005–11021. doi: 10.1002/2017JD026947

CrossRef Full Text | Google Scholar

Weidemann, S., Sauter, T., Schneider, L., and Schneider, C. (2013). Impact of two conceptual precipitation downscaling schemes on mass-balance modeling of Gran Campo Nevado ice cap, Patagonia. J. Glaciol. 59, 1106–1116. doi: 10.3189/2013JoG13J046

CrossRef Full Text | Google Scholar

Yuter, S. E., Kingsmill, D. E., Nance, L. B., and Löffler-Mang, M. (2006). Observations of precipitation size and fall speed characteristics within coexisting rain and wet snow. J. Appl. Meteorol. Climatol. 45, 1450–1464. doi: 10.1175/JAM2406.1

CrossRef Full Text | Google Scholar

Zängl, G. (2007). Interaction between dynamics and cloud microphysics in orographic precipitation enhancement a high-resolution modeling study of two orth Alpine heavy-precipitation events. Month. Weather Rev. 135, 2817–2840. doi: 10.1175/MWR3445.1

CrossRef Full Text | Google Scholar

Ziemen, F., Hock, R., Aschwanden, A., Khroulev, C., Kienholz, C., Melkonian, A. K., et al. (2016). Modeling the evolution of the Juneau Icefield between 1971 and 2100 using the Parallel Ice Sheet Model (PISM). J. Glaciol. 62, 199–214. doi: 10.1017/jog.2016.13

CrossRef Full Text | Google Scholar