- 1Department of Forecasting Systems, Regional Agency for Environmental Protection of Piemonte, Turin, Italy
- 2National Research Council, Research Institute for Geo-Hydrological Protection, Padua, Italy
- 3Department of Environment, Land and Infrastructure Engineering, Politecnico di Torino, Turin, Italy
Debris flows are among the most dangerous natural processes affecting the alpine environment due to their magnitude (volume of transported material) and the long runout. The presence of structures and infrastructures on alluvial fans can lead to severe problems in terms of interactions between debris flows and human activities. Risk mitigation in these areas requires identifying the magnitude, triggers, and propagation of debris flows. Here, we propose an integrated methodology to characterize these phenomena. The methodology consists of three complementary procedures. Firstly, we adopt a classification method based on the propensity of the catchment bedrocks to produce clayey-grained material. The classification allows us to identify the most likely rheology of the process. Secondly, we calculate a sediment connectivity index to estimate the topographic control on the possible coupling between the sediment source areas and the catchment channel network. This step allows for the assessment of the debris supply, which is most likely available for the channelized processes. Finally, with the data obtained in the previous steps, we modeled the propagation and depositional pattern of debris flows with a 3D code based on Cellular Automata. The results of the numerical runs allow us to identify the depositional patterns and the areas potentially involved in the flow processes. This integrated methodology is applied to a test-bed catchment located in Northwestern Alps. The results indicate that this approach can be regarded as a useful tool to estimate debris flow related potential hazard scenarios in an alpine environment in an expeditious way without possessing an exhaustive knowledge of the investigated catchment, including data on historical debris flow events.
Introduction
In the last decades, several studies have focused on analyzing channel processes in relation to hydrological, geomorphological and ecological systems; in particular, the concepts of coupling and connectivity are largely adopted for studying the interaction of hillslope and channel flows in order to model the hydrological response of catchments (Rickenmann, 1999; Michaelides and Wainwright, 2002; Glade, 2005; Michaelides and Chappell, 2009) and sediment dynamics (Iverson, 2003; Rickenmann et al., 2003; Berti and Simoni, 2005).
Sediment connectivity is a measure of the degree of linkage between sediment sources and downstream areas (Cavalli et al., 2013) and its spatial characterization in a catchment gives an estimation of the possible paths of sediment to reach a target zone. The geomorphic effect of the rainfall acting on sediment deposits may result in debris flow occurrence. Debris flows are one of the most dangerous phenomena within the Italian alpine environment. In fact, they have been responsible for the 36% of fatalities in the Italian alpine region during the last century (Tropeano et al., 2006). Mitigation of debris flow effects on human life has become one of the most important challenges of the scientific community.
The complexity of such a type of catchment processes, resulted in several research field focused on particular aspects governing the behavior of these flows events.
The aspects related to debris flows are typically investigated with emphasis on:
1. triggering conditions (Ellen and Flaming, 1987; Gregoretti, 2000; Beylich and Sandberg, 2005; Wieczorek and Glade, 2005; Cannon et al., 2008; Tiranti et al., 2008; Stoffel et al., 2011, 2014; Kean et al., 2013; Brunetti et al., 2015; Marra et al., 2015; Cavalli et al., 2017a)
2. propagation and deposition (Chang and Chao, 2006; Rickenmann et al., 2006; Deangeli et al., 2015; Gregoretti et al., 2016);
3. magnitude evaluation (Bovis and Dagg, 1988; Marchi and D'Agostino, 2004; Jakob et al., 2005; Hungr et al., 2008; Brardinoni et al., 2012; Rickenmann, 2015; Tiranti et al., 2016a; Cavalli et al., 2017b);
4. rheological behavior (Pierson and Costa, 1987; Costa, 1988; Hungr, 1995, 2002; Ancey, 2007; Von Boetticher et al., 2016);
5. geomorphological and sedimentary processes (Moscariello et al., 2002; Wilford et al., 2004);
6. evolution mechanisms (Sassa, 1985; Segre and Deangeli, 1995; Prancevic et al., 2014);
7. hydrologic modeling (Johnson and Sitar, 1990; Harvey, 1994; Hürlimann et al., 2006; Gregoretti et al., 2016).
In this paper, an integrated study to gain insight into potential hazard linked to debris flows is presented. The proposed methodology starts from the classificati of the catchment and the characterization of the main active processes. Considering the characteristics of the dominant bedrock lithology in the area (Tiranti et al., 2014) it is possible to infer a potential frequency of occurrence of debris flows, the total rainfall needed for their triggering, together with the sedimentological and rheological characteristics of the flow (viscosity, evolution, and depositional style). The second step consists in the characterization of sediment source areas, including their degree of coupling to the main channel by using a sediment connectivity index (IC) proposed by Cavalli et al. (2013). The final step concerns the propagation and deposition of material from sediment source areas actually involved in debris flow process by a Cellular Automata Model (Deangeli, 2008) simulating the mechanisms of flow routing and deposition patterns. One of the advantages of the presented integrated approach relies on the fact that there's no need to simulate past debris flow events to define its deposition areas, but it takes into account a likely volume based on the availability and distribution of sediment source areas and a compatible deposition pattern with the alluvial fan architecture and the processes behavior characterizing the catchments, according to the CWI classification proposed by Tiranti et al. (2008, 2014, 2016a), Tiranti and Deangeli (2015). The aim of the simulations is to match the predominant observed depositional style on the alluvial fan and the channel bed. In this way, the model can be applied in absence of a detailed report (actual magnitude, deposition areas, etc.) of a debris flow event used as calibration test. In this way, it is possible to get close to the most likely behavior of a given catchment. The methodology has been applied to an alpine test-bed catchment, for which historical documentation on debris flow occurrence is available, thus helping in the validation of the obtained results.
Study Area
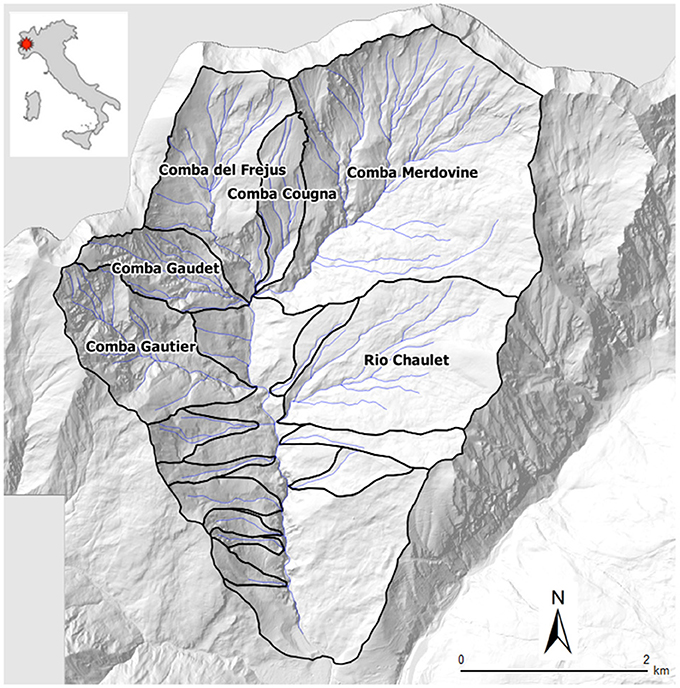
The Rio Frejus catchment, located at the head of Susa Valley (upper Susa Valley, Municipality of Bardonecchia, Turin, North-western Italy), covers an area of about 22 km2 and is composed by several sub-catchments: Comba Merdovine, Comba del Frejus, Comba Gaudet, Comba Cougna, Comba Gautier, and Rio Chaulet (Figure 1).
The upper Susa Valley is dominated by dry climate with average annual precipitations is under 800 mm, whereas the annual average is about 1,200 mm in Piemonte. The average number of annual rainy days is about 50 with a very low precipitation density, <10 mm/day (Fratianni and Motta, 2002).
Rio Frejus is characterized by a complex geomorphology due to the combined action of several processes, such as landslides, rock falls, debris flows and cryogenic processes (permafrost degradation and nival processes) at the head of catchments. Shallow deposits linked to the glacial activity are infrequent and almost completely reworked by the action of streams and landslides. For more details on geomorphological settings of Rio Frejus see Bosco et al. (2007) and Tiranti et al. (2016b).
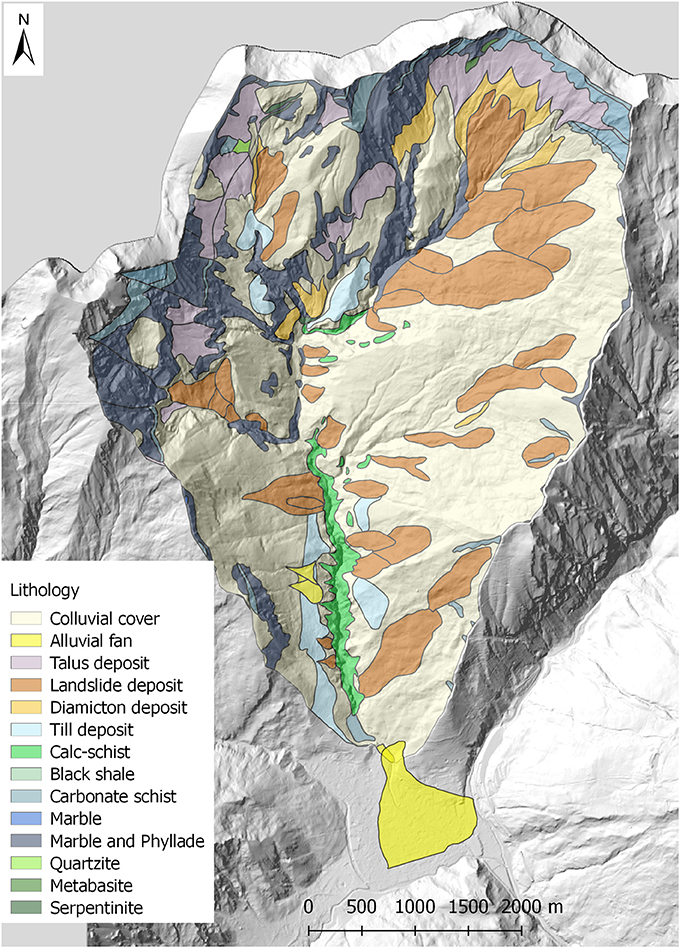
The pre-Quaternary bedrock of Rio Frejus belongs primarily to the Tectonostratigraphic Unit of the Lago Nero (Polino et al., 2002), formed by carbonate or phylladic calc-schists. The outcropping of thick-bedded serpentinites, ophicalcites and quartzites is subordinate. The outcrops percentages consist of 74.2% shallow deposits (including colluvial cover), 27.28 schists, 0.22% serpentinites/ophicalcites and 0.03% quartzites (Figure 2).
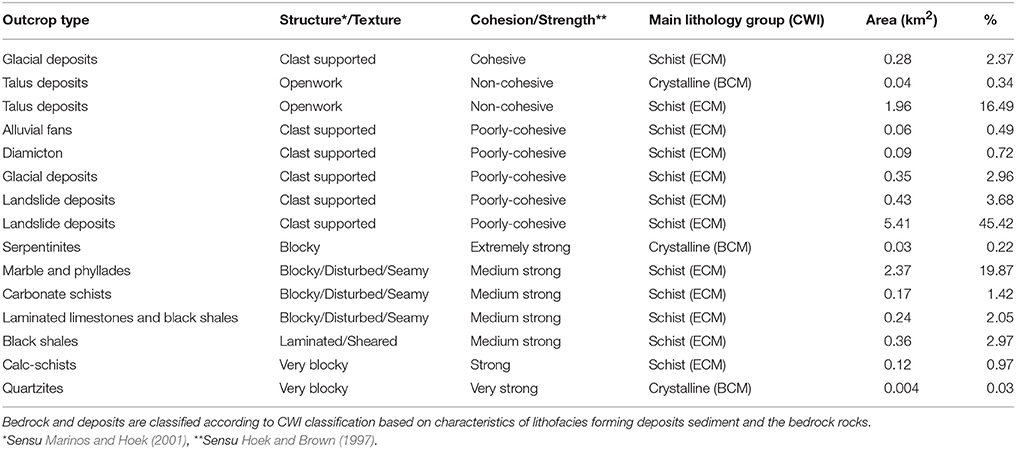
The main structural setting is represented by slightly-dip overthrust contacts and subvertical faults. The intensely fractured rock masses exhibit poor geomechanical characteristics. The phylladic-rich calc-schists are extremely degraded and can be classified as blocky/disturbed/seamy according to the Geological Strength Index (GSI; Marinos et al., 2005). Such conditions favor weathering with high generation of fine loose materials and slope instability. The main characteristics of Rio Frejus are reported in Table 1.
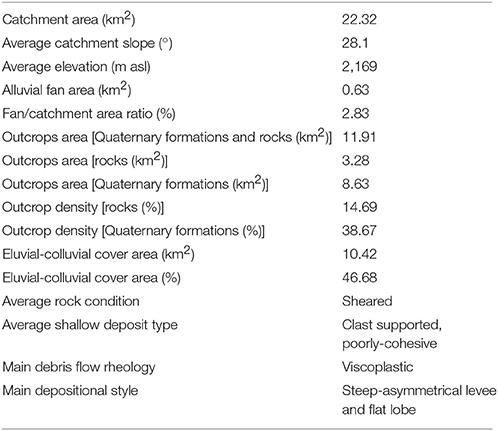
Table 1. A synthesis of the Rio Frejus catchment characteristics (modified from Tiranti and Deangeli, 2015).
Methods
Clay Weathering Index (CWI) and Catchment Classification
North-western alpine catchments were classified by Tiranti et al. (2014) into three main catchment lithology classes by using the Clay Weathering Index (CWI). This index defines the propensity of a certain lithotype to weather into clay or other fine minerals with clay-like rheology behavior (e.g., phyllosilicate groups). Following this approach, Excellent Clay Maker (ECM) catchments are characterized by particularly degradable rocks due to their weak geotechnical characteristics. Debris flow frequency for these catchments is therefore high (two events/year) due to the abundance of unconsolidated material available along the channel network in spring, summer and autumn with indicative minimum triggering rainfall threshold of 20 mm/h. In Good Clay Maker (GCM) catchments, rocks are degradable and consequently, the unconsolidated material is less abundant if compared to ECM ones. Debris flows for this class occur usually in late-spring, with an indicative minimum triggering rainfall threshold of 30 mm/h. In Bad Clay Maker (BCM) catchments, bedrocks are more resistant to the weathering and inclined to produce coarse debris (blocks and boulders in silt-sandy matrix). Debris flows are triggered by infrequently heavy rainfall. In this case, the debris flows average frequency is <1 event every 20 years and the main seasons of occurrence are fall and early spring (very uncommon during summer). Identified minimum triggering rainfall threshold is 50 mm/h.
Sediment Connectivity Index (IC)
The Sediment Connectivity Index (IC) was originally proposed by Borselli et al. (2008) with an application to agricultural catchments. Cavalli et al. (2013) made important modifications to this approach to take advantage of high-resolution Digital Terrain Models (DTMs) and to make it suitable for applications to mountain environment. IC is a distributed morphometric index focused on the topography influence on sediment connectivity representing the degree of coupling among different portions of the catchment with respect to a selected target (e.g., main channel network).
Mathematically IC is expressed by the logarithm of the ratio between the upslope and the downslope components (Equation 1):
This index indicates the potential for downward routing of sediments produced upslope and the (weighted) flow path length to the nearest target or sink.
To model the impedance to runoff and sediment fluxes, a weighting factor is included in both components of IC. In mountain catchments, high-resolution DTMs can represent an important input for deriving surface roughness in order to include an objective measure of flow impedance in the connectivity assessment. We computed the roughness index as the standard deviation of residual topography according to Cavalli et al. (2008). The roughness index was used to calculate the weighting factor by using the following equation (Equation 2; Cavalli et al., 2013):
Where RI is the roughness index value and RImax is the maximum value of RI in the study area.
As the DTM of the study area is at 5-m resolution, we considered as an optimal spatial scale a moving window of 3 × 3 pixel in order to derive a flow-impedance related roughness index and the related weighting factor.
The determination of the information necessary to identify sediment source areas were carried out with field surveys coupled with an analysis of the existent cartography (regional geologic and geomorphologic maps).
We carried out an assessment of sediment connectivity based on the computation of IC (Cavalli et al., 2013) in order to select the areas effectively coupled to the main channel system (i.e., areas accountable for sediment supply). The results of this analysis were interpreted and integrated with field observations to characterize connectivity patterns at the catchment scale with a focus on sediment source areas.
The main drainage system was extracted on an empirical basis from the DTM, adopting an area threshold approach (Figure 3) to extract a synthetic network corresponding to the presence of permanent drainage lines from field evidence. The main permanent drainage network was selected as a target for IC analysis.
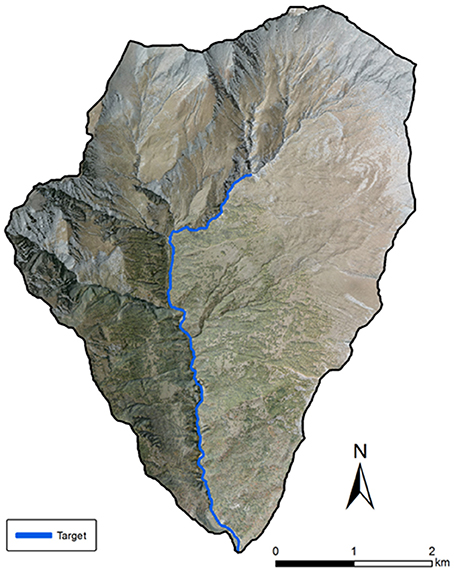
Figure 3. Frejus catchment study area, shaded relief map in transparency with aerial view of the study area. The main permanent drainage network is highlighted and has been selected as target for IC analysis.
We used the extent of the main channel system to determine the threshold area for the stream network extraction (i.e., 4.8 km2). IC map, surface roughness and the weighting factor were computed using the freely available SedInConnect application (Crema et al., 2015; Crema and Cavalli, 2018).
Cellular Automata Model
Debris flow propagation and deposition patterns were simulated by a 3D numerical code based on Cellular Automata Method (Segre and Deangeli, 1995; Deangeli, 2008). In this code, the computational domain is discretized into elementary squared cells. Each cell is characterized by columns of rigid substratum and mobilizable debris material. The volume of debris material is characterized by rheological parameters, depending on the selected constitutive law. Two constitutive laws are implemented: a frictional/collisional law (Segre and Deangeli, 1995), based on the Bagnold dilatant fluid behavior (Takahashi, 1978, 1991), and a viscoplastic law (Deangeli et al., 2013; Tiranti and Deangeli, 2015), based on Bingham fluid behavior. The solid-liquid mixture is considered as a single-phase fluid.
The linear momentum conservation equation, the mass balance, and the constitutive law are combined and integrated to obtain flow velocity. The average velocity is used for flow rate calculation at each cell.
The evolution of the system occurs in discrete time-steps, based on the Courant criterion. At each time-step, an initiation rule dependent on flow rheology is verified in each cell. If the initiation rule is satisfied for a cell, a sediment flow rate, proportional to the time-step, is calculated and stored. When all the cells are checked, the system is simultaneously updated, at the end of the time-step. Deposition and remobilization of debris can occur at each time-step and when no cell can receive or supply a rate of solid-liquid mixture the simulation ends. This numerical tool was successfully applied to analyze flume experiments (Deangeli, 2008) and the evolutive behavior of actual flows, occurred in different settings and contexts (Deangeli and Grasso, 1996; Deangeli and Giani, 1998; Deangeli et al., 2013, 2015; Tiranti and Deangeli, 2015).
The numerical analyses for the definition of depositional scenarios were carried out for each sub-catchment in the viscoplastic regime (Bingham fluid), as the basin was classified as an Excellent Clay Maker. The rheological parameters, i.e., the yield strength and the viscosity of the fluid, used in the numerical runs are based on a study of Tiranti and Deangeli (2015). In this study, the authors analyzed deposition styles and scenarios of different basins, and also the main Rio Frejus channel. They estimated the yield strength from the mean basal shear stress at the time of deposition, and the viscosity from the maximum debris flow velocity. Tiranti and Deangeli (2015) found that the yield strength was equal to τy = 1,400 Pa and the viscosity was equal to μ = 80 Pa*s, by assuming a solid concentration equal c = 0.4. An analysis of deposition style sensitivity to yield strength and viscosity, indicated that in the Rio Frejus the deposition pattern did not vary substantially in the range τy = 1,400–2,000 Pa and μ = 80–100 Pa*s. Based on this finding, in our numerical runs we used the following values of yield strength and the viscosity: τy = 1,400 Pa, μ = 80 Pa*s.
Results and Discussion
This section reports the results of the integrated study presented step-by-step to underline the single contribute for each method and how them can give some more exhaustive results compared with those resulting from more classical approaches based only on debris flow routing model output calibrated on debris flow events of the past (e.g., Bertolo and Bottino, 2008; Pirulli and Marco, 2010) applied in similar geological and geomorphological contest.
CWI Classification of Catchment
Based on the dominant bedrock lithology characteristics reported in section “Study Area,” Rio Frejus is classified as Excellent Clay Maker based on the Clay Weathering Index (CWI) classification (Tiranti et al., 2014; Table 2).
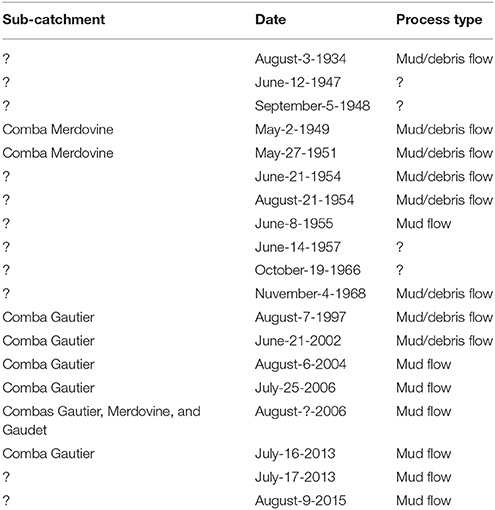
Due to the dominant lithology (phyllosilicates-rich schist), the catchment is characterized by a very high production of unconsolidated material which is rich in clay or clay-like minerals. This material favors the occurrence of cohesive debris flows showing a viscoplastic rheology, as resulting from the analysis of historical reports on torrential processes occurred in the Rio Frejus catchment (Table 3).
Debris flows occurred along the Rio Frejus show high viscosity and on average 45% of material is commonly deposited along the channels while only 55% of sediment reaches the alluvial fan as mud flow or mud/debris flow (Tiranti and Deangeli, 2015) as shown in Figure 4.

Figure 4. An example of main type of torrential process that most frequently reaches the Rio Frejus's alluvial fan area (6th August 2004).
For this reason, the Rio Frejus alluvial fan shows a rather small area (“starved alluvial fan” sensu Tiranti and Deangeli, 2015) compared to the feeding catchment (see Figure 2 and Table 1), according to CWI classification.
Index of Connectivity and Sediment Source Areas
We identified extensive sediment source areas primarily as landslide deposits (Figure 5), typically incised by several gullies (Figure 6a), covering 58% of the catchment, with 35% of active phenomena. The most frequent debris flow initiation points occur at the landslide deposits intersected by channel network. In these zones the sediments are chaotic and heterometric, characterized by a prevalent gravel and clayey silt-forming matrix. These deposits represent the main sediment source for erodible clayey sediments.
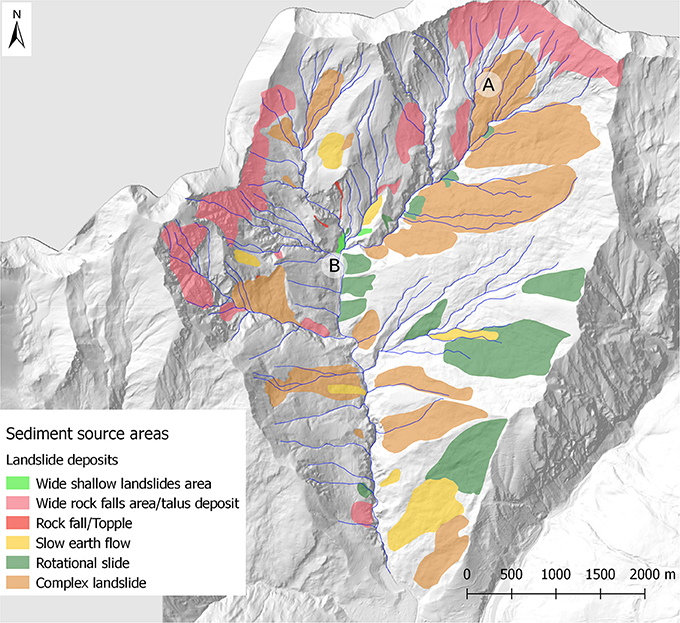
Figure 5. Distribution of sediment source areas within the Rio Frejus catchment. A and B represent the location of example deposits shown in Figure 7.

Figure 6. Example of deposits located at the head of Rio Frejus catchment: (a) A slow earth flow landslide deposit incised by gullies. (b) A thick debris flow deposit near a main incised channel located at the catchment head.
Moreover, the colluvial cover (<2 m) on steep slope is affected by shallow landslides and widespread rill erosion. Another important sediment source is represented by the abundant presence of past debris-flow deposits along the main incised channel (Figure 6b).
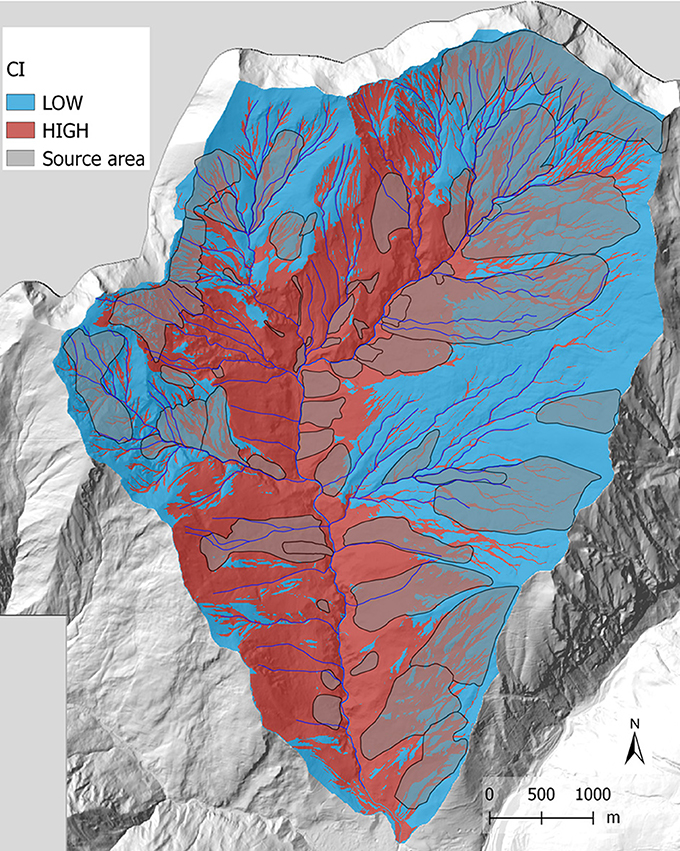
IC map (Figure 7A), resulting from the analysis reported in section “Methods,” was subdivided into 4 classes (i.e., Low, Medium-Low, Medium-High, High), using the Natural Breaks (Jenks, 1967) classification algorithm (Figure 7A) as proposed by Crema and Cavalli (2018) and Tiranti et al. (2016a).
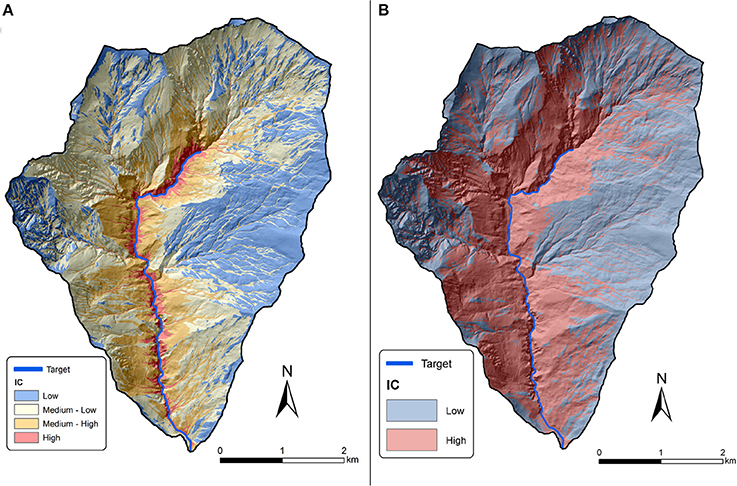
Figure 7. (A) Results of IC analysis with the main river as a target. Results are divided in four classes according to Natural Breaks algorithm. (B) Results of IC analysis grouping the values in two classes.
Figure 7B shows the results of IC analysis based on two classes (high/low) This analysis was carried out to highlight potentially coupled and decoupled areas. Figure 7 clearly shows that three sub-catchments seem characterized by a general decoupled behavior. Two of these sub-catchments, located in the upper and western portion of the study area, exhibit signs of geomorphic activity and active erosional processes, but also a structural decoupling barrier can be detected at the outlet of these sub-catchments. This physical barrier could account for the upstream low IC values playing an important role in the catchment morphological evolution. Unlike these two cases, the decoupled subcatchments in the eastern portion of the study area do not show important ongoing erosional processes. The disconnectivity here could be related to the presence of flatter areas and gentler slopes that affect primarily the flow paths in the downslope component of IC.
The comparison between coupled and decoupled results are shown in Figure 8. in which it is clear how the high connectivity distribution is mainly close to the gullies related to large sediment source areas.
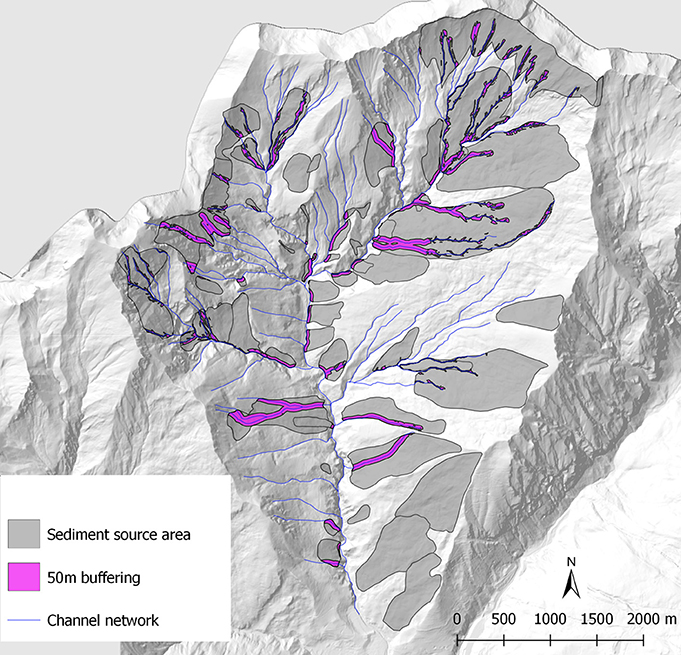
The most likely amount of sediment that actually can contribute to a debris flow of usual magnitude by selecting the source areas on the basis of the IC distribution and the intersection with the channel network within 50 m buffering from channels axes is showed in Figure 9, according to Bosco et al. (2007).
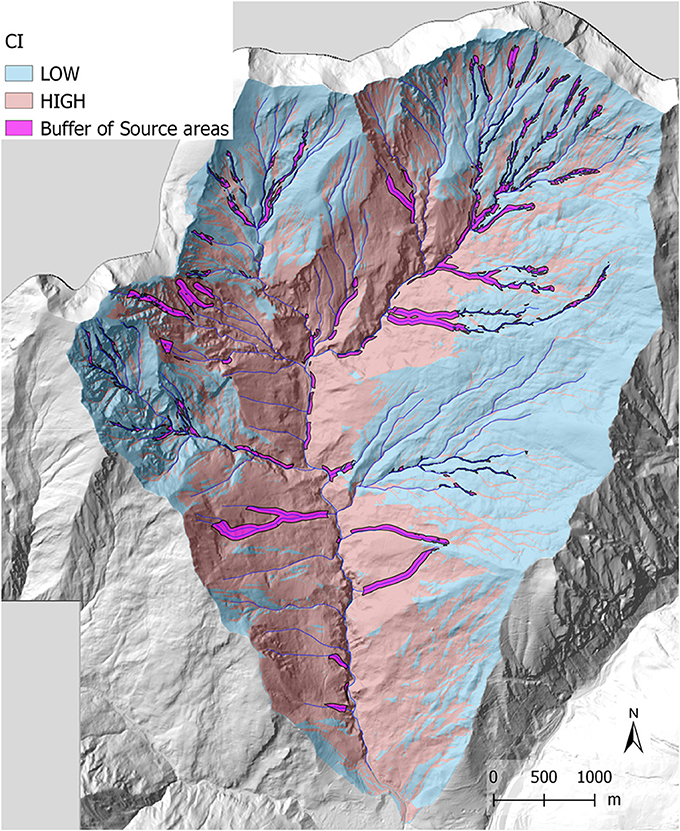
Figure 9. Sediment source areas resulting from intersection between source deposits and a 50 m buffer of the channel network.
Based on field observations, we estimated the average depth of detachment surfaces for each deposit in order to determine the mobilizable volume from slope sediment source areas.
We compared the resulting volumes with standard volumes of the same deposit types available in the literature (Hungr et al., 1984; Dadson et al., 2004; Marchi and D'Agostino, 2004; Guzzetti et al., 2009; Tiranti et al., 2016a). The identified portion of sediment source areas represents the effective total sediment volume potentially mobilizable by debris flows that can reach the channel network. In order to find the total sediment volume, we considered the average thickness for each type mobilizable deposit (1.5 m for rockfall accumulation areas, 1 m for areas subject to wide shallow landslides, 2.5–3 m for slow earth flows, 3–5 m for marginal/surficial portions of complex landslides, 2–7 m for rotational landslides) according to the method proposed by Tiranti et al. (2016a). We calculated a likely maximum sediment volume equal to 3,342,286 m3.
Routing Model (Cellular Automata Model)
Based on the results of IC analyses and field observations, the source areas and the volumes of sediments were identified for each sub-catchment. These outcomes were used as an input to simulate sub-catchment dynamics through deposition scenarios with the Cellular Automata Model. Figure 10 shows the initial sediment input determined from the intersection of buffered source areas and IC map.
In the numerical simulations, we subdivided the whole catchment area into a West area and East area. Each area was further subdivided into sub-catchments, characterized by a potential mobilizable volume of sediments:
• West area. Comba Merdovine sx_1 and Comba Merdovine sx_2 with potential mobilizable volume of 258,784 m3 and 323,856,32 m3 respectively; Rio Chaulet and unnamed channels (sx_3) with a mobilizable volume of 554,578 m3 (Figure 11).
• East area. Comba del Frejus (dx_1) with potential mobilizable volume of 678,918 m3; Comba Gaudet and Gautier (dx_2) with potential mobilizable volume of 827,388 m3; unnamed channels (dx_3) with potential mobilizable volume of 532,745 m3 (Figure 12).
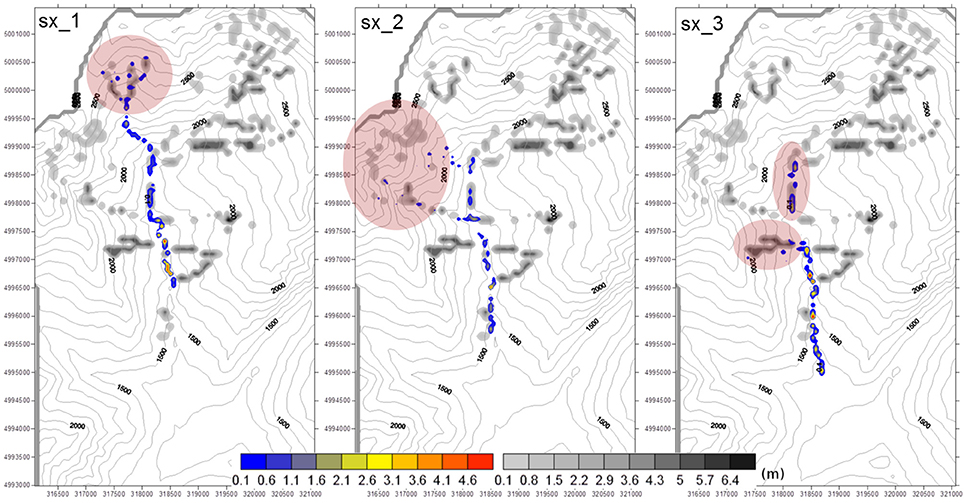
Figure 11. Results of the numerical runs performed in the West area. Colored scale: simulated deposition patterns. Gray scale: initial deposits of sediments.
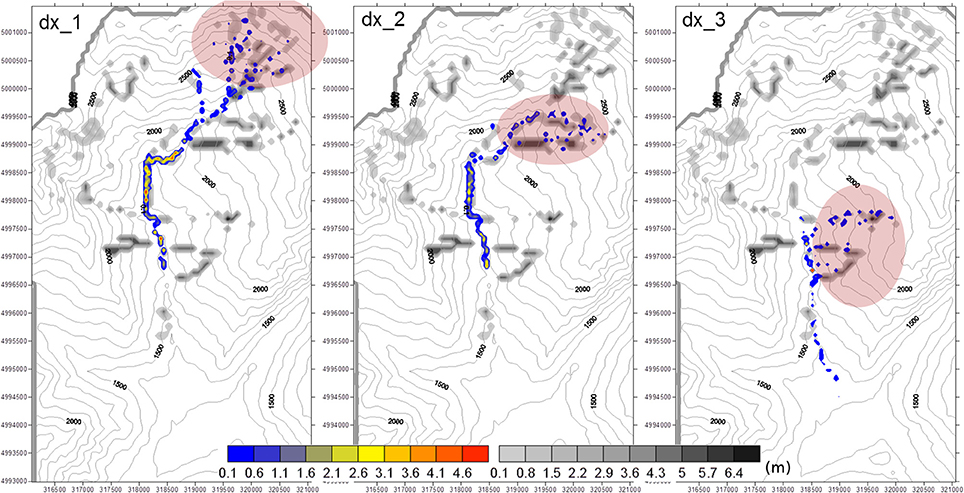
Figure 12. Results of the numerical runs performed in the East area. Colored scale: simulated deposition patterns. Gray scale: initial deposits of sediments.
Figures 11, 12 show the results of the simulations in the West area and East area, respectively. All the sediment flows reach the target channel, in agreement with the IC spatial pattern. A part of the initial deposits of sediments remains in the original place or propagates for a small distance on channels belonging to the sub-catchments. This outcome is related to the local morphology of each sub-catchment and to the viscoplastic rheology of the mixture and agrees with in situ observations. Furthermore, the results also show a significant sediment deposition along the main channel, in agreement with in situ observation and CWI class of catchments. Only the debris flows occurring in sub catchments with the higher initial sediment volumes reach the valley bottom, with very low deposition thicknesses. This result agrees with the characteristics of the fan highlighted from in situ observations.
For this reason, we stress herein the fact that the evaluation of debris flow hazard needs to be considered in a dynamic way as an evolving process, with continuous updates.
Conclusions
The presented integration of different methodology to characterize debris flows initiation, propagation and deposition allows to define hazard scenarios without refer the simulations to past debris flow events. Thanks to the application of the Clay Weathering Index classification it is possible to infer “a priori” the potential typology of torrential processes that can occur and its evolution according to flow rheology and transported sediment characteristics. The characterization of sediment source areas by applying of a sediment connectivity index permitted to include into the analysis a potential for the sediment to be coupled to the main drainage system. Finally, the scenarios of debris flow propagation and deposition can be modeled using a 3D cellular automata model. Through this third step, it is possible to obtain numerous propagation and deposition scenarios considering only the sediment source areas that can actually feed a debris flow. Thanks to the proposed integrated approach, it is possible to gain accurate insights into the most likely impacts of a debris flow, characterizing its dynamics from the initiation areas to the alluvial fan. Moreover, the study demonstrates that the maximum expected magnitude of a debris flow can be forecasted excluding all the sediment source areas not connected to the main channel network, with interesting applications also in urban planning and hazard mitigation strategies.
The limits of this integrated method are mainly linked to the availability of territorial dataset (detailed geological and geomorphological maps, high resolution DTM, knowledge of nature and distribution of potential sediment source areas).
Moreover, this study represents the beginning of the experimentation of the integrated method, which must be applied to catchments characterized by different geomorphological geologic contexts before being considered sufficiently reliable to be used as a decision makers' support tool.
Another point of future development will consist in comparing the here proposed method with others already widely tested and available in the literature.
At this moment, the presented study represents an interesting line of research that will provide a new and useful tool for debris flow hazard assessment.
Author Contributions
DT dealt with the characterization and classification of catchment, debris flow processes and sediment source areas. MC and SC determined the connectivity index to identify the sediment source areas available to generate debris flows. CD applied a Cellular Automata model to define the propagation and deposition scenarios of debris flows in the studied catchment.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Ancey, C. (2007). Plasticity and geophysical flows: a review. J. Nonnewton. Fluid Mech. 142, 4–35. doi: 10.1016/j.jnnfm.2006.05.005
Berti, M., and Simoni, A. (2005). Experimental evidences and numerical modelling of debris flow initiated by channel runoff. Landslides 2, 171–182. doi: 10.1007/s10346-005-0062-4
Bertolo, P., and Bottino, G. (2008). Debris-flow event in the Frangerello Stream-Susa Valley (Italy)-calibration of numerical models for the back analysis of the 16 October, 2000 rainstorm. Landslides 5, 19–30. doi: 10.1007/s10346-007-0099-7
Beylich, A. A., and Sandberg, O. (2005). Geomorphic effects of the extreme rainfall event of 20–21 July, 2004 in the Latnjavagge catchment, northern Swedish Lapland. Geogr. Ann. 87A, 409–419. doi: 10.1111/j.0435-3676.2005.00267.x
Borselli, L., Cassi, P., and Torri, D. (2008). Prolegomena to sediment and flow connectivity in the landscape: a GIS and field numerical assessment. CATENA 75, 268–277. doi: 10.1016/j.catena.2008.07.006
Bosco, F., Gandini, D., Giudici, I., Marco, F., Paro, L., Tararbra, M., et al. (2007). “The mass movement of the Rio Frejus (Bardonecchia, NW Italian Alps) on August 6th, 2004,” in Evaluation and Prevention of Natural Risks, eds S. Campus, S. Barbero, S. Bovo, and F. Forlati (London: Taylor and Francis Group, Balkema), 409–447.
Bovis, M. J., and Dagg, B. R. (1988). A model for debris accumulation and mobilization in steep mountain streams. Hydrol. Sci. 33, 589–604. doi: 10.1080/02626668809491292
Brardinoni, F., Church, M., Simoni, A., and Macconi, P. (2012). Lithologic and glacially conditioned controls on regional debris-flow sediment dynamics. Geology 40, 455–458. doi: 10.1130/G33106.1
Brunetti, M. T., Luino, F., Vennari, C., Peruccacci, S., Biddoccu, M., Valigi, D., et al. (2015). “Rainfall thresholds for possible occurrence of shallow landslides and debris flows in Italy,” in Dating Torrential Processes on Fans and Cones, Advances in Global Change Research, eds M. Schneuwly-Bollschweiler, M. Stoffel, and F. Rudolf-Miklau (Springer Science), 327–339.
Cannon, H. S., Gartner, J. E., Wilson, R. C., Bowers, J. C., and Laber, J. L. (2008). Storm rainfall conditions for floods and debris flows from recently burned areas in Southwestern Colorado and Southern California. Geomorphology 96, 250–269. doi: 10.1016/j.geomorph.2007.03.019
Cavalli, M., Crema, S., Trevisani, S., and Marchi, L. (2017a). GIS tools for preliminary debris-flow assessment at regional scale. J. Mt. Sci. 14, 2498–2510. doi: 10.1007/s11629-017-4573-y
Cavalli, M., Goldin, B., Comiti, F., Brardinoni, F., and Marchi, L. (2017b). Assessment of erosion and deposition in steep mountain basins by differencing sequential digital terrain models. Geomorphology 291, 4–16. doi: 10.1016/j.geomorph.2016.04.009
Cavalli, M., Tarolli, P., Marchi, L., and Dalla Fontana, G. (2008). The effectiveness of airborne LiDAR data in the recognition of channel-bed morphology. CATENA 73, 249–260. doi: 10.1016/j.catena.2007.11.001
Cavalli, M., Trevisani, S., Comiti, F., and Marchi, L. (2013). Geomorphometric assessment of spatial sediment connectivity in small Alpine catchments. Geomorphology 188, 31–41. doi: 10.1016/j.geomorph.2012.05.007
Chang, T. C., and Chao, R. J. (2006). Application of back-propagation networks in debris flow prediction. Eng. Geol. 85, 270–280 doi: 10.1016/j.enggeo.2006.02.007
Costa, J. E. (1988). “Rheologic, geomorphic, and sedimentologic differentiation of water floods, hyperconcentrated flows, and debris flows,” in Flood Geomorphology, eds V. R. Baker, R. C. Kochel, and R. C. Patton (New York, NY: John Wiley and Sons), 113–122.
Crema, S., and Cavalli, M. (2018). SedInConnect: a stand-alone, free and open source tool for the assessment of sediment connectivity. Comput. Geosci. 111, 39–45. doi: 10.1016/j.cageo.2017.10.009
Crema, S., Schenato, L., Goldin, B., Marchi, L., and Cavalli, M. (2015). Toward the development of a stand-alone application for the assessment of sediment connectivity. Rendiconti Online Della Soc. Geol. Ital. 34, 58–61. doi: 10.3301/ROL.2015.37
Dadson, S. J., Hovius, N., Chen, H., Dade, W. B., Lin, J. C., and Hsu, M. L. (2004). Earthquake-triggered increase in sediment delivery from an active mountain belt. Geology 32, 733–736. doi: 10.1130/G20639.1
Deangeli, C. (2008). Laboratory granular flows generated by slope failures. Rock Mech. Rock Eng. 41, 199–217. doi: 10.1007/s00603-007-0131-1
Deangeli, C., and Giani, G. P. (1998). “Physical and Numerical models to rehabilitate a waste disposal site,” in Proceedings of the 8th International Congress IAEG (Vancouver, BC; Balkema; Rotterdam), 1813–1818.
Deangeli, C., and Grasso, P. (1996). “The evolutive mechanism of debris flows: analysis and protection works,” in Proceedings of 7th International Symposium on Landslides (Trondheim; Balkema; Rotterdam), 1183–1188.
Deangeli, C., Paltrinieri, E., and Tiranti, D. (2013). Debris flow analysis: from lithological classification of the basin to deposition,” in Landslide Science and Practice, Vol. 3, Spatial Analysis and Modeling Chap. 2: Rapid Landslide Runout Analysis, eds C. Margottini, P. Canuti, and K. Sassa (Springer), 301–307.
Deangeli, C., Tiranti, D., Marco, F., and Volpato, M. (2015). “Comparison of Debris flow depositional scenarios using different DTMs,” in Engineering Geology for Society and Territory, Vol. 2, eds G. Lollino, D. Giordan, G. B. Crosta, J. Corominas, R. Azzam, J. Wasowski, and N. Sciarra (Springer International Publishing), 1667–1671.
Ellen, S. D., and Flaming, R. W. (1987). Mobilization of Debris Flows From Soil Slips, San Francisco Bay Region. GSA Reviews in Engineering Geology.
Fratianni, S., and Motta, L. (2002). Andamento Climatico in Alta Val Susa Negli Anni 1990-1999. Regione Piemonte; Studi Climatologici in Piemonte.
Glade, T. (2005). Linking debris-flow hazard assessment with geomorphology. Geomorphology 66. 189–213. doi: 10.1016/j.geomorph.2004.09.023
Gregoretti, C. (2000). Experimental evidence from the triggering of debris flow along a granular slope. J. Phys. Chem. Earth B Hydrol. Oceans Atmosphere 25, 387–390. doi: 10.1016/S1464-1909(00)00031-9
Gregoretti, C., Degetto, M., and Boreggio, M. (2016). GIS-based cell model for simulating debris flow runout on a fan. J. Hydrol. 534, 326–340. doi: 10.1016/j.jhydrol.2015.12.054
Guzzetti, F., Ardizzone, F., Cardinali, M., Rossi, M., and Valigi, D. (2009). Landslide volumes and landslide mobilization rates in Umbria, central Italy. Earth Planetary Sci. Lett. 279, 222–229. doi: 10.1016/j.epsl.2009.01.005
Harvey, A. M. (1994). “Influence of slope/stream coupling on process interactions on eroding gully slopes, Howgill Fells, Northwest England,” in Process Models and Theoretical Geomorphology, ed M. J. Kirkby (Chichester: John Wiley and Sons), 247–270.
Hoek, E., and Brown, E. T. (1997). Practical estimates of rock mass strength. Int. J. Rock Mech. Min. Sci. 34, 1165–1186. doi: 10.1016/S1365-1609(97)80069-X
Hungr, O. (1995). A model for the run out analysis of rapid flow slides, debris flows and avalanches. Can. Geotechnical J. 32, 610–623. doi: 10.1139/t95-063
Hungr, O. (2002). “Analytical Models for Slide Sand Flows,” in Proceedings of the International Symposium on Landslide Risk Mitigation and Protection of Cultural and Natural Heritage, ed K. Sassa (Kyoto: KyotoUniversity), 559–586.
Hungr, O., McDougall, S., Wise, M., and Cullen, M. (2008). Magnitude–frequency relationships of debris flows and debris avalanches in relation to slope relief. Geomorphology 96, 355–365. doi: 10.1016/j.geomorph.2007.03.020
Hungr, O., Morgan, G. C., and Kellerhals, R. (1984). Quantitative analysis of debris torrent hazard for design of remedial measures. Can. Geotech. J. 21, 663–677 doi: 10.1139/t84-073
Hürlimann, M., Copons, R., and Altimir, J. (2006). Detailed debris flow hazard assessment in Andorra: a multidisciplinary approach. Geomorphology 78, 359–372. doi: 10.1016/j.geomorph.2006.02.003
Iverson, R. M. (2003). “The debris flow rheology myth,” in Third International Conference on Debris-Flow Hazard Mitigation: Mechanics, Prediction and Assessment, eds Rickenmann and C. L. Chen (New York, NY: American Society of Civil Engineers), 303–314.
Jakob, M., Bovis, M., and Oden, M. (2005). The significance of channel recharge rates for estimating debris-flow magnitude and frequency. Earth Surf. Process. Landf. 30, 755–766. doi: 10.1002/esp.1188
Johnson, K. A., and Sitar, N. (1990). Hydrologic conditions leading to debris-flow initiation. Can. Geotech. J. 27, 789–801. doi: 10.1139/t90-092
Kean, J. W., McCoy, S. W., Tucker, G. E., Staley, D. M., and Coe, J. A. (2013), Runoff-generated debris flows: observations modeling of surge initiation, magnitude, frequency. J. Geophys. Res. Earth Surf. 118, 2190–2207. doi: 10.1002/jgrf.20148
Marchi, L., and D'Agostino, V. (2004). Estimation of debris-flow magnitude in the Estern Italian Alps. Earth Surf. Process. Landforms 29, 207–220. doi: 10.1002/esp.1027
Marinos, P., and Hoek, E. (2001). Estimating the geotechnical properties of heterogeneous rock masses such as flysch. Bull. Eng. Geol. Environ. 60, 85–92. doi: 10.1007/s100640000090
Marinos, V., Marinos, P., and Hoek, E. (2005). The geological strength index: applications and limitations. Bull. Eng. Geol. Environ. 64, 55–65. doi: 10.1007/s10064-004-0270-5
Marra, F., Nikolopoulos, E. I., Creutin, J. D., and Borga, M. (2015). Space–time organization of debris flows-triggering rainfall and its effect on the identification of the rainfall threshold relationship. J. Hydrol. 541, 246–255. doi: 10.1016/j.jhydrol.2015.10.010
Michaelides, K., and Chappell, A. (2009). Connectivity as a concept for characterising hydrological behaviour. Hydrological Process. 23, 517–522. doi: 10.1002/hyp.7214
Moscariello, A., Marchi, L., Maraga, F., and Mortara, G. (2002). Alluvial fans in the Alps: sedimentary facies and processes. Spec. Publ. Int. Ass. Sediment 32, 141–166.
Pierson, T. C., and Costa, J. E. (1987). A rheologic classification of subaerial sediment–water flows. Geol. Soc. Am. Rev. Eng. Geol. 7, 1–12. doi: 10.1130/REG7-p1
Pirulli, M., and Marco, F. (2010). Description and numerical modelling of the October 2000 Nora debris flow, Northwestern Italian Alps. Can. Geotech. J. 47, 135–146 doi: 10.1139/T09-082
Polino, R., Dela Pierre, F., Fioraso, G., Giardino, M., and Gattiglio, M. (2002). Foglio 132-152-153 “Bardonecchia” Carta Geologica d'Italia, scala 1:50,000. Servizio Geologico d'Italia.
Prancevic, J. P., Lamb, P. M., and Fuller, B. M. (2014). Incipient sediment motion across the river to debris-flow transition. Geology 42, 191–194, doi: 10.1130/G34927.1
Rickenmann, D. (2015). “Debris-flow hazard assessment and methods applied in engineering practice,” in International Conference on Debris-Flow Hazards Mitigation: Mechanics, Prediction, and Assessment, Proceedings, 23–24.
Rickenmann, D., Laigle, D., McArdell, B. W., and Hubl, J. (2006). Comparison of 2D debris-flow simulation models with field events. Comput. Geosci. 10, 241–264. doi: 10.1007/s10596-005-9021-3
Rickenmann, D., Weber, D., and Stepanov, B. (2003). “Erosion by debris flows in field and laboratory experiments,” in Debris-Flow Hazards Mitigation: Mechanics, Prediction, and Assessment, eds D. Rickenmann and C. L. Chen (Rotterdam: Millpress), 883–894.
Sassa, K. (1985). “The mechanism of debris flow,” in Proceedings of XI International Conference on Soil Mechanics and Foundation Engineering (San Francisco, CA), 1173–1176.
Segre, E., and Deangeli, C. (1995). Cellular automaton for realistic modelling of landslides. Nonlinear Process. Geophys. 2, 1–15. doi: 10.5194/npg-2-1-1995
Stoffel, M., Bollschweiler, M., and Beniston, M. (2011). Rainfall characteristics for periglacial debris flows in the Swiss Alps: past incidences–potential future evolutions. Clim. Change 105, 263–280. doi: 10.1007/s10584-011-0036-6
Stoffel, M., Tiranti, D., and Huggel, C. (2014). Climate change impacts on mass movements – case studies from the European Alps. Sci. Total Environ. 493, 1255–1266. doi: 10.1016/j.scitotenv.2014.02.102
Tiranti, D., Bonetto, S., and Mandrone, G. (2008). Quantitative basin characterization to refine debris-flow triggering criteria and processes: an example from the Italian Western Alps. Landslides 5, 45–57. doi: 10.1007/s10346-007-0101-4
Tiranti, D., Cavalli, M., Crema, S., Zerbato, M., Graziadei, M., Barbero, S., et al. (2016a). Semi-quantitative method for the assessment of debris supply from slopes to river in ungauged catchments. Sci. Total Environ. 554–555, 337–348. doi: 10.1016/j.scitotenv.2016.02.150
Tiranti, D., Cremonini, R., Asprea, I., and Marco, F. (2016b). Driving factors for torrential mass-movements occurrence in the Western Alps. Front. Earth Sci. 4:16. doi: 10.3389/feart.2016.00016
Tiranti, D., Cremonini, R., Marco, F., Gaeta, A. R., and Barbero, S. (2014). The DEFENSE (DEbris Flows triggEred by storms-Nowcasting SystEm): an early warning system for torrential processes by radar storm tracking using a Geographic Information System (GIS). Comput. Geosci. 70, 96–109. doi: 10.1016/j.cageo.2014.05.004
Tiranti, D., and Deangeli, C. (2015). Modeling of debris flow depositional patterns according to the catchments and source areas characteristics. Front. Earth Sci. 3:8. doi: 10.3389/feart.2015.00008
Tropeano, D., Luino, F., and Turconi, L. (2006). Eventi di Piena e Frana in Italia Settentrionale nel Periodo 2002-2004. CNR-IRPI/GNDCI.
Von Boetticher, A., Turowski, J. M., McArdell, B. W., Rickenmann, D., and Kirchner, J. W. (2016). DebrisInterMixing-2.3: a finite volume solver for three-dimensional debris-flow simulations with two calibration parameters-Part 1: model description. Geosci. Model Dev. 9, 2909–2923. doi: 10.5194/gmd-9-2909-2016
Michaelides, K., and Wainwright, J. (2002). Modelling the effects of hillslope–channel coupling on catchment hydrological response. Earth Surf. Process. Landforms 27, 1441–1457. doi: 10.1002/esp.440
Wieczorek, G. F., and Glade, T. (2005). “Climatic factors influencing occurrence of debris flow,” in Debris Flow Hazard and Related Phenomena, eds Jacob and Hungr (Springer), 325–352.
Keywords: torrential mass movement, sediment connectivity, cellular automata, hazard assessment, Northwestern Italy
Citation: Tiranti D, Crema S, Cavalli M and Deangeli C (2018) An Integrated Study to Evaluate Debris Flow Hazard in Alpine Environment. Front. Earth Sci. 6:60. doi: 10.3389/feart.2018.00060
Received: 29 January 2018; Accepted: 07 May 2018;
Published: 23 May 2018.
Edited by:
Daniel Nývlt, Masaryk University, CzechiaReviewed by:
Radek Tichavsky, University of Ostrava, CzechiaVincenzo Amato, University of Molise, Italy
Copyright © 2018 Tiranti, Crema, Cavalli and Deangeli. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Davide Tiranti, ZGF2aWRlLnRpcmFudGlAYXJwYS5waWVtb250ZS5pdA==
 Davide Tiranti
Davide Tiranti Stefano Crema
Stefano Crema Marco Cavalli
Marco Cavalli Chiara Deangeli
Chiara Deangeli