Forecasting Volcanic Eruptions: Beyond the Failure Forecast Method

Introduction

Most of the world’s active volcanoes are not regularly monitored (Tilling, 1995; Sparks et al., 2012), especially those that have been in repose for centuries or more. When such volcanoes reawaken, short-term forecasts of eruption are normally based on data from rudimentary monitoring networks installed after the start of unrest. Local microseismicity, or volcano-tectonic (VT) events, and ground deformation are the pre-eruptive phenomena most frequently detected (Zobin, 2003; McNutt, 2005; Dzurisin, 2007; White and McCausland, 2016) and forecasting strategies use accelerations in both signals to estimate when their rate will reach a critical pre-eruptive value. A popular approach follows the failure forecast method (FFM) developed by Voight (1988) and Cornelius and Voight (1994, 1995,1996). However, the best-fit trends for individual time series are not unique and statistical fits can yield ambiguous results (Bell et al., 2011, 2013; Boué et al., 2015; Vasseur et al., 2015). Here we argue that the precursory time series are governed by a deterministic parent relation between seismicity and deformation, subject to independent constraints on how the crust is loaded with time. The FFM then emerges as a particular form of the parent relation when rates of stress supply are constant. Because the parent relation is generic, it can be applied in the absence of information about previous unrest and offers the prospect of enhancing the reliability of forecasts by integrating deterministic estimates of eruption time with existing probabilistic evaluations. The physical basis for the parent relation is reviewed and updated, before it is used to propose new operational procedures for emergency forecasts of eruptions.

Seismic and Deformation Precursors to Eruption

Precursors to eruption describe how magma is able to overcome resistance to its ascent through the crust. When magma can utilize an existing open conduit, resistance is provided by the magma’s rheology and friction along the conduit’s walls (Figure 1). When an existing conduit is not used, resistance is dominated by the need to break open a new pathway for magma ascent; this so-called closed condition applies to long-dormant volcanoes, which have sealed previous conduits, and to volcanoes creating new pathways in addition to an existing conduit, such as flank eruptions through volcanic edifices that already have an open summit vent (Figure 1).

FIGURE 1

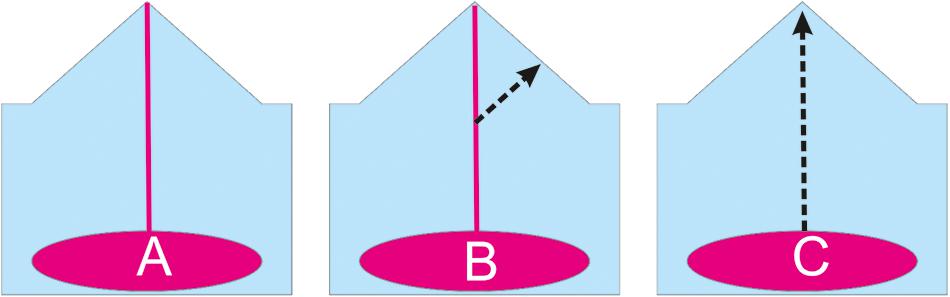
FIGURE 1. Resistance to magma ascent is governed (A) by magma rheology at open volcanoes that maintain a connection between their feeding body and the surface, but by the strength of the crust at closed volcanoes, when a new pathway (arrows) must be formed before (B) a flank eruption (even when an open conduit is also available) and (C) eruptions after an extended interval of repose.

A crustal control on opening new magmatic pathways favors similar patterns of precursory behavior, independent of a volcano’s tectonic setting, magma composition and style of eruption; similar patterns support the view that short-term forecasts of eruptions are feasible and can be quantified by rock mechanics; and the control of rock mechanics suggests that repeatable patterns are likely to be scale-independent. Voight (1988, 1989) was among the first to promote the importance of scale-independence by recognizing the similarities between precursors to eruptions and rock deformation in the laboratory. He argued that restricted ranges of precursory behavior are driven by a positive feedback between the rate (dΩ/dt) and acceleration (d²Ω/dt²) of a precursory signal Ω with time:

$$\begin{array}{c}{d}^2\Omega /d{t}^2 = A{(d\Omega /dt)}^{\alpha }\left(1\right)\end{array}$$

where A is a constant and α, which usually lies between 1 and 2, describes the strength of the feedback. As the rate increases, the acceleration becomes larger and increases the rate more quickly than before. The deterministic forecasting potential of the relation depends on estimating the time at which the rate tends to infinity. This singularity is interpreted to represent when a major change occurs in the structure of the deforming rock that ultimately favors an eruption, such as bulk failure and the formation of a pathway along which magma can reach the surface (Voight, 1988; Cornelius and Scott, 1993; Cornelius and Voight, 1994, 1995, 1996; Kilburn and Voight, 1998; De la Cruz-Reyna, 2001; Chastin and Main, 2003; Collombet et al., 2003; Kilburn, 2003; Bell and Kilburn, 2011).

Constrained by the limited test data available at the time, Voight (1988) proposed that individual precursory sequences are characterized by a single value of α, that α can take values from 1 to 2, and that the associated range of accelerations can be expected for any precursory signal related to ground deformation and fracturing. Subsequent studies, however, suggest that α can evolve from 1 to 2 during an individual precursory sequence (Figure 2; McGuire and Kilburn, 1997; Kilburn and Voight, 1998; Kilburn, 2003, 2012), and that different signals need not accelerate throughout a full sequence. For example, closed volcanoes and rock-physics experiments show that rates of fracturing can accelerate while the deformation rate remains constant (Figure 3; Kilburn, 2012; Robertson and Kilburn, 2016). Under such conditions, Eq. (1) may accommodate the VT event rate, but not the contemporaneous rate of deformation, and so describes only part of the precursory processes that lead to eruption.

FIGURE 2

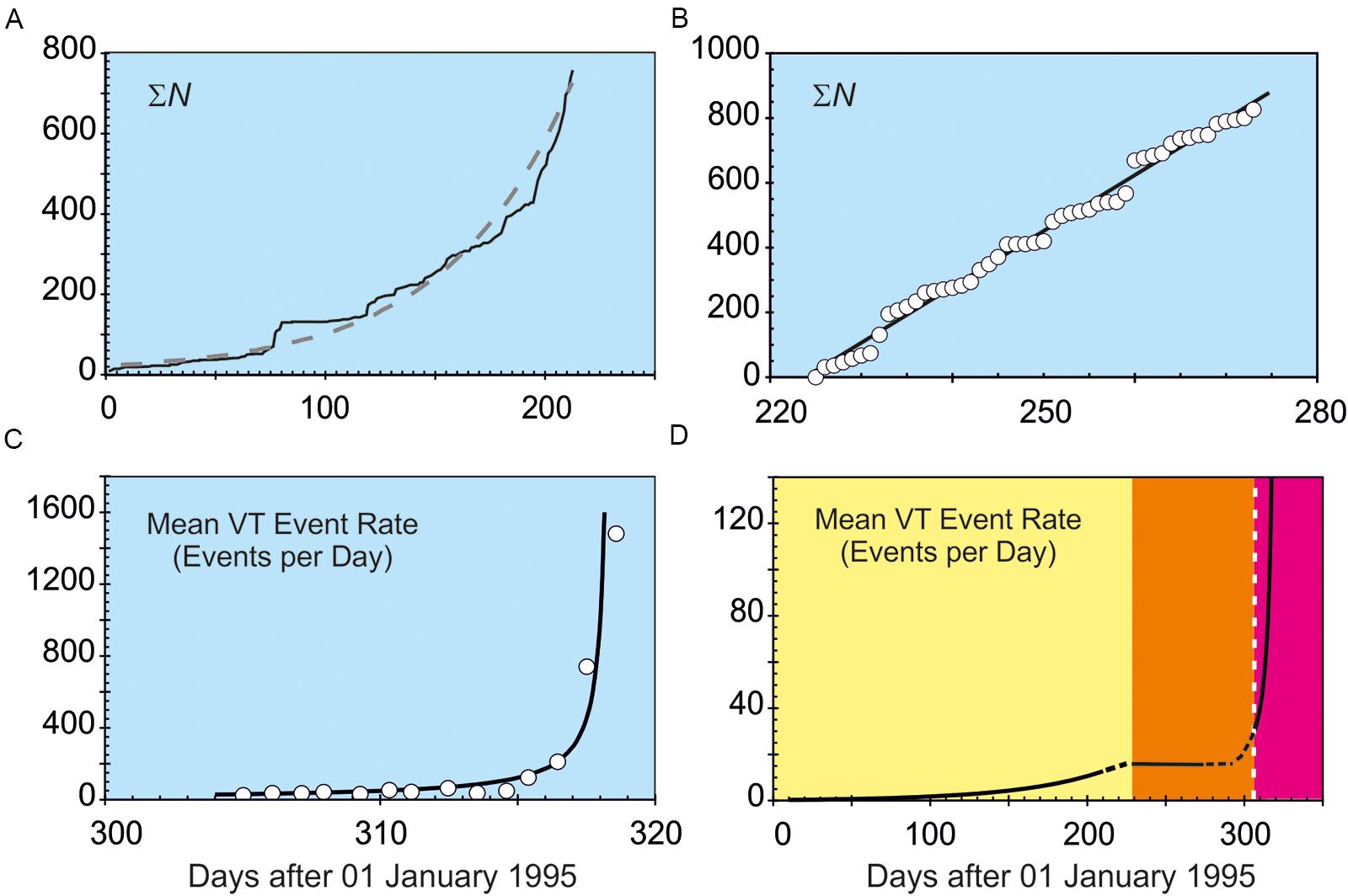
FIGURE 2. The andesitic-dacitic volcano Soufriere Hills, Montserrat, erupted on 15 November 1995 after 350 years of repose. VT data from three sources are consistent with initial and final episodes of accelerating VT event rate separated by an interval of constant event rate. (A) 01 January–31 July (time t = days 0–212 since 01 January). The mean daily VT event rate (dashed curve) increased exponentially as 16 exp (t/55.6) [data from Shepherd et al. (2002)]. (B) 13 August–30 September (t = days 225–273). Constant mean VT rate at c. 17 events per day [line; data from Gardner and White (2002)]. (C) 01–14 November (t = days 305–318). The mean daily rate increased hyperbolically (curve) as (0.037–0.0024t)^-1 until the eruption [curve; data from Kilburn and Voight (1998) and Kilburn (2003)]. Additional stations were added to the monitoring network between 18 and 31 July [days 200–212; Gardner and White (2002)] Most VT events had magnitudes between 1.3 and 2.7 (Power et al., 1998; Gardner and White, 2002). (D). The three datasets suggest that the mean VT trends evolved with time from quasi-elastic (yellow), through steady inelastic (orange) to accelerating inelastic (magenta); dashed portions of the curve are qualitative interpolations.

FIGURE 3

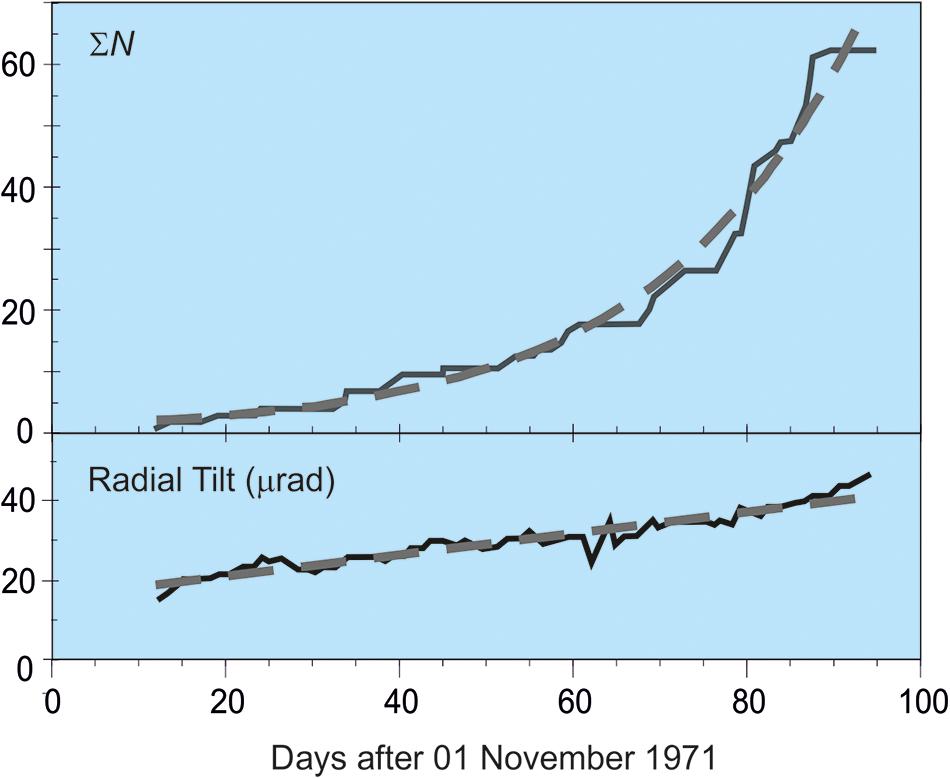
FIGURE 3. The number of VT events may accelerate with time (top), while the mean deformation rate remains constant (bottom, gradient of broken line). The example shows VT and deformation trends before the flank eruption of Mauna Ulu on Kilauea, Hawaii, on 04 February 1972 (most VT events had magnitudes between 1.5 and 4; Bell and Kilburn, 2011). In this case, the VT number, ΣN, increases exponentially with time t (in days; broken curve) as 1.17 exp (t/23.3); the mean daily VT event rate increases 0.05 exp (t/23.3). The combination of exponential VT rate and constant deformation rate is consistent with quasi-elastic brittle behavior under a constant rate of stress supply (Table 1). The eruption occurred almost immediately after the end of the quasi-elastic regime when t/23.3 ≈ 4.

Nevertheless, Eq. (1) has been fundamental in advancing the quality of short-term forecasts: it has revealed the control of rates of change in a precursory signal on determining the approach to eruption (rather than a threshold value of the precursor); it has showed that precursory mechanisms are expected to be scale-independent; and it has demonstrated that numerous, independent empirical relations for rock failure share common dynamic constraints (Main, 1999; Turcotte et al., 2003; Ojala et al., 2004; Davidsen et al., 2007; Schmid and Grasso, 2012). In addition, the preferred values of 1 and 2 for α correspond to exponential and hyperbolic increases with time. Both types of increase are common among self-accelerating processes in biological (Monod, 1949) and physico-chemical (Frank-Kamenetskii, 1939; Bowden and Yoffe, 1952; Gruntfest, 1963; Shaw, 1969) systems and so, in retrospect, ought not to be a surprising feature of accelerating rock failure.

Precursors Controlled by an Elastic-Brittle Crust

Precursory unrest is usually detected ∼1–10 months before eruption at closed strato-volcanoes (Zobin, 2003; McNutt, 2005; Dzurisin, 2007; Bell and Kilburn, 2011; White and McCausland, 2016), but may continue for decades at closed large calderas (Robertson and Kilburn, 2016). At strato-volcanoes, it commonly involves as many as ∼10⁴ VT events, which occur without systematic changes in hypocentral locations, and ground displacements of ∼0.01–1 m over distances of ∼1–10 km (Kilburn, 2003, 2012; Bell and Kilburn, 2011); at large calderas, the total number of detected VT events can be at least an order of magnitude greater (e.g., ∼10⁵ events at Rabaul before its eruption in 1994; Robertson and Kilburn, 2016) and ground displacements reach ∼1–10 m over distances of kilometers (Bellucci et al., 2006; Acocella et al., 2015; Di Vito et al., 2016; Robertson and Kilburn, 2016). Most of the detected VT events have magnitudes of 0–2 and are triggered by the movement of faults ∼10^-2–10^-1 km across, or ∼0.1–10% the size of deforming crust. VT events and ground deformation can thus be viewed as proxies for the inelastic and total deformation of a crust that contains a dispersed population of small faults.

The trends described by Eq. (1) can be incorporated into a general model by recognizing that deformation and VT events are mutually dependent and that their time series are the result of a parent relation between inelastic and total deformation, constrained by specified changes with time in loading the crust. The parent relation describes the potential for rock to fail when supplied with a mean differential stress S_sup. For each increment of supplied stress, ΔS_sup, a proportion ΔS is used elastically to deform atomic bonds, while the remainder, ΔS_loss, is lost inelastically by breaking bonds:

$$\begin{array}{c}\Delta S_{sup} = \Delta S + \Delta S_{los}{}_s\left(2\right)\end{array}$$

The total elastic component determines the mean, or bulk, differential stress S that is established across the deforming volume V of crust and, hence, also the amount of elastic energy being stored. Under idealized conditions, the dominant mode of deformation is initially elastic (without seismicity; ΔS_sup = ΔS) and, once faulting has begun, evolves with increasing differential stress from quasi-elastic to inelastic (Figure 4), as the additional energy being supplied is at first mostly stored elastically (quasi-elastic, ΔS_sup ≈ ΔS) and, later, mostly consumed by faulting (inelastic, ΔS_sup ≈ ΔS_loss). In the quasi-elastic regime, the mean deformation approximately increases in proportion to S until it reaches its maximum value S_F, when the amount of stored energy has reached its maximum capacity. Any additional stress (e.g., from a pressurizing magma body) is consumed in fracturing and fault movement and deformation continues under a constant maintained stress, which defines the inelastic regime. Bulk failure begins within one or more portions of the crust, where the stresses at fracture tips remain large enough to persistently overcome rock resistance and so allow fractures to grow and link together (Griffith, 1921).

FIGURE 4

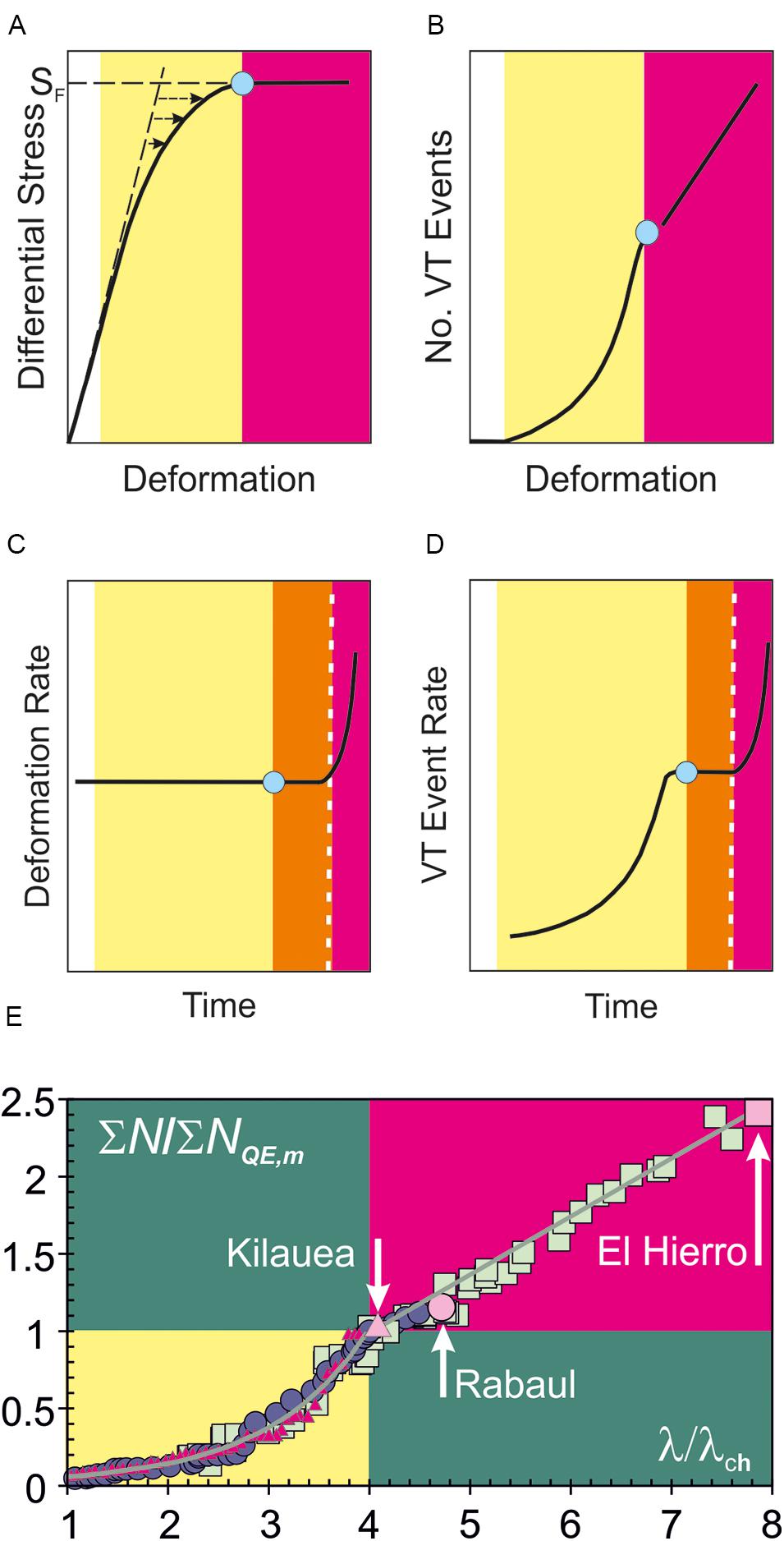
FIGURE 4. (A) The amount of deformation due to fault movement is given by the difference between the equilibrium (unbroken curve) and ideal elastic (broken line) deformation trends. As the differential stress increases to its failure value S_F, behavior evolves from elastic (white), through quasi elastic (yellow) to inelastic (magenta). This yields (B) accelerating quasi-elastic and linear inelastic increases in VT event with deformation. (C) For a constant rate of supplied stress, the deformation rate remains constant until a hyperbolic increase during inelastic behavior. The hyperbolic increase may be preceded by an interval of steady inelastic VT rate (orange). (D) The contemporaneous VT event rate increases from exponentially to hyperbolically with time, again possibly separated by an interval at constant rate (see Figure 2). (E) The model VT-deformation trends are consistent with normalized pre-eruptive sequences observed at El Hierro, Canary Islands, 18 July–12 October 2011 [squares; data from Istituto Geográfica Nacional [IGN] (2011) and Sagiya (2011)], Rabaul, Papua New Guinea, 1971–1994 [circles; data from Robertson and Kilburn (2016)], and Mauna Ulu on Kilauea, Hawaii, 14 November 1971–04 February 1972 [triangles; data from Bell and Kilburn (2011)]. See also Figure 3. Measures of ground movement (λ; displacement and tilt) and their characteristic values (λ_ch) are used as proxies for deformation. In all three cases, inelastic behavior (magenta) began when λ/λ_ch ≈ 4 and eruptions occurred (violet symbols) when λ/λ_ch ≥ 4. The trends were normalized using the total number of VT events at the end of the quasi-elastic regime, ΣN_QE,m, and the characteristic ground movement λ_ch. See Figure 5 for the non-normalized trends. Typical magnitude ranges for VT events were 0.5–2.0 for Rabaul, 1.0–2.5 for El Hierro and 1.5–4.0 for Mauna Ulu.

Deformation, rather than stress, is measured in the field, so that the quasi-elastic and inelastic regimes have to be identified indirectly from relations between VT seismicity and total ground movement. In the quasi-elastic regime, the number of VT events (a measure of inelastic deformation) is expected to accelerate with the total amount of ground movement (a measure of total deformation) as the proportion of inelastic deformation becomes larger. In the inelastic regime, net deformation continues by faulting, so that the ground movement is expected to increase in proportion to the number of VT events. A complete failure sequence is thus expected to show an accelerating and then linear increase in the number of fracturing events with ground movement (Figure 4).

Figures 4, 5 illustrate how similar failure sequences have been observed before eruptions under a wide range of closed conditions. The examples are from Kilauea, in Hawaii, El Hierro, in the Canary Islands, and Rabaul, in Papua New Guinea. The sequences continued for about 0.22–0.25 years (approximately 3 months) at Kilauea (Nakata, 2006; Bell and Kilburn, 2011) and El Hierro (Istituto Geográfica Nacional [IGN], 2011; Sagiya, 2011; Kilburn et al., 2017) and for 23 years at Rabaul (Johnson et al., 2010; Robertson and Kilburn, 2016); they include both strato-volcanoes (Kilauea and El Hierro) and large calderas (Rabaul); and the resulting eruptions ranged from basaltic effusive at Kilauea (Swanson et al., 1971) to andesitic phreato-Plinian at Rabaul (Rabaul Petrology Group, 1995). All three VT-deformation trends show the expected evolution from quasi-elastic to inelastic behavior, independent of the type of volcano, the duration of precursor, magma composition, style of eruption and, as discussed below, how VT event rate and deformation rate vary with time. Such similarity is compelling evidence that elastic-brittle failure of the crust determines the pattern of seismic and deformation precursors to eruptions at closed volcanoes.

FIGURE 5

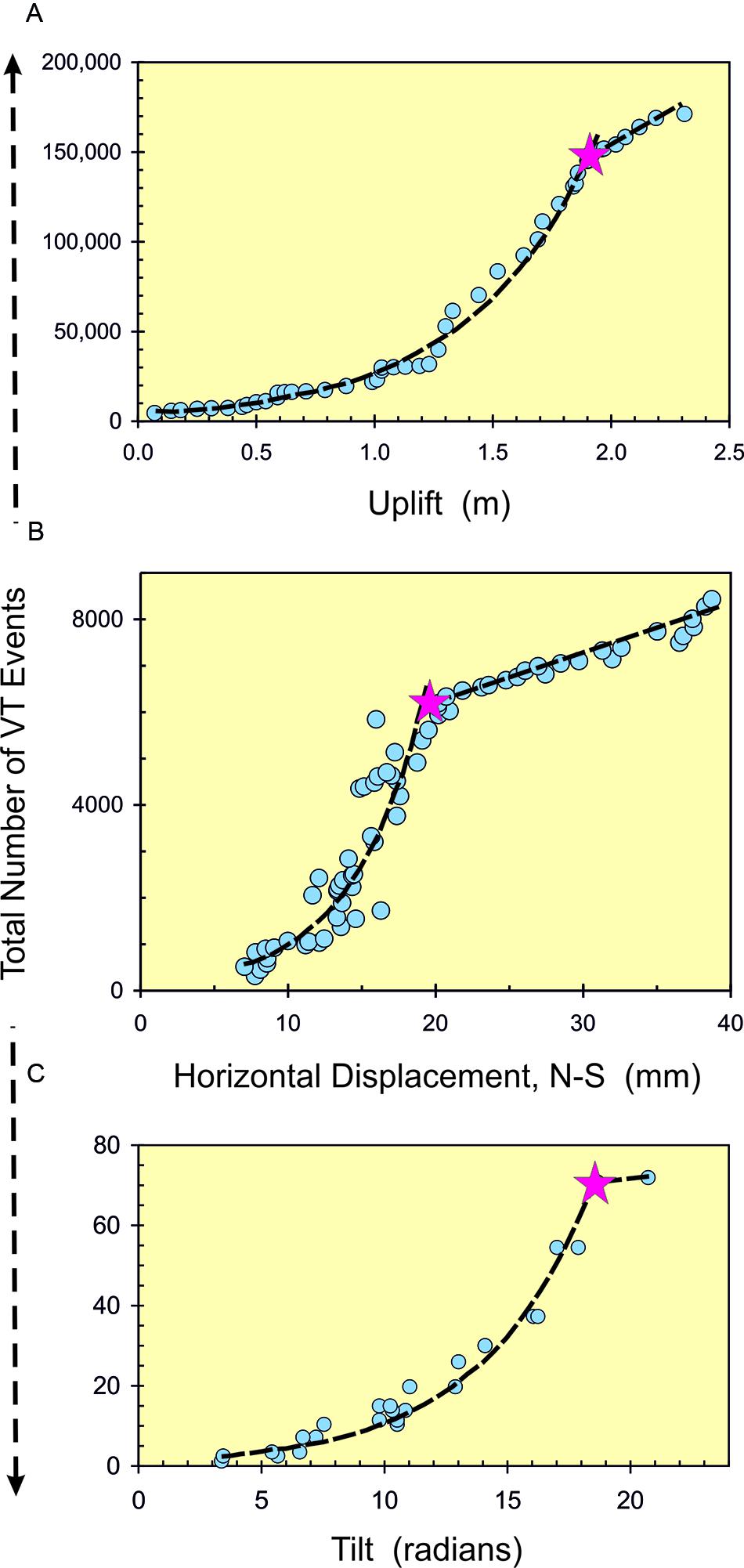
FIGURE 5. Changes in the total number of VT events with deformation for precursors to eruption at (A) Rabaul, Papua New Guinea, 1971–1994 [data from Robertson and Kilburn (2016)]: (B) El Hierro, Canary Islands, 18 July–12 October 2011 [data from Istituto Geográfica Nacional [IGN] (2011) and Sagiya (2011)]; and (C) Mauna Ulu, Kilauea, Hawaii, 14 November 1971–04 February 1972, [data from Bell and Kilburn (2011)]. The quasi-elastic regime shows exponential trends between VT number and the proxy for deformation, yielding characteristic values of 0.53 m for uplift at Rabaul [ΣN ∝ exp (λ/0.53)], 5 mm for displacement at El Hierro [ΣN ∝ exp (λ/5)] and 4.5 rad for tilt at Kilauea [ΣN ∝ exp (λ/4.5)]. The inelastic regime shows linear trends. The data are consistent with transition between regimes (star) when the ratio of total deformation to characteristic value (λ/λ_ch) is about 4. See Figure 4 for the normalized trends.

Elastic-brittle failure additionally favors the scale-independent behavior implicit by Voight’s analysis (Voight, 1988). VT events are produced by fault slip; slip is accommodated by extending the margin of a fault; and fault extension is controlled by cracking within the zone of stress concentration, or process zone, that develops around a fault’s tip (Atkinson, 1984; Main and Meredith, 1991; Lockner, 1993; Cowie and Shipton, 1998). Smaller discontinuities (both cracks and slip surfaces) grow in the process zone until it is broken, so extending the parent fault. Similarly, the discontinuities grow by cracking at a still smaller scale around their own process zones. Whatever the scale of observation (e.g., in the field or laboratory), slip can be viewed as an hierarchical process, in which the larger movements are the result of cracking at successively smaller scales. It is therefore expected that large-scale movements can ultimately be described by processes operating contemporaneously at the smallest scale (Kilburn, 2003, 2012).

Quantifying Regimes of Deformation

Parent Relations for Bulk Failure

Bulk failure begins when fracture growth becomes self-perpetuating within part of the stressed crust. It may occur when the failure stress, S_F, is first achieved, or after an extended interval of inelastic deformation under a stress maintained at S_F, during which the externally supplied stress replaces the stress lost by fracturing and fault movement, so resembling rock creep (Figure 4).

Applying well-known methods from classical statistical mechanics (Reif, 1985; Ruhla, 1992; Guénault, 1995), the magnitudes of local stresses are expected to follow a Boltzmann distribution about the bulk value, for which inelastic deformation 𝜀_in increases with supplied stress S_sup as (Kilburn, 2003, 2012):

$$\begin{array}{c}d{\text{ε}}_{in}/d{S}_{sup}\text{ = (}d{\text{ε}}_{in}/d{S}_{\sup }{)}_{a}exp(-S_{act}/S_{ch})\left(3\right)\end{array}$$

where the activation stress S_act is the additional stress required to initiate bulk failure, the characteristic stress S_ch is the atomic free energy per volume available for deformation, (d𝜀_in/dS_sup)_a is the rate at which natural fluctuations in atomic configuration attempt to initiate failure, and exp (-S_act/S_ch) measures the probability that an attempt is successful (Reif, 1985; Ruhla, 1992; Guénault, 1995).

The activation stress is S_F-S, the difference between the failure and applied differential stresses. In the quasi-elastic regime, it decreases to zero as S_F is approached and all local attempts to fracture are successful [d𝜀_in/dS_sup = (d𝜀_in/dS_sup)_a]. Fracturing continues to accelerate in the inelastic regime, owing to the local redistribution of stress around fractures (Lawn, 1993; Valkó and Economides, 1995). The redistribution concentrates stress at fracture tips and, as long as the bulk stress is maintained at S_F, increases the stress remaining after each increment of growth. A decreasing proportion of S_sup is required to continue fracture growth, so that the interval between growth steps persistently decreases, leading to runaway growth when the interval becomes infinitesimally small.

If ΔS_R is the mean amount of stress redistributed around fractures, then, from the viewpoint of fracture tips, the activation energy becomes (S_F-ΔS_R)-S = (S_F-ΔS_R)-S_F = -ΔS_R. The negative sign indicates the local surplus of stress at fracture tips (which is balanced by a local deficit where stress has been transferred from around the sides of a fracture). Although the failure strength is not changed, it appears to be decreasing by an amount equal to ΔS_R and so mimics fracturing promoted by progressive rock weakening. Interpretations that have qualitatively related accelerated fracturing to stress corrosion at fracture tips (Anderson and Grew, 1977; Atkinson, 1984; Main and Meredith, 1991; Lockner, 1993; McGuire and Kilburn, 1997; Kilburn and Voight, 1998; Kilburn, 2003) may thus alternatively be viewed in terms of increasing stress concentration around fractures in rock with unchanged strength. Setting 𝜀_in proportional to the number N of VT events, Eq. (3) yields for the quasi-elastic regime:

$$\begin{array}{c}dN\text{/}d{S}_{sup}\text{ = (}dN/d{S}_{sup}{)}_{a}exp\text{ [(}S-S_{\text{F}}\text{})/}{S}_{ch}\text{]}\left(4\right)\end{array}$$

and for the inelastic regime:

$$\begin{array}{c}dN/d{S}_{sup} = {(dN/d{S}_{sup})}_{a}exp(\Delta S_R/S_{ch})\left(5\right)\end{array}$$

Equations (4 and 5) are the basic expressions for deriving relations between VT event rate and both deformation and time. A first comparison with Eq. (3) suggests that the probability of bulk failure is proportional to exp [(S-S_F)/S_ch] and to exp (ΔS_R/S_ch) in the quasi-elastic and inelastic regimes, respectively. The exponential terms, however, do not represent the same type of probability. The quasi-elastic regime describes conditions before the start of bulk failure, so that exp [(S-S_F)/S_ch] measures the probability that bulk failure will begin under an applied differential stress S. As a result, the probability becomes one when S = S_F. The inelastic regime, in contrast, describes when the failure process will be completed, so that exp (ΔS_R/S_ch) measures the probability that failure will occur within a given time interval.

The Characteristic Stress

The value of the characteristic stress in Eqs (4 and 5) changes with the conditions of loading. Independent of the applied stress, atoms deform naturally as they oscillate around their equilibrium positions. The oscillations may randomly yield configurations that assist stress-induced deformation and so promote failure at a stress smaller than S_F. The total free energy per volume for oscillations is S^∗ = (3ϕT+P_c-P_p)/3, where T is absolute temperature (K), P_c and P_p are the confining and pore-fluid pressures, and the molecular energy per unit volume per temperature, ϕ, has a notional value of (7 ± 1) × 10⁴ J m^-3 K^-1 for common silicate rocks (Kilburn, 2012). How much of the total free energy is utilized determines the characteristic stress. Failure in compression is limited by shearing between atoms, but in tension by the tensile failure of bonds. Shearing requires the integrated deformation of all bonds and so utilizes the full amount of S^∗. Tension, however, requires deformation only among bonds in a particular direction and so utilizes a fraction of S^∗; the amount utilized in tension defines the rock’s tensile strength, σ_T.

The condition that S_ch = S^∗ in compression has been verified against laboratory experiments (Kilburn, 2012). It was also applied to VT precursors of the 1991 eruption of Pinatubo, in the Philippines, and 1995 eruption of Soufriere Hills, on Montserrat (Kilburn, 2003), implying the unlikely scenario of eruptions through crust in compression. Extensional stresses are instead anticipated in crust being deformed by a pressurizing magma body and, as demonstrated below, the precursory sequences at Pinatubo and Soufriere Hills can be explained more simply by equating S_ch instead with the tensile strength.

Applications to Field Data

Changes in Seismicity With Deformation

Equations (4 and 5) describe the change from an exponential to linear increase in VT number with deformation, corresponding to the evolution from quasi-elastic to inelastic behavior. In the quasi-elastic regime, ΔS_supp ≈ ΔS [Eq. (2)] and both S_sup and S can be set to E𝜀, the product of Young’s modulus and bulk deformation. If ground movement, λ, is proportional to the bulk deformation, Eq. (4) yields exponential increases with ground movement of both the change in VT seismicity and the total number of VT events [Table 1, Eqs (T1) and (T2)]. In the inelastic regime, the additional elastic strain supplied by S_sup is consumed in faulting (Section 3). Changes in N and λ now both measure VT events, so dN/dλ is constant and total VT number increases linearly with ground movement [Figures 4, 5 and Table 1, and Eq. (T3)].

TABLE 1

TABLE 1. Regimes for elastic-brittle precursors to eruption.

The transition from quasi-elastic to inelastic behavior occurs when the applied differential stress reaches its failure value, S_F. Since S_ch = σ_T for tensile deformation, the transitional value for S/S_ch in Eq. (4) is expected to be S_F/σ_T for crust being stretched. Applying the Mohr–Coulomb–Griffith criterion for bulk failure, S_F/σ_T is four or less in tension, between 4 and 5.6 in extension (combined tension and shear) and 5.6 or more in compression (Figure 6; Secor, 1965; Shaw, 1980; Sibson, 1998). In the quasi-elastic regime S is proportional to ground movement, so that S_F/σ_T can be obtained from λ/λ_ch at the end of the regime. The examples in Figures 4, 5 are consistent with values for λ/λ_ch of about four and, hence, with bulk failure in tension.

FIGURE 6

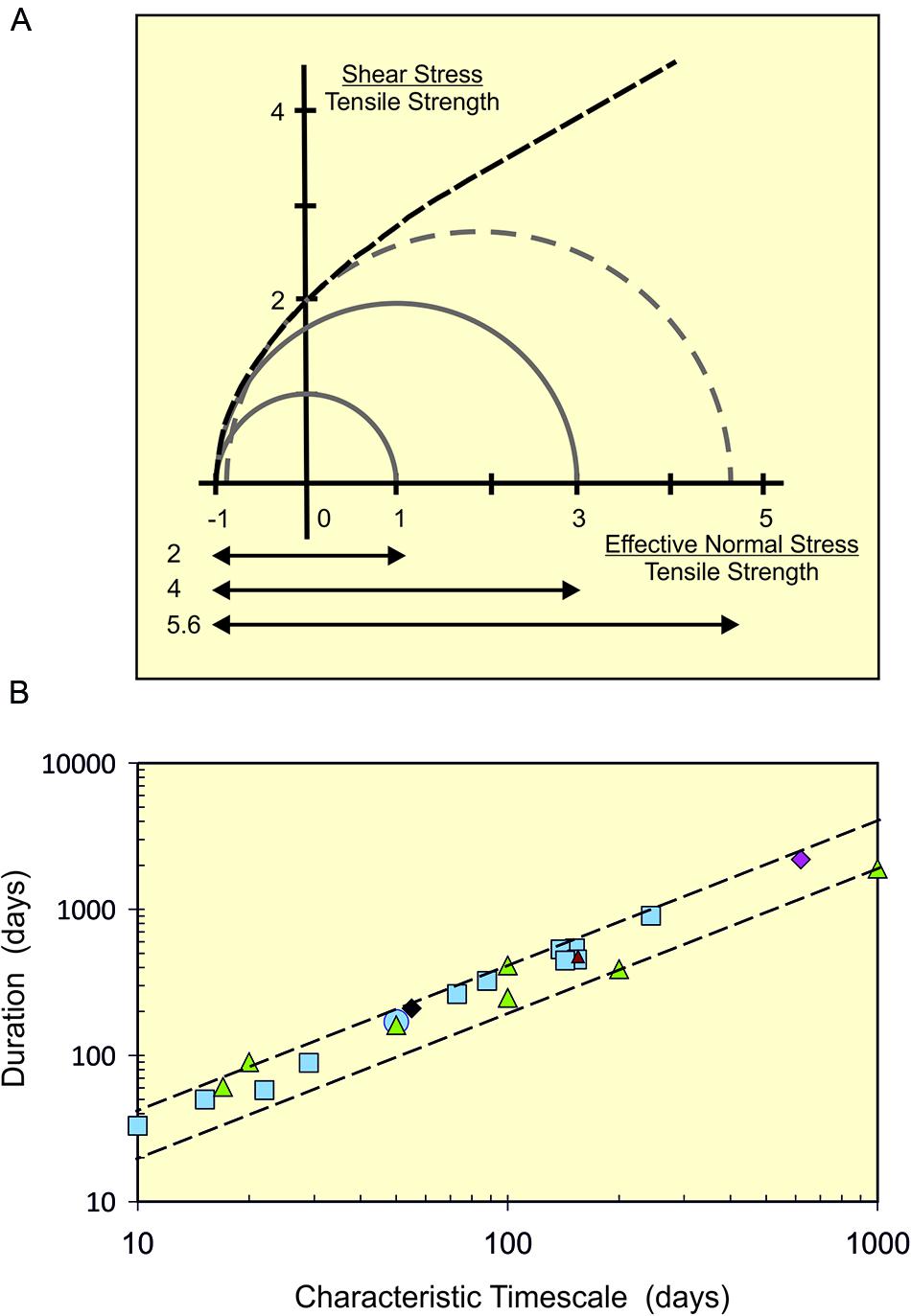
FIGURE 6. (A) The Mohr–Coulomb–Griffith representation of bulk failure in terms of applied normal and shear stresses. The outer dashed curve shows the parabolic form of the failure envelope [for mathematical treatments, see Secor (1965); Shaw (1980), and Sibson (1998)]. The Mohr circles (continuous and dashed semi-circles) describe states of stress between the maximum and minimum effective normal stresses; positive values are in compression, negative values in tension. The diameter of a circle gives the applied differential stress, S. Failure occurs when the minimum normal stress meets the failure envelope. Tensile failure corresponds to where the circles meet the envelope at zero shear stress (hence intersect the horizontal axis) and the minimum effective normal stress equals the tensile strength (with a normalized value of –1). To satisfy this condition, the Mohr circle must have a diameter less than or equal to 4σ_T (or normalized diameter of four; arrows beneath graph) The maximum value (larger continuous semi-circle) may represent the opening of a failure plane. For comparison, failure at the margins of a long vertical cylinder is shown with a normalized diameter of two (smaller continuous semi-circle). The dashed semi-circle (normalized diameter of 5.6) shows the Mohr circle at the transition between failure in extensional (tension and shear) and compression (shearing alone). (B) Values of T/t_ch for quasi-elastic pre-eruptive behavior at Etna, Sicily (blue squares; Wall, 2014), Kilauea, Hawaii (green triangles; Bell and Kilburn, 2011), Mauna Loa, Hawaii (magenta diamond; Lengliné et al., 2008), Piton de La Fournaise, Réunion (small dark red triangle; Lengliné et al., 2008) and Soufriere Hills, Montserrat (black diamond; Figure 2). Most of the values for T/t_ch lie between 2 and 4 (lower and upper dashed lines).

Quasi-Elastic Changes in Seismicity and Deformation With Time

The VT-deformation trends describe how the proportion of inelastic movement varies with total deformation. To transform the trends into time series, independent constraints must be introduced to specify how loading changes with time. The simplest condition is a constant rate of stress supply. Under this condition, Eq. (4) for quasi-elastic behavior leads to exponential increases with time in VT rate and the total number of VT events [Table 1, Eqs (T4)-(T5)]. The contemporaneous rate of ground movement is constant because S_sup is proportional to deformation [Table 1, Eq. (T8)]. Quasi-elastic behavior at a constant deformation rate thus naturally yields the exponential VT-time trends frequently observed at closed volcanoes (Figures 2, 3; Shepherd et al., 2002; Bell and Kilburn, 2011; Kilburn, 2012; Wall, 2014).

Under a constant deformation rate, the ratio λ/λ_ch is measured by t/t_ch, where t_ch is the characteristic timescale of the exponential VT time series. If T is the duration of the full exponential sequence, then T/t_ch = S_F/σ_T. Observations at closed volcanoes suggest preferred values for T/t_ch of 2–4 (Figure 6). The range is consistent with the limiting values for λ/λ_ch obtained from the VT-deformation trends (Figures 4, 5), so reinforcing the interpretation of deformation in tension (Figure 6).

The particular value of S_F/σ_T in tension changes with the geometry of failure. The generic Mohr–Coulomb–Griffith criterion applies to failure along a plane (e.g., creating a new failure plane or pulling opening a sealed fault) and values for S_F/σ_T are ≤4. Pressurized bodies, in contrast, rupture their margins at values of S_F/σ_T that change according to their shape; for example, S_F/σ_T is three for a sphere, but two for a long vertical cylinder (Jaeger, 1969; Saada, 2009). The preferred field values of 2–4 are thus consistent with the onset of bulk failure at the margins of magma bodies, as well as the opening of healed faults in crust being stretched by those bodies. In all cases, tensile bulk failure requires the effective principal stresses (normal stress-pore-fluid pressure) to be less than three times the tensile strength (Figure 6). For a notional strength of 10 MPa, therefore, the effective principal stress cannot exceed about 30 MPa, which corresponds to maximum lithostatic depths of about 1.2 and 2 km in dry and water-saturated crust. Tensile failure at greater depths thus implies deformation of super-saturated crust with pore-fluid pressures greater than hydrostatic (Shaw, 1980).

Inelastic Changes in Seismicity and Deformation With Time

In the inelastic regime, a constant rate of stress supply generates hyperbolic increases in VT and deformation rates with time [Table 1; Eq (T9)]. After a time τ, the rates tend to an infinite value, which is taken to be the mathematical equivalent of continuous fracture coalescence and successful bulk failure (Voight, 1988; Kilburn, 2003); τ therefore defines the duration of accelerating inelastic deformation, which is analogous to tertiary brittle creep under a constant external stress.

The hyperbolic trends are equivalent to linear decreases with time in the inverse VT and deformation rates. Applied to VT seismicity, principal episodes of fracture coalescence coincide with local peak rates (dN_p/dt) - or local minima in inverse-rates [(dN_p/dt)^-1] - during which the mean increase in stress concentration per event is B(S_F²/E), where E is Young’s modulus and the geometric constant B = π for straight-edged fractures (Kilburn, 2003). Hence ΔS_R = B(S_F²/E)N_p and so, after manipulation, the parent relation for inelastic deformation [Eq. (5)] yields dN_p/dt = (dN_p/dt)_a exp [B(S_F²/E)N_p/σ_T] for a constant rate of stress supply in extension. This form of relation can be re-expressed to show changes in VT event rate with time (Voight, 1988), leading to:

$$\begin{array}{c}{(d{N}_p/dt)}^{-}{}^1 = {(d{N}_p/dt)}_{0,}{{}_{IN}}^{-}{}^1 - {\text{γ}}^{*}(t-t_0{,}_{IN})\left(6\right)\end{array}$$

or, alternatively, to:

$$\begin{array}{c}{(d{N}_p/dt)}^{-}{}^1 = {(d{N}_p/dt)}_{0,}{{}_{IN}}^{-}{}^1[1 - (t-t_0{,}_{IN})/\tau ]\left(7\right)\end{array}$$

where the subscript 0,IN denotes values at the start of the inelastic regime.

The gradient for the inverse-rate VT minima in Eq. (6) has a magnitude γ^∗ = B(S_F/σ_T)²(σ_T/E) and units of “per VT event” (Table 1). For common crustal rocks, σ_T/E∼10^-4 (Mogi, 2007; Heap et al., 2009) and so, with B = π and S_F/σ_T between 2 and 4 (Figure 6), the gradient is expected to be ∼10^-3-10^-2 per event, which is consistent with the values of 6.4 × 10^-3 and 2.4 × 10^-3 per event found for inverse-rate minima at Pinatubo in 1991 and Soufriere Hills, Montserrat, in 1995 (Figure 7; Kilburn, 2003).

FIGURE 7

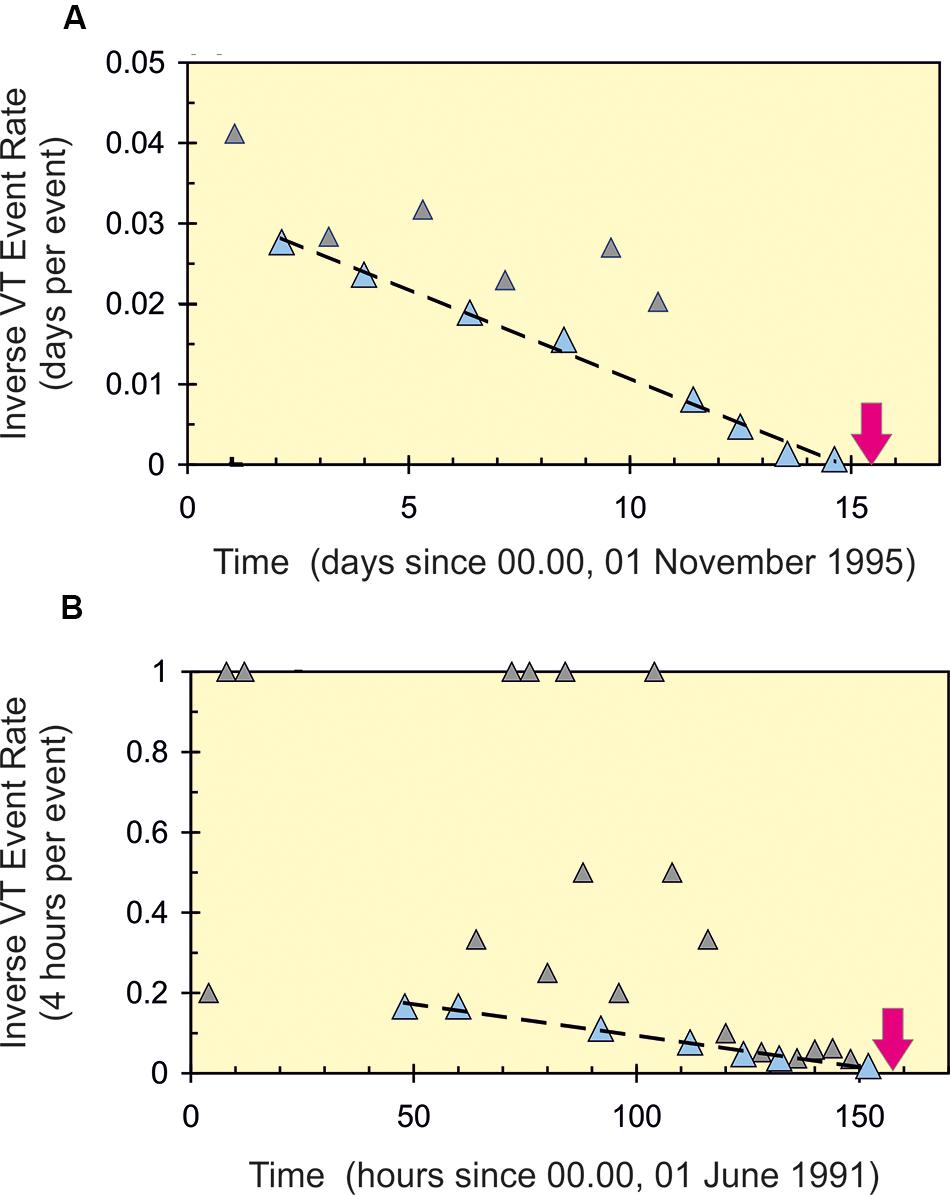
FIGURE 7. Linear decreases (dashed lines) in inverse-rate minima for VT events (large triangles) before magmatic eruptions (arrows) after centuries of repose at (A) Soufriere Hills, Montserrat (gradient –2.4 × 10^-3 per event), and (B) Pinatubo, Philippines (gradient –6.4 × 10^-3 per event). The trends are equivalent to the hyperbolic increases in VT rate expected for inelastic behavior; the inverse-rate minima thus correspond to local peaks in VT rate. Data from Kilburn (2003).

In Eq. (7), the duration of inelastic acceleration is given by τ = [γ^∗(dN_p/dt)]^-1 [so when (t-t₀,_IN) = τ, the inverse-VT rate tends to zero and the VT rate tends to infinite values]. At andesitic strato-volcanoes, observed values of dN_p/dt are ∼10 events per day, which, with typical values of γ^∗, give the observed durations on the order of 10 days (Kilburn, 2003). Hence, if about 30–50% of the total time is needed to confirm a hyperbolic increase in rate, realistic warning times at such volcanoes are on the order of days.

Elastic-Brittle Failure and Voight’s Relation

Equations (4 and 5) quantitatively capture the essential features of VT-deformation trends before eruptions. Their good agreement with field data confirms the mutual dependence of VT and deformation precursors and suggests that (a) precursory deformation evolves from quasi-elastic to inelastic, (b) when the rate of stress supply is constant, the increase in VT event rate with time changes from exponential (quasi-elastic behavior) to hyperbolic (inelastic behavior), and (c) precursory behavior can be interpreted in terms of elastic-brittle deformation, without the need to invoke additional rheological responses in the crust (such as plastic flow); this does not preclude the operation of additional processes, only that they need not be invoked unless field data indicate otherwise.

For a constant rate of stress supply, Equations (4 and 5) yield time series (Eqs. T4 and T6) that can be re-expressed as

$$\begin{array}{c}{d}^{2}N/d{t}^2 = (1/t_{ch}){({\text{γ}}^{*}{t}_{ch})}^{\alpha }{{}^{-}}^1{(dN/dt)}^{{}^{\alpha }}\left(8\right)\end{array}$$

which has the form of Voight’s original FFM Relation [Eq. (1)].

The exponential and hyperbolic VT rates coincide with Voight’s relation for α = 1 and 2, but it has yet to be confirmed whether intermediate values of α have any physical meaning. Indeed, it is possible that intermediate values are artifacts from seeking best-fit single trends to partial data sets that extend across the quasi-elastic and inelastic regimes. Comparison with Eq. (1) also shows that the term A in Voight’s FFM Relation is not a constant, but changes from 1/t_ch for α = 1 to γ^∗ for α = 2; in other words, 1/A is a characteristic timescale when α = 1, but a characteristic number of VT events when α = 2.

Applied to contemporaneous changes in rates of ground movement with time, an expression similar to Eq. (8) is available only for inelastic behavior, when the rate increases hyperbolically (α = 2) to yield d²λ/dt² = (γ^∗/β)dλ/dt (where β is the mean ground movement per VT event). Hence, the deformation and VT rates both favor α = 2 immediately before bulk failure, a feature noted in Voight’s original analysis (Voight, 1988). During quasi-elastic unrest, however, the deformation rate remains constant while the VT event rate increases and so Voight’s relation is not equally applicable to the two precursory signals.

When the rate of stress supply varies with time, the VT and deformation time series derived from Eqs (4 and 5) no longer follow Voight’s relation. Hence, the fact that the FFM has been found to describe numerous precursory sequences at closed stratovolcanoes (e.g., Cornelius and Voight, 1994, 1996; Kilburn and Voight, 1998; De la Cruz-Reyna, 2001; Kilburn, 2003; Bell and Kilburn, 2011; Wall, 2014; Boué et al., 2015) suggests that such sequences may often develop under a constant rate of stress supply.

Pre-eruptive sequences at strato-volcanoes commonly have durations of years or less. Longer sequences provide a greater opportunity for significant variations in the rates of stress supply, in particular the decadal time intervals for precursory sequences at large calderas, such as Rabaul (Robertson and Kilburn, 2016) and Campi Flegrei (Kilburn et al., 2017). For example, the full 23-year sequence of unrest before Rabaul’s 1994 eruption did not show changes with time in rates of VT event and of uplift consistent with Voight’s relation - even though it followed the trend between VT events and deformation expected for an evolution from quasi-elastic to inelastic behavior (Figures 4, 8). Thus the VT event rate and uplift rate both fluctuated by an order of magnitude or more (∼10²-10⁴ events per month and c. 0.015-0.4 m y^-1), and the peak rates occurred half-way through the sequence (Figure 8). During its final 2 years, however, the sequence did show changes in rates that were consistent with hyperbolic increases with time (Figure 8).

FIGURE 8

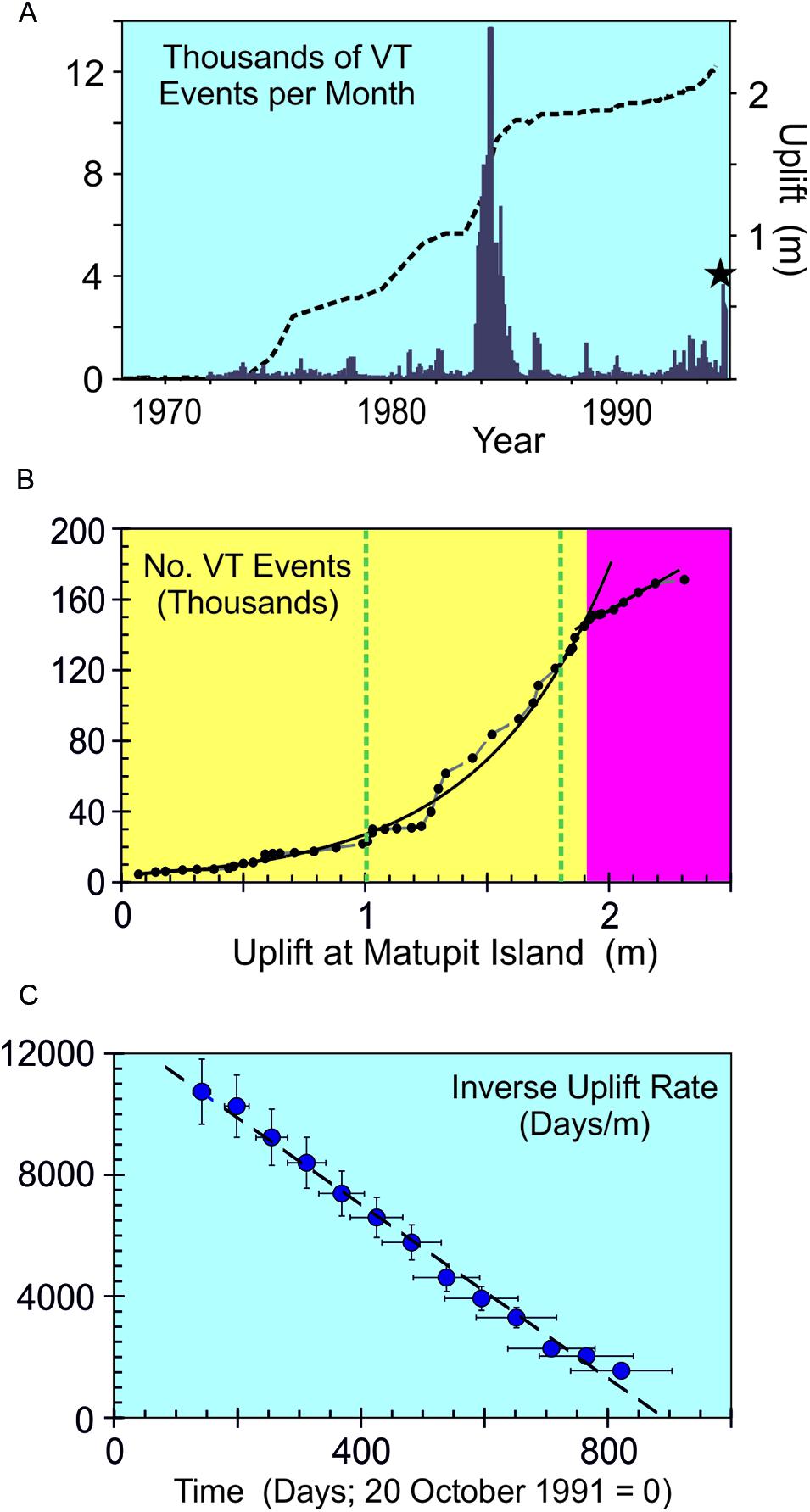
FIGURE 8. (A) VT event rate (columns) and uplift rate (gradient of dashed curve) both fluctuated unevenly with time during the 23-year approach to Rabaul’s eruption in 1994. (B) The change in number of VT events with uplift shows the evolution from accelerating quasi-elastic (yellow) to linear inelastic (magenta) behavior (a normalized version is shown in Figure 4). The dashed green lines show conditions corresponding to the 1983–1985 crisis when rates reached their peak values (see A). Note how the expected VT-uplift trends persist in spite of significant variations with time in rates of seismicity and ground movement. (C) The inverse mean rate of uplift decreased linearly with time during 1992–1994. The best-fit trend (dashed) is [Inverse Mean Rate of Uplift] = 12784–14.38t (r² = 0.99) for inverse-rates in days m^-1 and time t in days; the trend corresponds to a hyperbolic increase in the mean rate of uplift. The contemporaneous inverse VT rates showed a less clearly defined trend (Robertson and Kilburn, 2016).

The peak rates in the Rabaul sequence have been associated with the arrival of magma at a depth of about 2 km, possibly intruding into an existing magma chamber (McKee et al., 1984). The final rates have instead been associated with segments of the ring fault being torn open to allow magma to erupt (Robertson and Kilburn, 2016). The full sequence thus represents the caldera being stretched to breaking point under a variable rate of increasing magmatic pressure. A constant rate of stress supply was established during the final 2 years of deformation, when the crust had already entered the inelastic regime, so promoting the hyperbolic increase in rates with time (described by the Voight’s relation with α = 2). However, rates of stress supply were not constant for the first 20 years of unrest, during which time Voight’s relation could not be used to describe the precursory time series.

Deviations From Model Elastic-Brittle Conditions

By describing common trends among VT and deformation precursors, Eqs (4 and 5) provide a starting point also for identifying when the model cannot be applied without adjusting its underlying assumptions. For example, the model assumes that the crust’s mean behavior follows that of an elastic medium containing a dispersed population of small faults. It does not explicitly accommodate conditions when bulk deformation is controlled by movements of faults with lengths similar to that of the crust being deformed. Slip along such faults would favor the occurrence of a small number of large-magnitude VT earthquakes instead of a large number of small VT events; as a result, VT trends may be dominated by only a few earthquakes, whose total number is too small to yield repeatable mean behavior.

Even in the presence of large faults, VT seismicity may remain controlled by small earthquakes. For example, before Rabaul caldera’s 1994 eruption, VT seismicity was concentrated in an annulus related to ring faults extending to depths of 2–4 km and produced by caldera collapse about 1,400 years beforehand (Nairn et al., 1995; Jones and Stewart, 1997). Most of the VT events had magnitudes of 0.5–2, triggered by the slip of small faults in the crust surrounding the ring faults, rather than movements along the ring faults themselves (Robertson and Kilburn, 2016). Similar behavior has been argued for VT seismicity in the vicinity of ring faults at the Campi Flegrei caldera in southern Italy (Troise et al., 2003). In both cases, the large ring faults appear to have constrained the size and geometry of the crust being deformed, rather than to have contributed directly to rates of VT seismicity.

The initial application of Eqs (4 and 5) implicitly assumes that self-accelerating crack growth begins at the start of the inelastic regime. In this case, precursory VT event rates are anticipated to accelerate with time across the transition from quasi-elastic to elastic regimes. Such behavior is indeed observed in the field (Bell and Kilburn, 2011) and laboratory (Kilburn, 2012). However, the transition may also be marked by an interval of constant VT event rate between the quasi-elastic and inelastic accelerations (Figure 2). Such steady rates may develop in the inelastic regime when the coalescence of fractures, which favors accelerating rates, is temporarily retarded by stress barriers in rock between non-interacting fractures (Main, 2000; Heap et al., 2009; Girard et al., 2010). An accelerating transition may thus represent the limiting case when fracture coalescence dominates from the start of the inelastic regime. Hence, should a steady rate appear after quasi-elastic acceleration, it cannot be taken to indicate an approach to stability, but must be viewed as a temporary lengthening of unrest until the onset of hyperbolic accelerations to bulk failure (Figure 2).

Although bulk failure in the crust is necessary before eruption at a closed volcano, it does not ensure that an eruption will occur (Kilburn, 2003; Grasso and Zaliapin, 2004). For example, similar precursory sequences have been identified before eruptions and intrusions at Kilauea (Bell and Kilburn, 2011) and at Krafla in Iceland (Blake and Cortés, 2018). Failure may be initiated at the margin of a magma body, after which an eruption requires a magmatic overpressure large enough to drive magma to the surface (Jellinek and DePaolo, 2003). It may also begin at a more distant location where stresses are concentrated (e.g., the tips of a major fault) or where the crust is locally weak (e.g., altered rocks in a hydrothermal system), in which case the propagating fracture must additionally extend to the magma body itself. The probability of eruption can thus be expressed more generally as the product of the probability of bulk failure, the probability that failure breaches a magma body, and the probability that magma can erupt through the new breach. The elastic-brittle model addresses only the first of these and so, by itself, is a necessary but insufficient condition for guaranteeing an eruption.

In common with most analyses of VT and deformation precursors, the elastic-brittle model does not specify conditions within the magmatic, or other, systems driving volcanic unrest. One exception is the model by Lengliné et al. (2008), who investigate how specific conditions of magma accumulation may control rates of precursory signal at basaltic volcanoes. The acceleration in VT number with time may also increase with the size of the following eruption (Schmid and Grasso, 2012). Future models that couple crustal stresses with magmatic processes promise to yield new insights for refining and enhancing forecasting procedures.

Scale-Independent Fracturing

The elastic-brittle model is inherently scale-independent, because it expresses rates of VT seismicity and deformation in terms of the ratio of mean applied differential stress to characteristic stress. Applied stress measures changes in the free energy per volume available for atoms to do work (in this case to deform and break bonds); the characteristic stress measures the total free energy per volume already available for a specific type of deformation (e.g., tension or compression) before a differential stress is applied. Thus, if Δe is the change in free energy and e′ the free energy available, then S/S_ch = (Δe/V)/(e′/V), where V is the volume of deformation. At the atomic scale, V is the volume of an atom itself. At the macroscopic scale, it refers to the size of rock being deformed, including the volume of discontinuities. At any given scale, the same V is used to calculate both stresses from their respective energy terms, so that S/S_ch always measures the ratio of change in free energy to the reference free energy available. Hence, even though the values of individual stress terms may change with scale and amount of fracturing, their ratios remain the same.

The influence of fracturing is shown by the change from quasi-elastic to inelastic deformation regime, which appears to correspond to a change from weak to strong interactions among fractures (Vasseur et al., 2017) and favors the onset of self-accelerating crack growth. Exploring the interactions has generated an independent class of fracture models, most of which have focused on strong interactions immediately before bulk failure (Main, 1996, 2000; Molchan et al., 1997; Guarino et al., 1998; Amitrano et al., 2005; Girard et al., 2010). Applying statistical methodologies, they have shown that increases in seismic event rate with time in the inelastic regime are expected to follow a power-law trend of the form:

$$\begin{array}{c}dN/dt \propto {[1-(t-t_0)/{\tau }_f]}^{-}{}^p\left(9\right)\end{array}$$

where t₀ is the starting time, τ_f is the duration of the sequence before bulk failure and p is an undetermined empirical factor. The result is scale-independent because it depends on the interaction among fractures, regardless of size, and values of p between 0.5 and 2 have been obtained from field data (Amitrano et al., 2005; Schmid and Grasso, 2012). When p = 1, the result is identical to that obtained for the acceleration to failure in the inelastic regime [Eq. (7)] and corresponds to the limit of α = 2 in Voight’s analysis (Voight, 1988). The similarity of Eqs (7) and (9) suggests agreement between the different modeling strategies. Their future integration may thus yield enhanced procedures for general forecasts of bulk failure.

Precursors as Indicators of Energy Loss Before Eruptions

In addition to demonstrating the elastic-brittle features of unrest, precursory time series indicate preferred energy states in magmatic systems before eruption. Common quasi-elastic behavior suggests a preference for steady rates of deformation, which are a natural consequence of minimizing rates of energy dissipation. Primary controls on energy dissipation are VT seismicity in the crust and frictional resistance during the transport of magma. Under a constant deformation rate, the VT event rate increases exponentially with time and so is not an obvious minimizing factor. A constant deformation rate, however, is favored by a constant rate of pressurization in the magmatic source and this, in turn, is promoted by a constant flux of magma from depth. Approximately steady deformation rates may thus reflect a preference to minimize rates of energy loss during magma transport.

A second remarkable feature is the agreement between theory and observed inverse-VT rate gradients in the inelastic regime. The model VT expressions implicitly assume that the number of detected events is similar to the number of essential events for bulk failure. In principle, however, fault movement may be triggered in parts of the crust that do not directly affect the volume that will ultimately fail, so that the number of detected events is greater than the essential number. The difference will not affect expressions for VT events in the quasi-elastic regime, because it changes only pre-exponential terms and so cancels from both sides of the relevant equations. In the inelastic regime, however, N appears within the exponent itself [Eq. (T6)], so that the inverse-rate field gradient is given by γ^∗N_es/N - that is, the model gradient multiplied by the ratio of the number of essential (N_es) to detected (N) VT events - which is ≤γ^∗. At Pinatubo and Soufriere Hills, Montserrat, the observed gradients are within the expected theoretical range, suggesting that the proportion of non-essential VT events is small. Although such a condition may not be universal, the fact that it appears for these two examples implies that precursory deformation may tend to involve the minimum amount of crust possible for initiating bulk failure, which again indicates a preference for minimizing energy loss.

Potential Application to Operational Forecasts

Event trees have become a popular aid for deciding levels of alert during a volcanic emergency (Newhall and Hoblitt, 2002; Aspinall, 2006; Sandri et al., 2009; Marzocchi and Bebbington, 2012; Selva et al., 2012; Sobradelo et al., 2013, 2014). They pose a sequence of interconnected questions about interpreting precursory signals, the combined answers to which are used to estimate the probability of eruption. Critical pre-eruptive values for individual signals (e.g., number of VT events and amount of ground deformation) are identified empirically from observations of previous eruptions at the same volcano or at apparently analogous volcanoes elsewhere (Sobradelo and Martí, 2015).

The progression from quasi-elastic to inelastic behavior yields objective pre-eruptive criteria that complement the existing empirical evaluations. This is especially important at volcanoes for which no data are available from previous unrest. An example of how additional procedures may be applied is shown in Figure 9 and summarized below. It is based on the simplest conditions for a constant rate of stress supply and no steady VT rate between quasi-elastic and inelastic regimes.

FIGURE 9

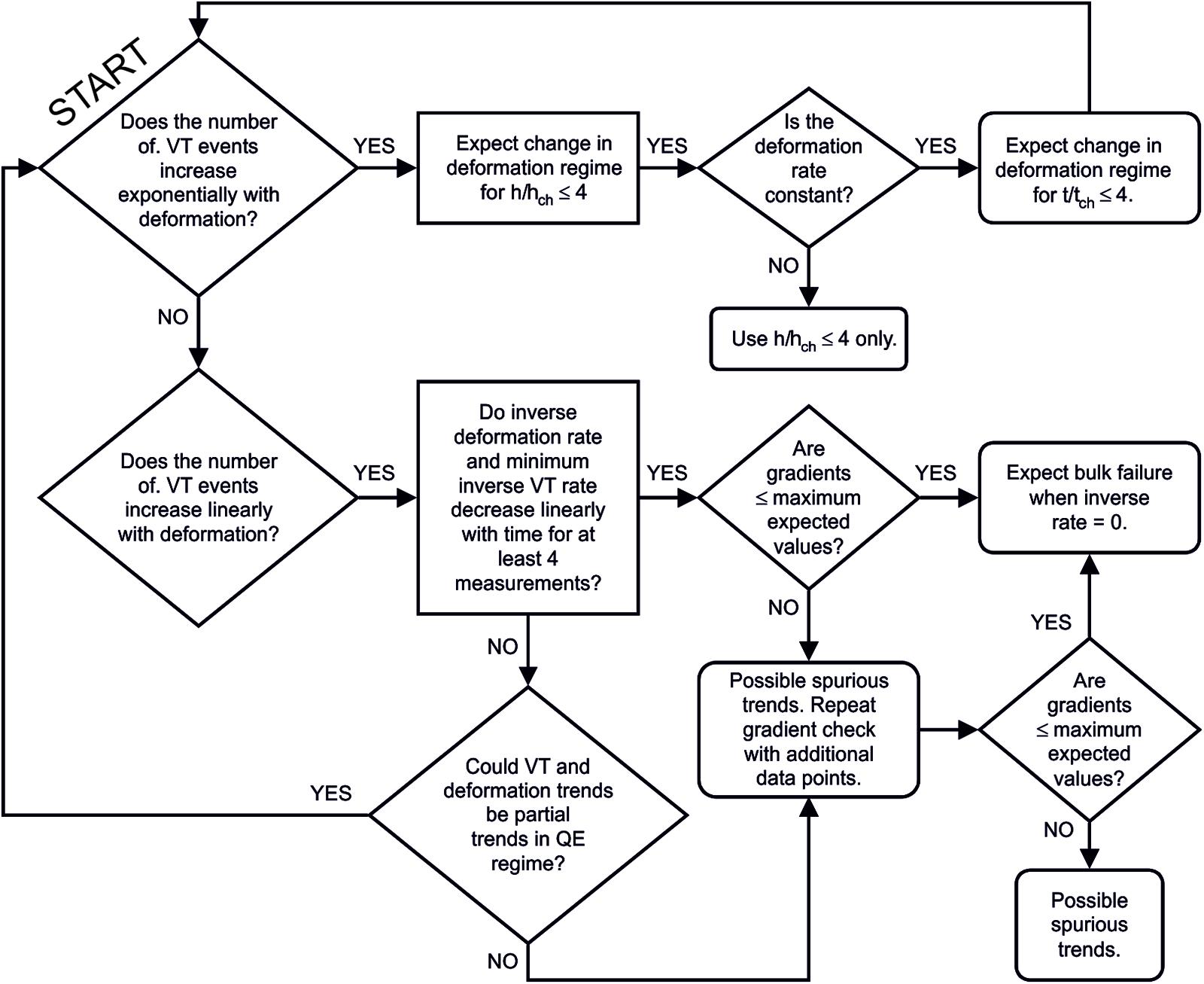
FIGURE 9. Flow-chart showing an example the proposed operational procedure for applying the elastic-brittle model to VT and deformation signals of unrest. It assumes a transition from exponential to hyperbolic VT event rates after an amount of ground movement 4h_ch and, for a constant rate of stress supply, after a time 4t_ch.

1. Identify the regime of deformation. Quasi-elastic behavior will show an exponential increase in VT number with ground movement and yield a characteristic movement, λ_ch. VT events and deformation will follow distinctly different time series. For a constant rate of stress supply, the deformation rate is constant and the VT rate will increase exponentially with time, yielding the characteristic timescale t_ch; following the VT rate here is crucial, because a constant deformation rate on its own may erroneously be interpreted as a sign of dynamic stability. Inelastic behavior will show a constant increase in VT number with ground movement and VT event rate maxima and deformation rate will both increase hyperbolically with time (equivalent to linear decreases with time in inverse event rate for VT minima and inverse deformation rate).

2. If behavior is quasi-elastic, the transition to inelastic behavior is expected when the total amount of ground movement is between 2λ_ch and 4λ_ch and, if deformation rate is constant, after corresponding times of 2t_ch and 4t_ch.

3. If behavior is inelastic, the magnitudes of the inverse-rate gradients will be in the range 10^-3-10^-2 for VT minima. Larger gradients may indicate that the linear trends are spurious. Extrapolating the trends to zero inverse-rate (i.e., infinite rate) provides the preferred time τ for bulk failure to be completed.

In all cases, observations must cover a minimum range of values to confirm that a trend is not spurious. For exponential trends, the minimum range is one characteristic interval (λ_ch or t_ch), because shorter observations may yield trends statistically indistinguishable from linear; at least one quarter of a trend’s total duration must therefore be used to identify its existence. For the inverse-rate trends, the smallest range is a decrease in inverse-rate minima by a factor of two (hence, at least half of a trend’s total duration) before a linear trend can be proposed.

Under the ideal conditions when unrest data follow a complete sequence from lithostatic equilibrium (without a differential stress) to bulk failure, the elastic-brittle model provides estimates of the maximum ground movement (2λ_ch–4λ_ch) before the emergence of inelastic deformation and the onset of bulk failure (and, for a constant rate of stress supply, also the maximum time to the transition, 2t_ch–4t_ch). For a continuous acceleration in VT rate across regimes (without at intervening interval at steady rate), bulk failure is expected after an additional time τ at most.

The probability that quasi-elastic behavior will lead to bulk failure increases exponentially with the amount of ground movement (and with time for a constant deformation rate); once it has started, the probability that failure will be completed before an additional interval τ increases hyperbolically with time (Figure 10). The ends of the quasi-elastic and inelastic regimes thus coincide with critical changes in the potential for eruption. They are natural stages for step-like increases in alert (Figure 10) and can readily be incorporated into existing forecasting event trees (Selva et al., 2012; Sobradelo et al., 2013, 2014) or measures of unrest (Potter et al., 2015).

FIGURE 10

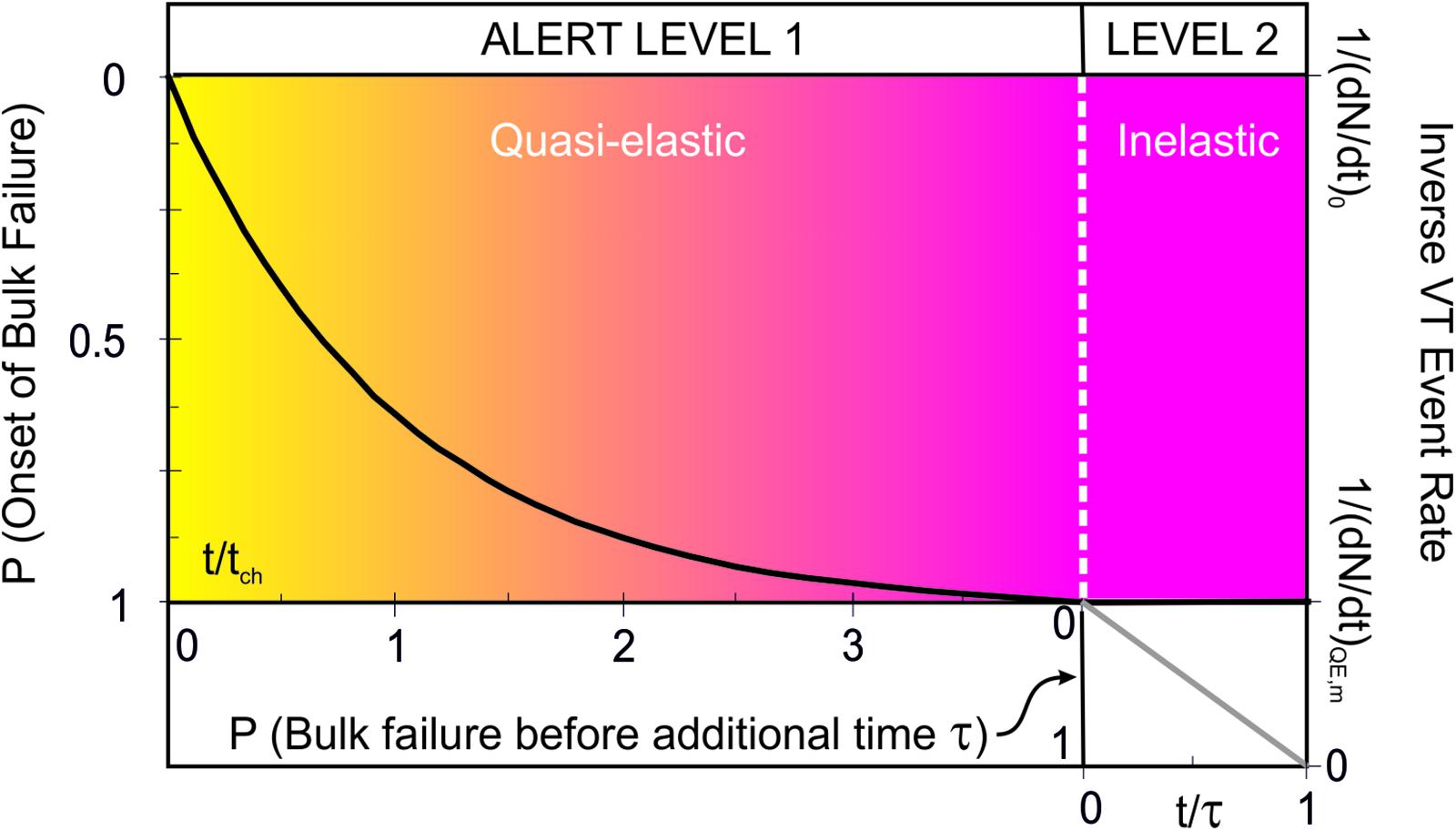
FIGURE 10. The elastic-brittle trends can be transformed into probabilities of bulk failure and levels of alert. The example here assumes a steady rate of stress supply and an immediate transition from exponential to hyperbolic VT event rates after a time 4t_ch. Inverse trends are plotted because changes from an exponential to a linear decrease is easier to visualize that a change from exponential to hyperbolic increase. The transition from quasi-elastic to inelastic regime marks a step increase in alert level. Each level may itself consist of gradational changes, as implied by the colored gradient. The probability being quantified changes from the probability that bulk failure begins in the quasi-elastic regime to the probability that failure will be complete before the time interval τ in the inelastic regime.

At volcanoes reawakening after long repose, emergency measurements are often gathered systematically a significant time after the start of unrest, so that the transition from quasi-elastic to elastic behavior will occur sooner than the ideal maximum time. In the least-favorable case, measurements may become available only when the crust is already in the inelastic regime.

Conclusion

The good agreement between field observation and parent model for changes in seismicity with deformation at closed volcanoes suggests that their behavior before eruptions is normally governed by the stretching of elastic-brittle crust. Immediate implications are that there is no starting requirement to invoke deformation mechanisms other than elastic-brittle, and that VT signals reflect how a population of small faults responds to changes in stress.

The trend between VT events and deformation persists independently from how seismicity and ground movement vary with time, as shown most clearly by the case for Rabaul (Figure 8). A corollary is that VT and deformation time series are mutually dependent and controlled by the rate at which the crust is being stressed. In particular, they reveal how a constant rate of stress (e.g., from magma pressurization) will yield the observed combinations of exponential VT event rate with constant deformation rate, and of hyperbolic VT event rate with hyperbolic deformation rate. These combinations show that the popular FFM model of Voight (1988) is a particular form of the parent VT-deformation model under a constant rate of stress supply. They also provide new criteria to be tested for integrating deterministic physical constraints into probabilistic forecasts of eruption.

The parent model, however, is still not a complete description of pre-eruptive conditions at closed volcanoes. It identifies conditions for bulk failure in the crust, which, although necessary to open a new pathway for magma ascent, do not guarantee that magma will reach the surface. It also focuses on conditions that favor continued acceleration in VT seismicity with time, without significant intervals of steady VT rate. The parent model thus provides a starting point for identifying additional precursory trends and pre-eruptive criteria. Outstanding goals include identifying whether precursory signals can distinguish between pre-eruptive and non-eruptive outcomes; whether VT rates will accelerate to bulk failure without an interval of steady behavior; and, indeed, whether final VT accelerations are inevitable a significant time before eruption. Achieving these goals will provide new constraints for coupling changes in crustal stresses with specific magmatic processes and, hence, yield greater insights for refining and enhancing current forecasting procedures.

Author Contributions

CK developed the elastic-brittle model for precursors to eruption and prepared the manuscript.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Careful reviews by Jérémie Vasseur, Jean-Robert Grasso, Raffaello Cioni and Valerio Acocella clarified and improved the original manuscript. The research was privately funded. Thanks are also due to Barry Voight, whose support and advice during the emergency at Soufriere Hills, Montserrat, in 1996 laid the foundations for the present work.

References

Acocella, V., Di Lorenzo, R., Newhall, C., and Scandone, R. (2015). An overview of recent (1988-2014) caldera unrest: knowledge and perspectives. Rev. Geophys. 53, 896–955. doi: 10.1002/2015RG000492

CrossRef Full Text | Google Scholar

Amitrano, D., Grasso, J. R., and Senfaute, G. (2005). Seismic precursory patterns before a cliff collapse and critical point phenomena. Geophys. Res. Lett. 32:L08314. doi: 10.1029/2004GL022270

CrossRef Full Text | Google Scholar

Anderson, O. L., and Grew, P. C. (1977). Stress corrosion theory of crack propagation with applications to geophysics. Rev. Geophys. Space Sci. 15, 77–104. doi: 10.1029/RG015i001p00077

CrossRef Full Text | Google Scholar

Aspinall, W. (2006). “Structured elicitation of expert judgement for probabilistic hazard and risk assessment in volcanic eruptions,” in Statistics in Volcanology, eds H. M. Mader, S. G. Coles, C. B. Connor, and L. J. Connor (Rome: IAVCEI Publications), 15–30.

Google Scholar

Atkinson, B. K. (1984). Subcritical crack growth in geological materials. J. Geophys. Res. 89, 4077–4114. doi: 10.1029/JB089iB06p04077

PubMed Abstract | CrossRef Full Text | Google Scholar

Bell, A., and Kilburn, C. R. J. (2011). Precursors to dyke-fed eruptions at basaltic volcanoes: insights from the spatiotemporal patterns of volcano-tectonic seismicity at Kilauea volcano, Hawaii. Bull. Volcanol. 74, 325–339. doi: 10.1007/s00445-011-0519-3

CrossRef Full Text | Google Scholar

Bell, A. F., Greenhough, J., Heap, M. J., and Main, I. G. (2011). Challenges for forecasting based on accelerating rates of earthquakes at volcanoes and laboratory analogues. Geophys. J. Int. 185, 718–723. doi: 10.1111/j.1365-246X.2011.04982.x

CrossRef Full Text | Google Scholar

Bell, A. F., Naylor, M., and Main, I. G. (2013). Convergence of the frequency-size distribution of global earthquakes. Geophys. Res. Lett. 40, 2585–2589. doi: 10.1002/grl.50416

CrossRef Full Text | Google Scholar

Bellucci, F., Woo, J., Kilburn, C. R. J., and Rolandi, G. (2006). “Ground deformation at Campi Flegrei, Italy: implications for hazard assessment,” in Mechanisms of Activity and Unrest at Large Calderas, Vol. 269, eds C. Troise, G. De Natale, and C. R. J. Kilburn (London: Geological Society of London), 141–158.

Google Scholar

Blake, S., and Cortés, J. A. (2018). Forecasting deflation, intrusion and eruption at inflating volcanoes. Earth Planet. Sci. Lett. 481, 246–254. doi: 10.1016/j.epsl.2017.10.040

CrossRef Full Text | Google Scholar

Boué, A., Lesage, P., Cortés, G., Valette, B., and Reyes-Dávila, G. (2015). Real-time eruption forecasting using the material Failure Forecast Method with a Bayesian approach. J. Geophys. Res. 120, 2143–2161. doi: 10.1002/2014JB011637

CrossRef Full Text | Google Scholar

Bowden, F. P., and Yoffe, A. D. (1952). The Initiation and Growth of Explosion in Liquids and Solids. Cambridge: Cambridge Univ. Press.

Google Scholar

Chastin, S. F. M., and Main, I. G. (2003). Statistical analysis of daily seismic event rate as a precursor to volcanic eruptions. Geophys. Res. Lett. 30:1671. doi: 10.1029/2003GL016900

CrossRef Full Text | Google Scholar

Collombet, M., Grasso, J.-R., and Ferrazzini, V. (2003). Seismicity rate before eruptions on Piton de la Fournaise volcano: implications for eruption dynamics. Geophys. Res. Lett. 30:2009. doi: 10.1029/2003GL017494

CrossRef Full Text | Google Scholar

Cornelius, R. R., and Scott, P. A. (1993). A materials failure relation of accelerating creep as empirical description of damage accumulation. Rock Mech. Rock Eng. 26, 233–252. doi: 10.1007/BF01040117

CrossRef Full Text | Google Scholar

Cornelius, R. R., and Voight, B. (1994). Seismological aspects of the 1989-1990 eruption at Redoubt volcano, Alaska: the materials failure forecast method (FFM) with RSAM and SSAM seismic data. J. Volcanol. Geotherm. Res. 62, 469–498. doi: 10.1016/0377-0273(94)90048-5

CrossRef Full Text | Google Scholar

Cornelius, R. R., and Voight, B. (1995). Graphical and PC-software analysis of volcano eruption precursors according to the Materials Failure Forecast Method (FFM). J. Volcanol. Geotherm. Res. 64, 295–320. doi: 10.1016/0377-0273(94)00078-U

CrossRef Full Text | Google Scholar

Cornelius, R. R., and Voight, B. (1996). “Real-time seismic amplitude measurement (RSAM) and seismic spectral amplitude measurement (SSAM) analyses with the Materials Failure Forecast Method (FFM), June 1991 explosive eruption at Mount Pinatubo,” in Fire and Mud: Eruptions and Lahars of Mount Pinatubo, Philippines. PHIVOLCS, Quezon City, and, eds C. G. Newhall and R. S. Punongbayan (Seattle, WA: University of Washington Press), 249–267.

Google Scholar

Cowie, P. A., and Shipton, Z. K. (1998). Fault tip displacement gradients and process zone dimensions. J. Struct. Geol. 20, 983–997. doi: 10.1016/S0191-8141(98)00029-7

CrossRef Full Text | Google Scholar

Davidsen, J., Stanchits, S., and Dresen, G. (2007). Scaling and universality in rock fracture. Phys. Rev. Lett. 98:125502. doi: 10.1103/PhysRevLett.98.125502

PubMed Abstract | CrossRef Full Text | Google Scholar

De la Cruz-Reyna, S., and Reyes-Davila G. A. (2001). A model to describe precursory material-failure phenomena: applications to short-term forecasting at Colima volcano, Mexico. Bull. Volcanol. 63, 297–308. doi: 10.1007/s004450100152

CrossRef Full Text | Google Scholar

Di Vito, M. A, Acocella, V., Aiello, G., Barra, D., Battaglia, M., et al. (2016). Magma transfer at Campi Flegrei caldera (Italy) before the 1538 AD eruption. Sci. Rep. 6:32245. doi: 10.1038/srep32245

PubMed Abstract | CrossRef Full Text | Google Scholar

Dzurisin, D. (2007). Volcano Deformation. Geodetic Monitoring Techniques. Chichester: Springer-Praxis.

Google Scholar

Frank-Kamenetskii, D. A. (1939). Diffusion and Heat Transfer in Chemical Kinetics. New York, NY: Plenum.

Google Scholar

Gardner, C. A., and White, R. A. (2002). Seismicity, gas emission and deformation from 18 July to 25 September 1995 during the initial phreatic phase of the eruption of Soufrière Hills Volcano. Montserrat. Mem. Geol. Soc. Lon. 21, 567–581. doi: 10.1144/GSL.MEM.2002.021.01.26

CrossRef Full Text | Google Scholar

Girard, L., Amitrano, D., and Weiss, J. (2010). Failure as a critical phenomenon in a progressive damage model. J. Stat. Mech. doi: 10.1088/1742-5468/2010/01/P01013

CrossRef Full Text | Google Scholar

Grasso, J. R., and Zaliapin, I. (2004). Predictability of volcano eruption: lessons from a basaltic effusive volcano. Geophys. Res. Lett. 31:L05602. doi: 10.1029/2003GL019022

CrossRef Full Text | Google Scholar

Griffith, A. A. (1921). The phenomenon of rupture and flow in solids. Philos. Trans. R. Soc. Lond. A 221, 163–198. doi: 10.1098/rsta.1921.0006

CrossRef Full Text | Google Scholar

Gruntfest, I. J. (1963). Thermal feedback in liquid flow; plane shear at constant stress. Trans. Soc. Rheol. 7, 195–207. doi: 10.1122/1.548954

CrossRef Full Text | Google Scholar

Guarino, A., Garcimartín, A., and Ciliberto, S. (1998). An experimental test of the critical behaviour of fracture precursors. Eur. Phys. J. B 6, 13–24. doi: 10.1007/s100510050521

CrossRef Full Text | Google Scholar

Guénault, A. M. (1995). Statistical Physics, 2nd Edn. Dordrecht: Kluwer. doi: 10.1007/978-1-4020-5975-9

CrossRef Full Text | Google Scholar

Heap, M. J., Baud, P., Meredith, P. G., Bell, A. F., and Main, I. G. (2009). Time-dependent brittle creep in darley dale sandstone. J. Geophys. Res. 114, B07203. doi: 10.1029/2008JB006212

CrossRef Full Text | Google Scholar

Istituto Geográfica Nacional [IGN] (2011). Serie El Hierro. Available at: http://www.ign.es/web/ign/portal/vlc-serie-hierro

Jaeger, J. C. (1969). Elasticiy, Fracure and Flow, 3rd Edn. London: Chapman & Hall.

Google Scholar

Jellinek, A. M., and DePaolo, D. J. (2003). A model for the origin of large silicic magma chambers:precursors of caldera-forming eruptions. Bull. Volcanol. 65, 363–381. doi: 10.1007/s00445-003-0277-y

CrossRef Full Text | Google Scholar

Johnson, R. W., Itikarai, I., Patia, H., and McKee, C. O. (2010). Volcanic Systems of the North-Eastern Gazelle Peninsula, Papua New Guinea. Rabaul Volcano Workshop Report, 1-84. DMPGM Gov. Papua: New Guinea andAusAID Gov.

Google Scholar

Jones, R. H., and Stewart, R. C. (1997). A method for determining significant structures in a cloud of earthquakes. J. Geophys. Res. 102, 8245–8254. doi: 10.1029/96JB03739

CrossRef Full Text | Google Scholar

Kilburn, C. R. J. (2003). Multiscale fracturing as a key to forecasting volcanic eruptions. J. Volcanol. Geotherm. Res. 125, 271–289. doi: 10.1016/S0377-0273(03)00117-3

CrossRef Full Text | Google Scholar

Kilburn, C. R. J. (2012). Precursory deformation and fracture before brittle rock failure and potential application to volcanic unrest. J. Geophys. Res. 117:B02211. doi: 10.1029/2011JB008703.

CrossRef Full Text | Google Scholar

Kilburn, C. R. J., and Voight, B. (1998). Slow rock fracture as eruption precursor at Soufriere Hills volcano. Montserrat. Geophys. Res. Lett. 25, 3665–3668. doi: 10.1029/98GL01609

CrossRef Full Text | Google Scholar

Kilburn, C. R. J, De Natale, G., and Carlino, S. (2017). Progressive approach to eruption at Campi Flegrei caldera in southern Italy. Nat. Comms. 8:15312. doi: 10.1038/ncomms15312

PubMed Abstract | CrossRef Full Text | Google Scholar

Lawn, B. (1993). Fracture of Brittle Solids, 2nd Edn. Cambridge: Cambridge University Press. doi: 10.1017/CBO9780511623127

CrossRef Full Text | Google Scholar

Lengliné, O., Marsan, D., Got, J.-L., Pinel, V., Ferrazzini, V., and Okubo, P. G. (2008). Seismicity and deformation induced by magma accumulation at three basaltic volcanoes. J. Geophys. Res. 113. doi: 10.1029/2008JB005937

CrossRef Full Text | Google Scholar

Lockner, D. (1993). Room temperature creep in saturated granite. J. Geophys. Res. 98, 475–487. doi: 10.1029/92JB01828

CrossRef Full Text | Google Scholar

Main, I. G. (1996). Statistical physics, seismogenesis, and seismic hazard. Rev. Geophys. 34, 433–462, doi: 10.1029/96RG02808

CrossRef Full Text | Google Scholar

Main, I. G. (1999). Applicability of time-to-failure analysis to accelerated strain before earthquakes and volcanic eruptions. Geophys. J. Int. 139, F1–F6. doi: 10.1046/j.1365-246x.1999.00004.x

CrossRef Full Text | Google Scholar

Main, I. G. (2000). A damage mechanics model for power-law creep and earthquake aftershock and foreshock sequences. Geophys. J. Int. 142, 151–161. doi: 10.1046/j.1365-246x.2000.00136.x

CrossRef Full Text | Google Scholar

Main, I. G., and Meredith, P. G. (1991). Stress corrosion constitutive laws as a possible mechanism of intermediate-term and short-term seismic event rates and b-values. Geophys. J. Int. 107, 363–372. doi: 10.1111/j.1365-246X.1991.tb00831.x

CrossRef Full Text | Google Scholar

Marzocchi, W., and Bebbington, M. S. (2012). Probabilistic eruption forecasting at short and long time scales. Bull. Volcanol. 74:805. doi: 10.1007/s00445-012-0633-x

CrossRef Full Text | Google Scholar

McGuire, W. J., and Kilburn, C. R. J. (1997). Forecasting volcanic events: some contemporary issues. Geol. Rundsch. 86, 439–445. doi: 10.1007/s005310050152

CrossRef Full Text | Google Scholar

McKee, C. O., Lowenstein, P. L., De Saint Ours, P., Talai, B., Itikari, I., and Mori, J. J. (1984). Seismic and ground deformation crises at Rabaul caldera: prelude to an eruption? Bull. Volcanol. 47, 397–411. doi: 10.1007/BF01961569

CrossRef Full Text | Google Scholar

McNutt, S. R. (2005). Volcano seismology. Annu. Rev. Earth Planet. Sci. 32, 461–491. doi: 10.1146/annurev.earth.33.092203.122459

CrossRef Full Text | Google Scholar

Mogi, K. (2007). Experimental Rock Mechanics. London: Taylor & Francis.

Google Scholar

Molchan, G., Kronrod, T., and Panza, G. F. (1997). Multi-scale seismicity model for seismic risk. Bull. Seis. Soc. Am. 87, 1220–1229.

Google Scholar

Monod, J. (1949). The growth of bacterial cultures. Annu. Rev. Microbiol. 3, 371–394. doi: 10.1146/annurev.mi.03.100149.002103

CrossRef Full Text | Google Scholar

Nairn, I. A., McKee, C. O., Talai, B., and Wood, C. P. (1995). Geology and eruptive history of the Rabaul Caldera area, Papua New Guinea. J. Volcanol. Geotherm. Res. 69, 255–284. doi: 10.1016/0377-0273(95)00035-6

CrossRef Full Text | Google Scholar

Nakata, J. (2006). Hawaiian Volcano Observatory Seismic Data, January to December 2005. Reston, CA: U.S. Geological Survey Open-File Report, 1–122. doi: 10.3133/ofr20061231

CrossRef Full Text | Google Scholar

Newhall, C. G., and Hoblitt, R. P. (2002). Constructing event trees for volcanic crises. Bull. Volcanol. 64, 3–20. doi: 10.1007/s004450100173

CrossRef Full Text | Google Scholar

Ojala, I. O., Ngwenya, B. T., Main, I. G., and Elphick, S. C. (2004). Correlation of microseismic and chemical properties of brittle deformation in Locharbriggs sandstone. J. Geophys. Res. 108:2268. doi: 10.1029/2002JB002277

CrossRef Full Text | Google Scholar

Potter, S. H., Scott, B. J., Jolly, G. E., Neall, V. E., and Johnston, D. M. (2015). Introducing the Volcanic Unrest Index (VUI): a tool to quantify and communicate the intensity of volcanic unrest. Bull. Volcanol. 77:77. doi: 10.1007/s00445-015-0957-4

CrossRef Full Text | Google Scholar

Power, J. A., Wyss, M., and Latchman, J. L. (1998). Spatial variations in the frequency-magnitude distribution of earthquakes at Soufrière Hills Volcano, Montserrat, West Indies. Geophys. Res. Lett. 25, 3653–3656. doi: 10.1029/98GL00430

CrossRef Full Text | Google Scholar

Rabaul Petrology Group (1995). Taking petrologic pathways toward understanding Rabaul’s restless caldera. EOS Trans. Am. Geophys. 76, 171, 180. doi: 10.1029/95EO00093

CrossRef Full Text | Google Scholar

Reif, F. (1985). Fundamentals of Statistical and Theirmal Physics, (International Edition). Auckland: McGraw-Hill.

Robertson, R. M., and Kilburn, C. R. J. (2016). Deformation regime and long-term precursors to eruption at large calderas: Rabaul, Papua New Guinea. Earth Planet. Sci. Lett. 438, 86–94. doi: 10.1016/j.epsl.2016.01.003

CrossRef Full Text | Google Scholar

Ruhla, C. (1992). The Physics of Chance. Oxford: Oxford University Press.

Google Scholar

Saada, A. S. (2009). Elasticity: Theory and Applications, 2nd Edn. Plantation, FL: J. Ross Andover.

Google Scholar

Sagiya, T. (2011). GPS Network in Canary Islands and Fogo, Cape Verde. Available at: http://www.seis.nagoya-u.ac.jp/~sagiya/Sagiyas_Page/Canary.html

Sandri, L., Guidoboni, E., Marzocchi, W., and Selva, J. (2009). Bayesian event tree (BET) for eruption forecasting at Vesuvius, Italy: a retrospective forward application to 1631 eruption. Bull. Volcanol. 71, 729–745. doi: 10.1007/s00445-008-0261-7

CrossRef Full Text | Google Scholar

Schmid, A., and Grasso, J.-R. (2012). Omori law for eruption foreshocks and aftershocks. J. Geophys. Res. 117:B07302. doi: 10.1029/2011JB008975

CrossRef Full Text | Google Scholar

Secor, D. T. (1965). Role of fluid pressure in jointing. Am. J. Sci. 263, 633–646. doi: 10.2475/ajs.263.8.633

CrossRef Full Text | Google Scholar

Selva, J., Marzocchi, W., Papale, P., and Sandri, L. (2012). Operational eruption forecsting at high-risk volcanoes: the case of Campi Flegrei, Naples. J. Appl. Volcanol. 1:5. doi: 10.1186/2191-5040-1-5

CrossRef Full Text | Google Scholar

Shaw, H. R. (1969). Rheology of basalt in the melting range. J. Petrol. 10, 510–535. doi: 10.1093/petrology/10.3.510

CrossRef Full Text | Google Scholar

Shaw, H. R. (1980). “The fracture mechanisms of magma transport from the mantle to the surface,” in Physics of Magmatic Processes, ed. R. B. Hargraves (Princeton: Princeton University Press), 201–264.

Google Scholar

Shepherd, J. B., Robertson, R., Latchman, J., and Lynch, L. (2002). “Precursory activity to the 1995 eruption of the Soufrière Hills volcano, Montserrat,” in Proceedings of the Beyond Walls: Multidisciplinary Perspectives. Montserrat Conference, School of Continuing Studies, University of the West Indies, 13-14 December 2002, Jamaica. Available at: http://www.open.uwi.edu/sites/default/files/bnccde/montserrat/conference/papers/pre-1995%20Montserrat.pdf

Sibson, R. H. (1998). Brittle failure mode plots for compressional and extensional tectonic regimes. J. Struct. Geol. 20, 655–660. doi: 10.1016/S0191-8141(98)00116-3

CrossRef Full Text | Google Scholar

Sobradelo, R., Bartolini, S., and Martí, J. (2013). HASSET: a probability event tree tool to evaluate future eruptive scenarios using Bayesian Inference. Bull. Volcanol. 76:770. doi: 10.1007/s00445-013-0770-x

CrossRef Full Text | Google Scholar

Sobradelo, R., and Martí, J. (2015). Short-term volcanic hazard assessment through Bayesian inference: retrospective application to the Pinatubo 1991 volcanic crisis. J. Volcanol. Geotherm. Res. 290, 1–11. doi: 10.1016/j.jvolgeores.2014.11.011

CrossRef Full Text | Google Scholar

Sobradelo, R., Martí, J., Kilburn, C. R. J., and López, C. (2014). Probabilistic approach to decision-making under uncertainty during volcanic crises: retrospective application to the El Hierro (Spain) 2011 volcanic crisis. Nat. Hazards 76, 979–998. doi: 10.1007/s11069-014-1530-8

CrossRef Full Text | Google Scholar

Sparks, R. S. J., Biggs, J., and Neuberg, J. W. (2012). Monitoring volcanoes. Science 335, 1310–1311. doi: 10.1126/science.1219485

PubMed Abstract | CrossRef Full Text | Google Scholar

Swanson, D. A., Jackson, D. B., Duffield, W. A., and Peterson, D. W. (1971). Mauna Ulu eruption, Kilauea Volcano. Geotimes 16, 12–16.

Google Scholar

Tilling, R. I. (1995). “The role of monitoring in forecasting volcanic events,” in Monitoring Active Volcanoes, eds W. J. McGuire, C. R. J. Kilburn, and J. B. Murray (London: UCL Press), 369–402.

Google Scholar

Troise, C., De Natale, G., and Pingue, F. (2003). Coulomb stress changes at calderas: modeling the seismicity of Campi Flegrei (southern Italy). J. Geophys. Res. 108:2292. doi: 10.1029/2002JB002006

CrossRef Full Text | Google Scholar

Turcotte, D. L., Newmanm, W. I., and Shcherbakov, R. (2003). Micro and macroscopic models of rock fracture. Geophys. J. Int. 152, 718–728. doi: 10.1046/j.1365-246X.2003.01884.x

CrossRef Full Text | Google Scholar

Valkó, P., and Economides, M. J. (1995). Hydraulic Fracture Mechanics. Chichester: John Wiley & Sons.

Google Scholar

Vasseur, J., Wadsworth, F. B., Heap, M. J., Lavallée, Y., and Dingwell, D. B. (2017). Does an inter-flaw length control the accuracy of rupture forecasting in geological materials? Earth Planet. Sci. Lett. 475, 181–189. doi: 10.1016/j.epsl.2017.07.011

CrossRef Full Text | Google Scholar

Vasseur, J., Wadsworth, F. B., Lavallée, Y, Bell, A. F., Main, I. G., and Dingwell, D. B. (2015). Heterogeneity: The key to failure forecasting. Sci. Rep. 5:13529. doi: 10.1038/srep13259

PubMed Abstract | CrossRef Full Text | Google Scholar

Voight, B. (1988). A method for prediction of volcanic eruptions. Nature 332, 125–130. doi: 10.1038/332125a0

CrossRef Full Text | Google Scholar

Voight, B. (1989). A relation to describe rate-dependent material failure. Science 243, 200–203. doi: 10.1126/science.243.4888.200

PubMed Abstract | CrossRef Full Text | Google Scholar

Wall, R. J. (2014) Precursors to Volcanic Eruptions in Extensional Stress Fields. PhD Thesis, University College London, London, 404.

Google Scholar

White, R., and McCausland, W. (2016). Volcano-tectonic earthquakes: a new tool for estimating intrusive volumes and forecasting eruptions. J. Volcanol. Geotherm. Res. 309, 139–155. doi: 10.1016/j.jvolgeores.2015.10.020

CrossRef Full Text | Google Scholar

Zobin, V. M. (2003). Introduction to Volcano Seismology. Amsterdam: Elsevier.