- 1Department of Earth and Planetary Sciences, Johns Hopkins University, Baltimore, MD, United States
- 2Department of Earth and Planetary Sciences, University of New Mexico, Albuquerque, NM, United States
- 3Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, University of Cambridge, Cambridge, United Kingdom
- 4Institut de Physique du Globe de Paris, Sorbonne Paris Cité, Université Paris-Diderot, Paris, France
- 5T-Mobile USA, Bellevue, WA, United States
The presence of stable stratification has broad implications for the thermal and compositional state of the outer core, the evolution of Earth's deep interior, and the energetics of the geodynamo. Yet the origin, strength, and depth extent of stratification in the region below the core-mantle boundary remain open questions. Here we compare magnetic fields produced by numerical dynamos that include heterogeneous stable thermal stratification below their outer boundary with models of the geomagnetic field on the core-mantle boundary, focusing on high latitude structures. We demonstrate that the combination of high magnetic field intensity regions and reversed magnetic flux spots, especially at high latitudes, constrains outer core stratification below the core-mantle boundary. In particular, we find that the negative contribution to the axial dipole from reversed flux spots is a strong inverse function of the stratification. Comparison of our numerical dynamo results to the structure of the historical geomagnetic field suggests up to 400 km of permeable, laterally heterogeneous thermal stratification below the core-mantle boundary.
1. Introduction
Stable stratification at the top the outer core has been inferred using both seismic and geomagnetic data, typically with divergent results. Some investigations find that the stratification is limited to a layer extending 100–200 km below the core-mantle boundary (Whaler, 1980; Lay and Young, 1990; Garnero et al., 1993; Gubbins, 2007; Tanaka, 2007; Buffett, 2014). However, other studies indicate the stratification extends to greater depths—300 km (Helffrich and Kaneshima, 2010) and possibly deeper (Gomi et al., 2013; Tang et al., 2015; Kaneshima, 2017), while still others find little evidence for stratification (Irving et al., 2018). Interpretations of the source of the stratification include stable (subadiabatic) thermal stratification (Gomi et al., 2013; Buffett et al., 2016) as well as stable compositional stratification due to anomalous light element concentrations (Gubbins and Davies, 2013; Helffrich and Kaneshima, 2013; Brodholt and Badro, 2017).
This raises multiple questions for the dynamics of the core. First, is the outer core stratification inferred by recent seismic studies compatible with the geomagnetic field and its secular variation? Core flow inversions based on the geomagnetic secular variation are best accommodated by including upwelling and downwelling motions extending very close to the core-mantle boundary (Gubbins, 2007; Amit, 2014; Lesur et al., 2015; Huguet et al., 2016). For example, Gubbins (2007) argued that the production of reversed flux spots on the core-mantle boundary, which are rapidly evolving in the present-day geomagnetic field (Olson and Amit, 2006; Olsen et al., 2014; Terra-Nova et al., 2015; Metman et al., 2018), limits the depth extent of the stratification to less than 150 km, assuming no radial motion in that layer and that the reversed flux spots on the core-mantle boundary result from the expulsion of magnetic flux from the outer core.
Second, can numerical dynamos provide independent constraints on the strength and depth extent of the stratification? There are relatively few systematic investigations of the geodynamo in the presence of stratification (Sreenivasan and Gubbins, 2008; Nakagawa, 2011, 2015; Olson et al., 2017; Christensen, 2018). However, stratification effects have been extensively studied in the context of the solar dynamo (e.g., Browning et al., 2006, 2007; Käpylä et al., 2008; Tobias et al., 2008; Brummell et al., 2010; Masada et al., 2013), Jupiter (Zhang and Schubert, 2000), Saturn (Christensen and Wicht, 2008; Stanley, 2010), and also Mercury (Christensen, 2006; Manglik et al., 2010). All these investigations found that the presence of a stratified layer affects the morphology of the magnetic field. In particular, a stratified layer below a convective region is key to generating a large-scale magnetic field in solar dynamo simulations (Browning et al., 2006, 2007; Käpylä et al., 2008), where strong zonal flows in the stratified layer stretch the poloidal magnetic field in the convective region into a large-scale toroidal magnetic field through an ω-effect. Other investigations have reported the generation of strong azimuthal flows within a stratified layer adjacent to a convective region (Zhang and Schubert, 2000; Takehiro and Lister, 2002; Couston et al., 2018), which attenuate high-frequency, non-axisymmetric magnetic field components in the stratified layer (Christensen, 2006; Christensen and Wicht, 2008; Stanley, 2010).
Because stratification affects the magnetic field structure, dynamo simulations are useful in constraining the stratification in Earth's core. In a previous paper (Olson et al., 2017) we conducted a systematic investigation of the flow and the time average magnetic field in the presence of thermal stratification. We showed that the high latitude structures of the time average magnetic fields in numerical dynamos are sensitive to the strength and depth extent of thermal stratification below the dynamo upper boundary. This sensitivity offers the means to infer the properties of stratification below the core-mantle boundary (CMB) in terms of the time average structure of the geomagnetic field. In this paper we quantitatively compare the high latitude CMB structure of the COV-OBS geomagnetic field model (Gillet et al., 2013) to a suite of thermally stratified numerical dynamos. Extending the analysis in Olson et al. (2017), we compute the correlation of the high latitude structures of the time average magnetic field in the COV-OBS model and in our numerical dynamos. In addition, we analyze the time varying field, focusing on the effects of reversed flux spots on the axial dipole. These comparisons favor the existence of stratification below the CMB but also indicate that substantial radial motions are present there, implying that the stratification is rather weak and permeable to outer core convection.
2. Numerical Dynamos With Thermal Stratification Below the Outer Boundary
The stratification analyzed in this study is due to thermal gradients that deviate from adiabatic (i.e., uniform entropy) conditions and are maintained by the heat flux imposed at the outer boundary. We include lateral variations of the boundary heat flux, following the results of mantle global circulation models (Nakagawa and Tackley, 2013, 2015; Zhong and Rudolph, 2015) that yield vigorous deep mantle convection with locally variable heat flux on the core-mantle boundary that is large enough in some places to sustain unstable thermal stratification (Olson et al., 2015), even if the thermal conductivity of the outer core is high (Ohta et al., 2016).
We model stratified thermochemical convection in the outer core with heterogeneous heat flux at the CMB using the formulation in Olson et al. (2017). Outer core density variations are expressed in terms of the codensity, i.e., density variations due to the combination of temperature and light element concentration variations:
where ρo is fluid mean density, T is temperature relative to the adiabat with mean To, χ is the fluid light element concentration with mean χo, and α and β are volumetric expansion coefficients for T and χ, respectively. In terms of these, the governing equations for thermochemical convection and dynamo action in a rotating spherical shell (with the Boussinesq approximation) include the following dimensionless control parameters:
Here E is the Ekman number, Pr is the Prandtl number, Pm is the magnetic Prandtl number, and ϵ is the volumetric codensity source. In (2), Ω denotes angular velocity of rotation, D = ro − ri is the depth of the fluid shell, ro and ri, the radii of the inner and outer fluid boundaries, with ν, η, and κ denoting kinematic viscosity, magnetic diffusivity, and codensity diffusivity, respectively.
At the inner boundary ri we assume no-slip velocity conditions and a uniform codensity Ci. At the outer boundary we also assume no-slip velocity conditions, zero light element flux, and we specify the heat flux q to be the sum of a spherical mean part (denoted by an overbar) and a deviation from the spherical mean (denoted by a prime):
where ϕ and θ are longitude and colatitude, respectively, and is measured relative to the heat flux down the adiabat, with being superadiabatic heat flux and being subadiabatic heat flux. This formulation yields three additional dimensionless parameters that control the convection: a Rayleigh number based on the rate of increase of light element concentration in the fluid
a second Rayleigh number based on the spherical mean heat flux at the outer boundary
and a third Rayleigh number based on the peak-to-peak variation Δq′ of the laterally varying boundary heat flux
In (4-6), g is gravity at the outer boundary and k is thermal conductivity. In the numerical dynamos, the factors and (where σ is electrical conductivity) non-dimensionalize codensity variations and magnetic field intensity, respectively, and ν/D non-dimensionalizes the fluid velocity. In what follows, we retain these scalings for codensity and magnetic field, but we use η/D to scale the fluid velocity. With these factors, the scaling for velocity and magnetic field intensities are referred to as magnetic Reynolds number and Elsasser number units, respectively.
In Olson et al. (2017) we introduced a parameter describing the spherical mean stratification:
defined to be positive when is negative, i.e., when the spherical mean boundary heat flux is stabilizing. There is also a related stratification parameter describing the effects of the boundary heat flux heterogeneity:
We analyze dynamos with E = 10−4, Pr = 1, Pm = 6, and ϵ = −0.8, the latter appropriate for dominantly compositional convection but with some secular cooling included. The aspect ratio of the fluid shell is fixed at ri/ro = 0.351. The solid region r ≤ ri representing the inner core is assumed to have the same electrical conductivity as the fluid, and the solid region r ≥ ro representing the mantle is assumed to be electrically insulating. The boundary heat flux pattern is defined by a spherical mean part plus a heterogeneous part consisting mostly of spherical harmonic degree ℓ = 2 components at orders m = 0 and m = 2, adjusted so as to produce a pattern with nearly bilateral (i.e., 2-fold) azimuthal symmetry. The resulting boundary heat flux pattern is shown in Figure 1A and corresponds to the largest scale of lower mantle heterogeneity structure determined by Dziewonski et al. (2010). It is basically the same planform used by Olson and Amit (2015) in their study of the influences of lower mantle piles on magnetic polarity reversal behavior.
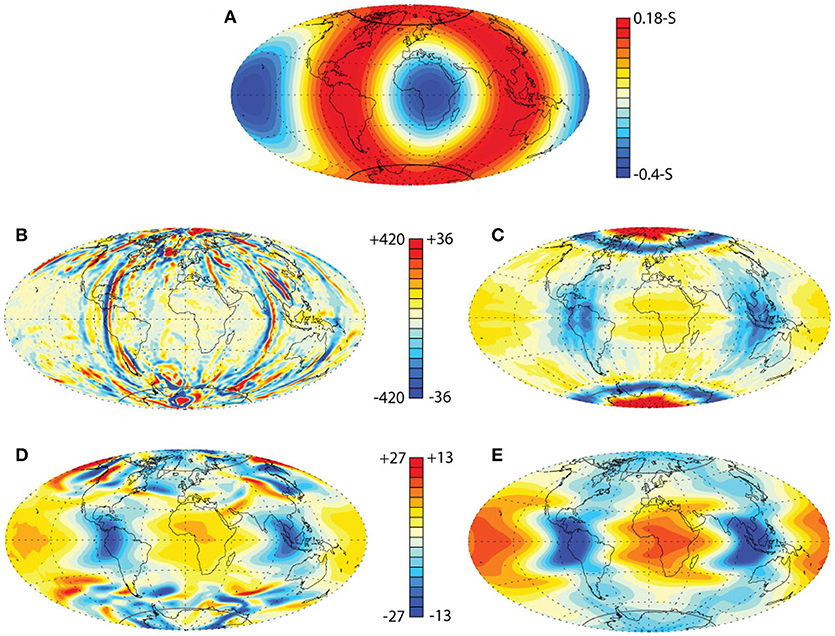
Figure 1. Numerical dynamo heat flux and radial velocities near the outer boundary ro at Ra = 9 × 107. (A) is the dimensionless heat flux imposed on the outer boundary; (B–E) are r = 0.95ro dimensionless radial velocity patterns. (B,C) are a snapshot and time average radial velocity for stratification parameter S = 0; (D,E) are a snapshot and time average radial velocity for stratification parameter S = 0.3. Maximum and minimum dimensionless outer boundary heat fluxes are 0.18-S and –0.4-S, respectively. Velocity scales are in magnetic Reynolds number units.
Dynamo calculations are made at Ra = 6 × 107 and Ra = 9 × 107 for stratification parameters S ranging from −0.1, corresponding to superadiabatic CMB heat flux, to +0.3, corresponding to strongly subadiabatic CMB heat flux, using the MAGIC dynamo code (Wicht, 2002). We assume a constant value of S′ = 0.58 for all cases. We find that by preserving S′, key properties of these dynamos such as the r.m.s. dipole axis tilt are nearly independent of S, while other properties such as the contribution of reversed flux to the axial dipole are relatively insensitive to Ra. We use a numerical grid with (nr, nθ, nϕ) = (81, 128, 256) in the fluid shell and spherical harmonic truncation (ℓ, m)max = 85. All the calculations were run for at least one magnetic diffusion time, in order that the run averages approximate true time averages.
3. Stratification Diagnostics
For comparison with the geomagnetic field, we focus on properties of the dynamo magnetic field structures, particularly at high latitudes. Previously, Olson et al. (2017) found that the high latitude dynamo magnetic fields are especially sensitive to stratification beneath the outer boundary, and the effects of stratification produce distinct and readily identifiable structures, both inside the tangent cylinder of the inner core and beyond, down to latitudes of approximately 45o. In contrast, some dynamo magnetic field structures at low latitudes are not so easily related to stratification. Accordingly, most of our comparisons between numerical dynamos and the geomagnetic field are based on the variable Br cos(θ), where θ is colatitude, which is the kernel of the axial dipole moment density on the CMB (Olson and Amit, 2006). For our applications, Br cos(θ) is superior to the radial component of the magnetic field Br because the cos(θ) factor adds weight to the high latitude field structure.
We characterize our numerical dynamos in terms of the structure of Br cos(θ) on the outer boundary, along with the magnitude of the stratification and the upwelling below the outer boundary. One important diagnostic is the ratio of reversed to normal polarity flux on the outer boundary. The two individual contributors to this ratio are given by
where the superscripts N and R denote the signs of Br (positive or negative) that define the dominant and the subordinate components, respectively, of the axial dipole moment, and A is the outer boundary surface area. The ratio of these two fluxes
is defined so that 0 ≤ F* ≤ 1, the lower limit indicating zero contribution to the axial dipole moment from reversed flux, the upper limit corresponding to a vanishingly small axial dipole. Another magnetic diagnostic we use is the distribution of high latitude, high intensity Br cos(θ)-structures. Our previous study (Olson et al., 2017) documented that the morphology of high latitude, high intensity Br-structures in time average dynamo magnetic fields can be used to constrain the stratification parameter S. In the next sections we demonstrate that Br cos(θ) is even more sensitive to S, both in snapshots and in time averages.
We measure the stratification in our numerical dynamos using the spherical mean thickness of the stratified region and its gravitational stability. The dimensionless spherical mean thickness of the stratified region of the dynamo is defined as
where rmin is the radius where the dimensionless spherical mean codensity reaches its local minimum value below the outer boundary. Likewise, we define the gravitational stability of the stratified layer in terms of the dimensionless buoyancy frequency squared:
where is the dimensionless codensity increase across the stratified region. In Olson et al. (2017) we derived the following scaling laws for these quantities:
in which (aδ, bδ) = (1.82, 1.2), plus
in which (aN, bN) = (0.72, 1). Lastly, the r.m.s. upwelling strength below the outer boundary is used to characterize the effects of stratification on the flow. We define the dimensionless outer boundary (or CMB) upwelling strength as
where ∇H and u are the dimensionless horizontal divergence and the fluid velocity, respectively, and ‖ denotes r.m.s. average over the spherical shell at 0.95ro.
4. Dynamos With Stratification
Figure 1 shows the pattern of heat flux applied to the outer dynamo boundary and the resulting radial velocity pattern from two dynamos with Ra = 9 × 107 but different amounts of stratification. Figure 1A shows the nearly bilaterally symmetric boundary heat flux in dimensionless form, with a great circle of elevated heat flux that includes both polar regions, separating two large, low latitude regions with reduced heat flux. The reduced heat flux regions correspond approximately to the Large Low Shear Velocity Provinces (LLSVPs) imaged by seismic tomography (Garnero and McNamara, 2008) and the elevated heat flux band approximately corresponds to the high shear velocity regions at the base of the mantle. Figures 1B,C show a snapshot and the time average radial velocity at a depth of 0.05ro below the outer boundary, for stratification parameter S = 0. Figures 1D,E are a snapshot and the time average radial velocity at the same depth for stratification parameter S = 0.3. The radial velocities are in dimensionless (magnetic Reynolds number) units.
In the snapshots, the effects of stratification are most evident in the difference in magnitude of the radial velocities. In the S = 0 dynamo, dimensionless radial velocities in Figure 1B exceed 400 in places, with an r.m.s. at this depth of approximately 180. In the S = 0.3 dynamo, in contrast, dimensionless radial velocities in Figure 1D nowhere exceed 30, and the r.m.s. at this depth is approximately 9. Clearly, the stabilizing effects of the boundary heat flux suppress the radial velocity below the outer boundary, reducing the r.m.s. strength of upwellings and downwellings there by a nearly a factor of 20 between the two cases.
The strong reduction in radial velocity caused by stratification that is seen in the snapshots is less extreme in the time averages in Figures 1C,E. Overall, the patterns of radial velocity are more similar in these time averages compared to their corresponding snapshots, because the boundary heat flux heterogeneity plays a relatively greater role in structuring the time average velocities. The greatest differences between the two dynamos in terms of their time average radial velocities are found at high latitudes. In the S = 0 dynamo, there are strong polar upwellings and strong downwellings along the inner core tangent cylinder in both hemispheres (Figure 1C), structures that are missing from the strongly stratified S = 0.3 dynamo (Figure 1E).
Figure 2 shows snapshots and time averages of the radial magnetic field intensity on the outer boundary at Ra = 9 × 107 for stratification parameter S varying between 0 and 0.3. Unlike the radial velocity, for which the amplitude of the upwellings and downwellings show the strongest influence of stratification, the magnetic field on the outer boundary mainly responds to the stratification through changes in its structure, rather than its amplitude. For example, in the snapshot field structures in Figure 2 there is a progressive reduction in the number and the intensity of reversed flux spots with increasing S, such that the S = 0.3 dynamo snapshot (Figure 2G) is entirely lacking in reversed flux at high latitudes in both hemispheres, yet the overall magnetic field intensity barely changes with S.
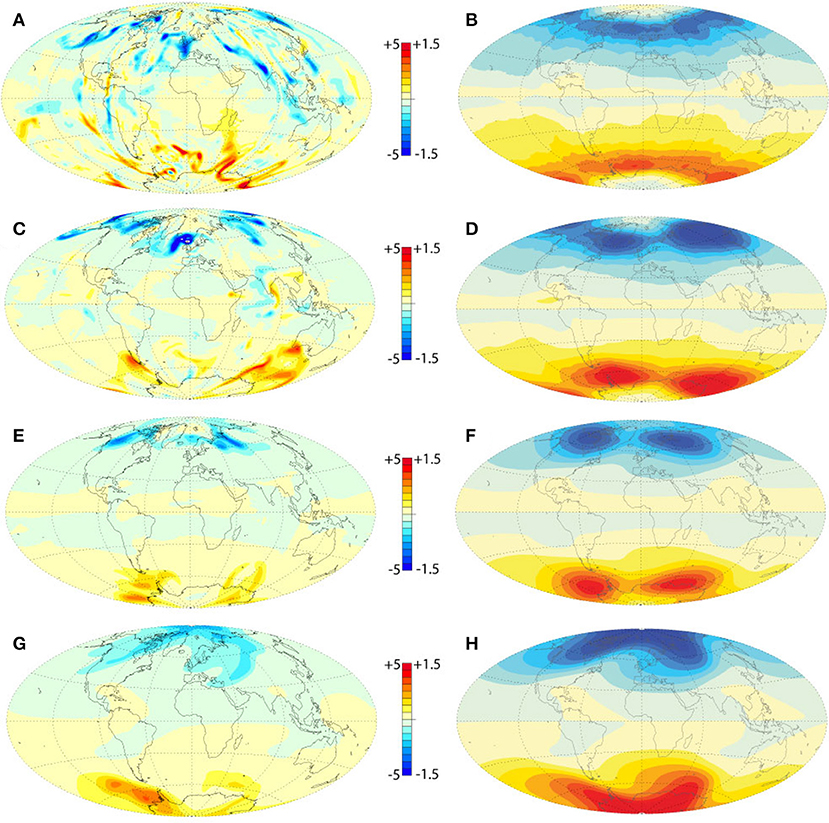
Figure 2. Numerical dynamo radial magnetic field intensity Br at the outer boundary and Ra = 9 × 107 for different stratification parameters S. (A,B) Snapshot and time average fields for S = 0; (C,D) Snapshot and time average fields for S = 0.1; (E,F) Snapshot and time average fields for S = 0.2; (G,H) Snapshot and time average fields for S = 0.3. Magnetic field intensities are in dimensionless Elsasser number units.
The other expression of structural change at high latitudes is seen in the time average field structures. In the S = 0 and S = 0.1 dynamos (Figures 2B,D) the high latitude structure consists of rings of high intensity field located near the tangent cylinder surrounding deep intensity minima, with localized reversed flux at the poles. In the S = 0.2 dynamo (Figure 2F) the polar minima are gone and the high intensity field is localized in patches, two in each hemisphere. Lastly, in the strongly stratified S = 0.3 case (Figure 2H) the two patches in each hemisphere have merged into a single high intensity lobe, positioned such that there is a field intensity maximum located at each pole.
The trends in the time average magnetic field structure in Figure 2 can be explained in terms of the changes in the internal dynamo structure with increasing stratification. Figure 3 compares the azimuthally averaged structure of Ra = 9 × 107 dynamos with S = 0 and S = 0.3, respectively. The internal structure of the S = 0 dynamo (Figures 3A–C) includes an adverse (i.e., destabilizing) codensity gradient, strong thermal wind circulations with meridional overturning inside the tangent cylinder in both hemispheres, and low magnetic field intensity near the outer boundary inside the tangent cylinder, locally reversed at each pole. The polar reversed flux, the low field intensity inside the tangent cylinder, and the high intensity field along the tangent cylinder, can be explained in this dynamo in terms of incomplete flux expulsion by the meridional circulations inside each tangent cylinder region. This circulation advects the poloidal magnetic field away from the poles and concentrates it along the tangent cylinder, producing the high latitude pattern seen in Figure 2B. In contrast, the azimuthally averaged internal structure of the S = 0.3 dynamo (Figures 3D–F) includes stable stratification below the outer boundary at all latitudes, a two-layer meridional circulation pattern at low and middle latitudes, and reversed circulations inside the tangent cylinder that exchange fluid with the meridional circulations outside. The meridional circulations inside the tangent cylinder region include polar downwellings that produce horizontal convergence beneath the outer boundary. These circulations concentrate poloidal magnetic flux close to the pole, producing polar intensity maxima in both hemispheres, as seen in Figure 2H.
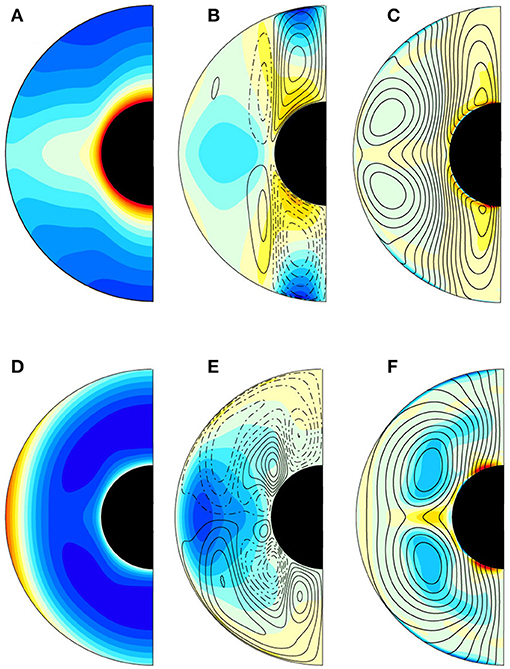
Figure 3. Zonal average numerical dynamo structures at Ra = 9 × 107 for two stratification parameters: S = 0 (A–C) and S = 0.3 (D–F). Images (A,D) show codensity contours; images (B,E) show meridional circulation streamlines (clockwise=dashed; counterclockwise=solid) over azimuthal velocity contours; images (C,F) show poloidal magnetic field lines over azimuthal electric current contours, all dimensionless. Red contours=positive, blue=negative.
5. Comparisons With the Geomagnetic Field at the CMB
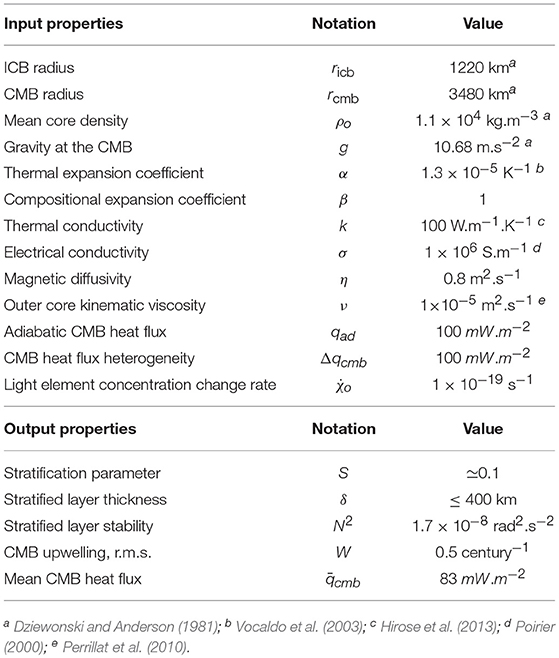
Figure 4 shows Br cos(θ) on the core-mantle boundary from the COV-OBS geomagnetic field model (Gillet et al., 2013; http://www.spacecenter.dk/files/magnetic-models/COV-OBS/COV-OBS-int.txt). Figures 4A,B are Northern and Southern hemisphere images at epoch 2014, whereas Figures 4C,D are 1840–2014 time averages for the Northern and Southern hemispheres, respectively. Data sources for this geomagnetic field model include space-borne magnetometer measurements during low altitude satellite orbits plus annual means from ground-based observatories. The COV-OBS core field is represented at epochs spaced 2 years apart, and is complete to spherical harmonic degree and order 14. We treat Figures 4A,B as snapshots of the present-day core field, for comparison with our dynamo snapshots. The maps of Br cos(θ) in Figures 4C,D are averages over 88 epochs, but their 174 year time span is far shorter than the averaging times in our dynamos, which are of the order of a few hundred thousand years. Nevertheless, in what follows we treat the geomagnetic field average as a true time average for purposes of comparison with the dynamo averages.
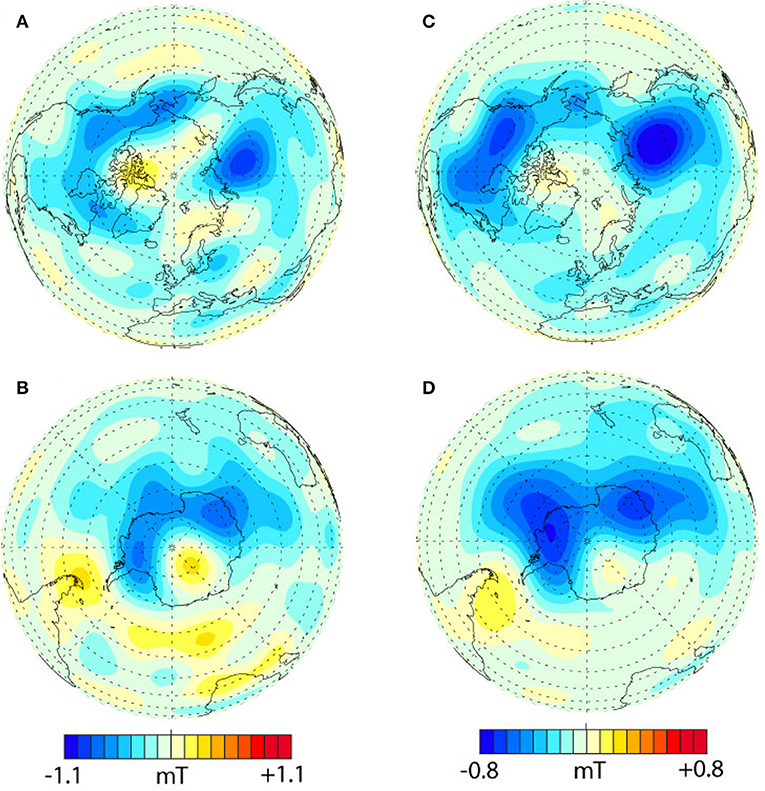
Figure 4. Br cos(θ) on the core-mantle boundary from the COV-OBS geomagnetic field model (Gillet et al., 2013). (A,B) are Northern and Southern hemisphere snapshots, respectively, at epoch 2014; (C,D) are 1840-2014 time averages of the Northern and Southern hemispheres, respectively. Contours are in millitesla, mT.
Figure 5 shows snapshots and time averages of Br cos(θ) from numerical dynamos at Ra = 6 × 107 for stratification parameters ranging from S = −0.1, corresponding to a superadiabatic thermal gradient at the CMB, to S = 0.3, corresponding to a strongly subadiabatic thermal gradient at the CMB. The top row of maps in Figure 5 are Northern hemisphere Br cos(θ) snapshots, the middle row are Southern hemisphere snapshots at the same times, and the bottom row are Northern hemisphere time averages. Southern hemisphere time averages differ insignificantly from their northern counterparts and are not shown.
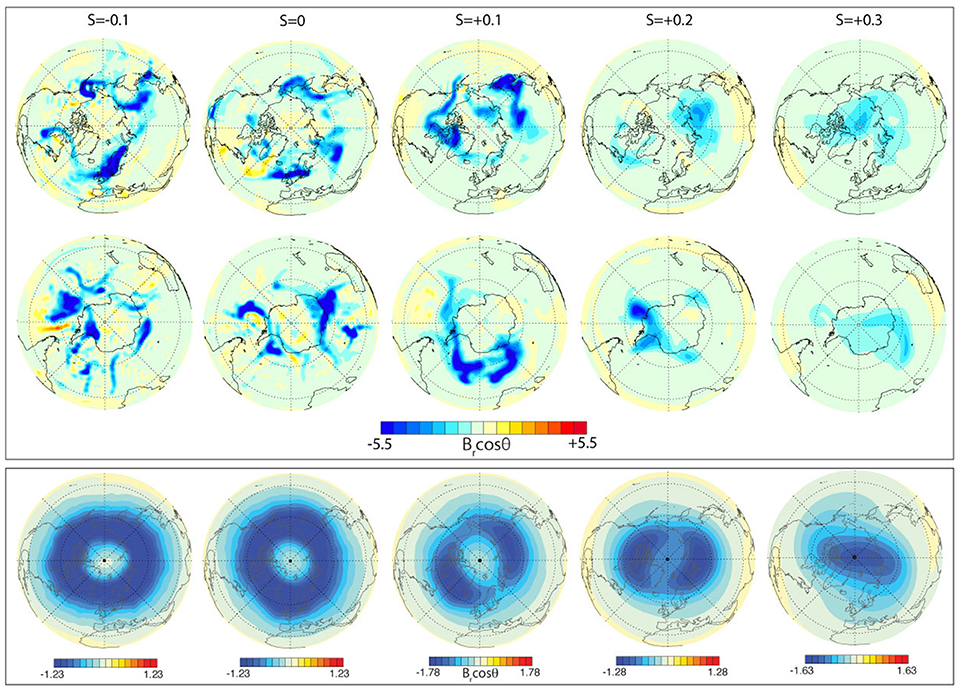
Figure 5. Snapshots and time averages of Br cos(θ) from numerical dynamos at Ra = 6 × 107 for different stratification parameters S. Top row: Northern hemisphere snapshots; middle row: Southern hemisphere snapshots at the same times; bottom row: Northern hemisphere time averages. Magnetic field intensities are in dimensionless Elsasser number units.
The top and middle rows in Figure 5 show the same qualitative trends as in Figure 2 in terms of the disappearance of reversed flux with increasing stratification parameter. To demonstrate this quantitatively, Figure 6 shows F*, the ratio of reversed to normal flux defined by Equations (9) and (10) vs. stratification parameter S, for the Ra = 6 × 107 dynamos in Figure 5 and the Ra = 9 × 107 dynamos in Figure 2. The error bars indicate the standard deviation of F* based on six to eight snapshots from each dynamo. Although there is some dependence on the Rayleigh number at S = 0 and S = −0.1, the reversed to normal flux ratios at both Rayleigh numbers decrease strongly with increasing S, rapidly converging toward zero at larger S. Reversed flux patches are generally non-axisymmetric structures. Therefore, this decrease in F* with increasing S agrees with previous studies that found that stratification removes not only reversed flux (Sreenivasan and Gubbins, 2008), but also other non-axisymmetric components of the magnetic field (Christensen, 2006; Christensen and Wicht, 2008; Stanley, 2010). We also show in Figure 6 the reversed to normal flux ratio on the CMB from the Gillet et al. (2013) COV-OBS geomagnetic field model at epoch 2014. Dynamos with S = 0.1 best match the present-day geomagnetic field structure in terms of the relative contribution of reversed flux to the axial dipole.
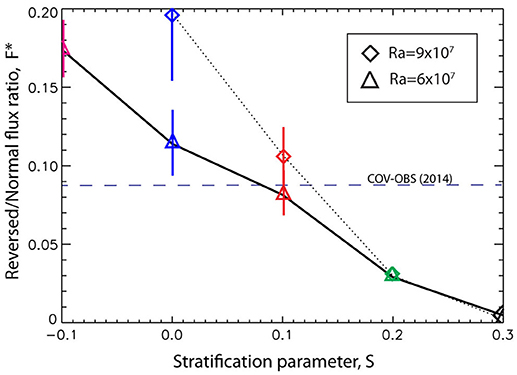
Figure 6. Ratios of reversed to normal flux contributions to the axial dipole F* vs. stratification parameter S from numerical dynamos (symbols), compared to F* from the COV-OBS geomagnetic field model on the core-mantle boundary at epoch 2014 (dashed line). Error bars denote one standard deviation of dynamo snapshots.
There are several important differences between the numerical dynamos and the core field model that need to be factored out in order to make the comparison in Figure 6 more direct. First, the core field model is truncated at spherical harmonic degree 14, whereas the numerical dynamos used for F* in Figure 6 represent the field to spherical harmonic degree 85. Second, ambiguities arise in the calculation of F* that depend on the choice of the geographic equator vs. the magnetic equator. All of the values of F* in Figure 6 are based on the geographic equator, whereas the standard methods for calculating reversed flux on the CMB make use of the magnetic equator (Terra-Nova et al., 2015; Metman et al., 2018). The most obvious consequence of the choice of equator is the contribution to reversed flux from the tilt of the dipole axis. Dipole axis tilt contributes to the inventory of reversed flux when using the geographic equator, but it need not when using the magnetic equator. Third, the value of F* changes with time in the core field model, being generally smaller in the past, whereas the averaging of widely spaced snapshots removes most (or all) of the secular drift in F* from the numerical dynamos.
For these reasons, we show in Figure 7 comparisons between numerical dynamos, the COV-OBS core field model, and two other core field models, based on a modified reversed to normal flux ratio, . For the core field model COV-OBS, is just F* with the equatorial dipole terms removed. Removing the equatorial dipole represents the lowest order correction to the magnetic equator. from COV-OBS is shown at epochs 2014 and 1964, to illustrate the magnitude of the drift in this parameter with time. MLM in Figure 7 corresponds to the mean value of calculated by Metman et al. (2018) for epoch 2015 using their definition of magnetic equator on core field model COV-OBS.x1 (Gillet et al., 2015). TN in Figure 7 corresponds to the value of calculated by Terra-Nova et al. (2015) using their definition of magnetic equator on the present-day (zero age) limit of archeomagnetic field model CALSk.4b (Korte and Constable, 2011). For the numerical dynamos, in Figure 7 is F* with the equatorial dipole terms removed and with a crustal filter applied, such that the magnetic field amplitude decreases by a factor of e with each spherical harmonic degree above 14. We note that the effects of removing the equatorial dipole from the numerical dynamos and the modern core field models are comparable, because the r.m.s. dipole axis tilt of the numerical dynamos (10 degrees at Ra = 6 × 107 and 12 degrees at Ra = 6 × 107) are comparable to the time average dipole axis tilt in the historical geomagnetic field. Finally, we calculate for the dynamos and for field model COV-OBS using the same 1.5 x 1.5 degree grid.
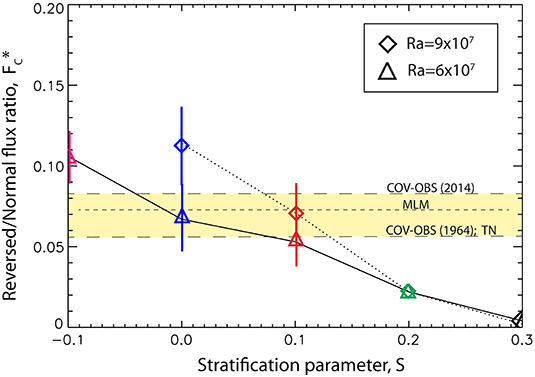
Figure 7. Modified ratios of reversed to normal flux contributions to the axial dipole vs. stratification parameter S from numerical dynamos (symbols), compared to from geomagnetic field models on the core-mantle boundary. Geomagnetic field values labeled COV-OBS, MLM, and TN are explained in the text. Symbol error bars denote one standard deviation of dynamo snapshots.
The effects of crustal filtering and correction to the magnetic equator are to reduce relative to F*, for the core field models as well as the numerical dynamos. Yet the same trends evident in Figure 6 are seen in Figure 7, with perhaps greater clarity. The numerical dynamos with S = 0.1 are compatible with all three core field models, in spite of the differences in processing that went into calculating reversed and normal flux in each case. There is some suggestion in Figure 7 that neutrally stratified dynamos with S = 0 may also be compatible, although this comparison is less convincing. And, just like Figure 6, this comparison argues against the more strongly stratified dynamos with S = 0.2 and greater. In short, Figures 6, 7 imply that strong thermal stratification below the CMB, characterized by S ≥ 0.2, as well as strongly superadiabatic conditions below the CMB characterized by S ≤ −0.1, are incompatible with the present-day structure of the geomagnetic field insofar as the amount of reversed flux is concerned, whereas on this same basis, the present-day field is compatible with weak stratification characterized by S = 0.1 or perhaps a bit less.
Disappearance of reversed flux with increasingly strong stratification is a direct consequence of the reduction in strength of the radial velocity below the outer boundary. Figure 8 shows vs. the CMB upwelling strength W* defined by (15). The CMB upwelling is given in dimensionless form, in units of η/D2. The color and symbol schemes in Figure 8 are the same as in Figure 6, and only the snapshot averaged values of W* are plotted because the variation between snapshots is no larger than the symbols. Figure 8 shows a strong, positive and approximately linear correlation between the dynamo reversed to normal flux ratio and CMB upwelling. CMB upwelling less than a few hundred hardly produces any reversed flux, whereas for CMB upwelling above W* ≃ 1700, reversed flux reduces the axial dipole by 10% or more. Figure 8 also shows the range in from the core field models in Figure 7. The best matching S = 0.1 and S = 0 dynamos intersect the dynamo trend at dimensionless CMB upwelling strengths of W* = 800–1500, with W* ≃ 1000 being a representative value.
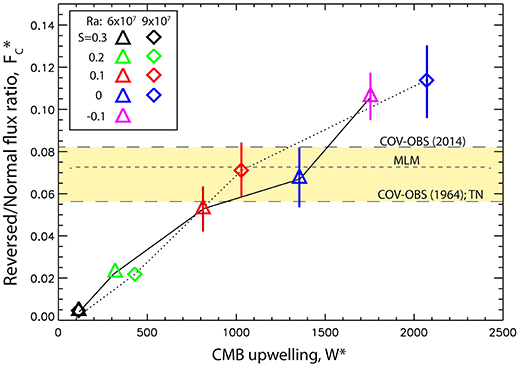
Figure 8. Modified ratios of reversed to normal flux contributions to the axial dipole vs. dimensionless r.m.s. upwelling W* below the core-mantle boundary from numerical dynamos (symbols), compared to the geomagnetic field models on the core-mantle boundary described in the text.
In addition to reversed flux in snapshots, the polar structure of the time average geomagnetic field is also sensitive to core stratification. Based on visual comparison of the time averages in Figures 4, 5, the S = 0.1 dynamo best replicates the polar field structure of COV-OBS geomagnetic field model. The high latitude structure of that dynamo in Figure 5 includes two partially isolated high field intensity patches enclosing a polar intensity minimum, much like the high latitude geomagnetic field structures in Figure 4. In contrast, the dynamos with S ≤ 0 in Figure 5 have ring-shaped high intensity field regions, while the dynamos with S ≥ 0.2 lack polar intensity minima or in the extreme case, have polar intensity maxima.
A quantitative test of this visual interpretation can be made using the cross correlation between a time average dynamo magnetic field and a 174 year geomagnetic field average. Figure 9 shows global cross correlations of time average Br cos(θ) between the Ra = 6 × 107 dynamos and the COV-OBS geomagnetic field model vs. longitude shift in degrees, with positive and negative denoting westward and eastward shifts, respectively, of the dynamo relative to the geomagnetic field model. It is helpful to include longitude pattern shifts in this analysis, since the longitudes of the high field intensity patches vary with the dynamo control parameters. Allowance for some longitude pattern shift mitigates the bias from this variation. The spectra of the time average dynamo fields on the outer boundary contain little power above spherical harmonic degree 14, so crustal filtering is not necessary here. The cross correlations were preconditioned for weak field suppression by masking boundary regions with field intensity below 20% of the maximum intensity, in order to add weight to the high field intensity regions. Figure 9 indicates there is some dependence of the correlation on longitude shift, but for shifts of 20o or less the effect is relatively minor. More significantly, there is a substantial difference in this correlation between unstratified and weakly stratified dynamos vs. the strongly stratified dynamos, with the former group correlating above 0.5 and the latter group below 0.5. Interestingly, the best correlation is found for the unstratified S = 0 dynamo and the second best is the S = −0.1 dynamo, although their correlations differ very little from the S = 0.1 dynamo overall.
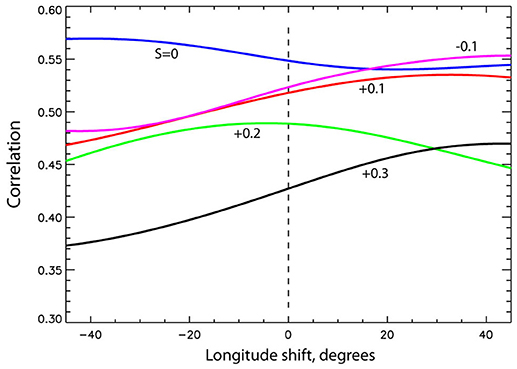
Figure 9. Br cos(θ) cross correlations of the 1840-2014 time average COV-OBS CMB geomagnetic field model vs. numerical dynamo time averages at Ra = 6 × 107, for various stratification parameters S.
6. Implications for Outer Core Stratification
Our comparisons between numerical dynamos and the geomagnetic field on the CMB favor the existence of outer core stratification with stratification parameter S close to 0.1. Equally significant, these same comparisons argue against stronger outer core stratification, as would be characterized by S ≥ 0.2, say. Although our study does not consider situations in which the stabilizing effects of stratification vastly outweigh the destabilizing effects of inner core growth, as would be the case for strong compositional stratification (Landeau et al., 2016; Nakagawa, 2017; Christensen, 2018), the fact that we can exclude thermally stratified dynamos with large S suggests our results might also be applicable for constraining outer core compositional stratification.
Assuming that S = 0.1 in the region below the CMB, our previously-derived dynamo scaling laws yield estimates of the thickness of the stratified layer and its gravitational stability. In dimensional terms, our scaling laws for stratified layer thickness (13) and squared buoyancy frequency (14) are, for the outer core
plus
and from the definition (7) of S, the subadiabatic heat flux on the CMB is
Using the core property values in Table 1 with S = 0.1, (16) gives δ ≃ 400 km, (18) gives 17 mW.m−2, and (17) gives N2 ≃ 1.7 × 10−8 rad2.s−2.
A 400 km layer may seem excessively thick for a thermal stratification, but it is important to note that this value refers to the full spherical mean thickness of the layer, from the CMB to the depth where the spherically averaged codensity profile has a local minimum. Furthermore, although our results favor S = 0.1 stratification, they are also marginally consistent with somewhat weaker stratification, S = 0.05 for example. In that case, the stratified layer would be substantially thinner, with δ ≃ 170 km.
In dynamical terms, such a layer would not prevent upward radial motions reaching close to the CMB, as evidenced by our finding that the r.m.s. CMB upwelling strength W* ≃ 1000. For the geodynamo, in dimensional units, , where the subscripts cmb and icb denote outer and inner core radii, respectively. In terms of the values of core properties in Table 1, this corresponds to W ≃ 0.5/century for the r.m.s upwelling below the CMB, within the range of the estimates of the r.m.s. CMB upwelling obtained from frozen flux inversions of the geomagnetic secular variation, which vary between 0.1/century and 4/century r.m.s. (Amit and Olson, 2006; Amit and Pais, 2013). Even with S = 0.1 stratification, superadiabatic thermal conditions may be present beneath approximately 5% of the CMB, according to the boundary heat flux pattern in Figure 1. If so, thermal instabilities originating at the CMB can penetrate the layer in these regions, making the thermal stratification somewhat permeable to outer core convection and allowing the formation of reversed flux spots as observed in the geomagnetic core field.
Permeable stratification distributed over several hundred kilometers beneath the CMB is consistent with other fluid dynamical effects, in particular, the upward penetration of convection through a weakly stratified layer (Takehiro and Lister, 2002; Rogers and Glatzmaier, 2005). Two scalings for the penetration distance have been proposed; because it is unclear which applies best to the core, we consider both. The first, by Takehiro and Lister (2002), predicts that convection penetrates a distance given by δp ~ 2Ωλ/N, where λ is the horizontal flow length scale. Using (17), we estimate 2Ω/N ~ 1 for thermal stratification in the Earth's core. This implies a weak stratification, where the effects of stable stratification below the CMB are only about as strong as Coriolis effects from rotation. With this stratification, the Takehiro and Lister (2002) scaling predicts that convective eddies wider than about 400 km will penetrate to the CMB. The second scaling is derived from numerical models of solar convection (Hurlburt et al., 1994; Rogers and Glatzmaier, 2005). These studies find that the penetration distance scales with the ratio of the unstable to the stable stratification, i.e., in our notation. This scaling also predicts that convective motions easily penetrate a 400 km layer with S = 0.1.
The Rayleigh number Ra, the Ekman number E and the magnetic Prandtl number Pm in our numerical dynamos are orders of magnitude away from Earth's core values. This raises a standard question for dynamo modelers: How sensitive are our conclusions to our parameter choices? Assuming reversed flux spots originate from toroidal flux expulsion (Gubbins, 2007), we expect the flux ratio at the CMB (either F* or ) to scale as the flux ratio measured in the underlying convective region modulated by the radial velocity in the stratified region relative to that in the convective region. For dipole-dominated dynamos, the relative strength of the dipole varies only marginally with Ra, E, and Pm (Aubert et al., 2009). We hypothesize that the flux ratios in the convective region are only weakly sensitive to these parameters. In addition, the radial velocity in the stratified region relative to that in the convective region depends only on the ratio of the stratified layer thickness δ to the penetration distance of the convection δp. Using the scalings discussed above for δp and relation (16), we infer that δ/δp, and therefore F* and depend only on S and possibly Ω/N. And, in contrast to Ra, E, and Pm, the values of Ω/N and S in our dynamos are in the range expected for thermal stratification at the top of Earth's core (Takehiro and Lister, 2002; Buffett et al., 2016). Provided these expectations are met, our conclusions about stratification are applicable to the core. This can be tested by extending our analysis to stratified dynamos with more realistic values of Ra, E, and Pm.
Author Contributions
PO and ML designed the study, did the analysis, and wrote the paper. ER managed the dynamo calculations and produced the dynamo data products.
Conflict of Interest Statement
ER, is currently employed by T-Mobile USA. At the time this research was done, ER was employed by the Johns Hopkins University, under the grant listed in the acknowledgments of our paper.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research was supported in part by Frontiers in Earth System Dynamics grant EAR-1135382 from the National Science Foundation. Additional support for ML came from the European Union's Horizon 2020 Research and Innovation Programme under the Marie Sklodowska-Curie grant agreement 703767. The dynamo calculations were made at the Maryland Advanced Research Computer Center (MARCC). We thank Nicolas Gillet for directing us to the COV-OBS geomagnetic field model. This paper benefited from thoughtful reviews by M. Metman, B. Sreenivasan, and editor H. Amit.
References
Amit, H. (2014). Can downwelling at the top of the Earth's core be detected in the geomagnetic secular variation? Phys. Earth Planet. Int. 229, 110–121. doi: 10.1016/j.pepi.2014.01.012
Amit, H., and Olson, P. (2006). Time-average and time-dependent parts of core flow. Phys. Earth Planet. Int. 155, 120–139. doi: 10.1016/j.pepi.2005.10.006
Amit, H., and Pais, M. A. (2013). Differences between tangential geostrophy and columnar flow. Geophys. J. Int. 194, 145–157. doi: 10.1093/gji/ggt077
Aubert, J., Labrosse, S., and Poitou, C. (2009). Modelling the palaeo-evolution of the geodynamo. Geophys. J. Int. 179, 1414–1428. doi: 10.1111/j.1365-246X.2009.04361.x
Brodholt, J., and Badro, J. (2017). Composition of the low seismic velocity E′ layer at the top of the core. Gephys. Res. Lett. 44, 8303–8310. doi: 10.1002/2017GL074261
Browning, M., Brun, A. S., Miesch, M., and Toomre, J. (2007). Dynamo action in simulations of penetrative solar convection with an imposed tachocline. Astrophys. J. 648, 157–160. doi: 10.1002/asna.200710849
Browning, M., Miesch, M., Brun, A. S., and Toomre, J. (2006). Dynamo action in the solar convection zone and tachocline: pumping and organization of toroidal fields. Astron. Nachr. 328, 1100–1103. doi: 10.1086/507869
Brummell, N., Tobias, S., and Cattaneo, F. (2010). Dynamo efficiency in compressible convective dynamos with and without penetration. Geophys. Astrophys. Fluid Dyn. 104, 565–576. doi: 10.1080/03091929.2010.495067
Buffett, B. (2014). Geomagnetic fluctuations reveal stable stratification at the top of the Earth's core. Nature 507, 484–487. doi: 10.1038/nature13122
Buffett, B., Knezek, N., and Holme, R. (2016). Evidence for MAC waves at the top of Earth's core and implications for variations in length of day. Geophys. J. Int. 204, 1789–1800. doi: 10.1093/gji/ggv552
Christensen, U. (2006). A deep dynamo generating mercury's magnetic field. Nature 444, 1056–1058. doi: 10.1038/nature05342
Christensen, U. (2018). Geodynamo models with a stable layer and heterogeneous heat flow at the top of the core. Geophys. J. Int. 215, 1338–1351. doi: 10.1093/gji/ggy352
Christensen, U., and Wicht, J. (2008). Models of magnetic field generation in partly stable planetary cores: applications to Mercury and Saturn. Icarus 196, 16–34. doi: 10.1016/j.icarus.2008.02.013
Couston, L.-A., Lecoanet, D., Favier, B., and Le Bars, M. (2018). Order out of chaos: slowly reversing mean flows emerge from turbulently generated internal waves. Phys. Rev. Lett. 120, 16–34. doi: 10.1103/PhysRevLett.120.244505
Dziewonski, A. M., and Anderson, D. L. (1981). Preliminary reference Earth model. Phys. Earth Planet. Int 25, 297–356.
Dziewonski, A. M., Lekic, V., and Romanowicz, B. A. (2010). Mantle anchor structure: an argument for bottom up tectonics. Earth Planet. Sci. Lett. 299, 69–79. doi: 10.1016/j.epsl.2010.08.013
Garnero, E. J., Helmberger, D. V., and Grand, S. P. (1993). Constraining outermost core velocity with SmKS waves. Geophys. Res. Lett. 20, 2463–2466.
Garnero, E. J., and McNamara, A. (2008). Structure and dynamics of Earth's lower mantle. Science 320, 626–628. doi: 10.1126/science.1148028
Gillet, N., Barrois, O., and Finlay, C. C. (2015). Stochastic forecasting of the geomagnetic field from the COV-OBS.x1 geomagnetic field model, and candidate models for IGRF-12. Earth Planets Space 76:71. doi: 10.1186/s40623-015-0225-z
Gillet, N., Jault, D., Finlay, C. C., and Olsen, N. (2013). Stochastic modeling of the Earth's magnetic field: inversion for covariances over the observatory era. Geochem. Geophys. Geosyst. 14, 766–786. doi: 10.1002/ggge.20041
Gomi, H., Ohta, K., Hirose, K., Labrosse, S., Caracas, R., Verstraete, M. J., et al. (2013). The high conductivity of iron and thermal evolution of the Earth's core. Phys. Earth Planet. Int. 224, 88–103. doi: 10.1016/j.pepi.2013.07.010
Gubbins, D. (2007). Geomagnetic constraints on stratification at the top of Earth's core. Earth Planet. Space 59, 661–664. doi: 10.1186/BF03352728
Gubbins, D., and Davies, C. (2013). The stratified layer at the core-mantle boundary caused by barodifusion of oxygen, sulfur and silicon. Phys. Earth Planet. Int. 215, 21–28. doi: 10.1016/j.pepi.2012.11.001
Helffrich, G., and Kaneshima, S. (2010). Outer-core compositional stratification from observed core wave speed profiles. Nature 468, 807–810. doi: 10.1038/nature09636
Helffrich, G., and Kaneshima, S. (2013). Causes and consequences of outer core stratification. Phys. Earth Planet. Int. 223, 2–7. doi: 10.1016/j.pepi.2013.07.005
Hirose, K., Labrosse, S., and Hernlund, J. (2013). Composition and state of the core. Annu. Rev. Earth Planet. Sci. 41, 657–691. doi: 10.1146/annurev-earth-050212-124007
Huguet, L., Amit, H., and Alboussiere, T. (2016). Magnetic to magnetic and kinetic to magnetic energy transfers at the top of the Earth's core. Geophys. J. Int. 207, 934–948. doi: 10.1093/gji/ggw317
Hurlburt, N., Toomre, J., Massaguer, J., and Zahn, P. (1994). Penetration below a convective zone. Astrophys. J. 421, 245–260. doi: 10.1086/173642
Irving, J. C. E., Cottarr, S., and Lekic, V. (2018). Seismically determined elastic parameters for Earth's outer core. Sci. Adv. 4:eaar2538. doi: 10.1126/sciadv.aar2538
Kaneshima, S. (2017). Array analyses of SmKS waves and the stratification of Earth's outermost core. Phys. Earth Planet. Int. 276, 234–246. doi: 10.1016/j.pepi.2017.03.006
Käpylä, P., Korpi, M., and Brandenburg, A. (2008). Large-scale dynamos in turbulent convection with shear. Astron. Astrophys. 491, 353–362. doi: 10.1051/0004-6361:200810307
Korte, M., and Constable, C. (2011). Improving geomagnetic field reconstructions for 0-3 ka. Phys. Earth Planet. Int. 188, 247–259. doi: 10.1016/j.pepi.2011.06.017
Landeau, M., Olson, P., Deguen, R., and Hirsh, B. (2016). Core merging and stratification after giant impacts. Nat. Geosci. 9, 786–789. doi: 10.1038/ngeo2808
Lay, T., and Young, C. (1990). The stably-stratified outermost core revisited. Geophys. Res. Lett. 17, 2001–2004.
Lesur, V., Whaler, K., and Wardinski, I. (2015). Are geomagnetic data consistent with stably stratified flow at the core-mantle boundary? Geophys. J. Int. 201, 929–946. doi: 10.1093/gji/ggv031
Manglik, A, Wicht, J., and Christensen, U. (2010). A dynamo model with double diffusive convection for Mercury's core. Earth Planet. Sci. Lett. 289, 619–628. doi: 10.1016/j.epsl.2009.12.007
Masada, Y., Yamada, K., and Kageyama, A. (2013). Effects of penetrative convection on solar dynamo. Astrophys. J. 778:16. doi: 10.1088/0004-637X/778/1/11.
Metman, M. C., Livermore, P. W., and Mound, J. E. (2018). The reversed and normal flux contributions to axial dipole decay for 1880-2015. Phys. Earth Planet. Int. 276, 106–117. doi: 10.1016/j.pepi.2017.06.007
Nakagawa, T. (2011). Effect of a stably stratified layer near the outer boundary in numerical simulations of a magnetohydrodynamic dynamo in a rotating spherical shell and its implications for Earth's core. Phys. Earth Planet. Int. 187, 342–352. doi: 10.1016/j.pepi.2011.06.001
Nakagawa, T. (2015). An implication for the origin of stratification below the core-mantle boundary region in numerical dynamo simulations in a rotating spherical shell. Phys. Earth Planet. Int. 247, 94–104. doi: 10.1016/j.pepi.2015.02.007
Nakagawa, T. (2017). On the thermo-chemical origin of the stratified region at the top of the Earth's core. Phys. Earth Planet. Int. 276, 172–181. doi: 10.1016/j.pepi.2017.05.011
Nakagawa, T., and Tackley, P. J. (2013). Implications of high core thermal conductivity on Earth's coupled mantle and core evolution. Geophys. Res. Lett. 40, 2652–2656. doi: 10.1002/grl.50574
Nakagawa, T., and Tackley, P. J. (2015). Influence of combined primordial layering and recycled MORB on the coupled thermal evolution of Earth's mantle and core. Geochem. Geophys. Geosyst. 15, 619–633. doi: 10.1002/2013GC005128
Ohta, K., Kuwayama, Y., Hirose, K., Shimizu, K., and Ohishi, Y. (2016). Experimental determination of the electrical resistivity of iron at earth's core conditions. Nature 534, 95–98. doi: 10.1038/nature17957
Olsen, N., Luhr, H., Finlay, C., Sabaka, T., Michaelis, I., Rauberg, J., et al. (2014). The chaos-4 geomagnetic feld model. Geophys. J. Int. 197, 815–827. doi: 10.1093/gji/ggu033
Olson, P., and Amit, H. (2006). Changes in Earth's dipole. Naturwissenschaften 93, 519–542. doi: 10.1007/s00114-006-0138-6
Olson, P., and Amit, H. (2015). Mantle superplumes induce geomagnetic superchrons. Front. Earth Sci. 3:38. doi: 10.3389/feart.2015.00038
Olson, P., Deguen, R., Rudolph, M. L., and Zhong, S. (2015). Core evolution driven by mantle global circulation. Phys. Earth Planet. Int. 243, 44–55. doi: 10.1016/j.pepi.2015.03.002
Olson, P., Landeau, M., and Reynolds, E. (2017). Dynamo tests for stratification below the core-mantle boundary. Phys. Earth Planet. Int. 271, 1–18. doi: 10.1016/j.pepi.2017.07.003
Perrillat, J.-P., Mezouar, M., Garbarino, G., and Bauchau, S. (2010). In situ viscometry of high-pressure melts in the Paris-Edinburgh cell: application to liquid FeS. High Pressure Res. 30, 415–423. doi: 10.1080/08957959.2010.494844
Poirier, J.-P. (2000). Introduction to the Physics of the Earth's Interior, 2nd Edn. Cambridge: Cambridge University Press.
Rogers, T., and Glatzmaier, G. (2005). Penetrative convection within the anelastic approximation. Astrophys. J. 620, 432–441. doi: 10.1086/423415
Sreenivasan, B., and Gubbins, D. (2008). Dynamos with weakly convecting outer layers: implications for core-mantle boundary interaction. Geophys. Astrophys. Fluid Dyn. 102, 395–407. doi: 10.1080/03091920801900047
Stanley, S. (2010). A dynamo model for axisymmetrizing Saturn's magnetic field. Geophys. Res. Lett. 37:L05201. doi: 10.1029/2009GL041752
Takehiro, S., and Lister, J. (2002). Surface zonal flows induced by thermal convection trapped below a stably stratified layer in a rapidly rotating spherical shell. Geophys. Res. Lett. 29:50. doi: 10.1029/2002GL015450
Tanaka, S. (2007). Possibility of a low p-wave velocity layer in the outermost core from global smks waveforms. Earth Planet. Sci. Lett. 259, 486–499. doi: 10.1016/j.epsl.2007.05.007
Tang, V., Zhao, L., and Hung, S. (2015). Seismological evidence for a non-monotonic velocity gradient in the topmost outer core. Sci. Rep. 5:8613. doi: 10.1038/srep08613
Terra-Nova, F., Amit, H., Hartmann, G. A., and Trindade, R. I. F. (2015). The time dependence of reversed archeomagnetic flux patches. J. Geophys. Res. Solid Earth 120, 691–704. doi: 10.1002/2014JB011742
Tobias, S., Cattaneo, F., and Brummell, N. (2008). Convective dynamos with penetration, rotation, and shear. Astrophys. J. 685, 596–605. doi: 10.1086/590422
Vocaldo, L., Alfe, D., Gillan, M. J., and Price, G. D. (2003). The properties of iron under core conditions from first principles calculations. Phys. Earth Planet. Int. 140, 101–125. doi: 10.1016/j.pepi.2003.08.001
Wicht, J. (2002). Inner-core conductivity in numerical dynamo simulations. Phys. Earth Planet. Inter. 132, 281–302. doi: 10.1016/S0031-9201(02)00078-X
Zhang, K., and Schubert, G. (2000). Teleconvection: remotely driven thermal convection in rotating stratified spherical layers. Science 290, 1944–1947. doi: 10.1126/science.290.5498.1944
Keywords: thermally stratified dynamos, outer core stratification, core-mantle boundary, core heat flux, geomagnetic field
Citation: Olson P, Landeau M and Reynolds E (2018) Outer Core Stratification From the High Latitude Structure of the Geomagnetic Field. Front. Earth Sci. 6:140. doi: 10.3389/feart.2018.00140
Received: 28 May 2018; Accepted: 05 September 2018; Published: 01 October 2018.
Edited by:
Hagay Amit, University of Nantes, FranceReviewed by:
Maurits Cornelis Metman, University of Leeds, United Kingdom Binod Sreenivasan, Indian Institute of Science, IndiaCopyright © 2018 Olson, Landeau and Reynolds. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Peter Olson, b2xzb25Aamh1LmVkdQ==
 Peter Olson
Peter Olson Maylis Landeau3,4
Maylis Landeau3,4