- Department of Planets and Comets, Max Planck Institute for Solar System Research, Göttingen, Germany
Many celestial objects are thought to host interfaces between convective and stable stratified interior regions. The interaction between both, e.g., the transfer of heat, mass, or angular momentum depends on whether and how flows penetrate into the stable layer. Powered from the unstable, convective regions, radial flows can pierce into the stable region depending on their inertia (overshooting). In rapidly rotating systems, the dynamics are strongly influenced by the Coriolis force and radial flows penetrate in stratified regions due to the geostrophic invariance of columnar convection even in the limit of vanishing inertia. Within this study, we numerically investigate both mechanisms and hence explore the nature of penetrative convection in rapidly rotating spherical shells. The study covers a broad range of system parameters, such as the strength of the stratification relative to the Coriolis force or the inertia. Guided by the application to Saturn, we model a sandwiched stable stratified layer (SSL) surrounded by two convective zones. A comprehensive analysis of the damping behavior of convective flows at the edges of the SSL showed that the mean penetration depth is controlled by the ratio of stratified and unstratified buoyancy gradients and is hence independent of rotation. A scaling law is derived and suggests that the penetration depth decreases with the square root of the ratio of unstabilizing and stabilizing entropy gradients. The influence of the Coriolis force, however, is evident by a modulation of the penetration depth along latitude, since convective columns are elongated vertically and hence pierce predominantly into the SSL around mid-latitudes and outside the tangent cylinder. Our result also show that the penetration depth decreases linearly with the flow length scale (low pass filter), confirming predictions from the linear theory of rotating partially stratified convection.
1. Introduction
When the local temperature gradient is steeper than the one associated with an adiabat, small perturbations from the hydrostatic equilibrium amplify to the well-known Rayleigh-Taylor convective instability. This leads to vigorous convection that very rapidly re-establishes bulk adiabatic gradients of density and temperature due to the inherent mixing and heat transport efficiency.
However, stable stratified regions, in which the heat flux is conductive or radiative, are widespread phenomena in stars and planets. Those regions are caused by either subadiabatic temperature or positive heavy element gradient. In stars, the large efficiency of radiative heat transport induces stratified regions, e.g., in the radiative part of the solar interior (e.g., Zahn, 1991; Brun et al., 2011). Stable stratification due to temperature inversion or subadiabatic temperature lapse rates are known for the Gas Giants (Jupiter Galileo probe, Atkinson et al., 1996) and outermost atmosphere of terrestrial planets, where radiation is most efficient. In the Earth's liquid outer core, the outermost layer seems stratified caused by either a subadiabatic temperature gradient or a local enrichment of light elements (Fearn and Loper, 1981; Lister and Buffett, 1998). Such a layer would have profound consequences for core convection and dynamo action in the core and be traceable in the geomagnetic field (Nakagawa, 2011; Buffett, 2014). A potential effect of electrically conducting, stable stratified layers surrounding a dynamo region are weak amplitude, strongly axisymmetric surface magnetic fields and are often proposed for Mercury's or Saturn's dynamo regions (Stevenson, 1982; Schubert et al., 1988; Christensen, 2006).
For Saturn a particular interesting scenario, consisting of a stratified layer between two convective ones is favored by the H/He demixing behavior (Stevenson and Salpeter, 1977; Püstow et al., 2016; Schöttler and Redmer, 2018) and in agreement with several observational constraints, such as the peculiarly axisymmetric magnetic field (e.g., Cao et al., 2012), the apparently impeded thermal evolution (Leconte and Chabrier, 2013; Nettelmann et al., 2013) and the detection of gravity wave induced pulsations in Saturn's rings (Hedman and Nicholson, 2013; Fuller, 2014). Saturn's interior might have been homogeneously mixed in the early, hot stages of the thermal evolution. Once the adiabatic temperature gradient crosses the demixing curve, He droplets form, sink downwards and are remixed at greater depth. This process builds up a compositional gradient roughly around mid-depth bridging from He-depleted outer to He-enriched inner convective zone (Stevenson and Salpeter, 1977; Schöttler and Redmer, 2018).
Radial, convective flows originating from the unstable regions might penetrate into the stratified region due to inertia or the geostrophy of the columnar convective structures. It is useful to distinguish qualitatively the different end-members scenarios in terms of the dominant forces. In rotating, partially stratified convection, the three main forces, each associated with a timescale, are the Coriolis force (τrot), the buoyancy of the rising fluid parcel (τbuo) and the inverse buoyancy due to the stratification (τstrat). The time scales are given by the rotation rate Ω, , the Brunt-Väisälä frequency N, and the time scale of buoyancy to accelerate fluid parcels , respectively. Here ρ′ is the density fluctuation of a buoyant fluid parcel, ρ the ambient density, D a typical length scale and g the local gravity. For our setup, τbuo characterizes the convective and τstrat the stratified regions. The ratio of the time scales can be expressed as the convective Rossby number Roc and the stratification parameter Is:
In slowly rotating systems, rotational forces are less important (Is < 1, Roc > 1) and a hot fluid parcel is accelerated by the buoyancy in the convective region, rises radially upwards and eventually pierces into the SSL, where the depth of penetration depends on the previously gained inertia. This represents the classical case of non-rotating penetrative convection, typically called overshooting or inertia penetration. For this end-member, the penetration depth should be independent of colatitude, and may be the dominant form of penetration close to the rotation axis for Roc < 1 and in the equatorial regions in our models.
In rapidly rotating systems, convective flows are strongly modified by the rotation (Roc < 1). The dominant Coriolis force constrains the flow to be invariant along the rotation axis leading to the well-known convective columns and strongly geostrophic zonal flows. This implies that the flows extend into the stratified layer independent of inertia, but with a characteristic colatitudinal modulation. When the Coriolis force is stronger than the gravity force associated with the stratification (i.e., Is > 1, Roc < 1), rotational penetration is strong and acts predominantly at mid-latitudes and outside the tangent cylinder (TC), where convective columns can vertically extend through the whole spherical shell. Since in the equatorial regions and close to the rotation axis no convective columns can be extended into the SSL, rotational penetration yields a characteristic colatitude dependence. If, on the other hand, Is < 1 and Roc < 1 the SSL should be devoid of radial flows since the stratification is strong enough to efficiently break the vertical stiffness of geostrophic flows.
A fundamental understanding of penetrative convection in rapidly rotating spherical shells is of ample importance in geo- and astrophysics. The efficiency or vigor of penetrative convection controls the transport of heat, mass, angular momentum, and magnetic fields across the interface between unstable and stable stratified regions. If the penetration is strong and the associated heat transport efficient, adiabatic regions are extended into the stratified layers (e.g., Browning et al., 2004). This means that stratified layers can be eroded by the permanent entrainment of convective flows and subsequent efficient mixing (e.g., Ellison and Turner, 1959; Levy and Fernando, 2002). Another complication arises from the combination of spherical geometry and rapid rotation. If rotational forces dominate over the inverse buoyancy associated with the stratification, piercing radial flows are non-uniform along colatitude leading to latitudinal entropy (density) gradients and hence drive baroclinic instabilities. Those in turn will act as a boundary condition for the differential rotation in the convective regions and potentially alter the magnetic field (Stevenson, 1982).
Classic studies of penetrative convection dealt with non-rotating cartesian setups of Rayleigh-Bénard convection (Veronis, 1963). The effect of rotation was firstly considered in the framework of oceanic dynamics (e.g., Julien et al., 1996). The investigation of rotating convection in spherical shells below or above a stable stratified layer was mainly driven by studies on the interaction and efficiency of radiative and/or convective heat transport in solar or stellar interiors (e.g., Zahn, 1991; Brummell et al., 2002; Rogers et al., 2006). For rapidly rotating A-type stars, where a convective core is surrounded by a radiative outer envelope, Browning et al. (2004) reported that rotational and overshooting penetrative convection generates adiabatic regions in the radiative zone preferentially at higher latitudes (prolate adiabatic core).
Several numerical investigations tuned to the solar setup with a convective envelope enclosing a deeper radiation dominated zone, investigate the parameter dependence of penetrative convection (Zahn, 1991; Hurlburt et al., 1994; Rogers et al., 2006). Since the stratification originates from enhanced radiative heat transport, it is typically assumed that penetration depth is largely characterized by two parameters, one being the Péclet number given by Pe = UD/κ, where U is a typical flow speed, D a length scale and κ the thermal diffusivity measuring the radiative heat transport (Zahn, 1991; Brummell et al., 2002). The other parameter, S is the ratio of sub- and superadiabaticity in the stable and unstable region (Hurlburt et al., 1994). However, different scaling relations between the penetration depth and S have been reported (Hurlburt et al., 1994; Brummell et al., 2002; Rogers et al., 2006). Interestingly, in models that take spherical geometry and rotation into account, the associated Coriolis forces appear unimportant for the magnitude of the penetration depth.
In the planetary context, the Galileo Probe revealed subadiabatic temperature gradients and non-ceasing zonal flows in Jupiter's outermost atmosphere down to roughly 20 bar of atmospheric pressure. This suggests that zonal flows are not damped, but rather maintained in stratified regions yet disconnected from their potential sources, such as convection or irradiation gradients. Assuming that the axisymmetric winds are driven from correlations of the deep convection (i.e., Reynolds stresses, Zhang and Schubert, 1996, 1997) showed that zonal mean flows are vertically extended by the Coriolis forces in accordance with the Taylor-Proudman theorem, but non-axisymmetric convective flows are damped by the inverse buoyancy gradients due to the stratification. From a more theoretical point of view, the linearized model of inviscid, inertia-less, rapidly rotating penetrative convection as studied by Takehiro and Lister (2001) shows a linear length scale dependence of penetration depth such that larger scale flows (like differential rotation) are less damped than short length scale flows typically associated with convective motions. The overall damping amplitude depends on the gravity force associated with the stable stratification relative to the Coriolis force (Is). Subsequent studies including nonlinear inertia showed a more complex damping behavior (Takehiro and Lister, 2002), but the results offered an attractive explanation how zonal flows are extended through stratified regions.
The major aim of the present study is to understand how overshoot and rotational penetration act across the interface between stratified and unstratified regions in rapidly rotating, spherical shell models, which are most suitable for interiors of planets. Even though the effects of stratification on differential rotation and magnetic fields as far as the emerging waves inside the SSL are left aside in this study, the investigation of fundamental properties of rapidly rotating, penetrative convection serves as a basis of upcoming research. Our models cover a comprehensive part of the parameter space, such that the different regimes appropriate for planets are reached in terms of Is and Roc. The general setup featuring a thin, sandwiched stratified layer centered at mid-depth and surrounded by two thick convective zones is motivated from the application to Saturn.
2. Model
The non-dimensional governing equations for conservation of mass, momentum and thermal energy for an ideal gas in the anelastic approximation are given by (Jones, 2011; Gastine and Wicht, 2012; Verhoeven et al., 2015; Wicht et al., 2018):
where p⋆ is the reduced pressure, Fν is the viscous force,
and Qν represents viscous heating given by
where σij is the stress tensor. The non-dimensional parameters are given by
These equations were formulated for an adiabatic background state. In our model, a prescribed non-adiabaticity of the background state powers or suppresses convection. The amplitude of these destabilizing and stabilizing entropy gradients must remain small relative to the adiabat to make sure the equations still hold. The non-adiabaticity of the new background state is thus scaled with ϵs ≪ 1,
where is the dimensionless analytically prescribed stratification profile and Γ the Grüneisenparameter which is in an ideal gas related to the polytropic index n and specific heats by
The background state is characterized by the relative deviation from an adiabat ϵs and the dissipation number Di, which sets the background density variation
where is the dimensional reference entropy gradient at the inner boundary. The background entropy gradient is prescribed analytically and sets convective (unstable stratified, ) and stable () regions. The -profile is given by
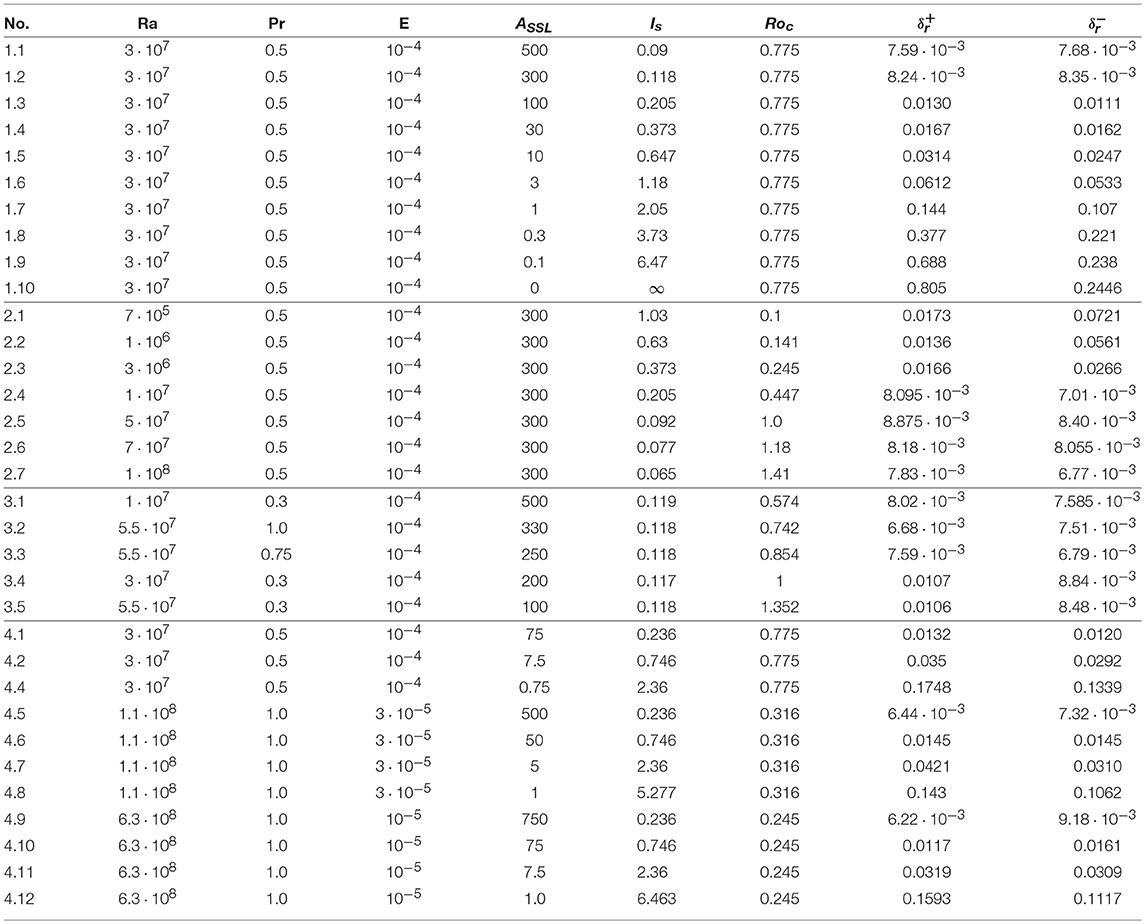
where ASSL is the amplitude of stable stratification (basically setting the BV frequency, see Equation 17), rlb and rub are lower and upper boundary of the SSL. The parameter ds defines the slope of the profile. When choosing the stratification amplitude, ϵsASSL ≪ 1 is required to be compliant with the treatment in the framework of the anelastic approximation, which is based on an adiabatic and steady background state. The gravity profile and Γ are fitted to an interior model of Saturn by Nettelmann et al. (2013) (see also Figure 1), where a polynomial of second order is used for the former:
with
Γ characterizes the nature of the ideal gas and is found by fitting p-T-curves from Nettelmann et al. (2013) with polytropic laws such that
yielding a best fitting Γ = 0.513 for the deep interior. The mean density contrast is set by Di = 3, corresponding to a top-to-bottom ratio of ρi/ρo ≈ 38. Then the temperature and density gradient are set by a chosen entropy gradient profile and Equation 9. Figure 1B) shows the so derived background state, indicating sub- and superadiabatic temperature gradients (middle panel, upper row). The black, dashed line corresponds to an isentropic () model for reference. Note, that the non-adiabaticity in the figure is strongly exaggerated using ϵs = 0.5 and ASSL = 1.0. For production runs, the relative deviation from an adiabatic background must remain small (ϵsASSL ≪ 1). To ensure that the newly defined background state is steady, the heat flux must be constant on every radius. Hence a thermal conductivity profile () is set such that
where Qo is the heat flux at the outer boundary. The profile of is shown in Figure 1B) bottom left plot.
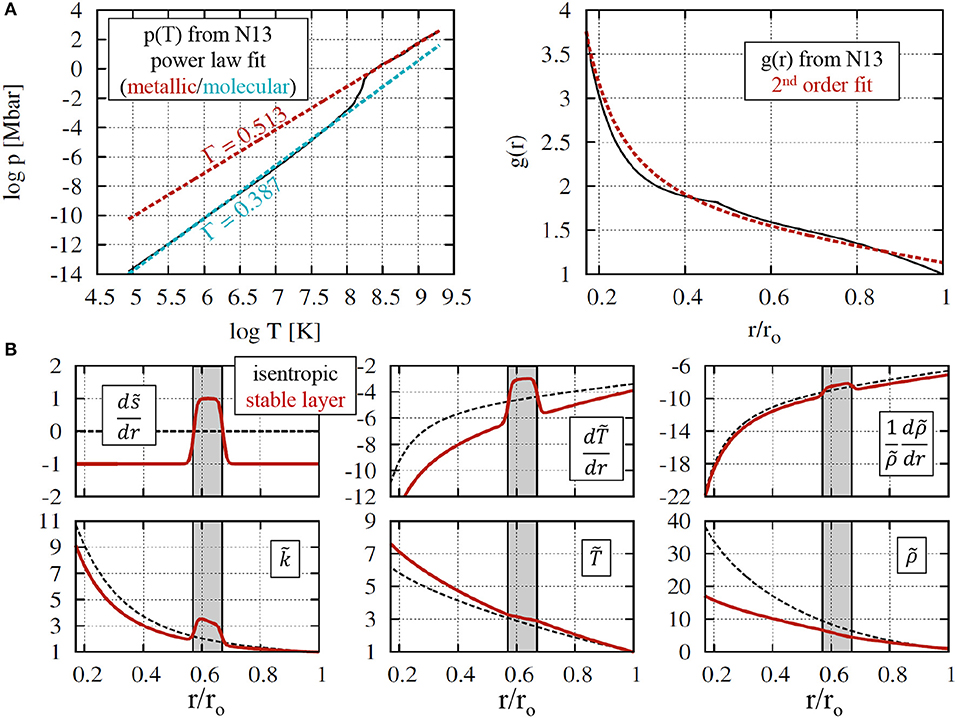
Figure 1. (A) power law (Γ) and 2nd order polynomial (gravity) fits to the interior state model from Nettelmann et al. (2013) (B) the non-adiabatic background state is characterized by a prescribed entropy gradient profile () setting the temperature, density and thermal conductivity. For visualization purposes the relative non-adiabaticity is strongly exaggerated (parameters ϵs = 0.5, ASSL = 1.0, Di = 3.0, Γ = 0.513).
The equations are non-dimensionalized by scaling length with the shell thickness d = ro−ri, time by the viscous diffusion time and entropy by . To avoid radius dependent control parameters, reference values for , , , are taken at the outer boundary. The convective Rossby number Roc, the non-dimensional Brunt-Väisälä frequency and the non-dimensional stratification parameter are
3. Numerical Results
Equations 3, 4 are solved numerically using MagIC 5.6 (Wicht, 2002; Gastine and Wicht, 2012; Schaeffer, 2013) which is modified such that the non-adiabatic background state relations (Equation 9) are integrated. The mechanical confinement yields impenetrable and free-slip conditions at both walls. The entropy boundary conditions are fixed-flux in accordance with the stratification profile (Equation 12), which sets unstable and stable regions. The stratified layer is located between rlb/ro = 0.57 and rub/ro = 0.67. The numerical grid resolution is Nr×Nϑ×Nϕ = 145 × 256 × 512 for E = 10−4, 193 × 320 × 640 at E = 3·10−5 and 241 × 320 × 640 at E = 10−5. The spectral resolution is limited to Nℓ = 2/3Nϑ. Fixed parameter values are the aspect ratio β = ri/ro = 0.17, , ds = 75, gravity according to Equation 13, Di = 3 and Γ = 0.513.
The other parameters, Ra, E, Pr, ASSL are varied to explore the parameter dependencies. Figure 2 provides an overview of Roc and Is for the four sets of models. In models from group 1 the stratification amplitude (hence Is) is varied and Roc kept fixed. Group 2 investigates the influence of more vigorous convection, where increasing Ra yields a decrease of Is, but an increase of Roc. For group 3, Is is kept constant, but with different combinations of Pr, Ra, and ASSL. Finally, group 4 investigates the Ekman number (E) dependence.
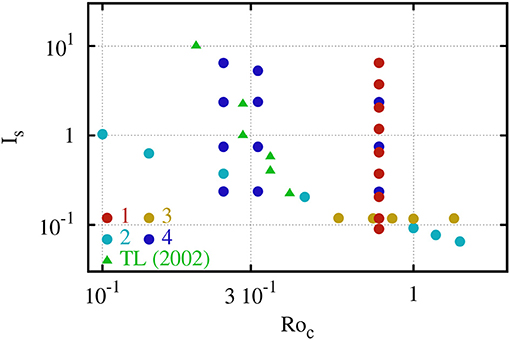
Figure 2. Regime diagram of the numerical models from Table 1 sorted by their respective convective Rossby (Roc) and the stratification relative to rotation rate (Is). The colors indicate simulations from different groups. The green triangles mark the cases used in Takehiro and Lister (2002).
The immediate effect of adding a stratified layer can be seen in the radial profiles of non-axisymmetric poloidal kinetic energy for models from group 1 displayed in Figure 3. For instance, the dark-red profile indicates that the non-axisymmetric poloidal kinetic energy is suppressed by up to four orders of magnitude relative to a model without stratification (gray). Along both edges of the SSL region (highlighted in gray), the kinetic energy drops sharply. The inverse buoyancy in the SSL also reduces the flow amplitude outside of the stable zone. This might be linked to the columnar structures of the convective flows since their vertical extension along the rotation axis is limited by an increasing stratification in the SSL. In addition an asymmetry between the lower and upper interface is clearly visible when the stratification is stronger, where for the upper one the radial flows seem to require more buoyancy to replenish after being reflected at the SSL underneath. This might be due to the fact, that the SSL itself acts as solid bottom wall hence providing a virtual tangent cylinder at rub/ro = 0.67.
Figure 3. Time averaged radial profiles of the non-axisymmetric poloidal energy for various stratification strength ASSL (Left) and horizontally averaged intensity of non-axisymmetric flow components vr, vϕ, vϑ for model 1.2 with ASSL = 300 (Right). The dashed lines denote the assumed exponential decay laws.
The inverse buoyancy force in stratified regions directly acts to damp radial flows, which are consequently diverged into horizontal directions. Hence, the effect of the SSL should be clearly visible in each of the non-axisymmetric flow components. For example is the time-averaged intensity of radial flows vr given by:
where the prime indicates non-axisymmetric flow. vϑ and vϕ are defined accordingly. Figure 3, right shows the radial profiles of vr, vϕ and vϑ for model 1.2 (red profile in panel a). It is obvious, that the poloidal energy is a rather good proxy of the radial flow intensity. Since the radial flows are mainly deflected into horizontal directions, vϕ and vϑ appear muss less damped inside the SSL. Those represent wave-like, horizontal flows with frequencies smaller than the rotation or Brunt-Väisälä frequency. The strong decay of vr allows to investigate the damping behavior. For guidance, the dashed lines in the figure represent exponential functions suggestive of exponential damping at the edges of the stratified regions. Their decay exponents are the penetration depths from Table 1. The actual determination of the penetration depth is more involved and discussed in section 3.2 and Figure 9.
Those models might be biased by the choice of a somewhat large Ekman number (too viscous). For a more detailed inspection, a model with smaller Roc hence stronger rotational constraints is favored (model 4.10). Figure 4 shows the instantaneous radial flow along a meridional cut (a) and in the equatorial plane (b). For this particular model, Is = 0.746 and Roc = 0.245. It is obvious that the stratification breaks the geostrophy of the convective columns and efficiently wipes out radial flows in the SSL. This shows that in the SSL the inverse buoyancy exceeds the Coriolis force (Is < 1). For both convective regions, the vertical length scale is clearly larger than the horizontal ones showing the effect of Roc < 1. Further, the convective structures outside the tangent cylinders given by ri/ro and rub/ro, respectively, are vertically more extended than the corresponding convective flows inside the TCs. Furthermore, Figure 4C) indicates that the zonal flow is connected through the SSL between the convective shells. At the outer boundary of the model domain representing the planetary surface, the equatorial region features a wide prograde jet reminiscent of Saturn's equatorial super-rotating jet.
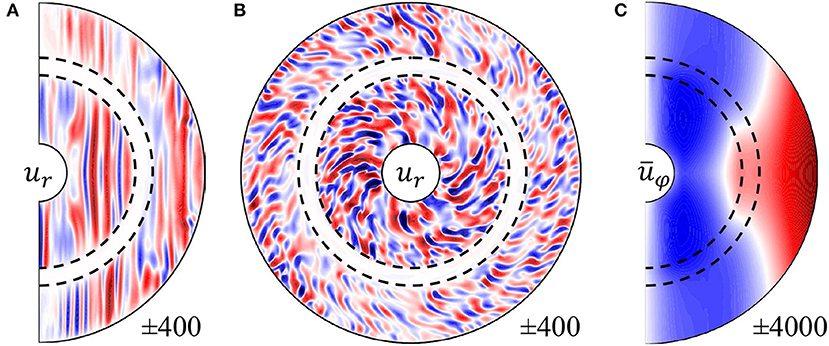
Figure 4. Instantaneous radial flow in a meridional slice (A) and in the equatorial plane (B) as far as the axisymmetric zonal flow averaged over time (C) for model 4.10 from Table 1.
3.1. Radial Flows in the Vicinity of Stratified Layers
The spherical surface projections (Figures 5A–I) reveal more details of the damping mechanisms. The nine maps represent several radial levels ranging from below the SSL (a), to the center r/ro = 0.62 (e), and on top of the SSL at r/ro = 0.695 (i). The typical columnar structures in the lower convective layer are apparent outside TC (a, b). As those are more rotationally constrained by the Coriolis force they can penetrate deeper into the stable layer than the spiraling structures at higher latitudes and though cause the radial flow peaks around ±60° colatitude (b, c). Deeper inside the SSL, in the equatorial regions, large length scale flows appear more dominant (c), even exceeding the remaining columnar patterns found in higher latitudes (d, e). The rms radial flow amplitude decreases drastically toward the center of the SSL, but at unequal rates for different colatitudes and different length scales. In the center of the SSL (Figure 5E) the flow is of weak amplitude and apparently dominated by the larger length scale. The amplitude has been decreased by a factor of 35, where the strongest remaining flows are concentrated in a broad belt around the equator. This is unlikely linked to rotational penetration as no columns can be vertically extended. For inertia penetration to be efficient, the flow must be energetic, what does not seem to be the case for those large scale and weak amplitude flows. Toward the outer edge of the SSL (f-g), the flow amplitudes keep increasing featuring columnar elongated structures outside and small-scale, spiraling convection patterns inside the effective tangent cylinder (h-i). The effective TC is now attached to the upper edge of the SSL at rub, hence the columnar flows are confined to a much smaller colatitude range.

Figure 5. Instantaneous radial flow on spherical surfaces taken at various radii indicated at the top left of each panel, ranging from r = 0.545 (A) over the center of the SSL at r = 0.62 (E) to r = 0.695 (I). The min/max velocity contour is indicated at the lower right. The velocity scale is the Reynolds-number. Parameters: model 4.10 from Table 1, Is = 0.746, Roc = 0.245.
This indicates that when columns touch on the stratified layer, they penetrate deeper, likely due to the rotational penetration or the Taylor-Proudman theorem. However, in the inner equatorial region and inside the inner TC, this effect is secondary. Even more so for the penetration at the outer boundary, where columns may only directly touch the stratified layer at a low-latitude band. As a result, the inertia penetration dominates, but is somewhat modified by latitudinal effects.
For a more detailed analysis of the apparent colatitudinal variation and the length scales dependencies, a FFT transforms from vr(r, ϑ) to , where ℓ is the spherical harmonic degree. For a few radii, this is shown as a function of either colatitude or spectral degree in Figure 6. The radial flow intensity drops slightly before reaching the lower SSL edge at rlb/ro = 0.57 (top left), though with weak modulation along colatitude ϑ. At the edge (blue line), the damping is strongest close to the rotation axis and around the equatorial region. In between rotational penetration somewhat reduces the damping of radial flows (profiles are closer to each other). This is the expected behavior, as the Coriolis forces act to extend convective columns into the stratified region predominantly at mid-latitudes outside TC. For the upper edge (top left), the region inside TC is larger and spans roughly the upper half of the colatitude domain. There the radial flows decrease strongly with colatitude toward the poles, but are rather constant outside TC. In general, the radial flows close the equator remain strongest in the center of the SSL.
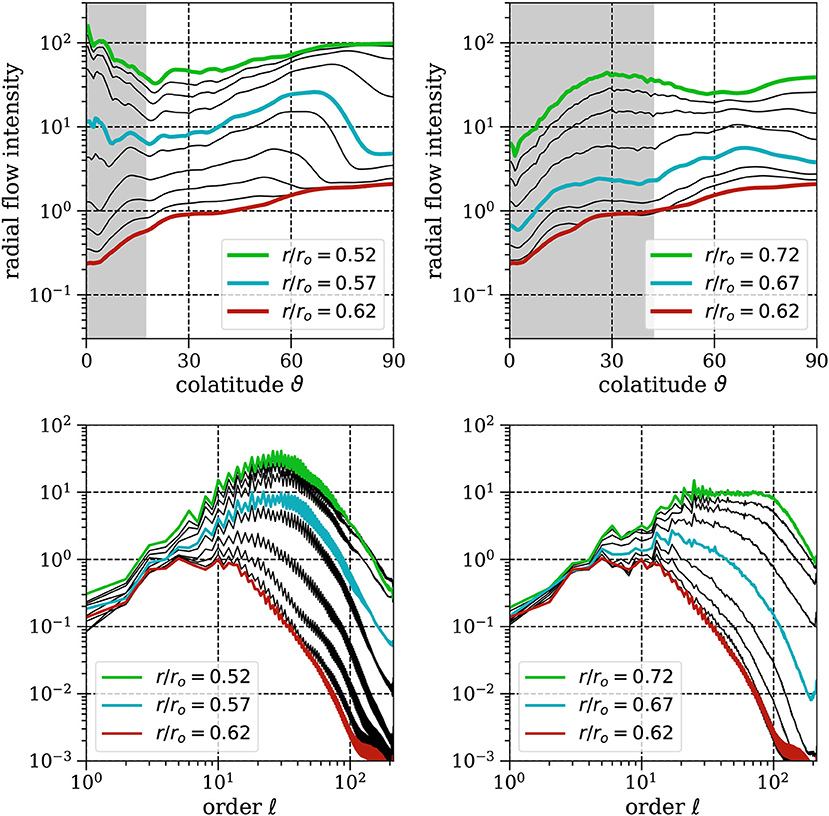
Figure 6. Time and azimuthally averaged intensity of radial flows at various depth around the edge of the SSL rlb = 0.57 (Left) and rub = 0.67 (Right). The upper plot show profiles along colatitude, the lower for spectral degree (length scale). The gray shaded areas mark colatitude bands inside the tangent cylinder set in the inner convective shell by sinϑTC = ri/rlb (top left) and in the outer convective shell by sinϑTC = rub/ro.
In the bottom plot of Figure 6, the radial flow per spectral degree ℓ is shown at the same depth levels used before. The broad peaks around ℓ = 10−50, indicate the mean convective horizontal length scales outside the SSL (green profiles). In this representation, it is obvious that small length scale flows are stronger suppressed by the inverse buoyancy gradients. Whereas, at the short length scale end of the spectrum at ℓ ≈ 100 the total drop exceeds two orders of magnitude, the large length scales are damped less than one order of magnitude. Especially for the intermediate length scales around ℓ ≈ 5−50 the suppression seems most efficient. Comparing the spectra outside the SSL (green profile, Figure 6) with those at the bottom of SSL (red) clarifies why the flows seen before in Figure 5E are so large scale. This behavior appears rather similar for both edges of the SSL (bottom left). The effects of viscosity are only visible at the largest length scales, where the spectra follow different slopes. At the largest length scales, the flow amplitudes are not damped at all, but rather maintained across the stable layer. This points toward an additional source of radial flows powered by the convergence and dissipation of horizontal flows, which manifest as gravito-inertial waves.
3.2. Penetration Depth
For a qualitative assessment we assume that the penetration depth of radial flows is a linear function of the radial flow intensity itself (Takehiro and Lister, 2001) and potentially varying along colatitude. This implies, that
where the penetration depth δ is defined by the e-fold decay scale height
Figure 3, right show that the radial profiles vr drops exponentially in the vicinity of the neutral buoyancy radii located at rlb/ro = 0.57 and rub/ro = 0.67, respectively. The penetration depth is calculated as a function of radius using Equation 20 while averaging over the colatitude ϑ
or as function of colatitude taken at the lower edge of the stratified region
Finally, we also investigate the length scale dependence in terms of the spherical harmonic degree ℓ as used in the linear theory study by Takehiro and Lister (2001):
where is the Fourier-transformed.
Figure 7 shows the colatitude dependence of δϑ for the nine cases (group 4 in Table 1). The reference model (no. 4.10) previously being subject of a detailed investigation, is placed left in the middle row. The other cases are set up such that Roc is constant for each column and Is for each row (both indicated at the top right). Inertia increases from left to right, the stratification strength relative to the rotation rate from top to bottom.
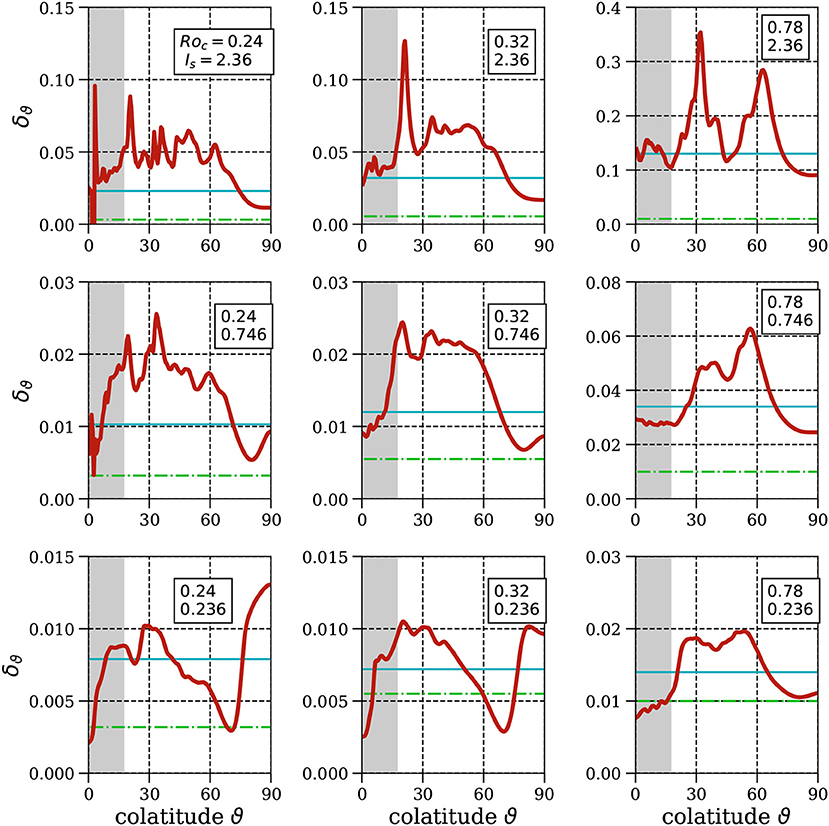
Figure 7. Penetration depth of radial flows as a function of colatitude for nine cases from Table 1, group 4 taken at the lower edge of the SSL r = rlb. The green line shows the thickness of an Ekman layer . The gray shaded areas mark colatitude bands inside the tangent cylinder set by sinϑTC = ri/rlb.
The overall penetration depth decreases with decreasing inertia (Roc) and increasing stratification (Is). For the top right model, the inertia is strong and the stratification weak (Roc = 0.78, Is = 2.36), such that the penetration depth exceeds significantly the thickness of the SSL (0.1ro). If Is is ten-fold decreased (bottom right) the penetration depth is reduced to a fraction of the SSL width and the radial flows are hence tiny deep inside the SSL. For the other columns, smaller Ekman numbers provide smaller Roc and consequently smaller penetration depth as the efficiency of overshooting convection is reduced. All models seem to share significant higher penetration depths at mid-latitudes. Inside the TC and in equatorial regions the penetration depth is typically smaller. However, the penetration depth is bounded by the viscosity (horizontal green lines, ) and apparently cannot be reduced far below this value. We conclude that the penetration depth at intermediate colatitudes of 30−60° can easily reach twice its mean value, indicated by the blue lines, what is most clearly seen in the bottom right panel. It was shown before that large scale flows remain most dominant in the equatorial regions. Those are obviously only weakly damped (Figure 6), bottom, yield larger penetration depth in the equatorial regions (Figure 7, left bottom) and might originate from collision of horizontal flows.
Takehiro and Lister (2001) concluded that the stable layer acted as a spectral filter with low pass nature, more precisely they predict that δℓ should decay like 1/|ℓ|. Figure 8 shows δℓ for the nine cases from group 4 (see Table 1, Figure 7). The blue horizontal lines denote the mean value listed in Table 1, the green one marks the thickness of the Ekman layer.
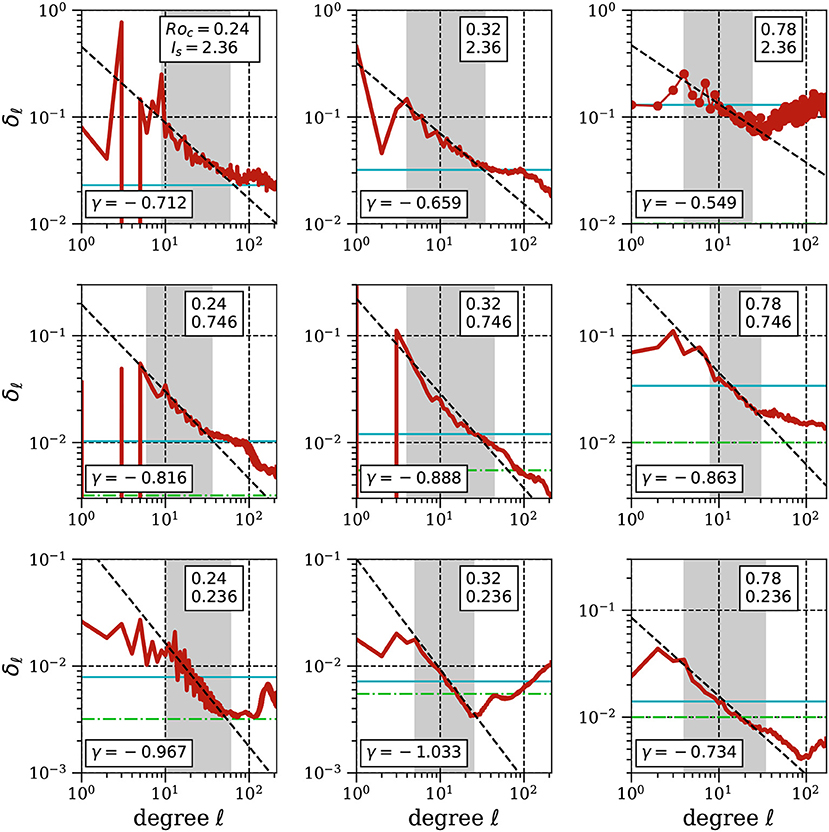
Figure 8. Penetration depth as a function of spectral degree ℓ for the nine case of group 4 in Table 1. The horizontal blue lines indicate the mean values. The green line shows the thickness of an Ekman layer . The black lines show power laws fitted over the gray-shaded length scale ranges resulting into a decay exponent γ added at the bottom of each figure.
It can be seen, that penetration depth clearly decays for smaller length scales even for cases with rather large inertia and weak stratification (top right). As shown for the case 4.10 in Figure 6, the largest (small ℓ) and smallest length scales (large ℓ) contain little kinetic energy and are excluded from the analysis. Therefore, power laws of the form
are fitted over an intermediate ℓ-range that is highlighted in gray. The resulting spectral decay exponent is added on the bottom of each panel. The slopes are all negative and spread amongst γ = [−0.55, −1.03], where models with weak inertia and strong stratification approach the (γ = −1)-scaling predicted by the linear theory of Takehiro and Lister (2001). Those models are most effectively controlled by rotational penetration and not overly biased by inertia. This indicates that the results of Takehiro and Lister (2001) can only be applied to an intermediate length scale range, for which the agreement is striking. The large ℓ part, which has been excluded from the fit, might be controlled by the viscosity and hence the penetration depth is not decreasing below the thickness of the Ekman layer. For the small ℓ part of the spectrum, the associated flows are controlled by other means, where the large scale patterns found in the equatorial regions (compare Figure 5E) or meridional circulation induced by the latitude-dependent penetration might play a role. Also other typical flows found in stratified regions, such as gravito-inertial waves could be taken into account. Those might then be the same features seen before in the equatorial regions (Figure 5E) deep inside the SSL around the equator. If applicable, the radial waves are then excited by dissipating or diverging the horizontal counterparts preferentially in the equatorial belt.
Finally, the dependence of the mean penetration depth on the model parameters (Ra, E, Pr and ASSL) is studied. The penetration depth at the lower and upper boundary of the SSL are indicated by and . Those are derived by taking the minimal value of δr in the vicinity (±0.01ro) of rlb and the maximal value of −δr near rub (see also Figure 9).
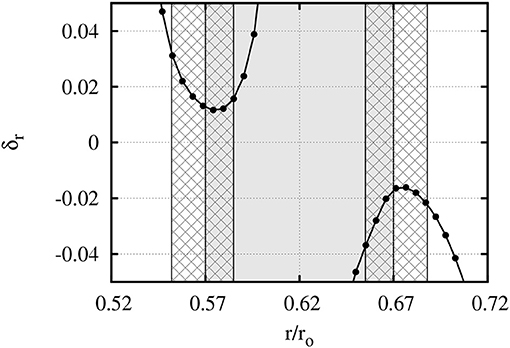
Figure 9. Mean penetration depth along radius for model 4.10. The gray shaded area marks the SSL; the hatched areas indicate the radius range in which the extrema of δr are taken.
Figure 10 shows and for all models from Table 1. It can be clearly seen, that δr decreases with increasing stratification and settles somewhat below δr = 0.01. This lower boundary is due to viscosity and hence depending on the Ekman number. For all studied Ekman numbers δr can be decreased to values approximatively the Ekman layer thickness () suggesting that our numerical setup is only limited by the viscosity. Models with δr larger than the width of SSL (0.1ro) are robustly constrained, as the mean radial flow intensity drops noticeable across the SSL, yet less than e-fold. As shown by the dark-blue profile in the left panel of Figure 3, even models with neutral buoyancy gradient (ASSL = 0) in the SSL create a strong dimple in the poloidal energy. Apparently and are nearly identical, suggesting that there is no major dynamic difference between a scenario where the stable region is on top of the convective one and the opposite situation. As the Coriolis force clearly dominates the flows in convective regions (Roc < 1), it appears reasonable to expect that Is = τstrat/τrot is the appropriate force ratio to estimate the penetration depth (Figure 10, left). However, this does not seem to hold for all Ekman numbers. The right hand plot of Figure 10 shows an alternative scaling attempt relative to IsRoc = τstrat/τbuo, i.e., the rotational time scale is replaced with the inertia time scale. This indicates that the penetration depth δr is independent of rotation and depends, as in a non-rotating system, only on the ratio of inertia and stratification. Further, a power law fit of the form
results in a = 0.121±0.008 and b = 0.989±0.1162 and hence suggesting a linear dependence. For the least-squares fitting procedure only data points were considered for which IsRoc>0.1, since they are not biased by viscosity (thick black, dot-dashed line in Figure 10, right).
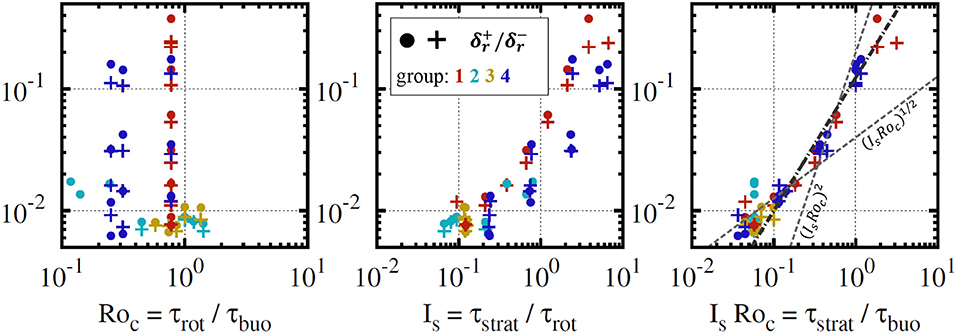
Figure 10. Mean penetration depth at the lower edge (, filled circles) and upper edge (, plus markers) as a function of time scale ratios. Plotted are models from Table 1, colors indicate various groups. For the right hand plot a power law is fitted to the data for IsRoc>0.1 (thick black, dot-dashed line), showing the almost linear dependence of δr∝IsRoc. The thin gray power laws indicate previously published scaling suggestions. For details, see text.
Previous studies targeted to the radiative-convective boundary in the Sun, such as (Hurlburt et al., 1994; Brummell et al., 2002; Rogers et al., 2006) controlled the degree of stratification by reducing or increasing the local polytropic index ni below or above the adiabatic one na. Using the polytropic relations (e.g., , where ξ is a function of r), the deviation from the adiabat can be expressed by logarithmic density gradients and polytropic indices
where index a refers to the adiabat. Consequently, the stratification measure S defines the ratio of subadiabatic (positive) to superadiabatic (negative) entropy gradients and is compatible with our stratification amplitude S ≈ ASSL. Whereas, the numerical models in the previous study cover stratifications between S = 1 and S = 30, our parameter space with respect to ASSL spans from 0 to 750 (see Table 1). Further the scaling above suggested that
Hence, our results show that the penetration depth increases with the square root of the ratio of positive and negative entropy gradients. Firstly reported by (Hurlburt et al., 1994), comparable models found different scaling exponents, which changed as a function of S. Typically for small S the penetration depth scales with , but for larger S with a significantly shallower S−1/4 (Hurlburt et al., 1994). Other studies only found the weak scaling throughout the studied S-range (Brummell et al., 2002; Rogers et al., 2006). For guidance, both scaling laws are drawn into Figure 10, right, thin gray dashed lines. Indeed those predictions seem to approximate the data in local sub-regions of the parameter space. However, the general trend appears much better reproduced by a single scaling law with an exponent of roughly S−1/2.
4. Summary and Discussion
We have performed an extensive numerical modeling campaign of rapidly rotating convection in a spherical shell that exhibits a sandwiched stable stratified layer between two convective zones. Such a system is most suitable for Saturn, where the H/He demixing generates a compositional gradient around mid-depth and though suppresses thermal convection locally. Our numerical models cover a large fraction of the appropriate parameter space, e.g., in the terms of the stratification relative to rotational forces 2Ω/N, where N is the Brunt-Väisälä frequency or relative to the inertia characterized by Roc (see also Table 1).
Stratification acts directly to suppress radial flows, but radial flows can pierce across the interface by different mechanisms. The classic overshooting penetration depends on the inertia a fluid parcel has gained from buoyancy instabilities. Furthermore, rapid rotation and the spherical geometry allows convective columns to be vertically extended into the stratified regions in accordance with the Taylor-Proudman theorem. We investigate and distinguish the potential effects of both penetration mechanisms by altering the leading order force balances. Our results indicate that the mean penetration depth depends linearly on the square root of the ratio of destabilizing and stabilizing entropy gradients (). This builds on the rather diverse results derived in the solar context (Zahn, 1991; Hurlburt et al., 1994; Brummell et al., 2002; Rogers et al., 2006), where different scaling exponents with stronger scaling for weaker stratification were reported. The exponents in those studies range from −1/4 to −1, but the robust −1/2-scaling suggested in the present study reproduces the results convincingly. In addition, and in contrast to the expectations from Takehiro and Lister (2001), the magnitude of the penetration depth appears largely unaffected by the rotation.
The Coriolis force, however, adds a characteristic latitudinal modulation of the penetration depth amplifying to ±(40−50)% of the mean value, where the strongest penetration resides at mid-latitudes (outside TC). This clearly reflects the action of columnar structures vertically extended by the Coriolis force and hence represents rotational penetration. Therefore, latitudinal density gradients are expected to build up at the edges of stratified regions. Such gradients are known to drive baroclinic instabilities, e.g., thermal winds.
Alongside original studies using linear waves, such as Takehiro and Lister (2001), a spectral (length scale) dependence of the penetration depth is expected and this is indeed found in our strongly non-linear simulations. The decay exponent γ approaches unity, what confirms the expected value from linear theory (Takehiro and Lister, 2001). The SSL though clearly shows the quality of a low pass filter. Consequently, radial flow in the SSL, even though weak in amplitude, must be expected to be of larger length scale than the convective flows pummeling into the SSL. However, the striking agreement with the theoretical predictions is limited to an intermediate length scale range.
As a peculiar result, we have identified wave-like radial flows that seem to somewhat resist the inverse buoyancy forces in the stratified layer. Those are non-geostrophic, of large length scale, weak in amplitude, and predominantly driven in the equatorial regions of the stratified layer. We showed that the required additional source of radial flow is likely not due to the length scale filtering effect of the rotational penetration or due to inertia penetration, but is potentially powered from the convergence of horizontal flows in the shape of gravito-inertial waves.
Finally, we have shown that viscous effects only play a role for very shallow penetration depth and at the smallest length scales. The overall results should not depend on the fact that we have only explored an Ekman number rage limited by the numerical constraints. More important is the spherical geometry. We speculate that a thin stable stratified layer will be significantly penetrated by Coriolis force induced columnar flows vertically extending into the SSL and hence more closely obey the linear theory by Takehiro and Lister (2001).
As an outlook for future work, a thorough investigation of the gravito-inertial waves generated in the SSL, the emergence of thermal winds due to latitude-dependent penetrative convection and consequently how differential rotation is paused through stratified zones. In addition, the effect on a dynamo process originating from underneath will help to understand the dynamics and magnetic fields of partly stratified rapidly rotating convection, which is most suitable for the planetary atmospheres and interiors.
Author Contributions
WD designed and carried out the numerical experiments, analyzed the data, and wrote the paper manuscript. JW provided physical insights, fluid dynamics expertise, and significantly contributed to the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors would like to thank the reviewers for their valuable comments and suggestions to improve the manuscript. This work was supported by the Deutsche Forschungsgemeinschaft (DFG) in the framework of the priority programs SPP 1488 “Planetary Magnetism” and SPP 1992 “Diversity of Exoplanets”. MagIC is available at an online repository (https://github.com/magic-sph/magic).
References
Atkinson, D. H., Pollack, J. B., and Seiff, A. (1996). Galileo doppler measurements of the deep zonal winds at jupiter. Science 272, 842–843. doi: 10.1126/science.272.5263.842
Browning, M. K., Brun, A. S., and Toomre, J. (2004). Simulations of core convection in rotating A-Type stars: differential rotation and overshooting. Astrophys. J. 601, 512–529. doi: 10.1086/380198
Brummell, N. H., Clune, T. L., and Toomre, J. (2002). Penetration and Overshooting in Turbulent Compressible Convection. Astrophys. J. 570, 825–854. doi: 10.1086/339626
Brun, A. S., Miesch, M. S., and Toomre, J. (2011). Modeling the dynamical coupling of solar convection with the radiative interior. Astrophys. J. 742:79. doi: 10.1088/0004-637X/742/2/79
Buffett, B. (2014). Geomagnetic fluctuations reveal stable stratification at the top of the Earth's core. Nature 507, 484–487. doi: 10.1038/nature13122
Cao, H., Russell, C. T., Wicht, J., Christensen, U. R., and Dougherty, M. K. (2012). Saturn's high degree magnetic moments: evidence for a unique planetary dynamo. Icarus 221, 388–394. doi: 10.1016/j.icarus.2012.08.007
Christensen, U. R. (2006). A deep dynamo generating Mercury's magnetic field. Nature 444, 1056–1058. doi: 10.1038/nature05342
Ellison, T. H., and Turner, J. S. (1959). Turbulent entrainment in stratified flows. J. Fluid Mech. 6, 423–448. doi: 10.1017/S0022112059000738
Fearn, D. R., and Loper, D. E. (1981). Compositional convection and stratification of earth's core. Nature 289:393. doi: 10.1038/289393a0
Fuller, J. (2014). Saturn ring seismology: evidence for stable stratification in the deep interior of Saturn. Icarus 242, 283–296. doi: 10.1016/j.icarus.2014.08.006
Gastine, T., and Wicht, J. (2012). Effects of compressibility on driving zonal flow in gas giants. Icarus 219, 428–442. doi: 10.1016/j.icarus.2012.03.018
Hedman, M. M., and Nicholson, P. D. (2013). Kronoseismology: using density waves in Saturn's C ring to probe the planet's interior. Astron. J. 146:12. doi: 10.1088/0004-6256/146/1/12
Hurlburt, N. E., Toomre, J., Massaguer, J. M., and Zahn, J.-P. (1994). Penetration below a convective zone. Astrophys. J. 421, 245–260. doi: 10.1086/173642
Jones, C. A. (2011). Planetary magnetic fields and fluid dynamos. Ann. Rev. Fluid Mech. 43, 583–614. doi: 10.1146/annurev-fluid-122109-160727
Julien, K., Legg, S., McWilliams, J., and Werne, J. (1996). Penetrative convection in rapidly rotating flows: preliminary results from numerical simulation. Dynam. Atmos. Oceans 24, 237–249. doi: 10.1016/0377-0265(95)00449-1
Leconte, J., and Chabrier, G. (2013). Layered convection as the origin of Saturn's luminosity anomaly. Nat. Geosci. 6, 347–350. doi: 10.1038/ngeo1791
Levy, M. A., and Fernando, H. J. S. (2002). Turbulent thermal convection in a rotating stratified fluid. J. Fluid Mech. 467, 19–40. doi: 10.1017/S0022112002001350
Lister, J. R., and Buffett, B. A. (1998). Stratification of the outer core at the core-mantle boundary. Phys. Earth Planet. Inter. 105, 5–19. doi: 10.1016/S0031-9201(97)00082-4
Nakagawa, T. (2011). Effect of a stably stratified layer near the outer boundary in numerical simulations of a magnetohydrodynamic dynamo in a rotating spherical shell and its implications for Earth's core. Phys. Earth Planet. Inter. 187, 342–352. doi: 10.1016/j.pepi.2011.06.001
Nettelmann, N., Püstow, R., and Redmer, R. (2013). Saturn layered structure and homogeneous evolution models with different EOSs. Icarus 225, 548–557. doi: 10.1016/j.icarus.2013.04.018
Püstow, R., Nettelmann, N., Lorenzen, W., and Redmer, R. (2016). H/He demixing and the cooling behavior of Saturn. Icarus 267, 323–333. doi: 10.1016/j.icarus.2015.12.009
Rogers, T. M., Glatzmaier, G. A., and Jones, C. A. (2006). Numerical simulations of penetration and overshoot in the sun. Astrophys. J. 653, 765–773. doi: 10.1086/508482
Schaeffer, N. (2013). Efficient spherical harmonic transforms aimed at pseudospectral numerical simulations. Geochem. Geophys. Geosys. 14, 751–758. doi: 10.1002/ggge.20071
Schöttler, M., and Redmer, R. (2018). Ab initio calculation of the miscibility diagram for hydrogen-helium mixtures. Phys. Rev. Lett. 120:115703. doi: 10.1103/PhysRevLett.120.115703
Schubert, G., Ross, M. N., Stevenson, D. J., and Spohn, T. (1988). Mercury's Thermal History and the Generation of its Magnetic Field. Tucson, AZ: University of Arizona Press.
Stevenson, D. J. (1982). Reducing the non-axisymmetry of a planetary dynamo and an application to Saturn. Geophys. Astrophys. Fluid Dyn. 21, 113–127. doi: 10.1080/03091928208209008
Stevenson, D. J., and Salpeter, E. E. (1977). The dynamics and helium distribution in hydrogen-helium fluid planets. Astrophys. J. 35, 239–261. doi: 10.1086/190479
Takehiro, S., and Lister, J. R. (2002). Surface zonal flows induced by thermal convection trapped below a stably stratified layer in a rapidly rotating spherical shell. Geophys. Res. Lett. 29:1803. doi: 10.1029/2002GL015450
Takehiro, S.-I., and Lister, J. R. (2001). Penetration of columnar convection into an outer stably stratified layer in rapidly rotating spherical fluid shells. Earth Planet. Sci. Lett. 187, 357–366. doi: 10.1016/S0012-821X(01)00283-7
Verhoeven, J., Wiesehöfer, T., and Stellmach, S. (2015). Anelastic versus fully compressible turbulent Rayleigh-Bénard convection. Astrophys. J. 805:62. doi: 10.1088/0004-637X/805/1/62
Wicht, J. (2002). Inner-core conductivity in numerical dynamo simulations. Pepi 132, 281–302. doi: 10.1016/S0031-9201(02)00078-X
Wicht, J., French, M., Stellmach, S., Nettelmann, N., Gastine, T., Duarte, L., et al. (2018). “Modeling the interior dynamics of gas planets,” in Magnetic Fields in the Solar System Vol 448, Astrophysics and Space Science Library, eds H. Lühr, J. Wicht, S. A. Gilder, and M. Holschneider (Cham: Springer), 7–81.
Zhang, K., and Schubert, G. (1996). Penetrative convection and zonal flow on jupiter. Science 273, 941–943. doi: 10.1126/science.273.5277.941
Keywords: stable stratification, rapidly rotating spherical shells, penetrative convection, numerical simulation, scaling laws
Citation: Dietrich W and Wicht J (2018) Penetrative Convection in Partly Stratified Rapidly Rotating Spherical Shells. Front. Earth Sci. 6:189. doi: 10.3389/feart.2018.00189
Received: 18 July 2018; Accepted: 16 October 2018;
Published: 08 November 2018.
Edited by:
Renaud Deguen, Claude Bernard University Lyon 1, FranceReviewed by:
Moritz Heimpel, University of Alberta, CanadaDaniel Lecoanet, Princeton University, United States
Copyright © 2018 Dietrich and Wicht. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wieland Dietrich, ZGlldHJpY2h3QG1wcy5tcGcuZGU=
 Wieland Dietrich
Wieland Dietrich Johannes Wicht
Johannes Wicht