- 1Department of Geography and Sustainable Development, University of St Andrews, St Andrews, United Kingdom
- 2Department of Geography, University of Sheffield, Sheffield, United Kingdom
- 3School of Geosciences, University of Edinburgh, Edinburgh, United Kingdom
Coupling between runoff, hydrology, basal motion, and mass loss (“hydrology-dynamics”) is a critical component of the Greenland Ice Sheet system. Despite considerable research effort, the mechanisms by which runoff influences ice dynamics and the net long-term (decadal and longer) dynamical effect of variations in the timing and magnitude of runoff delivery to the bed remain a subject of debate. We synthesise key research into land-terminating ice sheet hydrology-dynamics, in order to reconcile several apparent contradictions that have recently arisen as understanding of the topic has developed. We suggest that meltwater interaction with subglacial channels, cavities, and deforming subglacial sediment modulates ice flow variability. Increasing surface runoff supply to the bed induces cavity expansion and sediment deformation, leading to early-melt season ice flow acceleration. In the ablation area, drainage of water at times of low runoff from high-pressure subglacial environments toward more efficient drainage pathways is thought to result in reductions in water pressure, ice-bed separation and sediment deformation, causing net slow-down on annual to decadal time-scales (ice flow self-regulation), despite increasing surface melt. Further inland, thicker ice, small surface gradients and reduced runoff suppress efficient drainage development, and a small net increase in both summer and winter ice flow is observed. Predicting ice motion across land-terminating sectors of the ice sheet over the twenty-first century is confounded by inadequate understanding of the processes and feedbacks between runoff and subglacial motion. However, if runoff supply increases, we suggest that ice flow in marginal regions will continue to decrease on annual and longer timescales, principally due to (i) increasing drainage system efficiency in marginal areas, (ii) progressive depression of basal water pressure, and (iii) thinning-induced lowering of driving stresses. At higher elevations, we suggest that minor year-on-year ice flow acceleration will continue and extend further into the interior where self-regulation mechanisms cannot operate and if surface-to-bed meltwater connections form. Based on current understanding, we expect that ice flow deceleration due to the seasonal development of efficient drainage beneath the land-terminating margins of the Greenland Ice Sheet will continue to regulate its future mass loss.
Introduction
Future variations in the dynamics and mass balance of the Greenland Ice Sheet will influence rates of sea level rise, ocean circulation and climate (Cazenave and Llovel, 2010; Rignot et al., 2011; Gillet-Chaulet et al., 2012; Bamber and Aspinall, 2013; Nick et al., 2013). Recent observations have revealed that runoff-induced ice flow variations can occur over timescales as short as hours (e.g., Zwally et al., 2002; Das et al., 2008; Shepherd et al., 2009; Doyle et al., 2014), can be of high magnitude (daily mean flow of up to 400% above mean winter values; e.g., van de Wal et al., 2008) and effect an extensive area of the ice sheet (e.g., Joughin et al., 2008; Palmer et al., 2011; Fitzpatrick et al., 2013). Marginal ice flow acceleration induces drawdown of inland ice (termed “dynamic thinning”; Krabill et al., 2004; Pritchard et al., 2009), exposing more ice to higher atmospheric temperatures and ablation rates, thus increasing runoff, thereby creating a potential positive feedback.
However, the net effect of future increases in surface runoff production on ice flow is uncertain. A wealth of observations from a land-terminating sector of western Greenland (Figure 1) have demonstrated that runoff input to the bed increases ice flow early in the melt season (e.g., Zwally et al., 2002; Joughin et al., 2008), but that a commensurate decrease in ice flow as melt water supply declines may offset this speed-up throughout the ablation area (e.g., Sole et al., 2013; van de Wal et al., 2015; Stevens et al., 2016) but not further inland (e.g., Phillips et al., 2013; Sole et al., 2013; Doyle et al., 2014). Over the last three decades, this seasonal pattern has been superimposed on a decline in annual ice velocity in the ablation area (van de Wal et al., 2008, 2015; Tedstone et al., 2015). The mechanisms by which variations in runoff supply produce these velocity fluctuations have recently been the subject of considerable debate (e.g., Phillips et al., 2013; Bougamont et al., 2014; Tedstone et al., 2015; Hoffman et al., 2016; Christoffersen et al., 2018). Seemingly conflicting lines of evidence have indicated different mechanisms, with contrasting implications for the future stability of the ice sheet in a changing climate (e.g., Shannon et al., 2013; Koziol and Arnold, 2018). This uncertainty hinders our ability to accurately predict the future dynamic behaviour of land-terminating sectors of the ice sheet. Therefore, we believe that a thorough review of this research area is timely.
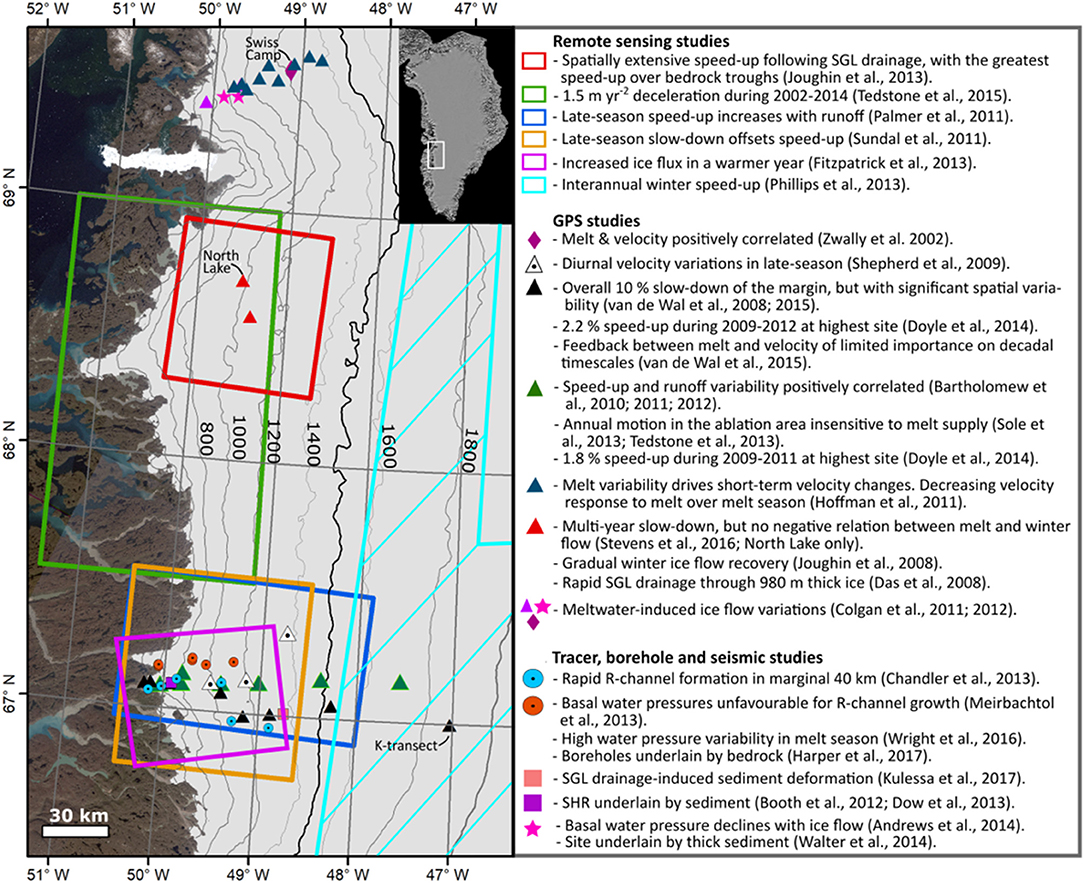
Figure 1. Overview of key observations. Coloured boxes delimit the approximate study area of corresponding text. Also shown are: Swiss Camp (lilac diamond, data presented in Zwally et al., 2002); FOXX and GULL GPS and borehole sites (pink stars, Andrews et al., 2014); K-transect sites (black triangles); Leverett GPS sites (dark green triangles); Russell GPS sites (white dotted triangles, Shepherd et al., 2009); Lake F (pale pink square); moulins used for gas tracer injection (blue dotted circles, Chandler et al., 2013); boreholes presented in Wright et al. (2016) (orange dotted circles). Contours (200 m intervals) are from the GIMP DEM (Howat et al., 2014), overlaid on a true colour composite Landsat 7 image mosaic (Howat et al., 2014). Inset is a MEaSUREs MODIS mosaic (Haran et al., 2015). The bold contour (1,500 m) represents the approximate elevation of the equilibrium line during 1991–2011 [1,553 m above sea level in van de Wal et al. (2012)]. “SGL” is supraglacial lake. Note the study area of Phillips et al. (2013) extends off the figure.
This review aims to reconcile the apparent contradictions of recent research and develop a conceptual model of the coupling between runoff, hydrology, basal motion and mass loss (“hydrology-dynamics”) of the land-terminating Greenland Ice Sheet. To achieve this, we begin with a brief discussion of the ways in which surface-derived meltwater accesses the ice sheet bed (for a thorough overview of water transport pathways, see Chu, 2014; Flowers, 2015; Greenwood et al., 2016; for an overview of the importance of meltwater to the ice sheet system in general, see Nienow et al., 2017). Secondly, we summarise theoretical and conceptual subglacial hydrological drainage system morphology (section Subglacial Hydrology). We then outline the observed ice flow variations throughout this land-terminating sector of west Greenland (section Land-Terminating Ice Dynamics; Figure 1) and discuss the mechanisms that have been proposed to explain them (section Mechanisms Controlling Ice Flow Variability). We then discuss the possible future dynamic behaviour of the ice sheet at high-elevations (section The Inland Limit of Melt-Induced Ice Flow Variations) and how bed topography may modulate ice flow variability (section Roughness Modulation of Hydrology-Dynamics). These sections provide a basis for our conceptual model of hydrology-dynamics (section A Conceptual Model of Subglacial Hydrology and Ice Dynamic Variability). Finally, we highlight several areas that we believe require further work (section Key Issues and Future Research), before presenting our conclusions.
Whilst ice sheet dynamics is a relatively new field of study, the motion of mountain glaciers has long been investigated (e.g., Forbes, 1846). Indeed, many parallels can be drawn between hydrology-dynamic hypotheses developed for mountain glaciers and those for the ice sheet; such pioneering work provided much inspiration for contemporary ice sheet investigations. Although at times in this review we draw on this earlier body of literature to provide relevant context, we focus on the latter; the reader is directed toward Hubbard and Nienow (1997), Fountain and Walder (1998), and Irvine-Fynn et al. (2011) for reviews of mountain glacier hydrology.
Before proceeding, we provide here a few clarifications. Although runoff-induced ice flow acceleration is associated with summer, we refrain from using seasonal descriptors because the precise timing of variations in melt onset, peak, and cessation varies between years and location on the ice sheet. Instead, we use the terms “early-melt season” and “late-melt season” to refer to the rising and descending limbs of an idealised runoff hydrograph (Figure 2). In addition, “post-melt season” refers to the period of the mass balance year during which surface melting has ceased but its legacy is still of importance dynamically (and so extends into the following calendar year). This is similar to the approach used in Stevens et al. (2016). Areas within ~50 km of the margin and from ~50 km inland to the equilibrium line are here referred to as the lower and upper ablation areas, respectively. Areas further inland are collectively referred to as the lower accumulation area. Although we make these distinctions for convenience, we note that runoff supply, rather than the mass balance regime, is of principal importance for hydrology-dynamics. It is also worth stressing here that direct observations of the subglacial environment are limited to relatively few moulins and boreholes; therefore, our understanding has been primarily developed from theoretical studies and inferences from geophysical exploration and observations of ice surface motion. Ice-dynamic proxies for subglacial water pressure comprise a large proportion of these observations. These are based on theoretical and observed linkages between subglacial discharge, hypothesised drainage system morphology, subglacial water pressure, and basal motion (Röthlisberger, 1972; Iken, 1981; Iken and Bindschadler, 1986; Kamb, 1987; Schoof, 2010).
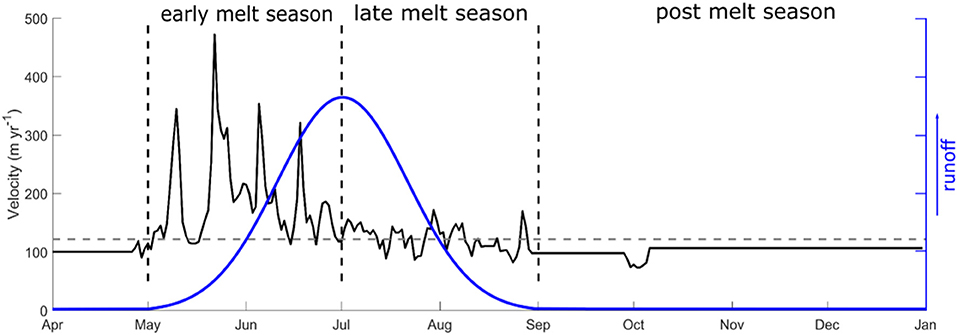
Figure 2. Greenland Ice Sheet velocity and runoff. Twenty-four hour mean horizontal velocity (solid black line) during 2010 at Leverett site 3 [20 km inland from the ice margin; see Sole et al. (2013)] and idealised runoff hydrograph (solid blue line), showing the early, late, and post-melt season periods, as described in text, separated by dashed vertical lines. As discussed in text, the positions of the seasonal boundaries are based on the runoff hydrograph, not the time of year. Dashed horizontal grey line indicates mean annual ice velocity.
Runoff Access to the Ice Sheet Bed
For transient surface melt-induced ice flow variations to occur, surface-derived meltwater must reach the ice sheet bed. In west Greenland, crevasses, and moulins appear to be the most important surface-to-bed connections, draining 47 and 39% of surface meltwater, respectively (Koziol et al., 2017), with crevasses of greatest importance where they are most abundant close to the margin (Clason et al., 2015; Koziol et al., 2017). The remaining surface meltwater is either stored at or near the surface or flows off the ice sheet edge (Koziol et al., 2017). Moulins are formed due to melting, by fast-flowing water, of a previously opened preferential flow pathway such as a crevasse. Surface fractures (or crevasses) may be extended to the ice sheet bed by “hydrofracture”— meltwater-induced downward propagation of pre-existing fractures (Weertman, 1972; van der Veen, 1998; Alley et al., 2005; Krawczynski et al., 2009).
Supraglacial lakes (henceforth “lakes”) often provide this meltwater to drive hydrofracture, particularly in the upper ablation area (Banwell et al., 2012; Doyle et al., 2013; Arnold et al., 2014; Clason et al., 2015; Koziol et al., 2017). Lake drainage due to hydrofracture is rapid (i.e., <1 day; e.g., Das et al., 2008) and creates new surface-to-bed connections (Christoffersen et al., 2018; Hoffman et al., 2018). The distribution of lakes and the causes and impacts of rapid lake drainage have, therefore, received considerable research attention (e.g., Banwell et al., 2016).
Lakes form in bed-topographically controlled surface depressions (Echelmeyer et al., 1991; Lampkin and VanderBerg, 2011; Sergienko, 2013; Ignéczi et al., 2018) during the melt season across much of the ablation area (McMillan et al., 2007; Selmes et al., 2011). Up to 55% of lakes drain rapidly, often in clusters (Box and Ski, 2007; Selmes et al., 2011) and progressively away from the ice sheet margin as the melt season progresses (Sundal et al., 2009; Morriss et al., 2013; Fitzpatrick et al., 2014). Although the total area of lakes increased during 2000–2015, the occurrence of rapid drainage varies inter-annually (Sneed and Hamilton, 2007; Fitzpatrick et al., 2014; Cooley and Christoffersen, 2017) and regionally (our Figure 3; Selmes et al., 2011). The remainder of lakes either drain slowly overland or freeze over (Selmes et al., 2013; Kingslake et al., 2015; Koziol et al., 2017).
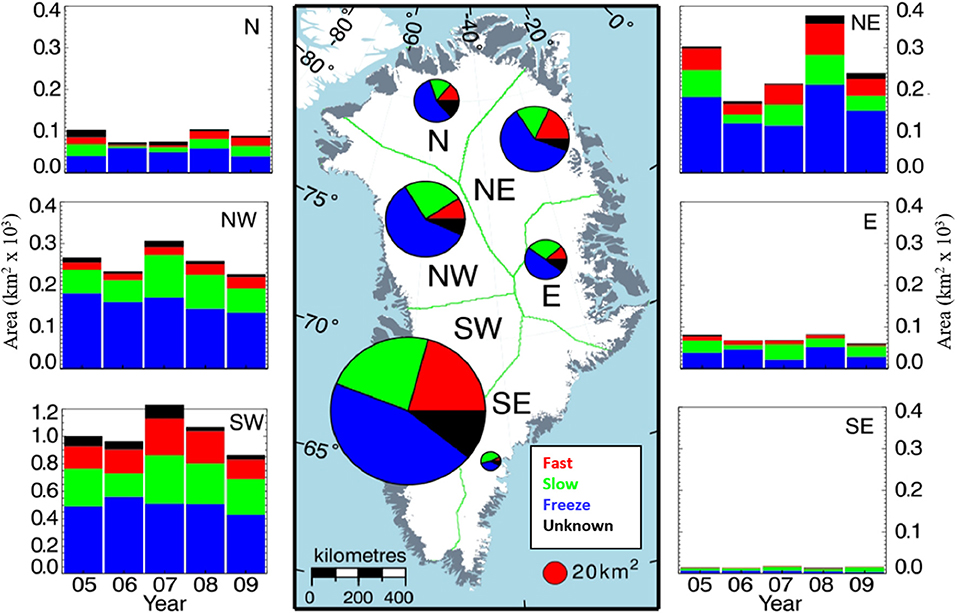
Figure 3. The distribution of supraglacial lake (SGL) area and drainage type on the Greenland Ice Sheet. The central plot shows the mean area of fast draining SGLs (red), slow draining SGLs (green), SGLs that freeze over during winter (blue), and SGLs of an unknown drainage type (black) during 2005–2009. Bar charts show area and proportion of SGL drainage types per year. Adapted from Selmes et al. (2013).
Although it is not yet possible to predict rapid lake drainage (e.g., Williamson et al., 2018), the associated processes are becoming clearer. Rapid lake drainage appears to be initiated by transient stress perturbations of sufficient magnitude to cause ice fracturing. Fractures may form in lakes due to enhanced basal sliding (Doyle et al., 2013; Carmichael et al., 2015) caused by remote runoff input to the bed (Smith et al., 2015; Stevens et al., 2015), which induces extensional flow and fracturing of upstream ice through longitudinal stress coupling (Price et al., 2008; Christoffersen et al., 2018). Such a process is argued to have a cascading effect, whereby the drainage of one cluster of lakes results in the drainage of another cluster, often further upstream, which expands the area of extensional flow, thereby encompassing yet more lakes (Christoffersen et al., 2018). Subsequent downward fracture propagation can theoretically occur if the fracture remains ≥92% full of water, due to the density difference between ice and water (van der Veen, 2007; Clason et al., 2015).
Subglacial Hydrology
Water Routing and Effective Pressure
Once runoff accesses the bed, the ice dynamic implications depend on the subglacial drainage system encountered, via its modulation of runoff-induced changes in basal water pressure. Theory developed from observations at mountain glaciers suggests that increased basal water pressure reduces the effective pressure at the bed (defined as ice overburden minus basal water pressure). Increasing water pressure can reduce the ice-bed contact area (Lliboutry, 1968; Bindschadler, 1983), cause “hydraulic jacking” of the overlying ice (Iken, 1981) and (where sediment is present) increase subglacial sediment deformation, thereby increasing basal motion rates (e.g., Engelhardt et al., 1978; Hodge, 1979; Iken and Bindschadler, 1986; Fowler, 1987; Iverson et al., 1999; Bingham et al., 2008). As we will discuss later, the rate of change of water pressure (e.g., Iken, 1981; Cowton et al., 2016), water storage (e.g., Chu et al., 2016a) and the connectivity of the drainage system (e.g., Iken and Truffer, 1997; Hoffman et al., 2016) are also important in the ice sheet setting. However, we focus here on effective pressure because it illustrates the importance of the subglacial drainage system and how it may respond to changes in runoff supply.
Runoff-induced perturbations in effective pressure depend on the balance between water supply to, storage in and discharge from the subglacial drainage system (e.g., Iken et al., 1983; Kamb et al., 1985; Nienow et al., 1998). The capacity and efficiency of the subglacial drainage system is, therefore, a key parameter controlling ice flow variability. For example, an increase in water supply to a given subglacial drainage system is evacuated by increasing water pressure at the location of water input to the bed, which in turn decreases effective pressure and increases the hydraulic gradient in the system, driving faster water flow. However, a different subglacial drainage system with a greater capacity will induce a smaller increase in water pressure (and therefore a smaller decrease in effective pressure) to evacuate the same increase in runoff. We discuss below how this theoretical relationship is complicated by spatial and temporal variations in subglacial drainage system efficiency.
Conceptualised Subglacial Drainage Morphologies
A conceptual framework for end-member subglacial drainage configurations has been developed for alpine glaciers (see Hubbard and Nienow, 1997). These are broadly classified into “efficient” and “inefficient” forms (Figure 4) and have been inferred to also exist beneath the ice sheet from observations of water tracer transit times (Chandler et al., 2013; Cowton et al., 2013), proglacial runoff characteristics (e.g., Bhatia et al., 2011), ice-dynamic proxies (e.g., Cowton et al., 2016), and borehole water pressure (e.g., Meierbachtol et al., 2013, 2016). Inefficient forms of subglacial drainage have been variously termed “slow,” “un-channelised,” “non-arborescent,” “distributed,” or “anastomosing,” but for simplicity they are here referred to as “inefficient.” Efficient forms have been variously termed “fast,” “channelised,” or “arborescent,” but here we simply use “efficient.” The various efficient and inefficient forms are illustrated in Figure 4 and summarised below.
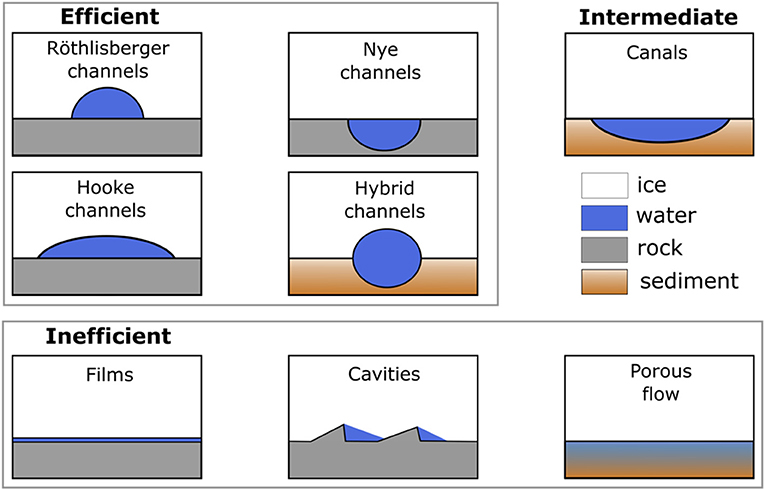
Figure 4. Conceptualised efficient, inefficient, and example intermediary subglacial drainage forms, as described in text. Channels and cavities are depicted as filled with water, but they may not be if they are not in steady-state. Ice flow is into the page, except for inefficient cavities, where ice flow is left-to-right.
Three forms of inefficient drainage have been postulated in the literature (Figure 4): films (Weertman, 1962), linked-cavity systems (Kamb, 1987), and porous (or Darcian) flow (Boulton and Jones, 1979). Sedimentary canals (Walder and Fowler, 1994) may also be inefficient but they are here classified as intermediate because they may at times evacuate water efficiently (Ng, 2000). A continuous, millimetre thick, subglacial water film was described by Weertman (1962, 1972) to explain glacier sliding by regelation, where water is produced by melting of ice under high pressure on the stoss side of basal undulations and obstacles. Films of this type are unlikely to contribute significantly to subglacial water transport, however, because theory suggests that thick films (greater than several millimetres) are unstable (Walder, 1982; Weertman and Birchfield, 1983), unless the overlying ice is partially supported by bedrock clasts (Creyts and Schoof, 2009).
Sliding of ice over small-scale (decimetres) bed roughness elements can create lee-side subglacial cavities connected by narrow orifices (Lliboutry, 1968; Walder and Hallet, 1979; Kamb, 1987; Sharp et al., 1989). Most models of subglacial water flow (e.g., Hewitt, 2013; Werder et al., 2013) assume that linked cavities are the only or dominant inefficient subglacial drainage form. Cavity size is theoretically controlled by ice sliding speed, ice viscosity, subglacial discharge and effective pressure, with faster sliding, higher viscosity, greater subglacial discharge, and lower effective pressure producing larger cavities (Walder, 1986; Kamb, 1987). Specifically, an increase in runoff supply reduces effective pressure, thereby forcing cavity expansion, which in turn expedites runoff evacuation (e.g., Kamb, 1987; Schoof, 2010). Therefore, as discharge in linked-cavity systems increases, effective pressure decreases.
Some subglacial hydrology models (e.g., Kyrke-Smith and Fowler, 2014; Bueler and van Pelt, 2015) now include drainage through sediment because a growing body of evidence suggests that the substrate underlying the ice sheet is characterised both by areas of bedrock (e.g., Harper et al., 2017) and sediment (e.g., Booth et al., 2012; Dow et al., 2013; Walter et al., 2014; Kulessa et al., 2017). These models implement Darcian flow (e.g., Boulton and Jones, 1979; Walder and Fowler, 1994), canals and shallow streams (e.g., Stone and Clarke, 1993; Ng, 2000; Kyrke-Smith and Fowler, 2014) and linked cavities emerging from the sediment (Bueler and van Pelt, 2015).
Röthlisberger channels (R-channels) are hydraulically efficient, semi-circular conduits melted up into the base of the ice (Figure 4; Röthlisberger, 1972). The cross-sectional area of R-channels is determined by the balance of channel opening by viscous dissipation of heat into the ice due to turbulent water flow, and the rate of ice-creep closure due to the effective pressure of the overlying ice (Röthlisberger, 1972). Low subglacial discharge, high effective pressure and weak hydropotential gradients (caused primarily by shallow ice-surface slopes) act to suppress R-channel growth. Conversely, increased subglacial discharge enhances channel opening rates, requiring higher creep closure rates (and therefore effective pressure) at steady-state, resulting in a positive steady-state relationship between discharge and effective pressure (Röthlisberger, 1972; Nye, 1976; Schoof, 2010). Though this relationship is not a sensitive one, it means that in steady-state there is no increase in water pressure with discharge in an R-channel (Röthlisberger, 1972). However, because the theoretical timescale of R-channel adjustment (typically days to weeks) is longer than variations in runoff supply (hours), they may be overwhelmed at times of increasing runoff supply and only partially filled at times of decreasing runoff supply. The latter situation likely results in preferential melting of channel sides, theoretically creating broader, low Hooke-channels (H-channels; Figure 4; Hooke et al., 1990). R- and H-channels are not usually distinguished in the hydrology-dynamics literature and we henceforth refer simply to efficient channels, in most cases.
Persistent subglacial water routing may incise channels into the underlying bedrock (Nye or N-channels; Figure 4; Nye, 1976). On the basis that surface-to-bed connections seem to form in the same locations year-to-year (e.g., Clason et al., 2015) and that channels incised into bedrock have been observed in deglaciated regions (e.g., Walder and Hallet, 1979; Sharp et al., 1989), we think it is likely that N-channels exist in some locations beneath the ice sheet (e.g., Beaud et al., 2018) and may provide preferential flow pathways. Water flow along water-filled N-channels will melt the overlying ice, possibly forming an N-R-channel hybrid (i.e., a channel partially melted into the overlying ice and partially eroded into bedrock). Similarly, persistent water routing in a spatially stable R-channel will presumably eventually lead to the incision of an N-channel. R- and N-channels may therefore comprise two end members of a spectrum. Such a possibility is supported by observations of transitions between inferred R- and N-channels in paleo-subglacial environments (e.g., Livingstone et al., 2016).
Spatial Variations in Subglacial Hydrological Structure
Though it is useful initially to conceptualise the above drainage forms as independent entities, they are likely frequently and extensively hydraulically connected (e.g., Hubbard et al., 1995; Andrews et al., 2014). When and where subglacial water flow is turbulent enough to cause channel opening, efficient channels should begin to form (e.g., Kamb, 1987; Bingham et al., 2005; Schoof, 2010; Chandler et al., 2013), thereby increasing the efficiency of the drainage system and increasing effective pressure. In steady-state, theory suggests that water will flow from surrounding high pressure regions toward channels. In addition, across-flow transects of ice velocity (Bingham et al., 2006; Tedstone et al., 2014) and borehole water pressure (Hubbard et al., 1995; Fudge et al., 2008), and modelling (e.g., Schoof, 2010; McGrath et al., 2011), suggest that sufficiently large or rapid pulses of runoff can cause transient spikes in channel water pressure of sufficient magnitude to reverse the hydraulic gradient between channels and the surrounding inefficient drainage system. The pressure gradient reversal could force water out of the channel into the adjacent inefficient drainage system across a “variable pressure axis” (Hubbard et al., 1995; Nienow et al., 2005; Tedstone et al., 2014). The inefficient system in the variable pressure axis is envisioned to take the form of one or a combination of linked cavities and films, where sediment cover is thin or absent, or Darcian flow and canals, where sediment cover is both thick and pervasive (e.g., Stone and Clarke, 1993; Kyrke-Smith and Fowler, 2014).
Efficient Channel Formation
The spatial extent of efficient channel formation beneath the ice sheet has been considerably debated. As described in section Conceptualised Subglacial Drainage Morphologies, shallower surface slopes, lower runoff and thicker ice hinder channel development by reducing hydropotential gradients and channel wall melt rates and increasing creep-closure rates, respectively (e.g., Röthlisberger, 1972). Based on this reasoning and numerical modelling, some authors (e.g., Meierbachtol et al., 2013; Dow et al., 2014) have argued that channels are not a major component of the subglacial drainage system beneath thick ice where surface slopes are shallow and runoff supply sparse.
Observations of borehole water pressure and tracer transit times provide some constraints on the extent of efficient channel formation. Two independent water pressure records are consistent with channel formation beneath ice up to at least ~600 m thick. Firstly, water pressure in boreholes at site SHR (location in Figure 1; van de Wal et al., 2015) was generally low and variable throughout the 2011 melt-season (compared to before and after the melt season), other than a transient increase coincident with melt-onset, indicating an efficient drainage system that may at times be over-pressurised. Similarly, water pressure in moulins near the GULL Global Positioning System (GPS) site (location in Figure 1; Andrews et al., 2014), increased during melt events and declined rapidly afterwards; indicating that although the drainage system was transiently over-pressurised, drainage efficiency was relatively high. However, water pressure in boreholes spanning a range of ice thicknesses (100–800 m), located primarily on bedrock highs, was generally high throughout the year, indicating a persistently inefficient subglacial drainage system (Meierbachtol et al., 2013; Wright et al., 2016). Although these are point observations, they indicate a drainage system of spatially varying efficiency and connectivity. Water tracer transit times in the same region suggest that efficient channels form rapidly (Cowton et al., 2013) and can extend up to at least 41 km from the margin (Chandler et al., 2013), indicating that channels can form along the principal flow paths throughout the lower ablation area.
Numerical modelling investigations generally support these inferences. R-channel formation has been modelled up to ~50 km inland [nearly 1,200 m above sea level (a.s.l), beneath ~900 m thick ice; (de Fleurian et al., 2016; Koziol and Arnold, 2018)], but not in a setup representative of conditions ~70 km inland and ~1,400 m a.s.l (1,200 m thick ice; Dow et al., 2014). This would suggest that there is a transition in potential drainage system efficiency between areas overlaid by ~900 and ~1,200 m thick ice. However, observations of the subglacial environment and constraints on crucial model parameters are sparse, leading to uncertainty in inferences from models: modelled R-channels can form under conditions representative of the upper ablation area if a large (~1 m2) initial conduit size is used (e.g., Hewitt, 2011; Gulley et al., 2012). Such conditions may occur due to uplift during rapid lake drainage (Das et al., 2008; Pimentel and Flowers, 2010; Andrews et al., 2018) or may be facilitated if persistent surface-to-bed hydrological connections (Catania and Neumann, 2010) enable erosion of preferential flow pathways into the substrate (Gulley et al., 2012; Beaud et al., 2018). In addition, the spatial pattern of surface-to-bed connections (moulins) strongly influences the spatial organisation of modelled subglacial channels, with a high density of moulins producing widespread and rapid channelisation beneath ice up to 815 m thick (Banwell et al., 2016).
Large inputs of meltwater to the bed during rapid lake drainage events also appear to influence the subglacial drainage system. Observations indicate ice sheet uplift during and immediately following rapid lake drainage (e.g., Das et al., 2008; Doyle et al., 2013; Andrews et al., 2018), followed by lowering within a few hours (e.g., Das et al., 2008; Bartholomew et al., 2012) to days (Doyle et al., 2013; Andrews et al., 2018), and sustained flow deceleration (Andrews et al., 2018). The uplift of the ice sheet-surface implies that the initial influx of runoff exceeds the capacity of the local subglacial drainage system (e.g., Das et al., 2008; Stevens et al., 2015) and likely spreads out radially from the point of input as a “blister” (Tsai and Rice, 2010; Dow et al., 2015). The subsequent subsidence suggests that this runoff can be evacuated relatively rapidly, possibly in a turbulent sheet (Adhikari and Tsai, 2015; Dow et al., 2015), whilst the subsequent slow-down implies persistent, efficient drainage formation at low elevations (below ~900 m) or changing pressures within inefficient parts of the drainage system at high elevations (see section Modulation of Ice Flow by the Weakly-Connected Subglacial Drainage System; Andrews et al., 2018). Whether efficient channels develop during rapid lake drainage is uncertain and will depend on local ice thickness and hydropotential gradient. Large and turbulent fluxes of subglacial runoff would theoretically cause rapid channel opening (Röthlisberger, 1972; Schoof, 2010), which would be followed by sustained flow deceleration (Andrews et al., 2018); however, the short duration of drainage events may limit channel growth (e.g., Dow et al., 2015). A modelled lake drainage event through 1,200 m thick ice (Dow et al., 2015) did not generate substantial channel growth; however, the sensitivity of this finding to key properties (such as ice thickness and pre-drainage basal hydrology) remains unclear. In summary, observations indicate that efficient channels can form along principal water flow paths beneath large areas of the ablation area (up to at least ~40 km from the margin), but their formation and persistence appears to be suppressed and may even be precluded with increasing ice thickness and distance from the margin.
The “Weakly Connected” Drainage System
Outside variable pressure axes, observations and modelling of both mountain glaciers (e.g., Murray and Clarke, 1995; Gordon et al., 1998; Fudge et al., 2008; Schoof et al., 2014; Lefeuvre et al., 2015, 2018) and the ice sheet (Meierbachtol et al., 2013, 2016; Andrews et al., 2014; Ryser et al., 2014a; Hoffman et al., 2016) indicate that there are potentially large areas of inefficient drainage that are not directly connected to surface runoff supply. These areas operate at higher water pressures than other parts of the subglacial drainage system. We suggest that this “weakly connected” drainage system (as described in Hoffman et al., 2016) exists throughout the subglacial environment where water is present (e.g., from basal melting and/or storage) but is superseded along preferential subglacial water flow pathways during the melt season by a “connected” drainage system, fed by surface runoff inputs, comprised of an efficient core surrounded by a mixture of inefficient drainage forms. It is worth stressing that because observations of the subglacial environment are sparse, it is not clear what drainage forms the “weakly-connected” system is comprised of, nor whether subglacial drainage system “connectivity” varies continuously or discretely in space.
Temporal Variations in Subglacial Hydrological Structure
Observations and modelling suggest that the configuration of the subglacial drainage system varies over sub-daily to millennial timescales in response to variations in runoff supply, ice surface slope and sliding velocity (e.g., Chandler et al., 2013; Livingstone et al., 2013; Lindbäck et al., 2015; Chu et al., 2016b). During the post-melt season period, runoff supply to the bed is at an annual minimum and channel-creep closure rates likely exceed channel-wall melt rates. Therefore, an inefficient drainage mosaic of films, linked-cavities and Darcian flow through subglacial till (where present) potentially dominates during this time.
Shortly following surface melt onset, runoff accesses the bed, perturbing the inefficient winter drainage system at and downstream of surface-to-bed hydraulic connections, and generating local variations in basal water pressure (Andrews et al., 2014; Wright et al., 2016). Efficient channels should begin to form if subglacial discharge becomes sufficiently turbulent to cause melting of the overlying ice faster than the rate of creep closure (Kamb, 1987; Bingham et al., 2005; Schoof, 2010). Although one study (Sundal et al., 2011) has suggested a fixed threshold surface melt volume above which channelisation occurs, this ignores the influence of variable creep closure and cavity opening rates caused by spatial and temporal variations in effective pressure, ice viscosity and basal sliding.
As surface melting occurs at increasingly high elevations, channels are thought to form and extend progressively inland (as in Nienow et al., 1998), as inferred from an up-glacier progression of relatively rapid observed water flow velocities (>1 m s−1) (Chandler et al., 2013) and high correlations between diurnal surface melting and both proglacial discharge (e.g., Bartholomew et al., 2010) and moulin water pressure (e.g., Andrews et al., 2014) in the lower ablation area. Theory suggests that as channels grow in diameter through the melt season, water flow should become increasingly concentrated into fewer channels, further increasing the efficiency of the subglacial drainage system (Röthlisberger, 1972; Hock and Hooke, 1993; Hewitt, 2011; Koziol and Arnold, 2018), but this has not been confirmed by observations in the ice sheet setting. The growth of channels would progressively decrease the extent of the weakly-connected system. Efficient channels should persist as long as subglacial discharge generates sufficient ice-wall melting to offset ice creep-closure. Therefore, channels should start to close as surface melting decreases toward the end of the melt season. The capacity and efficiency of drainage forms within the variable pressure axis may also seasonally increase because of runoff-induced cavity growth (Kamb, 1987; Schoof, 2010) and increased till porosity and sedimentary canal formation, where sediment is present (Kyrke-Smith and Fowler, 2014; Damsgaard et al., 2015).
Despite receiving little runoff, the putative weakly-connected drainage system should also evolve throughout the melt season. In many places, water pressure has been observed to decline in boreholes inferred to be connected to the weakly-connected system, albeit with considerable variability, through all or part of the melt season (Smeets et al., 2012; Meierbachtol et al., 2013; Andrews et al., 2014; Wright et al., 2016) and become anti-correlated with water pressure in the connected drainage system on diurnal timescales (Andrews et al., 2014; Lefeuvre et al., 2015). The diurnal variations in pressure are thought to be due to stress-transfer induced increases in basal sliding, leading to cavity expansion (Andrews et al., 2014) and/or mechanical stress redistribution (e.g., Murray and Clarke, 1995; Ryser et al., 2014b; Meierbachtol et al., 2016; Lefeuvre et al., 2018). The general decline of water pressure in the weakly-connected system during the melt season is thought to be due to the seasonal establishment of a water pressure gradient, which gradually drains water from the weakly-connected to the connected system (Hoffman et al., 2016). In the lower accumulation area, where surface slopes are small and ice thick, water flow between the connected and weakly-connected system should theoretically be suppressed due to the weak pressure gradients and rapid closure (or absence) of connections between the two systems.
When runoff supply ceases, we envisage relatively rapid closure of channels (hours to days, depending on ice thickness), re-establishment of the weakly-connected, inefficient system and a consequent increase in subglacial water pressure and water storage. Theory suggests that re-pressurisation of the subglacial drainage system, due to basal melting and cavity closure, should be slow and gradual; however, observations of re-pressurisation are sparse and so are usually inferred from ice velocity observations. The gradual ice flow recovery throughout much of the ablation area (e.g., Joughin et al., 2008; Colgan et al., 2011; Sole et al., 2013) and increasing borehole water pressures ~15 km inland (van de Wal et al., 2015) during the post-melt season period corroborate this view. On the other hand, Wright et al. (2016) observed rapid recovery of borehole water pressures during the late-melt season and only a slight increase in water pressure over winter at some sites. These contrasting observations suggest that the degree and timing of post-melt season re-pressurisation varies both spatially and inter-annually (as also evidenced by Figure 13 in Colgan et al., 2011). This may be due to spatial variability in ice thickness and temperature, drainage system efficiency, the degree to which water has been drained from the weakly-connected drainage system and local cavity geometry. These factors are related: for example, a more efficient end-of-season connected drainage system will likely be associated with greater water drainage from the weakly-connected system, due to steeper hydraulic gradients between the two (Hoffman et al., 2016).
In addition to the hypothesised seasonal and shorter-term changes in the subglacial drainage system discussed above, there may also be broad changes in the size and location of subglacial catchments in response to both seasonal changes in basal water pressure and changes in ice surface slope over centennial-and-longer timescales. Chu et al. (2016b) and Lindbäck et al. (2015) modelled large changes in subglacial catchments in response to changing basal water pressure. Such changes would alter the magnitude and timing of water flow beneath neighboring glaciers, thereby potentially affecting the temporal and spatial evolution of subglacial drainage forms discussed above. On longer timescales (centuries to millennia), changes in ice sheet geometry will also affect the routing and storage of water at the bed (e.g., Livingstone et al., 2013).
Land-Terminating Ice Dynamics
Ice motion is due in part to ice sliding over the bed and by deformation of subglacial sediments, both of which are directly influenced by subglacial hydrology. In the following two sections, key turning points, developments, and debates from observations and modelling over the last 15 years are discussed (Figure 1).
Short-Term Ice Speed-Ups
Short-term speed-ups (lasting hours to several days) of ice sheet flow occur in response to variations in surface runoff supply (e.g., Shepherd et al., 2009) and lake drainage (e.g., Das et al., 2008). Each year, after an initial melt-induced speed-up (often termed a “spring-event”; section Seasonal and Inter-Annual Variability of Ice Flow), ice velocity in the lower ablation area typically varies diurnally with an amplitude of up to ~300% of pre-melt speeds. Diurnal fluctuations have the highest amplitude near the margin and decrease steadily inland within the lower ablation area. Occasionally, ice flow will increase (by >100%) and remain elevated for several days in response to major increases in runoff supply (e.g., van de Wal et al., 2008; Hoffman et al., 2011; Bartholomew et al., 2012; Tedstone et al., 2013).
Rapid lake drainage events cause most short-term speed-ups in the upper ablation area, particularly during the late-melt season (Hoffman et al., 2011; Doyle et al., 2013; Joughin et al., 2013). Although the temporal patterns of ice dynamic response to lake drainage events are complex (e.g., Das et al., 2008; Joughin et al., 2013), direct observations of ice sheet motion during and after rapid lake drainage reveal a typical pattern of ice sheet uplift by decimetres to metres, lasting less than a few hours (e.g., Tedesco et al., 2013), and concurrent short-lived (<24 h) ice flow acceleration by 100–400% above pre-melt season values (e.g., Das et al., 2008; Shepherd et al., 2009; Bartholomew et al., 2012). This is usually followed by rapid (<few hours) deceleration to below pre-lake drainage velocities and then recovery to pre-drainage velocities (e.g., Das et al., 2008), producing a small net speed-up (~1 m year−1; Das et al., 2008; Doyle et al., 2013).
Not all lakes drain rapidly - many drain slowly over the ice sheet-surface via channels into down-glacier moulins and lakes, augmenting the locally-derived surface runoff supply (Selmes et al., 2013; Kingslake et al., 2015; Koziol et al., 2017). Modelling suggests that the effect of lake surface drainage on ice velocity depends on the rate of drainage and whether the lake drains partially or entirely (Kingslake et al., 2015). One study (Tedesco et al., 2013), suggested that so-called “slow-draining” lakes produce less than half the speed-up of their fast-draining counterparts.
Seasonal and Inter-annual Variability of Ice Flow
Following localised surface melt onset, ice velocities increase considerably (the “spring event”). In southwest Greenland, this initial speed-up typically begins in early May, close to the margin, and occurs progressively later further inland (Bartholomew et al., 2010, 2011b; Fitzpatrick et al., 2013; Sole et al., 2013; van de Wal et al., 2015). In the lower ablation area, this speed-up is of high magnitude (up to 300–400% above pre-melt speeds) but lasts only a few days to a week before ice velocity falls to near pre-melt speeds (e.g., Sole et al., 2013). Further inland, the initial speed-up is damped (~50–100%) but more sustained (Bartholomew et al., 2012). During the late-melt season, ice velocity typically decreases at times when meltwater supply is steady or falling. This slow-down may, however, be interrupted by short-lived accelerations during exceptional warm periods and rainfall events (Tedstone et al., 2013; Doyle et al., 2015) and rapid lake drainage (Shepherd et al., 2009). Together, these typically increase mean melt season ice flow relative to the post-melt period by ~65% in the lower ablation area (Sole et al., 2013), declining to ~7% in the lower accumulation area (Sole et al., 2013; Doyle et al., 2014).
Post-melt season, ice flow throughout the ablation area initially slows to an annual minimum before gradually returning to pre-melt season speeds over several months (e.g., Joughin et al., 2008; Sole et al., 2013; van de Wal et al., 2015). One set of Global Navigation Satellite System (henceforth also GPS) observations near the Kangerlussuaq, or K-, transect (Figure 1) showed that although ice displacement and runoff during the melt season are positively correlated, post-melt season ice velocities are negatively correlated with runoff during the latter part of the preceding melt season, such that annual ice velocity is not significantly related to annual runoff (Sole et al., 2013). This finding applied even during the extreme melt year of 2012 (Tedstone et al., 2013). A similar relationship has been observed in a large area of the lower ablation area (Sundal et al., 2011) and over 20 years at K-transect sites in the ablation area (van de Wal et al., 2015). A detailed set of GPS observations near North Lake (location in Figure 1), showed a similar pattern of ice flow variability; however, post-melt season ice velocities were unrelated to preceding mean melt season characteristics (Stevens et al., 2016). The inter-annual stability of ice flow in the ablation area, despite elevated melt season ice flow during warmer years, due to the post-melt season deceleration has been termed “ice flow self-regulation” (Sole et al., 2013; van de Wal et al., 2015). However, at K-transect sites at and above the approximate elevation of the equilibrium line, the late-melt season deceleration is short lived or non-existent (Doyle et al., 2014; van de Wal et al., 2015).
The 20-year time-series of GPS ice displacement data along and adjacent to the K-transect suggests, therefore, that ice flow self-regulation varies throughout the ablation area (van de Wal et al., 2015). In the lower ablation area, annual ice flow exhibits no statistically significant relationship with surface melt (Sole et al., 2013; van de Wal et al., 2015). In the upper ablation area, early-melt season and post-melt season velocities are positively and negatively correlated with runoff supply, respectively, but the influence of lower ice velocity during the longer winter season produces an overall, weak negative correlation between annual ice velocity and runoff supply (van de Wal et al., 2015). In contrast, annual ice flow at a K-transect site 140 km from the margin increased by 2.2% during 2009–2012, during which time lake extent also increased, implying an increase in runoff supply (Doyle et al., 2014). A similar (1.8%) speed-up was observed during 2009–2011 at a site 117 km from the margin (Figure 3 in Sole et al., 2013). The mechanisms controlling this seasonal response are discussed in section Mechanisms Controlling Ice Flow Variability.
Decadal Ice Flow Variability
Both high-temporal resolution and spatially-extensive observations have shown that ice flow in the majority of the ablation area is slowing on multi-year timescales, despite a concurrent increase in modelled runoff supply (van de Wal et al., 2008, 2015; Tedstone et al., 2015; Stevens et al., 2016). van de Wal et al. (2008) reported a 10% decline in the annual average ice velocity along the K-transect from 1991 to 2007, which was tentatively attributed to decreases in surface slope or ice thickness and, on the basis of those observations, suggested that dynamic thinning does not significantly increase the ablation rate in their study area. van de Wal et al. (2015) showed that the long-term pattern of ice velocity change varies throughout the ablation area, with the greatest net slow-down occurring in the upper ablation area, due to the strong negative correlation between winter flow speeds and melt supply described above—behaviour also noted by Sole et al. (2013). In the lower accumulation area, there was not a discernible positive correlation between annual melt supply and annual ice velocity during 1991–2012 (van de Wal et al., 2015); however, Doyle et al. (2014), using more precise GPS receivers, did observe a modest year-on-year acceleration from 2009 to 2012, possibly as a direct response to increased runoff supply, or indirectly via hydrologically-induced warming of basal ice (e.g., Phillips et al., 2013). Furthermore, ice flow within ~50 km of the margin across a large land-terminating sector of west Greenland was on average 12% slower during 2007–2014 than 1985–1994 (Tedstone et al., 2015), despite a concurrent 50% increase in surface meltwater production (Wilton et al., 2017). Only ~30% of this slow-down was explicable by changes in ice thickness and surface slope (Tedstone et al., 2015). Similarly, Stevens et al. (2016) observed at North Lake net annual flow deceleration of 1.1% per year during 2009–2013. Analogous multi-year slow-down trends of glaciers have been observed in Alaska (Truffer et al., 2005; Burgess et al., 2013) and Canada (Thomson and Copland, 2017).
Mechanisms Controlling Ice Flow Variability
The ice flow fluctuations described above are difficult to reconcile. A suitable hypothesis must explain (i) the timing and magnitude of short-term accelerations as well as the late-melt season and decadal slow-downs in the ablation area, and; (ii) the contrasting behaviour further inland. Robust process-understanding of the mechanisms controlling ice flow variability is essential if we are to reliably predict the future behaviour of the ice sheet. There are three principal hypotheses that seek to explain this behaviour. The first states that ice flow variability is due to runoff-induced weakening and strengthening of subglacial sediment, leading respectively to increasing and decreasing sediment deformation rates (Figure 5; Bougamont et al., 2014; Kulessa et al., 2017); the second states that efficient channels and inefficient cavities modulate runoff-induced variations in water pressure (Figure 6; Bartholomew et al., 2010, 2012; Sole et al., 2013; Tedstone et al., 2015; Cowton et al., 2016); and the third, which seeks to explain only the late-melt season slow-down, draws on leakage of water from the weakly-connected drainage system (Figure 7; Andrews et al., 2014; Hoffman et al., 2016).
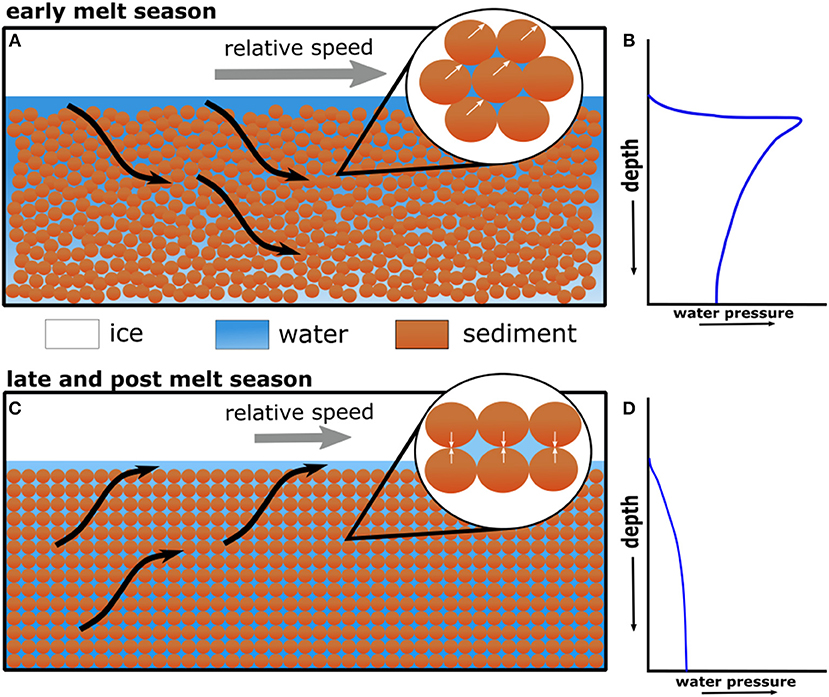
Figure 5. Schematic of the sediment deformation mechanism proposed by Bougamont et al. (2014). (A) Pulses of meltwater (black arrows) during the early-melt season force water downward along a vertical hydraulic gradient (idealised in B). A consequent reduction in sediment shear strength facilitates particle displacement (white arrows, top zoom), leading to (C) grain rearrangement, increased sediment porosity, and (D) lower water pressure and therefore stronger inter-particle contacts (white arrows, bottom zoom) during the late-melt season.
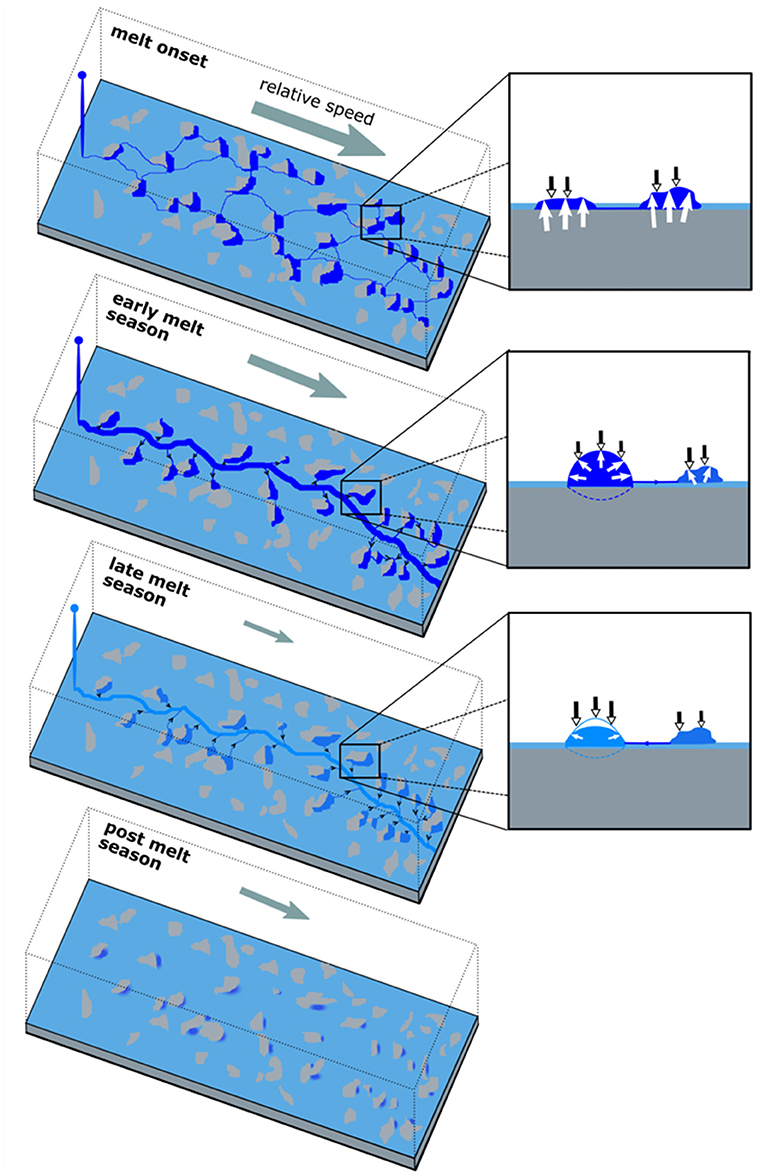
Figure 6. Schematic of active drainage system hydrology-dynamic interactions. (Left) Black arrays indicate water flow direction. (Right) Cavity cross-sections—black and white arrows indicate closing and opening mechanisms, respectively. Size of grey arrow in left panels indicates relative velocity change from preceding period. Blue shading indicates basal water pressure (darker equals higher pressure).
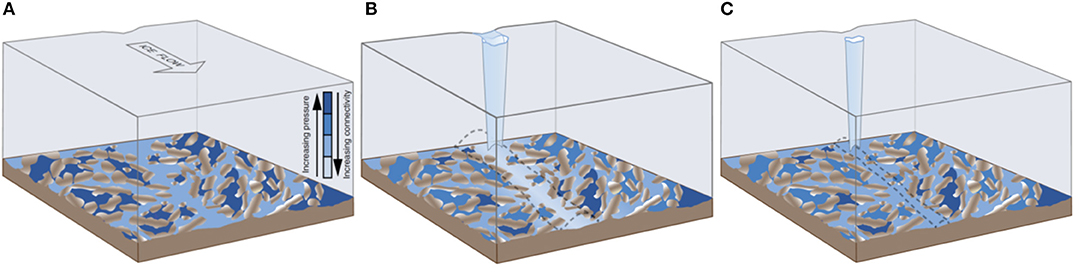
Figure 7. Conceptual model of ice flow self-regulation by the inactive subglacial drainage system. (A) At the onset of the melt season, a large fraction of the bed is comprised of high pressure, weakly connected cavities. (B) By the middle of the melt season, efficient subglacial drainage has developed (dashed grey outline) and the extent and pressure of the inactive system have decreased, leading to relative ice flow slow-down. (C) At the end of the melt season, channels collapse soon after surface melt cessation and water pressure in the inactive drainage system begins to increase, leading to gradual ice flow speed-up. Adapted from Hoffman et al. (2016).
Runoff-Induced Variations in Sediment Shear Strength
Subglacial sediment may respond to runoff supply in a manner that could explain some aspects of ice flow variability (Figure 5; Dow et al., 2013; Bougamont et al., 2014; Walter et al., 2014; Kulessa et al., 2017). According to this hypothesis, pulses of runoff to the bed create a vertical hydraulic gradient between (high pressure) subglacial water at the ice-sediment interface and the (low pressure) underlying sediment, leading to downward migration of water into the sediment (Boulton et al., 2001; Damsgaard et al., 2016). This increases sediment pore-water pressure, reduces sediment shear strength and increases sediment deformation and thus ice flow (Figure 5; Boulton et al., 2001; Bougamont et al., 2014; Damsgaard et al., 2016). Subsequent evacuation of water through the efficient drainage system then leads to a reversal of vertical hydraulic gradients, upward migration of water out of the sediment and a reduction in sediment pore-water pressure. Modelling (Bougamont et al., 2014; Damsgaard et al., 2015, 2016) suggests that runoff-induced sediment grain rearrangement acts to increase sediment porosity. This in turn leads to a subsequent drop in pore-water pressure, increased sediment shear strength and basal traction and therefore slower basal motion (Figure 5) (Bougamont et al., 2014; Kulessa et al., 2017).
Modelling (Bougamont et al., 2014) suggests that the rate and duration of runoff input to a sediment-rich subglacial environment strongly influences the resultant ice velocity response. Modelled and inferred variations in subglacial sediment shear strength can be induced by rapid lake drainage, which produces realistic seasonal variations in modelled ice velocity (Bougamont et al., 2014; Kulessa et al., 2017). Bougamont et al. (2014) also argue that increases in runoff supply may in the future affect sediment shear strength and ice velocity: a modelled 50% increase (relative to that in 2010) in both runoff and lake drainages resulted in an early-melt season acceleration that was not compensated for by a late-melt season deceleration, thereby increasing mean annual ice velocity.
Subglacial sediments appear to be concentrated in troughs but are thin on the adjacent plateaus (e.g., Harper et al., 2017; Kulessa et al., 2017). Dilatant till in subglacial troughs has been inferred from seismic surveys in some areas of west Greenland (Booth et al., 2012; Dow et al., 2013; Walter et al., 2014; Kulessa et al., 2017; Hofstede et al., 2018). While the thickness of this till is largely unknown, subglacial sediment tens of metres thick has been inferred (Walter et al., 2014; Doyle et al., 2018; Hofstede et al., 2018). However, observations from an array of boreholes through relatively thin ice over bedrock highs in parts of the Kangerlussuaq sector (Harper et al., 2017) and from radar tomography of areas of west Greenland (Jezek et al., 2011, 2013) were inconsistent with the presence of a thick sediment substrate, at least on the extensive plateaus between troughs.
Although it is likely that runoff-induced variations in subglacial sediment shear strength will occur, we advise caution when interpreting suggestions that ice flow may accelerate in future in response to pervasive subglacial sediment weakening (Bougamont et al., 2014). Firstly, net sediment weakening has not, as far as we are aware, been inferred beneath the land-terminating ice sheet, though observations are sparse (Kulessa et al., 2017). Secondly, although till deformation is non-linear and sensitive to driving stress (e.g., Iverson et al., 1999), there is no evidence that the short-term subglacial sediment strengthening inferred in Kulessa et al. (2017) occurs on annual timescales nor that the mechanism is effective over multi-year timescales. Furthermore, the hypothesis that future increases in runoff supply will cause net speed-up is predicated on a modelled speed-up in response to runoff forcing above 2010 levels (Bougamont et al., 2014). Such a relationship is directly at odds with observations: ice sheet wide runoff was approximately 30% greater during 2012 than in 2010 (Cullather et al., 2016), but annual ice motion during 2010 averaged across all sites presented in Sole et al. (2013) was ~5% slower than in 2010. In addition, ice flow in a large land-terminating sector of west Greenland slowed over 30 years, despite increasing surface melt (Tedstone et al., 2015).
Ice Flow Modulation by the Connected Drainage System
The observed ice flow fluctuations have been attributed by some authors (e.g., Bartholomew et al., 2010; Sole et al., 2013; Cowton et al., 2016; Koziol and Arnold, 2018) to runoff input to a subglacial environment underlain principally by hard bedrock and characterised by a network of efficient channels and linked cavities (Figure 6). Much of the evidence for this hypothesis comes from ice-dynamic proxies for subglacial water pressure. We note that changes in ice velocity can occur that are apparently unrelated to changes in basal water pressure (e.g., Iken and Truffer, 1997; Harper et al., 2007).
According to this hypothesis, the short-term dynamic response of the ice sheet to variations in surface runoff production (van de Wal et al., 2008; Bartholomew et al., 2012) results from the differing timescales of variability in subglacial channel evolution and runoff supply (e.g., Cowton et al., 2016). Although channel initiation and growth occur relatively early in the melt season [depending on ice thickness, surface slope, and viscosity (Schoof, 2010; Cowton et al., 2013)], the timescale of variability in runoff supply (hours) is typically much shorter than that of channel adjustment (days to weeks), hence channels are typically not in steady-state (Pimentel and Flowers, 2010; Schoof, 2010; Bartholomew et al., 2012). The implication is that, regardless of time of year, if runoff supply exceeds the rate at which it can be evacuated, then there will be an increase in water pressure and ice acceleration (Bartholomew et al., 2011a, 2012).
When runoff supply to a full channel increases, water pressure in the channel should rise, forcing water away from the channel across the variable pressure axis into the surrounding inefficient drainage system. This should, theoretically, induce cavity expansion (and therefore vertical and down-glacier displacement of overlying ice) and reduce ice-bed coupling (Figure 6; Figure 10 in Cowton et al., 2016). This inference is supported by observations of changes in channel water pressure that are well-correlated with changes in ice velocity and water pressure of the surrounding area (Andrews et al., 2014). The sensitivity of water pressure in channels to runoff input decreases as channel cross-sectional area expands during the early-melt season: much greater increases in runoff input are required during the middle of the melt season (and after any period of relatively sustained surface melting) to generate the same velocity response as during the early-melt season (Röthlisberger, 1972; Cowton et al., 2016). In regions of the ice sheet where channels are sufficiently dense and/or the variable pressure axes sufficiently wide, short-term flow acceleration may be dominated by this mechanism, particularly when longitudinal stress coupling is considered (Kamb and Echelmeyer, 1986; Price et al., 2008). There is observational and modelling evidence to suggest that, at least in the ablation area of western Greenland, this is indeed the case. Firstly, GPS observations along transects parallel and transverse to ice flow show that the patterns of short-term speed-up in response to runoff variations were strikingly similar up to at least ~75 km from the margin (~1,500 m a.s.l, ~1,200 m ice thickness; Bartholomew et al., 2011a) and extend at least 2.8 km transverse to an inferred subglacial channel (Tedstone et al., 2014). Secondly, Hewitt (2011) suggested a theoretical subglacial channel spacing of ~2–15 km depending on the permeability of the substrate—similar to the spacing of Canadian eskers, which are interpreted as relict subglacial drainage pathways (Storrar et al., 2014). This theoretical spacing is reduced when downstream variations in ice flow velocity are also considered (Meyer et al., 2016), as has been reproduced in a modelling study in which subglacial channels were extensive below 1,000 m a.s.l. (Koziol and Arnold, 2018).
Sole et al. (2013) proposed that the late-melt season slow-down is due to channel-induced de-pressurisation of the inefficient subglacial drainage system surrounding efficient channels (Figure 6). During the late-melt season, channels are thought to be initially well-developed and maintained by continued (albeit declining) runoff supply. They are therefore likely to be capable of evacuating this runoff without becoming over-pressurised. Due to relatively slow channel closure rates (compared to variations in runoff supply), water pressure in channels will, therefore, often be low, creating a steep hydraulic gradient toward channels from surrounding high pressure regions. Consequent water flow toward the channels would lead to an overall reduction in basal water pressure, an increase in effective pressure and, therefore, reduced basal sliding across the variable pressure axis and surrounding dynamically-coupled ice (Price et al., 2008). Water volumes in variable pressure axes should therefore decline throughout the late-melt season, leading to an annual velocity minimum near the end of the melt season (Sole et al., 2013; van de Wal et al., 2015; Stevens et al., 2016). Once channels are closed [which may take hours to weeks depending principally on ice thickness (Chandler et al., 2013)], basal meltwater is hypothesised to gradually re-pressurise the now inefficient drainage system (e.g., van de Wal et al., 2015), thereby slowly restoring ice flow to pre-melt season values (e.g., Joughin et al., 2008; Colgan et al., 2012; Sole et al., 2013). Importantly, the late-melt season increase in effective pressure and thus slow-down is argued to be (i) greater and relatively prolonged if the late-melt-season channels are larger and (ii) is more pervasive if the subglacial channel network is more extensive (Sole et al., 2013; Tedstone et al., 2014; van de Wal et al., 2015). This negative relationship between late-season runoff (and by inference the extent and efficiency of the subglacial drainage system) and subsequent ice motion has also been observed on nearly all major glaciers in Alaska (Burgess et al., 2013). In addition, inferences from ice velocity observations (Tedstone et al., 2015) and modelling (Hoffman et al., 2016) indicate that the inferred post-melt season recovery of water pressure may be incomplete, leading to year-on-year decreases in ice velocity that are greater than would be expected from thinning alone (Pritchard et al., 2009; Helm et al., 2014; Tedstone et al., 2015; van de Wal et al., 2015).
Efficient channels must form and persist for a sufficiently long time to affect subglacial water pressures (but not for the duration of the velocity recovery and inferred re-pressurisation) for this self-regulation mechanism to operate; however, it is uncertain where and for how long subglacial channels can form and persist with minimal water flux. Before we proceed, it is worth reiterating that the temporal pattern of ice velocity we are seeking to explain extends up to ~80 km along the K-transect (Sole et al., 2013; van de Wal et al., 2015). In the lower ablation area, there is some observational evidence to suggest that channels can induce depressurisation of the surrounding area. Water pressure in a moulin ~20 km from the margin, inferred to be connected to a channel, was lower than neighboring boreholes and was characterised by generally higher pressure during melt events and lower pressure during periods of steady or declining air temperature, with large diurnal variability superimposed (Andrews et al., 2014). In addition, water pressure in a borehole thought to intersect a hydrologically active part of the drainage system declined during the early-melt season and then gradually recovered through the post-melt season period (van de Wal et al., 2015). These observations are broadly consistent with channel-induced depressurisation—lower channel water pressure relative to the surroundings, particularly during periods of steady or declining runoff supply, would result in increased drainage of water from variable pressure axes until channels close after the melt season, allowing re-pressurisation to begin. As discussed in section Spatial Variations in Subglacial Hydrological Structure, observations, and modelling of channel formation in the upper ablation area are sparse and equivocal (Bartholomew et al., 2011a; Chandler et al., 2013; Dow et al., 2014; Koziol and Arnold, 2018). In the upper ablation area, similar mechanisms may operate that do not require channel formation, but which produce similar seasonal ice velocity patterns (Andrews et al., 2014; Hoffman et al., 2016)—these are discussed below.
Modulation of Ice Flow by the Weakly-Connected Subglacial Drainage System
In section Subglacial Hydrology, we suggested that there are potentially large regions of the subglacial drainage system that are not directly affected by runoff reaching the ice bed (the “weakly-connected” drainage system; Andrews et al., 2014; Hoffman et al., 2016). The late-melt season slow-down throughout the ablation area has been attributed to declining water pressure in this weakly-connected drainage system (Figure 7; Hoffman et al., 2016). Observations of water pressure in boreholes inferred to be connected to the weakly-connected system indicate higher water pressure than in connected regions of the bed (Meierbachtol et al., 2013; Andrews et al., 2014; Wright et al., 2016). As discussed in section Spatial Variations in Subglacial Hydrological Structure, it is proposed that this high pressure is due to low hydraulic conductivity—although water can flow toward the connected subglacial drainage system, the rate of flow is sufficiently low that water pressures in the connected and weakly-connected regions of the bed do not equalise within a melt season (Murray and Clarke, 1995; Iken and Truffer, 1997; Ryser et al., 2014a; Lefeuvre et al., 2015; Hoffman et al., 2016; Wright et al., 2016).
During the melt season, the extent of the weakly-connected system will, according to this hypothesis, decrease, and the rate of water flow out of the weakly-connected system will increase, leading to a reduction in water pressure during the late-melt season (Andrews et al., 2014; Hoffman et al., 2016). As discussed in sections Spatial Variations in Subglacial Hydrological Structure and Ice Flow Modulation by the Connected Drainage System, water pressure in the connected drainage system is thought to increase when runoff supply exceeds the capacity of the efficient core (e.g., Bartholomew et al., 2012). As well as causing cavity expansion in the inefficient parts of the connected drainage system (discussed in the previous section), this may increase the efficiency of hydraulic connections in proximal parts of the weakly-connected drainage system. Such “connection” events have been suggested based on observations of sudden drops in borehole water pressure followed by diurnal variations correlated with surface melting on mountain glaciers (e.g., Murray and Clarke, 1995; Gordon et al., 1998; Rada and Schoof, 2018) and on the ice sheet (Andrews et al., 2014; Wright et al., 2016). Water flow out of the remaining weakly-connected system should theoretically increase throughout the melt season as increasing connected drainage system efficiency (Chandler et al., 2013) acts to increase the hydraulic gradient and therefore water flow between the two systems (Hoffman and Price, 2014; Hoffman et al., 2016). We note that this latter hypothesis draws on the same processes as channel-induced depressurisation of the variable pressure axis (section Ice Flow Modulation by the Connected Drainage System; Sole et al., 2013), but does not necessarily require efficient channels to form. Using an ice flow model, Hoffman et al. (2016) parameterised these processes as a gradual water pressure reduction across extensive areas of the model domain, enabling realistic reproduction of the observed late-melt season flow deceleration. They further hypothesised that the decline in water pressure during the late-melt season is not entirely replenished over winter, potentially providing an explanation for the observed multi-year slow-down of the ablation area (Hoffman et al., 2016). Such temporal and spatial variations in hydraulic conductivity are not included in most subglacial hydrological studies (hydraulic conductivity is typically used as a tuning parameter; e.g., Werder et al., 2013; Flowers, 2015), leading to an under-prediction of winter basal water pressure compared to observations (Downs et al., 2018).
At increasingly high elevations and beneath increasingly thick ice, we suggest that both connection events and leakage of water out of the weakly-connected system are suppressed. For example, in the lower accumulation area, surface runoff supply is sparse and the melt season is shorter than in the ablation area (van de Wal et al., 2015). As such, the connected system is likely to be less frequently or persistently overwhelmed, providing limited opportunity for connection events to occur. Similarly, water pressure gradients between the connected and weakly-connected parts of the drainage system are likely to be weaker than at lower elevations, thereby limiting the rate of water flow out of the weakly-connected system. The implications of this for the dynamic behaviour of high elevation areas to potential future increases in surface runoff supply are discussed in sections The Inland Limit of Melt-Induced Ice Flow Variations and A Conceptual Model of Subglacial Hydrology and Ice Dynamic Variability. We stress that there are very few observations of ice motion and no observations of subglacial water pressure that we are aware of in the lower accumulation area, and that the above points are, therefore, speculation based on existing theory and observations from the ablation area. It is likely that the contrasting character of runoff supply and ice geometry in the lower accumulation area will produce a subglacial drainage system that is different than in the ablation area; however, if and how they differ is not clear.
The Inland Limit of Melt-Induced Ice Flow Variations
A key question that remains unanswered is the propensity for melt-induced ice flow variations to expand further inland. The recognition that lakes are forming further inland (Howat et al., 2013; Carrivick and Quincey, 2014; Fitzpatrick et al., 2014; Cooley and Christoffersen, 2017), and that seasonal melt-induced ice speed-up is greater and occurs at higher-elevation sites in warmer years compared to cooler years (Sole et al., 2013; Doyle et al., 2014), highlights the potential for inland penetration of runoff-induced ice flow acceleration. Nevertheless, the spatial limits and magnitude of possible future runoff-induced ice flow variations are not well understood or constrained.
Lakes are predicted to expand inland during the twenty-first century (Leeson et al., 2015; Ignéczi et al., 2016); however, it is uncertain whether the same is true of rapid lake drainage. Rapid lake drainage can only occur in areas susceptible to crevasse formation, which typically requires tensile stresses >90 kPa (see Colgan et al., 2016 and references therein) and surface tensile stresses are governed in large part by spatial variations in ice flow and surface topography. With increasing distance from the ice sheet margin, short wavelength high amplitude ice surface topography gives way to longer wavelength, low amplitude topography, which is not generally conducive to generating high tensile stresses. In addition, zones of high tensile stress (topographic highs) are located further from potential lake locations (Poinar et al., 2015). Therefore, with increasing distance from the margin, crevasses may be less likely to intersect lakes, with hydrofracture correspondingly less common. A recent modelling study (Christoffersen et al., 2018) showed, however, that the transient tensile stresses in response to daily-aggregated rapid lake drainage events causes seasonal inland progression of rapid lake drainage and furthermore, found no inland limit for rapid lake drainage. Observations show that fractures can form at very high elevations on the ice sheet (e.g., over 200 km from the margin; Scheick, 2012) and although fewer lakes form at high elevations, the proportion of lakes draining rapidly is relatively insensitive to elevation (Cooley and Christoffersen, 2017). The emerging picture, therefore, is that rapid lake drainage will likely occur at higher elevations in future.
The second element to understanding the inland limit of melt-induced ice velocity variations regards the magnitude and variability of the ice velocity response of high elevation areas. Current observations are a good starting point for this. One hundred forty kilometres from the margin, the highest elevation at which observations of ice velocity are available, Doyle et al. (2014) observed faster ice flow during and following the 2012 extreme melt season relative to cooler years. While faster ice flow during the melt season is directly attributable to runoff forcing, faster winter ice flow is not. Instead, water input to the potentially frozen bed of the interior ice sheet is hypothesised to decouple frozen sticky spots and/or warm basal ice, thereby increasing internal deformation, leading to faster winter flow (Phillips et al., 2010, 2013; Bell et al., 2014; Doyle et al., 2014; Colgan et al., 2015). The extreme melt during 2012 is expected to be the norm by the end of the century (Nghiem et al., 2012), which suggests that “normal” conditions in future will induce a similar velocity response at high elevations (i.e., a modest year-on-year acceleration).
Roughness Modulation of Hydrology-Dynamics
Bed topography may modulate ice flow variability at local to regional spatial scales. The effect of bed topography on ice flow variations is not well understood (Bamber et al., 2013; Prescott, 2013; Lindbäck and Pettersson, 2015), not least because the bed topography itself is poorly constrained, despite major ongoing mapping efforts (Leuschen et al., 2010, updated 2017; Allen, 2013), and improved assimilation techniques (Morlighem et al., 2017). Bed topography affects: (i) subglacial channel location via hydropotential gradients (Shreve, 1972); (ii) surface topography (Gudmundsson, 2003; Ignéczi et al., 2018; Ng et al., 2018) and therefore surface strain rates, supraglacial water routing and lake formation and drainage (Karlstrom and Yang, 2016; Crozier et al., 2018; Ignéczi et al., 2018); (iii) sediment distribution, which may be concentrated in troughs (Bullard and Austin, 2011; Booth et al., 2012; Dow et al., 2013; Jezek et al., 2013; Harper et al., 2017), and; (iv) subglacial cavity geometry, which should affect the magnitude of ice displacement during cavity expansion (Cowton et al., 2016). Observations suggest that although ice flow during the early-melt season is typically fastest overlying deep troughs (Joughin et al., 2013) and spatial variations in ice flow relate to bed topography via its effect on the routing of surface water (Bartholomew et al., 2011b; Palmer et al., 2011), relative annual and inter-annual ice flow variability is broadly consistent over scales characterised by spatially varying bed topography (Tedstone et al., 2014, 2015). Lindbäck et al. (2015) observed a negative correlation between bed roughness and ice velocity in west Greenland, but the effect of roughness on modulating the dynamic variability of the ice sheet has not yet been investigated.
A Conceptual Model of Subglacial Hydrology and Ice Dynamic Variability
We describe here a conceptual model of land-terminating Greenland Ice Sheet hydrology-dynamics, informed by the interactions of runoff and ice flow discussed above (Figure 8).
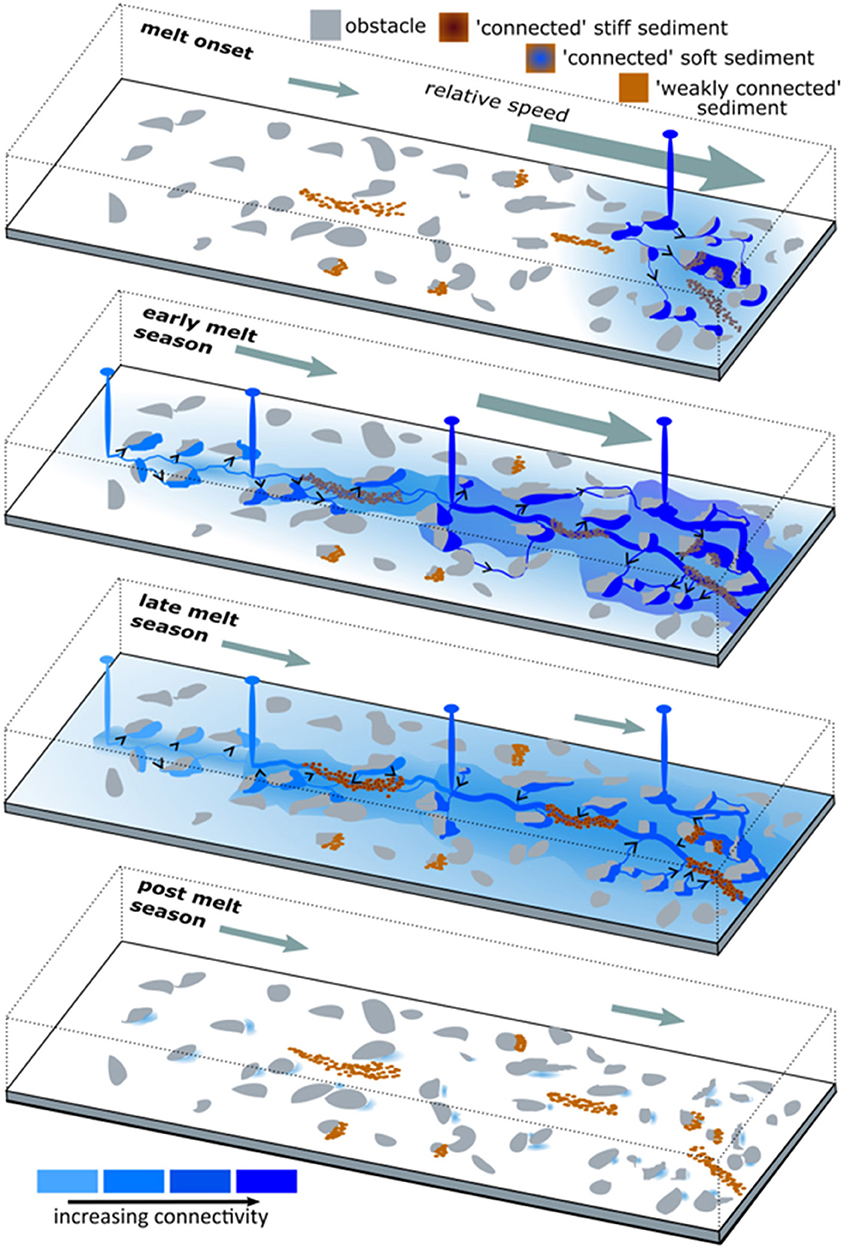
Figure 8. Conceptual model of land-terminating Greenland Ice Sheet seasonal hydrology and dynamics. Melt onset activates part of the weakly-connected drainage system (white background) and subsequent fluctuations in runoff supply lead to cavity expansion, increased sediment deformation and consequent rapid speed-up (grey arrow). In the early-melt season, meltwater accesses the bed at progressively higher elevations and the efficiency and extent of the connected drainage system increases (blue shading), likely forming channels at lower elevations. Surface runoff supply frequently exceeds the capacity of the core of the connected drainage system at progressively higher elevations during the early-melt season, causing speed-up. During the late-melt season, runoff supply declines, and water drains across variable pressure axes and from the weakly-connected system toward efficient drainage forms at lower elevations, but not higher elevations, where drainage system efficiency remains low throughout the melt season. Basal water pressure and cavity size gradually increase during the post-melt season.
Each year, surface runoff accesses the subglacial environment via moulins and crevasses progressively further inland throughout the melt season. Regardless of the substrate, the initial flux of runoff overwhelms the existing inefficient subglacial drainage system, leading to rapid and large speed-up due to cavity expansion (Cowton et al., 2016) and sediment deformation, where present (e.g., Kulessa et al., 2017). This speed-up occurs across large swathes of the ice sheet, beginning later and declining in magnitude with increasing distance from the margin. In the lower ablation area, we suggest that efficient subglacial channels (incised into the overlying ice, the bed, or both) develop progressively inland after surface-to-bed connections form and as runoff supply increases (Figure 9). In the upper ablation area, the basal drainage configuration, specifically whether or not efficient channels form, is currently unknown. There is nevertheless likely to be water exchange in the connected drainage system between a relatively efficient core and surrounding inefficient drainage forms. Throughout the melt season, sufficiently large, and/or rapid pulses of runoff into the efficient parts of the connected drainage system throughout the ablation area are forced laterally across variable pressure axes (e.g., Tedstone et al., 2014), causing cavity expansion (Cowton et al., 2016), sediment deformation (Kulessa et al., 2017), and increasing drainage system connectivity (e.g., Hoffman et al., 2016). During times of steady or declining runoff supply in the ablation area (particularly during the late-melt season), we suggest that water in variable pressure axes and the weakly-connected drainage system drains toward efficient parts of the connected drainage system along hydraulic gradients, leading to a regional reduction in water pressure and an increase in the ice-bed contact area as water storage decreases. During the late-melt season this net water pressure reduction is argued to cause regional ice flow slow-down of the ablation area (Figure 9; Sole et al., 2013; Bougamont et al., 2014; Tedstone et al., 2015; Hoffman et al., 2016). We suggest that water pressure, storage and ice velocity continue to decline on average until the rate of meltwater recharge (from groundwater and frictional and geothermal heat) exceeds runoff evacuation, which allows slow (possibly partial) re-pressurisation, storage replenishment and ice flow recovery to occur before the following melt season (Figure 9; Joughin et al., 2008; Colgan et al., 2011; Sole et al., 2013). Progressively inland, the amplitude of this seasonal cycle and of water transfer between the connected and weakly-connected systems diminishes, until at high elevations, there is no compensatory late-melt season slow-down (Figure 9; van de Wal et al., 2008, 2015; Phillips et al., 2013; Doyle et al., 2014). These seasonal patterns produce annual variations in ice motion that are negatively correlated with runoff supply in the ablation area and positively correlated with runoff supply further inland, though these relationships are statistically weak other than within 30 km of the margin (van de Wal et al., 2015).
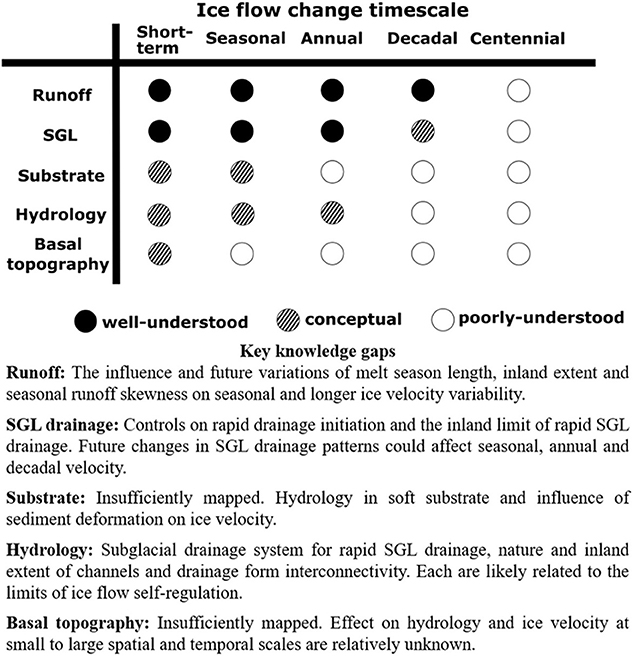
Figure 9. Summary of current understanding of the influence of system components on ice flow variations. Note, that although the processes discussed in the main text may be applicable at the centennial time scale, they are not usually incorporated into model simulations of Greenland Ice Sheet dynamics at this time scale.
We suggest that if future runoff supply increases, as is currently predicted (e.g., Fettweis et al., 2013a,b), future variations in ice flow will likely be characterised by the following key patterns. Mean annual ice flow in areas where there is inferred net drainage of water out of variable pressure axes and the weakly-connected drainage system toward the efficient parts of the connected system will, in all likelihood, continue to decline due to increased connected drainage system efficiency, continued depression of regional basal water pressure and declining driving stresses, in response to thinning (the “self-regulation zone”). Superimposed on this trend will likely be large seasonal variations, which are expected to become more pronounced in response to atmospheric warming (see e.g., Figure 13 in Colgan et al., 2011). Further inland, annual ice flow will likely continue to increase in response to increasing surface melt, unless self-regulation mechanisms become operative. We expect that this zone of inter-annual acceleration should migrate and expand inland with surface-to-bed hydrological connections, whilst the self-regulation zone should also expand inland as far as sufficiently efficient and extensive connected drainage systems can form and remain open long enough to affect basal water pressure and storage and therefore ice flow. Based on the above conceptual model, we would expect that the net response of the land-terminating ice sheet will largely be governed by future changes in the balance of net acceleration in the accumulation area and net deceleration in the ablation area, as well as by changes in ice sheet geometry.
Key Issues and Future Research
There are several key areas that remain poorly understood yet have important implications for understanding ice sheet dynamics. A summary of the relative understanding of key components of the hydrology-dynamic system is shown in Figure 9.
Firstly, continued observations of ice motion in response to changes in the timing and magnitude of runoff delivery will allow better characterisation of the ice dynamic response to runoff supply in a changing climate. Efforts in the field should ideally work to: (i) extend existing high-temporal resolution observations obtained at key sites, and; (ii) supplement these with additional observations at high elevation sites and in contrasting areas. Point (ii) is particularly important given that the vast majority of observations are available only from a relatively small part of the ablation area, which may behave differently to other areas if there are, for example, spatial variations in runoff supply, bed topography and substrate.
Similarly, the limits and thresholds (for initiation) of ice flow self-regulation should be constrained. Ice flow self-regulation is currently operative throughout the ablation area, even in years with extreme melt water supply. In contrast, ice flow self-regulation is not currently observed in the accumulation area; however, it is not clear if future changes in the magnitude and timing of runoff supply will initiate ice flow self-regulation at high elevations. Efforts in the field, such as those recommended above, as well as spatially-extensive velocity estimates throughout the post-melt season period (which are now achievable with the European Space Agency Sentinel satellite constellation) will improve process-understanding of ice flow self-regulation.
Finally, the relative rates at which surface-to-bed hydrologic connections (created by hydrofracture) and surface melt extent will migrate inland under projected future warming scenarios should be further investigated. If both surface melt extent and surface-to-bed hydrologic connections form further inland in future, then the spatial extent of surface runoff-induced velocity variations would likely also increase. However, evaluating the likelihood of this possibility is currently limited by our inability to predict rapid lake drainage.
Conclusions
We have synthesised over 15 years of investigations into the impacts of surface runoff and hydrology on the dynamics of a land-terminating sector of the Greenland Ice Sheet, motivated by a need to understand the net long-term impact of projected future warming on dynamic-thinning and associated enhanced ablation, runoff and sea level rise.
We suggest that ice flow variations arise due to the aggregated effect of several mechanisms by which subglacial water flow influences ice dynamics. Changes in subglacial water pressure and water storage, irrespective of the substrate, are key controls on ice flow variability. Meltwater-induced speed-up appears to be due to reductions in ice-bed contact area, cavity growth and sediment deformation in hydraulically connected parts of the subglacial drainage system. Late-melt season slow-down appears to be due to several mechanisms: in the lower ablation area, efficient channels may induce drainage of water from surrounding inefficient areas. In addition, increasing leakage of water from weakly-connected areas of the drainage system is argued to cause further slow-down, and may be particularly important where channels do not form. We suggest these mechanisms are not mutually exclusive and their combined effect is to drive the observed and statistically significant annual slow-down extending from the ice sheet margin across the lower ablation area and, to a lesser degree, into the upper ablation area, despite increasing runoff supply. In the lower accumulation area, runoff inputs to the bed likely cause hydraulic jacking and reduced ice-bed contact, but do not induce compensatory slow-down effects in the drainage system. Runoff potentially also contributes to warming of basal ice or thawing of the ice-bed interface. Together, these effects result in modest year-on-year increases in both winter and summer flow that are observed.
Under continued warming, annual ice flow in the ablation area will likely continue to decrease on average. We suggest that future reductions in annual flow speed in the ablation area will result primarily from water drainage from large areas of the subglacial drainage system, thereby increasing ice-bed coupling, and from thinning. The future dynamic response of high elevation areas to warming is unclear and requires further investigation, but current observations and modelling indicate small annual speed-up will continue as the climate warms. We suggest however that minor increases in surface melting caused by dynamic thinning in the lower accumulation area are unlikely to considerably impact ice sheet surface mass balance in the twenty-first century and are likely to be dwarfed by those caused by climate change. Therefore, if hydraulic interactions across variable pressure axes and between the connected and weakly-connected systems do dominate ice velocity variations (as we currently infer), then the land-terminating ice sheet is not expected to exhibit net annual ice flow acceleration or associated dynamic thinning over the twenty-first century.
We acknowledge that large swathes of the subglacial environment are as-yet unobserved, that the behaviour of high elevation areas is unclear and that the ice sheet bed is likely characterised by considerable spatial variability in its substrate and roughness, which may mean that other areas of the ice sheet behave differently. Continued monitoring of ice motion and further characterisation of the subglacial environment in response to runoff input, particularly across high elevation areas and in other regions of the ice sheet, along with comparison to model results, are thus essential to constrain the limits and thresholds of self-regulation mechanisms, the character and sensitivity of the weakly-connected subglacial drainage system and to elucidate those hydro-thermo-mechanical subglacial processes that appear to operate within the interior regions of the ice sheet. These will enable better understanding of ice sheet dynamic response to changes in melt season intensity, duration and structure.
Author Contributions
BD wrote the original manuscript and made the figures, with guidance from AS. All authors contributed to editing the manuscript.
Funding
The Scottish Alliance for Geoscience, Environment and Society (SAGES) provided financial support for this work in the form of a studentship for BD.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors would like to acknowledge insightful discussions with L. Andrews, M. Hoffman, R. Bingham and S. Marion, and we are grateful to A. Shepherd and M. McMillan for trying to provide positions of key GPS sites at short notice. We would also like to thank M. Truffer, S. Doyle, A. Hubbard and one other reviewer for providing thorough feedback on the manuscript.
References
Adhikari, S., and Tsai, V. C. (2015). A model for subglacial flooding through a pre-existing hydrological network during the rapid drainage of supraglacial lakes. J. Geophys. Res. Earth Surface 120, 580–603. doi: 10.1002/2014JF003339
Allen, C. (2013). IceBridge MCoRDS L3 Gridded Ice Thickness, Surface, and Bottom, Version 2. Boulder, CO: NASA National Snow and Ice Data Center Distributed Active Archive Center.
Alley, R. B., Dupont, T. K., Parizek, B. R., and Anandakrishnan, S. (2005). Access of surface meltwater to beds of sub-freezing glaciers: preliminary insights. Ann. Glaciol. 40, 8–14. doi: 10.3189/172756405781813483
Andrews, L. C., Catania, G. A., Hoffman, M. J., Gulley, J. D., Lüthi, M. P., Ryser, C., et al. (2014). Direct observations of evolving subglacial drainage beneath the Greenland Ice sheet. Nature 514, 80–83. doi: 10.1038/nature13796
Andrews, L. C., Hoffman, M. J., Neumann, T. A., Catania, G. A., Lüthi, M. P., Hawley, R. L., et al. (2018). Seasonal evolution of the subglacial hydrologic system modified by supraglacial lake drainage in Western Greenland. J. Geophys. Res. Earth Surface 123, 1479–1496. doi: 10.1029/2017JF004585
Arnold, N. S., Banwell, A. F., and Willis, I. C. (2014). High-resolution modelling of the seasonal evolution of surface water storage on the Greenland ice sheet. Cryosphere 8, 1149–1160. doi: 10.5194/tc-8-1149-2014
Bamber, J. L., and Aspinall, W. P. (2013). An expert judgment assessment of future sea level rise from the ice sheets. Nat. Clim. Chang. 3, 424–427. doi: 10.1038/Nclimate1778
Bamber, J. L., Griggs, J. A., Hurkmans, R. T. W. L., Dowdeswell, J. A., Gogineni, S. P., Howat, I., et al. (2013). A new bed elevation dataset for Greenland. Cryosphere 7, 499–510. doi: 10.5194/tc-7-499-2013
Banwell, A., Hewitt, I., Willis, I., and Arnold, N. (2016). Moulin density controls drainage development beneath the Greenland Ice Sheet. J. Geophys. Res. Earth Surface 121, 2248–2269. doi: 10.1002/2015JF003801
Banwell, A. F., Arnold, N. S., Willis, I. C., Tedesco, M., and Ahlstrøm, A. P. (2012). Modeling supraglacial water routing and filling on the Greenland Ice Sheet. J. Geophys. Res. 117, F04012. doi: 10.1029/2012JF002393
Bartholomew, I., Nienow, P., Sole, A., Mair, D., Cowton, T., and King, M. A. (2012). Short-term variability in Greenland Ice sheet motion forced by time-varying meltwater drainage: Implications for the relationship between subglacial drainage system behaviour and ice velocity. J. Geophys. Res. Earth Surface 117:F03002. doi: 10.1029/2011JF002220
Bartholomew, I., Nienow, P., Sole, A., Mair, D., Cowton, T., Palmer, S., et al. (2011b). Supraglacial forcing of subglacial drainage in the ablation area of the Greenland ice sheet. Geophys. Res. Lett. 38:L08502. doi: 10.1029/2011GL047063
Bartholomew, I. D., Nienow, P., Mair, D., Hubbard, A., King, M. A., and Sole, A. J. (2010). Seasonal evolution of subglacial drainage and acceleration in a Greenland outlet glacier. Nat. Geosci. 3, 408–411. doi: 10.1038/ngeo863
Bartholomew, I. D., Nienow, P., Sole, A., Mair, D., Cowton, T., King, M. A., et al. (2011a). Seasonal variations in Greenland Ice sheet motion: Inland extent and behaviour at higher elevations. Earth Planet. Sci. Lett. 307, 271–278. doi: 10.1016/j.epsl.2011.04.014
Beaud, F., Venditti, J. G., Flowers, G. W., and Koppes, M. (2018). Excavation of subglacial bedrock by seasonal meltwater flow. Earth Surface Process. Landforms. 43, 1960–1972. doi: 10.1002/esp.4367
Bell, R. E., Tinto, K., Das, I., Wolovick, M., Chu, W., Creyts, T. T., et al. (2014). Deformation, warming and softening of Greenland's ice by refreezing meltwater. Nat. Geosci. 7, 497–502. doi: 10.1038/ngeo2179
Bhatia, M. P., Das, S. B., Kujawinski, E. B., and Henderson, P. (2011). Seasonal evolution of water contributions to discharge from a Greenland outlet glacier: insights from a new isotope-mixing model. J. Glaciol. 57, 929–941. doi: 10.3189/002214311798043861
Bindschadler, R. A. (1983). The importance of pressurized subglacial water in separation and sliding at the glacier bed. J. Glaciol. 29, 3–19. doi: 10.1017/S0022143000005104
Bingham, R. G., Hubbard, A. L., Nienow, P. W., and Sharp, M. J. (2008). An investigation into the mechanisms controlling seasonal speedup events at a High Arctic glacier. J. Geophys. Res. 113:F02006. doi: 10.1029/2007JF000832
Bingham, R. G., Nienow, P. W., Sharp, M. J., and Boon, S. (2005). Subglacial drainage processes at a High Arctic polythermal valley glacier. J. Glaciol. 51, 15–24. doi: 10.3189/172756505781829520
Bingham, R. G., Nienow, P. W., Sharp, M. J., and Copland, L. (2006). Hydrology and dynamics of a polythermal (mostly cold) High Arctic glacier. Earth Surface Process. Landforms 31, 1463–1479. doi: 10.1002/esp.1374
Booth, A. D., Clark, R. A., Kulessa, B., Murray, T., Carter, J., Doyle, S., et al. (2012). Thin-layer effects in glaciological seismic amplitude-versus-angle (AVA) analysis: implications for characterising a subglacial till unit, Russell Glacier, West Greenland. Cryosphere 6, 909–922. doi: 10.5194/tc-6-909-2012
Bougamont, M., Christoffersen, P. A. L., Hubbard Fitzpatrick, A. A., Doyle, S. H., and Carter, S. P. (2014). Sensitive response of the Greenland Ice sheet to surface melt drainage over a soft bed. Nat. Commun. 5:5052. doi: 10.1038/ncomms6052
Boulton, G. S., Dobbie, K. E., and Zatsepin, S. (2001). Sediment deformation beneath glaciers and its coupling to the subglacial hydraulic system. Quat. Int. 86, 3–28. doi: 10.1016/S1040-6182(01)00048-9
Boulton, G. S., and Jones, A. S. (1979). Stability of temperate ice caps and ice sheets resting on beds of deformable sediment. J. Glaciol. 24, 29–43. doi: 10.1017/S0022143000014623
Box, J. E., and Ski, K. (2007). Remote sounding of Greenland supraglacial melt lakes: implications for subglacial hydraulics. J. Glaciol. 53, 257–265. doi: 10.3189/172756507782202883
Bueler, E., and van Pelt, W. (2015). Mass-conserving subglacial hydrology in the Parallel Ice Sheet Model version 0.6. Geosci. Model Dev. 8, 1613–1635. doi: 10.5194/gmd-8-1613-2015
Bullard, J. E., and Austin, M. J. (2011). Dust generation on a proglacial floodplain, West Greenland. Aeolian Res. 3, 43–54. doi: 10.1016/j.aeolia.2011.01.002
Burgess, E. W., Larsen, C. F., and Forster, R. R. (2013). Summer melt regulates winter glacier flow speeds throughout Alaska. Geophys. Res. Lett. 40, 6160–6164. doi: 10.1002/2013GL058228
Carmichael, J. D., Joughin, I., Behn, M. D., Das, S., King, M. A., Stevens, L., et al. (2015). Seismicity on the western Greenland Ice sheet: Surface fracture in the vicinity of active moulins. J. Geophys. Res. Earth Surface 120, 1082–1106. doi: 10.1002/2014JF003398
Carrivick, J. L., and Quincey, D. J. (2014). Progressive increase in number and volume of ice-marginal lakes on the western margin of the Greenland Ice sheet. Glob. Planet. Change 116, 156–163. doi: 10.1016/j.gloplacha.2014.02.009
Catania, G. A., and Neumann, T. A. (2010). Persistent englacial drainage features in the Greenland Ice Sheet. Geophys. Res. Lett. 37:L02501. doi: 10.1029/2009GL041108
Cazenave, A., and Llovel, W. (2010). Contemporary sea level rise. Ann. Rev. Mar. Sci. 2, 145–173. doi: 10.1146/annurev-marine-120308-081105
Chandler, D. M., Wadham, J. L., Lis, G. P., Cowton, T., Sole, A., Bartholomew, I., et al. (2013). Evolution of the subglacial drainage system beneath the Greenland Ice sheet revealed by tracers. Nat. Geosci. 6, 195–198. doi: 10.1038/ngeo1737
Christoffersen, P., Bougamont, M., Hubbard, A., Doyle, S. H., Grigsby, S., and Pettersson, R. (2018). Cascading lake drainage on the Greenland Ice Sheet triggered by tensile shock and fracture. Nat. Commun. 9:1064. doi: 10.1038/s41467-018-03420-8
Chu, V. W. (2014). Greenland ice sheet hydrology: a review. Prog Phys. Geogr. 38, 19–54. doi: 10.1177/0309133313507075
Chu, W., Creyts, T. T., and Bell, R. E. (2016b). Rerouting of subglacial water flow between neighbouring glaciers in West Greenland. J. Geophys. Res. Earth Surface 121, 925–938. doi: 10.1002/2015JF003705
Chu, W., Schroeder, D. M., Seroussi, H., Creyts, T. T., Palmer, S. J., and Bell, R. E. (2016a). Extensive winter subglacial water storage beneath the Greenland Ice Sheet. Geophys. Res. Lett. 43, 12484–12492. doi: 10.1002/2016GL071538
Clason, C. C., Mair, D. W. F., Nienow, P. W., Bartholomew, I. D., Sole, A., Palmer, S., et al. (2015). Modelling the transfer of supraglacial meltwater to the bed of Leverett Glacier, Southwest Greenland. Cryosphere 9, 123–138. doi: 10.5194/tc-9-123-2015
Colgan, W., Rajaram, H., Abdalati, W., McCutchan, C., Mottram, R., Moussavi, M. S., et al. (2016). Glacier crevasses: Observations, models and mass balance implications. Rev. Geophys. 54, 119–161. doi: 10.1002/2015RG000504
Colgan, W., Rajaram, H., Anderson, R. S., Steffen, K., Zwally, H. J., Phillips, T., et al. (2012). The annual glaciohydrology cycle in the ablation zone of the Greenland ice sheet: part 2. Observed and modeled ice flow. J. Glaciol. 58, 51–64. doi: 10.3189/2012JoG11J081
Colgan, W., Sommers, A., Rajaram, H., Abdalati, W., and Frahm, J. (2015). Considering thermal-viscous collapse of the Greenland ice sheet. Earth's Future 3, 252–267. doi: 10.1002/2015EF000301
Colgan, W., Steffen, K., McLamb, W. S., Abdalati, W., Rajaram, H., Motyka, R., et al. (2011). An increase in crevasse extent, West Greenland: hydrologic implications. Geophys. Res. Lett. 38:L18502. doi: 10.1029/2011GL048491
Cooley, S. W., and Christoffersen, P. (2017). Observation bias correction reveals more rapidly draining lakes on the Greenland Ice Sheet. J. Geophys. Res. Earth Surface 122, 1867–1881. doi: 10.1002/2017JF004255
Cowton, T., Nienow, P., Sole, A., Bartholomew, I., and Mair, D. (2016). Variability in ice motion at a land-terminating Greenlandic outlet glacier: the role of channelized and distributed drainage systems. J. Glaciol. 62, 451–466. doi: 10.1017/jog.2016.36
Cowton, T., Nienow, P., Sole, A., Wadham, J., Lis, G., Bartholomew, I., et al. (2013). Evolution of drainage system morphology at a land-terminating Greenlandic outlet glacier. J. Geophys. Res. Earth Surface 118, 29–41. doi: 10.1029/2012JF002540
Creyts, T. T., and Schoof, C. G. (2009). Drainage through subglacial water sheets. J. Geophys. Res. Earth Surface 114:F04008. doi: 10.1029/2008JF001215
Crozier, J., Karlstrom, L., and Yang, K. (2018). Basal control of supraglacial meltwater catchments on the Greenland Ice Sheet. Cryosphere 12, 3383–3407. doi: 10.5194/tc-12-3383-2018
Cullather, R. I., Mowicki, S. M. J., Zhao, B., and Koenig, L. S. (2016). A characterization of Greenland Ice Sheet surface melt and runoff in contemporary reanalyses and a regional climate model. Front. Earth Sci. 4:10. doi: 10.3389/feart.2016.00010
Damsgaard, A., Egholm, D. L., Beem, L. H., Tulaczyk, S., Larsen, N. K., Piotrowski, J. A., et al. (2016). Ice flow dynamics forced by water pressure variations in subglacial granular beds. Geophys. Res. Lett. 43, 2165–12173. doi: 10.1002/2016GL071579
Damsgaard, A., Egholm, D. L., Piotrowski, J. A., Tulaczyk, S., Larsen, N. K., and Brædstrup, C. F. (2015). A new methodology to simulate subglacial deformation of water-saturated granular material. Cryosphere 9, 2183–2200. doi: 10.5194/tc-9-2183-2015
Das, S. B., Joughin, I., Behn, M. D., Howat, I. M., King, M. A., Lizarralde, D., et al. (2008). Fracture propagation to the base of the Greenland Ice sheet during supraglacial lake drainage. Science 320, 778–781. doi: 10.1126/science.1153360
de Fleurian, B., Morlighem, M., Seroussi, H., Rignot, E., van den Broeke, M. R., Munneke, P. K. Tedstone, et al. (2016). A modeling study of the effect of runoff variability on the effective pressure beneath Russell Glacier, West Greenland. J. Geophys. Res. Earth Surface 121, 1834–1848. doi: 10.1002/2016JF003842
Dow, C. F., Hubbard, A., Booth, A. D., Doyle, S. H., Gusmeroli, A., and Kulessa, Y. B. (2013). Seismic evidence of mechanically weak sediments underlying Russell Glacier, West Greenland. Ann. Glaciol. 54, 135–141. doi: 10.3189/2013AoG64A032
Dow, C. F., Kulessa, B., Rutt, I. C., Doyle, S. H., and Hubbard, A. (2014). Upper bounds on subglacial channel development for interior regions of the Greenland ice sheet. J. Glaciol. 60, 1044–1052. doi: 10.3189/2014JoG14J093
Dow, C. F., Kulessa, B., Rutt, I. C., Tsai, V. C., Pimentel, S., Doyle, S. H., et al. (2015). Modeling of subglacial hydrological development following rapid supraglacial lake drainage. J. Geophys. Res. Earth Surface 120, 1127–1147. doi: 10.1002/2014JF003333
Downs, J. Z., Johnson, J. V., Harper, J. T., and Meierbachtol, T. (2018). Dynamic hydraulic conductivity reconciles mismatch between modeled and observed winter subglacial water pressure. J. Geophys. Res. Earth Surface. 123, 818–836. doi: 10.1002/2017JF004522
Doyle, S. H., Hubbard, A., Fitzpatrick, A. A. W., van As, D., Mikkelsen, A. B., Pettersson, R., et al. (2014). Persistent flow acceleration within the interior of the Greenland ice sheet. Geophys. Res. Lett. 41, 899–905. doi: 10.1002/2013GL058933
Doyle, S. H., Hubbard, A., Van De Wal, R. S., van As, D., Scharrer, K., Meierbachtol, T. W., et al. (2015). Amplified melt and flow of the Greenland ice sheet driven by late-summer cyclonic rainfall. Nat. Geosci. 8, 647–653. doi: 10.1038/ngeo2482
Doyle, S. H., Hubbard, A. L., Dow, C. F., Jones, G. A., Fitzpatrick, A., Gusmeroli, A., et al. (2013). Ice tectonic deformation during the rapid in situ drainage of a supraglacial lake on the Greenland Ice sheet. Cryosphere 7, 129–140. doi: 10.5194/tc-7-129-2013
Doyle, S. H., Hubbard, B., Christoffersen, P., Young, T. J., Hofstede, C., Bougamont, M., et al. (2018). Physical conditions for fast glacier flow: 1. Measurements from boreholes drilled to the bed of Store glacier, West Greenland. J. Geophys. Res. Earth Surface 123, 324–328. doi: 10.1002/2017JF004529
Echelmeyer, K., Clarke, T. S., and Harrison, W. D. (1991). Surficial glaciology of Jakobshavns Isbrae, West Greenland: Part I. Surface morphology. J. Glaciol. 37:368–382. doi: 10.1017/S0022143000005803
Engelhardt, H., Harrison, W., and Kamb, B. (1978). Basal sliding and conditions at the glacier bed as revealed by bore-hole photography. J. Glaciol. 20, 469–508. doi: 10.1017/S002214300002089X
Fettweis, X., Franco, B., Tedesco, M., Van Angelen, J. H., Lenaerts, J. T. M., Van den Broeke, M. R., et al. (2013a). Estimating Greenland ice sheet-surface mass balance contribution to future sea level rise using the regional atmospheric climate model MAR. Cryosphere 6, 3101–3147. doi: 10.5194/tcd-6-3101-2012
Fettweis, X., Hanna, E., Lang, C., Belleflamme, A., Erpicum, M., and Gallée, H. (2013b). Brief communication “Important role of the mid-tropospheric atmospheric circulation in the recent surface melt increase over the Greenland ice sheet”. Cryosphere 7, 241–248. doi: 10.5194/tc-7-241-2013
Fitzpatrick, A. A., Hubbard, A., Joughin, I., Quincey, D. J., Van As, D., Mikkelsen, A. P., et al. (2013). Ice flow dynamics and surface meltwater flux at a land-terminating sector of the Greenland ice sheet. J. Glaciol. 59, 687–696. doi: 10.3189/2013JoG12J143
Fitzpatrick, A. A. W., Hubbard, A. L., Box, J. E., Quincey, D. J., van As, D., Mikkelsem, A. P. B., et al. (2014). A decade (2002-2012) of lake volume estimates across Russell Glacier, West Greenland. Cryosphere 8, 107–121. doi: 10.5194/tc-8-107-2014
Flowers, G. E. (2015). Modelling water flow under glaciers and ice sheets. Proc. Math. Phys. Eng. Sci. 471:20140907. doi: 10.1098/rspa.2014.0907
Forbes, J. (1846). Illustrations of the viscous theory of glacier motion. Part II. An attempt to establish by observation the plasticity of glacier ice. Philos. Trans. R. Soc. Lond. 136, 157–175.
Fountain, A. G., and Walder, J. S. (1998). Water flow through temperate glaciers. Rev. Geophys. 36, 299–328. doi: 10.1029/97RG03579
Fowler, A. (1987). Sliding with cavity formation. J. Glaciol. 33, 131–141. doi: 10.1017/S0022143000008820
Fudge, T., Humphrey, N., Harper, J., and Pfeffer, W. (2008). Diurnal fluctuations in borehole water levels: configuration of the drainage system beneath Bench Glacier, Alaska, USA. J. Glaciol. 54, 297–306. doi: 10.3189/002214308784886072
Gillet-Chaulet, F., Gagliardini, O., Seddik, H., Nodet, M., Durand, G., Ritz, C., et al. (2012). Greenland ice sheet contribution to sea-level rise from a new-generation ice sheet model. Cryosphere 6, 1561–1576. doi: 10.5194/tc-6-1561-2012
Gordon, S., Sharp, M., Hubbard, B., Smart, C., Ketterling, B., and Willis, I. (1998). Seasonal reorganization of subglacial drainage inferred from measurements in boreholes. Hydrol. Process. 12, 105–133. doi: 10.1002/(SICI)1099-1085(199801)12:1%3C105::AID-HYP566%3E3.0.CO;2-%23
Greenwood, S. L., Clason, C. C., Helanow, C., and Margold, M. (2016). Theoretical, contemporary observational and palaeo-perspectives on ice sheet hydrology: Processes and products. Earth Sci. Rev. 155, 1–27. doi: 10.1016/j.earscirev.2016.01.010
Gudmundsson, G. H. (2003). Transmission of basal variability to a glacier surface. J. Geophys. Res. Solid Earth 108, 1–19. doi: 10.1029/2002JB002107
Gulley, J. D., Grabiec, M., Martin, J. B., Jania, J., Catania, G., and Glowacki, P. (2012). The effect of discrete recharge by moulins and heterogeneity in flow-path efficiency at glacier beds on subglacial topography. J. Glaciol. 58, 926, 940. doi: 10.3189/2012JoG11J189
Haran, T., Bohlander, J., Scambos, T., Painter, T., and Fahnestock, M. (2015). MEaSUREs MODIS Mosaic of Greenland 2005 (MOG2005) Image Map. Boulder, CO: National Snow and Ice Data Center.
Harper, J. T., Humphrey, N. F., Pfeffer, W. T., and Lazar, B. (2007). Two modes of accelerated glacier sliding related to water. Geophys. Res. Lett. 34, L12503. doi: 10.1029/2007GL030233
Harper, J. T., Humpohrey, N. F., Meirerbachtol, T. W., Graly, J. A., and Fischer, U. H. (2017). Borehole measurements indicate hard bed conditions, Kangerlussuaq sector, western Greenland Ice Sheet. J. Geophys. Res. Earth Surface 122, 1605–1618. doi: 10.1002/2017JF004201
Helm, V., Humbert, A., and Miller, H. (2014). Elevation and elevation change of Greenland and Antarctica derived from CryoSat-2. Cryosphere 8, 1539–1559. doi: 10.5194/tc-8-1539-2014
Hewitt, I. J. (2011). Modelling distributed and channelized subglacial drainage: the spacing of channels. J. Glaciol. 57, 302–314. doi: 10.3189/002214311796405951
Hewitt, I. J. (2013). Seasonal changes in ice sheet motion due to meltwater lubrication. Earth Planet. Sci. Lett. 371, 16–25. doi: 10.1016/j.epsl.2013.04.022
Hock, R., and Hooke, R. L. (1993). Evolution of the internal drainage system in the lower part of the ablation area of Storglaciären, Sweden. Geol. Soc. Am. Bull. 105, 537–546. doi: 10.1130/0016-7606(1993)105<0537:EOTIDS>2.3.CO;2
Hodge, S. M. (1979). Direct measurements of basal water pressures: progress and problems. J. Glaciol. 23, 309–319. doi: 10.1017/S0022143000029920
Hoffman, M., and Price, S. (2014). Feedbacks between coupled subglacial hydrology and glacier dynamics. J. Geophys. Res. Earth Surface 119, 414–436. doi: 10.1002/2013JF002943
Hoffman, M. J., Andrews, L. C., Price, S. A., Catania, G. A., Neumann, T. A., Lüthi, M. P., et al. (2016). Greenland subglacial drainage evolution regulated by weakly connected regions of the bed. Nat. Commun. 7:13903. doi: 10.1038/ncomms13903
Hoffman, M. J., Catania, G. A., Neumann, T. A., Andrews, L. C., and Rumrill, J. A. (2011). Links between acceleration, melting, and supraglacial lake drainage of the western Greenland Ice Sheet. J. Geophys. Res. 116:F04035. doi: 10.1029/2010JF001934
Hoffman, M. J., Perego, M., Andrews, L. C., Price, S. F., Neumann, T. A., Johnson, S. V., et al. (2018). Widespread moulin formation during supraglacial lake drainages in Greenland. Geophys. Res. Lett. 45, 778–788. doi: 10.1002/2017GL075659
Hofstede, C., Christoffersen, P., Hubbard, B., Doyle, S. H., Young, T. J., Diez, A., et al. (2018). Physical conditions of fast glacier flow: 2. Variable extent of anisotropic ice and soft basal sediment from seismic reflection data acquired on Store Glacier, west Greenland. J. Geophys. Res. Earth Surface 123, 349–362. doi: 10.1002/2017JF004297
Hooke, R. L., Laumann, T., and Kohler, J. (1990). Subglacial water pressures and the shape of subglacial conduits. J. Glaciol. 36, 62–71. doi: 10.1017/S0022143000005566
Howat, I., Negrete, A., and Smith, B. (2014). The Greenland Ice Mapping Project (GIMP) land classification and surface elevation data sets. Cryosphere 8, 1509–1518. doi: 10.5194/tc-8-1509-2014
Howat, I. M., Peña, S., Van Angelen, J. H., Lenaerts, J. T. M., and Van den Broeke, M. R. (2013). Brief Communication“ Expansion of meltwater lakes on the Greenland ice sheet”. Cryosphere 7, 201–204. doi: 10.5194/tc-7-201-2013
Hubbard, B., and Nienow, P. (1997). Alpine subglacial hydrology. Quat. Sci. Rev. 16, 939–955. doi: 10.1016/S0277-3791(97)00031-0
Hubbard, B. P., Sharp, M. J., Willis, I. C., Nielsen, M. T., and Smart, C. C. (1995). Borehole water-level variations and the structure of the subglacial hydrological system of Haut Glacier d'Arolla, Valais, Switzerland. J. Glaciol. 41, 572–583. doi: 10.1017/S0022143000034894
Ignéczi, A., Sole, A. J., Livingstone, S. J., Leeson, A. A., Fettweis, X., Selmes, N., et al. (2016). Northeast sector of the Greenland Ice Sheet to undergo the greatest inland expansion of supraglacial lakes during the 21st century. Geophys. Res. Lett. 43, 9729–9738. doi: 10.1002/2016GL070338
Ignéczi, Á., Sole, A. J., Livingstone, S. J., Ng, F. S., and Yang, K. (2018). Greenland Ice Sheet surface topography and drainage structure controlled by the transfer of basal variability. Front. Earth Sci. 6:101. doi: 10.3389/feart.2018.00101
Iken, A. (1981). The effect of subglacial water pressure on the sliding velocity of a glacier in an idealised numerical model. J. Glaciol. 32, 110–421.
Iken, A., and Bindschadler, R. A. (1986). Combined measurements of subglacial water pressure and surface velocity of Findelengletscher, Switzerland: conclusions about drainage system and sliding mechanism. J. Glaciol. 32, 101–119. doi: 10.1017/S0022143000006936
Iken, A., Röthlisberger, H., Flotron, A., and Haeberli, W. (1983). The uplift of Unteraargletscher at the beginning of the melt season - a consequence of water storage at the bed? J. Glaciol. 29, 28–47. doi: 10.1017/S0022143000005128
Iken, A., and Truffer, M. (1997). The relationship between subglacial water pressure and velocity of Findelengletscher, Switzerland, during its advance and retreat. J. Glaciol. 43, 328–338. doi: 10.1017/S0022143000003282
Irvine-Fynn, T. D. L., Hodson, A. J., Moorman, B. J., Vatne, G., and Hubbard, A. L. (2011). Polythermal glacier hydrology: a review. Rev. Geophys. 49:RG4002. doi: 10.1029/2010RG000350
Iverson, N. R., Baker, R. W., Hooke, R. L., Hanson, B., and Jansson, P. (1999). Coupling between a glacier and a soft bed: I. A relation between effective pressure and local shear stress determined from till elasticity. J. Glaciol. 45, 31–40. doi: 10.1017/S0022143000003014
Jezek, K., Wu, X., Gogineni, P., Rodriguez, E., Freeman, A., Rodriguez-Morales, F., et al. (2011). Radar images of the bed of the Greenland Ice Sheet. Geophys. Res. Lett. 38, L01501. doi: 10.1029/2010GL045519
Jezek, K., Wu, X., Paden, J., and Leuschen, C. (2013). Radar mapping of Isunnguata Sermia, Greenland. J. Glaciol. 59, 1135–1146. doi: 10.3189/2013JoG12J248
Joughin, I., Das, S. B., Flowers, G. E., Behn, M. D., Alley, R. B., King, M. A., et al. (2013). Influence of ice sheet geometry and supraglacial lakes on seasonal ice flow variability. Cryosphere 7, 1185–1192. doi: 10.5194/tc-7-1185-2013
Joughin, I., Das, S. B., King, M., Smith, B. E., Howat, I. M., and Moon, T. (2008). Seasonal speedup along the western flank of the Greenland Ice Sheet. Science 320, 781–783. doi: 10.1126/science.1153288
Kamb, B. (1987). Glacier surge mechanism based on linked cavity configuration of the basal water conduit system. J. Geophys. Res. Solid Earth 92, 9083–9100. doi: 10.1029/JB092iB09p09083
Kamb, B., and Echelmeyer, K. A. (1986). Stress-gradient coupling in glacier flow: I. Longitudinal averaging of the influence of ice thickness and surface slope. J. Glaciol. 32, 267–284. doi: 10.1017/S0022143000015604
Kamb, B., Raymond, C., Harrison, W., Engelhardt, H., Echelmeyer, K., Humphrey, N., et al. (1985). Glacier surge mechanism: 1982-1983 surge of Variegated Glacier, Alaska. Science 227, 469–479. doi: 10.1126/science.227.4686.469
Karlstrom, L., and Yang, K. (2016). Fluvial supraglacial landscape evolution on the Greenland Ice Sheet. Geophys. Res. Lett. 43, 2683–2692. doi: 10.1002/2016GL067697
Kingslake, J., Ng, F., and Sole, A. (2015). Modelling channelized surface drainage of supraglacial lakes. J. Glaciol. 61, 185–199. doi: 10.3189/2015JoG14J158
Koziol, C., Arnold, N., Pope, A., and Colgan, W. (2017). Quantifying supraglacial meltwater pathways in the Paakitsoq region, West Greenland. J. Glaciol. 63, 464, 476. doi: 10.1017/jog.2017.5
Koziol, C. P., and Arnold, N. (2018). Modelling seasonal meltwater forcing of the velocity of land-terminating margins of the Greenland Ice Sheet. Cryosphere 12, 971–991. doi: 10.5194/tc-12-971-2018
Krabill, W., Hanna, E., Huybrechts, P., Abdalati, W., Cappelen, J., Csatho, B., et al. (2004). Greenland ice sheet: increased coastal thinning. Geophys. Res. Lett. 31:L24402. doi: 10.1029/2004GL021533
Krawczynski, M. J., Behn, M. D., Das, S. B., and Joughin, I. (2009). Constraints on the lake volume required for hydro-fracture through ice sheets. Geophys. Res. Lett. 36:L10501. doi: 10.1029/2008GL036765
Kulessa, B., Hubbard, A. L., Booth, A. D., Bougamont, M., Dow, C. F., Doyle, S. H., et al. (2017). Seismic evidence for complex sedimentary control of Greenland Ice Sheet flow. Sci. Adv. 3:e1603071. doi: 10.1126/sciadv.1603071
Kyrke-Smith, T. M., and Fowler, A. C. (2014). Subglacial swamps. Proc. Math. Phys. Eng. Sci. 470:20140340. doi: 10.1098/rspa.2014.0340
Lampkin, D. J., and VanderBerg, J. (2011). A preliminary investigation of the influence of basal and surface topography on supraglacial lake distribution near Jakobshavn Isbrae, western Greenland. Hydrol. Process. 25, 3347–3355. doi: 10.1002/hyp.8170
Leeson, A. A., Shepherd, A., Briggs, K., Howat, I., Fettweis, X., Morlighem, M., et al. (2015). Supraglacial lakes on the Greenland ice sheet advance inland under warming climate. Nat. Clim. Chang. 5, 51–55. doi: 10.1038/nclimate2463
Lefeuvre, P.-M., Jackson, M., Lappegard, G., and Hagen, J. O. (2015). Interannual variability of glacier basal pressure from a 20 year record. Ann. Glaciol. 56, 33–44. doi: 10.3189/2015AoG70A019
Lefeuvre, P.-M., Zwinger, T., Jackson, M., Gagliardini, O., Lappegard, G., and Hagen, J. O. (2018). Stress redistribution explains anti-correlated subglacial pressure variations. Front. Earth Sci. 5:110. doi: 10.3389/feart.2017.00110
Leuschen, C., Gogineni, P., Rodriguez-Morales, F., Paden, J., and Allen, C. (2010). IceBridge MCoRDS L2 Ice Thickness, Version 1. Boulder, CO: NASA National Snow and Ice Data Center Distributed Active Archive Center.
Lindbäck, K., Pettersson, R., Hubbard, A. L., Doyle, S. H., van As, D., Mikkelsen, A. B., et al. (2015). Subglacial water drainage, storage, and piracy beneath the Greenland ice sheet. Geophys. Res. Lett. 42, 7606–7614. doi: 10.1002/2015GL065393
Lindbäck, K. R., and Pettersson, R. (2015). Spectral roughness and glacial erosion of a land-terminating section of the Greenland Ice Sheet. Geomorphology 238, 149–159. doi: 10.1016/j.geomorph.2015.02.027
Livingstone, S. J., Clark, C. D., Woodward, J., and Kingslake, J. (2013). Potential subglacial lakes and meltwater drainage pathways beneath the Antarctic and Greenland ice sheets. Cryosphere 7, 1721–1740. doi: 10.5194/tc-7-1721-2013
Livingstone, S. J., Utting, D. J., Ruffell, A., Clark, C. D., Pawley, S., Atkinson, N., et al. (2016). Discovery of relic subglacial lakes and their geometry and mechanism of drainage. Nat. Commun. 7:11767. doi: 10.1038/ncomms11767
Lliboutry, L. (1968). General theory of subglacial cavitation and sliding of temperate glaciers. J. Glaciol. 7, 21–58. doi: 10.1017/S0022143000020396
McGrath, D., Colgan, W., Steffen, K., and Lauffenburger, P. (2011). Assessing the summer water budget of a moulin basin in the Sermeq Avannarleq ablation region, Greenland ice sheet. J. Glaciol. 57, 954–964. doi: 10.3189/002214311798043735
McMillan, M., Nienow, P., Shepherd, A., Benham, T., and Sole, A. (2007). Seasonal evolution of supra-glacial lakes on the Greenland Ice sheet. Earth Planet. Sci. Lett. 262, 484–492. doi: 10.1016/j.epsl.2007.08.002
Meierbachtol, T. W., Harper, J. T., and Humphrey, N. F. (2013). Basal drainage system response to increasing surface melt on the Greenland Ice Sheet. Science 341, 777–779. doi: 10.1126/science.1235905
Meierbachtol, T. W., Harper, J. T., Humphrey, N. F., and Wright, P. J. (2016). Mechanical forcing of water pressure in a hydraulically isolated reach beneath Western Greenland's ablation area. Ann Glaciol. 57, 62–70. doi: 10.1017/aog.2016.5
Meyer, C. R., Fernandes, M. C., Creyts, T. T., and Rice, J. R. (2016). Effects of ice deformation on Röthlisberger channels and implications for transitions in subglacial hydrology. J. Glaciol. 62, 750–762. doi: 10.1017/jog.2016.65
Morlighem, M., Williams, C. N., Rignot, E., An, L., Arndt, J. E., Bamber, J. L. Zinglersen, et al. (2017). BedMachine v3: Complete bed topography and ocean bathymetry mapping of Greenland from multi-beam echo sounding combined with mass conservation. Geophys. Res. Lett. 44, 11051–11061. doi: 10.1002/2017GL074954
Morriss, B. F., Hawley, R. L., Chipman, J. W., Andrews, L. C., Catania, G. A., Hoffman, M. J., et al. (2013). A ten-year record of supraglacial lake evolution and rapid drainage in West Greenland using an automated processing algorithm for multispectral imagery. Cryosphere 7, 1869–1877. doi: 10.5194/tc-7-1869-2013
Murray, T., and Clarke, G. K. C. (1995). Black-box modelling of the subglacial water system. J. Geophys. Res. Solid Earth 100, 10231–10245. doi: 10.1029/95JB00671
Ng, F. S., Ignéczi, Á., Sole, A. J., and Livingstone, S. J. (2018). Response of surface topography to basal variability along glacial flowlines. J. Geophys. Res. Earth Surface 123, 2319–2340. doi: 10.1029/2017JF004555
Ng, F. S. L. (2000). Canals under sediment-based ice sheets. Ann. Glaciol. 30, 146, 152. doi: 10.3189/172756400781820633
Nghiem, S. V., Hall, D. K., Mote, T. L., Tedesco, M., Albert, M. R., Keegan, K., et al. (2012). The extreme melt across the Greenland ice sheet in 2012. Geophys. Res. Lett. 39:L20502. doi: 10.1029/2012GL053611
Nick, F. M., Vieli, A., Andersen, M. L., Joughin, I., Payne, A., Edwards, T. L., et al. (2013). Future sea-level rise from Greenland's main outlet glaciers in a warming climate. Nature 497, 235–238. doi: 10.1038/nature12068
Nienow, P., Sharp, M., and Willis, I. (1998). Seasonal changes in the morphology of the subglacial drainage system, Haut Glacier d'Arolla, Switzerland. Earth Surface Process. Landforms 23, 825–84. doi: 10.1002/(SICI)1096-9837(199809)23:9<825::AID-ESP893>3.0.CO;2-2
Nienow, P. W., Hubbard, A. L., Hubbard, B. P., Chandler, D. M., Mair, D. W. F., Sharp, M. J., et al. (2005). Hydrological controls on diurnal ice flow variability in valley glaciers. J. Geophys. Res. Earth Surface 110:F04002. doi: 10.1029/2003JF000112
Nienow, P. W., Sole, A. J., Slater, D. A., and Cowton, D. A. (2017). Recent advances in our understanding of the role of meltwater in the Greenland Ice Sheet System. Curr. Clim. Change Rep. 3, 330–344. doi: 10.1007/s40641-017-0083-9
Nye, J. (1976). Water flow in glaciers: jökulhlaups, tunnels and veins. J. Glaciol. 17, 181–207. doi: 10.1017/S002214300001354X
Palmer, S., Shepherd, A., Nienow, P., and Joughin, I. (2011). Seasonal speed-up of the Greenland Ice sheet linked to routing of surface water. Earth Planet. Sci. Lett. 302, 423–428. doi: 10.1016/j.epsl.2010.12.037
Phillips, T., Rajaram, H., Colgan, W., Steffen, K., and Abdalati, W. (2013). Evaluation of cryo-hydrologic warming as an explanation for increased ice velocities in the wet snow zone, Sermeq Avannarleq, West Greenland. J. Geophys. Res. Earth Surface 118, 1241–1256. doi: 10.1002/jgrf.20079
Phillips, T., Rajaram, H., and Steffen, K. (2010). Cryo-hydrologic warming: a potential mechanism for rapid thermal response of ice sheets. Geophys. Res. Lett. 37:L20503. doi: 10.1029/2010GL044397
Pimentel, S., and Flowers, G. (2010). A numerical study of hydrologically driven glacier dynamics and subglacial flooding. Proc. Math. Phys. Eng. Sci. 467, 537–558. doi: 10.1098/rspa.2010.0211
Poinar, K., Joughin, I., Das, S. B., Behn, M. D., Lenaerts, J., and Broeke, M. R. (2015). Limits to future expansion of surface-melt-enhanced ice flow into the interior of western Greenland. Geophys. Res. Lett. 42, 1800–1807. doi: 10.1002/2015GL063192
Prescott, P. (2013). Quantifying subglacial roughness and its link to glacial geomorphology and ice speed. Doctoral dissertation, Durham University.
Price, S. F., Payne, A. J., Catania, G. A., and Neumann, T. A. (2008). Seasonal acceleration of inland ice via longitudinal coupling to marginal ice. J. Glaciol. 54, 213–219. doi: 10.3189/002214308784886117
Pritchard, H. D., Arthern, R. J., Vaughan, D. G., and Edwards, L. A. (2009). Extensive dynamic thinning on the margins of the Greenland and Antarctic ice sheets. Nature 461, 971–975. doi: 10.1038/nature08471
Rada, C., and Schoof, C. (2018). Channelized, distributed, and disconnected: subglacial drainage under a valley glacier in the Yukon. Cryosphere 12, 2609–2636. doi: 10.5194/tc-12-2609-2018
Rignot, E., Velicogna, I., Van den Broeke, M. R., Monaghan, A., and Lenaerts, J. T. M. (2011). Acceleration of the contribution of the Greenland and Antarctic ice sheets to sea level rise. Geophys. Res. Lett. 38:L05503. doi: 10.1029/2011GL046583
Röthlisberger, H. (1972). Water Pressure in Intra-and Subglacial Channels. J. Glaciol. 11, 177–203. doi: 10.1017/S0022143000022188
Ryser, C., Luthi, M. P., Andrews, L. C., Catania, G. A., Funk, M., Hawley, R., et al. (2014a). Caterpillar-like ice motion in the ablation area of the Greenland Ice Sheet. J. Geophys. Res. Earth Surface 119, 2258–2271. doi: 10.1002/2013JF003067
Ryser, C., Luthi, M. P., Andrews, L. C., Hoffman, M. J., Catania, G. A., Hawley, R. L., et al. (2014b). Sustained high basal motion of the Greenland ice sheet revealed by borehole deformation. J. Glaciol. 60, 647–660. doi: 10.3189/2014JoG13J196
Scheick, J. (2012). Investigating Greenland Crevasses at Raven Camp. Field Notes, Polar Field Services Newsletter. Available online at: http://www.polarfield.com/blog/blog/investigating-greenland-crevasses-raven-camp
Schoof, C. (2010). Ice sheet acceleration driven by melt supply variability. Nature 468, 803–806. doi: 10.1038/nature09618
Schoof, C., Rada, C. A., Wilson, N. J., Flowers, G. E., and Haseloff, M. (2014). Oscillatory subglacial drainage in the absence of surface melt. Cryosphere 8, 959–976. doi: 10.5194/tc-8-959-2014
Selmes, N., Murray, T., and James, T. D. (2011). Fast draining lakes on the Greenland Ice sheet. Geophys. Res. Lett. 38:L15501. doi: 10.1029/2011GL047872
Selmes, N., Murray, T., and James, T. D. (2013). Characterizing supraglacial lake drainage and freezing on the Greenland Ice sheet. Cryosphere Discuss. 7, 475–505. doi: 10.5194/tcd-7-475-2013
Sergienko, O. V. (2013). Glaciological twins: basally controlled subglacial and supraglacial lakes. J. Glaciol. 59, 3–8. doi: 10.3189/2013JoG12J040
Shannon, S. R., Payne, A. J., Bartholomew, I. D., van den Broeke, M. R., Edwards, T. L., Fettweis, X., et al. (2013). Enhanced basal lubrication and the contribution of the Greenland ice sheet to future sea-level rise. Proc. Natl. Acad. Sci. U.S.A. 110, 14156–14161. doi: 10.1073/pnas.1212647110
Sharp, M., Gemmel, J. C., and Tison, J.-L. (1989). Structure and stability of the former subglacial drainage system of the Glacier de Tsanfleuron, Switzerland. Earth Surface Process. Landforms 14, 119–134. doi: 10.1002/esp.3290140204
Shepherd, A., Hubbard, A., Nienow, P., King, M., McMillan, M., and Joughin, I. (2009). Greenland ice sheet motion coupled with daily melting in late summer. Geophys. Res. Lett. 36, 2–5. doi: 10.1029/2008GL035758
Shreve, R. L. (1972). Movement of water in glaciers. J. Glaciol. 11, 205–214. doi: 10.1017/S002214300002219X
Smeets, C. J. P. P., Boot, W., Hubbard, A., Pettersson, R., Wilhelms, F., van den Broeke, M. R., et al. (2012). A wireless subglacial probe for deep ice applications. J. Glaciol. 58, 841–848. doi: 10.3189/2012JoG11J130
Smith, L. C., Chu, V. W., Yang, K., Gleason, C. J., Pitcher, L. H., Rennermalm, A. K., et al. (2015). Efficient meltwater drainage through supraglacial streams and rivers on the southwest Greenland ice sheet. Proc. Natl. Acad. Sci. U.S.A. 112, 1001–1006. doi: 10.1073/pnas.1413024112
Sneed, W. A., and Hamilton, G. S. (2007). Evolution of melt pond volume on the surface of the Greenland Ice sheet. Geophys. Res. Lett. 34, 4–7. doi: 10.1029/2006GL028697
Sole, A., Nienow, P., Bartholomew, I., Mair, D., Cowton, T., Tedstone, A., et al. (2013). Winter motion mediates dynamic response of the Greenland Ice sheet to warmer summers. Geophys. Res. Lett. 40, 3940–3944. doi: 10.1002/grl.50764
Stevens, L. A., Behn, M. D., Das, S. B., Joughin, I., Noël, B. P., Broeke, M. R., et al. (2016). Greenland Ice Sheet flow response to runoff variability. Geophys. Res. Lett. 43, 11295, 11303. doi: 10.1002/2016GL070414
Stevens, L. A., Behn, M. D., McGuire, J. J., Das, S. B., Joughin, I., Herring, T., et al. (2015). Greenland supraglacial lake drainages triggered by hydrologically induced basal slip. Nature 522, 73–76. doi: 10.1038/nature14480
Stone, D. B., and Clarke, G. K. C. (1993). Estimation of subglacial hydraulic properties from induced changes in basal water pressure: a theoretical framework for borehole-response tests. J. Glaciol. 39, 327–340. doi: 10.1017/S0022143000015999
Storrar, R. D., Stokes, C. R., and Evans, D. J. A. (2014). Morphometry and pattern of a large sample (>20,000) of Canadian eskers and implications for subglacial drainage beneath ice sheets. Quat. Sci. Rev. 104, 1–25. doi: 10.1016/j.quascirev.2014.09.013
Sundal, A. V., Shepherd, A., Nienow, P., Hanna, E., Palmer, S., and Huybrechts, P. (2009). Evolution of supra-glacial lakes across the Greenland Ice sheet. Remote Sens. Environ. 113, 2164–2171. doi: 10.1016/j.rse.2009.05.018
Sundal, A. V., Shepherd, A., Nienow, P., Hanna, E., Palmer, S., and Huybrechts, P. (2011). Melt-induced speed-up of Greenland ice sheet offset by efficient subglacial drainage. Nature 469, 521–524. doi: 10.1038/nature09740
Tedesco, M., Willis, I. C., Hoffman, M. J., Banwell, A. F., Alexander, P., and Arnold, N. S. (2013). Ice dynamic response to two modes of surface lake drainage on the Greenland ice sheet. Environ. Res. Lett. 8:034007. doi: 10.1088/1748-9326/8/3/034007
Tedstone, A. J., Nienow, P. W., Gourmelen, N., Dehecq, A., Goldberg, D., and Hanna, E. (2015). Decadal slow-down of a land-terminating sector of the Greenland Ice sheet despite warming. Nature 526, 692–695. doi: 10.1038/nature15722
Tedstone, A. J., Nienow, P. W., Gourmelen, N., and Sole, A. J. (2014). Greenland ice sheet annual motion insensitive to spatial variations in subglacial hydraulic structure. Geophys. Res. Lett. 41, 8910–8917. doi: 10.1002/2014GL062386
Tedstone, A. J., Nienow, P. W., Sole, A. J., Mair, D. W., Cowton, T. R., Bartholomew, I. D., et al. (2013). Greenland ice sheet motion insensitive to exceptional meltwater forcing. Proc. Natl. Acad. Sci. U.S.A. 110, 19719–19724. doi: 10.1073/pnas.1315843110
Thomson, L. I., and Copland, L (2017). Changing contribution of peak velocity events to annual velocities following a multi-decadal slowdown at White Glacier. Ann. Glaciol. 58, 145–154. doi: 10.1017/aog.2017.46
Truffer, M., Harrison, W. D., and March, R. S. (2005). Correspondence: Record negative glacier balances and low velocities during the 2004 heat wave in Alaska, USA: Implications for the interpretation of observations by Zwally and others in Greenland. J. Glaciol. 51, 663–664. doi: 10.3189/172756505781829016
Tsai, V. C., and Rice, J. R. (2010). A model for turbulent hydraulic fracture and application to crack propagation at glacier beds. J. Geophys. Res. 115:F03007. doi: 10.1029/2009JF001474
van de Wal, R. S. W., Boot, W., Smeets, C. J. P. P., Snellen, H., van den Broeke, M. R., and Oelemans, J. (2012). Twenty-one years of mass balance observations along the K-transect, West Greenland. Earth Syst. Sci. Data 4, 31, 35. doi: 10.5194/essd-4-31-2012
van de Wal, R. S. W., Boot, W., Van den Broeke, M. R., Smeets, C. J. P. P., Reijmer, C. H., Donker, J. J. A., et al. (2008). Large and rapid melt-induced velocity changes in the ablation area of the Greenland Ice sheet. Science 321, 111–113. doi: 10.1126/science.1158540
van de Wal, R. S. W., Smeets, C. J. P. P., Boot, W., Stoffelen, M., van Kampen, R., Doyle, S. H., et al. (2015). Self-regulation of ice flow varies across the ablation area in south-west Greenland. Cryosphere 9, 603–611. doi: 10.5194/tc-9-603-2015
van der Veen, C. J. (1998). Fracture mechanics approach to penetration of surface crevasses on glaciers. Cold region science technology 27, 31–47.
van der Veen, C. J. (2007). Fracture propagation as means of rapidly transferring surface meltwater to the base of glaciers. Geophys. Res. Lett. 34:L01501. doi: 10.1029/2006GL028385
Walder, J., and Fowler, A. (1994). Channelized subglacial drainage over a deformable bed. J. Glaciol. 40, 3–15. doi: 10.1017/S0022143000003750
Walder, J., and Hallet, B. (1979). Geometry of former subglacial water channels and cavities. J. Glaciol. 23, 335–346. doi: 10.1017/S0022143000029944
Walder, J. S. (1982). Stability of sheet flow of water beneath temperate glaciers and implications for glacier surging. J. Glaciol. 28, 273–293. doi: 10.1017/S0022143000011631
Walder, J. S. (1986). Hydraulics of subglacial cavities. J. Glaciol. 32, 439–445. doi: 10.1017/S0022143000012156
Walter, F., Chaput, J., and Lüthi, M. P. (2014). Thick sediments beneath Greenland's ablation area and their potential role in future ice sheet dynamics. Geology 42, 487–490. doi: 10.1130/G35492.1
Weertman, J. (1962). “Catastrophic glacier advances,” in Symposium of Obergurgl–Variations of the Regime of Existing Glaciers, International Association of Scientific Hydrology (Obergurgl), 31–39.
Weertman, J. (1972). General theory of water flow at the base of a glacier or ice sheet. Rev. Geophys. 10, 287–333. doi: 10.1029/RG010i001p00287
Weertman, J., and Birchfield, G. E. (1983). Stability of sheet water flow under a glacier. J. Glaciol. 29, 374–382. doi: 10.1017/S002214300003029X
Werder, M. A., Hewitt, I. J., Schoof, C. G., and Flowers, G. E. (2013). Modeling channelized and distributed subglacial drainage in two dimensions. J. Geophys. Res. Earth Surface 118, 2140–2158. doi: 10.1002/jgrf.20146
Williamson, A. G., Willis, I. C., Arnold, N. S., and Banwell, A. F. (2018). Controls on rapid supraglacial lake drainage in West Greenland: an exploratory data analysis approach. J. Glaciol. 64, 208–226. doi: 10.1017/jog.2018.8
Wilton, D. J., Jowett, A., Hanna, E., Bigg, G. R., van den Broeke, M. R., Fettweis, X., et al. (2017). High resolution (1 km) positive degree-day modelling of Greenland ice sheet surface mass balance, 1870–2012 using reanalysis data. J. Glaciol. 63, 76–193. doi: 10.1017/jog.2016.133
Wright, P. J., Harper, J. T., Humphrey, N. F., and Meierbachtol, T. W. (2016). Measured basal water pressure variability of the western Greenland Ice Sheet: Implications for hydraulic potential. J. Geophys. Res. Earth Surface 121, 1134–1147. doi: 10.1002/2016JF003819
Keywords: subglacial hydrology, ice dynamics, land-terminating, supraglacial lakes, Greenland Ice Sheet, glaciers
Citation: Davison BJ, Sole AJ, Livingstone SJ, Cowton TR and Nienow PW (2019) The Influence of Hydrology on the Dynamics of Land-Terminating Sectors of the Greenland Ice Sheet. Front. Earth Sci. 7:10. doi: 10.3389/feart.2019.00010
Received: 14 January 2018; Accepted: 23 January 2019;
Published: 21 February 2019.
Edited by:
Alun Hubbard, UiT The Arctic University of Norway, NorwayReviewed by:
Martin Truffer, University of Alaska Fairbanks, United StatesSamuel H. Doyle, Aberystwyth University, United Kingdom
Copyright © 2019 Davison, Sole, Livingstone, Cowton and Nienow. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Benjamin Joseph Davison, YmQ0MUBzdC1hbmRyZXdzLmFjLnVr
 Benjamin Joseph Davison
Benjamin Joseph Davison Andrew John Sole
Andrew John Sole Stephen John Livingstone
Stephen John Livingstone Tom R. Cowton1
Tom R. Cowton1 Peter William Nienow
Peter William Nienow