Limitations Posed by Free DEMs in Watershed Studies: The Case of River Tanaro in Italy

Introduction

One of the most critical elements in the hydrological response of a river basin is its topography. Among other implications, topography can significantly control the distribution of environmental variables (Sørensen and Seibert, 2007) and play a crucial role in the modeling of runoff generation and routing (e.g., Zhang and Montgomery, 1994). Its complexity can greatly influence predicted discharges and how water flows over the floodplain, making it largely responsible for the accuracy of flood maps (e.g., Horritt and Bates, 2001). In fact, the great progress experienced in the modeling of both hydrological and hydraulic processes in the last decades cannot be dissociated from the advances in terrain information in the form of DEM datasets.

Digital elevation models (DEMs) are digital elevation datasets representing the Earth’s surface. They may be termed more precisely as digital terrain models (DTM) or bare earth DEMs when not accounting for vegetation and buildings; otherwise, they are called digital surface models (DSM). DEMs are distributed as gridded data, where each cell, or pixel, contains a value representing the local terrain elevation. DEMs can be produced from a variety of data sources, most commonly from survey data, digitized maps, and remote sensing. Every source has its trade-offs, but remote sensing is the most versatile one, as it is able to deliver products with different areal coverages, resolutions and accuracies in an operational way – prime reason for the traction it gained in the last decades. Obviously, this popularity might not have been attained had advances in remote sensing not been on a par with those in computational power and software, as well as with the release of other important datasets, land use and land cover, for example.

Within the large variety of remote sensing techniques, we focus on the two most disruptive technologies for generating DEMs: synthetic aperture radar (SAR) and light detection and ranging (LiDAR). The greatest assets of SAR appear to be the use of long wavelengths by the active sensor, which allows imaging under all-weather conditions, and the variation of wavelengths, allowing for different degrees of reflection, e.g., by canopy or ground surface. Its major drawbacks are the presence of geometric distortions and shadows due to the side-looking antennas. On the other hand, LiDAR can be ineffective during heavy rain or in the presence of clouds, although it does not share SAR’s shortcomings of geometric distortions and shadows. Both systems are capable of fast data collection, can be mounted on airborne aircrafts or satellites, can operate during day and night and can resolve the presence of canopy. They are also relatively expensive to operate and maintain (up to millions of euros). The acquisition of a LiDAR DEM can typically cost on average 140 €/km², while a SAR acquisition can cost approximately 60 €/km² (Croneborg et al., 2015).

The open access licensing of DEMs is capable of breaking financial barriers that are frequently experienced by users, contributing to a faster advancement of science and innovation across fields. However, publicly released, freely available datasets differ in characteristics such as spatial resolution, digital terrain processing decisions and vertical accuracy, which may introduce a range of errors in the modeling of hydrological and hydraulic processes. A number of authors have assessed these errors and conjectured new ways to move forward. For example, Sanders (2007) analyzed the sensitivity of flood modeling to DEM characteristics. The author studied the Santa Clara and Buffalo Bayou rivers, US, using elevation data from LiDAR, interferometric SAR, the USGS national elevation dataset and the SRTM DEM. It was concluded that LiDAR was the best source of terrain data for that particular application and that, although very useful, the free SRTM DEM had serious limitations related to noise and data gaps. Jarihani et al. (2015) evaluated the SRTM and ASTER GDEM datasets in terms of vertical accuracy against survey marks and altimeter data, spatial resolution and digital terrain processing decisions. They demonstrated the significant impact that an underlay DEM has on flood modeling and found that the ASTER GDEM presented higher vertical accuracies in the Diamantina/Cooper river basins in Australia, while hydrologically reconditioned DEMs performed better when compared against vegetation-smoothed or unprocessed counterparts. More recently, Archer et al. (2018) compared flood modeling outcomes in a river basin in Fiji, using a commercial version of the TanDEM-X dataset (12 m spatial resolution), its vegetation-smoothed derivatives, the SRTM and the MERIT datasets against LiDAR data. The authors found that the TanDEM-X with vegetation smoothed by image classification of the amplitude map and progressive morphological filtering outperformed other datasets.

In this paper, the limiting nature of publicly released, freely available DEMs is evaluated, using LiDAR data as benchmark. However, it is done in the context of hydrogeomorphology, in other words of the study of landforms caused by the action of water, rather than focusing explicitly on flood modeling. In specific, for each DEM dataset, the upslope contributing area, the local slope, and the H and D geomorphic terrain descriptors are computed and the differences produced in terms of their cumulative frequency curves within the Tanaro river basin, in Italy, are evaluated.

The terrain descriptors analyzed are frequently used to characterize hydrological or hydraulic processes. For instance, the upslope contributing area can be associated with runoff volume, while the local slope reflects surface flow velocities (Chow, 1959), infiltration rates (Fox et al., 1997), erosional power (Knighton, 1999), drainage density (Tarboton et al., 1992), and response times (Maidment, 1993). In addition, the combination of the upslope contributing area and local slope values can be used to predict soil water content and runoff producing areas (see the topographic wetness index by Beven and Kirkby, 1979), as well as the location of channel initiation points (Montgomery and Dietrich, 1989).

The H and D terrain descriptors have also found numerous applications; for instance, Westerhoff et al. (2013) used H as topographic correction of water mapping based on SAR imagery, Nobre et al. (2016) matched a stage height to an H contour to obtain a proxy of flood extents, Elshorbagy et al. (2017) reclassified both H and D and used the product of their classes to define levels of flood hazard, Rebolho et al. (2018) and Zheng et al. (2018) used H to estimate reach-average hydraulic geometries and derive synthetic rating curves, and, finally, Clubb et al. (2017) and Nardi et al. (2019) used similar approaches to Manfreda et al. (2015) to delineate floodplains and terraces. Moreover, the terrain descriptor D can also be associated with the width function (defined as the flow path distance of any given point in a catchment to the outlet; Kirkby, 1976; Lee and Delleur, 1976), which represents a fully distributed residency time (Rodríguez-Iturbe and Rinaldo, 1997) used in the modeling of the hydrological response of a catchment. In particular, under the assumption of constant velocity, the width function can be used to estimate a geomorphological instantaneous unit hydrograph (e.g., Mesa and Mifflin, 1986; Moussa, 2008).

In addition to investigating the intrinsic characteristics of freely accessible DEMs and given the importance of river networks in the modeling of hydrological and hydraulic processes, DEM-based river networks are delineated and compared to a photo-interpreted river network. Last, the vertical accuracy of each DEM is quantified in relation to LiDAR data.

Free Digital Elevation Models

Open access licensing has allowed DEMs to be distributed online, free of charge to the public. This access policy not only allowed the lowering of research costs and the lifting of financial barriers to their use, but also promoted equality between individuals and institutions. As a possible indication of this, Figure 1 plots the number of scientific publications mentioning the term “digital elevation model” per year, starting before the very first public release of a global DEM (named the Global 30 arc second Elevation Data; GTOPO30, EROS/USGS/USDOI, 1997) in 1996. It can be seen that references to “digital elevation model” have increased from less than 60 publications per year to about 800 in 2018. We note that access to global DEMs before 1996 was either restricted or inexistent and that this trend in publication records probably reflects the use of DEMs in a range of fields, amongst which the modeling of hydrological and hydraulic processes (e.g., Kumar et al., 2000). However, benefits to science and technology of publicly releasing global DEMs may be constrained, as the most popular free DEMs are now seriously dated or lack the desired spatial resolution, accuracy, correction and conditioning to keep enhancing research.

FIGURE 1

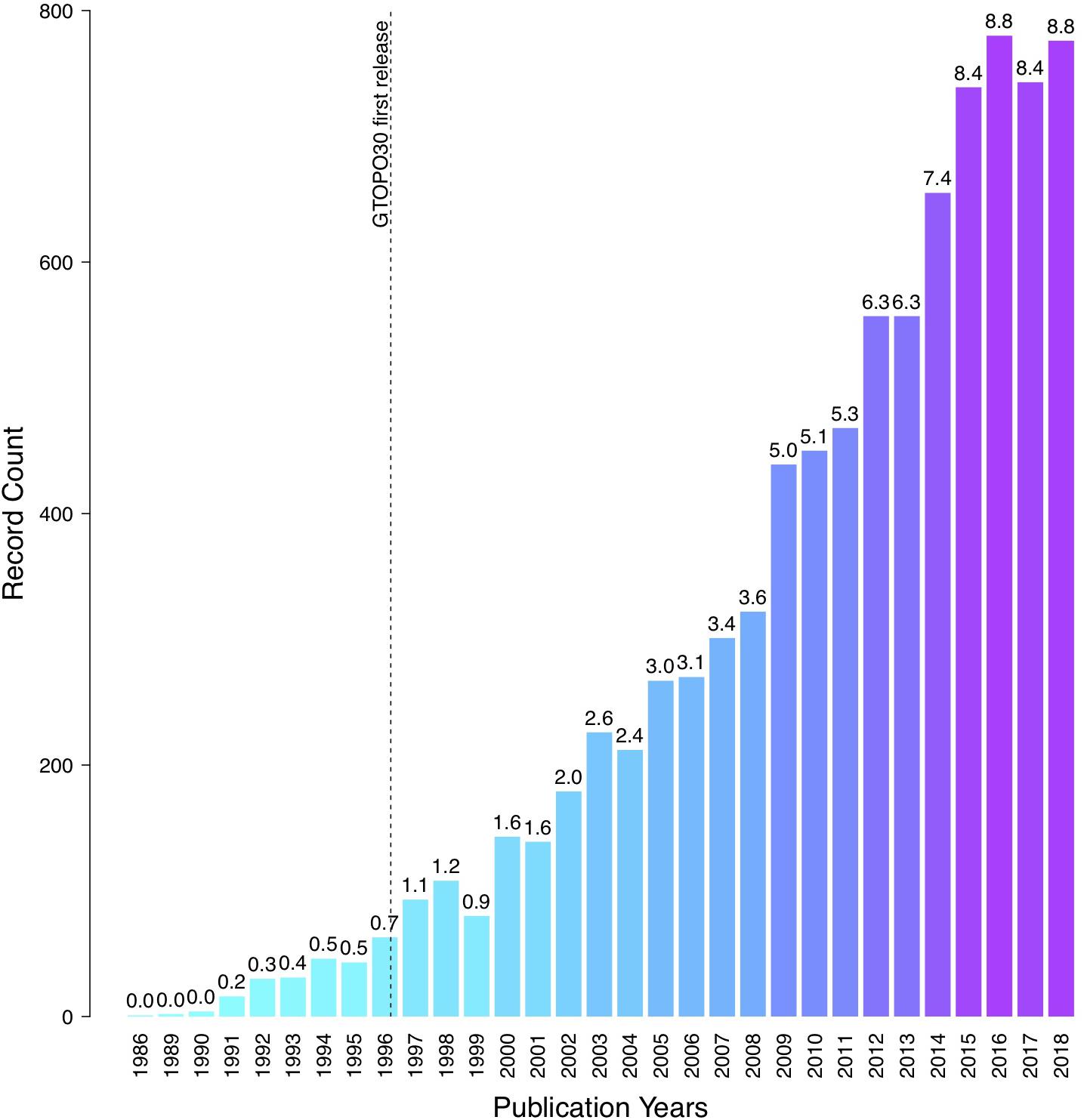
Figure 1. Number of scientific publications mentioning the words “digital elevation model.” Values on top of bars correspond to percentage of total records (data source: Web of Science, Clarivate Analytics, 2018).

Materials and Methods

Tanaro River Basin

With inception in the Ligurian Alps close to France and located in north-western Italy, the Tanaro river is the most significant right-side tributary to the Po River in terms of length (c.a. 276 km) and drainage area (c.a. 8000 km²), presenting a highly variable discharge (Degiorgis et al., 2012). The Tanaro river basin is characterized by steep mountainous terrain and a nearly flat alluvial region (Figure 2). The river itself is highly prone to flooding; indicatively, during the 1994 historical Piedmont flood and landslide, 44 persons lost their lives, 2000 were displaced and a whopping 8.8 billion € in damages were estimated (Luino, 1999).

FIGURE 2

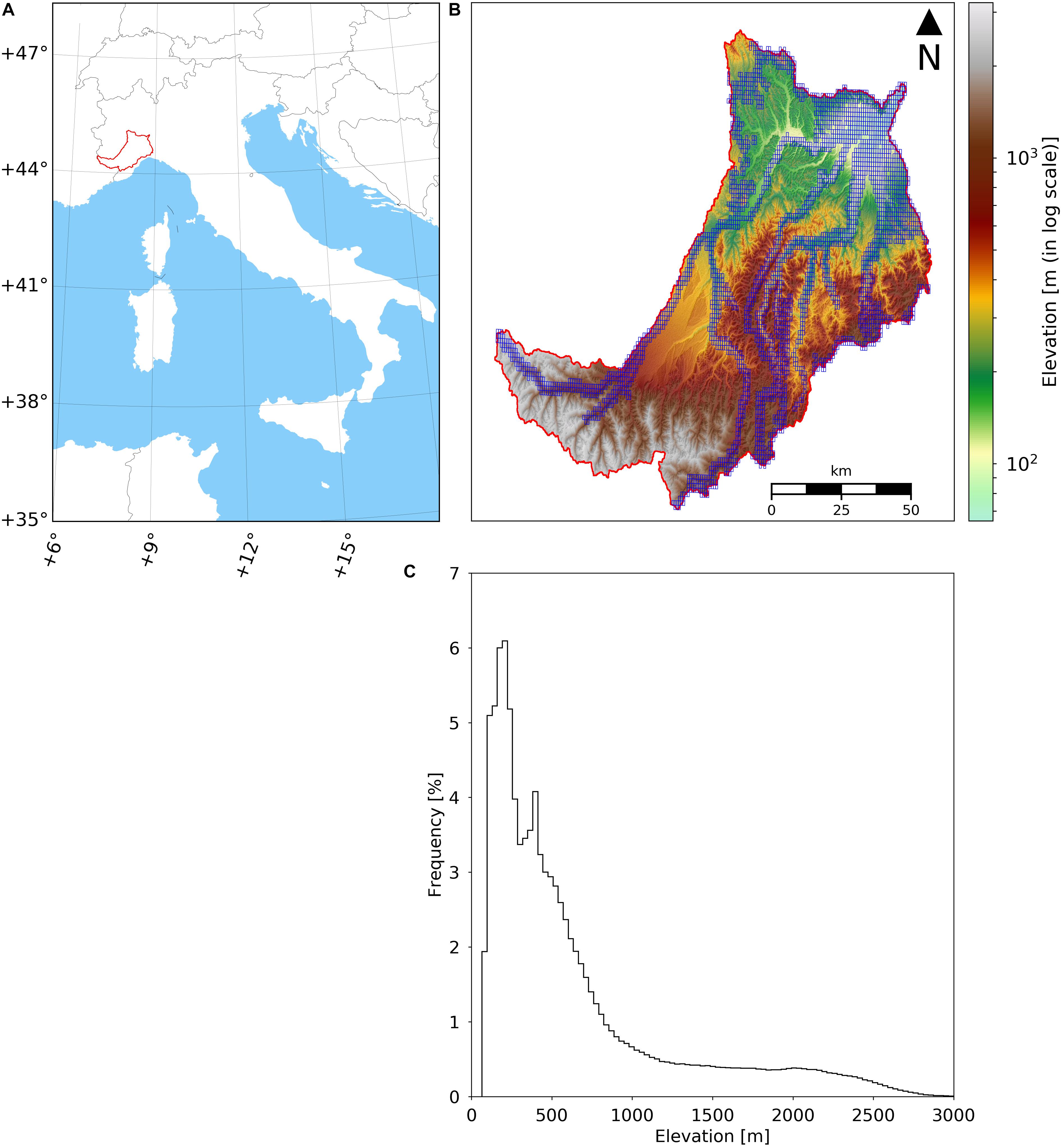
Figure 2. Representation of the study area. (A) Location of the Tanaro river basin in the Piedmont region, NW Italy, with the drainage divide highlighted in red; (B) digital elevation model (DEM) of the Tanaro river basin and footprint of the light detection and ranging (LiDAR) dataset in blue; (C) histogram of elevations within the Tanaro river basin.

The Tanaro river basin was chosen as case study due to its peculiar characteristics and history of disastrous events. In this work, the DEMs listed in Table 1 were clipped with the Tanaro river catchment polygon obtained from the Italian Environmental Agency (ISPRA – Istituto Superiore per la Protezione e la Ricerca Ambientale) in shapefile format. The clipped DEMs are used to extract the terrain descriptors within the study area, namely (1) the upslope contributing area, (2) the local slope, (3) the flow path elevation difference to the nearest stream, H, and (4) the flow path distance to the nearest stream, D, used for comparison in terms of cumulative frequency curves. In addition, river networks are delineated from the clipped DEMs for visual inspection and comparison with the EU-Hydro photo-interpreted river network (EEA, 2015b). As a final step, vertical accuracies of the free DEMs are reassessed using LiDAR data.

TABLE 1

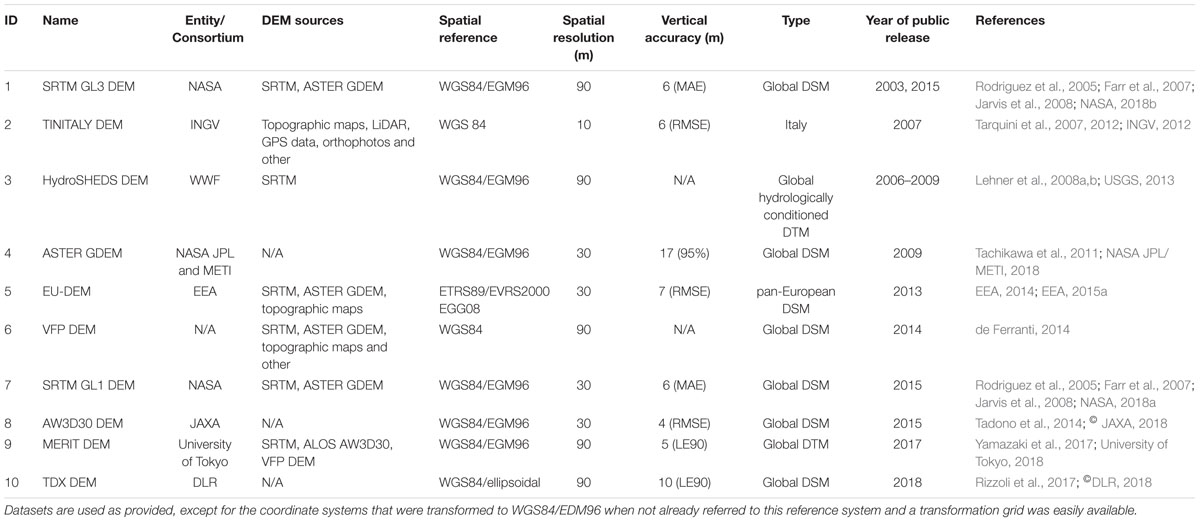
Table 1. Digital elevation models (DEM) currently available free of charge with spatial resolutions below 3 arc seconds.

Description of DEM Datasets

In Table 1, an overview of some of the most common DEMs with spatial resolutions of the order of 3 arc seconds (c.a. 90 m) or less is provided. These datasets are currently in the public domain or available upon request mostly for research or other non-commercial purposes. Table 1 is organized by ascending order of year of public release. In this work, all datasets in Table 1 are taken into consideration:

(1) The open-access SRTM GL3 (NASA, 2018a) released by the United States (US) National Aeronautics and Space Administration (NASA) in 2003 (Rodriguez et al., 2005; Farr et al., 2007; Jarvis et al., 2008).

(2) The TINITALY (INGV, 2012), a seamless DEM for the whole Italian territory developed by Tarquini et al. (2007, 2012) at the Italian National Institute of Geophysics and Volcanology (INGV – Istituto Nazionale di Geofisica e Vulcanologia). This DEM is based on the interpolation of heterogeneous data sources, including contour lines and spot heights from Italian topographic maps, global positioning system (GPS) and LiDAR data. The TINITALY is distributed as a non-commercial product available upon request.

(3) The open-access HydroSHEDS (USGS, 2013), a suite of hydrological geo-reference datasets produced and released between 2006 and 2009 by Conservation Science Program of World Wildlife Fund (WWF), within which a seamless hydrologically conditioned global DEM can be found (Lehner et al., 2008a,b). This DEM is derived from the SRTM GL3, but has been hydrologically conditioned using a sequence of automated procedures, namely the deepening of open water surfaces, weeding of coastal zones, stream burning, filtering, molding of valley courses, sink filling, carving through barriers, and manual corrections.

(4) The open-access ASTER GDEM (NASA JPL/ METI, 2018), a dataset produced by a consortium between the NASA Jet Propulsion Laboratory (JPL) and Japan’s Ministry of Economy, Trade and Industry (METI) produced and released in 2009 (Tachikawa et al., 2011).

(5) The EU DEM (EEA, 2015a) released by the European Environmental Agency (EEA) in 2013, consisting of a seamless open-access pan-European DEM that combines data from the SRTM and ASTER missions with other sources (EEA, 2014).

(6) The VFP made available to the public in 2014 as open-access by de Ferranti (2014), consisting of a global DEM produced by fusion of SRTM, ASTER GDEM and other elevation data sources.

(7) The open-access SRTM GL1 (NASA, 2018b) released by NASA in 2018 as an updated version of the SRTM GL3 (Rodriguez et al., 2005; Farr et al., 2007; Jarvis et al., 2008).

(8) The open-access AW3D30 global DEM (©JAXA, 2018) by the Japan Aerospace Exploration Agency (JAXA) publicly available since 2015 (Tadono et al., 2014).

(9) The MERIT DEM (University of Tokyo, 2018) by Yamazaki et al. (2017), consisting of a seamless global DEM that combines SRTM with AW3D30 and VFP data and has been available upon request since 2017.

(10) The open-access TDX (Rizzoli et al., 2017; ©DLR, 2018) released by the German Aerospace Centre (DLR – Deutsches Zentrum für Luft- und Raumfahrt e.V.) free of charge in 2018.

LiDAR Dataset for Italy (Benchmark)

As benchmark for the assessment of vertical accuracies, a LiDAR dataset that partially covers the Tanaro river basin (footprint in Figure 2) is used and was obtained from the Italian Ministry of Environment, Land and Sea (Ministero dell’Ambiente e della Tutela del Territorio e del Mare). The LiDAR data was resampled to the corresponding spatial resolution of each DEM in Table 1. The LiDAR dataset (with spatial reference WGS84/ITALGEO95) is available to the general public upon formal request and upon payment of a processing fee (to visualize its areal coverage, please visit the Italian National Geoportal – Geoportale Nazionale).

Terrain Descriptors

The extraction of the selected terrain descriptors from the free DEMs follows a simple workflow using the TauDEM toolbox (see Figure 3; Tarboton, 2015). A clipped DEM is first corrected by identifying sinks and by raising cell elevation values to the level of the lowest pour point in the eight surrounding cells of the structured grid. This is deemed necessary in order to avoid interference with flow routing. From this corrected layer, flow directions from each cell to one of its eight neighbors are determined by following the steepest descent (also known as convergent eight direction flow model, abbreviated as D8 flow directions) and a counter-clockwise coding from 1 (flow to the East) to 8. Using the D8 flow model, the local slope or tangent of the angle of incline, 𝜃, is calculated as the drop, Δy, over distance, Δx, between a cell and its neighbors in the flow path:

FIGURE 3

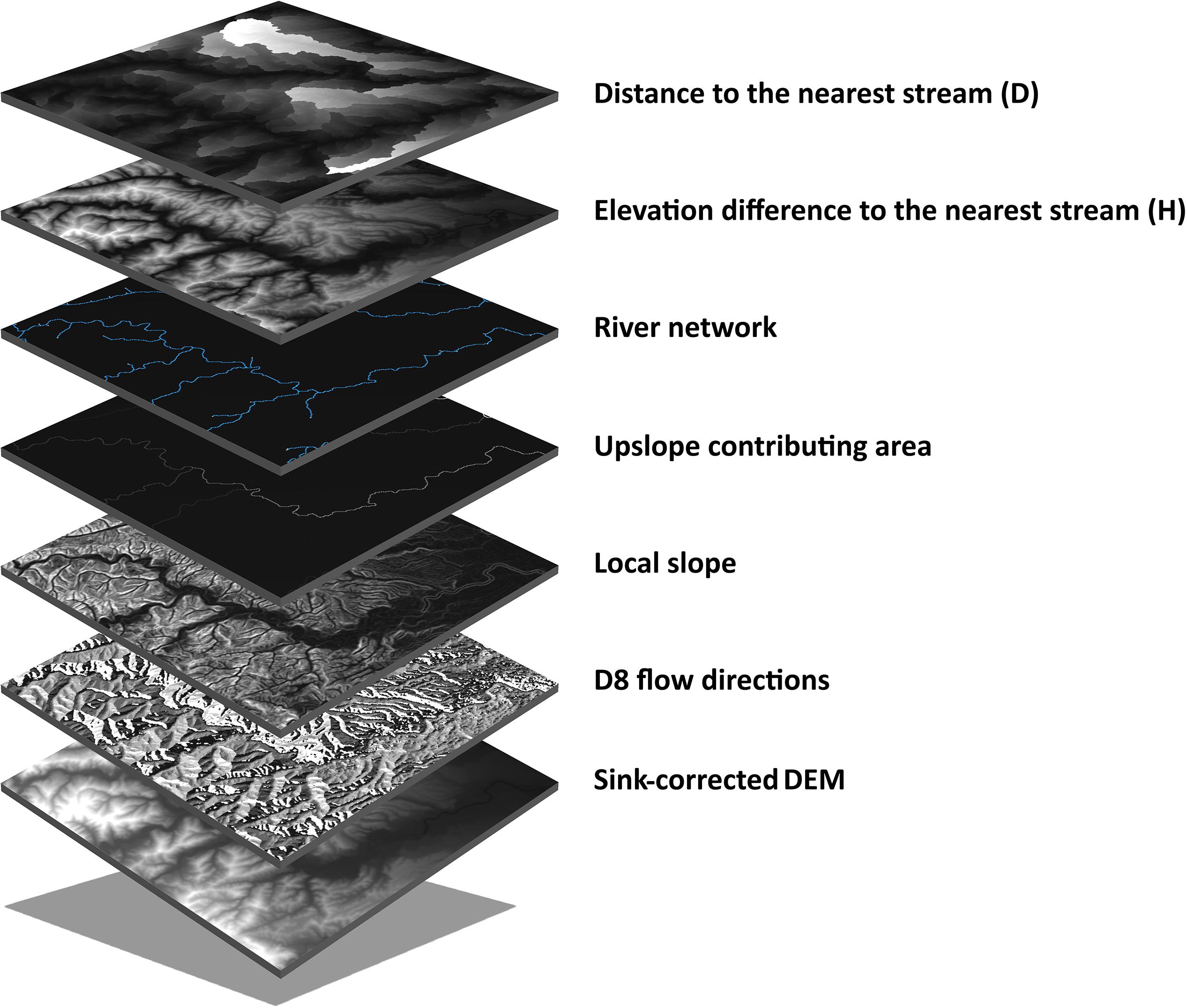
Figure 3. Layers involved in the extraction of terrain descriptors from digital elevation models (DEM).

$$\text{tan}\left(\theta \right)=\frac{\Delta y}{\Delta x}\left(1\right)$$

In turn, the upslope contributing area is obtained by simply accumulating cells following the D8 flow directions.

To delineate river networks from the free DEMs, channel heads are first identified by imposing a threshold of 10⁵ m² (Giannoni et al., 2005) on an area-slope criterion that characterizes the transition between transport mechanisms (Montgomery and Dietrich, 1988, 1989). This criterion is defined as the product of upslope contributing area and local slope raised to an exponent k responsible for drainage density changes, assuming k = 1.75 throughout this study (Giannoni et al., 2005). Starting at the channel heads, river networks are delineated following the D8 flow directions to the outlet.

With the river network delineated from the free DEMs, the computation of H and D is programmed in Python following the description in Manfreda et al. (2015) and making use of the Geospatial Data Abstraction Library (GDAL) for raster I/O. H is obtained by calculating the elevation difference between each cell in the DEM raster and the connected river network cell, following the D8 flow directions. D is obtained by counting the number of cells from each position in the DEM raster to the connected river network cell, still following the D8 flow directions. Furthermore, for each unique flow path, adjacent cell counts need to be distinguished from diagonal ones, so that lengths can be obtained by multiplication with the spatial resolution or with the product of spatial resolution and 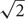, respectively. The total flow path distance from each location in the raster to the stream is simply the sum of corresponding adjacent and diagonal lengths.

Accuracy Assessment

In order to assess the vertical accuracy of the free DEMs, three common error measures were selected to be used with continuous variables, in this case the elevation data. Different error measures are report in this study as they may complement each other (Chai and Draxler, 2014). The systematic error or statistical bias is defined as the simple difference between DEM, 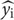, and LiDAR, y_i, elevations (here assumed as the truth):

$$\text{BIAS}=\widehat{y_i}-y_i\left(2\right)$$

where i the index of an individual cell in a flattened raster. The MAE is defined as:

$$\text{MAE}=\frac{1}{n}\sum _{i=1}^n\left|\widehat{y_i}-y_i\right|\left(3\right)$$

where n is the total number of cells. The MAE represents the average absolute difference between DEM and LiDAR elevations and gives an indication of the magnitude of error. Finally, the RMSE is defined as:

$$\text{RMSE}=\sqrt{\frac{1}{n}\sum _{i=1}^n{\left(\widehat{y_i}-y_i\right)}^2}\left(4\right)$$

where the mean square error is the second moment of the bias. The RMSE also measures the magnitude of error, but with a higher sensitivity to outliers, thus putting stronger emphasis to unfavorable conditions (Chai and Draxler, 2014). Its normalized version that is less sensitive to outliers is given by:

$$\text{NRMSE}={100}^{*}\frac{RMSE}{y_{max}-y_{min}}\left(5\right)$$

Finally, the linear correlation between 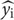and y_i is also reported and measured using the Pearson’s correlation coefficient (PC) defined as:

$$\text{PC}=\frac{{\sum }_{i=1}^n\left(y_i-\overline{y}\right)\left(\widehat{y_i}-\overline{\widehat{y}}\right)}{\sqrt{{\sum }_{i=1}^n{\left(y_i-\overline{y}\right)}^2{\sum }_{i=1}^n{\left(\widehat{y_i}-\overline{\widehat{y}}\right)}^2}}\left(6\right)$$

PC takes values between -1 and 1, with PC = -1 corresponding to a perfect inverse correlation, PC = 1 corresponding to a perfect direct correlation and PC = 0 corresponding to no linear correlation.

Results

In this section, the outcomes of the method proposed above are examined. The cumulative frequency curves of terrain descriptors presented in Figure 4 show important differences within the Tanaro river basin and the reader can also refer to Figure 5 for the average values of the terrain descriptors. Note that the upslope contributing area and D have not been computed for the LiDAR data, as both indicators proved to be meaningless within the limited extent of the LiDAR footprint.

FIGURE 4

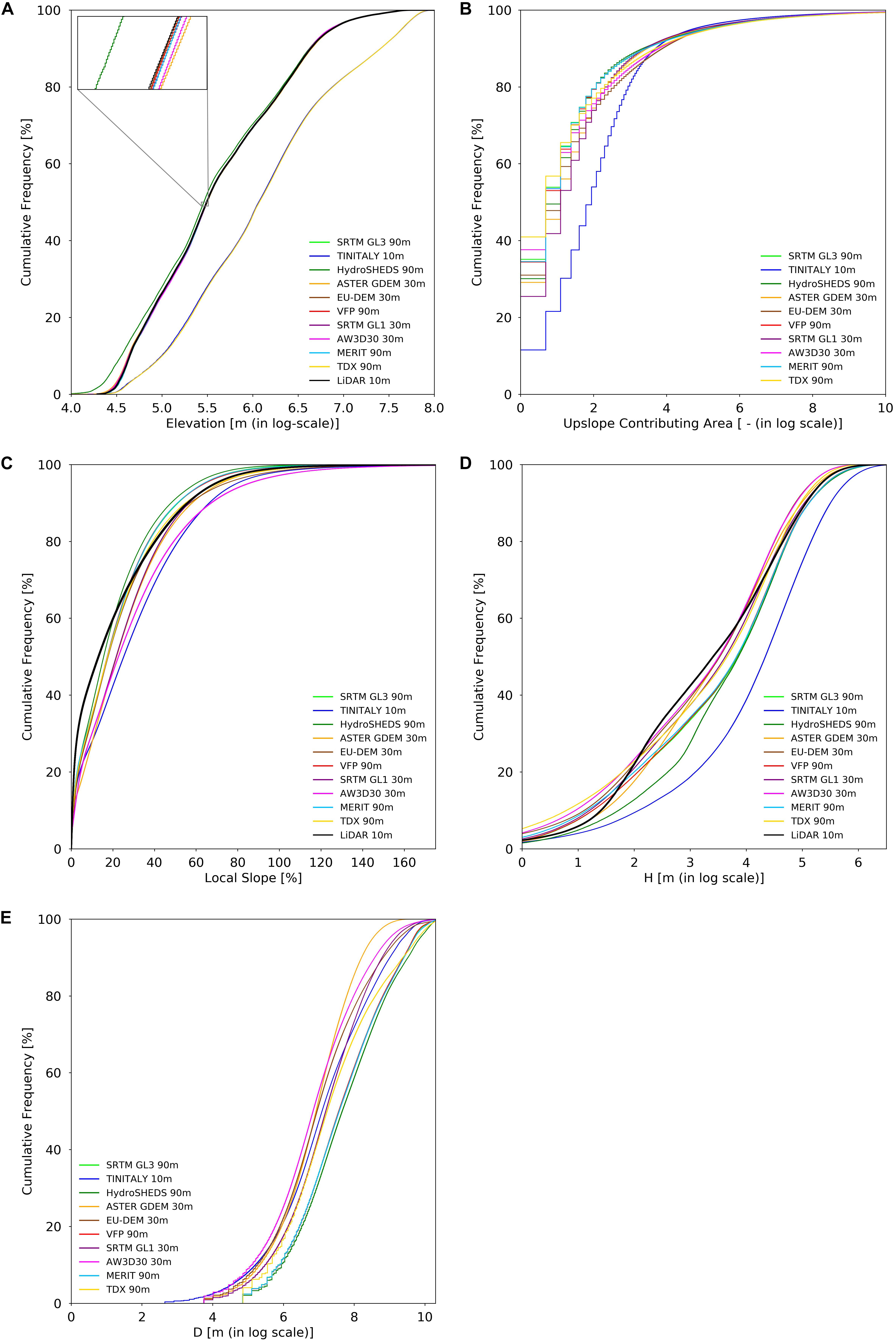
Figure 4. Cumulative frequency curves of terrain descriptors extracted from free digital elevation models (DEM) within the Tanaro river basin, in Italy. (A) Terrain elevations within the light detection and ranging (LiDAR) footprint; (B) upslope contributing area; (C) local slope within the LiDAR footprint; (D) elevation difference to the nearest stream, H, within the LiDAR footprint; and (E) distance to the nearest stream, D. Logarithmic scales refer to the natural logarithm.

FIGURE 5

Figure 5. Overlay of river networks for three distinct regions in the Tanaro river basin, Italy, derived from free digital elevation models (DEM). For each region, the corresponding EU-Hydro photo-interpreted river network is shown on the right. (A,B) are sample regions representative of flatter terrain; and (C) is a sample region representative of mountainous terrain. On the bottom left, the locations of the three regions within the Tanaro river basin are marked with red boxes. On the bottom right, the average values of the terrain descriptors are presented.

The cumulative frequency curves of elevation within the LiDAR footprint (Figure 4A) show that a large number of free DEMs approximate well the curve obtained from LiDAR data at 10 m spatial resolution. Namely, the EU DEM, the VFP DEM, the SRTM GL1 and GL3 and the MERIT DEM provide the best approximation and are very closely followed by the ASTER GDEM and the AW3D30 DEM. Minor differences may be observed between these datasets at lower elevations. In the lower part of the LiDAR footprint the HydroSHEDS hydrologically conditioned DEM has a different cumulative frequency curve than the previous mentioned datasets; in particular, below a certain elevation value, a slightly higher frequency may be expected for the HydroSHEDS DEM in comparison to the LiDAR (or lower elevation values for a certain frequency). Nevertheless, for the remaining 80% of the LiDAR footprint, the HydroSHEDS DEM provides a reasonable approximation of the LiDAR frequency curve. The TDX and the TINITALY DEMs present surprisingly similar cumulative frequency curves between themselves but, at the same time, significantly different from the LiDAR data and the remaining free DEMs; in specific, below a certain elevation value, a lower frequency may be expected for the TDX and the TINITALY DEMs (or higher elevation values for a certain frequency).

In terms of the upslope contributing area, the frequency distribution within the entire Tanaro river basin (and therefore not merely within the LiDAR footprint as before), Figure 4B, shows that all curves start to converge at around 150 accumulated cells (i.e., areas up to 1.2 km²) and that 90% of the cells have contributing areas below such value. Within the remaining upper 10%, DEMs with finer spatial resolution present higher upslope contributing areas than DEMs with coarser spatial resolution, as more cells are accumulated downstream in the former.

For the cumulative frequency curves of the local slope within the LiDAR footprint (Figure 4C), it is possible to observe that for slopes steeper than 22% (c.a. 40°) the TDX DEM gives the best overall approximation of the LiDAR data, followed by the SRTM GL1, the EU DEM and the ASTER GDEM. In the same range, the MERIT and the VFP DEMs overlap and follow closely the cumulative frequency curve of the HydroSHEDS and the SRTM GL3 DEMs, with higher frequencies relative to the LiDAR; while the remaining DEMs present lower frequencies relative to the LiDAR. For slopes values below 22%, every DEM curve presents a lower frequency relative to the LiDAR. Of all datasets, the AW3D30 and the TINITALY DEMs present the least representative approximation of the LiDAR curve, with lower frequencies. In general, all datasets have more than 90% of the cells with slope falling below 45°, approximately. Instead, if one looks at the average values of local slopes (Figure 5) within the LiDAR footprint the best approximation is given by the HydroSHEDS, followed by the SRTM GL3, the VFP and the MERIT DEM.

Figure 4D shows the cumulative frequency curve of H. In the case of the DEMs, the curve is S-shaped with a sharp increase from 50 (c.a. 10% frequency) to 150 m (c.a. 90% frequency), approximately. Contrarily, the LiDAR curve does not present a perfect S-shape; instead, there is a bump around 12 m. The best approximation of the curve from LiDAR data is given by the ASTER GDEM with a perfect match at low H values, followed by the SRTM GL1 and the TDX DEM with very close representation at high H values. Nevertheless, between 5 m and 12 m not a single DEM can faithfully represent the curve obtained from LiDAR data. In turn, the AW3D30 and the EU DEMs have similar curves that, for the same H value, consistently present a higher frequency relative to the MERIT, the SRTM GL3, the VFP (all three of them overlapping in the graph) and the HydroSHEDS DEM. The ASTER GDEM, the SRTM GL1 and the TDX DEM fall more or less between the previous cases, while the TINITALY, for a same H value, presents the lowest frequency of all DEMs and has the curve that is furthest apart from that of the LiDAR. In general, all datasets have more than 90% of the cells with H falling below 150 m, approximately. By looking at the average values of H (Figure 5), no single DEM within the LiDAR footprint can approximate the LiDAR value of 59 m, the closest one being the AW3D30 DEM, but still with a difference of 28 m.

The cumulative frequency curve of D is also S-shaped, with a sharp increase after 400 m (c.a. 10% frequency) and up to 5 km (c.a. 90% frequency), approximately. By looking at how the DEMs compare between themselves, it was found that the AW3D30 DEM and the ASTER GDEM have frequency curves that consistently present a higher frequency for the same D value relative to the MERIT, the SRTM GL3, the VFP (all three overlapping) and the HydroSHEDS DEM. The SRTM GL1 and the TDX DEM fall more or less in between the curves of the remaining free DEMs.

In Figure 5, we look into sample regions of the Tanaro river basin in Italy, where the DEM-derived river networks are overlaid. To the side of each sample region, the corresponding portion of the EU-Hydro photo-interpreted river network is presented for visual comparison. In the first sample region (Figure 5A), located in a flat area, it is clear that no single dataset can faithfully reproduce the photo-interpreted river network. Although all DEM-derived river networks are able to represent the river confluence in the region, they generally fail to match the location: they appear further upstream compared to the photo-interpreted river network. Furthermore, there is a tendency of a few datasets, namely the ASTER GDEM, the AW3D30 and the SRTM GL1, to create what seem to be spurious tributaries in the region.

In the second sample region (Figure 5B), another flat area, the only two datasets capable of representing the EU-Hydro are the HydroSHEDS and the EU DEM. The VFP, which once again matches perfectly the SRTM GL3, as well as the SRTM GL1 and the MERIT DEM, fails to properly locate the river confluence (further upstream compared to the EU-Hydro). The same happens with the TDX DEM, but with a more unrealistic meandering. Last, the AW3D30, the TINITALY DEM and the ASTER GDEM completely fail to represent the river network in the sample region, displaying a significant offset from the photo-interpreted river network, unrealistic meandering, unrealistic placement of the river confluence and even no confluence at all in the case of the AW3D30 DEM.

In the third sample region (Figure 5C), located in a mountainous area, all datasets are capable of a faithful representation of the photo-interpreted river network and specifically of the river confluence. However, a number of datasets, namely the TINITALY, the AW3D30, the TDX, the EU DEM and the ASTER GDEM, present possibly spurious tributaries in the sample region.

In Figure 6A, the spatial distribution of bias for the SRTM GL3 is presented. In this figure there appears to be a trend toward overestimating elevation in mountainous areas and a trend toward underestimating elevation in flatter terrain. All other DEM datasets follow more or less this same pattern, with the exception of HydroSHEDs DEM (Figure 6B), where there is a pronounced overall trend for underestimation, with a more limited overestimation in mountainous regions. Figure 6C shows that all free DEMs are linearly correlated with the LiDAR data, even though different degrees of dispersion can be noted, particularly in the TINITALY, HydroSHEDS, and the AW3D30 DEM. Figure 6D shows the cumulative bias as a function of H, which should help to differentiate between flatter and mountainous terrain, or floodplains and hillslopes, at any given elevation. It becomes clear that there is a lower bias in flatter terrain, where small H values are found, and higher bias in hillslopes. For all DEM datasets, the cumulative bias appears to be similar in the floodplains (c.a. 30 m H), with the VFP and SRTM GL3 presenting the smallest value and the AW3D30 DEM the highest one, while the remaining DEMs present values that fall in between. In hillslopes (above c.a. 30 m H), a similar behavior can be found, with the difference that the SRTM GL3 DEM accuracy tends to degrade faster than that of the VFP DEM. The SRTM GL3 DEM cumulative bias is matched by the MERIT DEM at c.a. 100 m H and by the HydroSHEDS DEM at c.a. 300 m H. The ASTER GDEM, the EU DEM and the TDX DEM share similar curves. Similarly, the TINITALY DEM, the SRTM GL1 and the HydroSHEDS DEM have curves that nearly overlap.

FIGURE 6

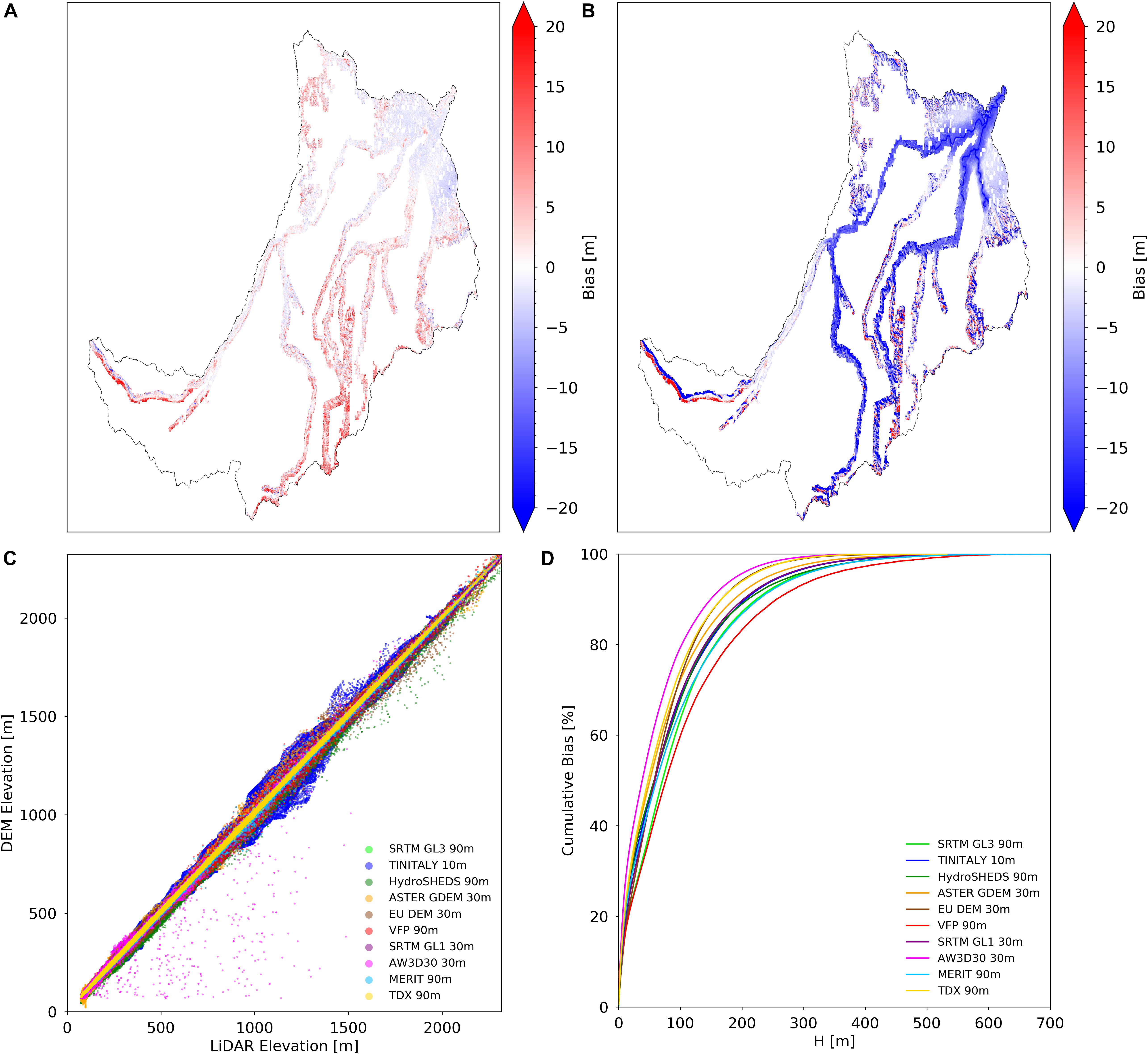
Figure 6. (A) Map of statistical bias between the SRTM GL3 digital elevation model (DEM) and the light detection and ranging (LiDAR) data in the Tanaro river basin, Italy; (B) map of statistical bias between the HydroSHEDS DEM and the LiDAR data; (C) DEM elevations plotted against LiDAR elevations; (D) cumulative frequency of absolute BIAS plotted against the elevation difference to the nearest stream, H.

In Table 2, results in terms of MAE and RMSE are presented. The lowest MAE is presented by the MERIT DEM, followed closely by TINITALY, the SRTM GL3, the SRTM GL1, the AW3D30, TDX, VFP and the EU-DEM. The ASTER GDEM and the HydroSHEDS DEM present the highest MAE among all datasets, more than double the MAE of the MERIT DEM. In terms of RMSE (and NRMSE), the lowest value is presented by the SRTM GL3, followed closely by the MERIT, SRTM GL1, TINITALY and TDX. The EU DEM, the VFP and the AW3D30 DEMs are found to have RMSE values with c.a. 2.5 m more than that of the SRTM GL3. The ASTER GDEM and the HydroSHEDS DEM, as with the MAE, present the highest value among all, more than double the RMSE of the SRTM GL3. Discrepancies found among datasets are explained to a limited degree by the lack of transformation of the LiDAR data and of the EU DEM to the EGM96 model, from the national and regional geoids, respectively. Unfortunately, an easily accessible transformation grid was not available to perform this step.

TABLE 2

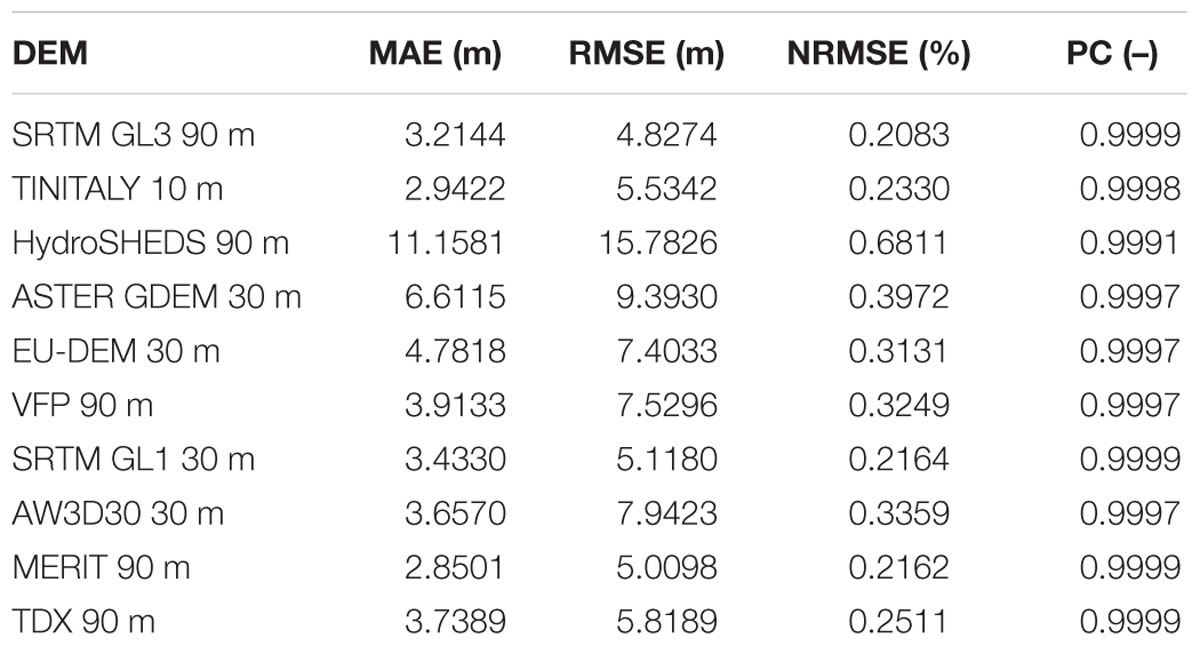
Table 2. Vertical accuracy assessment of the free digital elevation models (DEM) in the Tanaro river basin, Italy, expressed as mean absolute error (MAE), root mean squared error (RMSE), normalized RMSE (NRMSE), and Pearson correlation (PC), with the light detection and ranging data (LiDAR) data used as benchmark.

Discussion and Conclusion

In this analysis, the use of different DEMs is shown to result in some noteworthy discrepancies in the extracted terrain descriptors. In fact, the ability of each free DEM to capture a particular erosional or depositional landform caused by the action of water may vary with spatial resolution, hydrological reconditioning and vertical accuracy. This can impact any subsequent hydrogeomorphic analysis that requires a faithful representation of geomorphic features or the modeling of hydrological and hydraulic processes.

By looking at the cumulative frequency curves of elevation, it is found that the EU DEM, the VFP, the SRTM GL1 and GL3, the MERIT, the ASTER GDEM and the AW3D30 DEMs approximate the LIDAR data curve well. However, this is not necessary or sufficient to assert a faithful representation of geomorphic features. On the other hand, it is also observed that the HydroSHEDS DEM is significantly different from the LiDAR data at lower elevations and that the TDX and TINITALY DEMs is consistently different from LiDAR throughout the entire range of elevations.

In the case of the upslope contributing area within the whole Tanaro river basin, it is found that for areas below 1 km² (c.a. 90% of the basin) DEMs with a finer spatial resolution seem to present lower area values than DEMs with a coarser spatial resolution, while for areas above 1.2 km² (c.a. 10% of the basin) DEMs with finer spatial resolutions seem to present larger values than DEMs with coarser ones. The same conclusion can also be drawn by looking at the average values, where the TINITALY DEM, with a spatial resolution of 10 m, presents the highest upslope contributing area. The smaller fraction of cells with higher upslope contributing areas can generally be associated with cells belonging to the river network, and channel initiation may occur further upstream in DEMs of finer resolution.

The local slope differs from the LiDAR data to some degree, except in the case of HydroSHEDS, followed closely by the SRTM GL3, the VFP and the MERIT DEM. The best approximations are given by the TDX, the SRTM GL1, the EU DEM and the ASTER GDEM. The average values of local slope show that differences can reach about 10%.

The cumulative frequency curve of H is characterized by a sharp increase around 5 m, followed by a slower increase around 12 m and finally by another sharp increase from 30 m upward. DEMs with spatial resolution of 30 m, in addition to the TDX DEM, give the best approximation of the LiDAR H curve. In particular, the ASTER GDEM perfectly matches the LiDAR cumulative frequency curve at low H values. TINITALY, followed closely by HydroSHEDS at lower H values, presents a significantly different curve from LiDAR, while average values of H are significantly different between every DEM and the LiDAR.

The cumulative frequency curve of D is characterized by a sharp increase between 400 m and 5 km. The AW3D30 and the ASTER GDEM present consistently higher cell counts per D contour with respect to the remaining DEMs, while HydroSHEDS and the MERIT DEM present consistently lower cell counts; the SRTM GL1 and the TDX DEM fall more or less between all the other curves.

Regarding the DEM-based river network, it is confirmed that in the Tanaro river basin the river network extraction can be more problematic in flatter terrain. In particular, the location of river confluences and meanders can be significantly misrepresented. Over flat areas, coarser spatial resolution DEMs tend to better approximate the photo-interpreted river network, while hydrologically reconditioning a DEM (e.g., the HydroSHEDS) also seems to help.

In terms of BIAS, a tendency to overestimate elevation values in hillslopes and a tendency to underestimate elevations in floodplains appear to exist, except for the HydroSHEDS DEM that tends to underestimate elevations in a more generalized way. In spite of the BIAS found – less in the case of the SRTM GL3 and VFP DEMs – it is shown that DEMs are highly correlated to the LiDAR data, with the TINITALY, HydroSHEDS and AW3D30 showing some noticeable dispersion.

Finally, vertical accuracy measures were computed from each DEM. The lowest MAE has been obtained by the MERIT DEM, 2.85 m, while the ASTER GDEM and the HydroSHEDS DEM have presented the highest MAE of all the datasets, 11.16 and 6.61 m, respectively. The lowest RMSE, has been presented by the SRTM GL3, 4.83 m, or 0.21% NRMSE, while the ASTER GDEM and the HydroSHEDS DEM have presented, once again, the highest RMSE values among all datasets, 15.78 and 9.39 m, or 0.40 and 0.68% NRMSE, respectively.

In practice, differences found may affect several aspects of the modeling of hydrological and hydraulic processes, resulting in diverse outcomes. For instance, differences in upslope contributing area may influence scaling regimes that depend directly on it (Dodov and Foufoula-Georgiou, 2005) or may have an impact on the faithful representation of a river network and of channel hydraulic geometry. The slope may affect channel initiation and the flow of surface water. H may significantly influence the outcomes in low-complexity flood modeling (e.g., Rebolho et al., 2018; Zheng et al., 2018), flood mapping (Degiorgis et al., 2012; Manfreda et al., 2014) and flood detection (e.g., Westerhoff et al., 2013), while D may impact hydrological modeling (e.g., Mesa and Mifflin, 1986; Moussa, 2008).

Concerning the Tanaro river basin, finer spatial resolutions have not always improved the representation of the morphology. With respect to the hydrological reconditioning of DEMs, and even though only the HydroSHEDS DEM was given as an example, the procedure has appeared helpful in achieving a better definition of the river network, but it might also hinder the representation of fluvial landforms, something evidenced by Callow et al. (2007). In the case of vertical accuracy, elevation-based terrain features were affected by the magnitude of the vertical error. Indeed, error metrics can be misleading, since low values may hide significant problems in the representation of the terrain in different parts of the basin, as shown by the BIAS.

Ideally, a good DEM should aim for an optimal balance between spatial resolution, vertical accuracy and DEM reconditioning. Considering the numerous applications that free DEMs have and the fast evolution of instruments and techniques experienced over the past years, one might expect that new and improved datasets, as well as their derivatives, would be released more regularly. The lack of systematic updating constitutes a major hurdle. Operational flood forecasting systems that authorities rely on for early warning and which are as good as their margin of error, as well as flood maps, are only a few examples of applications that may suffer from the lack of timely DEM updates. It is shown that there is still substantial work to be done an there is some indication that a new generation of free DEMs can form the foundations on which to sustain and even accelerate progress in several fields. Therefore, we would like to use this opportunity not only to call for high-accuracy, open-access global DEMs, but also for the systematic processing of new and existing datasets, based on state-of-the-art techniques, with an exhaustive error quantification, the inclusion of comprehensive documentation and the production of terrain derivatives that can prove indispensable for saving valuable resources. Last, it is also recommended the fusion of existing free DEMs and LiDAR data, where the latter is available (e.g., Italy and United Kingdom), as this process may enhance the quality of the digital terrain representation.

Author Contributions

RT conceptualized the work, carried out the analysis, and wrote the manuscript. PM and SB reviewed and provided the comments.

Funding

This work was supported by the European Union’s EU Framework Programme for Research and Innovation Horizon 2020 under Grant Agreement No. 676027.

Disclaimer

This publication reflects only the authors’ views and the European Union is not liable for any use that may be made of the information contained therein.

Conflict of Interest Statement

RT is employed by company GECOsistema Srl. PM and SB are owners of the company GECOsistema Srl and declare no competing interests.

Acknowledgments

We would like to thank the European Union’s Horizon 2020 Research and Innovation Program under the Marie Skłodowska-Curie System-Risk ETN (https://www.system-risk.eu/) grant, the European Union’s Earth Observation Programme Copernicus, NASA for the release of the SRTM DEMs, INGV for TINITALY, the USGS for the HydroSHEDS dataset, NASA/METI for the release of ASTER GDEM, the European Union’s Copernicus Programme for the EU-DEM and EU-Hydro, Mr. de Ferranti for the VFP DEM, JAXA for the AW3D30 DEM, Dr. Dai Yamazaki and the University of Tokyo for the MERIT DEM, DLR for the TDX DEM, and the Italian Ministry of Environment, Land and Sea for the LiDAR dataset for Italy. We would also like to thank Dr. David Tarboton (Utah State University) for TauDEM utilities, the Python Software Foundation for the Python programming language, the Open Source Geospatial Foundation for the GDAL.

References

Archer, L., Neal, J. C., Bates, P. D., and House, J. I. (2018). Comparing TanDEM-X data with frequently used DEMs for flood inundation modeling. Water Res. Res. 54, 10205–10222. doi: 10.1029/2018WR023688

CrossRef Full Text | Google Scholar

Beven, K. J., and Kirkby, M. J. (1979). A physically based, variable contributing area model of basin hydrology. Hydrol. Sci. Bull. 24, 43–69. doi: 10.1080/02626667909491834

PubMed Abstract | CrossRef Full Text | Google Scholar

Callow, J. N., Van Niel, K. P., and Boggs, G. S. (2007). How does modifying a DEM to reflect known hydrology affect subsequent terrain analysis? J. Hydrol. 332, 30–39. doi: 10.1016/j.jhydrol.2006.06.020

CrossRef Full Text | Google Scholar

Chai, T., and Draxler, R. R. (2014). Root mean square error (RMSE) or mean absolute error (MAE)? – arguments against avoiding RMSE in the literature. Geosci. Model Dev. 7, 1247–1250. doi: 10.5194/gmd-7-1247-2014

CrossRef Full Text | Google Scholar

Chow, V. T. (1959). Open-Channel Hydraulics. New York, NY: McGraw-Hill, 680.

Google Scholar

Clarivate Analytics (2018). Clarivate Analytics. Available at: https://www.webofknowledge.com/ (accessed July, 2018).

Clubb, F. J., Mudd, S. M., Milodowski, D. T., Valters, D. A., Slater, L. J., Hurst, M. D., et al. (2017). Geomorphometric delineation of floodplains and terraces from objectively defined topographic thresholds. Earth Surf. Dynam. 5, 369–385. doi: 10.5194/esurf-5-369-2017

CrossRef Full Text | Google Scholar

Croneborg, L., Saito, K., Matera, M., McKeown, D., and van Aardt, J. (2015). A guidance note on how Digital Elevation Models are created and used – includes key definitions, sample terms of reference and how best to plan a DEM-mission. New York, NY: International Bank for Reconstruction and Development, 104.

de Ferranti, J. (2014). Viewfinder Panorama. Available at: http://www.viewfinderpanoramas.org/ (accessed July, 2018).

Degiorgis, M., Gnecco, G., Gorni, S., Roth, G., Sanguineti, M., and Taramasso, A. C. (2012). Classifiers for the detection of flood-prone areas using remote sensed elevation data. J. Hydrol. 47, 302–315. doi: 10.1016/j.jhydrol.2012.09.006

CrossRef Full Text | Google Scholar

DLR (2018). The TanDEM-X 90m Digital Elevation Model. Available at: https://geoservice.dlr.de/web/dataguide/tdm90/ (accessed July, 2018).

Dodov, B., and Foufoula-Georgiou, E. (2005). Fluvial processes and streamflow variability: interplay in the scale-frequency continuum and implications for scaling. Water Res. Res. 41:W05005. doi: 10.1029/2004WR003408

CrossRef Full Text | Google Scholar

EEA (2014). EU-DEM Statistical Validation. EEA Report. Copenhagen: European Environment Agency.

EEA (2015a). Copernicus Land Monitoring Service, European Digital Elevation Model (EU-DEM, Version 1.0). Available at: http://land.copernicus.eu/pan-european/satellite-derived-products/eu-dem (accessed May, 2018).

EEA (2015b). Copernicus Land Monitoring Service, EU-Hydro. Available at: https://land.copernicus.eu/pan-european/satellite-derived-products/eu-hydro (accessed July, 2018).

Elshorbagy, A., Bharath, R., Lakhanpal, A., Ceola, S., Montanari, A., and Lindenschmidt, K.-E. (2017). Topography- and nightlight-based national flood risk assessment in Canada. Hydrol. Earth Syst. Sci. 21, 2219–2232. doi: 10.5194/hess-21-2219-2017

CrossRef Full Text | Google Scholar

EROS/USGS/USDOI (1997). USGS 30 ARC-second Global Elevation Data, GTOPO30. Boulder, CO: Computational and Information Systems Laboratory.

Farr, T. G., Rosen, P. A., Caro, E., Crippen, R., Duren, R., Hensley, S., et al. (2007). The shuttle radar topography mission. Rev. Geophys. 45:RG2004. doi: 10.1029/2005RG000183

CrossRef Full Text | Google Scholar

Fox, D. M., Bryan, R. B., and Price, A. G. (1997). The influence of slope angle on final infiltration rate for interrill conditions. Geoderma 80, 181–194. doi: 10.1016/S0016-7061(97)00075-X

CrossRef Full Text | Google Scholar

Giannoni, F., Roth, G., and Rudari, R. (2005). A procedure for drainage network identification from geomorphology and its application to the prediction of the hydrologic response. Adv. Water Res. 28, 567–581. doi: 10.1016/j.advwatres.2004.11.013

CrossRef Full Text | Google Scholar

Horritt, M. S., and Bates, P. D. (2001). Effects of spatial resolution on a raster based model flood flow. J. Hydrol. 253, 239–249. doi: 10.1016/S0022-1694(01)00490-5

CrossRef Full Text | Google Scholar

INGV (2012). TINITALY/01. Istituto Nazionale di Geofisica e Vulcanologia [Dataset]. Available at: http://tinitaly.pi.ingv.it/ (accessed July, 2018).

Jarihani, A. A., Callow, J. N., McVicar, T. R., Van Niel, T. G., and Larsen, J. R. (2015). Satellite-derived digital elevation model (DEM) selection, preparation and correction for hydrodynamic modelling in large, low-gradient and data-sparse catchments. J. Hydrol. 524, 489–506. doi: 10.1016/j.jhydrol.2015.02.049

CrossRef Full Text | Google Scholar

Jarvis, A., Reuter, H. I., Nelson, A., and Guevara, E. (2008). Hole-filled seamless SRTM data V4. International Centre for Tropical Agriculture (CIAT) [Dataset]. Available at: http://srtm.csi.cgiar.org (accessed May, 2018).

JAXA (2018). ALOS Global Digital Surface Model ALOS World 3D - 30m (AW3D30). Japan Aerospace Exploration Agency (JAXA) [Dataset]. Available at: https://www.eorc.jaxa.jp/ALOS/en/aw3d30/index.htm (accessed July, 2018).

Kirkby, M. J. (1976). Tests of the random network model, and its application to basin hydrology. Earth Surf. Process. 1, 197–212. doi: 10.1002/esp.3290010302

CrossRef Full Text | Google Scholar

Knighton, A. D. (1999). Downstream variation in stream power. Geomorphology 29, 293–306. doi: 10.1016/S0169-555X(99)00015-X

CrossRef Full Text | Google Scholar

Kumar, P., Verdin, K. L., and Greenlee, S. K. (2000). Basin level statistical properties of topographic index for North America. Adv. Water Res. 23, 571–578. doi: 10.1016/S0309-1708(99)00049-4

CrossRef Full Text | Google Scholar

Lee, M. T., and Delleur, J. W. (1976). A variable source area model of the rainfall-runoff process based on the watershed stream network. Water Res. Res. 12, 1029–1036. doi: 10.1029/WR012i005p01029

CrossRef Full Text | Google Scholar

Lehner, B., Verdin, K., and Jarvis, A. (2008a). HydroSHEDS Technical Documentation. Washington, DC: World Wildlife Fund, 27.

Google Scholar

Lehner, B., Verdin, K., and Jarvis, A. (2008b). New global hydrography derived from spaceborne elevation data. Eos 89:93. doi: 10.1029/2008EO100001

CrossRef Full Text | Google Scholar

Luino, F. (1999). The flood and landslide event of November 4-6 1994 in piedmont region (northwestern italy): causes and related effects in tanaro valley. Phys. Chem. Earth 24, 123–129. doi: 10.1016/S1464-1895(99)00007-1

CrossRef Full Text | Google Scholar

Maidment, D. (ed.) (1993). Handbook of Hydrology. New York, NY: McGraw Hill.

Google Scholar

Manfreda, S., Nardi, F., Samela, C., Grimaldi, S., Taramasso, A. C., Roth, G., et al. (2014). Investigation on the use of geomorphic approaches for the delineation of flood prone areas. J. Hydrol. 517, 863–876. doi: 10.1016/j.jhydrol.2014.06.009

CrossRef Full Text | Google Scholar

Manfreda, S., Samela, C., Gioia, A., Consoli, G. G., Iacobellis, V., Giuzio, L., et al. (2015). Flood-prone areas assessment using linear binary classifiers based on flood maps obtained from 1D and 2D hydraulic models. Nat. Hazards 79, 735–754. doi: 10.1007/s11069-015-1869-5

CrossRef Full Text | Google Scholar

Mesa, O. J., and Mifflin, E. R. (1986). “On the relative role of hillslope and network geometry in hydrologic response,” in Scale Problems in Hydrology. Water Science and Technology Library, Vol. 6, eds V. K. Gupta, I. Rodríguez-Iturbe, and E. F. Wood (Dordrecht: Springer).

Google Scholar

Montgomery, D. R., and Dietrich, W. E. (1988). Where do channels begin? Nature 336, 232–234. doi: 10.1038/336232a0

CrossRef Full Text | Google Scholar

Montgomery, D. R., and Dietrich, W. E. (1989). Source areas drainage density and channel initiation. Water Res. Res. 25, 1907–1918. doi: 10.1029/WR025i008p01907

CrossRef Full Text | Google Scholar

Moussa, R. (2008). What controls the width function shape, and can it be used for channel network comparison and regionalization? Water Res. Res. 44:W08456. doi: 10.1029/2007WR006118

CrossRef Full Text | Google Scholar

Nardi, F., Annis, A., Di Baldassarre, G., Vivoni, E. R., and Grimaldi, S. (2019). GFPLAIN250m, a global high-resolution dataset of Earth’s floodplains. Sci. Data 6:180309. doi: 10.1038/sdata.2018.309

PubMed Abstract | CrossRef Full Text | Google Scholar

NASA (2018a). Shuttle Radar Topography Mission (SRTM) Global 1 arc second (GL1). United States National Aeronautics and Space Administration (NASA) [Dataset]. Available at: https://search.earthdata.nasa.gov/search (accessed July, 2018).

NASA (2018b). Shuttle Radar Topography Mission (SRTM) Global 3 arc second (GL3). United States National Aeronautics and Space Administration (NASA) [Dataset]. Available at: https://search.earthdata.nasa.gov/search (accessed July, 2018).

NASA JPL/ METI (2018). Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) Global Digital Elevation Model (GDEM). United States National Aeronautics and Space Administration (NASA) Jet Propulsion Laboratory and Ministry of Economy, Trade, and Industry (METI) of Japan [Dataset]. Available at: https://search.earthdata.nasa.gov/search (accessed July, 2018).

Nobre, A. D., Cuartas, L. A., Momo, M. R., Severo, D. L., Pinheiro, A., and Nobre, C. A. (2016). HAND contour: a new proxy predictor of inundation extent. Hydrol. Process. 30, 320–333. doi: 10.1002/hyp.10581

CrossRef Full Text | Google Scholar

Rebolho, C., Andréassian, V., and Le Moine, N. (2018). Inundation mapping based on reach-scale effective geometry. Hydrol. Earth Syst. Sci. 22, 5967–5985. doi: 10.5194/hess-2018-146

CrossRef Full Text | Google Scholar

Rizzoli, P., Martone, M., Gonzalez, C., Wecklich, C., Borla Tridon, D., Bräutigam, B., et al. (2017). Generation and performance assessment of the global TanDEM-X digital elevation model. ISPRS J. Photogramm. Remote Sens. 132, 119–139. doi: 10.1016/j.isprsjprs.2017.08.008

CrossRef Full Text | Google Scholar

Rodriguez, E., Morris, C. S., Belz, J. E., Chapin, E. C., Martin, J. M., Daffer, W., et al. (2005). An assessment of the Srtm Topographic Products. Pasadena, CA: Jet Propulsion Laboratory. .

Google Scholar

Rodríguez-Iturbe, I., and Rinaldo, A. (1997). Fractal River Networks: Chance and Self-Organization. New York: Cambridge University Press, 547.

Google Scholar

Sanders, B. F. (2007). Evaluation of on-line DEMs for flood inundation modeling. Adv. Water Res. 30, 1831–1843. doi: 10.1016/j.advwatres.2007.02.005

CrossRef Full Text | Google Scholar

Sørensen, R., and Seibert, J. (2007). Effects of DEM resolution on the calculation of topographical indices: TWI and its components. J. Hydrol. 347, 79–89. doi: 10.1016/j.jhydrol.2007.09.001

CrossRef Full Text | Google Scholar

Tachikawa, T., Kaku, M., Iwasaki, A., Gesch, D., Oimoen, M., Zhang, Z., et al. (2011). ASTER Global Digital Elevation Model Version 2 – Summary of Validation Results. Washington, DC: NASA.

Google Scholar

Tadono, T., Ishida, H., Oda, F., Naito, S., Minakawa, K., and Iwamoto, H. (2014). Precise global DEM generation by ALOS PRISM. ISPRS Ann. Photogramm. Remote Sens. Spat. Information Sci. 4, 71–76. doi: 10.5194/isprsannals-II-4-71-2014

CrossRef Full Text | Google Scholar

Tarboton, D. (2015). Terrain Analysis Using Digital Elevation Models (TauDEM, Version 5). Hydrology Research Group, Utah State University. Available at: http://hydrology.usu.edu/taudem/taudem5/ (accessed July 1, 2018).

Tarboton, D. G., Bras, R. L., and Rodriguez-Iturbe, I. (1992). A physical basis for drainage density. Geomorphology 5, 59–76. doi: 10.1016/0169-555X(92)90058-V

PubMed Abstract | CrossRef Full Text | Google Scholar

Tarquini, S., Isola, I., Favalli, M., Mazzarini, F., Bisson, M., Pareschi, M. T., et al. (2007). TINITALY/01: a new triangular irregular network of Italy. Ann. Geophys. 50, 407–425. doi: 10.4401/ag-4424

CrossRef Full Text | Google Scholar

Tarquini, S., Vinci, S., Favalli, M., Doumaz, F., Fornaciai, A., and Nannipieri, L. (2012). Release of a 10-m-resolution DEM for the italian territory: comparison with global-coverage DEMs and anaglyph-mode exploration via the web. Comput. Geosci. 38, 168–170. doi: 10.1016/j.cageo.2011.04.018

CrossRef Full Text | Google Scholar

University of Tokyo (2018). MERIT DEM: Multi-Error-Removed Improved-Terrain DEM [Dataset]. Available at: http://hydro.iis.u-tokyo.ac.jp/~yamadai/MERIT_DEM/ (accessed July, 2018).

USGS (2013). Hydrological data and maps based on SHuttle Elevation Derivatives at multiple Scales. Available at: https://hydrosheds.cr.usgs.gov/index.php (accessed July, 2018).

Google Scholar

Westerhoff, R. S., Kleuskens, M. P. H., Winsemius, H. C., Huizinga, H. J., Brakenridge, G. R., and Bishop, C. (2013). Automated global water mapping based on wide-swath orbital synthetic-aperture radar. Hydrol. Earth Syst. Sci. 17, 651–663. doi: 10.5194/hess-17-651-2013

CrossRef Full Text | Google Scholar

Yamazaki, D., Ikeshima, D., Tawatari, R., Yamaguchi, T., O’Loughlin, F., Neal, J. C., et al. (2017). A high accuracy map of global terrain elevations. Geophys. Res. Lett. 44, 5844–5853. doi: 10.1002/2017GL072874

CrossRef Full Text | Google Scholar

Zhang, W., and Montgomery, D. R. (1994). Digital elevation model grid size, landscape representation, and hydrologic simulations. Water Res. Res. 30, 1019–1028. doi: 10.1029/93WR03553

CrossRef Full Text | Google Scholar

Zheng, X., Tarboton, D. G., Maidment, D. R., Liu, Y. Y., and Passalacqua, P. (2018). River channel geometry and rating curve estimation using height above the nearest drainage. J. Am. Water Res. Assoc. 54, 785–806. doi: 10.1111/1752-1688.12661

CrossRef Full Text | Google Scholar