Wetting Behavior of Iron–Carbon Melt in Silicates at Mid-Mantle Pressures With Implications for Earth’s Deep Carbon Cycle

Introduction

Iron–carbon alloys represent reduced forms of carbon and are important components of Earth’s long-term carbon cycle. Metallic iron may have been actively produced in the lower mantle (e.g., Frost et al., 2004), the mantle transition zone, and deep part of the upper mantle (e.g., Rohrbach et al., 2007), due to disproportionation of ferrous iron (Fe²⁺) in silicates into iron metal (Fe⁰) and ferric iron (Fe³⁺). At depths greater than ∼250 km, metallic iron may reduce subducted carbonates to produce elemental carbon or carbide (MgCO₃ + 2 Fe⁰ = 3 (Fe, Mg)O + C, e.g., Rohrbach and Schmidt, 2011). Studies of diamond inclusions show that metallic melt containing Fe and C is present in the deep mantle (e.g., Kaminsky and Wirth, 2011; Smith et al., 2016). Depending on its wetting behavior, such melt may be trapped locally or drain into greater depths. Furthermore, carbon is a candidate for the light alloying element for the Earth’s iron-rich core, which likely constitutes the predominant carbon reservoir of the planet (e.g., Wood et al., 2013; Li and Fei, 2014). If the Fe–C melt could form an interconnected network, it may eventually segregate to the core-mantle boundary (CMB), possibly merging into the liquid outer core. It has been proposed that slab-derived Fe–C melt in isolated patches can match seismically observed density and velocity features of some ultralow velocity zones (ULVZs) (Liu et al., 2016). For these reasons, knowledge of the wetting behavior of Fe–C is crucial for assessing the fate of slab-derived metallic liquid in deep Earth.

The wetting behavior of iron-rich melt containing sulfur, oxygen, and silicon at high pressures has been studied previously in order to understand the mechanisms of core formation (e.g., Takafuji et al., 2004; Terasaki et al., 2008; Shi et al., 2013). However, that of Fe–C melt in silicate matrix remains poorly understood. Experimental data on the wetting behavior of Fe–C melt at mid-mantle conditions is scarce and limited to <6 GPa (Duncan and Fei, 2017; Zhimulev et al., 2018). In this study, we conduct experiments to investigate the wetting behavior of Fe–C melt in a matrix of polycrystalline olivine polymorphs and bridgmanite/ferropericlase at the conditions of Earth’s mid-mantle between 10 and 23 GPa and 1600 and 1800°C. The results are applied to assess the feasibility of percolative drainage of iron–carbon melt through the mantle.

Materials and Methods

Experimental

High pressure experiments were carried out using the 1000-ton Walker-type multi-anvil press at the University of Michigan. Experiments at pressures up to 17 GPa used Toshiba-Tungaloy F-grade tungsten carbide (WC) cubes with 5 mm truncation edge length (TEL) and those at pressures up to 23 GPa used similar WC cubes with 3 mm TEL (Figure 1). Temperature was monitored using the power curves determined by previous multi-anvil experiments with type-C (W95Re5-W74Re26) thermocouples. The pressure uncertainty is estimated to be ±2 GPa and the temperature uncertainty is estimated to be ±100 K, on the basis of duplication experiments (Li and Li, 2015).

FIGURE 1

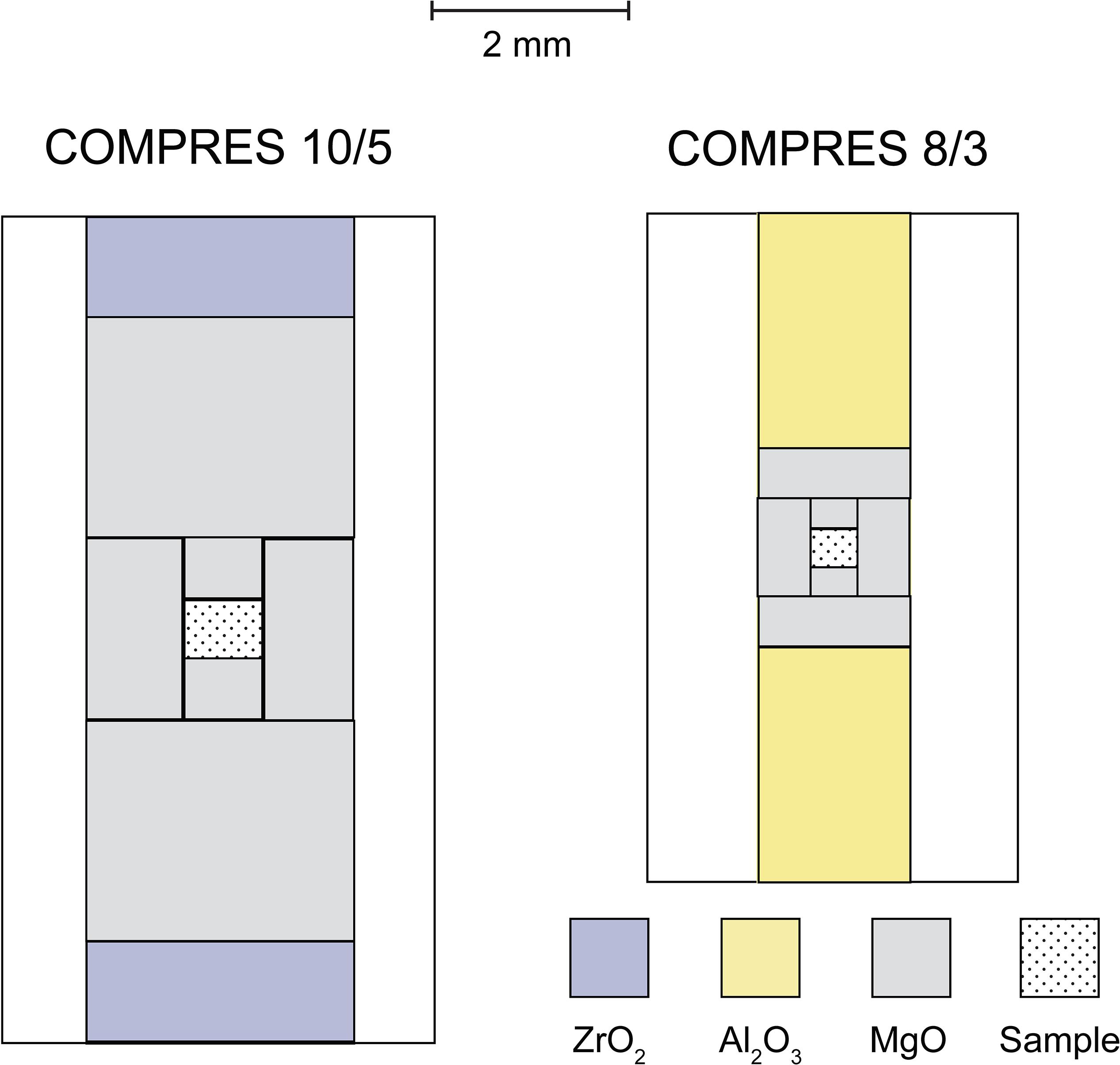
Figure 1. Configurations of cell assemblies for high-pressure experiments. Left: cross-section of modified COMPRES 10/5 assembly showing the sample (dotted) with a MgO container (gray), MgO spacers (gray), and zirconia end-plugs (blue). Right: cross-section of modified COMPRES 8/3 assembly showing the sample (dotted) with a MgO container (gray), MgO spacers (gray), and alumina end-plugs (yellow).

The starting material of the experiments consists of a powder mixture of San Carlos olivine, iron, and graphite. The olivine powder was prepared by grinding natural grains under ethanol in an agate mortar for 1 h and then dried at 110°C. Its composition is approximately (Mg_0.9Fe_0.1)₂SiO₄ with 2900 ppm Ni (Herzberg et al., 2016). An Fe–C mixture with 96 wt% Fe and 4 wt% graphite, corresponding to the eutectic composition of the Fe–C binary system at 10 GPa (Fei and Brosh, 2014) was homogenized and then mixed with the olivine power with a ratio of approximately 97:3 in volume. The volume fraction of Fe–C in the starting material was increased above 7% in one run for comparison. The sample was packed into a MgO capsule, which was dried at 950°C for approximately 2 h before loading to minimize trapped moisture. COMPRES 10/5 and 8/3 assemblies were used for experiments up to 17 GPa and those above 20 GPa, respectively (Leinenweber et al., 2012).

In each experiment, the sample was first pressurized to 5 GPa and then sintered at 800–1000°C for 8–12 h during further compression to the target pressure. Target temperature was set below the melting temperature of the silicate phase and above the melting temperature of the iron-rich mixture. The sample was held at target pressure and temperature for approximately 30 min and then quenched by cutting power to the heater and slowly decompressed to ambient pressure.

Analytical

Recovered experimental products were examined for texture, structure, and composition using optical microscopes, micro-Raman spectroscope, and scanning electron microscope (SEM) with energy dispersive spectrometer (EDS). The sample was first mounted in epoxy, sectioned and polished for analyses using optical microscopes. Raman analysis was then performed using a Renishaw inVia confocal Raman Microscope with a 532 nm continuous wave laser. The input laser power varied between 4 and 40 mW and the laser beam was focused through a 50× Mitutoyo objective lens to a diameter of 3–5 microns or through a 20× Olympus objective lens to a beam diameter of 7–12 microns. Raman signal was dispersed with an 1800 grooves/cm grating to achieve spectral resolution of 1–2 wave number (wn). The spectral window was centered at 520 wn. The signal was recorded with a Peltier cooled CCD. Acquisition time is typically 1 s per CCD window. Replicate measurements were conducted to evaluate heterogeneity. For composition and further texture analyses, the polished sample was aluminum-coated and examined using a JOEL 700FLV field emission SEM in the Central Campus Electron Microbeam Analysis Laboratory (EMAL) at the University of Michigan.

Apparent dihedral angles were measured from back scattered electron (BSE) images of the recovered samples by using the thresholding and protractor functions of the image processing software Fiji (Schindelin et al., 2012). To establish a consistent criterion and hence to increase reproducibility of dihedral angle measurement, the BSE images of the measured areas were converted into binary format. Each individual dihedral angle was measured by the “protractor” function in Fiji. The actual fraction of Fe–C in each experiment was estimated from the polished cross-sections of recovered samples using the “Analyze Particles…” function in Fiji.

Results and Discussion

Four experiments at pressures between 10 and 23 GPa and temperatures at 1600°C or 1800°C produced domains of quenched Fe–C melt dispersed in solid matrix (Table 1 and Figure 2). The molten state of the Fe–C phase is inferred from the spherical shape and/or the dendritic texture of interspersed carbon-rich and carbon-poor domains. The solid state of the silicate or oxide is inferred from the euhedral or sub-hedral shapes. The coexistence of Fe–C melt with solid silicate and oxide at the experimental pressures and temperatures are consistent with known melting behavior of silicates and iron–carbon binary system (Figure 3).

TABLE 1

Table 1. Summary of experimental conditions and results.

FIGURE 2

Figure 2. Back scattered electron (BSE) image of the experimental products. Upper: products showing Fe–C melt (gray) dispersed in olivine (Ol) in M053016, ringwoodite (Rw) in M052417, and bridgmanite (Bdg) and ferropericlase (Fp) in M013017. Lower: product of experiment M060316 showing Fe–C melt (gray with dendritic texture on the left, bright on the right) in a matrix of bridgmanite (Bdg) and ferropericlase (Fp). Some Fe–C melt partially connected to form larger domains but small melt pockets remain trapped in the solid matrix.

FIGURE 3

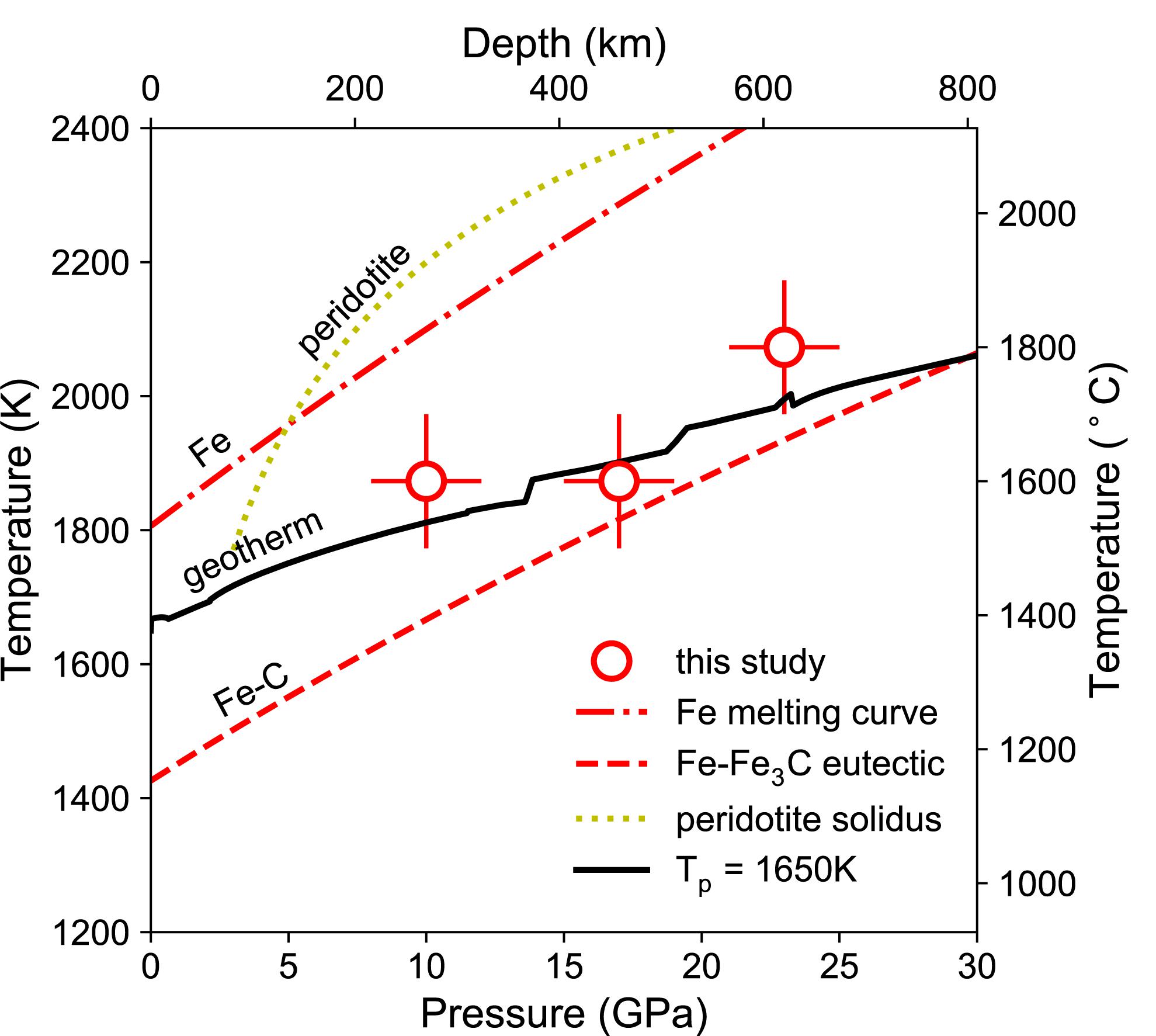
Figure 3. Experimental pressures and temperatures with respect to the geotherm. The temperatures of the experiments (open circle with error bars) are near the estimated mantle temperatures (solid, Stixrude and Lithgow-Bertelloni, 2011) and fall between the melting curve of iron (dashed dotted, fitted from Williams et al., 1987) and the eutectic melting curve of Fe–C binary system (dashed, fitted from Hultgren et al., 1963; Hirayama et al., 1993; Lord et al., 2009; Fei and Brosh, 2014; Liu et al., 2016), and they are below the solidus of peridotite (dotted, Herzberg et al., 2000).

In all experiments, the Fe–C melt after quench formed isolated pockets at the grain boundaries of silicate or silicate and oxide matrix. The volume fraction of the Fe–C melt ranged from 0.5 to 7.3%. At small melt fractions between 0.5 and 2.6%, the Fe–C melt assumed nearly spherical shape with a radius of R = 0.2–1 micron (R, radius of an equal area circle) and showed no connectivity at all (Figure 2, upper). The Fe–C sphere appear somewhat distorted at 17 and 23 GPa. Although some large melt domains (R ≥ 5 micron) were formed at a melt fraction of 7.3%, the dihedral angles of the small isolated melt pockets (R ≤ 1 micron) remained large and full connectivity was not developed (Figure 2, lower). All the textures suggest that Fe–C melt does not wet silicate or silicate plus oxide at the conditions of the mid-mantle.

Raman analyses showed that the olivine converted into ringwoodite at 17 GPa, and dissociated into bridgmanite and ferropericlase at 23 GPa (Figure 4). The carbon contents of the Fe–C melt phases were only estimated semi-quantitatively from EDS data because the domains are typically sub-micron in size. They are consistent with the expected 4 ± 2 wt%. The Fe–C melt phases sometimes contained a small amount of nickel, likely originating from San Carlos olivine in the starting materials.

FIGURE 4

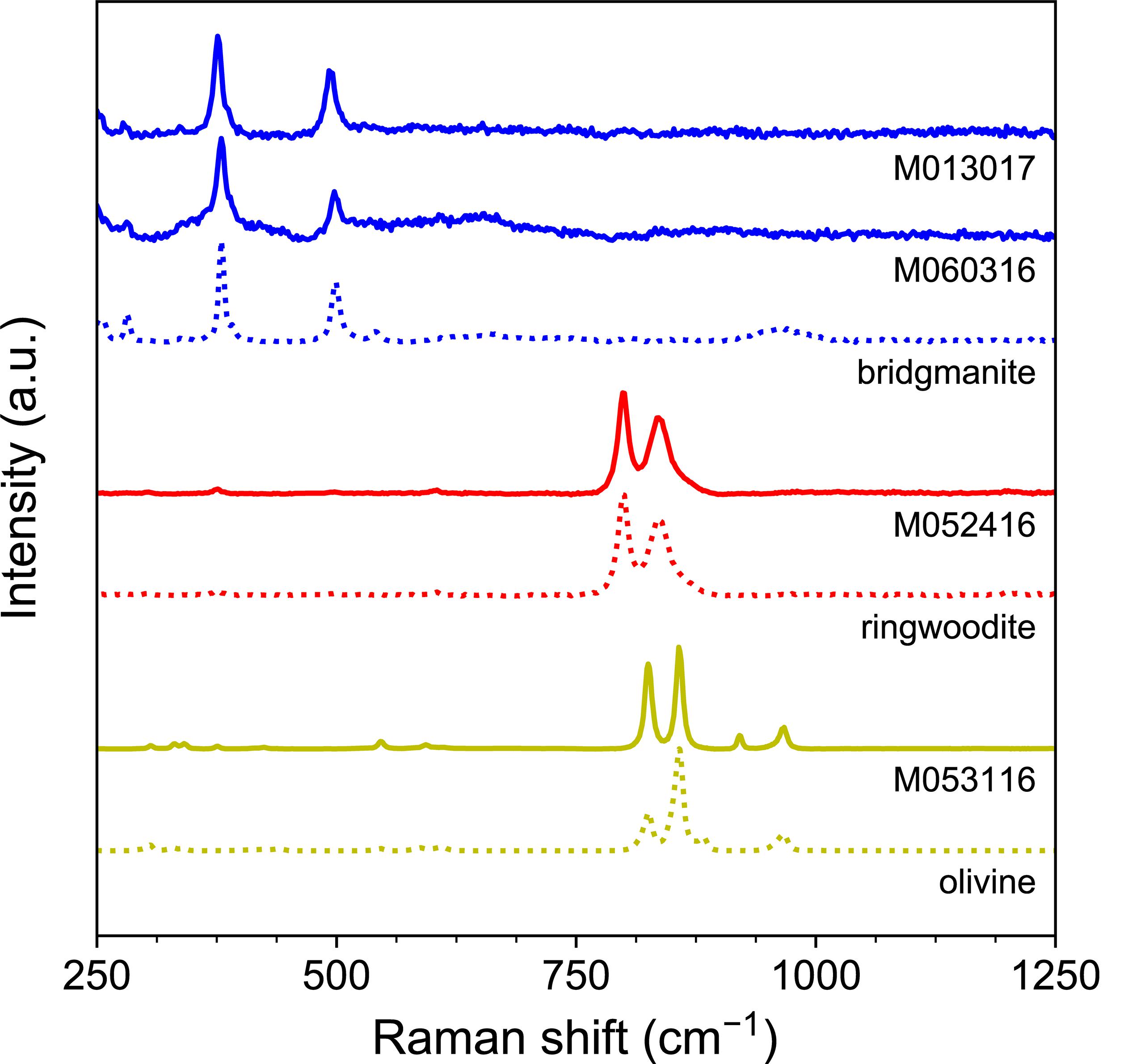
Figure 4. Raman spectra of silicate phases in experimental products. Reference spectra (dashed) are plotted for comparison.

Dihedral Angle of Fe–C Melt in Mantle Silicate

The apparent dihedral angles of Fe–C melt in silicate matrix at mid-mantle conditions are measured in cross-sections of the experimental products. Dihedral angle is defined as the angle between the junction of two solid grains and melt pocket in the plane normal to the junction of the two solid grains (e.g., Porter et al., 2009). Previous studies suggested that a large number of measurements (50–100) are adequate to determine the effective dihedral angles reliably (Holness and Lewis, 1997). Here, between 91 and 257 measurements yielded distributions close to Gaussian (Table 1 and Figure 5). The mean value of the apparent dihedral angle distribution is taken as the effective dihedral angle, with one standard deviation as the associated uncertainty. The dihedral angles of Fe–C melt in olivine, ringwoodite, and bridgmenite-ferropericlase are 117 ± 14° at 10 GPa, 120 ± 14° at 17 GPa, and 107 ± 16° at 23 GPa, respectively. In previous studies, the median is sometimes taken as the effective dihedral angle of the system when the distribution is not near Gaussian. For comparison, we also report the medians of the measured dihedral angles in each experiment with a 95% confidence interval around the medians (Stickels and Hucke, 1964), which are 116⁺⁴_–2° at 10 GPa, 119⁺⁴_–4° at 17 GPa, and 108⁺²_–2° at 23 GPa, respectively.

FIGURE 5

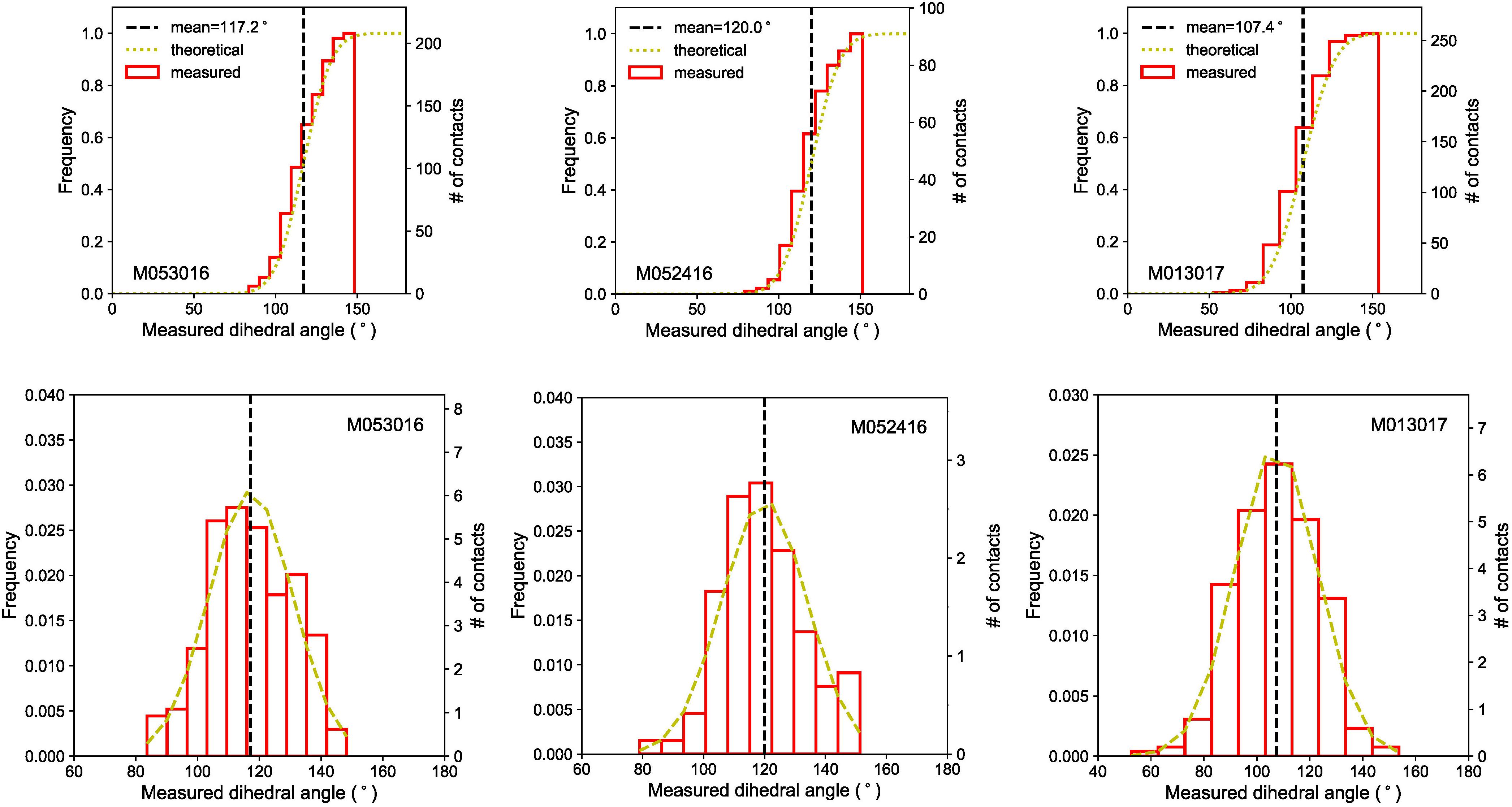
Figure 5. Cumulative (upper panel) and simple (lower panel) frequency distributions of apparent dihedral angles. The apparent dihedral angles measured from the BSE images of the cross-section for each experiment (red solid line) are compared with the theoretical frequency curves (yellow dashed line). The vertical dashed lines represent the mean values of the apparent dihedral angle distributions.

Textural Equilibrium

The measured dihedral angle is accurate only when the system has reached textural equilibrium so that with time the microstructures will only change in size but not in type or shape. At textural equilibrium, the distribution of the apparent dihedral angels formed by the liquid phase assumes a Gaussian pattern, with a single peak that drops off rapidly on both sides (Holzheid et al., 2000). Moreover, the distribution of grain sizes approaches the theoretically expected pattern, and the apparent angles formed by the solid grains at triple junction center around 120°, also dropping off rapidly above or below the mean value. Assuming that the effect of solid silicate matrixes is negligible, the dihedral angle measured in an equilibrated phase assembly is characteristic of the composition at specific pressure and temperature conditions.

Time series studies showed that iron-rich melt in solid silicate matrix reached steady-state texture within 12 min at 25 GPa and 2500 K (Takafuji et al., 2004) in laser-heated diamond anvil cells, and within 50 min at 14 GPa and 1700°C in multi-anvil apparatus (Shannon, 1998). In this study, the experiments were sintered at 5 GPa and 800–1000°C for 8–12 h and then held at 10–23 GPa and 1600–1800°C for about 30 min. The pressure and temperature conditions and experimental durations are comparable to the studies with demonstrated textural equilibrium. Moreover, the distributions of the apparent angles can be fitted by Gaussian curves (Figure 5), indicating sufficient approach to texture equilibrium. Equilibrium is further supported by the nearly 120° of dihedral angles at triple junctions of solid grains (Figure 2). Although the equilibrated triple junctions of solid grains may have formed at the pre-annealing or sintering stage, textural re-equilibration between solid grains at a slightly higher temperature would take shorter time than starting from ambient temperature, and the Fe–C melt is expected to establish textural equilibrium with the solid phases much faster than within the solid grains.

Interfacial Energy and Surface Tension Between Fe–C Melt and Mantle Silicate

The measured dihedral angles allow us to estimate the interfacial energy and surface tension between Fe–C melt and various mantle silicate phases at high pressure and high temperature conditions. The dihedral angle of a liquid in a solid matrix is governed by the interfacial energy per unit area between the liquid and the solid, γ_sl, and that between the solid phases, γ_ss. In an isotropic system, force balance at the triple junction can be described by the Cahn’s equation (e.g., Porter et al., 2009):

$$\frac{{\text{γ}}_{\text{ss}}}{{\text{γ}}_{\text{sl}}}=2\cdot \cos \frac{\text{θ}}{2}(1)$$

The interfacial energy between solid silicate grains (olivine) is estimated at about 0.9 J/m² with a relatively large uncertainty of ±30% (Stevenson, 1990). If this value is applicable to silicates at high pressures and high temperatures, then the measured dihedral angles of 107–120° yield the interfacial energy between Fe–C melt and major mantle silicates at approximately 0.76–0.9 J/m² at 10–23 GPa. The surface tension of Fe–C melt on mantle silicate, which has the identical numerical value to the interfacial energy between liquid and solid (Shannon, 1998), is 0.76–0.9 N/m.

The relation 2⋅cos θ/2 = γ_ss/γ_sl is derived for simple systems containing a single isotropic solid phase, and therefore it does not hold accurately for anisotropic mantle silicates such as olivine and bridgmanite. Laporte and Watson (1995) showed that with sufficiently high anisotropy the melt may form isolated plane-faced pockets at grain corners. A few experimental studies examined the anisotropy of γ_sl at olivine-basalt interface at low pressures (e.g., Schäfer and Foley, 2002), but the influence of anisotropy on the wetting behavior of iron-rich melt system remains to be explored.

According to the relationship between dihedral angle and interfacial energies, θ = 120° when γ_ss = γ_sl. Below 120°, θ decreases rapidly with the ratio and reaches the critical value of 60° when $\mathrm{\gamma }{}_{\text{ss}}=\sqrt{3}{\mathrm{\gamma }}_{\text{sl}}\sim 1.7{\mathrm{\gamma }}_{\text{sl}}$ or γ_sl∼0.6γ_ss. This relationship can be applied to understand the effects of composition, pressure, temperature on the wetting properties of Fe–C melt, as will be discussed below.

Composition Effect on the Dihedral Angles of Iron-Rich Melt

Our results show that the measured dihedral angles of Fe–C melt in silicates remained near 120°, indicating that the Fe–C melt does not wet major silicate phases in the mantle. The surface-avoiding or surface-phobic behavior of carbon is similar to that observed in metallurgical studies at ambient pressure (Halden and Kingery, 1955; Iida and Guthrie, 2015). It has been shown that at ambient pressure adding carbon to an iron liquid has little effect on the surface tension of liquid iron, which remains high even with more than 10 wt% of carbon (Figure 6A). In contrast, metallurgical studies showed that the surface tension of iron-rich liquid on aluminum oxide is sensitive to the presence of alloying elements such as O and S. At 1 bar and 1843 K, adding 0.1 wt% oxygen rapidly reduces the surface tension of liquid iron on alumina to by about 35%, whereas adding the same amount of sulfur to liquid iron reduces the surface tension by 30% (Figure 6A). These elements are therefore known as surface-loving elements or surfactants.

FIGURE 6

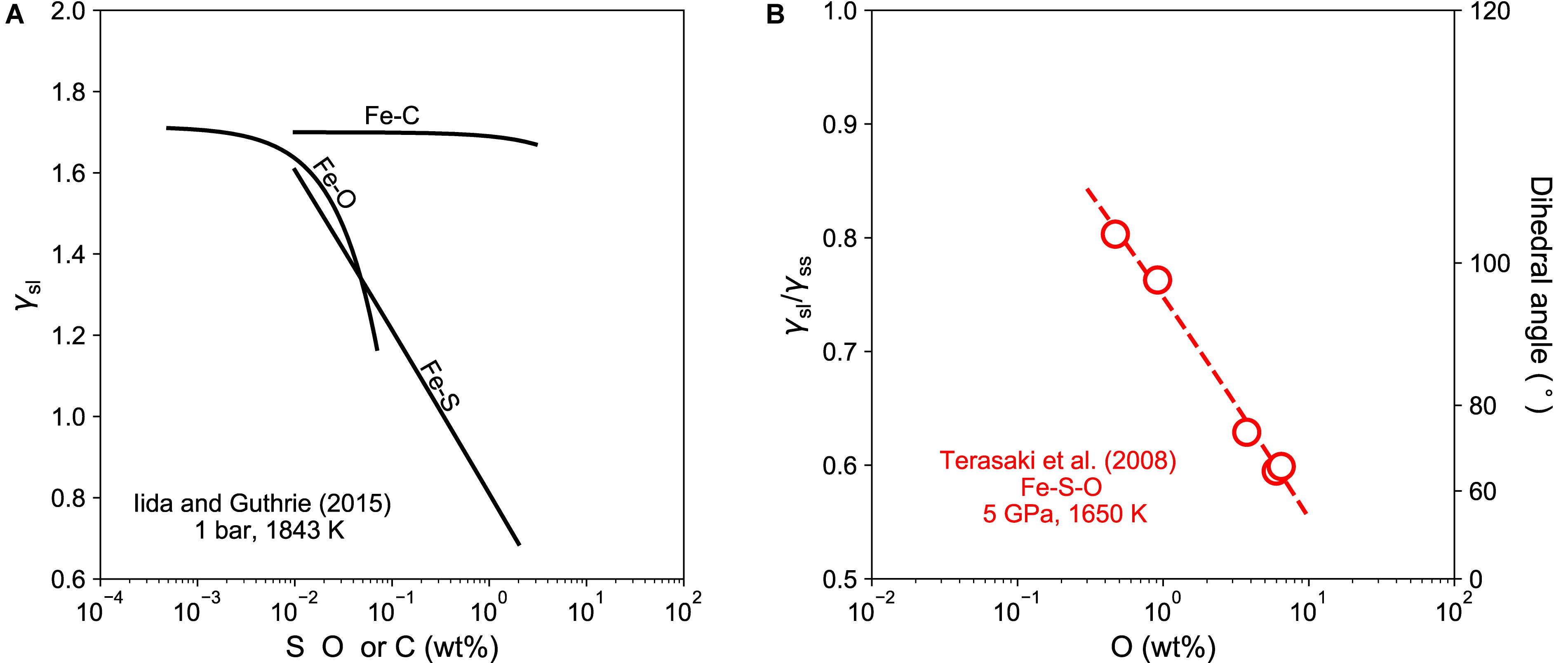
Figure 6. (A) Surface tension of iron-rich melt on aluminum oxide surface as a function of the concentration of lighter alloying element at 1 bar and 1843 K (Halden and Kingery, 1955; Iida and Guthrie, 2015). (B) Ratio of surface tensions and dihedral angles of iron-rich melt in mantle silicate as a function of the concentration of lighter alloying element at 5 GPa and 1650 K (Terasaki et al., 2008).

At high pressures, the dihedral angle of iron-rich melt in silicate is also influenced by the presence of alloying elements such as O and S (Figure 6B). For example, adding oxygen to an Fe–S melt lowers its dihedral angle in silicate matrix, which could fall below the critical value of 60° at sufficiently high oxygen concentrations (Terasaki et al., 2005, 2007, 2008). Other non-metal elements, such as S (e.g., Terasaki et al., 2005), Si (e.g., Mann et al., 2008), and P (e.g., Terasaki et al., 2007) can also reduce the dihedral angle of iron-rich melt in silicate, although the effect is weaker than oxygen.

Previous studies found that oxidized starting material or moistures trapped in sample capsule may introduce oxygen to the melt, as revealed by the presence of tiny FeO blobs exsolved from iron-rich melt upon quench (e.g., Terasaki et al., 2005). Carbon and oxygen are likely incompatible in iron-rich melt (Fischer et al., 2015). In this study, no tiny blob was observed in the quenched Fe–C melt, suggesting little influence of oxygen on the measured dihedral angles.

Effect of Pressure on the Dihedral Angle of Fe–C Melt in Silicate

The results from this study show little pressure dependence of the dihedral angle of Fe–C melt in mantle silicate between 10 and 23 GPa, with the variations from 107 to 120° falling within the measurement uncertainty of ±14–16° (Figure 7). The measured angles are also comparable to the dihedral angle of 115° between Fe–C melt with 4.3 wt% carbon and olivine at 3 GPa and 1400°C (Duncan and Fei, 2017).

FIGURE 7

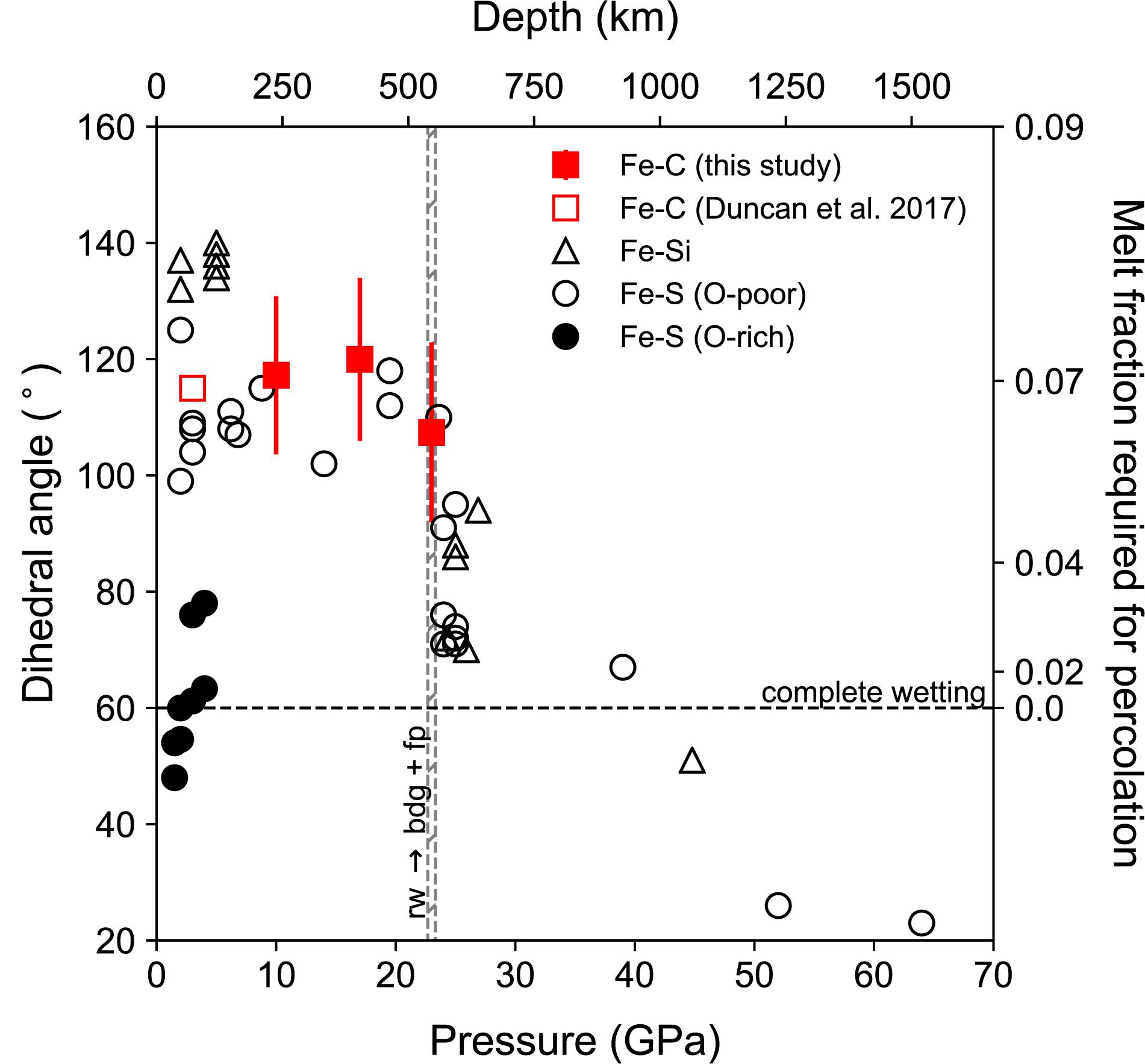
Figure 7. Dihedral angle of Fe-rich melt in silicate or silicate plus oxide matrix as a function of pressure. The dihedral angles of Fe–C melt from this study (solid squares with error bar) and that of between an Fe–C melt containing 4.3 wt% carbon in olivine (open square, Duncan and Fei, 2017) are above 100°. Plotted for comparison are data on oxygen-poor Fe–S melt (open circles, Terasaki et al., 2008), oxygen-rich Fe–S melt (closed circle, Shannon and Agee, 1996, 1998; Shi et al., 2013), and Fe–Si melt (Open triangles, Takafuji et al., 2004; Mann et al., 2008). Dashed horizontal line marks the critical angle of 60° for complete wetting. The vertical bar marks the boundary where ringwoodite (Rw) breaks down to form bridgmanite (Bdg) and ferropericlase (Fp). The melt fraction required for percolation at a given dihedral angle, known as the percolation threshold, is marked on the right Y-axis.

Pressure can influence the dihedral angle of Fe-rich melt in silicate in a number of ways (Shannon, 1998). Misalignment of crystal lattices produces excess volume or gap, which contributes to interfacial energy γ_ss. The excess volume between melt and crystal is likely smaller because atoms in the melt are not constrained by a lattice and hence moves more freely to fill space. Upon compression, the amount of lattice misalignment may change as a result of pressure-induced preferred orientation, polymorphic structural transformation, or even chemical reaction such as the breakdown of ringwoodite into bridgmanite and ferropericlase. Compression likely reduces the difference between the two excess volumes, leading to a smaller γ_ss/γ_sl, hence larger dihedral angle.

Compression may also affect the chemical properties of the interface such as the partitioning of surface-active elements between the coexisting melt and solid. For instance, significant chemical change such as enhanced solubility of oxygen in iron-rich alloy may have reduced γ_sl, thus lowering the dihedral angle (Terasaki et al., 2008). Even if the solubilities of surface-active elements remain constant, their surface activities may change with pressure (Shannon, 1998). The same amount of sulfur affects dihedral angle less significantly at high pressure (Shannon, 1998) than at 1 bar (Iida and Guthrie, 2015). Furthermore, segregation of certain species into the grain boundary may occur as a result of compression (Shannon, 1998). These changes could affect γ_ss and γ_sl and thus the dihedral angle.

The absence of pressure effect on the dihedral angle of Fe–C melt in mantle silicates suggests that ratio of interfacial energies remain nearly unchanged between 3 and 23 GPa, unless various pressure-induced effects on the ratio fortuitously offset each other. Within the pressure range of the upper mantle and transition zone, the dihedral angle of Fe–S melt with 12–14 wt% S in silicate also falls between 100 and 120°, showing little pressure dependence (Figure 7; Shannon and Agee, 1996). For Fe–Si melt in silicate, available data at pressure below 5 GPa do not show any pressure dependence either (Figure 7; e.g., Mann et al., 2008).

At higher pressures, diamond-anvil cell experiments on Fe–Si melt up to 47 GPa and 3000 K (Takafuji et al., 2004) and on Fe–S melt up to 64 GPa and 3300 K (Shi et al., 2013) showed that the dihedral angles of molten iron-alloys in bridgmanite matrix decreased rapidly with increasing pressure and temperature to below the critical value of 60° (Figure 7). The large negative pressure effect may be related to large deviatoric stress in solid phases, which would increase γ_ss significantly and therefore reducing θ (Figure 5; Rubie and Jacobson, 2016). Alternatively, significant chemical change such as enhanced solubility of oxygen in the iron-rich alloy may have reduced γ_sl, thus reducing the dihedral angle (Terasaki et al., 2008). It is also possible that temperature effect plays an important in the observed reduction of dihedral angle, as discussed below.

Effect of Temperature on the Wetting Behavior of Fe–C Melt in Mantle Silicate

No temperature effect on the dihedral angle of Fe–C melt in mantle silicate was observed between 1600 and 1800°C, at 10–23 GPa. Strong temperature dependence of surface tension was reported in metallurgical studies on iron alloys at 1 bar (e.g., Passerone and Sangiorgi, 1985). At 25 GPa, the dihedral angle of Fe–Si melt in bridgmanite decreases from 94° at 2400 K to 70° at 2800 K (Takafuji et al., 2004), also suggesting potentially significant temperature effect on the surface tension of compressed iron-rich melt, especially at temperatures approaching the melting point of the solid phase. In this study, the experimental temperatures were near the eutectic temperatures of Fe–C binary systems and far below the melting point of the silicate matrixes. The relatively low temperatures and small temperature range may explain the absence of temperature effect in our data.

At deep Earth conditions, it is often difficult to separate the effects of pressure, temperature, and composition on the dihedral angle. The temperature of a dihedral angle experiment must fall above the liquidus of iron-rich alloy and below the solidus of silicates, leaving a relatively narrow temperature range at which iron-rich melt coexists with solid silicate. This range usually shifts upward as pressure increases (Figure 3), and therefore it may be impossible to isolate the pressure and temperature effects. For Fe–S, the pressure rise from 25 to 64 GPa is accompanied by an increase of temperature from 2300 to 3300 K (Shi et al., 2013); thus it remains unclear if temperature, pressure, or both are responsible for the decrease in the dihedral angle of Fe–S in silicates.

Effect of Crystalline Structure on the Dihedral Angle of Fe–C Melt in Silicate

Our results show that the dihedral angle of Fe–C melt is not affected by pressure-induced polymorphic transition or decomposition of silicate at mid-mantle conditions. In the experiments, olivine powder grew in crystal size at 10 GPa, and transformed into ringwoodite at 17 GPa. At 23 GPa, ringwoodite broke down to form bridgmanite and ferropericlase. The measured dihedral angles of Fe–C melt remained near 115°. In contrast, the wetting behavior of Fe–S changed abruptly upon the break-down of ringwoodite, with the dihedral angle of Fe–S melt with 12–14 wt% S dropping from approximately 108° at upper mantle conditions to 71° at 25 GPa (Shannon and Agee, 1998). It is possible that the presence of ferropericlase increased the solubility of oxygen in the Fe–S melt, thus lowering its surface tension, whereas oxygen remains highly insoluble in the Fe–C melt, which is more reducing than the Fe–S melt.

Melt Connectivity and Percolation Threshold

The dihedral angles of Fe–C melt in silicate matrix at 3–23 GPa are well above the critical value of 60°, implying that Fe–C melt can only flow through mantle silicate when its volume fraction exceeds ∼7%. Dihedral angle measures the ability of liquid to wet a solid matrix. A dihedral angle of 60° or smaller implies complete wetting, where an interconnected network of liquid forms regardless of the melt fraction. A dihedral angle that is greater than 60° implies that a fraction of melt may be stranded in the solid matrix as isolated pockets. The minimum volume fraction of liquid to form a network that enables passage is known as the percolation threshold, f_p. For homogeneously distributed melt in solid matrix, f_p can be estimated from θ through the following relationship:

$$f_p\sim \mathrm{\hspace{0.33em}0.009}\sqrt{\mathrm{\theta }-60}(2)$$

With θ∼ 120°, the percolation threshold is estimated at ∼7 vol% (e.g., von Bargen and Waff, 1986; Stevenson, 1990). It should be noted that dihedral angle is a function of interfacial energy ratio (Eq. 1) while connectivity can be affected by both dihedral angle and melt fraction. Full connectivity of Fe-rich melt in silicate will develop at a wetting angle of >60° if the melt fraction is sufficiently large. However, at very low melt fractions, as relevant to the amount of metallic melt in the Earth’s mantle, percolative drainage (forming an interconnected network) can only occur when the wetting angle of Fe-rich melt is below 60°.

Below the threshold, percolation of iron-rich melt through silicate may still occur if the silicate matrix becomes partially molten (e.g., Duncan and Fei, 2017) or deforms under shear stress (e.g., Todd et al., 2016). Although the presence of partial melt of silicate does not change the dihedral angles of iron-rich melt (e.g., Holzheid, 2013), droplets of dense iron-rich melt can sink through molten silicate, especially when the amount of silicate melt is large enough to create channels (Duncan and Fei, 2017). The presence of non-wetting silicate melt may also raise the percolation threshold of iron-rich melt (Yoshino et al., 2004).

A number of studies have investigated if shear deformation can enhance connectivity of iron-rich melt and facilitate its percolation through silicate, but the effect remains poorly constrained. Walte et al. (2011) suggested that deformation only promote Fe–S melt segregation at high strain rates, with no influence at geologically relevant strain rates. Todd et al. (2016) also showed that the ability of Fe–S melt to flow through olivine matrix did not change with the amount of shear deformation. Cerantola et al. (2015) further suggested that the onset of silicate melting nullifies any effect of deformation on melt segregation and may hinter segregation of Fe-rich melt by reducing its connectivity. In contrast, Berg et al. (2017) suggested that deformation aided percolation at high pressure over a very large range of strain rates.

Implications for Earth’s Deep Carbon Cycle

The measured large dihedral angles and estimated high percolation thresholds imply that percolation may not be a viable mechanism to segregate Fe–C melt from the mantle into the core. The amount of Fe–C melt in the mid-mantle was estimated at no more than 1 wt% (Frost et al., 2004). This is well below the percolation threshold of ∼7 vol%, and therefore the Fe–C melt is expected to be stranded as isolated pockets at the mid-mantle pressures.

The presence of other alloying elements such as sulfur, hydrogen, and/or oxygen may allow Fe–C melt to percolate through surrounding silicates toward greater depths. Metallic phases in diamond inclusions consist not only Fe and C but also S and H (Smith et al., 2016). Adding sulfur may reduce the interfacial energy of Fe–C melt and lower the percolation threshold. The effect of hydrogen is not known. While oxygen is effective in lowering the surface tension of iron-rich melt, its solubility in Fe–C melt is likely negligible because of the reducing condition.

Partial melt of silicates may also facilitate percolation of iron-rich melt (Duncan and Fei, 2017). However, the present-day mantle temperature is too low to cause extensive melting of the silicates, thus segregation of Fe–C melt through channels of molten silicate is unlikely.

Given that the percolation threshold of Fe–C binary melt is much higher than the amount of Fe–C melt in the mid-mantle, and that partial melting of silicate matrix is unlikely with the present-day geotherm, we conclude that the slab-derived Fe–C melt is most likely to be retained within the subducting slab at mid-mantle depths during diamond growth, unless its wetting behavior is sufficiently modified by the presence of other alloying elements to allow percolation.

Although slab-derived Fe–C melt may not be able to percolate through the mantle, it may still reach the CMB if the sinking slab materials can survive viscous stirring associated with mantle plumes and remain largely unmixed with the ambient mantle. Liu et al. (2016) proposed that near the base of the mantle, the presence of slab-derived iron–carbon melt in isolated patches may explain seismically observed density excess and velocity features of some ULVZs. Here, we found that the dihedral angle of Fe–C in mid-mantle is larger than 100°. If applicable at the conditions near the CMB, then more than 10 vol% Fe–C is needed to match the ULVZ observations (Liu et al., 2016). This amount is, however, larger than the percolation threshold, implying that not enough Fe–C can be retained in silicate matrix to produce long-lived ULVZs, unless its drainage is hindered by the presence of silicate partial melt (Cerantola et al., 2015). Alternatively, metallic melt may be replenished through on-going subduction or infiltration of core melt back into ferropericlase matrix due to morphological instability (Otsuka and Karato, 2012).

Once at the CMB, Fe–C melt may segregate into the core if the high temperature at the base of the lower mantle lowers its dihedral angle and percolation threshold sufficiently. With an estimated 1 wt% Fe–C in the mantle (e.g., Wood et al., 2013), loss of Fe–C from 40% of the mantle corresponds to 0.8% growth in core mass at the expense of 0.4% reduction in mantle mass, which is equivalent to about 10-km expansion in core radius over Earth’s history. This is insignificant for the iron-rich core but would be a major leak for carbon in the silicate Earth.

Conclusion

The wetting behavior of Fe–C melt in silicates at mid-mantle conditions have been studied using multi-anvil experiments. The dihedral angles of Fe–C melt in olivine, ringwoodite, and bridgmanite/ferropericlase matrixes are measured at 117° at 10 GPa, 120 ± 14° at 17 GPa, and 107 ± 16° at 23 GPa, respectively. Carbon is found to behave as a surface-avoiding element in silicates at pressures up to 23 GPa, consistent with the high surface tension of Fe–C melt on alumina at 1 bar. Within the experimental ranges, no effect of pressure or temperature was observed.

The measure dihedral angles and estimated percolation thresholds are applied to assess the behavior of Fe–C alloys at deep Earth conditions. The percolation threshold of Fe–C melt in silicates is estimated at 7 vol%, much larger than the amount produced in the mantle. Consequently, Fe–C melt is expected to be retained within subducting slabs at mid-mantle depths (Figure 8), unless its surface tension is sufficiently lowered by the presence of other alloying elements such as sulfur. The amount of Fe–C melt needed to match the low shear wave velocity of the ULVZs, however, exceeds the percolation threshold. As a result, continuous replenishment, dynamic stirring, or the presence of non-wetting silicate melt is needed to generate ULVZ through slab-derived metallic melt. The non-wetting behavior of Fe–C implies that active core growth through percolation is unlikely, even though limited draining of Fe–C to the core remains feasible and may cause significant carbon loss from the silicate Earth.

FIGURE 8

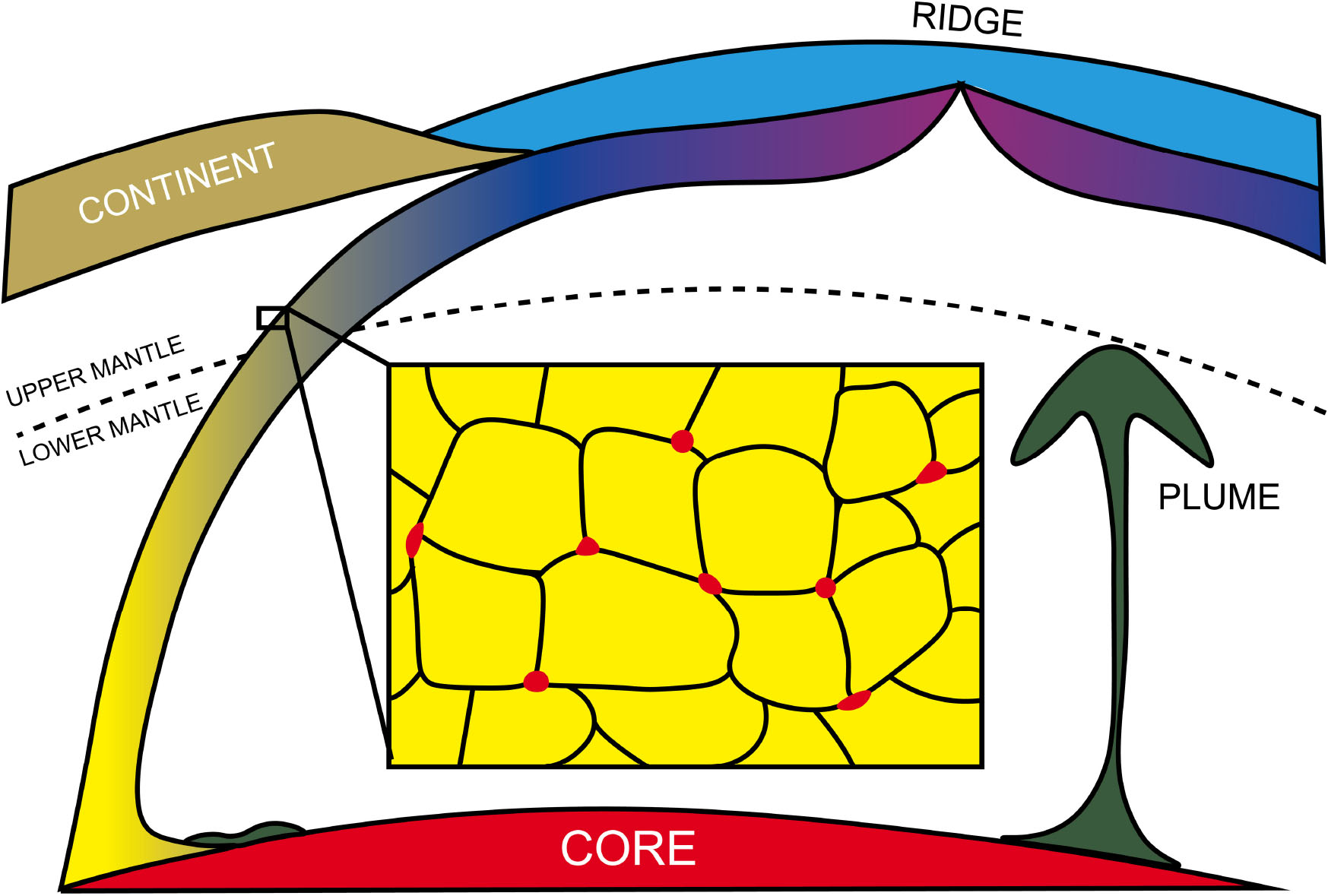
Figure 8. In Earth’s mid-mantle (up to 23 GPa), slab-derived Fe–C melt is expected to be trapped as isolated pockets and would not percolate through silicate matrix.

Further investigations are necessary to fully assess the wetting behavior of Fe–C melt during core formation and deep carbon cycle. This study only reached the pressure at the uppermost lower mantle. The wetting behavior of Fe–C melt in main stretch of the lower mantle remains to be studied. Additional work is also needed to demonstrate equilibrium texture through time-series experiments, quantify the composition of the Fe–C melt, evaluate the effect of temperature, and to explore the influence of anisotropy on the wetting behavior of iron-rich melts.

Data Availability Statement

All datasets generated for this study are included in the manuscript/supplementary files.

Author Contributions

JL and JD conceived the idea and designed the project. JD performed the experiments and analyzed the data, as part of his undergraduate honors thesis under the supervision of JL. JD and JL wrote the manuscript. FZ helped with the experiments.

Funding

This work was partially supported by the National Science Foundation Grants AST 1344133 and EAR 1763189, and the Alfred P. Sloan Foundation Deep Carbon Observatory Grant G-2017-9954 to JL; and a Turner Undergraduate Award from the Department of Earth and Environmental Sciences at University of Michigan, a James Mills Peirce Fellowship from the Graduate School of Arts and Sciences at Harvard University, open access publication funding from the Harvard Open-Access Publishing Equity (HOPE) office, and the Department of Earth and Planetary Sciences (EPS) at Harvard University to JD.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank the reviewers, GB and VC, for their reviews that helped to improve and clarify the manuscript; Hidenori Terasaki, Shun-ichiro Karato, Rebecca A. Fischer, Wendy L. Mao, Carl B. Agee, and David (Dave) Walker for discussions and comments; and Paul Kelley, the Harvard Open-Access Publishing Equity (HOPE) office, and the Frontiers Wavier Office for providing open-access funding opportunities.

References

Berg, M. T., Bromiley, G. D., Butler, I. B., Frost, M., Bradley, R., Carr, J., et al. (2017). Deformation-aided segregation of Fe-S liquid from olivine under deep earth conditions: implications for core formation in the early solar system. Phys. Earth Planet. Inter. 263, 38–54. doi: 10.1016/j.pepi.2017.01.004

CrossRef Full Text | Google Scholar

Cerantola, V., Walte, N. P., and Rubie, D. C. (2015). Deformation of a crystalline olivine aggregate containing two immiscible liquids: implications for early core–mantle differentiation. Earth Planet. Sci. Lett. 417, 67–77. doi: 10.1016/j.epsl.2015.02.014

CrossRef Full Text | Google Scholar

Duncan, M. S., and Fei, Y. (2017). “Experimental constraints on metal percolation through silicate: implications for core formation on asteroids and planetesimals,” in Lunar and Planetary Science Conference, Vol. 48, (Houston, TX).

Google Scholar

Fei, Y., and Brosh, E. (2014). Experimental study and thermodynamic calculations of phase relations in the Fe–C system at high pressure. Earth Planet. Sci. Lett. 408, 155–162. doi: 10.1016/j.epsl.2014.09.044

CrossRef Full Text | Google Scholar

Fischer, R. A., Nakajima, Y., Campbell, A. J., Frost, D. J., Harries, D., Langenhorst, F., et al. (2015). High pressure metal–silicate partitioning of Ni, Co, V, Cr, Si, and O. Geochim. Cosmochim. Acta 167, 177–194. doi: 10.1073/pnas.1108544108

PubMed Abstract | CrossRef Full Text | Google Scholar

Frost, D. J., Liebske, C., Langenhorst, F., McCammon, C. A., Trønnes, R. G., and Rubie, D. C. (2004). Experimental evidence for the existence of iron-rich metal in the Earth’s lower mantle. Nature 428, 409–412. doi: 10.1038/nature02413

PubMed Abstract | CrossRef Full Text | Google Scholar

Halden, F. A., and Kingery, W. D. (1955). Surface tension at elevated temperatures. II. Effect of C, N, O and S on liquid iron surface tension and interfacial energy with Al2O3. J. Phys. Chem. 59, 557–559. doi: 10.1021/j150528a018

CrossRef Full Text | Google Scholar

Herzberg, C., Vidito, C., and Starkey, N. A. (2016). Nickel–cobalt contents of olivine record origins of mantle peridotite and related rocks. Am. Mineral. 101, 1952–1966. doi: 10.2138/am-2016-5538

CrossRef Full Text | Google Scholar

Herzberg, C., Raterron, P., and Zhang, J. (2000). New experimental observations on the anhydrous solidus for peridotite KLB−1. Geochem., Geophys., Geosyst. 1:1051. doi: 10.1029/2000GC000089

CrossRef Full Text | Google Scholar

Hirayama, Y., Fujii, T., and Kurita, K. (1993). The melting relation of the system, iron and carbon at high pressure and its bearing on the early stage of the Earth. Geophys. Res. Let. 20, 2095–2098. doi: 10.1029/93gl02131

CrossRef Full Text | Google Scholar

Holness, M. B., and Lewis, S. (1997). The structure of the halite-brine interface inferred from pressure and temperature variations of equilibrium dihedral angles in the halite-H₂O-CO₂ system. Geochim. Cosmochim. Acta 61, 795–804. doi: 10.1016/s0016-7037(96)00370-5

CrossRef Full Text | Google Scholar

Holzheid, A. (2013). Sulphide melt distribution in partially molten silicate aggregates: implications to core formation scenarios in terrestrial planets. Eur. J. Mineral. 25, 267–277. doi: 10.1127/0935-1221/2013/0025-2264

CrossRef Full Text | Google Scholar

Holzheid, A., Schmitz, M. D., and Grove, T. L. (2000). Textural equilibria of iron sulfide liquids in partly molten silicate aggregates and their relevance to core formation scenarios. J. Geophys. Res.: Solid Earth 105, 13555–13567. doi: 10.1029/2000jb900046

CrossRef Full Text | Google Scholar

Hultgren, R., Orr, R. L., Anderson, P. D., and Kelley, K. K. (1963). Selected Values of Thermodynamic Properties of Metals and Alloys. New York, NY: John Wiley and Sons, Inc, 107.

Google Scholar

Iida, T., and Guthrie, R. I. (2015). The Thermophysical Properties of Metallic Liquids: Fundamentals, Vol. 1. Oxford: Oxford University Press.

Google Scholar

Kaminsky, F. V., and Wirth, R. (2011). Iron carbide inclusions in lower-mantle diamond from Juina. Brazil. Can. Mineral. 49, 555–572. doi: 10.3749/canmin.49.2.555

CrossRef Full Text | Google Scholar

Laporte, D., and Watson, E. B. (1995). Experimental and theoretical constraints on melt distribution in crustal sources: the effect of crystalline anisotropy on melt interconnectivity. Chem. Geol. 124, 161–184. doi: 10.1016/0009-2541(95)00052-n

CrossRef Full Text | Google Scholar

Leinenweber, K. D., Tyburczy, J. A., Sharp, T. G., Soignard, E., Diedrich, T., Petuskey, W. B., et al. (2012). Cell assemblies for reproducible multi-anvil experiments (the COMPRES assemblies). Am. Mineral. 97, 353–368. doi: 10.2138/am.2012.3844

CrossRef Full Text | Google Scholar

Li, J., and Fei, Y. (2014). Experimental constraints on core composition. Treatise Geochem. 2, 568–546.

Google Scholar

Li, Z., and Li, J. (2015). Melting curve of NaCl to 20 GPa from electrical measurements of capacitive current. Am. Mineral. 100, 1892–1898. doi: 10.2138/am-2015-5248

CrossRef Full Text | Google Scholar

Liu, J., Li, J., Hrubiak, R., and Smith, J. S. (2016). Origins of ultralow velocity zones through slab-derived metallic melt. Proc. Natl. Acad. Sci. U.S.A. 113, 5547–5551. doi: 10.1073/pnas.1519540113

PubMed Abstract | CrossRef Full Text | Google Scholar

Lord, O. T., Walter, M. J., Dasgupta, R., Walker, D., and Clark, S. M. (2009). Melting in the Fe–C system to 70 GPa. Earth Planet. Sci. Lett. 284, 157–167. doi: 10.1016/j.epsl.2009.04.017

CrossRef Full Text | Google Scholar

Mann, U., Frost, D. J., and Rubie, D. C. (2008). The wetting ability of Si-bearing liquid Fe-alloys in a solid silicate matrix-percolation during core formation under reducing conditions? Phys. Earth Planet. Int. 167, 1–7. doi: 10.1016/j.pepi.2007.12.002

CrossRef Full Text | Google Scholar

Otsuka, K., and Karato, S.-I. (2012). Deep penetration of molten iron into the mantle caused by a morphological instability. Nature 492, 243–246. doi: 10.1038/nature11663

PubMed Abstract | CrossRef Full Text | Google Scholar

Passerone, A., and Sangiorgi, R. (1985). Solid-liquid interfacial tensions by the dihedral angle method. A mathematical approach. Acta Metallurgica 33, 771–776. doi: 10.1016/0001-6160(85)90100-2

CrossRef Full Text | Google Scholar

Porter, D. A., Easterling, K. E., and Sherif, M. (2009). Phase Transformations in Metals and Alloys, (Revised Reprint). CRC press.

Google Scholar

Rohrbach, A., Ballhaus, C., Golla–Schindler, U., Ulmer, P., Kamenetsky, V. S., and Kuzmin, D. V. (2007). Metal saturation in the upper mantle. Nature 449, 456–458. doi: 10.1038/nature06183

PubMed Abstract | CrossRef Full Text | Google Scholar

Rohrbach, A., and Schmidt, M. W. (2011). Redox freezing and melting in the Earth’s deep mantle resulting from carbon–iron redox coupling. Nature 472, 209–212. doi: 10.1038/nature09899

PubMed Abstract | CrossRef Full Text | Google Scholar

Rubie, D. C., and Jacobson, S. A. (2016). Mechanisms and geochemical models of core formation. Deep Earth: Physics and Chemistry of the Lower Mantle and Core 217, 181–190. doi: 10.1002/9781118992487

CrossRef Full Text | Google Scholar

Schäfer, F. N., and Foley, S. F. (2002). The effect of crystal orientation on the wetting behaviour of silicate melts on the surfaces of spinel peridotite minerals. Contrib. Mineral. Petrol. 143, 254–262. doi: 10.1007/s00410-001-0339-0

CrossRef Full Text | Google Scholar

Schindelin, J., Arganda-Carreras, I., Frise, E., Kaynig, V., Longair, M., Pietzsch, T., et al. (2012). Fiji: an open-source platform for biological-image analysis. Nat. Methods 9, 676–682. doi: 10.1038/nmeth.2019

PubMed Abstract | CrossRef Full Text | Google Scholar

Shannon, M. C. (1998). Percolation of Iron Melts Through Mantle Minerals at High Pressure: Implications for Core Formation. Ph.D. Dissertation, Harvard University, Cambridge, MA.

Google Scholar

Shannon, M. C., and Agee, C. B. (1996). High pressure constraints on percolative core formation. Geophys. Res. Lett. 23, 2717–2720. doi: 10.1029/96gl02817

CrossRef Full Text | Google Scholar

Shannon, M. C., and Agee, C. B. (1998). Percolation of core melts at lower mantle conditions. Science 280, 1059–1061. doi: 10.1126/science.280.5366.1059

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, C. Y., Zhang, L., Yang, W., Liu, Y., Wang, J., Meng, Y., et al. (2013). Formation of an interconnected network of iron melt at Earth’s lower mantle conditions. Nat. Geosci. 6, 971. doi: 10.1038/ngeo1956

CrossRef Full Text | Google Scholar

Smith, E. M., Shirey, S. B., Nestola, F., Bullock, E. S., Wang, J., Richardson, S. H., et al. (2016). Large gem diamonds from metallic liquid in Earth’s deep mantle. Science 354, 1403–1405. doi: 10.1126/science.aal1303

PubMed Abstract | CrossRef Full Text | Google Scholar

Stevenson, D. J. (1990). “Fluid Dynamics of Core Formation,” in Origin of the Earth. Oxford: Oxford University Press, 231–249.

Google Scholar

Stickels, C. A., and Hucke, E. E. (1964). Measurement of dihedral angles. Trans. Metallurgical Soc. AIME 230:795.

Google Scholar

Stixrude, L., and Lithgow-Bertelloni, C. (2011). Thermodynamics of mantle minerals-II. Phase equilibria. Geophys. J. Int. 184, 1180–1213. doi: 10.1111/j.1365-246x.2010.04890.x

CrossRef Full Text | Google Scholar

Takafuji, N., Hirose, K., Ono, S., Xu, F., Mitome, M., and Bando, Y. (2004). Segregation of core melts by permeable flow in the lower mantle. Earth Planet. Sci. Lett. 224, 249–257. doi: 10.1016/j.epsl.2004.05.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Terasaki, H., Frost, D. J., Rubie, D. C., and Langenhorst, F. (2005). The effect of oxygen and sulphur on the dihedral angle between Fe–O–S melt and silicate minerals at high pressure: implications for Martian core formation. Earth Planet. Sci. Lett. 232, 379–392. doi: 10.1016/j.epsl.2005.01.030

CrossRef Full Text | Google Scholar

Terasaki, H., Frost, D. J., Rubie, D. C., and Langenhorst, F. (2007). Interconnectivity of Fe–O–S liquid in polycrystalline silicate perovskite at lower mantle conditions. Phys. Earth Planet. Int. 161, 170–176. doi: 10.1016/j.pepi.2007.01.011

CrossRef Full Text | Google Scholar

Terasaki, H., Frost, D. J., Rubie, D. C., and Langenhorst, F. (2008). Percolative core formation in planetesimals. Earth Planet. Sci. Lett. 273, 132–137. doi: 10.1073/pnas.1707580114

PubMed Abstract | CrossRef Full Text | Google Scholar

Todd, K. A., Watson, H. C., Yu, T., and Wang, Y. (2016). The effects of shear deformation on planetesimal core segregation: results from in-situ X-ray micro-tomography. Am. Mineral. 101, 1996–2004. doi: 10.2138/am-2016-5474

CrossRef Full Text | Google Scholar

von Bargen, N., and Waff, H. S. (1986). Permeabilities, interfacial areas and curvatures of partially molten systems: results of numerical computations of equilibrium microstructures. Journal of Geophysical Research: Solid Earth, 91, 9261–9276. doi: 10.1029/JB091iB09p09261

CrossRef Full Text | Google Scholar

Walte, N. P., Rubie, D. C., Bons, P. D., and Frost, D. J. (2011). Deformation of a crystalline aggregate with a small percentage of high-dihedral-angle liquid: implications for core–mantle differentiation during planetary formation. Earth Planet. Sci. Lett. 305, 124–134. doi: 10.1016/j.epsl.2011.02.049

CrossRef Full Text | Google Scholar

Williams, Q., Jeanloz, R., Bass, J., Svendsen, B., and Ahrens, T. J. (1987). The melting curve of iron to 250 gigapascals: a constraint on the temperature at Earth’s center. Science 236, 181–182. doi: 10.1126/science.236.4798.181

PubMed Abstract | CrossRef Full Text | Google Scholar

Wood, B. J., Li, J., and Shahar, A. (2013). Carbon in the core: its influence on the properties of core and mantle. Rev. Mineral. Geochem. 75, 231–250. doi: 10.1126/sciadv.1701840

PubMed Abstract | CrossRef Full Text | Google Scholar

Yoshino, T., Walter, M. J., and Katsura, T. (2004). Connectivity of molten Fe alloy in peridotite based on in situ electrical conductivity measurements: implications for core formation in terrestrial planets. Earth Planet. Sci. Lett. 222, 625–643. doi: 10.1016/s0012-821x(04)00182-7

CrossRef Full Text | Google Scholar

Zhimulev, E. I., Chepurov, A. I., Sonin, V. M., Litasov, K. D., and Chepurov, A. A. (2018). Experimental modeling of percolation of molten iron through polycrystalline olivine matrix at 2.0–5.5 GPa and 1600°C. High Press. Res. 38, 153–164. doi: 10.1080/08957959.2018.1458847

CrossRef Full Text | Google Scholar