Theoretical Analysis of Longitudinal Wave Attenuation in a Stressed Rock With Variable Cross-Section

Introduction

Natural rock mass consists of rock blocks and discontinuous interfaces (e.g., joints and fractures). In some special in situ stress field, conjugate joints, namely one type of the shear joints, are conceived and sprout. Distinguished from those the rock blocks between parallel joints, the shapes of rock blocks between conjugate joints are variable. This caused the variation of areas of cross-sections perpendicular to the wave propagation path, and it is believed to have an effect on wave propagation. On the other hand, rock masses are naturally stressed by gravitational and tectonic stress. The initial stress conditions may affect the property of rock, and therefore, affect the dynamic response of and wave propagation in rock. To deeply understand the wave propagation in natural rock blocks, it is necessary to explore the combined effects of geometry and static stress on the wave propagation. However, related researches have been rarely reported.

Many efforts have been made to explore the wave propagation in rock mass, and previous works mainly focus on the wave transmission across a joint or a fracture (Ma et al., 2011; Wu et al., 2013a, b, 2014; Chen et al., 2015). Notably, in the literatures, the rock blocks are generally believed to be elastic, and only the attenuation across the rock joints are considered. However, wave energy dissipation usually occurs in the rock blocks due to the existence of microcracks, micropores and viscosity (Fan et al., 2012). In addition, the geometry of research object is also a non-negligible factor affecting the wave propagation. Several researchers (Benveniste, 1975; Moodie and Barclay, 1975; Shorr, 1995) explored the wave propagation in rods with variable cross-section theoretically. Akkas et al. (1980) and Barez et al. (1980) carried out the wave propagation experiments in rods with variable-section for the first time, and the analytical predication of wave propagation was also presented. Dose and Skews (2014) also observed the shock wave propagation in the shock tube with decreasing areas. Fu and Scott (1994) analyzed the propagation of a simple wave and shock wave in a semi-infinite rod with a slowly varying cross-sectional area. Gan et al. (2014) investigated the frequency-dependent propagation of a P-wave in an elastic rod with a variable cross-section.

The mechanical behaviors of rocks under coupling static and dynamic loads have been systematically investigated (Li et al., 2008, 2009, 2018; Gong et al., 2010; Tao et al., 2017; Weng et al., 2018). They observed that the dynamic compressive strength, dynamic elastic modulus, failure mode and energy absorption of rocks are significantly influenced by the static stress. Notably, at a lower level of static stress, the dynamic compressive strength and deformability are strengthened, while they are degraded under a higher stress condition. In the aspect of wave propagation, considering the compressibility of filled joint, Li et al. (2010) and Fan and Sun (2015) investigated the wave energy transmission across the joint in a static stressed rock mass analytically. The wave speed is a basic wave parameter of rock, and numerous research works showed that the prestress alters the wave speed of rock due to the closure and opening of interior micropores and/or microcracks (Holt et al., 1997; Selim and Ahmed, 2006; Grana, 2016; Sahane et al., 2016). Li and Tao (2015) investigated the effects of the initial stress and initial stress gradient on the wave propagation, and the results showed that homogenous stress affects the elastic coefficients of medium while the 1D P-wave equation is unchanged in form. Liu et al. (2012) explored the effect of stress on the phase velocity, group velocity, energy reflection and refraction coefficients of plane wave at the interface between fluid and stressed rock. Notably, the previous works mainly focus on the effect of homogeneous prestress on wave propagation in a rock. However, for a static stressed rock block with variable cross-section, the initial stresses are axial gradient. The combined effects of the static stress and variable cross-section on wave propagation have been rarely reported yet.

The present work provides a theoretical exploration of wave propagation in a static stressed rock with variable cross-section. Firstly, the 1-D longitudinal wave propagation equation considering the combined effects of the static stress and variable cross-section is established. To reflect the closure and opening of interior micropores and/or microcracks under the effect of static stress, the key point in the establishment of wave propagation equation is summarizing stress-dependent dynamic elastic modulus. The energy dissipation is reflected by the employed modified viscoelastic model. Then, the attenuation coefficients in amplitude of 1-D harmonic wave are calculated based on the established wave propagation equation. Finally, the combined effects of static stress and variable cross-section on both amplitude attenuation and its frequency-dependence are discussed.

Establishment and Solution of Wave Equation

Establishment of Wave Equation

Figure 1 displays the physical problem that the stress wave propagates in a stressed rod with variable cross-section. This work assumes that the static and dynamic stresses in an arbitrary section of the rod are homogenous, and the lateral deformation of the rod is neglected. In this way, the wave propagation in the rod is supposed to be a problem of 1-D longitudinal wave propagation. In classic theory of wave propagation, 1-D wave propagation equation describes the wave propagation in medium analytically. The establishment of wave propagation equation is generally based on the continuity equation, motion equation and stress-strain relation equations. The strain and particle velocity are the first derivatives of the displacement u with respect to spatial variable x and temporal variable t, respectively. According to the conditions of both single-value and continuity of the displacement, the continuity equation as Eq. 1 can be obtained.

$$\frac{\partial v}{\partial x}=\frac{\partial \mathrm{\epsilon }}{\partial t}(1)$$

FIGURE 1

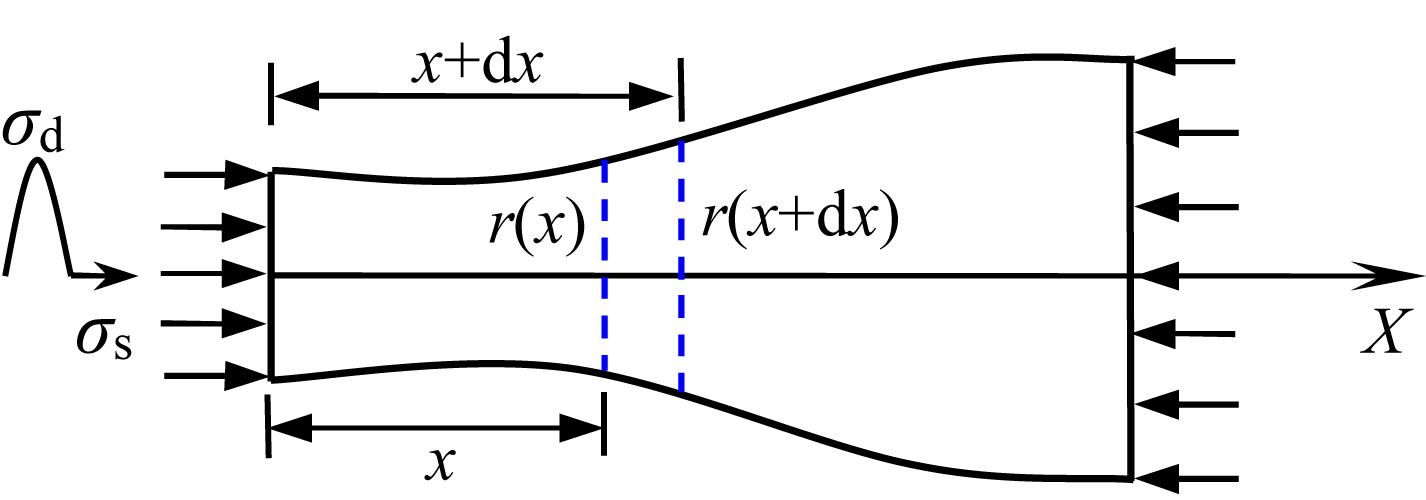
Figure 1. Sketch map of a pre-stressed rod with variable cross-section under coupling static-dynamic loads.

where v is the particle velocity; ε is the strain; and x, t are the spatial and temporal variables, respectively.

To obtain the motion equation, we choose a micro element with a width of dx from the rod shown in Figure 1 as the research object. According to the Newton’s second law, the motion equation can be written as following:

$$A(x)\left[{\text{σ}}_{\text{d}}(x)+{\text{σ}}_{\text{s}}(x)\right]+\text{ρ}A(x)\frac{\partial v}{\partial t}\text{d}x=\left[A(x)+\frac{\text{d}A(x)}{\text{d}x}\text{d}x\right]\left[{\text{σ}}_{\text{d}}(x)+\frac{\partial {\mathrm{\sigma }}_{\text{d}}}{\partial x}\text{d}x+{\text{σ}}_{\text{s}}(x)+\frac{\partial {\text{σ}}_{\text{s}}}{\partial x}\text{d}x\right](2)$$

where A(x) is the cross-sectional area; ρ is the mass density of medium; and σ denotes the stress. The subscripts “d” and “s” represent dynamic and static, respectively.

Expanding Eq. 2 and ignoring the higher-order infinitesimal with respect to spatial variable x yields Eq. 3 as following:

$$\text{ρ}A(x)\frac{\partial v}{\partial t}=\frac{\partial }{\partial x}\left[{\text{σ}}_{\text{d}}(x)A(x)+F\right](3)$$

where F represents the axial static force, and it is a space- and time-independent constant. Then, the motion equation of the physical problem shown in Figure 1 can be expressed as following:

$$\text{ρ}\frac{\partial v}{\partial t}=\frac{\partial {\text{σ}}_{\text{d}}(x)}{\partial x}+{\text{σ}}_{\text{d}}(x)\frac{1}{A(x)}\frac{\text{d}A(x)}{\text{d}x}(4)$$

As respect to different medium, the continuity equations and motion equations are similar, while the stress-strain relation equations may be remarkably different; therefore, the wave propagation equations are also different. To describe the wave propagation correctly, it is a crucial issue to establish the proper equation of stress-strain relation describing the variation in force versus deformation.

Intact rocks with natural micro defects, e.g., micropores and microcracks, behave non-linearly in mechanics (Jaeger et al., 2007). During the process of uniaxial compression, the volume percentage of defects decreases in the initial stage of compressive deformation due to the closure of natural micropores and microcracks (Hudson and Harrison, 2005); subsequently, it remains nearly constant close to zero in the intermediate stage because the closure of micropores and microcracks reaches a maximum. Finally, the volume percentage of defects increases again due to the initiation and propagation of stress-induced cracks. The volume of these interior defects is sensitive to the variation in the uniaxial stress; moreover, the dynamic compressive strength and deformability of rock are determined by the compaction of defects to some extent. Naturally, for the physical problem shown in Figure 1, the static stress can alter the dynamic elastic coefficients of rock, and then, the wave propagation in rock is remarkably different compared with that under unstressed condition.

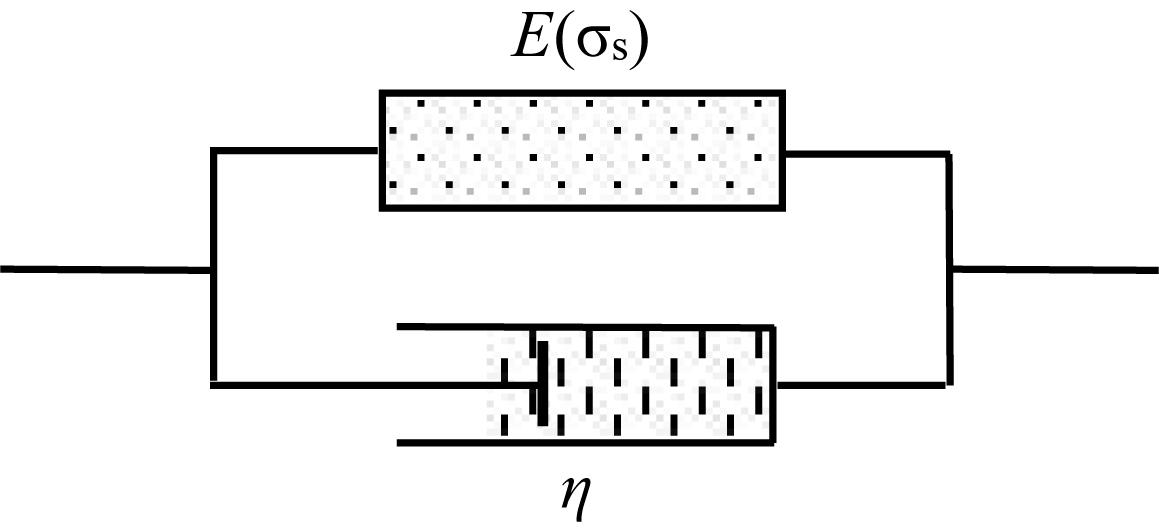
In the present work, the stress-strain relation of rock is described using a modified viscoelastic constitutive model. As is shown in Figure 2, the rock is assumed as a composition of the porous elastic body in parallel with the Newtonian viscous body. For the porous elastic body, the dynamic elastic modulus E(σ_s) changes with the static stress. And for the Newtonian viscous body, the viscosity coefficient η is assumed as a constant whatever the static stress is. Then, the dynamic stress-strain relation can be expressed as Eq. 5

$${\text{σ}}_{\text{d}}=E({\text{σ}}_{\text{s}})\mathrm{\epsilon }+\text{η}\frac{\partial \mathrm{\epsilon }}{\partial t}(5)$$

FIGURE 2

Figure 2. Simplified mechanical model of a rock.

where ε is the dynamic strain, η denotes the viscosity coefficient, t is the time variable, and E(σ_s) is the dynamic elastic modulus related to the static stresses, when σ_s = 0, it is the initial dynamic modulus E₀.

Similarly with the expression of the elastic coefficient for damage body, to describe the variation in dynamic elastic modulus of the porous body in Figure 2 versus static stresses, the E(σ_s) is written as following:

$$E({\text{σ}}_{\text{s}})=E_0[1-\text{δ}({\text{σ}}_{\text{s}})](6)$$

where δ(σ_s) is an employed variation coefficient of the dynamic modulus, and its value is mainly related to the actual static stress. Within a lower stress, the internal micropores and microcracks are compressed, and the negative values of δ(σ_s) represent the strengthened dynamic elastic modulus. The initiation and propagation of stress-induced microcracks occurs once the stress level is over the elastic limitation of the rock, correspondingly, the positive values of δ(σ_s) indicate the weakened dynamic elastic modulus under higher static stresses.

For a stressed rock with variable cross-section, the normal static stress is correlated with the spatial variable x, therefore, the dynamic elastic modulus also changes with x. By taking derivative with respect to x, Eq. 5 can be deformed into Eq. 7 as following:

$$\frac{\partial {\text{σ}}_{\text{d}}}{\partial x}=\mathrm{\epsilon }\frac{\partial E(x)}{\partial x}+E(x)\frac{\partial \mathrm{\epsilon }}{\partial x}+\text{η}\frac{{\partial }^2\mathrm{\epsilon }}{\partial x\partial t}(7)$$

Substituting Eqs 5 and 7 into Eq. 4 yields:

$$\text{ρ}\frac{{\partial }^{2}u}{\partial t^2}=E(x)\frac{{\partial }^{2}u}{\partial x^2}+\left[\frac{\partial E(x)}{\partial x}+\frac{E(x)}{A(x)}\frac{\text{d}A(x)}{\text{d}x}\right]\frac{\partial u}{\partial x}+\frac{\text{η}}{A(x)}\frac{\text{d}A(x)}{\text{d}x}\frac{{\partial }^{2}u}{\partial x\partial t}+\text{η}\frac{{\partial }^{3}u}{\partial x^2\partial t}(8)$$

Equation 8 is the one-dimensional longitudinal wave equation of a stressed rock with variable cross-section. And we can see that if the dynamic modulus is a stress-independent constant and the viscosity coefficient η = 0, Eq. 8 will degrade into the wave equation of an elastic bar with variable cross-section.

Solution to the Wave Equation

To obtain the analytical solution of the one-dimensional longitudinal wave equation, many methods such as the separation of variables, traveling wave approach, Fourier transform method, Laplace transform method and so on have been introduced. Notably, Eq. 8 is a homogeneous partial differential equation with variable coefficients, it is difficult to obtain the accurate analytical solution to this equation, and the effective methods to solve it have been rarely reported. In this work, an attempt to consider the harmonic wave propagation in a stressed rock with variable cross-section is conducted.

The particle displacement u(x, t) is assumed as Eq. 9 as following,

$$u(x,t)=u_0{\text{e}}^{-\mathrm{\alpha }x}{\text{e}}^{\text{i}(kx-\mathrm{\omega }t)}(9)$$

where u₀ is the initial amplitude of displacement, k denotes the wave number, ω is the angular frequency, and i is the imaginary unit. α is the variation coefficient of particle displacement amplitude. Notably, α is a comprehensive characterization of geometric and physical effect, which is different from the attenuation coefficient for a rock with constant cross-sectional areas. When the wave propagates from the end with smaller cross-section to the end with larger cross-section, the value of α is positive and it is named spatial attenuation coefficient in amplitude (SAC); otherwise, α is called spatial increase coefficient in amplitude (SIC).

Substituting Eq. 9 into Eq. 8 yields:

$$-\mathrm{\rho }{\mathrm{\omega }}^2=E(x)({\text{α}}^2-k^2)-2\mathrm{\omega }\mathrm{\eta }\mathrm{\alpha }k-\xi (x)\text{α}+\text{χ}(x)\mathrm{\omega }\mathrm{\eta }k+\mathrm{\omega }\mathrm{\eta }(k^2-{\text{α}}^2)\text{i}-2E(x)\text{α}k\text{i}+\mathit{\text{ξ}}(x)k\text{i}+\text{χ}(x)\mathrm{\omega }\mathrm{\eta }\mathrm{\alpha }\mathrm{i}(10)$$

where $\mathit{\text{ξ}}(x)=\frac{\partial E(x)}{\partial x}+\frac{E(x)}{A(x)}\frac{\partial A(x)}{\partial x},\mathrm{\chi }(x)=\frac{1}{A(x)}\frac{\partial A(x)}{\partial x}.$

To satisfy the equilibrium of Eq. 10, the real and imaginary parts of both sides should be equal, respectively. Therefore, we can obtain two equations related to variables α and k as following:

$$E(x)({\text{α}}^2-k^2)-2\mathrm{\omega }\mathrm{\eta }\mathrm{\alpha }k-\mathit{\text{ξ}}(x)\text{α}+\text{χ}(x)\mathrm{\omega }\mathrm{\eta }k+\mathrm{\rho }{\mathrm{\omega }}^2=0(\mathrm{11a})$$

$$\mathrm{\omega }\mathrm{\eta }({\text{α}}^2-k^2)+2E(x)\text{α}k-\text{χ}(x)\mathrm{\omega }\mathrm{\eta }\mathrm{\alpha }-\mathit{\text{ξ}}(x)k=0(\mathrm{11b})$$

The analytical solution of unknown variables α and k can be solved by uniting Eqs. 11a and 11b. However, the solutions of α and k are complicated in form; therefore, for convenience of description, the numerical results are straightly presented in next sections.

Results and Discussion

This section presents the effects of static stress and variable cross-section on the space- and frequency-dependent variation coefficients of particle displacement amplitude in a rock. The wave propagation in rocks with exponentially increasing areas is mainly discussed, and the differences of wave propagation caused by changing form of cross-sectional areas are also considered.

In the present work, main parameters utilized in the numerical calculation include: the mass density is ρ = 2388 kg/m³, the initial dynamic elastic modulus is E₀ = 20 GPa, and the viscosity coefficient is η = 60 MPa s. The axial calculation length of the rock is L = 1.5 m. The radius of an arbitrary cross-section of the rock is assumed as an exponential function with respect to the spatial variable x as following,

$$r(x)=r_0{\text{e}}^{\mathrm{\gamma }x/L},\mathrm{\gamma }=\ln (r_L/r_0),\mathrm{\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0}\le x\le L(12)$$

where r(x) denotes the radius of an arbitrary cross-section along the propagation path. r₀ and r_L are the radius of cross-sections at x = 0 and x = L, respectively. L is the axial calculation length of a rock. γ is a dimensionless parameter correlated with r₀ and r_L, and it is employed to describe the variation magnitude of radius along the propagation path.

In Gong’s work (Gong et al., 2010), axial static stresses including σ_s = 0 MPa, σ_s = 60 MPa, σ_s = 80 MPa and σ_s = 90 MPa were applied to the sandstone specimens, and it is observed that the dynamic elastic modulus of the sandstone under σ_s = 60 MPa increases by approximately 56% of the modulus under σ_s = 0 MPa. While the axial static stress is 80 and/or 90 MPa, the dynamic modulus decreases reversely. The dynamic elastic modulus may undergo a non-linear variation of “from increase to decrease” during the increasing in the axial static stress. In the present work, to describe this characteristic of dynamic elastic modulus quantitatively, the variation coefficient δ(σ_s) of dynamic elastic modulus is assumed as Eq. 13.

$$\text{δ}({\text{σ}}_{\text{s}})=a{\text{σ}}_{\text{s}}^2+b{\text{σ}}_{\text{s}},\mathrm{\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0}\le {\text{σ}}_{\text{s}}\le {\text{σ}}_{\text{c}}(13)$$

where a and b are empirical coefficients, and –b/2a means the elastic limitation of rock. In this work, a is assigned a value of 0.0018, and b is assigned a value of –0.053. σ_c denotes the uniaxial compressive strength (UCS).

Effect of Static Stress on the Wave Attenuation

In blasting excavation engineering, the damage of surrounding rock is straightly related to the amplitudes of blasting waves. To design proper blasting hole spacing and assess the safety of surrounding rock, it is a significant issue to predict the variation of wave amplitudes versus traveling distance.

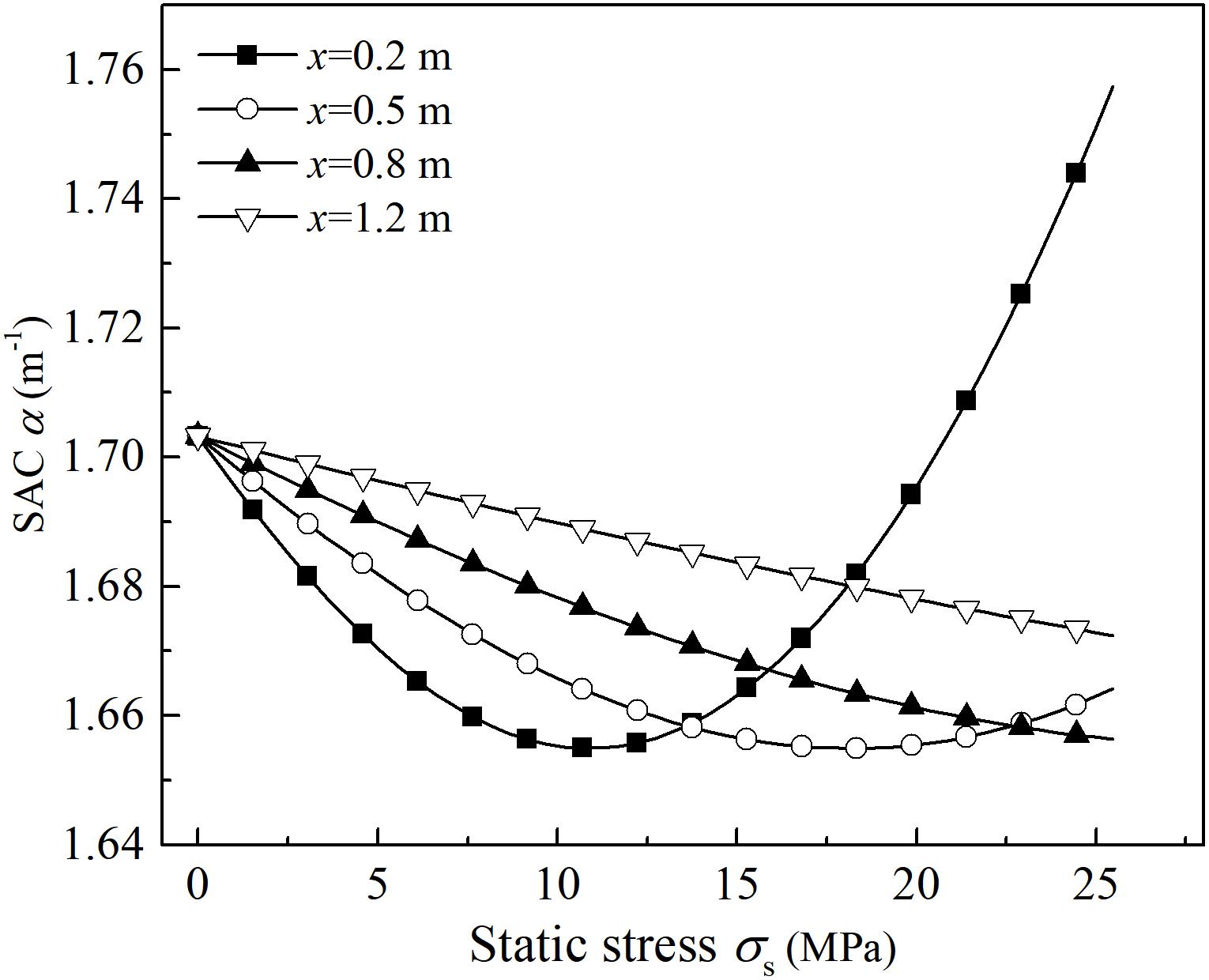
By fixing the angular frequency of waves to ω = 628.3 Hz and the radiuses of both end sections to r₀ = 0.025 m, r_L = 0.09 m, the changing trends of SAC versus static stresses are presented in Figure 3. Notably, the variable of horizontal axis σ_s is the normal static stress at the smaller end section.

FIGURE 3

Figure 3. Variation in spatial attenuation coefficient versus static stress.

Figure 3 shows that, with the increase in static stress, the SAC decreases within a lower level of static stress. When the static stresses increase to a higher level, the SAC keeps increasing. The reason for this result can be derived from the variation of dynamic modulus versus axial compression. According to Eqs 6 and 14, with the increase in uniaxial static stresses, the dynamic elastic modulus of rock tends to increase first, and then decreases. Within a lower level of uniaxial static stress, the closure of internal voids and cracks in the rock is strengthened, leading to an increase in dynamic elastic modulus. Furthermore, the elastic wave velocity is positively correlated with the dynamic elastic modulus. As a result, the wave energy dissipation decreases with the increase in static stress, which can be reflected from the attenuation of amplitudes. On the contrary, under a higher level of uniaxial static stress, the internal damage causing from initiation and propagation of new micro cracks begins to increase, and the dynamic elastic modulus of the rock gradually decreases. Correspondingly, the wave energy dissipation and amplitude attenuation start to increase.

Additionally, Figure 3 also reveals that the changing processes of SAC at different traveling distance x are also different. Under a certain normal static stress, the actual normal static stress in an arbitrary section is negatively correlated with the traveling distance. The smaller the traveling distance is, the larger the normal static stress of the cross-section is. Therefore, the variation ranges of actual static stress at different cross-sections are different, leading to the different dynamic elastic modulus at different cross-sections. Differences in actual stress result in the different changing process of SAC.

Space-Dependent Wave Attenuation

Due to the continuously changing cross-sectional areas, the actual static stresses vary along the propagation path. The influences of static stress on the wave attenuation are different at different traveling distance. To predict the amplitudes accurately along the propagation path, it is another important issue to investigate the space-dependent attenuation of wave propagation in rock with variable cross-section.

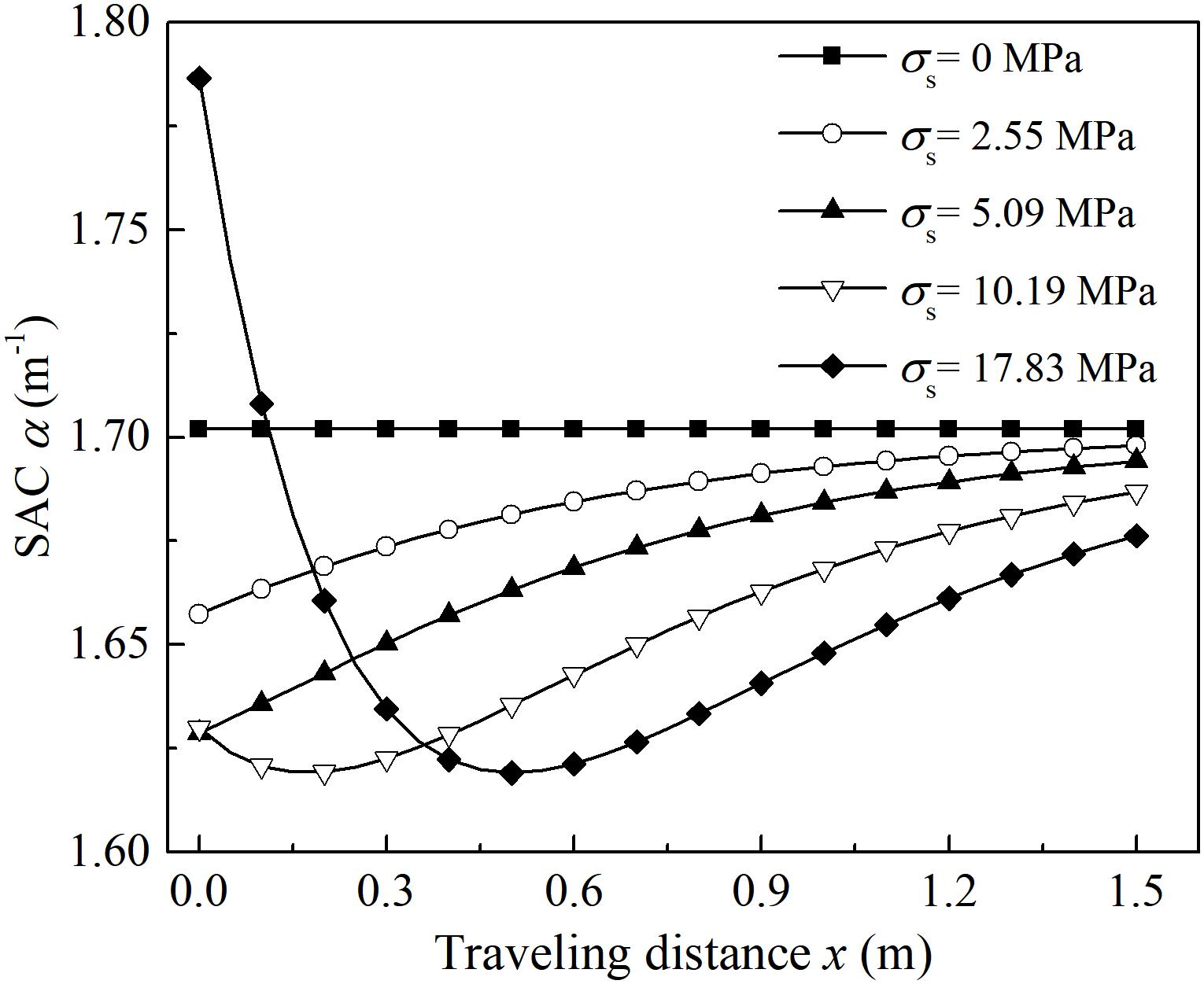
The calculated SAC at different traveling distance under different static stresses are presented in Figure 4. As can be seen from this figure, when the rock is unstressed, the SAC is a constant along the propagation path, and the amplitude attenuation is only related to the geometry and viscosity of the rock. As the static stresses increase, the variation of SAC along the propagation path occurs. In terms of the varying magnitude of the spatial attenuation coefficient, Figure 4 shows that the smaller the traveling distance, the more the variation in spatial attenuation coefficient. Apparently, under the same σ_s, the actual normal stresses in sections near the smaller end are higher than the stresses in sections near the larger end. Therefore, the dynamic elastic modulus and spatial attenuation coefficients change more obviously in sections near the smaller end.

FIGURE 4

Figure 4. Spatial attenuation coefficients versus traveling distance.

On the other hand, as is shown in Figure 4, under a lower uniaxial static stress, such as σ_s = 2.55 and 5.09 MPa, the SAC keep increasing along with the traveling distance. However, when the static stress reaches a higher level, such as σ_s = 10.19 and 17.83 MPa, the variation of SAC appears a characteristic of “from decrease to increase” along the propagation path. This result is also possibly related to the actual stress in different sections along the propagation path.

By fixing the radius of the smaller end section to r₀ = 0.025 m and changing the larger radius r_L, the SAC at different traveling distance are calculated and their variations along with the static stress are shown in Figure 5. It can be observed that the higher the value of γ, the larger the spatial attenuation coefficient. The reason for this result is that the SAC is positively correlated with the changing rate of cross-sectional area; and the higher the value of γ, the larger the changing rate of cross-sectional area. The variation characteristics in SAC along the propagation path are similar although the values of γ are remarkably different, while the variation magnitude is positively correlated with γ.

FIGURE 5

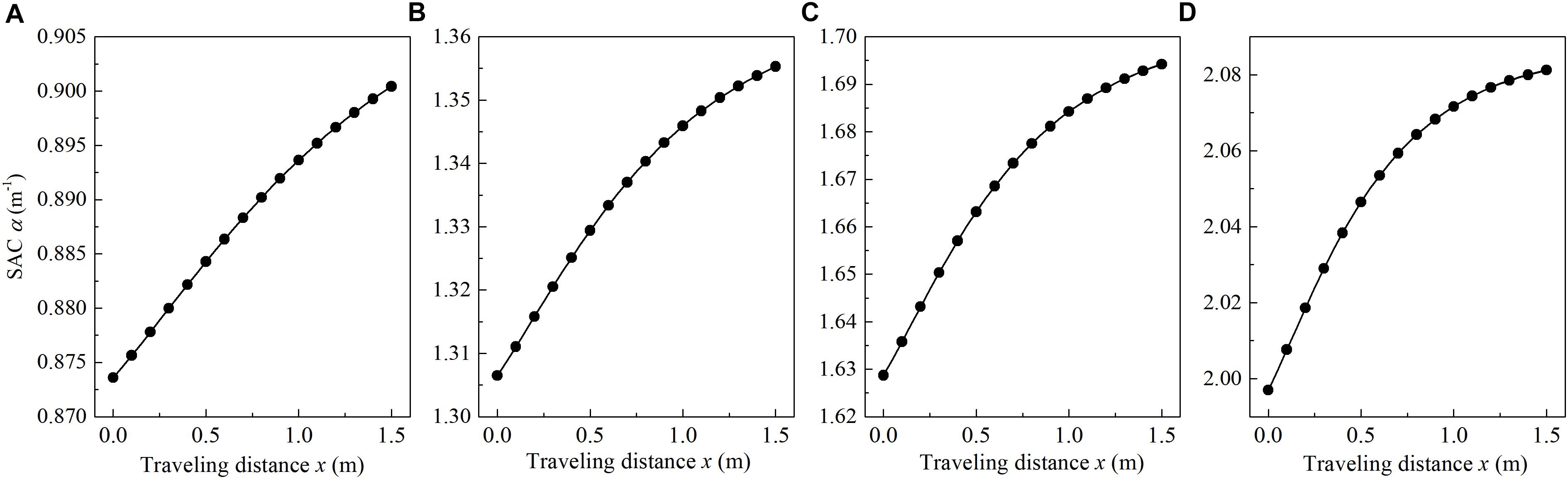
Figure 5. Spatial attenuation coefficient versus traveling distance at different γ. (A) γ = 2.0; (B) γ = 2.8; (C) γ = 3.6; (D) γ = 4.8. (σ_s = 5.09 MPa).

Frequency-Dependent Wave Attenuation

The blasting waves and or seismic waves are generally composed of many components with different frequencies. Frequency-dependent attenuation of wave propagation is a common characteristic in viscoelastic medium. It is common that the higher the frequency of wave component, the more susceptible the attenuation is (Kjartansson, 1979; Jones, 1986; Zhou et al., 2016). However, whether the influence of the uniaxial static stress on the attenuation of different wave components is similar or not is a rarely covered issue.

Figure 6 plots the variation in spatial attenuation coefficient along with the traveling distance under different frequency conditions. Obviously, the SAC of lower-frequency wave are smaller than that of higher-frequency wave. It means that the attenuation of wave propagating in the rock rod is frequency-dependent. In addition, the variation magnitude of SAC along the propagation path is correlated with the wave frequency. For instance, when the angular frequency ω is 628.3 and 1256.6 Hz, the spatial attenuation coefficients increase sharply as the traveling distance increases. However, when angular frequency ω increases to 3141.6 or 6283.2 Hz, the variation of SAC along the propagation path is trivial.

FIGURE 6

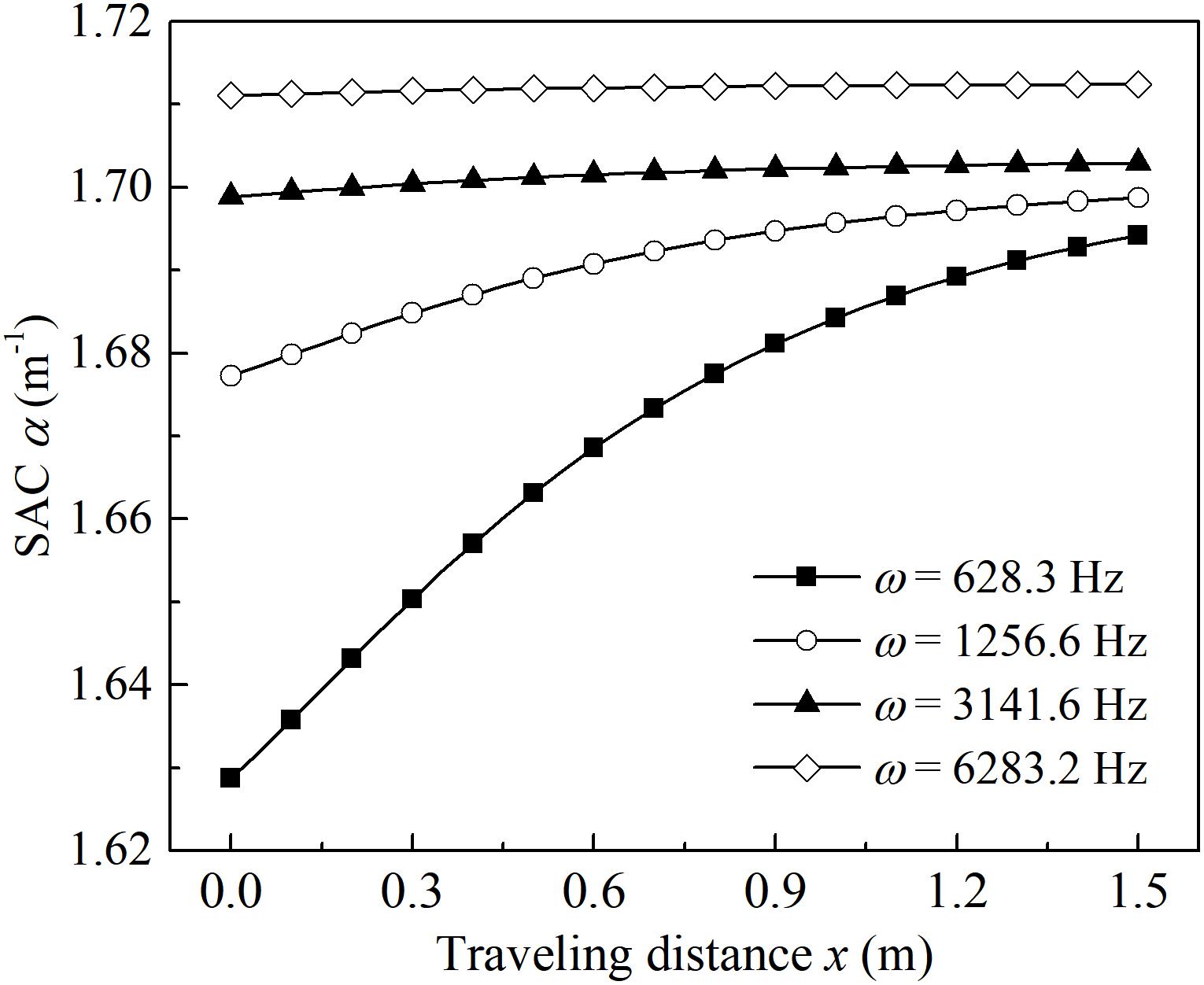
Figure 6. Frequency-dependent spatial attenuation coefficients versus traveling distance (σ_s = 5.09 MPa).

Figure 7 presents the variation in spatial attenuation coefficients of harmonic waves with different frequencies versus static stress. Similarly with Figures 6, 7 also show that the high-frequency waves are more susceptible to attenuate compared with the low-frequency ones. Additionally, as can be seen from this figure, under a lower frequency (e.g., ω = 628.3 Hz), the variation characteristic of “from decrease to increase” in SAC is apparent. With the frequency increasing, the variation magnitude of spatial attenuation coefficient decreases sharply. When the angular frequency ω is 6283.2 Hz, the effect of uniaxial static stress on the spatial attenuation coefficient is almost trivial.

FIGURE 7

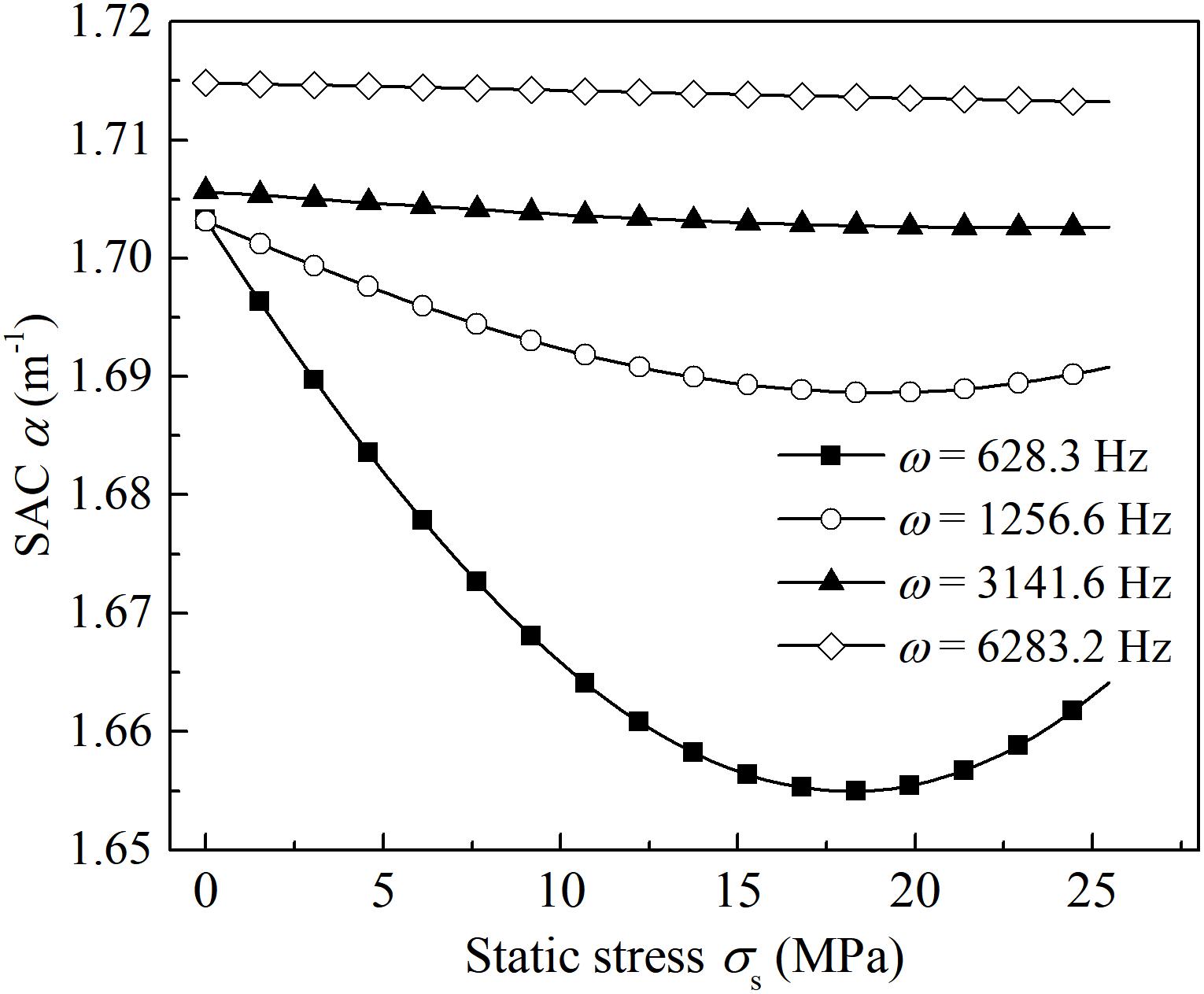
Figure 7. The variation in spatial attenuation coefficient versus static stress under different frequencies (x = 0.5 m).

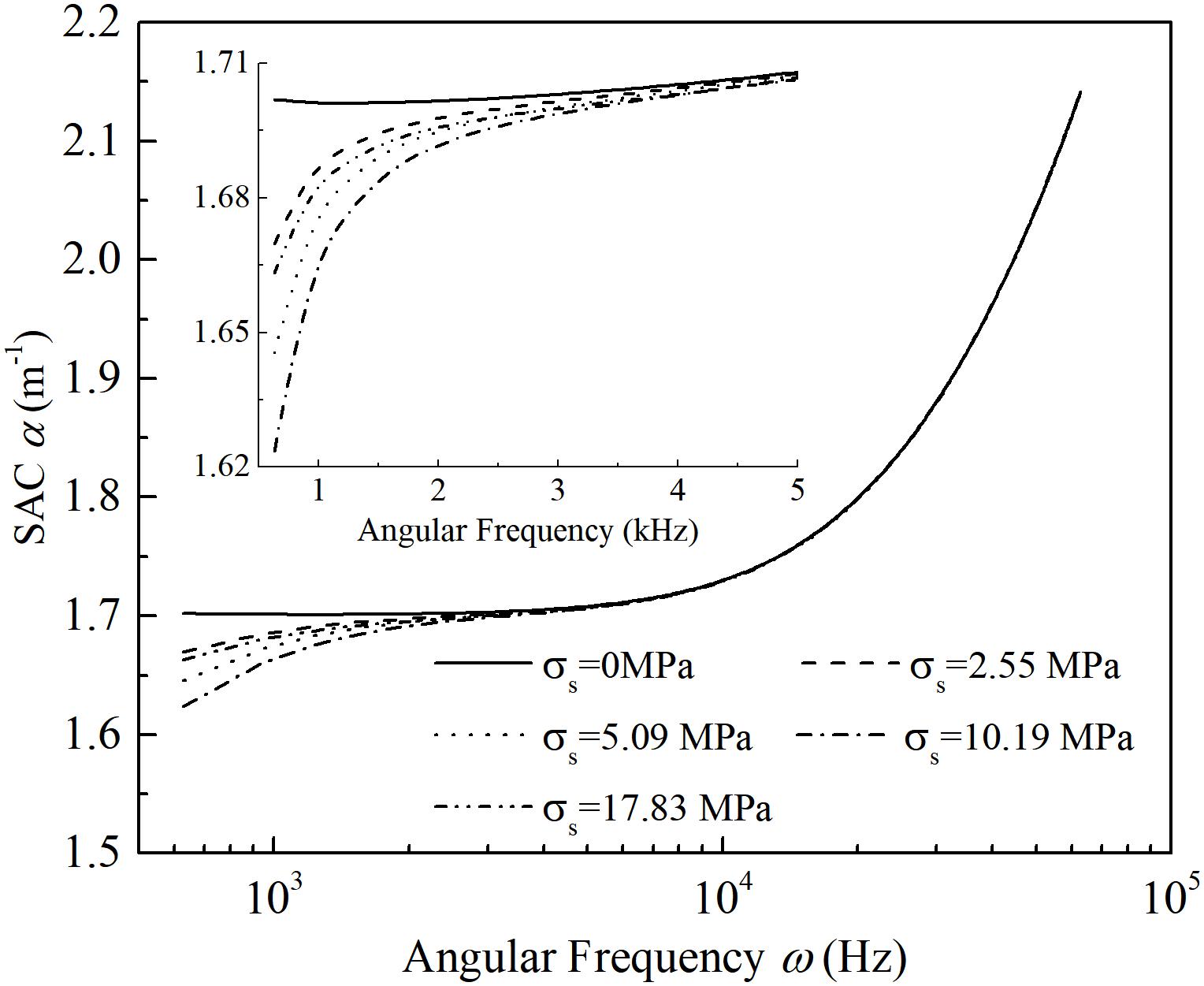
As is shown in Figure 8, the SAC generally increases with the increase in frequency. Within a lower frequency band (ω < 5 kHz), the variation of wave attenuation is gentle; on the contrary, within a higher frequency band, the spatial attenuation coefficients increase sharply. Additionally, within a lower frequency band (ω < 5 kHz), when the rock is unstressed, the attenuation coefficient is nearly a constant. As the static stress increases, the variation as is described above gradually occurs. The effect of uniaxial static stress on the variation in spatial attenuation coefficient is more remarkable compared with that of higher frequency. And the lower the frequencies of the harmonic waves are, the more apparent the changes of spatial attenuation coefficient are.

FIGURE 8

Figure 8. Frequency-dependent spatial attenuation coefficients (x = 0.2 m).

Effect of Geometry on the Wave Attenuation

Based on the results presented above, the variation of spatial attenuation coefficient is straightly correlated with the actual normal stress. The geometry of natural rock block is various, and the variation type of cross-section is various. For the convenience of investigation, the simplification of geometry of rock block is necessary. In this work, the intact rock blocks with different geometries are abstracted as concave, straight and convex rods as shown in Figure 9. As respect to rock with a circular cross-section, the radius of cross-section is chosen to describe the radial size of the rock, and the varying rules of radius along the propagation path decide the distribution of normal static stress. In this section, the differences of wave attenuation in concave, straight and convex rock bars are discussed in detail.

FIGURE 9

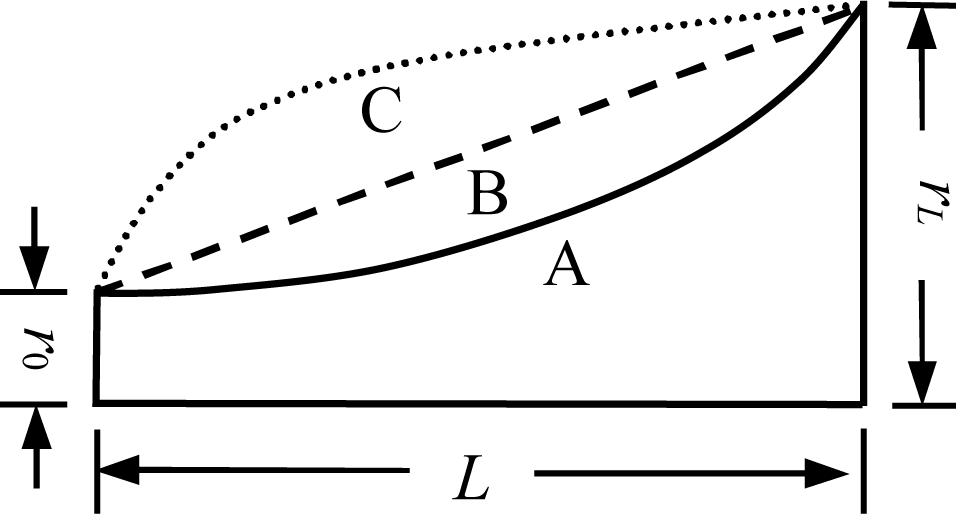
Figure 9. Schematic illustration of diffuse rock rod with variable cross-section. Because the rock rod is axisymmetric, only a half of the rock is presented. Type A: concave rod, the relation between the radius and the traveling distance is r(x) = r₀exp[xln(r_L/r₀)/L]; Type B: straight rod, the relation between the radius and the traveling distance is r(x) = r₀ + (r_L−r₀)x/L; Type C: convex rod, the relation between the radius and the traveling distance is r(x) = r₀ + (r_L−r₀)(x/L)^1/3.

As is shown in Figure 9, three types of varying rules of radius are mainly considered in this work. For type A, the rock is a concave rod and the relation between radius and traveling distance is assumed as r(x) = r₀exp[xln(r_L/r₀)/L]. For type B, the rock is a straight rod and the radius increases linearly with the increase in traveling distance, and the expression of radius of an arbitrary cross-section is shown in Eq. 14. As for type C, the rock is a convex rod and the relation between radius and traveling distance can be expressed as Eq. 15. From Figure 9, it is not hard to learn that the changing rates in radius of all types of rock are different at the same travel distance.

$$r(x)=r_0+(r_L-r_0)\frac{x}{L}(14)$$

$$r(x)=r_0+(r_L-r_0){\left(x\mathrm{/}L\right)}^{1/3}(15)$$

Figure 10 provides a comparison of spatial attenuation coefficients in different types of rock bars. Apparently, the wave attenuation is related to the changing rules in the radius along the propagation path. In the area near the smaller end, the changing rate in the radius of the convex rock rod is the biggest, and the wave attenuation of the convex rock is also the most serious. On the contrary, in the area near the larger end, the SAC of the concave rock rod is higher than that of the straight and convex rock rod. As the traveling distance of harmonic wave increases, in the area near the smaller end of the convex rock rod, the variation in SAC appears a characteristic of sharp decreasing; however, the SAC decreases gently in the area near the larger end. Comparing Figures 10A–C, we can see that obvious differences in the spatial distribution of the attenuation coefficient do not occur even though the static stress increases.

FIGURE 10

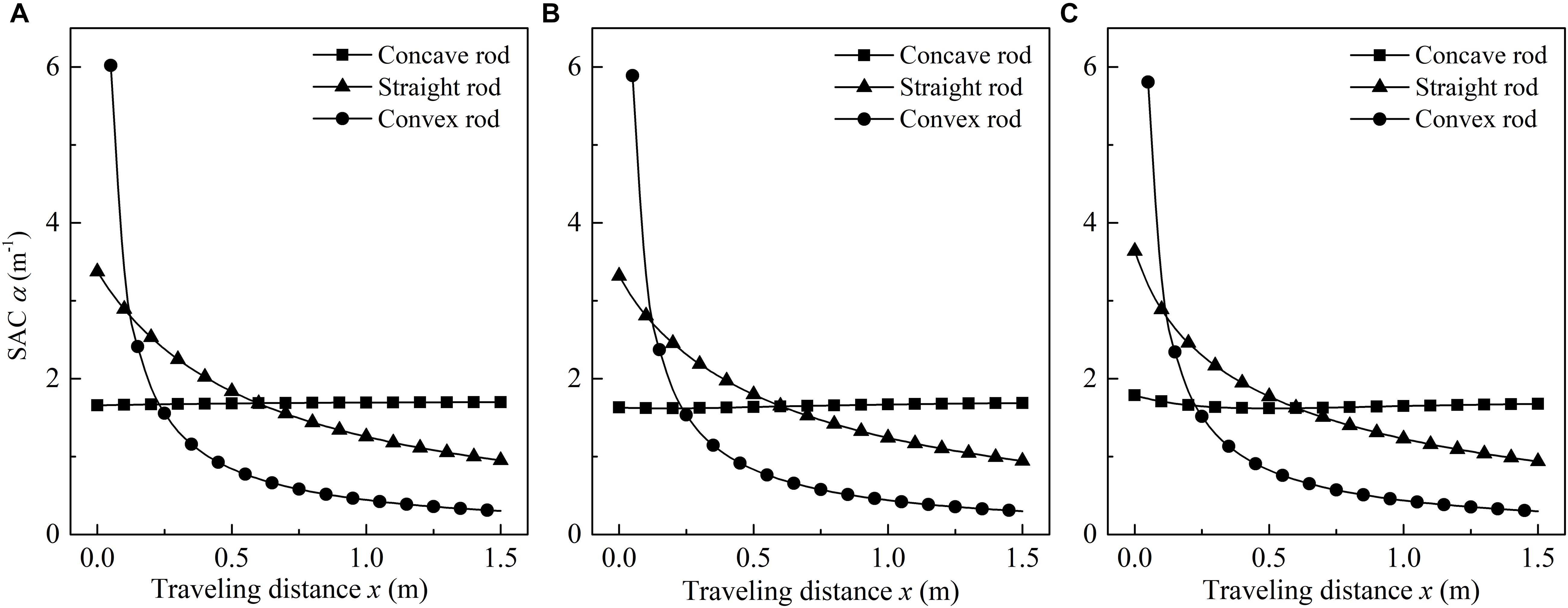
Figure 10. Spatial attenuation coefficient versus traveling distance in concave, straight and convex rock bars (r₀ = 0.025 m, r_L = 0.09 m, ω = 628.3 Hz) (A) σ_s = 2.55 MPa; (B) σ_s = 5.09 MPa; (C) σ_s = 10.19 MPa.

However, the changing rules in radius have a remarkable influence on the variation of wave attenuation versus static stress. As is presented in Figure 11, at the same traveling distance, the SAC of the concave and straight rock undergo a changing process of “from decrease to increase”; while the variation in attenuation coefficient of convex rock appears a characteristic of “monotonically decreasing.” As is shown in Figure 9, both of the radius and cross-sectional area in the convex rock are bigger than those of the concave and straight rocks at the same traveling distance x (0 < x < L), therefore, the actual normal stresses in the convex rock are lower than that of the others at the same location. The difference of actual normal stress results in the difference of variation in wave attenuation.

FIGURE 11

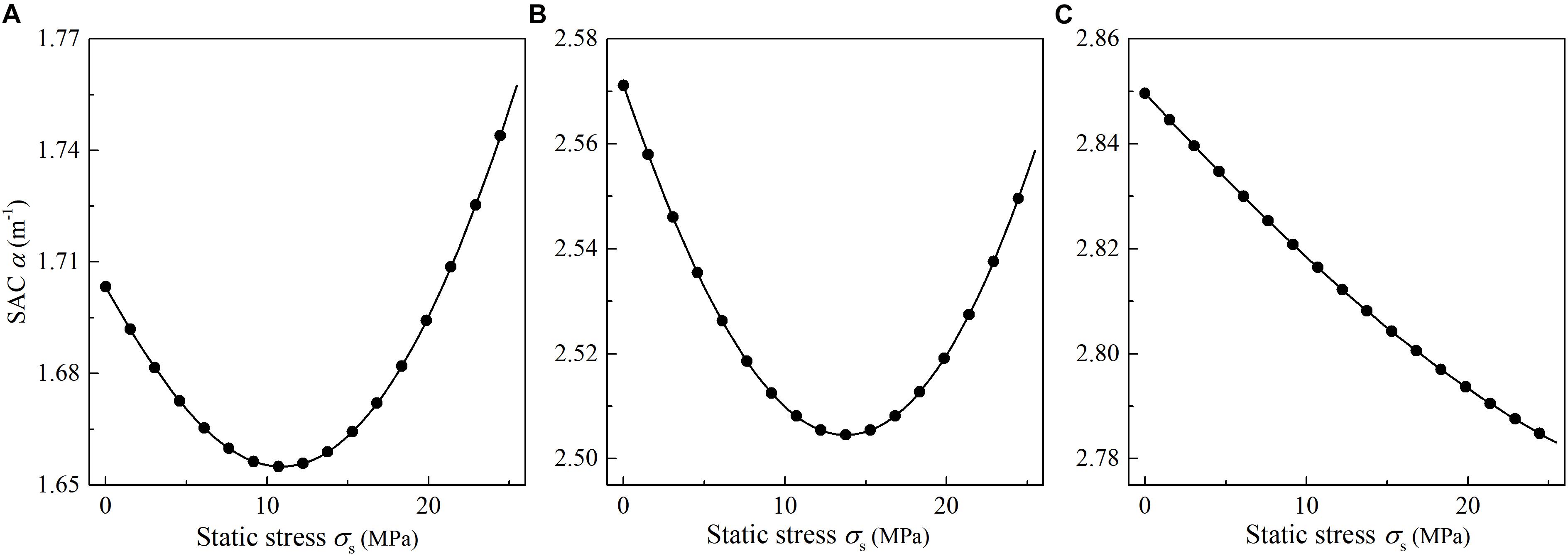
Figure 11. Comparison of variation in the spatial attenuation coefficient versus the static stress (x = 0.2 m, r₀ = 0.025 m, r_L = 0.09 m, ω = 628.3 Hz) (A) Concave rock bar; (B) Straight rock bar; (C) Convex rock bar.

Comparing the results in Figures 10, 11, we can draw a conclusion that both of the static stress and variable cross-section have a significant effect on the wave attenuation in the rock. The spatial distribution of the attenuation coefficient is mainly decided by the changing rules in the radius of a cross-section. While the variation of the spatial attenuation coefficient is mainly affected by the actual normal stress, and the distribution of the actual normal stress is also dependent on the changing rules of the radius of a cross-section. Overall, the variable cross-section is the root cause of variation in wave attenuation.

Conclusion

In this work, the wave equation in a stressed rock with variable cross-section is established on the basis of a modified constitutive model of the viscoelastic body. The spatial attenuation coefficients in amplitude of harmonic waves propagating in the rock are investigated by numerical calculation.

It is concluded that the amplitude attenuation in of lower-frequency waves decreases first within a lower static stress range; while the static stress is sufficiently large, the wave attenuation increases reversely. The variable normal static stresses along the propagation path result in the space-dependent attenuation coefficients. Additionally, the variation characteristics of space-dependent attenuation coefficient along the propagation path are different under different levels of static stress.

The wave attenuation in a stressed rock with variable cross-section is frequency-dependent. Lower-frequency harmonic waves are susceptible to be affected by static stress. When the frequency is sufficiently high, the spatial attenuation coefficients increase sharply, however, the effect of static stress on wave attenuation can be neglected.

The changing rules in the radius of cross-section also have an effect on the wave attenuation. The spatial distribution of the attenuation coefficient and its variation versus static stress are dependent on the distribution of actual normal static stress, the cross-sectional areas and the changing rates of cross-sectional area.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

WY completed the establishment and solution of the wave equation and the writing of the manuscript. JJ provided the guide of stress wave propagation theory for the study and economically supported the project. ZG and YW were responsible for data processing and figure plotting.

Funding

This work was financially supported by the National Natural Science Foundation of China (Grant Nos. 51664017 and 51964015), the Program of Qingjiang Excellent Young Talents, Jiangxi University of Science and Technology (JXUSTQJBJ2017007), and Science and Technology Project of Jiangxi Provincial Department of Education (Grant Nos. GJJ160616 and GJJ171490).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Akkas, N., Barez, F., and Goldsmith, W. (1980). Elastic wave propagation in an exponential rod. Int. J. Mech. Sci. 22, 199–208. doi: 10.1016/0020-7403(80)90035-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Barez, F., Goldsmith, W., and Sackman, J. L. (1980). Longitudinal wave propagation in axisymmetric structures with material and/or aereal discontinuity. Exp. Mech. 20, 325–333. doi: 10.1007/BF02321119

PubMed Abstract | CrossRef Full Text | Google Scholar

Benveniste, Y. (1975). Wave propagation in a nonlinearly elastic compressible rod with variable cross section. Acta Mech. 22, 197–208. doi: 10.1007/BF01170676

CrossRef Full Text | Google Scholar

Chen, X., Li, J. C., Cai, M. F., Zou, Y., and Zhao, J. (2015). Experimental study on wave propagation across a rock joint with rough surface. Rock Mech. Rock Eng. 48, 2225–2234. doi: 10.1007/s00603-015-0716-z

CrossRef Full Text | Google Scholar

Dose, J., and Skews, B. (2014). Area change effects on shock wave propagation. Shock Waves 24, 365–373. doi: 10.1007/s00193-014-0501-z

CrossRef Full Text | Google Scholar

Fan, L. F., Ren, F., and Ma, G. W. (2012). Experimental study on viscoelastic behavior of sedimentary rock under dynamic loading. Rock Mech. Rock Eng. 45, 433–438. doi: 10.1007/s00603-011-0197-7

CrossRef Full Text | Google Scholar

Fan, L. F., and Sun, H. Y. (2015). Seismic wave propagation through an in-situ stressed rock mass. J. Appl. Geophys. 121, 13–20. doi: 10.1016/j.jappgeo.2015.07.002

CrossRef Full Text | Google Scholar

Fu, Y. B., and Scott, N. H. (1994). Propagation of simple waves and shock waves in a rod of slowly varying cross-sectional area. In. J. Eng. Sci. 32, 35–44. doi: 10.1016/0020-7225(94)90147-3

CrossRef Full Text | Google Scholar

Gan, C. B., Wei, Y. M., and Yang, S. X. (2014). Longitudinal wave propagation in a rod with variable cross-section. J. Sound Vib. 333, 434–445. doi: 10.1016/j.jsv.2013.09.010

CrossRef Full Text | Google Scholar

Gong, F. Q., Li, X. B., Liu, X. L., and Zhao, J. (2010). Experimental study of dynamic characteristics of sandstone under one-dimensional coupled static and dynamic loads. Chin. J. Rock Mech. Eng. 29, 2076–2085.

Google Scholar

Grana, D. (2016). Pressure–velocity relations in reservoir rocks: modified MacBeth’s equation. J. Appl. Geophys. 132, 234–241. doi: 10.1016/j.jappgeo.2016.07.020

CrossRef Full Text | Google Scholar

Holt, R. M., Furre, A. K., and Horsrud, P. (1997). Stress dependent wave velocities in sedimentary rock cores: why and why not? International. J. Rock Mech. Min. Sci. 34, 128.e1–e128.e12. doi: 10.1016/S1365-1609(97)00059-2

CrossRef Full Text | Google Scholar

Hudson, J. A., and Harrison, J. P. (2005). Engineering Rock Mechanics: an Introduction to the Principles. New York: Elsevier.

Google Scholar

Jaeger, J. C., Cook, N. G. W., and Zimmerman, R. W. (2007). Fundamentals of Rock Mechanics. Malden: Blackwell Publishing.

Google Scholar

Jones, T. D. (1986). Pore fluids and frequency-dependent wave propagation in rocks. Geophysics 51, 1939–1953. doi: 10.1190/1.1442050

CrossRef Full Text | Google Scholar

Kjartansson, E. (1979). Constant Q-Wave propagation and attenuation. J. Geophys. Res. Solid Earth 84, 4737–4748. doi: 10.1029/JB084iB09p04737

CrossRef Full Text | Google Scholar

Li, J. C., Ma, G. W., and Huang, X. (2010). Analysis of wave propagation through a filled rock joint. Rock Mech. Rock Eng. 43, 789–798. doi: 10.1007/s00603-009-0033-5

CrossRef Full Text | Google Scholar

Li, X. B., and Tao, M. (2015). The influence of initial stress on wave propagation and dynamic elastic coefficients. Geomech. Eng. 8, 377–390. doi: 10.12989/gae.2015.8.3.377

CrossRef Full Text | Google Scholar

Li, X. B., Wang, S. F., and Wang, S. Y. (2018). Experimental investigation of the influence of confining stress on hard rock fragmentation using a conical pick. Rock Mech. Rock Eng. 51, 255–277. doi: 10.1007/s00603-017-1309-9

CrossRef Full Text | Google Scholar

Li, X. B., Zhou, Z. L., Lok, T. S., Hong, L., and Yin, T. (2008). Innovative testing technique of rock subjected to coupled static and dynamic loads. Int. J. Rock Mech. Min. Sci. 45, 739–748. doi: 10.1016/j.ijrmms.2007.08.013

CrossRef Full Text | Google Scholar

Li, X. B., Zhou, Z. L., Zhao, F. J., Zuo, Y., Ma, C., Ye, Z., et al. (2009). Mechanical properties of rock under coupled static-dynamic loads. J. Rock Mech. Geotech. Eng. 1, 41–47. doi: 10.3724/SP.J.1235.2009.00041

CrossRef Full Text | Google Scholar

Liu, J. X., Cui, Z. W., and Wang, K. X. (2012). Effect of stress on reflection and refraction of plane wave at the interface between fluid and stressed rock. Soil Dyn. Earthq. Eng. 42, 47–55. doi: 10.1016/j.soildyn.2012.05.022

CrossRef Full Text | Google Scholar

Ma, G. W., Li, J. C., and Zhao, J. (2011). Three-phase medium model for filled rock joint and interaction with stress waves. Int. J. Numer. Anal. Methods Geomech. 35, 97–110. doi: 10.1002/nag.941

CrossRef Full Text | Google Scholar

Moodie, T. B., and Barclay, D. W. (1975). Wave propagation in inhomogeneous variable-section viscoelastic bars. Acta Mech. 23, 199–217. doi: 10.1007/BF01174019

CrossRef Full Text | Google Scholar

Sahane, D., Santare, M. H., Powers, B. M., and Gazonas, G. A. (2016). Computational simulations of wave propagation in microcrack-damaged media under prestress. Int. J. Fract. 199, 185–198. doi: 10.1007/s10704-016-0103-0

CrossRef Full Text | Google Scholar

Selim, M. M., and Ahmed, M. K. (2006). Propagation and attenuation of seismic body waves in dissipative medium under initial and couple stresses. Appl. Math. Comput. 182, 1064–1074. doi: 10.1016/j.amc.2006.05.005

CrossRef Full Text | Google Scholar

Shorr, B. F. (1995). Analysis of wave propagation in elastic-plastic rods of a variable cross section using direct mathematical modeling. Arch. Appl. Mech. 65, 537–547. doi: 10.1007/BF00789095

CrossRef Full Text | Google Scholar

Tao, M., Ma, A., Cao, W. Z., Li, X., and Gone, F. (2017). Dynamic response of pre-stressed rock with a circular cavity subject to transient loading. Int. J. Rock Mech. Min. Sci. 99, 1–8. doi: 10.1016/j.ijrmms.2017.09.003

CrossRef Full Text | Google Scholar

Weng, L., Li, X. B., Taheri, A., Wu, Q., and Xie, X. (2018). Fracture evolution around a cavity in brittle rock under uniaxial compression and coupled static-dynamic loads. Rock Mech. Rock Eng. 51, 531–545. doi: 10.1007/s00603-017-1343-7

CrossRef Full Text | Google Scholar

Wu, W., Li, J. C., and Zhao, J. (2013a). Seismic response of adjacent filled parallel rock fractures with dissimilar properties. J. Appl. Geophys. 96, 33–37. doi: 10.1016/j.jappgeo.2013.06.009

CrossRef Full Text | Google Scholar

Wu, W., Zhu, J. B., and Zhao, J. (2013b). A further study on seismic response of a set of parallel rock fractures filled with viscoelastic materials. Geophys. J. Int. 192, 671–675. doi: 10.1093/gji/ggs055

CrossRef Full Text | Google Scholar

Wu, W., Li, J. C., and Zhao, J. (2014). Role of filling materials in a P-wave interaction with a rock fracture. Eng. Geol. 172, 77–84. doi: 10.1016/j.enggeo.2014.01.007

CrossRef Full Text | Google Scholar

Zhou, J. R., Lu, W. B., and Yan, P. (2016). Frequency-dependent attenuation of blasting vibration waves. Rock Mech. Rock Eng. 49, 4061–4072. doi: 10.1007/s00603-016-1046-5

CrossRef Full Text | Google Scholar