- 1China Energy Investment Corporation (China Energy) Co., Ltd., Beijing, China
- 2College of Water Resource and Hydropower, Sichuan University, Chengdu, China
- 3Guodian Dadu River Hydropower Development Co., Ltd., Chengdu, China
- 4State Key Laboratory of Hydraulics and Mountain River Engineering, Sichuan University, Chengdu, China
To get a better understanding of failure mechanism of slopes in soils that exhibit expansive characteristics subjected to any type of inundations, particularly, when the soils switch from unsaturated to saturated states, the field study may severe as a rather effective method for providing the most representative information. However, field investigation is usually time-consuming and expensive. While, numerical simulation provides a faster way for producing quantitative interpretation of several complicated mechanisms. In this paper, a field experiment is studied numerically, which involves simulation of water flow within the slope profile by finite element method, followed by quantification of the stability of potential failure mass by the classic slices Method. Special emphasis is placed on the effects of cracks on the flow behavior in the shallow layer, which is one of the most essential characteristics in expansive soils. The Bimodal Soil Water Characteristic curve, together with the Bimodal permeability functions, is found to be more effective in reproducing the change of flow regime (pore water pressure and water content) from the finite element water flow analyses, in comparison to the Unimodal functional properties. The stability analyses illustrate that the shear behavior of soils within the shallow layer should be better described by strength parameters measured under lower confining pressure close to the field conditions. This implies the actual mobilized shear strength of expansive soils in shallow layer should be better modeled with a non-linear strength model that is able to accommodate the low stress conditions.
Introduction
Expansive soils that swell significantly upon wetting and shrink during drying are found on every continent. Instability of slopes constructed of expansive soils are frequently reported in many countries around the world. The key triggering factor of expansive soil slopes failure is primarily the water infiltration due to snow melting or rainfall during wet season. Although the infiltration-induced failures usually have a shallow slip surface, it still can cause distress to the nearby infrastructures and contribute to huge economic losses (Wang et al., 2017). Understanding the failure mechanism of expansive soil slopes remains one of greatest challenges to both the researchers and the practitioners (Bao and Ng, 2000; Ng et al., 2003).
For example, in China, hundreds and thousands of expansive soil slopes have been formed either from the natural terrain or from excavations for supporting the growing needs of the increasing engineering activities in recent years. Over the same time period, the failures of expansive soils slopes and the associated destructive consequences have also been frequently reported, of which the fundamental mechanism is quite complicated. Several field tests were conducted to study the responses and behaviors of expansive soil slopes subjected to rainfall infiltration in China (Zhang et al., 2010; Cheng et al., 2011). Lessons learnt from these field tests were then used as guidelines in the design of the infrastructure in expansive soils area, for example, the world’s greatest water transfer project, the South-to-North Water Transfer Project (SNWTP), which involves many canals formed by excavation in expansive soil areas (Ng et al., 2003; Zhan et al., 2007; Zhang et al., 2010). These slopes investigated were usually well instrumented to monitor the changes in pore water pressure, suction, stress regime within the potential failure mass, and rainwater infiltration intensity on the slope ground surface, etc. The suction loss and engineering property degradations (i.e., decrease in shear strength and increase in permeability) of expansive soil resulting from environmental changes were identified as the key factors that contribute to expansive soil slopes failure.
In situ tests are costly and usually require a long period of time. Comparatively, numerical analysis is a cheaper and fast alternative to investigation of the behaviors of expansive soil slopes to various infiltration conditions. Several researchers (Alonso et al., 2003; Rouainia et al., 2009; Hamdhan and Schweiger, 2012; Qi and Vanapalli, 2016) used the advanced numerical techniques to simulate the field studies from the literature, most of which were based on saturated-unsaturated seepage analyses. One of the most striking findings is the importance of selecting proper hydraulic properties of the soil, in particular, when the soil structure is altered by environmental factors. For example, Qi and Vanapalli (2015a, b) recently suggested that the hydraulic behavior of cracked expansive soils might be better described using the bimodal soil-water characteristic curve (SWCC), together with a bimodal permeability function. The development of cracks, due to shrinkage-swelling of soils induced by drying-wetting cycles (Wang et al., 2019), is one of the most common issues concerned in expansive soil slopes, i.e., the soil cracking is a typical consequence of cyclic variations of water content. The mechanical cracking can, in turn, affect significantly the soils’ hydraulic properties/responses, and can gradually induce the deterioration of soil’s mechanical properties. This series of chain reactions involves complicated hydro-mechanical coupling that is highly non-linear in terms of the mathematical description (e.g., for both the shear strength and the hydraulic properties).
This paper will focus on the non-linear hydraulic behavior of cracked soils using the non-linear Bimodal hydraulic models. Starting from this perspective, numerical simulations are performed to investigate the hydro-mechanical response of expansive soil slope to rainfall, and to study its influence on slope stability based on the non-linear the shear strength behavior. In particular, the hydraulic behavior of an expansive soil slope under an artificial rainfall condition at an in situ test presented by Zhang et al. (2010) is first modeled using the commercial software, SEEP/W (Geo-Slope International Ltd., 2007a). Emphasis is placed on influence of soil cracking on the changes of flow regime within the shallow soil layer, which constituted a significant part of the failure mass. Meanwhile, the non-linearity of shear strength is considered by relating it to the adopted bimodal hydraulic models. The results of hydraulic variations (suction or negative pore water pressure and water content changes) using unimodal and bimodal SWCCs and their respective permeability functions are compared with the measurements. Based on the seepage analysis, the factors of safety calculated using the Limit Equilibrium Method, with the non-linear shear strength model linked to the soil water characteristic curve, are also presented and discussed.
Instrumentation and Monitoring
The Monitoring Area
The monitoring area is located near the city of Xinxiang, Henan, China, where a huge project transferring water from South China to North China (i.e., the South-to-North Water Transfer Project) goes through. Design of safe and economical dimensions for canals constructed in expansive soils was one of the major geotechnical problems in this area. The average annual rainfall in this region is about 800 mm, of which 60–70% of the rainfall is distributed from June to August (Zhang et al., 2010). Consequently, numerous slope failures were triggered by the rainfalls with high intensity during the wet seasons.
Field Study
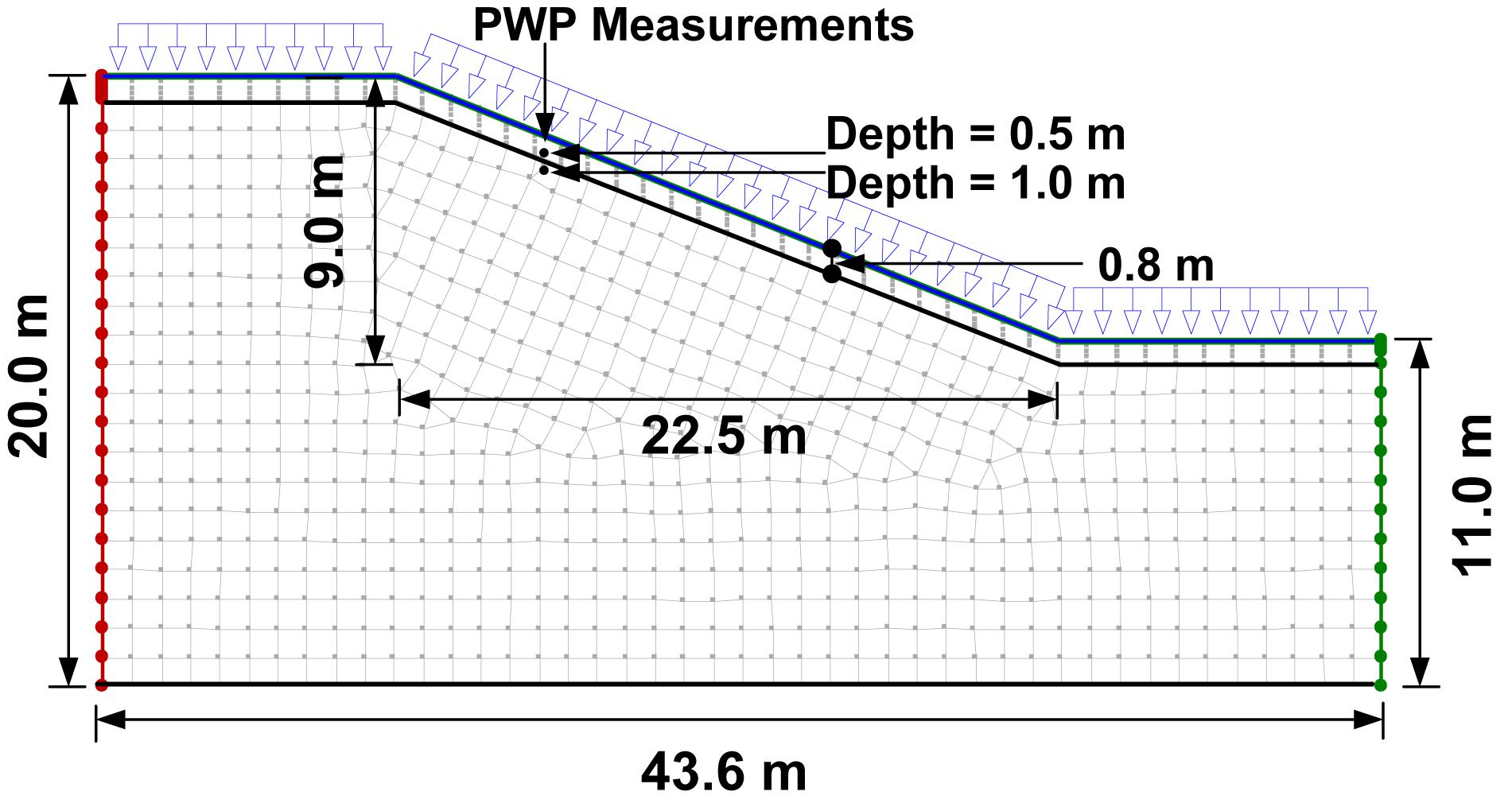
Several field tests were conducted in this area by Zhang et al. (2010) to investigate the sliding mechanisms of expansive slopes under artificial rainfalls. One of the field slopes is selected for numerical simulation in the present study. The test slope was formed by excavation and had a height of 9 m, and the slope following excavation was 1:2.5. The monitoring area affected by the artificial rainfall was 28 m length and 16 m width. Borehole tests showed that slope profile consisted primarily of the expansive clayey soils with a small portion of silty loamy soils. The laboratory tests indicated that the expansive soils had a natural water content of 21.7%, specific gravity of 2.78 and dry density of 1.7 g/cm3. The average Liquid Limit and Plastic Limit were measured to be 54.9 and 25.0%, respectively. The particles with sizes smaller than 0.005 and 0.002 mm accounted for 61.6 and 40.9%, respectively. The free swelling percentage was around 60.4%. The instrumentation included Tensiometer and ThetaProbe probe for measuring suction and volumetric water content, respectively, and rain gauge for measuring the rainfall intensity. The layout and locations of the instrumentation along a section profile of the slope are shown in Figure 1.
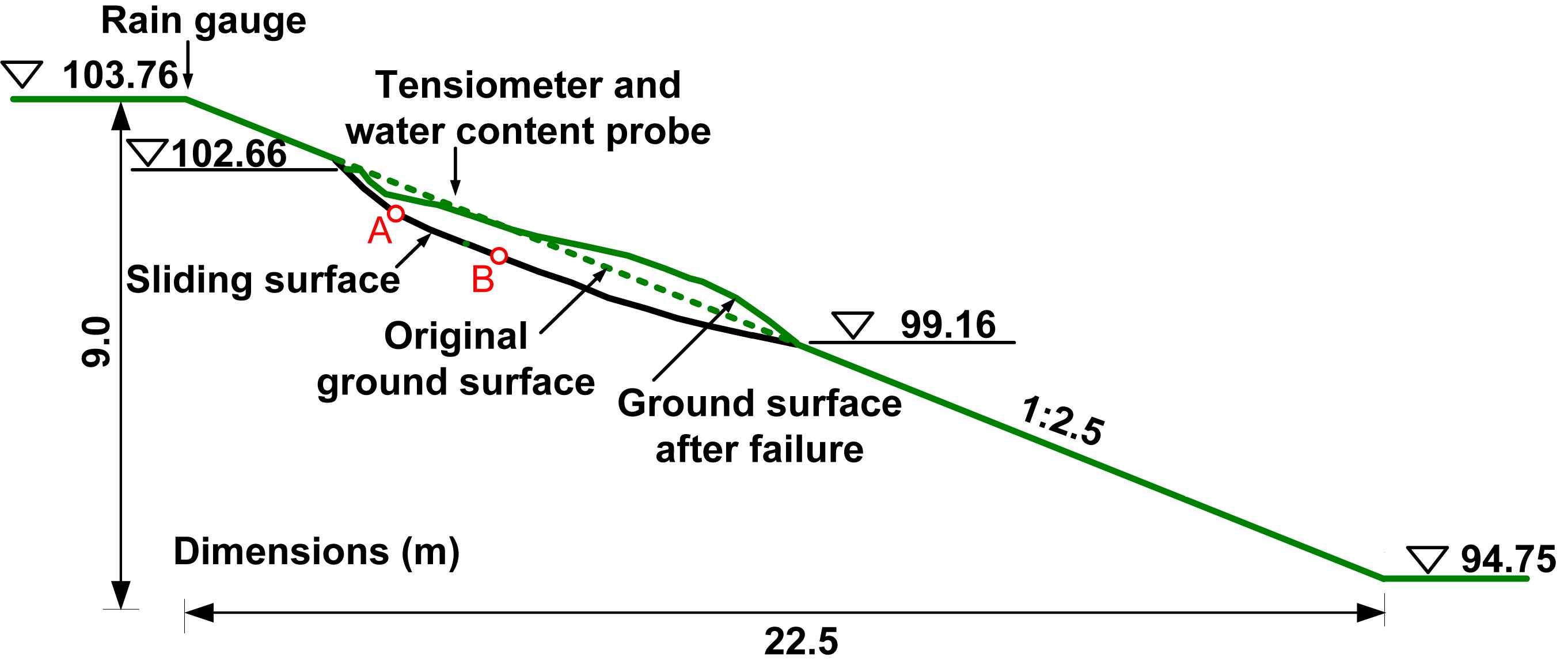
Figure 1. Cross section of studied slope from Zhang et al. (2010).
In order to model the infiltration process, a sprinkler system was specially designed for artificial rainfall, which consisted of 1 pump, 2 water-supply pipes, 15 branches, and 75 sprinkler heads (5 Rows × 15 Columns evenly distributed over the test area). The distances between two adjacent rows and columns were 4 and 2 m, respectively, along the slope and canal directions. This designed system covered more than 760 m2 of the sloping surface and almost the entire slope cross-section from the crest to the toe shown in Figure 1. This system was used to generate three periods of rainfall with a constant intensity of around 8 mm/h. In the first two rainfalls, evident sliding displacements were measured, the final collapse near the slope crest occurred during the third rainfall period. Figure 1 depicts the slip surface and ground surface after failure. It was reported from Zhang et al. (2010) that a significant section of the slip surface was located at the depths ranging from 0.6 to 1.0 m, over which the shallow failure mass was severely destroyed by the abundant cracks and fissures well developed due to previous wetting and drying cycles. The primary cracks were observed to have widths as large as 12 mm and depths of around 0.8 m, accompanied by many other smaller fissures with varying dimensions. It can be deduced that the presence of cracks has increased the apparent permeability of the surficial soils in this shallow layer. Consequently, significant fluctuations in the water contents mostly occurred within this shallow layer subjected to the simulated rainfalls, while little hydraulic response was observed in the underlying layer which was quite intact and relatively impermeable. Meanwhile, the abundance of cracks has led to a significant reduction in the shear strength (Lin et al., 2019), which might have brought the shallow layer to a critical state quite susceptible to failure subjected to rainfall condition. One of the focus of this work is to investigate these coupling effects of cracks on both hydraulic and mechanical behaviors of the surficial soils, as well as the stability of surficial layer.
Seepage Analysis
Theory of Water Infiltration
The processes of water infiltration and flow through saturated and unsaturated soil systems can be modeled analytically (Srivastava and Yeh, 1991; Wu and Zhang, 2009) or numerically (Alonso et al., 2003; Oh and Vanapalli, 2010). The analytical methods are able to provide accurate solutions to infiltration problems with a regular geometry and simple boundary conditions. Comparatively, the numerical solutions can simulate various complicated saturated and unsaturated seepage processes. Both the solutions are given for the equation describing the mass conversation of water, which reads as follows:
where, qw is volumetric water content, t is time, k is the permeability of soils, uw is the value of pore water pressure, gw is the density of water, g is the gravitational acceleration, and y is the elevation. ∇ is the del operator and defined as:
Equation (1) suggests that the difference between the flow entering and leaving an elemental volume is equal to the rate of change in the volumetric water content with respect to time (Fredlund and Rahardjo, 1993). In order to make Eq. 1 determinate, a continuous relationship needs to be specified to link the volumetric water content and suction, which is called the SWCC. Besides, the permeability of unsaturated soils, k, is no longer a constant, unlike that of un-deformable saturated soils, but varies with water content or suction, which constitutes another functional hydraulic parameter for seepage analysis. These two functional parameters (i.e., SWCC and the permeability function) make Eq. 1 highly non-linear. Analytical solution is nearly impossible to obtain for complicated boundary conditions that are common in practice. Furthermore, use of bimodal SWCC and permeability function in the present study will increase complexities associated with non-linearity. Therefore, the numerical solution to Eq. 1 in two dimensions is adopted and obtained using the commercial finite element-based software SEEP/W (Geo-Slope International Ltd., 2007b).
The Soil Water Characteristic Curve and Permeability
The SWCC, also known as soil water retention curve, is essentially a non-linear functional relationship between volumetric water content (gravimetric water content or degree of saturation) and suction for soils under unsaturated condition. Since the mechanical behavior of soils is strongly controlled by the amount of meniscus water in the soils and its bridge effects between solid particles, the SWCC often plays the role as a fundamental property for predicting the mechanical properties, for example, shear strength (Vanapalli et al., 1996) and stiffness (Qi and Vanapalli, 2016). The SWCC is also coupled with mechanical model to form a fully coupled model to describe the coupled hydro-mechanical response of soils subjected to variations of external hydraulic and/or mechanical factors. Thus, a good model for SWCC is of particularly importance in various types of geotechnical engineering applications using the mechanics for unsaturated soils.
A number of mathematical equations of SWCC (e.g., van Genuchten, 1980; Fredlund and Xing, 1994) have been established where the model parameters can be obtained by fitting to the experimental data, a majority of these existing functions have a sigmoid and unimodal form. In this work the Fredlund and Xing (1994) model is first used in seepage analysis:
where, ua − uw is the soil suction (kPa), the pore air pressure, ua, is assumed to be zero (atmospheric) and constant in this study. This assumption is acceptable, since the air phase in the unsaturated soil elements near the slope surface (the area of interest) is essentially connected to atmosphere. e is the natural logarithm (base 2.71828 …), θs is the saturated volumetric water content, a, n, and m are three fitting parameters, which are related to the air-entry value of the soil (kPa), the slope at the inflection point of the SWCC and the residual water content of the soil, respectively. The residual volumetric water content is simply taken as 10% of the saturated value.
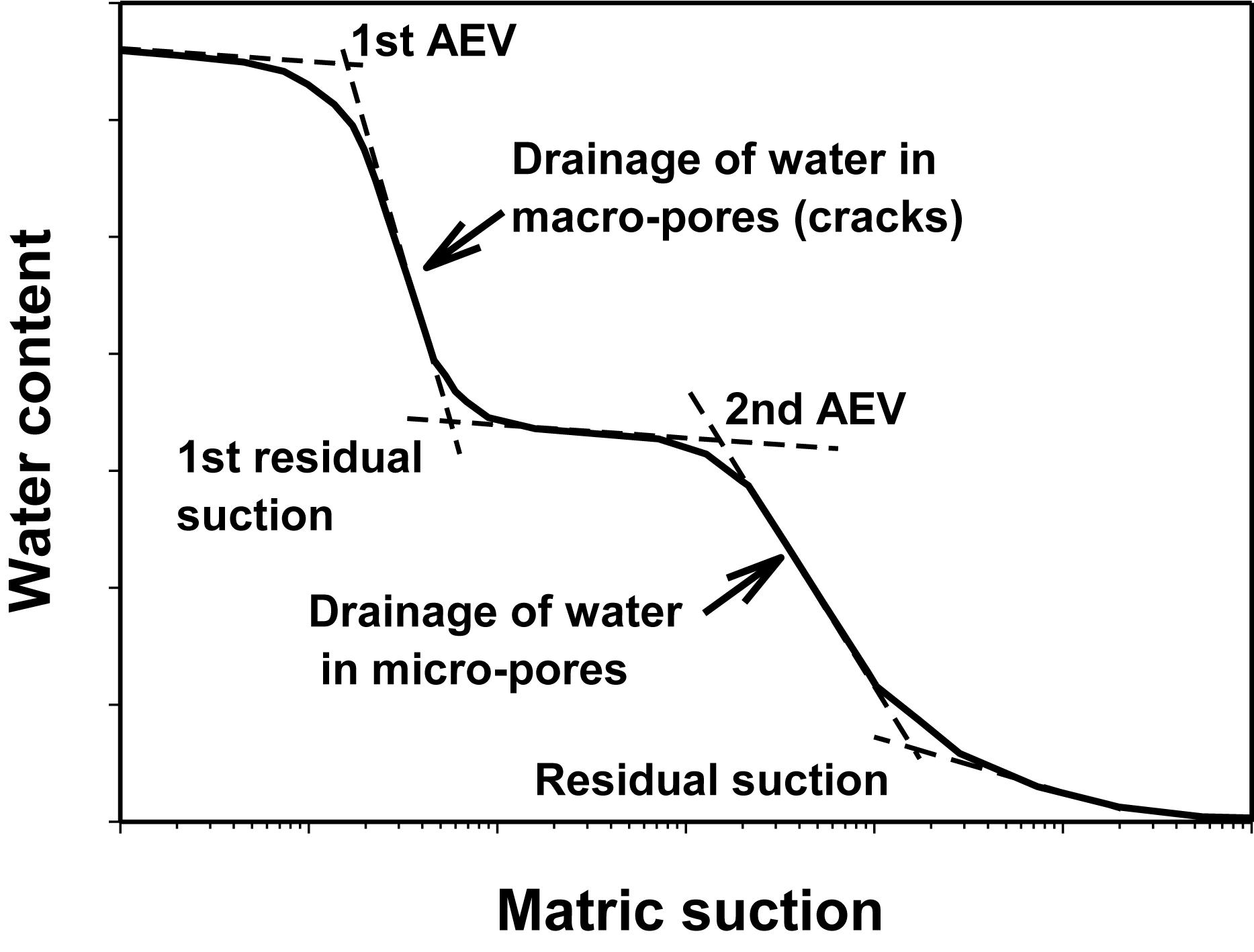
However, it is found that Eq. 3 is not able to fit experimental SWCC data sets from soil sample with two distinct pore-size distributions due to various factors. For example, the bimodal pore-size distributions of soil can be formed by compacting coarse colluvial soils, mixing the residual soil with sand, and/or due to desiccation cracking. Since the shape of SWCC is strongly correlated to the pore-size distributions (recalling water is stored in the pore between the soil particle), the SWCC data for these types of soil samples needs to be fitted/described using a Bimodal function, as typically shown in Figure 2. There are two air entry values (AEVs) corresponding to two distinct sizes of pores. As suction rises beyond these two AEVs, the water drainage through soil matrix can be divided into two phases, i.e., flowing out of the larger and smaller pores, respectively. Since the cracks can be regarded as larger pores, water drainage in the cracked soils exhibits similar characteristics as shown in Figure 2. Thus, the SWCC of a cracked soil is also of typical bimodel (Fredlund et al., 2010; Li et al., 2011), which has been observed in several cracked expansive soils (Azam and Ito, 2011; Elkady, 2014).
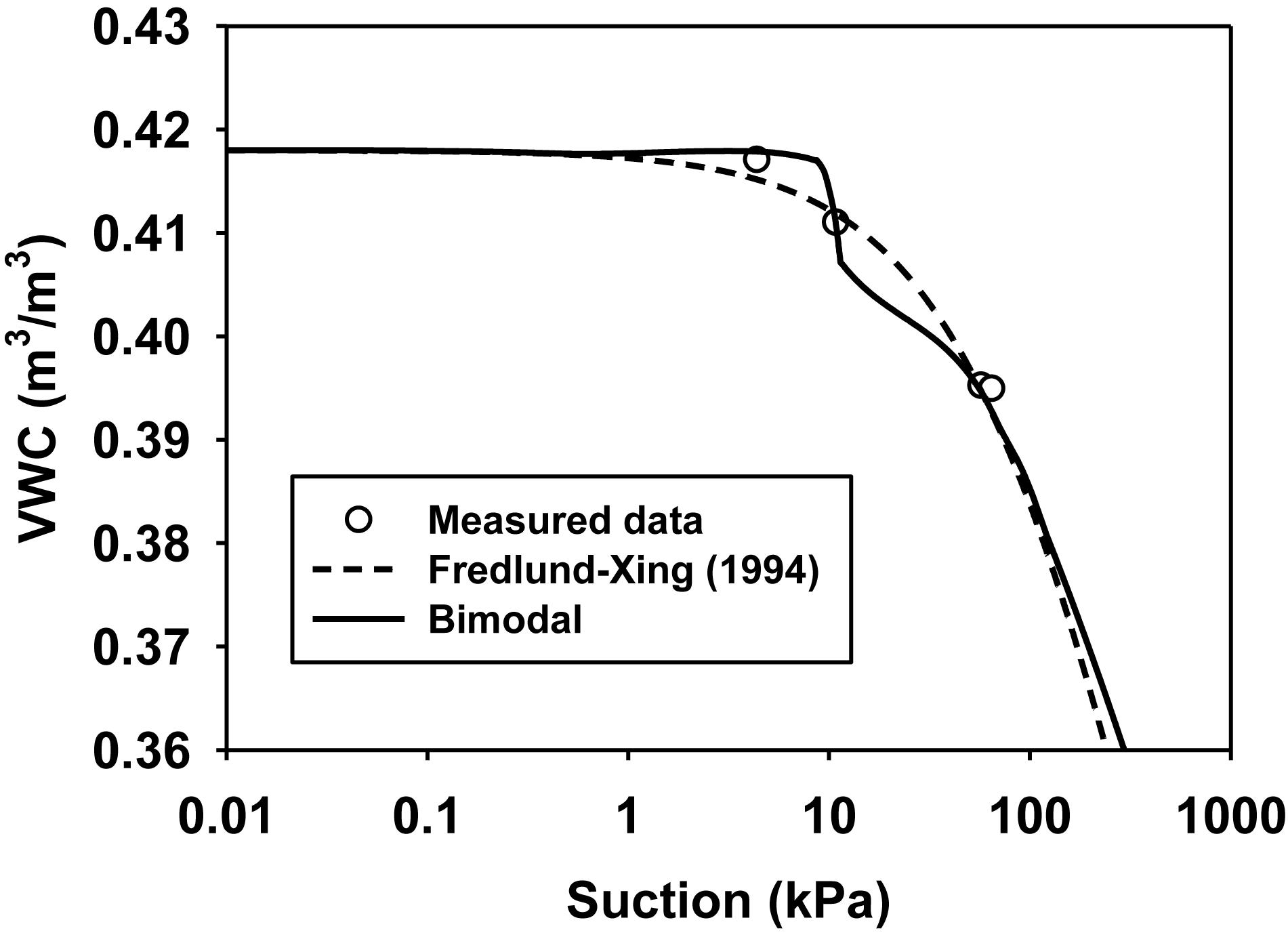
For the present work, the surficial layer of studied slope is strongly affected by wetting and drying cycles, which are likely to induce the development of cracks due to the substantial swelling and shrinking behaviors, the bimodal SWCCs are used for this surficial layer as shown in Figure 3. For unimodal SWCC, the parameters, a = 100 kPa, n = 0.888, m = 0.293, together with the saturated volumetric water content, θs = 41.8%, are used to fit the measured data of volumetric water content and suction in the field study in Zhang et al. (2010). Although there are several closed-form equations proposed very recently for Bimodal SWCC (e.g., Li et al., 2009; Fredlund et al., 2010), these functions are mostly based on the superposition of two unimodal SWCCs (e.g., Eq. 3), in which a high number of model parameters require to be determined. In this study, the bimodal SWCC is represented by the spline functions which has been built in the software to facilitate the generation of continuous curves with any shape. This is a simpler and sufficiently flexible way to describe the soil water characteristics of the complicated cracking soils’ structure.
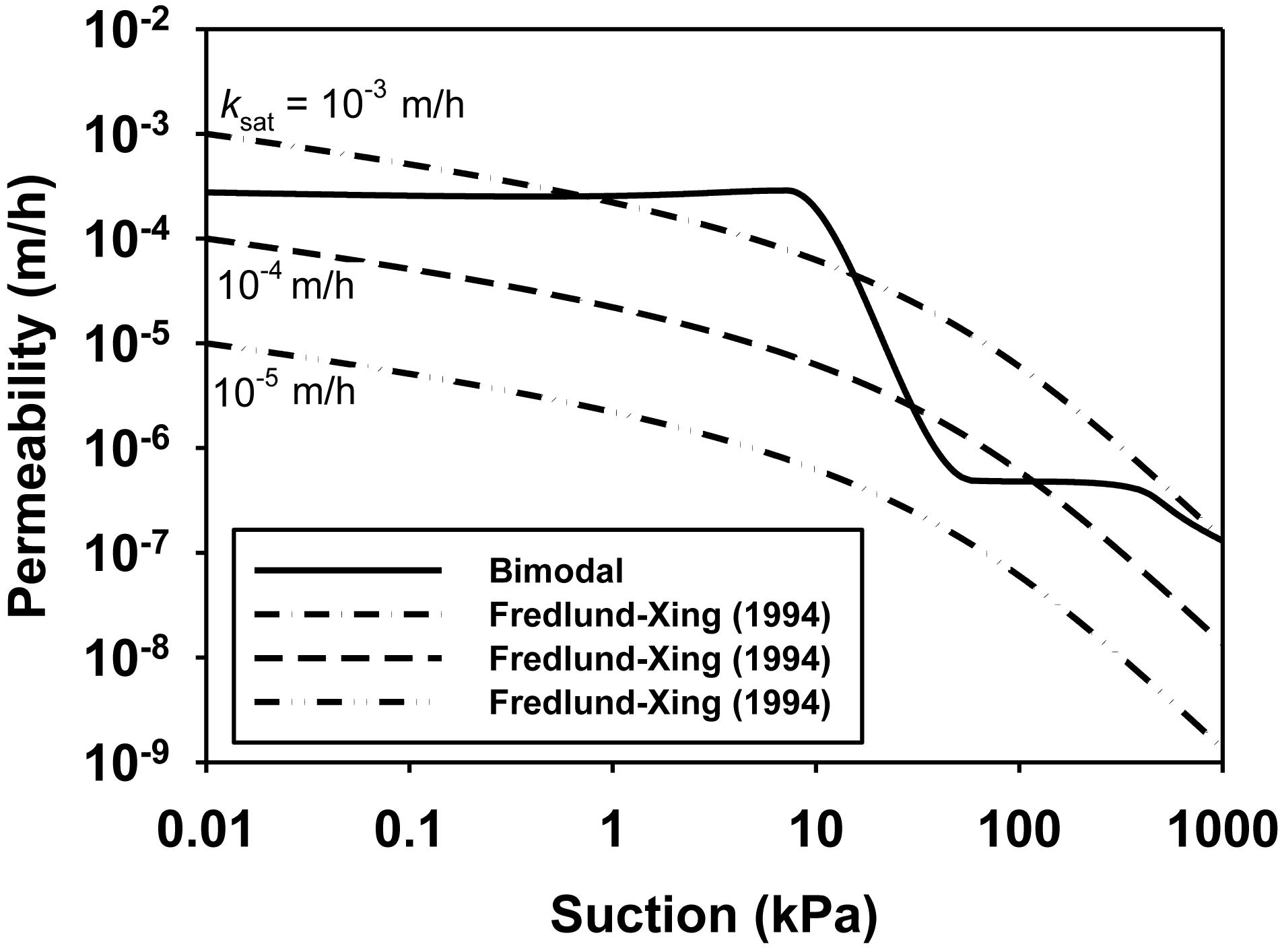
It is well known that the permeability function of an unsaturated soil bears a strong relationship to the corresponding SWCC (Leong and Rahardjo, 1997). Fredlund et al. (1994) proposed a procedure to estimate the permeability function by integrating along the SWCC. The Fredlund et al. (1994) permeability model is used to represent the unimodal permeability function in the present study, as illustrated in Figure 4. Similar to the Bimodal SWCC, i.e., the relatively simple spline function is used to describe the bimodal permeability function, which is flexible enough to follow the fundamental physics that the flow rate should be closely linked to the amount of water content transmitting movement of water itself. It should be noted that use of the measured permeability of the cracked soil sample would be desirable, However, accurate measurements often require more advanced apparatus, e.g., the large-scale infiltration column described in Chen et al. (2019) that can accommodate large samples with enough development of crack network. Due to the absence of the data, three values of saturated permeability (ksat = 10–3, 10–4, 10–5 m/h) are first used here (Figure 4), which are assumed based on the theoretical works by Li et al. (2009) and Tommasi et al. (2013) for cracked clays, and the values of similar type of cracked expansive soil measured by Zhan et al. (2007) in a field test. As will be discussed in later, a saturated permeability in the order of 10–3 to10–4 m/h is found to be able to represent the hydraulic conductivity of this cracked expansive soil, which is consistent with the findings from previous numerical study (e.g., Qi and Vanapalli, 2015a, b). Also, this assumption is considered acceptable based on numerical simulation of other earthworks including fissures subjected to rainfall (e.g., Chen et al., 2018).
The Numerical Model
A finite element-based computational model slope is established (using SEEP/W) as shown in Figure 5. The geometry of the slope is consistent with that of studied slope from Zhang et al. (2010). The model slope consists of two layers, i.e., the surficial cracked layer underlain by a relatively intact layer. According to Zhang et al. (2010), the simulated artificial rainfall had substantial influence on the hydraulic response of soils within the shallow layer, but negligible effect on that of soils below the depth of 0.8 m or deeper. This is probably attributed to the fact that cyclic drying and wetting-induced cracks only develop within the soil near the ground surface. Thus, it is assumed that the surficial cracked layer has thickness of 0.8 m for the model slope (see Figure 5). The locations of Pore Water Pressure (PWP) measurements at the depths of 0.5 and 1.0 m conducted by Zhang et al. (2010) are also indicated in Figure 5. The quadrilateral elements with vertically oriented nodes are used to discretize the surficial cracked layer for dealing with the dramatic hydraulic response to water infiltration. For the other zone (i.e., the intact layer), the mixed regular quadrilateral and triangle elements are used.
The initial hydraulic condition for the slope model is generated using spatial function according to the measured pore-water pressures just before the commencement of the artificial rainfall. A spatial function is built in SEEP/W to assist the users in setting up the initial condition accurately since the pore water pressure may distribute non-linearly or irregularly within the slope profile for most real cases. The consistent hydraulic heads are applied to both the right and left lateral boundaries during rainfall infiltration. The bottom boundary of the computational domain for water flow has a zero flux. A total of three rainfalls were simulated using the sprinkler system in the test. During the intervals of these artificial rainfalls the slope surficial layer was likely to lose water due to evaporation, which, is, however, difficult to estimate due to the absence of accurate local climate data. To reduce the possible uncertainties, the simulation is focused on the response of the slope subjected to the first rainfall, which is considered to be sufficient for the purpose of the current study. In the established model, the infiltration from first artificial rainfall is simulated using a constant influx with an intensity of 0.008 m/h for 28 h on slope ground surface without allowing any ponding.
Numerical Results
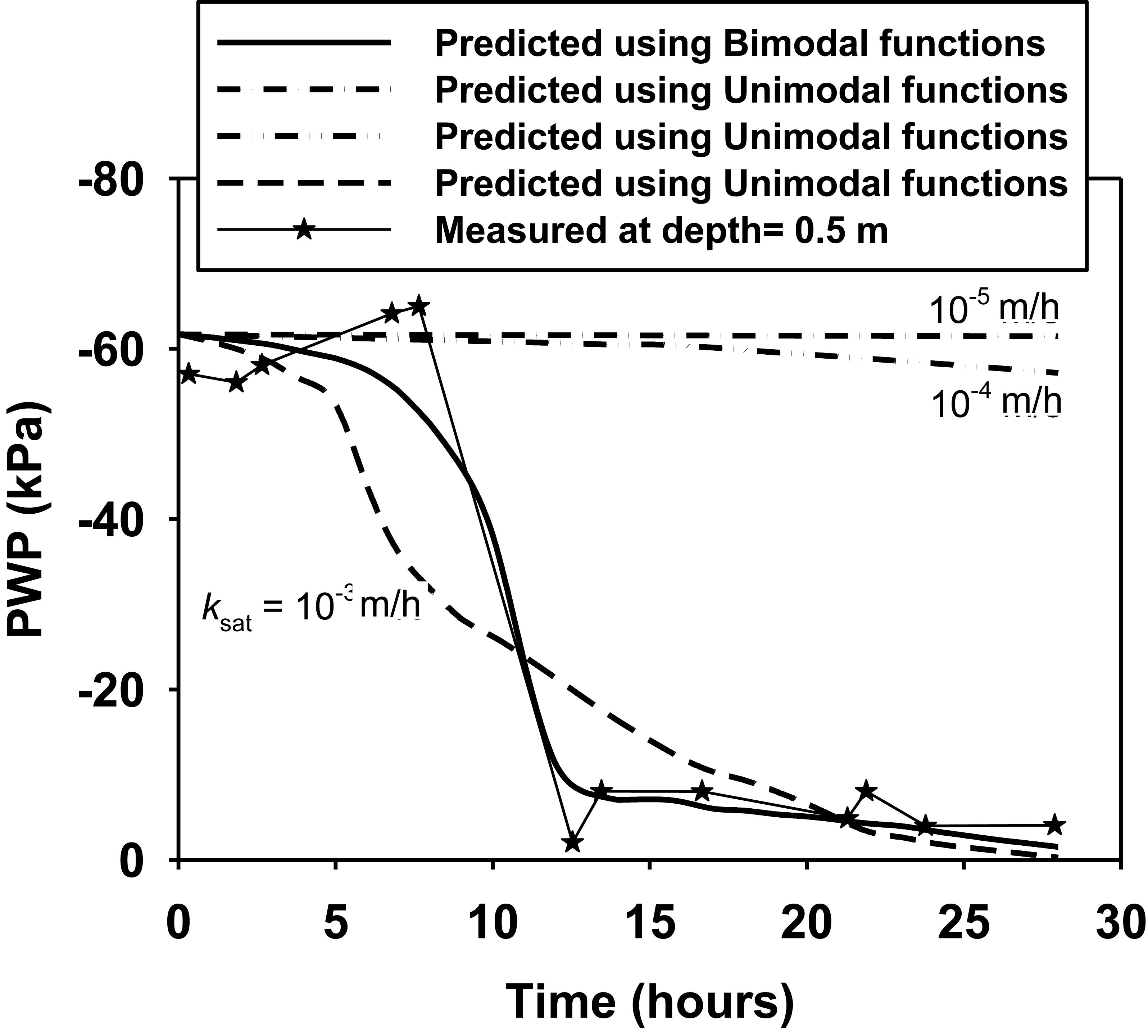
Figure 6 compares the time history of PWPs predicted using seepage analysis within measured values at the depth of 0.5 m near ground surface. It indicates that there is a rapid drop in the measured suction (i.e., negative PWP) from around 60 kPa at the seventh hour to less than 10 kPa at the around 12th hour. After that, the suction at the depth of 0.5 m remains almost constant. As explained by Zhang et al. (2010), the hydraulic regime near the ground surface was greatly affected by the artificial rainfall, since the presence of cracks at this layer provides pathways for preferential flow. For numerical simulation using unimodal SWCC and permeability function, slight decreases in the suction are observed when the relatively lower saturated permeability (i.e., 10–4 or 10–5 m/h) is used, which do not match the measured values. When the saturated coefficient of permeability is increased to 10–3 m/h, the predicted suction gradually decreases with respect to time. However, the discrepancy between the predictions and measurements is still apparent. Specifically, the model overpredicts the rate of suction loss (rate of pore water pressure increases) over the initial 12 h of the test, while underpredicts the rate of suction loss thereafter in comparison to the measurements, it is difficult for the unimodal model (for relatively uniform soil matrix without cracks) to simulate the sharp drop of the suction around 12 h after the commencement of the test. When the bimodal hydraulic properties (as shown in Figures 3, 4) are used, a good match is obtained between predicted and measured suction values. In other words, the dramatic decrease in the suction value at the depth of 0.5 m is successfully reproduced in the numerical simulation by using the bimodal hydraulic properties.
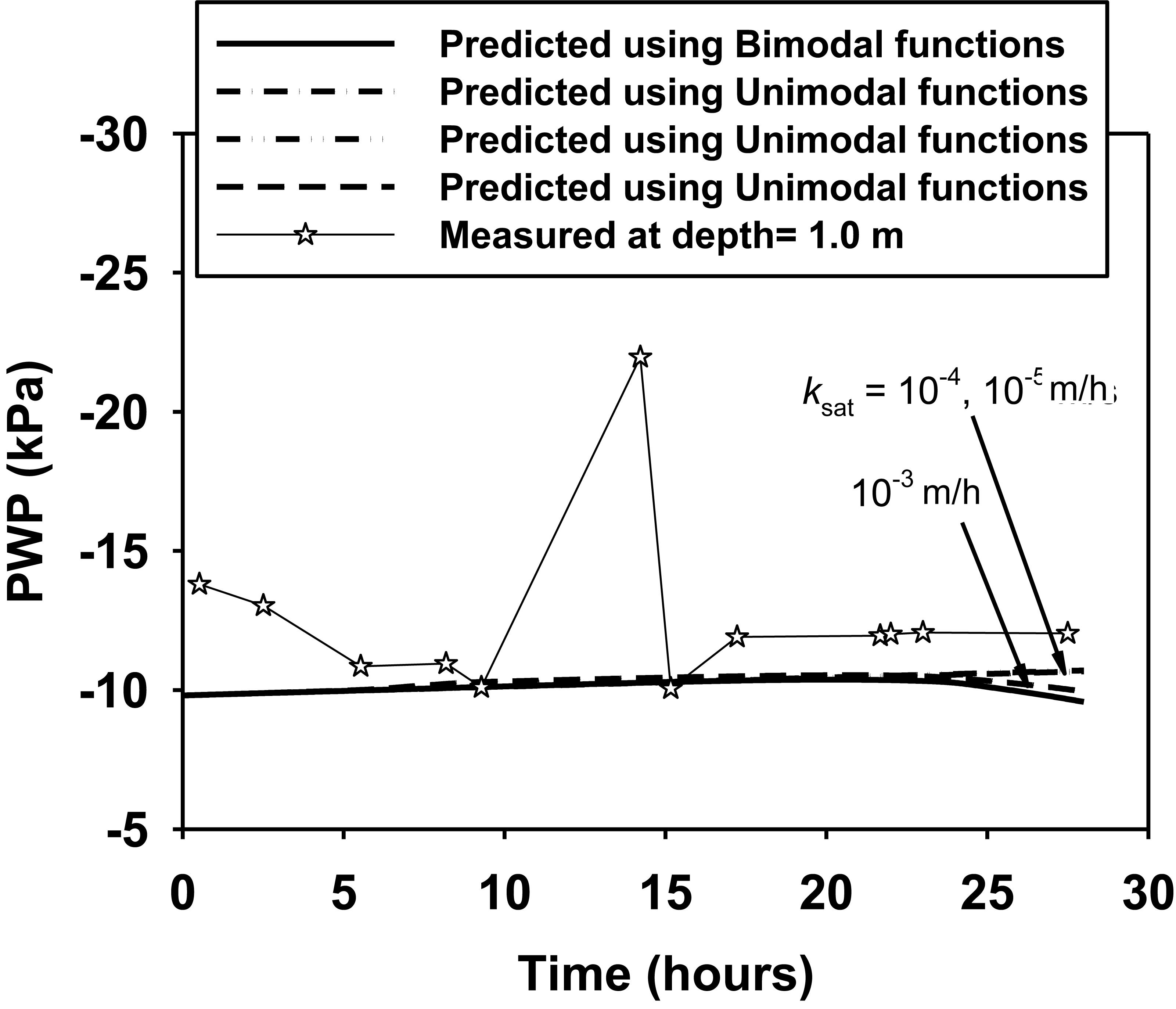
Figure 7 compares the time history of PWPs predicted using seepage analysis within measured values at the depth of 1.0 m near ground surface. It can be seen that the measured value of suction (negative PWPs) remains essentially at around 10 kPa. The PWP at this depth is not significantly affected by the rainfall, since the cracks were not developed at deeper depth as suggested by Zhang et al. (2010). For all numerical simulation, when the unimodal SWCC and permeability function (as shown in Figures 3, 4) with a lower saturated coefficient of permeability (10–5 m/h) for the intact layer are used, the predicted PWPs remain constant and show good agreements with the measured values, independent of the hydraulic properties assigned to the surficial cracked layer. Negligible decrease in the suction at the depth of 1.0 m is, therefore, attributed to the low permeability of intact layer. Figure 8 compares the variations of predicted depth profiles of PWP between unimodal and bimodal functions. It is seen that the profiles of PWP from Bimodal functions show sharper transitions (e.g., the wetting fronts from unsaturated to saturated conditions) over the depth than those from unimodal functions, which is consistent with the fast drop in suction at the depth of 0.5 m shown in Figure 6. Further, the more evident wetting front (from bimodal functions in Figure 8B) and its advancement over time are important indications for the location of critical slip surface for shallow slope failures.
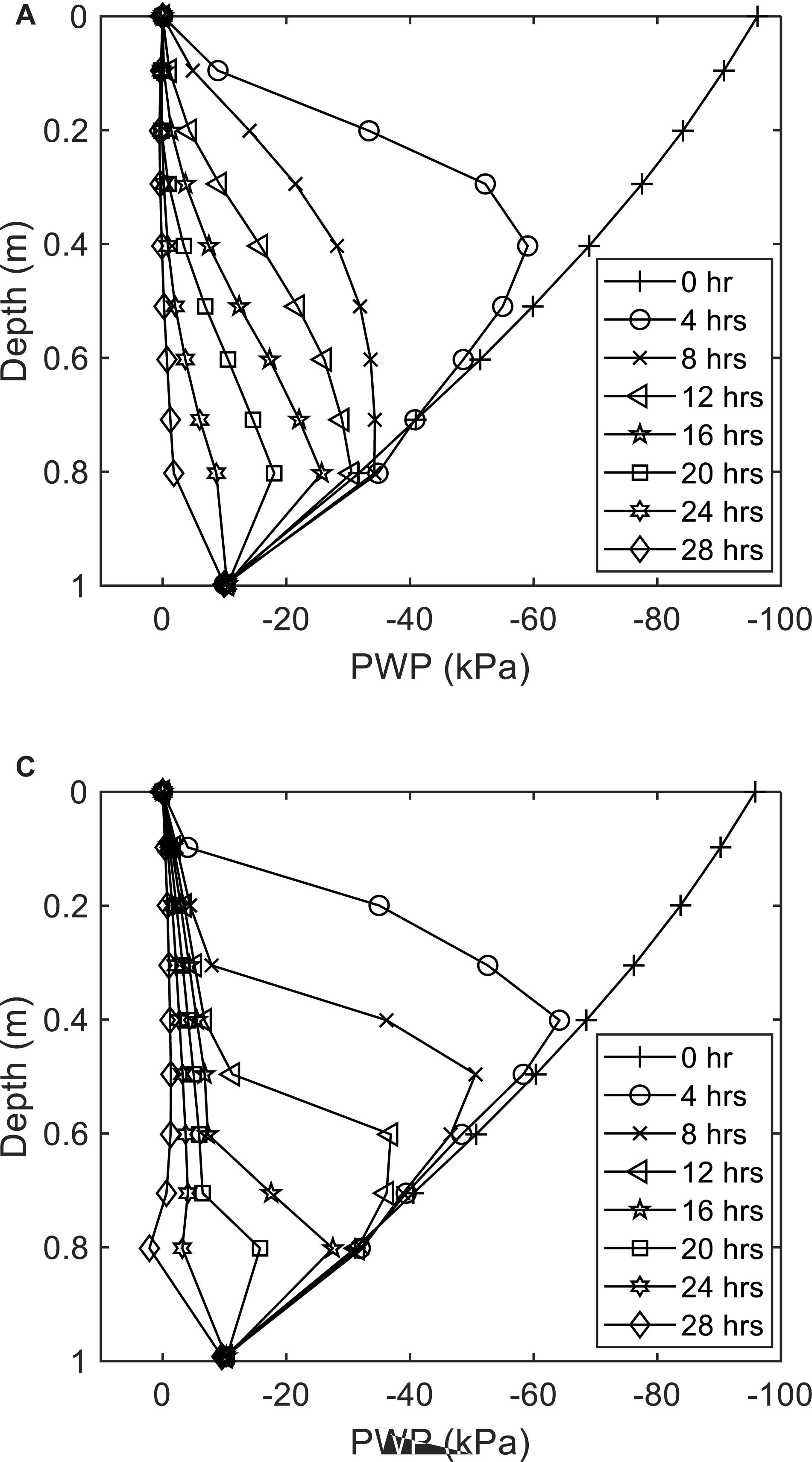
Figure 8. The predicted variation of pore water pressure profiles with: (A) unimodal functions with ksat = 10–3 m/h; and (B) bimodal functions.
Figures 9, 10 compare the time histories of volumetric water contents predicted using seepage analysis within measured values at the depth of 0.5 and 1.0 m, respectively. Similar to the pore water pressures, the numerical simulation with bimodal hydraulic functions outperforms that with unimodal hydraulic functions (saturated permeability = 10–3 m/h) in reproducing the measured volumetric water content variation, particularly, the dramatic (sharp) rise at relatively shallow depth (i.e., 0.5 m). Meanwhile, insignificant hydraulic responses (water content variations) are simulated at greater depth (1.0 m), which is consistent with both the predicted suction and the measurement. Thus, with a low permeability (10–5 m/h) the intact layer in all numerical analyses only acts as a relatively impermeable boundary for the domain of interest, i.e., the surficial layer, of which the stability is the major concern as discussed in the following section.
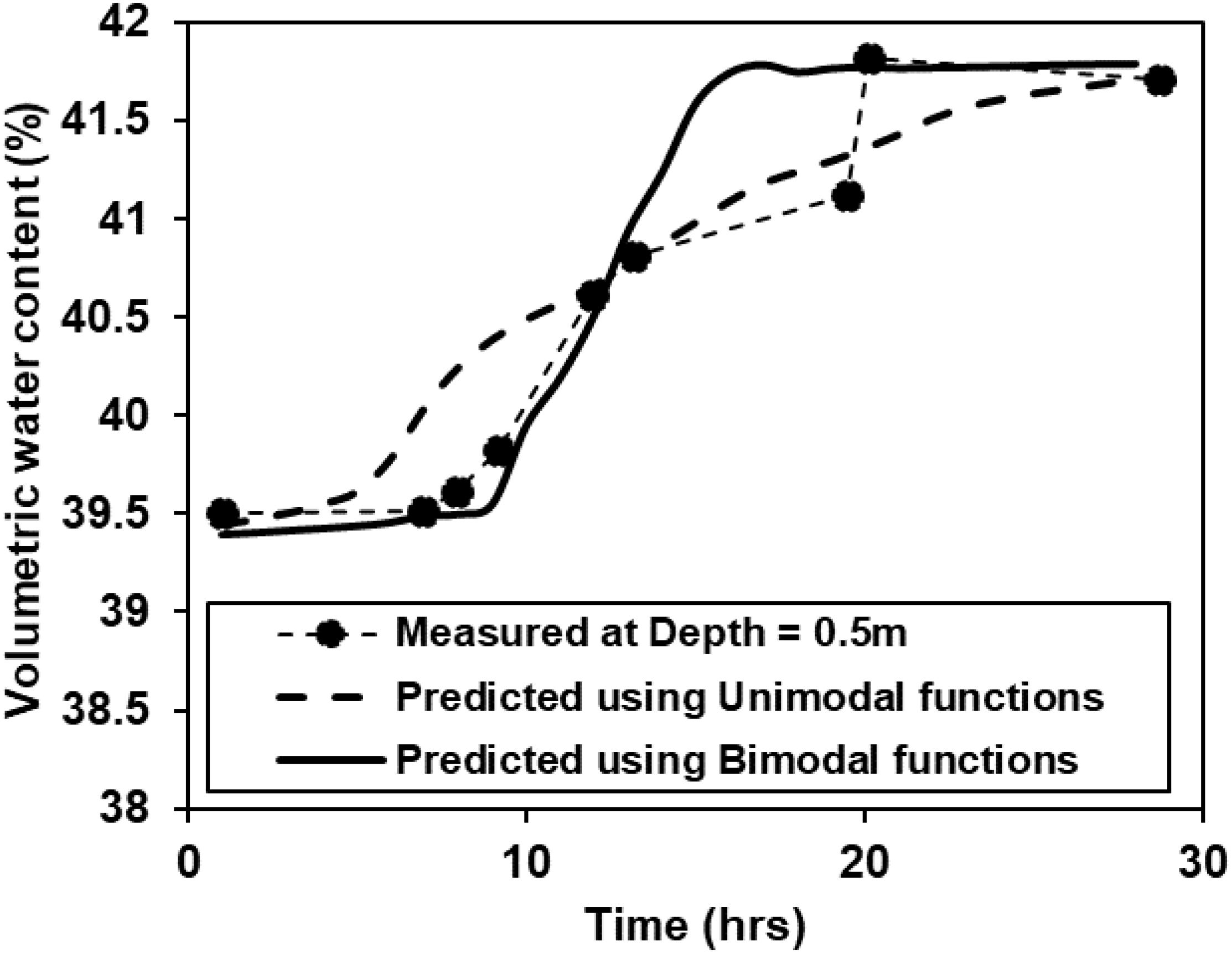
Figure 9. Comparison between measured and predicted (ksat = 10–3 m/h for unimodal function) volumetric water content at the depth of 0.5 m.
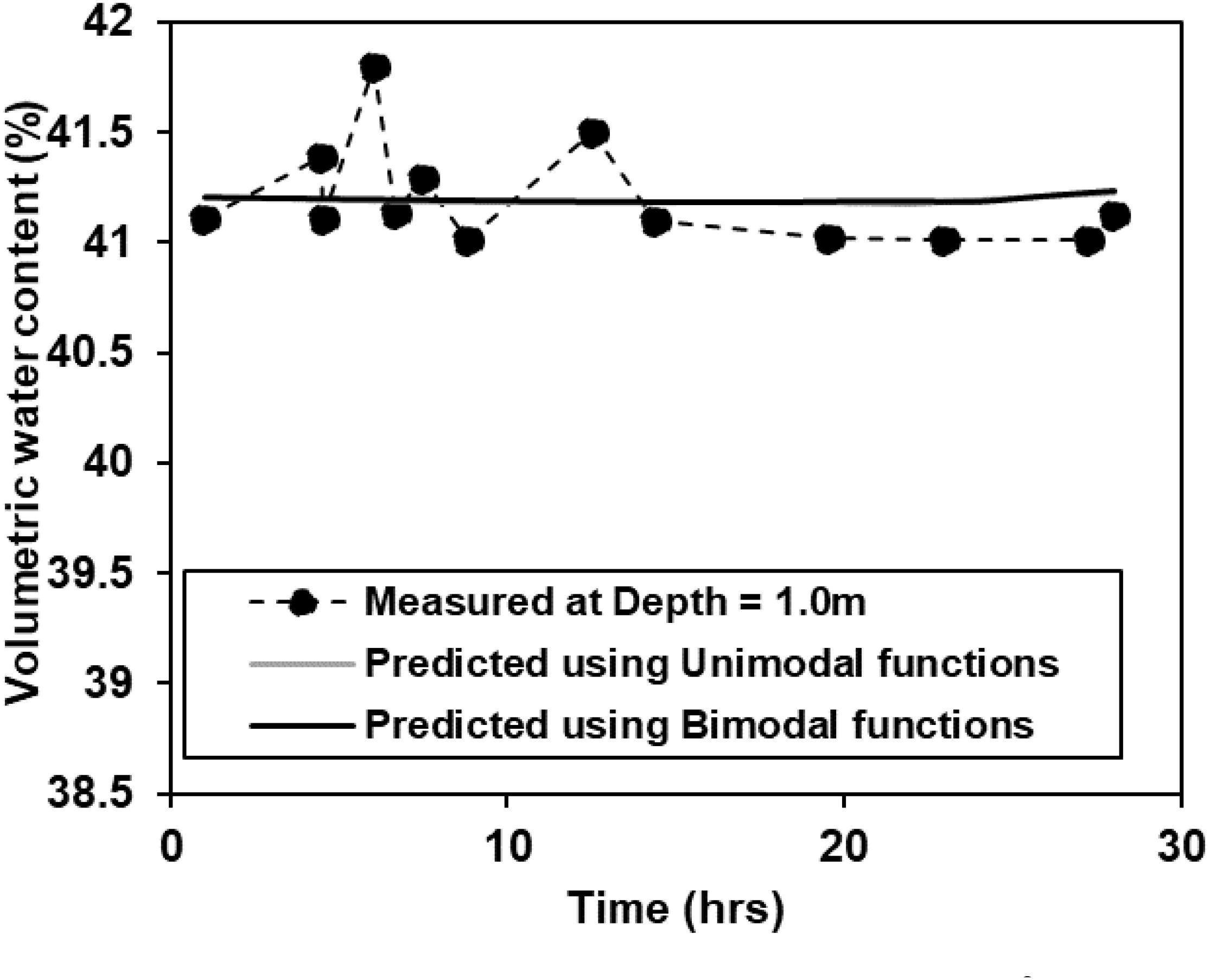
Figure 10. Comparison between measured and predicted (ksat = 10–3 m/h for unimodal function) volumetric water content at the depth of 1.0 m.
Slope Stability Analysis
Method for Calculating FS
Deterministic methods are widely used for analysis of slope stability with a scalar, called factor of safety (FS), being calculated and used as an indication/index for the stability of the slope. There are dozens of methods proposed in the literature for determining the FS. These methods generally fall into the following categories according to different theories; namely: (i) the limit equilibrium methods based on rigid block equilibrium analysis; (ii) the limit analysis methods based on upper bound plasticity theorem; (iii) finite element stress based method; (iv)finite element strength reduction method; and (v) finite element gravity increase method [e.g., in Chen and Lin (2019)]. Among all these methods, the limit equilibrium methods are most preferable for practical applications due to its long history as well as simplicity.
There are several commonly used variants of limit equilibrium methods in the literature, such as the Bishop’s simplified method (Bishop, 1955) satisfying only the moment equilibrium of failure mass, the Janbu’s simplified method (Janbu, 1954) satisfying only the force equilibrium, and the Morgenstern-Price Method (Morgenstern and Price, 1965) satisfying both the force and moment equilibrium conditions. Although the methods that satisfy both equilibrium conditions appear to be able to provide the most reliable FS, especially for slopes with complicated geometry, they, however, may encounter numerical non-convergence problems in some cases. In the present study, the slip surface detected in the field study by Zhang et al. (2010) is well defined and relative shallow, which categorizes this slope slide into a typical translational type. To capture this well-defined translational sliding mode, the position of the slip surface is fixed to be consistent with pre-detected one in this field thought use of the “Fully Specified Slip Surface” option. For translational type of slope failure, the Janbu’s simplified method (Janbu, 1954) is able to produce a satisfactory result, and is, therefore, used here to calculate the FS.
For saturated soils, the basic procedure and formulation of Janbu’s simplified method can be found elsewhere and are not detailed here. It should be noted that, for unsaturated soils, the shear strength contribution due to suction requires to be considered in the slope stability analysis formulation. The semi-empirical model proposed by Vanapalli et al. (1996) (Eq. 4) has been widely used by both the researchers and practitioners, which quantifies the non-linear behavior of shear strength of unsaturated soil using the saturated effective shear strength parameters and the SWCC as a tool.
where, c′ is effective cohesion, ϕ′ is effective internal friction angle, s is normal stress acting on the slip surface, θw is volumetric water content, θs and θr are saturated and residual volumetric water content, respectively. By replacing the c′ by ca = (c′ + (ua −uw)(θw − θr)/(θs − θr) tanϕ′) in the formulations of slope stability analysis for saturated soils, all the existing limit equilibrium methods, including the Janbu’s simplified method used in this study, can be used to evaluate the slope stability for unsaturated soils.
Factor of Safety Results
Calculation of FS variation over time is performed using SLOPE/W (Geo-Slope International Ltd., 2007b). The hydraulic response under the rainfall condition predicted using SEEP/W can be directly incorporated into SLOPE/W for stability analysis. We only used here the results of seepage analysis with bimodal hydraulic properties and unimodal hydraulic properties with the saturated permeability of 10–3 m/h. By using the semi-empirical model for shear strength of unsaturated soils (Vanapalli et al., 1996), the input parameters only include the saturated cohesion and effective internal frictional angle. It should be noted that the cracking has a significant effect on the shear resistance behavior of the expansive soils from a number of laboratory tests on samples under various conditions. The values c′ = 5 kPa and ϕ′ = 17° suggested by Liu (1997) for cracked expansive soils with basic soil properties similar to those of soils in this study is first used for the stability analysis. The variation of FS with respect to time is shown in Figure 11. It can be seen that the FS calculated using the bimodal hydraulic properties is initially higher than that based on unimodal hydraulic properties (saturated permeability = 10–3 m/h). However, the FS based on bimodal hydraulic properties decreases in a faster rate and becomes lower than that based on unimodal hydraulic properties after the 15th day. This phenomenon is generally consistent with that observed in the suction variations over time illustrated in Figure 12, which compares the variations of suctions predicted using the bimodal and unimodal hydraulic properties at two points (see Figure 1 for their positions, identified by red circles) along the slip surface. The relatively large drop in the predicted suction at upper part (e.g., point A in Figure 1) is believed to be mainly responsible for the initiation and development of the slip surface, where a collapse with several cracks were observed in the field (Zhang et al., 2010).
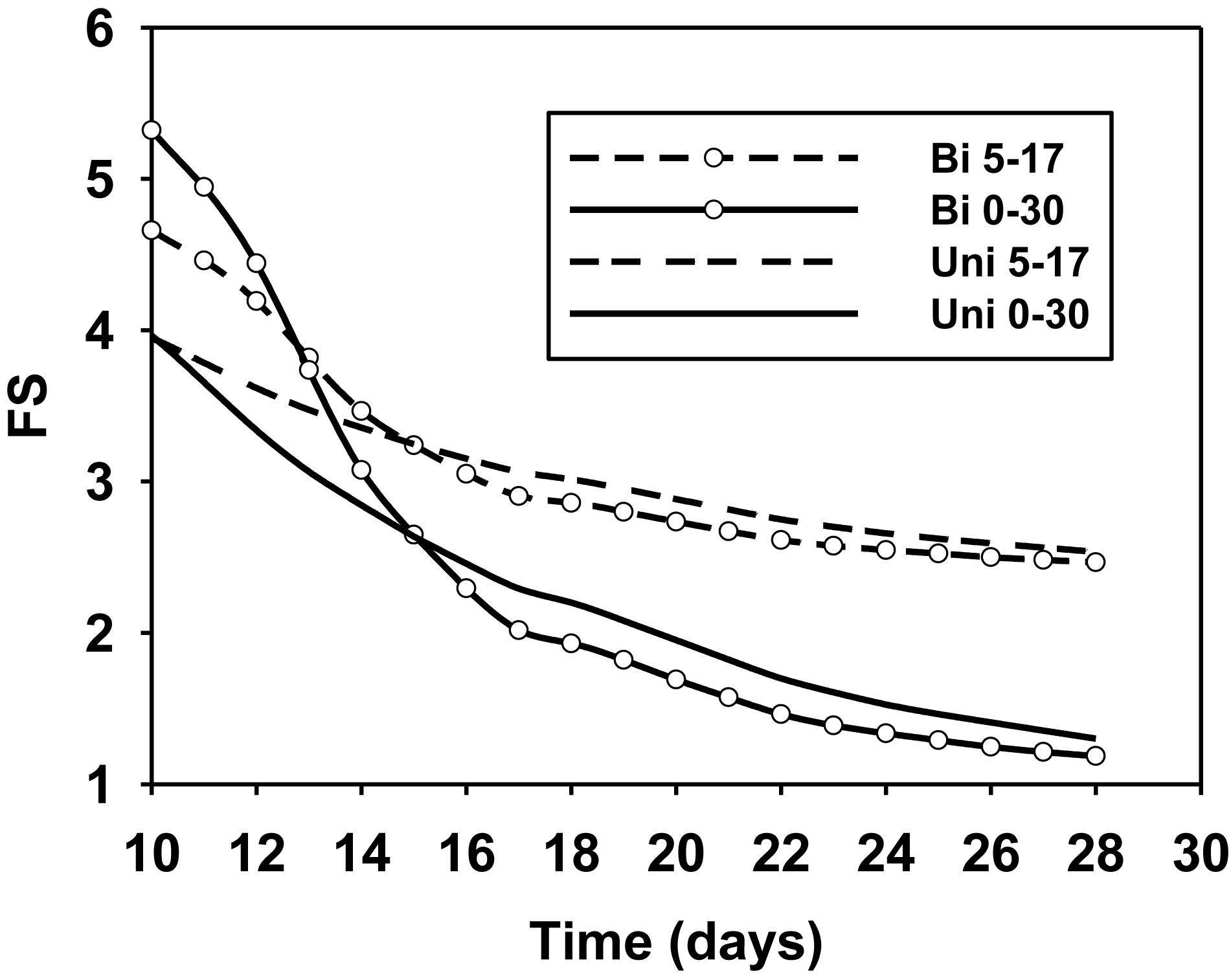
Figure 11. Factors of safety using the bimodal and unimodal hydraulic properties, where, the “Bi” and “Uni” represent the Bimodal and Unimodal functions, respectively, the following pair of numbers represent the values of cohesion (kPa) and internal friction angle (°), respectively.
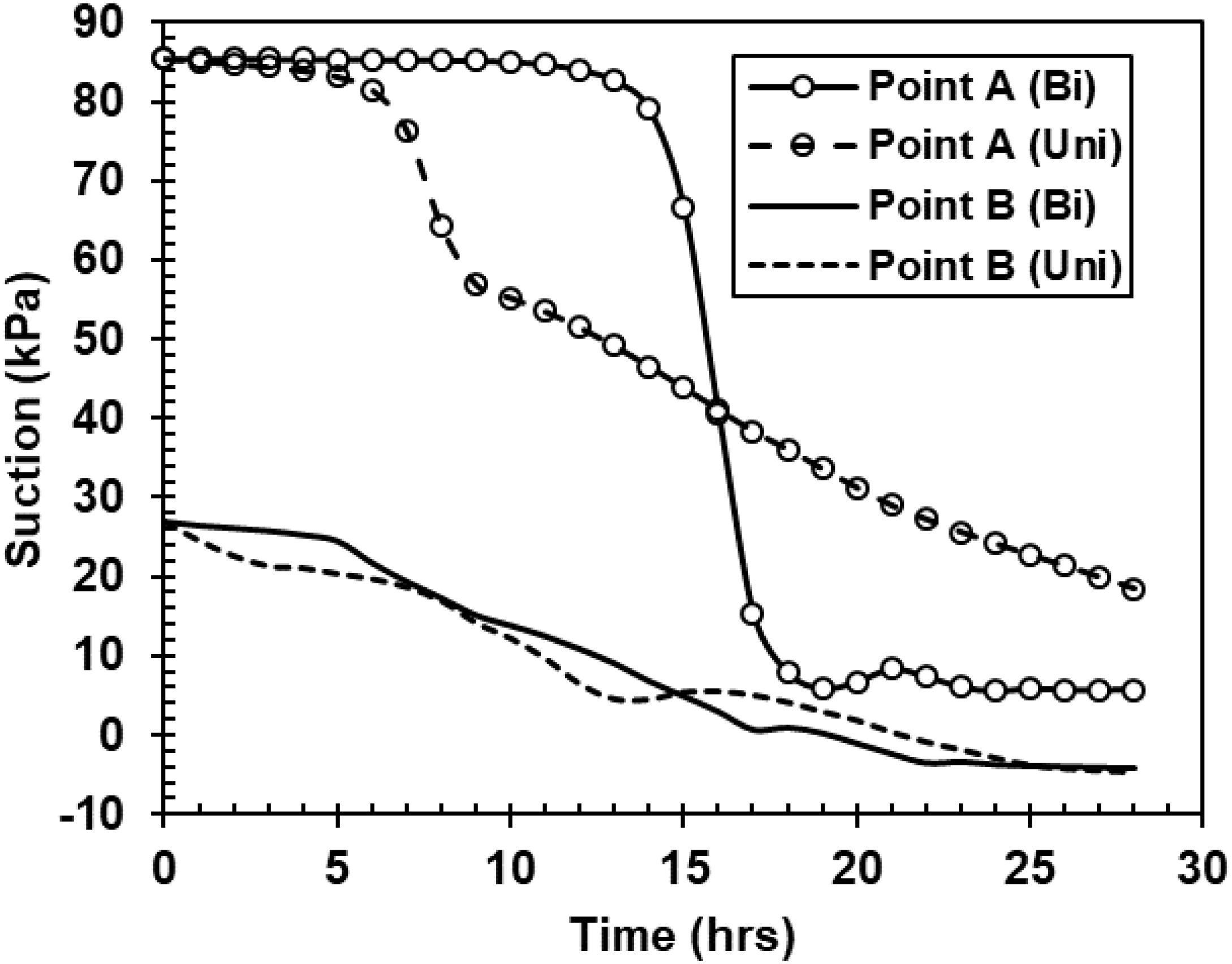
Figure 12. Variations of suctions predicted using the bimodal and unimodal hydraulic properties at two points along the slip surface, where, the “Bi” and “Uni” represent the Bimodal and Unimodal functions, respectively.
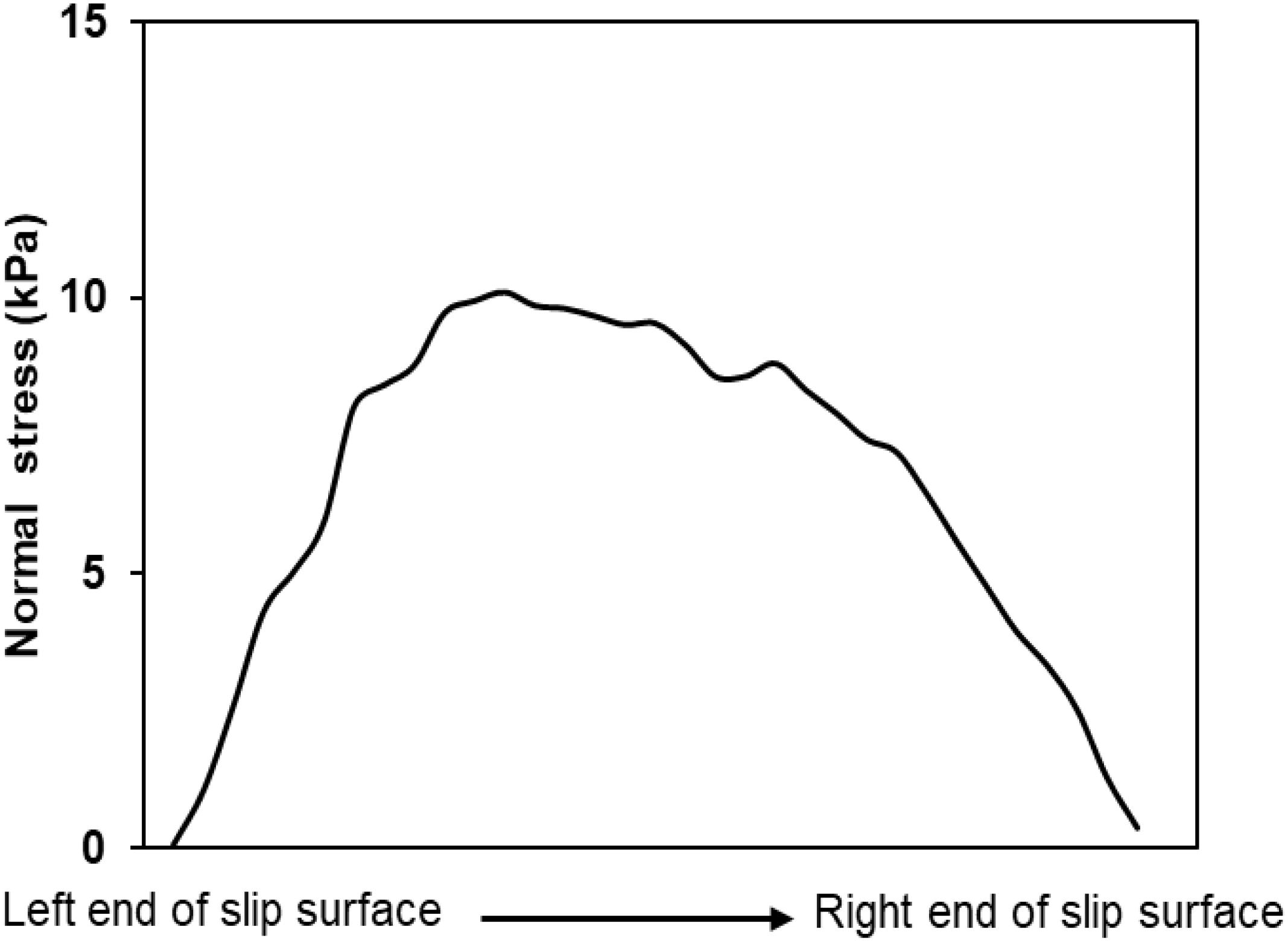
The FS calculated with c′ = 5 kPa and ϕ′ = 17° at the end of rainfall condition is around 2.8, indicating a fairly stable condition. This value cannot reflect the actual condition that some sliding displacements occurred, although an entire collapse was not observed (Zhang et al., 2010). A number of back-analyses of slope failures conducted previously in expansive soils areas indicated that the shear strength parameters mobilized in the field conditions were significantly lower than those measured in the laboratory (Day, 1994; Liu, 1997), it is therefore suggested a simple reduction of the strength parameters should be made for relevant engineering designs. For example, the c′ = 2 kPa (based on back-analysis) reduced from c′ = 20 kPa (from triaxial test) was used in the final design of an excavated slope consisting of yellow-brown cracked expansive soils in the project of SNWT (Liu, 1997). However, some researchers (e.g., Lade, 2010) believed that the relatively low mobilized values are linked to the low confining stress conditions (lower than those in most laboratory tests) from the theoretical point of view, i.e., the non-linear shear strength Mohr-Coulomb model should be more appropriate for soils in the shallow layer. It has, therefore, been argued that the shear strength parameters for shallow slope stability analysis should be determined from the specimens under low confining stress conditions considering the actual ground condition, under which a non-linear or bi-linear strength model with zero or extremely low cohesion may provide better fit to the measured shear strength data. For the case considered in the present study, the slip surface is quite shallow, over which the maximum normal stress is estimated to be around 10 kPa (see Figure 13). Thus, the strength parameters, c′ = 0 kPa and ϕ′ = 30° as representative values at low confining stress condition are used to repeat the FS calculation based on the same hydraulic simulation outlined above. Figure 14 shows graphically the magnitudes of mobilized shear strength that can been overestimated by using the shear strength parameters measured at relatively high confining stresses. It is also illustrated that the non-linear strength envelope can better describe the real available shear strength over both low and high confining stress levels (Lade, 2010). With the adopted simple approximation, the calculated FS are also compared with the previously obtained results in Figure 11. At the end of rainfall period, the FSs based on both bimodal and unimodal hydraulic properties decrease to values slight larger than one, which may better reflect the field observation by Zhang et al. (2010).
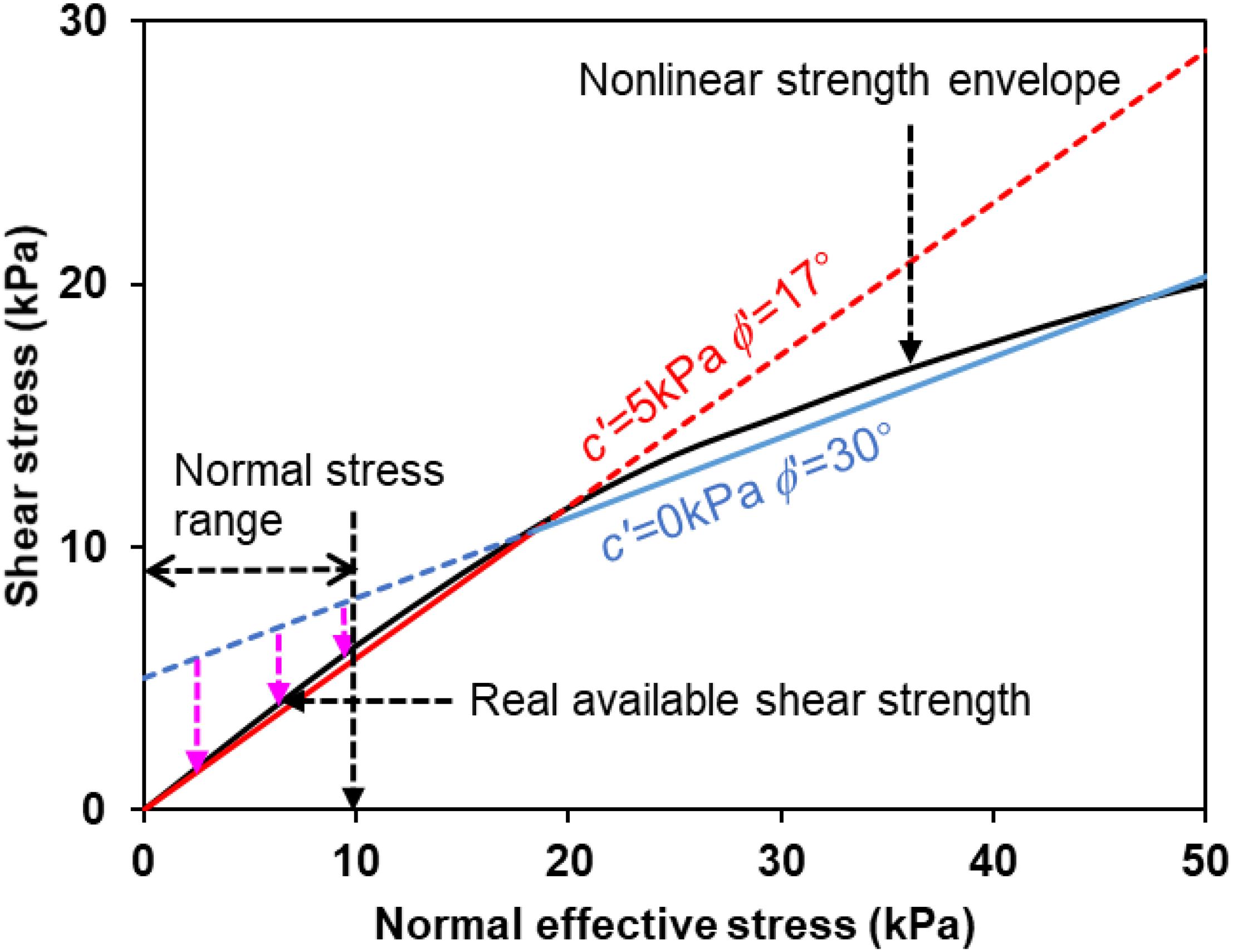
Figure 14. Illustration of the non-linear behavior of mobilized shear strength at low confining stress level.
Conclusion
The response of an expansive soil slope to an artificial rainfall infiltration in the in situ study conducted by Zhang et al. (2010) is numerically simulated in the present study. The hydraulic behavior within the slope profile is reproduced using the Finite Element Method-based software SEEP/W, while the slope stability analysis is carried out using the Limit Equilibrium Method-based software SLOPE/W. In the hydraulic analysis, effort is put into selecting the proper SWCC and permeability functions to represent the effect of cracks, i.e., the influence of mechanical cracking on the hydraulic (e.g., the water content variation) response in the shallow layer is considered from this perspective. In the slope stability analysis, the simplified Janbu’s method is selected to calculate the FS variation over time along a prescribed slip surface according to field study. The effects of the reduction of shear resistance, due to wetting and suction loss, are considered by coupling the strength model at local level to the SWCC, and by incorporating the flow regime at the global level calculated from the seepage analysis. These aspects of the coupling involved in expansive soils slope are investigated with the focus on adoption of highly non-linear hydraulic models, and their influence on evolutions of both the flow regime and shear strength field in the slope profile. The following conclusions can be derived from the results presented in this paper:
1. The cracks can significantly increase the permeability of surficial layer. However, it is difficult to reproduce the measured time history of pore water pressure at shallow depth using the unimodal SWCC and the related coefficient of permeability.
2. The dramatic decrease over time in the suction at the shallow depth is successfully predicted by using the bimodal SWCC and permeability function. This indicates bimodal SWCC and permeability function can better account for the effect of cracks on the hydraulic behavior of surficial layer.
3. The FSs calculated based on bimodal hydraulic properties are initially higher, but become lower, than those based on unimodal hydraulic properties, i.e., The Bimodal functions provide a better match between the prediction and field data. This phenomenon is consistent with suctions and water contents predicted from Finite Element Analysis.
4. Selection of appropriate shear strength parameters from laboratory tests under low confining stress conditions is required for the slope stability analysis of shallow layer in expansive soils during rainfall period.
Data Availability Statement
All datasets generated for this study are included in the article/supplementary material.
Author Contributions
RY conceived the conceptual framework. PX and SQ conducted the numerical analysis, analyzed the data, and wrote the manuscript.
Funding
The authors gratefully acknowledge the support from the National Key Research and Development Program of China (2018YFC1508601 and 2017YFC1501102) and the National Natural Science Foundation of China (51909182). This work was also supported by the Funds for Double First-Class University Plan for Sichuan University and by the Fundamental Research Funds for the Central Universities.
Conflict of Interest
RY and PX were employed by China Energy Investment Corporation (China Energy) Co., Ltd. PX was also employed by Dadu River Hydropower Development Co., Ltd.
The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Alonso, E. E., Gens, A., and Delahaye, C. H. (2003). Influence of rainfall on the deformation and stability of a slope in over consolidated clays: a case study. Hydrogeol. J. 11, 174–192.
Azam, S., and Ito, M. (2011). “Unsaturated soil properties of a fissured expansive clay,” in Proceedings of the 14th Pan-American Conference on Soil Mechanics and Geotechnical Engineering, Regina, SK.
Bao, C. G., and Ng, C. W. W. (2000). “Some thoughts and studies on the prediction of slope stability in expansive soils in unsaturated soils for Asia,” in Proceedings of the Asian Conference on Unsaturated Soils, UNSAT-ASIA 2000 (Singapore: AA Balkema).
Bishop, A. W. (1955). The use of the slip circle in the stability analysis of slopes. Géotechnique 5, 7–17. doi: 10.1680/geot.1955.5.1.7
Chen, R. P., Qi, S., Wang, H. L., and Cui, Y. J. (2019). Microstructure and hydraulic properties of coarse-grained subgrade soil used in high-speed railway at various compaction degrees. J. Mater. Civil Eng. 31:04019301. doi: 10.1061/(asce)mt.1943-5533.0002972
Chen, R. P., Wang, H. L., Hong, P. Y., Cui, Y. J., Qi, S., and Cheng, W. (2018). Effects of degree of compaction and fines content of the subgrade bottom layer on moisture migration in the substructure of high-speed railways. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 232, 1197–1210. doi: 10.1177/0954409717710838
Chen, Y. F., and Lin, H. (2019). Consistency analysis of hoek-brown and equivalent mohr-coulomb parameters in calculating slope safety factor. Bull. Eng. Geol. Environ. 78, 4349–4361. doi: 10.1007/s10064-018-1418-z
Cheng, Z. L., Li, Q. Y., Guo, X. L., and Gong, B. W. (2011). Study on the stability of expansive soil slope. J. Yangtze River Sci. Res. Inst. 28, 102–111.
Day, R. W. (1994). Surficial stability of compacted clay: case study. J. Geotech. Eng. 120, 1980–1990. doi: 10.1061/(asce)0733-9410(1994)120:11(1980)
Elkady, T. Y. (2014). Unsaturated characteristics of undisturbed expansive shale from Saudi Arabia. Arab. J. Geosci. 7, 2031–2040. doi: 10.1007/s12517-013-0915-4
Fredlund, D. G., Houston, S. L., Nguyen, Q., and Fredlund, M. D. (2010). Moisture movement through cracked clay soil profiles. Geotech. Geol. Eng. 28, 865–888. doi: 10.1007/s10706-010-9349-x
Fredlund, D. G., and Rahardjo, H. (1993). Soil Mechanics for Unsaturated Soils. Hoboken, NJ: John Wiley and Sons.
Fredlund, D. G., and Xing, A. (1994). Equations for the soil-water characteristic curve. Can. Geotech. J. 31, 521–532. doi: 10.1139/t94-061
Fredlund, D. G., Xing, A., and Huang, S. (1994). Predicting the permeability function for unsaturated soils using the soil-water characteristic curve. Can. Geotech. J. 31, 533–546. doi: 10.1139/t94-062
Geo-Slope International Ltd., (2007a). Seep/W Users Guide for Finite Element Seepage Analysis. Calgary: GEO-SLOPE International Ltd.
Geo-Slope International Ltd., (2007b) Slope/W User’s Guide for Slope Stability Analysis. Calgary: GEO-SLOPE International Ltd.
Hamdhan, I. N., and Schweiger, H. F. (2012). Finite element method–based analysis of an unsaturated soil slope subjected to rainfall infiltration. Int. J. Geomech. 13, 653–658. doi: 10.1061/(asce)gm.1943-5622.0000239
Janbu, N. (1954). Application of composite slip surfaces for stability analysis. InProc. European Conf. on Stability of Earth Slopes. Stockholm 3, 43–49.
Lade, P. V. (2010). The mechanics of surficial failure in soil slopes. Engineering Geology 114, 57–64. doi: 10.1016/j.enggeo.2010.04.003
Leong, E. C., and Rahardjo, H. (1997). Review of soil-water characteristic curve equations. J. Geotech. Geoenviron. Eng. 123, 1106–1117 doi: 10.1061/(asce)1090-0241(1997)123:12(1106)
Li, J. H., Zhang, L. M., and Li, X. (2011). Soil-water characteristic curve and permeability function for unsaturated cracked soil. Can. Geotech. J. 48, 1010–1031. doi: 10.1139/t11-027
Li, J. H., Zhang, L. M., Wang, Y., and Fredlund, D. G. (2009). Permeability tensor and representative elementary volume of saturated cracked soil. Can. Geotech. J. 46, 928–942. doi: 10.1139/t09-037
Lin, H., Xie, S. J., Yong, R., Chen, Y. F., and Du, S. G. (2019). An empirical statistical constitutive relationship for rock joint shearing considering scale effect. C. R. Mec. 347, 561–575. doi: 10.1016/j.crme.2019.08.001
Liu, T. H. (1997). Problems of Expansive Soils in Engineering Construction. Beijing: Architecture and Building Press of China.
Morgenstern, N. R., and Price, V. E. (1965). The analysis of the stability of general slip surfaces. Géotechnique 15, 79–93. doi: 10.1680/geot.1965.15.1.79
Ng, C. W. W., Zhan, L. T., Bao, C. G., Fredlund, D. G., and Gong, B. W. (2003). Performance of an unsaturated expansive soil slope subjected to artificial rainfall infiltration. Géotechnique 53, 143–157. doi: 10.1680/geot.53.2.143.37272
Oh, W. T., and Vanapalli, S. K. (2010). Influence of rain infiltration on the stability of compacted soil slopes. Comput. Geotech. 37, 649–657. doi: 10.1016/j.compgeo.2010.04.003
Qi, S. C., and Vanapalli, S. K. (2015a). Hydro-mechanical coupling effect on surficial layer stability of unsaturated expansive soil slopes. Comput. Geotech. 70, 68–82. doi: 10.1016/j.compgeo.2015.07.006
Qi, S. C., and Vanapalli, S. K. (2015b). Stability analysis of an expansive clay slope: a case study of infiltration induced shallow failure of an embankment in Regina, Canada. Int. J. Geohazards Environ. 1, 7–19. doi: 10.15273/ijge.2015.01.003
Qi, S. C., and Vanapalli, S. K. (2016). Influence of swelling behavior on the stability of an infinite unsaturated expansive soil slope. Comput. Geotech. 76, 154–169. doi: 10.1016/j.compgeo.2016.02.018
Rouainia, M., Davies, O., O’Brien, T., and Glendinning, S. (2009). Numerical modelling of climate effects on slope stability. Proc. ICE Eng. Sustain. 162, 81–89.
Srivastava, R., and Yeh, T. C. J. (1991). Analytical solutions for one-dimensional, transient infiltration toward the water table in homogeneous and layered soils. Water Resour. Res. 27, 753–762. doi: 10.1029/90wr02772
Tommasi, P., Boldini, D., Caldarini, G., and Coli, N. (2013). Influence of infiltration on the periodic re-activation of slow movements in an overconsolidatedclayslope. Can. Geotech. J. 50, 54–67. doi: 10.1139/cgj-2012-0121
van Genuchten, M. T. (1980). A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 44, 892–898.
Vanapalli, S. K., Fredlund, D. G., Pufahl, D. E., and Clifton, A. W. (1996). Model for the prediction of shear strength with respect to soil suction. Can. Geotech. J. 33, 379–392. doi: 10.1139/t96-060
Wang, Y. X., Guo, P. P., Ren, W. X., Yuan, B. X., Yuan, H. P., Zhao, Y. L., et al. (2017). Laboratory investigation on strength characteristics of expansive soil treated with jute fiber reinforcement. Int. J. Geomech. 17:04017101. doi: 10.1061/(asce)gm.1943-5622.0000998
Wang, Y. X., Shan, S. B., Zhang, C., and Guo, P. P. (2019). Seismic response of tunnel lining structure in a thick expansive soil stratum. Tunnel. Undergr. Space Technol. 88, 250–259.
Wu, L. Z., and Zhang, L. M. (2009). Analytical solution to 1D coupled water infiltration and deformation in unsaturated soils. Int. J. Numer. Anal. Methods Geomech. 33, 773–790. doi: 10.1002/nag.742
Zhan, T. L., Ng, C. W., and Fredlund, D. G. (2007). Field study of rainfall infiltration into a grassed unsaturated expansive soil slope. Can. Geotech. J. 44, 392–408. doi: 10.1139/t07-001
Keywords: slope stability, expansive soil, rainfall infiltration, limit equilibrium method, suction
Citation: Yang R, Xiao P and Qi S (2019) Analysis of Slope Stability in Unsaturated Expansive Soil: A Case Study. Front. Earth Sci. 7:292. doi: 10.3389/feart.2019.00292
Received: 14 August 2019; Accepted: 25 October 2019;
Published: 08 November 2019.
Edited by:
Hang Lin, Central South University, ChinaReviewed by:
Zhendong Shan, China Earthquake Administration, ChinaFubin Tu, China University of Geosciences (Wuhan), China
Han-Lin Wang, Cardiff University, United Kingdom
Copyright © 2019 Yang, Xiao and Qi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shunchao Qi, c2h1bmNoYW9xaUBzY3UuZWR1LmNu
 Rong Yang1
Rong Yang1 Shunchao Qi
Shunchao Qi