Insight Into the Wave Scattering Properties of the Solfatara Volcano, Campi Flegrei, Italy

Introduction

Imaging techniques applied to volcanoes allow to obtain static images of the structure and to track changes with time that can be a signature of the unrest status of the volcano. Specifically, methods applied to shallow part of the volcanoes can provide information about the upper hydrothermal system, fluid type and concentration, fluid migration, and possible magma pathways, thus improving eruption scenarios for volcanic hazard evaluation and eruption forecast. In this study we apply an imaging technique based on seismic wave scattering to the Solfatara volcano, located in the Campi Flegrei caldera a volcanic region located in Southern Italy, nearby the city of Naples. The Campi Flegrei is composed of more than 60 vents of different size, which erupted several times over the volcanic history of the caldera. The two largest eruptions were the Campanian Ignimbrite (39 ka) and the Neapolitan Yellow Tuff (15 ka) while the last one was the Monte Nuovo eruption (1538) (Di Vito et al., 1999; Deino et al., 2004; Pappalardo and Mastrolorenzo, 2012). The central part of the caldera (the Pozzuoli bay) was affected by a strong bradyseismic activity that recursively uplifted and lowered the ground. Usually, the bradyseism has also been accompanied by seismic activity. During the 1982–1984 episode, more than 10,000 seismic events were detected, with an earthquake of magnitude larger than 4.0 (Aster and Meyer, 1988; Aster et al., 1992; De Siena et al., 2017). After the 1982–1984 bradyseismic episode, no relevant seismicity has been recorded, indicating a possible change in the state of the caldera (Di Luccio et al., 2015). At present, the area is experiencing uplift and a change in the chemical composition of emitted gases and of degassing pattern was detected from geochemical analysis (Chiodini et al., 2012, 2016).

Different studies were performed in the area with the aim of providing velocity and attenuation images of the large-scale structure using data from active seismic surveys, such as the offshore SERAPIS experiment (Zollo et al., 2003) and from earthquakes (Judenherc and Zollo, 2004; Vanorio et al., 2005; Zollo and Judenherc, 2005; Battaglia et al., 2008; Zollo et al., 2008; Serlenga et al., 2016). These analyses pointed out the presence of two main discontinuities beneath the caldera. The deeper one, at about 8 km depth, is believed to be the top of a magma layer that was likely the source of the largest past eruptions, while the shallower one, at about 3 km, is interpreted as the separation between the hydrothermal system and the older rocks derived from magma solidification. The region below this interface can behave as a shallow magma chamber before the eruptions (D’Auria et al., 2015; Trasatti et al., 2015).

The shallow hydrothermal system of the Campi Flegrei is due to the interaction of meteoric water and magmatic fluids coming from depth. This results in an intense and almost continuous fumarolic activity localized in two areas of the Campi Flegrei Caldera: Solfatara and Pisciarelli. Specifically, the Solfatara crater is believed to be at the top of a hydrothermal plume (Chiodini et al., 2001; De Siena et al., 2010) whose base is fed by the primary hot fluid reservoir at about 2 km depth (De Siena et al., 2018; Siniscalchi et al., 2019). The crater is characterized by two areas of strong gas emission, e.g., Bocca Grande and Bocca Nuova (Chiodini et al., 2005; Chiodini, 2009) and several fumaroles, releasing the gas rising along faults (Bianco et al., 2004). Because of the connection between the hydrothermal system and the meteoric water, seasonal variations are also expected in this area.

The structure of the Solfatara is strongly heterogeneous. Delineating the morphology of the interfaces and interpreting the complex interaction between the diverse components of the hydrothermal system require a multidisciplinary approach (Bruno et al., 2007). Several active and passive seismic (Bruno et al., 2007; Letort et al., 2012; Serra et al., 2016; Amoroso et al., 2018), geoelectric (Byrdina et al., 2014; Gresse et al., 2018), and magnetotelluric surveys (Siniscalchi et al., 2015) were performed to constrain the subsoil stratification. From analysis of refracted waves (Bruno et al., 2007), ambient noise (Letort et al., 2012; Petrosino et al., 2012), and surface waves (Letort et al., 2012; Serra et al., 2016) a description of the shallow structure of the Solfatara was provided, with a very thin shallow low-velocity layer (2–4 m thick) above a sequence of interfaces with strong velocity contrasts. These layers correspond to poorly consolidated clays and tephra (Isaia et al., 2009). They are responsible for the low S wave and Rayleigh wave velocities (Petrosino et al., 2012; Serra et al., 2016). Below this low velocity layer, the evidence of a geological boundary with a strong velocity contrast was also suggested by a sharp variation of the temperature profile (Letort et al., 2012). Finally, 3D analysis of P (De Landro et al., 2017, 2019) and surface waves (Serra et al., 2016), and inspection of 2D profiles (Bruno et al., 2017; Gammaldi et al., 2018) pointed out a separation of the central part of the crater in two domains, with the NE sector having higher velocities than the SW one. As suggested by geoelectric measurements (Byrdina et al., 2014; Gresse et al., 2018), which are more sensitive to the presence of liquid/gas phases, this separation can be ascribed to a different concentration of water, which is more abundant in the SW domain. At larger depths several near-vertical normal faults individuated in the reflection profiles likely represent the pathways for ascending gas. Finally, the basement of the Solfatara crater can be found at about 400 m depth (Bruno et al., 2017).

Waves propagating in a strongly heterogeneous medium, such as the Solfatara, lose their coherence owing to the interaction with velocity anomalies and obstacles (scatterers) at different scales. Therefore, classical imaging methods based either on the arrival time or on the waveform of ballistic waves might provide too smooth images as compared to the real geological structure. Techniques based on single or multiple scattering approaches can instead provide insights into the small-scale properties of the medium and constrain mechanical properties or fluid type/concentration (e.g., Campillo and Margerin, 2010). Standard scattering techniques are based on the modeling of the decay of the seismic coda generated by earthquakes occurring beneath the volcanic edifice or by shots during active seismic surveys (e.g., Prudencio et al., 2013; De Siena et al., 2017) and may constrain fluid accumulation at depth (Prudencio et al., 2015). These techniques have been also applied to the whole Campi Flegrei caldera, using the seismicity occurring during the last strong bradiseismic activity. They adopt either a single scatterer model (Tramelli et al., 2006), or 2D space-weighted functions (De Siena et al., 2017) or 3D kernels from the radiative transfer equation (Akande et al., 2019), to detect the rim of the caldera and reveal the source of the unrest episodes, likely related to magma intrusion at about 4 km depth (Amoruso et al., 2014; De Siena et al., 2017). In several cases, such methods do not allow to localize and characterize single scatterers, but they rather provide a statistical description of the medium in terms of some relevant parameters such as the scattering mean free path l_s and the transport mean free path l^∗.

The scattering mean free path, defined as the average distance traveled by a wave between two scattering events, can be estimated using a regular dense array to reconstruct a plane wave and to measure its decay across the receiver grid (Gouédard et al., 2011). Although straightforward, this approach hides some drawbacks, such as the a priori knowledge of the anelastic attenuation (Sato et al., 2012). The scattering mean free path can be also computed through the evaluation of the ratio between the coherent and incoherent intensities, estimated on a single phase propagating across a set of stations (Roux and De Rosny, 2001; Gouédard et al., 2011; Chaput et al., 2015). The use of the intensity ratio allows us to rule out the effect of the absorption, due to both anelasticity and scattering (Roux and De Rosny, 2001). In this case, l_s can be better constrained when illuminating the scatterers under different experimental configurations, this condition being obtained either fixing the source and moving the scatterers (Roux and De Rosny, 2001) or fixing the scatterers and moving the source position (Snieder and Vrijlandt, 2005). However, when dealing with sharp changes in the scattering properties of the medium, the setup of appropriate boundary conditions is required to characterize the scattering mean-free path and the transport mean free path (De Siena et al., 2013).

In order to detect and track changes in the elastic properties of the shallow structure of the Solfatara down to depths of 15–30 m, using diverse imaging techniques, the “RICEN” experiment was organized in the framework of the European “Mediterranean Supersite Volcanoes” (MED-SUV¹) project. For the survey, three campaigns of active and passive seismic experiments were carried out in September 2013, May 2014, and November 2014. For each campaign, more than 25,000 seismograms and several days of continuous ambient noise were recorded. In the present study, we provide for the first time an estimation of the scattering mean free path at the Solfatara, making use of the large dataset acquired during the RICEN campaigns. The paper is organized as follows: the data acquisition and processing are described in the section “Data and Processing”; in the section “Scattering Mean Free Path Estimation,” we provide an estimate of l_s by inspection of the data, organized in seismic sections; in section “Inversion of the Scattering Mean Free Path,” we infer statistical properties of the scatterers distribution. Finally, in section “Discussion,” we provide an appraisal of the results to constrain the mechanical behavior of the Solfatara area at shallow depths.

Data and Processing

The present study is limited to analysis of active seismic data acquired in September 2013, during the first phase of RICEN (Serra et al., 2016), with the goal of defining the background scattering properties of the area. The experiment covered an area of 90 × 115 m, by a regular grid of 240 vertical sensors. The receivers were arranged in a grid composed of 10 lines of 24 sensors, with in-line inter-station distance of 5 m, and cross-line distance (distance between two contiguous lines) of 10 m. For the acquisition, the GS-11D 4.5 Hz vertical-component geophones were employed. We used the Vibroseis truck as a seismic source, and the source geometry was composed of about 100 shot-points on a staggered grid with respect to the receiver grid, for which both the in-line and cross-line distances were 10 m. The location of the survey area and the experimental setup are shown in Figure 1.

FIGURE 1

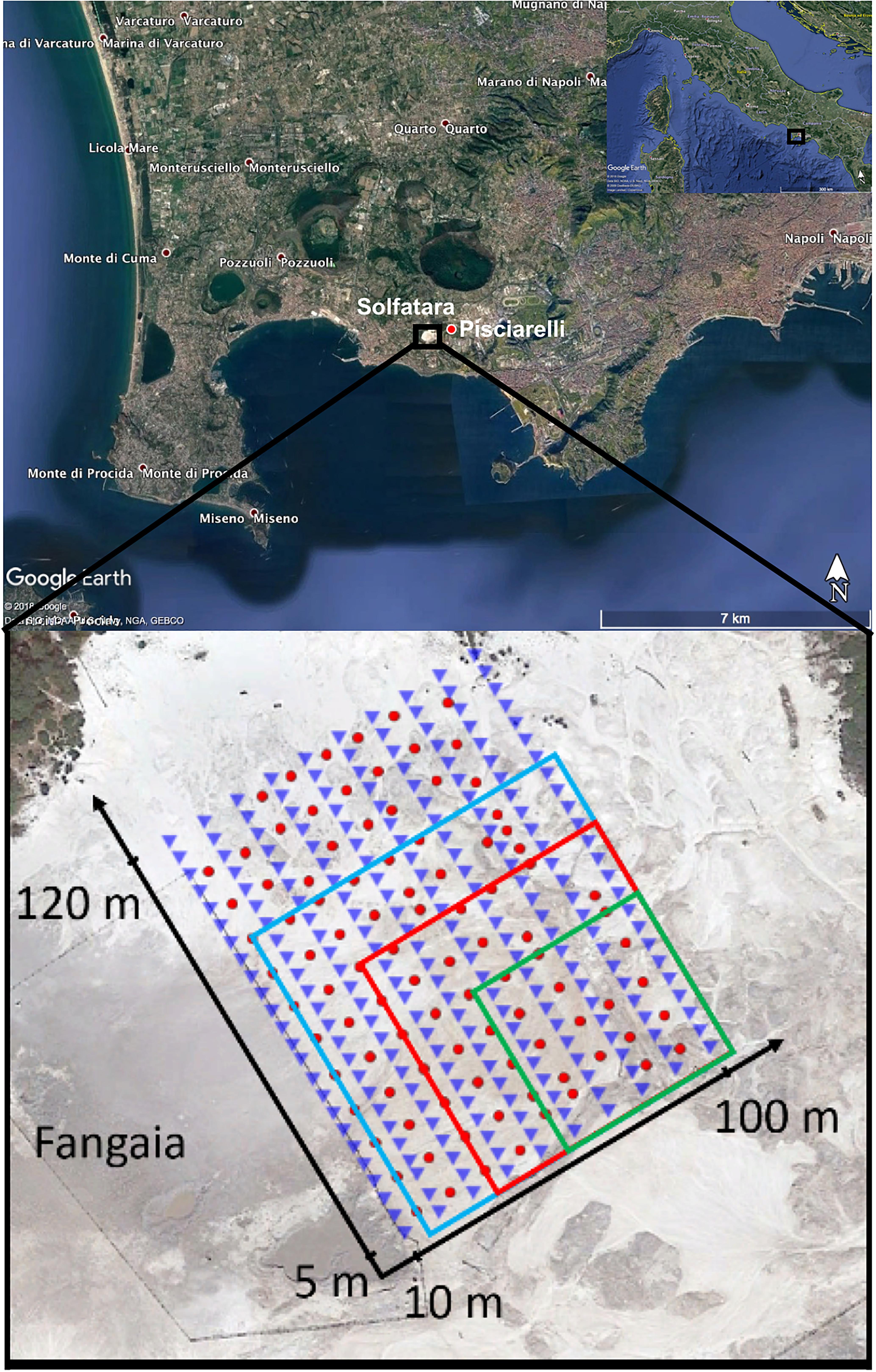
Figure 1. Location of the Solfatara volcano where the experiment has been performed. In the inset the experimental setup, with stations (blue triangles) and shots (red circles) positions. The green, red, and cyan squares represent the subgrids used to evaluate the scattering mean free path l_s.

The acquisition system was fully automatized, and synchronization provided by a radio-signal sent from the source to the control center of the instrumentation. Moreover, three successive transmissions were performed at each source location and received signals were stacked in order to increase the signal to noise ratio. The source was a vertical force with a time function of 15 s lasting linear sweep with the dominant frequency linearly increasing with time from 5 to 125 Hz.

The acquired velocigrams at each station are the convolution of the Green’s function of the medium by the source time function and the instrumental response. To study the properties of the medium, removal of both instrumental, and source effects is required.

Since the geophones have their high-pass cutoff-frequency at 4.5 Hz, while the source cut-off is at 5 Hz, we can assume a flat instrumental response in the frequency domain excited by the source. Therefore, to transform data into physical units, we just accounted for the ADC conversion and the transduction factors (Serra et al., 2016). The standard procedure to remove the source time function from seismic records is the deconvolution. When this procedure is applied in the frequency domain through a spectral ratio, instabilities may arise from small values of the spectral amplitude of the source time function and a water-level regularization is additionally required (Brittle et al., 2001).

However, because of the specific shape of the source sweep, an estimation of the Green’s function can be obtained by cross-correlation of the recorded signals by the relative sweep.

Specifically, the acquired velocigram v(x,t) is the convolution of the source time function S(x,t) by the medium Green’s function $G(x,t;\overrightarrow{\xi })$:

$v(x,t)=S(\overrightarrow{\xi },t)*G(x,t;\overrightarrow{\xi })(1)$

where x is the receiver position, $\overrightarrow{\xi }$ the source location and the symbol * denotes time convolution. The auto-correlation of a linearly swept frequency-modulated sinusoidal signal is the Klauder wavelet K(t), which has an almost flat amplitude spectrum in the domain 5–125 Hz (Sheriff, 1990):

$S(\overrightarrow{\xi },t)\times S(\overrightarrow{\xi },t)=K(\overrightarrow{\xi },t)(2)$

where the symbol × denotes the time correlation. Thus, cross-correlating the Eq. 1 with the sweep allows us to retrieve the Green’s function filtered by the function K(t):

$\overline{v}(x,t)=S(\overrightarrow{\xi },t)\times v(x,t)=K(\overrightarrow{\xi },t)*G(x,t;\overrightarrow{\xi })(3)$

Although the response of the Klauder wavelet is flat in the frequency range excited by the source, it is a zero-phase filter. Hence to preserve the causality in the data, a minimum phase filter was added (Robinson and Saggaf, 2001). The resulting seismogram is thus the Green’s function of the medium in velocity $G^{*}(x,t;\overrightarrow{\xi })$ in the frequency band excited by the source.

Because problems in the sweep recording may arise from radio transmission and at the interface between transmission and acquisition, the sweep functions were checked both in time and frequency domains. If some specific source time function did not show the expected shape either in time or in frequency, it was replaced by the average value of all the sweep functions (Serra et al., 2016).

Finally, the Green’s functions were normalized by their maximum to remove site effects, owing to the different coupling of the geophones with the ground. In fact, because of the strong variability of ground conditions at very shallow depths, going from stiff to unconsolidated soils, the local site effect strongly controls the amplitude of waves at the receiver. Normalization also removes at the first order the effect of geometrical spreading and intrinsic attenuation in the largest amplitude wave, which is the Rayleigh wave, while preserving its phase. As a consequence of the normalization, it is worth to note that in the scattering analysis performed in this study we only account for delays in the wave arrivals, and we neglect changes in the amplitude due to the interaction of the Rayleigh wave with the scatterers.

In Figure 2, we represent the Green’s functions $G^{*}(x,t;\overrightarrow{\xi })$, recorded for a single shot. Here we can identify the signature of P and Rayleigh waves as well as significant amount of energy in the coda (right panel).

FIGURE 2

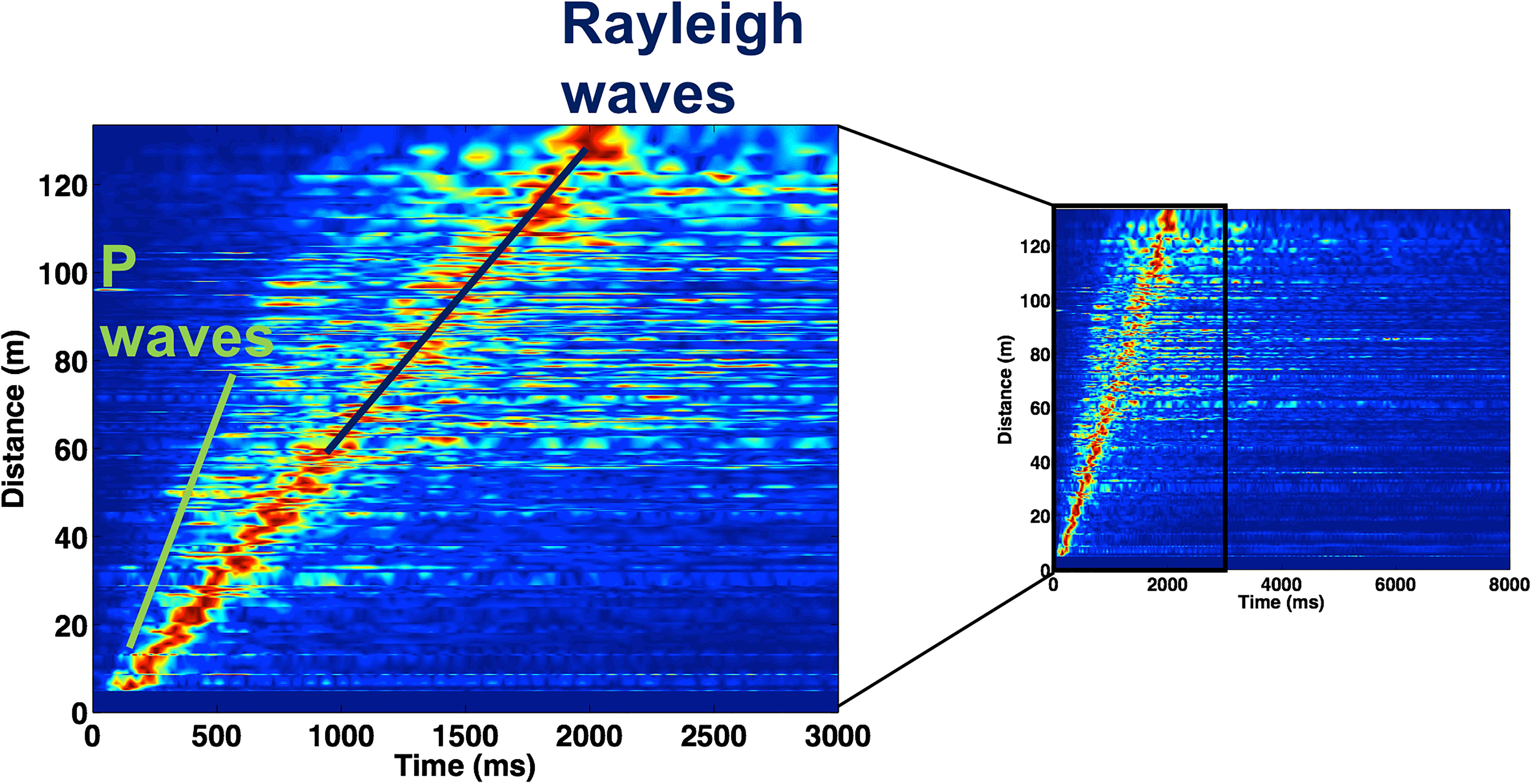
Figure 2. Normalized trace envelopes recorded for a fixed source as a function of the offset. In the zoom on the left (first 3 s) the P and Rayleigh phase arrivals are marked by green and blue lines respectively.

Scattering Mean Free Path Estimation

For the computation of the scattering mean free path, we evaluated the ratio between the coherent and incoherent intensities on the direct Rayleigh wave, which is the largest amplitude wave in our experiment, following the approach of Roux and De Rosny (2001). In the case of a 1D layered medium with scatterers, the incoherent intensity I_t, defined as the average intensity of the velocity field, exponentially decays as the source-receiver distance increases:

$I_t=G_n^{*2}{(t,r)}_{dn}=I_0{e}^{-r/l_a}g(r)(4)$

Here, G^∗ is the Green’s function as defined above, I₀ is the intensity of the velocity field at the source, r is the source–receiver distance, g(r) is the geometrical spreading, which is specific to the wave that we are considering and l_a is the absorption mean free path that accounts for both dissipation in the medium and inelastic effects due to the scatterers. The average is performed over receivers for the same source–receiver distance and then over all the sources, these averages being referred in the formula to the subscripts d and n, respectively.

The coherent intensity I_c, defined as the intensity of the averaged velocity field, can be expressed as:

$I_c=G_n^{*}{(t,r)}_{dn}^2=I_0{e}^{-r/l_a}{e}^{-r/l_s}g(r)(5)$

where l_s is the scattering mean free path that provides an estimate of the elastic scattering behavior of the medium.

These relationships hold when the number of sources n is large enough that the average is independent of the specific location and of the size of the scatterers for a homogeneous or a horizontally layered medium. In this case, the average elastic properties are also independent of the absolute location of sources and receivers, when the source-receiver distance is fixed. Therefore, the stack of traces having the same source–receiver distance but coming from different positions in the grid rules out local-scale coupling effects.

At the Solfatara we do not expect a prevalently 1D propagation medium (De Landro et al., 2017; Gresse et al., 2018). Indeed, the scattered waves are both associated with the presence of scatterers in the media as well as with 2D/3D structural effects. Furthermore, since the source-receiver grid is rectangular, a binning of the data is required to gather data from almost the same source-receiver distance. From the analysis of Serra et al. (2016), we collected data in distance bins with size of 1 m.

The ratio of the two intensities only depends on the scattering mean free path:

$H(r)=\frac{I_c}{I_t}=e^{-r/l_s}(6)$

For the more generic case of a finite number of source positions the above equation writes:

$H_N\left(r\right)=e^{-\frac{r}{l_s}}+\frac{1}{N}\left(1-e^{-\frac{r}{l_s}}\right)(7)$

N represents the number of independent realizations and may depend on the scatterer distribution, on the source location and on the investigated frequency range (Roux and De Rosny, 2001; Chaput et al., 2015). Using a characteristic average wave velocity c and defining the scattering mean free time ${\mathrm{\tau }}_s=\frac{l_s}{c}$ as the average time between two scattering events, we can represent the intensity ratio as a function of time:

$H_N\left(t\right)=e^{-\frac{t}{{\mathrm{\tau }}_s}}+\frac{1}{N}\left(1-e^{-\frac{t}{{\mathrm{\tau }}_s}}\right)(8)$

In the left panels of Figure 3, we represented the function H_N(t) in a seismic section as a function of the distance, for data filtered in the band 7–10 Hz, the smallest frequency band analyzed in this study. The four panels (A, C, E, G) correspond to a stack performed in four different subgrids, with size of 40 × 40 m², 60× 60 m², 80 × 80m² and 90 × 115m² (the whole network), respectively; these subgrids are also indicated in Figure 1. In the panels we observe that the largest amplitude of H_N(t) corresponds to surface waves and it significantly decreases along the section as the distance increases. Along these sections, we estimated the group velocity value from the best fit line crossing the maxima of the intensity ratio measured at distances r≤50m.

FIGURE 3

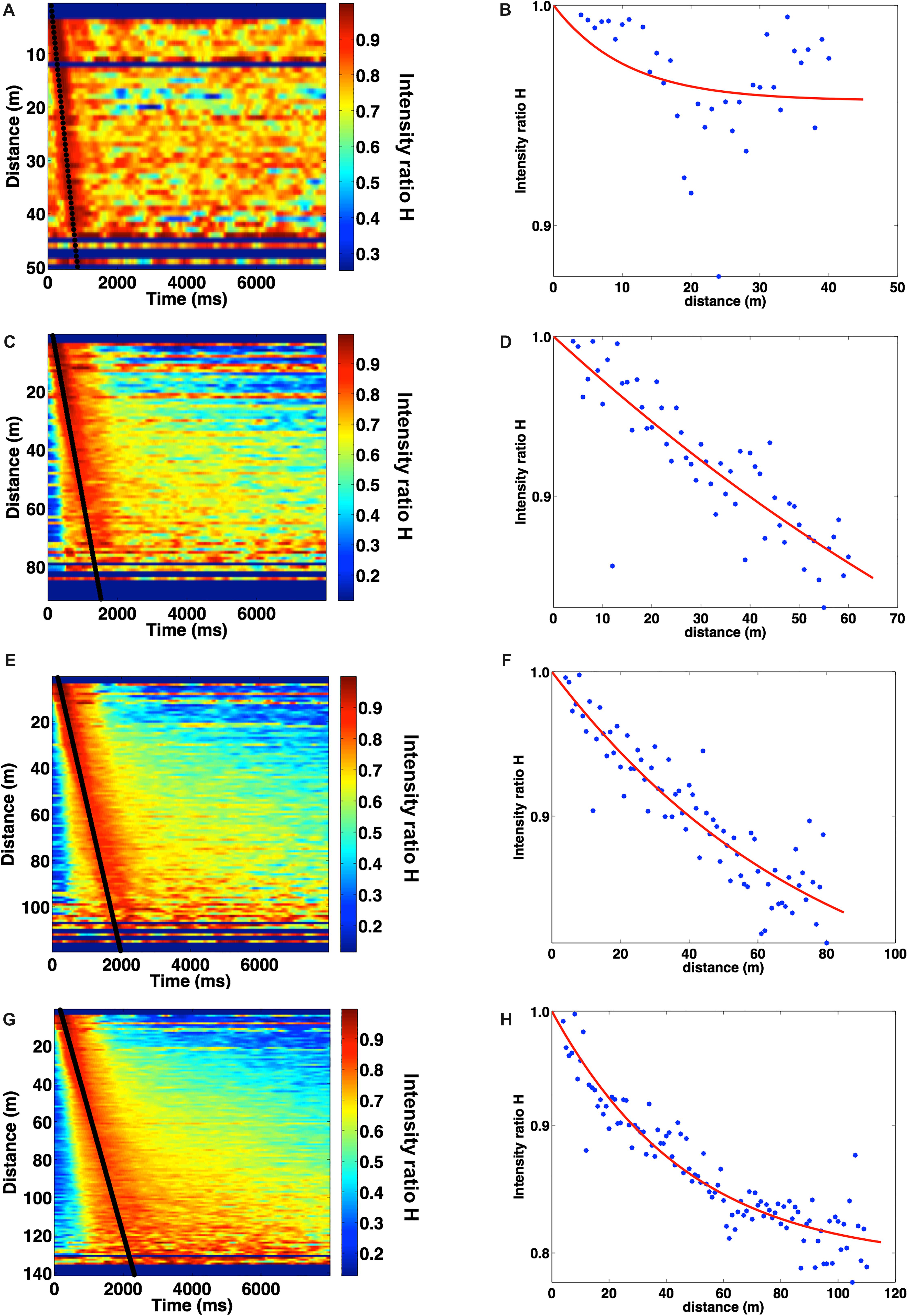
Figure 3. Ratio between coherent and incoherent intensities for different subgrids: panels (A,C,E,G) are computed for the 40× 40 m², 60× 60 m², 80× 80 m², and 90× 115 m² grid sizes, respectively in the frequency band 7–10 Hz. Panels (B,D,F,H) show the fit with an exponential curve across the points extracted from the corresponding left panels, using a velocity of V_g = 65 m/s. The time scale in Figure is milliseconds (ms).

In the panels (B-D-F-H) of Figure 3, we show the intensity ratio for Rayleigh wave as a function of distance for the same subgrids represented in left panels. In these plots, we expect that the points will follow the relation of Eq. 7, and thus we model the intensity ratio curves as a function of distance using a least-squares parametric fitting with the model of Eq. 7. For the smallest grid, we do not recover any particular trend. Referring to the fit of Figure 3B, the estimated scattering mean free path in the lowest frequency band is unconstrained since the dispersion of the points leads to a relative uncertainty of ∼70%. For the second and the third grids of Figures 3D,F, the estimate of the scattering mean free path in the same frequency band is of ∼120 m and ∼70 m, respectively, with a relative uncertainty of ∼65% and ∼20%. For these cases, the values of the scattering mean free path is larger than the maximum source-station distance and thus the model does not catch the asymptotic part of the intensity ratio as a function of the distance. The exponential behavior clearly appears only when the data are averaged over the whole grid, indicating that the scattering behavior can be analyzed only when we average over space scales comparable with the grid size (Figure 3H). For this grid and for the lowest frequency band, we found a scattering mean free path l_s = (43 ± 3) m.

We thus analyzed different frequencies bands, with their central frequency ranging from 8.5 to 21.5 Hz, averaging the intensity ratio over the whole grid. The frequency bands are selected maintaining constant the ratio between the central frequency and the bandwidth. In Figure 4, we plot the intensity ratio as a function of distance in the frequency bands 11.9–17.1 Hz and 17.7–25.3 Hz. As the frequency increases, we better recognize the exponential trend in the data, with the final plateau level clearly identified. The change in the decay rate owes to the sensitivity of surface waves to scatterers of smaller size as the frequency increases. For each frequency band, we estimate the average value of the Rayleigh wave group velocity from the best fit line crossing the maxima of the intensity ratio as a function of distance. In Figure 5A, we represent the values of the group velocity as a function of frequency. These values range between 56 and 70 m/s and they are close to the constant, frequency independent value of V_g = 65 m/s, retrieved by Serra et al. (2016).

FIGURE 4

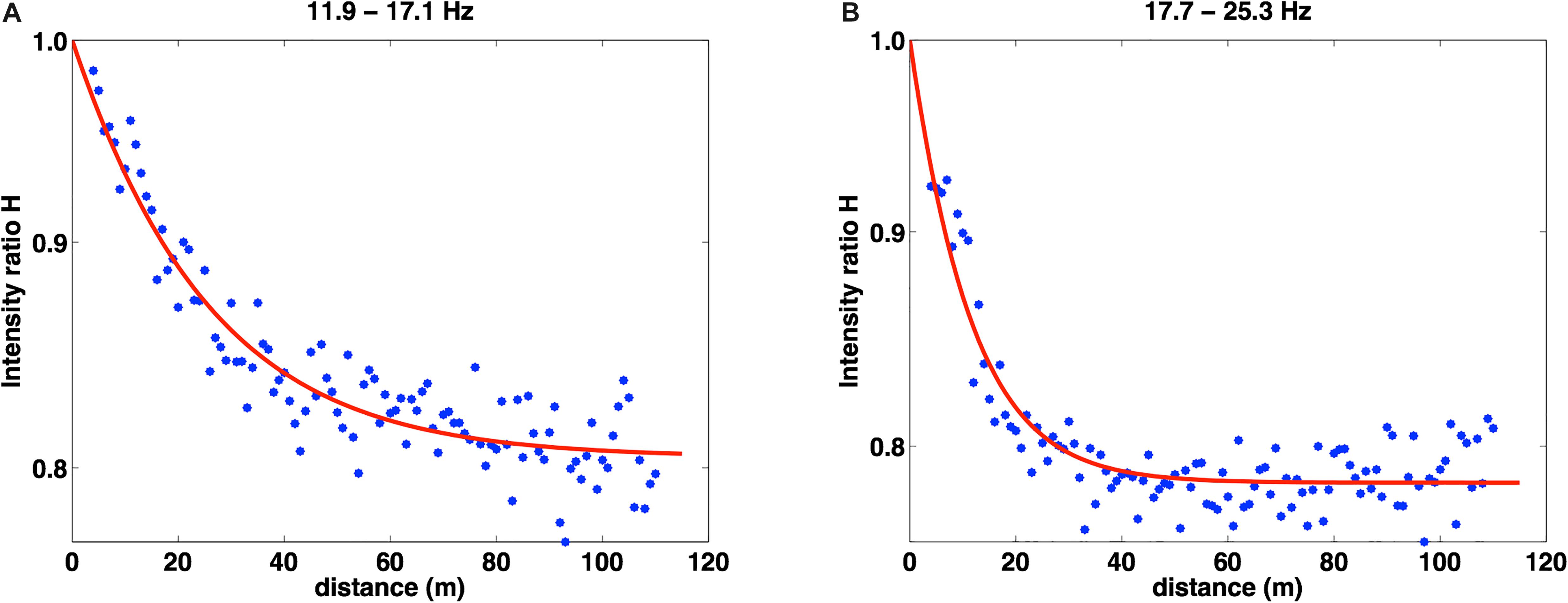
Figure 4. Exponential fits evaluated in two different frequency bands for the whole grid. Results for frequency bands ranging from 11.9 to 17.1 Hz and from 17.7 to 25.3 Hz are shown in panels (A) and (B), respectively.

FIGURE 5

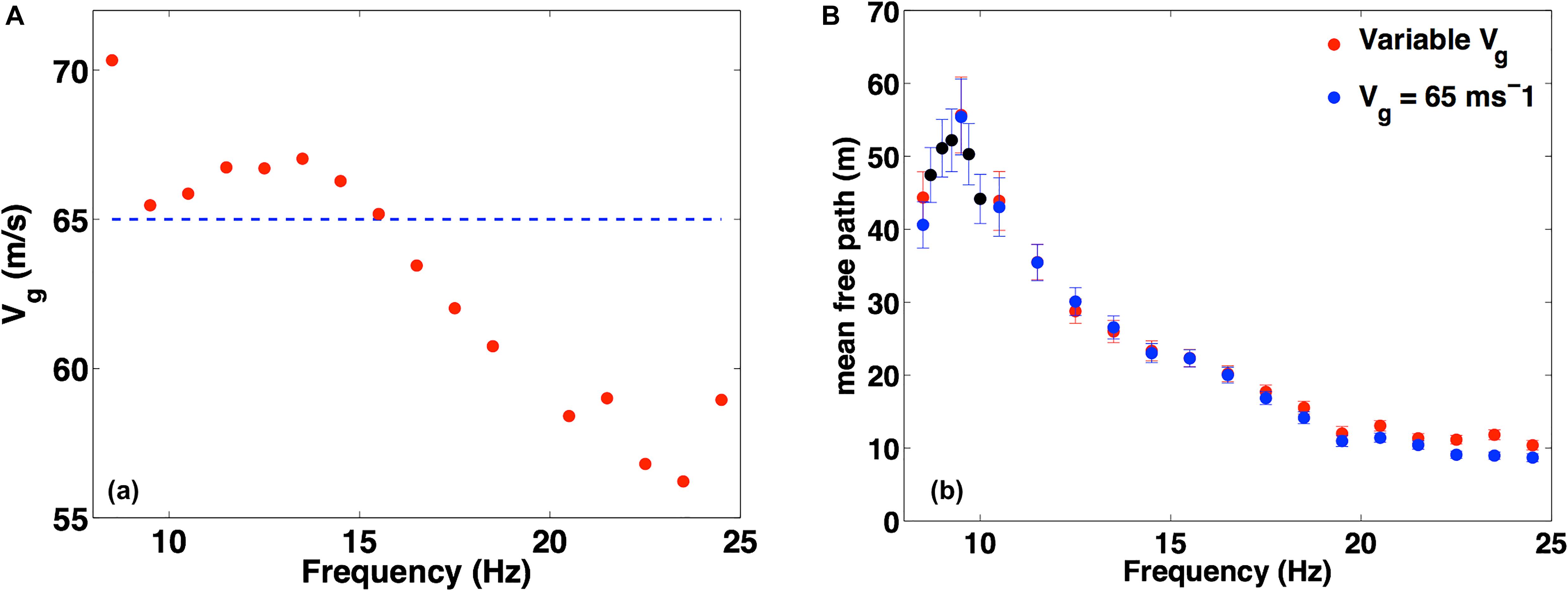
Figure 5. (A) Group velocity V_g as inferred from the maxima of the intensity ratio (red dots) compared to the fixed, average value of V_g = 65 m/s (blue dashed line). (B) l_s as a function of frequency for the two cases of the panel (A). A hump at low frequency emerges from the scattering mean free path computation.

Finally, in Figure 5B we show the evolution of l_s as a function of frequency. The red and blue points represent l_s considering for the Rayleigh wave group velocity the specific frequency-dependent value V_g retrieved from the best-fit procedure and assuming the constant value V_g = 65m/s, respectively. The two curves are almost superimposed, indicating that a constant value for the group velocity can be assumed in the interpretation of the scattering mean free path.

We find a scattering mean free path decreasing from 50 m at 8 Hz to 10 m at 25 Hz, with a small hump between 8.5 and 9.5 Hz, where the mean free path reaches its maximum of 60 m. We investigate in detail the initial small increase of l_s. A finer sampling in this frequency interval effectively confirms the small hump in this range, as evidenced by the black dots in the Figure 5B.

From the exponential modeling of the intensity ratio as a function of time via a least-squares fit, we can also estimate the number of independent realizations. We find a small N (N ∼1.2–1.3) despite the large number of source and receivers involved in the experiment. Such small values are also retrieved in other active seismic experiments, where the l_s is at maximum one order of magnitude smaller than the size of the survey (Gouédard et al., 2011).

Inversion of the Scattering Mean Free Path

The scattering mean free path dependence on frequency may provide information about the statistical properties of the scatterers, such as their density, velocity and average size. The scattering mean free path l_s can be analytically related to the scattering cross-sectionσ by the relationship:

$l_s^{theo}=\frac{1}{n\mathrm{\sigma }}(9)$

where n is the number of scatterers by surface unit. To interpret the retrieved dependence of l_s on frequency, we model the scattering cross-section for a single scatterer of size a. Since we investigate the scattering of the Rayleigh wave that propagates along the free surface, we assume a cylindrical anomaly embedded in a homogeneous medium. We additionally consider an acoustic interaction with the scatterer, assuming limited conversion between P and S waves.

The computation of the scattering cross section is dependent on the scatterer model through the parameter σ_θ:

$\mathrm{\sigma }={\int }_0^{2\mathrm{\pi }}{\mathrm{\sigma }}_{\mathrm{\theta }}\mathit{d}\mathrm{\theta }(10)$

where σ_θ is the differential scattering cross-section.

As a first trial, we model the interaction of the surface wave with an impenetrable cylindrical anomaly having rigid boundaries. For the forward model, we compute the differential scattering cross section using the formulation from Ingard and Morse (1968, p. 400). The intensity of the scattered wavefield has been computed with a truncation of the series of the Bessel functions to the order 30, in order to guarantee a truncation error well below the uncertainty on the scattering mean free path. We then numerically integrate Eq. 10 to obtain the scattering cross section, while the scattering mean free path is retrieved from Eq. 9. The theoretical scattering mean free path is characterized by two parameters, the size of the scatterer a and the number of the scatterers for surface unit n, while the wave velocity has been fixed to V_g = 65m/s. For the comparison with the scattering mean free path curve inferred from data, we compute the theoretical expectation, exploring both parameters on a 2D grid. We never get a good fit along the whole curve. By changing a and n, we are never able to model the whole experimental curve; we either model the initial trend of l_s curve or the final one, and in any case we never fit the small hump at low frequencies. If we define the normalized misfit as $M=\frac{{\sum }_k{(l_s^{theo}(f_k)-l_s(f_k))}^2}{{\sum }_k{(l_s(f_k))}^2}$, where f_k are the set of central frequencies at which the scattering mean free path is computed, the minimum value is M = 0.15.

We then move to the more sophisticated model of the penetrable cylinder as a scatterer. For the forward model, we use the analytical formulation of Montroll and Hart (1951). The series is truncated at the same order as in the previous case and the theoretical scattering mean free path is obtained following the same steps as for the impenetrable cylinder.

For a penetrable cylinder, the theoretical scattering mean free path is characterized by five parameters: the size of the scatterer, the number of scatterers per surface unit, the density ratio ρ_s/ρ₀, where ρ_s is the density of the scatterer and ρ₀ the density of the medium, respectively, and the velocities of the scatterer and of the domain. To limit the exploration of the parameters and thus the emergence of multiple solutions in the inverse problem, we fix the medium velocity to V_g = 65m/s. The inversion is performed by setting 80 diverse initial models and by adopting a linearized approach around the initial solution, that minimizes the misfit function M. The initial guesses are obtained by regularly sampling the four remaining parameters (a, n, ρ_s/ρ₀ and the wave velocity inside the scatterer V_s) on a regular grid. In about half of the cases, the final solution does not converge to a local minimum and the solution is discarded. Other solutions are also discarded because the size and/or the density of the scatterers are not compatible with the investigation area. The remaining solutions appear clustered in the parameter space and for solutions in this cluster the misfit is comparable. The minimum misfit is obtained for the following set of parameters: radius size a = 6.4 ± 0.1 m; V_s = 69.0 ± 0.6 m/s; n = 0.0050 ± 0.0015 m^–2; ρ_s/ρ₀ = 0.51 ± 0.03; the value of the misfit in this case is M = 4.5⋅10⁻³, significantly lower than the one provided by other solutions and this set of solutions is the only one that also models the hump at low frequencies. Also, it is two orders of magnitude smaller than the one obtained for the impenetrable cylinder. The best fit solution along with the experimental values of l_s is plotted in Figure 6.

FIGURE 6

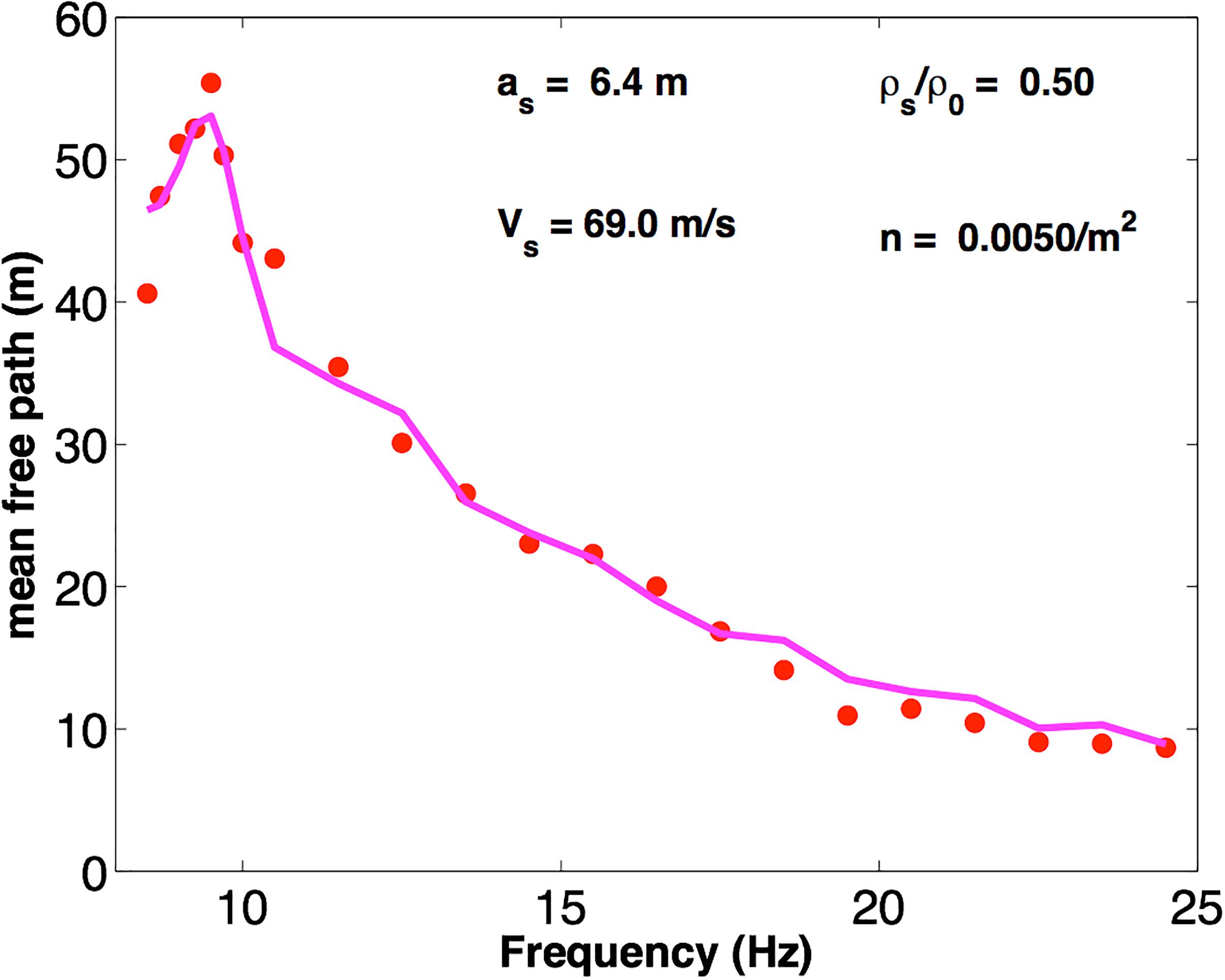
Figure 6. The best-fit solution for the mean free path using the penetrable single scatterer model. The figure shows the fit between the experimental l_s (red dots) and the one predicted by the model as a function of the frequency; the scatterer properties are reported within the panel.

We find that the horizontal size of the scatterers is well constrained by this model and it is of the order of several meters. The number of scatterers in the area covered by the survey is about n_s = 50. We have a slight increase of the group velocity in the scatterer of about 3%, while the density decreases. The change in density and the number of scatterers per surface unit are less constrained in the solutions.

Discussion

From the analysis of the intensity ratio, we retrieve a scattering mean free path which decreases from about 50 m at 8 Hz to 10 m at 25 Hz. The associated values of the scattering mean free time range between 0.15 and 0.77 s and they are comparable with values retrieved for other volcanic regions in the same frequency range, both for body and surface waves (Yamamoto and Sato, 2010; Obermann et al., 2014; Chaput et al., 2015). The modeling of the scattering mean free path as a function of the frequency allowed to infer a size of the scatterers, which is of about 10 m (the radius is 6 m) associated with a slight increase in the group velocity of the Rayleigh wave. According to Serra et al. (2016) the penetration depth of the Rayleigh waves in this frequency band is 10–15 m; thus, our scatterers appear as anomalies in the volume down to this depth. In addition, in the maps of Serra et al. (2016), positive variations of the group velocity with respect to the average value mostly occur in the Southern region of the Solfatara, where we can recognize a water-rich domain. Here the water also outcrops at the southern boundary of the domain, in the Fangaia pool. The amplitude of these variations is also of few percent larger than the average, as retrieved for the scatterers. Thus, the scatterers that determine the scattering mean free path in the analyzed frequency range could be associated with sacks/anomalies where the water content is larger than elsewhere. In this domain the average P wave velocity (Bruno et al., 2007; De Landro et al., 2017) is much smaller than the sound velocity in the water, and thus the P wave velocity is expected to increase with the increase of the water content. Also, in the group velocity maps the size of the anomalies is of the order of 10–20 m, which is comparable with the scatterer size found in this study. It is worth to note, however, that a comparison between the size of the scatterers retrieved here and the size of the anomalies in Serra et al. (2016) should be done with caution, since the group velocity maps are smoothed to guarantee continuity among nearby regions and the above size should be seen as an upper limit for the anomaly size in those models. Higher resolution resistivity maps (Serra et al., 2016; Gresse et al., 2018) also point out the presence of anomalies in the same volume whose size is about 10 m. These anomalies clearly appear as strong changes in the resistivity and they are interpreted in those studies as a sequence of water-rich and gas-rich areas. What we see as scatterers could be associated to the paths that condensed steam runs across to reach the Fangaia pool, outside the southern boundary of our domain (Gresse et al., 2018).

Another possible cause for changes in the surface wave velocity could be associated to temperature changes, whose surficial gradient is very relevant (Gresse et al., 2018). An increase in the wave velocity could be associated with a decrease in the temperature. This mechanism may exist at the Solfatara but here it is strictly correlated with the fluid type and content. A thermal anomaly in a compositionally homogeneous medium should drive a change in the density in the same direction as the velocity, which is not observed in this case.

The presence of scatterers could be also related to compositional anomalies in the investigated area. Several authors (Isaia et al., 2015; Mayer et al., 2016) have shown very different P-wave speeds for rock samples collected at the Solfatara and measured in laboratory. However, such strong lateral variation in both the P and S wave speed has not been retrieved in seismic tomographic images (Serra et al., 2016; Bruno et al., 2017; De Landro et al., 2017) nor it has been observed in this study. Small changes of few percent in the Rayleigh wave velocity could instead be associated to local chemical alteration of rocks (Mayer et al., 2016), to local changes in the morphology of the interfaces or to changes in the crack population and geometry.

Additional constraints on the scattering properties of the medium could be retrieved analyzing the decay of the incoherent intensity in the coda of the seismograms. We found that for a fixed frequency range, the incoherent intensity shows the same decay with time, for all the source-receiver distances, such that after renormalization by the geometrical spreading, all the curves show the same trend with increasing time. Thus, for this time window, the wave has lost the memory of its initial source. In Figure 7, we represent the incoherent ratio measured in the lowest (Figure 7A) and highest (Figure 7B) frequency bands. The energy is represented in a log-linear scale, to enhance the exponential decay with time, that would appear here as a straight line. We adopt the single scatter model to interpret the coda (e.g., Aki and Chouet, 1975). However, we retrieve that the exponent of the time function t^−m in the single scatter model decreases fast with frequency, moving to values larger than 3 and thus indicating a complexity in the coda contribution and a possible superposition of body and surface waves governed by anelastic attenuation in this regime. An exponent m=1, typical of surface waves, could fit the coda decay only for the lowest frequencies in our domain. Also, a multiple-scattering model does not reproduce the trend of the energy with time. Additional elements should be included in the coda modeling such as the effect of the anelastic attenuation and the coupling between surface and body waves.

FIGURE 7

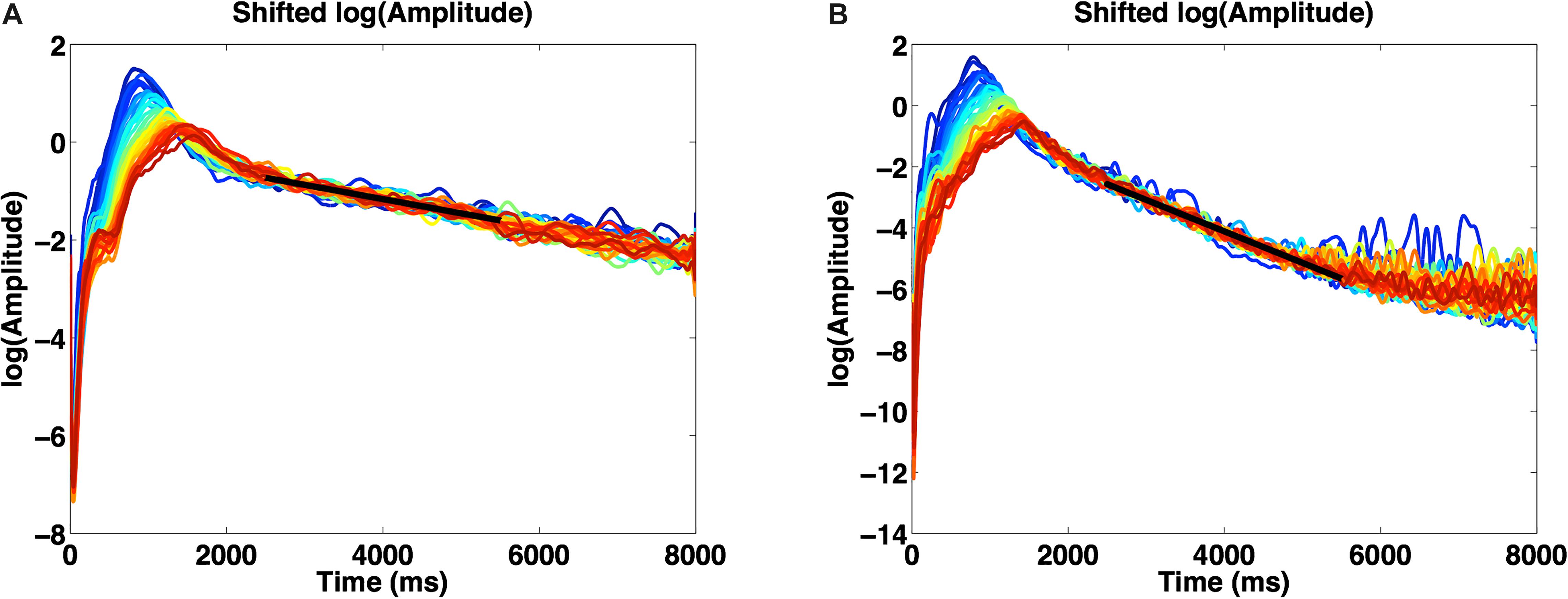
Figure 7. Logarithm of the incoherent amplitude at all available distances as a function of time. The curves show an almost linear trend in the coda. The left panel corresponds to the lowest frequency band (A), the right one to the highest frequency band (B). The time scale in Figure is milliseconds (ms).

Using the penetrable cylinder as the single scatterer model, we can derive an estimation of quality factor due to the scattering of surface waves Q_s from the computation of the theoretical transport mean free path l^∗. This latter parameter can be derived again as $l^{*}=\frac{1}{n{\mathrm{\sigma }}^{*}}$, where the scattering cross-section is now:

${\mathrm{\sigma }}^{*}={\int }_0^{2\mathrm{\pi }}{\mathrm{\sigma }}_{\mathrm{\theta }}(1-\cos \mathrm{\theta })\mathit{d}\mathrm{\theta }(11)$

Estimation of Q_s range between 100 and 160 in the selected frequency range.

The modeling of the scattering mean free path in the Solfatara has shown to discriminate water-rich areas as compared to gas-rich regions and provided a gross estimation of their ratio in the area. A continuous monitoring of this quantity by permanent instruments or temporary repeated surveys will allow to investigate changes in the shallow structure of the area, which may be connected to changes in the provision mechanism or amount of magmatic fluids from depth and may provide an indication of an unrest status of the volcano. Finally, upscaling the technique at kilometric size areas, such as the whole Campi Flegrei caldera, is expected to provide constrains on fluid migration, magma injection and potential evolution of the volcano toward any eruption.

Conclusion

In this study, we analyzed the scattering properties of the Solfatara crater, in the Campi Flegrei caldera, Southern Italy. We used active seismic data recorded during the RICEN experiment to evaluate the ratio between coherent and incoherent intensities. The evolution of this ratio with time enabled us to estimate the contribution of the scattering mean free path as a function of the frequency. Since seismograms are dominated by Rayleigh waves, the computed mean free path is referred to these surface waves. We found that the exponential decay of the intensity ratio at low frequencies can be constrained if the average over sources and receivers is performed on the whole area hosting the experiment. We found that the scattering mean free path decreases in the investigated frequency domain (7.5–21.5 Hz) from 50 to 10 m, with the exception of a small hump at about 10 Hz, where it reaches its maximum of 60 m. We modeled the scattering mean free path using a single, penetrable, cylindrical scatterer, under acoustic approximation. We found that the average size of the scatterer is about 10 m, with a small increase of the Rayleigh wave velocity inside the scatterer. We interpret these scatterers as due to domains richer in water. The regions can be associated with the paths run across by condensed steam to reach the Fangaia pool.

Connection between the scattering mean-free path and the fluid type/content is of fundamental importance to understand the volcanic structure; upscaling this technique to a kilometric size area would allow to provide constraints about the magma chamber and related feeding mechanism. In addition, monitoring changes in the scattering mean free path by repeated surveys can indeed bring information on changes in the very shallow hydrothermal system, eventually related the amount and type of magmatic fluid provision from depth, which is responsible for fumaroles and gas emissions at the Solfatara. Tracking these changes at larger scale can also provide information about magma injection and migration and ultimately about any future eruption in the investigated area.

Data Availability Statement

The dataset generated for this study can be found at the following address: https://doi.org/10.6084/m9.figshare.9114467.

Author Contributions

AS and MS analyzed the data and provided methodological implementation. MS built the database. GF and PR contributed to the methodological setup. GF provided interpretation. All authors contributed to the organization and writing of this manuscript.

Funding

This study was carried out within the framework of the project “Detection and tracking of crustal fluid by multi-parametric methodologies and technologies” which received funding from MIUR (Italian Ministry of University and Research), under grant agreement no. 20174X3P29.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We gratefully acknowledge the editor, Yosuke Aoki, and the reviewers, Luca De Siena, Hisashi Nakahara, and Jesus M. Ibanez, for their comments and suggestions. They have definitely contributed to improve the quality of the analysis and the whole manuscript.

Footnotes

1. ^ http://www.med-suv.eu

References

Akande, W. G., De Siena, L., and Gan, Q. (2019). Three-dimensional kernel-based coda attenuation imaging of caldera structures controlling the 1982–84 Campi Flegrei unrest. J. Volc. Geotherm. Res. 381, 273–283. doi: 10.1016/j.jvolgeores.2019.06.007

CrossRef Full Text | Google Scholar

Aki, K., and Chouet, B. (1975). Origin of coda waves: source, attenuation, and scattering effects. J. Geophys. Res. 80, 3322–3342. doi: 10.1029/jb080i023p03322

CrossRef Full Text | Google Scholar

Amoroso, O., Festa, G., Bruno, P. P., D’Auria, L., De Landro, G., Di Fiore, V., et al. (2018). Integrated tomographic methods for seismic imaging and monitoring of volcanic caldera structures and geothermal areas. J. App. Geoph. 156, 16–30. doi: 10.1016/j.jappgeo.2017.11.012

CrossRef Full Text | Google Scholar

Amoruso, A., Crescentini, L., Sabbetta, I., De Martino, P., Obrizzo, F., and Tammaro, U. (2014). Clues to the cause of the 2011–2013 Campi Flegrei caldera unrest, Italy, from continuous GPS data. Geophys. Res. Lett. 41, 3081–3088. doi: 10.1002/2014gl059539

CrossRef Full Text | Google Scholar

Aster, R. C., and Meyer, R. P. (1988). Three-dimensional velocity structure and hypocenter distribution in the Campi Flegrei caldera, Italy. Tectonophysics 149, 195–218. doi: 10.1016/0040-1951(88)90173-4

CrossRef Full Text | Google Scholar

Aster, R. C., Meyer, R. P., De Natale, G., Zollo, A., Martini, M., Del Pezzo, E., et al. (1992). Seismic investigation of the Campi Flegrei: a summary and synthesis of results. Volc. Seismol. 462–483. doi: 10.1007/978-3-642-77008-1_28

CrossRef Full Text | Google Scholar

Battaglia, J., Zollo, A., Virieux, J., and Dello Iacono, D. (2008). Merging active and passive data sets in traveltime tomography: the case study of Campi Flegrei caldera (Southern Italy). Geophys. Prospect. 56, 555–573. doi: 10.1111/j.1365-2478.2007.00687.x

CrossRef Full Text | Google Scholar

Bianco, F., Del Pezzo, E., Saccorotti, G., and Ventura, G. (2004). The role of hydrothermal fluids in triggering the July–August 2000 seismic swarm at Campi Flegrei, Italy: evidence from seismological and mesostructural data. J. Volc. Geotherm. Res. 133, 229–246. doi: 10.1016/S0377-0273(03)00400-1

CrossRef Full Text | Google Scholar

Brittle, K. F., Lines, L. R., and Dey, A. K. (2001). Vibroseis deconvolution: a comparison of cross-correlation and frequency-domain sweep deconvolution. Geophys. Prosp. 49, 675–686. doi: 10.1046/j.1365-2478.2001.00291.x

CrossRef Full Text | Google Scholar

Bruno, P. P., Maraio, S., and Festa, G. (2017). The shallow structure of Solfatara Volcano, Italy, revealed by dense, wide-aperture seismic profiling. Sci. Rep. 7:17386. doi: 10.1038/s41598-017-17589-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Bruno, P. P., Ricciardi, G. P., Petrillo, Z., Di Fiore, V., Troiano, A., and Chiodini, G. (2007). Geophysical and hydrogeological experiments from a shallow hydrothermal system at Solfatara Volcano, Campi Flegrei, Italy: response to caldera unrest. J. Geophys. Res. 112:B06201. doi: 10.1029/2006JB004383

CrossRef Full Text | Google Scholar

Byrdina, S., Vandemeulebrouck, J., Cardellini, C., Legaz, A., Camerlynck, C., Chiodini, G., et al. (2014). Relations between electrical resistivity, carbon dioxide flux, and self-potential in the shallow hydrothermal system of Solfatara (Phlegrean Fields, Italy). J. Volc. Geoth. Res. 283, 172–182. doi: 10.1016/j.jvolgeores.2014.07.010

CrossRef Full Text | Google Scholar

Campillo, M., and Margerin, L. (2010). “Mesoscopic seismic waves, in new directions in linear acoustics and vibration,” in Quantum Chaos, Random Matrix Theory and Complexity, eds M. Wright, and R. Weaver (Cambridge: Cambridge University Press). doi: 10.1017/CBO9780511781520

CrossRef Full Text | Google Scholar

Chaput, J., Campillo, M., Aster, R. C., Roux, P., Kyle, P. R., Knox, H., et al. (2015). Multiple scattering from icequakes at Erebus volcano, Antarctica: implications for imaging at glaciated volcanoes. J. Geophys. Res. 120, 1129–1141. doi: 10.1002/2014JB011278

CrossRef Full Text | Google Scholar

Chiodini, G. (2009). CO2/CH4 ratio in fumaroles a powerful tool to detect magma degassing episodes at quiescent volcanoes. Geophys. Res. Lett. 36:L02302. doi: 10.1029/2008GL036347

CrossRef Full Text | Google Scholar

Chiodini, G., Caliro, S., De Martino, P., Avino, R., and Gherardi, F. (2012). Early signals of new volcanic unrest at Campi Flegrei caldera? Insights from geochemical data and physical simulations. Geology 40, 943–946. doi: 10.1130/G33251.1

CrossRef Full Text | Google Scholar

Chiodini, G., Frondini, F., Cardellini, C., Granieri, D., Marini, L., and Ventura, G. (2001). CO2 degassing and energy release at Solfatara volcano, Campi Flegrei, Italy. J. Geophys. Res. 106, 16213–16221. doi: 10.1029/2001JB000246

CrossRef Full Text | Google Scholar

Chiodini, G., Granieri, D., Avino, R., Caliro, S., and Costa, A. (2005). Carbon dioxide diffuse degassing and estimation of heat release from volcanic and hydrothermal systems. J. Geophys. Res 110:B08204. doi: 10.1029/2004JB003542

CrossRef Full Text | Google Scholar

Chiodini, G., Paonita, A., Aiuppa, A., Costa, A., Caliro, S., De Martino, P., et al. (2016). Magmas near the critical degassing pressure drive volcanic unrest towards a critical state. Nat. Commun. 7:13712. doi: 10.1038/ncomms13712

PubMed Abstract | CrossRef Full Text | Google Scholar

D’Auria, L., Pepe, S., Castaldo, R., Giudicepietro, F., Macedonio, G., Ricciolino, P., et al. (2015). Magma injection beneath the urban area of Naples: a new mechanism for the 2012–2013 volcanic unrest at Campi Flegrei caldera. Sci. Rep. 5:13100. doi: 10.1038/srep13100

PubMed Abstract | CrossRef Full Text | Google Scholar

De Landro, G., Serlenga, V., Amoroso, O., Russo, G., Festa, G., and Zollo, A. (2019). High resolution attenuation images from active seismic data: the case study of Solfatara volcano (southern Italy). Front. Earth Sci. 7:295. doi: 10.3389/feart.2019.00295

CrossRef Full Text | Google Scholar

De Landro, G., Serlenga, V., Russo, G., Amoroso, O., Festa, G., Bruno, P. P., et al. (2017). 3D ultra-high resolution seismic imaging of shallow Solfatara Crater in Campi Flegrei (Italy): new insights on deep hydrothermal fluid circulation processes. Sci. Rep. 7:3412. doi: 10.1038/s41598-017-03604-0

PubMed Abstract | CrossRef Full Text | Google Scholar

De Siena, L., Chiodini, G., Vilardo, G., Del Pezzo, E., Castellano, M., Colombelli, S., et al. (2017). Source and dynamics of a volcanic caldera unrest: Campi Flegrei, 1983–84. Sci. Rep. 1:8099. doi: 10.1038/s41598-017-08192-7

PubMed Abstract | CrossRef Full Text | Google Scholar

De Siena, L., Del Pezzo, E., and Bianco, F. (2010). Seismic attenuation imaging of Campi Flegrei: evidence of gas reservoirs, hydrothermal basins and feeding systems. J. Geophys. Res. 115:B09312. doi: 10.1029/2009JB006938

CrossRef Full Text | Google Scholar

De Siena, L., Del Pezzo, E., Thomas, C., Curtis, A., and Margerin, L. (2013). Seismic energy envelopes in volcanic media: in need of boundary conditions. Geophysi. J. Int. 195, 1102–1119. doi: 10.1093/gji/ggt273

CrossRef Full Text | Google Scholar

De Siena, L., Sammarco, C., Cornwell, D. G., La Rocca, M., Bianco, F., Zaccarelli, L., et al. (2018). Ambient seismic noise image of the structurally controlled heat and fluid feeder pathway at Campi Flegrei caldera. Geophys. Res. Lett. 45, 6428–6436. doi: 10.1029/2018gl078817

CrossRef Full Text | Google Scholar

Deino, A. L., Orsi, G., de Vita, S., and Piochi, M. (2004). The age of the Neapolitan yellow tuff caldera – forming eruption (Campi Flegrei Caldera-Italy) assessed by 40Ar/39Ar dating method. J. Volc. Geoth. Res. 133, 157–170. doi: 10.1016/S0377-0273(03)00396-2

CrossRef Full Text | Google Scholar

Di Luccio, F., Pino, N., Piscini, A., and Ventura, G. (2015). Significance of the 1982–2014 Campi Flegrei seismicity: preexisting structures, hydrothermal processes, and hazard assessment. Geophys. Res. Lett. 42, 7498–7506. doi: 10.1002/2015GL064962

CrossRef Full Text | Google Scholar

Di Vito, M. A., Isaia, R., Orsi, G., Sounthon, J., de Vita, S., D’Antonio, M., et al. (1999). Volcanism and deformation since 12,000 years at the Campi Flegrei caldera (Italy). J. Volc. Geoth. Res. 91, 221–246. doi: 10.1016/S0377-0273(99)00037-2

CrossRef Full Text | Google Scholar

Gammaldi, S., Amoroso, O., D ’Auria, L., and Zollo, A. (2018). High resolution, multi-2D seismic imaging of Solfatara crater (Campi Flegrei Caldera, southern Italy) from active seismic data. J. Volcanol. Geotherm. Res. 357, 177–185. doi: 10.1016/j.volgeores.2018.03.025

CrossRef Full Text | Google Scholar

Gouédard, P., Roux, P., Campillo, M., Verdel, A., Yao, H., and van der Hilst, R. (2011). Source depopulation potential and surface-wave tomography using a crosscorrelation method in a scattering medium. Geophysics 76. doi: 10.1190/1.3535443

CrossRef Full Text | Google Scholar

Gresse, M., Vandemeulebrouck, J., Byrdina, S., Chiodini, G., Roux, P., Rinaldi, A. P., et al. (2018). Anatomy of a fumarolic system inferred from a multiphysics approach. Sci. Rep. 8:7580. doi: 10.1038/s41598-018-25448-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Ingard, K. U., and Morse, P. M. (1968). Theoretical Acoustics. Princeton University Press 949:150.

Google Scholar

Isaia, R., Marianelli, P., and Sbrana, A. (2009). Caldera unrest prior to intense volcanism in Campi Flegrei (Italy) at 4.0 ka B.P.: implications for caldera dynamics and future eruptive scenarios. Geophys. Res. Lett. 36:L21303. doi: 10.1029/2009GL040513

CrossRef Full Text | Google Scholar

Isaia, R., Vitale, S., Di Giuseppe, M. G., Iannuzzi, E., Tramparulo, F. D. A., and Troiano, A. (2015). Stratigraphy, structure, and volcano-tectonic evolution of Solfatara maar-diatreme (Campi Flegrei, Italy). GSA Bull. 127, 1485–1504. doi: 10.1130/b31183.1

CrossRef Full Text | Google Scholar

Judenherc, S., and Zollo, A. (2004). The Bay of Naples (southern Italy): constraints on the volcanic structures inferred from a dense seismic survey. J. Geophys. Res. 109:B10312. doi: 10.1029/2003JB002876

CrossRef Full Text | Google Scholar

Letort, J., Roux, P., Vandemeulebrouck, J., Coutant, O., Cros, E., Wathelet, M., et al. (2012). High-resolution shallow seismic tomography of a hydrothermal area: application to the Solfatara, Pozzuoli. Geophys. J. Int. 189, 1725–1733. doi: 10.1111/j.1365-246X.2012.05451.x

CrossRef Full Text | Google Scholar

Mayer, K., Scheu, B., Montanaro, C., Yilmaz, T. I., Isaia, R., Assbichler, D., et al. (2016). Hydrothermal alteration of surficial rocks at Solfatara (Campi Flegrei): petrophysical properties and implications for phreatic eruption processes. J. Volc. Geotherm. Res. 320, 128–143. doi: 10.1016/j.jvolgeores.2016.04.020

CrossRef Full Text | Google Scholar

Montroll, E. W., and Hart, R. W. (1951). Scattering of plane waves by soft obstacles. II. Scattering by cylinders, spheroids, and disks. J. Appl. Phys. 22, 1278–1289. doi: 10.1063/1.1699840

CrossRef Full Text | Google Scholar

Obermann, A., Larose, E., Margerin, L., and Rossetto, V. (2014). Measuring the scattering mean free path of Rayleigh waves on a volcano from spatial phase decoherence. Geophys. J. Int. 197, 435–442. doi: 10.1093/gji/ggt514

CrossRef Full Text | Google Scholar

Pappalardo, L., and Mastrolorenzo, G. (2012). Rapid differentiation in a sill-like magma reservoir: a case study from the Campi Flegrei caldera. Sci. Rep. 2:712. doi: 10.1038/srep00712

PubMed Abstract | CrossRef Full Text | Google Scholar

Petrosino, S., Damiano, N., Cusano, P., Di Vito, M. A., de Vita, S., Del Pezzo, E., et al. (2012). Subsurface structure of the Solfatara volcano (Campi Flegrei caldera, Italy) as deduced from joint seismic-noise array, volcanological and morphostructural analysis. Geochem. Geophys. Geosyst., 13:Q07006. doi: 10.1029/2011GC004030

CrossRef Full Text | Google Scholar

Prudencio, J., Del Pezzo, E., García-Yeguas, A., and Ibáñez, J. M. (2013). Spatial distribution of intrinsic and scattering seismic attenuation in active volcanic islands–I: model and the case of Tenerife Island. Geophys. J. Int. 195, 1942–1956. doi: 10.1093/gji/ggt361

CrossRef Full Text | Google Scholar

Prudencio, J., Del Pezzo, E., Ibáñez, J. M., Giampiccolo, E., and Patané, D. (2015). Two-dimensional seismic attenuation images of Stromboli Island using active data. Geophys. Res. Lett. 42, 1717–1724. doi: 10.1002/2015gl063293

CrossRef Full Text | Google Scholar

Robinson, E. A., and Saggaf, M. (2001). Klauder wavelet removal before vibroseis deconvolution. Geophys. Prosp. 49, 335–340. doi: 10.1046/j.1365-2478.2001.00260.x

CrossRef Full Text | Google Scholar

Roux, P., and De Rosny, J. (2001). Multiple scattering in a reflecting cavity: application to fish counting in a tank. J. Acoust. Soc. Am. 109:2431. doi: 10.1121/1.4744602

CrossRef Full Text | Google Scholar

Sato, H., Fehler, M. C., and Maeda, T. (2012). Seismic Wave Propagation and Scattering in the Heterogeneous Earth, 2nd Edn. Berlin: Springer. doi: 10.1007/978-3-642-23029-5

CrossRef Full Text | Google Scholar

Serlenga, V., di Lorenzo, S., Russo, G., Amoroso, O., Garambois, S., Virieux, J., et al. (2016). A three-dimensional QP imaging of the shallowest subsurface of Campi Flegrei offshore caldera, southern Italy. Geophys. Res. Lett. 43, 209–218. doi: 10.1002/2016GL071140

CrossRef Full Text | Google Scholar

Serra, M., Festa, G., Roux, P., Gresse, M., Vandemeulebrouck, J., and Zollo, A. (2016). A strongly heterogeneous hydrothermal area imaged by surface waves: the case of Solfatara, Campi Flegrei, Italy. Geophys. J. Int. 205, 1813–1822. doi: 10.1093/gji/ggw119

CrossRef Full Text | Google Scholar

Sheriff, R. E. (1990). Encyclopedic Dictionary of Exploration Geophysics. Tulsa, OK: Society of Exploration Geophysicists.

Google Scholar

Siniscalchi, A., Carlucci, M., D’Auria, L., Petrillo, Z., Romano, G., and Tripaldi, S. (2015). AMT Investigation in the Solfatara-Pisciarelli-Agnano Area: Results and Further Outlook. Vienna: EGU General Assembly.

Google Scholar

Siniscalchi, A., Tripaldi, S., Romano, G., Chiodini, G., Improta, L., Petrillo, Z., et al. (2019). Reservoir structure and hydraulic properties of the Campi Flegrei geothermal system inferred by audiomagnetotelluric, geochemical, and seismicity study. J. Geophys. Res. 124, 5336–5356.

Google Scholar

Snieder, R., and Vrijlandt, M. (2005). Constraining the source separation with coda wave interferometry: theory and application to earthquake doublets in the Hayward fault, California. J. Geophys. Res. 110:B04301. doi: 10.1029/2004JB003317

CrossRef Full Text | Google Scholar

Tramelli, A., Del Pezzo, E., Bianco, F., and Boschi, E. (2006). 3D scattering image of the Campi Flegrei caldera (Southern Italy): new hints on the position of the old caldera rim. Phys. Earth Planet. Int. 155, 269–280. doi: 10.1016/j.pepi.2005.12.009

CrossRef Full Text | Google Scholar

Trasatti, E., Polcari, M., Bonafede, M., and Stramondo, S. (2015). Geodetic constraints to the source mechanism of the 2011-2013 unrest at Campi Flegrei (Italy) caldera. Geophys. Res. Lett. 42, 3847–3854. doi: 10.1002/2015GL063621

CrossRef Full Text | Google Scholar

Vanorio, T., Virieux, J., Capuano, P., and Russo, G. (2005). Three-dimensional seismic tomography from P-wave and S-wave microearthquake travel times and rock physics characterization of the Campi Flegrei caldera. J. Geophys. Res. 110:B03201. doi: 10.1029/2004JB003102

CrossRef Full Text | Google Scholar

Yamamoto, M., and Sato, H. (2010). Multiple scattering and mode conversion revealed by an active seismic experiment at Asama volcano, Japan. J. Geophys. Res. 115:B07304.

Google Scholar

Zollo, A., Judenherc, S., Auger, E., D’Auria, L., Virieux, J., Capuano, P., et al. (2003). Evidence for the buried rim of Campi Flegrei caldera from 3-d active seismic imaging. Geophys. Res. Lett. 30. doi: 10.1029/2003GL018173

CrossRef Full Text | Google Scholar

Zollo, A., and Judenherc, S. (2005). Reply to comment by A. Rapolla on “The Bay of Naples (southern Italy): constraints on the volcanic structures inferred from a dense seismic survey”. J. Geophys. Res. 110:B06308. doi: 10.1029/2005JB003740

CrossRef Full Text | Google Scholar

Zollo, A., Maercklin, N., Vassallo, M., Dello Iacono, D., Virieux, J., and Gasparini, P. (2008). Seismic reflections reveal a massive melt layer feeding Campi Flegrei caldera. Geophys. Res. Lett. 35:L12306. doi: 10.1029/2008GL034242

CrossRef Full Text | Google Scholar