- 1School of Resource Environment & Safety Engineering, Hunan University of Science and Technology, Xiangtan, China
- 2Hunan Key Lab of Coal Safety Mining Technology, Xiangtan, China
In order to study the effects of stress and water pressure on the permeability of fractured sandstone, an ultra-deep gas layer of fractured tight sandstone in WengFu Mine in GuiZhou province, was selected for experimental design and research, and the effects of confining pressure, internal pressure, effective stress, and water pressure on gas permeability were studied. The results show that the effective stress and slippage effect compete with each other when the confining pressure is kept fixed and the internal pressure is increased in the fractured tight sandstone reservoir. At the beginning of the experiment, the gas slippage effect is strong while the rock stress sensitivity is weak. The gas permeability increasingly decreases with the increase of internal pressure. The effective stress is stronger than slippage effect, and the gas permeability increases with the increase of internal pressure when crossing the low point of permeability. The greater the confining pressure is, the greater the internal pressure needed to reach the low permeability point will be. With the increase of axial stress, horizontal contact hydraulic hole increasingly closed. Horizontal hydraulic holes are more sensitive to axial stress than vertical ones.
Introduction
Tight sandstone gas is considered unconventional gas in general conditions, but it can also be considered conventional gas for extracting when the burial depth is shallow and the mining conditions are good (Gao et al., 2010). Compared with coalbed methane and shale gas, China is far ahead in the development of tight gas. Although China has abundant reserves of tight gas resources, the abundance of tight sandstone gas reserves is low, the rate of production decline is quite fast, and economic development is difficult. The tight sandstone gas reservoir in China not only contains the general characteristics of the continental associated clastic rock reservoir, but also has the engineering geological characteristics of low porosity and low permeability, fracture, local water saturation, high capillary pressure, abnormal formation pressure, high damage potential, and so on. After years of unremitting efforts, China has developed a series of technologies for shielding and blocking of fractured tight sandstone gas reservoirs, technologies for gas drilling and complete underbalanced completion protection, and the latest gas drilling horizontal well-development technology for tight sandstone gas reservoirs etc., which greatly promoted the survey and development process of a number of tight sandstone gas fields in the Sichuan Basin, such as Xinchang, Luodai, Bajiaochang, Yuxi, Ordos Basin, Yulin, and Daniudi (Xiang et al., 2019).
As a kind of important unconventional reservoirs, fractured tight sandstone gas reservoirs have attracted increasing attention due to their considerable productivity and high economic benefits (Li et al., 2018). The gas permeability of fractured tight sandstone reservoirs is dynamic permeability, which changes with the change of environmental pressure, and it is an important reservoir parameter that impacts the exploitation of tight sandstone gas (Yang et al., 2012). Since the main space and seepage channel of gas in fractured tight sandstone reservoirs are micro-nano pores and fractures, compared with conventional reservoirs, there are obvious gas slippage effect (You et al., 2018). In addition, due to the extensive development of fractures, reservoirs usually have strong stress sensitivity (Benjamin et al., 2019), which makes the mechanism of gas permeability change with pressure complicated.
Since the 20th century, domestic and foreign scholars have made rich achievements in studying the relationship between the slippage effect of unconventional gas and the effective stress. A great number of methods have been used to study rock permeability, including field measurement, triaxial seepage experiment, and numerical simulation. It is usually reliable to measure the rock permeability on the scene. However, because of the complexity of the geological environment, repeated mining interference and the expensive testing required, these methods are not widely used. Instead, most rock samples are tested for permeability in the laboratory. In the past few years, the permeability evolution of rock in stress-strain process has been widely studied. Zhao et al. studied the rheological fracture behavior of rock fractures through a series of calculations and analyses of crack rheological fractures under different water pressure, and proposed the equivalent boggs model of rock fracture rheological fracture, laying a foundation for revealing the rheological characteristics of fractured rock under the combined action of water pressure and stress (Zhao et al., 2017b, 2018, 2019). Zhao et al. demonstrated the mechanical and permeability characteristics of fractured limestone in the complete stress-strain process by using water-mechanical coupling tests under different differential pressure and steady pressure, and verified the effectiveness of the mohr-coulomb yield criterion considering the effective stress effect under hydrodynamic coupling conditions (Zhao et al., 2016). Zhao et al. conducted transient pulse tests on single rock fractures under different pressures, and found that both mechanical and hydraulic apertures decreased with the increase of pressure, and proposed a data analysis method based on polynomial fitting to study the relationship between flow velocity and hydraulic gradient (Zhao et al., 2017c). Zhao Yanlin and Fu Chengcheng, etc., when studying the mechanical and permeability characteristics of fractured limestone during the full stress-strain process, performed hydraulic-hydraulic coupling tests on fractured limestone under different combinations of osmotic pressure and confining pressure. The existence of pressure reduces the strength and deformation modulus of fissured limestone to varying degrees, and intensifies its lateral deformation (Zhao et al., 2017a). Lin et al. verified the stress field of the crack tip under compressive and shear conditions, determined the formula of the compressive stress field of the open crack tip, and deduced the relationship between the crack initiation angle at the crack tip and the pretilt crack inclination angle. The scale effects of joint shear and cyclic freeze-thaw on the mechanical properties of non-persistent joint shear are studied. The method for determining the constitutive relationship parameters and the change rule with scale are discussed (Chen and Lin, 2019; Lei et al., 2019; Lin et al., 2019,a,b). Zhu and Wong (1997) conducted a triaxial seepage experiment on porous sandstone and analyzed the influence of stress and failure mode on the axial permeability of sandstone. The results show that permeability is highly correlated with stress. Wang and Park (2002) studied the permeability evolution in the whole stress-strain process and found that the permeability decreased with the increase of stress before reaching the peak strength. Worthington (2008) analyzed the relationship between axial permeability and effective stress of samples and determined that the relationship between the two could be described by cubic polynomial functions. Davies et al. (1999) studied the permeability stress sensitivity characteristics of different cores. The results show that the greater the porosity and permeability of sandstone core are, the smaller the permeability of cemented rock will be, and the greater the pressure sensitivity is. Wu et al. (2005) conducted CT scanning to observe the sandstone in real time by permaling-stress coupling, and studied the relationship between porosity and permeability. They found that the permeability increased as the appearance of microcracks and peaked after the macroscopic failure. Yu et al. (2013) conducted a triaxial test of rocks with different confining pressures and osmotic pressures, and determined the permeability curve to prove three trends: increase, flatness and decrease. Baghbanan and Jing (2007) used discrete fracture network models and trace length of various sizes to simulate the effects of fracture aperture and trace length on the permeability of fractured rocks. Wang (2000) analyzed the seepage-stress coupling process by analyzing the fracture network model and the discrete element method, and combined the seepage of the rock mass to establish a seepage-stress coupling model. Jing et al. (2001) studied the coupling deformation analysis of rock mass and discontinuous rock mass during the process of seepage stress excavation. Blessent et al. (2009) used a combination of geological modeling and numerical modeling to calculate fractured rock masses in 3D seepage fields. Guglielmi et al. (2008), respectively, studied the seepage-stress coupling of numerical boundary elements, discrete element and continuous element methods, and established discrete element numerical coupling models for fluid mechanics.
The relationship between volume change and permeability is very close. Ord (1990) showed that the increase of expansion rate or volume indicated the increase of porosity, therefore, the permeability increases the possibility of fluid flow with the increase of porosity. This interaction can also be conceptually summarized as the permeability caused by expansion. Understanding the interaction between volume change and permeability in rock mass has become a broadly used tool in geological engineering to ensure the stability of underground structures, assess geological carbon stocks or natural resource exploration, and predict rockburst and seismicity. Lots of studies have researched the interaction between deformation and fluid flow by using experimental methods or numerical models (Hakan, 2009). In this study, the interaction between physical properties, pore pressure, and bedding anisotropy was assessed to describe the interaction between permeability evolution and volume change.
Firstly, the volume change (or volume strain) of a compressed rock is a continual process with continual deformation phases, which are divided into regions of volume reduction (compression) or volume increase (expansion). In a word, the process of volume change starts with fracture closure and elastic compression, followed by the collapse of pore structure and the increase of microcrack density. The point of turnover between the compaction and expansion stages is often referred as the expansion boundary. Due to the disturbance of the original stress distribution, the expansion boundary of rock depends on its mechanical and hydraulic characteristics. Geological environment, temperature and time are also important factors for expansionary development. With the increase of steam and gas pressure, the expansion rate tends to increase with the increase of temperature, which will increase the tensile stress at the crack tip and facilitate the crack opening. The time-varying effect is characterized by a significant static quiescent period, resulting in a sudden energy release and pressure drop (Li et al., 2017; Liu et al., 2019).
During fault slip events, mechanical expansion leads to the creation of pores, which vary widely in fault zones, depending on rock type and rheology, stress state, displacement and so on. Many scholars have carried out research on rock permeability. Oda et al. (2002) used the transient pulse method to conduct permeability tests on the damaged granite samples, and concluded that, despite the preferred growth of cracks, rocks under stress can be roughly idealized into isotropic porous media. Mitchell and Faulkner (2008) studied the permeability evolution of two complete low-porosity crystalline rocks through conventional triaxial deformation experiments, and continuously monitored the permeability and pore volume. They proposed a positive correlation between permeability and strain, in which the permeability increased with different stresses and strains until the stress decreased by two order of magnitude. The interaction between swelling anisotropy and permeability may also be significantly affected by planar anisotropic rock fabrics. Naumann et al. (Marcel et al., 2007) conducted a true triaxial compression test to detect the expansion of clay cube samples with two different bedding directions. They point out that short-term strength and expansion are directional. However, the failure strength has a more obvious anisotropic mechanical response than the dilatancy behavior.
For this reason, this paper adopts the method that from low pressure to high pressure environment to conduct experimental research on non-steady-state method of high-pressure helium gas permeability measurement for the first time, and further discusses the slippage effect and effective stress of fractured tight sandstone reservoir permeability comprehensive control effect, which provides a new understanding for the study of mechanism of fractured tight sandstone gas reservoir permeability change. At the same time, it also has a certain practical guiding significance for predicting and improving gas reservoir of the gas production.
Materials and Methods
Experimental Samples
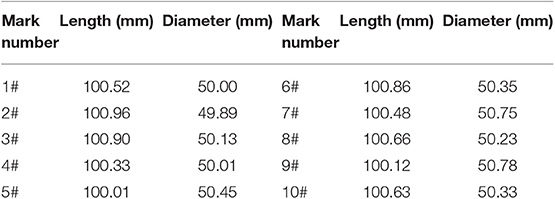
The samples were derived from the ultra-deep fractured tight sandstone gas layer which depths 4,525 m in the Wongfu Mine area of Guizhou province, and the samples were cylindrical samples with a length of 100 mm and a diameter of 50 mm. There were 10 groups, which were washed with oil and dried at 150°C. The experimental sample is shown in Figure 1. The sample parameters and number are shown in Table 1.
Permeability Measurement
Permeability is an inherent property of porous media materials, and it is a mark to measure the difficulty of sandstone gas flow. Measuring sandstone permeability has important guiding significance for the development of tight sandstone gas. Permeability is evaluated based on laminar flow state and hydraulic head. The flow rate at a point is defined as the volume of fluid(q) passing through the unit area per unit time (A) and is proportional to the pore pressure gradient at that point. The effect of pressure gradients in samples is known, and it is difficult to measure the gradients under triaxial test conditions, especially to express this change with an equation. Therefore, the permeability of hydraulic coefficient should be taken into cautiously consideration. This paper uses the Darcy formula to measure permeability using the steady state method, that is:
q is the flow through the rock at a pressure difference of Δp, cm3/s; A is the cross-sectional area of the rock, cm2; l is the contact length between the rocks, cm; μ is the viscosity of the fluid passing through the rock, mPa·s; Δp is the pressure difference before and after the fluid passes through the rock, atm; K is the proportionality coefficient, which is called the absolute permeability of the porous medium.
Model Application
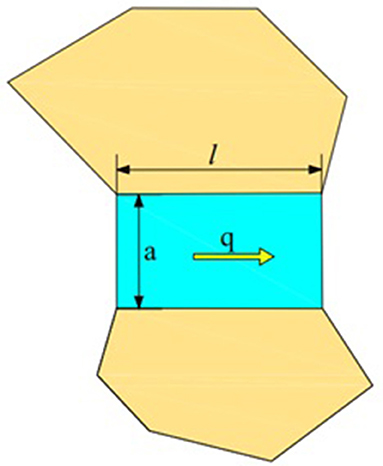
The sandstone permeability test experimental simulation model is shown in Figure 2, For a single fracture, where a is the crack width (pore diameter), b is the empirical coefficient, μ is the viscosity of the fluid, l is the contact length between domains, and Δp is the pressure between domains. The flow q1 can be obtained from the Poiseulle equation:
For n fractures, the cross-sectional area of the rock is A, and the flow qn can be determined by the following equation:
Comparing Equations (1) with (3), the following equation can be obtained:
Considering , (6) can be showed as:
Measurement of Sandstone Gas Permeability
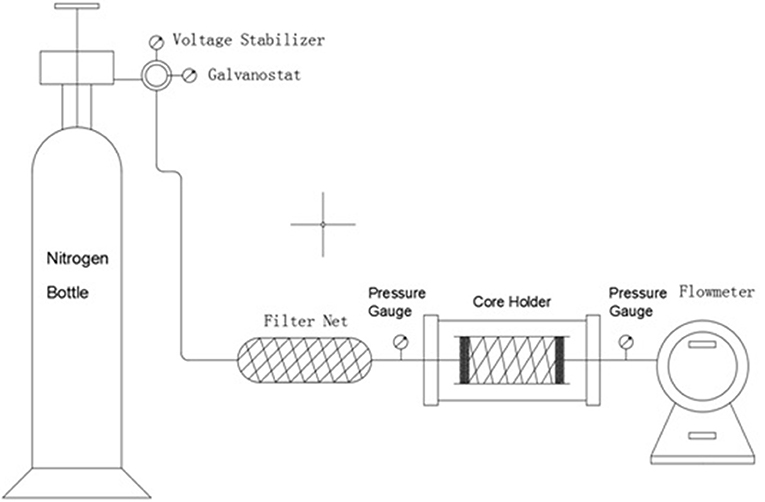
This experiment mainly uses a nitrogen bottle, a pressure gauge, an intermediate container, a core holder, and a flow meter to measure the gas permeability of a sandstone sample. The experimental flow chart is shown in Figure 3. The gas source is supplied by a high-pressure nitrogen bottle. After the pressure reducing valve and the constant flow device, the upstream pressure remains stable. When the gas passes through the core of the sandstone sample, a certain pressure difference is generated at both ends of the core. After the airflow is stable, the pressure at both ends of the core and the export flow is measured. It can be calculated by the following formula:
K is the gas permeability, μm2; Q0 is the gas flow at the core outlet end, cm3/s; L is the core length, cm; A is the cross-sectional area of the core, cm2; P0 is the absolute atmospheric pressure, MPa; P1 is the absolute core inlet end Pressure, MPa; P2 is the absolute pressure at the outlet end of the core, MPa; μ is the viscosity of the gas at the experimental temperature and atmospheric pressure, mPa·s.
Results and Discussion
The response surface method uses a series of deterministic experiments to approximate the implicit limit state function with a polynomial function, which can greatly reduce the number of experiments, improve the efficiency of the experiment, and explore the relationship between multiple input variables and dependent variables. In this paper, Design-Expert 8.0.6 software is used to compare and analyze the change law of gas permeability under the interaction of water pressure, effective stress, confining pressure, and internal pressure.
Effect of Effective Stress on Gas Permeability
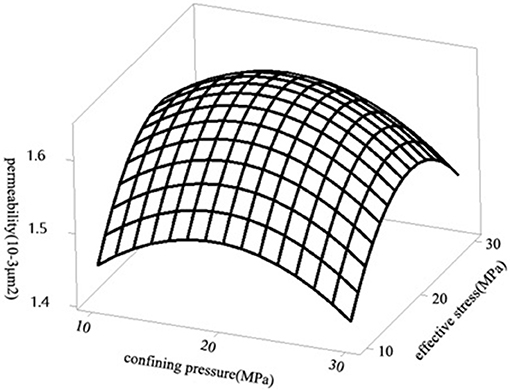
As is shown in the Figure 4 that when the axial stress is 0–10 MPa, the osmotic pressure plays a major role, while the role of the axial pressure is not clear. When the axial stress is 10–20 MPa, the flow rate drops quickly, as many horizontal contact hydraulic orifices begin to reach residual values and some seepage channels are closed.
It can be seen from Figure 5 that when the effective stress value is maintained at 10, 20, and 30 MPa, respectively, when the internal pressure increases, the gas permeability value decreases as the internal pressure increases. When the limiting stress is <10 MPa, the flow rate change curve can be divided into three stages: the descending stage (axial stress is 5–10 MPa), the sharp descending stage (axial stress is 10–25 MPa), and the steady state stage (axial stress is 25–30 MPa). When the confining pressure is 10–20 MPa, the contact hydraulic hole is reduced. The reseason is that in the fractured tight sandstone reservoir, the effective stress maintains constant, the matrix pores and fractures under the same pressure, and the reservoir space remains unchanged. At this time, the effective stress does not have any effect on gas permeability, and it also rules out the change of slippage effect which was caused by the pore throat radius and the crack opening these two factors, and the slippage effect is only affected by internal pressure.
Effect of Confining Pressure on Gas Permeability
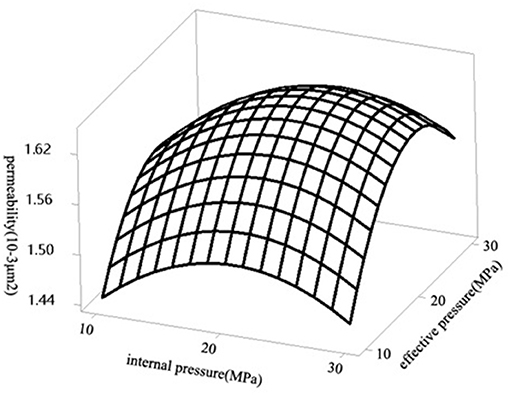
Figures 6, 7 show that: keeping the internal pressure constant, gradually increasing the confining pressure, and continuously increasing the effective stress, the gas permeability gradually decreases with the increase of the effective stress. According to the Klinkenberg slippage effect formula, when the internal pressure is constant, the influence of pressure on gas slippage effect is eliminated. At this time, slippage effect is only affected by the change of pore throat radius and fracture opening caused by the change of effective stress. With the increase of effective stress, the compaction of pores and fractures becomes stronger, the reservoir space becomes smaller, the radius of pore throat and fracture opening decrease, and the slippage effect increases, resulting in the increase of gas permeability. The increase of effective stress will cause the gradual decrease of gas permeability, and the two will compete with each other. The effective stress changes from large to small, and the damage to the pore structure is irreversible, and the loss of gas permeability is large. While the effective stress changes from small to large, the destruction of pore structure is progressive, and the loss of gas permeability is relatively small.
Variation of the Influence of Internal Pressure on Gas Permeability
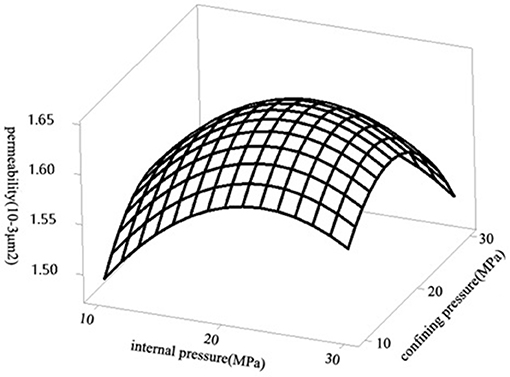
It can be seen from Figure 8 that when the confining pressure remains constant and the internal pressure continues to increase, in the process of the effective stress decreasing: the opening of the fracture and the radius of the pore throat gradually increase with the reduction of the effective stress and pressure relief, thus resulting in the increase of gas permeability. However, the increase of pore throat radius, crack opening and the increase of internal pressure leads to the decrease of gas slippage effect and the decrease of gas permeability. The two compete with each other and affect the gas permeability of the fractured tight sandstone samples. At the beginning of the experiment, the slippage effect is stronger than the effective stress, Slippage effect is stronger than the effective stress. The apparent permeability value of the gas gradually decreases with the increase of the internal pressure. When the gas permeability reached a low value, the effective stress will be stronger than slippage effect, thus making the increase of absolute permeability be dominant, while the weakening of slippage effect becomes unimportant, and the permeability of the gas value is gradually increasing with the increase of the internal pressure.
Effect of Water Pressure on Gas Permeability
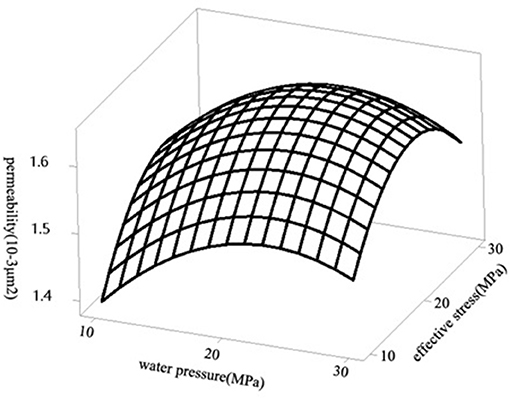
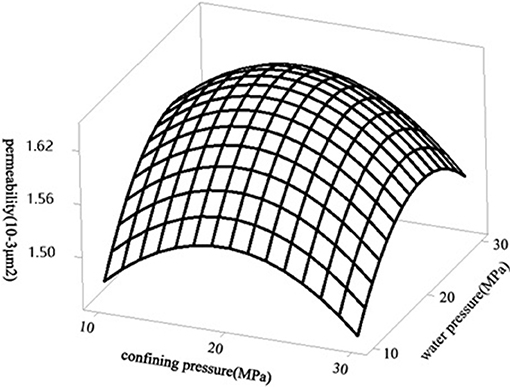
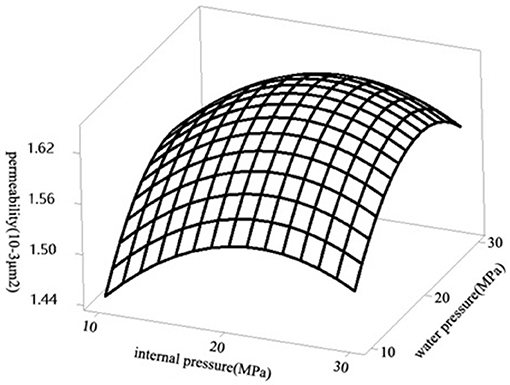
In this study, a coupling model was used to research the effect of water pressure on gas permeability. The model provides information on the effects of pressure and water pressure changes on permeability of fractured sandstone (Figure 9). The results show that the horizontal contact hydraulic hole gradually closes with the increase of axial stress. Horizontal hydraulic holes are more sensitive to axial stress than vertical ones. The pore size and pore structure of the fracture exert the main control over the pressure sensitivity, and the main seepage channels also affect the seepage characteristics, and there is a non-linear relationship.
Conclusion
An ultra-deep fractured tight sandstone gas layer from Wengfu mine in Guizhou province was selected for experimental design and study, and the effects of confining pressure, internal pressure, effective stress, and water pressure on gas permeability were investigated. The results show that in the fractured tight sandstone reservoir, keeping the confining pressure constant and constantly increasing the internal pressure, the effective stress and slippage effect compete with each other. At the beginning of the experiment, the gas slippage effect was strong while the rock stress sensitivity was relatively weak, and the gas permeability gradually decreased with the increase of internal pressure. When crossing the low point of permeability, the effective stress is stronger than slippage effect, and the gas permeability increases with the increase of internal pressure. The greater the confining pressure is, the greater the internal pressure needed to reach the low permeability point will be. With axial stress increasing, horizontal contact hydraulic hole increasingly closed. Horizontal hydraulic holes are more sensitive to axial stress than vertical ones. The damage which caused by the effective stress changing from large to small to the pore structure is irreversible, and the loss of gas permeability is large. However, the effective stress changes from small to large, and the destruction of pore structure is progressive, the loss of gas permeability is relatively small.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
BY designed the tests and wrote the paper. JX performed the tests and processed the data. SS provided funds and experimental apparatus. HLiu performed the lab tests and optimized the experimental scheme. YL collected samples. HLi was responsible for contacting the journal editor.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors gratefully acknowledge the support from the National Natural Science Foundation of China (51704110) and the Key Scientific Research Project of Hunan Education Department (18A183). The reviewers are gratefully acknowledged for their valuable comments on the manuscript.
References
Baghbanan, A., and Jing, L. (2007). Hydraulic properties of fractured rock masses with correlated fracture length and aperture. Int. J. Rock Mech. Min. 44, 704–719. doi: 10.1016/j.ijrmms.2006.11.001
Benjamin, B., Ivy, B., Bastian, K., Dirk, A., and Christoph, H. (2019). Porosity evolution of two Upper Carboniferous tight-gas-fluvial sandstone reservoirs: Impact of fractures and total cement volumes on reservoir quality. Mar. Petrol. Geol. 100, 376–390. doi: 10.1016/j.marpetgeo.2018.10.051
Blessent, D., Therrien, R., and Macquarrie, K. (2009). Coupling geological and numerical models to simulate groundwater flow and contaminant transport in fractured media. Comput. Geosci. 35, 1897–1906. doi: 10.1016/j.cageo.2008.12.008
Chen, Y. F., and Lin, H. (2019). Consistency analysis of Hoek-Brown and equivalent Mohr-coulomb parameters in calculating slope safety factor Bull. Eng. Geol. Environ. 78, 4349–4361. doi: 10.1007/s10064-018-1418-z
Davies, J. P., and Davies, D. K. (1999). “Stress-dependent permeability: characterization and modeling,” in Proceedings SPE Annual Technical Conf and Exhibition. doi: 10.2118/56813-MS
Gao, S. H., Xiong, W., Liu, X. G., Hu, Z. M., and Xue, H. (2010). Experimental research status and several novel understandings on gas percolation mechanism in low-permeability sandstone gas reservoirs. J. Nat. Gas Industry 30, 52–55.
Guglielmi, Y., Cappa, F., Rutqvist, J., Tsang, C. F., and Thoraval, A. (2008). Mesoscale characterization of coupled hydromechanical behavior of a fractured-porous slope in response to free water-surface movement. Int. J. Rock Mech. Min. 45, 862–878. doi: 10.1016/j.ijrmms.2007.09.010
Hakan, A. (2009). Percolation model for dilatancy-induced permeability of the excavation damaged zone in rock salt. Int. J. Rock Mech. Min. Sci. 46, 716–724. doi: 10.1016/j.ijrmms.2008.08.002
Jing, L., Ma, Y., and Fang, Z. (2001). Modeling of fluid flow and solid deformation for fractured rocks with discontinuous deformation analysis (DDA) method. Int. J. Rock Mech. Min. 38, 343–55. doi: 10.1016/S1365-1609(01)00005-3
Lei, D., Lin, H., Chen, Y., Cao, R., and Wen, Z. (2019). Effect of cyclic freezing-thawing on the shear mechanical characteristics of nonpersistent joints. Adv. Mater. Sci. Eng. 2019:9867681. doi: 10.1155/2019/9867681
Li, H., Li, Z. P., Wang, X. Z., Liu, Z. H., and Zhang, T. T. (2018). Imbibition model of tight sandstone based on distribution characteristics of roar. J.Sci. Technol. Eng. 18, 50–54.
Li, J., Wang, M. Y., Xia, K. W., Zhang, N., and Huang, H. X. (2017). Time-dependent dilatancy for brittle rocks. J. Rock Mech. Geotech. Eng. 9, 1054–1070. doi: 10.1016/j.jrmge.2017.08.002
Lin, H., Ding, X., Yong, R., Xu, W., and Du, S. (2019). Effect of non-persistent joints distribution on shear behavior. Compt. Rend. Mécaniq. 347, 477–489. doi: 10.1016/j.crme.2019.05.001
Lin, H., Xie, S. J., Yong, R., Chen, Y. F., and Du, S. G. (2019a). An empirical statistical constitutive relationship for rock joint shearing considering scale effect. Comp. Rend. Mecaniq. 347, 561–575. doi: 10.1016/j.crme.2019.08.001
Lin, H., Yang, H., Wang, Y., Zhao, Y., and Cao, R. (2019b). Determination of the stress field and crack initiation angle of an open flaw tip under uniaxial compression. Theoret. Appl. Fract. Mech. 104:102358. doi: 10.1016/j.tafmec.2019.102358
Liu, W., Fan, J. Y., Jiang, D. Y., Yi, L., et al. (2019). Stability study and optimization design of small-spacing two-well (SSTW) salt caverns for natural gas storages. J. Energy Storage. 27:101131. doi: 10.1016/j.est.2019.101131
Marcel, N., Udo, H., and Otto, s. (2007). Experimental investigation on anisotropy in dilatancy, failure and creep of Opalinus Clay. Phys. Chem. Earth 32, 889–895. doi: 10.1016/j.pce.2005.04.006
Mitchell, T. M., and Faulkner, D. R. (2008). Experimental measurements of permeability evolution during triaxial compression of initially intact crystalline rocks and implications for fluid flow in fault zones. J. Geophys. Res. 113:208–215. doi: 10.1029/2008JB005588
Oda, M., Takemura, T., and Aoki, T. (2002). Damage growth and permeability change in triaxial compression tests of Inada granite. Mech. Mater. 34, 313–331. doi: 10.1016/S0167-6636(02)00115-1
Ord, A. (1990). Mechanical Controls on dilatant shear zones. Geol. Soc. Lond. Spec. Publ. 54, 183–192. doi: 10.1144/GSL.SP.1990.054.01.18
Wang, H. T. (2000). Analysis of the stability of water-filled rock slope with fracture networks seepage and discrete element coupling. Hydrogeol. Eng. Geol. 27, 30–33.
Wang, J. A., and Park, H. D. (2002). Fluid permeability of sedimentary rocks in a complete stress-strain process. Eng. Geol. 63, 291–300. doi: 10.1016/S0013-7952(01)00088-6
Worthington, P. F. (2008). A diagnostic approach to quantifying the stress sensitivity of permeability. J. Petrol. Sci. Eng. 61, 49–57. doi: 10.1016/j.petrol.2008.03.003
Wu, Y. Q., Cao, G. Z., and Ding, W. H. (2005). Experimental study on relation between seepage and stress of sandstone in CT scale. Chin. J. Rock Mech. Eng. 23, 4204–4209.
Xiang, Z. W., Qiao, X. Y., Mi, N. Z., and Wang, R. G. (2019). Technologies for the benefit development of low-permeability tight sandstone gas reservoirs in the Yan'an Gas Field, Ordos Basin. J. Natural Gas Industry B 6, 272–281. doi: 10.1016/j.ngib.2018.11.017
Yang, F., Zhang, G. C., Fan, S. S., Xiao, C. W., and Chen, W. Z. (2012). The permeability of fractured tight sandstone reservoirs is evaluated by stoneley wave. J. Oil Gas Technol. 34, 88–92.
You, L., Wang, Z., Kang, Y., Zhao, Y., and Zhang, D. (2018). Experimental investigation of porosity and permeability change caused by salting out in tight sandstone gas reservoirs. J. Nat. Gas Geosci. 3, 347–352. doi: 10.1016/j.jnggs.2018.12.003
Yu, J., Li, H., and Chen, X. (2013). Triaxial experimental study of associated permeability-deformation of sandstone under hydromechanical coupling. China. J. Rock Mech. Eng. 32, 1204–1213. doi: 10.3969/j.issn.1000-6915.2013.06.014
Zhao, Y. l, Wang, Y. X., Wang, W. J., Tang, L. M., and Liu, Q. (2019). Modeling of rheological fracture behavior of rock cracks subjected to hydraulic pressure and far field stresses. Theor. Appl. Fract. Mech. 101, 59–66. doi: 10.1016/j.tafmec.2019.01.026
Zhao, Y. L., Tang, J. Z., Chen, Y., Zhang, L. Y., Wang, W. J., Wan, W., et al. (2017a). Hydromechanical coupling tests for mechanical and permeability characteristics of fractured limestone in completestress–strain process. Environ. Earth Sci. 76, 1–18. doi: 10.1007/s12665-016-6322-x
Zhao, Y. L., Wang, Y. X., Wang, W. J., Wan, W., and Tang, J. Z. (2017b). Modeling of non-linear rheological behavior of hard rock using triaxial rheological experiment[J]. Int. J. Rock Mech. Min. Sci. 93, 66–75. doi: 10.1016/j.ijrmms.2017.01.004
Zhao, Y. L., Zhang, L. Y., Wang, W. J., Pu, C. Z., Wan, W., and Tang, J. Z. (2016). Cracking and stress-strain behavior of rock-like material containing two flaws under uniaxial compression. Rock Mech. Rock Eng. 49, 2665–2687. doi: 10.1007/s00603-016-0932-1
Zhao, Y. L., Zhang, L. Y., Wang, W. J., Tang, J. Z., Lin, H., and Wan, W. (2017c). Transient pulse test and morphological analysis of single rock fractures. Int. J. Rock Mech. Min. Sci. 91, 139–154. doi: 10.1016/j.ijrmms.2016.11.016
Zhao, Y. L., Zhang, L. Y., Wang, W. J., Wan, W., and Ma, W. (2018). Separation of elastoviscoplastic strains of rock and a nonlinear creep model. Int. J. Geomech. 1:04017129. doi: 10.1061/(ASCE)GM.1943-5622.0001033
Keywords: fractured sandstone, stress, the water pressure, gas permeability, the response surface method
Citation: You B, Xu J, Shi S, Liu H, Lu Y and Li H (2020) Effect of Stress and Water Pressure on Permeability of Fractured Sandstone Based on Response Surface Method. Front. Earth Sci. 8:11. doi: 10.3389/feart.2020.00011
Received: 13 December 2019; Accepted: 20 January 2020;
Published: 06 February 2020.
Edited by:
Hang Lin, Central South University, ChinaCopyright © 2020 You, Xu, Shi, Liu, Lu and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bo You, NDk0OTA3MzM2QHFxLmNvbQ==
 Bo You
Bo You Jiaxin Xu1
Jiaxin Xu1