Crack Failure Characteristics of Different Rocks Under the Action of Frost Heaving of Fissure Water

Introduction

Coupled with the complex geological conditions, the freezing and thawing problems in the alpine mountains are incredibly prominent with the large-scale construction of projects in the alpine mountains. Engineering problems related to freezing–thawing urgently need to be solved (Chen and Lin, 2019). The problem of freezing and thawing in the alpine mountains comes not only from the temperature difference between day and night during the construction process, but also from the influence of severe weather such as freezing rain, snow, hail, chemical corrosion, and so on (Style and Peppin, 2012; Lin et al., 2019a,b). These factors cause the freezing–thawing effect in fractured rock mass to be more intense (Brideau et al., 2006; Matsuoka and Murton, 2008; Liu et al., 2016). The influence of water on rock brittleness and rock mass stability is studied here. The weakening effects of water and the influence of underground water on the stability of surrounding rock were studied from an energy viewpoint (Chen et al., 2017, 2019). The frequent freezing and thawing of pore water inside rock expands the cracks and pores and promotes the development of new micro-fractures (Park et al., 2015) and thus does excessive damage to rock engineering (Demirdag, 2013; Wang et al., 2019). In the process of the freezing–thawing cycle, rainfall infiltration causes microscopic rock damage, frost heave, and instability.

At present, the research on freezing–thawing effect has made many achievements. The research results mainly focus on the theoretical model of freeze–thaw damage, the mechanism of freeze–thaw damage, and the influencing factors of damage. Yavuz et al. (2006) did experiments on the freezing–thawing cycle and mechanical properties of 12 kinds of carbonate rocks. The degradation model of a rock was obtained by multiple regression analyses. A series of freeze–thaw damage models based on laboratory tests and theoretical deduction was proposed (Yang et al., 2002; Pudasaini and Krautblatter, 2014). The parties listed above conducted research on the freeze–thaw damage model. Following this, research of freeze–thaw damage mechanism and influencing factors was conducted. It was found that water content has a certain influence on freezing–thawing damage of rock through the freezing–thawing failure test of tuff with different water contents (Chen et al., 2004). Wang et al. (2016) reviewed the freeze–thaw weathering of rocks in cold regions. They pointed out that the process of ice segregation in the crack was the main cause of crack growth. The results of the deformation and failure characteristics under single and multiple freezing–thawing cycles were also obtained (Yamabe and Neaupane, 2001; Stacey, 2016; Lu et al., 2019). However, most of the above studies focus on the effect of micro-fractures in intact rocks. There are few studies on macroscopic fractures, especially on freezing–thawing experiments after water fills in fractures. However, it has been shown that the structural surface—or the large crack—often plays a controlling role in the stability of a rock mass (Zhao et al., 2016, 2017a,b,c). Thus, the freezing and thawing on the macroscopic fractures is worth further study in the alpine region. Based on the theory of fracture mechanics, the fracture characteristics of different lithological specimens caused by local damage under the freezing–thawing cycle were analyzed using the numerical simulation software FLAC3D. It was found that the joint structure in the rock controls the damage path of the freezing–thawing damage. The structure of rock itself has a significant influence on crack propagation. The following research results can provide a reference for the freezing–thawing splitting effect caused by rainwater infiltration in the alpine area.

Test Program and Results

Preparation of Rock Specimens

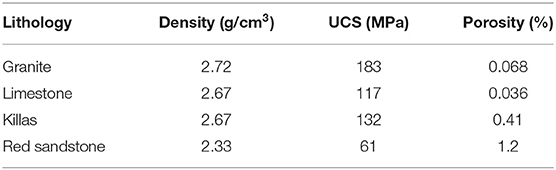
The rocks used in the experiment are four different lithologic rocks (granite, limestone, killas, and red sandstone) commonly found in the Zheduo Mountain (101°48′E, 30°06′N) within the Sichuan–Tibet line research area (Figure 1). Located in Ganzi Prefecture in Sichuan province, China, the Zheduo mountain is 4,298 meters above sea level. The mountain is an important geographical dividing line, with the plateau uplift to the west and the mountain canyon to the east. The specimens were obtained by using the water-drilling method, and the specimens were prepared as cylinders with a diameter of 50 mm and a height of 100 mm. The allowable deviation of non-parallelism of the two ends is ± 0.05 mm, and the allowable deviation of perpendicularity is ± 0.25°. We performed acoustic tests on the rock to ensure its integrity and uniformity. Integrity and uniformity met the test requirements. The experimental parameters of the intact rock specimen are shown in Table 1.

FIGURE 1

Figure 1. Satellite image of Zheduo mountain.

TABLE 1

Table 1. Basic rock parameters.

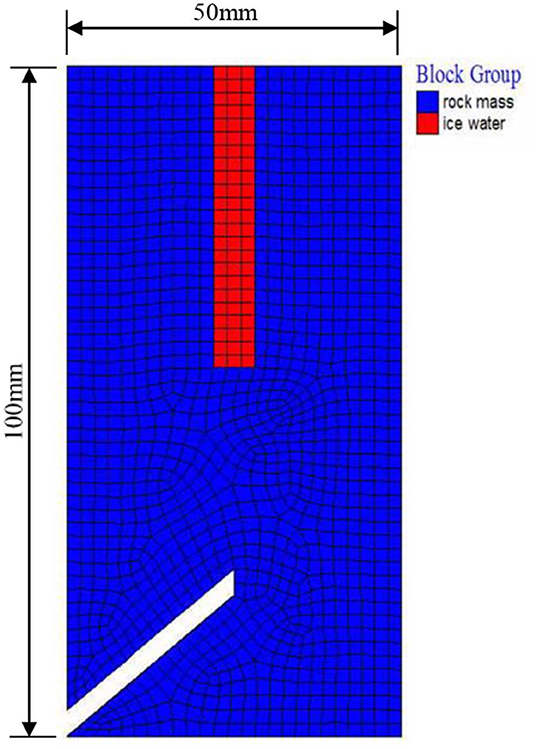
The pre-formed crack specimen was processed on the basis of the complete test piece. The purpose was to simulate the tension crack at the top of the slope and the unloading crack at the bottom of the slope, and to study the freezing and thawing ice-splitting effect caused by rainfall through the infiltration rock mass at the top of the slope. The specimen had two joints, one of which ran vertically downward from the middle of the upper top surface and the other which ran obliquely upward 45° from the lower-left corner of the specimen. The depth and width of the upper crack were 45 and 6 mm, respectively; the length of the rock bridge was 30 mm; and the width of the lower crack was 3 mm. The prepared rock specimen is shown in Figure 2. In order to reduce the experimental error caused by the defects of the specimen itself, the longitudinal wave velocity test and the density test were performed on all the specimens prior to the test, and the specimens with relatively close wave speed and density were selected for testing. The test divided the specimens into four groups according to the number of freezing–thawing cycles they were subjected to: 20 times, 45 times, and 60 times, respectively. Four types of lithology were tested in each group, with three specimens of each lithology (parallel test) and 27 specimens in total. The test was conducted in accordance with the Chinese standard for test methods of engineering rock mass (GBT 50266-2013).

FIGURE 2

Figure 2. Cracked rock specimen preparation. (A) Cracked rock specimen. (B) Cracked specimen model.

Test Program

A freeze–thaw tester with a TEMI 580 temperature and humidity regulator was used. This device uses a programmable controller to set the temperature and humidity, which can significantly eliminate the errors caused by human factors. The temperature control scope ranges from −40 to 150°C, with an accuracy of ± 0.1°C; humidity control ranges from 0 to 100% RH with a precision of ± 0.1% RH.

The freezing temperature in the automatic freeze–thaw cycle test chamber is −20°C. The melting temperature is 20°C. The temperature drop rate is set to V = 4°C/min. The freezing–thawing cycles were 15, 30, 45, and 60 min, respectively. Due to the large temperature difference between daytime and nighttime in the research area of the Zheduo mountain, the test set the freezing time for 1 h and the thawing time for 1 h in order to study the failure characteristics of the rock freezing–thawing cycle in a short period. The cycle time was 2 h. The 2 h cycle meets the requirements of complete freezing and complete ablation of water through the pre-test. The upper crack of the rock specimen was sealed with 704 silicone rubber paste and flexible material. The water with the same height as the crack was injected. In time, water was injected to avoid excessive evaporation. The rock specimen was placed in the freeze–thaw test chamber. The crack propagation and failure of different lithologic rock specimens were observed.

Test Results

The characteristics of cracked rock specimens after different cycles (20, 45, and 60 min) of freezing–thawing were observed according to the photos of typical rock specimens. The types of crack damage caused by freeze–thaw were classified into the following four types (Table 2).

TABLE 2

Table 2. Freeze–thaw failure processes with different cycles.

It can be seen from the red sandstone failure processes that the depth of crack penetration along the rock bridge is deepened with the increase of the number of freeze–thaw cycles (Table 2). No secondary cracks and wing cracks appear during the crack propagation process.

Stress concentration was formed at the end of the upper crack in limestone. The crack expands at a low angle. It can be seen from the limestone failure processes that the depth of crack penetration along the rock bridge is deepened with an increase in the number of freeze–thaw cycles (Table 2). No secondary cracks and wing cracks appeared during the crack propagation process.

The length of the circumferential crack in killas increased with the increase of the number of freeze–thaw cycles (Table 2). The crack of the killas freezing–thawing 60 times from the half-circle crack of the freeze–thaw cycle became a ring crack. The killas under 60 freezing–thawing cycles developed from a half-circle cracks with 20 freezing–thawing cycles to a circle of cracks.

The granite show no obvious signs of deformation and failure (Table 2). However, this does not mean that the freezing–thawing does not affect and destroy granite. Freezing–thawing of crack water will positively affect the mechanical properties of granite.

It is helpful to take reasonable measures to prevent and control the freezing–thawing damage in alpine and cold mountain areas by analyzing the causes of damage in cracked rocks under the action of the freezing–thawing cycle. It can be observed from Figure 3 that the rocks of four lithologies correspond to four failure types. Red sandstone mineral particles are evenly distributed without an obvious soft surface. Stress concentration is formed at the tops crack tip under the repeated action of freezing–thawing load. As a relatively weak part of the rock, the crack continues to expand downward along the rock bridge and has a tendency to penetrate the rock bridge. Three sets of nearly vertical joints are developed in limestone, which are potential weak parts of the rock. The limestone may develop a set of weak faces along the tip of the upper crack with the opposite dip to the lower crack. It leads to crack propagation and penetration failure along the shortest path and the surface with lower strength. Killas develop parallel planes perpendicular to the vertical direction, which are potential weak surfaces with low strength and softening when exposed to water. The water in the upper crack has the horizontal load of reciprocating action under the freezing–thawing cycle. This is the reason why the rock initiates cracks along the weak surface and expands along the ring. Granite has high strength and excellent mechanical properties. It is hard, with low porosity. Therefore, less water seeps into the rock. The frost-heaving force produced by water in the upper crack is unlikely to initiate the crack. Frost heaving has a weak effect on rocks.

FIGURE 3

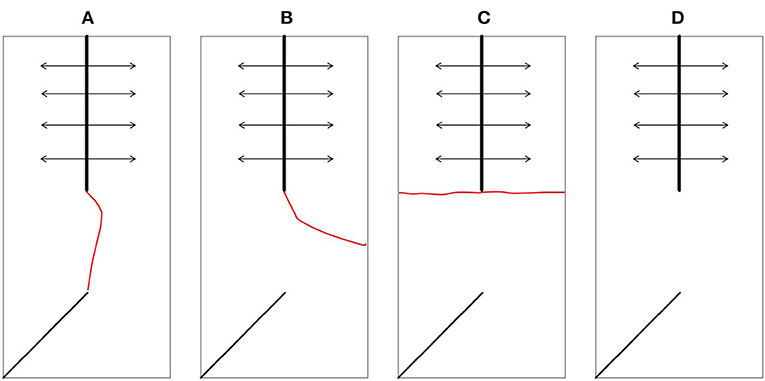
Figure 3. Freezing–thawing failure characteristics of specimens. (A) Red Sandstone. (B) Limestone. (C) Killas. (D) Granite.

Failure Characteristics of Cracked Rock

Fracture Mechanics Analysis of Cracked Rock

Due to the existence of the crack, the rock mass easily produced directional damage along the ends of the cracks under the action of external loads, thus exhibiting typically localized damage phenomena. The experimental research object was simplified into a plane strain problem. For the equal-width, vertical, and fully frozen fractures, the internal frost heave model can be simplified to the normal-strain tension model before the macro-cracks are produced (Zhou et al., 2011). It is a pure mode-I fracture based on the idea of fracture mechanics. The corresponding stress intensity factor expression is

$\begin{array}{ll}{K}_1={\sigma }_y\sqrt{\pi a}& (1)\end{array}$

where σ_f is the effective frost-heaving stress inside and outside of the crack, σ_y is the difference between the frost-heaving stress inside the crack [σ_y(in)] and the frost heaving stress outside the crack [σ_y(out)]. a is the semi-length (m) of the crack.

For a pure mode-I fracture, K₁ > K_1c when (stress intensity factor threshold), the crack begins to break under the action of repeated freeze–thaw cycles. The breaking angle β is 0°. Therefore, the critical value of the maximum principal stress in the initial crack zone is the tensile strength (σ_t) of the rock. The corresponding initial crack growth length r₀ is

$\begin{array}{ll}{r}_0=\frac{1}{2}\pi \left(\frac{K_{IC}}{{\sigma }_t}\right)& (2)\end{array}$

Considering the size estimation of the plastic zone, and starting from the progressive damage zone at the crack tip, the expressions of the three principal stresses at the tip of the mode-I fracture are as follows

$\begin{array}{ll}\begin{array}{c}{\sigma }_1=\frac{K_I}{2\sqrt{2\pi r}}\text{c}\text{o}\text{s}\frac{\theta }{2}(3-\text{cos}\theta )\\ {\sigma }_2=\frac{K_{{}_I}}{2\sqrt{2\pi r}}\text{c}\text{o}\text{s}\frac{\theta }{2}(1+\text{c}\text{o}\text{s}\theta )\\ {\sigma }_3=\frac{K_{{}_I}}{2\sqrt{2\pi r}}\text{c}\text{o}\text{s}\frac{\theta }{2}sin\theta \end{array}& (3)\end{array}$

where r is the polar coordinate radius; θ is the polar coordinate angle.

According to the maximum circumferential tensile stress criterion, the crack propagates in the direction of theta corresponding to σ_2max. The direction meets the following conditions:

$\begin{array}{ll}\frac{\partial {\sigma }_2}{\partial \theta }\text{=}0,\frac{{\partial }^2{\sigma }_2}{\partial {\theta }^2}<0& (4)\end{array}$

Differentiate the second formula in (2). The breaking Angle is determined by the following equation: K₁ sin θ = 0 Therefore, θ = 0.

When θ = 0, the size of the plastic zone along the direction of the breaking angle is

$\begin{array}{ll}{r}_{0y}=\frac{K_I^2}{2\pi {\sigma }_2^2}& (5)\end{array}$

When both K_Iand σ_y reach the critical state of fracture, the progressive damage in this direction is transformed into a macroscopic fracture.

This theory can explain the fracture process of red sandstone with good uniformity. The initial crack can be considered as the fracture process of a pure mode-I fracture in the freezing–thawing cycle. The initial expansion direction should be approximately consistent with the strike angle. Extension length is related to fracture toughness and tensile strength of rock. When the critical state is reached, the crack breaks and the progressive damage zone is transformed into the fracture zone. The conclusion is consistent with the laboratory test. The initial expansion of the crack extends from the end along the crack while under the process of freezing and thawing.

Numerical Simulation of Freeze–Thaw Cycle

In order to further study rocks with natural bedding, the finite difference calculation software FLAC3D was used for numerical simulation. The frost-heaving force in cracked rock mass is closely related to the properties of rock mass and water–ice medium. This is mainly reflected in the Poisson's ratio, elastic modulus of rock and water-ice medium, and the equivalent volume expansion coefficient of water–ice medium (Liu et al., 2016; Zhou et al., 2018). Killas specimens with natural bedding are selected as representatives for simulation. FLAC3D numerical simulation software was used to approximate the killas as a transversely isotropic material. The rock mechanics model was adopted as a spreading joint model. The foliation plane is perpendicular to the rock bridge. Joint surface, rock cohesion, internal friction angle, and tensile strength were determined, respectively. The ice mechanics model uses an elastic model. The ice mechanics model adopts elastic model. The hydraulic model adopts the empty model. All thermal models adopt isotropic temperature models. Relevant parameters are shown in Table 3: E is the modulus of elasticity (GPa); μ is Poisson's ratio; c is cohesion (MPa); ϕ is the internal friction angle (°); σ_t is the tensile strength (MPa); cohesion, internal friction angle, and tensile strength were assigned to the rock and joint, respectively; k is the coefficient of heat conduction [W ▪ (^m°C)−1]; α_t is the coefficient of linear expansion (10⁻⁶ ▪ °C⁻¹); ρ is density (kg ▪ m^-3); and C_v is the specific heat capacity [J ▪ (k^g°C)−1].

TABLE 3

Table 3. Model mechanical and thermal parameters.

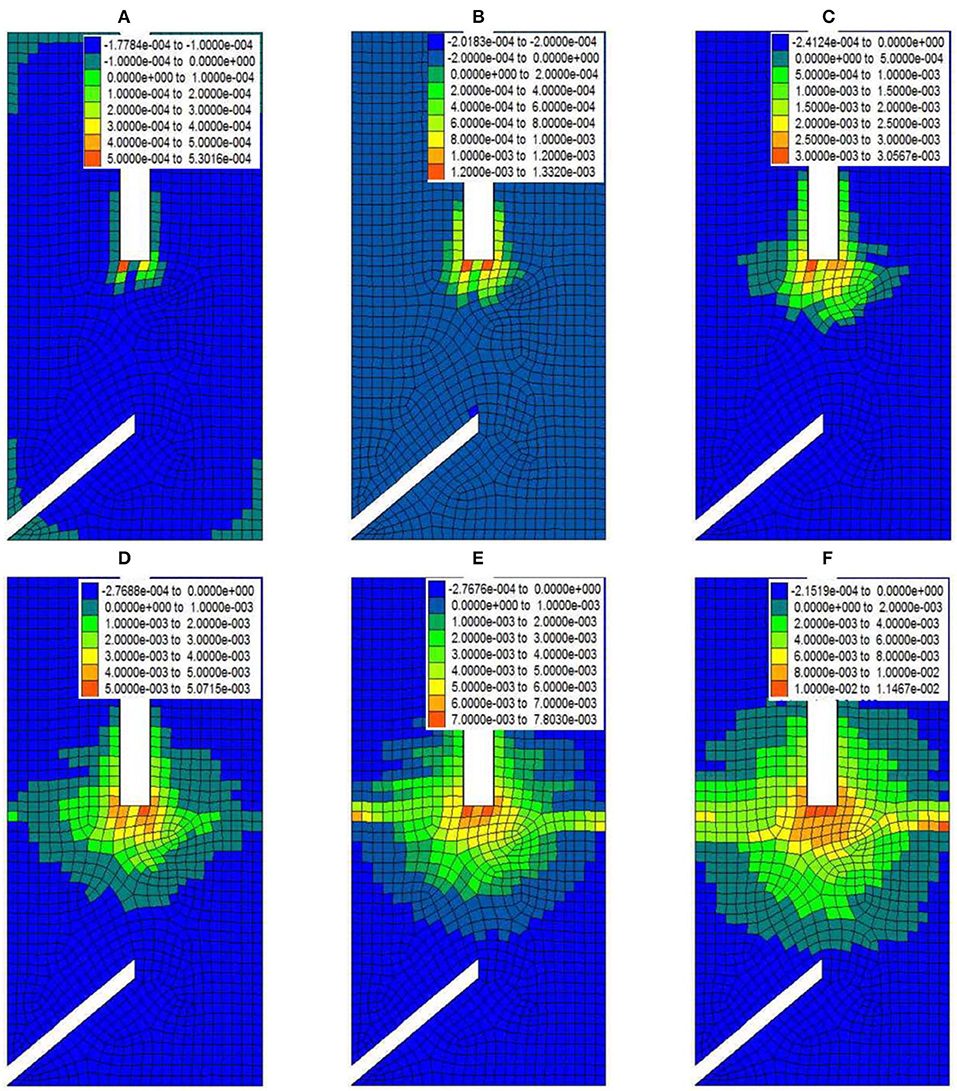
The grid division of the plane model is shown in Figure 4. It is divided into two groups, rock mass and ice water, with a total of 1,270 units and 2,726 nodes. The blue grid is the rock mass. The red grid is the ice water. The green grid is the fracture. The mesh size is 2 mm. The boundary condition is the bottom vertical constraint. The temperature boundary condition is constant temperature around. The change in temperature with time is shown in Table 4.

FIGURE 4

Figure 4. Model meshing.

TABLE 4

Table 4. Boundary temperature varies with time.

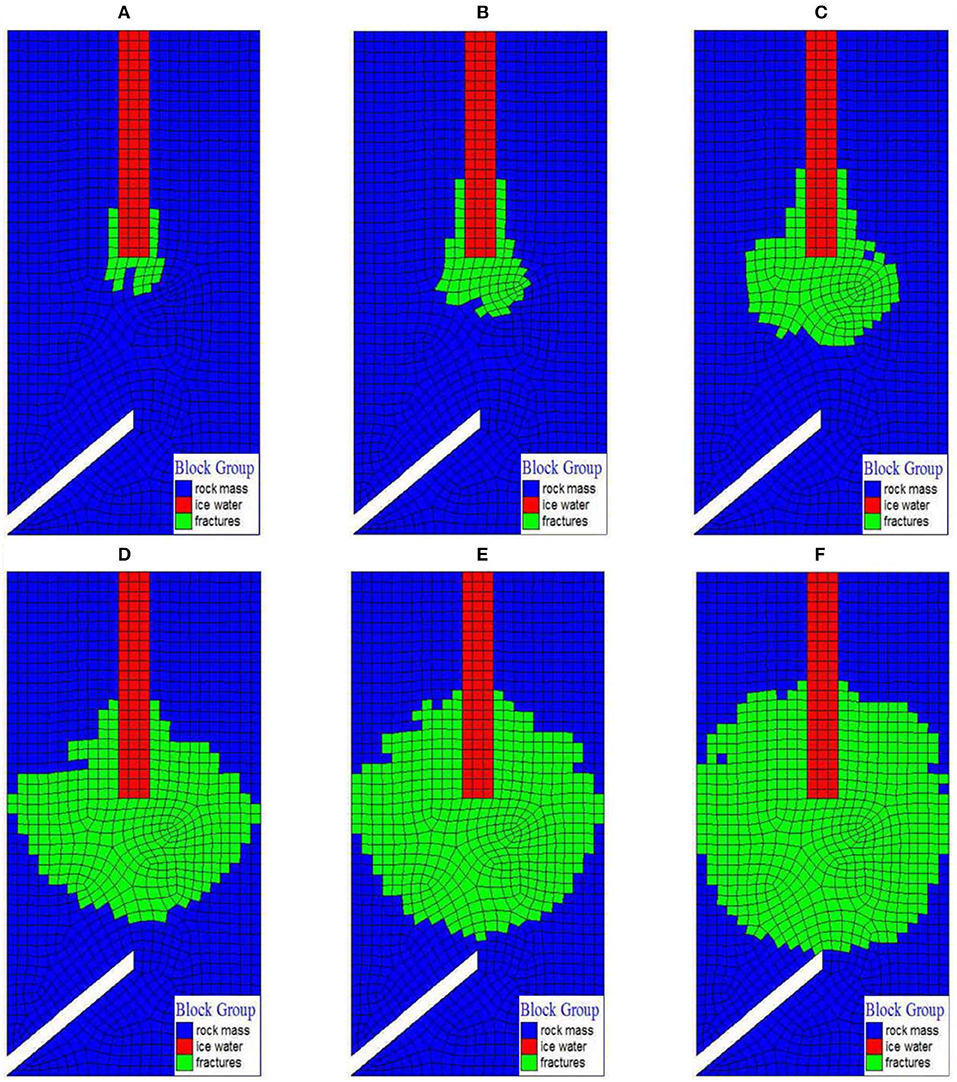
The frost-heaving force in the freezing–thawing process causes the tensile stress inside the rock mass to exceed its tensile strength. The frost-heaving force can result in tensile failure in the freezing–thawing process. The volume of rock and soil increases. Therefore, it is appropriate to use volumetric strain increment (VSI) as a quantitative indicator of tensile cracks in rocks. The yielding rock mass group unit is redefined as the fracture group. Based on the dynamic distribution process diagram of fractures group and VSI indicators, the propagation trend of cracks with the increase of the number of freezing–thawing cycles was analyzed. The simulation results are shown in Figures 5, 6.

FIGURE 5

Figure 5. (A–F) Distribution process diagram of killas specimen fractures' formation.

FIGURE 6

Figure 6. (A–F) Diagram of VSI distribution process of killas specimen.

It can be seen from Figure 5 that the killas specimen is first destroyed at the upper crack tip as the number of freeze–thaw cycles increase. Then, it expands to both sides, gradually passing through the loop, and finally the rock specimen is damaged. It can be observed from Figure 1 that the maximum value of volumetric strain increment starts from the tip of the upper crack, then it expands to both sides along the rock bridge and penetrates in a circle. Finally, the rock specimen is damaged. It can be seen from Figures 5, 6 that the crack growth of the specimen killas model starts from the top of the rock bridge and extends along the vertical rock bridge. This is basically consistent with the results of the freeze–thaw test. The fracture mechanics analysis results of red sandstone and the numerical simulation results of killas show that, under the action of freezing–thawing cycle, the crack of the fractured rock mass will expand along the direction of the weak structural plane when the rock mass has an obvious weak structural plane. Killas and limestone belong to this type of damage. The crack will expand along the direction of the rock bridge when the rock mass is homogeneous. Red sandstone belongs to this type of damage.

Discussion

The freezing–thawing cycle is a very important inducement of rock mass failure in the alpine mountains. Most of the studies related to freezing–thawing are conducted with intact rocks under different cycles of freezing–thawing (Tan et al., 2011; Song et al., 2015; Wang et al., 2017).

The damage mechanism of micro-cracks in rocks under freezing–thawing action is studied, without considering that macro-cracks may have a more significant impact. In this paper, freezing–thawing tests were carried out at different times after water was filled in the cracks for specimens of four different types of lithology.

The experimental results show that the internal structure of the rock largely determines the failure type of the rock, especially the control function of the weak structure surface. The rock structure has more influence on the rock failure mode compared with the influence of pre-fabricated cracks. The repeated freezing–thawing cycle of fissure water is a process of repeated fatigue loading and unloading on the end of the fissure, which does not necessarily exceed the tensile strength of rock. The initial crack propagation length of homogeneous rock is related to fracture toughness and tensile strength of rock. Indeed, Park and colleagues came to the same conclusion (Park et al., 2015). The influence of water in freezing–thawing cycles in macroscopic cracks is highlighted compared with the previous research results (Zhang et al., 2004; Fatih, 2012; Lai et al., 2012).

However, there are some shortcomings in this paper. During testing, less water permeated into the rock through the upper crack, turning into pore water. The effects of freezing and thawing on the pore water have not been considered. The frost heaving force generated by pore water in the rock may cause some damage to the rock. However, due to the small porosity and less water infiltration of the selected specimen in this test, it was ignored in this paper. The experimental conditions are still different from the real rock mass environment. Not only that, the fracture arrangement has some particularity. It can only represent one fracture combination. But the distribution of cracks in engineering varies greatly. Therefore, whether the research results can be directly applied to actual engineering practices remains to be further studied. The research results can provide a reference for the freezing–thawing splitting effect caused by rainwater infiltration in the alpine area. In future studies, we will consider how to avoid this situation and how to conduct further research on the effect of fissure water.

Conclusion

After water filled the cracks of rocks, freeze–thaw cycle tests of different times were carried out, and the failure characteristics of four different lithological specimens were analyzed by means of fracture mechanics and numerical simulation. The following conclusions were obtained:

(1) There are four types of fracture rock freeze–thaw failures: passing through the rock bridge along the tip of the upper crack; expanding in the opposite direction of the lower crack along the upper crack tip; extending circumferentially along the tip of the upper crack; and no visible damage to the rock specimen.

(2) The type of crack propagation is obviously influenced by the structure and strength of rock mass. Rocks with good homogeneity tend to spread along rock bridges; it expands along the weak structural plane when there is a weak structural plane (or natural bedding) in the rock. The fracture water freeze–thaw cycle is essentially a process of repeated fatigue loading and unloading of fracture ends. The crack propagation depth increases with the increase of freezing–thawing times, and all of them germinate from the tip of the upper crack.

(3) Based on fracture mechanics, the fracture characteristics of the initial extension end of cracks in red sandstone under the freezing–thawing cycle were analyzed. The initial crack in homogeneous rock specimen can be considered as a pure mode-I fracture. Crack propagation length is related to fracture toughness and tensile strength of rock.

Data Availability Statement

All datasets for this study are included in the article/supplementary material.

Author Contributions

GZ and ZX did the majority of rock sample collection. GC carries out the numerical modeling writing for this paper. YY and ZL carry out the Freeze-thaw test. All authors contributed extensively to the review and revision of this paper.

Funding

This work was supported by the National Key R&D Program of China (2017YFC1501301), National Natural Science Foundation of China (Grant Nos. 41521002 and 41972284), and Funding of Science and Technology Office of Sichuan Province (Grant No. 2017TD0018).

Conflict of Interest

GZ, ZX, and ZL were employed by company China Railway Eryuan Engineering Group Co. Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Brideau, M. A., Stead, D., and Couture, R. (2006). Structural and engineering geology of the East Gate Landslide, Purcell Mountains, British Columbia, Canada. Eng. Geol. 84, 183–206. doi: 10.1016/j.enggeo.2006.01.004

CrossRef Full Text | Google Scholar

Chen, G., Li, T., Guo, F., and Wang, Y. (2017). Brittle mechanical characteristics of hard rock exposed to moisture. Bull. Eng. Geol. Environ. 76, 219–230. doi: 10.1007/s10064-016-0857-7

CrossRef Full Text | Google Scholar

Chen, G., Li, T., Wang, W., Zhu, Z., Chen, Z., and Tang, O. (2019). Weakening effects of the presence of water on the brittleness of hard sandstone. Bull. Eng. Geol. Environ. 78, 1471–1483. doi: 10.1007/s10064-017-1184-3

CrossRef Full Text | Google Scholar

Chen, T. C., Yeung, M. R., and Mori, N. (2004). Effect of water saturation on deterioration of welded tuff due to freeze-thaw action. Cold Reg. Sci. Technol. 38, 127–136. doi: 10.1016/j.coldregions.2003.10.001

CrossRef Full Text | Google Scholar

Chen, Y., and Lin, H. (2019). Consistency analysis of Hoek–brown and equivalent mohr–Coulomb parameters in calculating slope safety factor. Bull. Eng. Geo. Environ. 78, 4349–4361. doi: 10.1007/s10064-018-1418-z

CrossRef Full Text | Google Scholar

Demirdag, S. (2013). Effects of freezing–thawing and thermal shock cycles on physical and mechanical properties of filled and unfilled travertines. Constr. Build Mater. 47, 1395–1401. doi: 10.1016/j.conbuildmat.2013.06.045

CrossRef Full Text | Google Scholar

Fatih, B. (2012). Predicting mechanical strength loss of natural stones after freeze–thaw in cold regions. Cold Reg. Sci. Technol. 83–84, 98–102. doi: 10.1016/j.coldregions.2012.07.003

CrossRef Full Text | Google Scholar

Lai, Y., Zhang, S., and Yu, W. (2012). A new structure to control frost boiling and frost heave of embankments in cold regions. Cold Reg. Sci. Technol. 79–80, 53–66. doi: 10.1016/j.coldregions.2012.04.002

CrossRef Full Text | Google Scholar

Lin, H., Xie, S., Yong, R., Chen, Y., and Du, S. (2019a). An empirical statistical constitutive relationship for rock joint shearing considering scale effect. Comptes Rendus Mécanique 347, 561–575. doi: 10.1016/j.crme.2019.08.001

CrossRef Full Text | Google Scholar

Lin, H., Yang, H., Wang, Y., Zhao, Y., and Cao, R. (2019b). Determination of the stress field and crack initiation angle of an open flaw tip under uniaxial compression. Theor. Appl. Fract. Mech. 104:102358. doi: 10.1016/j.tafmec.2019.102358

CrossRef Full Text | Google Scholar

Liu, J., Chang, D., and Yu, Q. (2016). Influence of freeze-thaw cycles on mechanical properties of a silty sand. Eng. Geol. 210, 23–32. doi: 10.1016/j.enggeo.2016.05.019

CrossRef Full Text | Google Scholar

Lu, Z., Xian, S., Yao, H., Fang, R., and She, J. (2019). Influence of freeze-thaw cycles in the presence of a supplementary water supply on mechanical properties of compacted soil. Cold Reg. Sci. Technol. 157, 42–52. doi: 10.1016/j.coldregions.2018.09.009

CrossRef Full Text | Google Scholar

Matsuoka, N., and Murton, J. (2008). Frost weathering: recent advances and future directions. Permafr. Periglac. Process. 19, 195–210. doi: 10.1002/ppp.620

CrossRef Full Text | Google Scholar

Park, J., Hyun, C. U., and Park, H. D. (2015). Changes in microstructure and physical properties of rocks caused by artificial freeze–thaw action. Bull. Eng. Geol. Environ. 74, 555–565. doi: 10.1007/s10064-014-0630-8

CrossRef Full Text | Google Scholar

Pudasaini, S. P., and Krautblatter, M. (2014). A two-phase mechanical model for rock-ice avalanches. J. Geophys. Res. Earth Surf. 119, 2272–2290. doi: 10.1002/2014JF003183

CrossRef Full Text | Google Scholar

Song, D., Wang, E., Li, Z., Liu, J., and Xu, W. (2015). Energy dissipation of coal and rock during damage and failure process based on EMR. Int. J. Min. Sci. Technol. 25, 787–795. doi: 10.1016/j.ijmst.2015.07.014

CrossRef Full Text | Google Scholar

Stacey, T. R. (2016). Addressing the consequences of dynamic rock failure in underground excavations. Rock Mech. Rock Eng. 49, 4091–4101. doi: 10.1007/s00603-016-0922-3

CrossRef Full Text | Google Scholar

Style, R. W., and Peppin, S. S. (2012). The kinetics of ice-lens growth in porous media. J. Fluid Mech. 692, 482–498. doi: 10.1017/jfm.2011.545

CrossRef Full Text | Google Scholar

Tan, X., Chen, W., Yang, J., and Cao, J. (2011). Laboratory investigations on the mechanical properties degradation of granite under freeze–thaw cycles. Cold Reg. Sci. Technol. 68, 130–138. doi: 10.1016/j.coldregions.2011.05.007

CrossRef Full Text | Google Scholar

Wang, P., Xu, J., and Fang, X. (2017). Energy dissipation and damage evolution analyses for the dynamic compression failure process of red-sandstone after freeze-thaw cycles. Eng. Geol. 221, 104–113. doi: 10.1016/j.enggeo.2017.02.025

CrossRef Full Text | Google Scholar

Wang, P., Xu, J., Liu, S., Liu, S., and Wang, H. (2016). A prediction model for the dynamic mechanical degradation of sedimentary rock after a long-term freeze-thaw weathering: considering the strain-rate effect. Cold Reg. Sci. Technol. 131, 16–23. doi: 10.1016/j.coldregions.2016.08.003

CrossRef Full Text | Google Scholar

Wang, Y., Lin, H., Zhao, Y., Li, X., Guo, P., and Liu, Y. (2019). Analysis of fracturing characteristics of unconfined rock plate under edge-on impact loading. Eur. J. Environ. Civil Eng. 1–16. doi: 10.1080/19648189.2018.1509021

CrossRef Full Text | Google Scholar

Yamabe, T., and Neaupane, K. M. (2001). Determination of some thermomechanical properties of Sirahama sandstone under subzero temperature condition. Int. J. Rock Mech. Mining Sci. 38, 1029–1034. doi: 10.1016/S1365-1609(01)00067-3

CrossRef Full Text | Google Scholar

Yang, G. S., Yibin, P. U., and Wei, M. A. (2002). Discussion on the damage propagation for the rock under the frost and thaw condition of frigid zone. J. Exp. Mech. 17, 220–226.

Google Scholar

Yavuz, H., Altindag, R., Sarac, S., Ugur, I., and Sengun, N. (2006). Estimating the index properties of deteriorated carbonate rocks due to freeze–thaw and thermal shock weathering. Int. J. Rock Mech. Min. Sci. 43, 767–775. doi: 10.1016/j.ijrmms.2005.12.004

CrossRef Full Text | Google Scholar

Zhang, S., Lai, Y., Zhang, X., Pu, Y., and Yu, W. (2004). Study on the damage propagation of surrounding rock from a cold-region tunnel under freeze–thaw cycle condition. Tunnel. Underground Space Technol. 19, 295–302. doi: 10.1016/j.tust.2003.11.011

CrossRef Full Text | Google Scholar

Zhao, Y., Wang, Y., Wang, W., Wan, W., and Tang, J. (2017a). Modeling of non-linear rheological behavior of hard rock using triaxial rheological experiment. Int. J. Rock Mech. Min. Sci. 93, 66–75. doi: 10.1016/j.ijrmms.2017.01.004

CrossRef Full Text | Google Scholar

Zhao, Y., Zhang, L., Wang, W., Pu, C., Wan, W., and Tang, J. (2016). Cracking and stress–strain behavior of rock-like material containing two flaws under uniaxial compression. Rock Mech. Rock Eng. 49, 2665–2687. doi: 10.1007/s00603-016-0932-1

CrossRef Full Text | Google Scholar

Zhao, Y., Zhang, L., Wang, W., Tang, J., Lin, H., and Wan, W. (2017b). Transient pulse test and morphological analysis of single rock fractures. Int. J. Rock Mech. Min. Sci. 91, 139–154. doi: 10.1016/j.ijrmms.2016.11.016

CrossRef Full Text | Google Scholar

Zhao, Y., Zhang, L., Wang, W., Wan, W., and Ma, W. (2017c). Separation of elastoviscoplastic strains of rock and a nonlinear creep model. Int. J. Geomechanics 18:04017129. doi: 10.1061/(ASCE)GM.1943-5622.0001033

CrossRef Full Text | Google Scholar

Zhou, Y. X., Xia, K. W., Li, X. B., Li, H. B., Ma, G. W., Zhao, J., et al. (2011). “Suggested methods for determining the dynamic strength parameters and mode-I fracture toughness of rock materials,” in The ISRM Suggested Methods for Rock Characterization, Testing and Monitoring: 2007–2014, eds Y. X. Zhou, K. Xia, X. B. Li, H. B. Li, G. W. Ma, J. Zhao, Z. L. Zhou, and F. Dai (Cham: Springer), 35–44.

Google Scholar

Zhou, Z., Ma, W., Zhang, S., Mu, Y., and Li, G. (2018). Effect of freeze-thaw cycles in mechanical behaviors of frozen loess. Cold Reg. Sci. Technol. 146, 9–18. doi: 10.1016/j.coldregions.2017.11.011

CrossRef Full Text | Google Scholar