Adaptive Localization for Tropical Cyclones With Satellite Radiances in an Ensemble Kalman Filter

Introduction

Tropical cyclones (TCs) are convective systems featuring multiscale interactions and have diameters ranging from a few hundred to several thousand kilometers. The TC forecasts have been improved in recent decades with benefits from the advanced numerical weather prediction models, improved observations, and better data assimilation techniques (Alley et al., 2019). TCs feature multi-scale interactions, since the tracks are closely related to the large-scale environment while the intensities are dominated by the internal dynamics and environmental flow. Nystrom et al. (2018) showed that the initial condition (IC) within 300 km from the center of Hurricane Joaquin (2015) dominated the early intensity changes, while the IC between 600–900 km from the center contributed more to the track changes. Munsell and Zhang (2014) found that the mean tropical flow is more important for Hurricane Sandy (2012) than the mid-latitude environment. Thus to achieve better TC forecasts, the multi-scale features of TCs should be considered.

The ensemble Kalman filter (EnKF; Evensen, 1994; Burgers et al., 1998) has been widely used in atmospheric applications (e.g., Whitaker et al., 2008; Aksoy et al., 2009; Buehner et al., 2010a, b; Houtekamer et al., 2014), especially for TCs (e.g., Zhang et al., 2011; Weng and Zhang, 2012; Kunii, 2015). The EnKF uses an ensemble of forecasts to estimate the flow-dependent background error covariances, which determine the analysis increment given assimilated observations including conventional observations, radar and satellite observations, etc. For regions with sparse conventional observations, assimilation of satellite radiances has been proven to have large positive impacts on the forecast skill (e.g., Le Marshall et al., 2006; McCarty et al., 2009; Collard and McNally, 2009), because satellite radiances provide important information of the atmospheric state. Since TCs spend most of their lifetimes over ocean, satellite observations have significant impact on the prediction of TCs.

The EnKF is subject to sampling errors when it is applied in high-dimensional atmospheric models, because the practical ensemble size (∼10²) is much smaller than the number of state variables (∼10⁸). The sampling errors can cause rank deficiency of the estimated background error covariances and filter divergence, and further degrade analyses and forecasts. One strategy to combat sampling errors is covariance localization that preserves meaningful impact of observations on nearby state variables but limits detrimental impact of observations on remote state variables caused by spurious correlations (e.g., Houtekamer and Mitchell, 2001). For a serial EnKF that assimilates observations singly or in batches, covariance localization is often implemented by multiplying a localization value to the sample covariance between an observation and a state variable (e.g., Hamill et al., 2001).

However, for non-local observations like satellite radiances, the concepts of the vertical location and separation are not well defined, thus covariance localization is not straightforward. A pioneer work of assimilating the Advanced Microwave Sounding Unit-A (AMSU-A) radiance observations in an EnKF treated the radiance observations as local observations and assigned the levels where the weighting functions maximize as the vertical locations (Houtekamer et al., 2005; Houtekamer and Mitchell, 2005). The commonly used localization function is the Gaspari and Cohn (GC; Gaspari and Cohn, 1999) function, which is a compactly supported polynomial approximation of a normal distribution. Miyoshi and Sato (2007) and Miyoshi et al. (2010) used normalized sensitivity functions as the vertical localization functions for radiance observations from different satellite platforms, and obtained positive impacts. Although previous studies suggested that localizing the impact of radiance observations in model space is superior to localizing in observation space (Campbell et al., 2010; Lei et al., 2018), the opposite can be true when there are significant negative background error covariances (Lei and Whitaker, 2015).

There have been theoretical studies on the adaptive covariance localization (e.g., Anderson and Lei, 2013; Lei and Anderson, 2014a, b; Flowerdew, 2015; Ying et al., 2018). Extended from the hierarchical ensemble filter introduced by Anderson (2007), Lei et al. (2016) proposed a global group filter (GGF) that can provide adaptive estimation of vertical localization functions for every channel of AMSU-A radiances. The GGF localization functions improved the assimilation of AMSU-A radiance observations and obtained better forecasts. To practically implement the GGF localization functions for various types of satellite radiances, Lei et al. (in review) investigated parameters that measure the properties of the estimated vertical localization functions, which include the localization widths, maximum values, and vertical locations of the radiance observations. Using the adaptively estimated localization parameters for each assimilated channel of every satellite platform leads to improved forecasts. Previous studies of adaptive localization were demonstrated in global models, but the application of the adaptive localization in regional models needs further investigation.

Moreover, TCs have multi-scale features, whose tracks are mainly controlled by the large-scale environment while intensities are primarily determined by the internal dynamics and environmental flow. To improve the assimilation of radar observations for multi-scale systems like the hurricanes, Zhang et al. (2009) proposed a successive covariance localization that utilizes broader localization length-scales for larger-scale features and narrower localization length-scales for smaller-scale characteristics. Lei et al. (2015) found that compared to non-precipitating regions, precipitating regions have narrower horizontal localization length scales but broader vertical localization length scales. Thus the adaptive localization functions for regions inside and outside TCs are also explored in this study.

The remainder of this paper is organized as follows. The methodology of GGF and the construction of GGFs for TC and non-TC regions are described in Section “Methodology.” Section “Experimental Design” presents the experimental design. Section “Adaptively Estimated Localization Parameters” discusses the estimated localization functions for radiance observations in an evolving multiscale system. The assimilation results using the adaptive localization functions are analyzed and discussed in Section “Results.” Section “Discussions and Summaries” summarizes the results.

Methodology

The Global Group Filter (GGF) Localization

Satellite radiances are integral observations in the vertical, thus the vertical localization functions and associated parameters for the radiance observations are investigated here. The adaptive vertical localization functions for radiance observations are estimated using the global group filter (GGF) method following Lei and Anderson (2014a) and Lei et al. (2016). The GGF in Lei et al. (2016) is computed from sample correlations based on climatological perturbations of ensemble prior estimates of observations and state variables. To capture the spatial and temporal variations of GGF, sample correlations directly from a cycling ensemble are adopted here.

Given an ensemble simulation, let K denote the model vertical levels, N the ensemble size and L the number of one kind of radiance observations. Let y_l,n represent the l^thobservation from the n^thensemble member (l ∈ {1,…,L} andn ∈ {1,…,N}). For the observation y_l,n, the ensemble perturbation Δy_l,n is given by $\mathrm{\Delta }{y}_{l,n}=y_{l,n}-\overline{y_l}$, where $\overline{y_l}$ is the ensemble mean. By interpolating one type of state variables to the horizontal locations of this kind of radiance observations, the ensemble perturbation of the model variable $x_{l,n}^k$ (i.e., the variable at the k^th vertical level from the n^thensemble member interpolated to the horizontal locations of the l^th observation) can be defined in a similar manner, $\mathrm{\Delta }{x}_{l,n}^k=x_{l,n}^k-\overline{x_l^k}$ (l ∈ {1,…,L}, n ∈ {1,…,N}, k ∈ {1,…,K}), where $\overline{x_l^k}$ denotes the ensemble mean of $x_{l,n}^k$. The correlation $r_l^k$ between the l^th observation y_l and the state variable $x_l^k$ can be computed by

$$r_l^k=\frac{{\sum }_{n=1}^N\mathrm{\Delta }{x}_{l,n}^k\mathrm{\Delta }{y}_{l,n}}{\sqrt{{\sum }_{n=1}^N\mathrm{\Delta }{x}_{l,n}^k{}^2\sum _{n=1}^N\mathrm{\Delta }{y}_{l,n}^2}}.$$

For a given type of radiance observation and a given kind of state variable, the correlations at each vertical level k are then subset to M samples with G groups in each sample. Thus L = M*G, and the correlations $r_l^k$ are now represented by $r_{m,g}^k$, m = 1,…,M and g = 1,…,G. Following Lei and Anderson (2014a), if the correlation $r_{m,g}^k$ can be seen as the “truth” in the g^th group, the root-mean-square (RMS) difference between the estimated correlations and the “truth” for all M samples of G groups can be written as

$$J^k=\sqrt{\sum _{m=1}^M\sum _{i=1}^G\sum _{j=1,j\ne i}^G{({\mathrm{\alpha }}^k{r}_{m,j}^k-r_{m,i}^k)}^2}.$$

The RMS difference minimizes when

$${\mathrm{\alpha }}^k=\frac{\frac{{\sum }_{m=1}^M{({\sum }_{g=1}^G{r}_{m,g}^k)}^2}{{\sum }_{m=1}^M{\sum }_{g=1}^G{(r_{m,g}^k)}^2}-1}{G-1}.$$

Thus α^k gives the confidence factor for the estimated correlations at vertical level k for this kind of radiance observations and type of state variables. The α^k (k ∈ {1,…,K}) profile forms the adaptively estimated vertical localization function for this radiance observation type and state variable kind, known as the GGF function hereafter. The GGF method succeeds in reducing sampling errors, since the grouping procedure serves as a secondary sampling (Anderson, 2007). In this study, the group size G is empirically set to 4.

It is impractical to incorporate the adaptively estimated localization functions for each channel of every type of radiance observations onboard different satellites. Using the National Centers for Environmental Prediction (NCEP) Global Forecast System (GFS), Lei et al. (in review) fitted the adaptively estimated GGFs with the GC localization function and obtained three localization parameters based on the fitted GC localization function. The localization parameters are the vertical location of the radiance observation p° that is the pressure level at which the maximum localization value occurs, the GC width c° that is determined by the fitted GC localization function with the smallest RMS difference compared to the GGF, and the GC maximum value lmax° that is given by the GGF value at p°. Lei et al. (in review) found that for radiance observations, using the adaptively estimated localization width c° and vertical observation location p° produced better forecast than including the maximum localization value lmax°. Therefore, the localization width c° and vertical observation location p° are explored here for TCs using a regional model.

Spatial and Temporal Variations of the Localization Parameters

Previous studies (Lei et al., 2016, Lei et al., in review) provided a globally uniform and static GGF localization function for a given type of observations. But Lei et al. (2015) demonstrated that different localization functions are needed for regions with and without precipitation. Since the TC has multi-scale features and varying intensity during its lifetime, the adaptively estimated localization parameters are examined for regions inside and outside a TC, and also explored on-the-fly along with the cycling assimilation.

The observations inside (outside) the TC region are used to compute the GGFs and associated localization parameters for TC (non-TC) region. The TC region is defined as a square area around the TC location with half side length of 10 degrees. The TC region is chosen based on the TC size and sample size of GGFs inside TC regions, because there are limited numbers of radiance observations within the TC region and a decent sample size M is needed to compute the GGFs. The radius of maximum wind of typhoon Yutu is approximately 100 km, thus the half side length of 10 degrees is chosen to consider both the inner core and outer rain band of typhoon Yutu and also to include sufficient sample sizes for the GGFs inside TC regions. The TC location is obtained from the Joint Typhoon Warning Center (JTWC) advisory Tropical Cyclone Vitals (TCVitals; Trahan and Sparling, 2012).

The GGFs used by Lei et al. (in review) and here are based on the ensemble priors of observations and state variables from a cycling ensemble assimilation experiment. Thus it is a natural extension to allow the GGFs and associated localization parameters varying with time. The GGFs and localization parameters can be computed before assimilating observations for each data assimilation cycle.

Experimental Design

The adaptive localization functions are examined for typhoon Yutu (2018). Experiments are conducted using the Weather Research and Forecasting (WRF v3.4; Skamarock et al., 2008) model and the National Oceanic and Atmospheric Administration (NOAA) operational ensemble Kalman filter (EnKF) system¹. The WRF model has an outer domain with an 18-km horizontal grid spacing and 520 × 660 grid points, and a vortex following domain of 6-km horizontal grid spacing and 180 × 180 grid points. The whole domain coverage is shown in Figure 7. There are 56 vertical levels with model top at 10 hPa. The following parameterization schemes are used: the WRF single-moment 6-class microphysics scheme (Hong and Lim, 2006), the Yonsei University Scheme (YSU) planetary boundary layer (PBL) scheme (Hong et al., 2006), the Rapid Radiative Transfer Model for GCMs (RRTM-G) shortwave and longwave schemes (Iacono et al., 2008), and the unified Noah land surface model (Tewari et al., 2004). The Kain Fritsch cumulus parameterization scheme (Kain, 2004) is only used for the 18-km outer domain.

Both conventional observations² and radiance observations³ from the NCEP Global Data Assimilation System (GDAS) are assimilated every 6 h. Conventional observations include all in situ observations and cloud motion vectors. Clear-sky radiance observations including the Advanced Microwave Sounding Unit-A (AMSU-A), the Atmospheric Infrared Sounder (AIRS), the Microwave Humidity Sounder (MHS) and the High-resolution Infrared Radiation Sounder (HIRS/4), are assimilated. The observation error variance R uses the same values as in the NCEP GDAS. The Community Radiative Transfer Model (CRTM; Weng, 2007; Han et al., 2007) is used to compute the observation forward operator H and save the values of Hx^b for the ensemble mean and each ensemble member separately.

The ensemble square root filter (EnSRF; Whitaker and Hamill, 2002) is used for assimilating observations. The ensemble size is 80. To remedy sampling errors with a limited ensemble size and also account for model error, localization and inflation are applied. The default horizontal and vertical localization length-scales and the inflation coefficient are optimally tuned, based on sensitivity experiments from which the smallest 6-h prior errors comparing to the conventional observations are obtained. The horizontal localization uses the Gaspari and Cohn (1999) localization function with a length-scale of 1000 km. The default vertical localization also uses the GC localization function, with a length-scale of 1.5 ln(hPa). Adaptively estimated localization parameters are used in additional assimilation experiments. Inflation uses the relaxation to prior ensemble spread (RTPS) (Whitaker and Hamill, 2012) method, where the relaxation coefficient is set to 1.15.

The cycling WRF/EnKF experiments extend from 1200 UTC 19 October 2018 to 1200 UTC 2 November 2018. The ensemble initial conditions at 1200 UTC 19 October 2018 are adapted from a cycling WRF/EnKF experiment with starting date of 0600 UTC 30 June 2018. Ensemble lateral boundary conditions are generated from the NCEP GFS forecasts of 0.25° resolution using the fixed-covariance perturbation technique (Torn et al., 2006). For all assimilation experiments, the first 2-day simulations are discarded to avoid spin-up impact, and the following simulations are used for verification.

The control experiment (CTRL) uses the optimally tuned default assimilation parameters. Three additional assimilation experiments are conducted, which use the adaptively estimated localization parameters in the vertical and the same horizontal GC localization length-scale as the CTRL experiment. Consistent results between the CTRL experiment and the assimilation experiments with a different horizontal GC localization length-scale are expected, since only the vertical localization parameters vary among the experiments. Details of the adaptively estimated localization parameters are explained below. As shown by Table 1, experiment GGF-Domain utilizes constant localization parameters through time and space. Experiment GGF-TC has temporally invariant localization parameters but differing for TC and non-TC regions. Experiment GGF-Time has constant localization parameters over the domain but with temporal variations. State variables of perturbation dry air mass in column, temperature, specific humidity, u- and v-winds are updated by assimilated observations in all experiments. For simplicity and avoiding imbalances, the same set of localization parameters is used for all updated state variables.

TABLE 1

Table 1. Details of localization parameters for the assimilation experiments.

The GGF localization functions and associated localization parameters for radiance observations of experiments GGF-Domain and GGF-TC are estimated from the output of the CTRL experiment, including four cycles before the rapid intensification of typhoon Yutu (from 0000 UTC 22 October to 1800 UTC 22 October) and four cycles after (from 1800 UTC 23 October to 1200 UTC 24 October). The GGF localization functions and associated localization parameters of experiment GGF-Time are estimated along with the assimilation cycle and updated every 6 h. To eliminate the impact of diffusion closed to the model top, sample correlations above 30 hPa are not used to fit the GC function, and the default localization parameters are used for radiances whose vertical locations are above 30 hPa. The GGF localization functions and localization parameters are computed for each channel of every satellite platform with state variables of temperature and specific humidity. The estimated localization parameters from the state variable that has the largest absolute value of mean sample correlation are used in additional assimilation experiments.

Adaptively Estimated Localization Parameters

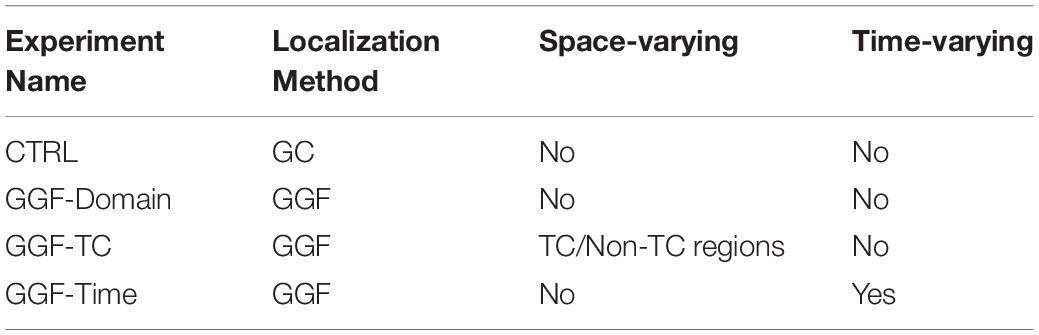
As described in previous sections, the GGF localization functions and associated localization parameters for each channel of every satellite are first computed based on the data from the eight assimilation cycles. As an example, the GGF localization functions and parameters for channels of NOAA-15 AMSU-A radiances with state variable of temperature are shown in Figure 1. The GGFs have similar shapes to the absolute values of correlations, which are either unimodal or polymodal. Based on the GGFs, the estimated vertical locations of the AMSU-A radiances increase with height when the channel number increases. The estimated GC widths are larger than the default value [1.5 ln(hPa)], especially for channels 8 and 9. For other microwave sounders like MHS and infrared sounders like AIRS and HIRS4, adaptive localization functions for each channel are also estimated (Figures are not shown).

FIGURE 1

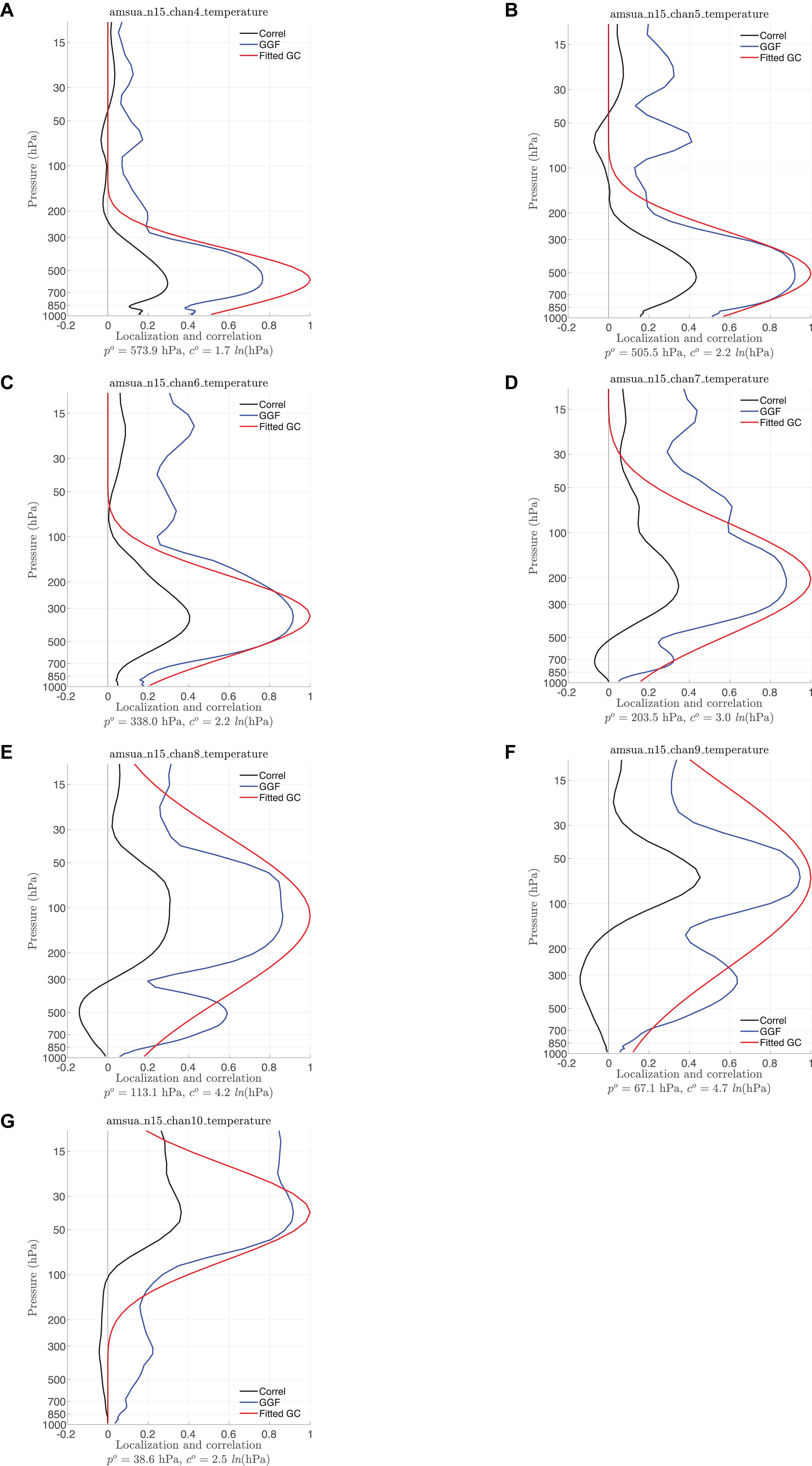
Figure 1. The mean sample correlations (black), estimated GGF localization functions (blue), and fitted GC localization functions (red) for (A–G) channels 4–10 of the NOAA-15 AMSU-A radiances with state variable temperature. The estimated localization parameters p° and c° are denoted at the bottom.

To summarize the estimated localization parameters, Figure 2 shows the mean (dots) and one standard deviation (bars) of the estimated localization parameters for AMSU-A and MHS onboard different satellite platforms. The localization parameters for AMSU-A radiances are associated with state variable temperature. The localization parameters for MHS radiances are associated with state variable specific humidity, since MHS radiances are more correlated with specific humidity than temperature. The vertical locations and localization widths obtained here from the regional model WRF are similar to those from the global model GFS (Lei et al., in review). There are fewer variations of the localization parameters among different satellite platforms in the regional model WRF than the global model GFS.

FIGURE 2

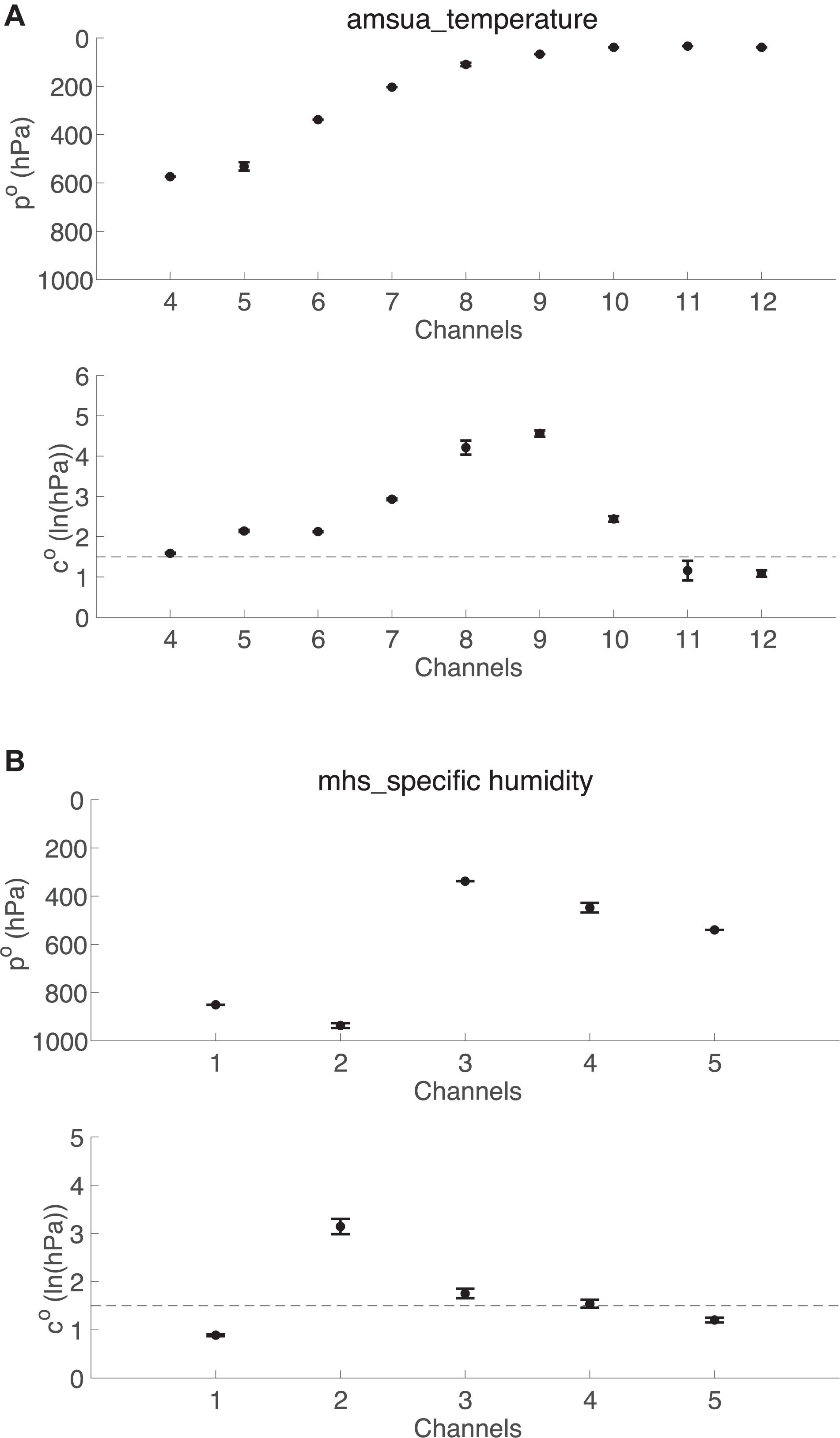
Figure 2. The mean (dots) and one standard deviation (bars) of the estimated localization parameters for (A) AMSU-A and (B) MHS radiance observations. The dashed line denotes the default GC localization width.

To account for different correlation characteristics inside and outside a TC, the GGF localization functions and associated localization parameters for each channel of every satellite are now computed for regions inside and outside the TC respectively. To avoid spurious correlations resulting from limited samples, the GGFs for regions inside a TC are computed when the sample size is larger than an empirically chosen threshold of 100. Figure 3 displays the GGFs and localization parameters inside and outside the TC for channel 3 of MHS onboard Metop-A and channel 185 of AIRS onboard AQUA. For the MHS radiance observations, the GGF localization profile inside the TC has similar shape to that outside the TC, but the former has slightly higher observation location than the latter. The broader correlations with larger magnitudes inside the TC lead to a larger localization width, comparing to those outside the TC. For the AIRS radiance observations, correlation profiles for TC and non-TC regions are similar, except that inside the TC there are prominent negative correlations between 150 and 50 hPa and also larger localization width. Similar correlation patterns are also obtained for several other channels from the infrared sounders AIRS and HIRS. For all radiance observations, the localization widths for TC regions are generally larger than those for non-TC regions.

FIGURE 3

Figure 3. Same as Figure 1, but for (A,B) channel 3 of MHS onboard MetOP-A and (C,D) channel 185 of AIRS onboard AQUA, for TC (right) and non-TC (left) regions respectively.

Similar to Figures 2, 4 shows the mean and one standard deviation of the estimated localization parameters for AMSU-A and MHS onboard different satellite platforms inside and outside the TC regions respectively. The estimated observation locations and localization widths for non-TC regions are very similar to those in the whole domain (Figure 2), since the sample sizes for non-TC regions are much larger than those for TC regions. As shown by Figure 4A, the estimated vertical locations for AMSU-A radiances are similar for TC and non-TC regions. The estimated GC widths for TC regions are generally larger than those for non-TC regions. This result is consistent with Lei et al. (2015), in which larger localization scales are found for precipitating regions than for non-precipitating regions. One possible reason is the enhanced vertical motion inside TC regions. The large standard deviation of localization width for channel 12 is resulted from limited samples. The estimated vertical locations for MHS radiances inside TC regions are slightly higher than outside TC regions (Figure 4B). Similar to AMSU-A, the estimated GC widths for MHS inside TC regions are larger than those for non-TC regions, except for channel 2.

FIGURE 4

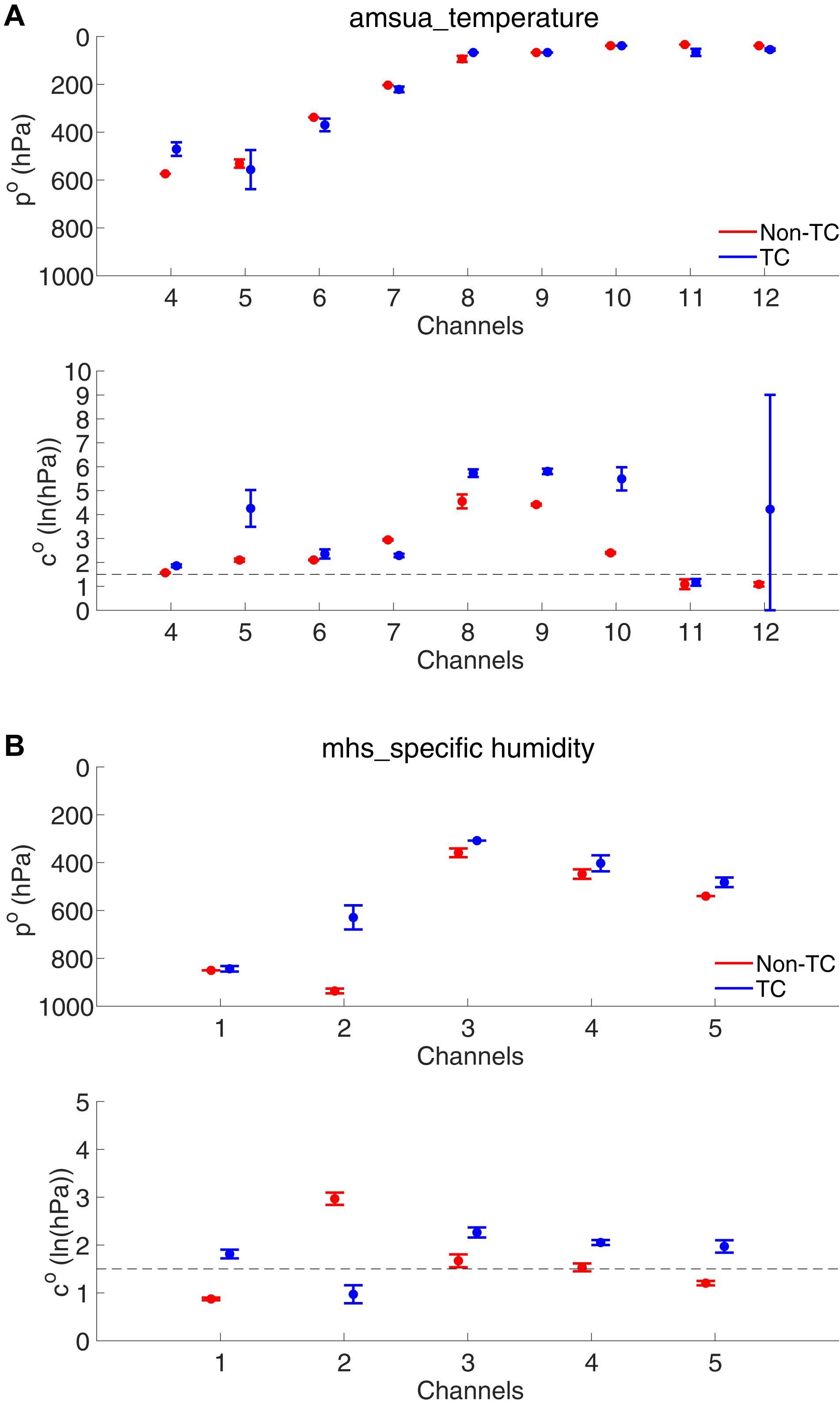
Figure 4. Same as Figure 2 for (A) AMSU-A and (B) MHS radiance observations, but with blue (red) denotes TC (non-TC) regions.

The GGF localization functions and associated parameters can also be computed along with the assimilation cycles and updated every 6 h. Due to limited sample size inside TC regions for one assimilation cycle, the GGF localization functions and parameters are not differentiated for TC and non-TC regions. The GGFs and estimated localization parameters are generally consistent with those in Figures 1, 2, and there are no significant temporal variations (figures are not shown). However, the cycling process may exaggerate the influence resulted from slightly different localization parameters in time.

Results

Verification Relative to Conventional and Radiance Observations

The RMS errors (RMSEs) of the 6-h priors from the assimilation experiments verified relative to the conventional and radiance observations are examined. Figure 5 shows the temporally and spatially averaged and platform averaged RMSEs for channels of AMSU-A. The RMSEs of the experiment CTRL are displayed in Figure 5A, and the differences of the RMSEs between the GGF experiments and CTRL are shown in Figure 5B. Thus negative (positive) values in Figure 5B denote smaller (larger) errors of the GGF experiments compared to the experiment CTRL. The bars on the right denote the channel averaged values. Experiment CTRL has errors between 0.2 and 0.5 for all channels, and the average error across the channels is 0.36. The three GGF experiments have similar RMSEs to each other, and they often have errors smaller than or closed to experiment CTRL, when verified relative to radiance observations.

FIGURE 5

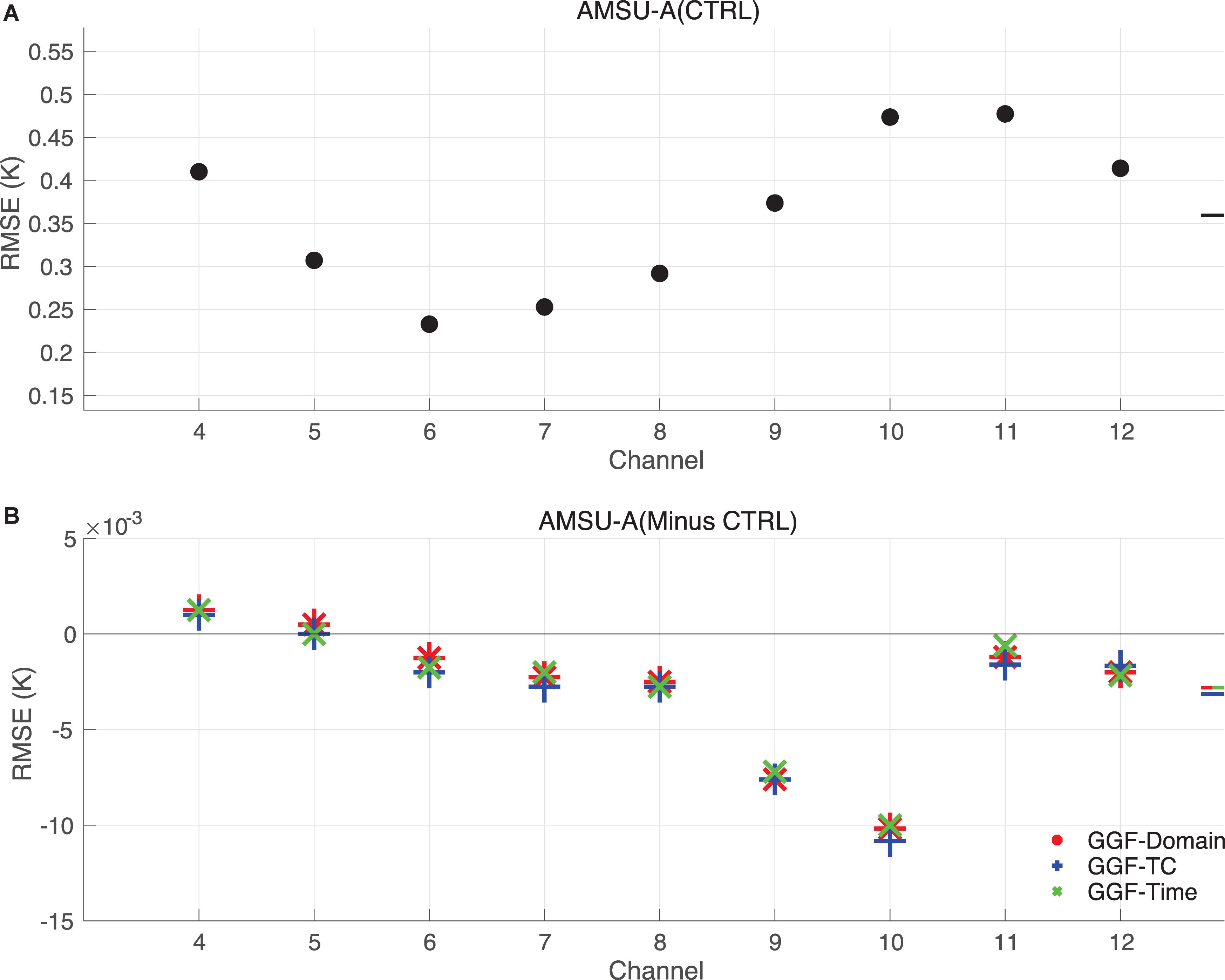
Figure 5. Verified relative to the AMSU-A radiances, (A) RMSEs of 6-h priors of experiment CTRL, and (B) error differences between the GGF experiments and experiment CTRL. The bars on right denote the channel average values.

Figure 6 shows the temporally and spatially averaged profiles of RMSEs for conventional observations, including temperature, wind speed and specific humidity. The temperature error of experiment CTRL decreases with height till 400 hPa and then increases to model top (Figure 6A). The three GGF experiments have similar temperature errors, and they have smaller temperature errors than experiment CTRL above 600 hPa, but slightly larger temperature errors than CTRL below 600 hPa (Figure 6B). The vertically averaged wind error of experiment CTRL is approximately 3.3 (Figure 6C). Experiment GGF-domain has smaller wind error than CTRL, except for between 600 and 300 hPa (Figure 6D). Experiments GGF-TC and GGF-Time have similar wind errors, and both have smaller wind errors than experiments CTRL and GGF-Domain, especially above 600 hPa. Experiment CTRL has errors of specific humidity decreasing with height since water vapor decreases with height (Figure 6E). GGF experiments generally have smaller errors of specific humidity than CTRL, especially between 900 and 500 hPa (Figure 6F). Experiment GGF-TC has smaller errors of specific humidity than the other two GGF experiments below 500 hPa. In general, the GGF experiments have smaller errors than experiment CTRL, and experiment GGF-Time has slightly smaller errors than GGF-Domain, and experiment GGF-TC outperforms the other two GGF experiments.

FIGURE 6

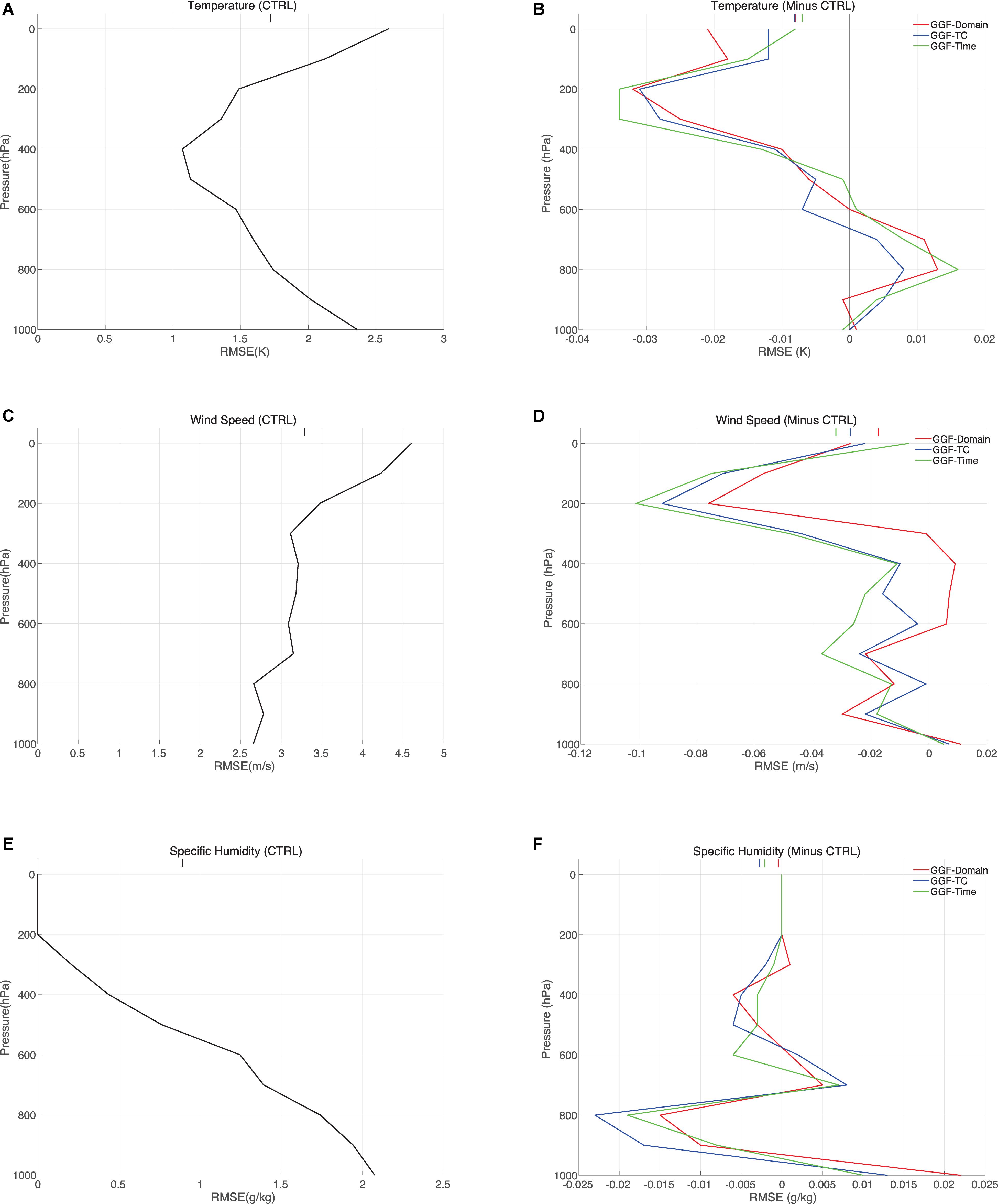
Figure 6. RMSEs of 6-h priors verified relative to (A) temperature, (C) wind speed and (E) specific humidity of experiment CTRL, and error differences between the GGF experiments and experiment CTRL for (B) temperature, (D) wind speed, and (F) specific humidity. The bars on top denote the average values.

FIGURE 7

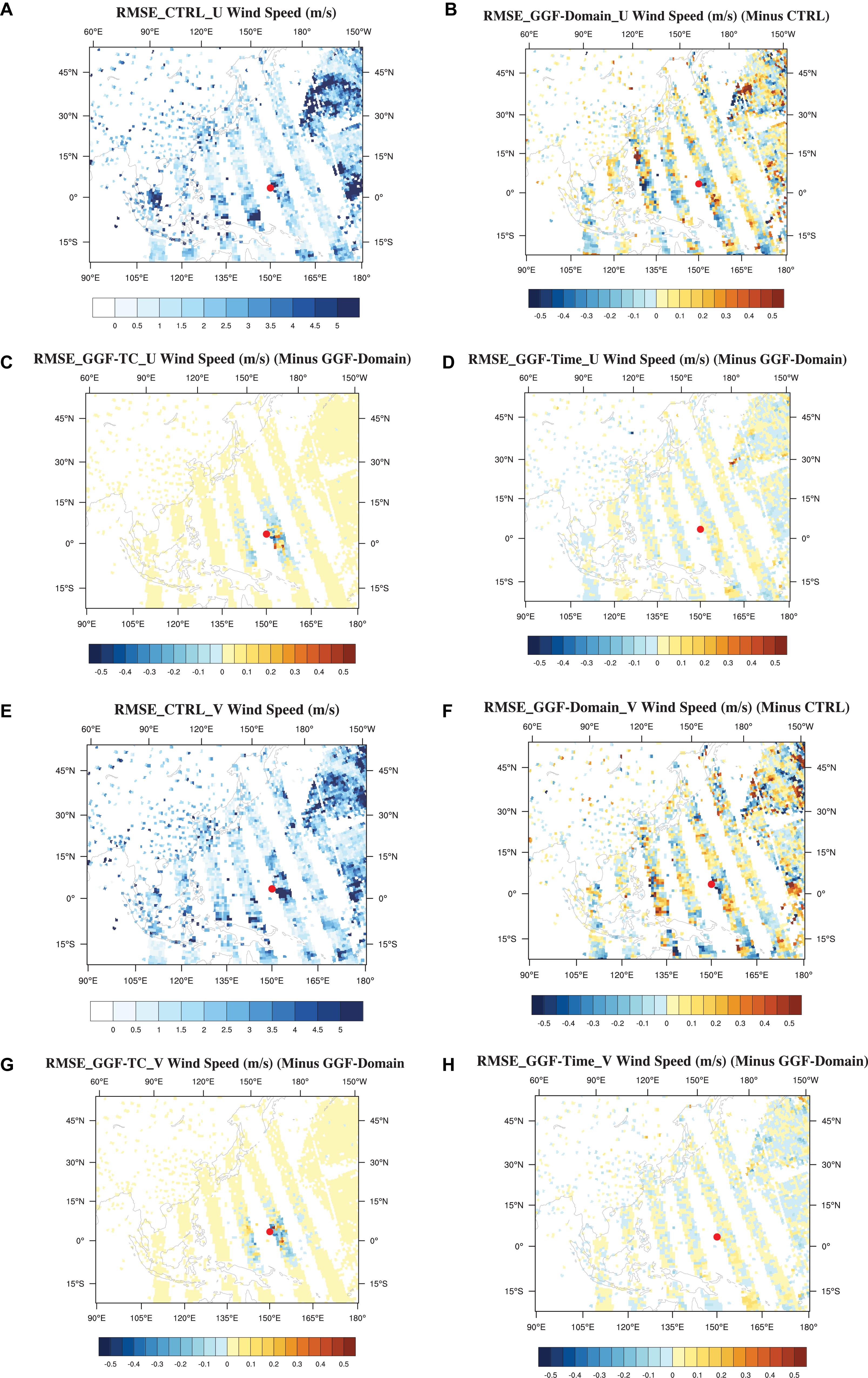
Figure 7. Vertically averaged analysis errors of (A) u- and (E) v-winds from experiment CTRL, analysis error differences between experiments GGF-Domain and CTRL for (B) u- and (F) v-winds, and analysis error differences between experiments GGF-TC (GGF-Time) and GGF-Domain for (C)((D)) u- and (G)((H)) v- winds.

To further examine the impact of adaptive localization parameters, radiance observations are assimilated with different localization parameters using the same ensemble priors from experiment CTRL on 1200 UTC 22 October 2018. Differences of the posteriors verified relative to observations show direct influences from the adaptive localization parameters. The vertically averaged analysis errors of u- and v-winds from experiment CTRL are shown by Figures 7A,E, from which the locations of cloud track wind observations are clearly seen. The red dot denotes the observed location of typhoon Yutu (2018), which is adapted from the TCVitals. The differences of the analysis errors between experiments GGF-Domain and CTRL are displayed by Figures 7B,F. Blue (red) dots indicate that experiment GGF-Domain has smaller (larger) errors than experiment CTRL. Over most observation locations, experiment GGF-Domain produces smaller wind errors than the CTRL. The differences of the analysis errors between experiments GGF-TC (GGF-Time) and GGF-Domain are shown by Figures 7C,G(D,H). It is obvious that GGF-TC obtains smaller wind errors than GGF-Domain inside the TC regions, which demonstrates the advantages of differentiating localization parameters for TC and non-TC regions. On average GGF-Time has similar wind errors to GGF-Domain, which is as expected since localization parameters for non-TC regions are very close to those for the whole domain.

The temporally and vertically averaged prior errors of u-wind from experiment CTRL and error differences between the GGF experiments and CTRL are displayed in Figures 8A–D. The black line denotes the observed track of typhoon Yutu (2018). Figure 8E shows the averaged error differences along the TC track (3 degrees to the north and 13 degrees to the south), and the mean error differences are denoted on the side. Experiment GGF-Domain generally produces smaller u-wind errors than the CTRL along the TC track, especially to the east of 135°E and to the south of the TC track. Compared to the differences between experiment GGF-Domain and CTRL, experiment GGF-Time produces smaller u-wind errors to the east of 135°E and to the south of the TC track. Compared to experiments GGF-Domain and GGF-Time, GGF-TC obtains smaller u-wind errors along the TC track, especially when approaching the end of TC track. Therefore, verifications from one assimilation cycle and multiple cycles show that GGF-TC has slightly advantages over GGF-Time, and both GGF-TC and GGF-Time are superior to GGF-Domain, especially for the TC regions.

FIGURE 8

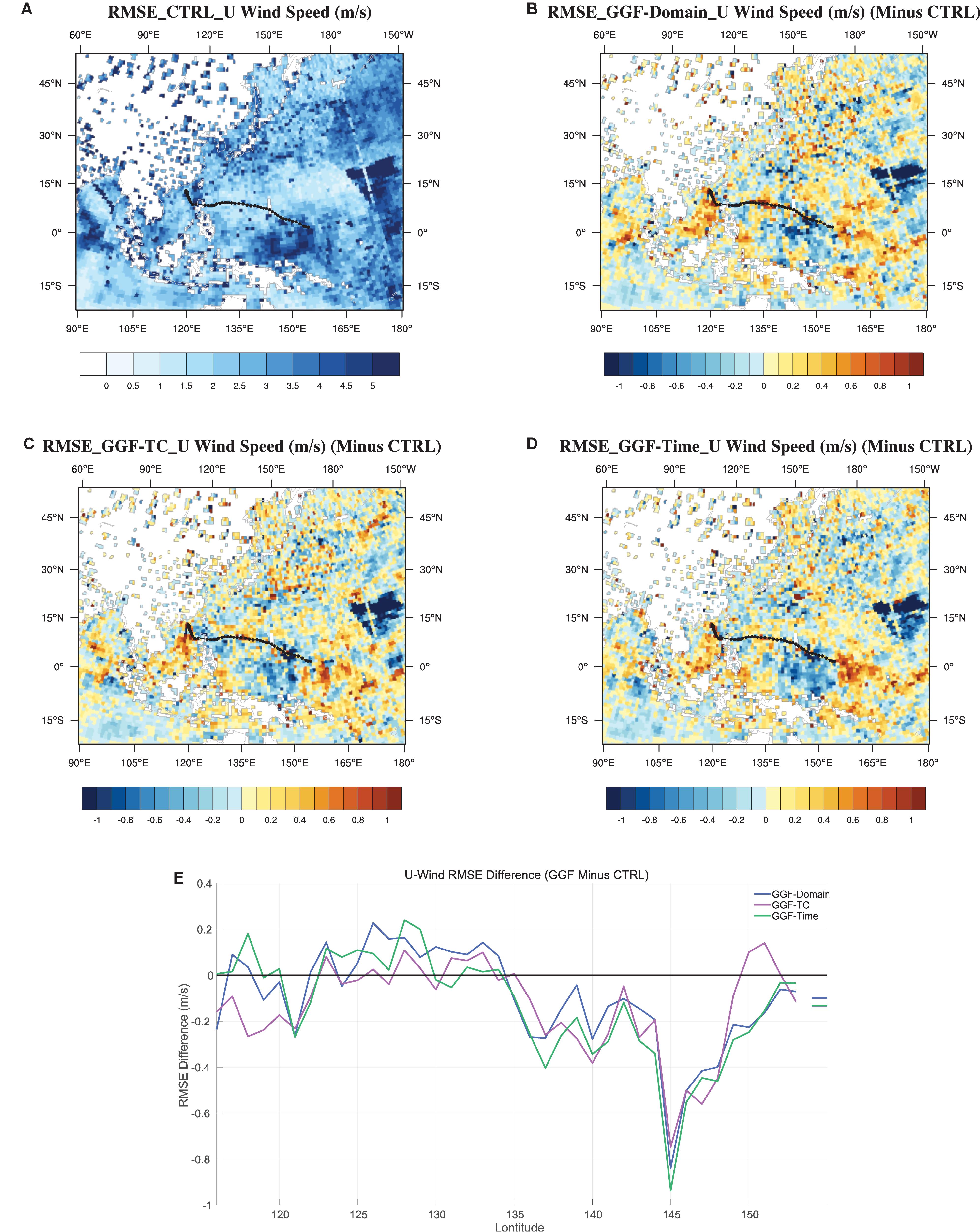
Figure 8. Temporally and vertically averaged prior errors of u-wind (A) from experiment CTRL, and error differences (B) between experiments GGF-Domain and CTRL, (C) between experiments GGF-TC and CTRL, (D) between experiments GGF-Time and CTRL. The black line denotes the observed track of typhoon Yutu (2018). The averaged error differences along the TC track (3 degrees to the north and 13 degrees to the south) are shown in (E), and the mean error differences are denoted on the side.

Verification of TC Track and Intensity

Information about the location and intensity of the vortex from the TCVitals is used as observations to verify the assimilation experiments. The observed and 6-h prior track, minimum sea level pressure (SLP) and maximum wind speed of typhoon Yutu (2018) are shown by Figure 9. Experiments CTRL and GGFs produce similar track forecasts to the observations, except that at the beginning of the storm GGF experiments have slightly better track forecasts than experiment CTRL (Figure 9A). For both minimum SLP and maximum wind speed, GGF experiments are more closed to the observed values than experiment CTRL. GGF experiments better capture the rapid intensification (RI) than the CTRL. But the peak intensity forecasted by GGF experiments are still lower than the observed values, which may be resulted from insufficient model resolution that cannot resolve the gradient of mass and wind fields or model physical parameterizations. In general, GGF experiments have similar track and intensity forecasts, and they have better track and intensity forecasts than experiment CTRL.

FIGURE 9

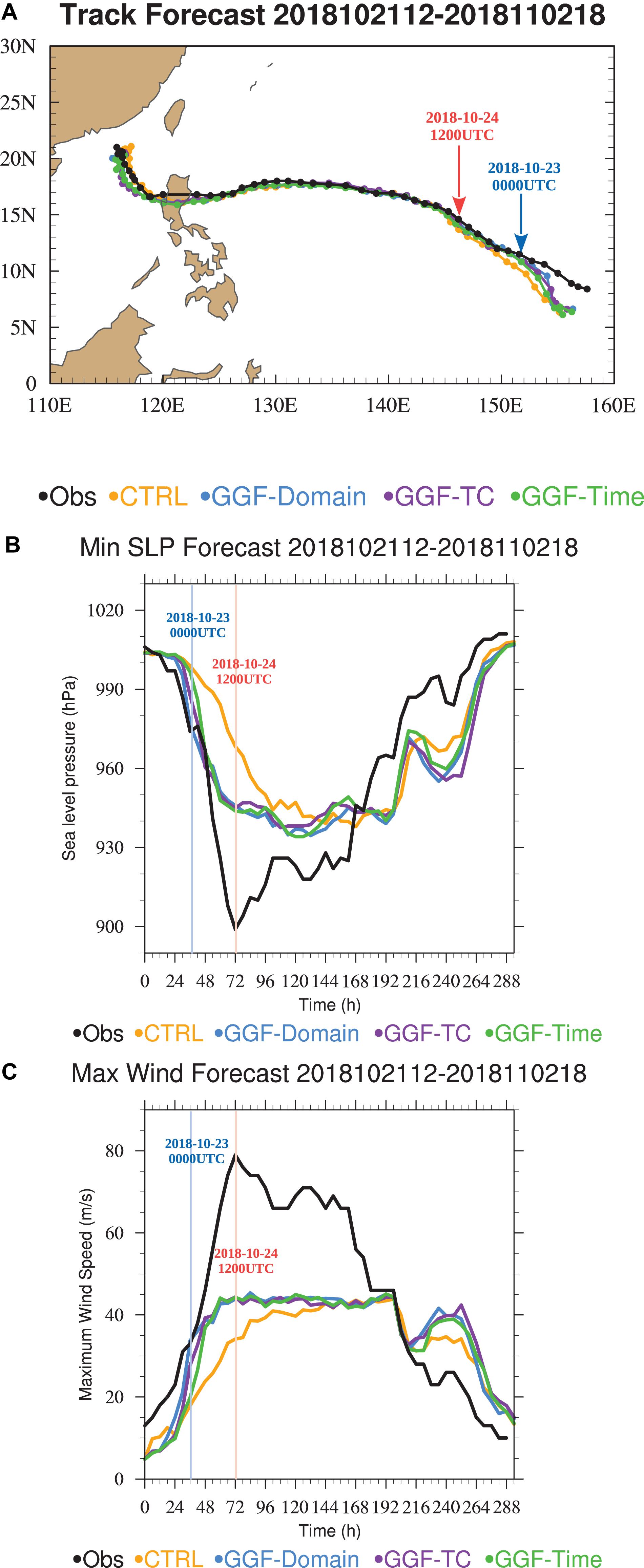
Figure 9. Six hour ensemble mean forecasts of (A) track, (B) minimum sea level pressure, and (C) maximum wind speed for typhoon Yutu (2018). Black line denotes the observed value, orange, blue, purple and green lines display the results of experiments CTRL, GGF-Domain, GGF-TC and GGF-Time respectively.

To understand the impact of the adaptive localization parameters on TC intensity and structure, the priors and posteriors of experiments CTRL and GGF-TC before and after RI are analyzed. The priors and posteriors of experiments GGF-Domain and GGF-Time are not shown, since the general patterns obtained by these two experiments are similar to those of experiment GGF-TC. Figures 10, 11 show the radius-height cross sections of prior temperature anomaly that has the mean temperature in a 1000 km radius deducted for each level, specific humidity, radial and tangential winds at 0000 UTC 23 October and 1200 UTC 24 October, respectively. Please note that in order to better display the structure of temperature anomaly, log pressure is used as vertical axes for panels a and b while pressure is used for the other panels in Figures 10, 11.

FIGURE 10

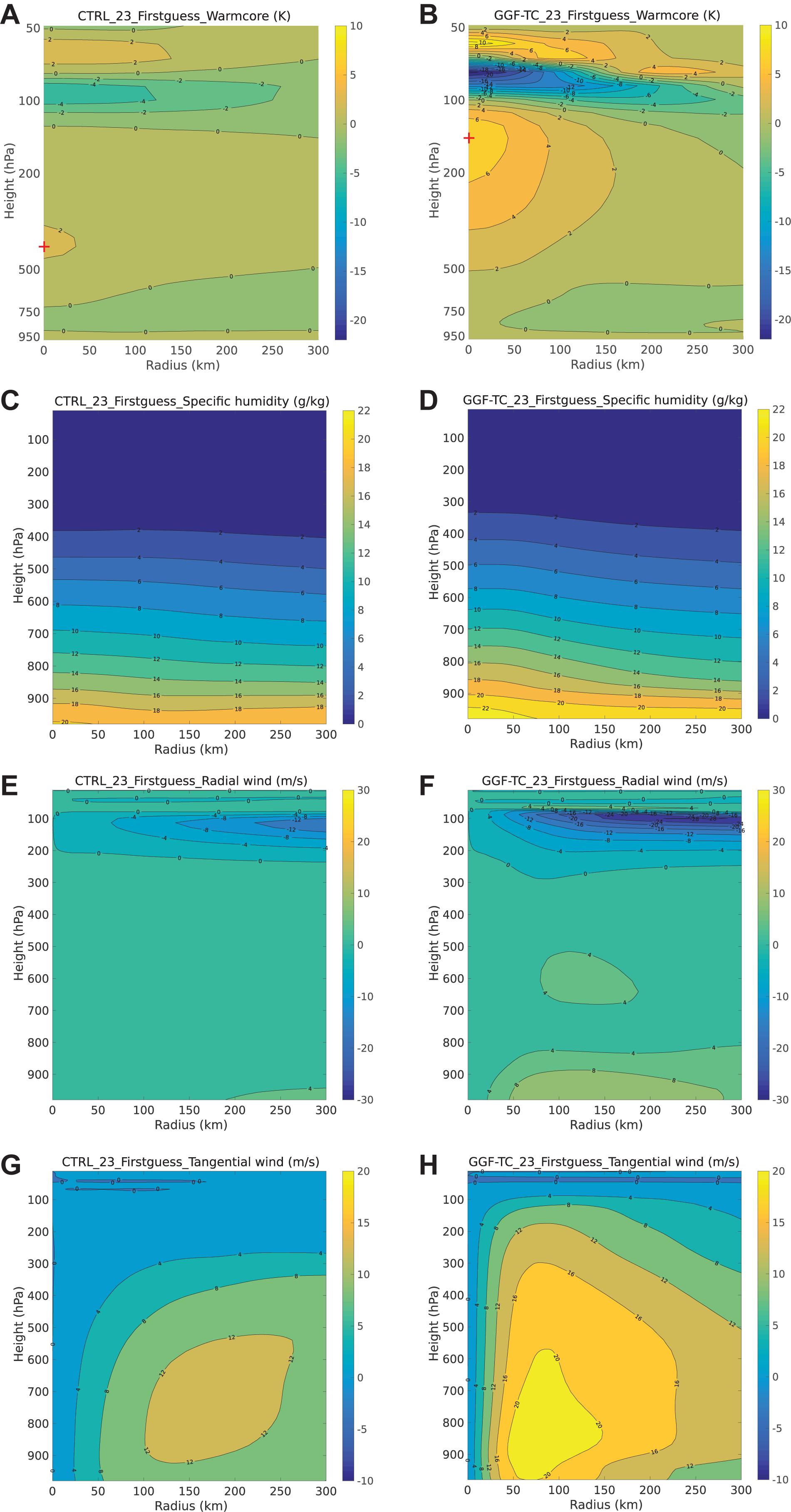
Figure 10. Radius-height cross sections of (A,B) temperature anomaly that has the mean temperature in a 1000 km radius deducted for each level, (C,D) specific humidity, (E,F) radial wind, and (G,H) tangential wind at 0000 UTC 23 October 2018. Left panels for experiment CTRL, and right panels for experiment GGF-TC. The red plus in (A,B) denotes the location of warm core. Please note that in order to better display the structure of temperature anomaly, log pressure is used as vertical axes for panels (A,B) while pressure is used for the other panels.

FIGURE 11

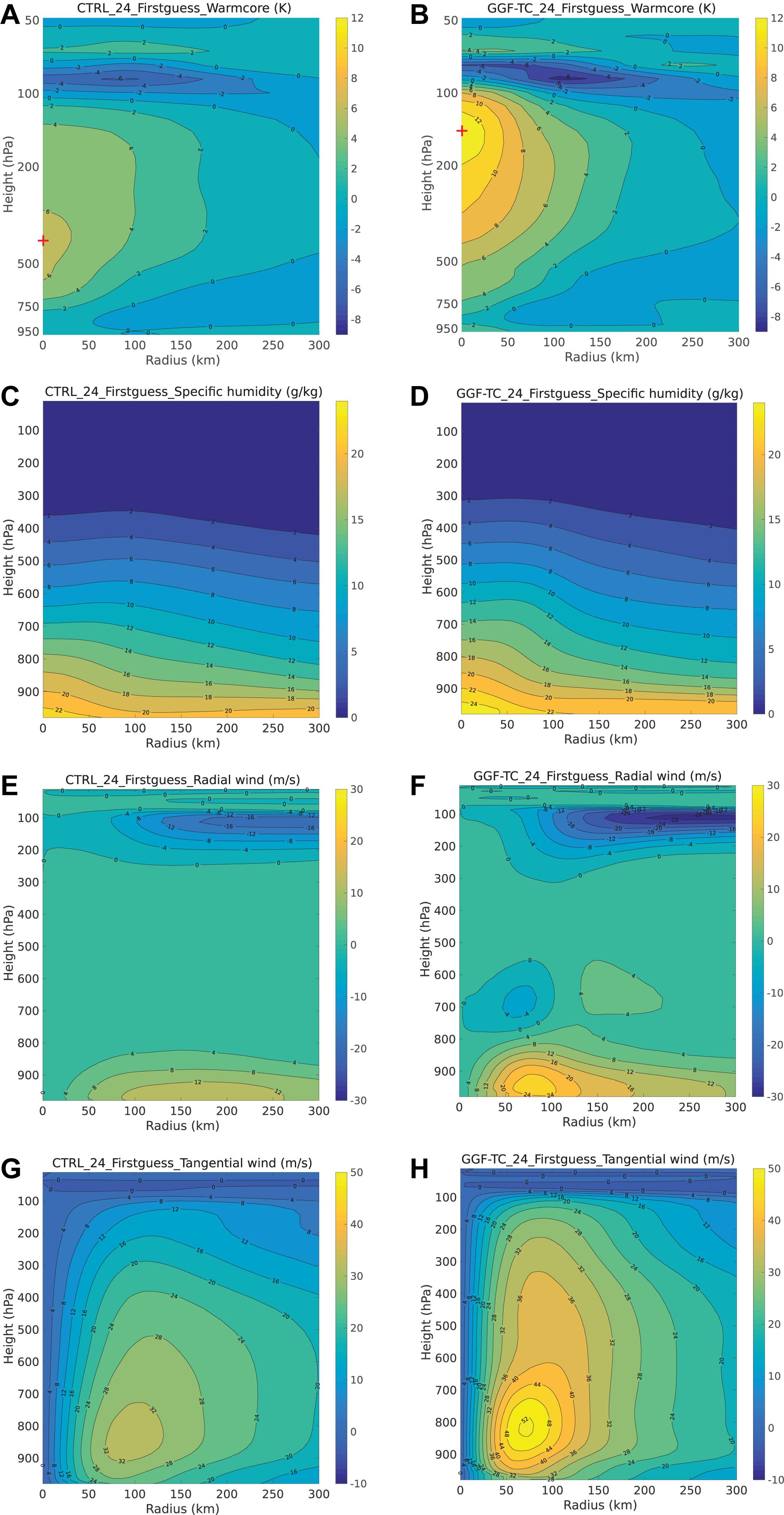
Figure 11. Same as Figure 10, radius-height cross sections of (A,B) temperature anomaly that has the mean temperature in a 1000 km radius deducted for each level, (C,D) specific humidity, (E,F) radial wind, and (G,H) tangential wind at 1200 UTC 24 October 2018. Left panels for experiment CTRL, and right panels for experiment GGF-TC.

Before the onset of RI (at 0000 UTC 23 October), the temperature anomalies of the priors from experiment GGF-TC prominently show a warm core at around 150 hPa, while experiment CTRL only has a weak warm core at around 400 hPa (Figures 10A,B). The stronger and higher upper-level warming shown in experiment GGF-TC is more favorable for the RI process (Hirschberg and Fritsch, 1993; Zhang and Chen, 2012). Compared to experiment CTRL, experiment GGF-TC has larger values of specific humidity, i.e., increased moisture, around the eyewall at low levels (Figures 10C,D), which could play an important role for TC intensification (Emanuel and Zhang, 2017). Experiment GGF-TC has stronger inflow at low levels and stronger outflow at high levels, and stronger primary circulations than experiment CTRL (Figures 10E–H). These features of wind filed from experiment GGF-TC indicate a more coherent storm wind structure, and can lead to later increase of pressure intensity (Ren et al., 2019). Comparisons of the posteriors at 0000 UTC 23 October between experiments GGF-TC and CTRL (figures are not shown) are consistent with those of the priors, except that the primary and secondary circulations, warm cores and humidity of the posteriors are more prominent than those of the priors due to data assimilation.

When typhoon Yutu (2018) reached its maximum intensity (at 1200 UTC 24 October), the temperature anomalies of the priors from experiment GGF-TC show a strong warm core at around 150 hPa, while experiment CTRL has a weak warm core at around 400 hPa (Figures 11A,B). Compared to experiment CTRL, experiment GGF-TC has increased moisture around the eyewall at low levels, a stronger primary circulation around the radius of maximum wind, and stronger inflow at low levels and stronger outflow at high levels (Figures 11C–H). These differences are consistent with the results of priors before the onset of RI. Therefore, the application of the adaptive localization parameters can better capture the onset of RI, and also improve the forecast of storm structures.

Discussion and Summaries

Tropical cyclones have multi-scale features, thus an adaptive localization function (GGF) is explored here for regions inside and outside a TC and for different assimilation times. Based on sample correlations between ensemble priors of observations and state variables, the GGF is computed by minimizing sampling errors of sample correlations. To practically implement the adaptive localization function for each radiance observation, the estimated vertical locations of radiance observations and localization widths are used. These adaptively estimated localization parameters can be obtained for each channel and every satellite platform of radiance data with different regions and times.

The adaptive localization parameters are examined for typhoon Yutu (2018). The GGF method can provide adaptively estimated localization parameters for both microwave and infrared sounders in the regional model WRF, which are similar to those in the global model GFS but with less variations among different satellite platforms. The GGF method can also estimate the localization parameters for regions inside and outside the TC separately. For all radiance observations, the localization widths for TC regions are generally broader than those for non-TC regions. Moreover, the GGF method can capture the temporal variations of the localization parameters by computing the localization parameters along with the assimilation cycles, although only slight temporal variations of the localization parameters are obtained.

Three assimilation experiments that use different localization parameters (GGF-Domain, GGF-TC, and GGF-Time) are conducted. The GGF experiments have similar errors verified relative to radiance observations, and they generally outperform the experiment CTRL that utilizes optimal GC localization. When verified against the conventional observations, the GGF experiments in general have smaller errors than experiment CTRL. Experiment GGF-Time has slightly smaller errors than GGF-Domain, and experiment GGF-TC is superior to the other two GGF experiments. The advantages of GGF experiments over experiment CTRL are more prominent for TC regions. For the track and intensity forecasts of typhoon Yutu (2018), the GGF experiments have similar forecasts to each other, and they have improved forecasts compared to experiment CTRL. Compared to the experiment CTRL, the GGF experiments better capture the onset of RI. The GGF experiments also produce more coherent TC structures than CTRL, including stronger warm cores, increased moisture around the eyewall at low levels, a stronger primary circulation around the radius of maximum wind, and stronger inflow at low levels and stronger outflow at high levels.

The adaptive method has also been applied to typhoon Meranti (2016), and similar results are obtained (Figures are not shown). The GGF experiments produce better forecasts than experiment CTRL when verified relative to radiance and conventional observations. For typhoon Meranti (2016), the GGF experiments can provide improved intensity forecasts and better capture the intensification process than experiment CTRL. Therefore, the advantages of adaptive localization parameters, especially for regions inside and outside the TC, have been demonstrated.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

CW performed the assimilation experiments and wrote the experimental design and results. LL performed the control experiments, developed the adaptive localization algorithm, and wrote the Introduction, Methodology, and Discussion and Summaries. Z-MT and KC analyzed the results and revised the manuscript.

Funding

This work was jointly sponsored by the National Key R&D Program of China through Grant 2017YFC1501603 and the National Natural Science Foundation of China through Grants 41675052 and 41675053.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Thanks to the two reviewers whose insightful comments significantly improve this report.

Footnotes

1. ^ https://dtcenter.org/EnKF/users/docs/enkf_users_guide/EnKF_UserGuide_v1.3.pdf
2. ^ http://www.emc.ncep.noaa.gov/mmb/data_processing/prepbufr.doc/table_2.htm
3. ^ http://www.emc.ncep.noaa.gov/mmb/data_processing/prepbufr.doc/table_18.htm

References

Aksoy, A., Dowell, D. C., and Snyder, C. (2009). A multicase comparative assessment of the ensemble Kalman filter for assimilation of radar observations. Part I: storm-scale analyses. Mon. Weather Rev. 137, 1805–1824. doi: 10.1175/2008MWR2691.1

CrossRef Full Text | Google Scholar

Alley, R. B., Emanuel, K. A., and Zhang, F. (2019). Advances in weather prediction. Science 363, 342–344. doi: 10.1126/science.aav7274

PubMed Abstract | CrossRef Full Text | Google Scholar

Anderson, J. L. (2007). Exploring the need for localization in ensemble data assimilation using a hierarchical ensemble filter. Phys. D 230, 99–111. doi: 10.1016/j.physd.2006.02.011

CrossRef Full Text | Google Scholar

Anderson, J. L., and Lei, L. (2013). Empirical localization of observation impact in ensemble Kalman filters. Mon. Weather Rev. 141, 4140–4153. doi: 10.1175/MWR-D-12-00330.1

CrossRef Full Text | Google Scholar

Buehner, M., Houtekamer, P. L., Charette, C., Mitchell, H. L., and He, B. (2010a). Intercomparison of variational data assimilation and the ensemble Kalman filter for global deterministic NWP. Part I: description and single-observation experiments. Mon. Weather Rev. 138, 1550–1566. doi: 10.1175/2009MWR3157.1

CrossRef Full Text | Google Scholar

Buehner, M., Houtekamer, P. L., Charette, C., Mitchell, H. L., and He, B. (2010b). Intercomparison of variational data assimilation and the ensemble Kalman filter for global deterministic NWP. Part II: one-month experiments with real observations. Mon. Weather Rev. 138, 1567–1586. doi: 10.1175/2009MWR3158.1

CrossRef Full Text | Google Scholar

Burgers, G., Van Leeuwen, P. J., and Evensen, G. (1998). Analysis scheme in the ensemble Kalman filter. Mon. Weather Rev. 126, 1719–1724. doi: 10.1175/1520-04931998126

PubMed Abstract | CrossRef Full Text | Google Scholar

Campbell, W. F., Bishop, C. H., and Hodyss, D. (2010). Vertical covariance localization for satellite radiances in ensemble Kalman filters. Mon. Weather Rev. 138, 282–290. doi: 10.1175/2009MWR3017.1

CrossRef Full Text | Google Scholar

Collard, A. D., and McNally, A. P. (2009). The assimilation of infrared atmospheric sounding interferometer radiances at ECMWF. Quat. J. R. Meteorol. Soc. 135, 1044–1058. doi: 10.1002/qj.410

CrossRef Full Text | Google Scholar

Emanuel, K., and Zhang, F. (2017). The role of inner-core moisture in tropical cyclone predictability and practical forecast skill. J. Atmos. Sci. 74, 2315–2324. doi: 10.1175/JAS-D-17-0008.1

CrossRef Full Text | Google Scholar

Evensen, G. (1994). Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. Oceans 99, 10143–10162. doi: 10.1029/94JC00572

CrossRef Full Text | Google Scholar

Flowerdew, J. (2015). Towards a theory of optimal localisation. Tellus A 67:25257. doi: 10.3402/tellusa.v67.25257

PubMed Abstract | CrossRef Full Text | Google Scholar

Gaspari, G., and Cohn, S. E. (1999). Construction of correlation functions in two and three dimensions. Quat. J. R. Meteorol. Soc. 125, 723–757. doi: 10.1002/qj.49712555417

PubMed Abstract | CrossRef Full Text | Google Scholar

Hamill, T. M., Whitaker, J. S., and Snyder, C. (2001). Distance-dependent filtering of background error covariance estimates in an ensemble Kalman filter. Mon. Weather Rev. 129, 2776–2790. doi: 10.1175/1520-04932001129<2776:DDFOBE<2.0.CO;2

CrossRef Full Text | Google Scholar

Han, Y., Weng, F., Liu, Q., and van Delst, P. (2007). A fast radiative transfer model for SSMIS upper atmosphere sounding channels. J. Geophys. Res. Atmos. 112:D11121. doi: 10.1029/2006JD008208

CrossRef Full Text | Google Scholar

Hirschberg, P. A., and Fritsch, J. M. (1993). On understanding height tendency. Mon. Weather Rev. 121, 2646–2661. doi: 10.1175/1520-0493(1993)121<2646:ouht>2.0.co;2

CrossRef Full Text | Google Scholar

Hong, S. Y., and Lim, J. O. J. (2006). The WRF single-moment 6-class microphysics scheme (WSM6). J. Korean Met. Soc. 42, 129–151.

Google Scholar

Hong, S. Y., Noh, Y., and Dudhia, J. (2006). A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 134, 2318–2341. doi: 10.1175/MWR3199.1

CrossRef Full Text | Google Scholar

Houtekamer, P. L., Deng, X., Mitchell, H. L., Baek, S. J., and Gagnon, N. (2014). Higher resolution in an operational ensemble Kalman filter. Mon. Weather Rev. 142, 1143–1162. doi: 10.1175/MWR-D-13-00138.1

CrossRef Full Text | Google Scholar

Houtekamer, P. L., and Mitchell, H. L. (2001). A sequential ensemble Kalman filter for atmospheric data assimilation. Mon. Weather Rev. 129, 123–137. doi: 10.1175/1520-04932001

CrossRef Full Text | Google Scholar

Houtekamer, P. L., and Mitchell, H. L. (2005). Ensemble kalman fieltering. Quat. J. R. Meteorol. Soc. 131, 3269–3289. doi: 10.1256/qj.05.135

CrossRef Full Text | Google Scholar

Houtekamer, P. L., Mitchell, H. L., Pellerin, G., Buehner, M., Charron, M., Spacek, L., et al. (2005). Atmospheric data assimilation with an ensemble Kalman filter: results with real observations. Mon. Weather Rev. 133, 604–620. doi: 10.1175/MWR-2864.1

CrossRef Full Text | Google Scholar

Iacono, M. J., Delamere, J. S., Mlawer, E. J., Shephard, M. W., Clough, S. A., and Collins, W. D. (2008). Radiative forcing by long–lived greenhouse gases: calculations with the AER radiative transfer models. J. Geophys. Res. 113, D13103. doi: 10.1029/2008JD009944

CrossRef Full Text | Google Scholar

Kain, J. S. (2004). The Kain–Fritsch convective parameterization: an update. J. Appl. Meteorol. 43, 170–181. doi: 10.1175/1520-045020040432

CrossRef Full Text | Google Scholar

Kunii, M. (2015). Assimilation of tropical cyclone track and wind radius data with an ensemble Kalman filter. Wea Forecast. 30, 1050–1063. doi: 10.1175/WAF-D-14-00088.1

CrossRef Full Text | Google Scholar

Le Marshall, J., Jung, J., Derber, J., Chahine, M., Treadon, R., Lord, S. J., et al. (2006). Improving global analysis and forecasting with AIRS. Bull. Am. Meteorol. Soc. 87, 891–895. doi: 10.1175/BAMS-87-7-891

CrossRef Full Text | Google Scholar

Lei, L., and Anderson, J. L. (2014a). Comparisons of empirical localization techniques for serial ensemble kalman filters in a simple atmospheric general circulation model. Mon. Weather Rev. 142, 739–754. doi: 10.1175/MWR-D-13-00152.1

CrossRef Full Text | Google Scholar

Lei, L., and Anderson, J. L. (2014b). Empirical localization of observations for serial ensemble Kalman filter data assimilation in an atmospheric general circulation model. Mon. Weather Rev. 142, 1835–1851. doi: 10.1175/MWR-D-13-00288.1

CrossRef Full Text | Google Scholar

Lei, L., Anderson, J. L., and Romine, G. S. (2015). Empirical localization functions for ensemble Kalman filter data assimilation in regions with and without precipitation. Mon. Weather Rev. 143, 3664–3679. doi: 10.1175/MWR-D-14-00415.1

CrossRef Full Text | Google Scholar

Lei, L., Anderson, J. L., and Whitaker, J. S. (2016). Localizing the impact of satellite radiance observations using a global group ensemble filter. J. Adv. Model Earth Syst. 8, 719–734. doi: 10.1002/2016MS000627

CrossRef Full Text | Google Scholar

Lei, L., and Whitaker, J. S. (2015). Model space localization is not always better than observation space localization for assimilation of satellite radiances. Mon. Weather Rev. 143, 3948–3955. doi: 10.1175/MWR-D-14-00413.1

CrossRef Full Text | Google Scholar

Lei, L., Whitaker, J. S., and Bishop, C. (2018). Improving assimilation of radiance observations by implementing model space localization in an ensemble Kalman filter. J. Adv. Model. Earth Syst. 10, 3221–3232. doi: 10.1029/2018MS001468

CrossRef Full Text | Google Scholar

McCarty, W., Jedlovec, G., and Miller, T. L. (2009). Impact of the assimilation of atmospheric infrared sounder radiance measurements on short-term weather forecasts. J. Geophys. Res. Atmos. 114:D18122. doi: 10.1029/2008JD011626

CrossRef Full Text | Google Scholar

Miyoshi, T., and Sato, Y. (2007). Assimilating satellite radiances with a local ensemble transform Kalman filter (LETKF) applied to the JMA global model (GSM). SOLA 3, 37–40. doi: 10.2151/sola.2007-010

CrossRef Full Text | Google Scholar

Miyoshi, T., Sato, Y., and Kadowaki, T. (2010). Ensemble Kalman filter and 4D-Var intercomparison with the Japanese operational global analysis and prediction system. Mon. Weather Rev. 138, 2846–2866. doi: 10.1175/2010MWR3209.1

CrossRef Full Text | Google Scholar

Munsell, E. B., and Zhang, F. (2014). Prediction and uncertainty of hurricane sandy (2012) explored through a real-time cloud-permitting ensemble analysis and forecast system assimilating airborne Doppler radar observations. J. Adv. Model. Earth Syst. 6, 38–58. doi: 10.1002/2013MS000297

CrossRef Full Text | Google Scholar

Nystrom, R. G., Zhang, F., Munsell, E. B., Braun, S. A., Sippel, J. A., Weng, Y., et al. (2018). Predictability and dynamics of Hurricane Joaquin (2015) explored through convection-permitting ensemble sensitivity experiments. J. Atmos. Sci. 75, 401–424. doi: 10.1175/JAS-D-17-0137.1

CrossRef Full Text | Google Scholar

Ren, S., Lei, L., Tan, Z. M., and Zhang, Y. (2019). Multivariate ensemble sensitivity analysis for super typhoon haiyan (2013). Mon. Weather Rev. 147, 3467–3480. doi: 10.1175/MWR-D-19-0074.1

CrossRef Full Text | Google Scholar

Skamarock, W. C., Klemp, J. B., Dudhia, J., Gill, D. O., Barker, D. M., Wang, W., et al. (2008). A Description of the Advanced Research WRF Version 3. NCAR Technical Note-475+ STR. Boulder, CO: University Corporation for Atmospheric Research.

Google Scholar

Tewari, M., Chen, F., Wang, W., Dudhia, J., LeMone, M. A., Mitchell, K., et al. (2004). “Implementation and verification of the unified NOAH land surface model in the WRF model,” in Proceedings of the 20th Conference on Weather Analysis and Forecasting/16th Conference on Numerical Weather Prediction, Seattle.

Google Scholar

Torn, R. D., Hakim, G. J., and Snyder, C. (2006). Boundary conditions for limited-area ensemble Kalman filters. Mon. Weather Rev. 134, 2490–2502. doi: 10.1175/MWR3187.1

CrossRef Full Text | Google Scholar

Trahan, S., and Sparling, L. (2012). An analysis of NCEP tropical cyclone vitals and potential effects on forecasting models. Wea Forecast. 27, 744–756. doi: 10.1175/WAF-D-11-00063.1

CrossRef Full Text | Google Scholar

Weng, F. (2007). Advances in radiative transfer modeling in support of satellite data assimilation. J. Atmos. Sci. 64, 3799–3807. doi: 10.1175/2007JAS2112.1

CrossRef Full Text | Google Scholar

Weng, Y., and Zhang, F. (2012). Assimilating airborne doppler radar observations with an ensemble Kalman filter for convection-permitting hurricane initialization and prediction: Katrina (2005). Mon. Weather Rev. 140, 841–859. doi: 10.1175/2011MWR3602.1

CrossRef Full Text | Google Scholar

Whitaker, J. S., and Hamill, T. M. (2002). Ensemble data assimilation without perturbed observations. Mon. Weather Rev. 130, 1913–1924. doi: 10.1175/1520-0493(2002)130<1913:EDAWPO>2.0.CO;2

CrossRef Full Text | Google Scholar

Whitaker, J. S., and Hamill, T. M. (2012). Evaluating methods to account for system errors in ensemble data assimilation. Mon. Weather Rev. 140, 3078–3089. doi: 10.1175/MWR-D-11-00276.1

CrossRef Full Text | Google Scholar

Whitaker, J. S., Hamill, T. M., Wei, X., Song, Y., and Toth, Z. (2008). Ensemble data assimilation with the NCEP global forecast system. Mon. Weather Rev. 136, 463–482. doi: 10.1175/2007MWR2018.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Ying, Y., Zhang, F., and Anderson, J. L. (2018). On the selection of localization radius in ensemble filtering for multiscale quasigeostrophic dynamics. Mon. Weather Rev. 146, 543–560. doi: 10.1175/MWR-D-17-0336.1

CrossRef Full Text | Google Scholar

Zhang, D. L., and Chen, H. (2012). Importance of the upper-level warm core in the rapid intensification of a tropical cyclone. Geophy. Res. Lett. 39:L02806. doi: 10.1029/2011GL050578

CrossRef Full Text | Google Scholar

Zhang, F., Weng, Y., Gamache, J. F., and Marks, F. D. (2011). Performance of convection-permitting hurricane initialization and prediction during 2008–2010 with ensemble data assimilation of inner-core airborne Doppler radar observations. Geophys. Res. Lett. 38:L15810. doi: 10.1029/2011GL048469

CrossRef Full Text | Google Scholar

Zhang, F., Weng, Y., Sippel, J. A., Meng, Z., and Bishop, C. H. (2009). Cloud-resolving hurricane initialization and prediction through assimilation of Doppler radar observations with an ensemble Kalman filter. Mon. Weather Rev. 137, 2105–2125. doi: 10.1175/2009MWR2645.1

CrossRef Full Text | Google Scholar