An Assessment of Continuous Modeling for Robust Design Flood Estimation in Urban Environments

Introduction

Catchment management is a complex task that, over the past decade, has become increasingly important to the community. This is particularly the case for urban environments. Of the many catchment management issues, estimation of the magnitude and likelihood of flood events is one that remains an issue in many urban environments. There are many different issues requiring design flood estimation; see, for example, Audisio and Turconi (2011), Hettiarachchi et al. (2018), and Andimuthu et al. (2019) who present different aspects of the need to estimate design floods in urban environments. As a consequence, design flood estimation remains a significant problem for management of many urban catchments.

While the flood characteristics important for management of a drainage system will vary between problems, Ball (2014) suggests that, typically, the flood characteristic of concern will be one of the following:

• Flood flow rate – the peak flow rate of the flood hydrograph is a common design flood hydrograph characteristic used, for example, to size drainage system components;

• Flood level – the peak flood level during a flood hydrograph is a common design flood hydrograph characteristic used, for example, in setting minimum floor levels;

• Flood rate of rise – this design flood characteristic is a concern when planning for evacuation;

• Flood volume – this design flood characteristic becomes a concern when storage of the design flood is being considered as part of a flood management system; or

• System failure – the usual design flood problem is located at a single point. There are numerous design problems, however, where the critical concern is prediction of system failure. Examples of these problems include urban drainage systems and transportation routes with multiple cross drainage structures.

In Australia, a risk management approach provides the foundation for flood management (Ball et al., 2016). When a risk management approach is used, it is necessary to estimate both the magnitude of the hazard and the likelihood of the hazard. In other words, there is a need to consider the relationship between the magnitude and the exceedance probability of a design flood characteristic. An example of this relationship is shown in Figure 1.

FIGURE 1

Figure 1. Relationship between flood hazard and likelihood.

Arising from the need for predictions of the relationship between flood hazard and its likelihood, a number of alternative approaches have been developed. Smithers (2012), discusses these approaches and categorizes the approaches considered as being either “analysis of streamflow data” or “rainfall based”; herein, similar categories are used although they are referred to as “catchment monitoring approaches” and “catchment modeling approaches”. In reviewing rainfall-based approaches, Smithers (2012) notes that continuous simulation approaches have been proposed to overcome inherent biases introduced through use of single event approaches.

While estimation of the relationship between the magnitude and the likelihood, or probability, of a flood hazard can be achieved through alternative approaches, a fundamental need for all approaches is the availability of suitable data. This data can be obtained from catchment monitoring or catchment modeling. The aim of a catchment monitoring is the collection of data about the desired flood characteristics within the catchment over multiple storm events. Typically, the data obtained will include time-series data at various time scales and spatial data, during and post events, of differing resolutions. To obtain relevant information about the flood risk within the catchment, as explained by Ball (2018) this collected data is mined to extract relevant information about the relationship between the magnitude and the likelihood of the flood hazard.

The alternative approach to catchment monitoring is catchment modeling. Conceptually, the aim of catchment modeling is to generate data that would have been recorded if catchment monitoring had been in place for the event, or sequence of events, at the locations being considered. Hence, the generated data should have the same characteristics as the historical data that could have been monitored at the site or sites of interest. Where changes in catchment management, e.g., land-use, or changes in climatic conditions are to be considered, catchment modeling techniques are required; catchment monitoring approaches can be used only when a physical catchment exists. Finally, similar to data obtained from catchment monitoring, mining of the data obtained from catchment modeling is required to extract relevant information about the likelihood of a flood hazard.

As implied in the previous discussion, catchment modeling can be used to provide data at locations remote from monitoring locations. The converse is also valid; catchment monitoring can be used to validate predictions obtained from catchment modeling. Hence, effective flood management for a catchment requires data from both catchment monitoring and catchment modeling programs. Presented herein will be a discussion of the use of monitored and modeled data in the estimation of the flood risk in the Powells Creek catchment located in the inner west suburbs of Sydney, Australia. Of particular interest is the viability of predicting flood risk from analysis of data generated through continuous simulation of catchment processes.

Powells Creek Catchment

Catchment Description

The Powells Creek catchment, sometimes referred to as the Strathfield catchment, is an 841 ha catchment situated 10 km west of Sydney’s central business district. The location of this catchment is shown in Figure 2. The catchment lies within the Sydney suburbs of Homebush West, North Strathfield, Rookwood and Strathfield, and is administered by the local government areas of Strathfield, Canada Bay and Auburn. The drainage network comprises a closed piped system that opens out to a lined channel and then into the Parramatta River. The main open channel was established in 1892 (Meutia, 2002) and the closed pipe system was established in the 1920s.

FIGURE 2

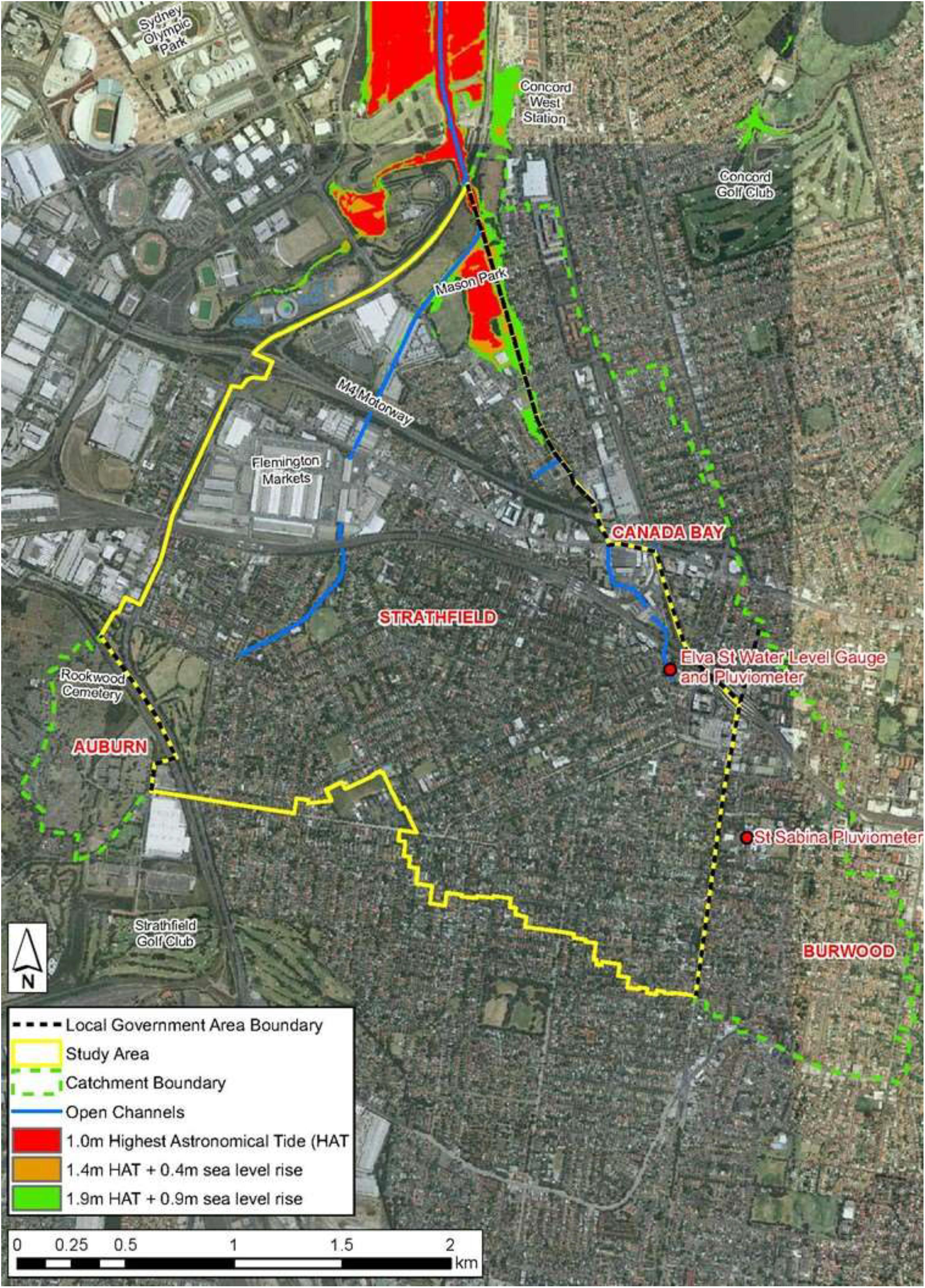
Figure 2. Powells Creek catchment (after WMAwater, 2016).

Shown in Table 1 are the land-use classifications within the Powells Creek catchment as outlined by Meutia (2002). From a topographic perspective, the catchment is classified as having gentle slopes between 4 and 6% with a maximum elevation of 40 m AHD; the minimum elevation is governed by the tidal regime of the Parramatta River.

TABLE 1

Table 1. Land use in the Powells Creek catchment (after Meutia, 2002).

Available Data

The School of Civil and Environmental Engineering at The University of New South Wales operated a gauging station on the main Powells Creek Stormwater Channel during the period 1958 to 2005. The location of this gauging station is shown in Figure 2. The catchment area draining to this gauging station consists of 2.3 km² of the total 8.41 km² catchment area. Initially this gauging station monitored only the flow quantity but since the early 1990s monitored water quality parameters as well.

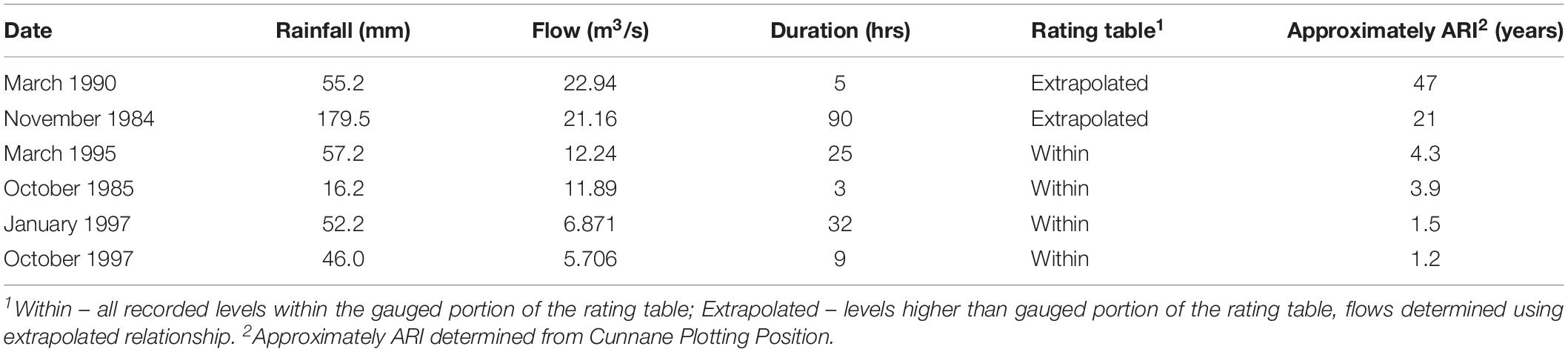
Numerous stream gaugings have been taken at this gauging station to define the rating curve for translation of level to recorded flows. There are 14 gaugings below 0.5 m and 14 gaugings between 0.5 and 1.0 m; the highest traditional gauging used in developing the rating curve was 1.35 m (13.8 m³/s). Gauging data above 1.35 to 1.65 m used the technique presented by Tilley et al. (2000) for gauging in rapidly varying flows; no gauge data is available above 1.65 m to validate the rating curve for the peak flood flows.

In addition to the flow data, continuous rainfall data was collected at two locations within the gauged portion of the catchment; these locations were at the centroid of the gauged catchment and at the flow gauging station. While this rainfall data was collected for the same period as the flow data, only rainfall data for the period 1981 to 1998 from the flow gauging station was available for this study.

Flow and rainfall data for individual events were extracted from this dataset for model calibration. Details of this data are presented in Table 2.

TABLE 2

Table 2. Calibration events.

Catchment Model

There are numerous alternative software systems suitable for process-based modeling of existing and potential urban catchments. After considering these alternatives, the SWMM system (Rossman, 2005) was used herein for data generation. This model has received extensive application; see, for example, Leutnant et al. (2019) and Broekhuizen et al. (2020) for recent applications.

SWMM is a physically distributed catchment modeling system consistent with the conceptual components of a catchment modeling system proposed by Ball (1992); these components are:

• Generation – this component of the modeling system is concerned with spatial and temporal models necessary to convert point data into spatial-temporal data. An example is the conversion of point rainfall records into spatial rainfall models over the catchment at suitable resolution;

• Collection – the component of the model where those processes concerned with the generation of runoff are dominant. This is the hydrologic component of the modeling system;

• Transport – the component of the model where the processes concerned with the movement of water through the drainage system are dominant. This is the hydraulic component of the modeling system; and

• Disposal – the component of the modeling system concerned with the discharge of water from the drainage system into receiving waters.

For construction of the catchment model, the Powells Creek catchment was divided into 103 subcatchments and a similar number of channels. SWMM has the capacity for each subcatchment and channel to have unique parameter values. This capacity was utilized during calibration of the model.

There are many different parameters necessary for operation of a catchment modeling system; these parameters can be categorized arbitrarily into:

• Measured parameters. These are parameters that are physically measured such as pipe diameters, catchment areas, rainfall depth or rainfall intensity, etc.; and

• Inferred parameters. These are parameters that are not measured and are determined from the application of a model. Examples of inferred parameters are Manning’s roughness for catchment surfaces or channels, depression storage, catchment or subcatchment imperviousness.

While the interface between these categories may appear as an absolute division, the interface between these categories is vague with parameters oscillating between the categories depending on the viewpoint of the user. For example, rainfall depth in the above discussion is defined as a measured parameter, but this measurement is only at the rainfall gauge itself with rainfall at other locations within the catchment (assuming the rain gauge is within the catchment) being inferred by application of a spatial rainfall model; see Ball and Luk (1998) for a discussion of the potential errors introduced through different inference models for the spatial distribution of rainfall over a catchment. Consideration of other parameters such as the catchment, or subcatchment, area also reveals a variability in measured parameters depending on, for example, the scale of the map from which the area was measured. In general, the values of inferred parameters are considered those that need to be adjusted during calibration, while measured parameters are assumed error free during the calibration process.

For the purposes of calibrating the Powells Creek model used in this study, the parameters considered are shown in Table 3. A previously calibrated model of Powells Creek was available from Meutia (2002). These parameter values were used as a search starting point for the most generic parameter values and their uncertainty. Initial feasible parameter values were defined as ± 50% of the values obtained by Meutia (2002); in other words, all parameter values tested were within ± 50% of the calibrated values obtained by Meutia (2002).

TABLE 3

Table 3. Parameter considered during model calibration.

Previously Fang and Ball (2007) used a genetic algorithm (GA) to search the parameter space for feasible parameter sets within a GLUE framework; a similar approach was used herein with a GA population of 1000. More details of the GA are presented by Fang and Ball (2007) and, hence, are not presented herein.

There are numerous alternative metrics that can be used to assess the suitability of the calibration obtained. Shown in Table 4 are the calibration metrics if Nash-Sutcliffe Efficiency (NSE), Root Mean Square Error (RMSE), and Peak Discharge (Q_peak) are used to assess the calibration. A visual comparison for some of the predicted hydrographs using the best parameter sets (i.e., the minimum error) for two events is shown in Figure 3. It should be noted that the best parameter set differed between events and between alternative calibration metrics.

TABLE 4

Table 4. Powells Creek calibration metrics.

FIGURE 3

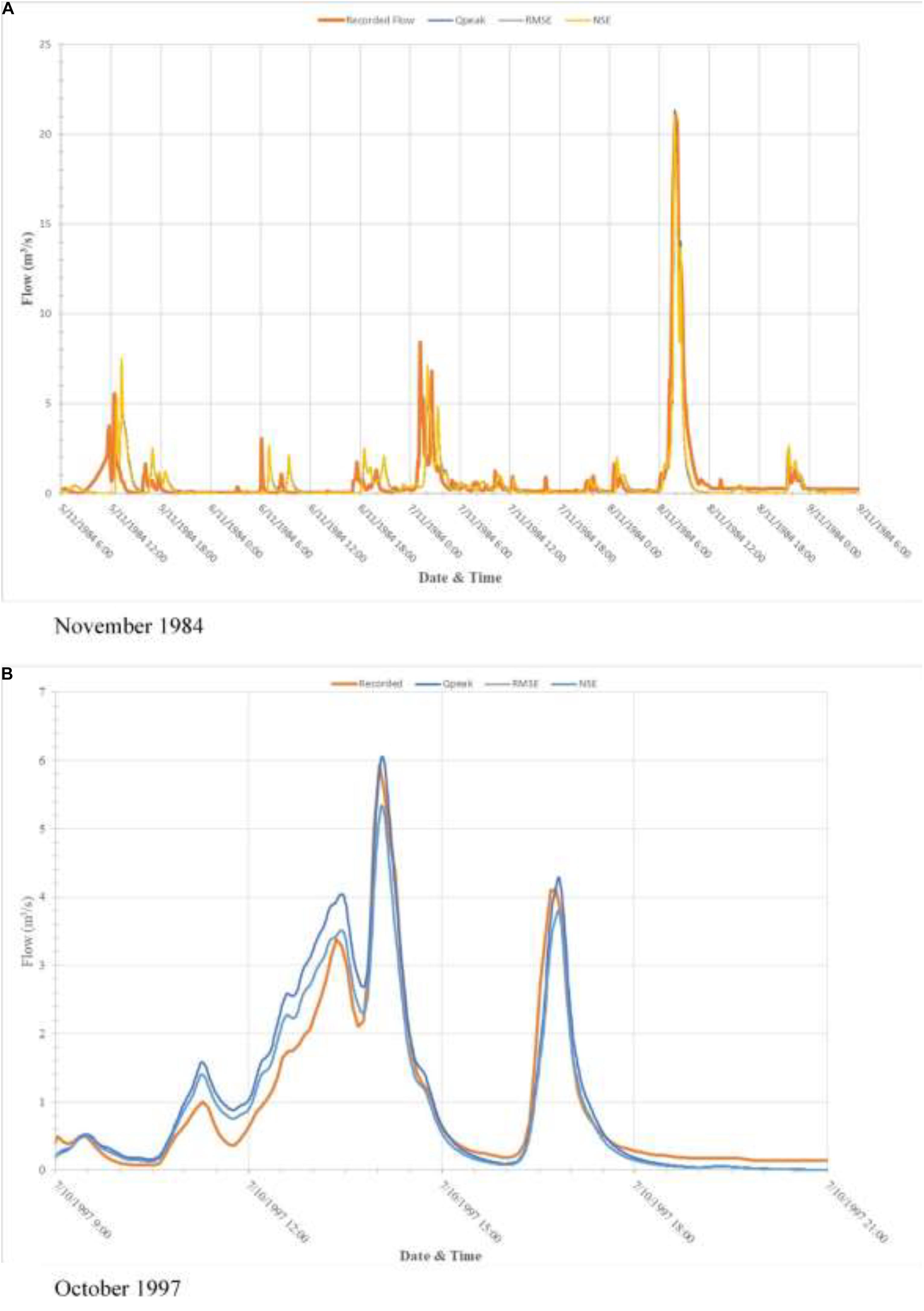
Figure 3. Predicted hydrographs for selected calibration events, (A) November 1984, (B) October 1997.

Analysis of Field Data

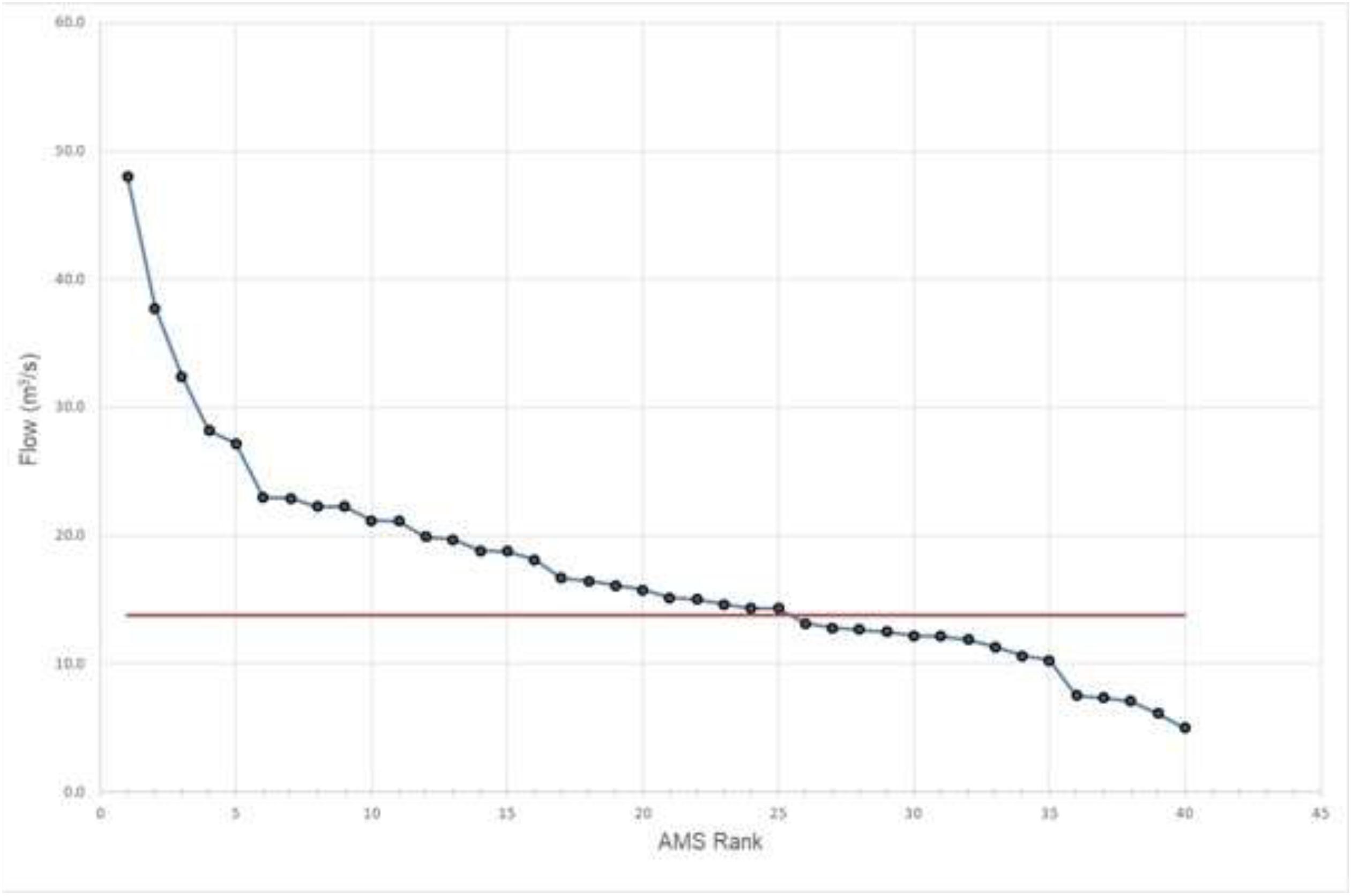
A common analysis approach for design flood estimation based on monitored data is the use of At-Site flood frequency analysis (FFA). While the period of record extended for 47 years, an annual maximum series (AMS) could be extracted only for a continuous 40 year period. Shown in Figure 4 is the ranked AMS. As can be seen from consideration of this figure, the highest 25 recorded flows are in the extrapolation zone of the rating curve; in other words, 25 of the AMS data points are above the highest validated point on the rating curve. This means that the Mean Annual Flood (Median of the AMS) lies within the extrapolation zone of the rating curve; note that the Mean Annual Flood is important for estimation of the value of the location parameter for most three parameter statistical models of the relationship between flood magnitude and likelihood.

FIGURE 4

Figure 4. Powells Creek ranked AMS.

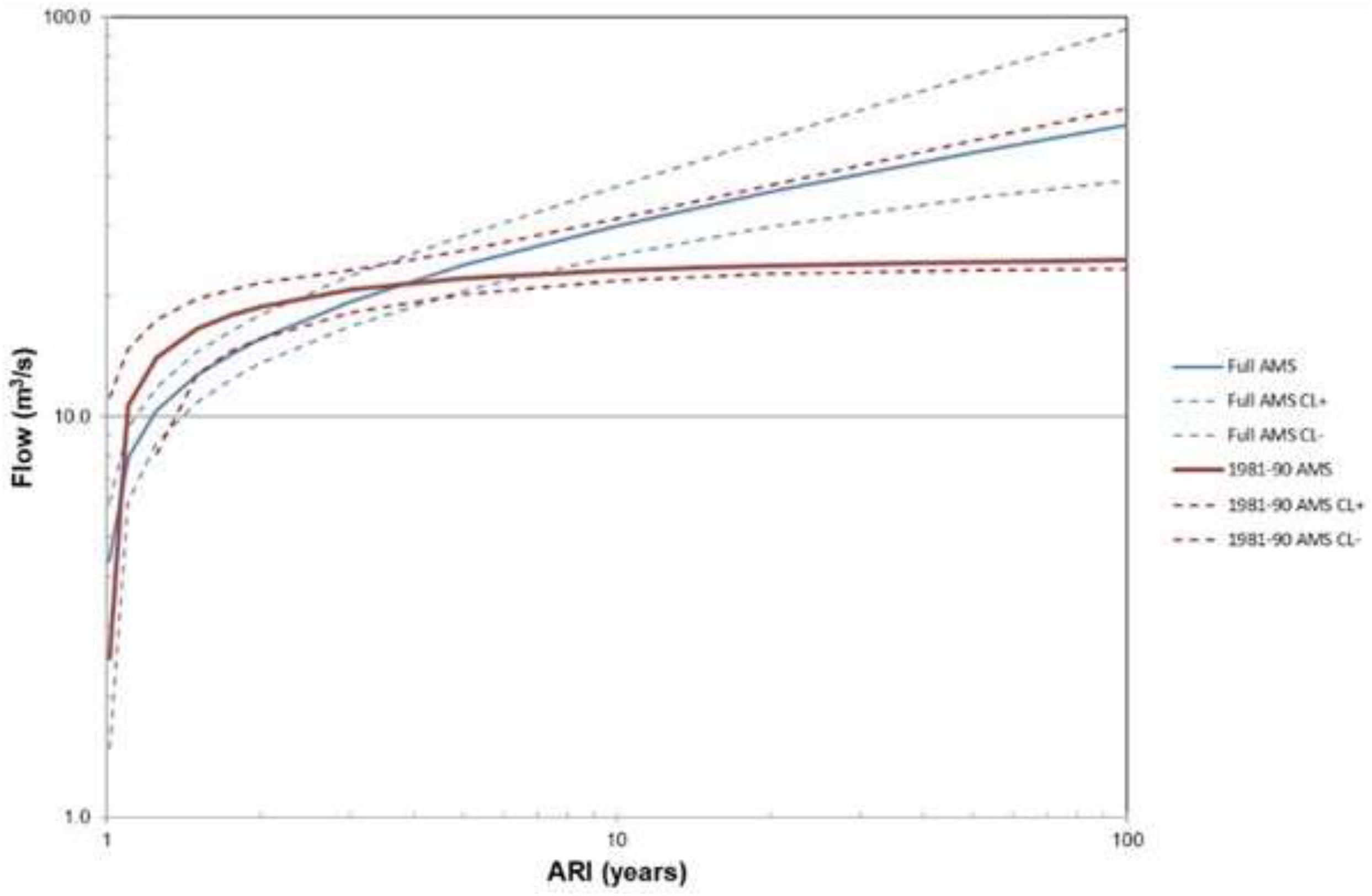
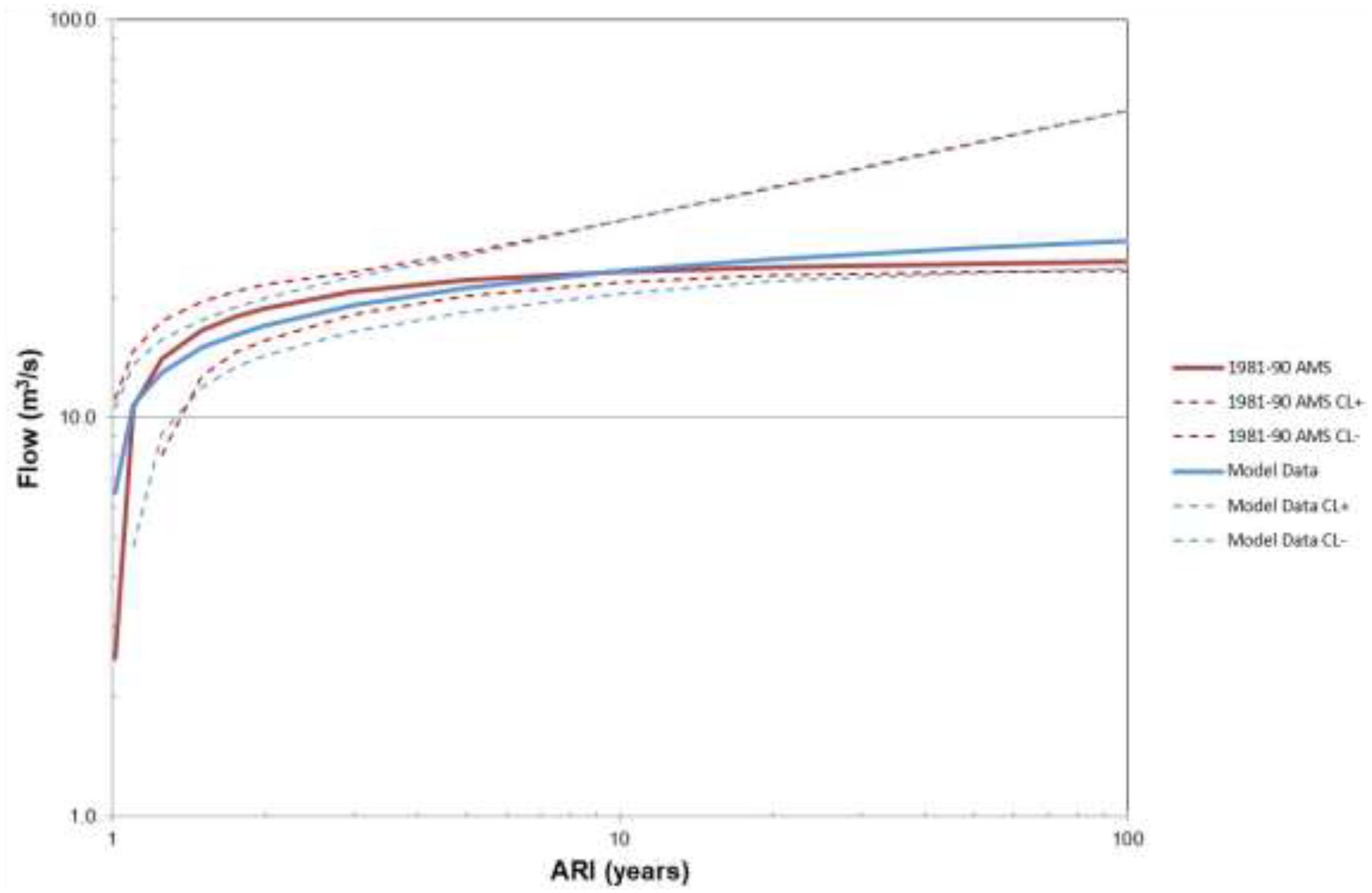
Undertaking an FFA for this site using the full 40 year AMS in accordance with guidance presented in Australian Rainfall and Runoff (Ball et al., 2016) results in the flood frequency shown in Figure 5. In this case, the three parameter GEV distribution was fitted to the 40 available data points. Shown in Table 5 are the estimated values for these parameters together with their estimated variability.

TABLE 5

Table 5. GEV parameters for annual maxima series of 40 and 10 years duration.

FIGURE 5

Figure 5. Flood frequency for Powells Creek gauging station.

Also shown in Figure 5 and Table 5 are the flood frequency predictions and the relevant statistical model parameters if the 10-year period, 1981–1990, were used in lieu of the full period of record. As can be seen in Figure 4 and as suggested by the values presented in Table 2, there are considerable differences in the predicted relationships even though the shorter period AMS occurs within the period of the longer AMS. This highlights the need, when assessing flood frequency relationships, to ensure consistency of data sources and periods.

Analysis of Modeled Data

As noted earlier, the aim of most physically based catchment models is the reproduction of the data that would have been recorded if monitoring were being undertaken at that location for the desired catchment conditions and climate state. While generation of both continuous and event specific data is feasible, for purposes of generating data for prediction of flood risk, techniques considering a single burst (or event) have been the more popular.

When catchment modeling using a single event or burst approach is employed, there are two alternative interpretations, namely AEP neutrality and event reproduction. These alternatives are shown in Figure 6.

FIGURE 6

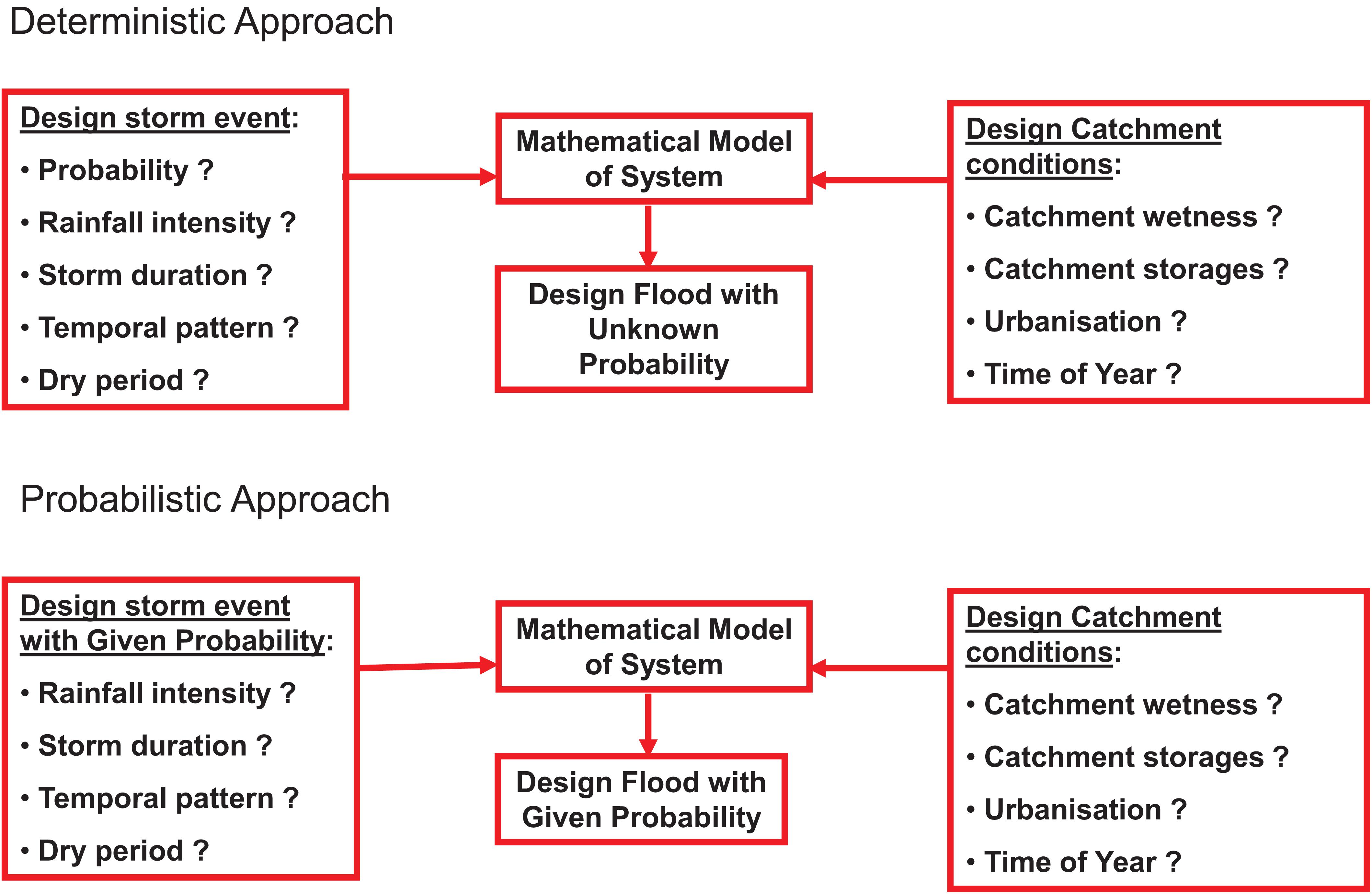
Figure 6. Alternative conceptual usage of catchment models for flood risk assessment (after Ball, 2017).

Where the single burst approach has been implemented with the assumption that the frequency of the rainfall is transformed to the frequency of the resultant flood characteristic, it can be argued that the approach is a Regional Flood Frequency Estimation technique; in other words, the catchment model is used to provide a regression ensuring consideration of the main catchment factors. An example of this approach is provided by Hill et al. (1998) who developed a method of estimating loss model parameters that are likely to result in the frequency of the rainfall being transferred to the frequency of the design flood flow.

It is possible to use a single event or burst approach without the assumption of AEP neutrality. In these circumstances, the catchment model is used to analyze the catchment response to a design rainfall event with the probability of the resultant flood characteristics being unknown.

The alternative to simulation of single events is continuous simulation resulting in continuous time series data; to estimate the flood risk, it is necessary to analyze this data using Flood Frequency. Previously, the calibration of the SWMM model to individual events was discussed. Since the focus of the data generation is the estimation of the flood risk, successful prediction of higher flows and flow depths was required and lower flows that were not likely to influence the statistical analysis did not need similar prediction reliability. Hence, the parameter sets derived from the event calibration were employed in the generation of the continuous time series data.

The model generated time series data were analyzed in a similar manner to the field monitored data to develop a flood hazard magnitude likelihood relationship. Shown in Figure 7 is a graphical representation of this relationship. Also shown in this figure is the same relationship developed from the field monitored data for the same period of record. Inspection of this figure suggests a visual similarity of the two relationships. This similarity of relationship is confirmed if the parameters for the GEV relationship, shown in Table 6, are considered.

TABLE 6

Table 6. FFA parameters for 10 year AMS.

FIGURE 7

Figure 7. Comparison of FFA from monitored and modeled data.

Conclusion

Management of floods in urban catchments is a complex task. Data for this management task can come from a variety of sources, namely monitoring and modeling of the catchment. Catchment modeling here refers to modeling aimed at reproducing data that would have been recorded if field monitoring were undertaken at that location for that catchment condition and rainfall record; many catchment modeling approaches do not meet this definition as the models are used in a statistical context rather than a physical process context. Management of data from both sources requires definition of the metadata about the data to enable assessment of data uncertainty and to enable appropriate data mining to determine flood risk. Finally, using the Powells Creek catchment in Sydney, Australia as a case study, it was shown that design flood predictions from data mining of both field monitored and model generated data were similar provided consistent periods of record were utilized for the same catchment conditions; in other words, the rain records and catchment conditions were from the same period.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

JB made substantial contributions to the conception, design of the work; drafted the work for important intellectual content; provided approval for publication of the content; and agrees to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Andimuthu, R., Kandasamy, P., Mudgal, B. V., Jeganathan, A., Balu, A., and Sankar, G. (2019). Performance of urban storm drainage network under changing climate scenarios: flood mitigation in Indian coastal city. Sci. Rep. 9:7783. doi: 10.1038/s41598-019-43859-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Audisio, C., and Turconi, L. (2011). Urban floods: a case study in the Savigliano area (North-Western Italy). Nat. Hazards Earth Syst. Sci. 11, 2951–2964. doi: 10.5194/nhess-11-2951-2011

CrossRef Full Text | Google Scholar

Ball, J. E. (1992). A Review of Numerical Models for Prediction of Catchment Water Quantity and Quality. Research Report No. 180, Water Research Laboratory, Dept. of Water Engineering, School of Civil Engineering. Sydney: The University of New South Wales.

Google Scholar

Ball, J. E. (2014). “Flood estimation under changing climates,” in Proeedings of the. 2014 IAHR-APD Congress, Hanoi.

Google Scholar

Ball, J. E. (2017). “Urban Flood Modelling – Process or Regression,” in Proceedings 37^th IAHR World Congress, Kuala Lumpur, Malaysia.

Google Scholar

Ball, J. E. (2018). “A classic hydroinformatic problem - floods,” in Proceedings of the 2018 International Conference on Hydroinformatics, Palermo.

Google Scholar

Ball, J. E., and Luk, K. C. (1998). Modelling the spatial variability of rainfall over a catchment. ASCE J. Hydrol. Eng. 3, 122–130.

PubMed Abstract | Google Scholar

Ball, J. E., Babister, M., Nathan, R., Weeks, W., Weinmann, E., Retallick, M., et al. (2016). Australian Rainfall and Runoff: A Guide to Flood Estimation. Canberra: Commonwealth of Australia.

Google Scholar

Broekhuizen, I., Leonhardt, G., Marsalek, J., and Viklander, M. (2020). Event selection and two-stage approach for calibrating models of green urban drainage systems. Hydrol. Earth Syst. Sci. 24, 869–885. doi: 10.5194/hess-24-869-2020

CrossRef Full Text | Google Scholar

Fang, T., and Ball, J. E. (2007). Evaluation of spatially variable control parameters in a complex catchment modelling system: a genetic algorithm application. J. Hydroinform. 9, 163–173. doi: 10.2166/hydro.2007.026

CrossRef Full Text | Google Scholar

Hettiarachchi, S., Wasko, C., and Sharma, A. (2018). Increase in flood risk resulting from climate change in a developed urban watershed – the role of storm temporal patterns. Hydrol. Earth Syst. Sci. 22, 2041–2056. doi: 10.5194/hess-22-2041-2018

CrossRef Full Text | Google Scholar

Hill, P. I., Mein, R. G., and Siriwardena, L. (1998). How Much Rainfall Becomes Runoff? - Loss Modelling for Flood Estimation. Industry Report 98/5, Cooperative Research Centre for Catchment Hydrology. Clayton: Monash University.

Google Scholar

Leutnant, D., Döring, A., and Uhl, M. (2019). swmmr - an R package to interface SWMM. Urban Water J. 16, 68–76. doi: 10.1080/1573062X.2019.1611889

CrossRef Full Text | Google Scholar

Meutia, E. Z. (2002). Development of a Catchment Modelling System for the Powells Creek Catchment. Unpublished Master of Engineering Science Report, The University of New South Wales, Sydney.

Google Scholar

Rossman, L. A. (2005). Storm Water Management Model - User’s Manual, Version 5.0. Report EPA/600/R-05/040. Cincinnati: U.S. Environmental Protection Agency.

Google Scholar

Smithers, J. C. (2012). Methods for design flood estimation in South Africa. Water SA 38, 633–646. doi: 10.4314/wsa.v38i4.19

CrossRef Full Text | Google Scholar

Tilley, J. H., Coates, A., Wojcik, A., Ball, J. E., and Abustan, I. (2000). Development of a stage-discharge relationship for rapidly varying flows in urban streams. Austral. J. Water Resour. 4, 139–145.

Google Scholar

WMAwater. (2016). Powells Creek and Saleyards Creek Revised Flood Study. Unpublished Report. Sydney, Australia: Strathfield Municipal Council.

Google Scholar