GNSS Meteorology for Disastrous Rainfalls in 2017–2019 Summer in SW Japan: A New Approach Utilizing Atmospheric Delay Gradients

We studied disastrous heavy rainfall episodes in 2017–2019 summer in SW Japan, especially in the Kyushu region using tropospheric delay data from the Japanese dense global navigation satellite system (GNSS) network GEONET (GNSS Earth Observation Network). This region often suffers from extremely heavy rains associated with stationary fronts during summer. In this study, we first analyze behaviors of water vapor on July 6, 2018, using tropospheric parameters obtained from the database at the University of Nevada, Reno. The data set includes tropospheric delay gradient vectors (G), as well as zenith tropospheric delays (ZTD), estimated every 5 min. At first, we interpolated G to obtain those at grid points and calculated their convergence, similar to the quantity proposed by Shoji (2013) as water vapor concentration (WVC) index. We obtained zenith wet delay (ZWD) from ZTD by removing zenith hydrostatic delay. The raw ZWD values do not really reflect the wetness of the atmosphere above the GNSS station because they largely depend on the station altitudes. To study the dynamics of water vapor before heavy rains, we estimated ZWD converted to the values at sea level. In the inversion scheme, we used G at all GEONET stations and ZWD data at low-altitude (<100 m) GEONET stations as the input. Then we assumed that spatial change of ZWD is proportional to G (e.g., G_x = H ∂ZWD/∂x, where H is the water vapor scale height) and estimated sea-level ZWD at grid points all over Japan. At last, we tried to justify our working hypothesis that heavy rain occurs when both WVC and sea-level ZWD are high by analyzing hourly water vapor distributions in all the days in July 2017, July 2018, and August 2019. We found that both two values showed maxima in the studied period when the three heavy rainfall (>50 mm/h) episodes occurred, that is, July 5, 2017, July 6, 2018, and August 27, 2019. Next, we performed high time resolution analysis (every 5 min) on the days of heavy rain. The results suggest that both WVC and sea-level ZWD go up prior to the onset of the rain, and ZWD decreases rapidly once the heavy rain started. It is a future issue, however, how far these two quantities contribute to forecast heavy rains.

Introduction

Disastrous heavy rains in summer 2017 to 2019 in SW Japan caused a lot of damage to property and human lives. The Japan Meteorological Agency (JMA) officially named the extreme rainfall event in 2018 July as “The Heavy Rain Event of July 2018.” Precipitation records at meteorological stations show extreme rainfalls from June 28 to July 8, 2018, especially in the northern part of the Kyushu District. Figure 1 shows the precipitation rate in the high-resolution nowcast rainfall map at 17:00 JST (08:00 UT), July 6, 2018, from JMA. This was obtained by a weather radar with a 250-m resolution every 5 min. Such meteorological radars have been operated by JMA at 20 stations throughout Japan. The heavy rain occurred over a patchy region elongated in NE-SW and overlap with the stationary front. Water vapor transported along the front from SW is thought to have caused the heavy rain.

FIGURE 1

Figure 1. High-resolution map of the rainfall rate at 17:00 JST (08:00 UT) July 6, 2018, from JMA (https://www.data.jma.go.jp/fcd/yoho/meshjirei/jirei01/high resorad/index.html).

The concept of ground-based global navigation satellite system (GNSS) meteorology was proposed initially by Bevis et al. (1992), and meteorological utilization of the Japanese GEONET has been sought (e.g., Tsuda et al., 1998). Nowadays, GNSS meteorology has become one of the essential means to observe precipitable water vapor (PWV), and PWV data from GEONET have been assimilated in the mesoscale model of JMA to improve weather forecast accuracy since 2009 (e.g., Shoji, 2015). In this study, we apply a new method of GNSS meteorology to utilize atmospheric delay gradients, reflecting azimuthal asymmetry of water vapor (MacMillan, 1995), for the 2017–2019 heavy rain cases in SW Japan.

Miyazaki et al. (2003) focused on such atmospheric delay gradients and showed that the temporal and spatial variations of the gradients were compatible with the humidity fields derived from zenith wet delay (ZWD) and with the meteorological conditions in 1996 summer over the Japanese Islands (especially during a front passages). Shoji (2013) and Brenot et al. (2013) demonstrated the important role of the atmospheric delay gradients to detect smaller scale structures of the troposphere than ZWD.

Recently, Zus et al. (2019) have successfully processed the Central Europe GNSS network data to show that the interpolation of ZWD observed with a sparse network can be improved by utilizing tropospheric delay gradients. They showed significant accuracy improvement for the simulation of the numerical weather model, and for the agreement of the simulation results with real observations, relative to the cases without utilizing tropospheric delay gradients.

In this study, we propose a new method to use tropospheric delay gradients to study heavy rain phenomena in Japan using the data from the GEONET data. At first, we analyze behaviors of water vapor on July 6, 2018, using tropospheric parameters obtained from the database at the University of Nevada, Reno (UNR; Blewitt et al., 2018). The data set includes tropospheric delay gradient vectors (G), as well as zenith tropospheric delays (ZTDs), estimated every 5 min. We interpolate G to obtain those at grid points and calculated their convergence, similar to the index proposed by Shoji (2013) as water vapor concentration (WVC). Then, taking advantage of the dense GNSS network, we try to reconstruct ZWD in inland regions (especially in high-altitude regions) by spatially integrating G.

The purpose of this study is to show the implication of utilizing tropospheric delay gradients, in addition to ZWD, to improve our understanding of water vapor dynamics during heavy rains. For this purpose, we reconstruct ZWD and calculate WVC and compare them with in situ rainfall data from AMEDAS (Automated Meteorological Data Acquisition System) stations of JMA. Finally, we study the behaviors of these quantities common for the three heavy rain cases in SW Japan in summer 2017–2019.

Data and Methods: Case Study for the 2018 Heavy Rain

We use the data from the dense GNSS network GEONET for the entire country operated by the Geospatial Information Authority (Tsuji and Hatanaka, 2018). It consists of more than 1,300 continuously observing stations in Japan with a typical separation distance of 15 to 30 km. Because its official solution (F3 solution) does not include tropospheric parameters in high temporal resolution (Nakagawa et al., 2009), we used tropospheric delay data from the UNR database (Blewitt et al., 2018). They estimated tropospheric parameters using the GIPSY/OASIS-II version 6.1.1 software with the Precise Point Positioning technique (Zumberge et al., 1997) using the products for satellite orbits and clocks from Jet Propulsion Laboratory. They employ the elevation cutoff angle of 7° and estimate ZTD and the atmospheric delay gradients every 5 min (Vaclavovic and Dousa, 2015). They follow the 2010 IERS convention (Petit and Luzum, 2010), and used the Global Mapping Function (Böhm et al., 2006), and troposphere gradient model of Chen and Herring (1997).

ZWD and Tropospheric Delay Gradients

The equation below is formulated by MacMillan (1995) and explains that the slant path delay (SPD) at the elevation angle θ and the azimuth angle φ measured clockwise from north can be expressed as follows.

$$\begin{array}{c}\hfill \text{SPD}(\mathrm{\theta },\mathrm{\varphi })=m(\mathrm{\theta })\cdot [\text{ZTD}+\text{cot}\mathrm{\theta }(G_{\text{n}}\text{cos}\mathrm{\varphi }+G_{\text{e}}\text{sin}\mathrm{\varphi })]+\mathrm{\epsilon }\hfill \end{array}(1)$$

There, m(θ) is the isotropic mapping function that shows the ratio of SPD to ZTD, and G_n and G_e are the north and east components, respectively, of the tropospheric delay gradient vectors G, and ε is the modeling error. ZTD is the refractivity of the atmosphere integrated in the vertical direction and is the sum of zenith hydrostatic delay (ZHD) and ZWD. In this study, we calculated surface pressure at the GNSS stations assuming 1 atm at the sea level. Then, we calculated ZHD and subtracted it from ZTD to isolate ZWD. Considering average variability of surface pressure, errors by this approximation for summer ZWD remain within a few percent.

Tropospheric delay gradients are also the sum of hydrostatic and wet contributions. Because we analyze summer data, we assumed that the latter is dominant and used the gradient as those representing the water vapor. Because of the low scale height of water vapor (∼2.5 km), ZWD highly depends on the station altitude; that is, small ZWD observed at highland does not always imply low humidity of the troposphere above that station. On the other hand, atmospheric delay gradients are observed by directly comparing atmospheric delays in different azimuths and hardly suffer from the station altitude (Shoji, 2013). This is the reason why we use troposphere gradients to reconstruct ZWD converted to sea level.

Water Vapor Concentration

Shoji (2013) suggested that two new quantities, WVC and WVI (water vapor inhomogeneity) indices, provide valuable information on non-uniform distribution of atmospheric water vapor in meso-β and meso-γ scales in addition to PWV representing water vapor distribution in meso-α scale. WVI is derived from the post–fit phase residuals in the processing of geodetic GNSS data analysis, and it is impossible to derive such information in the UNR database. WVC indices can be derived as the spatial derivative of ZWD. However, as explained in the previous section, low scale height of water vapor makes ZWD highly dependent on station height, and it is difficult to calculate WVC from ZWD in the mountainous Japanese Islands owing to large topographic slopes throughout the region. Shoji (2013) suggested that WVC can be calculated directly using the atmospheric delay gradient vector field, which is immune from the height problem and is readily available in the UNR database.

Following Shoji (2013), we use WVC to discuss its relationship with heavy rainfalls. WVC index expresses the degree of divergence/convergence of the atmospheric delay gradient and represent the short-wavelength concentration of PWV.

$$\begin{array}{c}\hfill \text{WVC}=-{\nabla }^2\text{PWV}\hfill \end{array}(2)$$

∇PWV is the spatial gradient of PWV. We here use the observed tropospheric gradient G, divided by the scale height H of water vapor.

$$\begin{array}{c}\hfill \nabla \text{PWV}=\mathrm{\Pi }\times \nabla \text{ZWD}=\mathrm{\Pi }\times G/H\hfill \end{array}(3)$$

Π is the coefficient to convert ZWD to PWV and is a function of temperature. ∇ZWD is the spatial gradient of ZWD and can be expressed as G/H (Ruffini et al., 1999). We here assumed 2.5 km for H. In our study, first, we obtained the vector G at grid points with east–west separation of 0.20° and north–south separation of 0.15° all over the country. Here we calculated G at grid points as the weighted mean of G at all the GEONET stations. Larger weight was given to nearer stations. The weight was taken proportional to the Gaussian function of the interstation distance with one-sigma of 20 km.

Unlike the original definition of WVC by Shoji (2013), we did not convert the wet delay to PWV by multiplying with Π in (3). So, our WVC index is actually −∇²ZWD and is calculated numerically as the convergence of G, that is,

$$\begin{array}{c}\hfill -{\nabla }^2\text{ZWD}=-(\partial G_{\text{e}}/\partial x+\partial G_{\text{n}}/\partial y)/H\hfill \end{array}(4)$$

using G at grid values.

Figure 2 shows the tropospheric delay gradient vectors at the grid points and its convergence (WVC) calculated by Eq. (4). As the first case study, we investigate water vapor in the heavy rainfall episode at 08 UT (17 JST) July 6, 2018. There are strong southward gradients in southern Hokkaido and central Tohoku, suggesting southwestward increase of water vapor. In northern Kyushu, we can see large gradient vectors line up, suggesting high concentration of water vapor there.

FIGURE 2

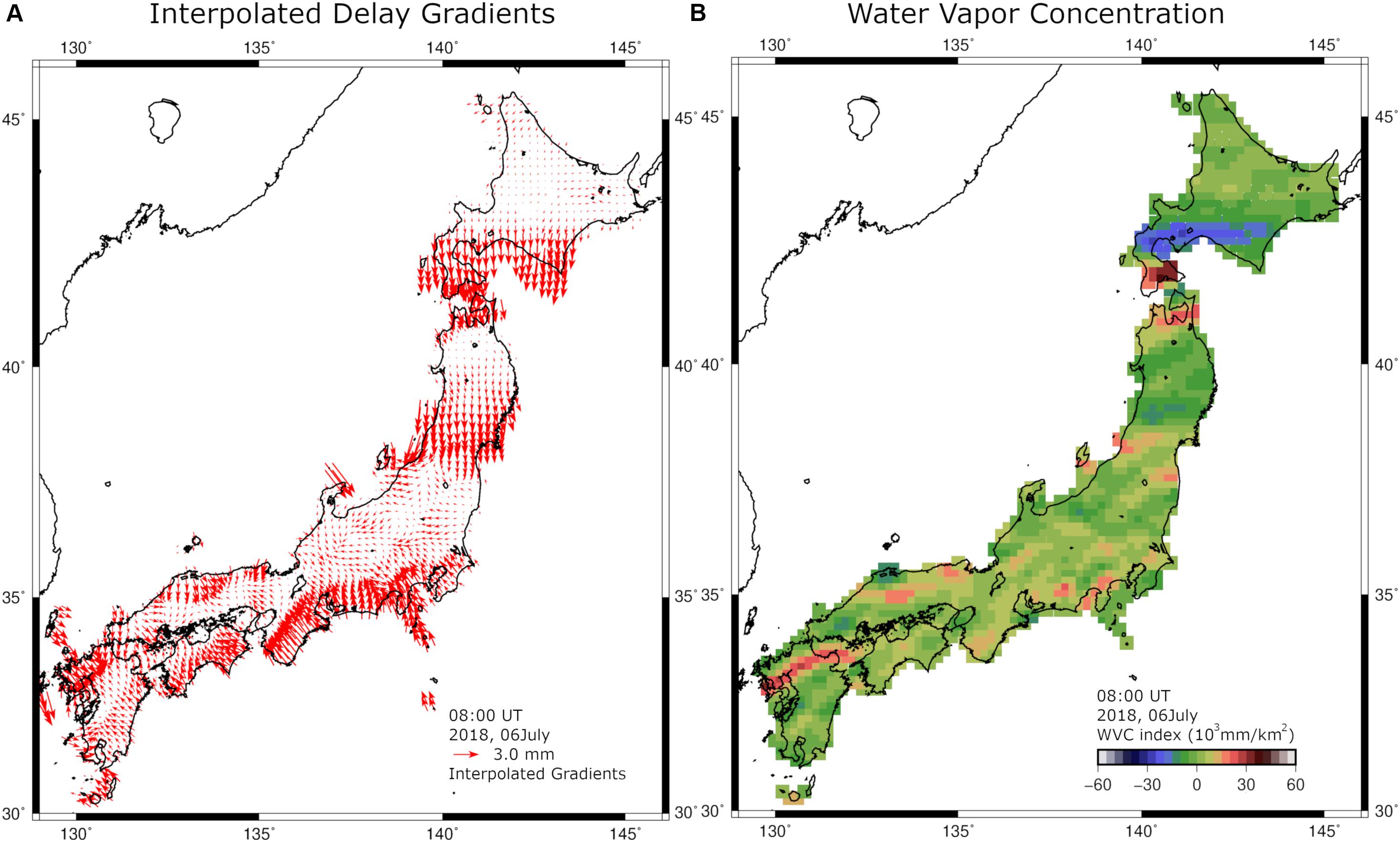
Figure 2. (A) Atmospheric delay gradients at grid points at 17 JST (08 UT) on July 6, 2018 (raw gradient data are shown in Figure 4A). Using these gradient vectors at grid points, we calculated their convergence shown in (B), similar to WVC index defined by Shoji (2013).

Sea-Level ZWD

In our study, in addition to WVC, we also reconstruct sea-level ZWD using the observed tropospheric delay gradients and ZWD at low elevation (<100 m) stations (they are assumed to be identical to sea-level ZWD there). Although the concept of WVC is adopted from Shoji (2013), it is our original technique to estimate the sea-level ZWD using the gradient vector data as the input. Below we provide the detailed explanation of this new inversion technique.

In the inversion, we estimate x(i, j; i = 1,2,…, m_e, j = 1,2…,m_n), the sea-level ZWD at the grid point with coordinates (i, j; i = 1,2… m_e, j 1,2,…, m_n). The input data are G (G_n, G_e) at all the GEONET stations. Suppose the situation in Figure 3, that is, the k’th GNSS station is located within a rectangle made of four corners (i, j–1; i + 1, j–1; i, j; and i + 1, j). Then, the observation equation to relate G at this GNSS station G(k) to the sea-level ZWD at grid points x(i, j) is,

FIGURE 3

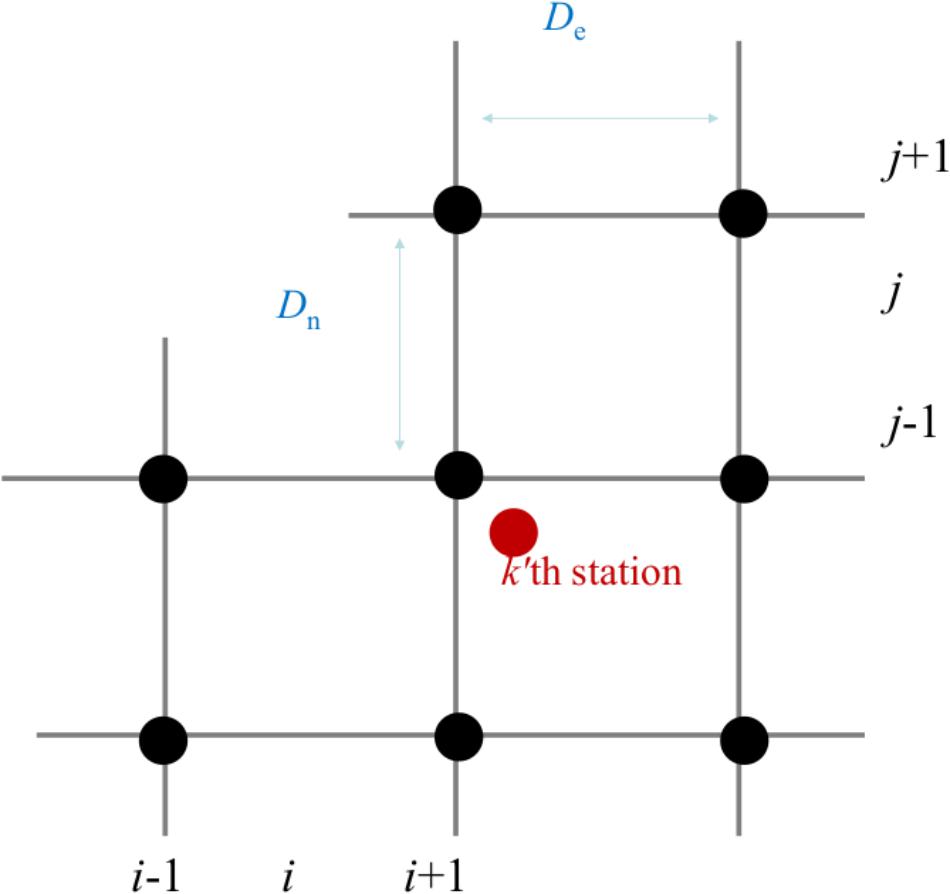
Figure 3. Inversion scheme of the sea-level ZWD. We estimate ZWD at grid points, with the east–west separation of D_e (0.20°), and north-south separation of D_n (0.15°), as the parameters. We used G at all the stations and ZWD at stations with altitudes lower than 100 m as the input data. The observation equation of the ZWD at the central grid (i, j) is given by Eq. (5).

$$\begin{array}{c}\hfill G_{\text{e}}\left(k\right)=\{x(i+\mathrm{\hspace{0.33em}1},j)-x(i,j)\}H/D_{\text{e}}\mathit{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} }(5a)\hfill \end{array}(\mathrm{5a})$$

$$\begin{array}{c}\hfill G_{\text{n}}(k)=\{x(i,j)-x(i,j-\mathrm{\hspace{0.33em}1})\}H/D_{\text{n}}.\mathit{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} }(5b)\hfill \end{array}(\mathrm{5b})$$

To regularize the inversion, we constrain the sea-level ZWD at the grids closest to the GNSS stations with altitude less than 100 m to the observed ZWD. They indicate that the sea-level ZWD at the grid point x(i, j) is the same as the ZWD y(k) observed at the k’th GNSS station, that is,

$$\begin{array}{c}\hfill x(i,j)=y\left(k\right).\mathit{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.5em}}(6)\hfill \end{array}(6)$$

We then performed inversion also applying a continuity constraint. When we estimate the sea-level ZWD over the entire Japanese Islands, the number of parameters is ∼1,600, and the number of observations is twice as large as the number of GNSS stations, ∼2,600. The number of GNSS stations with altitudes of less than 100 m is ∼100. In Figures 4, 5, we show inputs and outputs of the inversion, respectively. In Figure 5B, we confirm that the atmospheric delay gradient vectors at GNSS stations calculated using the estimated distribution of sea-level ZWD. They are similar to the input shown in Figure 4A, suggesting that the inversion is successful. The root-mean-square error between the observed and calculated atmospheric delay gradient is ∼0.65 mm in this case.

FIGURE 4

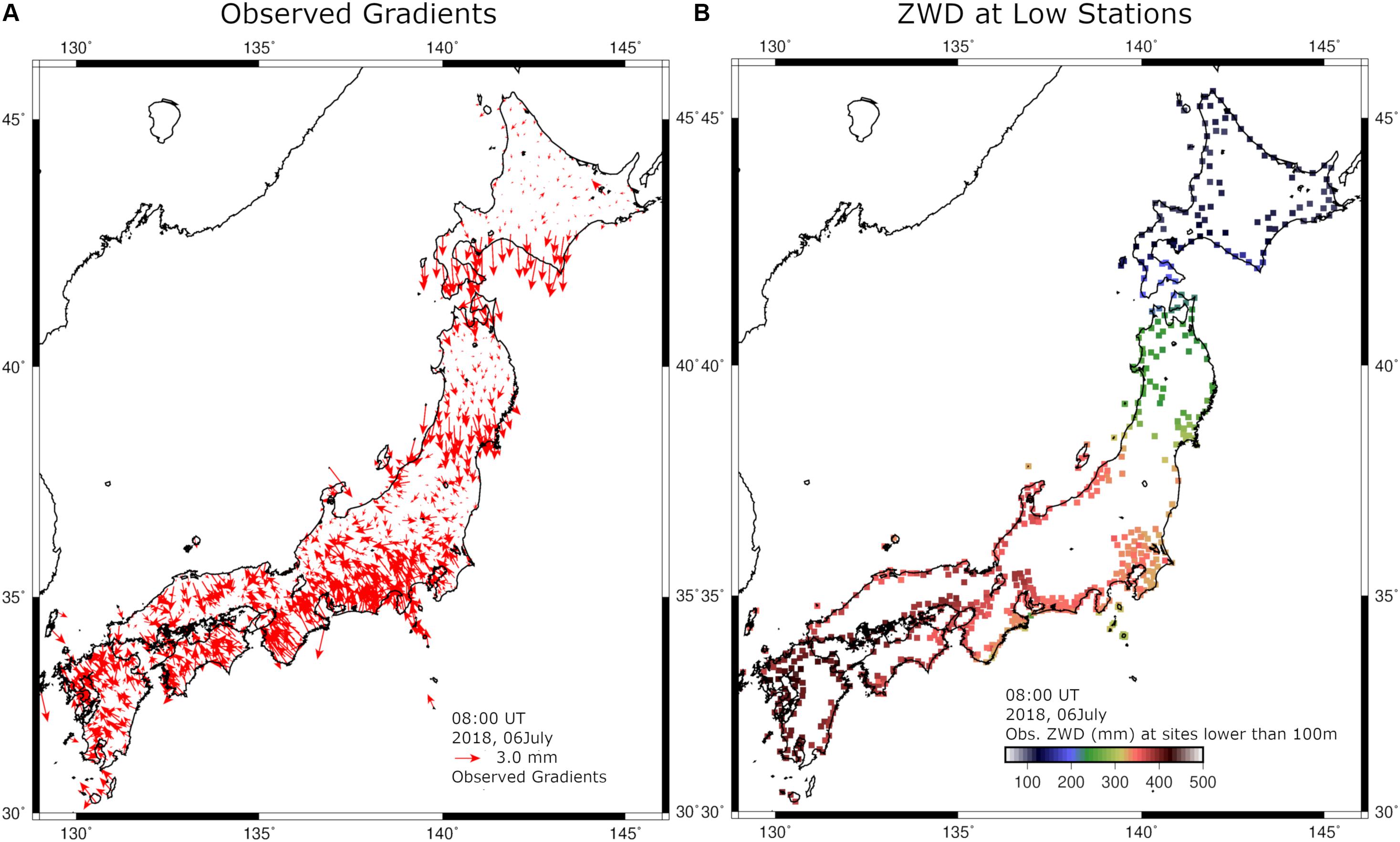
Figure 4. Input data for the inversion of sea-level ZWD at 17 JST (08 UT) on July 6, 2018. (A) shows the tropospheric delay gradients at all the GEONET stations, and (B) is the ZWD at stations with elevations <100 m. Using these inputs, we estimated sea-level ZWD at all the grid points shown in Figure 5A.

FIGURE 5

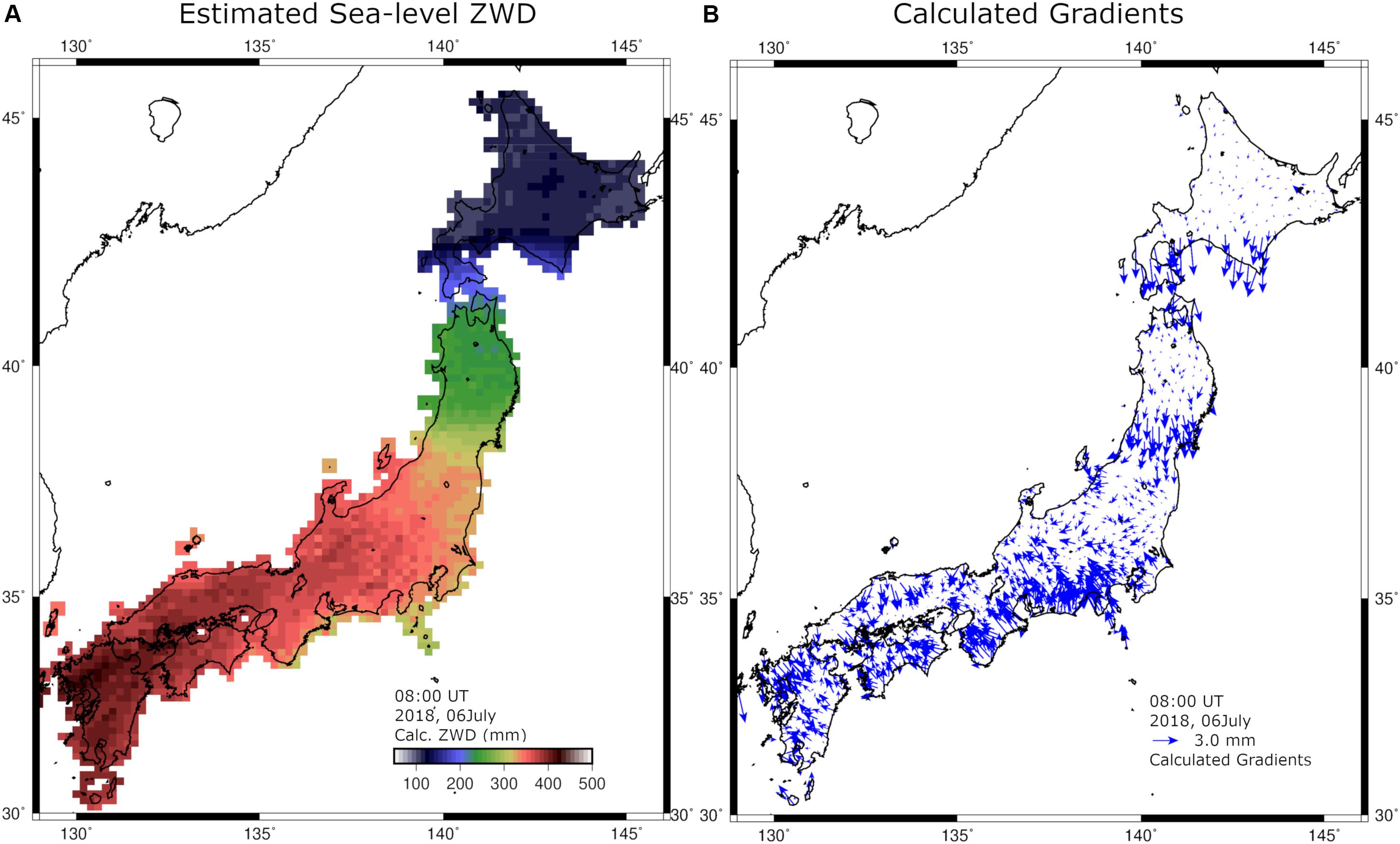
Figure 5. (A) Output of the inversion, that is, sea-level ZWD at grid points at 08 UT (17 LT) on July 6, 2018. (B) shows the atmospheric gradient vectors calculated at GEONET stations using Eq. (5) and the estimated ZWD shown in (A). They are consistent with the observed gradients shown in Figure 4A.

Results and Discussion

Figure 5A shows high ZWD throughout SW Japan, but such a ZWD map still lacks spatial resolution to pinpoint heavy rain as indicated in Figure 1. At a glance, WVC in Figure 2B shows good coincidence with the heavy rain given in red and orange colors in Figure 1. However, there are regions where WVC is high but heavy rain does not occur. This suggests that both two quantities need to be high for the occurrence of heavy rains. In this section, we study long- and short-term behaviors of the two quantities in several recent heavy rain episodes in SW Japan. For the former, we see hourly changes of WVC and sea-level ZWD over 1-month periods including the heavy rain episodes. For the latter, we study the change of these quantities every 5 min over the days of heavy rain.

The 2017 and 2019 Heavy Rain Cases

In Figures 2B, 5B, we show the WVC index and sea-level ZWD at 08.00 UT (17 JST) when heavy rain occurred. This can be compared with the rain images from the JMA, as shown in Figure 1. By comparing Figures 1, 2B, we can see that the WVC index successfully pinpoints the heavy rain. This is also consistent with the detailed report of this heavy rain episode compiled by Japan Meteorology Agency [JMA] (2018).

Here we perform the same calculation for a heavy rain episode on July 5, 2017, at 07 UT (16 JST) and show the results in Figure 6. These figures also show, like in the 2018 case, that both the sea-level ZWD and WVC are high where it rains heavily as shown in Japan Meteorology Agency [JMA] (2017).

FIGURE 6

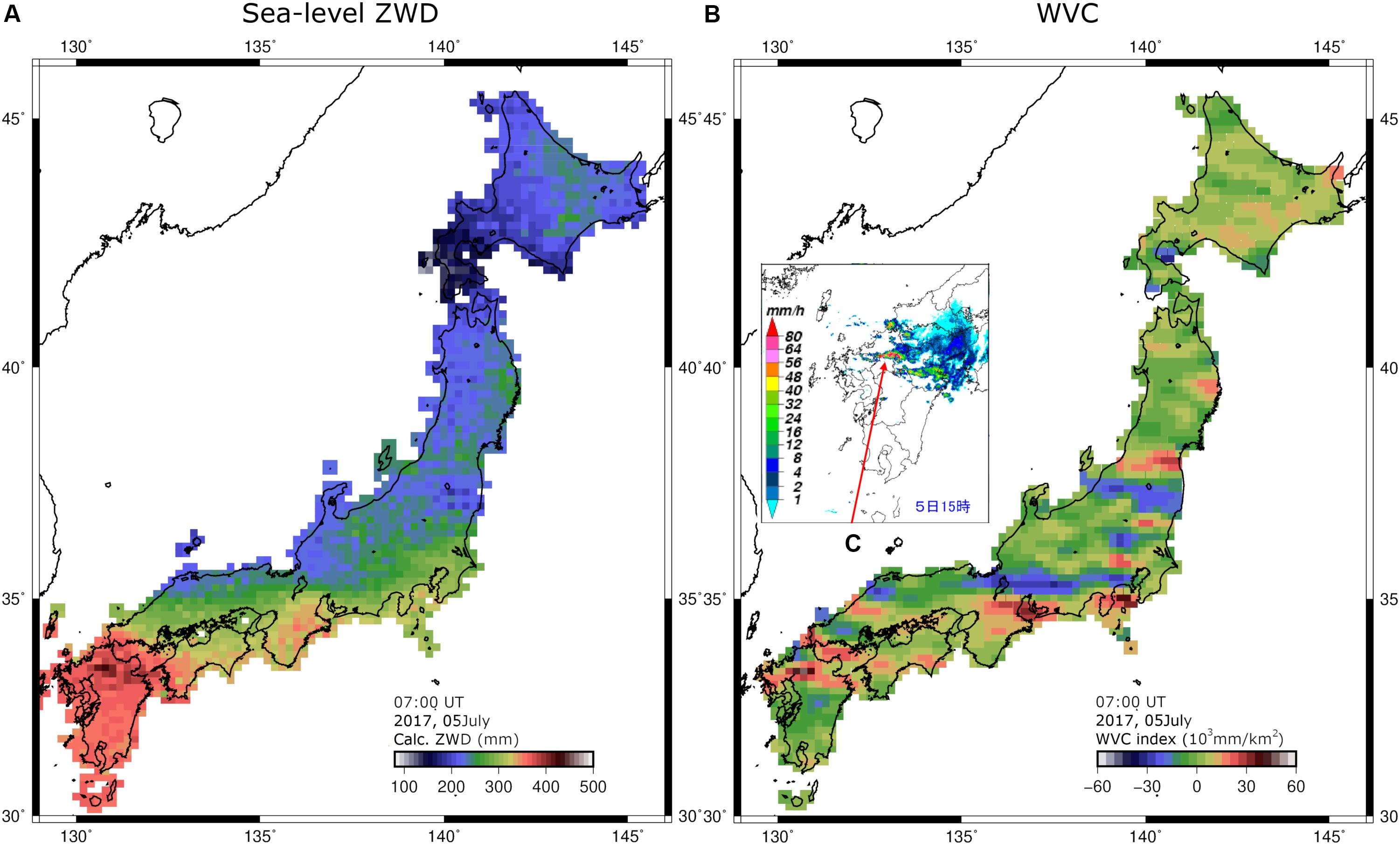
Figure 6. Estimated sea-level ZWD (A) and WVC (B) at 07 UT (16 JST) on July 5, 2017. (C) shows the rain rate map from Japan Meteorology Agency [JMA] (2017) at the epoch 1 h earlier (06 UT) than (A,B).

Likewise, Figure 7 shows the sea-level ZWD and WVC for a heavy rainfall episode in August 2019. WVC index pinpoints heavy rainfall, consistent with the information compiled by Japan Meteorological Agency [JMA] (2019).

FIGURE 7

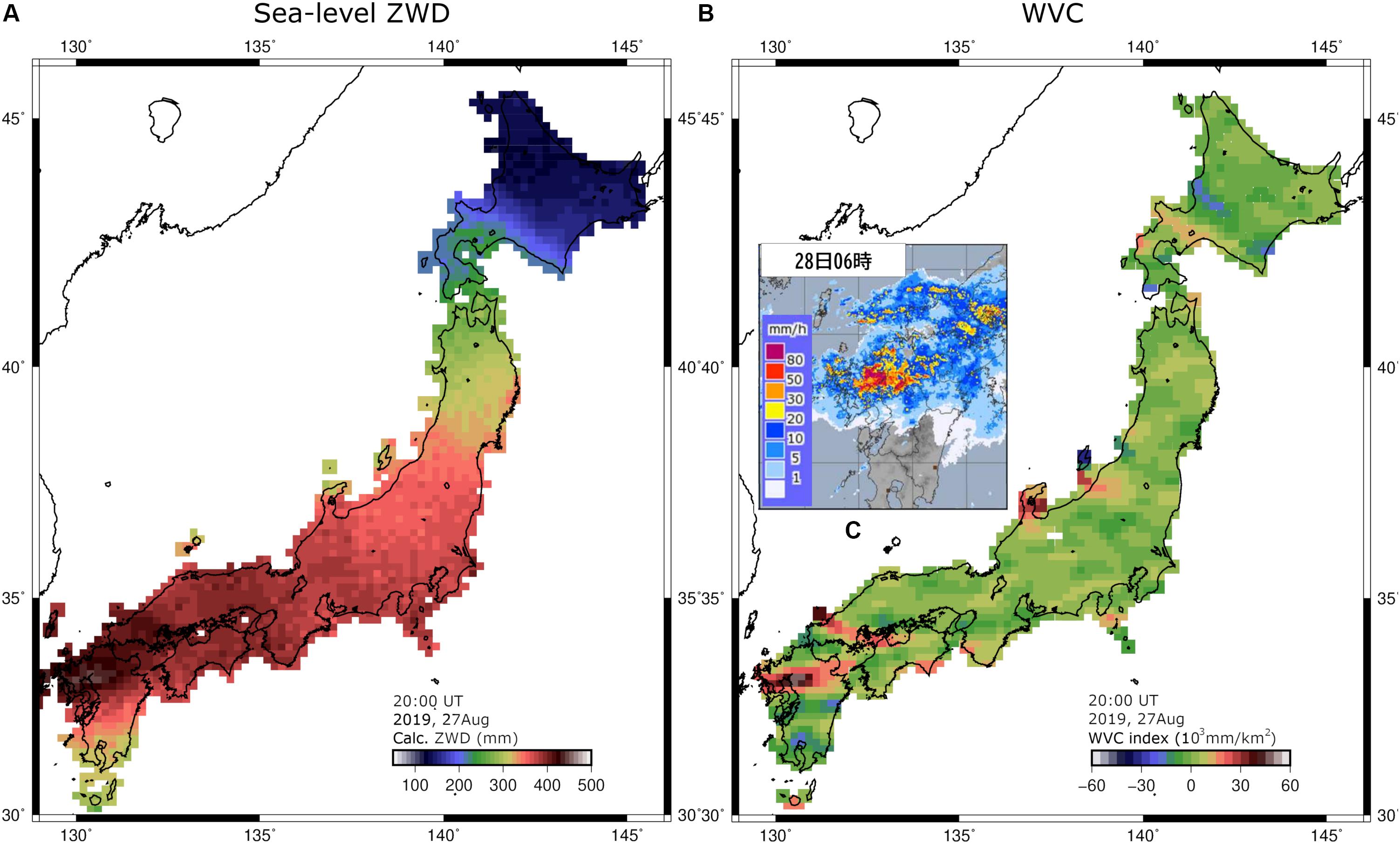
Figure 7. Estimated sea-level ZWD (A) and WVC index (B) at 20 UT (05 JST) on August 27 (August 28 in JST), 2019. (C) shows the rain rate map from Japan Meteorological Agency [JMA] (2019) at the epoch 1 h later (21UT) than (A,B).

From these results, we hypothesize that heavy rainfall occurs when both the ZWD and WVC are high. Next, we try to test the hypothesis by studying time series of the two quantities and rain rate.

WVC, Sea-Level ZWD, and Heavy Rain

Here we try to justify our working hypothesis that heavy rains occur when the WVC index and sea-level ZWD are both high by analyzing the distribution of water vapor every hour in the three cases, July 2017, July 2018, and August 2019. We present the results in Figure 8, which explains the scatter plot of sea-level ZWD and WVC, along with hourly rainfall data based on observations at the AMEDAS station of JMA.

FIGURE 8

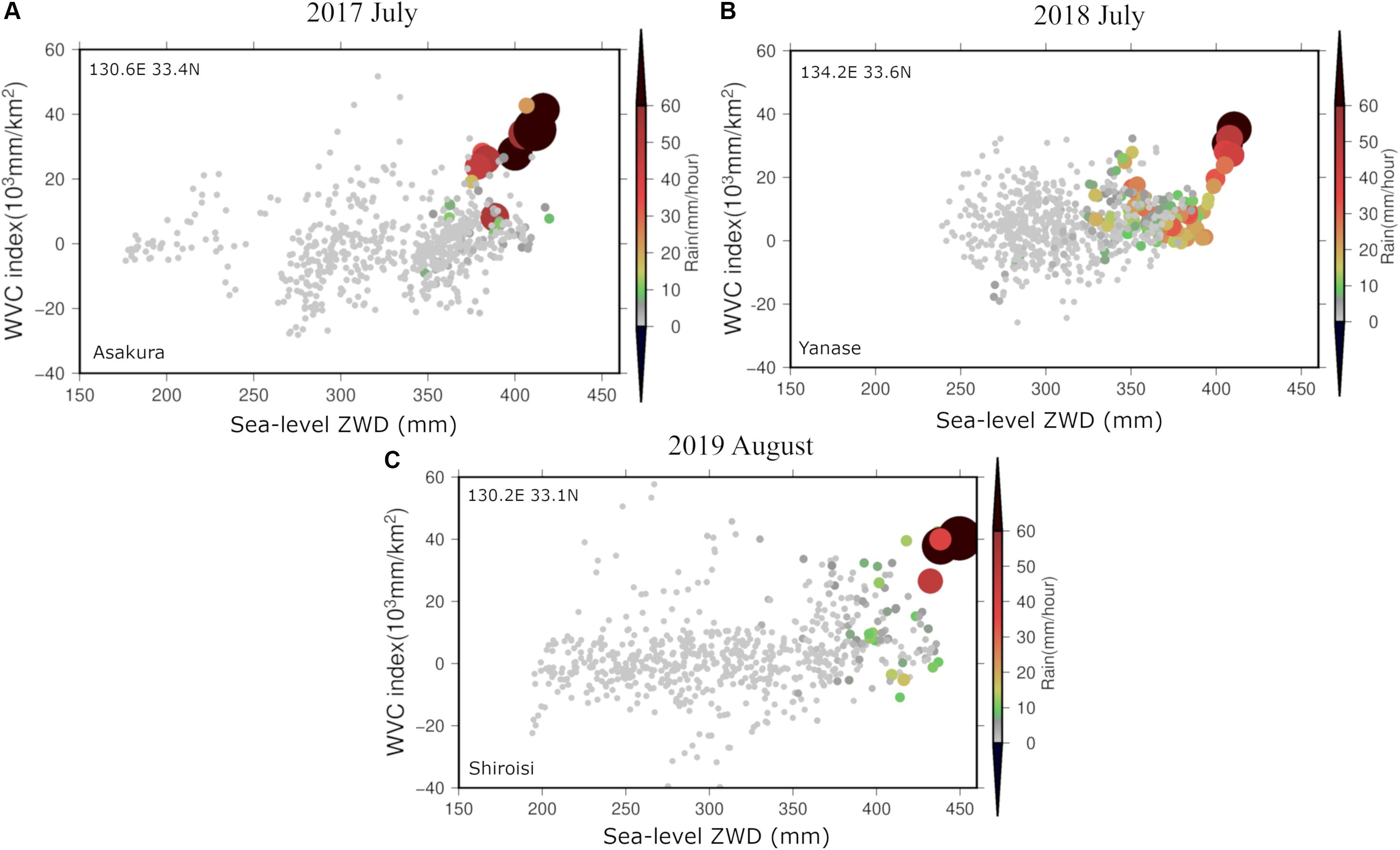
Figure 8. Distribution of hourly values of WVC (vertical axis), sea-level ZWD (horizontal axis), and hourly rain rate (color and circle size) for July 2017 (A), July 2018 (B), and August 2019 (C). The rain rate was measured at the Asakura, Yanase, and Shiroishi AMEDAS stations, respectively, and WVC and ZWD are the values at their nearest grid points (coordinates given at the upper left corners).

We selected the AMEDAS station showing the largest rain for the three episodes, that is, the Asakura station for 2017, the Yanase station for 2018, and the Shiroishi station for 2019. These three stations are all located in northern Kyushu and recorded heavy rains exceeding 50 mm/h. Then we picked up the grid point closest to these AMEDAS and compare the three quantities over a month, that is, July 2017, July 2018, and August 2019. We can see that ZWD values are high up to 400 mm, and WVC index goes up to 40 × 10³ mm/km² when heavy rain exceeding 50 mm/h occurred on July 5, 2017, July 6, 2018, and August 27, 2019 (Figure 8).

Next, we look for data from more AMEDAS stations in Japan on the same days showing hourly rain rates exceeding 50 mm/h and found 12 stations for the 2018 July and 5 stations for the 2019 August, the months including heavy rain episodes. The 2017 heavy rain was quite local (limited to northern Kyushu); we could not find enough number of AMEDAS stations showing rains exceeding 50 mm/h. From Figure 9A, we find that the probability of the heavy rain (>50 mm/h) was 14% for the range of ZWD (400–450 mm) and WVC index (35–50 × 10³ mm/km²), for July 2018. Likewise, for August 2019, the heavy rain occurred 50% for the same range of ZWD and WVC index. If we count rains exceeding 20 mm/h, then the percentages go up to 71% for July 2018 and 78% for August 2019. These results indicate that both the WVC index and sea-level ZWD are high when heavy rains occur. The results also suggest that heavy rains may not occur even when these two quantities are high. Next, we will show time series of these quantities.

FIGURE 9

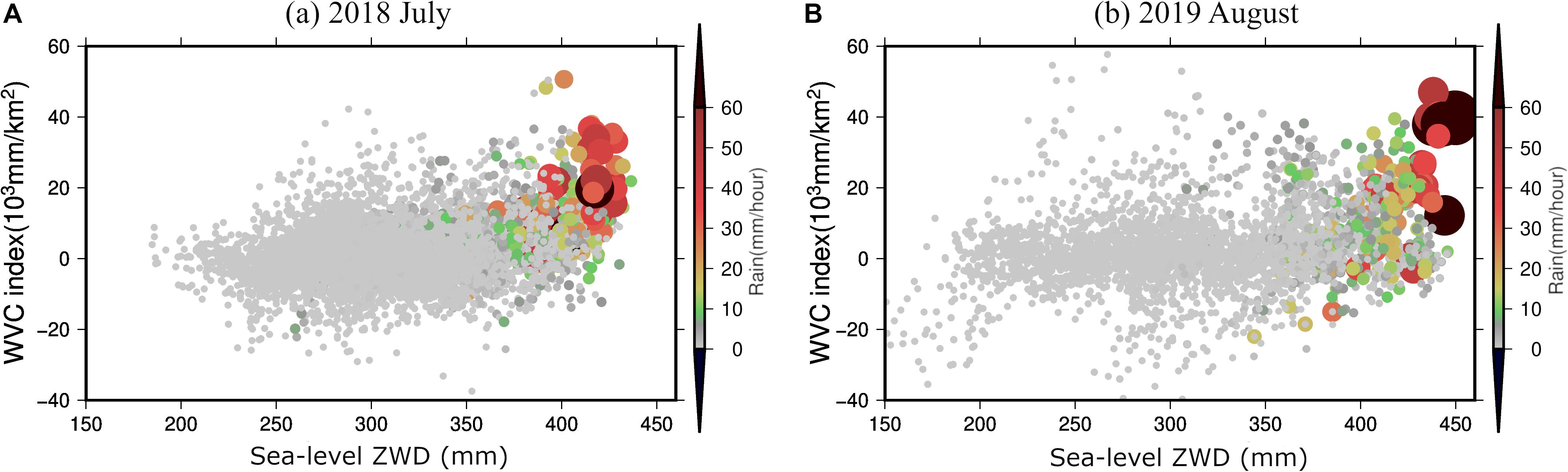
Figure 9. Same as Figures 8B,C, but we stacked data for 12 and 5 AMEDAS stations showing hourly rain rate exceeding 50 mm in July 2018 (A) and August 2019 (B), respectively. Again, we compare hourly rain rates with the WVC and ZWD, calculated at the nearest grid points of the AMEDAS stations.

Time-Series Analysis

In Figure 10, we plot the quantities in Figure 8 as the functions of time. The two quantities WVC and sea-level ZWD are given at the top, whereas the rain rate is given at the bottom. The bottom panels also include the time series labeled as “deviation.” This quantity indicates the sum of the deviations of WVC and sea-level ZWD from their averages normalized by their standard deviations. For example, if both quantities deviate from the means by 2σ, the deviation is 4.

FIGURE 10

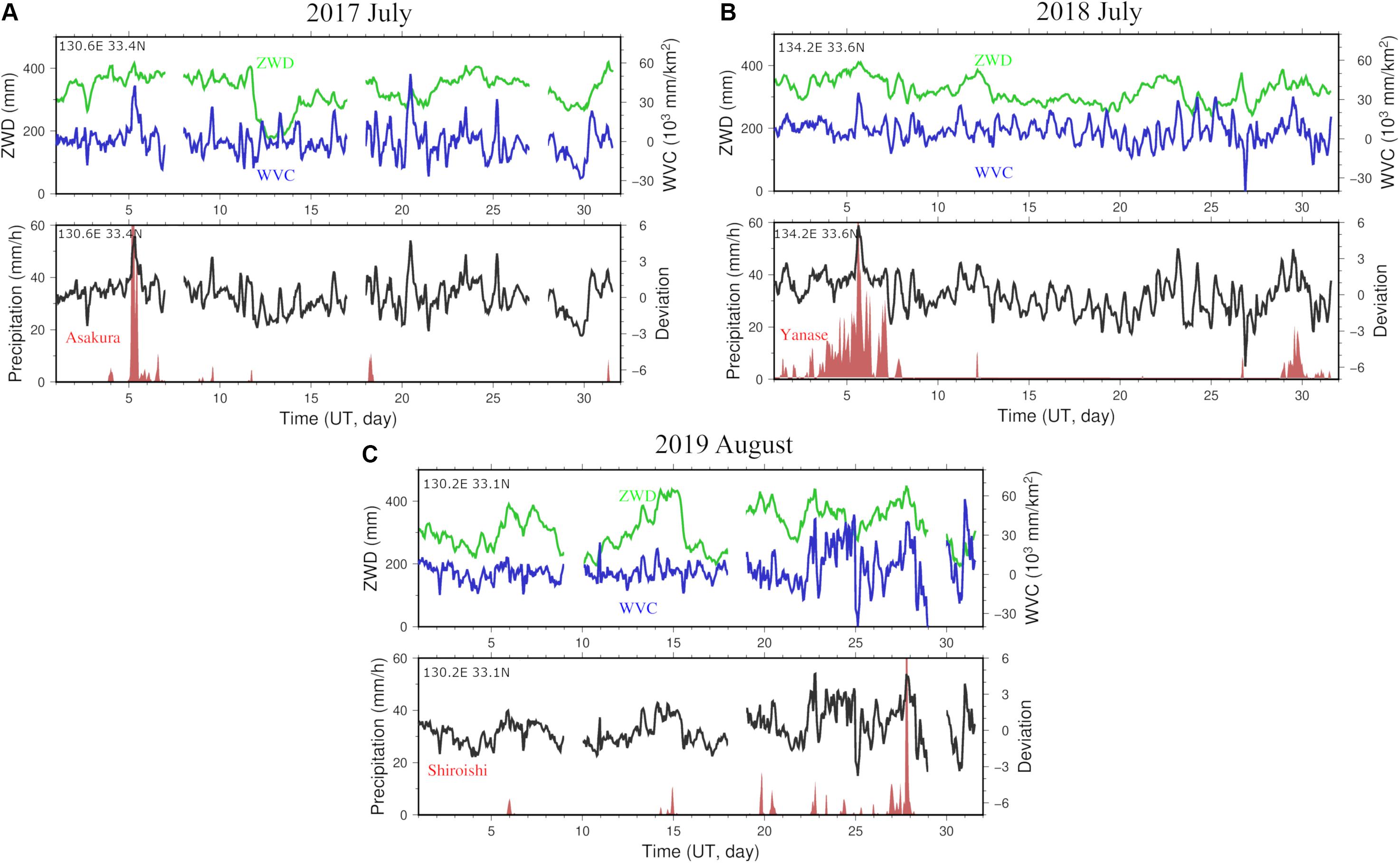
Figure 10. Time series of the two quantities shown in Figure 8, WVC and sea level ZWD (blue and green in the top panels), and rain rate at the nearest AMEDAS stations (red in the bottom panels). The bottom panels also show a new quantity (labeled as “Deviation”) in black, the sum of the standard deviation of the two quantities. They are for July 2017 (A), July 2018 (B), and August 2019 (C). High hourly rain rates occur when both the WVC and ZWD record very high values.

Figure 10 clearly shows that the two quantities show large deviations from the average values whenever heavy rains occur. We also see sometimes that high deviation does not coincide with a heavy rain, for example, July 20, 2017, and July 23, 2018. Regarding the time sequence, the high WVC/ZWD times seem to “coincide” with heavy rains rather than “precede” them. Hence, the usefulness of monitoring these quantities for weather forecast is not clear from this figure.

Lastly, we analyzed high time resolution (every 5 min) behaviors of WVC, ZWD, and rain rate, for the three heavy rain days in July 5, 2017, July 6, 2018, and August 27, 2019, selecting two AMEDAS stations from each episode (Figure 11). We estimated the sea-level ZWD and WVC every 5 min for these 3 days. The results show that both WVC indices and sea-level ZWD show large values at the start of the heavy rains. However, for many cases (e.g., Figures 11A,E,F), heavy rains already started before the two quantities reach their peaks, suggesting limited applicability of these quantities for weather forecast. ZWD often showed rapid declines after the start of the heavy rainfalls possibly because of the transformation of water vapor to liquid water.

FIGURE 11

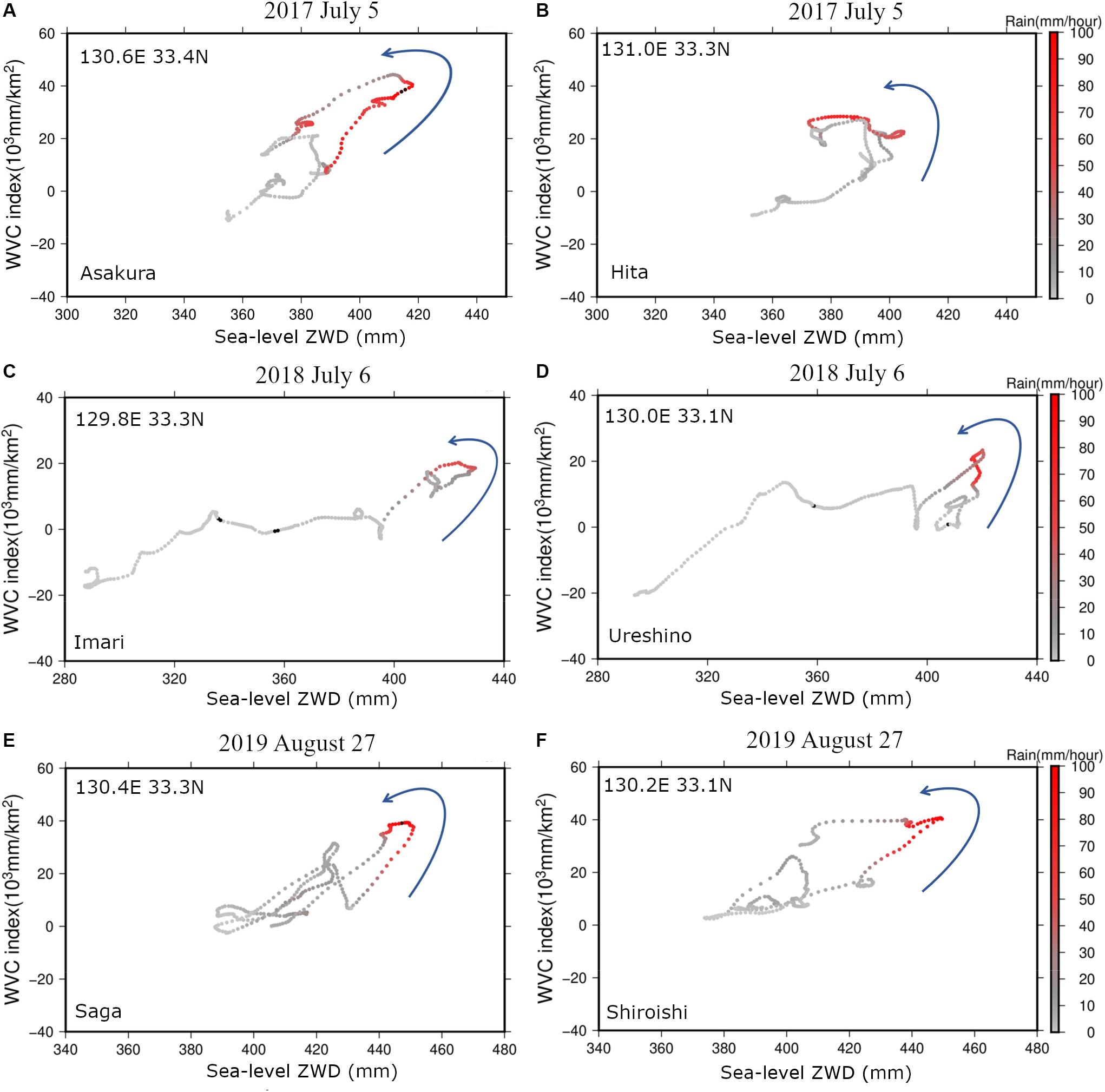
Figure 11. High time resolution (5-min resolution) behaviors of rain rate in the sea-level ZWD-WVC space during the heavy rain days, July 5, 2017 (A: Asakura, B: Hita), July 6, 2018 (C: Imari, D: Ureshino), and August 27, 2019 (E: Saga, F: Shiroishi). The color indicates hourly precipitation of AMEDAS stations interpolated to match the time resolution of sea-level ZWD and WVC.

Conclusion

The atmospheric delay gradients are little influenced by station altitudes and provide useful information of spatial gradient of relative humidity in lower atmosphere. By using atmospheric delay gradients, we could estimate distributions of sea-level ZWD, reflecting relative humidity of the air column above the station. This is possible only in regions with dense GNSS networks like Japan, because we relate tropospheric delay gradient to horizontal spatial gradient of ZWD. We also showed the importance of the WVC index reflecting small-scale enhancement of water vapor. As seen in the scatter diagrams in Figures 8, 9, sea-level ZWD and WVC are not correlated; that is, high sea-level ZWD does not always mean high WVC and vice versa. We showed that heavy rain occurs only when both quantities show high values.

The results suggest that monitoring these quantities is useful for the nowcast of heavy rains. However, their potential to forecast heavy rains is yet to be studied. As the next step, we will need to explore the way to use these two quantities for weather forecast, for example, by putting them to numerical weather models by some means. Computation time of sea-level ZWD and WVC is short, and we can convert ZTD values estimated by GNSS data analysis in near real time to sea-level ZWD and WVC.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author. Tropospheric parameters used in this study are available from geodesy.unr.edu.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This research was funded by the Ministry of Research, Technology, and Higher Education (Kemenristekdikti), Indonesia, in collaboration with the World Bank conducting Research and Innovation in Science and Technology Project (RISET-Pro) through Loan No. 8245-ID.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank RISET-Pro Kemenristekdikti, and Nevada Geodetic Laboratory (NGL) – University of Nevada, Reno, for providing tropospheric parameters for worldwide GNSS stations (ftp://gneiss.nbmg.unr.edu/). We also thank Japan Meteorological Agency (JMA) for operating Automated Meteorological Data Acquisition System (AMeDAS) stations. We thank Yoshinori Shoji, MRI, for useful discussions, and two referees for constructive comments.

References

Bevis, M., Businger, S., Herring, T. A., Rocken, C., Anthes, R. A., and Ware, R. H. (1992). GPS meteorology: remote sensing of atmospheric water vapor using the global positioning system. J. Geophys. Res. 97, 15787–15801.

Google Scholar

Blewitt, G., Hammond, W. C., and Kreemer, C. (2018). Harnessing the GPS data explosion for interdisciplinary science. EOS 99, 1–2. doi: 10.1029/2018EO104623

CrossRef Full Text | Google Scholar

Böhm, J., Niell, A., Tregoning, P., and Schuh, H. (2006). Global Mapping Function (GMF): a new empirical mapping function based on numerical weather model data. 33, 3–6. doi: 10.1029/2005GL025546

CrossRef Full Text | Google Scholar

Brenot, H., Neméghaire, J., Delobbe, L., Clerbaux, N., De Meutter, P., Deckmyn, A., et al. (2013). Preliminary signs of the initiation of deep convection by GNSS. Atmos. Chem. Phys. 13, 5425–5449. doi: 10.5194/acp-13-5425-2013

CrossRef Full Text | Google Scholar

Chen, G., and Herring, T. A. (1997). Effects of Atmospheric Azimuthal Asymmetry on the Analysis of Space Geodetic Data. J. Geophys. Res. 102, 20489–20502. doi: 10.1029/97jb01739

PubMed Abstract | CrossRef Full Text | Google Scholar

Japan Meteorological Agency [JMA] (2019). A Heavy Rain Episode Brought by a Stationary Front (2019 Aug. 26-29). Tokyo: Japan Meteorological Agency.

Google Scholar

Japan Meteorology Agency [JMA] (2017). On the 2017 July Heavy Rain in Northern Kyushu. Tokyo: Japan Meteorological Agency.

Google Scholar

Japan Meteorology Agency [JMA] (2018). 2018 July Heavy Rain (heavy rain etc, by the stationary front and the typhoon no. 7). Tokyo: Japan Meteorological Agency.

Google Scholar

MacMillan, D. S. (1995). Atmospheric Gradients from very long baseline interferometry observations. Geophys. Res. Lett. 22, 1041–1044. doi: 10.1029/95GL00887

CrossRef Full Text | Google Scholar

Miyazaki, S., Iwabuchi, T., Heki, K., and Naito, I. (2003). An impact of estimating tropospheric delay gradients on precise positioning in the summer using the Japanese nationwide GPS array. J. Geophys. Res. 108:4315. doi: 10.1029/2000JB000113

CrossRef Full Text | Google Scholar

Nakagawa, H., Toyofuku, T., Kotani, K., Miyahara, B., Iwashita, C., Kawamoto, S., et al. (2009). Development and validation of GEONET new analysis strategy (Version 4). J. Geogr. Surv. Inst. 118, 1–8.

Google Scholar

Petit, G., and Luzum, B. (2010). IERS Conventions 2010. France: Bureau International Des Poids Et Mesures Sevres, 1–179.

Google Scholar

Ruffini, G., Kruse, L. P., Rius, A., Biirki, I. B., and Cucurulll, L. (1999). A Flores. “Estimation of Tropospheric Zenith Delay and Gradients over the Madrid Area Using GPS and WVR Data.”. Geophys. Res. Lett. 26, 447–450. doi: 10.1029/1998gl900238

CrossRef Full Text | Google Scholar

Shoji, Y. (2013). Retrieval of water vapor inhomogeneity using the Japanese Nationwide GPS array and its potential for prediction of convective precipitation. J. Meteorol. Soc. Jpn. 91, 43–62. doi: 10.2151/jmsj.2013-103

PubMed Abstract | CrossRef Full Text | Google Scholar

Shoji, Y. (2015). Water vapor estimation using ground-based GNSS observation network and its application for meteorology. Tenki 62, 3–19.

Google Scholar

Tsuda, T., Heki, K., Miyazaki, S., Aonashi, K., Hirahara, K., Nakamura, H., et al. (1998). GPS meteorology project of Japan – Exploring frontiers of geodesy -. Earth Planet. Space 50, 1–5.

Google Scholar

Tsuji, H., and Hatanaka, Y. (2018). GEONET as Infrastructure for Disaster Mitigation. J. Dis. Res. 13, 424–432. doi: 10.20965/jdr.2018.p0424

CrossRef Full Text | Google Scholar

Vaclavovic, P., and Dousa, J. (2015). Backward Smoothing for Precise GNSS Applications. Adv. Space Res. 56, 1627–1634. doi: 10.1016/j.asr.2015.07.020

CrossRef Full Text | Google Scholar

Zumberge, J. F., Heftin, M. B., Jefferson, D. C., Watkins, M. M., and Webb, F. H. (1997). Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. 102, 5005–5017. doi: 10.1029/96JB03860

CrossRef Full Text | Google Scholar

Zus, F., Douša, J., Kaèmaøík, M., Václavovic, P., Balidakis, K., Dick, G., et al. (2019). Improving GNSS Zenith Wet Delay Interpolation by Utilizing Tropospheric Gradients: Experiments with a Dense Station Network in Central Europe in the Warm Season. Remote Sens. 11:674. doi: 10.3390/rs11060674

CrossRef Full Text | Google Scholar