- 1Faculty of Geosciences and Environment, Institute of Earth Surface Dynamics, University of Lausanne, Lausanne, Switzerland
- 2Department of Information Technologies for Innovative Services, Luxembourg Institute of Science and Technology—LIST, Belvaux, Luxembourg
Complex non-linear time series are ubiquitous in geosciences. Quantifying complexity and non-stationarity of these data is a challenging task, and advanced complexity-based exploratory tool are required for understanding and visualizing such data. This paper discusses the Fisher-Shannon method, from which one can obtain a complexity measure and detect non-stationarity, as an efficient data exploration tool. The state-of-the-art studies related to the Fisher-Shannon measures are collected, and new analytical formulas for positive unimodal skewed distributions are proposed. Case studies on both synthetic and real data illustrate the usefulness of the Fisher-Shannon method, which can find application in different domains including time series discrimination and generation of times series features for clustering, modeling and forecasting. The paper is accompanied with Python and R libraries for the non-parametric estimation of the proposed measures.
1. Introduction
The ubiquity and extensive growth of available temporal data requires the development of reliable techniques to extract knowledge from them and to understand multifaceted time-dependent phenomena. Over the last decades, an increasing attention was payed toward the use of Fisher-Shannon information as a measure to characterize the complexity and non-stationarity of non-linear time series. Originally proposed for statistical estimation purposes (Fisher, 1925), the Fisher information measure (FIM) has been extensively used in theoretical physics (Frieden, 1990). FIM and Shannon entropy power (SEP) (Shannon, 1948) are closely related, as shown by information theory (Dembo et al., 1991; Cover and Thomas, 2006). The Fisher-Shannon complexity (FSC)—the FIM and SEP product—was proposed as a possible definition of atom complexity (Angulo et al., 2008; Esquivel et al., 2010).
Following Frieden work, FIM has found applications in non-linear time-series analysis. Martin et al. (1999) analyzed complex non-stationary electroencephalographic signals and showed that FIM can have better discrimination performance than Shannon entropy. FIM was also used to detect behavior changes of dynamical systems (Martin et al., 2001). Vignat and Bercher (2003) showed that a joint analysis of both SEP and FIM can be required to perform effective discrimination of non-stationary signals.
The Fisher-Shannon method has been used to analyse complex dynamical processes in geophysics. Discrimination between the electric and magnetic components of magnotelluric signals is performed in Telesca et al. (2011). Tsunamigenic and non-tsunamigenic earthquakes were efficiently separated in the Fisher-Shannon information plane, using FSC (Telesca et al., 2013). Micro-tremors time series were identified depending on the soil characteristics of the measurement sites (Telesca et al., 2015b). Telesca et al. (2015a) proposed a classifier of (non-)tsunamigenic potential of earthquake build on several time series features, including FIM, SEP, FSC. Finally, FIM was also used dynamically with sliding window techniques in order to study precursory patterns in seismology (Telesca et al., 2009b) and volcanology (Telesca et al., 2010).
Many environmental processes have also been studied using the Fisher-Shannon method. Lovallo et al. (2013) and Pierini et al. (2011) studied climatic regimes identification in rainfall time series. Hydrological regimes discrimination have also been investigated (Pierini et al., 2015). Analyzing remotely sensed sea surface temperature, Pierini et al. (2016) have shown that the Fisher-Shannon method is able to clearly identify the Brazil-Malvinas Confluence Zone, which is known to be one of the most energetic area of oceans. Telesca and Lovallo (2011) analyzed more than 10 years of hourly wind speed data in the Fisher-Shannon information plane. The same authors studied yearly variation of the FIM, the SEP and the FSC on wind measurements (Telesca and Lovallo, 2013). Guignard et al. (2019b) have found correlations between daily variance of temperature and daily FSC of high-frequency wind speed records in urban area. Authors have also pointed out relationships between Fisher-Shannon analysis of wind speed daily means and topographical features—height and slope—in complex mountainous regions (Guignard et al., 2019a). Telesca et al. (2009a) discriminated some pollutants, including cadmium, iron, and lead, in the Fisher-Shannon plane. Similarly, Amato et al. (2020) have shown a relationship between the Fisher-Shannon analysis outputs of three air pollutants—Nitrogen dioxide, Ground level ozone and Particulate Matter—and measurement location in term of land use and of anthropogenic sources of pollutant emission.
The research involving Fisher-Shannon method is rather scattered and comes from various fields, e.g., information theory, physics, dynamical systems, machine learning, and statistics. Therefore, the present paper contributes to the methodological studies on Fisher-Shannon information measures along with some applications.
The main objectives of this research can be summarized as follows:
• discussing the state-of-the-art of Fisher-Shannon information measures and their applications,
• identifying FSC as a sensitivity measure of the SEP and as a scale-independent non-Gaussianity measure of data,
• presenting some new theoretical results on FIM and SEP,
• developing operational FIM and SEP tools for the nonlinear time-series analysis,
• demonstrating through two case studies, based on simulated (chaotic) and real data (high frequency wind speed measurements), the efficiency and usefulness of the proposed methods.
The remainder of the paper is organized as follows. Concepts of Fisher-Shannon analysis, including SEP, FIM, FSC, and information plane, are presented and reviewed in section 2. Section 3 provides analytical formula for such quantities in the particular cases of random variables following some positive skewed distributions, namely Gamma, Weibull, and log-normal ones. Then, a non-parametric kernel based estimation of the density function—for which Python and R packages are proposed—is presented in section 4. Experiments on simulated and real-world data are performed in section 5. Finally, section 6 concludes the paper.
2. Fisher-Shannon Analysis
2.1. Shannon Entropy Power and Fisher Information Measure
Let us consider a univariate continuous random variable X with its probability density function (PDF) f (x), which is supposed to be sufficiently regular for the exposition of our purpose. Its differential entropy (Cover and Thomas, 2006) is defined as
For example, if X is a centered Gaussian random variable of variance σ2, a direct computation gives . However, it will be more convenient to work with the following quantity, called the Shannon Entropy Power (SEP) (Dembo et al., 1991),
which is a strictly monotonically increasing transformation of HX. The SEP is constructed such that in the Gaussian case we have . Very often, entropies HX and NX are interpreted as global measures of disorder / uncertainty / spread of f (x). The higher the entropy, the higher the disorder.
The Fisher Information Measure (FIM) (Vignat and Bercher, 2003), also known as the Fisher information of X with respect to a scalar translation parameter (Dembo et al., 1991), is defined as
This quantity should not be confused with the Fisher information of a distribution parameter. In particular, the derivative of the log-density is relative to x and not to some parameter. However, the FIM is equivalent to the Fisher information of a location parameter of a parametric distribution (Cover and Thomas, 2006). Under mild regularity conditions, one has the following alternative formulation (Lehmann, 1999),
The quantity IX is sometimes interpreted as a measure of order / organization / narrowness of X. If X is Gaussian, . It should be noted that HX, NX, and IX only depend on the distribution f (x).
2.2. Properties
The SEP and the FIM respect several properties. First, both quantities are positive. It is also easy to see the scaling properties of the SEP and the FIM (Rioul, 2011),
for any real number a ≠ 0, by change of variable. Notice also that the SEP and the FIM are invariant under additive deterministic constant, by the same argument. Harder to show are the entropy power inequality (Dembo et al., 1991) and its dual the Fisher information inequality (Zamir, 1998),
for a random variable Y independent of X, with equality if X and Y are Gaussian.
Moreover, several relationships show that the FIM closely interact with the SEP and the differential entropy. Let Z be a random variable independent of X with finite variance . The de Bruijn's identity (Cover and Thomas, 2006; Rioul, 2011) states that
i.e., the variation of the differential entropy of a perturbed X is proportional to IX. Therefore, a possible interpretation of the FIM is that it quantifies the sensitivity of HX to a small independent additive perturbation Z. Using the entropy power inequality (6) and de Bruijn identity (8), one can show the isoperimetric inequality for entropies,
with equality if and only if X is Gaussian. The proof and the nomenclature motivation of equation (9) can be found in Dembo et al. (1991), where a remarkable analogy is done with geometry. This shows that SEP and FIM are intimately interlinked.
2.3. Fisher-Shannon Complexity
The joint FIM/SEP analysis has been used as a statistical complexity measure, albeit there is no clear consensus about the definition of signal complexity (Esquivel et al., 2010). The Fisher-Shannon Complexity (FSC) is defined as CX = NXIX (Angulo et al., 2008). From the scaling properties (5), it is easy to show that the FSC is constant under scalar multiplication and addition. In particular, normalization or standardization of X has no effect on the FSC. Additionally, the isoperimetric inequality for entropies (9) states that CX ≥ 1, with equality if and only if X is Gaussian. An interpretation of this quantity is the following. If Z is independent of X and has a finite variance , one obtains the following relationship by using the de Bruijn identity (8),
Hence, the FSC can be interpreted as a sensitivity measure of NX to a small independent additive perturbation.
2.4. Fisher-Shannon Information Plane
The PDF of X can be analyzed displaying the SEP and FIM within the so-called Fisher-Shannon Information Plane (FSIP), see Figure 1 (Vignat and Bercher, 2003). Although standard linear scale plot are very often used for the FSIP in the literature, a log-log plot is more adequate in practice. In the FSIP, the only reachable values are in the set , due to (9). Vignat and Bercher (2003) showed that for any point , it exists a random variable X (from an exponential power distribution) such that NX = N and IX = I.
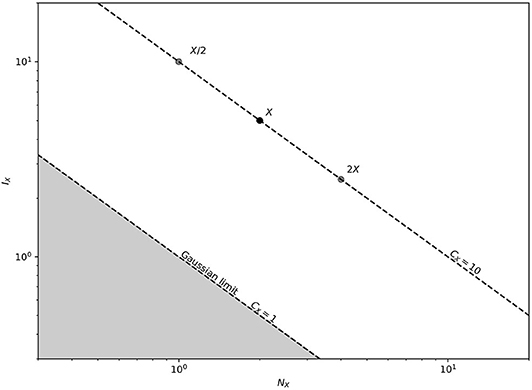
Figure 1. The Fisher-Shannon information plane with a random variable X of FSC equal to 10. Scalar multiplication of X corresponds to a displacement along the iso-complex curve passing through X. The unreachable points are in gray. Note the logarithmic scale.
A curve in is said to be iso-complex if the FSC along the curve is constant. As CX is constant up to a multiplicative factor a ≠ 0, and looking up at the scaling properties (5), one can move on any iso-complex curve by varying a. Figure 1 shows the iso-complex curve of complexity CX = 10 as an example. The boundary of is the iso-complex curve with FSC equal to 1, and is reached if and only if X is Gaussian, as states by (9). On this boundary, the standard deviation σ (which plays the role of the scaling parameter in the Gaussian case) is equivalent to the multiplicative factor a. Hence, while a point in the FSIP is described by (NX, IX), one can also describe it by (a, CX). In the light of this, one can also think of FSC as a scale-independent measure of non-Gaussianity of X.
3. Analytical Solutions for Some Distributions
In this section, we propose analytical formulas for the SEP, FIM and FSC for several parametric distributions. They can be used directly for parametric estimations. Vignat and Bercher (2003) obtained analogous results for the Student's t-distribution and the exponential power distribution (also known as generalized Gaussian distribution). The Gaussian case was already presented in section 2 as an example.
The differential entropy of the distributions proposed in this section have been computed by Lazo and Rathie (1978), from which the SEP is directly obtained. However, to our knowledge, the FIM-based calculations for Gamma, Weibull and log-normal distributions were never presented. Proofs can be found in the Appendix.
3.1. Gamma Distribution
The PDF of a Gamma random variable X is given by
and f (x) = 0, for x < 0, where Γ denotes the gamma function and θ, k > 0 are, respectively, the scale and shape parameters.
Proposition 1. The SEP of the Gamma distribution with scale θ > 0 and shape k > 0 is
where ψ is the digamma function.
The FIM and the FSC of the Gamma distribution with scale θ > 0 and shape k > 2 are, respectively,
3.2. Weibull Distribution
The PDF of a Weibull random variable is
and f (x) = 0, for x < 0, where μ is the location parameter, λ > 0 is the scale parameter and k > 0 is the shape parameter.
Proposition 2. The SEP of the Weibull distribution with location μ, scale λ > 0 and shape k > 0 is
where and γ is the Euler-Mascheroni constant.
The FIM and the FSC of the Weibull distribution with location μ, scale λ > 0 and shape k > 2 are, respectively
3.3. Log-Normal Distribution
The log-normal PDF with parameters μ and σ > 0 is
and f (x) = 0, for x ≤ 0.
The notation of the parameters μ and σ are motivated by the fact that the logarithm of a log-normal random variable follows a normal distribution of mean μ and variance σ2. However, μ and σ play, respectively, the role of the scale parameter and the shape parameter for the log-normal distribution.
Proposition 3. The SEP, the FIM and the FSC of the log-normal distribution with μ and σ > 0 are given by
4. Data Driven Non-Parametric Estimation
Complex real-world data sets rarely follow parametric distributions. Providing enough data, it is also possible to carry out Fisher-Shannon analysis with a non-parametric estimation of density, which release parametric assumptions on the distribution (Telesca and Lovallo, 2017). In this paper, integral estimates of the SEP and the FIM are considered, which consist of substituting the kernel density estimators (KDE) of both f (x) and its derivative in the integral forms of (1) and (3) (Bhattacharya, 1967; Dmitriev and Tarasenko, 1973; Prakasa Rao, 1983; Györfi and van der Meulen, 1987; Joe, 1989). Python and R implementations of this section content are proposed, see the software availability section at the end of this paper.
Following (Wand and Jones, 1994), let X1, …, Xn be a random sample of size n from a PDF f (x). Consider also the kernel K(u), a bounded PDF which is symmetric around zero, has a finite fourth moment and is differentiable. The KDE of f (x) is
where h > 0 is the bandwidth parameter. In this paper, the Gaussian kernel defined by K(u) = (2π)−1/2exp(−u2/2) is used and the estimator (10) becomes
The integral estimate of (2) is
Let us note f′, the derivative of f with respect to x. Usually, f′ is estimated by . With the Gaussian kernel we obtain
Then, the integral estimate of (3) is
The FSC is estimated by multiplying by ÎX.
Several techniques exist in order to automatize the bandwidth choice (Wand and Jones, 1994). In the following, the 2-stages direct plug-in method (Sheather and Jones, 1991) is used. This method estimates the optimal bandwidth regarding the asymptotic mean integrated squared error of . The interested reader can found further technical details in (Wand and Jones, 1994) and (Sheather and Jones, 1991).
5. Case Studies
In this section we explore two applications of SEP, FIM and FSC to time series. First, a synthetic experiment is used to show the usefulness of the method in detecting the dynamical behavior of chaotic systems. Then, an example of application of the proposed method to real complex environmental data is discussed.
5.1. Logistic Map
A synthetic experiment is designed to investigate how SEP, FIM, and FSC can be used to detect behavioral changes in non-linear dynamical systems. In the present research, the well-known logistic map is considered as a benchmark simulated case study, that illustrates and helps to understand important features of the considered measures.
Following the experiment proposed by Martin et al. (2001), the logistic map defined by
where c is the control parameter, is analyzed using sliding window technique. Analysis within the sliding window pursues the goal of revealing dynamical evolution of properties of time series like Gaussianity and non-stationarity.
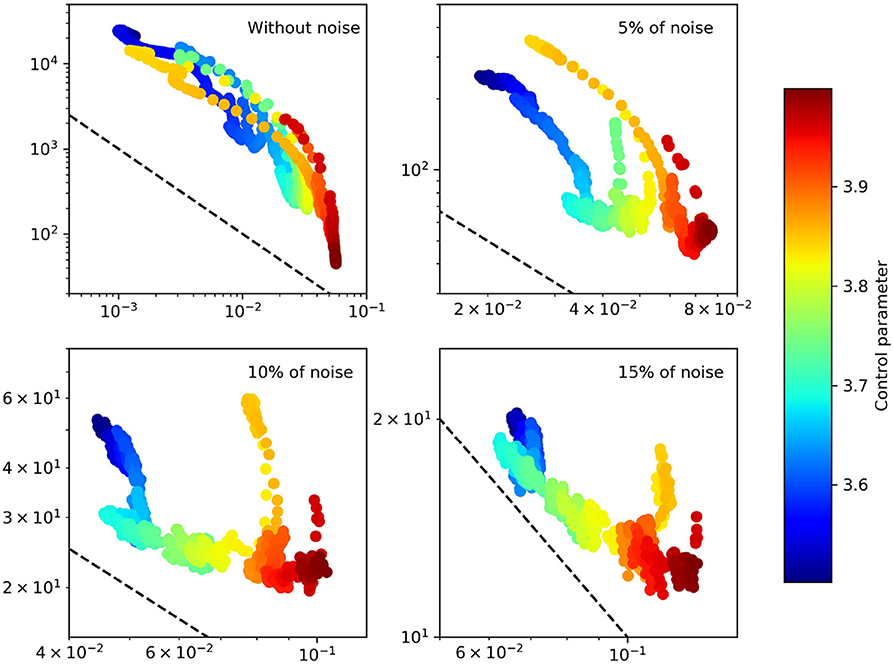
The sequence (xn) is computed up to n = 1, 000 for c ∈ [3.5, 4]. Centered Gaussian noise with different level of variance, 0.05, 0.10, 0.15, is added to xn. The well-known bifurcation diagram of the logistic map is displayed in Figure 2. The SEP, FIM, and FSC are computed on data included in the overlapping windows of width 2.5·10−3 along the control parameter, and the results are shown in the same figure. The Lyapunov exponent is also added for comparison reasons (Kantz and Schreiber, 2004). The results are also displayed in the FSIP, see Figure 3.
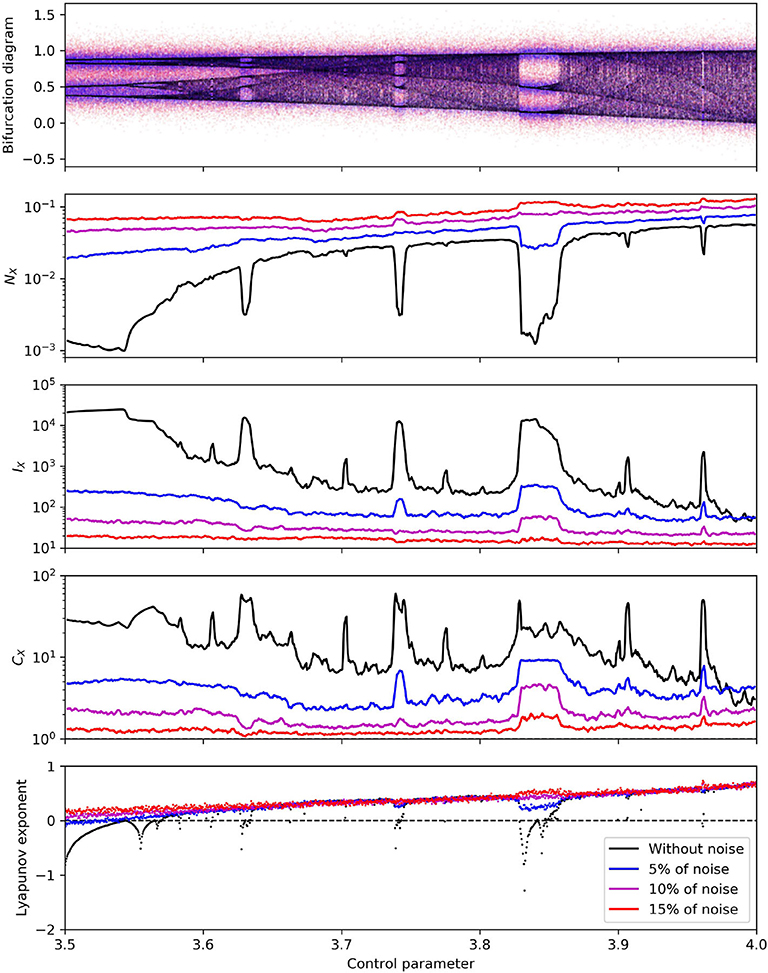
Figure 2. Logistic map with different level of noise. From top to bottom : bifurcation diagram, SEP, FIM, FSC, and Lyapunov exponent sliding windows. Note the logarithmic scale on the y-axis for SEP, FIM, and FSC.
Analyzing the results obtained from the data without noise, it is easy to see how the SEP, FIM and FSC peak occurrences correspond to dynamic changes shown by the bifurcation diagram and the Lyapunov exponent. With the logarithmic scale on the y-axis, the behavior of the SEP is somewhat symmetric to the behavior of the FIM, i.e., the FIM seems to be inversely proportional to the SEP. However, this is not exactly the case, otherwise the FSC would be constant. In some sense, the perturbations in the FSC reflect the departure from the inverse proportionality between the SEP and the FIM. In the FSIP, perfect inverse proportionality corresponds to iso-complex curves. Indeed, the trajectory of the logistic map in the FSIP is stretched along iso-complex curves, see Figure 3.
Adding noise shows that most of the peaks become undetectable, see Figure 2. However, FSC seems to be the measure which suffers the least to noise in data. Note also, that FIM is less impacted than SEP. The noise effect is more interesting in the FSIP, see Figure 3. While the uncorrupted data is quite hard to interpret due to the superposition of the trajectory with itself, adding some noise seems to clarify complexity and trajectory behaviors in the FSIP. Noise stimulates the emergence of protuberances roughly corresponding to “islands of stability” of the (uncorrupted) bifurcation diagram, where Lyapunov exponent is negative. This emergence is due to the fact that FIM is less impacted than SEP, as it was seen above.
5.2. Application to High Frequency Wind Data
The Fisher-Shannon information method can find a wide application in the geo-environmental domains. In the present section, we demonstrate how they can be applied to retrieve relevant knowledge from environmental time series. Specifically, high frequency wind speed data are analyzed. The time series consists of 1Hz frequency wind speed data, from 28 November 2016 to 29 January 2017 (Figure 4). The data (motus.epfl.ch) were measured at 25.5 m above the ground by a sensor which is placed on meteorological mast located on the campus of the Ecole Polytechnique Fédérale de Lausanne (EPFL), Switzerland. Notice that the mast is surrounded by a building layout of 10 m average height. More information on these measurements can be found in Mauree et al. (2017a,b).
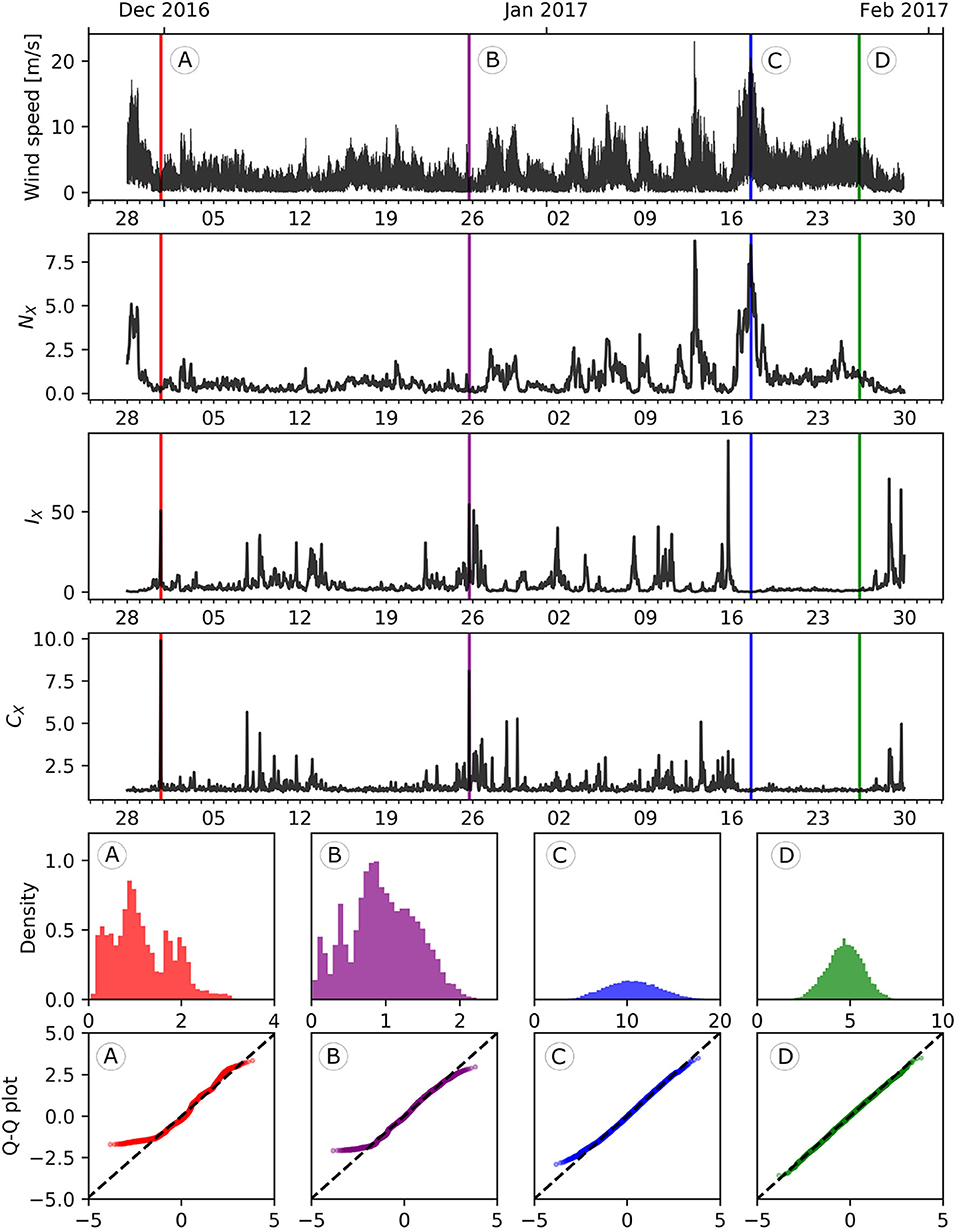
Figure 4. High-frequency wind speed time series. From top to bottom : time series, SEP, FIM, and FSC moving windows, histograms and Q-Q plots of some time series subsets.
The Fisher-Shannon quantities are computed with non-overlapping moving windows of 1 hour width along the time axis. Globally, all quantities vary with time, indicating non-stationarity, see Figure 4. The SEP seems to roughly replicate the behavior of the original time series. This is due to a proportional effect between the mean and the variance of the data, as shown in Figure 5. As for the logistic map case, the FIM is roughly inversely proportional to the SEP (not shown in logarithmic scale). The FSC is close to 1 during long period of time, e.g., between the 17th and the 27th January 2017. This should indicate a local behavior of wind speed close to a Gaussian one. During these periods, wind speed is not necessarily calm, e.g., the 17th January. Conversely, The FSC also exhibits some peaks where wind speed is rather low, which should indicate a more complex distribution of the data.
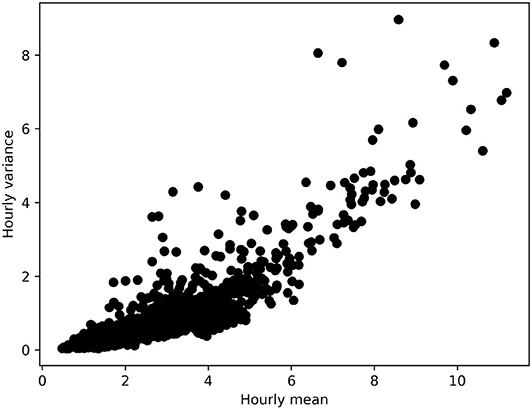
Figure 5. Scatter plot of hourly variance against hourly mean of the high-frequency wind speed data.
To verify this, a closer exploration of the data is required. To this aim, we considered four subsets of 3 hours length, denoted by A, B, C, and D and represented on Figure 4 by color red, purple, blue, and green, respectively. Histograms and quantile-quantile (Q-Q) plots of these data subsets are also plotted with the corresponding colors. The subset D is chosen during the period of almost unitary FSC. The corresponding histogram and Q-Q plot confirms the very-close-to-Gaussian behavior of the data. The subset C is also chosen with a FSC close to 1, but centered on the maximum of SEP of the 17th January 2017 which corresponds also to a high wind speed activity. The histogram shows again a distribution close to a Gaussian one, but with a higher variance than C. This was an expected output, since for Gaussian distribution the SEP equals to the variance and C was chosen with a high SEP. The Q-Q plot shows little departure for the left tail, but the data are still relatively close to what was expected. The subset B is centered on a peak of FSC. The histogram shows a distribution which is very far from Gaussianity. It is clearly asymmetric and has at least two modes—maybe three. The Q-Q plot shows a strong departure from the Gaussian distribution, especially on the left tail. The subset A is centered on the highest FSC value. Its histogram shows three—maybe four—modes. The corresponding Q-Q plot shows how for this subset data are even farther from Gaussianity than for the previous subset.
These results show the high complexity of these data, whose behavior can rapidly change locally in time or even during calm weather. Further analysis on a larger set of these measurements using the FSC can be found in Guignard et al. (2019b), where authors analyzed wind speed and temperature data gathered by sensors similar to the one used to collect the data analyzed in this section, fixed along a mast located in a urban canyon. A FSC analysis suggested different wind dynamics induced by the building layout. The daily variation of temperature was also found to be an important predictor for high-frequency wind speed daily complexity. Moreover, FSC was used to show that wind speed and height are related by a non-linear relationship. More generally, this demonstrates the high versatility of analysis based on Fisher-Shannon information, which had yield numerous and various insight on these data.
6. Conclusions
The paper discusses the Fisher-Shannon information method as an effective data exploration tool able to give diverse insights into complex non-stationary time series. The Fisher-Shannon method was presented in a unified framework and new interpretations of FSC were pointed out. In particular, the FSC was identified as a sensitivity measure of the SEP and as a scale-independent non-Gaussianity measure, which both provide interpretation of this quantity as well. The detection of potential Gaussian behavior in the data was successfully showed on high-frequency wind speed data.
In the methodological part of the paper, FIM and FSC were computed in closed forms for several parametric distributions which are widely used in geo-environmental data analyses. Theoretical formulas for other random variables can be derived depending on the problem at hand. Furthermore, it was also shown—by injecting noise in the logistic map—how these information measures can be used to detect potential dynamic changes in a quite robust manner—especially with FSC. While SEP, FIM and FSC were presented as versatile information-based exploratory tools, they can also be used as time series discrimination or, more generally, to generate time series features for clustering, modeling, and forecasting.
The Fisher-Shannon method has been widely used in geosciences, as shown in the first part of this paper. However, according to our opinion, its full potential is still unexploited and underestimated. To simplify the access to this method for environmental data analysis and foster reproducibility, open source libraries written in R and Python for the computation of the three measures via a non-parametric kernel density estimation are provided.
From a theoretical point of view, future studies should involve generalization of the Fisher-Shannon method to the multivariate case. Several numerical investigations could be carried out for the KDE of the FIM. In particular, other estimates could be provided by re-substitution techniques as with entropy. Optimal bandwidth choice regarding to asymptotic mean squared error of FIM—or even FSC—could be derived. More practically, a challenging exploratory analysis of spatio-temporal data is planned.
Software Availability
A Python package is proposed on PyPI and GitHub (https://github.com/fishinfo/FiShPy), as well as an R package available on CRAN and GitHub (https://github.com/fishinfo/FiSh). They allow interested users to compute non-parametric estimation of the SEP, FIM and FSC.
Data Availability Statement
The data presented in this article are not readily available as the authors are not their owners. Requests to access the data should be directed to the responsible parties of the MoTus experiment (motus.epfl.ch), Dasaraden Mauree (ZGFzYXJhZGVuLm1hdXJlZUBlcGZsLmNo).
Author Contributions
FG conceived the main conceptual ideas, conduct investigations, developed the theoretical formalism, performed the calculations, interpreted the computational results, and wrote the original draft. FG and ML developed Python and R packages. FG, FA, and MK wrote the final version of the paper. MK carried out the supervision, project administration, and funding acquisition. All authors discussed the results, provided critical feedback, commented, reviewed and edited the original manuscript, and gave final approval for publication.
Funding
FG and MK acknowledge the support of the National Research Programme 75 Big Data (PNR75) of the Swiss National Science Foundation (SNSF), project no. 167285.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors are grateful to Dasaraden Mauree from the Ecole Polytechnique Fédérale de Lausanne, Switzerland, for providing the high-frequency wind speed data, and to Sylvain Robert for analytical computation checking. They also thank Luciano Telesca from Institute of Methodologies for Environmental Analysis of the Italian National Research Council for profitable discussions, and the reviewers for their constructive comments, which contributed to improve the paper.
References
Amato, F., Laib, M., Guignard, F., and Kanevski, M. (2020). Analysis of air pollution time series using complexity-invariant distance and information measures. Phys. A Stat. Mech. Appl. 547:124391. doi: 10.1016/j.physa.2020.124391
Angulo, J., Antolín, J., and Sen, K. (2008). Fisher-Shannon plane and statistical complexity of atoms. Phys. Lett. A 372, 670–674. doi: 10.1016/j.physleta.2007.07.077
Bhattacharya, P. K. (1967). Estimation of a probability density function and its derivatives. Sankhy = a Indian J. Stat. Ser. A 29, 373–382.
Cover, T. M., and Thomas, J. A. (2006). Elements of Information Theory. New York, NY: Wiley-Interscience.
Dembo, A., Cover, T. M., and Thomas, J. A. (1991). Information theoretic inequalities. IEEE Trans. Inform. Theory 37, 1501–1518. doi: 10.1109/18.104312
Dmitriev, Y., and Tarasenko, F. (1973). On the estimation of functionals of the probability density and its derivatives. Theory Probabil. Appl. 18, 628–633. doi: 10.1137/1118083
Esquivel, R. O., Angulo, J. C., Antolín, J., Dehesa, J. S., Lopez-Rosa, S., and Flores-Gallegos, N. (2010). Analysis of complexity measures and information planes of selected molecules in position and momentum spaces. Phys. Chem. Chem. Phys. 12, 7108–7116. doi: 10.1039/b927055h
Fisher, R. A. (1925). Theory of statistical estimation. Math. Proc. Cambridge Philos. Soc. 22, 700–725. doi: 10.1017/S0305004100009580
Frieden, B. R. (1990). Fisher information, disorder, and the equilibrium distributions of physics. Phys. Rev. A 41, 4265–4276. doi: 10.1103/PhysRevA.41.4265
Guignard, F., Lovallo, M., Laib, M., Golay, J., Kanevski, M., Helbig, N., et al. (2019a). Investigating the time dynamics of wind speed in complex terrains by using the Fisher-Shannon method. Phys. A Stat. Mech. Appl. 523, 611–621. doi: 10.1016/j.physa.2019.02.048
Guignard, F., Mauree, D., Lovallo, M., Kanevski, M., and Telesca, L. (2019b). Fisher-Shannon complexity analysis of high-frequency urban wind speed time series. Entropy 21:47. doi: 10.3390/e21010047
Györfi, L., and van der Meulen, E. C. (1987). Density-free convergence properties of various estimators of entropy. Comput. Stat. Data Anal. 5, 425–436. doi: 10.1016/0167-9473(87)90065-X
Joe, H. (1989). Estimation of entropy and other functionals of a multivariate density. Ann. Instit. Stat. Math. 41, 683–697. doi: 10.1007/BF00057735
Kantz, H., and Schreiber, T. (2004). Nonlinear Time Series Analysis, Vol. 7. Cambridge, MA: Cambridge University Press. doi: 10.1017/CBO9780511755798
Lazo, A. V., and Rathie, P. (1978). On the entropy of continuous probability distributions (corresp.). IEEE Trans. Inform. Theory 24, 120–122. doi: 10.1109/TIT.1978.1055832
Lehmann, E. (1999). Elements of Large-Sample Theory. Springer Texts in Statistics. New York, NY: Springer-Verlag. doi: 10.1007/b98855
Lovallo, M., Shaban, A., Darwich, T., and Telesca, L. (2013). Investigating the time dynamics of monthly rainfall time series observed in northern Lebanon by means of the detrended fluctuation analysis and the Fisher-Shannon method. Acta Geophys. 61, 1538–1555. doi: 10.2478/s11600-012-0094-9
Martin, M., Pennini, F., and Plastino, A. (1999). Fisher's information and the analysis of complex signals. Phys. Lett. A 256, 173–180. doi: 10.1016/S0375-9601(99)00211-X
Martin, M., Perez, J., and Plastino, A. (2001). Fisher information and nonlinear dynamics. Phys. A Stat. Mech. Appl. 291, 523–532. doi: 10.1016/S0378-4371(00)00531-8
Mauree, D., Deschamps, L., Bequelin, P., Loesch, P., and Scartezzini, J. L. (2017a). “Measurement of the impact of buildings on meteorological variables,” in Building Simulation Application Proceedings (Bolzano: BU Press).
Mauree, D., Lee, D. S. H., Naboni, E., Coccolo, S., and Scartezzini, J. L. (2017b). Localized meteorological variables influence at the early design stage. Energy Proc. 122, 325–330. doi: 10.1016/j.egypro.2017.07.331
Pierini, J. O., Lovallo, M., Gomez, E. A., and Telesca, L. (2016). Fisher-Shannon analysis of the time variability of remotely sensed sea surface temperature at the brazil-malvinas confluence. Oceanologia 58, 187–195. doi: 10.1016/j.oceano.2016.02.003
Pierini, J. O., Restrepo, J. C., Lovallo, M., and Telesca, L. (2015). Discriminating between different streamflow regimes by using the Fisher-Shannon method: an application to the colombia rivers. Acta Geophys. 63, 533–546. doi: 10.2478/s11600-014-0229-2
Pierini, J. O., Scian, B., Lovallo, M., and Telesca, L. (2011). Discriminating climatological regimes in rainfall time series by using the fisher-Shannon method. Int. J. Phys. Sci. 6, 7799–7804. doi: 10.5897/IJPS11.737
Prakasa Rao, B. (1983). Nonparametric Functional Estimation. Probability and Mathematical Statistics: A Series of Monographs and Textbooks. Academic Press.
Rioul, O. (2011). Information theoretic proofs of entropy power inequalities. IEEE Trans. Inform. Theory 57, 33–55. doi: 10.1109/TIT.2010.2090193
Shannon, C. E. (1948). A mathematical theory of communication. Bell Syst. Tech. J. 27, 379–423. doi: 10.1002/j.1538-7305.1948.tb01338.x
Sheather, S. J., and Jones, M. C. (1991). A reliable data-based bandwidth selection method for kernel density estimation. J. R. Stat. Soc. Ser. B 53, 683–690. doi: 10.1111/j.2517-6161.1991.tb01857.x
Telesca, L., Caggiano, R., Lapenna, V., Lovallo, M., Trippetta, S., and Macchiato, M. (2009a). Analysis of dynamics in Cd, Fe, and Pb in particulate matter by using the Fisher-Shannon method. Water Air Soil Pollut. 201, 33–41. doi: 10.1007/s11270-008-9924-4
Telesca, L., Chamoli, A., Lovallo, M., and Stabile, T. A. (2015a). Investigating the tsunamigenic potential of earthquakes from analysis of the informational and multifractal properties of seismograms. Pure Appl. Geophys. 172, 1933–1943. doi: 10.1007/s00024-014-0862-3
Telesca, L., and Lovallo, M. (2011). Analysis of the time dynamics in wind records by means of multifractal detrended fluctuation analysis and the Fisher-Shannon information plane. J. Stat. Mech. Theory Exp. 2011:P07001. doi: 10.1088/1742-5468/2011/07/P07001
Telesca, L., and Lovallo, M. (2013). Fisher-Shannon analysis of wind records. Int. J. Energy Stat. 01, 281–290. doi: 10.1142/S2335680413500208
Telesca, L., and Lovallo, M. (2017). On the performance of Fisher information measure and Shannon entropy estimators. Phys. A Stat. Mech. Appl. 484, 569–576. doi: 10.1016/j.physa.2017.04.184
Telesca, L., Lovallo, M., Alcaz, V., and Ilies, I. (2015b). Site-dependent organization structure of seismic microtremors. Phys. A Stat. Mech. Appl. 421, 541–547. doi: 10.1016/j.physa.2014.11.061
Telesca, L., Lovallo, M., and Carniel, R. (2010). Time-dependent Fisher information measure of volcanic tremor before the 5 April 2003 paroxysm at Stromboli volcano, Italy. J. Volcanol. Geothermal Res. 195, 78–82. doi: 10.1016/j.jvolgeores.2010.06.010
Telesca, L., Lovallo, M., Chamoli, A., Dimri, V., and Srivastava, K. (2013). Fisher-Shannon analysis of seismograms of tsunamigenic and non-tsunamigenic earthquakes. Phys. A Stat. Mech. Appl. 392, 3424–3429. doi: 10.1016/j.physa.2013.03.049
Telesca, L., Lovallo, M., Hsu, H. L., and Chen, C. C. (2011). Analysis of dynamics in magnetotelluric data by using the Fisher-Shannon method. Phys. A Stat. Mech. Appl. 390, 1350–1355. doi: 10.1016/j.physa.2010.12.005
Telesca, L., Lovallo, M., Ramirez-Rojas, A., and Angulo-Brown, F. (2009b). A nonlinear strategy to reveal seismic precursory signatures in earthquake-related self-potential signals. Phys. A Stat. Mech. Appl. 388, 2036–2040. doi: 10.1016/j.physa.2009.01.035
Vignat, C., and Bercher, J. F. (2003). Analysis of signals in the Fisher-Shannon information plane. Phys. Lett. A 312, 27–33. doi: 10.1016/S0375-9601(03)00570-X
Wand, M., and Jones, M. (1994). Kernel Smoothing. Boca Raton: Chapman & Hall; Taylor & Francis. doi: 10.1201/b14876
Zamir, R. (1998). A proof of the Fisher information inequality via a data processing argument. IEEE Trans. Inform. Theory 44, 1246–1250. doi: 10.1109/18.669301
7. Appendix
The differential entropy HX for Gamma, Weibull and log-normal distributions can be found in (Lazo and Rathie, 1978) and (Cover and Thomas, 2006). The SEP is simply a non-linear transform of HX.
Proof of proposition 1: Computing the second derivative of logf (x), one has
and then, using (4), the variable change x = θy and the properties of the Gamma function,
yielding the FIM for the Gamma distribution. The FSC is directly obtained by multiplying the SEP and the FIM.□
Proof of proposition 2: Starting from the Weibull PDF, one has
and with the variable change ,
□
Proof of proposition 3: The second derivative of logf (x) is
and using the variable change y = logx − μ, one have
Note that
Using this and the definition of a Gaussian distribution ,
and the FIM is obtained. The FSC is
□
Keywords: Fisher-Shannon complexity, Fisher-Shannon information plane, Shannon entropy power, Fisher information measure, statistical complexity, non-linear time series, dynamical behavior characterization, high frequency wind speed
Citation: Guignard F, Laib M, Amato F and Kanevski M (2020) Advanced Analysis of Temporal Data Using Fisher-Shannon Information: Theoretical Development and Application in Geosciences. Front. Earth Sci. 8:255. doi: 10.3389/feart.2020.00255
Received: 04 December 2019; Accepted: 09 June 2020;
Published: 14 July 2020.
Edited by:
Juergen Pilz, Alpen-Adria-Universität Klagenfurt, AustriaReviewed by:
Hwa-Lung Yu, National Taiwan University, TaiwanLuis Gomez, University of Las Palmas de Gran Canaria, Spain
Copyright © 2020 Guignard, Laib, Amato and Kanevski. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fabian Guignard, ZmFiaWFuLmd1aWduYXJkQHVuaWwuY2g=
 Fabian Guignard
Fabian Guignard Mohamed Laib
Mohamed Laib Federico Amato
Federico Amato Mikhail Kanevski
Mikhail Kanevski