Numerical Simulation of Dam-Break Flood Impacting Buildings by a Volume of Fluid and Immersed Boundary Method

A three-dimensional hydrodynamic model is developed to study the propagation of dam-break-induced flood and the interaction between floods and buildings. In the proposed mathematical model, the volume of fluid (VOF) method and the immersed boundary (IB) method are used to address the air/water interface and fluid/structure interface, respectively. Barely a limited number of publications focus on 3D simulations of the dam-break flood impacting buildings in the long flume heretofore, for researching the dam-break flood impacting buildings involves some hard issues like wave breaking phenomena, flood–building interaction, and computational efficiency. Therefore, the highlights to this paper are as follows: (1) The THINC/SW (THINC with Slope Weighting), which is extremely simple and efficient and meanwhile can also solve the wave breaking process, is adopted in the paper. Furthermore, its numerical accuracy is comparable with the conventional VOF schemes that use geometrical reconstructions. (2) The direct forcing IB method, which can be easily applied to three-dimensional simulation, is adopted to promote the computational efficiency of the three-dimensional numerical model and handle flood–building interaction interface treatment. The proposed VOF/IB model is validated by the physical experiment results and is also compared with the two-dimensional depth-averaged Shallow-Water Equations, and Coupled Level Set/Volume of Fluid and Immersed Boundary models in terms of accuracy and efficiency.

Introduction

Catastrophic consequences such as the losses of human life and properties can occur when severe flood propagate to downstream areas (Schubert and Sanders, 2012). Also, a strong influence can be found on the inundation dynamics and the flood characteristics on account of the buildings in the flooding area. The present research is therefore undertaken to construct an effective and accurate three-dimensional (3D) multi-phase solver to comprehensively understand the fluid/structure interaction and its flow characteristics that arise in dam-break-induced flood events.

These factors, various hydraulic quantities including water depth, velocity field, flood arrival time, and duration of the flood, are of significance to the buildings in flooded areas that need to be figured out. So numerical simulations are considered because of their universality and practicability, which cannot solely predict force actions on structures located in the flow domain (Aureli et al., 2015) precisely but also tackle irregular topography, and wetting and drying flow with high efficiency. Two-dimensional (2D) Shallow-Water Equations (SWEs) model that considers hydrostatic pressure assumption is supposed to be simple and requires less computational cost to simulate dam-break flow. Thus, the high resolutions of space and time can be sufficiently obtained for real long rivers (Chang et al., 2011). The main concerns regarding numerical challenges of modeling dam-break flow by 2D shallow water equations include the treatment of the propagation of free-surface discontinuities and the resolution of rapidly varying open channel flows interacting with the building. A reliable numerical scheme must have the ability to suppress numerical instability which is particularly severe when transient flows with steep gradients over bumpy dry beds or free-surface discontinuities occur. One way to resolve this difficulty is to apply the Godunov scheme (Savic and Holly, 1993), high-resolution non-oscillatory scheme (Sanders, 2001), Riemann Solvers (Guinot et al., 2009), and total variation diminishing (TVD) scheme (Ying et al., 2004; Liang et al., 2006). While a construction is conducted by the simulation of rapidly varying open channel flows in the buildings or topographical singularities with the 2D SWEs, it is usually categorized as a rigid block with impervious walls or equivalently as a hole in the computational domain (Schubert and Sanders, 2012). Otherwise, the concept of porosity of a built-up area is required (Sanders et al., 2008; Soares-Frazao et al., 2008) to obtain an acceptable level of accuracy for the prediction of the effects of buildings on flood propagation. The weaknesses of the shallow water models are no density or velocity variations in the vertical direction, and, meanwhile, are inadequate to simulate flows involving significant variations of flow depth and wave breaking because 2D shallow water models originate from depth-integrating the 3D continuity and momentum equations. Moreover, they assume that the viscous force is negligible and the vertical acceleration is small, so the pressure field is purely hydrostatic. In other words, the depth-averaged approach cannot be used to simulate flows with significant variations in the vertical direction and the 3D is locally obvious in this phenomenon, which demonstrates strong curvatures of the free surface with non-hydrostatic distribution of pressure along the vertical direction. The alternative to the numerical method is to numerically solve the 3D Navier–Stokes equations for simulating dam-break flow impacting buildings.

The computational method for 3D dam-breaking floods with complex bodies can be generally divided into three categories: the moving grid approach, the fixed grid approach, and meshless approach. In the moving grid methods, body-fitted grids are attached to the solid surfaces or even the interfaces between two different fluids, whereas the overall grids can be unstructured or overlapping grids, which were normally applied to free-surface flows with a single stationary structure. Great progress has been made in moving grid methods. However, it is still time consuming and prone to errors during the process of the grid deformation, re-generation, and overlapping interpolation. A considerable number of studies on this approach for 3D dam-break problem have been done (Hou et al., 2013; Guo et al., 2018; Fourtakas et al., 2019) during the development of a meshless approach (e.g., smoothed particle hydrodynamics, SPH). The basic idea of the SPH method is to describe continuous fluids (or solids) in groups of interacting particles, and each of them can carry various physical quantities (such as mass and velocity), and the mechanical behavior of the whole system can be obtained by solving the kinetic equation and tracing the motion orbit of each particle. The robust numerical simulation of dam-break flow applications depends on the performance of the boundary conditions employed within the SPH model. In the SPH method (Fourtakas et al., 2019) proposed by Fourtakas et al., hence, the new solid boundary formulation adopts a local uniform stencil (LUST) of fictitious particles that surround and move with each fluid particle and are only activated when they are located inside a boundary. The simulation of dam-break flow is achieved by incompressible SPH (Guo et al., 2018) with the advent of high-speed computers. For a comprehensive literature review, see the research work for SPH of Hou et al. (2013) and Cao et al. (2017). SPH, within the entire calculation process, is able to enhance the conservative property without advection errors. Nevertheless, high demand for computational cost is needed and the modeling of boundary conditions is still challenging. Moreover, the SPH method is unstable when tracking interfaces with large deformations.

The VOF/IB method belongs to fixed grid approach. Solid boundaries and phase interfaces can have unrestricted motions across the underlying fixed grid lines, which are usually not aligned with the solid–fluid and/or the fluid–fluid interfaces. Also, in most cases, Cartesian grids, which further simplify the gridding requirements, are used to cover the whole computational domain. In other words, a fixed grid approach has become feasible and is greatly important to simulate 3D dam-break flow problems. For example, 3D Reynolds-averaged Navier–Stokes model, a non-hydrostatic pressure assumption, is developed to complete the simulation of dam-break flow. This model is used to capture the free surface with the volume of fluid (VOF) approach. Kurioka and Dowling present a level set (LS) method which combines with high-order Weighted Essentially Non-Oscillatory scheme to capture free surface evolution for dam-break flows (Kurioka and Dowling, 2009). It is developed as an unstructured-mesh finite element 3D model for simulating dam-break floods through several cases, whose advantage is that the vertical inertia is considered in its 3D model (Zhang et al., 2018). A macroscopic model for describing the interaction between dam-break waves and porous media is presented in Hu et al. (2012). The two-phase model, which uses the LS method with second-order accuracy, is evolved to simulate dam-break flow with the consideration of the total pressure or hydrostatic pressure assumption in Navier–Stokes solutions (Monteiro et al., 2019). From above, the fluid–fluid interface is usually treated in literature utilizing interface capturing methods, such as the VOF (Hirt and Nichols, 1981; Zeng et al., 2010; Wang et al., 2012) and the LS method (Osher and Sethian, 1988; Gu et al., 2018a,b). Both can tackle topology changes or the phases between air and water on account of solving advection equations that use a color function. Furthermore, air entrainment effects and wave breaking phenomena can also be predicted accurately, so the employment of the interface capturing method is advisable.

When the free surface is tracked by the LS method, the mass conservation will rapidly deteriorate as time goes by. This loss of mass problem arises from the use of a lower-order spatial discretization scheme to approximate the highly oscillatory and the dissipation character of the propagating solutions. A mass conservation method, proposed by Olsson et al. (2007), is named as the conservative Level Set (CLS) method. On account of the intrinsic shortage of the Heaviside function, the normals and curvatures of interfaces are sensitive to small spurious oscillations, though the mass conservation property of the advection step can be ensured for the CLS method. To address this issue, an improved CLS method is proposed (Bahbah et al., 2019) for the 3D simulations of the axisymmetric and non-axisymmetric merging of two bubbles. Coupled Level Set and Volume of Fluid (CLSVOF) methods are noteworthy for their ability to overcome mass loss and meanwhile present strong curvatures of the free surface (Sun and Tao, 2010; Wang et al., 2013; Gu et al., 2019; Li and Yu, 2019).

Regarding the simulation of dam-break flow impacting buildings (or fluid–structure interaction), the treatment of fluid–structure interfaces is crucial (Yang and Stern, 2009). The immersed boundary (IB) method, which is advisable to do with problems with irregular solid objects and is not necessarily supposed to conform to Cartesian grids, can be adopted (Yang and Stern, 2009) to simulate fluid–structure interface problems. Namely, the boundary condition is enforced at the immersed boundary as long as an immersed boundary is identified, which is trivial for a body-fitted grid method as the grid lines are made to follow the phase interface. Based on the pioneering work by interface capturing/immersed boundary methods of Zhang et al. (2010), Zhang et al. (2014), and Li (2016), Yu et al. (2019) proposed a Coupled Level Set and Volume of Fluid and an Immersed Boundary (CLSVOF/IB) method for the 3D Navier–Stokes equation to resolve dam-break flow impacting a stationary obstacle problem. In comparison with the 2D shallow equations, the 3D model requires more computational cost and therefore is not the main framework of the dam-break flow computation in the urban area.

Only a limited number of publications focus on 3D simulations of the dam-break flood impacting buildings in the long flume heretofore. The objectives to this paper are (1) to improve the efficiency of the three-dimensional numerical model in Yu et al. (2019) based on VOF and IB methods to, respectively, solve the interface problems of fluid/fluid and fluid/solid, and to address the problem of excessive calculation time in Yu et al. (2019). Moreover, the model can accurately estimate the front location of the dam break and the depth of the downstream water, and reproduce the wave breaking phenomena in the long straight water channel. (2) To compare the result of 2D shallow water and 3D modeling the unsteady multi-phase flow with the outcome of the experiment by Soares-Frazão and Zech (2008) from the University of Leuven. The offered hydraulic quantities forming the experiment are used for model validation in terms of efficiency and accuracy.

This paper is organized as follows: section Mathematical Model presents the 2D shallow water equations, 3D Navier–Stokes equations, and the developed VOF/IB solution algorithm; section Numerical Results and Discussion presents numerical results as the standard practice, and we validate the code against the test case, which is amenable to experiments (Soares-Frazao et al., 2008); concluding remarks are given in section Concluding Remarks.

Mathematical Model

To calculate flood propagation, two mathematical models, depth-averaged water model and depth-resolving simulation model, are useful. Flood whose length is substantially larger than its depth can frequently be approximated by depth-averaged water models. Song et al. (2011) introduced this approach for shallow water flows and later extended to shallow water flows that adopt unstructured grids (Meneveau and Katz, 2000). Various modeling approaches for dam breaking have evolved, spanning the entire range from dimensional analysis to high-resolution DNS, owing to this multitude of, to some extent, relevant flow regimes. Besides VOF-IB method (depth-resolving simulation model), the paper has proposed a way to deal with flooding through buildings with depth-averaged water model (see section Two-Dimensional Depth-Averaged Shallow-Water Equations (SWEs) Model) and compared their accuracy as well. Indeed, the Large-Eddy Simulation (LES), a turbulence model, belongs to depth-resolving simulation model, which can show the turbulent process. In addition, fewer computational resources are required than direct numerical simulations (DNSs) because LES, instead of modeling all of the scales of motion below a cutoff, resolve merely the energy-containing large eddies. This approach often results in the majority of the dissipative scales being modeled (Meneveau and Katz, 2000). The cutoff is determined by a filter width that depends on the grid spacing employed in the LES. DNS represents the most accurate computational approach for studying dam-break flood despite its need for more computational resources. In DNS, all scales of motion are explicitly resolved even which are from the integral scales dictated by the boundary conditions down to the dissipative Kolmogorov scale determined by viscosity are explicitly resolved. Hence, the N-S equation described in this paper is still referred to as DNS.

Depth-Resolving Simulation Model

The paper presents the VOF/IB method in the sequence of solving the VOF equation (Equation 1) at first and then the momentum equation (Equation 4). The step of introducing the CLSVOF/IB method first needs to work out the VOF equation (Equation 1) and then the LS equation $\frac{\partial \varphi }{\partial t}+\text{u}·\nabla \varphi =0$ and the momentum equation (Equation 4).

Volume of Fluid (VOF) Method

In the VOF method, the interface is regarded as the cell-wise geometrical reconstruction that can separate the two distinct fluids (e.g., air and water) in the cell. The volume fraction C occupied by the water within each cell with a value between 0 and 1 is advected by the following transport equation under a velocity field u:

$\begin{array}{ll}\frac{\partial C}{\partial t}+\nabla ·(uC)-C\nabla ·u=0& (1)\end{array}$

It is notable that the geometrical reconstruction procedure that computes the numerical fluxes can be performed through the simple line interface calculation (Noh and Woodward, 1976), piecewise linear interface calculation (Harvie and Fletcher, 2000, 2001), or weighted line interface calculation (Yokoi, 2007) reconstruction. Still, it usually prevents them from being immediately adopted by the users that a geometrical reconstruction makes the computer coding complex and be filled with “if” logic operations. One way of circumventing this geometrical reconstruction procedure is to use the so-called THINC (Tangent of Hyperbola for INterface Capturing) (Xiao et al., 2005) to compute moving interfaces, thus the needed geometrical reconstruction procedures being avoided. With the utilization of the hyperbolic tangent function, the THINC can compute the numerical flux for the fluid fraction function, and also present a solution, which is conservative, oscillation-less, and smearing-less, to the fluid fraction function even for the extremely distorted interfaces of arbitrary complexity. Yet for all that, the interface will be ruffled when flow direction parallels the interface. How to use a scheme to result in a simpler and more accurate algorithm becomes the main subject of the present study. Based on the attractive feature of the 1D THINC building block, the THINC with Slope Weighting (THINC/SW) (Xiao et al., 2011) is adopted by this paper. Our goal of solving the VOF transport equation is to obtain solutions with higher accuracy and less computational cost.

Coupled Level set and Volume of Fluid (CLSVOF) Method

The algorithm for CLSVOF is as follows: The CLSVOF method advects the level set function ϕ and the volume fraction C by solving LS and VOF equations, respectively, from tⁿ to tⁿ⁺¹. In other words, the evolution of the air/water interface can be tracked by solving the VOF equation (Equation 1) and the level set equation $\frac{\partial \varphi }{\partial t}+\text{u}·\nabla \varphi =0$, where u accounts for the fluid velocity field obtained by solving the Navier–Stokes equations. The interface needs to reconstruct, subsequent to the advection of ϕ and C, so that the two interfaces predicted by ϕ and C are close to each other. The reconstruction procedure of LS and VOF functions can be found in Yu et al. (2019).

Navier–Stokes Equations and the Immersed Boundary Method

The following dimensionless Navier–Stokes equations are considered:

$\begin{array}{ll}\frac{\partial u}{\partial t}+(u·\nabla )u=-\frac{\nabla p}{\rho (C)}+\frac{1}{Re}\frac{\nabla ·(2\mu (C)D)}{\rho (C)}+\frac{1}{F{r}^2}{\widehat{e}}_g& (2)\end{array}$

In this equation, u represents velocity fields, p represents pressure, and Re and Fr denote the Reynolds number and Froude number. Physical properties (density ρ and viscosity μ) are the function of C and defined in the following equations:

$\begin{array}{l}\rho =C+\left(\frac{{\rho }_a}{{\rho }_w}\right)(1-C)\\ \mu =C+\left(\frac{{\mu }_a}{{\mu }_w}\right)(1-C)& (3)\end{array}$

where ρ_a and ρ_w are air and water density, respectively.

In the IB method, the momentum forcing which is introduced to enforce the boundary condition of the body in the fluid can be prescribed on a fixed mesh (Zhang et al., 2010). Momentum equations can be discretized via the following second-order Adams–Bashforth scheme and the immersed boundary method:

$\begin{array}{ll}\frac{u^{n+1}-u^n}{\Delta t}+\left(\frac{3}{2}{A}^n-\frac{1}{2}{A}^{n-1}\right)+\frac{1}{\rho (C)}\nabla p^{n+1}=\eta f^{n+1}& (4)\end{array}$

where

$\begin{array}{l}A=(u·\nabla )u-\frac{1}{Re}\frac{\nabla ·(2\mu (C)D)}{\rho (C)}-\frac{1}{F{r}^2}{\widehat{\text{e}}}_g\end{array}$

given that the forcing vector ηf with the solid volume fraction η is introduced as a source term to the momentum equation through the IB method. To calculate the solid volume fraction η accurately, refining the mesh on solid is considered to satisfy this requirement (Yu et al., 2019). In the framework of the projection method discussed in Yu et al. (2019), the velocity uⁿ⁺¹ given by the following equations will be obtained:

$\begin{array}{ll}\frac{u^{*}-u^n}{\Delta t}+\left(\frac{3}{2}{A}^n-\frac{1}{2}{A}^{n-1}\right)=0& (5)\end{array}$

$\begin{array}{ll}\nabla ·\left(\frac{1}{\rho (C)}\nabla p^{n+1}\right)=\frac{\nabla ·u^{\text{*}}}{\Delta t}& (6)\end{array}$

$\begin{array}{ll}{u}^{n+1}=u^{*}-\frac{\Delta t}{\rho (C)}\nabla p^{n+1}& (7)\end{array}$

where u^* is intermediate velocity. The point-successive over-relaxation (PSOR) method is applied to solve the discretized linear system of the Poisson pressure equation. The iterative procedures for the PSOR method will not stop until the user's specified tolerance is reached. Moreover, the relaxation factor is set as 1.5 in our calculation. Note that the virtual force fⁿ⁺¹ can be calculated as Yu et al. (2019).

$\begin{array}{ll}{f}^{n+1}=\frac{u_s-u^{*}}{\Delta t}+\frac{\nabla p^{n+1}}{\rho (C)}& (8)\end{array}$

where u_s symbolizes the velocity of buildings. Note that all the buildings are set in a static state, so u_s = 0. While we are calculating the convection terms in the momentum equations, points at the upwind side are considered. Also, in previous experiments, there are no apparent improvements on a prediction for the position of dam-break fronts under a discretization made by Navier–Stokes equations with the discrete scheme over a second-order precision. Therefore, the second-order accuracy scheme is enough to discretize the convection terms in this study. The viscous terms are discretized by the second-order central difference scheme.

Two-Dimensional Depth-Averaged SWE Model

Governing Equations

When the flood occurs in the urban area, the governing equation is expressed as Wu (2008):

(1) Continuity equation

$\begin{array}{ll}\frac{\partial \left[(1-c)\eta \right]}{\partial t}+\frac{\partial \left[(1-c)h{u}_x\right]}{\partial x}+\frac{\partial \left[(1-c)h{u}_y\right]}{\partial y}=0& (9)\end{array}$

(2) Momentum equation

To direction X:

$\begin{array}{l}\frac{\partial }{\partial t}\left[(1-c)u_{x}h\right]+\frac{\partial }{\partial x}\left[(1-c)u_x^{2}h+(1-c)\frac{g}{2}{h}^2\right]\\ +\frac{\partial }{\partial y}\left[(1-c)u_x{u}_{y}h\right]\\ =-(1-c)gh\frac{\partial z_b}{\partial x}-(1-c)\frac{{\tau }_{b,x}}{\rho }+\frac{g{h}^2}{2}\frac{\partial (1-c)}{\partial x}\\ -\frac{f_{d,x}h}{\rho }+\frac{\partial }{\partial x}\left[(1-c)v_e\frac{\partial u_x}{\partial x}\right]+\frac{\partial }{\partial y}\left[(1-c)v_e\frac{\partial u_x}{\partial y}\right]& (10)\end{array}$

To direction Y:

$\begin{array}{l}\frac{\partial }{\partial t}\left[\left(1-c\right)u_{y}h\right]+\frac{\partial }{\partial x}\left[\left(1-c\right)u_x{u}_{y}h\right]\hfill \\ +\frac{\partial }{\partial y}\left[\left(1-c\right)u_y^{2}h+\left(1-c\right)\frac{g}{2}{h}^2]\right]\hfill \\ =-\left(1-c\right)gh\frac{\partial z_b}{\partial x}-\left(1-c\right)\frac{{\tau }_{b,y}}{\rho }+\frac{g{h}^2}{2}\frac{\partial \left(1-c\right)}{\partial y}-\frac{f_{d,y}h}{\rho }\hfill \\ +\frac{\partial }{\partial x}\left[\left(1-c\right)v_e\frac{\partial u_y}{\partial x}\right]+\frac{\partial }{\partial y}\left[\left(1-c\right)v_e\frac{\partial u_y}{\partial y}\right]\hfill & (11)\end{array}$

in which t is time; η is water level; h is water depth; ρ is water flow density; g is gravity acceleration; u_x and u_y represent the velocity components of water flow in direction x and direction y, respectively; z_b is bed elevation; ∂z_b/∂x and ∂z_b/∂y are slopes of the bed; and c represents the distribution density of water blocking obstacles. In Equations (10) and (11), v_e = v + v_t, where v is the kinematic viscosity of water flow and v_t is eddy current viscosity produced by turbulent flow; v_t = 1/6κu_fh, where κ is von Karman constant and u_f is the friction velocity, generally expressed as $u_f=n(\sqrt{u^2+v^2})h^{1/6}$ (n symbolizes Manning coefficient).

f_d,x and f_d,y are the resistances of water obstacles along the direction x and direction y on the unit volume, which can be, respectively, expressed as $F_{d,x}=\frac{1}{2}{C_b}_{,x}\rho A_{b,x}\left|U\right|U_x$ and $F_{d,y}=\frac{1}{2}{C_b}_{,y}\rho A_{b,y}\left|U\right|U_y$ ($U=\sqrt{u_x^2+u_y^2}$). A_b,x = L_xh, A_b,y = L_yh; L_x and L_y are the projected length of the building in the direction x and y. C_b,x and C_b,y are two drag coefficients of two directions, which can be indicated as C_b,x = ξ_x/L_x and C_b,y = ξ_y/L_y ○ ξ_x and ξ_y are the local head loss coefficients in their corresponding direction ○; τ_b,x and τ_b,y are bed frictions toward direction x and directions y, which can be expressed as ${\tau }_{b,x}=\rho g\frac{n^{2}U}{R^{1/3}}{u}_x$ and ${\tau }_{b,y}=\rho gh\frac{n^{2}U}{R^{1/3}}{u}_y$ where R is hydraulic radius, but represents the water depth h in this study.

The governing Equations (9), (10), and (11) can also be expressed in the form of a vector:

$\begin{array}{l}\frac{\partial }{\partial t}\left[(1-c)\Phi \right]+\frac{\partial }{\partial x}\left[(1-c)f(\Phi )\right]\\ +\frac{\partial }{\partial y}\left[(1-c)g(\Phi )\right]=S+D\hfill & (12)\end{array}$

in which Φ is conserved variable; f(Φ) and g(Φ) are fluxes in direction x and direction y; S and D are, respectively, the source item and the diffusion term, which can be expressed as

$\begin{array}{l}\Phi ={\left[\eta ,h{u}_x,h{u}_y\right]}^T\\ f(\Phi )={\left[h{u}_x,h{u}_x{u}_x+\frac{1}{2}g{h}^2,h{u}_x{u}_y\right]}^T\\ g(\Phi )={\left[h{u}_y,h{u}_x{u}_y,h{u}_y{u}_y+\frac{1}{2}g{h}^2\right]}^T\\ S={\left[0,S_{p,x}+S_{f,x},S_{p,y}+S_{f,y}\right]}^T\\ D={\left[0,\frac{\partial }{\partial x_j}\left[(1-c)v_e\frac{\partial u_x}{\partial x_j}\right],\frac{\partial }{\partial x_j}\left[(1-c)v_e\frac{\partial u_y}{\partial x_j}\right]\right]}^T& (13)\end{array}$

S are made up of two factors, S_p,x and S_p,y, which are the source terms generated by the change of bottom gradient and permeable density in direction x and direction y, and its specific calculation formula is

$\begin{array}{ll}\begin{array}{c}{S}_{p,x}=-(1-c)gh\frac{\partial z_b}{\partial x}+g\frac{h^2}{2}\frac{\partial (1-c)}{\partial x}\\ S_{p,y}=-(1-c)gh\frac{\partial z_b}{\partial y}+g\frac{h^2}{2}\frac{\partial (1-c)}{\partial y}\end{array}& (14)\end{array}$

In Equation (13), S_f,x and S_f,y are drag source terms of bottom bed friction and water blocking obstacles in direction x and direction y, which can be calculated through the following formula:

$\begin{array}{l}{S}_{f,x}=-(1-c)gh\frac{n^2{u}_x\sqrt{u_x^2+u_y^2}}{h^{4/3}}-\frac{f_{d,x}h}{r}\\ S_{f,y}=-(1-c)gh\frac{n^2{u}_y\sqrt{u_x^2+u_y^2}}{h^{4/3}}-\frac{f_{d,y}h}{r}& (15)\end{array}$

Equation (12) can be also written as

$\begin{array}{ll}\frac{\partial }{\partial t}\left[(1-c)\Phi \right]+\frac{\partial }{\partial x}\left[F(\Phi )\right]+\frac{\partial }{\partial t}\left[G(\Phi )\right]=S+D& (16)\end{array}$

where F(Φ) = (1 − c)f(Φ) and G(Φ) = (1 − c)g(Φ).

Finite-Volume Discretization

The governing Equation (16) of the fixed bed flood motion can be discretized by finite volume method:

$\begin{array}{l}{\Phi }_{i,j}^{n+1}={\Phi }_{i,j}^n-\frac{\Delta t\left(F_{i+1/2,j}^n-F_{i-1/2,j}^n\right)}{\Delta x(1-c)}\\ -\frac{\Delta t\left(G_{i,j+1/2}^n-G_{i,j-1/2}^n\right)}{\Delta y(1-c)}+\frac{\Delta t}{1-c}\left(S_{i,j}^n+D_{i,j}^n\right)& (17)\end{array}$

in which the superscript n represents time step; Δt represents the time step, Δx and Δy represent the sizes of grids in direction x and direction y, respectively; $F_{i-1/2,j}^n$ and $F_{i+1/2,j}^n$ represent the fluxes of grid interfaces (i – 1/2,j) and (i + 1/2,j); $G_{i,j+1/2}^n$ and $G_{i,j-1/2}^n$ represent the fluxes of grid interfaces (i,j + 1/2) and (i,j – 1/2); S_i,j and D_i,j, respectively, represent the source term and the diffusion term at the unit center (i,j). The central-upwind format proposed by Kurganov and Petrova (2007) is applied to calculate the interface fluxes $F_{i+1/2,j}^n$ and $G_{i,j+1/2}^n$. In order to enable the model to spatially reach a second-order accuracy, the linear reconstruction technique of Liang (2011) is adopted in this paper to reconstruct the conserved variables at both sides of the interface and the bed elevation of the interface. Numerical stability conditions should limit the computational time step since the developed solution procedure is explicit, such as the Courant–Friedrichs–Lewy (CFL) condition for flow computation. The time step should satisfy the following CFL condition:

$\begin{array}{ll}{N}_{CFL}={\displaystyle \underset{i,j}{max}}\left\{\frac{\Delta t}{\Delta x}(|u_x|+\sqrt{gh}),\frac{\Delta t}{\Delta y}(|u_y|+\sqrt{gh})\right\}\le 0.25& (18)\end{array}$

Numerical Results and Discussion

The main contents of this chapter are as follows: (1) validate the accuracy of the 3D model through grid convergence study; (2) analyze the characteristics of the 3D flow fields; (3) compare accuracies and efficiencies amid the proposed VOF/IB, CLSVOF/IB (Yu et al., 2019), and SWE models.

Parameters and Setting of Numerical Simulations

Soares-Frazão and Zech (2008) from the Catholic University of Leuven experimented the evolution process simulation of outburst flood on the urban ground with dense buildings. This experimentation is a classic example of urban flood under fixed-bed condition, where the building here is architectural complex. The experimental area occupies a trapezoidal channel which is 36 m long, 3.6 m wide with a zero slope. The initial water depth in the upstream reservoir is 0.4 m, and that downstream of the reservoir is 0.011 m, as shown in Figure 1. In their experiment, water depth was measured by means of several resistive level gauges. As shown in Section B-B in Figure 1, 16 liquid level gauges are placed in Section B-B by Soares-Frazão and Zech. As the gate opens, those begin to record the evolution of the free surface. In this simulation, the continuous water depth of Section B-B is extracted and compared with the water depth data of 16 measuring points of Soares-Frazão and Zech experiments, in which the length range of the section in the x-axis is actually within 4 m from 11.5 to 15.5 m of the x-axis.

FIGURE 1

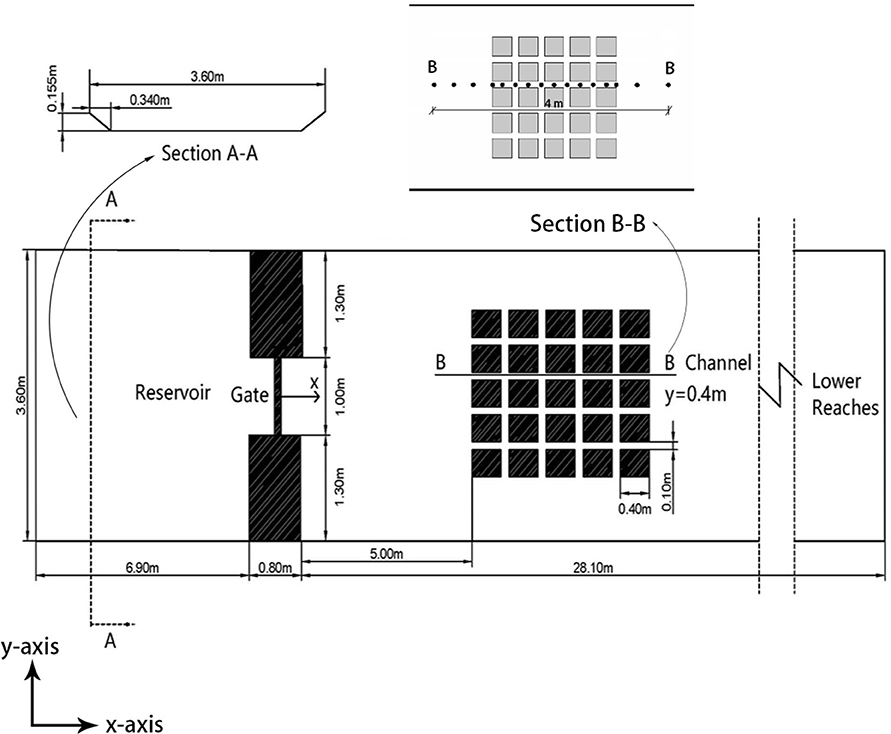
Figure 1. Parameters and setting of numerical simulations after (Yu et al., 2019).

Grid Convergence Study

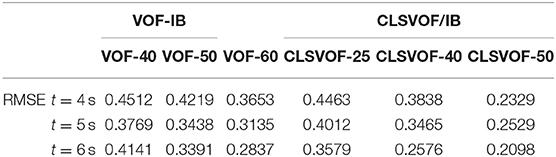
When the grid intervals (h) are 40, 50, and 60, the temporal evolution of water depth over time is proved in Figure 2. Both CLSVOF/IB and VOF/IB methods are able to accurately simulate water depth when the grid is finer enough. The relative root means square error (RMSE) between measured values and numerical results obtained from CLSVOF/IB and VOF/IB methods is shown in Table 1. The RMES mentioned in Table 1 is defined as $\mathrm{\text{RMSE}}=\sqrt{(1/m_R){\displaystyle \sum _{i=1}^{m_R}}{\left[(f_{simu,i}-f_{meas,i})/f_{meas,i}\right]}^2}$, where m_R is the number of measured values; f_meas,i is the ith measured value, and f_simu,i is the ith simulated value. The smaller the RMES value, the smaller the error between the simulated value and the measured value will be, and the more accurate the simulation result will be. From Figure 2, Table 1, it is shown that compared with the coarse grid (h = 40), with CLSVOF/IB and VOF/IB methods, the resulting error of water depth at each moment is relatively smaller as the grid is finer (h = 50). Therefore, the mesh density has a great influence on the calculation results of the model when the mesh is relatively finer, and the simulation consequences of water depth is more consistent with the measured values.

FIGURE 2

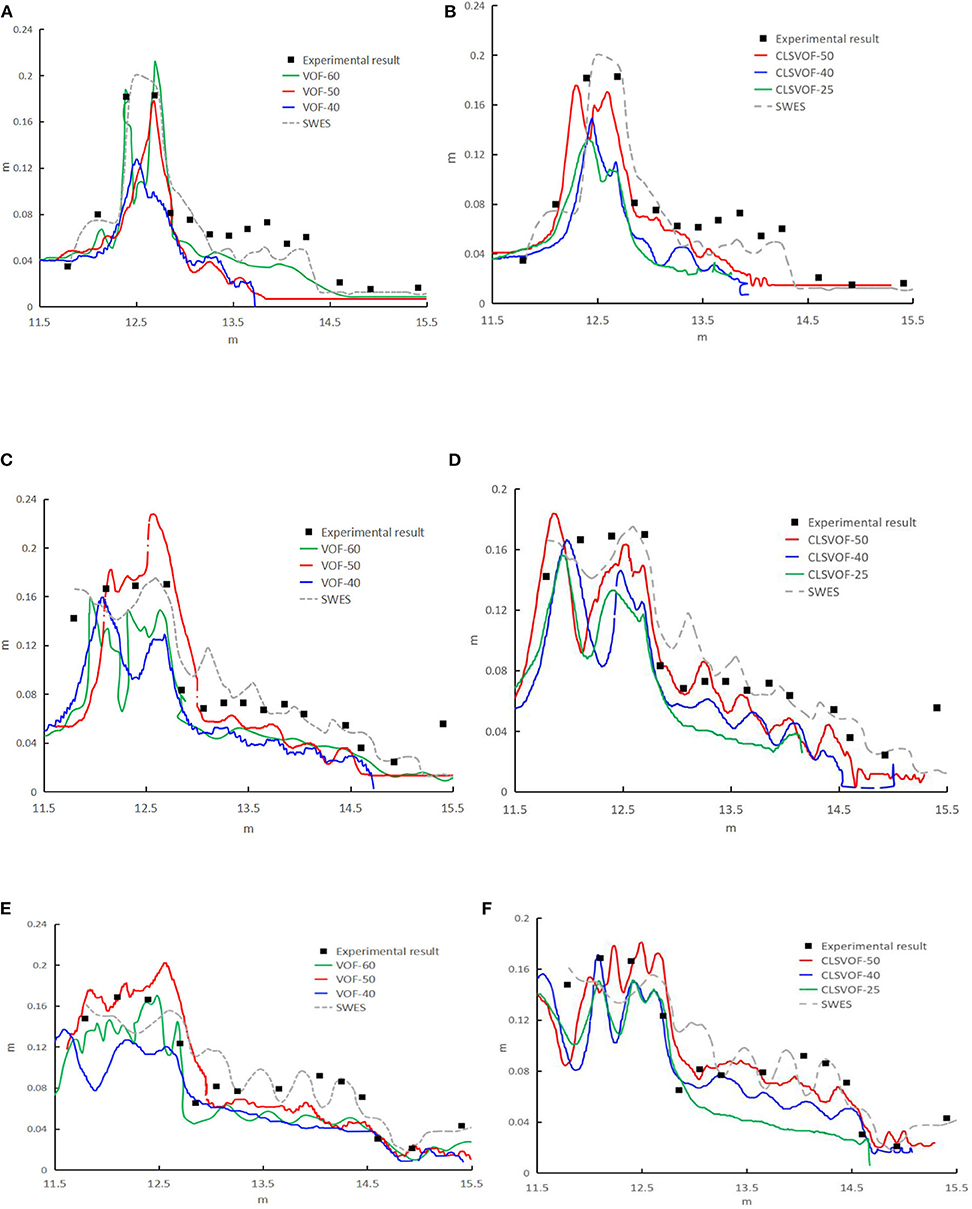
Figure 2. The free surface profile at different time in Section B-B (A,B) t = 4 s; (C,D) t = 5 s; (E,F) t = 6 s.

TABLE 1

Table 1. Numerical error estimation.

Free Surface Evolution and Flow Characteristic

After ensuring that the grids are independent of water level, the time-evolving free surface of the flood–building interaction at the grid interval h = 50 is carried out for free surface evolution. Figure 3 shows the time evolution of the free surface at several instants where results of fine grids are proved. The flooding wave approximately touches the buildings on time t = 2.5 s. The run-up jet will break up as Figure 3B shows and start to detach from the vertical wall overturning backward as Figure 3C shows, when it reaches the maximum elevation under the acceleration of gravity. In Figure 3D, the falling jet then collapses onto the water surface of the incoming dam-break wave. New surges, which are created by the spattering of the plunging jet on the back flow, that rebound on the water surface cause a strong free surface mixing with air entrainment as shown in Figure 3E. In Figure 3F, flood wave (secondary wave) propagate in the upstream at gradually between t = 5.0 and 6.0 s.

FIGURE 3

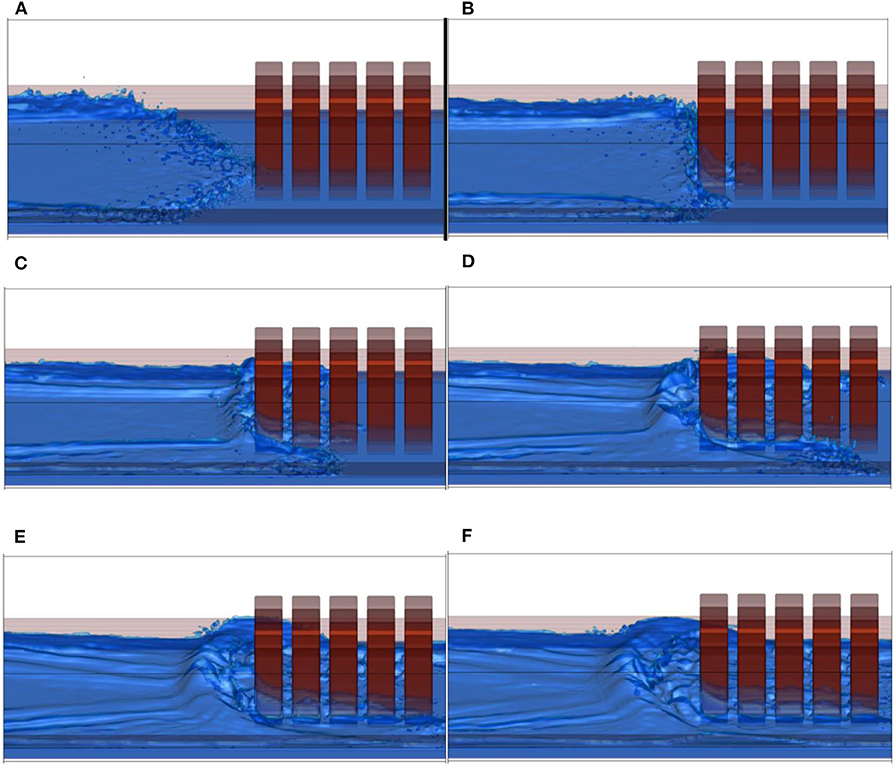
Figure 3. Time evolution of the free surface at different times. (A) t = 2.5 s; (B) t = 3.0 s; (C) t = 3.5 s; (D) t = 4.0 s; (E) t = 4.5 s; (F) t = 5.0 s.

Figures 4, 5 show the temporal evolution of water depth and velocity magnitude calculated in the plane using VOF/IB methods. It can be indicated that the flood is incapable to flow out rapidly because of the hurdle of multiple buildings, which raises the water level and the flow speed at both sides of the wall. A symmetric and steady wake of velocity magnitude is not demonstrated behind the buildings because of the flow becoming unstable at high Reynolds number and toward being inertial force-dominated. The x–z plane at Section B-B (see Figure 2) is compared with the velocity fields diagram of CLSVOF/IB and VOF/IB methods. As Figures 6A,B show, the velocity fields experience the most drastic change where the flood first impacts the building at around x = 12m. The velocity of the flow intruding into the buildings changes quite significantly. After x = 12m, the velocity attenuates greatly because of the buildings in the front.

FIGURE 4

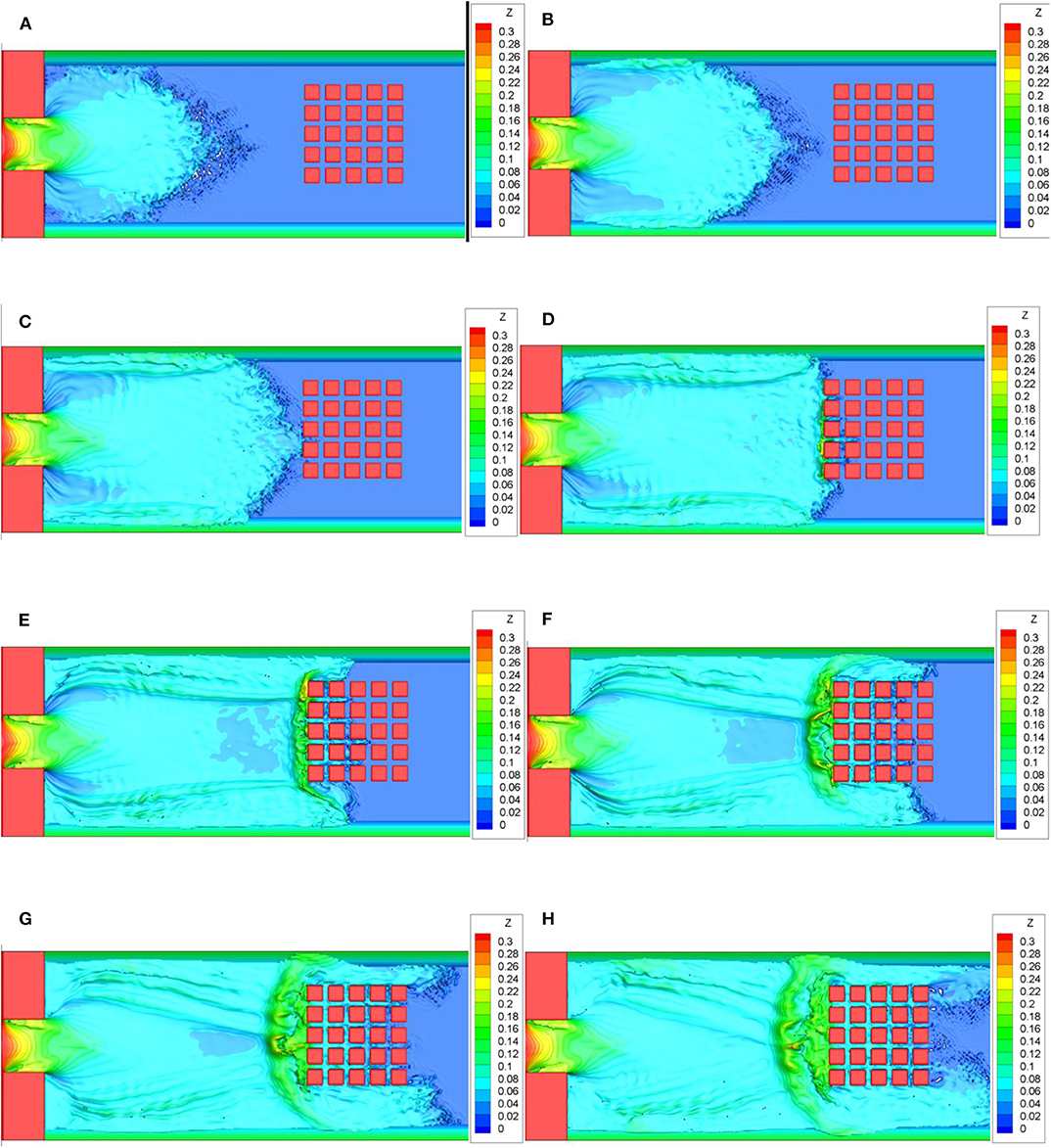
Figure 4. Water depth of the dam-break flow in the x − y plane. (A) t = 1.5 s; (B) t = 2.0 s; (C) t = 2.5 s; (D) t = 3.0 s; (E) t = 3.5 s; (F) t = 4.0 s; (G) t = 4.5 s; (H) t = 5.0 s. The unit is set as m.

FIGURE 5

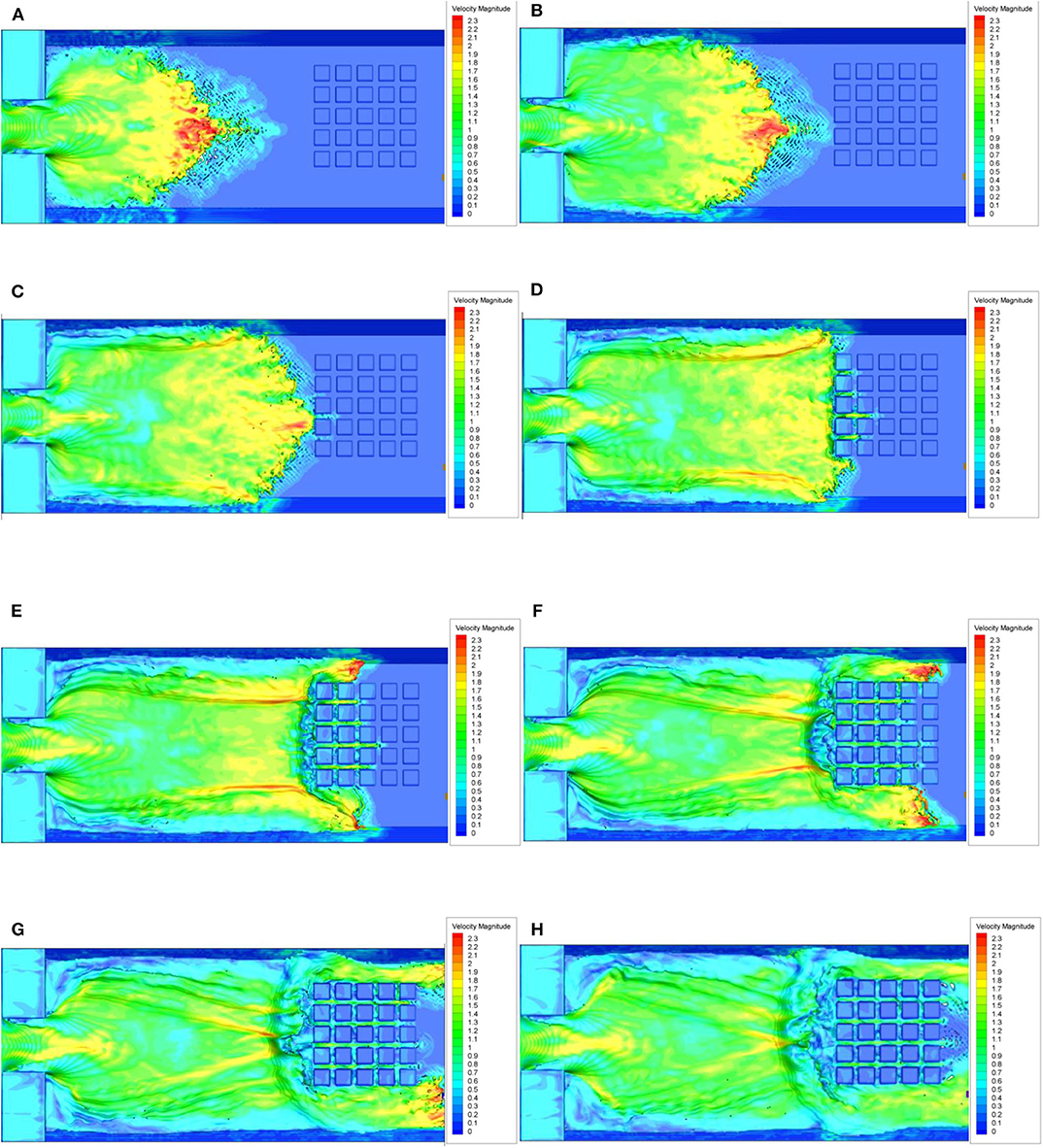
Figure 5. Velocity magnitude of the dam-break flow in the x − y plane. (A) t = 1.5 s; (B) t = 2.0 s; (C) t = 2.5 s; (D) t = 3.0 s; (E) t = 3.5 s; (F) t = 4.0 s; (G) t = 4.5s; (H) t = 5.0 s. The unit is set as m/s.

FIGURE 6

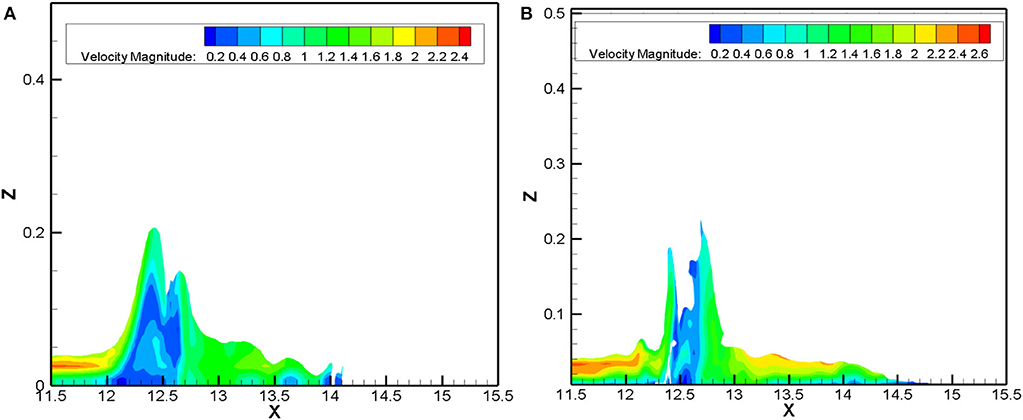
Figure 6. Velocity magnitude of the dam-break flow in the x − z plane. (A) t = 4.0 s (CLSVOF/IB method); (B) t = 4.0 s (VOF/IB method). The unit is set as m/s.

Comparison of Efficiency, Mass Conservation, and Free Surface Evolution

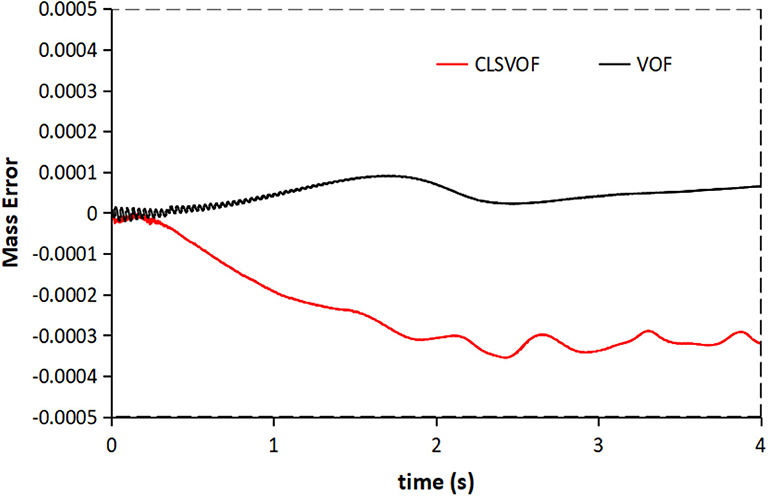
From Table 2, we can notice that VOF/IB is more efficient than CLSVOF/IB because there is no calculation time spent in solving the level set in the solver of VOF/IB. Compared with other solvers in the aspect of serial computing time, we have come to the conclusion that VOF/IB solver possesses the advantage of saving time. A comparison between the present VOF/IB method and the CLSVOF/IB method in mass conservation shows that both methods perform quite well as Figure 7 shows.

TABLE 2

Table 2. CPU time for different methods until t = 4.0 s.

FIGURE 7

Figure 7. Mass conservation against times for both methods.

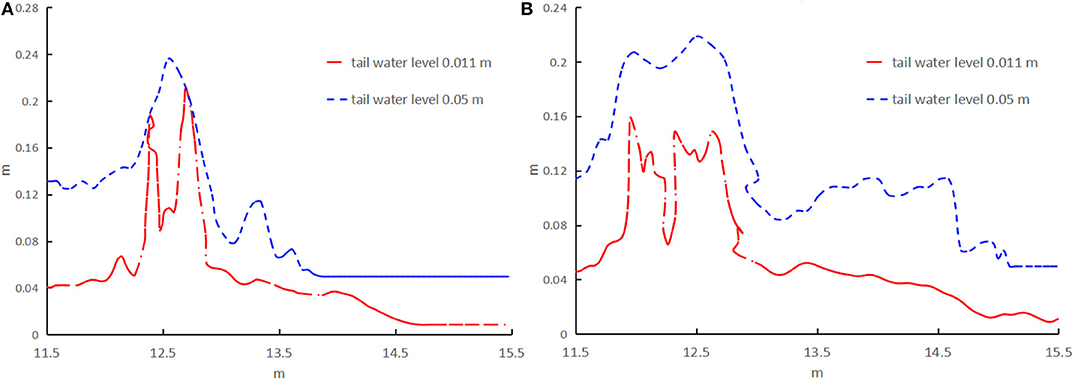
Figure 8 shows the free surface at (a) t = 4 s and (b) t = 5 s. The downstream water depth (or tailwater level) is 0.05 m in the blue line and 0.011 m in the red line. Because of the greater resistance imposed by the larger water depth in the blue line, the discharged water moves slower in the blue line than in the red line. For example, at t = 4 s as shown in Figure 8A, the front moves to 13.7 m in the blue line and 14.6 m in the red line. This implies that the front velocity decrease with increasing downstream water depth.

FIGURE 8

Figure 8. The free surface profile at different times: (A) t = 4.0 s; (B) t = 5.0 s.

The evolution of x-force acting on the buildings is plotted in Figure 9A. The VOF/IB results with the finest spatial resolution are almost identical to those obtained with CLSVOF/IB method for up to t = 4.0 s. However, we found that the VOF/IB method overestimates the peak force slightly at t = 4.0 s. At that time, the flow has already hit the right wall of the tank and, consequently, has generated several complex fluid structures with air entrapment. Two stages for the evolution of x-force acting on the buildings with different initial water depth in the downstream reservoir (i.e., different tailwater level) can be identified in Figure 9B. The first stage exists during t = 1~2 s before intrusion happens. During this stage, the water is discharged through the left of the dam, but the flow has not reached the downstream buildings, and the impacting force in the buildings is nearly zero. During the second stage t = 2~7 s, the discharge begins to intrude into the building from the left and flows around the buildings. The discharge calculated in the red line moves with a greater front velocity and enters the second stage earlier, but has a smaller impacting force in the buildings. Two reasons account for this phenomenon. First, a greater front velocity induces a larger viscous dissipation and kinematic energy loss. Second, the larger water depth difference makes it easier for flow to intrude into the buildings.

FIGURE 9

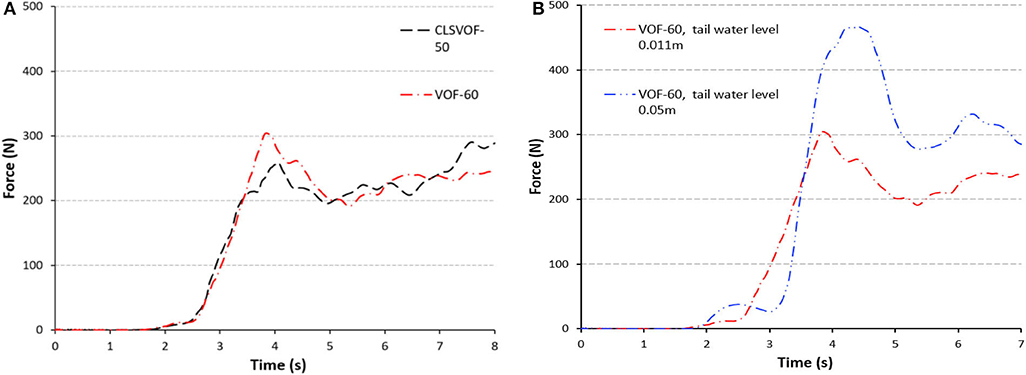
Figure 9. (A) Evolution of x-force acting on the buildings using CLSVOF/IB and VOF/IB methods. (B) Evolution of x-force acting on the buildings using VOF/IB method with different tail water level.

Concluding Remarks

Adopting a three-dimensional mathematical model, this paper exerts algebraic VOF (THINC/SW) method on free liquid surface tracking, which is simpler and more efficient than the traditional VOF method that needs interface reconstruction. In addition, to tackle liquid (flood) and solid (buildings) interface problems, this method is combined with IB method. The accuracy of the CLSVOF/IB method is higher than VOF/IB methods. However, the main idea of the paper is to develop a mathematical model with high computational efficiency and the ability to deal with wave breaking so that the matter of the dam-break flood with a larger kilometer scale can also be addressed. In other words, the VOF/IB method developed in this paper mainly aims to overcome the disadvantages of CLSVOF/IB (e.g., poor computational efficiency) and the shallow water models (e.g., inability to handle complex flow conditions). This paper first presents the VOF/IB method in the sequence of solving the VOF equation (Equation 1), and then it presents the momentum equation (Equation 4). While getting the CLSVOF/IB method, it needs to solve the VOF equation (Equation 1), the LS equation, and the momentum equation (Equation 4). The latter possesses a lower calculation efficiency on account of one more step to solve LS equations. Also, the CLSVOF/IB method is mainly applied to tackle the problem of surface tension (e.g., the bubble rising and water droplet collision). Also owing to LS equations included, this method can effectively calculate air bubbles or water droplets free liquid surface curvature. Without constantly considering surface tension concerning the dam-break flood problem, the issue of the dam-break flood is more suitable to be addressed by the VOF/IB method. Cases of irregular buildings can be predicted by the performed VOF/IB method, which induces the formation of wave breaking and wave reflections in flow behavior. However, in numerical simulation, fine mesh is needed to well-represent the irregular topography. Large computational domains are still attracted by SWE-based numerical models because of less computational efforts and time over DNS models.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

RA contributed conception and design of the study. CY and WM wrote the manuscript. YL organized the database.

Funding

This research was funded by National Key R&D Program of China (2016YFC0502207), National Natural Science Foundation of China (No. 51979178), Department of Science and Technology of Sichuan Province (No. 2019YJ0118), Fundamental Research Funds for the Central Universities (No. YJ201837), and Innovation spark project (No. SCUH0049).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Aureli, F., Dazzi, S., Maranzoni, A., Mignosa, P., and Vacondio, R. (2015). Experimental and numerical evaluation of the force due to the impact of a dam-break wave on a structure. Adv. Water Resour. 76, 29–42. doi: 10.1016/j.advwatres.2014.11.009

CrossRef Full Text | Google Scholar

Bahbah, C., Khalloufi, M., Larcher, A., Mesri, Y., Coupez, T., Valette, R., et al. (2019). Conservative and adaptive level-set method for the simulation of two-fluid flows. Comput. Fluids. 191:104223. doi: 10.1016/j.compfluid.2019.06.022

CrossRef Full Text | Google Scholar

Cao, X. Y., Ming, F. R., Zhang, A. M., and Tao, L. (2017). Multi-phase SPH modelling of air effect on the dynamic flooding of a damaged cabin. Comput. Fluids. 163, 7–19. doi: 10.1016/j.compfluid.2017.12.012

CrossRef Full Text | Google Scholar

Chang, T. J., Kao, H. M., Chang, K. H., and Hsu, M. H. (2011). Numerical simulation of shallow-water dam break flows in open channels using smoothed particle hydrodynamics. J. Hydrol. 408, 78–90. doi: 10.1016/j.jhydrol.2011.07.023

CrossRef Full Text | Google Scholar

Fourtakas, G., Dominguez, J. M., Vacondio, R., and Rogers, B. D. (2019). Local uniform stencil (LUST) boundary condition for arbitrary 3-D boundaries in parallel smoothed particle hydrodynamics (SPH) models. Comput. Fluids. 190, 346–361. doi: 10.1016/j.compfluid.2019.06.009

CrossRef Full Text | Google Scholar

Gu, Z. H., Wen, H. L., Yao, Y., and Yu, C. H. (2019). A volume of fluid method algorithm for simulation of surface tension dominant two-phase flows. Numer. Heat Transfer Part B 76, 1–17. doi: 10.1080/10407790.2019.1642048

CrossRef Full Text | Google Scholar

Gu, Z. H., Wen, H. L., Ye, S., An, R. D., and Yu, C. H. (2018b). Development of a mass-preserving level set redistancing algorithm for simulation of rising bubble. Numer Heat Transfer Part B. 74:699–727. doi: 10.1080/10407790.2018.1525157

CrossRef Full Text | Google Scholar

Gu, Z. H., Wen, H. L., Yu, C. H., and Sheu, T. W. H. (2018a). Interface-preserving level set method for simulating dam-break flows. J. Comput. Phys. 374, 249–280. doi: 10.1016/j.jcp.2018.07.057

CrossRef Full Text | Google Scholar

Guinot, V., Delenne, C., and Cappelaere, B. (2009). An approximate Riemann solver for sensitivity equations with discontinuous solutions. Adv. Water Resour. 32, 61–77. doi: 10.1016/j.advwatres.2008.10.002

CrossRef Full Text | Google Scholar

Guo, X. H., Rogers, B. D., Lind, S., and Stansby, P. K. (2018). New massively parallel scheme for Incompressible Smoothed Particle Hydrodynamics (ISPH) for highly nonlinear and distorted flow. Comput. Phys. Commun. 233, 16–28. doi: 10.1016/j.cpc.2018.06.006

CrossRef Full Text | Google Scholar

Harvie, D. J. E., and Fletcher, D. F. (2000). A new volume of fluid advection algorithm: the stream scheme. J. Comput. Phys. 162, 1–32. doi: 10.1006/jcph.2000.6510

CrossRef Full Text | Google Scholar

Harvie, D. J. E., and Fletcher, D. F. (2001). A new volume of fluid advection algorithm: the defined donating region scheme. Int. J. Numer. Methods 35, 151–172. doi: 10.1002/1097-0363(20010130)35:2<151::AID-FLD87>3.0.CO;2-4

CrossRef Full Text | Google Scholar

Hirt, C. W., and Nichols, B. D. (1981). Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 39, 201–225. doi: 10.1016/0021-9991(81)90145-5

CrossRef Full Text | Google Scholar

Hou, J. M., Simons, F., Mahgoub, M., and Hinkelmann, R. (2013). A robust well-balanced model on unstructured grids for shallow water flows with wetting and drying over complex topography. Comput. Comput. Methods Appl. Mech. Eng. 257, 126–149. doi: 10.1016/j.cma.2013.01.015

CrossRef Full Text | Google Scholar

Hu, K. C., Hsiao, S. C., Hwung, H. H., and Wu, T. R. (2012). Three-dimensional numerical modeling of the interaction of dam-break waves and porous media. Adv. Water Resour. 47, 14–30. doi: 10.1016/j.advwatres.2012.06.007

CrossRef Full Text | Google Scholar

Kurganov, A., and Petrova, G. (2007). A second-order well-balanced positivity preserving central-upwind scheme for the Saint-Venant system. Commun. Math. Sci. 5:133–160. doi: 10.4310/CMS.2007.v5.n1.a6

CrossRef Full Text | Google Scholar

Kurioka, S., and Dowling, D. R. (2009). Numerical simulation of free surface flows with the level set method using an extremely high-order accuracy WENO advection scheme. Int. J. Comut. Fluid Dyn. 23, 233–243. doi: 10.1080/10618560902776786

CrossRef Full Text | Google Scholar

Li, Q. (2016). Numerical simulation of melt filling process in complex mold cavity with insets using IB-CLSVOF method. Comput. Fluids. 132, 94–105. doi: 10.1016/j.compfluid.2016.04.005

CrossRef Full Text | Google Scholar

Li, Y. L., and Yu, C. H. (2019). Research on dam-break flow induced front wave impacting a vertical wall based on the CLSVOF and level set methods. Ocean Eng. 178, 442–462. doi: 10.1016/j.oceaneng.2019.02.064

CrossRef Full Text | Google Scholar

Liang, D., Falconer, R. A., and Lin, B. (2006). Comparison between TVD-MacCormack and ADI-type solvers of the shallow water equations. Adv. Water Resour. 29, 1833–1845. doi: 10.1016/j.advwatres.2006.01.005

CrossRef Full Text | Google Scholar

Liang, Q. H. (2011). Flood simulation using a well-balanced shallow flow model. J Hydraulic Eng.- ASCE 136, 669–675. doi: 10.1061/(ASCE)HY.1943-7900.0000219

CrossRef Full Text | Google Scholar

Meneveau, C., and Katz, J. (2000). Scale-invariance and turbulence models for large-eddy simulations. Annu. Rev. Fluid Mech. 32, 1–32. doi: 10.1146/annurev.fluid.32.1.1

CrossRef Full Text | Google Scholar

Monteiro, L. R., Lucchese, L. V., and Schettini, E. B. C. (2019). Comparison between hydrostatic and total pressure simulations of dam-break flows. J. Hydraulic Res. doi: 10.1080/00221686.2019.1671509. [Epub ahead of print].

CrossRef Full Text | Google Scholar

Noh, W. F., and Woodward, P. (1976). “SLIC (simple line interface calculation),” in Proceedings of the Fifth International Conference on Numerical Methods in Fluid Dynamics, 5th, Enschede, Netherlands. (Berlin; New York, NY: Springer-Verlag), 330–340. doi: 10.1007/3-540-08004-X_336

CrossRef Full Text | Google Scholar

Olsson, E., Kreiss, G., and Zahedi, S. (2007). A conservative level set method for two phase flow II. J. Comput. Phys. 225, 785–807. doi: 10.1016/j.jcp.2006.12.027

CrossRef Full Text | Google Scholar

Osher, S., and Sethian, J. A. (1988). Fronts propagating with curvature dependent speed: algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 79, 12–49. doi: 10.1016/0021-9991(88)90002-2

CrossRef Full Text | Google Scholar

Sanders, B. F. (2001). High-resolution and non-oscillatory solution of the St. Venant equations in non-rectangular and non-prismatic channels. J Hydraulic Res. 39, 321–330. doi: 10.1080/00221680109499835

CrossRef Full Text | Google Scholar

Sanders, B. F., Schubert, J. E., and Gallegos, H. A. (2008). Integral formulation of shallow-water equations with anisotropic porosity for urban flood modeling. J. Hydrol. 362, 19–38. doi: 10.1016/j.jhydrol.2008.08.009

CrossRef Full Text | Google Scholar

Savic, L. J., and Holly, F. M. (1993). Dambreak flood waves computed by modified Godunov method. J. Hydraulic Res. 31, 187–204. doi: 10.1080/00221689309498844

CrossRef Full Text | Google Scholar

Schubert, J. E., and Sanders, B. F. (2012). Building treatments for urban flood inundation models and implications for predictive skill and modeling efficiency. Adv. Water Resour. 41, 49–64. doi: 10.1016/j.advwatres.2012.02.012

CrossRef Full Text | Google Scholar

Soares-Frazao, S., Lhomme, J., Guinot, V., and Zech, Y. (2008). Two-dimensional shallow-water model with porosity for urban flood modelling. J. Hydraulic Res. 46, 45–64. doi: 10.1080/00221686.2008.9521842

CrossRef Full Text | Google Scholar

Soares-Frazão, S., and Zech, Y. (2008). Dam-break flow through an idealised city. J Hydraulic Res. 46, 648–658. doi: 10.3826/jhr.2008.3164

CrossRef Full Text | Google Scholar

Song, L. X., Zhou, J. Z., Guo, J., Zou, Q., and Liu, Y. (2011). A robust well-balanced finite volume model for shallow water flows with wetting and drying over irregular terrain. Adv. Water Resour. 34, 915–932. doi: 10.1016/j.advwatres.2011.04.017

CrossRef Full Text | Google Scholar

Sun, D., and Tao, W. (2010). A coupled volume-of-fluid and level set (VOSET) method for computing incompressible two-phase flows. Int. J. Heat Mass Transf. 53, 645–655. doi: 10.1016/j.ijheatmasstransfer.2009.10.030

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, T., Li, H., Feng, Y., and Shi, D. (2013). A coupled volume-of-fluid and level set (VOSET) method on dynamically adaptive quadtree grids. Int. J. Heat Mass Transf. 67, 70–73. doi: 10.1016/j.ijheatmasstransfer.2013.08.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z., Yang, J., and Stern, F. (2012). A new volume-of-fluid method with a constructed distance function on general structured grids. J. Comput. Phys. 231, 3703–3722. doi: 10.1016/j.jcp.2012.01.022

CrossRef Full Text | Google Scholar

Wu, W. M. (2008). Computational River Dynamics. London: Taylor & Francis Ltd. doi: 10.4324/9780203938485

CrossRef Full Text | Google Scholar

Xiao, F., Honma, Y., and kono, T. (2005). A simple algebraic interface capturing scheme using hyperbolic tangent function. Int. J. Numer. Methods Fluids. 48, 1023–1040. doi: 10.1002/fld.975

CrossRef Full Text | Google Scholar

Xiao, F., Ii, S., and Chen, C. (2011). Revisit to the THINC scheme: a simple algebraic VOF algorithm. J. Comput. Phys. 230, 7086–7092. doi: 10.1016/j.jcp.2011.06.012

CrossRef Full Text | Google Scholar

Yang, J., and Stern, F. (2009). Sharp interface immersed-boundary/level-set method for wave-body interactions. J. Comput. Phys. 228, 6590–6616. doi: 10.1016/j.jcp.2009.05.047

CrossRef Full Text | Google Scholar

Ying, X., Khan, A. A., and Wang, S. Y. (2004). Upwind conservative scheme for the Saint Venant equations. J Hydraulic Eng-ASCE 130, 977–987. doi: 10.1061/(ASCE)0733-9429(2004)130:10(977)

CrossRef Full Text | Google Scholar

Yokoi, K. (2007). Efficient implementation of THINC scheme: a simple and practical smoothed VOF algorithm. J. Comput. Phys. 226, 1985–2002. doi: 10.1016/j.jcp.2007.06.020

CrossRef Full Text | Google Scholar

Yu, C. H., Wen, H. L., Gu, Z. H., and An, R. D. (2019). Numerical simulation of dam-break flow impacting a stationary obstacle by a CLSVOF/IB method. Commun. Nonlinear Sci. Numer. Simul. 79:104934. doi: 10.1016/j.cnsns.2019.104934

CrossRef Full Text | Google Scholar

Zeng, L., Luo, Z. L., Chen, B., Yang, Z. F., Li, Z., Lin, W. X., et al. (2010). Numerical analysis of a lock-release oil slick. Commun. Nonlinear Sci. Numerical. Simulat. 15, 2222–2230. doi: 10.1016/j.cnsns.2009.08.023

CrossRef Full Text | Google Scholar

Zhang, C., Lin, N., Tang, Y., and Zhao, C. (2014). A sharp interface immersed boundary/VOF model coupled with wave generating and absorbing options for wave-structure interaction. Comput. Fluids. 89, 214–231. doi: 10.1016/j.compfluid.2013.11.004

CrossRef Full Text | Google Scholar

Zhang, T., Peng, L., and Feng, P. (2018). Evaluation of a 3D unstructured-mesh finite element model for dam-break floods. Comput. Fluids. 160, 64–77. doi: 10.1016/j.compfluid.2017.10.013

CrossRef Full Text | Google Scholar

Zhang, Y., Zou, Q., Greaves, D., Reeve, D., Hunt-Raby, A., Graham, D., et al. (2010). A level set immersed boundary method for water entry and exit. Commun. Comput. Phys. 8, 265–288. doi: 10.4208/cicp.060709.060110a

CrossRef Full Text | Google Scholar