Investigation of Hilbert–Huang Transform and Fourier Transform for Horizontal-to-Vertical Spectral Ratio Analysis: Understanding the Shallow Structure in Mataram City, Lombok, Indonesia

Introduction

The evaluation of site-effect at a particular location using microtremor recordings was first introduced by Kanai (1957). The method was improved by Nogoshi and Igarashi (1971) and is recognized by the term Horizontal-to-Vertical Spectral Ratio (HVSR), which was popularized by Nakamura (1989). Although the theory behind it is still debatable, this method is widely used nowadays especially in earthquake hazard assessment because of its robustness and practicality. The original paper from Nakamura (1989) explained that HVSR is related to the resonance of S-wave in soft sedimentary layer with minor influence of surface wave. On the other hand, Bard (1999) preferred that HVSR is related to the surface wave, i.e., the ellipticity of the Rayleigh wave. The alternative physical interpretations of the HVSR were discussed by several authors depending on the analyzed wave (Bonnefoy-Claudet et al., 2006; Albarello and Lunedei, 2010; Sánchez-Sesma et al., 2011; Oubaiche et al., 2016).

The basic assumption used in this method is that the H/V value in the bedrock is equal to one because the particle movement in the bedrock is assumed to be the same horizontally and vertically. Based on this assumption, one can extract information about the impedance contrast beneath the surface by examining the peak location in the HVSR curve. One of the earliest methods of estimating the depth of the impedance contrast is a frequency-depth function derived from the regression of borehole data (Ibs-von Seht and Wohlenberg, 1999). The frequency-depth function proposed by Ibs-von Seht and Wohlenberg (1999) is defined as:

$$m=a{f}^b(1)$$

where f is the frequency of the main peak in the HVSR curve (in Hz) and m is the depth of the main impedance contrast (in m). a and b are the coefficients obtained through the regression of the pair of the frequency of the main peak in the HVSR curve and the observed depth of the main impedance contrast from the borehole data.

Inversion techniques of HVSR curves as an effort to estimate not only the depth of the impedance contrast but also the subsurface elastic parameters (e.g., P-wave and S-wave velocity) were developed in several studies (Bignardi et al., 2016; García-Jerez et al., 2016). Bignardi et al. (2016) used the same forward modeling routine from Herak (2008) which calculates the amplification spectrum of P- and S-waves under the assumption of vertically incident body waves on layered media to approximate the HVSR curve as follows:

$$HVSR(f)=\frac{AM{P}_S(f)}{AM{P}_S(f)}(2)$$

where AMP_P(f) and AMP_S(f) are the amplification spectra of P- and S-waves, respectively. Meanwhile, García-Jerez et al. (2016) used the same layered media representation but under the assumption of 3D-diffuse vector field of ambient noise established within the media. Research regarding the development of methods to estimate the depth of the impedance contrast is still ongoing, most are using various techniques of geophysical inversion. For example, Parolai et al. (2019) combined joint inversion of the HVSR curve and microtremor array measurement with various fitting techniques to reconstruct the subsurface structure in Almaty Basin, Kazakhstan. Büyük et al. (2020) used joint inversion of Rayleigh wave dispersion and HVSR with Pareto-based multiobjective particle swarm optimization to obtain Vs profile in both synthetic and field data of Bursa Basin in Turkey. Kumar and Mahajan (2020) provided a new empirical relationship of resonance frequency and pseudo-depth for Kangra Valley, India derived from joint inversion of HVSR curves and multichannel simulation with one receiver (MSOR) technique. In this study, we combine the application of Hilbert–Huang Transform (HHT) to remove the local noises in HVSR curves with the inversion technique developed by Bignardi et al. (2016) to obtain the subsurface elastic parameters. The combination of the powerful tool of the HHT and the dynamicity of the inversion technique should improve the inversion result as presented in this study.

The concept of the HVSR method is quite simple. Nakamura (1989) introduced the concept that the transfer function of a site can be calculated by taking the ratio of the frequency spectrum of the horizontal component of a microtremor recording to its vertical component. The original method uses a Fourier Transform to obtain the frequency spectrum of both components. However, Fourier Transforms, as described by Bowman and Lees (2013), assume that a time series extends from positive infinity to negative infinity (stationarity) and consists of a linear superposition of sinusoids (linearity), conditions that are rarely even impossible to be found in geophysical signals. Enforcing the use of Fourier Transform to non-stationary and non-linear signals could lead to the reduction of time or frequency resolution and the appearance of spurious harmonic waves. Bowman and Lees (2013) provided exhaustive explanation to this in his study. He compared the utilization of the Fourier Transform and the HHT on both synthetic and real data. The study concluded that HHT is outperformed Fourier Transform when handling non-stationary and non-linear signals. This is because Fourier Transform uses combination of sinusoidal-basis function in representing the signal, which can be troubling when processing non-sinusoidal signal. On the other hand, HHT uses an adaptive signal decomposition method that chooses the basis function from the properties of each individual signal, which in the end can prevent the bleeding of the spectral energy that can reduce the time-frequency resolution.

Hilbert–Huang Transform can be used to overcome the non-stationary and non-linearity problems of a signal for time-frequency analysis. Huang et al. (1998) shows that the Hilbert Spectrum obtained from HHT is more meaningful than the Fourier Spectrum when analyzing the frequency spectrum of a non-stationary signal. In terms of HVSR processing and analysis, Liu et al. (2015) shows that HHT is a powerful tool that can be used to enhance microtremor data. He demonstrates the usage of HHT to eliminate transient and monochromatic noise, which is common in microtremor data. It can also be used as an alternative approach to obtain the HVSR curve by utilizing the Hilbert-Huang Spectrum instead of the conventional Fourier Spectrum.

The utilization of HHT, rather than Fast Fourier Transform (FFT, a method to obtain Fourier spectrum), can give higher resolutions in HVSR analysis and can reduce uncertainties in estimations of sediment thickness, as demonstrated by Liu et al. (2015). However, the robustness and effectiveness of this method in obtaining a subsurface structure through the inversion process of HVSR curves have not yet proven. In this study, we compare the HVSR curve obtained by the conventional FFT method and the HHT method, while also utilizing the HHT to remove local noises. We apply the inversion process to both curves and compare the result to results from a previous study. The resulting subsurface structure is then interpreted based on the existing geological information.

In this study, we apply the HVSR Method to obtain the subsurface structure beneath Mataram City, Lombok Island, Indonesia. This area is unique because of the series of destructive earthquake events that took place there in 2018 as well as the complexity of its geological settings. According to data from the Meteorology, Climatology and Geophysics Agency of Indonesia (BMKG), 1,973 earthquakes were recorded (M > 3) in Lombok Island in August 2018, with four large magnitude earthquakes of M 6.4 (July 29, 2018), M 7.0 (August 5, 2018), M 6.3, and M 6.9 (August 19, 2018). If an earthquake occurred on Lombok Island, Mataram City, the biggest city on the island, has the potential to suffer greatly from the amplification of seismic waves as its lithology is covered by an alluvium deposit, a very soft sedimentary layer. When the underlying layer is a much harder rock, it can create a high impedance contrast; propagating waves can then be trapped inside the softer layer, causing multiple reflections and leading to amplification of those waves by the interference process.

Geological Setting

The results of the geological mapping conducted by Wafid et al. (2014) concluded that there were seven rock groups on the island of Lombok: alluvium deposit groups, inseparable volcanic rock groups, pumice tuff groups, breccia and lava groups, limestone groups, sandstone groups, and igneous rock groups. The northern part of Lombok Island is dominated by inseparable volcanic rock groups, while the southern part of the island is dominated by breccia and lava groups. There are accumulations of alluvium deposits in the western (the vicinity of Mataram City) and the eastern part of Lombok Island.

Mataram City is a lowland area that is occupied by alluvium deposits, consisting of pebble, granule, sand, clay, peat, and coral fragments (Mangga et al., 1994). This rock is the youngest in Mataram City. The hills that surround Mataram City in the northern, eastern, and southern areas are tertiary-aged rocks known as the Lekopiko Formation, which consist of pumiceous tuff, lahar breccia, and lava. The Lekopiko Formation overlaps the Kalibabak Formation which consists of breccias and lava. Beneath the Kalibabak Formation is the Kalipalung Formation, which consists of an alternation of calcareous breccia and lava. The geological map of Mataram City along with the tectonic environment and historical earthquakes in the region can be seen in Figure 1.

FIGURE 1

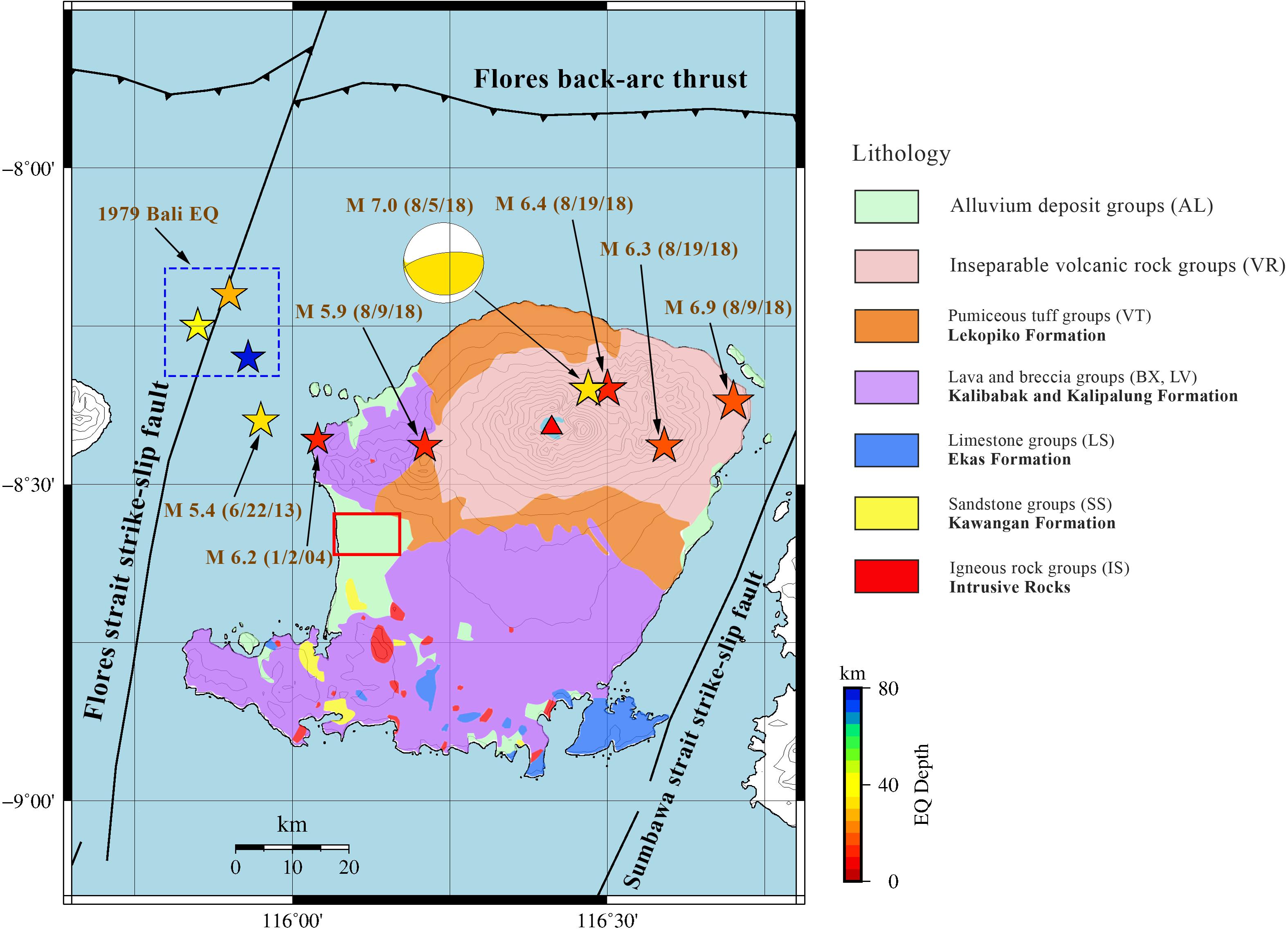
Figure 1. Geological map of Lombok Island, Indonesia (modified from Mangga et al., 1994; Wafid et al., 2014); the study area is marked by a red square. The red triangle represents volcano in the region. The black lines represent active fault in the region obtained from Irsyam et al. (2017). The stars represent significant earthquakes that occurred from 1979 to 2018, obtained from Supartoyo et al. (2014) and Badan Meteorologi Klimatologi dan Geofisika (Badan Meteorologi Klimatologi dan Geofisika [BMKG], 2019) with the color of each star indicates the depth of the earthquake according to the color scale in the bottom right of the map. The focal mechanism of the 5th August 2018 earthquake is taken from Global CMT catalog (Dziewonski et al., 1981; Ekström et al., 2012).

Lombok Island is located in a complex tectonic setting. There are four active faults that surround the island: the Flores back-arc thrust fault in the north, the Indo-Australian subduction in the south, the strike-slip fault of the Lombok Strait in the west, and the strike-slip fault of the Sumbawa Strait in the east (Irsyam et al., 2017). Recorded significant earthquakes near Mataram City, Lombok Island, occurred in 1979. There were three earthquakes, known as Bali earthquake, that caused quite devastating effect, occurring on May 21, 1979 with M 5.7 (Badan Meteorologi Klimatologi dan Geofisika [BMKG], 2019), May 30, 1979 with M 6.1 (Supartoyo et al., 2014; Badan Meteorologi Klimatologi dan Geofisika [BMKG], 2019), and October 20, 1979 with M 6.0 (Badan Meteorologi Klimatologi dan Geofisika [BMKG], 2019). In the 21st century, significant earthquakes near the region were recorded on January 2, 2004 with M 6.2 and June 22, 2013 with M 5.4 (Supartoyo et al., 2014) (Figure 1).

The 2018 earthquake series that shook Lombok Island was mainly driven by the movement of the Flores back-arc thrust fault and the Indo-Australian subduction. There are several strong earthquakes that occurred at a relatively close time, that are with magnitude of M 7.0 (August 5, 2018), M 6.9 and M 5.9 (August 9, 2018), and M 6.4 and M 6.3 (August 19, 2018) (Figure 1). This is possible because of the complex structure beneath the Lombok Island. McCaffrey and Nabelek (1987) showed the evidence of the existence of Flores oceanic crust located in the southern region of Flores back-arc thrust fault that subduct beneath Lombok Island. The hypocenters of the earthquake series in 2018 are distributed along the northern part of Lombok Island with east-west trend, but located to the south of the Flores back-arc thrust fault. Using the mainshock’s hypocenter distribution, the focal mechanism of the large earthquakes, and the aftershocks distribution, Sasmi et al. (2020) proposed that the earthquake series is generated by the movement between the subducting Flores oceanic crust with the overriding Lombok Island. The interaction between the two creates an east-west trending fault beneath the northern part of Lombok Island with thrust fault mechanism, adjacent to the Flores back-arc thrust fault. The study by Sasmi et al. (2020) also proposed that this structure of the Flores oceanic crust is segmented, and the failure of each successive segment triggers the next segment to fail, creating a large earthquake shortly afterward.

According to Robiana et al. (2018), the earthquake that occurred on August 5, 2018 and August 19, 2018 reached a maximum intensity of VIII-IX MMI (Modified Mercalli Intensity). BMKG and the National Disaster Management Agency of Indonesia (BNPB) reported that the region suffering the greatest damage was the northern region of Lombok Island, with 496 deaths and 178,122 refugees (as of April 2019). Even though Mataram City is located in the western region of Lombok Island, the seismicity near this region was able to create severe destruction. Sasmi et al. (2020) suggest that the Flores oceanic crust is divided into three segments, and the northwestern segment, which is relatively closer to Mataram City, has the largest magnitude of M 5.9 (August 9, 2018). This is relatively small compared to the M 7.0 earthquake (August 5, 2018) in the northern segment and M 6.9 earthquake (August 19, 2018) in the northeastern segment but does not rule out the possibility of creating an equally large, or even larger, magnitude earthquake in the future, considering the complex structure beneath the Lombok Island.

Data and Method

Data

We conducted a microtremor survey in Mataram City from August 8-12, 2019. The survey was conducted at 56 points, whose distribution can be seen in Figure 2, with an average spacing of 1 km. Data was collected using the three-component accelerometer Geotiny! Compact Digital Seismometer which has a measurement duration of ±60 min per point and a sampling rate of 100 Hz. The recording duration is adjusted based on the smallest dominant frequency target to be identified (Bard, 2004). Data was collected each morning until the afternoon (8:00 to 18:00 local time, GMT+ 8 h) for safety reasons. The measurement points were done as far as possible from the sources of noise. Placement of the equipment was attempted on hard and stable soil, according to guidelines from the Site Effects Assessment Using Ambient Excitations (SESAME). Another procedure undertaken when collecting data was filling in observation reports of probable noise contaminant around the measurement point as field notes. Some examples of microtremor data collection activities in Mataram City can be seen in Figure 2.

FIGURE 2

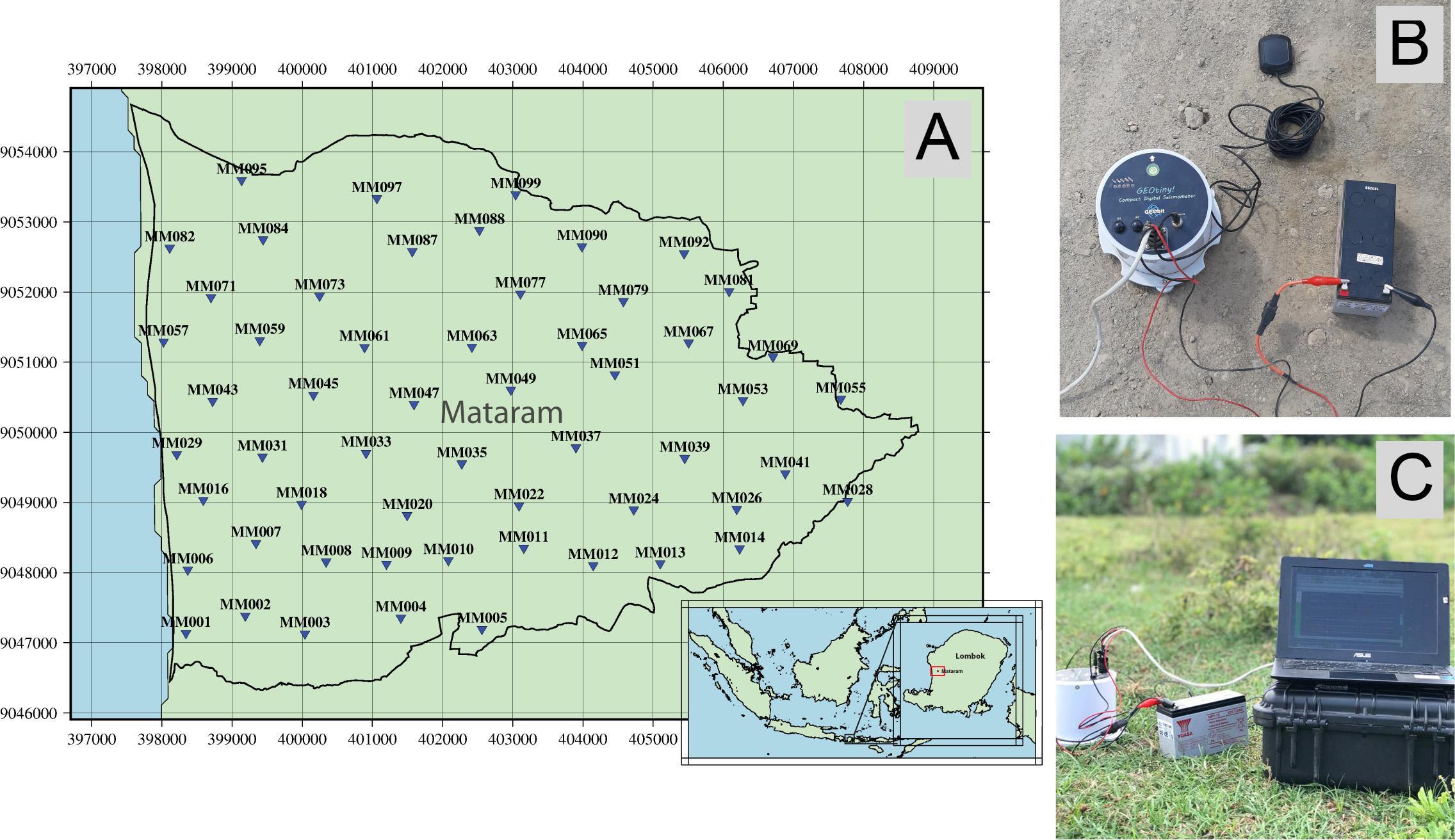
Figure 2. (A) Map showing the location of 56 microtremor measurements marked by blue inverted triangles. The inset shows a map of Indonesia and Lombok Island. (B) Instruments used in microtremor data collection at MM077. (C) Installation and setup of microtremor data collection.

Our study area is the capital of Nusa Tenggara Barat Province, which is a densely populated area. Therefore, we had to anticipate the introduction of man-made noise to the data, even more so knowing that data were collected during the day. After careful examination of the frequency spectrum of all data, we found that some stations were contaminated by a monochromatic noise source. Figure 3 shows the frequency spectrum of some examples of these stations. The time of the data acquisition of Station MM029 is at 11:00 local time and for Station MM099 is at 15:30 local time. In both vertical and horizontal component spectra, it was easy to observe narrow and sharp peaks at frequencies ±8 Hz and ±12 Hz on Station MM029 and ±9 Hz and ±13 Hz on Station MM099. The narrow and sharp peaks that were found in all three components are an indication of monochromatic noise due to man-made noise/machinery (Bard, 2004). We did further evaluation of these stations considering their locations and the observation reports and found that these stations are within the proximity of industrial areas and housing construction.

FIGURE 3

Figure 3. (A) The spectrum of the vertical and horizontal components at Station MM029. (B) The spectrum of the vertical and horizontal components at Station MM099. The red line represents the vertical component spectrum, while the green and blue lines represent the horizontal NS and EW component spectrums, respectively.

Moreover, analysis of variations of the frequency spectrum in Mataram City was also carried out for 24 h. This analysis was intended to observe the difference in the frequency spectrum of the recordings during busy times and quiet times. Figure 4 shows the variations of the frequency spectrum for 24 h from recordings at basecamp, which was located near the city center. As can be seen in Figure 4, there is a significant difference in the amplitude of the frequency spectrum between busy times (09:00 to 21:00 local time) and quiet times (21:00 to 09:00 local time). The difference can easily be observed, especially at a higher frequency range (>1 Hz), where the amplitude of the spectrum at busy times is higher than at quiet times. This difference in higher frequency might be due to the introduction of transient noise (Liu et al., 2015) that was generated by human activities, such as footsteps, passing vehicles, etc. During busy times, these transient noise sources are more likely to be found, especially in densely populated areas.

FIGURE 4

Figure 4. Frequency spectrum for various times in Mataram City at the same location. The solid line represents quiet times and the dashed line represents busy times.

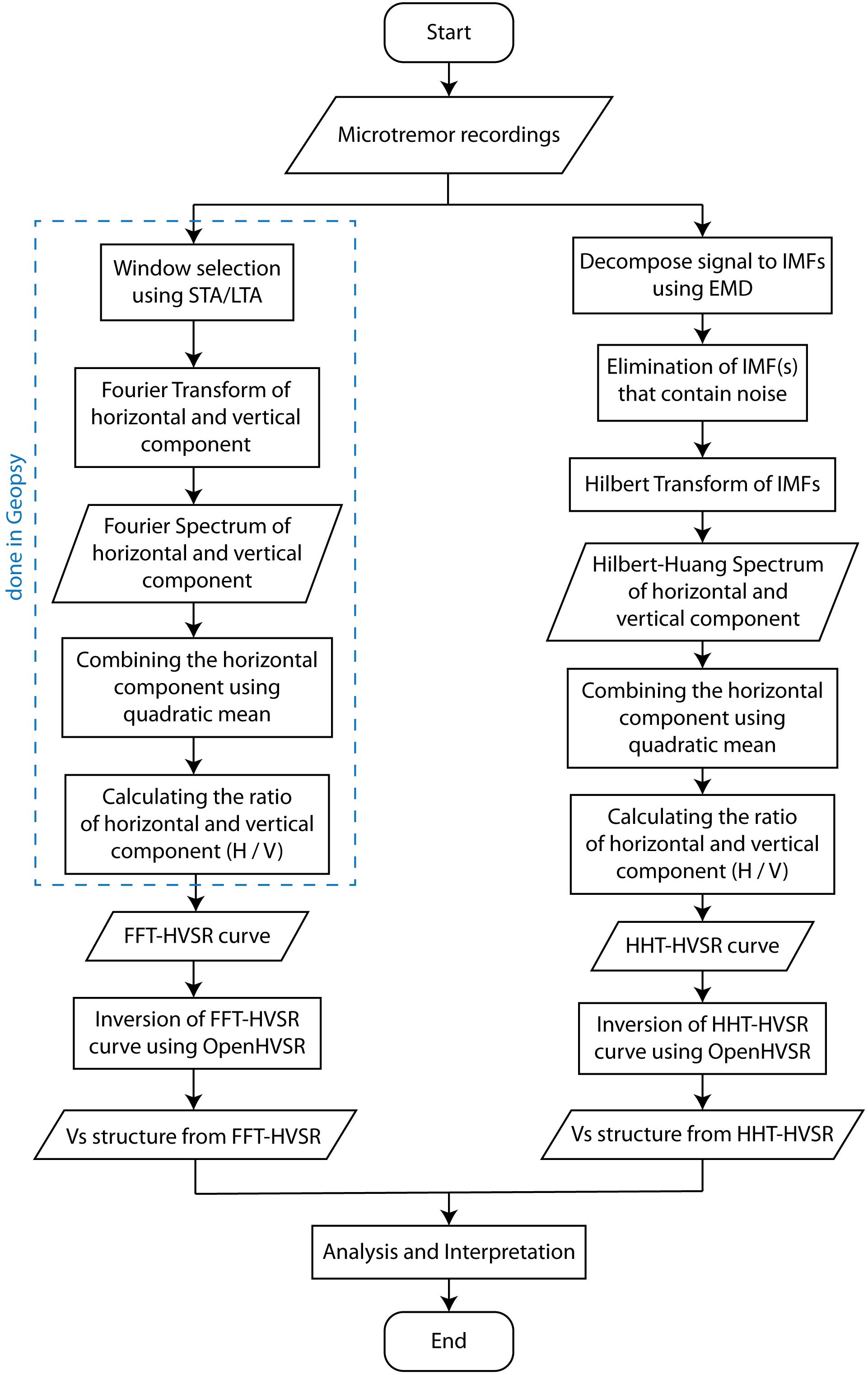
Only coherent noise from distant sources is useful when utilizing microtremor data to obtain information regarding geological structures near the surface (Liu et al., 2015). Therefore, there is a need to eliminate local noise in order to improve the quality of microtremor data, especially in urban areas, so that more reliable subsequent analyses can be obtained. In this study, we apply HHT to help eliminate transient and monochromatic noise in the microtremor recordings and increase the resolution in HVSR analysis, as demonstrated by Liu et al. (2015). These procedures will be explained in the following section. The flowchart of the processes done in this study is presented in Figure 5.

FIGURE 5

Figure 5. Flowchart of the processes done in this study.

FFT-HVSR Calculation

The Horizontal-to-Vertical Spectral Ratio Method was first used to analyze seismic risk in Japan (Nogoshi and Igarashi, 1971; Nakamura, 1989). The basic concept of this method is making a comparison between the spectrum of horizontal components and the spectrum of vertical components of a wave. Theoretically, the movement of the horizontal component particles will be greater than the movement of the vertical component particles in soft soil; whereas in hard soil both components (horizontal and vertical) will have the same value (Nakamura, 2008). The assumption used in this method is that the H/V value in bedrock is equal to one because the movement of the horizontal component particles and the movement of the vertical component particles in the bedrock are the same. This method is formulated in the following equation:

$$\mathit{HVSR}(f)/V=\frac{A_H(f)}{A_V(f)}(3)$$

where A_H(f) is the frequency spectrum in the horizontal component, and A_V(f) is the frequency spectrum in the vertical component. After obtaining the H/V value at each frequency, the HVSR curve can be obtained where the horizontal axis is the frequency and the vertical axis is the amplification factor (H/V).

The initial step in processing FFT-HVSR is to determine the length of the time window and STA/LTA parameters. The purpose of this step is to extract the signal at a certain period from all records that meet the specified criteria and to exclude the transient signals through this selection process. The length of the selected time window is 125 s, and the range of STA/LTA values is 0.5–2.0. In determining the value of the parameters, we followed the guideline from Site Effects Assessment Using Ambient Excitations (SESAME) by Bard (2004). The goal here is to extract the most stationary parts of ambient vibrations, i.e., the microtremor signal, and to avoid the transients associated with human activities.

The recommended maximum value of the STA/LTA as stated on the guideline is around 1.5 – 2 to select windows without any energetic transients. The guideline did not specify the recommended minimum value of the STA/LTA, but it did say that the minimum value of the STA/LTA must be determined to avoid vibration windows with abnormally low amplitudes. We tested several combination of minimum and maximum STA/LTA values and found that 0.5 – 2 is the best value to extract the required number of microtremor windows.

The time window is selected based on this criterion:

$$f_0>10/I_W(4)$$

Where f₀ is the H/V peak frequency (in Hz) and I_W is the window length (in s). We have to anticipate that the peak of the H/V is located at the lowest detectable frequency. Our instrument (Geotiny!) is able to detect signal with frequency as low as 0.1 Hz. Putting this value to the equation, the minimum value of the window length is 100 s. We increased the value to 125 s to anticipate edge effect.

The next step is carrying out the Fourier Transform Process for each signal in the selected time window. The purpose of this process is to change the signal from the time domain to the frequency domain. The two horizontal components (north-south and east-west) in the signal are then combined with the quadratic mean method, as shown in the following equation:

$$A_H(f)=\sqrt{\frac{A_{\mathit{NS}}^2(f)+A_{\mathit{EW}}^2(f)}{2}}(5)$$

where A_NS(f) and A_EW(f) are the amplitude spectrum of the horizontal component of the north-south and east-west directions, respectively. After the two horizontal components are combined, the calculation of the ratio of the horizontal component and the vertical component (H/V) can be calculated using Equation 3. The entire process is done automatically using Geopsy Software (Wathelet et al., 2020).

HHT-HVSR Calculation

The Hilbert-Huang Transformation (Hilbert-Huang Transform/HHT), developed by Huang et al. (1998), is a time-frequency analysis method that includes Empirical Mode Decomposition (EMD) and the Hilbert Spectrum to analyze signals. HHT is a reliable method that can be applied to non-linear and non-stationary signals which are commonly found in seismic signals. The final results from the HHT Method are the amplitude-frequency-time distribution, commonly known as the Hilbert-Huang Spectrum. The first step of HHT is EMD, which splits a complex signal into several Intrinsic Mode Functions (IMF). The IMF must meet the following conditions: (1) In all data, the number of extreme points and the number of intersection points at zero must be the same or have a difference of at most one. (2) At each point in the data, the mean value of the amplitude envelope must be zero (Huang and Wu, 2008). The IMF is obtained through the sifting process and iterations to obtain the signal with the shortest oscillation period. Hilbert Transform was then applied to each IMF to obtain instantaneous frequency and instantaneous amplitude. Hilbert Transform is expressed in the following equation:

$$y\left(t\right)=\frac{1}{\mathrm{\pi }}P\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\frac{x(\mathrm{\tau })}{t-\mathrm{\tau }}\mathit{d}\mathrm{\tau }(6)$$

where P is the Cauchy value for singular integrals and x represents the time function of the signal. Determining the y(t), instantaneous amplitude (a), and instantaneous phase (θ) can be done using the following equations:

$$a\left(t\right)={(x^2+y^2)}^{1/2}(7)$$

$$\mathrm{\theta }\left(t\right)={\tan }^{-1}\frac{y}{x}(8)$$

Instantaneous frequency (ω) can then be calculated using:

$$\mathrm{\omega }(t)=\frac{d\mathrm{\theta }}{\mathit{dt}}(9)$$

To obtain the marginal spectrum h(ω) from the Hilbert-Huang Spectrum (HHS), integration of the HHS function H(ω,t) with respect to time can be done. After obtaining the marginal spectrum for all components, the HVSR curve from HHT can be obtained using Equations 5 and 3.

The utilization of HHT to eliminate transient and monochromatic noise is done in the first procedure by obtaining the IMFs through the EMD process. The raw signal is separated into several IMFs based on the oscillation period, in which the first IMF has the shortest oscillation period (highest frequency), and the last IMF has the longest oscillation period (lowest frequency). Liu et al. (2015) states that transient noise is often associated with the IMF with the shortest oscillation period; i.e., the first IMF (IMF 1). Here we demonstrate the removal of IMF 1, which is assumed to be transient noise, from the raw signal, as shown in Figure 6. We calculated the frequency spectrum between 03:00 and 09:00 (local time) which represent quiet times and busy times, respectively. A significant amplitude difference can be seen at a frequency above 1 Hz. Through the removal of IMF 1, the spectrum at busy times agrees better with the spectrum at quiet times, especially at frequency > 5 Hz. Some discrepancies are still observed at frequency ranges 1-5 Hz, which might be related to other noise sources.

FIGURE 6

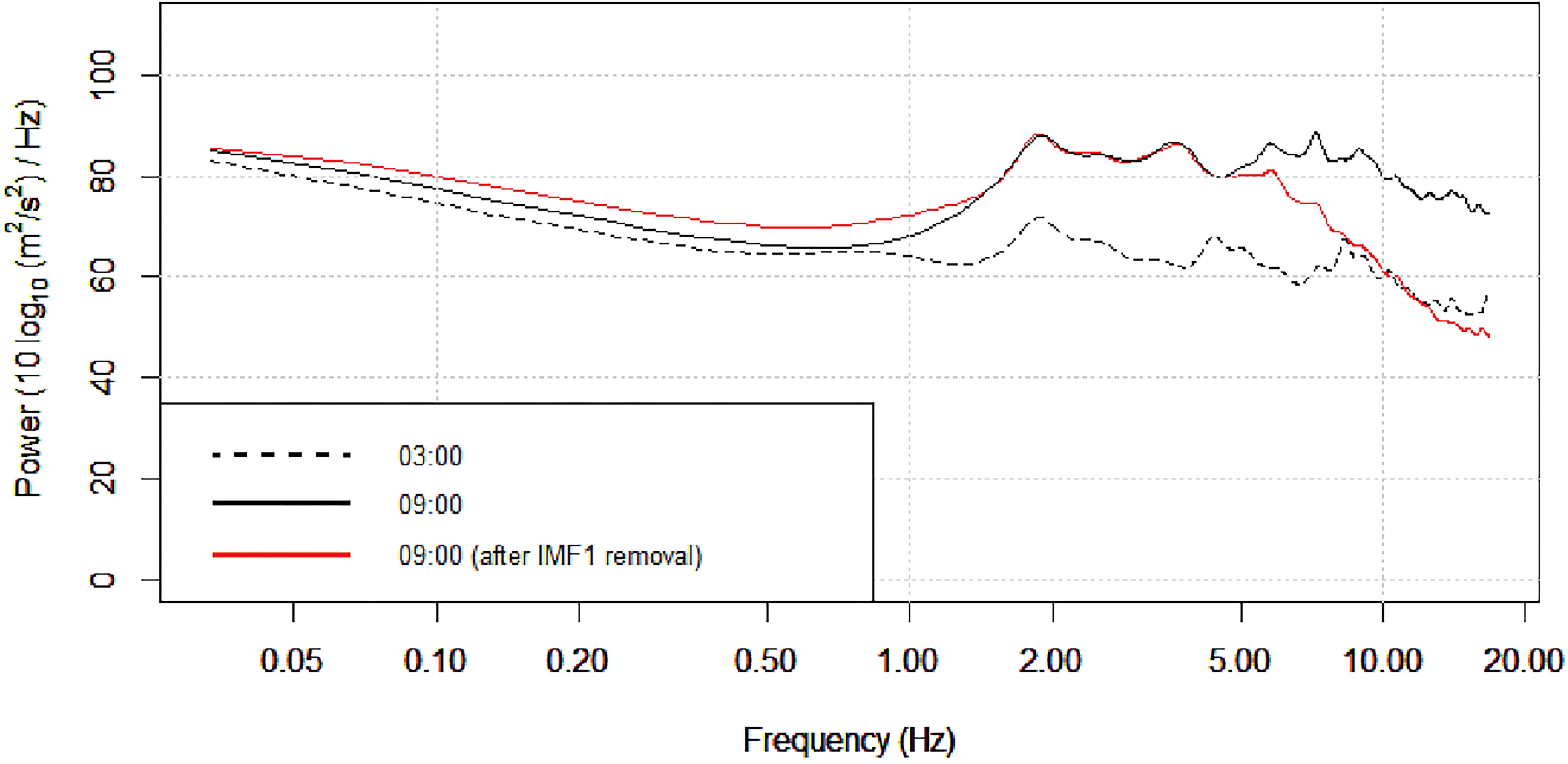
Figure 6. Results of transient noise removal. Dashed and solid black lines represent the frequency spectrum at a quiet and busy time, respectively. The red line represents the frequency spectrum at a busy time after the removal of transient noise.

Demonstration of monochromatic noise removal is conducted at Station MM099. Figure 7 shows the frequency spectrum of the vertical component at Station MM099 where amplitude spikes can be observed at frequencies ±9 Hz and ±13 Hz, indicating the contamination of monochromatic noise. After careful examination of the frequency spectrum of every IMF, we observed that monochromatic noise is associated with IMF 1 and IMF 2 (Figure 7). These IMFs were then removed before calculating the H/V Spectrum. To see the effect of transient and monochromatic noise removal on HHT-HVSR calculations, we plotted the HVSR curve at Station MM099, which is calculated using FFT and using HHT after noise removal (Figure 8). The removal of these noises successfully revealed the main peak at frequency ±12 Hz which was unclear before the noise removal process. This main peak location may contain important information; i.e., the depth of the main impedance contrast, which may lead to misinterpretations when further analyses of the unprocessed trace are carried out (e.g., obtaining subsurface information such as S-wave velocity through the inversion process).

FIGURE 7

Figure 7. Vertical components, IMF 1, and IMF 2 trace at Station MM099 (left) with its corresponding frequency spectrum (right).

FIGURE 8

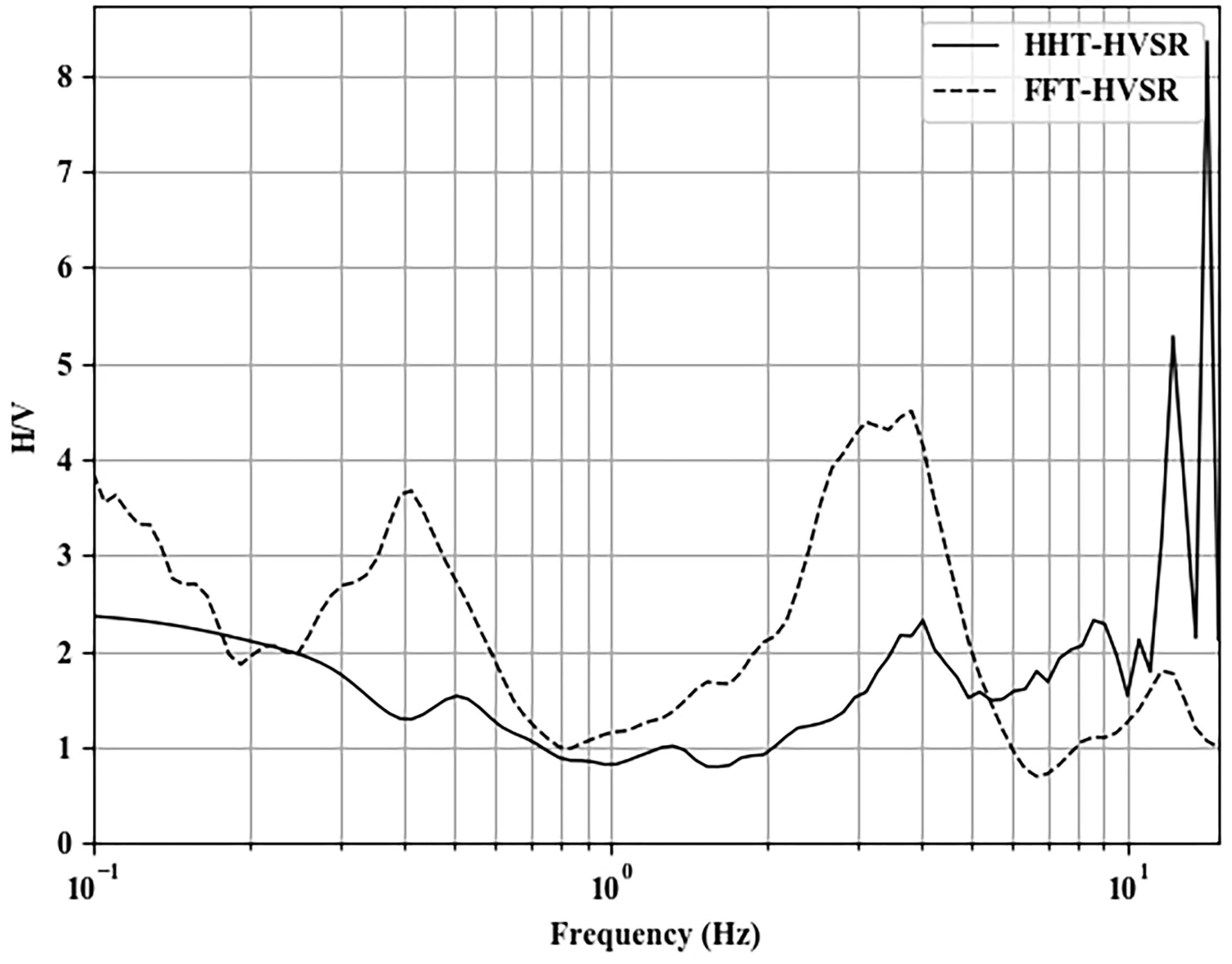
Figure 8. HVSR curve at Station MM099. The solid line represents the HHT-HVSR curve after the removal of local noises, and the dashed line represents the FFT-HVSR curve.

Inversion of HVSR Curves

The inversion of HVSR curves to obtain the S-wave velocity (Vs) structure is conducted using OpenHVSR, a MATLAB-based software, developed by Bignardi et al. (2016), that can perform forward and inverse computations of the HVSR curve. Forward calculations use the Tsai and Housner (1970) approach, which calculates the theoretical transfer function of a layered subsurface with a vertically incident body wave assumption. The layered subsurface is described as a stack of homogenous viscoelastic layers overlying a half-space, each layer having body wave velocities (Vp, Vs), density (ρ), thickness (H), and body wave attenuation factors (Qp, Qs). The software also accounts for the contribution of surface waves with a different approach, as proposed by Lunedei and Albarello (2010).

The optimum subsurface physical parameter model can be determined based on an objective function: a function that can assess the suitability of the data and the model. The objective function (E) used in OpenHVSR and expressed as a function of model parameter m is written as follows:

$$E(m)=aM(m)+bS(m)+\sum _{j=1}^5{\alpha }_j{R}_j(m)(10)$$

where the first term (M) is a misfit function defined as the misfit between calculated (from the observation data) and simulated (from the forward modeling using Equation 2) curves. The second term (S) is a novel strategy used to preserve the primary information of the HVSR curve; i.e., the location of the peaks, which the function itself has defined as the misfit between the partial derivative (with respect to frequency of the observation) of the calculated curve and simulated curves. Lastly, the third term (R) is a regularization factor used to implement lateral constraint in the inversion process. This last term is useful in accounting for the effect of lateral variations of subsurface parameters to the model, where a large lateral variation is expected in an area. Variables a, b, and α in front of each term are weighting constants that can be adjusted based on their importance.

The Monte Carlo Method is implemented in this software to search for the subsurface parameters which best fit the calculated curve. Starting from an initial model defined by the user, the software explores the parameters by randomly perturbing them for a percentage amount chosen by the user. If the perturbed set of parameters has a lower value objective function, as in Equation 10, the set of parameters becomes the current model, and so on. This allows the software to explore numerous combinations of a set of parameters until it reaches the best fitting curve. This will also allow the software to force the calculated curve to reach minimum misfit; even though the values are unreasonable and cannot be found in real geological situations. Therefore, careful judgment and evaluation must be made before interpreting the result of the inversion process.

The initial model for the inversion of HVSR curves is obtained from the work of Marjiyono (2016b), done in the same study area, which used microtremor array measurements and inversion to obtain the subsurface S-wave velocity structure in Mataram City. That study proposed a two-layer model to represent the alluvium deposits overlying the harder rocks. In this study, we added layers to make a total of five layers in order to account for the possible contribution of H/V amplification from a deeper layer and to increase the degree of freedom in the inversion process. We divided the inversion process into three steps. In the first step, we allow 15% perturbation for 5000 iterations under each HVSR curve. Successively, we allow 5% perturbation for 10,000 iterations to finalize the 1D local inversions. For the last step, we performed 15,000 laterally constrained iterations which allows 20% perturbation with respect to the best-fitting model.

Results

To compare the subsurface structure obtained from FFT-HVSR curves and HHT-HVSR curves, we performed the inversion process for both sets of curves (FFT-HVSR and HHT-HVSR), following the strategy explained in the previous section. Figure 9A shows the example of the inversion result of the FFT-HVSR curve at Station MM065 in which the calculated curve and simulated curve from the best-fitting model are displayed in the same graph. Figure 9B shows the inversion result of HHT-HVSR at the same location. It can be seen that the inversion result of the HHT-HVSR curve provides a better fit for the calculated curve than that of the FFT-HVSR curve. The peak amplitudes, especially the main peak, also constrained better in the inversion results of the HHT-HVSR curve than that of the FFT-HVSR curve. We observed that this also applies to other stations in which the utilization of HHT to HVSR curves, rather than using the conventional FFT method, can reduce the average misfit at all stations in the inversion process for up to 23%.

FIGURE 9

Figure 9. (A) Inversion result of FFT-HVSR curve at Station MM065. (B) Inversion result of the HHT-HVSR curve at Station MM065. The black line represents the calculated HVSR curve; the blue line represents the simulated HVSR curve for the last iteration on the model, and the red line represents the simulated HVSR curve for the best-fitting model.

Figures 10B,C show the vertical cross-sections of Vs structure from the inversion of FFT-HVSR curves and HHT-HVSR curves, respectively. The location and the extent of the cross-sections were made the same as in Figure 10A for easier comparison with the reference model. In general, the Vs structure from the inversion of HHT-HVSR curves shows better agreement with the reference model from Marjiyono (2016b) than the Vs structure from the inversion of FFT-HVSR curves. The HHT-HVSR Vs structure gives a better separation of a layer with lower Vs (∼100–500 m/s) on top and layers with higher Vs (>500 m/s) beneath it; while the FFT-HVSR Vs structure did not show these features. The continuity of the layer with higher Vs can also be fairly well observed in the HHT-HVSR Vs structure. Further examination of the HHT-HVSR Vs structure allows us to identify the diminishing trend of thickness in the lower Vs layer to the eastern side, which is also a feature of the reference model. The FFT-HVSR Vs structure shows a dike-shaped feature in the center with relatively large Vs (∼1000–1200 m/s). This large Vs feature is also found in the bottom right of the vertical cross-section of the FFT-HVSR Vs structure.

FIGURE 10

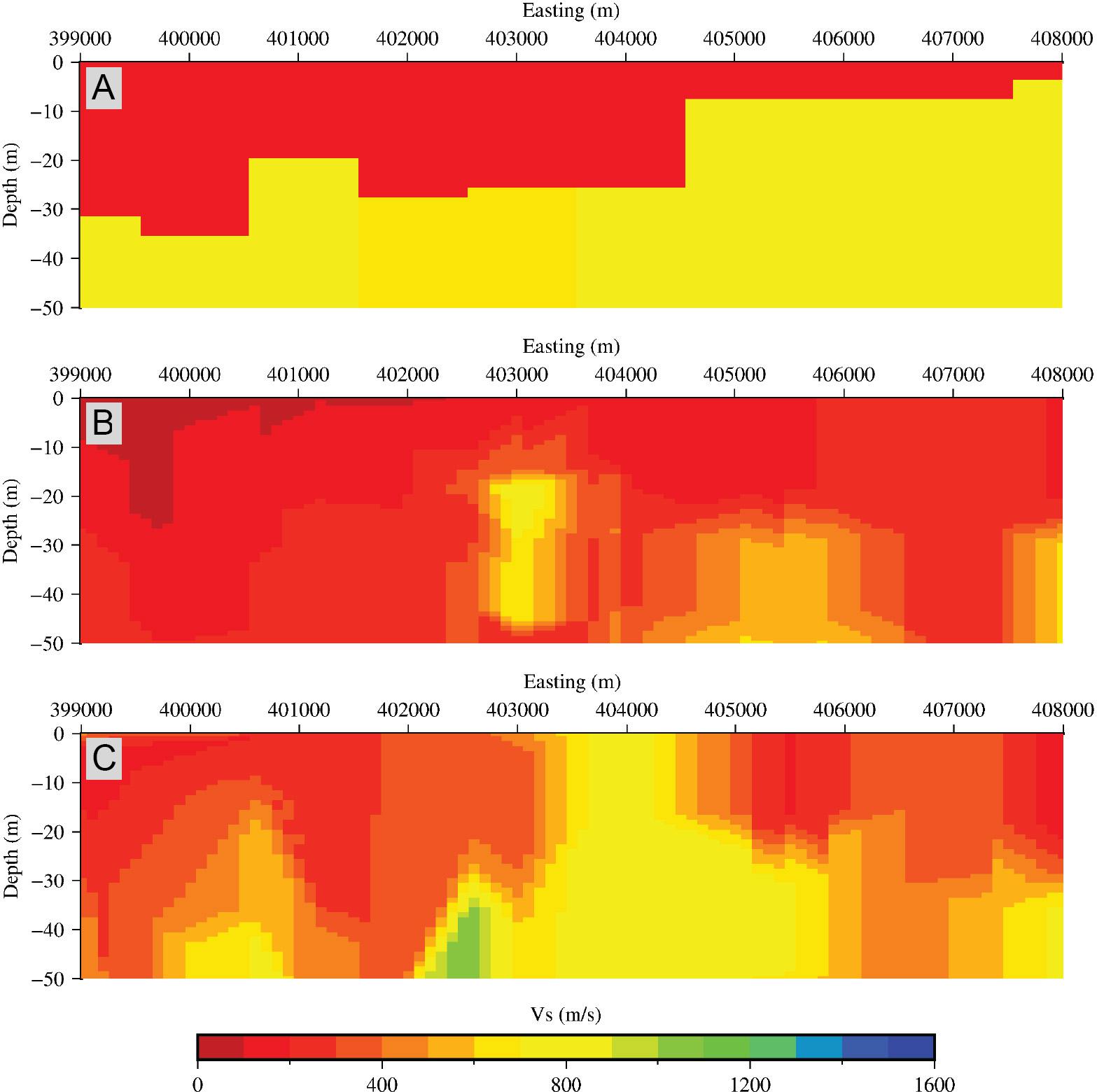
Figure 10. (A) Proposed Vs structure of Mataram City digitized from the study done by Marjiyono (2016b) which is used as a reference model in this study. (B) Vertical cross-section of Vs structure from the result of the inversion process of FFT-HVSR curves. (C) Same with point (B) but for HHT-HVSR curves.

Because of the better misfit of HHT-HVSR curve inversion results and the better agreement of shallow Vs structure resulting from the inversion process of the curves with reference to the model, this study provides a deeper depth and larger extent of vertical cross-section (up to 300 m depth) of HHT-HVSR Vs structures. In order to observe and conduct an analysis of lateral variations of the Vs structure in Mataram City, this study also provides the horizontal cross-section of the HHT-HVSR Vs structure up to depth 50 m, as shown in Figure 11. It can be seen from the horizontal cross-section that the Vs values generally have an increasing trend to the east of Mataram City. This feature can be fairly well observed at almost every depth of the cross-section. With increasing depth, the Vs values in the entire Mataram City area also increase. These results agree with the results of the study done by Marjiyono (2016b) using a two-layer model. The interpretation of the results, with consideration of the geological conditions in Mataram City, will be explained in the following section.

FIGURE 11

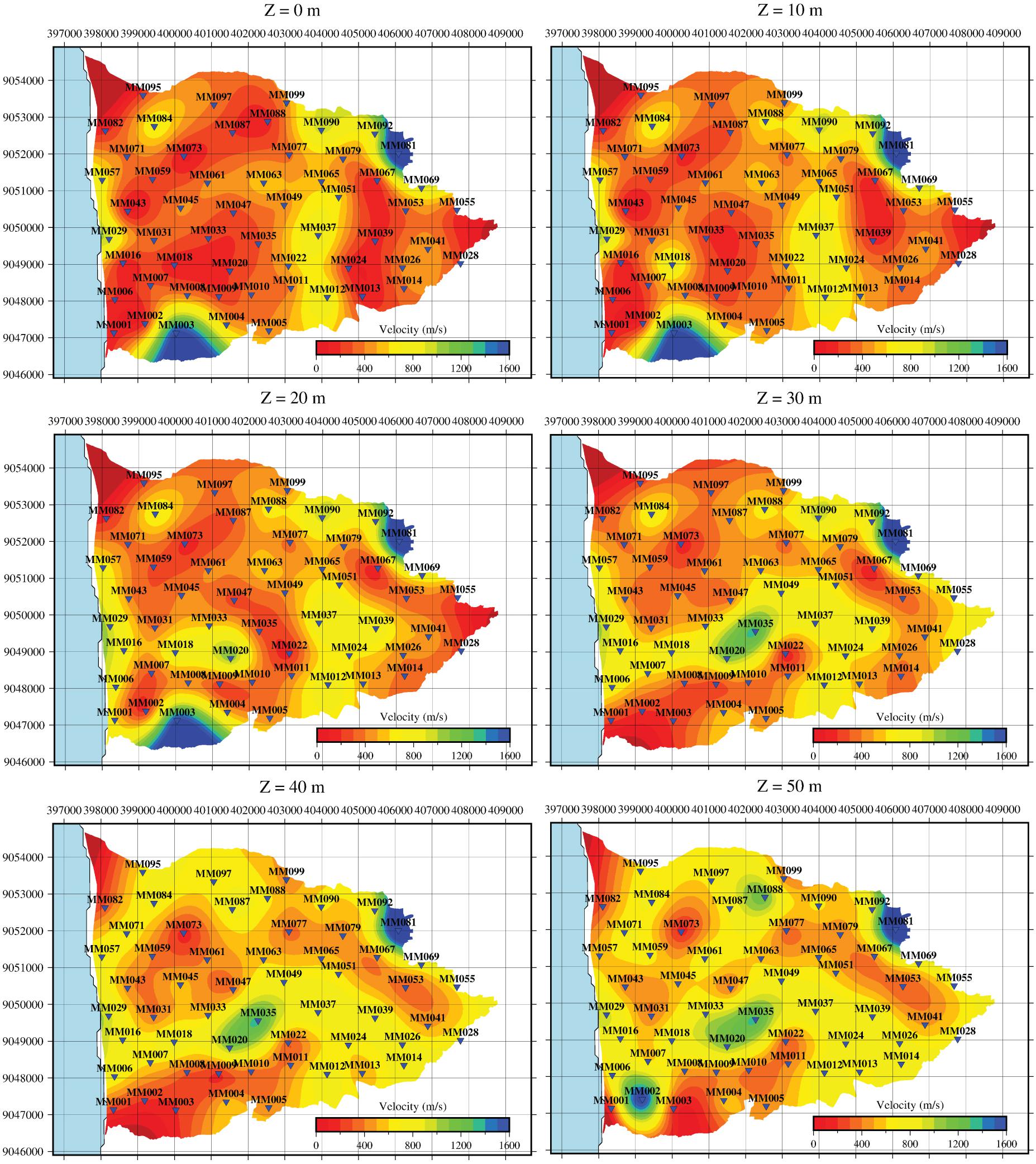
Figure 11. The horizontal cross-section of Vs structure in Mataram City from depths 0–50 m. The depth of each cross-section is displayed on top of the corresponding cross-section.

Discussion

In obtaining the HHT-HVSR curves, we did not use the Konno-Ohmachi smoothing like the Geopsy (the software to obtain the FFT-HVSR curves) does, so it looks like there are highly varying data point in high frequency in the HHT-HVSR curve (Figure 9B). As in the Geopsy documentation, the purpose of the Konno-Ohmachi smoothing is to increase the readability of the HVSR curves. Therefore, we believe that the use of this smoothing has very small impact upon the inversion process.

Mataram City is occupied by an alluvium deposit, which is a product of deposition from alluvial, beach, or swamp, and is the youngest rock in the region. The deposit may contain pebbles, granules, sand, clay, peat, or coral fragments (Mangga et al., 1994), which are all relatively soft materials. The combination of the young rock (which might be exposed to erosion and lack of compaction) and the soft materials contained within it make this layer most likely to have low seismic velocity. In Figure 12, low Vs value with a range of 100–500 m/s is observed at the top part of the vertical cross-section and has a fairly clear continuity throughout the cross-section. We interpret this layer to be the alluvium deposit layer because the characteristics correspond with the preceding explanation. The features of this layer diminish in thickness to the eastern side of Mataram City, which is in agreement with the previous work of Marjiyono (2016a) that successfully reconstruct the base structure of the alluvium deposits. According to this study, however, the thickness of the alluvium deposit on the eastern side of Mataram City reaches about 25 m, in contrast to the previous study which suggests a thickness of about 3 m. This discrepancy might be due to the different approaches and methods used to reconstruct the alluvium deposit structure. Another feature that can be observed is the increasing trend of Vs values to the eastern side of Mataram City, which can be seen in Figure 11. The lateral variation of Vs values might be caused by different grain sizes. The western side has a smaller grain size because it is farther from the source of the materials, as suggested by Marjiyono (2016a). The features of the diminishing thickness in the alluvium deposit and the increasing trend of Vs upon getting farther from the coast is also observed in other cities in Indonesia with similar situations and lithologies in the topmost layer (e.g., Thein et al., 2015; Ridwan et al., 2019), indicating that these features are characteristic of cities located in coastal areas and areas with alluvium deposits.

FIGURE 12

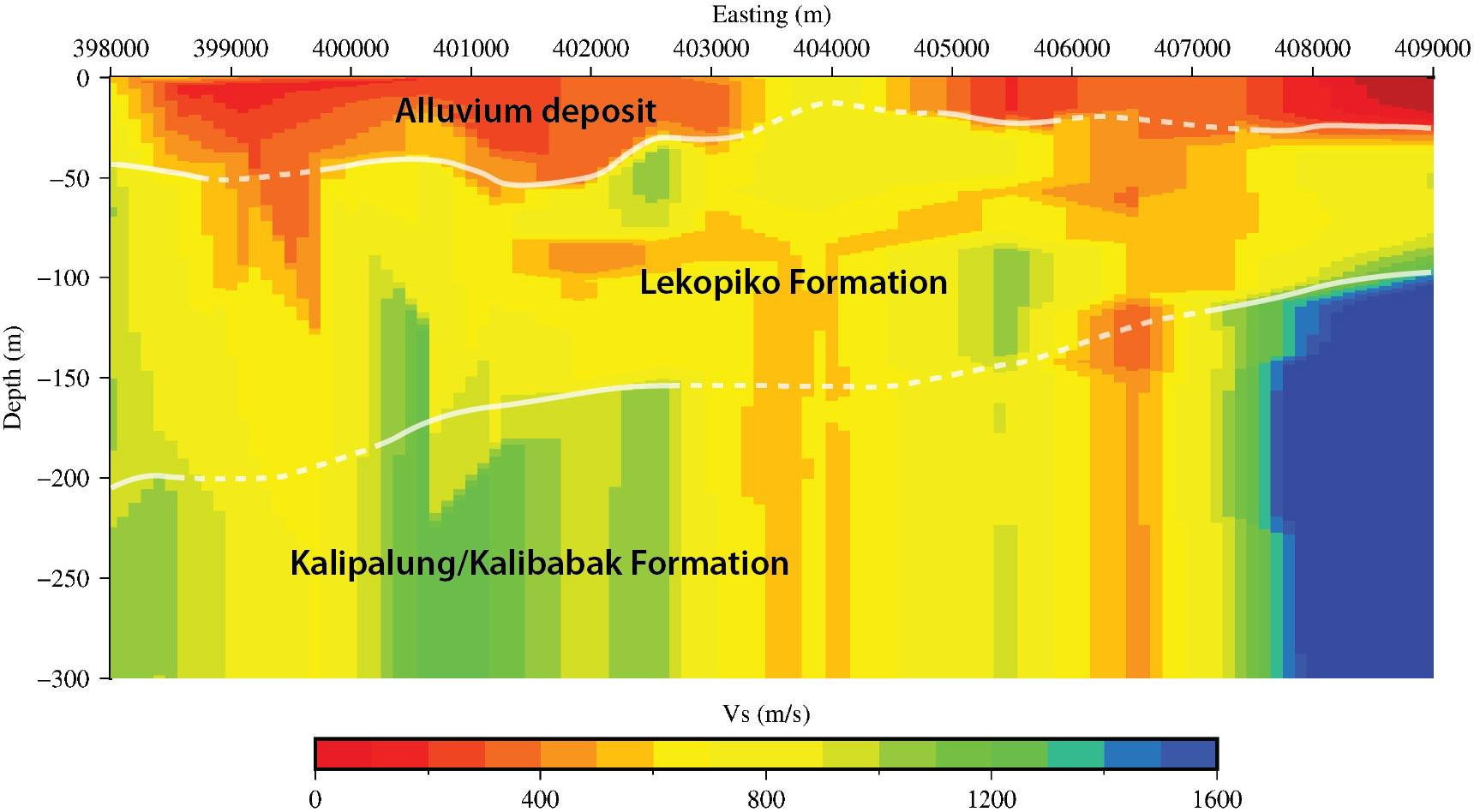
Figure 12. Vertical cross-section of Vs structure from the result of the inversion process of HHT-HVSR curves with a larger extent and deeper depth than that of Figure 10C along with the interpretation of the vertical cross-section.

Beneath the alluvium deposit layer, higher Vs can be found with values of more than 500 m/s. In this study, this layer was separated into two layers because of the significant velocity contrast that can be fairly well observed. The middle layer has Vs values ranging from ∼400 m/s to ∼1100 m/s, and the thickness of this layer varies from ∼75 m on the western side of Mataram City up to ∼150 m on the eastern side. Based on the borehole data from the previous study (Marjiyono, 2016a), this second layer is identified as rocks from the Lekopiko Formation. This formation consists of the products of volcanic activity, such as pumiceous tuff, lahar breccia, and lava. There is a high possibility that these rocks could have higher Vs value than that of alluvium deposits because of higher density and being older in age. From the borehole data obtained from the previous study (Marjiyono, 2016a), and the geological history of Lombok Island, it can be assumed that this layer of Lekopiko Formation is the base of the alluvium deposit.

The bottommost layer has Vs values ranging from ∼500 m/s up to 1600 m/s. The boundary of this layer with the Lekopiko Formation is identified through a fairly well observed velocity contrast. The continuity of the boundary is poorly observed compared to the alluvium-Lekopiko Formation, which might be caused by decreasing resolution at increasing depths. Based on the Vs values, this layer contains the same lithology as the Lekopiko Formation, but has older rocks. The most probable interpretation of this layer is either that it is the Kalibabak Formation or the Kalipalung Formation, which are rocks produced by volcanic activity (breccia and lava). This study was unable to determine whether this layer belongs to the Kalibabak or the Kalipalung Formations because of a lack of additional information. Further research using a different approach is required to give a more in-depth explanation and to provide a better understanding of this uncertain layer.

Conclusion

This study utilizes the HHT for removing noise which might affect the quality of microtremor recordings. We demonstrate the robustness of this method for removing transient and monochromatic noise from microtremor recordings and show that the method is quite effective for extracting microtremor signals. The presence of local noises in microtremor recordings may affect further analysis of the data and may lead to misinterpretations. Local noises mainly affect the higher frequency ranges in the HVSR curve that produce some of the main information from the HVSR curve; i.e., the location and amplitude of the concealed main peak. Removal of local noises could help to reveal the hidden peak in the HVSR curve.

In order to compare the quality of the HHT-HVSR curves in terms of estimating the subsurface structure beneath it, we apply the inversion process to both sets of FFT-HVSR and HHT-HVSR curves, using Open HVSR software developed by Bignardi et al. (2016). The resulting simulated curves show a better misfit to the calculated HHT-HVSR curves than the FFT-HVSR curves. The utilization of HHT to obtain HVSR curves can reduce the average misfit in the inversion process up to 23% as compared to the conventional method with FFT. From the cross-section of the subsurface structure, a better agreement can be observed in the inversion result of HHT-HVSR curves as compared to the FFT-HVSR curves. This result is also supported by the study done by Marjiyono (2016b) which uses a different approach and method to obtain the subsurface structure of Mataram City.

Based on our study, three layers are observed in the vertical cross-section which are identified through velocity contrast. The first layer is interpreted to be an alluvium deposit, which is characterized by low values of Vs (100–500 m/s) and a thickness ranging from 25 m on the eastern side of Mataram City to 50 m on the western side. The lateral variation of this layer is also observed in the horizontal cross-section with the increasing trend of Vs value to the east of Mataram City. The second layer is interpreted as rocks from the Lekopiko Formation, which are characterized by moderate values of Vs (400–1100 m/s) and a thickness ranging from 75 m on the eastern side of Mataram City up to 150 m on the western side. The third layer is interpreted as rocks from the Kalibabak/Kalipalung Formations, which are characterized by higher Vs values (500–1600 m/s). It is quite difficult to identify the boundary between this layer and the Lekopiko Formation layer due to the decreasing resolution of HVSR analysis with increasing depth. It is still uncertain whether the classification of this layer belongs to the Kalibabak Formation or the Kalipalung Formation due to the lack of additional information from deeper borehole data.

The results of this study, especially information regarding the structure of the alluvium deposit layer in Mataram City, are in good agreement with previous studies. This study gives new insight into the structure of the deeper layer in Mataram City, although the resolution still needs to be improved. Further research using a different approach is needed to provide better resolutions in order to reconstruct the subsurface structure in Mataram City and to give a better understanding of the subsurface conditions.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

MH, ZZ, AN, and AS conceived the microtremor survey in Mataram City, Lombok, Indonesia. MH, ZZ, AN, AS, and SR contributed to the writing of the manuscript. All the authors contributed to the preparation of the manuscript, read, and approved the final manuscript.

Funding

This work was supported by the Institute for Research and Community Service, Bandung Institute of Technology 2019 through a research grant from the Global Geophysics Research Group awarded to NP, and was partially supported by the Ministry of Research and Technology through SIMLITABMAS awarded to NP. Partially supported by “Hibah Penelitian Dasar Unggulan Perguruan Tinggi, Kemenristek/BRIN 2019-2021”, Republic of Indonesia and “Hibah Riset Institut Teknologi Bandung 2019-2020” awarded to AN.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors are grateful to the Institute for Research and Community Service, Bandung Institute of Technology, and the Ministry of Research and Technology. Generic Mapping Tools (Wessel and Smith, 1998) were used to produce the figures.

References

Albarello, D., and Lunedei, E. (2010). Alternative interpretations of horizontal to vertical spectral ratios of ambient vibrations: new insights from theoretical modeling. Bull. Earthquake Eng. 8, 519–534. doi: 10.1007/s10518-009-9110-0

CrossRef Full Text | Google Scholar

Badan Meteorologi Klimatologi dan Geofisika [BMKG] (2019). Katalog Gempa Bumi Signifikan dan Merusak Tahun 1821–2018, Pusat Gempa dan Tsunami BMKG. Available online at: https://www.bmkg.go.id/gempabumi/katalog-gempabumi-signifikan.bmkg (accessed June, 2020).

Google Scholar

Bard, P. Y. (1999). Microtremor measurements: a tool for site effect estimation. Effects Surf. Geol. Seismic Motion 3, 1251–1279.

Google Scholar

Bard, P. Y. (2004). Guidelines for The Implementation Of The H/V Spectral Ratio Technique On Ambient Vibrations Measurements, Processing And Interpretation, Site Effects Assessment Using Ambient Excitations (SESAME) European Research Project. Brussels: European Commission.

Google Scholar

Bignardi, S., Mantovani, A., and Abu Zeid, N. (2016). OpenHVSR: imaging the subsurface 2D/3D elastic properties through multiple HVSR modeling and inversion. Comput. Geosci. 93, 103–113. doi: 10.1016/j.cageo.2016.05.009

CrossRef Full Text | Google Scholar

Bonnefoy-Claudet, S., Cotton, F., and Bard, P. Y. (2006). The nature of noise wavefield and its applications for site effects studies: a literature review. Earth Sci. Rev. 79, 205–227. doi: 10.1016/j.earscirev.2006.07.004

CrossRef Full Text | Google Scholar

Bowman, D. C., and Lees, J. M. (2013). The Hilbert–Huang transform: a high resolution spectral method for nonlinear and nonstationary time series. Seismol. Res. Lett. 84, 1074–1080. doi: 10.1785/0220130025

CrossRef Full Text | Google Scholar

Büyük, E., Zor, E., and Karaman, A. (2020). Joint modeling of Rayleigh wave dispersion and H/V spectral ratio using Pareto-based multiobjective particle swarm optimization. Turk. J. Earth Sci. 29, 684–695. doi: 10.3906/yer-2001-15

PubMed Abstract | CrossRef Full Text | Google Scholar

Dziewonski, A. M., Chou, T. A., and Woodhouse, J. H. (1981). Determination of earthquake source parameters from waveform data for studies of global and regional seismicity. J. Geophys. Res. Solid Earth 86, 2825–2852. doi: 10.1029/jb086ib04p02825

CrossRef Full Text | Google Scholar

Ekström, G., Nettles, M., and Dziewoński, A. M. (2012). The global CMT project 2004–2010: centroid-moment tensors for 13,017 earthquakes. Phys. Earth Planet. Interiors 200, 1–9. doi: 10.1016/j.pepi.2012.04.002

CrossRef Full Text | Google Scholar

García-Jerez, A., Piña-Flores, J., Sánchez-Sesma, F. J., Luzón, F., and Perton, M. (2016). A computer code for forward calculation and inversion of the H/V spectral ratio under the diffuse field assumption. Comput. Geosci. 97, 67–78. doi: 10.1016/j.cageo.2016.06.016

CrossRef Full Text | Google Scholar

Herak, M. (2008). ModelHVSR—A Matlab§tool to model horizontal-to-vertical spectral ratio of ambient noise. Comput. Geosci. 34, 1514–1526. doi: 10.1016/j.cageo.2007.07.009

CrossRef Full Text | Google Scholar

Huang, N. E., Shen, Z., Long, S. R., Wu, M. C., Shih, H. H., Zheng, Q., et al. (1998). The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. 454, 903–995. doi: 10.1098/rspa.1998.0193

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, N. E., and Wu, Z. (2008). A review on hilbert-huang transform: method and its applications to geophysical studies. Rev. Geophys. 46:RG2006. doi: 10.1029/2007RG000228

CrossRef Full Text | Google Scholar

Ibs-von Seht, M., and Wohlenberg, J. (1999). Microtremor measurements used to map thickness of soft sediments. Bull. Seismol. Soc. Am. 89, 250–259.

Google Scholar

Irsyam, M., Widiyantoro, S., Natawidjaja, D. H., Meilano, I., Rudyanto, A., Hidayati, S., et al. (2017). Peta Sumber dan Bahaya Gempa Indonesia Tahun 2017. Indonesian: Badan Penelitian dan Pengembangan Kementerian Dalam Negeri Republik Indonesia.

Google Scholar

Kanai, K. (1957). The requisite conditions for the predominant vibration of ground. Bull. Earthq. Res. Inst. Univ. Tokyo 35, 457–471.

Google Scholar

Kumar, P., and Mahajan, A. K. (2020). New empirical relationship between resonance frequency and thickness of sediment using ambient noise measurements and joint-fit-inversion of the Rayleigh wave dispersion curve for Kangra Valley (NW Himalaya), India. Environ. Earth Sci. 79:256.

Google Scholar

Liu, L., Mehl, R., Wang, W., and Chen, Q. (2015). Applications of the Hilbert-Huang transform for microtremor data analysis enhancement. J. Earth Sci. 26, 799–806. doi: 10.1007/s12583-015-0594-z

CrossRef Full Text | Google Scholar

Lunedei, E., and Albarello, D. (2010). Theoretical HVSR curves from full wavefield modelling of ambient vibrations in a weakly dissipative layered Earth. Geophys. J. Int. 181, 1093–1108.

Google Scholar

Mangga, S. A., Atmawinata, S., Hermanto, B., Setyogroho, B., and Amin, T. C. (1994). Geological Map of the Lombok Sheet, West Nusatenggara. Bandung: Pusat Penelitian dan Pengembangan Geologi Kelautan.

Google Scholar

Marjiyono, M. (2016a). Konfigurasi cekungan kuarter wilayah kota mataram, nusa tenggara barat berdasarkan data mikrotremor. J. Geol. Sumberdaya Miner. 17, 51–60.

Google Scholar

Marjiyono, M. (2016b). Potensi penguatan gelombang gempabumi oleh sedimen permukaan kota mataram, Nusa Tenggara Barat. J. Lingkungan Bencana Geol. 7, 135–144.

Google Scholar

McCaffrey, R., and Nabelek, J. (1987). Earthquakes, gravity, and the origin of the Bali Basin: an example of a nascent continental fold-and-thrust belt. J. Geophys. Res. Solid Earth 92, 441–460.

Google Scholar

Nakamura, Y. (1989). A Method for Dynamic Characteristics Estimation of Subsurface using Microtremor on the Ground Surface. Tokyo: Railway Technical Research Institute.

Google Scholar

Nakamura, Y. (2008). “On the H/V spectrum,” in Proceedings of the The 14^th World Conference on Earthquake Engineering, Beijing.

Google Scholar

Nogoshi, M., and Igarashi, T. (1971). On the amplitude characteristics of microtremor. J. Seismol. Soc. Jpn. 24, 26–40. doi: 10.4294/zisin1948.24.1_26

CrossRef Full Text | Google Scholar

Oubaiche, E. H., Chatelain, J. L., Hellel, M., Wathelet, M., Machane, D., Bensalem, R., et al. (2016). The relationship between ambient vibration H/V and SH transfer function: some experimental results. Seismol. Res. Lett. 87, 1112–1119. doi: 10.1785/0220160113

CrossRef Full Text | Google Scholar

Parolai, S., Maesano, F. E., Basili, R., Silacheva, N., Boxberger, T., and Pilz, M. (2019). Fingerprint identification using noise in the horizontal-to-vertical spectral ratio: retrieving the impedance contrast structure for the Almaty Basin (Kazakhstan). Front. Earth Sci. 7:336. doi: 10.3389/feart.2019.00336

CrossRef Full Text | Google Scholar

Ridwan, M., Cummins, P. R., Widiyantoro, S., and Irsyam, M. (2019). Site characterization using microtremor array and seismic hazard assessment for Jakarta, Indonesia. Bull. Seismol. Soc. Am. 109, 2644–2657. doi: 10.1785/0120190040

CrossRef Full Text | Google Scholar

Robiana, R., Minarno, P. A., Hidayati, S., Supartoyo, S., and Nurfalah, F. (2018). Gempa Lombok Tanggal 29 Juli 2018 dan Dampaknya—Kajian Rangkaian Gempa Lombok Provinsi Nusa Tenggara Barat. Indonesian: Badan Penelitian dan Pengembangan.

Google Scholar

Sánchez-Sesma, F. J., Rodríguez, M., Iturrarán-Viveros, U., Luzón, F., Campillo, M., Margerin, L., et al. (2011). A theory for microtremor H/V spectral ratio: application for a layered medium. Geophys. J. Int. 186, 221–225. doi: 10.1111/j.1365-246x.2011.05064.x

CrossRef Full Text | Google Scholar

Sasmi, A. T., Nugraha, A. D., Muzli, M., Widiyantoro, S., Zulfakriza, Z., Wei, S., et al. (2020). Hypocenter and magnitude analysis of aftershocks of the 2018 lombok, indonesia, earthquakes using local seismographic networks. Seismol. Res. Lett. 91, 2152–2162. doi: 10.1785/0220190348

CrossRef Full Text | Google Scholar

Supartoyo, S., and Surono Tofani, E. (2014). Katalog Gempa Merusak Indonesia Tahun 1612–2014 (Edisi Kelima). Indonesian: Pusat Vulkanologi dan Mitigasi Bencana Geologi, Badan Geologi.

Google Scholar

Thein, P. S., Pramumijoyo, S., Brotopuspito, K. S., Kiyono, J., Wilopo, W., Furukawa, A., et al. (2015). Estimation of S-wave velocity structure for sedimentary layered media using microtremor array measurements in Palu City, Indonesia. Proc. Environ. Sci. 28, 595–605. doi: 10.1016/j.proenv.2015.07.070

CrossRef Full Text | Google Scholar

Tsai, N. C., and Housner, G. W. (1970). Calculation of surface motions of a layered half-space. Bull. Seismol. Soc. Am. 60, 1625–1651.

Google Scholar

Wafid, M., Sugiyanto, P., and Sarwondo, T. (2014). Resume Hasil Kegiatan Pemetaan Geologi Teknik Pulau Lombok Sekala 1:250.000. Indonesian: Pusat Sumber Daya Air Tanah dan Geologi Lingkungan, Badan Geologi.

Google Scholar

Wathelet, M., Chatelain, J. L., Cornou, C., Giulio, G. D., Guillier, B., Ohrnberger, M., et al. (2020). Geopsy: a user-friendly open-source tool set for ambient vibration processing. Seismol. Res. Lett. 91, 1878–1889. doi: 10.1785/0220190360

CrossRef Full Text | Google Scholar

Wessel, P., and Smith, W. H. F. (1998). New, improved version of the generic mapping tools released. EOS 79:579. doi: 10.1029/98eo00426

CrossRef Full Text | Google Scholar