Creep Experimental Study of Rocks Containing Weak Interlayer Under Multilevel Loading and Unloading Cycles

Introduction

The rheological mechanical properties of rocks have always been an important topic in rock mechanics, and it is closely related to the long-term stability of underground engineering. The deformation of rock mass after rock excavation, found by engineers, was not instantaneous but time-dependent. The experimental study of rheological mechanics of rock can be traced back to the 1930s; Griggs (1939) studied limestone, shale, and sandstone in 1939 and found that rheologic deformation occurs when the load reaches 12.5–80% of the failure load. When the rock mass was temporarily in a stable state, deformation and failure could still occur under the long-term load. It is found that during the process of rock mass deformation, the deformation of rock mass either tended to be stable or accelerated until failure (Griggs, 1939; Zhou et al., 2017a; Wang et al., 2020). The phenomenon that the rock mass deformation changes with time is called rheological deformation. In recent years, many scholars have studied the rheological mechanical properties of rocks (Maranini and Brignoli, 1999; Li and Xia, 2000; Ślizowski and Lankof, 2003; Zhou, 2005; Fabre and Pellet, 2006; Yang and Jiang, 2010; Zhao et al., 2016; Zhao et al., 2018; Lin et al., 2019; Wu et al., 2019a; Zhao et al., 2019c).

A weak interlayer (WI) refers to a rock’s relatively thin layer in which the lithology is weaker than that of the adjacent rock formation. The characteristics of strength, deformation, and failure of rock masses with weak interlayer often have significant time dependence directly influencing engineering design, construction, operation, stability, and reinforcement. It is of great theoretical significance and engineering value to study the influence of WI on the rheological characteristics of rock. To date, many researchers (Li et al., 2007; Jiang et al., 2009; Xu et al., 2009; Xiong and Yang 2010; Li A. et al., 2014; Li Y. et al., 2014; Triantafyllidis and Gerolymatou, 2014; Yang et al., 2014; Zhao et al., 2017a; Zhao et al., 2017b; Zhou et al., 2017; Ma et al., 2018; Zhou and Bi, 2018; Wang Y. X. et al., 2018; Wang C. et al., 2019; Hu et al., 2019; Wu et al., 2019b; Wang et al., 2020) have studied the mechanical properties of weak intercalated rock mass under uniaxial compression. Xu et al. (2009) studied the effects of simulated WI on the mechanical properties of layered rock salt in the laboratory and obtained the correlation between the mechanical properties of layered salt rock mass and the characteristics of the WI. Ma et al. (2018) conducted uniaxial and triaxial compression tests on mudstone specimens of layered features produced indoors, and the strength and deformation characteristics of the specimens were analyzed. Jiang et al. (2009) and Xiong and Yang (2010) established the viscoelastic-plastic rheological constitutive model and the viscoelastic rheological constitutive model for interbedded rock masses based on FLAC3D numerical simulation software, respectively. The results showed that the factors such as interlayer length, interlayer spacing, and interlayer thickness have great influence on the elastoplastic deformation and rheological deformation of rock. Li A. et al. (2014) used the FLAC3D numerical simulation software to analyze the fracture process of soft and hard interlayer composite rock mass under uniaxial compression stress as a function of the inclination angle of the layer. For layered rock masses, many uniaxial compression tests and analyses have been done (Xu et al., 2009; Triantafyllidis and Gerolymatou, 2014; Zhou and Yang, 2017; Zhou et al., 2017; Ma et al., 2018). However, fewer studies on rheological mechanical properties have been done (Li et al., 2007; Zhou et al., 2008; Yang et al., 2014; Zhao et al., 2017b; Hu et al., 2019; Zhao et al., 2020), and the creep characteristics of rock containing WI under multilevel loading and unloading cycles have barely been studied.

In this study, according to the literature (Fan and Gao 2005; Tsai et al., 2008; Zhao et al., 2017c; Wang C. L. et al., 2018; Wang R. H. et al., 2018; Zheng et al., 2018; Zhao et al., 2019a; Zhao et al., 2019b; Zhou et al., 2019; Zhou et al., 2020), using the cyclic loading and unloading method, the uniaxial compression rheological test under cyclic loading and unloading conditions was carried out on the intact rock and rock containing WI. The influence law of stress level and WI inclination angle on the rheological characteristics of the rock was studied. In addition, the failure modes of sandstones and composite sandstones were studied.

Experiments

Specimen Preparation

The experimental rock blocks (sandstone) were taken from an underground roadway construction site at the Meitanba Coal Mining Area located in southern China. The test rock sample is cyan sandstone, mainly composed of quartz and calcite, with relatively stable properties, uniform lithology, fine-grained structure, and no macroscopic visible joints and cracks. The AiniMR-60 nuclear magnetic resonance analyzer was used to test the porosity of the cyan sandstone specimens, and the average porosity of the cyan sandstone specimens was 4.26%. According to the method introduced in Kohlhauser and Hellmich (2013) and Karte et al. (2015), the primary velocity of the sample measured by the wave velocity tester is $\mathrm{2,551}\text{m}·{\text{s}}^{-1}$, and the secondary velocity is $\mathrm{1,453}\text{m}·{\text{s}}^{-1}$. The rock blocks were cut into 50 × 100 mm cylinder standard specimens in the laboratory [based on the recommendations of the International Society of Rock Mechanics on the dimensions of the test specimens (ASTM D2938, 2002)].

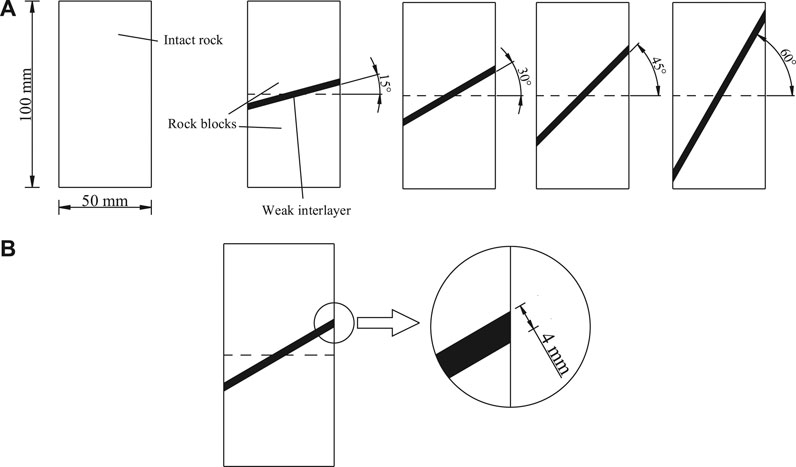
Twenty-eight specimens in total have been used in this study. Eight intact sandstone specimens No. 1–No. 8 were used for the conventional triaxial compression test with confining pressures of 6, 12, 18, and 24 MPa, respectively. Ten specimens (two intact sandstone specimens numbered S0-1 and S0-2, respectively, and eight composite sandstone specimens numbered S1-1, S1-2, S2-1, S2-2, S3-1, S3-2, S4-1, and S4-2, respectively) were used for the conventional uniaxial compression test. Ten specimens (two intact sandstone specimens numbered S0-3 and S0-4, respectively, and eight composite sandstone specimens numbered S1-3, S1-4, S2-3, S2-4, S3-3, S3-4, S4-3, and S4-4, respectively) were prepared to perform the uniaxial compression creep test. The composite sandstone specimens, containing WI with inclination angles 15°, 30°, 45°, and 60°, respectively, were prepared as follows:

(i) Rock blocks cutting: eight intact sandstone specimens were cut into two rock blocks with the cutting inclination angles 15°, 30°, 45°, and 60°, respectively (two intact sandstone specimens were cut for each inclination angle, respectively). The cutting position is shown in Figure 1. The surface of the cutting surface was smoothed by a polishing machine to ensure that the composite sandstone specimen with its WI had the same length as the intact sandstone specimen.

(ii) Cement mortar making: the WIs were prepared using cement mortar composed of C42.5 ordinary Portland cement, sand, and water at a mass ratio of 1:2:0.8.

(iii) Molding and shaping: the rock blocks were placed into PVC pipe mold. Then, using reference lines, the two rock blocks were moved to ensure that the gap had a 4 mm thickness (see Figure 2).

(iv) WI making: to prevent the rock blocks from moving in the mold, the two ends of the mold were fastened with transparent tape; the cement mortar was poured into the 4 mm gap between the two rock blocks in the mold, and the cement mortar was compacted by a wire to keep the surface of the composite sandstones containing a WI smooth. The WI thickness was 4 mm.

(v) Demoulding and maintenance: the sample was removed from the mold after 24 h of curing. The specimens were then held for 28 days in a curing room (at 20°C, 95% relative humidity, and an atmospheric pressure). Examples of prepared specimens are shown in Figure 3.

FIGURE 1

FIGURE 1. (A) Diagram of rock interlayer structure. (B) Diagram of rock interlayer thickness.

FIGURE 2

FIGURE 2. Molding and shaping.

FIGURE 3

FIGURE 3. The prepared specimens (a part of) used in the conventional uniaxial and triaxial compression test and creep test.

Testing Equipment

The conventional triaxial compression tests were performed using a servo-hydraulic Rock Mechanics Testing System (MTS 815) with axial loading in the range of 0–4,600 kN and confining pressure in the range of 0–200 MPa. The triaxial testing system (see Figure 4A) consists of four main units: triaxial cell, loading unit, deformation and pressure monitoring unit, and computerized data acquisition unit. The axial deformation of the specimen was measured with a pair of linear variable displacement transducers (LVDTs), and the circumferential deformation was measured with a circumferential extensometer connected to a roller chain assembly wrapped around the jacketed specimen. The conventional uniaxial compression tests and creep tests were performed using the MTS 815 uniaxial testing system. The uniaxial testing system (see Figure 4B) is mainly composed of an axial loading system, a compression loading frame, and a data acquisition system.

FIGURE 4

FIGURE 4. MTS 815 rock test machine: (A) triaxial testing system and (B) uniaxial testing system.

Experiment Method

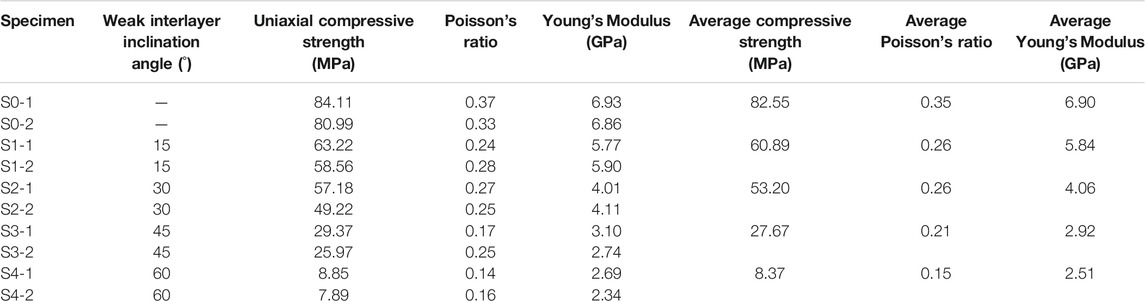
Before the multilevel cyclic loading and unloading tests, the conventional uniaxial compression tests are first performed to obtain mechanical parameters of the specimens. The average uniaxial compression strengths of these specimens are listed in Table 1, which provides the references for subsequent cyclic tests.

TABLE 1

TABLE 1. Rock mechanics parameters of specimens under uniaxial compression test.

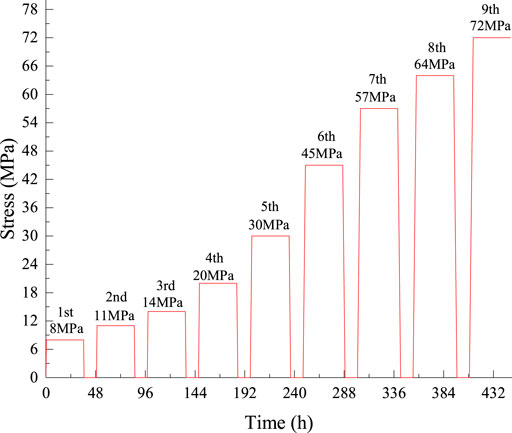
According to the average uniaxial compression strengths of these specimens, nine axial stress levels were used in the multilevel cyclic loading and unloading tests, with the first about the average uniaxial compressive strength of the specimens containing WI inclination angle of 60° and the last about 90% of the average uniaxial compressive strength of the intact specimens. The specific nine axial stress levels were 8, 11, 14, 20, 30, 45, 57, 64, and 72 MPa. Also, the rheological stress levels of the specimen are shown in Table 2.

TABLE 2

TABLE 2. Rheological loading stress level statistics of specimens.

The duration for each stress level (or each stage) was 36 h for the loading period and about 12 h for the unloading period, except for the ninth level which had no unloading period. During the loading period, the axial load increased monotonically at a rate of 0.05 MPa/s to achieve the targeted axial stress level and then remained constant. During the unloading period, the axial load decreases at a rate of 0.05 MPa/s to zero MPa and then remained 12 h. After the unloading period was completed, the next stage was started following the same sequence. The stress loading and unloading diagram is shown in Figure 5.

FIGURE 5

FIGURE 5. Multilevel loading and unloading cycles used in the creep test.

Viscoelastic-Plastic Strain Separation Method

In order to gain insight into the creep properties of rocks containing WI, a new creep data processing algorithm is proposed according to the literature (Mishra and Verma, 2015; Irfan-ul-Hassan, et al., 2016; Königsberger, et al., 2016; Irfan-ul-Hassan, et al., 2017; Zhao et al., 2017d; Göbel, et al., 2018; Wang Y. X. et al., 2019). Specifically, the total strain is divided into instantaneous elastic strain, instantaneous plastic strain, viscoelastic strain, and viscoplastic strains. Figure 6 shows a representative strain–time curve under a loading and unloading cycle (say cycle i). The total strain consists of the instantaneous strain ${\epsilon }_i^{\left(i\right)}$ and the creep strain ${\epsilon }_c^{\left(i\right)}$.

${\epsilon }^{\left(i\right)}={\epsilon }_i^{\left(i\right)}+{\epsilon }_c^{\left(i\right)}.(1)$

FIGURE 6

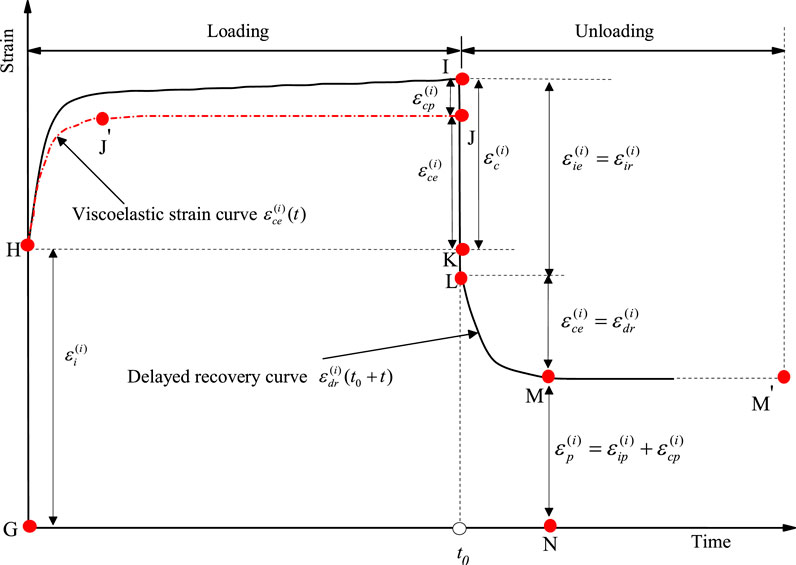
FIGURE 6. Viscoelastic-plastic strain separation diagram (Zhao et al., 2017b).

The instantaneous strain ${\epsilon }_i^{\left(i\right)}$ is the measured strain when the axial load reaches the targeted stress level, and the creep strain ${\epsilon }_c^{\left(i\right)}$ is the measured increase in strain with time during the stage when the load is maintained constant. The instantaneous strain ${\epsilon }_i^{\left(i\right)}$ is composed of the instantaneous elastic strain ${\epsilon }_{ie}^{\left(i\right)}$ (it is equal to the strain ${\epsilon }_{ir}^{\left(i\right)}$ recovered during unloading) and the instantaneous plastic strain ${\epsilon }_{ip}^{\left(i\right)}$:

${\epsilon }_i^{\left(i\right)}={\epsilon }_{ie}^{\left(i\right)}+{\epsilon }_{ip}^{\left(i\right)}.(2)$

The instantaneous strain ${\epsilon }_i^{\left(i\right)}$ is the strain due to the loading, namely, segment GH in Figure 6. The instantaneous elastic strain ${\epsilon }_{ie}^{\left(i\right)}$ is the recovery of strain due to unloading, namely, segment IL in Figure 6. The instantaneous strain ${\epsilon }_i^{\left(i\right)}$ induced by the loading is not completely recovered during the unloading, which means that segment IL is smaller than segment GH in Figure 6. Actually, the difference between segments GH and IL is the instantaneous plastic strain ${\epsilon }_{ip}^{\left(i\right)}$.

Similarly, the creep strain ${\epsilon }_c^{\left(i\right)}$ also consists of the recoverable viscoelastic strain ${\epsilon }_{ce}^{\left(i\right)}$ and the unrecoverable viscoplastic strain ${\epsilon }_{cp}^{\left(i\right)}$:

${\epsilon }_c^{\left(i\right)}={\epsilon }_{ce}^{\left(i\right)}+{\epsilon }_{cp}^{\left(i\right)}.(3)$

After the unloading, a part of the creep strain ${\epsilon }_c^{\left(i\right)}$ recovers with time as represented by segment LM in Figure 6. The delayed recovery of strain ${\epsilon }_{dr}^{\left(i\right)}$ (segment LM in Figure 6) is the recoverable component of the creep strain ${\epsilon }_c^{\left(i\right)}$ (called the viscoelastic strain ${\epsilon }_{ce}^{\left(i\right)}$). After a long enough time, only the unrecoverable strain ${\epsilon }_p^{\left(i\right)}$ (segment MN in Figure 6) remains, which consists of the unrecoverable instantaneous plastic strain ${\epsilon }_{ip}^{\left(i\right)}$ and the unrecoverable viscoplastic strain ${\epsilon }_{cp}^{\left(i\right)}$.

By assuming that the viscoelastic strain curve under loading (segment HJ′J in Figure 6) has the same shape as the delayed strain recovery curve after unloading (segment LMM′ in Figure 6) (Bai et al., 2014; Yang et al., 2015), the viscoelastic strain ${\epsilon }_{ce}^{\left(i\right)}\left(t\right)$ at time t is equal to the delayed recovery strain ${\epsilon }_{dr}^{\left(i\right)}\left(t_0+t\right)$ after unloading, and the viscoplastic strain ${\epsilon }_{cp}^{\left(i\right)}\left(t\right)$ at time t can be obtained by

${\epsilon }_{cp}^{\left(i\right)}\left(t\right)={\epsilon }_c^{\left(i\right)}\left(t\right)-{\epsilon }_{ce}^{\left(i\right)}\left(t\right)={\epsilon }_c^{\left(i\right)}\left(t\right)-{\epsilon }_{dr}^{\left(i\right)}\left(t_0+t\right).(4)$

However, the viscoelastic and viscoplastic strains cannot be separated due to the accelerating creep to failure. In this study, the viscoelastic strain ${\epsilon }_{ce}^{\left(i\right)}$ and the viscoplastic strain ${\epsilon }_{cp}^{\left(i\right)}$ were only considered before the failure of the specimen.

According to the viscoelastic-plastic strain separation method described above and the reversibility of viscoelastic deformation, the data of axial elastic strain and plastic strain of specimens under different stress levels can be obtained.

Results and Discussion

Conventional Uniaxial and Triaxial Compression Tests

From Table 1, one can see that the uniaxial compression strength, Poisson’s ratio, and elastic modulus of the intact rock are higher than those of the sandstones containing WI. Meanwhile, the uniaxial compression strength, Poisson’s ratio, and elastic modulus of the sandstones containing WI will decrease with the increase of inclination angle of WI. The average compressive strengths of intact sandstones and sandstones containing WI with inclination angles 15°, 30°, 45°, and 60° are 82.55, 60.89, 53.20, 27.67, and 8.37 MPa, respectively. Especially for sandstone containing WI with inclination angle 60°, the strength is weakened a lot, only 10.14% of intact rock. Poisson’s ratio of sandstone containing WI is much lower than that of intact sandstone, and Poisson’s ratio of sandstone containing WI with an inclination angle of 15° (S1-1) is 43.64% of intact sandstone. It is indicated that with the increase of inclination angle from 15° to 60° of WI, rocks are more prone to instability and damage. The conventional triaxial compression test results are used to calculate the internal friction angle and will not be analyzed in detail here.

The Effect of Weak Interlayer on Creep Curve

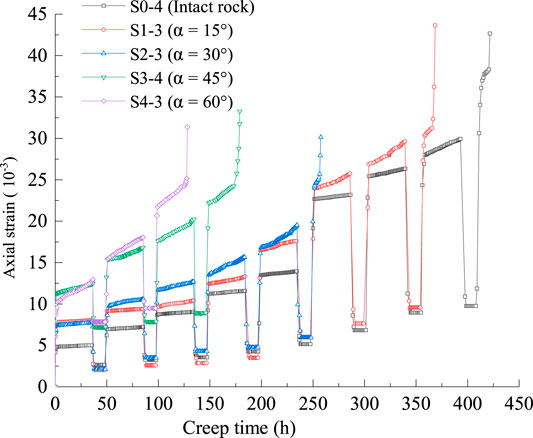
In this study, specimens numbered S0-4, S1-3, S2-3, S3-4, and S4-3 were selected for analysis. The maximum rheological load stress level of S0-4, S1-3, S2-3, S3-4, and S4-3 was 72, 64, 45, 20, and 8 MPa, respectively.

Because the strength of the specimen containing WI with inclination angle 60° is too low, the load of each stage was changed to 4, 6, and 8 MPa, respectively.

Figure 7 shows strain–time curves of specimens under the same stress level (A) and axial strain increment of specimens containing WI relative to intact specimen (B). For instance, under the 8 MPa stress level (see Figure 7A), the axial strain of the specimens containing WI is larger than the strain of the intact specimens, and the strain increases with the increase of the WI inclination angle.

FIGURE 7

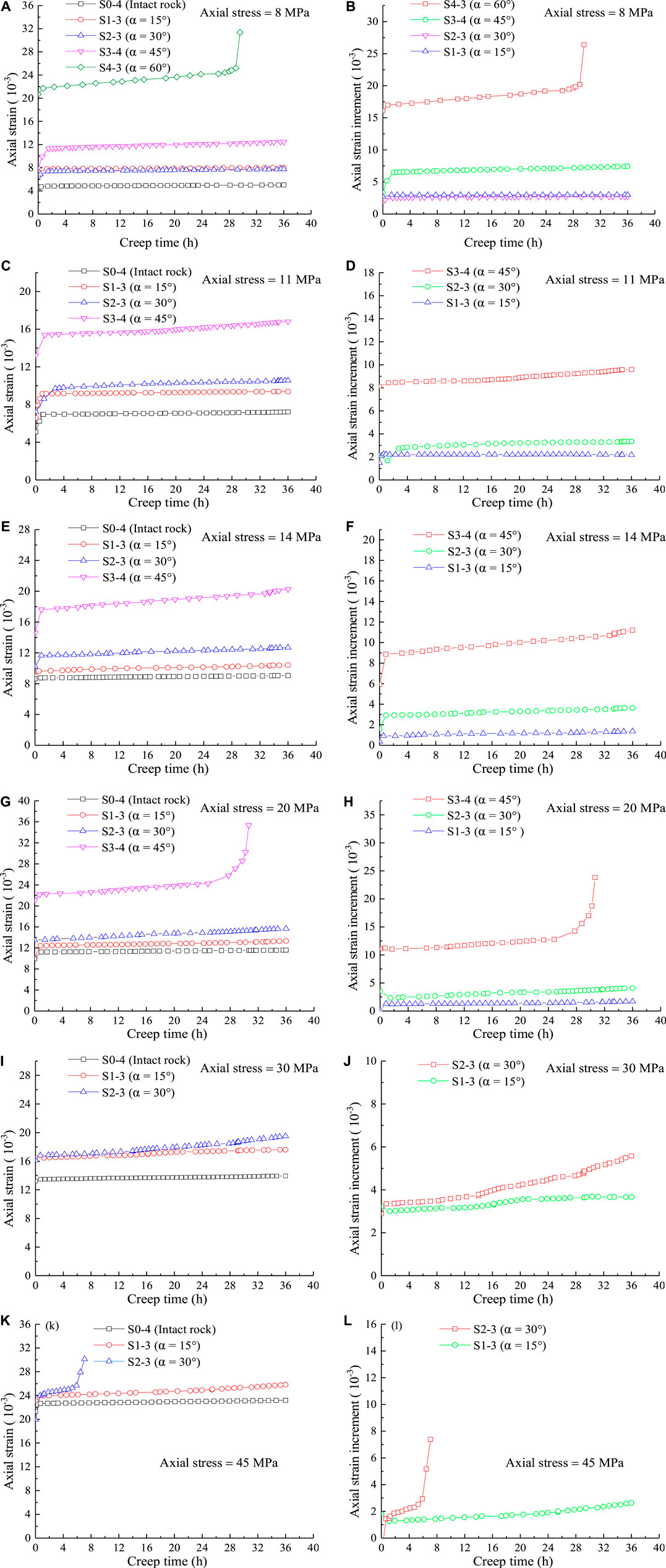
FIGURE 7. (A, C, E, G, I, K) Strain–time curves of specimens under the same stress level and (B, D, F, H, J, L) axial strain increment of specimens containing WI relative to intact specimens.

One can see that the axial strain increment of specimens containing WI relative to intact specimen is more than 50% (see Figure 7B).

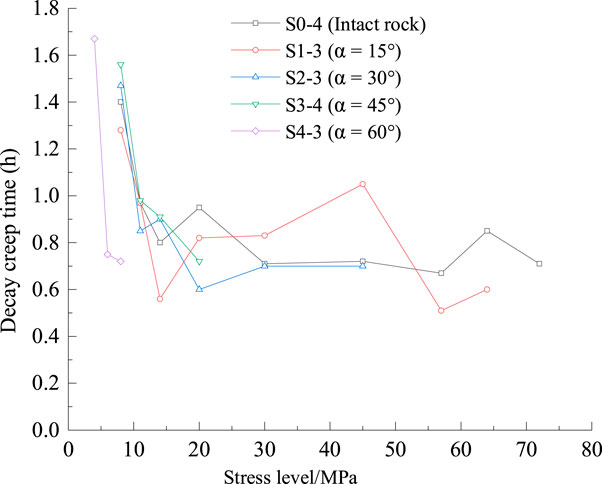
Figure 8 shows strain–time curves of specimens from the first to the last stress levels under multilevel loading and unloading cycles. Figure 9 shows decay creep time–stress curves of specimens from the first to last stress levels. All of the specimens have an obvious decay creep stage at the first stress level. Specimens S0-4, S1-3, and S2-3 pass the deceleration phase and directly enter the accelerated rheological phase until failure; specimens S3-4 and S4-3 pass a period of stable rheological phase after the deceleration rheological phase and then enter the acceleration phase until failure. At the moment of stress unloading, the axial strain of rock was restored immediately, and when the stress is unloaded to zero, the rock strain gradually decreases with time and viscoelastic recovery occurs. However, the rock has viscoplastic deformation, and as the stress increases, the viscoplastic deformation gradually increases.

FIGURE 8

FIGURE 8. Strain–time curves of specimens from the first to the last stress levels.

FIGURE 9

FIGURE 9. Decay creep time–stress curves of specimens from the first to the last stress levels.

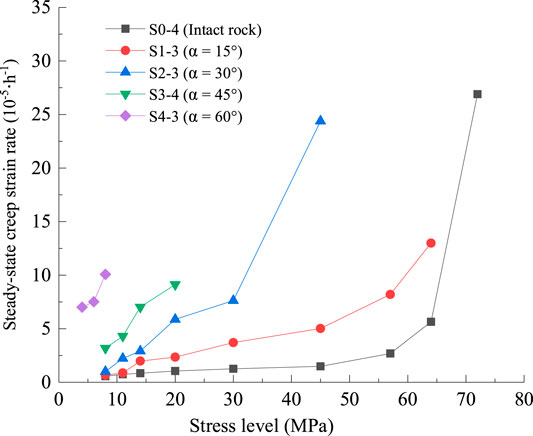
The steady-state creep strain rate can reflect the rheological properties well. Figure 10 shows the steady-state creep strain rate of specimens from the first to last stress levels. The steady-state creep strain rate of all the specimens are the lowest under the first stress level. No rheological acceleration stage occurs in intact specimens before failure; however, the specimens containing WI have an obvious rheological acceleration stage. When the rock is subjected to low loads, the strain rate is quickly attenuated to zero and shows only deceleration rheology.

FIGURE 10

FIGURE 10. Steady-state creep strain rate of specimens from the first to the last stress levels.

The Effect of Weak Interlayer on Instantaneous Strain

The data of axial viscoelastic-plastic strain of intact and WI-containing specimens at different stress levels can be obtained by the viscoelastic-plastic strain separation method. Figure 11 shows instantaneous elastic strain, instantaneous plastic strain, and instantaneous strain curves of specimens from the first to last stress levels. Obviously, with the increase of the WI inclination angle, the instantaneous elastic strain and instantaneous plastic strain will increase. It indicates that the presence of a WI is more likely to cause rheological deformation; the bigger the WI inclination angle, the greater the rheological deformation. One can see that the curve of the stress-instantaneous strain is nearly linear, and the instantaneous elastic modulus (which can be defined as the ratio of the instantaneous stress increment to the instantaneous strain increment under each level of load) of the specimen in the stepped loading creep test showed an overall trend of increasing with the increase of stress, which shows that during the staged loading test, the ability of specimen to resist instantaneous deformation gradually increases with the increase of load, showing obvious hardening characteristics.

FIGURE 11

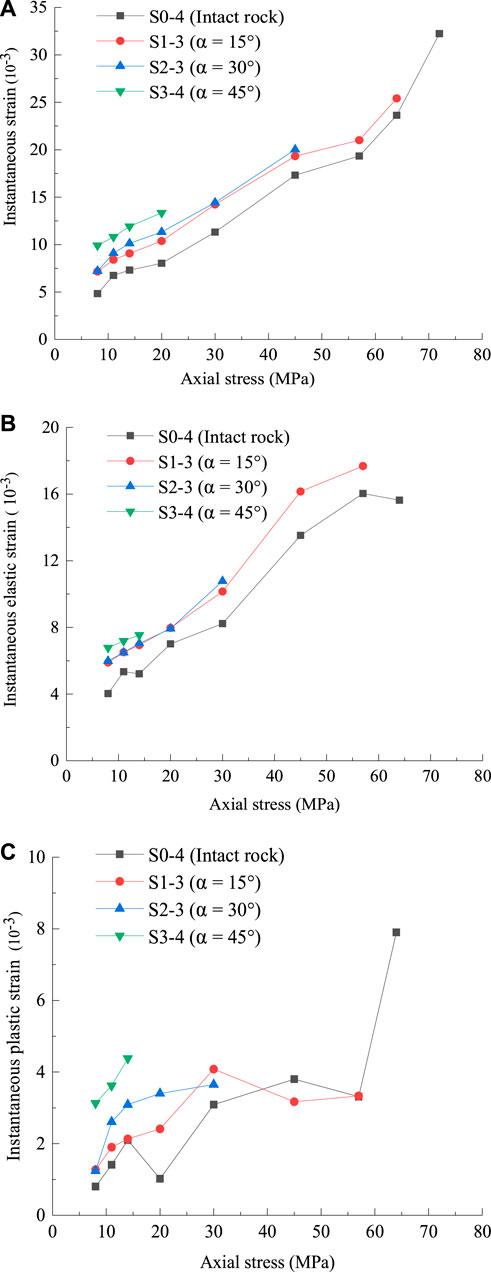
FIGURE 11. (A) Instantaneous strain, (B) instantaneous elastic strain, and (C) instantaneous plastic strain from the first to the last stress levels.

The Effect of Weak Interlayer on Viscoelastic Strain and Viscoplastic Strain

Similarly, creep strain, viscoelastic strain, and viscoplastic strain curves of specimens from the first to last stress levels are shown in Figure 12. As the stress increases, the viscoelastic strain, the viscoplastic strain, and the creep strain of the specimens increase. With the increase of stress, the viscoplastic strain of the intact specimen decreases at low stress levels and increases at high stress levels. However, the viscoplastic strain of specimens with WI always increases with the increase of stress. Also, the larger the WI inclination angle is, the more obvious the plastic deformation will be. With the increase of stress, the viscoelastic strain increases slowly for the intact specimen and decreases for the specimen containing WI. This means that the WI may promote the viscoplastic rheology of the rock mass. We can find that at the same axial stress the instantaneous strain, creep strain and total strain of the specimen containing WI are larger than those of the intact specimen, and the instantaneous strain, creep strain, and total strain increase with the increase of the WI inclination angle. Moreover, the WI inclination angle has a positive correlation with the viscoelastic strain and viscoplastic strain. It indicates that the presence of a WI is more likely to cause rheological deformation; the bigger the WI inclination angle, the greater the rheological deformation.

FIGURE 12

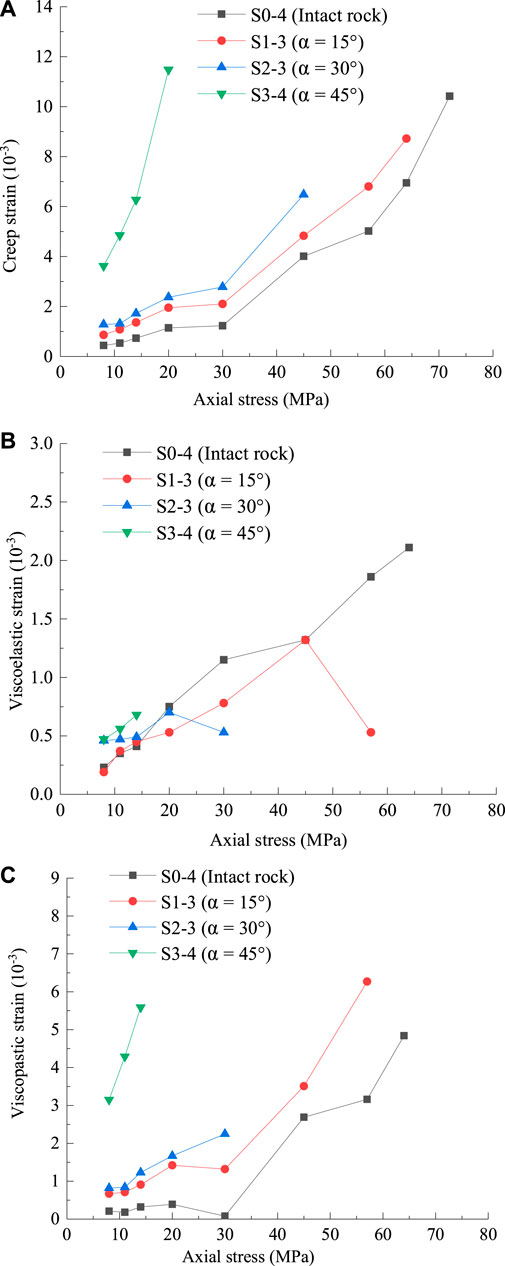
FIGURE 12. (A) Creep strain, (B) viscoelastic strain, and (C) viscoplastic strain curves of specimens from the first to the last stress levels.

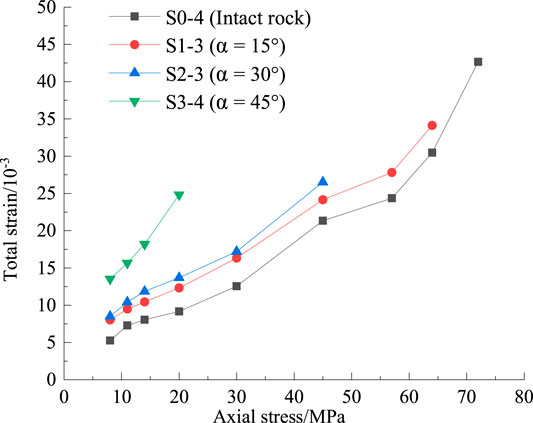
The proportion of creep strain to total strain is 25.3–60.5%. The minimum proportion of creep strain to total strain is specimen S1‐3 at 8 MPa, and the maximum case is specimen S3-4 at 20 MPa; as the stress increases, the proportion of creep strain to total strain increases. The proportion of creep strain to the total strain is more than 10% for all the specimens. Even considering the special case of specimen failure, the proportion of creep strain to total strain is up to 34% (specimen S3-4 at 14 MPa). Similarly, the relation of stress and total strain is shown in Figure 13. Obviously, as the stress increases, the total strain of the specimen increases.

FIGURE 13

FIGURE 13. Total strain curves of specimens from the first to the last stress levels.

The Effect of Weak Interlayer on the Rheological Failure Modes of Rocks

The rheological failure strengths of the rocks numbered S0-4, S1-3, S2-3, S3-4, and S4-3 are 72, 64, 45, 20, and 8 MPa, respectively. The rheological failure strengths of the specimens are about 72–96% of uniaxial compression strengths. Moreover, the WI promotes the rheological failure of the rock; the greater the WI inclination angle, the lower the rheological failure strength.

Figure 14 shows the failure modes of intact rock and rock containing WI. The intact specimens ar‐e mainly splitting and tensile failure. For the specimens containing WI, with the increase of the inclination angle, the specimen gradually transitions from the splitting failure to the shear failure. The specimens, containing small inclination angles (15° and 30°)WI, are mainly splitting failure, and the rheological failure mode is utter shear failure (see Figures 14D,E) when the inclination angle of WI becomes bigger. From triaxial compression tests, the internal friction angle of intact sandstone is 34.06°, the rock fracture angle is 62.03°. The rheological failure mode of the rock containing WI inclination angle 60° is an utter shear failure, which can be understood as that when the WI inclination angle of the rock is close to the rock fracture angle, the rock will failure along the inclination angle of the WI.

FIGURE 14

FIGURE 14. Failure mode of specimens.

Conclusion

(1) The rheological failure strength of sandstone containing WI decreases with the increase of WI inclination angle changing from 15° to 60°, and the decline is 86%. The failure strength, Poisson’s ratio, and elastic modulus of the intact rock are higher than those of the sandstones containing WI. Meanwhile, the uniaxial compressive strength, Poisson’s ratio, and Young’s modulus of the sandstones containing WI will decrease with the increase of inclination angle of WI. It is indicated that the rheological failure of rocks containing WI is faster and more severe than that of intact rocks.

(2) The steady-state creep strain rates of all the specimens are the lowest under the first stress level. When the rock is subjected to low loads, the strain rate is quickly attenuated to zero and shows only deceleration rheology. Whether it is intact sandstone or composite sandstone, the decay creep time at the first stress level is longer than that of other stress levels.

(3) At lower stress levels, the plastic strain of the intact specimen decreases with the increase of stress, and the plastic strain of the intact specimen increases with the increase of stress under high stress level. The plastic strain of the specimen containing WI always increases with the increase of the stress level. With the increase of stress level, the viscoelastic strain increases slowly for the intact specimen and decreases for the specimen containing WI; the larger the WI inclination angle is, the faster the viscoelastic strain decreases.

(4) The failure mode of intact specimen is splitting tensile failure, and the failure mode of rock containing WI is changed from splitting tensile failure to shear failure along the interface of WI. The larger the WI inclination angle, the more obvious the shear failure. Under the same axial stress level, the larger the WI inclination angle, the greater the rheological deformation, and the influence of rheological deformation on the stability of rock mass increases with the increase of WI inclination angle.

Data Availability Statement

All datasets generated for this study are included in the manuscript.

Author Contributions

LT conceived the conceptual framework and wrote the manuscript. YZ provided guidance for the strain analysis. JL and QL were responsible for data processing and figure plotting.

Funding

This work was financially supported by the National Natural Science Foundation of China (Nos. 51774131 and 51274097) and the CRSRI Open Research Program (CKWV2017508/KY).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer (HW) declared a shared affiliation with the authors to the handling editor at time of review.

References

ASTM D2938 (2002). Standard test method for unconfined compressive strength of intact rock core specimens. West Conshohocken, PA: Annual Book of ASTM Standards.

Google Scholar

Bai, F., Yang, X., and Zeng, G. (2014). Creep and recovery behavior characterization of asphalt mixture in compression. Constr. Build. Mater. 54, 504–511. doi:10.1016/j.conbuildmat.2013.12.088

CrossRef Full Text | Google Scholar

Fabre, G., and Pellet, F. (2006). Creep and time-dependent damage in argillaceous rocks. Int. J. Rock Mech. Min. Sci. 43, 950–960. doi:10.1016/j.ijrmms.2006.02.004

CrossRef Full Text | Google Scholar

Fan, Q. Z., and Gao, Y. F. (2005). Experimental study on creep properties of rocks under stepwise loading. Chin. J. Geotech. Eng. 27, 1273–1276. doi:1000%20134548(2005)11%20131273%201304

Google Scholar

Göbel, L., Osburg, A., and Pichler, B. (2018). The mechanical performance of polymer-modified cement pastes at early ages: ultra-short non-aging compression tests and multiscale homogenization. Constr. Build. Mater. 173, 495–507. doi:10.1016/j.conbuildmat.2018.04.033

CrossRef Full Text | Google Scholar

Griggs, D. (1939). Creep of rocks. J. Geol. 47, 225–251. doi:10.1086/624775

CrossRef Full Text | Google Scholar

Hu, B., Yang, S.-Q., Xu, P., and Cheng, J.-L. (2019). Cyclic loading-unloading creep behavior of composite layered specimens. Acta Geophys. 67, 449–464. doi:10.1007/s11600-019-00261-x

CrossRef Full Text | Google Scholar

Irfan-ul-Hassan, M., Königsberger, M., Reihsner, R., Hellmich, C., and Pichler, B. (2017). How water-aggregate interactions affect concrete creep: multiscale analysis. J. Nanomech. Micromech. 7 (4), 04017019. doi:10.1061/(asce)nm.2153-5477.0000135

CrossRef Full Text | Google Scholar

Irfan-ul-Hassan, M., Pichler, B., Reihsner, R., and Hellmich, C. (2016). Elastic and creep properties of young cement paste, as determined from hourly repeated minute-long quasi-static tests. Cem. Concr. Res. 82, 36–49. doi:10.1016/j.cemconres.2015.11.007

CrossRef Full Text | Google Scholar

Jiang, Y. Z., Xu, W. Y., Zhu, J. B., Wang, R. H., and Yang, S. Q. (2009). Rheology characteristics of rock with discontinuously weak intercalations. J. Yangtze River Sci. Res. Inst. 26, 71–75. doi:10.1007/s12040-018-1051-z

CrossRef Full Text | Google Scholar

Karte, P., Hlobil, M., Reihsner, R., Dörner, W., Lahayne, O., Eberhardsteiner, J., et al. (2015). Unloading-based stiffness characterisation of cement pastes during the second, third and fourth day after production. Strain 51 (2), 156–169. doi:10.1111/str.12129

CrossRef Full Text | Google Scholar

Kohlhauser, C., and Hellmich, C. (2013). Ultrasonic contact pulse transmission for elastic wave velocity and stiffness determination: influence of specimen geometry and porosity. Eng. Struct. 47, 115–133. doi:10.1016/j.engstruct.2012.10.027

CrossRef Full Text | Google Scholar

Königsberger, M., Irfan-ul-Hassan, M., Pichler, B., and Hellmich, C. (2016). Downscaling based identification of nonaging power-law creep of cement hydrates. J. Eng. Mech. 142 (12), 04016106. doi:10.1061/(asce)em.1943-7889.0001169

CrossRef Full Text | Google Scholar

Li, A., Shao, G. J., Fan, H. L., Du, P. R., and Zhu, Y. H. (2014). Investigation of mechanical properties of soft and hard interbedded composite rock mass based on meso-level heterogeneity. Chin. J. Rock Mech. Eng. 33, 3042–3049. doi:1000-6915(2014)Supplement 1-3042-06

Google Scholar

Li, W.-q., Li, X.-d., Han, B., and Shu, Y. (2007). Recognition of creep model of layer composite rock mass and its application. J Cent. South Univ. Technol. 14, 329–331. doi:10.1007/s11771-007-0275-x

CrossRef Full Text | Google Scholar

Li, Y., Liu, W., Yang, C., and Daemen, J. J. K. (2014). Experimental investigation of mechanical behavior of bedded rock salt containing inclined interlayer. Int. J. Rock Mech. Min. Sci. 69, 39–49. doi:10.1016/j.ijrmms.2014.03.006

CrossRef Full Text | Google Scholar

Li, Y., and Xia, C. (2000). Time-dependent tests on intact rocks in uniaxial compression. Int. J. Rock Mech. Min. Sci. 37, 467–475. doi:10.1016/s1365-1609(99)00073-8

CrossRef Full Text | Google Scholar

Lin, H., Yang, H. T., Wang, Y. X., Zhao, Y. L., and Cao, R. H. (2019). Determination of the stress field and crack initiation angle of an open flaw tip under uniaxial compression. Theor. Appl. Fract. Mech. 104, 102358. doi:10.1016/j.tafmec.2019.102358

CrossRef Full Text | Google Scholar

Ma, F. R., Zhang, X. G., Yan, L. E., and Yi, N. P. (2018). Influence of weak layer on the mechanical properties of stratified composite mudstone mass. Geotech. Investig. Survey. 46, 1–6.

Google Scholar

Maranini, E., and Brignoli, M. (1999). Creep behaviour of a weak rock: experimental characterization. Int. J. Rock Mech. Min. Sci. 36, 127–138. doi:10.1016/s0148-9062(98)00171-5

CrossRef Full Text | Google Scholar

Mishra, B., and Verma, P. (2015). Uniaxial and triaxial single and multistage creep tests on coal-measure shale rocks. Int. J. Coal Geol. 137, 55–65. doi:10.1016/j.coal.2014.11.005

CrossRef Full Text | Google Scholar

Ślizowski, J., and Lankof, L. (2003). Salt-mudstones and rock-salt suitabilities for radioactive-waste storage systems: rheological properties. Appl. Energy 75, 137–144. doi:10.1016/s0306-2619(03)00026-6

CrossRef Full Text | Google Scholar

Triantafyllidis, T., and Gerolymatou, E. (2014). Estimation of the strength of stratified rock mass. Rock Mech. Rock Eng. 47, 535–547. doi:10.1007/s00603-013-0431-6

CrossRef Full Text | Google Scholar

Tsai, L. S., Hsieh, Y. M., Weng, M. C., Huang, T. H., and Jeng, F. S. (2008). Time-dependent deformation behaviors of weak sandstones. Int. J. Rock Mech. Min. Sci. 45, 144–154. doi:10.1016/j.ijrmms.2007.04.008

CrossRef Full Text | Google Scholar

Wang, C., Pan, L., Zhao, Y., Zhang, Y., and Shen, W. (2019). Analysis of the pressure-pulse propagation in rock: a new approach to simultaneously determine permeability, porosity, and adsorption capacity. Rock Mech. Rock Eng. 52, 4301–4317. doi:10.1007/s00603-019-01874-w

CrossRef Full Text | Google Scholar

Wang, C. L., Zhao, Y., Zhao, Y. L., and Wan, W. (2018). Study on the interaction of collinear cracks and wing cracks and cracking behavior of rock under uniaxial compression. Adv. Civ. Eng. 2018, 5459307. doi:10.1155/2018/5459307

CrossRef Full Text | Google Scholar

Wang, R. H., Jiang, Y.Z., Yang, C., Huang, F., and Wang, Y. X. (2018). A nonlinear creep damage model of layered rock under unloading condition. Math. Probl Eng. 2018, 8294390. doi:10.1155/2018/8294390

CrossRef Full Text | Google Scholar

Wang, Y. X., Wang, S. Y., Zhao, Y. L., Guo, P. P., Liu, Y., and Cao, P. (2018). Blast induced crack propagation and damage accumulation in rock mass containing initial damage. Shock Vib. 2018, 3848620. doi:10.1155/2018/3848620

CrossRef Full Text | Google Scholar

Wang, Y. X., Wang, S. Y., Zhao, Y. L., Li, X., Guo, P. P., and Liu, Y. (2019). Analysis of fracturing characteristics of unconfined rock plate under edge-on impact loading. Eur. J. Environ. Civ. Eng. 2019, 1509021 doi:10.1080/19648189.2018.1509021

CrossRef Full Text | Google Scholar

Wang, Y., Zhang, H., Lin, H., Zhao, Y., and Liu, Y. (2020). Fracture behaviour of central-flawed rock plate under uniaxial compression. Theor. Appl. Fract. Mech. 106, 102503. doi:10.1016/j.tafmec.2020.102503

CrossRef Full Text | Google Scholar

Wu, Q., Chen, L., Shen, B., Dlamini, B., Li, S., and Y. J., Zhu. (2019a). Experimental investigation on rockbolt performance under the tension load. Rock Mech. Rock Eng. 52, 4605–4618. doi:10.1007/s00603-019-01845-1

CrossRef Full Text | Google Scholar

Wu, Q., Weng, L., Zhao, Y., Guo, B., and Luo, T. (2019b). On the tensile mechanical characteristics of fine-grained granite after heating/cooling treatments with different cooling rates. Eng. Geol. 253, 94–110. doi:10.1016/j.enggeo.2019.03.014

CrossRef Full Text | Google Scholar

Xiong, L. X., and Yang, D. L. (2010). Viscoelastic rheological model for interlayered rock mass and its numerical analysis. J. Tongji Univ. Nat. Sci. 38, 1281–1286. doi:10.3969/j.issn.0253-374x.2010.09.005

Google Scholar

Xu, S. G., Liang, W. G., Mo, J., and Zhao, Y. S. (2009). Influence of weak mudstone intercalated layer on mechanical properties of laminated salt rock. Chin. J. Undergr. Space Eng. 5, 878–883. doi:1001-5485(2009)12 -0071 -05

Google Scholar

Yang, S., and Jiang, Y. (2010). Triaxial mechanical creep behavior of sandstone. Min. Sci. Technol. 20, 339–349. doi:10.1016/s1674-5264(09)60206-4

CrossRef Full Text | Google Scholar

Yang, S.-Q., Xu, P., Ranjith, P. G., Chen, G.-F., and Jing, H.-W. (2015). Evaluation of creep mechanical behavior of deep-buried marble under triaxial cyclic loading. Arab J Geosci. 8, 6567–6582. doi:10.1007/s12517-014-1708-0

CrossRef Full Text | Google Scholar

Yang, T., Xu, T., Liu, H., Zhang, C., Wang, S., Rui, Y., et al. (2014). Rheological characteristics of weak rock mass and effects on the long-term stability of slopes. Rock Mech. Rock Eng. 47, 2253–2263. doi:10.1007/s00603-013-0527-z

CrossRef Full Text | Google Scholar

Zhao, Y., Zhang, L., Wang, W., Pu, C., Wan, W., and Tang, J., (2016). Cracking and stress-strain behavior of rock-like material containing two flaws under uniaxial compression. Rock Mech. Rock Eng. 49, 2665–2687. doi:10.1007/s00603-016-0932-1

CrossRef Full Text | Google Scholar

Zhao, Y. L., Tang, J. Z., Chen, Y., Zhang, L. Y., Wang, W. J., Wan, W., et al. (2017a). Hydromechanical coupling tests for mechanical and permeability characteristics of fractured limestone in complete stress–strain process. Environ Earth Sci. 76, 24. doi:10.1007/s12665-016-6322-x

CrossRef Full Text | Google Scholar

Zhao, Y., Wang, Y., Wang, W., Wan, W., and Tang, J. (2017b). Modeling of non-linear rheological behavior of hard rock using triaxial rheological experiment. Int. J. Rock Mech. Min. Sci. 93, 66–75. doi:10.1016/j.ijrmms.2017.01.004

CrossRef Full Text | Google Scholar

Zhao, Y., Zhang, L., Wang, W., Tang, J., Lin, H., and Wan, W. (2017c). Transient pulse test and morphological analysis of single rock fractures. Int. J. Rock Mech. Min. Sci. 91, 139–154. doi:10.1016/j.ijrmms.2016.11.016

CrossRef Full Text | Google Scholar

Zhao, Y., Zhang, L., Wang, W., Wan, W., Li, S., Ma, W., et al. (2017d). Creep behavior of intact and cracked limestone under multi-level loading and unloading cycles. Rock Mech. Rock Eng. 50, 1409–1424. doi:10.1007/s00603-017-1187-1

CrossRef Full Text | Google Scholar

Zhao, Y. L., Zhang, L. Y., Wang, W. J., Wan, W., and Ma, W. H. (2018). Separation of elastoviscoplastic strains of rock and a nonlinear creep model. Int. J. GeoMech. 18, 04017129. doi:10.1061/(asce)gm.1943-5622.0001033

CrossRef Full Text | Google Scholar

Zhao, Y., Wang, C., Zhang, Y., and Liu, Q. (2019a). Experimental study of adsorption effects on shale permeability. Nat. Resour. Res. 28, 1575–1586. doi:10.1007/s11053-019-09476-7

CrossRef Full Text | Google Scholar

Zhao, Y. L., Wang, Y. X., and Tang, L. M. (2019b). The compressive-shear fracture strength of rock containing water based on Druker- Prager failure criterion. Arab. J. Geosci. 12, 452. doi:10.1007/s12517-019-4628-1

CrossRef Full Text | Google Scholar

Zhao, Y., Wang, Y., Wang, W., Tang, L., Liu, Q., and Cheng, G. (2019c). Modeling of rheological fracture behavior of rock cracks subjected to hydraulic pressure and far field stresses. Theor. Appl. Fract. Mech. 101, 59–66. doi:10.1016/j.tafmec.2019.01.026

CrossRef Full Text | Google Scholar

Zhao, Y. L., Zhang, L. Y., Liao, J., Wang, W. J., Liu, Q., and Tang, L. M. (2020). Experimental study of fracture toughness and subcritical crack growth of three rocks under different environments. Int. J. GeoMech. 20 ( 8), 04020128. doi:10.1061/(asce)gm.1943-5622.0001779

CrossRef Full Text | Google Scholar

Zheng, W. X., Zhao, Y. L., and Bu, Q. W. (2018). The coupled control of floor heave based on a composite structure consisting of bolts and concrete antiarches. Math. Probl Eng. 2018, 3545423. doi:10.1155/2018/3545423

CrossRef Full Text | Google Scholar

Zhou, X. P. (2005). Localization of deformation and stress-strain relation for mesoscopic heterogeneous brittle rock materials under unloading. Theor. Appl. Fract. Mech. 44 ( 1), 27–43. doi:10.1016/j.tafmec.2005.05.003

CrossRef Full Text | Google Scholar

Zhou, X. P., and Bi, J. (2018). Numerical simulation of thermal cracking in rocks based on General Particle Dynamics. J. Eng. Mech. 144, 04017156. doi:10.1061/(asce)em.1943-7889.0001378

CrossRef Full Text | Google Scholar

Zhou, X. P., Bi, J., Deng, R. S., and Li, B. (2020). Effects of brittleness on crack behaviors in rock-like materials. J. Test. Eval. 48, 20170595. doi:10.1520/jte20170595

CrossRef Full Text | Google Scholar

Zhou, X. P., and Yang, H. Q. (2017). Dynamic damage localization in crack-weakened rock mass: strain energy density factor approach. Theor. Appl. Fract. Mech. 97, 289–302. doi:10.1016/j.tafmec.2017.05.006

CrossRef Full Text | Google Scholar

Zhou, X.-P., Zhang, Y.-X., Ha, Q.-L., and Zhu, K.-S. (2008). Micromechanical modelling of the complete stress-strain relationship for crack weakened rock subjected to compressive loading. Rock Mech. Rock Eng. 41( 5), 747–769. doi:10.1007/s00603-007-0130-2

CrossRef Full Text | Google Scholar

Zhou, Y.-Y., Feng, X.-T., Xu, D.-P., and Fan, Q.-X. (2017). An enhanced equivalent continuum model for layered rock mass incorporating bedding structure and stress dependence. Int. J. Rock Mech. Min. Sci. 97, 75–98. doi:10.1016/j.ijrmms.2017.06.006

CrossRef Full Text | Google Scholar

Zhou, Z. J., Zhan, H. C., Hu, J. Y., and Ren, C. N. (2019). Characteristics of unloading creep of tuffaceous sandstone in east Tianshan tunnel under freeze-thaw cycles. Adv. Mater. Sci. Eng. 2019, 7547564. doi:10.1155/2019/7547564

CrossRef Full Text | Google Scholar