Optimal Transponder Array and Survey Line Configurations for GNSS-A Observation Evaluated by Numerical Simulation

Introduction

The Global Navigation Satellite System-Acoustic ranging combination technique (GNSS-A) has realized the precise measurement of a reference point on the seafloor, expanding the crustal observation network into the ocean (Spiess, 1985; Asada and Yabuki, 2001; Fujita et al., 2006). In the GNSS-A observation of the Japan Coast Guard (JCG), the precise position of a survey vessel sailing along a survey line is measured using kinematic GNSS positioning, and the distances between the onboard transducer and the mirror transponders installed on the seafloor are measured using acoustic ranging (Figure 1A). Combining these data with the vessel attitude data and XBT/XCTD observations, the global coordinates of the virtual reference point (the centroid of the transponders) is precisely determined in the centimeter level. GNSS-A observation has revealed numerous tectonic phenomena such as the coseismic and postseismic movements of the 2011 Tohoku-oki earthquake $\left(M_{w}9.0\right)$ (Sato et al., 2011; Watanabe et al., 2014), interplate coupling in the Nankai Trough region (Yokota et al., 2016a), and shallow slow slip events that occurred near the Nankai Trough axis (Yokota and Ishikawa, 2020).

FIGURE 1

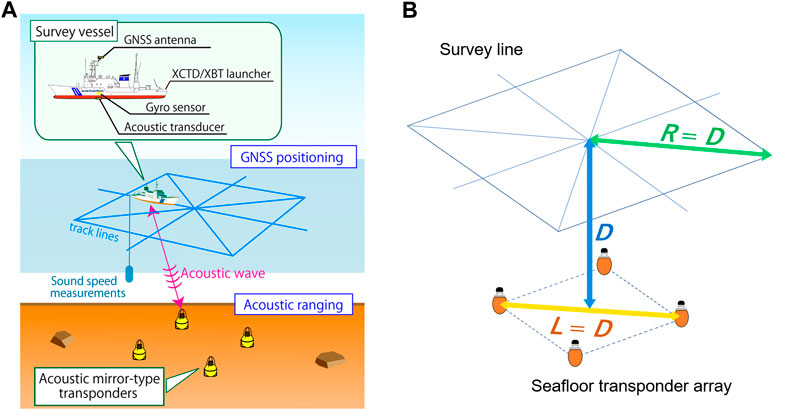
FIGURE 1. Schematic images of the current GNSS-A observation system conducted by the Japan Coast Guard. (A) is the overview of the entire GNSS-A observation system, and (B) indicates the configurations of the transponder array and the survey line. As shown in (B), the seafloor site depth (D), transponder array size (L), and survey line radius (R) are set to be equal.

The observation frequency has been a crucial matter for GNSS-A observation over the past 20 years, and we have been making significant efforts to improve the observation frequency. Despite the increase in the number of our seafloor sites, the observation frequency of the JCG group has improved from approximately one time per year per site in the early 2000s to 4 times per year per site by 2018 (Ishikawa et al., 2020). However, this frequency is still inadequate for observing tectonic phenomena with time scales less than few months (e.g. shallow short-term slow slip events).

One of the key factors that affects the observation efficiency is the size of the transponder array and the survey line, as shown in Figure 1B. In the early research by Spiess (1985), the proposed stationary observation system required at least three transponders, and the transponder array size has been defined that the circumdiameter of the transponder array should be approximately equal to the depth of the seafloor site.

However, the stationary system using a triangular transponder array proposed by Spiess (1985) was unable to detect the vertical displacement. To overcome this problem of detecting the vertical displacement, our research group has taken a different approach. We have developed an observation system that uses a vessel to perform a moving survey (Figure 1A), which is capable to detect both the horizontal and vertical displacements. In our system, although it is possible to detect the movement of only a single transponder, we deploy four transponders to form a square array as shown in Figure 1A to increase the positioning accuracy and stability. The transponder array size in our observation system is configured to be equal to the site depth, as done in Spiess (1985).

Regarding the survey line, theoretical studies by a research group in China have indicated that the optimal survey line radius is $\sqrt{2}$ times the depth of the seafloor site, which is the radius when the smallest geometric dilution of precision (GDOP) is achieved (Zhao et al., 2016). In the current observation system of our group, the survey line radius is set to be approximately equal to the depth of the seafloor site. Taking in account of the effects of vessel attitude and the seawater turbulence on the acoustic ranging, the maximum speed of the survey vessel during an observation is limited to approximately 6–7 knots. Therefore, deeper sites which have longer survey lines tend to take relatively longer observation times, and it is difficult to reduce the observation times of the deeper sites by increasing the vessel speed.

One possible approach to reduce the observation time for the deep sites is by reducing the transponder array size and the survey line radius which were empirically defined in the early studies (e.g. Spiess 1985). However, the effects of changing the transponder array size and the survey line radius on the accuracy of GNSS-A positioning have not been clearly investigated. In this study, we evaluated the effects of changing the transponder array size and the survey line radius on the accuracy of GNSS-A observation, by analyzing synthetically generated datasets.

We created a series of synthetic datasets with different transponder array sizes and survey line radii by using a numerical simulator (Yokota et al., 2016b) to evaluate the effects of changing these sizes on the positioning accuracy. In our numerical experiments, we assumed a simple square transponder array and assigned a symmetrical survey line. To focus only on the effects of changing the geometry of the observation system, we configured a simple sound speed structure with no horizontal and temporal variations. We analyzed these datasets like the actual GNSS-A datasets using the conventional linearized inversion method (Fujita et al., 2006).

Methods

The GNSS-A Simulator

We used a numerical simulator that has been developed to create synthetic GNSS-A observation datasets (Yokota et al., 2016b). In the GNSS-A simulator, the synthetic travel times are calculated between the synthetic vessel positions and the preconfigured transponder positions, and the outputs are formatted to be analyzed like an actual GNSS-A observation dataset. The GNSS-A simulator requires the following input files (also shown in Figure 2):

(I-1) Transponder position and error configuration file

(I-2) Survey line configuration file

(I-3) Sound speed profile configuration file (for synthetic acoustic travel time data)

(I-4) Sound speed profile configuration file (as pseudo-XBT data used in analysis)

FIGURE 2

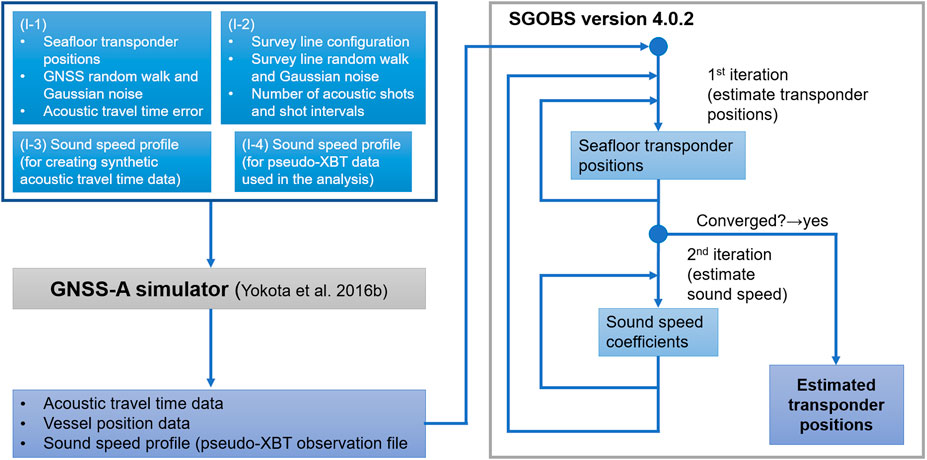
FIGURE 2. The flow chart of our numerical experiment. The input files (I-1), (I-2), (I-3), and (I-4) are used for the configurations of the numerical simulation by the GNSS-A simulator. The outputs of the GNSS-A simulator (the synthesized GNSS-A data) are analyzed using the analysis software SGOBS version 4.0.2, in which the linearized inversion method by Fujita et al. (2006) is implemented (right side of the figure).

In our simulation, the three-dimensional position is expressed by local East-North-Up (ENU) coordinates, with the origin at the sea surface directly above the centroid of the transponder array. Configuration file (I-1) contains the three-dimensional positions of the transponders, which are written in the local ENU coordinates. The acoustic travel time error, pseudo-random walk of the GNSS, and Gaussian noise of the GNSS are also configured in this file. Survey line configuration file (I-2) contains the survey line geometry and size, number of acoustic shots and shot interval for each survey line, and the pseudo-random walk and Gaussian noises of the survey line (which express random distortions of the survey line geometry). In the sound speed profile configuration file for the theoretical ray path calculation (I-3), the spatiotemporal variation of the sound speed profile can be configured. There is also a sound speed profile configuration file (I-4) for the pseudo-XBT data used in the analysis. The sound speed profile in (I-3) and (I-4) are configured at several depth layers; the sound speed at depths between these configured depth layers are either linearly interpolated or extrapolated. Settings for the vessel attitude and the offset between the GNSS antenna and the transducer are not implemented in this simulator; thus, the calculated vessel positions are equivalent to the transducer positions.

The resulting outputs of the calculated data are the acoustic travel time file, vessel position file, and the sound speed observation file. These output files can be analyzed like an actual GNSS-A dataset using the method of Fujita et al. (2006), as described in Figure 2 and Analysis of the Synthetic Datasets.

Configurations of the Numerical Experiments

In our study, we mainly edited input files (I-1) and (I-2) to configure the transponder positions and the survey line radius for each experimental run, and kept the settings in files (I-3) and (I-4) constant throughout all of the numerical experiments.

Since the focus of our study is on the possibility to reduce the observation times for the deep sites, we have set the depth of the seafloor site in file (I-1) to 3,000 m, which is a representative depth of the deepest seafloor sites installed by our research group. In our numerical experiments, the depths of all transponders were set to 3,000 m. This value was kept constant for all of the experimental runs. The transponder positions were set so that the transponders form a square array, with the centroid at position (0 m, 0 m, −3,000 m) in local ENU coordinates. For example, when we set the transponder array size to L, we assigned the transponders at (L/2, 0 m, −3,000 m) (−L/2, 0 m, −3,000 m) (0 m, L/2, −3,000 m), and (0 m, −L/2, 3,000 m), in local ENU coordinates. The transponder array size was changed depending on the experimental run.

In the survey line configuration file (I-2), a symmetrical survey line configuration currently adopted in our GNSS-A observation, as shown in Figure 1B, is configured. Like the transponder positions, the survey line radius was also changed depending on the type of the experimental run. For each trial of data synthesis and analysis, a total of four sets with each having 784 acoustic shots were simulated to create a single GNSS-A dataset with a total of 3,136 shots. The acoustic shots were created at a constant time interval, to synthesize a geometrically well-balanced data, as we do in the actual observations. The number of acoustic shots per line and the shot intervals were tuned so that the total simulated acoustic shots is 3,136 for each trial, regardless of the survey line radius.

We configured a simple sound speed structure in files (I-3) and (I-4) that has no horizontal sound speed gradient nor temporal variation. Such a simplified sound speed structure was used instead of a more realistic model (e.g. Munk, 1974), since our focus is on how the GNSS-A positioning accuracy is affected by changing the transponder array size and the survey line radius. The configured values for the ray path calculation in (I-3) were 1,505.00 m/s at 0 m, 1,494.30 m/s at 400 m, and 1,490.00 m/s at depths below 600 m, as shown in the left of Figure 3A. The acoustic shots calculated using these values have round-trip travel times ranging roughly 4–10 s and takeoff angles ranging roughly from $100°-180°$, depending on the transponder array size and the survey line radius. As shown in the right of Figure 3A, we configured values in (I-4) for the XBT data used in the analysis that were almost identical to the values configured in (I-3). Since the temporal variation estimated in SGOBS ver. 4.0.2 is much larger in magnitude compared to the XBT measurement errors, our settings of the XBT measurement errors should not affect the outcome of the simulation.

FIGURE 3

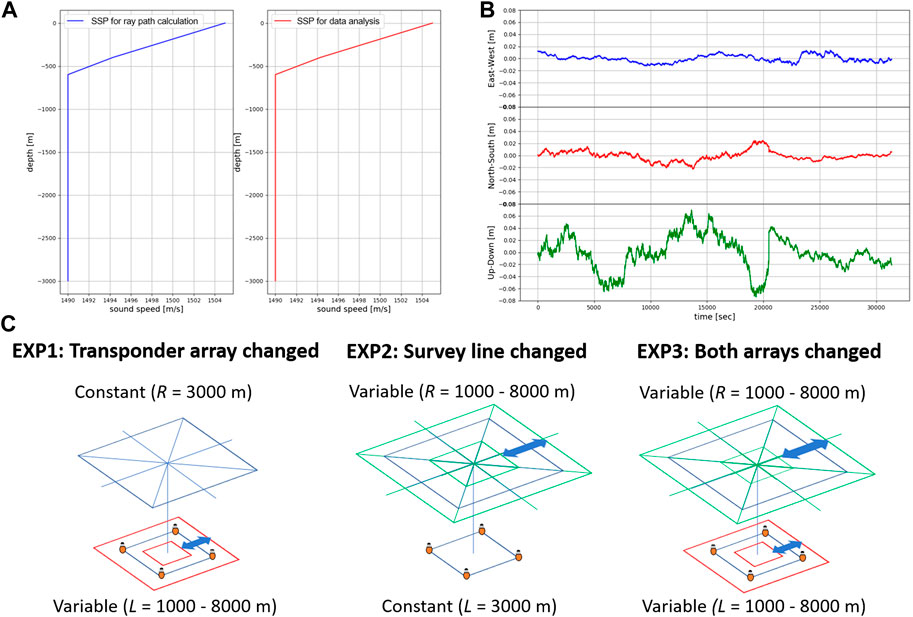
FIGURE 3. The configurations of our numerical experiment. (A) shows the vertical sound speed profile (SSP) configured for the ray path calculation (left, blue line) and the vertical SSP used in the data analysis (right, red line). Note that the difference between these two profiles is so small that the difference cannot be distinguished in this figure (see Configurations of the Numerical Experiments for details). (B) indicates sample waveforms of the GNSS pseudo-random walk added to the synthesized data (from top to bottom, the east-west, north-south, and up-down components). (C) is the schematic diagram of the settings of EXP1, EXP2, and EXP3, from left to right (see Configurations of the Numerical Experiments for details).

We created high-rate pseudo-GNSS noises using the Box-Muller’s method (Box and Muller, 1958). For the pseudo-GNSS noise, we assigned a Gaussian noise and a random walk for the vertical and horizontal components. Gaussian noise and random walk were empirically known to be included in the GNSS noises (Bilich et al., 2008). The values of 1$\sigma$ of the pseudo-GNSS noises, implemented in file (I-1), were 0.5 cm for the horizontal Gaussian noise, 1.5 cm for the vertical Gaussian noise, 2.5 cm for the horizontal random walk, and 7.5 cm for the vertical random walk. Sample waveforms of the random walk are shown in Figure 3B. To focus on how the transponder array size and the survey line radius affect the GNSS-A positioning accuracy, we have only added the pseudo-GNSS noises, and did not configure the travel time errors in our experiments.

We performed a series of experimental runs as shown in Figure 3C to evaluate the individual and the combined effects of changing the transponder array size and the survey line radius on the GNSS-A positioning accuracy. In our first experiment, only the transponder array size was changed from 1,000 m to 8,000 m at 1,000 m intervals, and the survey line radius was fixed to 3,000 m (EXP1 in Figure 3C). In our second experiment, only the survey line radius was changed from 1,000 m to 8,000 m at 1,000 m intervals, and the transponder array size was fixed to 3,000 m (EXP2 in Figure 3C). In the third experiment (EXP3 in Figure 3C), both the transponder array size and the survey line radius were simultaneously changed from 1,000 m to 8,000 m at 1,000 m intervals (e.g. when the transponder array size is configured to 8,000 m, the survey line radius is also configured to 8,000 m). Additionally, we have also performed an experiment with a transponder array size of 2,000 m and a survey line radius of 4,000 m, and another experiment with a transponder array size of 4,000 m and a survey line radius of 2,000 m, to closely examine the effects of transponder array sizes and survey line radii around 2,000–4,000 m. As stated above in this section, note that the site depth is fixed to 3,000 m for all experimental runs.

To evaluate the positioning accuracy, we conducted 300 trials of data synthesis and analysis for each experimental run. For each trial, we created pseudo-GNSS noises as assigned in file (I-1), and added the noises to the synthetic data, to create data variation among the trials.

Analysis of the Synthetic Datasets

For the analysis of the synthetic datasets, we used the analysis software SGOBS version 4.0.2, in which the method developed by Fujita et al. (2006) is implemented. SGOBS version 4.0.2 is regularly used in the observation and analysis routine of our group. In the method of Fujita et al. (2006), the sound speed structure and the three-dimensional transponder positions are alternately estimated using Bayesian inversion. As shown in the right of Figure 2, this algorithm first iterates to determine the positions of the seafloor transponders using the initial sound speed profile, and then the resulting residuals of the first loop are used in the second loop to determine the sound speed coefficient. Then, the transponder positions are determined again using the newly estimated sound speed coefficients, and so on. These iterations are repeated until both the sound speed and the transponder positions satisfy the convergence criteria. The centroid of the transponder positions is calculated from the final estimations of the transponder positions.

In the actual GNSS-A observations, acoustic shots with extremely small takeoff angles may be due to fake return signals, such as echoes from the seafloor. In order to remove such acoustic shots that may not be responses from the transponders, acoustic shots with takeoff angles less than $120°$ are removed in the algorithm of SGOBS version 4.0.2.

To evaluate the GNSS-A positioning accuracy, we defined three criteria as listed below:

The average horizontal error of the centroid (${\mu }_{Ch}$)

The average horizontal error of the four transponders (${\mu }_{\overline{M}}$)

The average vertical error of the centroid (${\mu }_{Cv}$)

The average horizontal error of the centroid (${\mu }_{Ch}$) is defined as the average displacement of the horizontal centroid positions of the $N$ trials from the “true” horizontal position of the centroid C₀. As explained in Configurations of the Numerical Experiments, the horizontal centroid position C₀ is always at (0 m, 0 m) regardless of the transponder array size. Let C_i be the estimated horizontal position of the centroid of the ith trial, and ${\mu }_{Ch}$ can be calculated as follows:

${\mu }_{Ch}=\frac{1}{N}{\displaystyle \sum _{i=1}^N\left|{\mathit{C}}_i-{\mathit{C}}_0\right|}.$

${\mu }_{\overline{M}}$ is calculated by averaging the horizontal errors of the four transponders numbered j (j = 1, 2, 3, 4, corresponding to the transponder in the east, west, north, and south of the centroid). Let M_i^j be the estimated horizontal position of the jth transponder in the ith trial, and M₀^j be the “true” horizontal position of the jth transponder configured in file (I-1), and the average horizontal error of the four transponders for the ith trial ${\overline{M}}_i$ is expressed as:

${\overline{M}}_i=\frac{1}{4}{\displaystyle \sum _{j=1}^4\left|{\mathit{M}}_i^j-{\mathit{M}}_0^j\right|}.$

Thus, the average horizontal error of the four transponders for $N$ trials, ${\mu }_{\overline{M}}$ can be simply calculated as the average of ${\overline{M}}_i$ for all trials:

${\mu }_{\overline{M}}=\frac{1}{N}{\displaystyle \sum _{i=1}^N{\overline{M}}_i}.$

The average vertical error of the centroid ${\sigma }_{Cv}$ is calculated by averaging the absolute value of the anomaly of the $N$ trials from the “true” vertical position of the centroid, $d$, configured in file (I-1), which is constantly $d=\mathrm{3,000}\text{m}$ for all trials in all experimental runs. Thus, when the vertical position of the centroid for the ith trial is defined as $u_{C_i}$, ${\mu }_{Cv}$ is simply calculated as below:

${\mu }_{Cv}=\frac{1}{N}{\displaystyle \sum _{i=1}^N\left|u_{C_i}-d\right|}.$

In Results and Discussion, the results will be evaluated by calculating and plotting the values of ${\mu }_{Ch}$, ${\mu }_{\overline{M}}$, ${\mu }_{Cv}$ of each experimental run. Since 300 trials were performed for each run, $N=300$ in these equations above for this study.

Results

Figures 4A–C indicate the values of ${\mu }_{Ch}$, ${\mu }_{\overline{M}}$, and ${\mu }_{Cv}$ obtained from the numerical experiments, respectively. Figure 4A indicates that the horizontal positioning accuracy of the centroid decreases when the survey line radius is shrunk to less than 3,000 m. When the survey line radius is fixed to 3,000 m, the change in the values of ${\mu }_{Ch}$ is small, regardless of the transponder array size. Overall, the values of ${\mu }_{Ch}$ fluctuate within the range of few centimeters, indicating that changing the transponder array size and the survey line radius do not significantly affect the horizontal positioning accuracy of the centroid.

FIGURE 4

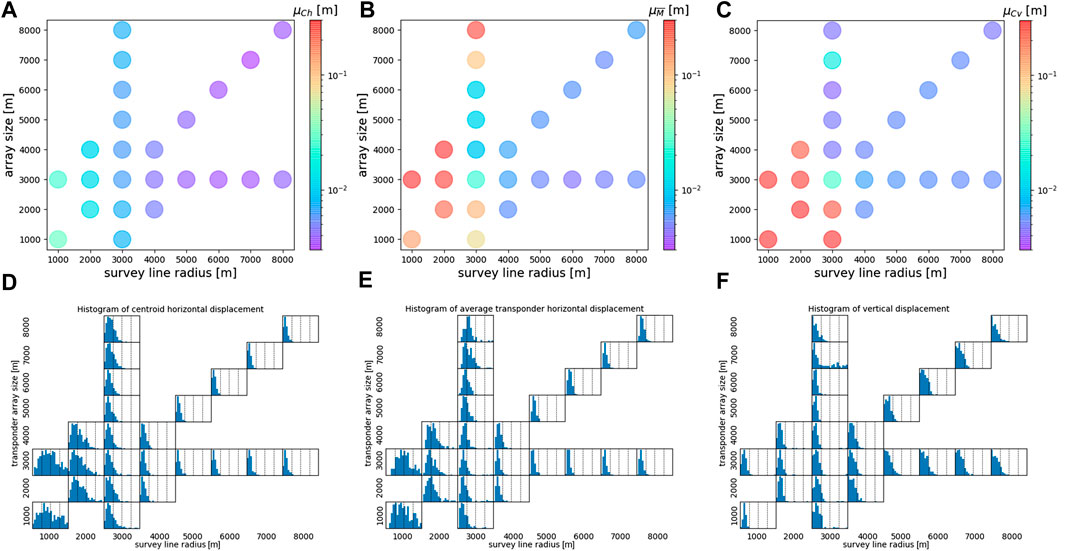
FIGURE 4. The results of the numerical experiments. Figure (A) is the plot of the average horizontal error of the centroid ${\mu }_{Ch}$, (B) is the plot of the average horizontal error of the four transponders ${\mu }_{\overline{M}}$, (C) is the plot of the average vertical error of the centroid ${\mu }_{Cv}$. Figure (D) is the histogram of the horizontal error of the centroid obtained from 300 trials for each experimental run, (E) is the histogram of the average horizontal error of the four transponders, and (F) is the histogram of the vertical error of the centroid. The range of these histograms are from 0 cm to 4 cm, and the dashed lines indicate 1 cm intervals. Note that Figures (D), (E), and (F) have outliers that exceed 4 cm.

Meanwhile, the values of ${\mu }_{\overline{M}}$ (Figure 4B) shows that the horizontal positioning accuracies of the individual transponders fluctuate in the order of decimeters. This indicates that unlike the centroid, the positioning accuracy of each transponder is clearly affected by changing the transponder array size and/or the survey line radius. ${\mu }_{\overline{M}}$ is approximately 2 cm for an array size of 3,000 m, but when the transponder array size is shrunk to less than 3,000 m, ${\mu }_{\overline{M}}$ becomes greater than 10 cm. The positioning accuracy is degraded even more when the survey line radius is shrunk to less than 3,000 m; ${\mu }_{\overline{M}}$ becomes greater than 20 cm ${\mu }_{\overline{M}}$ also increases when the survey line radius is fixed to 3,000 m and the transponder array size is greater than 6,000 m, exceeding 20 cm when the transponder array size is 8,000 m.

Figure 4C shows that the average error of the vertical position ${\mu }_{Cv}$ generally increases as the transponder array size and/or the survey line radius decrease. When the transponder array size and/or the survey line radius become smaller than 3,000 m, ${\mu }_{Cv}$ rapidly increases, and the values exceed 20 cm. This result indicates that the vertical positioning becomes inaccurate and unstable as these sizes decrease. However, when the transponder array size and the survey line radius become larger than 3,000 m, ${\mu }_{Cv}$ rapidly converges to values less than 1 cm.

Figures 4D–F shows the histograms of the horizontal error of the centroid, the average horizontal error of the four transponders, and the vertical error of the centroid, respectively. All histograms indicate the frequency of errors in the range of 0–4 cm. Figures 4D,E show that the distribution peaks of the horizontal errors become generally sharper, and the peak gradually shifts to 0 cm as the transponder array size and the survey line radius increase. This indicates that the horizontal positioning accuracy generally improves as these sizes increase. In Figure 4F, the histograms of the vertical error, the distribution peak shifts toward 0 cm as the transponder array size and the survey line radius increase. This result shows that the vertical positioning accuracy also improves by increasing these sizes.

Discussion

Effects of Changing the Transponder Array Size

Figure 4B indicates that ${\mu }_{\overline{M}}$ increases rapidly as the transponder array size becomes greater than 6,000 m, when the survey line radius is fixed to 3,000 m. Histograms in Figure 4E show that when the survey line radius is fixed to 3,000 m and the transponder array size becomes greater than 6,000 m, the distribution peak becomes wider and shifts away from 0 cm. These results imply that the horizontal positioning errors of each transponder becomes larger when the transponder array size becomes wider than the survey line radius. When the transponder array is larger than the area covered by the survey line, most of the acoustic shots will be taken from the inside of the transponder array. Since a geometrically well-balanced acoustic data is necessary for GNSS-A observation, such poorly balanced data would degrade the positioning accuracy, leading to the results shown in Figure 4B.

The values of ${\mu }_{\overline{M}}$ also increase when the transponder array size is shrunk to less than 3,000 m, as well as the vertical error ${\mu }_{Cv}$ (Figure 4C). Shrinking the transponder array size would eventually converge as observing a single transponder at the centroid. The position obtained by observing only a single transponder is unstable compared to the position of the centroid obtained by observing a square array of four transponders, which may be the cause of the decrease in positioning accuracy when the transponder array size is decreased.

However, the values of ${\mu }_{Ch}$ remain relatively stable throughout all array sizes when the survey line radius is kept constant at 3,000 m, each ranging between 6 and 10 mm (Figure 4A). The results of ${\mu }_{Ch}$ imply that the horizontal positioning of the centroid is not significantly affected by shrinking the transponder array size, despite the fact that ${\mu }_{\overline{M}}$ significantly increases by shrinking the array. This indicates that rather than determining the position of an individual transponder as the position of a seafloor site, determining the centroid of a square transponder array is an effective method for reducing observation errors and stably positioning a seafloor site.

Effects of Changing the Survey Line Radius

In general, larger survey line radius enhances the variation of the takeoff angles of the acoustic shots, which leads to improved positioning accuracy, as shown in Figure 4. This is analogous to a good constellation geometry in GNSS positioning; it is better that the GNSS satellites spread out evenly across the sky rather than being confined in a very small area.

Shrinking the survey line radius would eventually converge as a stationary observation at the sea surface directly above the centroid. The takeoff angle variation of the acoustic shots decreases since the survey range is confined to a smaller area. Unlike the transponder arrangement proposed by Tomita et al. (2019), our square transponder array cannot determine the vertical displacement by stationary observation. Our results shown in Figure 4C indicate that ${\mu }_{Cv}$ rapidly increases as the survey line radius is decreased below 3,000 m. The histogram (Figure 4F) also shows that the distribution peak gradually shifts away from 0 cm as the survey line radius decrease, implying the decrease in the positioning accuracy. ${\mu }_{\overline{M}}$ (Figure 4B) and the histograms (Figure 4E) indicate that the horizontal positioning of the individual transponders is degraded as well by decreasing the survey line radius. Nevertheless, the values of ${\mu }_{Ch}$ when the survey line radius is less than 3,000 m are much smaller compared to the values of ${\mu }_{\overline{M}}$. This indicates that positioning the centroid of the seafloor transponders forming a square array is an effective method to reduce the horizontal positioning error.

When the survey line radius is increased, all of the errors tend to become very small. However, it must be noted that the availability of the acoustic data in the analyses for a very large survey line radius is very poor. For example, when the survey line radius is 8,000 m, the data availability is around 30–50%. This is due to the takeoff angle limitation in our GNSS-A observation to exclude acoustic signals transmitted from takeoff angles that are less than $120°$, as explained in Analysis of the Synthetic Datasets. Thus, although very large survey line radii seem to perform well regarding the positioning accuracies, these radii are not suitable for the actual observation routine. Also, the improvement of the positioning accuracy when configuring a survey line radius larger than 3,000 m is small, improving only in order of millimeters, compared to the significant increase in the observation time, making the observation inefficient.

The Optimal Transponder Array Size and Survey Line Radius

We can imply from Figure 4 that when regarding the horizontal and vertical positioning accuracies, the transponder array size and the survey line radius should be as large as possible. However, due to the takeoff angle limitation explained in Effects of Changing the Survey Line Radius, the optimal transponder array size and survey line radius for our observation system is limited to approximately 3,000–4,000 m. When regarding both the observation time and the positioning accuracy, the transponder array size and survey line radius of 3,000 m, which is equal to the empirically defined sizes for a depth of 3,000 m, seems to be quite optimal. When the sizes are less than 3,000 m, the positioning errors become too large for crustal monitoring. When the sizes are greater than 3,000 m, the improvement of the positioning accuracy is small compared to the significant increase in the observation time. It can be concluded that the trade-off between the positioning accuracy and the observation time is well balanced at our empirically defined sizes. Also, it must be noted that in the real world, increasing the transponder array size and the survey line radius would increase errors due to the spatial variability of the sound speed structure.

Figure 4A has indicated that the horizontal positioning error of the centroid of the transponders remains stable when the transponder array size and/or the survey line radius is changed. This result implies that it is possible to obtain the horizontal positions of a site with a transponder array size and a survey line radius that is smaller than our empirically defined sizes. One of the limitations when installing a site is the seafloor topography; there are cases where we cannot install a site with the empirically defined transponder array size, due to the lack of a smooth seafloor. When regarding only the horizontal positioning accuracy, we can shrink the transponder array size to some degree, which would give us more valuable options when installing a site. Also, the result that the horizontal positioning is not significantly affected by shrinking the survey line radius indicates a possibility that we can reduce the observation time. By reducing the observation time and increasing the observation frequency, we can improve the accuracy of the time series of the horizontal positions. An improved time series of the horizontal positions would provide us valuable information on the temporal variation of the seafloor crustal deformation.

Our simulation results may also be applied to the observations of other institutions, with different survey line geometry. As explained in Effects of Changing the Survey Line Radius, assigning a large survey line radius enables us to obtain acoustic data with larger variation of takeoff angles, which is necessary for achieving high positioning accuracies for both the horizontal and the vertical components. Thus, it may be possible that the optimal sizes indicated in our study can be applied to other types of survey line geometry, if the survey line geometry is configured to obtain acoustic data with large variation of the takeoff angles.

Future Works

The results of the numerical experiments indicated that the positioning accuracy is degraded rapidly assuming transponder array size and survey line radius of less than 3,000 m for a site with 3,000 m of depth. Thus, shrinking the transponder array size and the survey line radius is not a suitable solution for improving observation frequency. In fact, the empirically defined sizes, which is equal to 3,000 m in the experiments of our study, are quite optimal values when regarding both the positioning accuracy and observation efficiency.

GNSS-A observation has numerous error sources other than those focused in this study. One of the main error sources is the spatiotemporal variation of the sound speed structure, which has been investigated in numerous studies (e .g. Yasuda et al., 2017; Honsho et al., 2019; Yokota et al., 2019). Assessing the effects of the temporal change of the sound speed structure and the horizontal sound speed gradient on the GNSS-A accuracy is one of the main topics for our future research using the GNSS-A simulator. Numerical experiments using different transponder arrangements such as those proposed by Tomita et al. (2019) is an important topic as well, since there is a possibility that the positioning accuracy may improve by changing the arrangement of the transponders. Also, a new analysis software that directly estimates the sound speed structure using a Bayesian approach is being developed (Watanabe et al., 2020). We can utilize the simulator to validate the capability of this new software to accurately determine the transponder positions and to properly estimate the sound speed structure. We plan to further investigate the GNSS-A observation errors by taking the approach using numerical simulation, as done in this study.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

YN designed the study and wrote this manuscript. YY developed and tuned the GNSS-A simulator. YN, YY, TI, SW discussed about the simulation configurations and the results, and commented to improving the manuscript.

Funding

The submission of this manuscript was funded by the Japan Coast Guard.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank the many staff members from the Hydrographic and Oceanographic Department, Japan Coast Guard, including the crew of the survey vessels Takuyo, Shoyo, Meiyo, and Kaiyo for their support in our observations and technological developments. We especially thank the active senior staff members from the Geodesy and Geophysics Office, Hydrographic and Oceanographic Department, Japan Coast Guard, for their devoted maintenance and management of the equipment.

References

Asada, A., and Yabuki, T. (2001). Centimeter-level positioning on the seafloor. Proc. Jpn. Acad. Ser. B 77, 7–12. doi:10.2183/pjab.77.7

CrossRef Full Text | Google Scholar

Bilich, A., Larson, K. M., and Axelrad, P. (2008). Modeling GPS phase multipath with SNR: case study from the salar de Uyuni, boliva. J. Geophys. Res. 113, B04401. doi:10.1029/2007JB005194

CrossRef Full Text | Google Scholar

Box, G. E. P., and Muller, M. E. (1958). A note on the generation of random normal deviates. Ann. Math. Stat. 29 (2), 610–611. doi:10.1214/aoms/1177706645

CrossRef Full Text | Google Scholar

Fujita, M., Ishikawa, T., Mochizuki, M., Sato, M., Toyama, S., Katayama, M., et al. (2006). GPS/acoustic seafloor geodetic observation: method of data analysis and its application. Earth Planets Space 58, 265–275. doi:10.1186/BF03351923

CrossRef Full Text | Google Scholar

Honsho, C., Kido, M., Tomita, F., and Uchida, N. (2019). Offshore postseismic deformation of the 2011 Tohoku earthquake revisited: application of an improved GPS-acoustic positioning method considering horizontal gradient of sound speed structure. J. Geophys. Res. Solid Earth 124. doi:10.1029/2018JB017135

CrossRef Full Text | Google Scholar

Ishikawa, T., Yokota, Y., Watanabe, S., and Nakamura, Y. (2020). History of on-board equipment improvement for GNSS-A observation with focus on observation frequency. Front. Earth Sci. 8, 150. doi:10.3389/feart.2020.00150

CrossRef Full Text | Google Scholar

Munk, W. H. (1974). Sound channel in an exponentially stratified ocean, with application to SOFAR. J. Acoust. Soc. Am. 55, 220. doi:10.1121/1.1914492

CrossRef Full Text | Google Scholar

Sato, M., Ishikawa, T., Ujihara, N., Yoshida, S., Fujita, M., Mochizuki, M., et al. (2011). Displacement above the hypocenter of the 2011 Tohoku-oki earthquake. Science 332, 1395. doi:10.1126/science.1207401

PubMed Abstract | CrossRef Full Text | Google Scholar

Spiess, F. N. (1985). Suboceanic geodetic measurements. IEEE Trans. Geosci. Remote Sensing, GE-23, 502–510. doi:10.1109/TGRS.1985.289441

CrossRef Full Text | Google Scholar

Tomita, F., Kido, M., Honsho, C., and Matsui, R. (2019). Development of a kinematic GNSS-Acoustic positioning method based on a state-space model. Earth Planets Space 71, 102. doi:10.1186/s40623-019-1082-y

CrossRef Full Text | Google Scholar

Watanabe, S., Ishikawa, T., Yokota, Y., and Nakamura, Y. (2020). GARPOS: analysis software for the GNSS-A seafloor positioning with simultaneous estimation of sound speed structure. Front. Earth Sci. 8, 597532. doi:10.3389/feart.2020.597532

CrossRef Full Text | Google Scholar

Watanabe, S., Sato, M., Fujita, M., Ishikawa, T., Yokota, Y., Ujihara, N., et al. (2014). Evidence of viscoelastic deformation following the 2011 Tohoku-oki earthquake revealed from seafloor geodetic observation. Geophys. Res. Lett. 41, 5789–5796. doi:10.1002/2014GL061134

CrossRef Full Text | Google Scholar

Yasuda, K., Tadokoro, K., Taniguchi, S., Kimura, H., and Matsuhiro, K. (2017). Interplate locking condition derived from seafloor geodetic observation in the shallowest subduction segment at the Central Nankai Trough, Japan. Geophys. Res. Lett. 44, 3572–3579. doi:10.1002/2017GL072918

CrossRef Full Text | Google Scholar

Yokota, Y., and Ishikawa, T. (2020). Shallow slow slip events along the Nankai Trough detected by GNSS-A. Science Advances 6, eaay5786. doi:10.1126/sciadv.aay5786

PubMed Abstract | CrossRef Full Text | Google Scholar

Yokota, Y., Ishikawa, T., and Watanabe, S. (2019). Gradient field of undersea sound speed structure extracted from the GNSS-A oceanography. Mar. Geophys. Res. 40 (4), 493–504. doi:10.1007/s11001-018-9362-7

CrossRef Full Text | Google Scholar

Yokota, Y., Ishikawa, T., Watanabe, S., Tashiro, T., and Asada, A. (2016a). Seafloor geodetic constraints on interplate coupling of the Nankai Trough megathrust zone. Nature 534, 374–377. doi:10.1038/nature17632

CrossRef Full Text | Google Scholar

Yokota, Y., Tashiro, T., Ishikawa, T., and Watanabe, S. (2016b). Development of numerical simulator for seafloor geodetic observation system [in Japanese]. Rep. Hydrogr. Oceanogr. Researches 53, 90–97.

Google Scholar

Zhao, J., Zou, Y., Zhang, H., Wu, Y., and Fang, S. (2016). A new method for absolute datum transfer in seafloor control network measurement. J. Mar. Sci. Technol. 21, 216–226. doi:10.1007/s00773-015-0344-z

CrossRef Full Text | Google Scholar