- 1State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Chengdu University of Technology, Chengdu, China
- 2Tarim Oilfield Company, PetroChina, Korla, Xinjiang, China
- 3CNPC Xibu Drilling Engineering Company Limited, Xinjiang, China
- 4PetroChina Research Institute of Petroleum Exploration and Development and Research Center of Sichuan Basin, Chengdu, China
We use analog experiments to investigate the influence of rapid filling of a foreland basin system during the development of a fold-and-thrust belt, in particular, the change of erosion–sedimentation along the strike in the Longmenshan foreland basin. A negative relationship between wedge geometries and the magnitude of erosion can be found; increased erosion results in out-of-sequence thrusting and fault reactivation in the wedge hinterland, to limit the forelandward propagation of the wedge. In contrast, increased sedimentation facilitates the forelandward propagation of the wedge. We focus on a natural example of the Longmenshan foreland basin, where a change in erosion–sedimentation along the strike during the Late Cretaceous to Cenozoic is well documented. The comparison between our model and seismic sections indicates that such along-strike variation results in a rejuvenated foreland basin restricted to the southwestern part of the western Sichuan Basin in the Cenozoic.
Introduction
Tectonic–erosion–sedimentation interaction controls the evolution of fold-and-thrust belt and foreland basin system at different time and space scales. This process plays an important role in controlling the material energy transfer and transportation process in the basin-mountain system, leading to the dynamic equilibrium of tectonic deformation, uplift, erosion, and sedimentation (Hack, 1975; Kooi and Beaumont, 1996). In the 1980s, the thrust belt and foreland basin system model was compared to that of “a pile of sand in front of a moving bulldozer” (Davis et al., 1983), of which the mechanical and structural evolution could be attributed to the critical Coulomb wedge theory (Chapple, 1978; Davis et al., 1983; Dahlen, 1984; Dahlen et al., 1984; Dahlen and Suppe, 1988; Decelles and Mitra, 1995), e.g., the Sevier orogenic wedge, Taiwan wedge, and Canadian Rockies wedge. Critical taper is attained when the angle between the base and surface of the wedge reaches a critical value with stable geometry and is maintained as the offsetting effects of deformation in the rear of the wedge and forward propagation in front of the wedge. When the critical taper remains, the wedge is considered to be stable (i.e., critical state). As a result, deformation is restricted to slide along the basal detachment. However, the erosion can decrease the wedge taper (i.e., subcritical state), and result in the locus of deformation shifting to the rear of the wedge in order to maintain a critical taper. Furthermore, the deformation at the rear of the wedge increases the wedge taper larger than the critical taper, causing a supercritical state and propagates forelandward over large distances to rebuild a critical taper (Decelles and Mitra, 1995).
Based on analog experiments and natural examples (e.g., Decelles and Mitra, 1995; Bonnet et al., 2007; Cruz et al., 2008; Wu and McClay, 2011; Graveleau et al., 2012 and references in), increased surface processes will transform the thrust belt and foreland basin system from a critical state to an unstable state (i.e., subcritical or supercritical state). This transformation will lead to the uplift and erosion of wedges, change in the geometry of wedges, multi-stage reactivation of faults, thermal convection, and unstable geomorphic construction processes (Willett et al., 1993; Persson et al., 2004; Hoth et al., 2006; Cruz et al., 2008; Konstantinovskaya and Malavieille, 2011). Cruz et al. (2008) suggested wedge erosion increases the density of fore-shears and controls the wedge geometry and its topographic divide migration. Fillon et al. (2013) and Erdõs et al. (2015) argued the first-order control of syntectonic sedimentation on wedge geometry and thrust spacing. However, analog experiments lack quantitative studies on the material flux in the process of tectonic erosion–sedimentation and their coupling process, and therefore, quantitative comparisons between stable and unstable surface processes of the foreland basin system are still not fully understood (Malavieille, 2010; Sieniawska et al., 2010; Konstantinovskaya and Malavieille, 2011).
The Longmenshan thrust belt and foreland basin system have the largest terrain gradient around the whole Tibetan Plateau. Controlled by multi-stage tectonic movements and sedimentary loading, a Late Cretaceous–Cenozoic rejuvenated foreland basin occurred at the southern segment of the western Sichuan basin, overlying the Late Triassic–Early Jurassic peripheral foreland basin across the western Sichuan basin (Liu et al., 1994, 2005; Jia et al., 2006; Deng et al., 2012). They are consistent with strong uplift and erosion that occurred at the southern segment of Longmenshan in the Cenozoic (Wang et al., 2012; Tian et al., 2013; Tan et al., 2017), as well as much larger topographic relief in the south. This indicates a significant influence of the surface process (i.e., erosion–sedimentation) on the foreland basin occurred in the late Mesozoic and Cenozoic time across the Longmenshan (Hubbard and Shaw, 2009; Wang et al., 2012). Based on analog experiments, Sun et al. (2016) argued that the along-strike topographic relief across the northern and southern Longmenshan had contributed significantly to the kinematics and deformation localization (e.g., the Xiaoyudong tear fault) of the Longmenshan. Hubbard et al. (2010) suggested a critical taper wedge for the Longmenshan fold-and-thrust belt; based upon this finding, Liu et al. (2020) further showed that the interaction between the late-Cenozoic shortening and the localized fluvial erosion of the Minjiang River resulted in the Dujiangyan recess in the central Longmenshan.
In this study, several sandbox analog experiments were carried out with syntectonic erosion and sedimentation, systematically expounding the surface process in a foreland basin system. Furthermore, a comparison between the Longmenshan fold-and-thrust belt and the western Sichuan foreland basin system and analog results revealed that the surface process and tectonics profoundly impacted the evolution of the foreland basin system.
Model Set-Up of Erosion and Sedimentation Processes
The critical-taper Coulomb wedge theory emphasizes that tectonic shortening produces a typical orogenic wedge and foreland basin system (Davis et al., 1983; Dahlen et al., 1984; Decelles and Mitra, 1995). The surface process not only results in the deposition of a large amount of eroded material in the foreland basin but also brings important changes to the structural geometry of the orogenic wedge (McClay and Whitehouse, 2004; Cruz et al., 2008; Wu and McClay, 2011). In particular, there are mutual feedback relationships between tectonics and surface processes in natural examples. Tectonic deformation, material transport, and the sedimentary model dynamically respond to the temporal and spatial extent of erosion. They jointly control the dynamic evolution process of imbricated thrust, tectonic shortening, and the aggradation and duplex structure in the orogenic wedges.
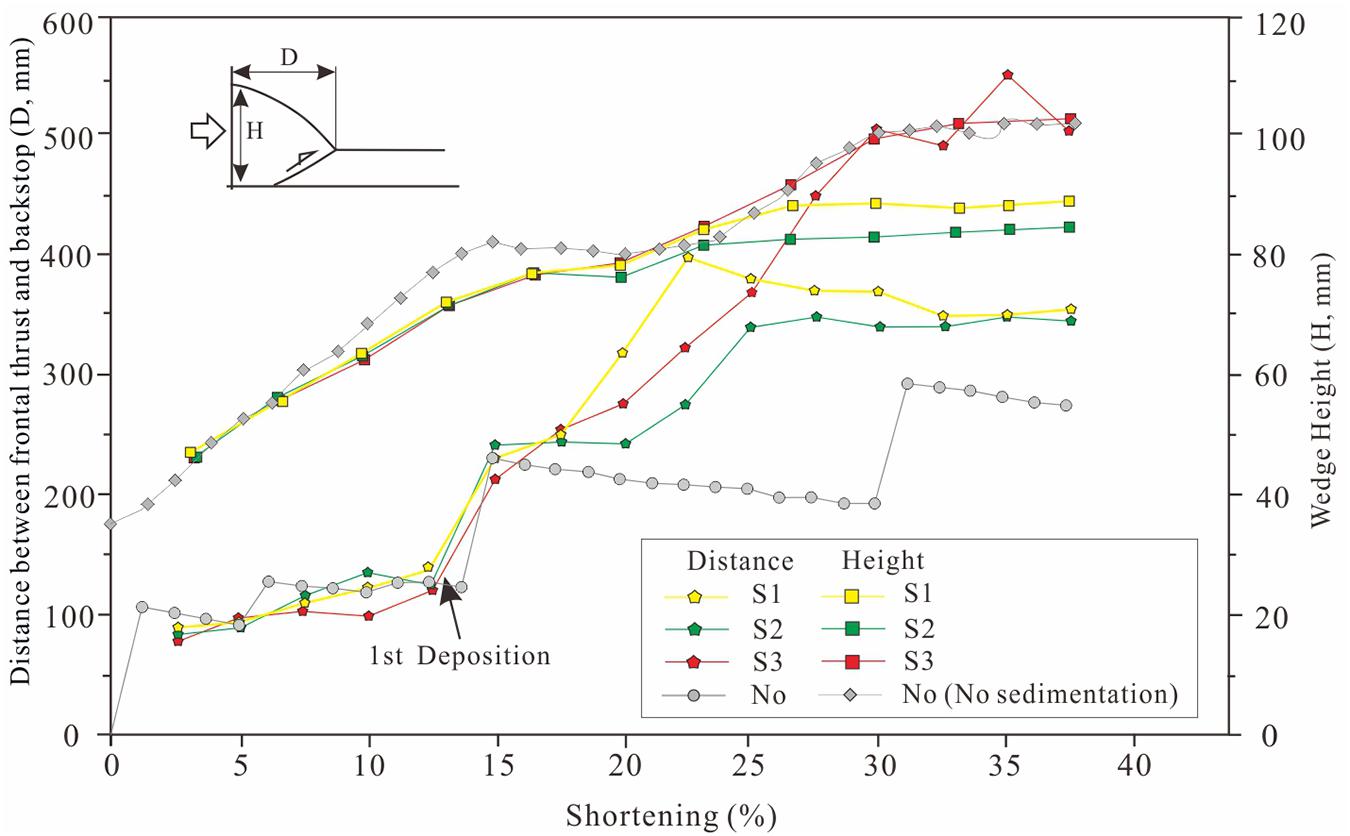
We have conducted two experiments in the tectonic modeling laboratory, which divided the surface process (i.e., erosion–sedimentation process) of the natural prototype into two independent models: erosion and sedimentation (Figure 1 and Table 1). Different lithologies have different anti-weathering abilities, and their sedimentation resulting from surface processes varies from one another. To eliminate the complications caused by lithologic dissimilarities, we used quartz sand as the experimental material in all analog models. The quartz sand we used was medium-rounded, well-sorted, and had an average grain size of 0.2–0.3 mm, a bulk density of 1.35 g cm–3, an internal friction angle of 29–31°, an internal coefficient of friction of 0.58, and a critical wedge taper angle of 10–12° (Deng et al., 2018). The quartz sand was evenly sieved into a sandbox to form an initial sand pack of 800 mm × 400 mm × 35 mm. Approximately 1 mm-thick colored quartz sand was laid in the sandbox at an interval of 7 mm vertically to ensure that the deformation process could be easily monitored and quantitated (Figure 1A).
Figure 1. (A) Diagram of the experimental apparatus. (B) Interpreted fold-thrust wedge showing the parameters measured in the experiment. Note that the distance between frontal thrust and backstop is about 7.5 mm shorter than the original definition of wedge length (Dahlen et al., 1984; Dahlen, 1990). (C) Erosion models with constant erosion slope angles to represent different rates of erosion. (D) Sedimentation models with constant deposited slope angle with different area to represent different rates of sedimentation.
Quartz sand has a linear Coulomb Mohr fracture deformation behavior and is nearly cohesionless. It enables sandbox models to effectively simulate brittle deformations in the upper 10 km of the crust (e.g., Davis et al., 1983; McClay and Whitehouse, 2004). The scaled coefficient of strain can be expressed by calculating the corresponding physical quantity between the analog model and the natural prototype. The strain-scaled coefficient σ∗ = ρ∗ L∗ g∗, where ρ∗, L∗, and g∗ are the proportion coefficients of density, length, and gravity between the analog model and the natural prototype, respectively. In this research, we obtained a strain-scaled coefficient of σ∗ = 0.74 × 10–6. Considering that the shear strength of natural rock is 1–20 MPa and the cohesion strength of the analog model is approximately 0–100 Pa, this implies that they are ideal models to simulate natural brittle deformation in the upper crust under normal gravity conditions.
When the compression shortening reaches 100 mm (corresponding to 12% shortening), a critical state of the wedge is attained at the movable cylinder in the sandbox. Meanwhile, the materials on the surface of the sandbox accept different syntectonic processes according to their location, which includes erosion (E1-3 group), and sedimentation (S1-3 group) models. For each erosion model, an inclined surface line set from the forefront thrust with different angles is determined by the critical taper angle (i.e., 12° based on our quartz sands) to represent a critical state of the erosional process (Figure 1C). Furthermore, we set a smaller slope angle of 4° and 8° to represent much strong erosion at the wedge top, following Konstantinovskaia and Malavieille (2005) and Wu and McClay (2011). All quartz sands above the inclined surface line (i.e., an erosion surface) are scraped off and removed by a vacuum cleaner for each 20 mm shortening. Erosion is allowed elsewhere about the erosion surface, however, no erosion is carried out if all quartz sands are under the surface until to next step (Table 1). It should be noted that a strong erosion decreases the wedge strength, and results in the wedge a sub- and super-critical state. The wedge thus tends to rebuild its critical taper after each syntectonic erosion. The E1 model with a 4° erosion surface is characterized with the strongest erosion (i.e., ten repetitions of erosion) occurred on the wedge top, while the E2 and E3 models with 8° and 12° (critical taper age) erosion surfaces respectively are characterized with medium- and low-rate of erosion, both of them have three repetitions of erosion (Table 1).
The sedimentation models are divided into three sets of models, starvation, transitional, and saturated to elucidate how syntectonic sedimentation influences the evolution and deformation of the foreland basin system. According to DeCelles and Giles (1996) and Allen and Allen (2005), a natural foreland basin system is composed of the wedge-top, foredeep, forebulge and back-bulge zones, however, a foreland basin system in an analog experiment usually lacks the last two zones due to the absence of lithospheric flexure-related deformation, so we assigned that the wedge-top and foredeep (separated by the forefront fault, in Figure 1B) are two parts of our foreland basin system. After the wedge attains the critical state, dry quartz sands are sieved by hand, to fill in the foreland basin system in each 20 mm shortening. In the model of starvation sedimentation (i.e., S1 model), quartz sands are filled in the foredeep zone, which is approximately 10 cm from the forefront fault toward the foreland. With increasing sedimentation, quartz sands are filled in the foredeep and wedge-top basins in the model of medium sedimentation (i.e., S2 model). Their deposited slope surface (i.e., an accommodation space) is restricted by the surface of the wedge taper angle (Figure 1D). Furthermore, we used a top slope surface of 12° (i.e., a critical wedge angle) to represent the maximum flux of syntectonic sedimentation in the model of saturated sedimentation (i.e., S3 model). In the three sets of sedimentation models, we carried out ten repetitions of sedimentation (Table 1).
During the experiment, the movable cylinder moved forward at a speed of 0.003 mm/s. The total shortening amount was 300 mm, corresponding to an overall shortening percent of ca. 38% for a natural thrust belt and foreland basin system. Progressive deformation of all experiments was monitored using high-resolution digital photographs taken after 1.0 mm increments of displacement. Using a graphic software package, wedge height and distance between frontal thrust and backstop were systematically measured at every 10 mm of incremental shortening to describe the evolving wedge configuration, following the methods used by Buiter et al. (2016) and Schreurs et al. (2016). However, it should be noted that the distance between frontal thrust and backstop is about 7.5 mm (i.e., 35 mm × tan12°) shorter than the original wedge length defined by Dahlen et al. (1984) and Dahlen (1990).
Experiment results
Results of Erosion Models
The deformation and evolution process of the model with a medium rate are illustrated by the E2 group (Figure 2). With the movable cylinder moving forward at a constant speed, several thrust faults were propagating forward in the sequence. After the critical–taper angle was attained, the T4 fault formed with a 12% shortening, as a result, the wedge taper angle reached approximately 13–15°, larger than the erosion surface we set. Therefore, the wedge surface was eroded along a sloped surface of 8° from the back of the wedge to the tip of the frontal fault (Figure 2A and Table 2). When the shortening was 15%, the T5 fault formed, and T2-T4 fault surfaces steepened. Because the wedge taper angle was exactly 8°, with no erosion occurred on the wedge surface at that moment. The T6 fault formed when the shortening was 18%, and the black layer was denuded up to the surface during the second erosion process (Figure 2B). Pre-existing faults were reactivated with a continuous compression process, resulting in a sharp decrease in the distance between frontal thrust and backstop (i.e., wedge length) and a gradual increase in the wedge height, to rebuild a critical wedge taper. The T7 fault and the second pop-up structure formed in the wedge frontier with a wedge taper angle of less than 8° when the shortening was 25%. When the shortening was 28%, the third erosion process caused the deepest red layer to be exposed on the surface (Figure 2C), and the wedge height decreased sharply. Until the end, the shortening was 38%. At this end stage, the T1–T7 fault surfaces at the back of the wedge are rotated and steepened strongly. In the final stage of this experiment, a wedge with a height of 80 mm and a length of 200 mm is attained.
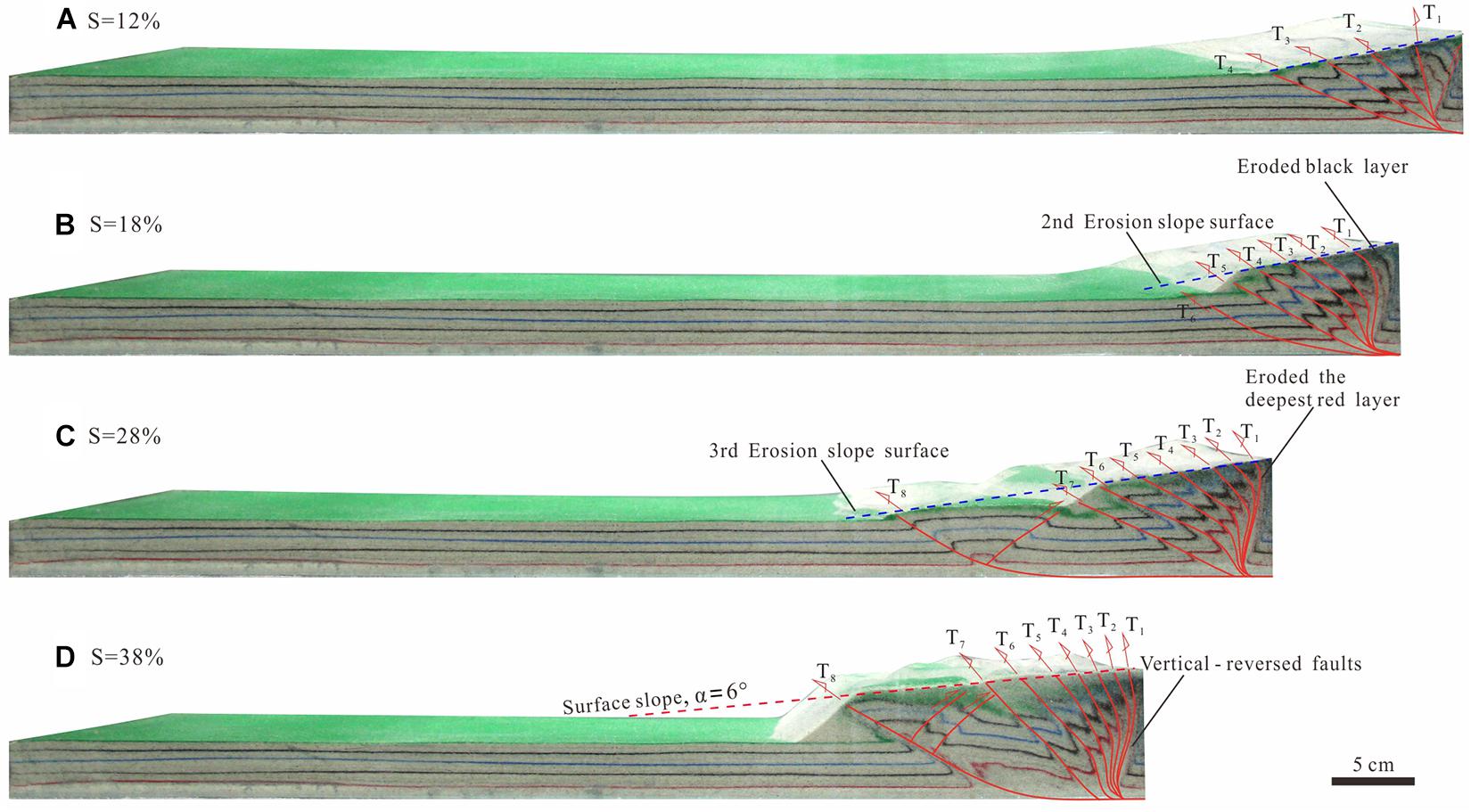
Figure 2. Experiment results of medium rate of erosion model (E2). (A–D) Sequential photopraphs showing the structural evolution of wedge.
In model E1, which is characterized by a high-rate erosion, a wedge taper of 13–15° was formed with the new T4 fault when the shortening arrived at 12% (Table 2). The first erosion was thus conducted on the wedge surface, to significantly reduce the wedge height to about 60 mm (Figure 3A). With the progressive shortening, the wedge tended to rebuild a critical wedge taper with strong reactivation of faults in the wedge hinterland (Figure 3A), e.g., T1-T4. A new T5 fault formed and the wedge taper increased to 8° when the shortening was 15%. The second erosion was carried on the wedge surface and decreased the wedge height by 5 mm. After each 20 mm shortening, the wedge taper increased to 8°-10°, which exceeded the erosion surface we set initially. Thus, we performed a total of ten repetitions of erosion in model E1 (Table 2), resulting in the distance between frontal thrust and backstop and wedge height to fluctuate between 100 mm and 60 mm, respectively. Ten imbricated faults formed in the whole and thrusted toward the foreland (Figure 3D and Table 2), with a final wedge height and distance between frontal thrust and backstop of 65 mm and 120 mm respectively.
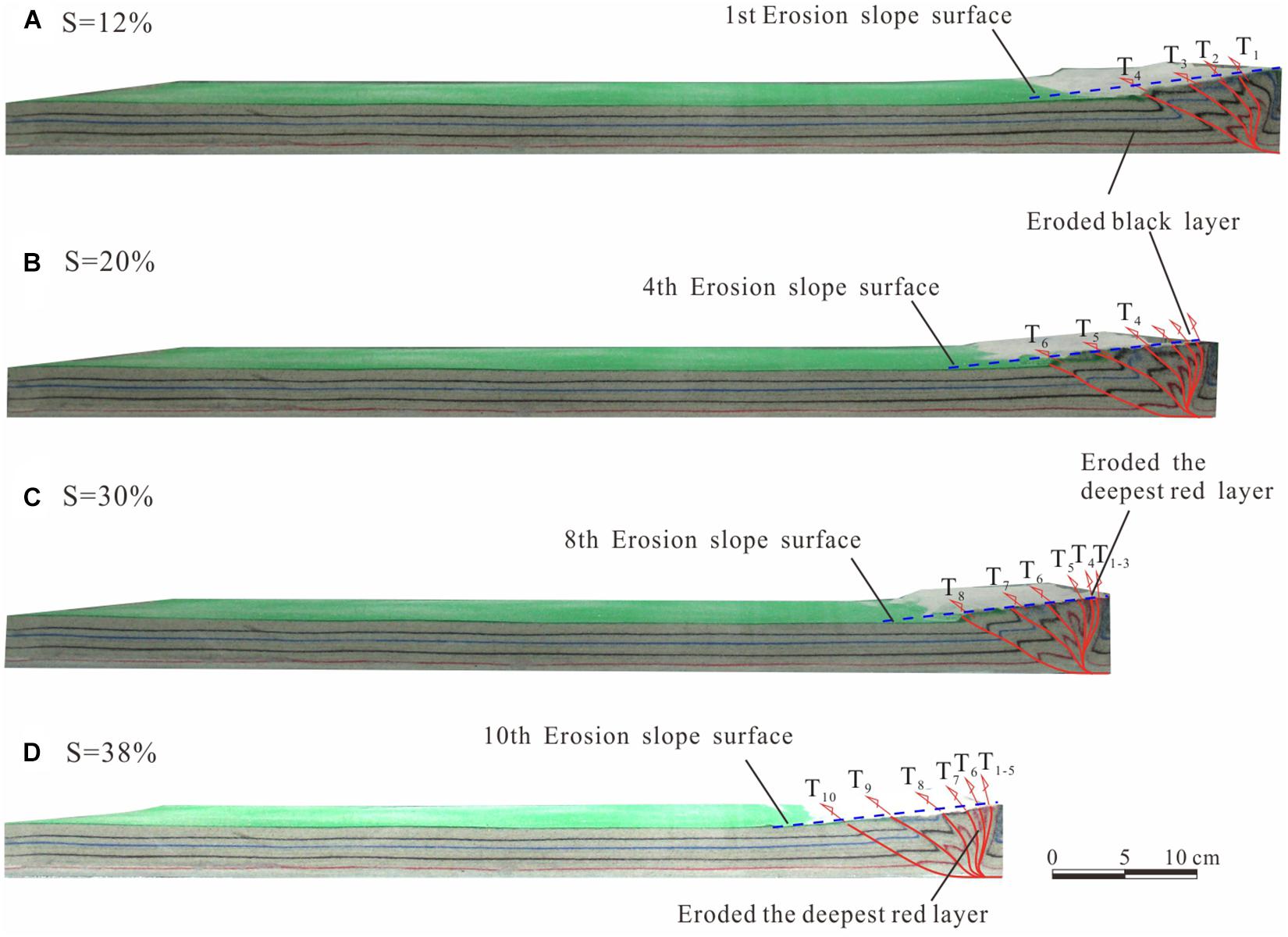
Figure 3. Experiment results of high rate of erosion model (E1). (A–D) Sequential photopraphs showing the structural evolution of wedge.
In the E3 model, the first erosion event occurred on the wedge surface when the wedge taper angle reached approximately 12–14° (Figures 4A,B and Table 2). Due to the erosion surface was set to an angle of 12°, the erosion decreased weakly the wedge height and the distance between frontal thrust and backstop. With a progressive shortening, the wedge taper increased to 12–14°, thus the second and the third erosion events occurred at the 23 and 25% shortening (Figure 4B), respectively. A new T5 fault formed with the second pop-up structure in the wedge frontier, and the fourth erosion event occurred at the shortening of 28% (Figure 4C), decreasing the wedge height by about 3-5 mm. After that, the wedge taper was roughly smaller than the critical taper, we performed no erosion anymore. In the final stage of this experiment, a wedge with a height of 100 mm and a length of 300 mm is attained (Figure 4D).
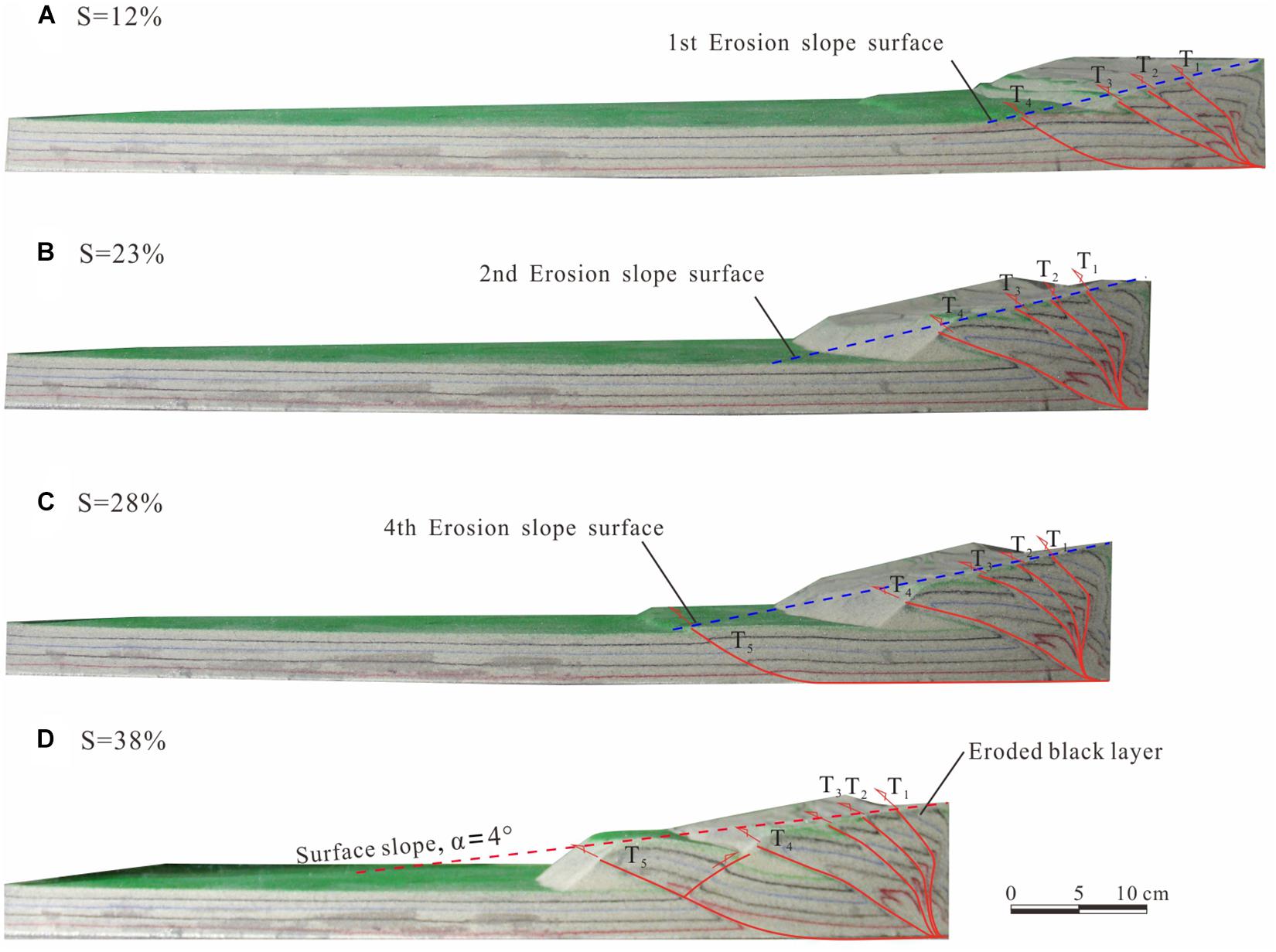
Figure 4. Experiment results of low rate of erosion model (E3). (A–D) Sequential photopraphs showing the structural evolution of wedge.
Overall, controlled by the variation of the erosion trigger angle set and the wedge taper angle, the distance between frontal thrust and backstop and wedge height were negatively correlated with the erosion rate (Figure 5). High-rate erosion could strengthen the thrusting deformation within the accretionary wedge. For example, we found that more thrust faults occurred in the E1 group than in the E3 group (Table 2).
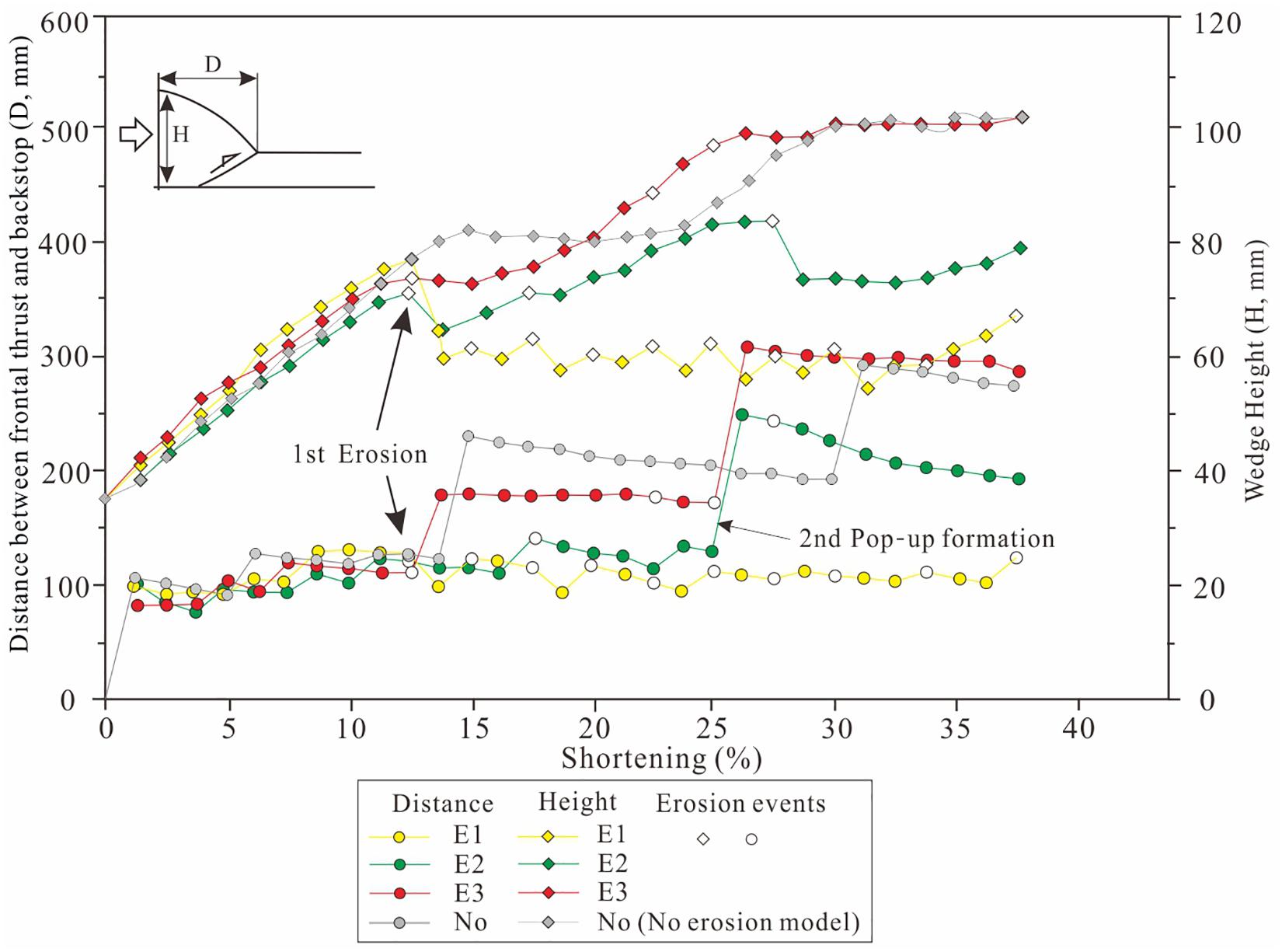
Figure 5. Plot of geometries of accretionary wedge versus shortening in three erosion models. It should be noted that the geometry of no erosion model shows much changes among our models.
Results of Sedimentation Models
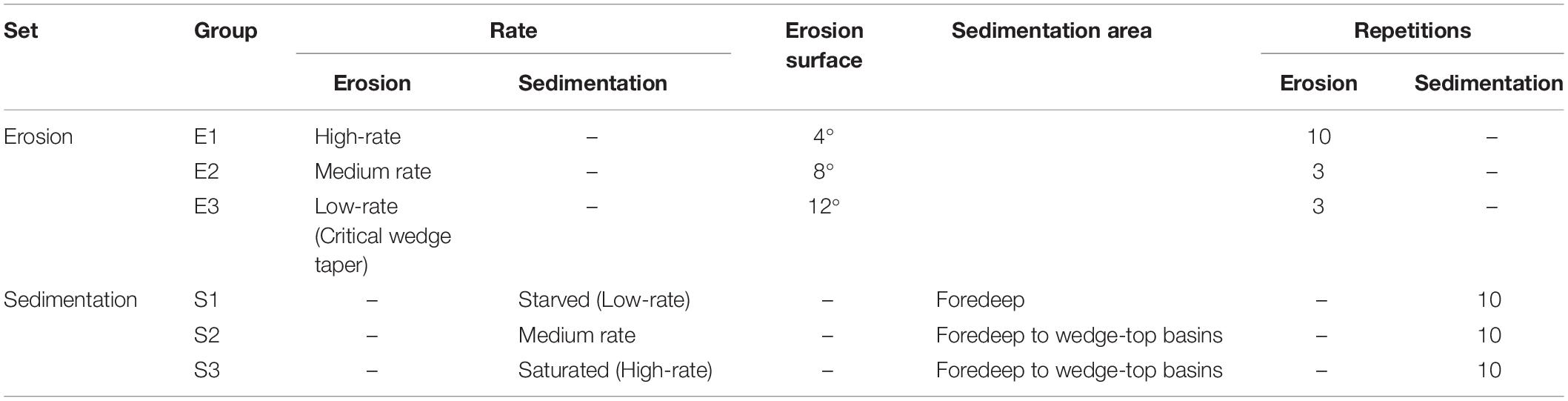
The evolution process of the high-rate sedimentation model is illustrated by the S3 group (Figure 6). After a critical wedge taper was attained when the shortening reached 12%, colored quartz sand was deposited at the foredeep to wedge-top basins to form a sloped surface of 12° (Figure 6A). With progressive shortening, the syntectonic depositions were deformed by thrusting and shortening to rebuild a critical wedge taper, resulting in the steepened faults in the hinterland and the increased wedge height (Figures 6B,C). A new T5 fault formed with an 18% shortening, which cut the second and third depositions, in contrast to three inactive faults (i.e., T1–3 faults) in the hinterland without cutoff the first depositions. Then a new T6 fault formed with a 23% shortening, in particular, the T5 fault was characterized by the maximum offset along the former depositions (Figure 6C). The T7 fault and second pop-ups formed when the shortening reached 30% (Figure 6D), to accommodate a piggy-back or wedge-top basin. Where the backthrust of T7 and T6 faults thrust and resulted in the early depositions deformed. The seventh and subsequent depositions took place in front of the tip of the T7 fault, rendering the distance between frontal thrust and backstop increased slowly and most of the faults in the wedge hinterland inactive (i.e., T1–6 faults). Until the end at a shortening of 38% with ten repetitions of deposition, the distance between frontal thrust and backstop and wedge height reached 500 mm and 100 mm, respectively (Figure 6D and Table 3). In the S3 group experiment, we found the dragging fold deformation preserved in the syntectonic sedimentation at the forelimb of the wedge.
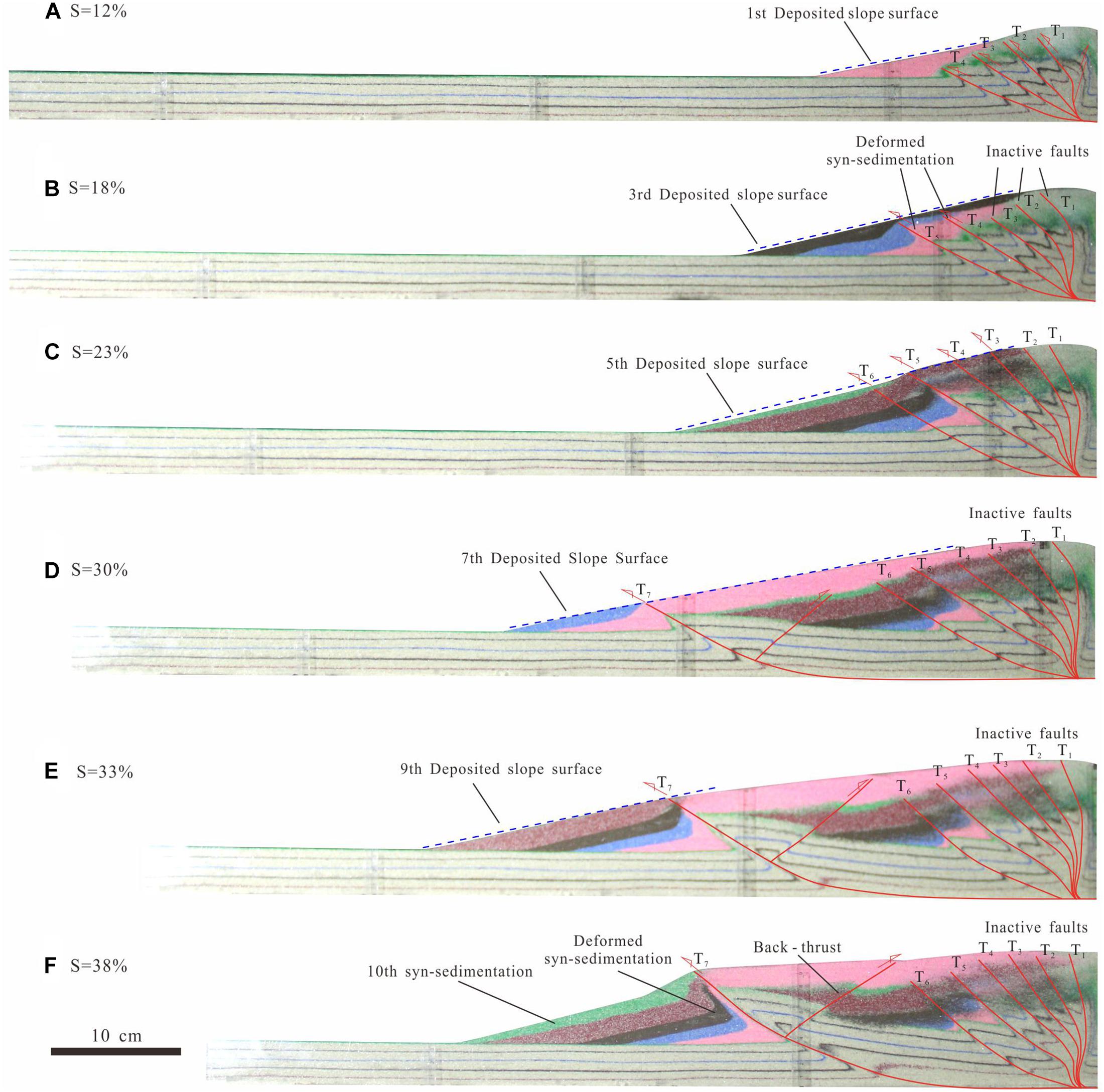
Figure 6. Experiment results of Saturated (high-rate) sedimentation model (S3). (A–F) Sequential photopraphs showing the structural evolution of wedge.
In model S2, which is characterized by medium-rate sedimentation, a critical wedge taper was formed with the new T4 fault at a shortening of 12%. We performed the first syn-sedimentation in the foredeep and wedge-top basin to increase the distance between frontal thrust and backstop to about 200 mm (Figure 7A). With a progressive shortening and sedimentation, the wedge increased the length and height to rebuild a critical wedge taper, compared with the second and third repetitions of deposition at the shortening of 15% and 18% respectively (Table 3). A new T5 fault and second pop-up formed when the shortening was 23%, subsequent with an out-of-sequence T6 fault (Figure 7C). The sixth and subsequent depositions took place in the wedge frontier (front of the T5 fault) with progressive deformation induced by the T5 fault thrusting. As a result of ten repetitions of deposition, the distance between frontal thrust and backstop and wedge height reached 350 mm and 85 mm, respectively (Figure 8 and Table 3). It should be noted that most of the faults in the wedge hinterland were inactive (i.e., T1–3 faults) as well as the T6 fault, however, the T4 fault was reactivated with increase offset in the syn-sedimentations (Figure 7D).
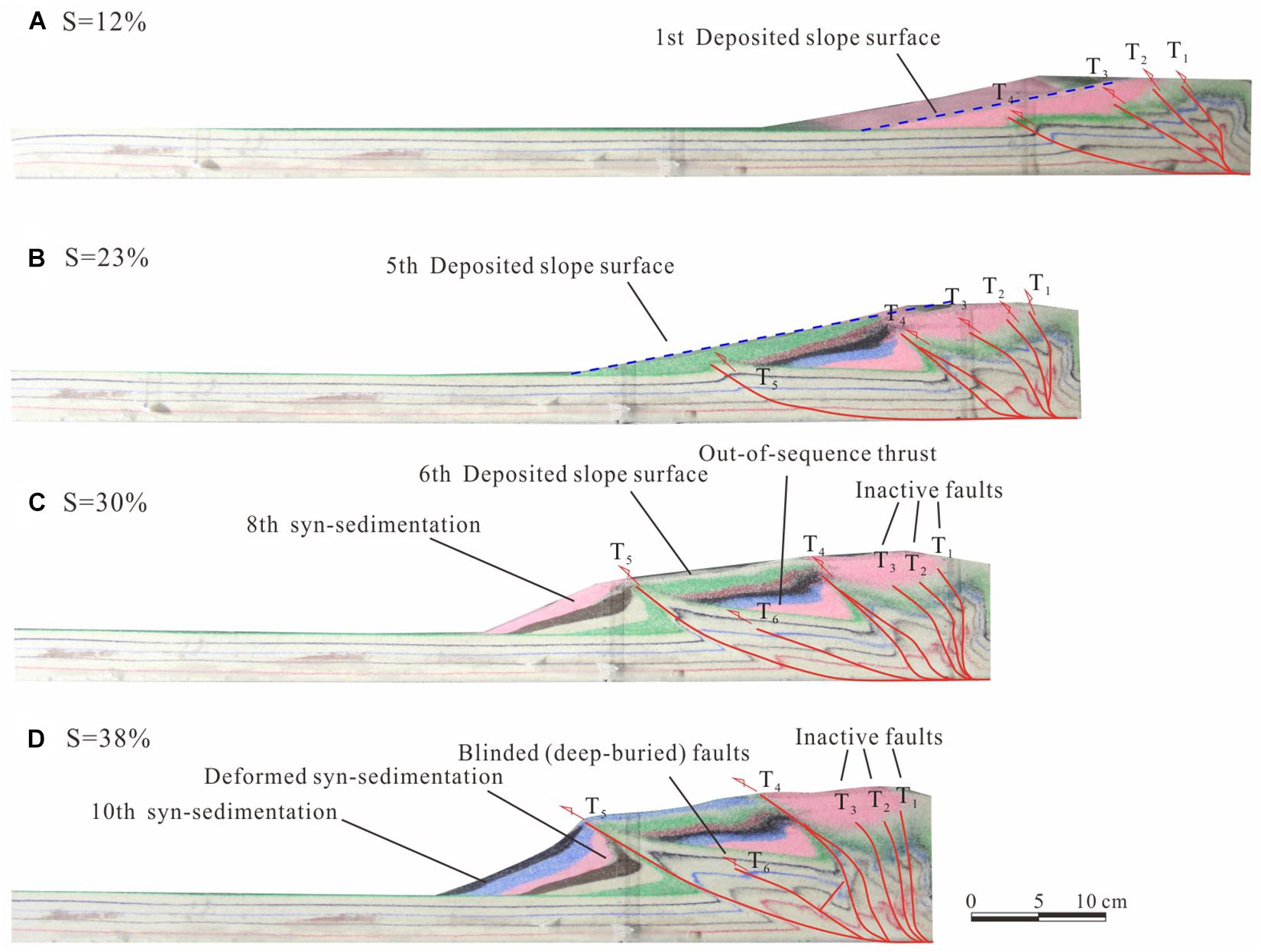
Figure 7. Experiment results of medium-rate sedimentation model (S2). (A–D) Sequential photopraphs showing the structural evolution of wedge.
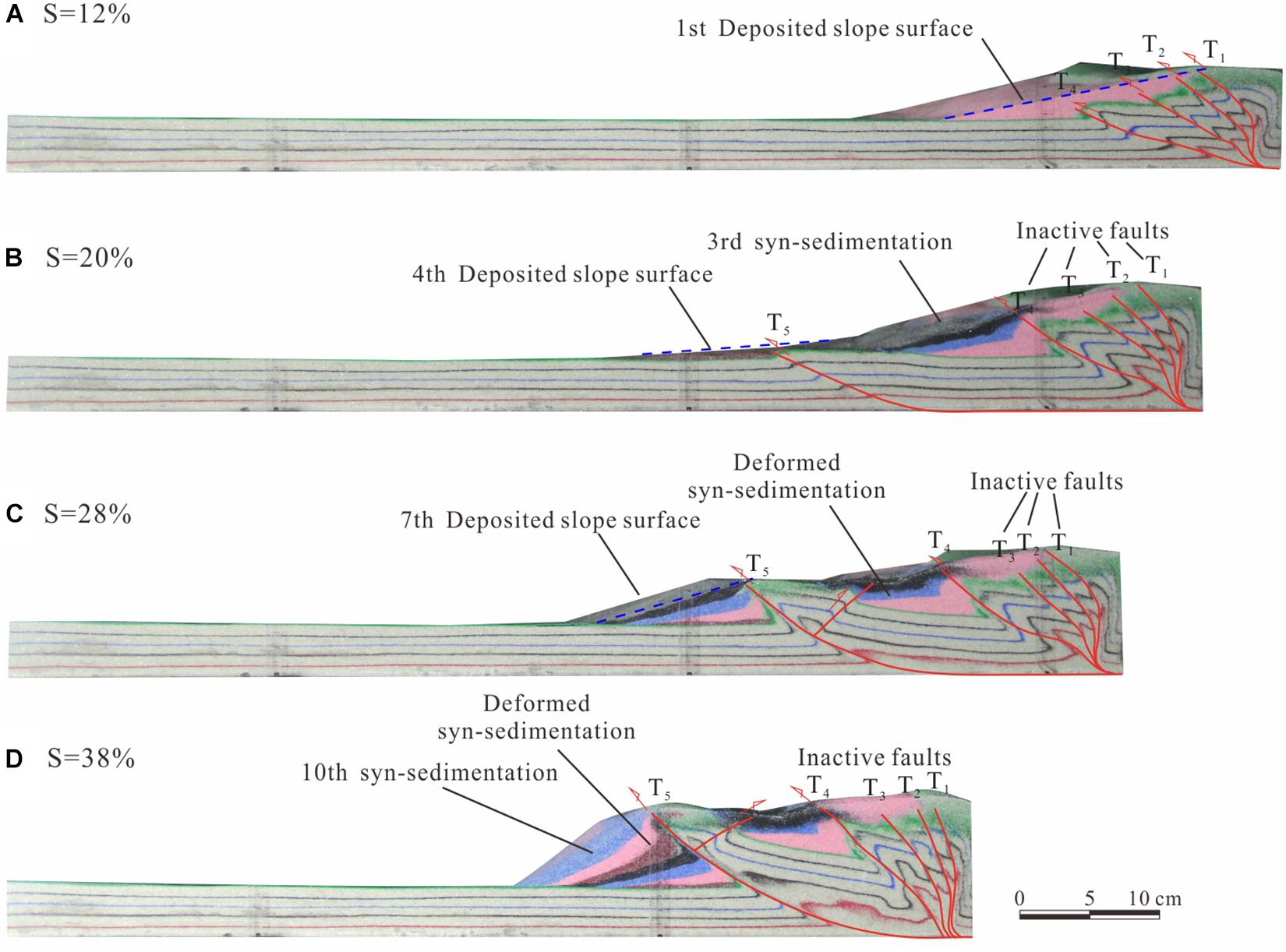
Figure 8. Experiment results of Staved (low-rate) sedimentation model (S1). (A–D) Sequential photopraphs showing the structural evolution of wedge.
In the S1 model characterized by low-rate sedimentation, a critical wedge taper formed with the new T4 fault at a shortening of 12%, and the first syn-sedimentation was thus deposited to increase the distance between frontal thrust and backstop to about 200 mm (Figure 8A). A new T5 fault and second pop-up formed when the shortening was 20%, followed by the fourth to ten repetitions of deposition in the wedge frontier (front of the T5 fault). Because of repetitions of deposition, the front pop-up was deformed substantially with the T5 fault thrusting, and a new backthurst of T5 fault formed to cut the early depositions in the wedge-top basin when the shortening was 28% (Figure 8C). As a result of ten repetitions of deposition, the distance between frontal thrust and backstop and wedge height reached 350 mm and 90 mm, respectively (Figure 8D and Table 3).
By contrasting the wedge height and the distance between frontal thrust and backstop between the S1, S2, and S3 groups, we found a distinct increase in wedge height and length in the saturated syntectonic sedimentation group (S3 group) (Figure 9). Furthermore, we argued that the synsedimentary process accelerated the propagation of the wedge to the foreland but restrained faults in the hinterland (Figures 6-8), as well as reactivation and out-of-sequence thrusting of faults.
Discussion
Influence of Erosion and Sedimentation on Deformation
Based on analog experiments, we argued that syntectonic erosion and sedimentation play an important influence on wedge geometry and kinematics. The syntectonic erosion process prohibited the wedge from propagating toward the foreland, the higher the erosion rate, the more intense the faults thrust in the hinterland. In other words, syntectonic erosion would enhance the uplift and consequent erosion of the deep material in the hinterland (Figure 5). The lowest red layer in E1 was partly denuded up to the surface in the hinterland (Figure 3). However, in the E3 group, the lowest red layer was still buried deep in the hinterland (Figure 4). The high-rate erosion led to the multi-stage reactivation of pre-existing faults in the hinterland. Previous researches have also revealed that shallow denudation results in multi-stage reactivation and out-of-sequence thrusting of faults in the hinterland (Persson and Sokoutis, 2002; McClay and Whitehouse, 2004; Cruz et al., 2008). In general, the reactivation of pre-existing faults was positively correlated with the thrusting deformation and erosion rate and negatively correlated with the wedge height and the distance between frontal thrust and backstop.
Syntectonic sedimentation increased the mass fluxes, deposition amount, and the distance between frontal thrust and backstop (Figure 9). It prohibited faults from thrusting in the hinterland, resulting in several dormant or deep-buried faults (Figures 6, 8). Generally, pre-existing faults and related pop-up structures were buried much deeper as the mass fluxes increased. Pop-up structures were specifically developed with deeper depths and smaller fault spacings in the S1 group than that of the S3 group. Wu and McClay (2011) suggested that syntectonic sedimentation results in conspicuous stratigraphic rotation in the front of the wedge, which is also similar to the change in the thickness and deformation of syn-sedimentation strata in our models (Figures 6-8). An earlier study revealed that the synsedimentary process would steepen thrust faults (Storti and McClay, 1995; Nieuwland et al., 2000). Syntectonic erosion leads to overlying unloading in the hinterland of the wedge, which tends to concentrate strain and trigger the reactivation of dormant faults. However, the syntectonic sedimentation increases overlying loads at the foredeep of the wedge, restricts the activation of pre-existing faults, and then propagates the wedge forward (Stockmal et al., 2007; Duerto and McClay, 2009). The deposition rate would also greatly influence the development of both fore-thrust and back-thrust (Bonnet et al., 2007).
The syntectonic erosion and sedimentation in analog experiments indicated that the erosion and sedimentation processes control the wedge deformation and evolution with an interactive influence on each other. Erosion and sedimentation control the coupling of the fore-thrust at the forelimb and passive back-thrust in the hinterland, which results in multi-stage reactivation and out-of-sequence thrusting of the faults (Mugnier et al., 1997; Bonnet et al., 2007; Malavieille and Trullenque, 2009).
Volume of Erosion and Sedimentation
Syntectonic erosion and sedimentation in the fold-and-thrust belt and foreland basin system have an important influence on the deformation of the compressed wedge and structural geometry of faults. In this study, we calculated the amount of both erosion and sedimentation and their relationship to unravel the erosion and sedimentation of the basin–mountain system in nature.
These tectonics-erosion analog experiments showed that the total erosion amount increased with the erosion repetitions (Figure 10A). The maximum cumulative erosion ratio in the E1 group increased to 20–25%. However, the cumulative erosion ratio was 5–10% in the E1 and E2 groups, representing the medium and low rate of erosion, respectively. The erosion amount at every time was approximately equal (i.e., 200-300 cm3) among the experiments with different erosion rates. Therefore, the differential erosion processes were controlled by erosion repetitions. Additionally, with the increased shortening, the cumulative erosion ratio increased in a step-type manner in the E1 group, but we found a linear correlation between the cumulative erosion ratio and the shortening in the other two groups (i.e., the E2 and E3).
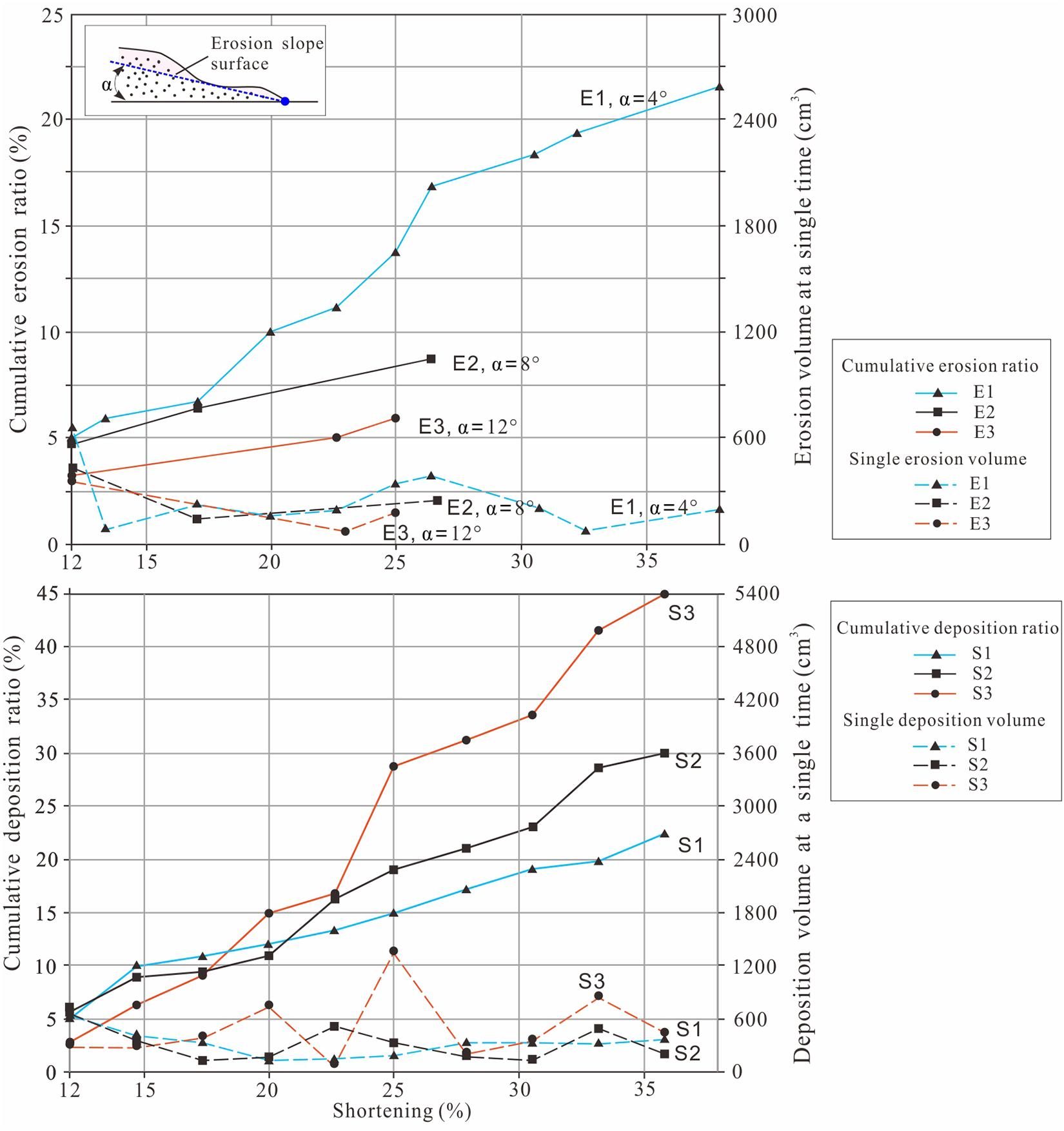
Figure 10. Volume of erosion and sedimentation versus shortening. The cumulative erosion ratio is the ratio of cumulative erosion volume to original volume of quartz sand in the model; the cumulative deposition ratio is the ratio of cumulative sedimentation volume to original volume of quartz sand in the model.
Similarly, the total amount of sedimentation was positively correlated with the shortening and the repetitions of sedimentation in the sedimentation analog experiments (Figure 10B). The most synsedimentary quartz sand was deposited in the S3 group, with a cumulative deposition ratio of 45%. In contrast, the cumulative deposition ratios of the S1 and S2 groups were between 20–30%. Sedimentation analog experiments revealed that the amount of each repetition of syntectonic deposition was different under different sedimentation rates. For instance, the deposition volume was significantly higher in the S3 group (i.e., 300-1500 cm3) than that in the S1 and S2 groups (i.e., 300-500 cm3). In addition, the total deposition amount in the S1 and S2 groups increased with a positive correlation with the shortening, which was different from the S3 groups. This difference was attributed to the different wedge taper angles set in these three groups.
Different erosion and sedimentation processes in the thrust belt and foreland basin systems have different mass fluxes. The mass flux in the high-rate erosion (i.e., E1 group) is approximately twice than that in the medium-to-low-rate erosion (i.e., E2-E3 groups). Similarly, the mass flux in the saturated deposition model (i.e., S1 group) is also twice to four-time than that of the starvation and transitional deposition models (i.e., S2-S3 groups). The critical-taper Coulomb wedge theory emphasizes that the erosion and sedimentation process can reach a critical state of the matter exchange (Dahlen and Suppe, 1988; Willett et al., 1993). However, both the erosion volume in each repetition of erosion and the cumulative erosion ratio of the low-rate erosion process (i.e., E3 group) was smaller than the deposition volume of the saturated sedimentation process (i.e., S3) (Figure 10). Therefore, we concluded that there must be a huge quantity of matter and energy from the deep lithosphere to maintain a critical state of the matte exchange in the thrust and foreland basin system (Konstantinovskaia and Malavieille, 2005; Vanderhaeghe, 2012; Jamieson and Beaumont, 2013).
Comparison of the Natural Example of Longmenshan Fold-and-Thrust Belt
At the eastern margin of the Tibetan Plateau (Figure 11), the peripheral foreland basin and rejuvenated foreland basin were formed in the Late Triassic–Early Jurassic and Late Cretaceous–Cenozoic, respectively (Burchfiel et al., 1995; Liu et al., 2005; Jia et al., 2006; Deng et al., 2012). During the Late Triassic to Early Jurassic, the Songpan Ganzi fold belt
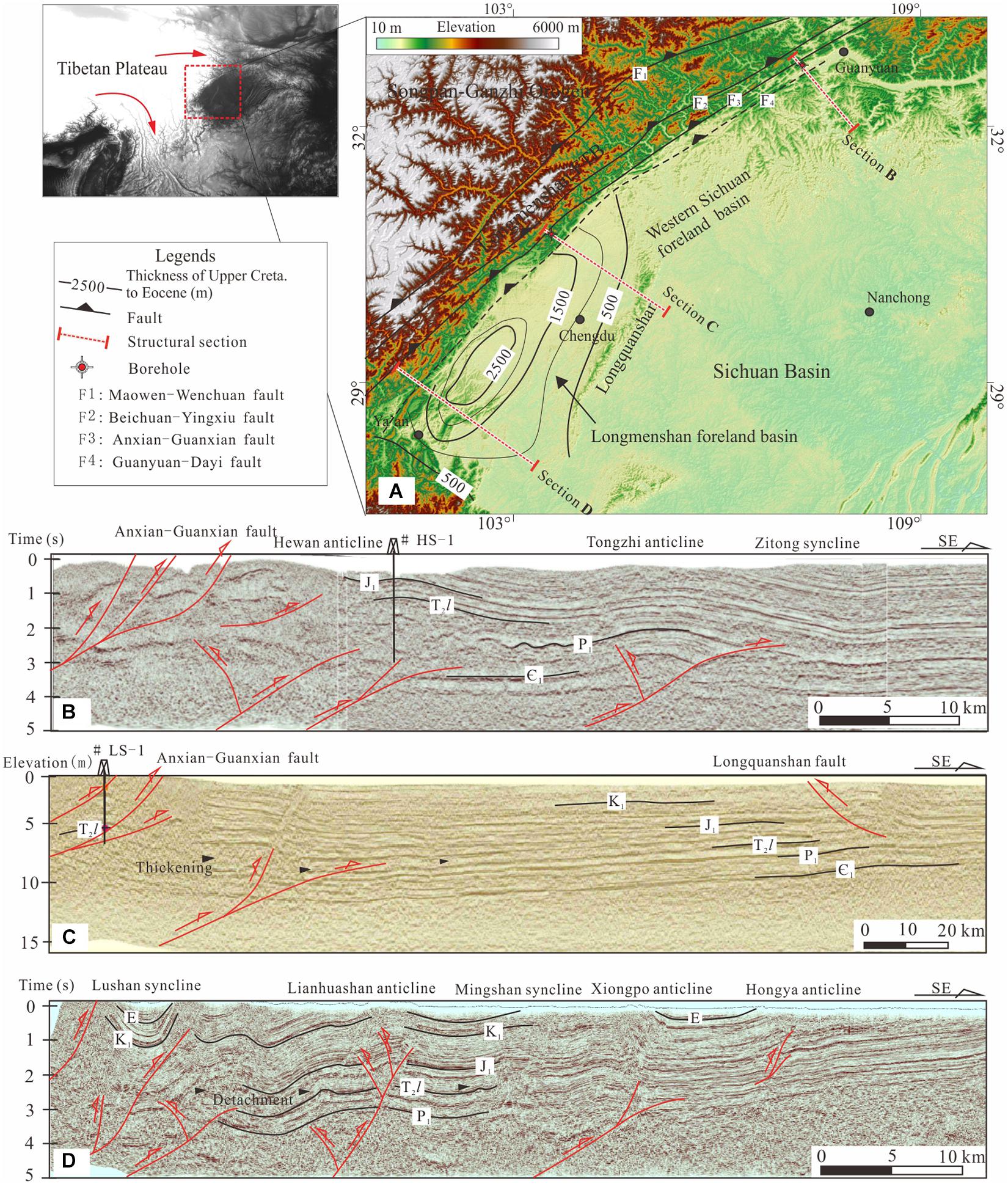
Figure 11. Natural example of the Longmenshan fold-and-thrust belt in the eastern margin of the Tibetan Plateau. (A) Topography of Longmenshan FTB (fold-and-thrust belt) with the thicknesses of upper Cretaceous to Eocene showing Longmenshan foreland basin. (B–D) Structural sections indicate different style of deformation occurred in the northern, middle, and southern segments of the Longmenshan FTB.
was thrust upon the western margin of the Yangtze Plate and accommodated the Longmenshan fold-and-thrust belt composed of the Maowen-Wenchuan ductile shear zone, Beichuan-Yingxiu Fault, and Anxian-Guanxian Fault (Figure 11A). Therefore, approximately 1–2 km of wedge-shaped molasse was deposited in the western Sichuan foreland basin, such as the Upper Triassic Xujiahe Formation and Lower Jurassic Baitianba Formation (Figure 11C). Many calcareous and quartzitic synorogenic conglomerates revealed a high rate of erosion and unroofing process of the Longmenshan fold-and-thrust belt (Cui et al., 1991; Deng et al., 2012). The Late Cretaceous–Cenozoic eastward extrusion process of the Tibetan Plateau caused the Longmenshan fold-and-thrust belt to rejuvenate, leading to an increased erosion (Wang et al., 2012; Tian et al., 2013; Deng et al., 2016). The outcrops of Precambrian basements, such as the Pengguan and the Baoxing complexes, indicate a strong uplift and erosion process at the southern and middle segments of the Longmenshan (Wang et al., 2012; Tian et al., 2013; Tan et al., 2017). Approximately 1–2 km of molasse was deposited in the Longmenshan foreland basin (Figure 11A). The Upper Cretaceous Jiaguan and Guankou formations and Eocene Mingshan Formation are characterized by wedge-shaped conglomerates, as a result of unroofing of the Longmenshan fold-and-thrust belt (Li and Ji, 1993; Gou, 2001).
Based on river sediment load data and denudation rates, Liu-Zeng et al. (2011) argued that the erosion of the Longmenshan margin has approached a steady state. It is consistent with a nearly constant surface slope and fault-related fold geometry along the Longmenshan described by Liu et al. (2020), to argue a critically-tapered thrust wedge along the eastern margin of the Tibetan Plateau. Combined with the critical taper wedge model, Hubbard et al. (2010) suggested that crustal shortening, structural relief, and topography are strongly correlated in the Lognmenshan, controlled by the mechanical strengths of rock and fault, and detachment. The Longmenshan fold-and-thrust belt has attained a steady state since the Pliocene or the latest Miocene. Although erosion rates deduced from cosmogenic 10Be, and low-temperature thermochronology and topography are similar about 0.2-0.8 mm/yr (e.g., Liu-Zeng et al., 2011; Tian et al., 2013; Tan et al., 2019), two-phase rapid exhumation occurred in the Longmenshan fold-and-thrust belt, beginning around 30 Ma (with a rate of 0.8 mm/yr) and about 10 Ma (0.4 mm/yr) respectively (Wang et al., 2012). It indicates an exhumation steady state (Willett and Brandon, 2002) occurred in the Late Miocene, as well as a steady state wedge of the Longmenshan.
The evolution of the Longmenshan fold-and-thrust belt is characterized by multi-stage thrusting and denudation, indicated by syn-sedimentations and low-temperature thermochronology (Li and Ji, 1993; Gou, 2001; Wang et al., 2012). In particular, the crustal thickness, fault geometry, and kinematics, and exhumation pattern all show along-strike variation in the Longmenshan at the eastern margin of the Tibetan Plateau (e.g., Hubbard et al., 2010; Sun et al., 2018; Lu et al., 2019; Tan et al., 2019). Which resulted in the kinematic and deformation more complicated than that of our experiments. It should be noted that the most distinct difference is along-strike topography and relief in the Longmenshan, probably as result of thrusting and surface processes in Cenozoic. Based on models of a critical taper wedge, Hubbard et al. (2010) argued that a much steeper topography in the southern segment of the Longmenshan is related to the localization of detachment within lower to middle Triassic evaporite sequence in the Longmenshan foreland basin. We found such a detachment deformation and related thickening strata are widespread in seismic sections (Figures 11C,D).
The along-strike variation of erosion–sedimentation in the Longmenshan fold-and-thrust belt has caused the southern and middle segments to be eroded more intensively than the north segment. Therefore, a Precambrian basement outcrops at the southern segment, and the lower Paleozoic strata outcrop to the north. The rejuvenated foreland basin developed in southwestern Sichuan could also be identified from the analog experiments. Similar to the syntectonic sedimentation at the foredeep of the wedge, the foredeep of the Longmenshan fold-and-thrust belt was filled with upper Cretaceous and Cenozoic depositions, causing thrust faults to become laterally gentler from north to south. For example, thrust faults in the Xiongpo and Lihuashan anticlines (Figure 11D) were gentler than those in the Hewan and Tongzhi anticlines (Figure 11B). Meanwhile, the back thrusting was more intensive in the southwest of the Sichuan basin than in the north. For example, typical back-thrusts are widespread in the Lianhuashan and Longquanshan anticline. In response to the differential erosion–sedimentation, we could find detached deformation, bulk shortening, and thickening in the Middle–Lower Triassic gypsum and mudstone at the central and northern segment of the foreland basin (Figures 11C,D).
Conclusion
Syntectonic erosion analog experiments indicated that the erosion decreased with increasing erosion surface among different groups (erosion surface of 4°, 8°, and 12°corresponding to S1, S2, and S3, respectively). The syntectonic erosion process concentrated deformation in the hinterland of the thrust belt, reactivated pre-existing faults, and weakened the propagation of the thrust toward the foreland. Syntectonic sedimentation analog experiments revealed a strong restriction of the deposition load, thereby stopping fault activities. Therefore, the syntectonic sedimentation process helped the wedge propagate toward the foreland. The saturated deposition (S3), in particular, resulted in a significant increase in wedge height and length. In particular, the comparison between the erosion and deposition volume revealed that both a single erosion volume and the cumulative erosion ratio of the erosion process were much smaller than the deposition volume of the saturated sedimentation process.
A rejuvenated foreland basin controlled by the along-strike variation of erosion and sedimentation in the Longmenshan fold-and-thrust belt was developed in the southwestern part of the Sichuan Basin in the Late Cretaceous to Cenozoic times. We further found thrusts with lower dip-angle and stronger back thrusting are widespread in the southwestern parts of the basin than that in the northern part.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
BD conceived and designed the experiments. QL, HY, YH, JH, and RY performed the experiments. BD and JH analyzed the data. QL, HY, and BD wrote the manuscript. All authors contributed to the article and approved the submitted version.
Funding
This work was supported by the National Natural Science Foundation of China (Nos. U19B6003 and 2017JQ0025). We would like to thank the two reviewers, for their reviews, constructive comments, and suggestions.
Conflict of Interest
QL, JH, RY, HY, and JZ were employed by the company PetroChina and YG was employed by the company CNPC Xibu Drilling Engineering Company Limited.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Allen, P. A., and Allen, J. R. (2005). Basin Analysis: Principles and Applications, 2nd Edn, Vol. 5. Hoboken, NJ: Blackwell Publishing, 191.
Bonnet, C., Malavieille, J., and Mosar, J. (2007). Interactions between tectonics, erosion, and sedimentation during the recent evolution of the Alpine orogen: analogue modeling insights. Tectonics. 26:TC6016. doi: 10.1029/2006TC002048
Buiter, S., Schreurs, G., Albertz, M., Gerya, T. V., Kaus, B., Landry, W., et al. (2016). Benchmarking numerical models of brittle thrust wedges. J. Struct. Geol. 92, 140–177. doi: 10.1016/j.jsg.2016.03.003
Burchfiel, B. C., Zhiliang, C., Yupin, L., and Royden, L. H. (1995). Tectonics of the Longmen Shan and adjacent regions, central China. Int. Geol. Rev. 37, 661–735. doi: 10.1080/00206819509465424
Chapple, W. M. (1978). Mechanics of thin-skinned fold and thrust belts. GSA Bull. 89, 1189–1198. doi: 10.1130/0016-7606(1978)89<1189:motfb>2.0.co;2
Cruz, L., Teyssier, C., Perg, L., and Fayon, A. (2008). Deformation, exhumation, and topography of experimental doubly-vergent orogenic wedges subjected to asymmetric erosion. J. Struct. Geol. 30, 98–115. doi: 10.1016/j.jsg.2007.10.003
Cui, B. Q., Long, X. M., and Li, Y. L. (1991). The subsidence of western Sichuan depression and the rise of Longmenshan Mountains. J. Chengdu Coll. Geol. 18, 39–45. (in Chinese with English abstract).
Dahlen, F. A. (1984). Non cohesive critical coulomb wedges: an exact solution. J. Geophys. Res. 89, 10125–10133. doi: 10.1029/jb089ib12p10125
Dahlen, F. A. (1990). Critical taper model of fold-and-thrust belts and accretionary wedges. Annu. Rev. Earth Planet. Sci. 18, 55–99. doi: 10.1146/annurev.ea.18.050190.000415
Dahlen, F. A., and Suppe, J. (1988). “Mechanics, growth, and erosion of mountain belts,” in Processes in Continental Lithospheric Deformation, Vol. 218, eds S. P. Clark <suffix>Jr.</suffix>, B. C. Burchfiel and J. Suppe (Boulder, CO: Geological Society of America), Geological Society of America Special Paper, 161–178. doi: 10.1130/spe218-p161
Dahlen, F. A., Suppe, J., and Davis, D. (1984). Mechanics of fold-and-thrust belts and accretionary wedges: cohesive coulomb theory. J. Geophys. Res. 89, 10087–10101. doi: 10.1029/jb089ib12p10087
Davis, D., Suppe, J., and Dahlen, F. A. (1983). Mechanics of fold-and-thrust belts and accretionary wedges. J. Geophys. Res. 88, 1153–1172. doi: 10.1029/jb088ib02p01153
DeCelles, P. G., and Giles, K. A. (1996). Foreland basin systems. Basin Res. 8, 105–123. doi: 10.1046/j.1365-2117.1996.01491.x
Decelles, P. G., and Mitra, G. (1995). History of the sevier orogenic wedge in terms of critical taper models, northeast Uta and southwest Wyoming. GSA Bull. 107, 452–462.
Deng, B., Jiang, L., Zhao, G. P., Huang, R., Wang, Y., and Liu, S. (2018). Insights into the velocity-dependent geometry and internal strain in accretionary wedges from analogue models. Geol. Mag. 155, 1089–1104. doi: 10.1017/S0016756816001266
Deng, B., Liu, S. G., Jansa, L., Cao, J., Cheng, Y., Li, Z., et al. (2012). Sedimentary record of Late Triassic transpressional tectonics of the longmenshan thrust belt, SW China. J. Asian Earth Sci. 48, 43–55. doi: 10.1016/j.jseaes.2011.12.019
Deng, B., Zhao, G. P., Wan, Y. B., Huang, R., Wang, X., Liu, S., et al. (2016). A review of tectonic sandbox modeling of fold-and-thrust belt. Geotectonica Metallogenia 40, 446–464. (in Chinese with English abstract).
Duerto, L., and McClay, K. R. (2009). The role of syntectonic sedimentation in the evolution of doubly vergent thrust wedges and foreland folds. Mar. Pet. Geol. 26, 1051–1069. doi: 10.1016/j.marpetgeo.2008.07.004
Erdõs, Z., Huismans, R. S., and Beek, P. (2015). First-order control of syntectonic sedimentation on crustal-scale structure of mountain belts. J. Geophys. Res. Solid Earth. 120, 5362–5377. doi: 10.1002/2014jb011785
Fillon, C., Huismans, R. S., and van der Beek, P. (2013). Syntectonic sedimentation effects on the growth of fold-and-thrust belts. Geology 40, 83–86.
Gou, Z. H. (2001). Characteristics of jurassic-tertiary conglomerates and depositional environment in the Dayi-Wenchuan area, Sichuan. Reg. Geol. China 20, 25–32. (in Chinese with English abstract)
Graveleau, F., Malavieille, J., and Dominguez, S. (2012). Experimental modelling of orogenic wedges: a review. Tectonophysics 538, 1–66. doi: 10.1016/j.tecto.2012.01.027
Hack, J. T. (1975). “Dynamic equilibrium and landscape evolution,” in Theories of Landform Evolution, eds W. N. Melhorn and R. C. Flemal (Boston: Allen and Unwin), 87–102.
Hoth, S., Adam, J., Kukowski, N., and Oncken, O. (2006). “Influence of erosion on the kinematics of bivergent orgens. Results from scaled sandbox simulations,” in Tectonics, Climate, and Landscape Evolution, eds S. D. Willett, N. Hovius, M. T. Brandon, et al. (Boulder, Co: The Geological Society of America), Geological Society of America, Special Paper no. 398, 201–225..
Hubbard, J., and Shaw, J. H. (2009). Uplift of the Longmen Shan and Tibetan plateau, and the 2008 Wenchuan (M = 7.9) earthquake. Nature. 458, 194–197. doi: 10.1038/nature07837
Hubbard, J., Shaw, J. H., and Klinger, Y. (2010). Structural Setting of the 2008 Mw 7.9 Wenchuan, China, EarthquakeStructural setting of the 2008 Mw 7.9 Wenchuan, China, Earthquake. Bull. Seismol. Soc. Am. 100, 2713–2735. doi: 10.1785/0120090341
Jamieson, R. A., and Beaumont, C. (2013). On the origin of orogens. GSA Bull. 125, 1671–1702. doi: 10.1130/b30855.1
Jia, D., Wei, G., Chen, Z., Li, B., Zeng, Q., and Yang, G. (2006). Longmen Shan fold-thrust belt and its relation to the western Sichuan Basin in central China: new insights from hydrocarbon exploration. AAPG Bull. 90, 1425–1447. doi: 10.1306/03230605076
Konstantinovskaia, E., and Malavieille, J. (2005). Erosion and exhumation in accretionary orogens: experimental and geological approaches. Geochem. Geophys. Geosys. 6:Q02006. doi: 10.1029/2004GC000794
Konstantinovskaya, E., and Malavieille, J. (2011). Thrust wedges with décollement levels and syntectonic erosion: a view from analog models. Tectonophysics. 502, 336–350. doi: 10.1016/j.tecto.2011.01.020
Kooi, H., and Beaumont, C. (1996). Large-scale geomorphology: classical concepts reconciled and integrated with contemporary ideas via a surface processes model. J. Geophys. Res. 101, 3361–3386. doi: 10.1029/95jb01861
Li, Y. L., and Ji, X. T. (1993). Petrological character of Daxi conglomerate in Lushan-Tianquan and its provenance. J. Mineral. Petrol. 13, 68–73. (in Chinese with English abstract)
Liu, H., Liang, H., Cai, L., and Shen, F. (1994). Structural styles of the Longmenshan thrust belt and evolution of the foreland basin in western Sichuan Province, China. Acta Geol. Sin. 68, 101–118. (in Chinese with English abstract)
Liu, S., Luo, Z., Zhao, X., Xu, G., Liu, S., Wang, G., et al. (2005). Discussion on essential characteristics of intracontinental-subduction type foreland basins in western China. Oil Gas Geol. 26, 37–48,56. (in Chinese with English abstract)
Liu, Y., Tan, X., Ye, Y., Zhou, C., Lu, R., Murphy, M. A., et al. (2020). Role of erosion in creating thrust recesses in a critical-taper wedge: an example from Eastern Tibet. Earth Planet. Sci. Lett. 540:116270. doi: 10.1016/j.epsl.2020.116270
Liu-Zeng, J., Wen, L., Oskin, M., and Zeng, L. S. (2011). Focused modern denudation of the Longmen Shan margin, eastern Tibetan Plateau. Geochem. Geophys. Geosyst. 12, 1–21.
Lu, R., Liu, Y., Xu, X., Tan, X., He, D., Yu, G., et al. (2019). Three-dimensional model of the lithospheric structure under the eastern Tibetan Plateau: implications for the active tectonics and seismic hazards. Tectonics 38, 1292–1307. doi: 10.1029/2018tc005239
Malavieille, J. (2010). Impact of erosion, sedimentation, and structural heritage on the structure and kinematics of orogenic wedges: analog models and case studies. GSA Today. 20, 4–10. doi: 10.1130/gsatg48a.1
Malavieille, J., and Trullenque, G. (2009). Consequences of continental subduction on forearc basin and accretionary wedge deformation in SE Taiwan: insights from analogue modeling. Tectonophysics. 466, 377–394. doi: 10.1016/j.tecto.2007.11.016
McClay, K. R., and Whitehouse, P. (2004). “Analogue modelling of doubly vergent thrust wedges,” in Thrust Tectonics and Hydrocarbon Systems, Vol. 82, ed. K. R. McClay (Tulsa, OK: AAPG Memoir), 184–206.
Mugnier, J. L., Baby, P., Colletta, B., Vinour, P., Bale, P., and Leturmy, P. (1997). Thrust geometry controlled by erosion and sedimentation: a view from analogue models. Geology 25, 427–430. doi: 10.1130/0091-7613(1997)025<0427:tgcbea>2.3.co;2
Nieuwland, D. A., Leutscher, J. H., and Gast, J. (2000). Wedge equilibrium in fold-and-thrust belts: prediction of out-of-sequence thrusting based on sandbox experiments and natural examples. Netherlands J. Geosci. 79, 81–91. doi: 10.1017/s0016774600021594
Persson, K. S., Garcia-Castellanos, D., and Sokoutis, D. (2004). River transport effects on compressional belts: first results from an integrated analogue-numerical model. J. Geophys. Res. 109:B01409. doi: 10.1029/2002JB002274
Persson, K. S., and Sokoutis, D. (2002). Analogue models of orogenic wedges controlled by erosion. Tectonophysics 356, 323–336. doi: 10.1016/s0040-1951(02)00443-2
Schreurs, G., Buiter, S., Boutelier, J., Burberry, J., Callot, J.-P., and Cavozzi, C. (2016). Benchmarking analogue models of brittle thrust wedges. J. Struct. Geol. 92, 116–139.
Sieniawska, I., Aleksandrowski, P., Rauch, M., and Koyi, H. (2010). Control of synorogenic sedimentation on back and out-of-sequence thrusting: insights from analog modeling of an orogenic front (Outer Carpathians, southern Poland). Tectonics. 29:TC6012.
Stockmal, G. S., Beaumont, C., Nguyen, M., et al. (2007). “Mechanics of thin-skinned fold-and-thrust belts: insights from numerical models,” in Whence the Mountains? Inquiries into the Evolution of Orogenic Systems: A Volume in Honor of Raymond A. Price, Vol. 433, eds J. W. Sears, T. A. Harms, and C. A. Evenchick (Boulder, CO: Geological Society of America), 63–98. doi: 10.1130/2007.2433(04)
Storti, F., and McClay, K. (1995). Influence of syntectonic sedimentation on thrust wedges in analogue models. Geology 23, 999–1002. doi: 10.1130/0091-7613(1995)023<0999:iossot>2.3.co;2
Sun, C., Jia, D., Yin, H. W., Chen, Z. X., Li, Z. G., Shen, L., et al. (2016). Sandbox modeling of evolving thrust wedges with different preexisting topographic relief: implications for the Longmen Shan thrust belt, eastern Tibet. J. Geophys. Res. Solid Earth 121, 4591–4614. doi: 10.1002/2016JB013013
Sun, M., Yin, A., Yan, D., Ren, H., Mu, H., Zhu, L., et al. (2018). Role of pre-existing structures in controlling the Cenozoic tectonic evolution of the eastern Tibetan plateau: new insights from analogue experiments. Earth Planet. Sci. Lett. 491, 207–215. doi: 10.1016/j.epsl.2018.03.005
Tan, X., Liu, Y., Lee, Y. H., Lu, R., Xu, X., Suppe, J., et al. (2019). Parallelism between the maximum exhumation belt and the Moho ramp along the eastern Tibetan Plateau margin: coincidence or consequence? Earth Planet. Sci. Lett. 507, 73–84. doi: 10.1016/j.epsl.2018.12.001
Tan, X. B., Xu, X. W., Lee, Y. H., Liu, Y., Xu, C., Li, K., et al. (2017). Late cenozoic thrusting of major faults along the central segment of Longmen Shan, eastern Tibet: evidence from low-temperature thermochronology. Tectonophysics 712, 145–155. doi: 10.1016/j.tecto.2017.05.016
Tian, Y. T., Kohn, B. P., Gleadow, A. J., and Hu, S. (2013). Constructing the longmen shan eastern tibetan plateau margin: insights from low-temperature thermochronology. Tectonics 32, 1–17. doi: 10.1016/j.tecto.2015.04.010
Vanderhaeghe, O. (2012). The thermal-mechanical evolution of crustal orogenic belts at convergent plate boundaries: a reappraisal of the orogenic cycle. J. Geodyn. 5, 124–145. doi: 10.1016/j.jog.2011.10.004
Wang, E. C., Kirby, E., Furlong, K. P., Van Soest, M., Xu, G., Shi, X., et al. (2012). Two-phase growth of high topography in eastern Tibet during the Cenozoic. Nat. Geosci. 5, 640–645. doi: 10.1038/ngeo1538
Willett, S. D., Beaumont, C., and Fullsack, P. (1993). Mechanical model for the tectonics of doubly vergent compressional orogens. Geology 21, 371–374. doi: 10.1130/0091-7613(1993)021<0371:mmftto>2.3.co;2
Willett, S. D., and Brandon, M. T. (2002). On steady states in mountain belts. Geology 30, 175–178. doi: 10.1130/0091-7613(2002)030<0175:ossimb>2.0.co;2
Keywords: surface process, syntectonic, foreland basin system, analog experiment, Longmenshan
Citation: Luo Q, Deng B, Guang Y, He Y, Guo H, Huang J, Yang R, Yu H and Zhang J (2021) Differential Erosion and Sedimentation Process at the Longmenshan Foreland Basin, Eastern Margin of the Tibetan Plateau: Evidence From Analog Experiments. Front. Earth Sci. 9:637927. doi: 10.3389/feart.2021.637927
Received: 04 December 2020; Accepted: 07 April 2021;
Published: 11 May 2021.
Edited by:
Renqi Lu, Institute of Geology, China Earthquake Administration, ChinaCopyright © 2021 Luo, Deng, Guang, He, Guo, Huang, Yang, Yu and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bin Deng, ZGVuZ2JpbjEzQG1haWwuY2R1dC5lZHUuY24=; ZGVuZ2JpbjMwMDBAMTYzLmNvbQ==
 Qiang Luo1,2
Qiang Luo1,2 Bin Deng
Bin Deng