- 1Department of Geography, Texas A&M University, College Station, TX, United States
- 2Department of Earth and Atmospheric Sciences, University of Alberta, Edmonton, AB, Canada
Understanding the climate-glacier dynamics of debris-covered glaciers is notoriously difficult given a multitude of controlling factors and feedback mechanisms involving climate forcing, debris-load properties, supraglacial water bodies, and multi-scale topographic effects. Recent studies have provided insights into controlling factors, and have reported the presence of anomalies that contradict the general consensus of the protective influence of debris loads on ablation dynamics. Nevertheless, numerous processes that regulate glacier dynamics at various spatial and temporal scales have not been adequately accounted for in statistical and numerical modeling studies. Furthermore, important feedbacks involving ablation, topography, irradiance, gravitational debris flux, and supraglacial ponding are often neglected or oversimplified in existing models, which poses a challenge to our understanding of conflicting field observations such as the accelerated mass loss of many Himalayan glaciers, and glacier-subsystem responses (ice-flow, debris flux, surface morphology, and supraglacial water bodies) to climate forcing. This paper provides insights into the complexity of debris-covered glacier systems by addressing concepts and issues associated with forcing factors and glacial processes, and highlights the importance of understanding system couplings and feedbacks. Specifically, we review recent studies on debris-covered glaciers and utilize simulation results based on the Baltoro Glacier in the central Karakoram to discuss important concepts and issues. Our results demonstrate that climate forcing, the properties and transport of debris, topography and supraglacial water bodies are the key controlling factors in a debris-covered glacier system, and that their coupled effects and positive feedbacks may increase the ice loss of a debris-covered glacier. We also recommend new research directions for future studies.
1. Introduction
Debris-covered glaciers (DCGs) present a series of unique and complex challenges to those investigating climate-glacier dynamics and their role in downstream impacts such as freshwater availability, hydroelectric power generation, natural hazards and landscape evolution (Bishop et al., 2002; Seong et al., 2009; Immerzeel et al., 2010; Reid and Brock, 2010; Bush et al., 2020). While debris-free glaciers are relatively well-understood and modeled, DCGs introduce a number of additional complex dynamical and thermodynamical feedbacks between the underlying glacier ice, the debris cover, the adjacent-terrain geomorphological conditions, and the overlying atmosphere. The thermal and radiative characteristics of the debris cover itself depend on geographic location and the surrounding lithology. The thickness of the debris cover, which so critically determines whether the debris acts as an insulator for the ice or accelerates ice ablation, depends on the steepness of the surrounding topography, regional erosion characteristics, and glacier dynamics, which in turn depend on atmosphere-glacier interactions that have not yet been fully quantified (Bolch et al., 2012; Dobreva et al., 2017; Farinotti et al., 2020).
Currently, we have not achieved an agreement on the state and fate of many DCGs in High-Mountain Asia due to uncertainties related to climate, topographic evolution, debris-load forcings, and the development of supraglacial water bodies and ice-cliffs. Most researchers agree that debris insulation makes a glacier less sensitive to climate change (e.g., Reid and Brock, 2014; Pratap et al., 2015; Anderson and Anderson, 2016; Vincent et al., 2016). Recent observations and simulations, however, show that many DCGs exhibit comparable ice-loss to debris-free glaciers despite the presence of supraglacial debris (Kääb et al., 2012; Immerzeel et al., 2013; Fujita et al., 2014; Salerno et al., 2017). Therefore, it appears that DCGs may be more sensitive to climate change than previously thought, as a multitude of processes and feedbacks have not been accurately characterized. Existing DCG models do not provide a satisfactory explanation to these conflicting interpretations of climate-glacier dynamics, which is partially due to the over-simplified assumptions of important processes and feedbacks that involve ablation dynamics, debris flux and property variation, surface ponding, and topographic evolution.
Mountains that exhibit DCGs typically have substantial vertical relief and erosional forces that produce significant mass flux from the sidewalls onto the glacier. In the central Karakoram in Pakistan, extreme relief and complex climate systems generate some of the largest DCGs in the world (Bishop et al., 2001; Hewitt, 2005; Copland et al., 2009). Precipitation rates can be highly variable in space and time caused by the dominance of regional climate systems and topography. A particular system such as the Westerlies or the Monsoon could dominate over an area over a specific time frame, and it is also possible that an area could receive precipitation from both systems for a period. Furthermore, topographic variation partially controls the degree of orographic precipitation and this would also vary depending upon which system dominants over an area (i.e., moisture conditions, wind velocity and direction). This very high degree of coupled climate-topographic interactions presents a challenge to the numerical modeling of climate-glacier dynamics.
The surface-energy balance determines the ablation rates on DCGs, and net long-wave and short-wave fluxes play a major role in that balance, but the atmospheric conditions through which that radiation must pass play an equally important role: if the atmosphere is cloudy then the incoming short- and long wave radiations are fundamentally altered. Additionally, atmospheric temperature above the surface is critical to determining precipitation type (rain, snow, or some combination of frozen/liquid water). For example, debris cover can provide a surface heat source that drives convection and precipitation in the overlying atmosphere (e.g., Collier et al., 2015); depending on the temperature, that precipitation may fall as snow which would accumulate on the glacier ice in the absence of the debris, but given the presence of the warm debris the snow may melt and percolate down to the glacier surface, thereby enhancing ablation.
Supraglacial ponding is another critical process on DCGs. Supraglacial ponds and lakes play an important role in glacier ice-loss as well as glacial hydrology (Fountain and Walder, 1998; Sakai et al., 2000; Wessels et al., 2002; Miles et al., 2016, 2018). Researchers have identified an increasing number of ponds on some large DCGs (Gibson et al., 2017). Studies have also indicated that the increase in spatial density of supraglacial ponds can be facilitated by localized thinning, insufficient drainage, collapse of water channels, and overall lowering that decreases the slope of the glacier altitude profile in the ablation zone (Sakai et al., 2000). Unfortunately, many of these important mechanisms have not been adequately studied and are often neglected in existing glacier models and simulations.
Such complexities are only now beginning to be understood through the use of numerical models (e.g., Collier et al., 2013; Rowan et al., 2015; Anderson and Anderson, 2016; Miles et al., 2018). Field observations of en-debris and sub-debris processes can be difficult to obtain given time, economic, and logistic constraints. Nevertheless, field observations are essential for understanding the magnitude of specific properties and processes, providing constraints for input into numerical models, and for validation and accuracy assessment of numerical modeling efforts. However, many mechanisms that govern glacier dynamics can not be fully understood through field observations and remote sensing data. Consequently, numerical modeling that evaluates new parameterization schemes to account for processes and important feedback is sorely needed to better understand complex climate-glacier dynamics of DCGs.
The objectives of this paper are therefore to discuss a multitude of complex interactions and uncertainties that limit our understanding of how DCGs may be responding to climate change. We review our current understanding of debris-covered glaciers and identify gaps in knowledge about some processes and feedbacks that appear to play important roles with respect to ablation dynamics. We also utilize numerical simulations to demonstrate various concepts and processes. We specifically discuss various issues and use our simulation results to identify future research pathways that can help eliminate uncertainty and promote new empirical and numerical-modeling research. We acknowledge that we cannot account for all processes, nor utilize fully comprehensive parameterization schemes that accurately predict process rates (an objective of numerical modeling research). Rather, we attempt to provide for a first-order characterization and understanding of processes and feedbacks based upon the simulations that we have incorporated into our discussion. Furthermore, it should be noted that this work should not be viewed as a formal modeling paper, complete with parameter sensitivity and uncertainty analyses, as this is beyond the scope of our objectives.
We synthesize our treatment of this complex topic by organizing the paper based upon concepts related to climate-glacier system components. We first address climate forcing and specifically address radiative and precipitation forcing, where we identify some processes that should be considered regarding the surface energy balance in high relief mountains. We then discuss debris load properties and debris transport dynamics. We finally address various feedback mechanisms and system couplings on the glacier surface with respect to ablation, supraglacial water bodies, ice cliffs, and surface topography.
2. Climate Forcing
Radiative and precipitation forcing govern glacier dynamics, although the partitioning of these forcing components in any particular geographic area is not well-known with any degree of certainty, given a multitude of multi-scale topographic effects and our inability to accurately characterize and account for radiative and precipitation processes (Bishop et al., 2019; Bush et al., 2020). For example, it is thought that radiative forcing dominates in the Eastern Himalaya, while precipitation forcing has the biggest influence in the western Himalaya (Bolch et al., 2012). Nevertheless, we require a much more detailed understanding of climate-glacier dynamics from an internal and external scale-dependent forcing perspective, as various aspects of climate, glacial, and geomorphological systems need to be accounted for. Unfortunately, we lack basic data regarding radiation transfer and precipitation components that govern glacier states, and we do not know the responses and sensitivity to climate change for many regions of the world (Bolch et al., 2012; Dobreva et al., 2017; Bishop et al., 2019; Bush et al., 2020; Farinotti et al., 2020). Furthermore, the data sets that we tend to rely upon for such information (e.g., climate simulations and re-analysis data) do not accurately characterize local-scale radiative and precipitation fluxes due to inadequate representation of topography and/or processes (Bush et al., 2020).
Energy balance calculation at the glacier surface (with or without debris) is the first step toward determining the low-level air temperature above the glacier, but it neglects potential temperature advection by atmospheric circulations (e.g., anabatic, katabatic, or frontal winds, which all advect temperature). Furthermore, during the daytime, heating of the debris cover itself can generate atmospheric convection above the debris leading to strong converging surface winds and potential precipitation, which can further alter the surface energy balance. Consequently, numerous radiative-transfer (RT) parameters, circulation dynamics and cloud properties, and convective, cyclonic and orographic precipitation mechanisms must be considered to understand glacier response and sensitivity to forcings.
2.1. Irradiant Fluxes
The short-wave and long-wave radiant energy components of the surface-energy balance strongly regulate ablation dynamics. The short-wave surface irradiance (E) components include the direct irradiance from the sun (Eb), the diffuse-skylight irradiance due to atmospheric scattering (Ed) and the adjacent-terrain irradiance (Et). All of these components are space-time-topography-wavelength dependent, and numerical modeling is the only way to account for the inherent scale-dependent operation of orbital, atmospheric and lithospheric processes that govern the variability of the magnitude of these RT parameters over glaciers (Bishop et al., 2019). These radiation fluxes significantly contribute to ablation at a particular location depending upon the surrounding land cover and topographic conditions. Studies have estimated that the shortwave radiation usually accounts for 75% or more of total irradiance on glacier surfaces (Oerlemans and Klok, 2002).
2.1.1. Short-Wave Direct Irradiance
The direct irradiance is the dominant short-wave irradiance component (Proy et al., 1989; Olson and Rupper, 2019). It is strongly controlled by local and meso-scale topographic effects. It can be represented as:
where λl is wavelength, E0 is the exo-atmospheric irradiance adjusted for Earth-Sun distance, T↓ is the downward atmospheric transmittance of radiation governed by atmospheric absorption and scattering, and θs is the solar zenith angle. Transmittance also accounts for the atmospheric optical depth that is partially governed by the relief structure of the landscape (i.e., altitude).
The cosine of the incidence angle (cosi) characterizes the local topographic effects on irradiance given solar and terrain geometry relationships. Specifically, the incidence angle of illumination (i) between the sun and normal to the ground surface is defined as:
where θs is the apparent solar zenith angle that accounts for altitude variations and atmospheric refraction given the atmospheric temperature and pressure profiles, θt represents the terrain slope angle, ϕs is the solar azimuth angle, and ϕt is the terrain slope-azimuth angle. Calculation of cosi is possible with the use of a digital elevation model, and negative values must be corrected to 0.0. Local topographic properties can have a significant effect on the magnitude of the direct irradiance that reaches the surface of a glacier. Ablation and meltwater transport, and gravitational sediment fluxes all alter the altitude, slope and slope azimuth of the ice and sediment surfaces of a glacier. A feedback between ablation-topography and surface irradiance controls the topographic evolution of a glacier surface (Huo et al., 2020). The importance of the local topographic conditions on the direct irradiance cannot be overlooked. The cosine of the incidence angle can range from 0 to 1 based upon slope angle and slope-azimuth angle variations caused by sediment transport and ablation processes. Based upon our simulations in the Karakoram (see Figure 1), direct irradiance values can be greater than 1,000 Wm−2. Consequently, rapidly evolving topography should be accounted for as this sub-parameter strongly regulates ablation, all other factors such as debris properties being equal.
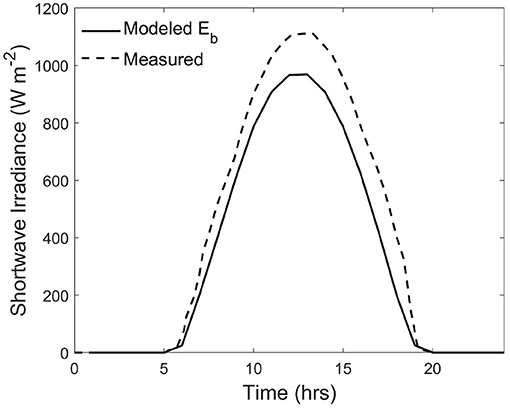
Figure 1. Simulated short-wave direct-beam irradiance (Eb) component (wavelength range: 0.3 μm to 3 μm) for the Baltoro Glacier, compared to field measurements of short-wave irradiance at the same location on July 24th 2004. The discrepancy in magnitude is mainly caused by the diffuse-skylight irradiance and the adjacent-terrain irradiance.
For many valley glaciers, the topographic shading on the direct solar radiation can be significant due to complex topography (Olson and Rupper, 2019). The S parameter in Equation (1) accounts for the meso-scale relief structure of the topography that governs the presence of cast shadows on the landscape. Cast shadows on the landscape are governed by the size of the solar disk and the Earth-Sun distance. More specifically, the solar angular width (αs(t),[degrees]) in relation to topographic relief, will govern the overall length of a cast shadow in the direction of ϕs. This angle and other geometry parameters can be used to compute the planimetric length of the umbra and penumbra subregions that collectively represent the total cast-shadow region. The umbra is the region over the landscape where Eb is totally obstructed by the topography. Conversely, the penumbra region receives a fraction of Eb because a portion of the solar disk is obstructed by the topography. In the penumbra region, the fraction of Eb is governed by the pixel location. Consequently, a location in the umbra region would exhibit a shadow coefficient of 0.0, while a location in the penumbra region would exhibit a coefficient value ranging from 0.0 < S < 1.0. Therefore, cast shadow locations can also include irradiance from Eb. Furthermore, because of the eccentricity of the Earth's orbit around the sun, the length of the cast shadow region varies non-linearly with time. Given the extreme relief in many mountain environments, cast shadows can significantly modulate direct irradiance over the course of a day, let alone over the course of an ablation season. The importance of cast shadows should also not be underestimated, as the S parameter strongly regulates the direct irradiance during the early morning and late afternoon, as governed by basin relief and solar geometry. Large areas of a glacier's surface can be in cast shadow (umbra) for hours during the day, thereby blocking the direct irradiance and decreasing the surface irradiance and ablation potential. It is more difficult to evaluate the significance of the penumbra on ablation, other than to say that the length of the penumbra in the direction of the solar azimuth angle causes a direct irradiance gradient that influences ablation depending upon its length. Numerical modeling and sensitivity analysis are required to have a better understanding of the entire S parameter. Consequently, the S parameter can have a significant to insignificant influence on glacier ablation depending upon environmental conditions and the total length of the umbra and penumbra and time that cast shadows are found over the glacier surface. Its modulating effects on ablation will increase during the ablation season as solar zenith angles increase.
Simulating the magnitude and distribution of Eb on a glacier surface is relatively straight-forward, given that topographic evolution resulting from ablation dynamics is accounted for with respect to local topographic properties and relief. We demonstrate relatively accurate simulated estimates of diurnal direct irradiance (1 day; July 24, 2004) using a SRTM 30 m DEM, and compared our simulation to field-based surface irradiance measurements collected on the same day by Mihalcea et al. (2008) for the same location on the Baltoro Glacier (Figure 1). We accounted for orbital parameters based upon Berger (1978) and used the apparent solar zenith angle accounting for parallax and atmospheric refraction, assuming the temperature and pressure profiles of the atmosphere. In this simulation, however, we did not utilize ray-tracing to account for cast shadows. The simulation results are reasonable, the modeled Eb is less than measured E values in the field, as we did not account for Ed and Et that is represented in the E values. Perhaps it is more important to notice the discrepancy in magnitude in the early morning and late afternoon, caused by cast shadows (i.e., shape at the base of the distribution is different). Rapidly changing magnitudes at these times clearly reveals the influence of cast shadows in E, vs. simulated Eb values. We would expect these differences to become more pronounced during the later stages of the ablation season as the solar zenith angles increases.
Challenges in estimating this dominant component more accurately involve better characterization of atmospheric conditions, use of higher-resolution DEMs for establishing initial conditions, and the development and evaluation of different parameterization schemes to account for those controlling parameters that govern the energy-balance at the glacier surface.
2.1.2. Short-Wave Diffuse-Skylight Irradiance
Atmospheric scattering will produce a hemispherical source of irradiance that contains isotropic and anisotropic components (Perez et al., 1986; Proy et al., 1989). The anisotropic nature of Ed has been the largest source of error for estimating this component, as it is governed by circumsolar brightening due to forward scattering by aerosols, and horizontal brightening due to Rayleigh scattering (Perez et al., 1986). A Two-stream approximation model assumes that there is a Rayleigh-scattering component (Er), an aerosol-scattering component (Ea), and a secondary ground/sky-backscattering component (Eg) caused by multiple interactions between the ground surface and the atmosphere (Proy et al., 1989; Gueymard, 1995; Zhang et al., 2015). One can account for single-scattering or a multiple-scattering Rayleigh atmosphere. The single-scattering albedo is required to account for aerosol scattering which is a function of both wavelength and humidity. Aerosol type and models such as rural, urban, maritime or tropospheric can also be accounted for Gueymard (1995). The ground backscatter component can be modeled by accounting for the zonal ground reflectance from the overall ground and sky reflectance (Gueymard, 1995). Numerous parameterization schemes are available that enable a reasonable characterization of this irradiance component for a horizontal surface (e.g., Bird and Riordan, 1986; Gueymard, 1995). Multi-scale topographic effects, however, need to be considered at each location on the landscape (Proy et al., 1989; Bishop et al., 2019).
Both local and meso-scale topographic properties govern Ed and Proy et al. (1989) provides a computation solution such that:
where L↓ is the downward radiance from sky-hemispherical incident directions θi and ϕi, and θi and ϕi are the zenith and azimuth angles from the hemisphere, αs is the solar-elevation angle (αs = π/2 − θs), and I is the incidence angle of the direction defined by sky-hemisphere and terrain geometry, similar to Equation (2) using incident geometry. Such a computation is computationally expensive given that Ed is wavelength dependent, and hemispherical topographic shielding must be accounted for by limiting the integration based upon the maximum relief angle for all hemispherical azimuth directions.
Basin relief production is primarily governed by paleo-glacier erosion and uplift history. There is a time disconnect such that the majority of the relief production occurred in the past, however the resulting relief (i.e., topographic shielding) partly influences the modern-day diffuse-skylight irradiance. Its altitudinal spatial variability can therefore govern the spatial variability in ablation. We demonstrate this topographic control using radiative and ablation simulations over the Baltoro Glacier in the central Karakoram (Figure 2). For this simulation, we did not perform the full integration of Ed because of the computational intensity of doing so over all wavelengths. Rather we used the algorithms from Bird and Riordan (1986) to estimate Ed on a horizontal surface, and then multiplied the results by the so-called skyview-factor coefficient that represents the relative magnitude of topographic shielding. The computation of this topographic parameter is highly scale dependent, and Bishop and Dobreva (2017) demonstrated that it is highly variable across mountain environments given the polygenetic nature of erosion dynamics and topographic evolution (for more parameter details see Dozier et al., 1981; Wilson and Bishop, 2013). Regarding the ablation simulations, we account for debris thickness distribution over the Baltoro Glacier from Mihalcea et al. (2008) and meltwater ponds to generate a temporally-averaged ablation rate over the glacier. We then compared the skyview-factor coefficient to simulated ablation over the glacier (Figure 2). Clearly there is a decrease in the ablation rate with altitude that accounts for the collective influence of cooler atmospheric temperatures and an increase in topographic shielding (lower skyview coefficient). At about 4, 400 − 4, 500 m (below Concordia; Concordia is at about 4,691 m) topographic shielding begins to decrease and is associated with the confluence of glacier tributaries. It then abruptly increases with maximum topographic shielding being spatially coincident with the minimum ablation rate for the profile. These simulation results suggest that meso-scale topographic effects also play an important role governing the magnitude of Ed and ablation depending upon paleo-glacier erosion dynamics and basin relief production (i.e., erosion-uplift dynamics).
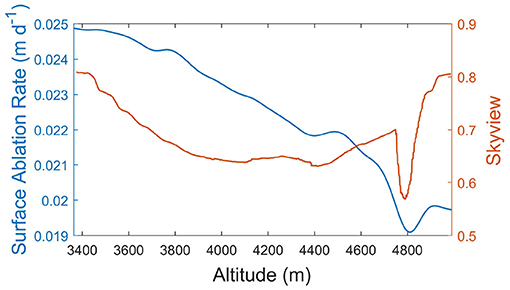
Figure 2. Topographic shading effect on the simulated surface ablation rates for the Baltoro Glacier in 2004. The ablation rates are averaged over 30 m altitude bins. The skyview factor represents the topographic shielding that governs the diffuse-skylight irradiance. The abrupt drop in the skyview is associated with the minimum ablation along the profile, which highlights this meso-scale topographic effect on glacier surface ablation.
The significance of this secondary surface-irradiance parameter on ablation is difficult to ascertain, as numerical simulation sensitivity analysis focused on irradiance partitioning is sorely needed. We have demonstrated, however, that mesoscale topographic effects on the diffuse irradiance potentially regulate ablation rates based upon glacier erosion histories (i.e., relief production). Simulation results indicate that the magnitude of this parameter can range from relatively low or moderate energy levels in the visible portion of the spectrum (generally 5–200 Wm−2) depending upon topographic conditions. Spatial distribution patterns of higher diffuse energy are most likely found at higher altitudes where basin relief significantly decreases. Furthermore, the influence of landcover conditions can also increase the magnitude of this component given high albedo surfaces (i.e., snow) and secondary scattering back to the surface.
2.1.3. Short-Wave Adjacent-Terrain Irradiance
The aforementioned irradiance components and surface Bi-Directional Reflectance Distribution Function (BRDF) interact with the surrounding terrain geometry to produce the adjacent-terrain irradiance (Et). This irradiance component is extremely complicated but important to characterize, because variations in land cover and topographic complexity strongly regulate its magnitude. Highly reflective materials such as felsic minerals, vegetation, and ice and snow coupled with steep slopes can cause significant irradiance that impacts ablation dynamics, and especially the retreat of ice-cliffs (Sakai et al., 2002; Buri et al., 2016).
The characteristics of surface reflectance properties can range between diffuse and specular (Iqbal, 1983; Zhang et al., 2015). We know, however, that the isotropic assumption of reflectance is not valid in mountains, and the surface BRDF (ρbrdf) must be accounted for at each location on the landscape, as reflectance from the surrounding terrain and other glacier surface locations can contribute to Et. The BRDF is used to describe the anisotropic nature of surface reflectance characteristics. It is a scattering function that describes anisotropic reflectance given all input-output angles. It is characterized as:
where, L is the surface radiance and E is the surface irradiance (E = Eb+Ed+Et). The effective illumination () and viewing directions () are a function of solar geometry and terrain geometry. Consequently, the topography has a significant affect on the BRDF (Zhang et al., 2015), and the intimate mixture of materials and structure of the surface also influence scattering direction. The BRDF, however, is difficult to measure accurately, and is also the basis for the computation of surface albedo, another important RT parameter that is difficult to estimate.
The irradiance component Et can be characterized in the following fashion:
where L is the adjacent surface reflected radiance coming from the effective incident direction, ϕi is the hemispherical incident azimuth angle, θi is the incident vertical hemispherical zenith angle to account for terrain radiance above and below a pixel location, T↓↑ is the atmospheric transmittance given the optical depth of the atmosphere due to relief and propagation zenith angle through the atmosphere (θv) between two locations, cosIt represents the terrain incidence angle given the influence of the local terrain geometry in relation to the incident directional geometry, and St representing terrain blocking of the adjacent surface radiance between any two points of the surrounding terrain. As a general rule-of-thumb, the computation of Et should account for the terrain conditions extending out to some distance (e.g., 5 km) from each pixel location (Proy et al., 1989). However, the appropriate distance in any direction can vary as a function of the anisotropic nature of the topography, given the orientation of the structural fabric of the topography related to differential erosion and tectonics. As such, the adjacent hemispherical distribution of locations that can contribute to Et for any particular location can be extremely scale dependent, given that it is also a function of altitude, such that the contributing zones of adjacent-terrain irradiance may be spatially contiguous or spatially fragmented. To our knowledge, this level of complexity has not been evaluated with respect to determining its impact on ablation dynamics, although it most likely plays a role in ice-cliff retreat when considering the coupled influence of the long-wave adjacent-terrain irradiance term.
The short-wave adjacent-terrain irradiance is thought to be a tertiary surface irradiance component that does not significantly affect ablation. However, given our parameterization scheme and the nature of highly directional and diffuse reflectance components associated with the BRDF, coupled with changing glacier surface topography, solar zenith and solar azimuth angles, the Et component is likely to be highly variable in space and time, and facilitate ablation in general. The significance of this component could be greater than the diffuse irradiance given specific topographic and adjacent land cover conditions, such as at depression areas that are surrounded by highly reflective felsic minerals and snow.
2.2. Precipitation
Precipitation in mountainous regions is partly modified by avalanche redistribution of snow, and is determined by uplift in traveling frontal zones or by orographic uplift. The former will move spatially with the frontal system while the latter will remain stationary given the topography and the wind direction. Determining where near-constant orographically-forced precipitation occurs may lead to an explanation of why a particular glacier exists at one location but not in another nearby location.
Separating orographic precipitation from frontal precipitation is difficult from observations (in which all precipitation is combined). For orographic precipitation one needs to know the wind direction, the atmospheric moisture content, and the topography itself but one also has to track the properties of the air parcels along their trajectories to keep track of the amounts of condensation, evaporation, and precipitation as the air travels up and perhaps over multiple peaks, potentially losing all of its water content along the way. Some attempts at quantifying this process have been made using a combination of a high resolution DEM and downscaled reanalysis climate data (e.g., Dobreva et al., 2017).
Regardless of the driving mechanism behind mountain precipitation, the precipitate-formation process is mostly a cold-based one given typical surface temperatures at high elevations and the adiabatic lapse rate, i.e., the precipitate-formation process occurs at temperatures below freezing and so is governed by the Bergeron-Findeisen process. According to this process, in a cloud that has a mix of ice crystals and supercooled water droplets, water vapor in the cloud preferentially deposits on the ice crystals because of the lower saturation vapor pressure over ice than over water. As the water vapor decreases through deposition on the ice, the supercooled droplets evaporate and lose their water to the growing ice crystals, which may then grow large enough to overcome any updrafts and fall to the surface. This process dominates mid-latitude precipitation (even during the summer) and at high altitudes.
Most precipitation in mountainous regions therefore begins frozen; whether it remains frozen on its way down to the surface is dependent on the atmospheric temperatures through which it falls. At high altitudes, it is more likely to remain frozen than, for example, at sea level in mid-latitudes, but if conditions are warm enough then it will melt completely and fall as rain (or, if the precipitate does not have enough time to melt completely it will fall as graupel, sleet, or freezing rain).
Snowfall above the equilibrium line altitude (ELA) is paramount for a glacier's survival. Climate change can alter the ELA up or down, depending on local conditions, but with a general warming trend ELAs on average are rising. If the ELA rises above the peak of the mountain then no glacier can exist. If atmospheric conditions above the ELA become conducive to rain then glacier ablation will be accelerated.
When debris cover is present additional factors must be taken into account. If the debris temperature is below freezing, snowfall would accumulate as on a debris-free glacier. If the debris cover is above freezing, however, then it will melt the snow leading to percolation of liquid water onto the glacier surface that can enhance ablation. Refreezing of the percolated water at the glacier surface is possible, with the release of latent heat into the interstitial spaces of the debris cover (Collier et al., 2014, 2015). The debris cover fundamentally alters the fluxes of sensible and latent heat to the overlying atmosphere (Collier et al., 2014). In addition, a relatively warm debris cover (through daytime solar heating) can trigger convection in the atmosphere above and produce precipitation that melts on contact and increases surface ablation (Collier et al., 2015). So DCGs have the potential to increase their own ablation rates through dynamic interactions with the overlying atmosphere as well as the underlying glacier.
3. Supraglacial Debris Load
3.1. Composition and Properties
Investigators are increasingly recognizing the significance of the supraglacial debris load as a major controlling factor in regulating ablation and the morphological evolution of DCGs (Adhikary et al., 2000; Nicholson and Benn, 2006; Reid et al., 2012; Rowan et al., 2015; Anderson and Anderson, 2016; Zhang et al., 2016; Gibson et al., 2017). Field data and numerical-modeling efforts (given various assumptions) demonstrate the general relationship between debris thickness and ablation rate, as thicker debris loads decrease the thermal energy available for ablation at the debris/ice interface, while thin and moisture laden debris can significantly accelerate ablation beyond that of debris-free conditions (Mattson, 1993; Kayastha et al., 2000; Reznichenko et al., 2010). This general relationship, however, does not account for a variety of debris-load properties, processes, and feedbacks regarding ablation dynamics, as supported by findings related to the “debris-covered glacier anomaly” (Salerno et al., 2017) and numerical modeling efforts (Anderson and Anderson, 2016; Zhang et al., 2016; Gibson et al., 2017; Huo et al., 2020). Consequently, the multi-faceted nature of this controlling factor is not adequately understood, as there are many unknowns with regard to properties and processes that govern ablation dynamics, and research clearly reveals the relatively high spatio-temporal variability in debris properties and processes that should be accounted for Scherler et al. (2011b); Reid et al. (2012); Rowan et al. (2015); Yue et al. (2017). The complexity of the problem is highlighted by the relatively large number of debris, near-surface and scale-dependent topographic parameters that partially govern ablation. Table 1 lists various physical and radiative-transfer properties that all contribute toward regulating the magnitude of ablation in space and time. It is also important to realize that location/scale specific parameters related to the topography and lithology beneath and surrounding a glacier also contribute to spatial and property variations in the debris load, as debris sources and mineralogical composition of debris and rocks is governed by the nature of the geological setting, and the geomorphological system within the glacial basin.
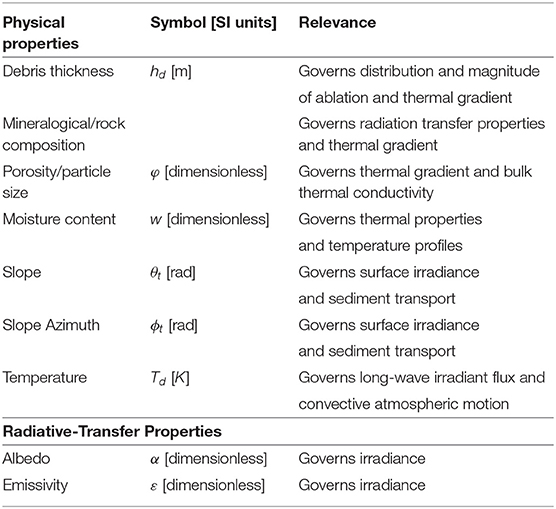
Table 1. Debris-cover physical and radiative-transfer properties that regulate ablation in space and time.
An important first-order property that requires consideration is the particle size/distribution of the debris load. This property can be highly spatio-temporally variable over a glacier, and is regulated by source and sediment-transport dynamics. It can have a significant impact on ablation dynamics, as “particles” can include dust, fines, gravel, cobbles, rocks, isolated boulders, and boulder fields (Figure 3; the full range of debris particle sizes). Such heterogeneous conditions are common on many glaciers around the world, and “particle” distributions can be significantly different on glaciers within a region, depending upon paleo-climate-glacier dynamics (Bush et al., 2020). Such variations are the result of polygenetic sediment-transport dynamics involving mass movements, aeolean, suprafluvial, englacial, gravitational, and ice-flow transport mechanisms. Spatio-temporal variations of this aspect of the debris load are usually not considered, and homogeneous unconsolidated debris conditions are assumed, which causes uncertainties in ablation estimates.

Figure 3. Supraglacial debris cover conditions on the Baltoro Glacier during the summer of 2005. The nature of the supraglacial debris load can vary significantly with respect to particle size, composition, and debris thicknesses. (A) Cryoconite holes at Concordia at 4,500 m. These features form as wind blown dust, soot and particles that absorb radiation generate holes that contain water that contributes further to increase ablation and the depth and width of the hole. (B) Wind blown silt and sand deposits at the terminus of the glacier. Wind turbulence caused by up valley winds and altitude variations between the pro-glacial valley floor and the glacier surface results in wind-sorted supraglacial debris. (C) Supraglacial debris load consisting of gravel, pebbles, and cobble-sized particles. Notice the felsic and mafic compositional variations of particles. (D) Supraglacial debris dominated by larger rocks over the glacier surface. Rock spatial density greatly governs the spatial variation in ablation dues to shadowing and rock mass influence on the vertical debris load thermal gradient. (E) Debris load consisting of sediment, rocks, and boulders. Debris thickness is about 5 m. Debris thickness can be highly variable over a glacier surface depending upon a multitude of controlling factors. (F) Debris loads in the Himalaya frequently consist of boulder fields, that make it difficult to accurately assess or model thermal gradients, given shadowing and alternation of the wind field. Photo credit: Michael P. Bishop.
The composition of the debris load is another important property. It is rarely accounted for, although it can be taken into consideration by using estimates of the debris bulk conductivity. It not only governs the bulk thermal properties of the debris, but also the surface reflectance properties and the surface energy balance of the short-wave irradiance (i.e., albedo). Consequently, remote sensing analysis and absorption-feature modeling can be used for mineral detection and determining the composition of the debris using hyperspectral data. This approach can provide more explicit estimates of the surface composition and distribution of moisture-laden debris. Such data regarding the debris load are too logistically difficult to acquire in the field, but high-resolution hyperspectral remote-sensing capabilities are now available using uncrewed aerial systems (UAS) to better assess “particle” distributions, surface mineralogy and other parameters that are not usually accounted for (e.g., Fyffe et al., 2020).
Debris load thickness has been shown to be highly variable (Mihalcea et al., 2008; Fyffe et al., 2020). Many glaciers exhibit low-frequency debris thickness variation (the generally thicker debris toward the terminus) controlled by surface ice-flow transport dynamics and englacial transport of sediment and rocks into the terminus region (Anderson and Anderson, 2016; Wirbel et al., 2018). Higher-frequency debris thickness variations must also be considered, as the debris load is modulated by supra-fluvial transport, topography-driven gravitational transport, and other ablation dynamics including supraglacial lake development and evolution. Furthermore, a high percentage of debris cover lowers the glacier surface albedo that partially counters the debris insulation effect (Fyffe et al., 2020). Such complexities have not been adequately investigated, and it is essential to note that complex feedbacks exist between sediment fluxes, ablation, topography and the surface-energy balance (Huo et al., 2020). Although several approaches have been developed to estimate the distribution of debris thickness (e.g., Mihalcea et al., 2008; Zhang et al., 2011; Reid et al., 2012; Rounce et al., 2018), higher-frequency variations in debris thickness and the spatial variability of ablation is not known with any degree of certainty on most DCGs.
Field measurements suggest that debris temperature gradients are approximately stable and linear with depth during the ablation season (Rowan et al., 2021), although the linearity and stability depend on the time scale, and linearity is also dependent upon the debris thickness. Assuming linearity, debris surface temperature can be used to estimate sub-debris ablation, which is also controlled by debris thickness, and thermal conductivity (Nakawo and Young, 1981; Nicholson and Benn, 2006). Given shallow debris thicknesses, relative homogeneity in particle distribution, and lack of moisture-laden sediment, this first-order approximation assumes isotropic conditions with respect to various properties. With greater debris load thicknesses, however, porosity variation has the potential to alter the thermal gradient given the translocation of the fine size-fraction of particles and presence of moisture-laden sediment. Therefore, the thermal conductivity of debris can be difficult to determine given the complex composition and pore-space conditions. Nicholson and Benn (2006) presented an approach to address this issue using measured temperature profiles. Based on this model, the bulk thermal conductivity of the debris layer (kd) can be written as:
where cd, ρd, cv, ρv are the specific heat capacity and density of debris, and specific heat capacity and density of the pore-space filler, respectively. φ is the porosity, and κ is the apparent thermal diffusivity of the debris, which can be determined using the thermal diffusion equation:
where Td is the debris temperature, which is a function of depth (z) and time (t). κ can then by determined from the measured temperatures-time and temperatures-depth variations. Another method was presented by Reid and Brock (2010), based on which, the debris was broken down to multiple thin layers to estimate the thermal conductivity and internal temperature profiles:
Debris moisture conditions, mineral mixing, debris surface structure, and surface topography can also significantly influence the surface albedo that regulates debris temperature and ablation (Pelto, 2000; Nicholson and Benn, 2006). Accurate estimation of the albedo based upon the surface BRDF is difficult to compute, and rapidly changing glacier-surface dynamics should cause the surface albedo to exhibit relatively high spatio-temporal variability (Takeuchi and Li, 2008; Yue et al., 2017). Therefore, better estimates of debris surface reflective parameters are required using more reliable parameterization schemes.
We demonstrate this using numerical simulations and accounting for the spectral reflectance of minerals that make of the debris load of the Baltoro Glacier. Specifically, we utilize a radiation-transfer approach (Coakley, 2003) to compute the broadband surface albedo (α) based on the mixing of sediments and water at each grid cell, such that:
where E is the total short-wave irradiance and L is the reflected surface radiance, which, based on an isotropic (Lambertian) assumption, can be written as (Bishop and Colby, 2011):
where rmc is the spectral reflectance of the mineralogical composite representing the debris, which is considered as a composite reflectance of different types of minerals. The debris lithological distribution over the Baltoro Glacier was based on Gibson et al. (2017), which indicates that the surface is mostly covered by a composite of gneiss (about 53%), granite (about 30%), and schist metasediment (about 17%). Simulated results in Figure 4 reveal significant spatial variations in the surface albedo over the lower ablation zone of the Baltoro Glacier caused by mineralogical and moisture variations. We performed the narrow-band to broad-band conversion of surface albedo using ASTER imagery based on the work of Liang (2001), and confirmed that our simulated values are very close to the remote-sensing approach. In the future, the use of semi-empirical BRDF models should be used with multi-angle reflectance imagery to generate higher quality albedo estimates for glacier surfaces.
Figure 4. Modeled surface albedo over the lower ablation zone of the Baltoro Glacier. The geomorphological conditions were estimated from an ASTER scene acquired on August 14th, 2004 (AST_08_00308142004054614).
3.2. Debris Transport
Debris loads are mobile due to ice-flow, gravitational movement, and fluvial processes (Anderson, 2000; Benn and Evans, 2014; Anderson and Anderson, 2016, 2018; Zhang et al., 2016; van Woerkom et al., 2019; Fyffe et al., 2020). Although the exact glacial debris production mechanisms have not been fully understood, most investigators consider the main sources are from headwalls, sidewalls, basal erosion and moraines (Anderson, 2000; Benn and Owen, 2002; Anderson and Anderson, 2016; van Woerkom et al., 2019). Studies have observed mass transport from landslides (Benn and Evans, 2014), avalanches (Benn and Lehmkuhl, 2000), and rockfalls from valley walls (Benn and Evans, 2014). Englacial debris loads and rock encapsulated by basal erosion also contribute to the total debris mass balance, and several models have been developed to investigate the transport of englacial debris loads (Anderson and Anderson, 2016; Wirbel et al., 2018).
One of the first models of supraglacial debris flux was developed by Anderson (2000), which describes the diffusive debris flux originated from medial moraines in valley glaciers. Anderson and Anderson (2016) and Anderson and Anderson (2018) developed a similar model that couples with ice dynamics to investigate the longer-term evolution of debris cover. Moore (2018) presented a comprehensive study on the gravitational debris transport across the ice surface, as the topography evolves due to melt. A theoretical framework was developed for assessing slope stability and gravitational mass transport accounting for meltwater balance on ablating ice. Modeled results provided insights into the geometry of stable slopes as a function of debris thickness and texture. Another recent study by Fyffe et al. (2020) provides valuable field observations on the rates and forms of debris transport. van Woerkom et al. (2019) studied the debris transport from lateral moraines using high resolution DEMs and found that the lateral moraines contribute to debris thickening along the margin of the glacier surface.
Here we discuss two dominant processes that govern debris movement on a glacier at different spatio-temporal scales: the gravitational process that operates at smaller spatio-temporal scales given complex glacier topography, and the advective-diffusive processes that control debris flux over larger spatio-temporal scales governed by the ice-flow.
3.2.1. Gravitational Debris Fluxes
Gravitational debris movement (such as sliding and slumping) occurs on hillslopes and on glacier surfaces (Benn and Evans, 2014; Fyffe et al., 2020). Gravity-driven debris flux regulates the local thickness distribution of supraglacial debris during the ablation season when the surface topography is constantly changing under rapid melting, especially around melt hotspots such as supraglacial ponds and ice-cliffs. Field observations have identified sediment sliding or slumping off steepening ice-cliffs due to ice-cliff retreat and supraglacial lake expansion (Buri et al., 2016; Miles et al., 2017).
Gravity, internal friction and basal resistance force govern the gravitational movement of debris. Based on the debris flow model by Chen and Lee (2000), the unit net force acting on a debris column, F, can be written as:
where ρd is debris density, g is the gravitational acceleration, zx and zy are the first derivatives of ice-surface elevation in the horizontal and vertical directions, respectively, k is the pressure ratio as defined by Chen and Lee (2000), ux and uy are debris velocity components, ru is the constant pore-pressure ratio, and ϕ is the dynamic internal friction angle of the debris. The first term on the right represents the gravitational force, the second term describes the internal friction of debris particles, and the third term represents the resistance force at the base of the debris column. Gravitational debris flux governs the local redistribution of debris thickness during the ablation season when the ice surfaces topography changes rapidly due to melt. The transport of a thin debris cover, however, is strongly controlled by more complex processes such as fluvial transport and rain wash (Fyffe et al., 2020).
3.2.2. Ice-Flow and Debris Advection
Ice-flow describes the glacier motion that governs the advective debris transport from the production zone to the terminus (Benn et al., 2012; Rowan et al., 2015; Anderson and Anderson, 2016; Wirbel et al., 2018). Therefore, ice-flow dynamics play a fundamental role in debris transport as demonstrated by recent numerical simulations (e.g., Anderson and Anderson, 2016; Wirbel et al., 2018).
Ice-flow velocity is governed by multiple factors such as the ice thickness and basal water pressure, and many DCGs exhibit high flow velocities even though they have stable termini (Copland et al., 2009; Quincey et al., 2009, 2011). The surface velocity field can be determined from remote sensing analysis, estimating englacial ice-flow velocities can be challenging, although estimates are usually sufficient for computing particle trajectories if far enough away from the bed (about 80% of the ice depth). Therefore, most studies use ice-flow models (such as the shallow ice approximation) to solve the englacial velocity field (Herman and Braun, 2008; Bueler and Brown, 2009; Anderson and Anderson, 2016), which usually requires ice thickness measurements from geophysical surveys using seismic or radio sounding (McNabb et al., 2012). Modeled ice-flow velocities often suffer from high uncertainty (Farinotti et al., 2017), however, more accurate models have been developed to account for basal melt, temperature-adjusted ice properties and rugged bed topography (e.g., Bueler and Brown, 2009; Egholm et al., 2011).
Debris advection is governed by the ice-flow velocity field (Benn and Evans, 2014; Anderson and Anderson, 2016; Wirbel et al., 2018). A recent model was developed by Anderson and Anderson (2016), in which the englacial and supraglacial debris advection were modeled under a steady debris input to understand the mechanisms in the debris-glacier-climate system. Simulations indicated that debris has significant control on glacier length and gradients of ice discharge, ice thickness, and surface velocities. Their model demonstrated that high debris flux slows down the glacier and contributes to extending its length. Based on this, the rate of change of supraglacial debris thickness in the ablation zone can be written as (Anderson, 2000; Anderson and Anderson, 2016, 2018):
where hd is the surface debris thickness, t is time, cs is the near-surface debris concentration, Ms is surface ablation rate, and us is surface ice velocity. The use of advection is valid for glacial debris transport because advection is defined as the transport of materials due to the bulk motion of a fluid, and glacier ice is a form of a viscoelastic fluid that is the basis for all modern ice-flow models. Figure 5D shows the simulated supraglacial debris advection based on Equation (13) given the initial debris thickness (Figure 5A) and surface velocity (Figure 5C).
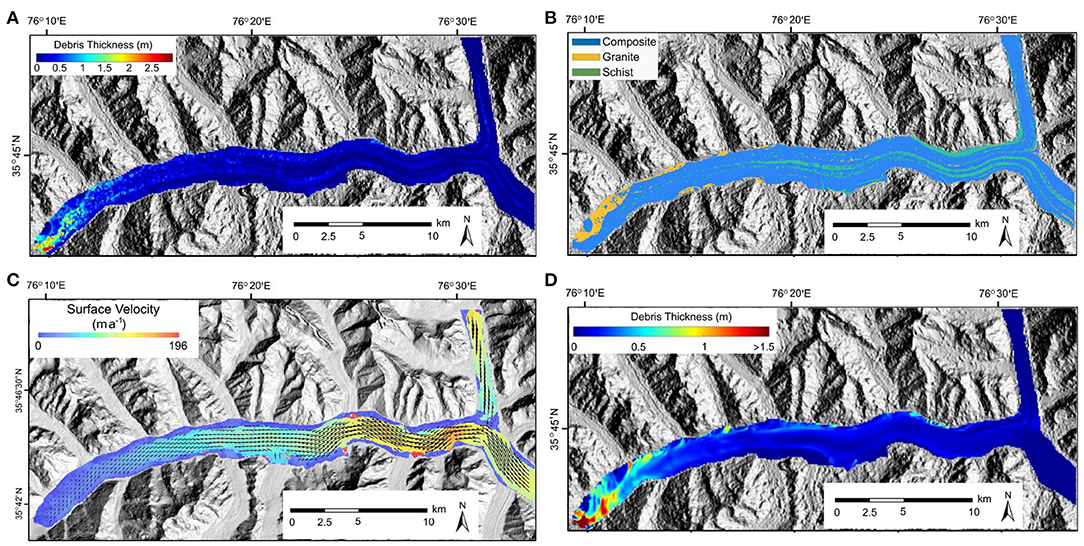
Figure 5. Supraglacial debris conditions for the Baltoro Glacier. (A) The debris-thickness distribution over the Baltoro glacier in summer 2004 computed from ASTER surface kinetic temperature data following the approach by Mihalcea et al. (2008). (B) Debris rock type distribution over the Baltoro Glacier in 2004 based on the remote-sensing analysis by Gibson et al. (2017). (C) Surface ice-flow velocity of the Baltoro Glacier estimated from a Landsat-8 OLI panchromatic image pair acquired on September 15, 2004 and September 2, 2005. (D) Simulated debris transport due to ice-flow (advection process) over a 50-year period. Result represents the debris thickness distribution for year 50.
The transport of englacial debris and its contribution to the surface debris load is controlled by ice-flow dynamics, given that the vertical component of ice velocity usually points upward in the lower glacier where ice thickness increases toward the terminus. These processes have been described by Anderson (2000), and demonstrated in the simulations by Anderson and Anderson (2016) and Wirbel et al. (2018). The contribution of englacial debris load may explain the debris mass balance issue discussed by van Woerkom et al. (2019). The most recent englacial debris transport model was presented by Wirbel et al. (2018), in which both the advection and diffusion of englacial debris are accounted for:
where ce is the concentration of englacial debris, D is the diffusion coefficient, ue is englacial ice velocity, and r represents englacial debris sources or sinks.
Remote-sensing approaches have been used to map debris thickness distributions (Mihalcea et al., 2008; Juen et al., 2014; Gibson et al., 2017; Rounce et al., 2018); the results, however, suffer from high uncertainties due to the instantaneous nature of satellite imagery and the complex properties of debris. Further investigations on debris production and transport modeling are required to better address the spatial patterns of surface melt and supraglacial morphological conditions.
4. Ablation Dynamics
Surface melt dominates the ablation of a DCG (Hambrey et al., 2008; Reid and Brock, 2014; Rowan et al., 2015). The melt rate is strongly affected by the properties of debris loads and the presence of supraglacial water bodies due to their strong impact on the energy transfer dynamics (Sakai et al., 2000; Nicholson and Benn, 2006; Reid and Brock, 2010; Fyffe et al., 2014; Miles et al., 2016).
Field measurement of ablation is usually conducted through monitoring ablation stakes at multiple locations on the glacier surface. Ablation rates at locations with different debris thickness are measured by several studies, and field data showed that debris thickness is a predominant factor that governs the sub-debris ablation rate (Mattson, 1993; Kayastha et al., 2000; Rounce et al., 2015). Given the complex debris effects, empirical approaches such as the degree-day method for estimating ablation may be highly unreliable for DCGs (Braithwaite and Olesen, 1990; Nicholson and Benn, 2006). Therefore, physics-based surface energy balance models are widely used for estimating sub-debris ablation (e.g., Nicholson and Benn, 2006; Reid and Brock, 2010, 2014; Fyffe et al., 2014; Miles et al., 2016), and several remote-sensing approaches have been developed to estimate the key parameters, such as the thickness and thermal properties of debris (e.g., Mihalcea et al., 2008; Zhang et al., 2011; Foster et al., 2012; Juen et al., 2014).
Several recent studies have successfully used the surface energy balance model to estimate ablation on DCGs. For example, Fyffe et al. (2014) used a distributed model to compute melt rate on the Miage glacier in Alps. Rounce et al. (2015) compared the influences of debris thermal conductivity, albedo, and surface roughness on the surface energy balance of the Imja-Lhotse Shar glacier in Nepal. These results highlighted that: (1) Unlike the thick debris layer, a thin debris is sensitive to air temperature variation and water content, therefore areas with wet thin debris must be identified. (2) Subdebris ablation is more sensitive to the changes in thermal conductivity than surface roughness and albedo. (3) It is important to account for the realistic topographic shielding and wind speed over the glacier surface in the energy balance model. (4) Many model parameters need to be calibrated using field measurements or remote sensing data as they can be highly site-specific. The energy balance model at the debris/air interface can be written as (Nakawo and Young, 1981; Nicholson and Benn, 2006; Zhang et al., 2011; Rounce et al., 2015):
where Qs is the net shortwave radiation flux, Ql is the net long-wave radiation flux, Qh is the net sensible-heat flux, Qe is the net latent-heat flux, and Qc is the conductive heat flux into the debris which governs the ablation rate. Net radiation fluxes dominate glacier surface energy balance and significantly control surface ablation rates (Nicholson and Benn, 2006; Cuffey and Paterson, 2010). The net shortwave radiation flux and the net long-wave radiation flux can be computed as:
where Eb is the direct-beam irradiance from the sun, Ed is the diffuse-skylight irradiance, Et is the adjacent-terrain irradiance, and α is the surface albedo. For the long-wave radiation fluxes, εa, εs and εt are the emissivity for the air, glacier surface and adjacent terrain, respectively, σ is the Stefan-Boltzmann constant, T0 is the air temperature which is a function of altitude, Ts is the glacier surface temperature, and Tt is the surface temperature of the surrounding terrain, which is responsible for the long-wave adjacent-terrain irradiance.
The energy balance at the debris/ice interface can be written as (Nakawo and Young, 1981):
where Qm is the heat flux used for sub-debris ice ablation, is the conductive heat flux from the debris, and is the heat flux toward the ice that is not used for ablation, which is often negligible under a temperate ice assumption (Cuffey and Paterson, 2010).
Most models assume constant heat storage and a linear debris-temperature gradient, then Qm during the ablation season can be computed using the simplified heat-flux approach based on daily mean values at a minimum 24 h timescale (Nakawo and Young, 1981; Nicholson and Benn, 2006):
where kd is the bulk thermal conductivity of the debris layer accounting for water in pore-spaces, Ti is the ice temperature. The sub-debris melt rate (Ms) can then be computed as (Nakawo and Young, 1981; Nicholson and Benn, 2006):
where Lf is the latent heat of fusion for ice, and ρi is the density of ice.
Precipitation can also contribute to surface melt (Fujita et al., 2014; Fyffe et al., 2014; Miles et al., 2016), and several methods have been used to account for this process (e.g., Reid and Brock, 2010; Fujita et al., 2014; Miles et al., 2016). Although more complicated processes have not been accounted for, such as the energy exchange between rainfall and heated debris that could eventually lead to additional ice melt. The latent and sensible heat fluxes have been found to be less significant with respect to melt variability compared to the shortwave and longwave fluxes in different climates (Sicart et al., 2008).
Using the aforementioned equations, Figure 6A shows the simulated ablation rates on the Baltoro Glacier in the Karakoram, using surface conditions presented by Mihalcea et al. (2008). Note that the modeled values are reasonably similar to field measurements on several Himalayan glaciers (Nicholson and Benn, 2006), including Barpu Glacier (Khan, 1989), Khumbu Glacier (Kayastha et al., 2000), and Rakhiot Glacier (Mattson, 1993). Figure 6B is an example of the temporal variation in ablation rate as a function of debris thickness over an ablation season, which highlights the important role of the dynamics involving debris redistribution in regulating local ablation rates on the glacier surface, especially for areas with water bodies and ice-cliffs. Figure 7 depicts simulated surface ablation rates compared to the remote-sensing-based estimates (Mihalcea et al., 2008). Both results show suppressed ablation in the terminus region and higher ablation around inter-moraine valleys corresponding to the difference in debris thickness (Figure 5A).
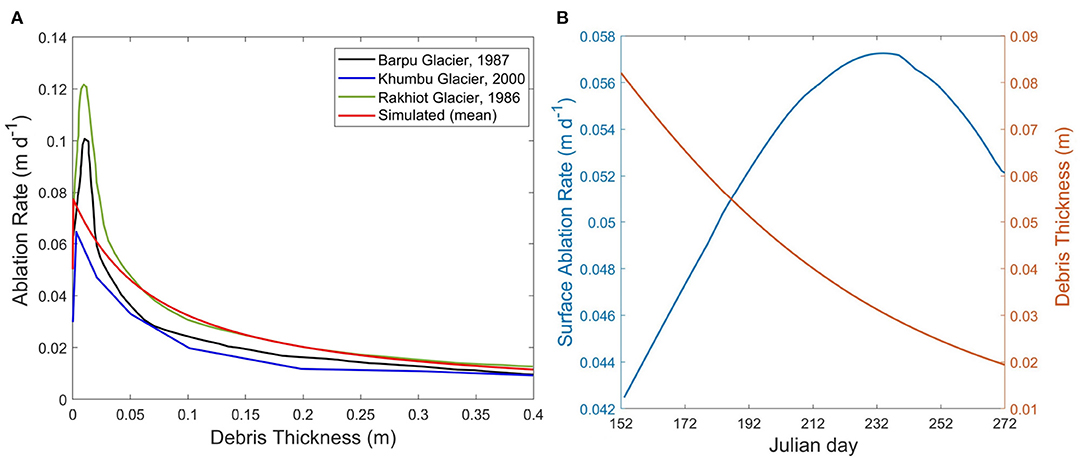
Figure 6. The debris-thickness control on surface ablation rates. (A) June-averaged ablation rate as a function of debris thickness on the Baltoro Glacier (red) compared to in-situ measurements in the ablation season on other Himalayan glaciers (replotted), including Barpu Glacier (Khan, 1989), Khumbu Glacier (Kayastha et al., 2000), and Rakhiot Glacier (Mattson, 1993). Note that the melt-enhancing effect of thin-debris is observed on all glaciers. (B) An example of the temporal variation in ablation rate vs. debris thickness around a supraglacial lake on the Baltoro Glacier. The debris layer is getting thinner as sediments are gradually sliding into the lake, which leads to an increase in ablation rate (the decrease of ablation rate in late ablation season is due to the decreasing irradiance).
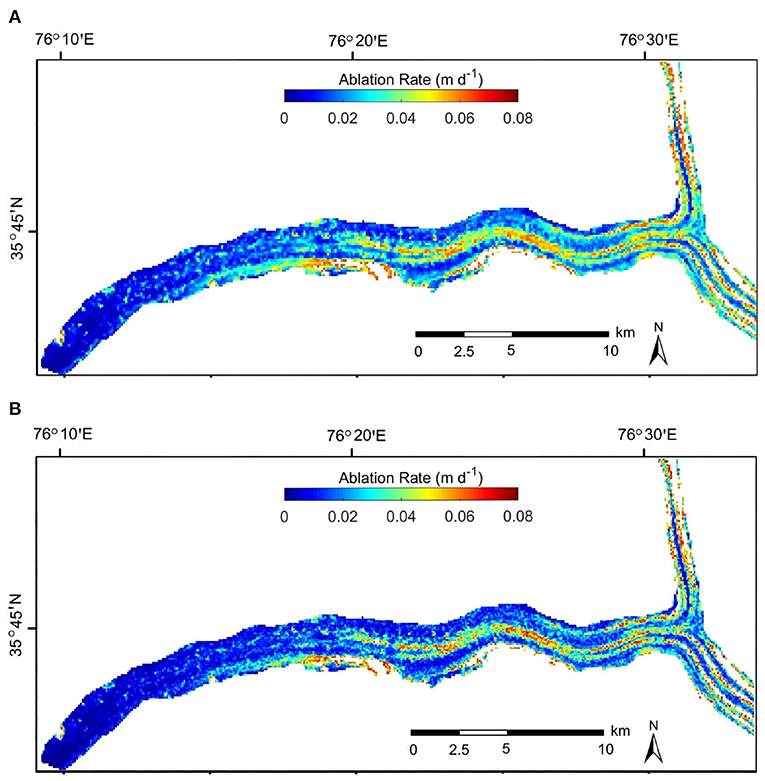
Figure 7. Surface ablation rates for the Baltoro Glacier modeled with two different methods: (A) The remote-sensing based approach (Mihalcea et al., 2008), which uses surface temperature data acquired by satellite. (B) The surface energy balance based approach, which uses modeled surface irradiance. Both results are based on the same debris thickness distribution, assuming no water bodies and were produced to represent rates on August 14 2004. Note the high spatial variability in ablation rate caused by the debris thickness distribution (Figure 5A).
5. Supraglacial Water Bodies and Ice Cliffs
Supraglacial water bodies and ice-cliffs elevate the ice loss of DCGs (Anderson, 2014; Reid and Brock, 2014; Steiner et al., 2015; Buri et al., 2016; Miles et al., 2016, 2018; Thompson et al., 2016; Dobreva et al., 2017; Mertes et al., 2017; Huang et al., 2018). The number of supraglacial ponds and lakes have been found to be increasing on many DCGs, which is related to the glacier morphological changes such as differential surface lowering and collapse of englacial channel roofs (Sakai et al., 2000, 2002; Benn et al., 2001; Quincey and Glasser, 2009; Gibson et al., 2017). These water bodies also play an important role in regulating water storage and drainage in a glacier system (Cuffey and Paterson, 2010; Benn and Evans, 2014), and cause englacial ablation via efficient heat transfer (Sakai et al., 2000; Gulley and Benn, 2007; Benn et al., 2012; Miles et al., 2016; Mertes et al., 2017).
Supraglacial lakes can be relatively large to moderate-sized water bodies (lake azimuthal distances have been observed to be up to 0.6 km in length on the Baltoro Glacier) that can be relatively short lived or exist over multiple years, and supraglacial ponds are smaller but more common water bodies that usually only appear during the ablation season. These water bodies are typically abundant in the ablation zone where the surface slope is gentle and heterogeneous surface lowering occurs (Reynolds, 2000; Sakai et al., 2002; Reid and Brock, 2014). The evolution of many supraglacial lakes and ponds are governed by filling and draining cycles, and hydrological connectivity that are controlled by glacier surface and internal structures (Benn et al., 2001, 2017; Wessels et al., 2002; Miles et al., 2017). Studies also found that proglacial lakes also have a significant control on the glacier dynamics (Sutherland et al., 2020). These processes have only been studied on a handful of glaciers in the field, and there are still many processes and feedbacks that need to be investigated.
Supraglacial ponds and lakes are efficient in transferring heat into glacier ice due to their low surface albedo and active convection (Lüthje et al., 2006; Miles et al., 2016). Studies have estimated that the ablation rates around the lakes can be much higher than that of most debris-covered areas (Sakai et al., 2000; Thompson et al., 2016). The simulations by Miles et al. (2018) revealed that ponds may be responsible for 1/8 of total ice loss in the Langtang valley, Nepal. Furthermore, supraglacial water bodies will most likely exhibit accelerated growth on Himalayan glaciers given current atmospheric temperature trends (Benn et al., 2001). For example, Gibson et al. (2017) estimated that the number of water bodies on the Baltoro Glacier has increased from 234 in 2001 to 570 in 2012, and the area has tripled, which suggests that supraglacial water bodies can expand quickly on DCGs.
One of the first energy-balance models for supraglacial ponds on DCGs was developed by Sakai et al. (2000), which was used to address field observations on the Lirung Glacier in the Langtang Valley, Nepal. The core of this model is the energy-balance of a supraglacial lake that accounts for heat flux input and output due to meltwater, heat storage of the lake, and the bare-ice vs. debris covered areas beneath the lake surface:
where Q is the net radiation heat flux on the lake surface, Qin is the input heat flux from meltwater inflow into the lake, which in most cases, can be neglected (Sakai et al., 2000), Qout is the output heat flux from the water outflow from the lake, which dominates the englacial ablation such as the expansion of conduits (Sakai et al., 2000), ΔQt is the change in heat storage of the lake, Qi is the heat flux for ice melt at subaqueous ice-cliff, and Qd is the heat flux for ice melt beneath the subaqueous debris layer.
A more recent model was presented by Miles et al. (2016), which improves the Sakai et al. (2000)'s model in several aspects, such as the energy flux due to rainfall, more accurate turbulent fluxes, and the free convection of water that may circulate within the pond. In addition to the energy-balance, Miles et al. (2016) used a mass balance model to account for the changes in pond volume (ΔV):
where Vin and Vout are the inflows and outflows, Vi is the subaqueous bare ice melt volume, Vd is the subaqueous subdebris melt volume, Vle is the volume of vapor exchanges, and Vr is the volume gained from rain. All terms in the energy-balance model and the mass-balance model have been discussed. Although some parameters are based on empirical relationships, this work provides the most comprehensive physics-based pond model to date. Figure 8 depicts the large number of supraglacial water bodies identified in the terminus region of the Baltoro Glacier. Our simulation results (Figures 8C,D) based on the above model suggest that supraglacial water bodies make a significant contribution to the total ice loss and surface lowering in the ablation zone, and exhibit a non-linear seasonal trend toward the end of the ablation season, as the extent and amount of lakes and ponds gradually expand to yearly maximum.
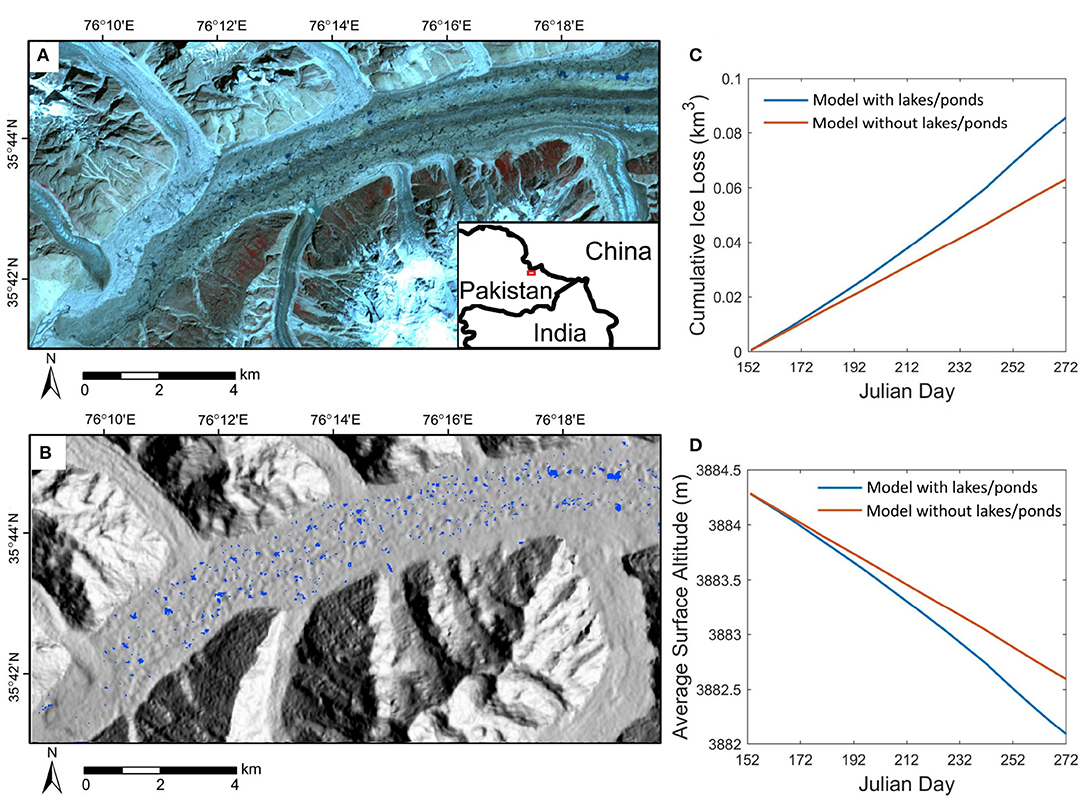
Figure 8. (A) ASTER false-color composite imagery (VNIR bands) of the lower ablation zone of the Baltoro Glacier acquired on August 14, 2004. (B) A large number of supraglacial ponds and lakes mapped from the satellite data using the normalized difference water index. (C) Temporal variation in the simulated cumulative ice-volume loss for this area over the ablation season of 2004. Two scenarios (with and without lakes/ponds) are compared. (D) Comparison of the mean surface altitude variations for the two simulations. Note the increased non-linearity in ice loss and surface lowering when supraglacial lakes/ponds are present.
The dynamics of supraglacial lakes and ponds is often coupled with the evolution of ice-cliffs around them. Studies have suggested that this cliff/lake system plays an important role in governing the mass balance of DCGs, and most field observations and modeling results confirmed that ice-cliffs can make a significant contribution to the total ice mass loss on a DCG (Sakai et al., 2002; Anderson, 2014; Steiner et al., 2015; Buri et al., 2016), although many questions remain unresolved (Sakai et al., 2002; Buri et al., 2016; Miles et al., 2016). Several forms of interactions exist between ice-cliffs and ponds/lakes. For example, lake undercut can cause the steepening of some ice-cliffs (Sakai et al., 2000, 2002), and the melt of ice-cliff below the water surface is strongly affected by water fluctuations (Miles et al., 2016).
Sakai et al. (2002) found that the orientation and inclination of ice-cliffs significantly control the evolution of ice cliffs given the solar geometry and cast shadows. The geometry of the ice-cliff also controls the thickness distribution of debris cover which regulates meltwater production. Ice-cliffs are also controlled by englacial processes, and studies have attributed the formation of some ice-cliffs to the collapses of englacial conduits (Sakai et al., 2000, 2002). Some recent simulations (Steiner et al., 2015; Buri et al., 2016) confirmed that the complex terrain around the cliff has a non-negligible effect on ice-cliff evolution due to the local shading and the adjacent terrain irradiance. Furthermore, ice-cliff evolution can also be governed by pond-water ablation that undercuts adjacent lake slopes. In addition, the ice topographic load coupled with the debris load causes significant variations in the ice stress fields, that partially control the process of calving. We have observed this process on a very large supraglacial lake near the terminus of the Liligo Glacier during the summer of 2005. Significant water depths coupled with wind and wave action can cause significant undercutting, thereby altering the ice stress fields which enables calving and the production of icebergs in glacial lakes. The ice cliffs that are generated from these processes typically have very steep slopes, and the debris loads above them are quickly transported. Collectively, various feedbacks promote ice-cliff retreat and rapid supraglacial lake expansion, that most likely represents a non-linear ablation response to climate forcing.
Understanding supraglacial water bodies and ice-cliff dynamics is critical to assessing DCG sensitivity to climate change, and valuable knowledge has been gained from the aforementioned studies. However, there are still many issues that need to be investigated including the filling and draining cycles that control the evolution of many supraglacial ponds, the connectivity between surface water bodies and englacial conduits, englacial ablation due to warm water outflow, rockfall from ice-cliffs, and modeling the edge effects and temperature gradients in ponds (Benn et al., 2001, 2017; Miles et al., 2016, 2017).
6. Feedback and System Couplings
The dynamics of a DCG system is controlled by the complex interactions between climate, debris load, ice dynamics, hydrologic conditions and topography (Scherler et al., 2011a,b; Dobreva et al., 2017; Gibson et al., 2017). Unfortunately, few studies have investigated the couplings and feedback mechanisms in a DCG system, which is a major issue in characterizing DCGs, because isolating a small number of processes out of the full system increases uncertainty in results, as system couplings and feedbacks can significantly affect glacier dynamics (Rowan et al., 2015; Anderson and Anderson, 2016). Studies are often limited in spatio-temporal scale (Anderson, 2014; Anderson et al., 2021), because they rely on instantaneous remote-sensing data or field measurements at limited sites that do not describe multi-year or longer-term variations in glacier conditions (such as ice thickness, debris distribution and topography). Furthermore, many system couplings and feedbacks operate at very different spatio-temporal scales, making them difficult to investigate in the field. Therefore, numerical modeling is required to address the feedbacks and non-linear relationships between major glacier components. Figure 9 is a conceptual diagram showing the major systems couplings we identified between climate, mass balance, supraglacial water bodies, debris load, ice flow, and topography that govern the dynamics of a DCG.
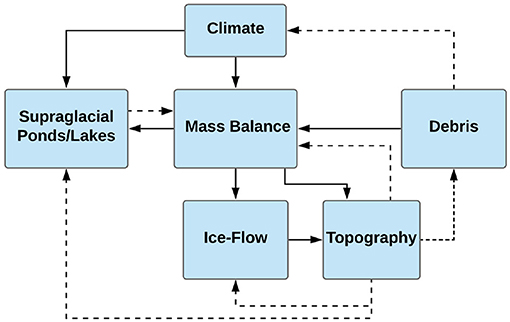
Figure 9. Diagram illustrating the interactions between key controlling factors discussed in this paper that govern the dynamics of a debris-covered glacier. The feedbacks (dashed lines) are important to the system as they may increase a glacier's sensitivity to climate change over time.
6.1. Feedbacks on Glacier Surface
Figure 10 is a conceptual diagram that illustrates the feedbacks we identified between ablation, surface ponding and debris thickness. The most obvious positive feedback describes the relationship between meltwater production and supraglacial pond expansion: as a pond grows, its surface area and surrounding ice-cliff area get larger, they absorb more solar energy due to the lower albedo, causing enhanced melt and calving, which in turn, leads to further expansion of the pond. Another feedback involves the differential lowering of the glacier surface, the distribution of debris and the increased ponding of surface water: the spatially heterogeneous distribution of supraglacial water bodies and ice-cliffs governs the differential elevation change, which in turn, facilities the expansion of existing ponds and the formation of new ponds as suggested by multiple studies (Benn and Owen, 2002; Benn et al., 2012; Reid and Brock, 2014; Rowan et al., 2015; Salerno et al., 2017; Miles et al., 2018). The presence of supraglacial ponds and lakes also increases the spatial heterogeneity of debris thickness. Rounce et al. (2018) found that debris thinning is usually associated with the formation of supraglacial lakes and ice-cliffs, then the heterogeneous distribution of debris thickness further enhances the differential surface lowering which creates more depression zones for new ponds.
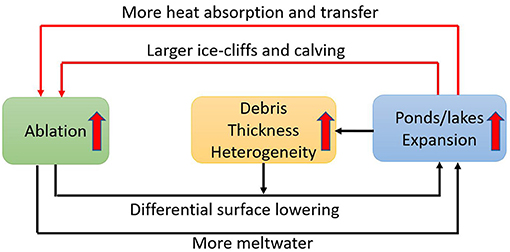
Figure 10. Conceptual diagram that illustrates the positive feedbacks between ablation, surface ponding and the spatial distribution of debris thickness.
Positive feedbacks also exist between the lowing of surface albedo and enhanced melt, as a wet surface often exhibits lower albedo. Pritchard et al. (2008) showed that this mechanism has significant influence on millennial-scale mass-loss of ice sheets. For certain locations on the glacier surface, such as on ice-cliffs, the decrease in albedo is more significant due to the thinner debris and high moisture content, i.e., the “dirty ice” that causes more ablation (Fyffe et al., 2020), which is also coupled with the topographic factors (such as the orientation of the cliff wall and the high adjacent terrain irradiance on the cliffs) to form positive feedback that accelerates melting, causing faster ice-cliff backwasting than previously thought (Sakai et al., 2000; Benn and Owen, 2002; Reid and Brock, 2014).
6.2. The Role of Glacier Surface Topography
Surface topography is an important factor that acts as a bridge between multiple components of a DCG, and studies have identified the following topographic effects on DCGs:
1. Surface topography has a direct impact on glacier surface ablation because slope, slope azimuth, and basin topographic shielding directly control the total amount of shortwave radiation received by the glacier surface (Arnold et al., 2006; Garg et al., 2017; Olson and Rupper, 2019).
2. Surface topographic conditions control supraglacial hydrology, especially the development of ponds and lakes (Huo et al., 2021). Water transport is enhanced with steeper gradients, while ponding is enhanced with lower gradients, therefore supraglacial water bodies are more abundant where the glacier surface is flatter (Reynolds, 2000; Sakai et al., 2002; Immerzeel et al., 2014; Reid and Brock, 2014). Topographic depressions caused by differential ablation and debris loading are also important, as they provide topographic sinks for meltwater to accumulate.
3. Topography also affects the distribution and transport of supraglacial debris. Observations and simulations have shown that the morphometric conditions of the sidewalls and headwalls of the glacial valley control sediment input to the glacier (Benn and Evans, 2014; Anderson and Anderson, 2016).
4. The adjacent-terrain irradiance due to complex topography coupled with debris cover contributes to the surface melt, and especially the retreat of ice-cliffs (Sakai et al., 2002; Wessels et al., 2002).
6.3. Basal Processes
The glacier bed is slowly evolving due to differential glacier erosion caused by variations in ice-flow dynamics, such that erosion is most likely at a maximum near the ELA due to relatively thick ice and high flow velocities (Herman et al., 2011; Steer et al., 2012). Another complexity is the basal hydrological conditions that govern sliding velocity, as high basal water pressure may lubricate the ice-bedrock interface (Cuffey and Paterson, 2010; Quincey et al., 2011). The higher sliding velocity leads to more frictional heating that further increases basal water pressure, which forms a positive feedback (Benn and Evans, 2014). Many details about the interactions between basal sliding, erosion, subglacial ablation, basal hydrology, and subglacial debris transport need to be investigated in future studies.
Collectively, the DCG system is complicated by interactions and feedbacks between debris load, ablation, topography, ice-flow, basal processes, and supraglacial water bodies. An integrated modeling of these processes may help explain field observations over High-Mountain Asia, such as the rapid lowering on Himalayan DCGs (Kääb et al., 2012; Immerzeel et al., 2013; Fujita et al., 2014) and the advancement of many glaciers in the Karakoram (Bolch et al., 2012; Bishop et al., 2014; Dobreva et al., 2017; Farinotti et al., 2020). Furthermore, it is also important to account for ice-flow dynamics being a potential cause of glacier thinning, as the re-distribution of ice mass, especially the declining ice discharge plays a dominant role in setting the thinning patterns on debris-free glaciers (e.g., Cuffey and Paterson, 2010), and has also been shown to be important for DCGs (Vincent et al., 2016; Brun et al., 2018; Anderson et al., 2021).
Improved parameterization schemes (more parameters and processes) suggest that climate glacier dynamics for DCGs are more complex than debris-free glaciers and that DCGs may be more sensitive to climate change than previously thought.
We recommend that more energy input components (e.g., the adjacent-terrain irradiance) and multi-scale topographic effects be accounted for in improved parameterization schemes. Our simulations indicate that scale dependent processes such as the gravitational debris transport and supraglacial ponding must also be accounted for given the coupling of climate and surface process and the non-linear responses in ablation and ice-mass loss. In all likelihood, our simulations probably underestimate the magnitude of non-linear responses due to these coupled processes/systems, as other processes such as calving were not accounted for. Furthermore, it is essential that future research focus on addressing questions about the significance of missing and existing processes so that we have an improved understanding of the degree of dominance and partitioning of key parameters and processes/systems that need to be incorporated into DCG models. This will require important comparative analysis of parameterization schemes and parameter sensitivity analysis to account for uncertainty in so many parameters and processes that govern climate-glacier dynamics.
More remote sensing and field-based studies are required to validate numerical modeling results. Further research is also required to determine if DCGs in different geographic locations exhibit similar or different sensitivity to climate change given variations in internal and external forcing factors. We speculate that such complex non-linear systems have the potential to reach tipping points based upon changing climate and geomorphological conditions within glacierized basins.
7. Conclusions
Debris-covered glaciers represent complex non-linear systems that operate given the coupling of climate, geomorphological and glaciological processes and feedbacks. Many important processes and systems have not been adequately characterized. Consequently, our current understanding of DCG sensitivity to climate change is most likely oversimplified, as numerous processes and scale dependencies have not been accounted for. This has resulted in conflicting views about these glaciers, such as the Karakoram anomaly and the “debris-covered glacier anomaly,” where the lack of data and information about climate forcing and ablation dynamics force us to rely on empirical measurements that represent a static snapshot in space and time. This paper and our simulations have attempted to provide a more integrated synthesis into the complexity of DCG systems by addressing important concepts associated with the key external and internal forcing factors and glacial processes, highlighting the importance of feedback mechanisms, system couplings, and recognition of the high degree of uncertainty related to numerous properties and parameters that need to be taken into consideration. Our simulation results based on the Baltoro Glacier in the central Karakoram combined with a review of literature reveal that climate-DCG dynamics and responses can be significantly attributed to the following factors:
1. Climate forcing: solar radiation and precipitation are the main driving forces for ice loss or gain. An accurate surface energy balance model for debris-covered glaciers needs to account for short-wave and long-wave irradiance. Our simulations showed that multi-scale topographic effects on surface ablation can be significant for debris-covered glaciers, given glacier surface topographic evolution and differential sky-view conditions in the glacier valley. Other meso-scale topographic effects such as cast shadows and adjacent-terrain influences should also be considered.
2. Supraglacial debris: physical properties of debris, such as thickness, lithology, grain size, moisture content and thermal conductivity strongly govern the surface ablation rates on debris-covered glaciers. Many of these factors, however, have not been adequately characterized or studied. We showed that there are significant spatial variability in debris thickness, albedo, particle size and composition, which are also coupled with the dynamic movement of debris due to gravity and ice-flow. Such complexity needs to be accounted for in models and field studies to better assess debris-related effects on glacier mass balance.
3. Supraglacial water bodies and ice-cliffs: supraglacial ponds, lakes, and surrounding ice-cliffs are melt hotspots on debris-covered glaciers and are expanding in size on many glaciers. Our simulations based on the Baltoro Glacier suggest that supraglacial water bodies make a significant contribution to the total ice-mass loss over the ablation season. Further investigations are needed to address the evolution of supraglacial water bodies and ice-cliffs, and their interactions with debris load, topography and englacial processes.
4. System coupling and feedback: positive feedbacks on debris-covered glaciers have been identified in numerical simulations, such as the surface melt-lowering-ponding feedback, and the atmospheric convection feedback. These couplings and especially the positive feedbacks may govern the non-linearity of the glacier's response to climate forcing, which are represented as an acceleration in ice-mass loss and heterogeneous surface lowering. The combined effect of these processes may lead to the beginning of a critical transition of the glacier system that signifies an increasing level of glacier sensitivity to climate change.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Author Contributions
DH conducted the model simulations, made the figures, and wrote the sections 3.2–6. MB proposed and designed the research, developed the parameterization schemes, wrote the sections 2.1 and 3.1, and edited the manuscript. AB wrote the section 2.2 and edited the manuscript. All authors contributed to the writing of the introduction and conclusions and the final editing.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We would like to thank Dr. Zhaohui Chi and Brennan Young at Texas A&M University for discussion. AB recognizes support from the Canadian Natural Sciences and Engineering Research Council and the computational resources of Compute Canada.
References
Adhikary, S., Masayoshi, N., Seko, K., and Shakya, B. (2000). “Dust influence on the melting process of glacier ice: experimental results from Lirung glacier, Nepal Himalayas, in Debris-Covered Glaciers: Proceedings of an International Workshop (Seattle, WA: IAHS), 43.
Anderson, L. S. (2014). Glacier response to climate change: modeling the effects of weather and debris-cover (Doctoral dissertation), University of Colorado at Boulder, Boulder, CO.
Anderson, L. S., and Anderson, R. S. (2016). Modeling debris-covered glaciers: response to steady debris deposition. Cryosphere 10:1105. doi: 10.5194/tc-10-1105-2016
Anderson, L. S., and Anderson, R. S. (2018). Debris thickness patterns on debris-covered glaciers. Geomorphology 311, 1–12. doi: 10.1016/j.geomorph.2018.03.014
Anderson, L. S., Armstrong, W. H., Anderson, R. S., and Buri, P. (2021). Debris cover and the thinning of Kennicott glacier, Alaska: in situ measurements, automated ice cliff delineation and distributed melt estimates. Cryosphere 15, 265–282. doi: 10.5194/tc-15-265-2021
Anderson, R. S. (2000). A model of ablation-dominated medial moraines and the generation of debris-mantled glacier snouts. J. Glaciol. 46, 459–469. doi: 10.3189/172756500781833025
Arnold, N. S., Rees, W. G., Hodson, A. J., and Kohler, J. (2006). Topographic controls on the surface energy balance of a high arctic valley glacier. J. Geophys. Res. Earth Surface 111. doi: 10.1029/2005JF000426
Benn, D., Bolch, T., Hands, K., Gulley, J., Luckman, A., Nicholson, L., et al. (2012). Response of debris-covered glaciers in the Mount Everest region to recent warming, and implications for outburst flood hazards. Earth Sci. Rev. 114, 156–174. doi: 10.1016/j.earscirev.2012.03.008
Benn, D., and Evans, D. J. (2014). Glaciers and Glaciation. London: Routledge. doi: 10.4324/9780203785010
Benn, D., Wiseman, S., and Hands, K. (2001). Growth and drainage of supraglacial lakes on debris-mantled Ngozumpa glacier, Khumbu Himal, Nepal. J. Glaciol. 47, 626–638. doi: 10.3189/172756501781831729
Benn, D. I., and Lehmkuhl, F. (2000). Mass balance and equilibrium-line altitudes of glaciers in high-mountain environments. Quat. Int. 65, 15–29. doi: 10.1016/S1040-6182(99)00034-8
Benn, D. I., and Owen, L. A. (2002). Himalayan glacial sedimentary environments: a framework for reconstructing and dating the former extent of glaciers in high mountains. Quat. Int. 97, 3–25. doi: 10.1016/S1040-6182(02)00048-4
Benn, D. I., Thompson, S., Gulley, J., Mertes, J., Luckman, A., and Nicholson, L. (2017). Structure and evolution of the drainage system of a Himalayan debris-covered glacier, and its relationship with patterns of mass loss. Cryosphere 11, 2247–2264. doi: 10.5194/tc-11-2247-2017
Berger, A. (1978). Long-term variations of daily insolation and quaternary climatic changes. J. Atmos. Sci. 35, 2362–2367. doi: 10.1175/1520-0469(1978)035<2362:LTVODI>2.0.CO;2
Bird, R. E., and Riordan, C. (1986). Simple solar spectral model for direct and diffuse irradiance on horizontal and tilted planes at the Earth's surface for cloudless atmospheres. J. Climate Appl. Meteorol. 25, 87–97. doi: 10.1175/1520-0450(1986)025<0087:SSSMFD>2.0.CO;2
Bishop, M. P., Bonk, R., Kamp, U. Jr., and Shroder, J. F. Jr. (2001). Terrain analysis and data modeling for alpine glacier mapping. Polar Geogr. 25, 182–201. doi: 10.1080/10889370109377712
Bishop, M. P., and Colby, J. D. (2011). Topographic normalization of multispectral satellite imagery. J. Glaciol. 55, 131–146. Available online at: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.727.9345&rep=rep1&type=pdf
Bishop, M. P., and Dobreva, I. D. (2017). “Geomorphometry and mountain geodynamics: issues of scale and complexity,” in Integrating Scale in Remote Sensing and GIS, eds D. A. Quattrochi, E. Wentz, N. S.N. Lam, and C. W. Emerson (Boca Raton, FL: Taylor and Francis), 189–228. doi: 10.1201/9781315373720-8
Bishop, M. P., Shroder, J. F., Ali, G., Bush, A. B. G., Haritashya, U. K., Roohi, R., et al. (2014). “Remote sensing of glaciers in Afghanistan and Pakistan,” in Global Land Ice Measurements from Space, eds J. S. Kargel, G. J. Leonard, M. P. Bishop, A. Kääb, and B. Raup (Berlin; Heidelberg: Springer), 509–548. doi: 10.1007/978-3-540-79818-7_23
Bishop, M. P., Shroder, J. F. Jr., Bonk, R., and Olsenholler, J. (2002). Geomorphic change in high mountains: a western himalayan perspective. Glob. Planet. Change 32, 311–329. doi: 10.1016/S0921-8181(02)00073-5
Bishop, M. P., Young, B. W., Colby, J. D., Furfaro, R., Schiassi, E., and Chi, Z. (2019). Theoretical evaluation of anisotropic reflectance correction approaches for addressing multi-scale topographic effects on the radiation-transfer cascade in mountain environments. Remote Sens. 11:2728. doi: 10.3390/rs11232728
Bolch, T., Kulkarni, A., Kääb, A., Huggel, C., Paul, F., Cogley, J. G., et al. (2012). The state and fate of Himalayan glaciers. Science 336, 310–314. doi: 10.1126/science.1215828
Braithwaite, R. J., and Olesen, O. B. (1990). Response of the energy balance on the margin of the greenland ice sheet to temperature changes. J. Glaciol. 36, 217–221. doi: 10.3189/S0022143000009461
Brun, F., Wagnon, P., Berthier, E., Shea, J. M., Immerzeel, W. W., Kraaijenbrink, P. D. A., et al. (2018). Ice cliff contribution to the tongue-wide ablation of Changri Nup glacier, Nepal, central Himalaya. Cryosphere 12, 3439–3457. doi: 10.5194/tc-12-3439-2018
Bueler, E., and Brown, J. (2009). Shallow shelf approximation as a “sliding law” in a thermomechanically coupled ice sheet model. J. Geophys. Res. Earth Surface 114. doi: 10.1029/2008JF001179
Buri, P., Miles, E. S., Steiner, J. F., Immerzeel, W. W., Wagnon, P., and Pellicciotti, F. (2016). A physically based 3-D model of ice cliff evolution over debris-covered glaciers. J. Geophys. Res. Earth Surface 121, 2471–2493. doi: 10.1002/2016JF004039
Bush, A. B. G., Bishop, M. P., Huo, D., Chi, Z., and Tiwari, U. (2020). “Issues in climate analysis and modeling for understanding mountain erosion dynamics,” in Reference Module in Earth Systems and Environmental Sciences (Amsterdam: Elsevier). doi: 10.1016/B978-0-12-818234-5.00022-5
Chen, H., and Lee, C. (2000). Numerical simulation of debris flows. Can. Geotech. J. 37, 146–160. doi: 10.1139/t99-089
Coakley, J. (2003). “Reflectance and albedo, surface,” in Encyclopedia of the Atmosphere Sciences eds. J. Holton, J. Curry (Amsterdam: Elsevier), 1914–1923. doi: 10.1016/B0-12-227090-8/00069-5
Collier, E., Maussion, F., Nicholson, L. I., Mölg, T., Immerzeel, W. W., and Bush, A. B. G. (2015). Impact of debris cover on glacier ablation and atmosphere-glacier feedbacks in the Karakoram. Cryosphere 9, 1617–1632. doi: 10.5194/tc-9-1617-2015
Collier, E., Mölg, T., Maussion, F., Scherer, D., Mayer, C., and Bush, A. B. G. (2013). High-resolution interactive modelling of the mountain glacier-atmosphere interface: an application over the Karakoram. Cryosphere 7, 779–795. doi: 10.5194/tc-7-779-2013
Collier, E., Nicholson, L. I., Brock, B. W., Maussion, F., Essery, R., and Bush, A. B. G. (2014). Representing moisture fluxes and phase changes in glacier debris cover using a reservoir approach. Cryosphere 8, 1429–1444. doi: 10.5194/tc-8-1429-2014
Copland, L., Pope, S., Bishop, M. P., Shroder, J. F., Clendon, P., Bush, A. B. G., et al. (2009). Glacier velocities across the central Karakoram. Ann. Glaciol. 50, 41–49. doi: 10.3189/172756409789624229
Dobreva, I. D., Bishop, M. P., and Bush, A. B. G. (2017). Climate-glacier dynamics and topographic forcing in the Karakoram Himalaya: concepts, issues and research directions. Water 9:405. doi: 10.3390/w9060405
Dozier, J., Bruno, J., and Downey, P. (1981). A faster solution to the horizon problem. Comput. Geosci. 7, 145–151. doi: 10.1016/0098-3004(81)90026-1
Egholm, D. L., Knudsen, M. F., Clark, C. D., and Lesemann, J. E. (2011). Modeling the flow of glaciers in steep terrains: the integrated second-order shallow ice approximation (isosia). J. Geophys. Res. Earth Surface 116. doi: 10.1029/2010JF001900
Farinotti, D., Brinkerhoff, D. J., Clarke, G. K. C., Fürst, J. J., Frey, H., et al. (2017). How accurate are estimates of glacier ice thickness? Results from ITMIX, the Ice Thickness Models Intercomparison experiment. Cryosphere 11, 949–970. doi: 10.5194/tc-11-949-2017
Farinotti, D., Immerzeel, W. W., de Kok, R. J., Quincey, D. J., and Dehecq, A. (2020). Manifestations and mechanisms of the Karakoram glacier anomaly. Nat. Geosci. 13, 8–16. doi: 10.1038/s41561-019-0513-5
Foster, L., Brock, B., Cutler, M., and Diotri, F. (2012). A physically based method for estimating supraglacial debris thickness from thermal band remote-sensing data. J. Glaciol. 58, 677–691. doi: 10.3189/2012JoG11J194
Fountain, A. G., and Walder, J. S. (1998). Water flow through temperate glaciers. Rev. Geophys. 36, 299–328. doi: 10.1029/97RG03579
Fujita, K.Sakai, A., et al. (2014). Modelling runoff from a himalayan debris-covered glacier. Hydrol. Earth Syst. Sci. 18, 2679–2694. doi: 10.5194/hess-18-2679-2014
Fyffe, C. L., Reid, T. D., Brock, B. W., Kirkbride, M. P., Diolaiuti, G., Smiraglia, C., et al. (2014). A distributed energy-balance melt model of an alpine debris-covered glacier. J. Glaciol. 60, 587–602. doi: 10.3189/2014JoG13J148
Fyffe, C. L., Woodget, A. S., Kirkbride, M. P., Deline, P., Westoby, M. J., and Brock, B. W. (2020). Processes at the margins of supraglacial debris cover: quantifying dirty ice ablation and debris redistribution. Earth Surface Process. Landforms 45, 2272–2290. doi: 10.1002/esp.4879
Garg, P. K., Shukla, A., and Jasrotia, A. S. (2017). Influence of topography on glacier changes in the central Himalaya, India. Glob. Planet. Change 155, 196–212. doi: 10.1016/j.gloplacha.2017.07.007
Gibson, M. J., Glasser, N. F., Quincey, D. J., Mayer, C., Rowan, A. V., and Irvine-Fynn, T. D. (2017). Temporal variations in supraglacial debris distribution on Baltoro glacier, Karakoram between 2001 and 2012. Geomorphology 295, 572–585. doi: 10.1016/j.geomorph.2017.08.012
Gueymard, C. (1995). SMARTS2, A Simple Model of the Atmospheric Radiative Transfer of Sunshine: Algorithms and Performance Assessment. Florida Solar Energy Center, Cocoa, FL.
Gulley, J., and Benn, D. (2007). Structural control of englacial drainage systems in himalayan debris-covered glaciers. J. Glaciol. 53, 399–412. doi: 10.3189/002214307783258378
Hambrey, M. J., Quincey, D. J., Glasser, N. F., Reynolds, J. M., Richardson, S. J., and Clemmens, S. (2008). Sedimentological, geomorphological and dynamic context of debris-mantled glaciers, Mount Everest (Sagarmatha) region, Nepal. Quat. Sci. Rev. 27, 2361–2389. doi: 10.1016/j.quascirev.2008.08.010
Herman, F., Beaud, F., Champagnac, J.-D., Lemieux, J.-M., and Sternai, P. (2011). Glacial hydrology and erosion patterns: a mechanism for carving glacial valleys. Earth Planet. Sci. Lett. 310, 498–508. doi: 10.1016/j.epsl.2011.08.022
Herman, F., and Braun, J. (2008). Evolution of the glacial landscape of the southern Alps of New Zealand: insights from a glacial erosion model. J. Geophys. Res. Earth Surface 113. doi: 10.1029/2007JF000807
Hewitt, K. (2005). The Karakoram anomaly? Glacier expansion and the “elevation effect,” Karakoram Himalaya. Mountain Res. Dev. 25, 332–340. doi: 10.1659/0276-4741(2005)025[0332:TKAGEA]2.0.CO;2
Huang, L., Li, Z., Han, H., Tian, B., and Zhou, J. (2018). Analysis of thickness changes and the associated driving factors on a debris-covered glacier in the tienshan mountain. Remote Sens. Environ. 206, 63–71. doi: 10.1016/j.rse.2017.12.028
Huo, D., Bishop, M. P., Young, B. W., Chi, Z., and Haritashya, U. K. (2020). “Numerical modeling issues for understanding complex debris-covered glaciers,” in Reference Module in Earth Systems and Environmental Sciences (Elsevier). doi: 10.1016/B978-0-12-818234-5.00019-5
Huo, D., Chi, Z., and Ma, A. (2021). Modeling surface processes on debris-covered glaciers: a review with reference to the high mountain asia. Water Amsterdam, 13:101. doi: 10.3390/w13010101
Immerzeel, W., Kraaijenbrink, P., Shea, J., Shrestha, A., Pellicciotti, F., Bierkens, M., et al. (2014). High-resolution monitoring of Himalayan glacier dynamics using unmanned aerial vehicles. Remote Sens. Environ. 150, 93–103. doi: 10.1016/j.rse.2014.04.025
Immerzeel, W., Pellicciotti, F., and Bierkens, M. (2013). Rising river flows throughout the twenty-first century in two Himalayan glacierized watersheds. Nat. Geosci. 6, 742–745. doi: 10.1038/ngeo1896
Immerzeel, W. W., Van Beek, L. P., and Bierkens, M. F. (2010). Climate change will affect the asian water towers. Science 328, 1382–1385. doi: 10.1126/science.1183188
Juen, M., Mayer, C., Lambrecht, A., Han, H., and Liu, S. (2014). Impact of varying debris cover thickness on ablation: a case study for KOXKAR glacier in the Tien Shan. Cryosphere 8:377. doi: 10.5194/tc-8-377-2014
Kääb, A., Berthier, E., Nuth, C., Gardelle, J., and Arnaud, Y. (2012). Contrasting patterns of early twenty-first-century glacier mass change in the Himalayas. Nature 488, 495–498. doi: 10.1038/nature11324
Kayastha, R. B., Takeuchi, Y., Nakawo, M., and Ageta, Y. (2000). Practical prediction of ice melting beneath various thickness of debris cover on Khumbu glacier, Nepal, using a positive degree-day factor. IAHS Publ. 264, 71–81.
Khan, M. I. (1989). Ablation on Barpu glacier, Karakoram Himalaya, Pakistan a study of melt processes on a faceted, debris-covered ice surface (Master thesis), Wilfrid Laurier University, Waterloo, ON.
Liang, S. (2001). Narrowband to broadband conversions of land surface albedo I: algorithms. Remote Sens. Environ. 76, 213–238. doi: 10.1016/S0034-4257(00)00205-4
Lüthje, M., Pedersen, L., Reeh, N., and Greuell, W. (2006). Modelling the evolution of supraglacial lakes on the west Greenland ice-sheet margin. J. Glaciol. 52, 608–618. doi: 10.3189/172756506781828386
Mattson, L. (1993). Ablation on debris covered glaciers: an example from the Rakhiot glacier, Punjab, Himalaya. Intern. Assoc. Hydrol. Sci. 218, 289–296.
McNabb, R., Hock, R., O'Neel, S., Rasmussen, L. A., Ahn, Y., Braun, M., et al. (2012). Using surface velocities to calculate ice thickness and bed topography: a case study at Columbia glacier, Alaska, USA. J. Glaciol. 58, 1151–1164. doi: 10.3189/2012JoG11J249
Mertes, J. R., Thompson, S. S., Booth, A. D., Gulley, J. D., and Benn, D. I. (2017). A conceptual model of supra-glacial lake formation on debris-covered glaciers based on GPR facies analysis. Earth Surface Process. Landforms 42, 903–914. doi: 10.1002/esp.4068
Mihalcea, C., Mayer, C., Diolaiuti, G., D'agata, C., Smiraglia, C., Lambrecht, A., et al. (2008). Spatial distribution of debris thickness and melting from remote-sensing and meteorological data, at debris-covered Baltoro glacier, Karakoram, Pakistan. Ann. Glaciol. 48, 49–57. doi: 10.3189/172756408784700680
Miles, E. S., Pellicciotti, F., Willis, I. C., Steiner, J. F., Buri, P., and Arnold, N. S. (2016). Refined energy-balance modelling of a supraglacial pond, Langtang Khola, Nepal. Ann. Glaciol. 57, 29–40. doi: 10.3189/2016AoG71A421
Miles, E. S., Steiner, J., Willis, I., Buri, P., Immerzeel, W. W., Chesnokova, A., et al. (2017). Pond dynamics and supraglacial-englacial connectivity on debris-covered Lirung glacier, Nepal. Front. Earth Sci. 5:69. doi: 10.3389/feart.2017.00069
Miles, E. S., Willis, I., Buri, P., Steiner, J. F., Arnold, N. S., and Pellicciotti, F. (2018). Surface pond energy absorption across four Himalayan glaciers accounts for 1/8 of total catchment ice loss. Geophys. Res. Lett. 45, 10–464. doi: 10.1029/2018GL079678
Moore, P. L. (2018). Stability of supraglacial debris. Earth Surface Process. Landforms 43, 285–297. doi: 10.1002/esp.4244
Nakawo, M., and Young, G. J. (1981). Field experiments to determine the effect of a debris layer on ablation of glacier ice. Ann. Glaciol. 2, 85–91. doi: 10.3189/172756481794352432
Nicholson, L., and Benn, D. I. (2006). Calculating ice melt beneath a debris layer using meteorological data. J. Glaciol. 52, 463–470. doi: 10.3189/172756506781828584
Oerlemans, J., and Klok, E. J. (2002). Energy balance of a glacier surface: analysis of automatic weather station data from the morteratschgletscher, switzerland. Arctic Antarct. Alpine Res. 34, 477–485. doi: 10.1080/15230430.2002.12003519
Olson, M., and Rupper, S. (2019). Impacts of topographic shading on direct solar radiation for valley glaciers in complex topography. Cryosphere 13, 29–40. doi: 10.5194/tc-13-29-2019
Pelto, M. S. (2000). Mass balance of adjacent debris-covered and clean glacier ice in the north Cascades, Washington. IAHS Publ. 35–42.
Perez, R., Stewart, R., Arbogast, C., Seals, R., and Scott, J. (1986). An anisotropic hourly diffuse radiation model for sloping surfaces: description, performance validation, site dependency evaluation. Solar Energy 36, 481–497. doi: 10.1016/0038-092X(86)90013-7
Pratap, B., Dobhal, D., Mehta, M., and Bhambri, R. (2015). Influence of debris cover and altitude on glacier surface melting: a case study on Dokriani glacier, central Himalaya, India. Ann. Glaciol. 56, 9–16. doi: 10.3189/2015AoG70A971
Pritchard, M. S., Bush, A. B. G., and Marshall, S. J. (2008). Neglecting ice-atmosphere interactions underestimates ice sheet melt in millennial-scale deglaciation simulations. Geophys. Res. Lett. 35. doi: 10.1029/2007GL031738
Proy, C., Tanré, D., and Deschamps, P. Y. (1989). Evaluation of topographic effects in remotely sensed data. Remote Sens. Environ. 30, 21–32. doi: 10.1016/0034-4257(89)90044-8
Quincey, D., Braun, M., Glasser, N. F., Bishop, M., Hewitt, K., and Luckman, A. (2011). Karakoram glacier surge dynamics. Geophys. Res. Lett. 38. doi: 10.1029/2011GL049004
Quincey, D., Copland, L., Mayer, C., Bishop, M., Luckman, A., and Belo, M. (2009). Ice velocity and climate variations for Baltoro glacier, Pakistan. J. Glaciol. 55, 1061–1071. doi: 10.3189/002214309790794913
Quincey, D. J., and Glasser, N. F. (2009). Morphological and ice-dynamical changes on the Tasman glacier, New Zealand, 1990-2007. Glob. Planet. Change 68, 185–197. doi: 10.1016/j.gloplacha.2009.05.003
Reid, T., and Brock, B. (2014). Assessing ice-cliff backwasting and its contribution to total ablation of debris-covered miage glacier, Mont Blanc Massif, Italy. J. Glaciol. 60, 3–13. doi: 10.3189/2014JoG13J045
Reid, T., Carenzo, M., Pellicciotti, F., and Brock, B. (2012). Including debris cover effects in a distributed model of glacier ablation. J. Geophys. Res. Atmos. 117. doi: 10.1029/2012JD017795
Reid, T. D., and Brock, B. W. (2010). An energy-balance model for debris-covered glaciers including heat conduction through the debris layer. J. Glaciol. 56, 903–916. doi: 10.3189/002214310794457218
Reynolds, J. M. (2000). On the formation of supraglacial lakes on debris-covered glaciers. IAHS Publ. 153–164.
Reznichenko, N., Davies, T., Shulmeister, J., and McSaveney, M. (2010). Effects of debris on ice-surface melting rates: an experimental study. J. Glaciol. 56, 384–394. doi: 10.3189/002214310792447725
Rounce, D., Quincey, D., and McKinney, D. (2015). Debris-covered energy balance model for Imja-Lhotse Shar glacier in the Everest region of Nepal. Cryosphere Discuss 9, 3503–3540. doi: 10.5194/tcd-9-3503-2015
Rounce, D. R., King, O., McCarthy, M., Shean, D. E., and Salerno, F. (2018). Quantifying debris thickness of debris-covered glaciers in the Everest region of Nepal through inversion of a subdebris melt model. J. Geophys. Res. Earth Surface 123, 1094–1115. doi: 10.1029/2017JF004395
Rowan, A., Nicholson, L., Quincey, D., Gibson, M., Irvine-Fynn, T., Watson, C., et al. (2021). Seasonally stable temperature gradients through supraglacial debris in the Everest region of Nepal, Central Himalaya. J. Glaciol. 67, 170–181. doi: 10.1017/jog.2020.100
Rowan, A. V., Egholm, D. L., Quincey, D. J., and Glasser, N. F. (2015). Modelling the feedbacks between mass balance, ice flow and debris transport to predict the response to climate change of debris-covered glaciers in the Himalaya. Earth Planet. Sci. Lett. 430, 427–438. doi: 10.1016/j.epsl.2015.09.004
Sakai, A., Nakawo, M., and Fujita, K. (2002). Distribution characteristics and energy balance of ice cliffs on debris-covered glaciers, Nepal Himalaya. Arctic Antarct. Alpine Res. 34, 12–19. doi: 10.1080/15230430.2002.12003463
Sakai, A., Takeuchi, N., Fujita, K., and Nakawo, M. (2000). Role of supraglacial ponds in the ablation process of a debris-covered glacier in the nepal himalayas. IAHS Publ. 119–132.
Salerno, F., Thakuri, S., Tartari, G., Nuimura, T., Sunako, S., Sakai, A., et al. (2017). Debris-covered glacier anomaly? Morphological factors controlling changes in the mass balance, surface area, terminus position, and snow line altitude of Himalayan glaciers. Earth Planet. Sci. Lett. 471, 19–31. doi: 10.1016/j.epsl.2017.04.039
Scherler, D., Bookhagen, B., and Strecker, M. R. (2011a). Hillslope-glacier coupling: the interplay of topography and glacial dynamics in high Asia. J. Geophys. Res. Earth Surface 116. doi: 10.1029/2010JF001751
Scherler, D., Bookhagen, B., and Strecker, M. R. (2011b). Spatially variable response of Himalayan glaciers to climate change affected by debris cover. Nat. Geosci. 4, 156–159. doi: 10.1038/ngeo1068
Seong, Y. B., Owen, L. A., Yi, C., and Finkel, R. C. (2009). Quaternary glaciation of Muztag Ata and Kongur Shan: evidence for glacier response to rapid climate changes throughout the late glacial and holocene in westernmost tibet. Geol. Soc. Am. Bull. 121, 348–365. doi: 10.1130/B26339.1
Sicart, J.-E., Hock, R., and Six, D. (2008). Glacier melt, air temperature, and energy balance in different climates: the Bolivian Tropics, the French Alps, and northern Sweden. J. Geophys. Res. Atmos. 113. doi: 10.1029/2008JD010406
Steer, P., Huismans, R. S., Valla, P. G., Gac, S., and Herman, F. (2012). Bimodal plio-quaternary glacial erosion of fjords and low-relief surfaces in scandinavia. Nat. Geosci. 5, 635–639. doi: 10.1038/ngeo1549
Steiner, J. F., Pellicciotti, F., Buri, P., Miles, E. S., Immerzeel, W. W., and Reid, T. D. (2015). Modelling ice-cliff backwasting on a debris-covered glacier in the Nepalese Himalaya. J. Glaciol. 61, 889–907. doi: 10.3189/2015JoG14J194
Sutherland, J. L., Carrivick, J. L., Gandy, N., Shulmeister, J., Quincey, D. J., and Cornford, S. L. (2020). Proglacial lakes control glacier geometry and behavior during recession. Geophys. Res. Lett. 47:e2020GL088865. doi: 10.1029/2020GL088865
Takeuchi, N., and Li, Z. (2008). Characteristics of surface dust on Ürümqi glacier no. 1 in the tien Shan mountains, China. Arctic Antarct. Alpine Res. 40, 744–750. doi: 10.1657/1523-0430(07-094)[TAKEUCHI]2.0.CO;2
Thompson, S., Benn, D. I., Mertes, J., and Luckman, A. (2016). Stagnation and mass loss on a himalayan debris-covered glacier: processes, patterns and rates. J. Glaciol. 62, 467–485. doi: 10.1017/jog.2016.37
van Woerkom, T., Steiner, J. F., Kraaijenbrink, P. D., Miles, E., and Immerzeel, W. W. (2019). Sediment supply from lateral moraines to a debris-covered glacier in the Himalaya. Earth Surface Dyn. 7, 411–427. doi: 10.5194/esurf-7-411-2019
Vincent, C., Wagnon, P. W., Shea, J. M., Immerzeel, W. W., Kraaijenbrink, P., Shrestha, D., et al. (2016). Reduced melt on debris-covered glaciers: investigations from Changri Nup Glacier, Nepal. Cryosphere 10, 1845–1858. doi: 10.5194/tc-10-1845-2016
Wessels, R. L., Kargel, J. S., and Kieffer, H. H. (2002). Aster measurement of supraglacial lakes in the Mount Everest region of the Himalaya. Ann. Glaciol. 34, 399–408. doi: 10.3189/172756402781817545
Wilson, J. P., and Bishop, M. P. (2013). “Geomorphometry,” in Remote Sensing and GIScience in Geomorphology, ed J. S. Bishop (Waltham, MA: Academic Press), 162–186. doi: 10.1016/B978-0-12-374739-6.00049-X
Wirbel, A., Jarosch, A. H., and Nicholson, L. (2018). Modelling debris transport within glaciers by advection in a full-stokes ice flow model. Cryosphere 12, 189–204. doi: 10.5194/tc-12-189-2018
Yue, X., Zhao, J., Li, Z., Zhang, M., Fan, J., Wang, L., et al. (2017). Spatial and temporal variations of the surface albedo and other factors influencing Urumqi glacier no. 1 in Tien Shan, China. J. Glaciol. 63, 899–911. doi: 10.1017/jog.2017.57
Zhang, Y., Fujita, K., Liu, S., Liu, Q., and Nuimura, T. (2011). Distribution of debris thickness and its effect on ice melt at Hailuogou glacier, southeastern Tibetan plateau, using in situ surveys and aster imagery. J. Glaciol. 57, 1147–1157. doi: 10.3189/002214311798843331
Zhang, Y., Hirabayashi, Y., Fujita, K., Liu, S., and Liu, Q. (2016). Heterogeneity in supraglacial debris thickness and its role in glacier mass changes of the mount Gongga. Sci. China Earth Sci. 59, 170–184. doi: 10.1007/s11430-015-5118-2
Keywords: debris-covered glaciers, climate-glacier dynamics, debris load, supraglacial water bodies, glacier model, Baltoro glacier
Citation: Huo D, Bishop MP and Bush ABG (2021) Understanding Complex Debris-Covered Glaciers: Concepts, Issues, and Research Directions. Front. Earth Sci. 9:652279. doi: 10.3389/feart.2021.652279
Received: 12 January 2021; Accepted: 23 April 2021;
Published: 24 May 2021.
Edited by:
Duncan Joseph Quincey, University of Leeds, United KingdomReviewed by:
Leif S. Anderson, University of Lausanne, SwitzerlandChristoph Mayer, Bavarian Academy of Sciences and Humanities, Germany
Copyright © 2021 Huo, Bishop and Bush. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Da Huo, ZGgyMUB0YW11LmVkdQ==
 Da Huo
Da Huo Michael P. Bishop1
Michael P. Bishop1 Andrew B. G. Bush
Andrew B. G. Bush