Test on the Reliability of the Subsurface Fault Geometry Estimated by Deformed River Terraces Along the Bailang River, North Front of the Qilian Shan (North West China)

The subsurface fault geometry is the base for understanding a process of crust deformation and mountain building. Based on kinematic models for fault-related folds, a geomorphic method is recently applied to estimate the subsurface fault geometry, while the validation on its reliability is lacking. In this study, we surveyed a suit of river terrace surfaces across an active fold at the north front of the Qilian Shan. According to the deformation geometry of the terraces, the fold deformation is interpreted by a listric fault fold model, and based on this kinematic model, the fault geometry underlying the fold is estimated. In comparison between the estimated fault geometry and a seismic reflection profile, we found that the decollement depth and the back thrust are highly consistent with each other. Although some small fault bends or internal shearing cannot be estimated solely by the terrace deformation, the overall fault geometry is successfully revealed by the terrace deformation. Using this fault geometry and the terrace dating results, the region deformation kinematics are re-evaluated, which suggest that the dip slip (in a rate of 1.8 ± 0.4 mm/a) along the decollement is mainly accommodated by two structures, one is the blind-back-thrust fault within the piggy basin in a dip-slip rate of 0.9 ± 0.3 mm/a and another is the thrust and fold at the west portion of the Yumu Shan range.

Introduction

The subsurface geometry of an active fault is the base for estimating the deformation kinematics (e.g., Whipple et al., 2016), to calculate the crust shortening rate (e.g., Lavé and Avouac, 2000), and thus to understand a process for mountain building (e.g., Hu et al., 2019b). For the extension of a fault from the surface to the deep crust, except definite evidence of the fault tip at the surface (if the fault breaks the surface) and a certain position at which a large earthquake happened (e.g., Burchfiel et al., 2008), most part of the fault geometry is hard to be definitely revealed. Up to now, the most popular method to acquire the subsurface fault geometry is a seismic reflection survey (e.g., Gao et al., 2013; Wang et al., 2013). Although it can supply relatively reliable data on sedimentary basins with layered strata (e.g., Wu et al., 2019), the results usually have great uncertainties in regions involving basement rocks (e.g., Gao et al., 2013). An extremely high cost in operating the seismic reflection is also a matter, which impedes its utilization in a wide area.

In the profit from the development of kinematic models for fault-related folds (Suppe, 1983; Suppe and Medwedeff, 1990; Erslev, 1991; Hardy and Poblet, 1994; Wickham, 1995; Allmendinger, 1998; Mitra, 2003; Cardozo, 2008; Hardy and Allmendinger, 2011; Poblet and Lisle, 2011; Brandes and Tanner, 2014), scholars try to estimate the active fold geometry using deformation patterns of geomorphic markers (Thompson et al., 2002; Gold et al., 2006; Scharer et al., 2006; Wilson et al., 2009; Burgess et al., 2012). Based on kinematic models for fault-related folds geometry and geomorphic deformation, the geometry of the related fault can also be estimated (Hu et al., 2015, 2017, 2019b; Liu et al., 2019; Wang et al., 2020; Zhong et al., 2020), which provides a more convenient way to investigate the subsurface fault geometry. Due to the uncertainty derived from the selection of the fold model and from the assumption of the fault dip close to the surface (e.g., Hu et al., 2015), the reliability of the estimated fault geometry is still questionable. Thus, it is highly necessary to verify the geomorphic method for the estimation of the subsurface fault geometry.

In this study, we conduct geomorphic investigations on a relatively new active fold, at the north front of the Qilian Shan, northwest China. This fold is named as the Dahe Anticline whose deformation is onset in recent 1 Ma (Hu et al., 2017). The deformed terrace surfaces along the Bailang River, which transect the active fold, are surveyed to obtain their deformation patterns and to estimate the fold and its related fault geometry. Then, the estimated fault geometry is compared to the available seismic reflection profile (Zuza et al., 2016) to verify the result. Furthermore, combining the ages of terrace surfaces, the deformation kinematic across the North Qilian Shan Fault (NQF), the piggy-back basin, and the Yumu Shan range is renewed.

Regional Tectonic Setting

The North Qilian Shan Fault

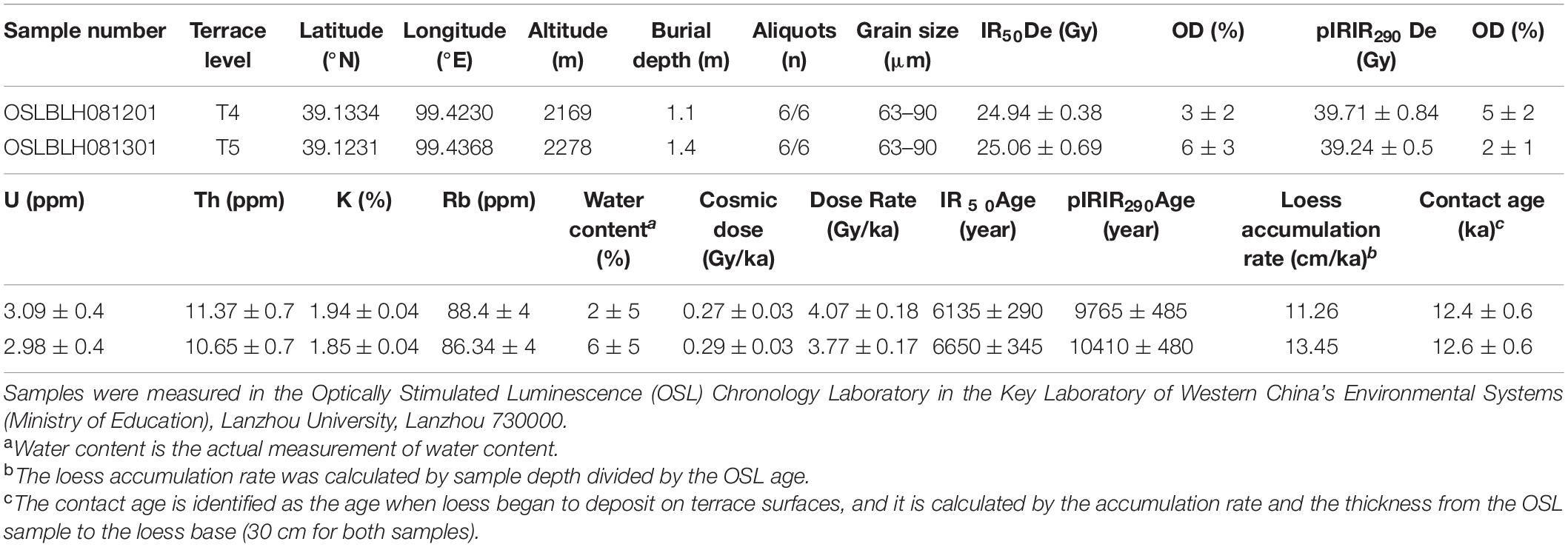
The North Qilian Shan Fault (NQF) is a geomorphic boundary between the Qilian Shan and the Hexi Corridor, which acts as a foreland basin (Yang, 2007) receiving sediments from the Qilian Shan range (Figure 1). This South West-dipping thrust fault (NQF) consists of a series of segments that lies ∼600 km long from the Altyn-Tagh Fault (in the west) to the city of Wuwei (in the east). Along the NQF, the surface deformation includes surface offsets by break-through thrusts (Palumbo et al., 2009; Liu et al., 2017; Xiong et al., 2017; Yang et al., 2018; Hetzel et al., 2019) and fault-related folds by blind thrusts (Yang et al., 2018; Cao et al., 2019) or by fault bending in the depth (Hu et al., 2015, 2017, 2019b; Liu et al., 2019; Wang et al., 2020). Through multiple dating methods, the optically stimulated luminescence (OSL), the in situ terrestrial cosmogenic nuclides (TCN), and ¹⁴C dating, the deformed Quaternary geomorphic surfaces at different segments are dated to yield vertical slip rates of 0.5–1.5 mm/a, inferring an average crust shortening rate of 1–2 mm/a (e.g., Xiong et al., 2017; Yang et al., 2018; Hu et al., 2019b; Wang et al., 2020). According to the continuous thrusting of the NQF from ∼10 Ma (Zheng et al., 2010), the Qilian Shan is uplifted to a peak elevation of ∼5,500 m and the pre-Cenozoic rock exposed in the range is placed on the Quaternary sedimentary rock in the Hexi Corridor. At the north front of the NQF, in the foreland basin, late Cenozoic sediments are deformed by several active thrust faults and/or folds, indicating that these structures are relatively new (to be onset in Pliocene and Quaternary; Palumbo et al., 2009; Zheng et al., 2013; Hu et al., 2017, 2019b; Zhao et al., 2017). These structures are interpreted as the result of north-ward propagation of the NQF system through new growing thrust faults, which root at the decollement connected to the NQF in the deep crust (Tapponnier et al., 1990; Hetzel, 2013; Cheng et al., 2019; Hu et al., 2019b).

FIGURE 1

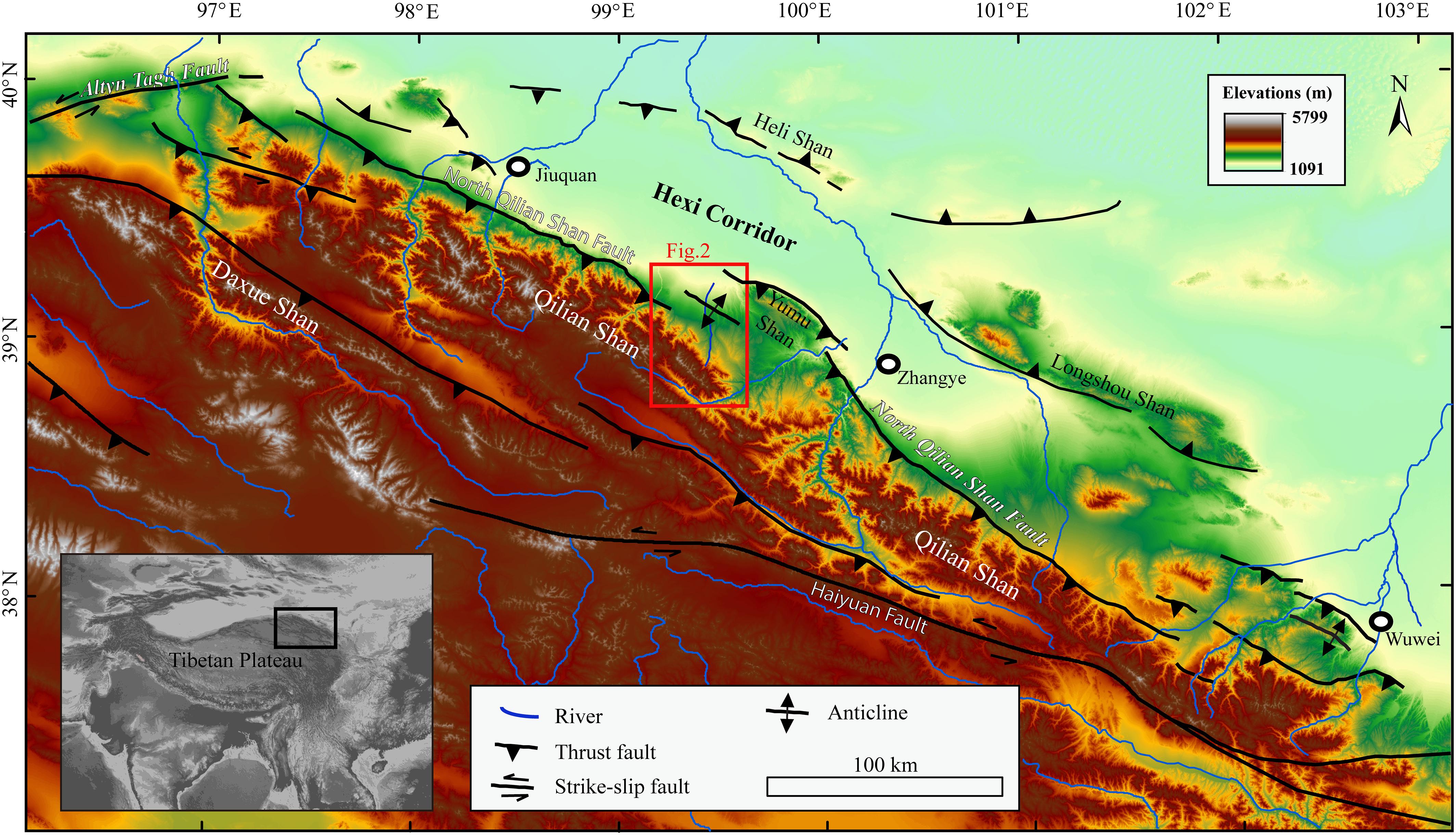
Figure 1. Topographic map of the Qilian Shan [derived from the Shuttle Radar Topography Mission (SRTM) digital elevation model with 90 m resolution] and the distributions of active faults. Fault data are from Meyer et al. (1998), Hetzel et al. (2002), Yuan et al. (2013), Zheng et al. (2013), and Hu et al. (2017).

The North Yumu Shan Fault and the Dahe Anticline

The uplift of the Yumu Shan is controlled by thrusting and its related folding on the North Yumu Shan Fault (Tapponnier et al., 1990; Palumbo et al., 2009; Hu et al., 2019b). In the core of the range, the Paleozoic sedimentary rocks are exposed with a summit of ∼3,200 m and on the west rim of the range, as the elevation decreases, Paleogene, Neogene, and Quaternary sediments are systematically exposed in the form of an anticline (Figure 2A). Through landform deformation and TCN dating, Palumbo et al. (2009) determined an uplift rate of ∼0.8 mm/a for the central part and ∼0.5 mm/a for the eastern tip and deduced an onset age of 3.7 ± 0.9 Ma for the activation of the NYF. Another geomorphic research on the eastern part of the Yumu Shan builds a fault-related model from the deformed river terraces and derived a relatively higher uplift rate of 1.2 ± 0.1 mm/a (Hu et al., 2019b), which inferred a relatively newer onset age of 2.5 ± 0.5 Ma for the uplift of the Yumu Shan. The thermo-modeling of the apatite fission track data indicates that the fast cooling of the Yumu Shan range began at ∼4.0 Ma (Wang et al., 2018). The sedimentary evidence in the foreland basin also records the Late Pliocene (∼3 Ma) uplift for the Yumu Shan (Hu et al., 2019a).

FIGURE 2

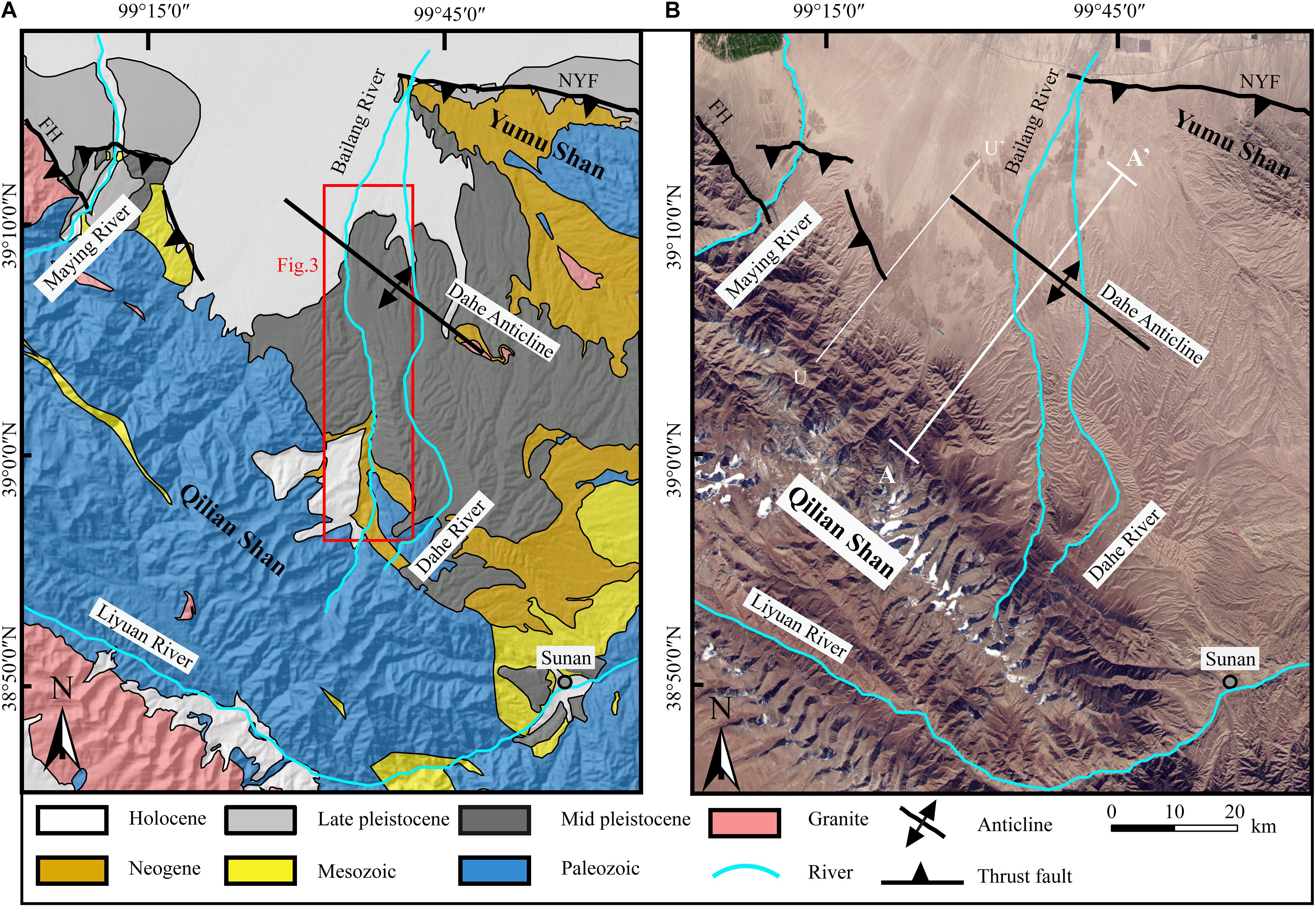
Figure 2. (A) Geologic map of the study region showing the lithology and active structures (lithology data are from 1:200,000 Chinese geologic maps, Ministry of Geology and Mineral Resources). (B) The Google Earth image of the study region showing the topography distribution from the Qilian Shan to the Yumu Shan. The line U–U′ shows the location of a seismic reflection profile in Zuza et al. (2016). FH is the Fodongmiao-Hongyazi Fault and NYF is the North Yumu Shan Fault, and both of these two faults are parts of the North Qilian Shan Fault (NQF).

At the region between the Yumu Shan and the Qilian Shan, widespread Pleistocene alluvial-fluvial sediments, mainly gravels with a depth of >150 m (Hu et al., 2017), cover on the surface of this region, which has an average elevation of 2,000–3,000 m. Based on the geology and geomorphic characters in this region, Hu et al. (2017) proposed a deformation model of the piggy-back basin, which began to be uplifted and deformed since 1.0–0.3 Ma associated with the west-ward extension of the NYF (Seong et al., 2011). The Dahe Anticline (Figure 2B) is formed by the thrusting on a north-dipping back-thrust fault, which is a blind fault rooting to the decollement that extends to the NYF in the north and to the NQF to the south (Tapponnier et al., 1990; Hu et al., 2017). Recently published seismic reflection profile to the west of this region (U–U′ profile in Zuza et al., 2016) shows a clear trace of a blind-back-thrust fault at the position of the Dahe Anticline, and the reflection profile also presents a trace for a possible decollement surface, which has an upward-convex shape that gradually increases its dip angle and extends to the deep crust under the Qilian Shan. Previous estimated shortening rate within this region is relatively low (0.14 + 0.14/-0.03 mm/a), which is calculated with an assumption of ∼7 km depth for the decollement (Hu et al., 2017).

Materials and Methods

Fluvial Terraces Along the Bailang River

Along the Bailang River, at least five levels of fluvial terraces are developed (Figures 3A–C), and we named the lowest (youngest) as T1 and the highest (oldest) as T5. Near the Dahe Anticline, T5 and T4 are continuously developed and have relatively wide surfaces that extend downstream until they are merged into T3. T3 is developed almost continuously along the studied reach, and its surface is relatively narrow upstream of the Dahe Anticline. Downstream the anticline, T3 surface is extending widely in a fan shape in a plan view. T2 and T1 are distributed relatively narrower and just adjacent to the active river channel.

FIGURE 3

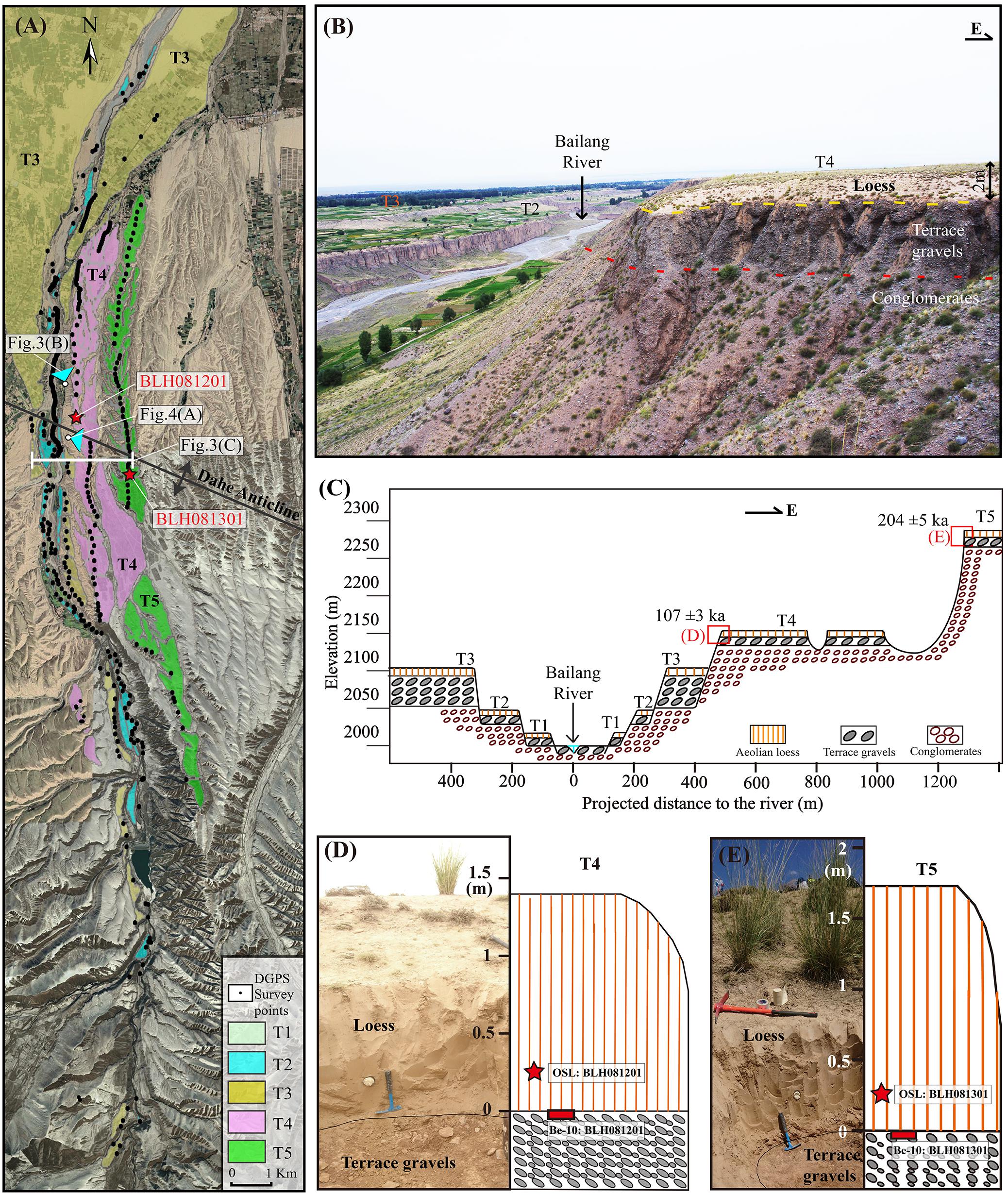
Figure 3. (A) Distributions of terraces along the Bailang River. (B) The photo showing the terrace staircases and the composition of terrace T4. (C) The sketched transect near the anticline (location shown in the Figure 3A) showing the stratigraphy and positions of the optically stimulated luminescence (OSL) and ¹⁰Be samples. (D) The photo showing the T4 surface of the gravel top at which the ¹⁰Be sample was taken and above which the OSL sample was taken close to the base of aeolian loess. (E) The photo showing the T5 surface of the gravel top, at where the ¹⁰Be sample was taken and above which the OSL sample was taken close to the base of aeolian loess.

From the transect (Figure 3C) across the river valley close to the crest of the anticline, the composition of the terrace staircases can be identified. T5 and T4 express as strath terraces that terrace gravels are beveled by Middle and Early Pleistocene conglomerates, which are interpreted as alluvial fan deposits before the region began to uplift from Middle Pleistocene (Hu et al., 2017). From the field investigation, we can find that the beveled conglomerates are relatively smaller and have a brownish color contrasting to the terrace gravels of gray color (Figure 3B). T3 is about 100 m above the river bed and has a thick terrace gravel deposition of 40–60 m, which is also beveled by the old conglomerates. The thick fluvial deposition of the T3 suggests that this terrace is a fill terrace with a fast following incision. Both terraces T2 and T1 are strath terraces and their surfaces are ∼30 and ∼10 m above the river bed, respectively. All these terrace surfaces are made to overlie by a thin layer of aeolian loess with a thickness of 1–3 m.

Deformation of Terrace Surfaces

In order to obtain accurate surface deformation characteristics, we used a differential Global Positioning System (GPS) with a vertical error of less than 5 cm to measure the elevations of terrace surfaces. Due to the relatively thin loess cover on the terrace surface, continuous terrace surface was surveyed on the loess top, and most of the discontinuous points were surveyed at the top of a gravel layer. After minus the loess thickness, longitudinal profiles for each terrace surface and modern river bed were plotted to find the deformation geometry (Figure 4B). In order to constrain the deformation amount, the distance for longitudinal profiles was projected in the direction of NE30° (Figure 2B), perpendicular to the fold strike. Furthermore, in order to eliminate the effect of the initial inclination of the terrace surface, elevations of the terrace surfaces are transformed to relative heights above the modern river bed (Figure 4C). The fold deformation at the Dahe Anticline is clearly recorded by the terraces T5 and T4 (Figure 4A), and a north-ward tilting of terrace surfaces to the south of the Dahe Anticline (upstream of 16-km point) is also illustrated from the terrace deformation geometry. From the geometry of T5 and T4, we can find that the width of the Dahe Anticline is about 6.6 km, from ∼16 to ∼23 km at the longitudinal profile (Figure 4B), and the crest of the anticline is at the 17-km point. The forelimb (south limb) is relatively short (Figure 4C), with a width of ∼1.3 km, and the backlimb (north limb) is relatively wide, with a width of ∼5.3 km. The dip angle for T5 at the backlimb is greatly larger than that of the modern river bed.

FIGURE 4

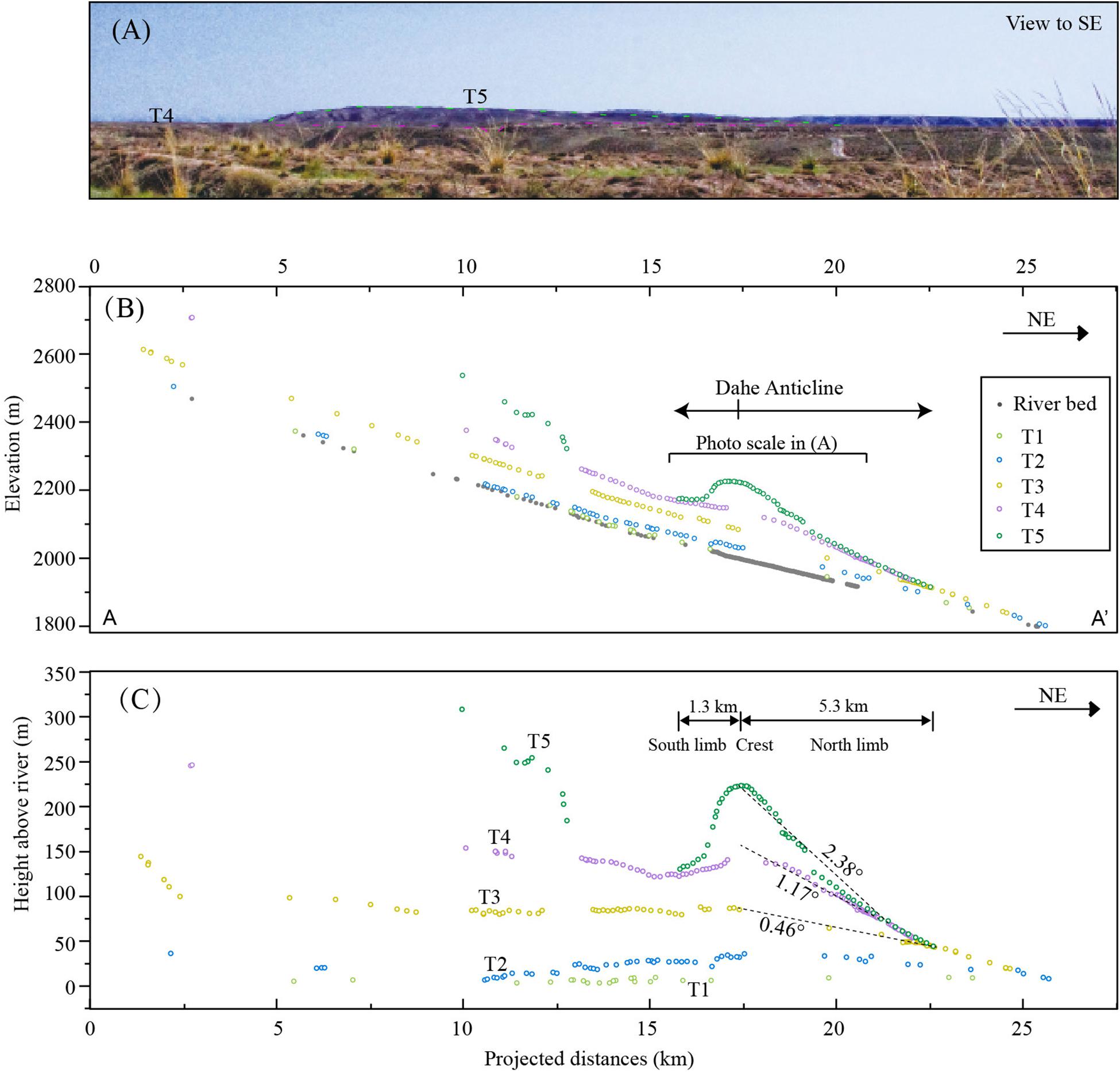
Figure 4. (A) The photo of the folded terrace surface of T5 at the anticline. (B) The longitudinal profiles of terrace surfaces and the modern river bed. The distance is along the straight line of A–A′ in Figure 2, and each surveyed point is projected to this line. (C) The heights of terrace surfaces along the Bailang River. The height data for the terrace surfaces are calculated by subtracting the elevation of modern river bed from the elevation of terrace surface.

We noticed that the T3 is a fill terrace, contrasting to the strath terraces for other terrace levels, and the thickness of the fill is up to ∼60 m, indicating significant aggradation in building the T3 surface and fast incision after the abandonment of the surface. This terrace also has a wide distribution downstream, composing the main fan along the Bailang River. These characteristics are similar with the terrace formed during 25–15 ka along the rivers to the west of the Bailang River, such as the Maying River (Yang et al., 2018), the Hongshuiba River (Yang et al., 2020), the Beida River (Wang et al., 2020), the Baiyang River (Liu et al., 2019), and the Shiyou River (Hetzel et al., 2006). The incision rate by this late Pleistocene terrace is estimated to be 6–10 mm/a, which is greatly higher than the regional rock uplift rate of 0.5–1.5 mm/a, and the fast incision is attributed to the climate transition after the last glacial maximum (Hetzel et al., 2006; Wang et al., 2020; Yang et al., 2020). In the upstream of the Bailang River, the luminescence study of T3 yielded an age of 16 ± 1 ka (Zhou et al., 2002), in good agreement with the ages obtained from other rivers for this climatic terrace, and thus we give the age of 16 ± 1 ka for T3. In order to eliminate the influence of climate (Wang et al., 2020), we can construct the deformation before T3 by subtracting the surface elevation of T3 from T4 and T5 (Figure 5A).

FIGURE 5

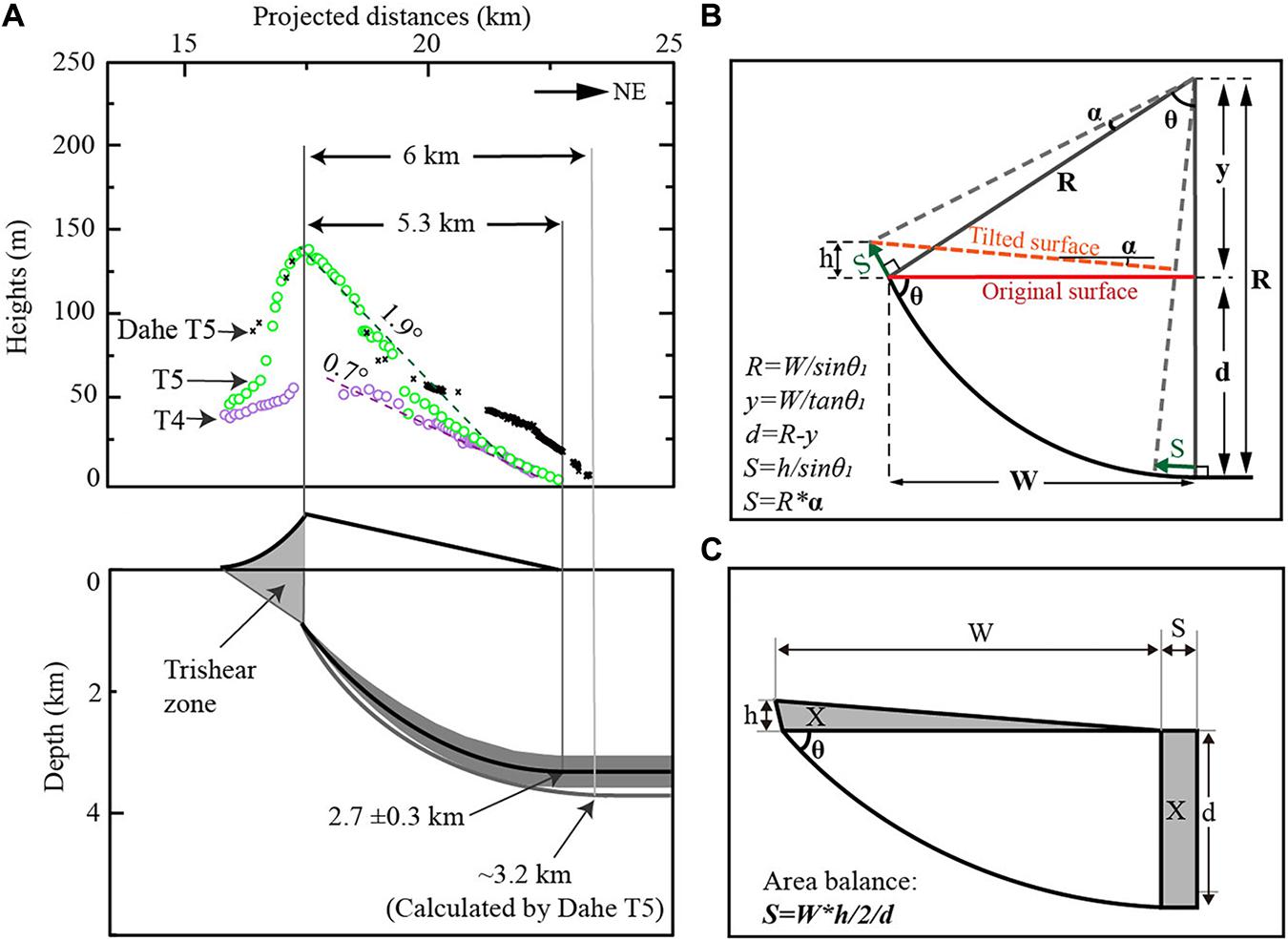
Figure 5. (A) Terrace heights relative to the T3 surface showing the deformation geometry of across the Dahe Anticline. The lower part showing the fault geometry deduced from the deformed terraces with the calculating method in (B). (B) The geometric method to calculate the subsurface fault geometry and to calculate the fault slip rate. R = radius of the curve, α = the tilt angle of the terrace surface, W = the width of the backlimb, θ = dip angle of the back thrust at the upper-most part, d = the depth to the decollement, y = the height from the surface to the center of rotation, S = the slip amount along the back thrust, h = terrace height at the anticline crest. (C) The illustration to show the area-mass-balance method to calculate the fault slip. X is the shortening area on a horizonal fault, and it equals to the uplifted area from the backlimb of the terrace surface.

Chronology of the Terraces

Abandonment times for T5 and T4 surfaces were determined by cosmogenic ¹⁰Be exposure dating, and the OSL samples were also collected at the base of the aeolian loess for the correction of ¹⁰Be exposure ages. Close to the terrace riser of T5 and T4 (Figure 3C), we excavated out the overlying loess to the top of the fluvial gravels (Figures 3D,E), and then we picked out at least 50 quartz grains with a size of 10–20 mm at the topmost surface of the fluvial gravels. In the meantime, close to the loess base (at the position 30 cm above the gravel layer), we collected one OSL sample from the loess deposit by a steel tube. The excavated gravel top is a flat surface, indicating limited post erosion on the gravel surface. Detailed information on chronology samples is presented in Tables 1, 2.

TABLE 1

Table 1. OSL samples from the overlying loess and dating results.

TABLE 2

Table 2. ¹⁰Be samples and analysis results for terraces of the Bailang River.

In calculating the exposure age, we follow the method proposed by Hetzel et al. (2004) to eliminate the influence from loess shielding, and the calculated equation can be expressed as:

$${\mathbf{\text{t}}}_{\mathbf{1}}=-\frac{\mathbf{1}}{\mathrm{\lambda }}\mathbf{\text{l}}n\left[\mathbf{1}-\frac{\mathrm{\lambda }}{\mathbf{\text{P}}}\left({\mathbf{\text{C}}}_{\mathbf{t}ot}{\mathbf{\text{e}}}^{\mathrm{\lambda }{\mathbf{t}}_{\mathbf{2}}}+\frac{\mathbf{\text{P}}}{\mathrm{\lambda }-\frac{\mathrm{\rho }\mathrm{\alpha }}{\mathrm{\Lambda }}}\left(\mathbf{1}-{\mathbf{\text{e}}}^{\left(\mathrm{\lambda }-\mathrm{\rho }\mathrm{\alpha }/\mathrm{\Lambda }\right){\mathbf{t}}_{\mathbf{2}}}\right)\right)\right]$$

where t₁ is the time span between the generation of the surface and the onset of loess accumulation and t₂ is the time span from the onset of loess accumulation to the present. λ is the decay constant (for ¹⁰Be: 4.998 × 10^–7 yr^–1, Korschinek et al., 2010). P is the production rate of the nuclide (with unit of atoms⋅g^–1⋅yr^–1), and it is calculated with the scaling model of Stone (2000), using the ¹⁰Be production rate of 5.1 atoms⋅g^–1⋅a^–1 at sea level and high latitude. C_tot is the concentration of the total cosmogenic ¹⁰Be nuclides in quartz from the original surface (atoms⋅g^–1). ρ is the loess density with the value of 1.4 g⋅cm^–3 (Hetzel et al., 2004; Cao et al., 2019). α is the accumulation rate of loess derived from the age and the depth. Λ is the decay length of cosmic ray (160 g/cm²; Balco et al., 2008). The sum of t₁ and t₂ is the total exposure time t.

Results

Geometry of the Subsurface Fault

According to the deformation pattern of terraces (Figure 4), the coupled deformation and related fault geometry can be separated into two parts: The first part is the Dahe Anticline deformation, relating to a back thrusting fault derived from the decollement (Zuza et al., 2016; Hu et al., 2017) and the second part is the monocline with north-ward tilting terraces on the south of the anticline and probably related to the thrusting on the base fault with a south-ward tilting shape (Hu et al., 2017).

Based on the factors of a gentle tilting and wide backlimb, a relatively short forelimb, and a blind fault under the anticline, we can interpret the anticline using a listric fault model (Amos et al., 2007; Hu et al., 2015) for the backlimb and using a trishear-fold model (Erslev, 1991) above the fault tip for the forelimb. In building the detailed fault-and-fold geometry, two boundary conditions, a dip angle at the upper tip of the blind fault and a dip angle of the decollement at the north boundary, are assumed based on local investigations. Previous investigations in this area showed that faults at the surface usually have steep dip angles of 40°–70° (Tapponnier et al., 1990; Yang et al., 2018; Cao et al., 2019; Ren et al., 2019), and a seismic reflection profile (Zuza et al., 2016) illustrated a dip angle of ∼55° for this fault tip. Thus, we assume a dip angle for the upper dip of the blind fault as 55° ± 5° (θ). According to the landform pattern that, all the terraces are merged into the fluvial plain to the north of the anticline, probably indicating no uplift at this region and suggesting a horizontal we assume a dip angle of 0° for the decollement at the north boundary, which is also in agreement with previous interpretation for the decollement dip at the south of the Yumu Shan (Tapponnier et al., 1990; Hu et al., 2017). Enclosed by the two axle surfaces, a listric fault geometry can be constructed (Figure 5B). By the width of the anticline (5.3 km) and the fault dip angle at the fault upper tip, the radius of the fan is estimated as ∼6.5 km, and then the fault depth of the decollement at the north can be estimated as ∼2.8 ± 0.3 km (the uncertainty is mainly derived from the uncertainty of the fault dip angle θ). The southward tilting at the forelimb of the anticline is simply interpreted by a trishear zone (Figure 5B) in the shallow depth and with a surface width of ∼1.3 km (Figure 4B).

The subsurface fault geometry at the second part is estimated by the kinematic theory of fault-bending fold that, the uplift rate is a function of the dip angle with a constant fault slip rate (Thompson et al., 2002; Hu et al., 2015). At the 15-km point, the river incised 40 m from T4 to T3. Using the incision amount and the age, the incision rate can be estimated as 0.3–0.4 mm/a. If we assume this relatively long-term river incision rate in equilibrium with the local rock uplift rate and using the fault slip rate of 1.8 ± 0.4 mm/a (detailed discussion for this value is in the section “Deformation rate”) for the base thrust in this region (Hetzel et al., 2019; Hu et al., 2019b), the dip angle of the base fault at this point can be calculated as 11° ± 2°. At the 10-km point, using the same method, the local uplift rate is calculated as 0.8–1.2 mm/a, and then the dip angle can be estimated as 34° ± 8°. With these two constraints for the fault dips and the horizontal fault surface under the Dahe Anticline, the subsurface fault geometry under the south monocline is constructed (Figure 6).

FIGURE 6

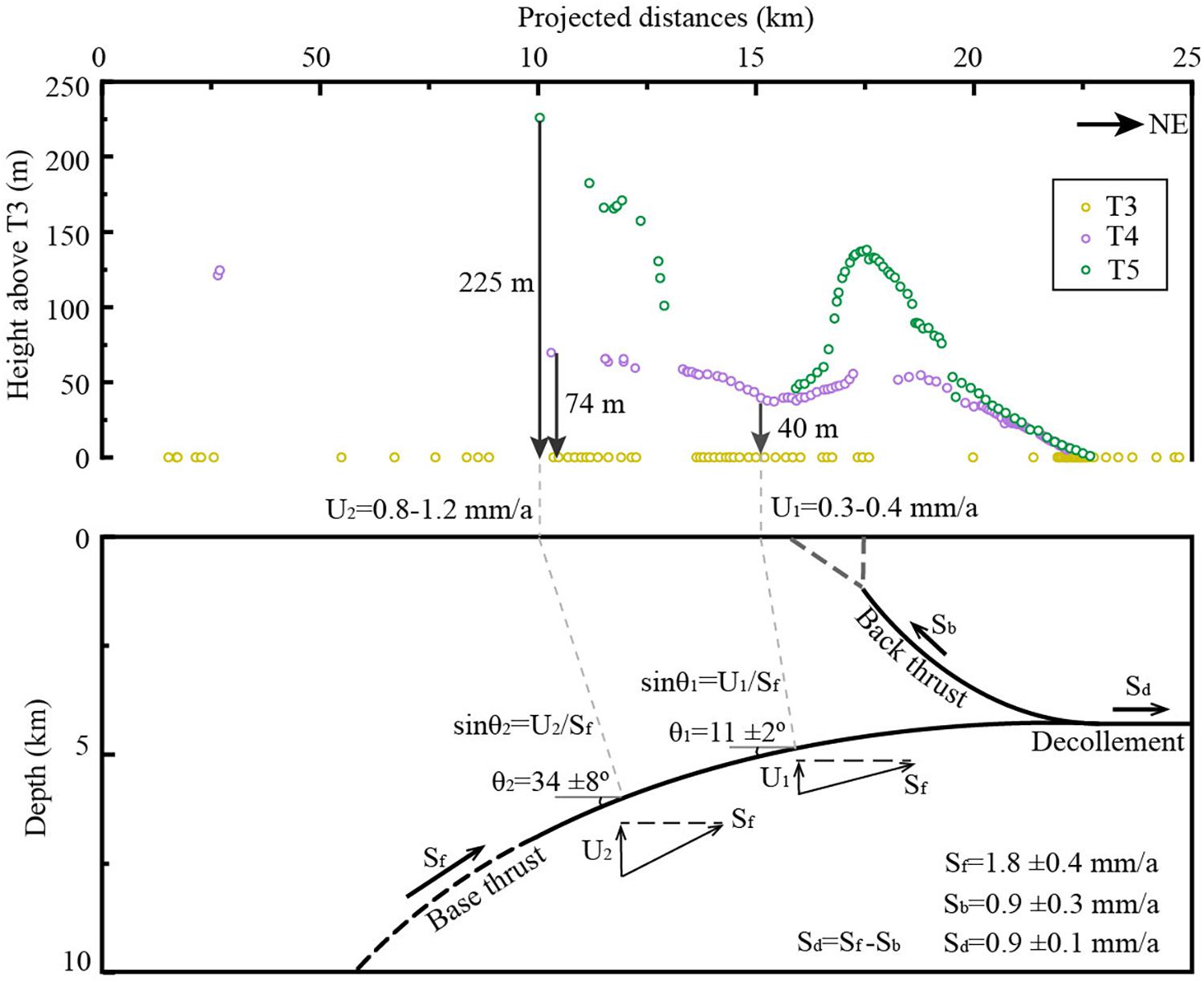
Figure 6. The overall geometry for the subsurface thrust fault. In calculating the fault dip, we assume that the river incision equal to the rock uplift. S_f = the full fault slip rate along the base thrust, S_b = the fault slip rate along the back thrust, S_d = the fault slip rate to the north of the back thrust, U = vertical component of the dip-slip rate or uplift rate, θ = the local fault dip angle.

From south to north, the overall geometry for the subsurface fault estimated by terrace deformations can be described as a convex-up curve changed to a horizontal decollement, and at the horizontal decollement, a concave-down curve of the back thrust grew. By comparing the geometry with the seismic reflection profile (Figure 7), the fault structure is closely match with each other, especially for the depth of the horizontal decollement, for the geometry of the curved back thrust, and for the curved south-dipping thrust. Although a natural fault is not following an ideal curve and shows some small fault bends and secondary fault traces (as illustrated in the seismic reflection profile, Figure 7), which cannot be estimated in this study, the overall geometry for the fault in controlling local deformation can be successfully estimated by the surface deformation pattern, and it verified the validation of the geomorphic method in estimating the subsurface fault geometry.

FIGURE 7

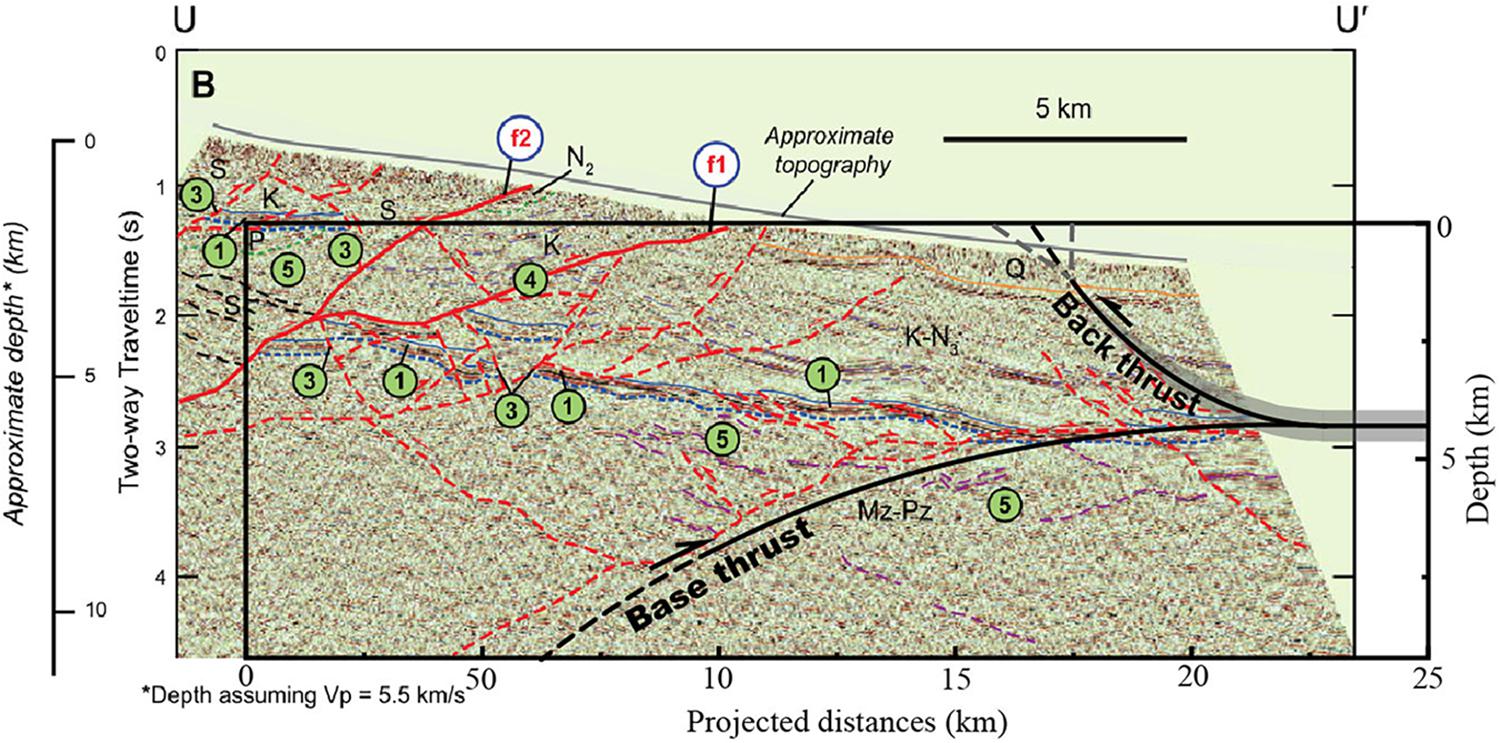
Figure 7. Comparison between the fault geometries estimated by terrace deformation, and the interpretation form the seismic reflection profile of Zuza et al. (2016).

Deformation Rate

The TCN exposure dating on the terrace surface yields an age of 204 ± 7 ka for T5 and an age of 109 ± 8 ka for T4 (Table 2). With the fault geometry, terrace deformation geometry, and terrace ages, the slip rate for the back thrust can be estimated. The first method (Figure 5B) for the estimation is using the tilting angle of terrace surfaces and the turning radius R (∼6.5 km). Relative to T3, the tilting of T5 surface is ∼1.9°, and this angle will yield a slip amount of 215 m. From T5 (∼204 ka) to T3 (∼16 ka), the slip rate can be estimated as 1.1–1.2 mm/a. The tilting angle of 0.7° for T4 surface (relative to T3) yields a slip rate 0.8–0.9 mm/a. The second method uses the terrace height at fold crest and θ (55° ± 5°) to calculate the total slip amount. In relation to T3, the estimated fault slip rate for T5 is 1.0 ± 0.2 mm/a and for T4 is 0.8 ± 0.2 mm/a by T4. For the connection of the back thrust to the horizonal decollement, the slip rate on the back thrust could be estimated as the shortening rate (part of the total shortening) at the horizonal decollement, thus we can apply the commonly used area-balance method (Lavé and Avouac, 2000) to calculate the slip rate (Figure 5C). The uplifted area of T5 and T4 also relative to T3 can be calculated by a triangle, and using the decollement depth estimated in the previous section, the slip rate is estimated as 0.8 ± 0.2 mm/a. We can find that these estimations for the fault slip rate by three methods are highly in agreement and give an average value of 0.9 ± 0.3 mm/a.

Discussion

Implications for Local Deformation Kinematics

Based on the geological (Tapponnier et al., 1990), seismic (Zuza et al., 2016), and geomorphic (Hu et al., 2017, 2019b) evidences, the deformation of the Yumu Shan and the piggy-back basin at its south is interpreted by thrusting along an upper crust decollement (Tapponnier et al., 1990; Hu et al., 2017). This base thrust fault is connected to the NQF at the south in a relatively deeper crust (Zuza et al., 2016). Furthermore, to the south margin of the piggy-back basin, no active fault has been found along the eastern extending trace of the Fodongmiao-Hongyazi Fault (FH), although a clear geology and topographic boundary can be identified along this line. This evidence probably suggests that the NQF had been active along this boundary before the thrust fault propagating to the north below the piggy-back basin and to the Yumu Shan. Thus, we can assume the NQF has been inactive after its north-ward propagation in this region, and the slip rate along the decollement and at the NYF (if without internal shortening in the piggy basin) should be equal to the slip rate on the NQF. On the west of the Bailang River, a dip-slip rate of 1.7 ± 0.3 mm/a for the FH fault can be estimated according to 1.2 ± 0.1 mm/a vertical slip rate (Yang et al., 2018; Hetzel et al., 2019) and 45° ± 5° dip angle for the fault close to the surface (Yang et al., 2018). At the eastern portion of the Yumu Shan, Hu et al. (2019b) estimated a full dip-slip rate of 1.8 ± 0.4 mm/a, which is in good consistency with the rate on the FH fault. Thus, we could assume that the full dip slip along the decollement under the piggy-back basin is in a rate of 1.8 ± 0.4 mm/a.

At the eastern portion of the Yumu Shan, this rate is probably fully concentrated on the faulting and the folding across the Yumu Shan range (Hu et al., 2019b), while it is not concentrated at the western portion of the Yumu Shan by the observation in this study. We suggest a 0.9 ± 0.4 mm/a shortening or fault slip is accommodated by the Dahe Anticline within the piggy-back basin, and the rest half-slip is accommodated by the western portion of the Yumu Shan range. After revisiting the terrace deformation pattern along the Dahe River (Hu et al., 2017), we find the anticline deformation could be extending to a wider width of ∼6 km with a relatively wide and gentle-tilting backlimb, rather than a folding with a width of 3 km. Thus, using a new method in this study, we estimated the subsurface fault geometry using T5 surface along the Dahe river, and it yields a similar geometry result (Figure 5A) as that along the Bailang River.

Advantages and Limitations in Estimation of the Fault Geometry Using a Geomorphic Method

Across tectonic active fault-and-fold belts, river terraces are usually widely distributed, which provide us available materials to constrain the deformation kinematics, such as the Himalaya (e.g., Lavé and Avouac, 2000; Burgess et al., 2012), the Tian Shan (e.g., Burchfiel et al., 1999; Goode et al., 2014), the Taiwan Range (e.g., Simoes et al., 2007), the New Zealand (e.g., Amos et al., 2007), and the Qilian Shan (e.g., Hu et al., 2015; Cao et al., 2019). These widely distributed materials were mostly used to determine the fold types and deformation rates, while this study along with other relative studies (Amos et al., 2007; Hu et al., 2015; Wang et al., 2020) indicate that the geometry of fold-related fault could be also successfully estimated based on the terrace deformation and kinematic models for fault-related folds (Brandes and Tanner, 2014). Thus, this geomorphic method could provide us a valuable way to estimate the subsurface fault geometry in a basement-involved range, where the seismic reflection data are usually lacking or have great uncertainty in determining the fault trace. From these studies, we can know that a geomorphic constraint on deformations not only gives us the availability to study the fold geometry and deformation rates, but also at the same time, it would provide us a new way to obtain the subsurface fault geometry.

In this study, we should notice that a listric fault-related fold model was applied to reconstruct the terrace deformation. Along the Bailiang and Dahe rivers, the tilted terrace surface at the backlimb is not strictly a planar surface (with a constant dip angle), which suggests that the subsurface fault probably is not an ideal curve, has some small fault bends or a certain amount of internal shearing (Hu et al., 2019b). The uncertainty with the chosen fold model can be also derived from the fold geometry, likewise, the terrace deformation may be interpreted by a hanging-wall shearing model along a fault-bend fold (Suppe et al., 2004; Wang et al., 2020). For the shear fault-bend folding, how to obtain the subsurface fault geometry is still a question; however, the listric fault-related fold (e.g., Hu et al., 2017) and classic fault-bend folding models (e.g., Stockmeyer et al., 2017) have been successfully applied to reconstruct the subsurface fault geometry based on the geomorphic deformation. In regard to a buried fault, another uncertainty in calculating the subsurface fault geometry is that we need an assumption for a dip angle of the upper-most fault trace. Here, the assumption depends on a seismic reflection profile, which gave us a robust boundary condition. While we do not have a seismic reflection profile, people usually made the assumption according to nearby investigations on the fault dips on the break-through thrusts at the surface (Hu et al., 2015; Liu et al., 2019). Although this assumption could be validated according to the similar lithology in a nearby region, the investigated dip angles of the thrust at the surface usually have a wide range (Yang et al., 2019), which could introduce a certain amount of uncertainty for this assumption. To resolve this problem, surveying by the Ground Penetrating Radar (GPR) would be an efficient method (Amos et al., 2007) to determine the shallow-buried thrust fault.

Conclusion

In comparison to a seismic reflection profile, the high consistency of the subsurface fault geometry estimated by the terrace deformation across an active folding region proved the validation of the geomorphic method in estimating the subsurface fault geometry. Although the uncertainty can be derived from the selection of fold kinematic models and from the assumption of the fault dip at one boundary, the overall geometry for the blind thrust fault is successfully estimated by a geomorphic deformation. Based on the fault geometry, a more reliable kinematic for local crust deformation can be constructed.

Data Availability Statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author and the first author.

Author Contributions

XH designed the study and wrote most of the manuscript. XJ conducted the field and lab work, wrote some part of the manuscript, and constructed the figures. XC led the field investigations and analyzed the data. JC conducted the field work and analyzed parts of the data. BP provided the funding and resources for this research. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This study was supported by the National Natural Science Foundation of China (NSFC; Grant Nos. 42071001 and 41730637) and the Second Tibetan Plateau Scientific Expedition and research program (STEP; Grant No. 2019QZKK0704).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We like to thank Changsheng Gong, Zhenling Wen, Jiakun Wu, Xin He, and Yanan Zhang for their assistance in field and lab-dating work. We also like to thank XL and another reviewer for their valuable suggestions.

References

Allmendinger, R. W. (1998). Inverse and forward numerical modeling of trishear fault-propagation folds. Tectonics 17, 640–656. doi: 10.1029/98tc01907

CrossRef Full Text | Google Scholar

Amos, C. B., Burbank, D. W., Nobes, D. C., and Read, S. A. L. (2007). Geomorphic constraints on listric thrust faulting: implications for active deformation in the Mackenzie Basin, South Island, New Zealand. J. Geophys. Res. 112:4291. doi: 10.1029/2006jb004291

CrossRef Full Text | Google Scholar

Balco, G., Stone, J. O., Lifton, N. A., and Dunai, T. J. (2008). A complete and easily accessible means of calculating surface exposure ages or erosion rates from 10Be and 26Al measurements. Q. Geochronol. 3, 174–195. doi: 10.1016/j.quageo.2007.12.001

CrossRef Full Text | Google Scholar

Brandes, C., and Tanner, D. C. (2014). Fault-related folding: a review of kinematic models and their application. Earth Sci. Rev. 138, 352–370. doi: 10.1016/j.earscirev.2014.06.008

CrossRef Full Text | Google Scholar

Burchfiel, B. C., Brown, E. T., Qidong, D., Xianyue, F., Jun, L., Molnar, P., et al. (1999). Crustal Shortening on the margins of the Tien Shan, Xinjiang, China. Intern. Geol. Rev. 41, 665–700. doi: 10.1080/00206819909465164

CrossRef Full Text | Google Scholar

Burchfiel, B. C., Nakov, R., Dumurdzanov, N., Papanikolaou, D., Tzankov, T., Serafimovski, T., et al. (2008). Evolution and dynamics of the Cenozoic tectonics of the South Balkan extensional system. Geosphere 4:919.

Google Scholar

Burgess, P. W., Yin, A., Dubey, C. S., Shen, Z.-K., and Kelty, T. K. (2012). Holocene shortening across the Main frontal thrust zone in the eastern Himalaya. Earth Planet. Sci. Lett. 357–358, 152–167. doi: 10.1016/j.epsl.2012.09.040

CrossRef Full Text | Google Scholar

Cao, X., Hu, X., Pan, B., Zhang, J., Wang, W., Mao, J., et al. (2019). A fluvial record of fault-propagation folding along the northern Qilian Shan front, NE Tibetan Plateau. Tectonophysics 755, 35–46. doi: 10.1016/j.tecto.2019.02.009

CrossRef Full Text | Google Scholar

Cardozo, N. (2008). Trishear in 3D. Algorithms, implementation, and limitations. J. Struct. Geol. 30, 327–340. doi: 10.1016/j.jsg.2007.12.003

CrossRef Full Text | Google Scholar

Cheng, F., Garzione, C. N., Mitra, G., Jolivet, M., Guo, Z., Lu, H., et al. (2019). The interplay between climate and tectonics during the upward and outward growth of the Qilian Shan orogenic wedge, northern Tibetan Plateau. Earth Sci. Rev. 198:102945. doi: 10.1016/j.earscirev.2019.102945

CrossRef Full Text | Google Scholar

Erslev, E. A. (1991). Trishear fault-propagation folding. Geology 19, 617–620.

Google Scholar

Gao, R., Wang, H., Yin, A., Dong, S., Kuang, Z., Zuza, A. V., et al. (2013). Tectonic development of the northeastern Tibetan Plateau as constrained by high-resolution deep seismic-reflection data. Lithosphere 5, 555–574. doi: 10.1130/l293.1

CrossRef Full Text | Google Scholar

Gold, R. D., Cowgill, E., Wang, X., and Chen, X. (2006). Application of trishear fault-propagation folding to active reverse faults: examples from the Dalong Fault, Gansu Province, NW China. J. Struct. Geol. 28, 200–219. doi: 10.1016/j.jsg.2005.10.006

CrossRef Full Text | Google Scholar

Goode, J. K., Burbank, D. W., and Ormukov, C. (2014). Pliocene-Pleistocene initiation, style, and sequencing of deformation in the central Tien Shan. Tectonics 33, 464–484. doi: 10.1002/2013tc003394

CrossRef Full Text | Google Scholar

Hardy, S., and Allmendinger, R. (2011). Trishear: a review of kinematics, mechanics, and applications. AAPG Memoir. 94, 95–119. doi: 10.1306/13251334M943429

CrossRef Full Text | Google Scholar

Hardy, S., and Poblet, J. (1994). Geometric and numerical model of progressive limb rotation in detachment folds. Geology 22, 371–374.

Google Scholar

Hetzel, R. (2013). Active faulting, mountain growth, and erosion at the margins of the Tibetan Plateau constrained by in situ-produced cosmogenic nuclides. Tectonophysics 582, 1–24. doi: 10.1016/j.tecto.2012.10.027

CrossRef Full Text | Google Scholar

Hetzel, R., Hampel, A., Gebbeken, P., Xu, Q., and Gold, R. D. (2019). A constant slip rate for the western Qilian Shan frontal thrust during the last 200 ka consistent with GPS-derived and geological shortening rates. Earth Planet. Sci. Lett. 509, 100–113. doi: 10.1016/j.epsl.2018.12.032

CrossRef Full Text | Google Scholar

Hetzel, R., Niedermann, S., Tao, M., Kubik, P. W., Ivy-Ochs, S., Gao, B., et al. (2002). Low slip rates and long-term preservation of geomorphic features in Central Asia. Nature 417, 428–432. doi: 10.1038/417428a

PubMed Abstract | CrossRef Full Text | Google Scholar

Hetzel, R., Niedermann, S., Tao, M., Kubik, P. W., and Strecker, M. R. (2006). Climatic versus tectonic control on river incision at the margin of NE Tibet:10Be exposure dating of river terraces at the mountain front of the Qilian Shan. J. Geophys. Res. Earth Surf. 111:F03012. doi: 10.1029/2005jf000352

CrossRef Full Text | Google Scholar

Hetzel, R., Tao, M., Stokes, S., Niedermann, S., Ivy-Ochs, S., Gao, B., et al. (2004). Late Pleistocene/Holocene slip rate of the Zhangye thrust (Qilian Shan, China) and implications for the active growth of the northeastern Tibetan Plateau. Tectonics 23, TC6006.1–TC6006.17. doi: 10.1029/2004tc001653

CrossRef Full Text | Google Scholar

Hu, X., Chen, D., Pan, B., Chen, J., Zhang, J., Chang, J., et al. (2019a). Sedimentary evolution of the foreland basin in the NE Tibetan Plateau and the growth of the Qilian Shan since 7 Ma. Geol. Soc. Am. Bull. 131, 1744–1760. doi: 10.1130/b35106.1

CrossRef Full Text | Google Scholar

Hu, X., Wen, Z., Pan, B., Guo, L., and Cao, X. (2019b). Constraints on deformation kinematics across the Yumu Shan, NE Tibetan Plateau, based on fluvial terraces. Glob. Planet. Chang. 182:103023. doi: 10.1016/j.gloplacha.2019.103023

CrossRef Full Text | Google Scholar

Hu, X., Pan, B., Fan, Y., Wang, J., Hu, Z., Cao, B., et al. (2017). Folded fluvial terraces in a young, actively deforming intramontane basin between the Yumu Shan and the Qilian Shan mountains, NE Tibet. Lithosphere 9, 545–560. doi: 10.1130/l614.1

CrossRef Full Text | Google Scholar

Hu, X., Pan, B., Kirby, E., Gao, H., Hu, Z., Cao, B., et al. (2015). Rates and kinematics of active shortening along the eastern Qilian Shan, China, inferred from deformed fluvial terraces. Tectonics 34, 2478–2493.

Google Scholar

Korschinek, G., Bergmaier, A., Faestermann, T., Gerstmann, U. C., Knie, K., Rugel, G., et al. (2010). A new value for the half-life of ¹⁰Be by heavy-ion elastic recoil detection and liquid scintillation counting. Nuclear Instrum. Methods Phys. Res. Sect. B 268, 187–191. doi: 10.1016/j.nimb.2009.09.020

CrossRef Full Text | Google Scholar

Lavé, J., and Avouac, J. P. (2000). Active folding of fluvial terraces across the Siwaliks Hills, Himalayas of central Nepal. J. Geophys. Res. Solid Earth 105, 5735–5770. doi: 10.1029/1999jb900292

CrossRef Full Text | Google Scholar

Liu, X., Yuan, D., and Su, Q. (2017). Late pleistocene slip rate of the northern Qilian Shan frontal thrust, western Hexi Corridor, China. Terra Nova 29, 238–244. doi: 10.1111/ter.12270

CrossRef Full Text | Google Scholar

Liu, X., Yuan, D., and Su, Q. (2019). Late Pleistocene slip rate on a blind thrust in the western Qilian Shan, NW China. Geomorphology 345:106841. doi: 10.1016/j.geomorph.2019.106841

CrossRef Full Text | Google Scholar

Meyer, B., Tapponnier, P., Bourjot, L., Métivier, F., Gaudemer, Y., Peltzer, G., et al. (1998). Crustal thickening in Gansu-Qinghai, lithospheric mantle subduction, and oblique, strike-slip controlled growth of the Tibet plateau. Geophys. J. Int. 135, 1–47. doi: 10.1046/j.1365-246x.1998.00567.x

CrossRef Full Text | Google Scholar

Mitra, S. (2003). A unified kinematic model for the evolution of detachment folds. J. Struct. Geol. 25, 1659–1673. doi: 10.1016/s0191-8141(02)00198-0

CrossRef Full Text | Google Scholar

Palumbo, L., Hetzel, R., Tao, M., Li, X., and Guo, J. (2009). Deciphering the rate of mountain growth during topographic presteady state: an example from the NE margin of the Tibetan Plateau. Tectonics 28, TC4017.1–TC4017.18. doi: 10.1029/2009tc002455

CrossRef Full Text | Google Scholar

Poblet, J., and Lisle, R. J. (2011). Kinematic evolution and structural styles of fold-and-thrust belts. Geol. Soc. Lond. Spec. Public. 349, 1–24.

Google Scholar

Ren, J., Xu, X., Zhang, S., Ding, R., Liu, H., Liang, O., et al. (2019). Late quaternary slip rates and Holocene paleoearthquakes of the eastern Yumu Shan fault, northeast Tibet: implications for kinematic mechanism and seismic hazard. J. Asian Earth Sci. 176, 42–56. doi: 10.1016/j.jseaes.2019.02.006

CrossRef Full Text | Google Scholar

Scharer, K. M., Burbank, D. W., Chen, J., and Weldon, R. J. (2006). Kinematic models of fluvial terraces over active detachment folds: constraints on the growth mechanism of the Kashi-Atushi fold system, Chinese Tian Shan. Geol. Soc. Am. Bull. 118, 1006–1021. doi: 10.1130/b25835

CrossRef Full Text | Google Scholar

Seong, Y. B., Kang, H. C., Ree, J. H., Choi, J. H., Lai, Z. P., Long, H., et al. (2011). Geomorphic constraints on active mountain growth by the lateral propagation of fault-related folding: a case study on Yumu Shan, NE Tibet. J. Asian Earth Sci. 41, 184–194. doi: 10.1016/j.jseaes.2011.01.015

CrossRef Full Text | Google Scholar

Simoes, M., Avouac, J. P., and Chen, Y. (2007). Slip rates on the Chelungpu and Chushiang thrust faults inferred from a deformed strath terrace along the Dungpuna river, west central Taiwan. J. Geophys. Res. 112:jb004200. doi: 10.1029/2005jb004200

CrossRef Full Text | Google Scholar

Stockmeyer, J. M., Shaw, J. H., Brown, N. D., Rhodes, E. J., Richardson, P. W., Wang, M., et al. (2017). Active thrust sheet deformation over multiple rupture cycles: a quantitative basis for relating terrace folds to fault slip rates. Geol. Soc. Am. Bull. 129, 1337–1356. doi: 10.1130/b31590.1

CrossRef Full Text | Google Scholar

Stone, J. O. (2000). Air pressure and cosmogenic isotope production. J. Geophys. Res. Earth Surf. 105, 23753–23759. doi: 10.1029/2000jb900181

CrossRef Full Text | Google Scholar

Suppe, J. (1983). Geometry and kinematics of fault-bend folding. Am. J. Sci. 283, 684–721. doi: 10.2475/ajs.283.7.684

PubMed Abstract | CrossRef Full Text | Google Scholar

Suppe, J., Connors, C. D., and Zhang, Y. (2004). “Shear fault-bend folding,” in Thrust Tectonics and Hydrocarbon Systems, ed. K. R. McClay (Tulsa, OK: American Association of Petroleum Geologists), 303–323. doi: 10.1306/m82813c17

CrossRef Full Text | Google Scholar

Suppe, J., and Medwedeff, D. A. (1990). Geometry and kinematics of fault-propagation folding. Ecl. Geol. Helvet. 83, 409–454. doi: 10.5169/seals-166595

CrossRef Full Text | Google Scholar

Tapponnier, P., Meyer, B., Avouac, J. P., Peltzer, G., Gaudemer, Y., Shunmin, G., et al. (1990). Active thrusting and folding in the Qilian Shan, and decoupling between upper crust and mantle in northeastern Tibet. Earth Planet. Sci. Lett. 97, 382–403. doi: 10.1016/0012-821x(90)90053-z

CrossRef Full Text | Google Scholar

Thompson, S. C., Weldon, R. J., Rubin, C. M., Abdrakhmatov, K., Molnar, P., and Berger, G. W. (2002). Late Quaternary slip rates across the central Tien Shan, Kyrgyzstan, central Asia. J. Geophys. Res. Solid Earth 107, ETG7-1–ETG7-32. doi: 10.1029/2001jb000596

CrossRef Full Text | Google Scholar

Wang, H., Gao, R., Yin, A., Xiong, X., Kuang, C., and Li, W. (2013). Deep structure geometry features of haiyuan fault and deformation of the crust revealed by deep seismic reflection profiling. Chin. J. Geophys. 55, 3902–3909. doi: 10.6038/j.issn.0001-5733.2012.12.003

CrossRef Full Text | Google Scholar

Wang, Y., Oskin, M. E., Zhang, H., Li, Y., Hu, X., and Lei, J. (2020). Deducing crustal-scale reverse-fault geometry and slip distribution from folded river terraces, qilian shan, china. Tectonics 39:e2019TC005901. doi: 10.1029/2019TC005901

CrossRef Full Text | Google Scholar

Wang, Y., Zheng, D., Pang, J., Zhang, H., Wang, W., Yu, J., et al. (2018). Using slope-area and apatite fission track analysis to decipher the rock uplift pattern of the Yumu Shan: new insights into the growth of the NE Tibetan Plateau. Geomorphology 308, 118–128. doi: 10.1016/j.geomorph.2018.02.006

CrossRef Full Text | Google Scholar

Whipple, K. X., Shirzaei, M., Hodges, K. V., and Ramon Arrowsmith, J. (2016). Active shortening within the Himalayan orogenic wedge implied by the 2015 Gorkha earthquake. Nat. Geosci. 9, 711–716. doi: 10.1038/ngeo2797

CrossRef Full Text | Google Scholar

Wickham, J. (1995). Fault displacement-gradient folds and the structure at Lost Hills, California (U.S.A.). J. Struct. Geol. 17, 1293–1302. doi: 10.1016/0191-8141(95)00029-d

CrossRef Full Text | Google Scholar

Wilson, L. F., Pazzaglia, F. J., and Anastasio, D. J. (2009). A fluvial record of active fault-propagation folding, Salsomaggiore anticline, northern Apennines, Italy. J. Geophys. Res. 114:984. doi: 10.1029/2008jb005984

CrossRef Full Text | Google Scholar

Wu, L., Lin, X., Cowgill, E., Xiao, A., Cheng, X., Chen, H., et al. (2019). Middle Miocene reorganization of the Altyn Tagh fault system, northern Tibetan Plateau. Geol. Soc. Am. Bull. 131, 1157–1178. doi: 10.1130/b31875.1

CrossRef Full Text | Google Scholar

Xiong, J., Li, Y., Zhong, Y., Lu, H., Lei, J., Xin, W., et al. (2017). Latest pleistocene to holocene thrusting recorded by a flight of strath terraces in the Eastern Qilian Shan, NE Tibetan Plateau. Tectonics 36, 2973–2986. doi: 10.1002/2017tc004648

CrossRef Full Text | Google Scholar

Yang, H., Yang, X., Huang, W., Li, A., Hu, Z., Huang, X., et al. (2020). 10Be and OSL dating of Pleistocene fluvial terraces along the Hongshuiba River: constraints on tectonic and climatic drivers for fluvial downcutting across the NE Tibetan Plateau margin, China. Geomorphology 348:106884. doi: 10.1016/j.geomorph.2019.106884

CrossRef Full Text | Google Scholar

Yang, H., Yang, X., Huang, X., Li, A., Huang, W., and Zhang, L. (2018). New constraints on slip rates of the Fodongmiao-Hongyazi fault in the Northern Qilian Shan, NE Tibet, from the 10 Be exposure dating of offset terraces. J. Asian Earth Sci. 151, 131–147. doi: 10.1016/j.jseaes.2017.10.034

CrossRef Full Text | Google Scholar

Yang, H., Yang, X., Zhan, Y., Cunningham, D., Zhao, L., Sun, X., et al. (2019). Quaternary Activity of the Beihewan Fault in the Southeastern Beishan Wrench Belt, western China: implications for crustal stability and intraplate earthquake hazards north of Tibet. J. Geophys. Res. Solid Earth 124, 13286–13309. doi: 10.1029/2018jb017209

CrossRef Full Text | Google Scholar

Yang, S. (2007). The Thrust Belt Structure and the Gas-Oil Bearing Perspective of the North Qilian Shan [in Chinese]. Beijing: Science Press.

Google Scholar

Yuan, D., Ge, W., Chen, Z., Li, C., Wang, Z., Zhang, H., et al. (2013). The growth of northeastern Tibet and its relevance to large-scale continental geodynamics: a review of recent studies. Tectonics 32, 1358–1370. doi: 10.1002/tect.20081

CrossRef Full Text | Google Scholar

Zhao, Z., Granger, D. E., Chen, Y., Shu, Q., Liu, G., Zhang, M., et al. (2017). Cosmogenic nuclide burial dating of an alluvial conglomerate sequence: an example from the Hexi Corridor, NE Tibetan Plateau. Q. Geochronol. 39, 68–78. doi: 10.1016/j.quageo.2017.02.007

CrossRef Full Text | Google Scholar

Zheng, D., Clark, M. K., Zhang, P., Zheng, W., and Farley, K. A. (2010). Erosion, fault initiation and topographic growth of the North Qilian Shan (northern Tibetan Plateau). Geosphere 6, 937–941. doi: 10.1130/ges00523.1

CrossRef Full Text | Google Scholar

Zheng, W., Zhang, P., He, W., Yuan, D., Shao, Y., Zheng, D., et al. (2013). Transformation of displacement between strike-slip and crustal shortening in the northern margin of the Tibetan Plateau: evidence from decadal GPS measurements and late Quaternary slip rates on faults. Tectonophysics 584, 267–280. doi: 10.1016/j.tecto.2012.01.006

CrossRef Full Text | Google Scholar

Zhong, Y., Xiong, J., Li, Y., Zheng, W., Zhang, P., and Lu, H. (2020). Constraining late quaternary crustal shortening in the eastern Qilian Shan from deformed river terraces. J. Geophys. Res. Solid Earth 125:e2020JB020631. doi: 10.1029/2020JB020631

CrossRef Full Text | Google Scholar

Zhou, S., Li, J., and Zhang, S. (2002). Quaternary glaciation of the Bailang River Valley, Qilian Shan. Q. Intern. 97–98, 103–110.

Google Scholar

Zuza, A. V., Cheng, X., and Yin, A. (2016). Testing models of Tibetan Plateau formation with Cenozoic shortening estimates across the Qilian Shan-Nan Shan thrust belt. Geosphere 12, 501–532. doi: 10.1130/ges01254.1

CrossRef Full Text | Google Scholar