Calculation of Deflection of Vertical and Gravity Anomalies Over the South China Sea Derived from ICESat-2 Data

Introduction

Deflection of vertical (DOV), which can be derived from sea surface height (SSH) measurements, is an important Earth gravity field parameter. It is widely used to calculate marine gravity anomalies based on the inverse Vening Meinesz formula and a fast Fourier transform (FFT) technique (Hwang and Hsu, 2003; Wang and Lu, 2008; Zhu et al., 2020). The achieved accuracies of DOV and gravity field measurements have a mutually beneficial symbiotic relationship (Hwang et al., 1998). There are several methods for measuring DOV using satellite altimetry data (Peng and Xia, 2004), and significant progress has been made in obtaining the directional components of DOV with higher accuracy and finer spatial resolution. However, there is still room for improvement. The accuracy of the obtained directional DOV components at gridding points is limited by the spatial distribution density of crossover points (Sandwell, 1992). Subsequently, the along-track vertical deflections solution was used to obtain gridded deflection of vertical (GDOV), but inconsistent estimated uncertainties were found between the meridional and prime components (Sandwell and Smith, 1997; Hwan et al., 2002). Previous studies have shown that the orbital inclination of the altimetry satellite will affect the accuracy of the directional component of DOV and that using a design with a low orbital inclination could help to improve the calculation of the prime component (Guo et al., 2016; Zhang et al., 2017; Wan et al., 2020a). However, the accuracy of the meridional component has still prevailed in the low-latitude sea for most cases of conventional satellite altimeter missions. Since the distribution of ground trajectories of low-orbital-inclination satellites in low-latitude waters still tends to be meridional, the sampling interval and application of observations in the cross-track direction of altimetry missions constrain the current solutions of DOV and the inversion of the ocean gravity field.

With the continuous launch of new satellites in recent years, different types of SSH observations have emerged (Zhang, 2017). Among these new types of observations, the Interferometric Radar Altimeter (InRA) model altimetry mission observations are promising for improving the accuracy of determining the prime component of the DOV. Wan et al. (2020b) used simulated data to show that, with InRA, the accuracy of the prime component solution can be consistent with the meridional component. However, these results still need to be verified practically using the National Aeronautics and Space Administration (NASA)’s Surface Water and Ocean Topography (SWOT) mission, which is due for launch in 2022. The SWOT mission will provide a new approach to solving the problem of the difference in the accuracy of the directional component.

The NASA Ice, Cloud, and Elevation Satellite-2 (often known as ICESat-2 but hereafter referred to as IS-2 for brevity), the orbital inclination is 92°, first along the flight direction using three groups of synchronous observation for reflecting surface height information. The sampling resolution of IS-2 along its trajectory is 0.7 m, which is a great improvement in the along-track spatial resolution compared with traditional radar altimetry missions (Markus et al., 2017). The simultaneous observation of three pairs in the cross-track aspect greatly reduces the influence of time-varying sea-surface topography between cross-track data, as well as the near-horizontal cross-track azimuth, so that more prime component information can be obtained. IS-2 is expected to significantly improve the accuracy of the directional components of DOV measurements.

In this study, the South China Sea (SCS; 0°–23°N, 103°–120°E) is used as the research area and IS-2 observation data is used for DOV measurements. Observation data from the Jason-2 satellite is used as a reference and 2159-order data with a spatial resolution of 2′ × 2′ (XGM 2019e_2159; eXperimental Gravity Field Model, hereafter referred to as XGM2019) (Zingerle et al., 2019; Zingerle et al., 2020) is used as the validation model to analyze the accuracy of the sub-section results in this study. Cross-analysis is also performed for the accuracy of the IS-2 SSH. Then, the along-track and cross-track deflection of vertical (ATDOV and CTDOV) are calculated. The calculation and analysis of DOV aim to provide a reference for improving the prime component of DOV. Finally, gravity anomaly data for the SCS is obtained by inversion using the directional components of DOV, and it is compared with the XGM2019 model and shipborne gravity measurements to verify the accuracy level of the inversion.

Data and Methodology

Study Area

The SCS is a deep marginal sea with many coastal islands; it has an undulating topography and an average water depth of about 1,212 m (Li et al., 2001). It has been a major research area for scholars worldwide for many years (Shaw and Chao, 1994; Jilan, 2004; Huang et al., 2006; Andersen et al., 2014; Zhu et al., 2019; Li et al., 2020). However, it is known that the inversion results of global models are not ideal in coastal areas and around island groups because the quality of satellite-derived gravity data decreases close to the coast (Hwang et al., 2006; Liu et al., 2015; Zhang et al., 2017; Albayrak et al., 2020).

IS-2 Data Introduction

The IS-2 mission has provided measurements that enable to estimate of the heights of ice sheets and sea-ice thickness (Kwok and Markus, 2017; Zhu et al., 2018). Despite it not being a formal project requirement (Abdalati et al., 2010), the IS-2 project office and science team are also dedicated to providing ocean-height data that are useful to the scientific community. The main instrument onboard the IS-2 is the Advanced Topographic Laser Altimeter System (ATLAS). This instrument uses a 532 nm (green) laser to actively map surface elevations.

The mapping between the strong and weak beams of ATLAS and their relative positions on the ground depends on the orientation (yaw) of the IS-2 observatory, which changes. The ATLAS laser emits six beams and is divided into three pairs. Each pair consists of strong and weak energy beams with an energy ratio of 4:1, respectively. As IS-2 orbits the Earth, these trace out six ground tracks that are typically about 14 m wide. Six ground tracks are numbered according to the left-to-right direction of the laser spot number that generates it, with ground track 1L (GT1L),1R (GT1R), 2L (GT2L), 2R (GT2R), 3L (GT3L), and 3R (GT3R). IS-2 will orbit with a yaw angle of 2° during nominal operations, setting left/right beam separation at ∼2.5 km in the along-track direction and beams within a pair by ∼90 m in the cross-track direction (Smith et al., 2019). The data is organized by ground track, with ground tracks 1L and 1R forming pair one, ground tracks 2L and 2R forming pair two, and ground tracks 3L and 3R forming pair three. The pair tracks are ∼3.3 km apart in the across-track direction (Neumann et al., 2019).

The yaw of IS-2 is changed twice a year to maximize the illumination of its solar panels. When the ATLAS instrument is traveling along the +x coordinate in the forward orientation, the weak beam leads the strong beam, and the weak beam is located at the left edge of the beam pattern. When the ATLAS instrument is traveling along the −x coordinate in the backward orientation, the strong beam leads the weak beam, and the strong beam is located at the left edge of the beam pattern. The data book shows that ATLAS performed its first yaw flip on December 28, 2018, placing the spacecraft in the backward orientation. The exact timing of subsequent flips is shown in the datasheets, and this is crucial for reading the strong-beam data in the six beams (Morison et al., 2020).

The IS-2 mission produces along-track geophysical products over select surface types that include land ice (ATL06), sea ice (ATL07), land/vegetation (ATL08), atmosphere (ATL09), oceans (ATL12), and inland water (ATL13). The ATL03 data is a geolocated photon-cloud product that serves as the input data for each of the aforementioned higher-level data products (Neuenschwander and Pitts, 2019). The ATL12 algorithm was developed specifically for the extraction of terrain and ocean heights from the ATL03 photon clouds (Neumann et al., 2018) and the background photon rate from ATL09. The ATL12 geophysical data for one photon is generated by approximately 100 photons (segment length 70 m) according to the ATL12 adaptive algorithm. Based on the distribution of signal photons, this algorithm estimates the ground- and sea-surface elevations and then subsequently; labels the individual photons as either data or noise. Currently, the open ocean has low reflectance in the visible spectrum (Moses et al., 2015), and the ocean signal rates are 0–4 per laser shot, similar to overland.

The ATL12 data product also includes flags that can improve the interpretability of the height estimates. The ATL12 data includes dynamic atmosphere correction, which is derived from ATL09 and indicates possible scattering in the atmosphere. Furthermore, when calculating the freeboard of sea ice, the accuracy of the water-surface height can be approximated by the inter-ice water (Friedl et al., 2010). The SSH measurements take into account ocean tide correction, sea state deviation, sea breeze, and other factors.

It is worth stating that in a pure ocean region, only the strong beams are active because of the low reflectance of the open ocean in the visible spectrum. In marginal ice zones and coastal zone overlap regions, the three weak beams are also valid, and these are processed in the same way as the strong beams and exported together with the strong-beam results as part of the ATL12 ocean product (Morison et al., 2020).

Jason-2 Data Introduction

The Jason-2 calibration experiment was successfully launched on 20 June 2008 as a continuation of the TOPEX/Poseidon and Jason-1 altimeter missions, in cooperation with Centre National d’Études Spatiales, the European Organization for the Exploitation of Meteorological Satellites, NASA, and the National Oceanic and Atmospheric Administration (Fu et al., 1994; Chander et al., 2012). Data from the Jason-2 satellite is often used by international scholars for high-quality comparisons with other satellite measurements due to the outstanding quality of its sea-surface data (Yang et al., 2016; Liu et al., 2020; Sun et al., 2021).

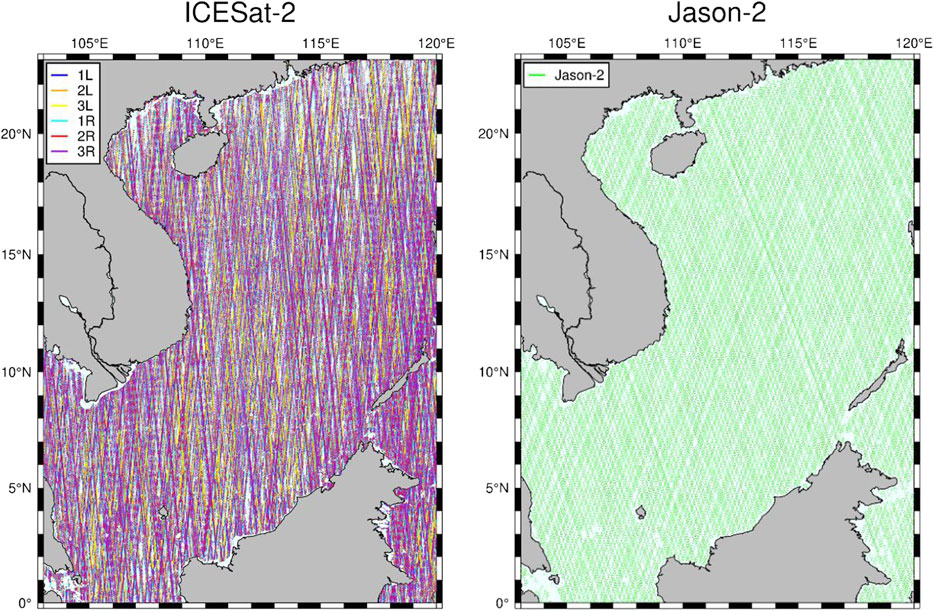
In our analysis, we combine these indices to represent SSH, and because the study area includes both open ocean and nearshore, we do not consider strong and weak beam effects. The IS-2 data used in this study are obtained through the National Snow and Ice Data Center, 2019 and are from release 003 (Neuenschwander et al., 2020a; Neuenschwander et al., 2020b), with the time series as 2018/10/13 to 2020/07/16 (strong beam including left and right). The Jason-2 SSH data used for validation have a repeat orbital period of 10 days, with the time series 2018/10/05 to 2019/02/16 and 2019/05/22 to 2019/10/01, respectively. The ground trajectories of both sets of data in the test area are shown in Figure 1.

FIGURE 1

FIGURE 1. Trajectories of IS-2 (left) and Jason-2 (right) over the SCS.

Along-Trajectory DOV

The computing methods mean sea-surface height (MSSH) and gravity anomalies in this paper use DOV as the data type. By definition, the ATDOV is the gradient of the geoid but with the opposite sign (Hwang et al., 2002). The great advantage of this method is that it is only based on geoid gradients computed along with the satellite profiles. Therefore, if there is a local bias between two arcs, it will not be affected the results, all long-wavelength errors have very small effects. As Sandwell (1992) showed, the orbit error, which is mostly of a long-wavelength nature, has a negligible effect, and no cross-over adjustment is needed.

We obtain the spherical distance s between the points p and q with the reference ellipsoid as the coordinate system according to the spherical distance formula:

$\epsilon =-\frac{\left(N_q-N_p\right)}{s}(1)$

where $\mathit{ϵ}$ is the along-trajectory DOV and N is the geoid, which is a surface function.

Obtaining the GDOV Directional Component

Based on the correlation between the along-trajectory DOV and the directional component of the DOV (Hwang et al., 2002), the relationship between $\mathit{\epsilon }$ along the specified direction and its meridian component $\xi$ and prime component $\eta$ is:

$\epsilon =\xi \cos \alpha +\eta \sin \alpha (2)$

where α is the azimuth of the altimetric point along the ground track direction, which can be calculated using the position information of adjacent altimetric points according to

$\tan \alpha =\frac{\cos {\phi }_q\sin \left({\lambda }_q-{\lambda }_p\right)}{\cos {\phi }_p\sin {\phi }_q-\sin {\phi }_p\cos {\phi }_q\cos \left({\lambda }_q-{\lambda }_p\right)}(3)$

where ${\phi }_p$,${\lambda }_p$ and ${\phi }_q$, ${\lambda }_q$ are the geodetic latitudes and longitudes of two adjacent points p and q, respectively, and point p is a point along the track of point q.

To calculate the GDOV components $\left(\begin{array}{cc}\overline{\xi }& \overline{\eta }\end{array}\right)$ from the observation point’s ATDOV $\mathit{\epsilon }$, the observation equation is given as:

${\epsilon }_i+v_i=\overline{\xi }\cos {\alpha }_i+\overline{\eta }\sin {\alpha }_i, i=1,···,n(4)$

where: $n$ is the number of high observation points along the track in the grid and its adjacent sea area; and $v_i$, ${\alpha }_i$, and ${\mathit{\epsilon }}_i$ are the residuals, azimuths, and DOVs along the specified direction for observation point i, respectively. This can be written in matrix form as:

$\mathbf{V}=\mathbf{A}\mathbf{X}-\mathbf{L}(5)$

where $\mathbf{V}={\left(v_1 \cdots v_n\right)}^{\text{T}}$, $\mathbf{X}=\left(\begin{array}{c}\overline{\xi }\\ \overline{\eta }\end{array}\right)$, $\mathbf{A}=\left[\begin{array}{cc}\cos {\alpha }_1& \sin {\alpha }_1\\ ⋮& ⋮\\ \cos {\alpha }_n& \sin {\alpha }_n\end{array}\right]$, and $\mathbf{L}={\left({\epsilon }_1\cdots {\epsilon }_n\right)}^T$

Using the indirect leveling method, the solution to this can be obtained using:

$\mathbf{X} ={\left({\mathbf{A}}^{\text{T}}\mathbf{P}\mathbf{A}\right)}^{-1}{\mathbf{A}}^{\text{T}}\mathbf{P}\mathbf{L}(6)$

Where p is the weight array of observations, $P_i=1/d_i$, where $d_i$ is the distance from the observation point i to the grid point.

Obtaining the ATDOV Directional Components

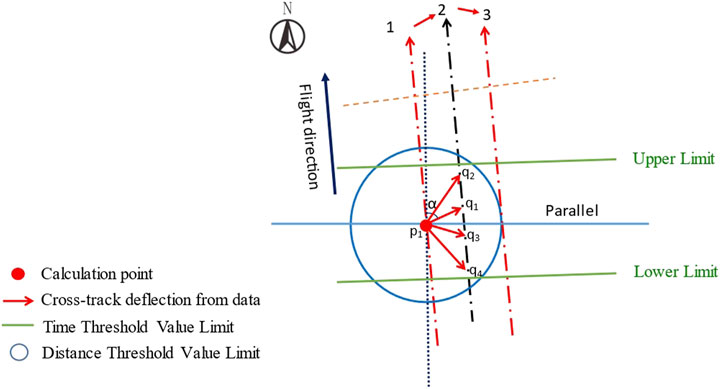
Scholars have solved for the directional components of the DOV at the intersections or grid points (Olgiati et al., 1995; Sandwell and Smith 1997; Hwang et al., 1998). The former approximates along-track points and cross-track points as ascending and descending arcs, the latter approximates along-track points as grid points and cross-track points as points calculated within the grid. Since in the subsequent solution, we have to compare the accuracy of the ATDOV directional components with the GDOV directional component, the latter method is proposed for calculating the ATDOV directional components in this study. The GDOV formula in Section Obtaining the GDOV Directional Component is used as the theoretical formula, and the distance between two points and the time threshold is set as constraints. There are four methods to distinguish the number of beams being computed and the associated directions, as shown in Figure 2.

FIGURE 2

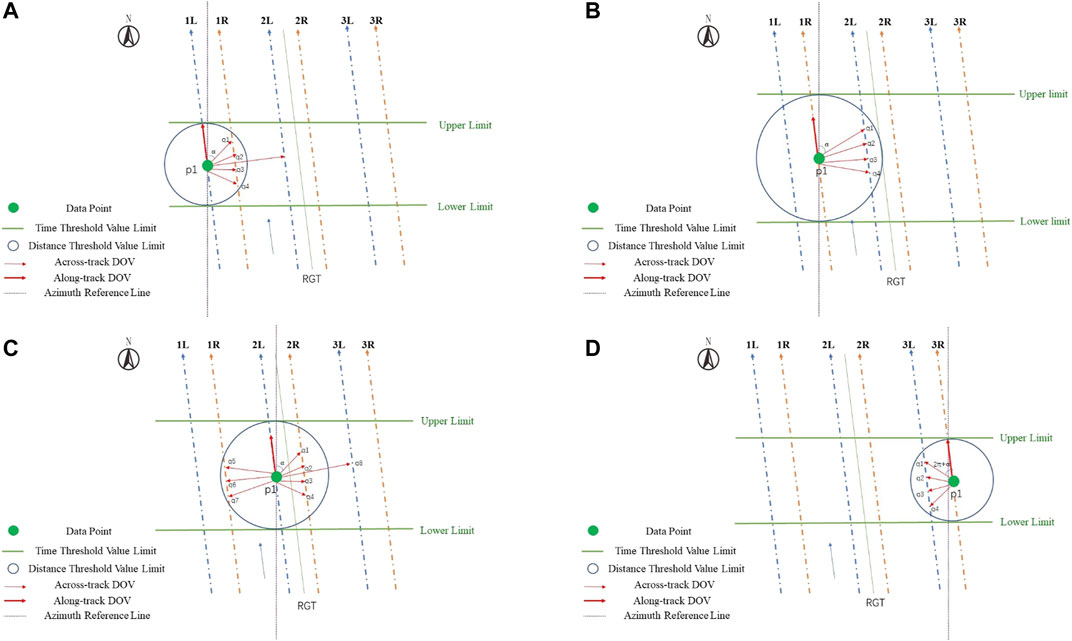
FIGURE 2. (A) Joint calculation between the same group of beams (left-to-right), (B) joint calculation between different groups of beams (left-to-right or right-to-left), (C) joint calculation between different groups and the same group of beams (left-to-right and right-to-left), (D) joint calculation between the same group of beams (right-to-left).

Obtaining Gravity Anomaly Data

The advantage of using the DOV method to obtain gravity anomaly data is that calculating the SSH difference between two points is essentially a high-pass filtering process (Wang and Wang, 2001), in which almost all the effects of long-wave errors are deducted, such as orbital errors, atmospheric propagation errors, tidal errors, the effects of sea surface steady-state topography, the effects of ocean circulation, and the effects of instrument errors, So as to reducing the requirements for pre-processing of altimetric satellite data.

Gravity anomaly data can be derived from DOV with the inverse Vening Meinesz formula (Hwang et al., 1998). Based on the grid data of the meridional component $\xi$ and the prime component $\eta$ of DOV, the formula for calculating the gravity anomaly $\Delta g$ using the inverse Vening Meinesz formula method through the 1-D fast Fourier transform (FFT) technique (Haagmans, 1993) can be expressed as

$\Delta g_{{\phi }_p}\left({\lambda }_p\right)=\frac{{\gamma }_0\Delta \varphi \Delta \lambda }{4\pi }{F}_1^{-1}{\displaystyle \sum }_{{\varphi }_q={\varphi }_1}^{{\varphi }_2}\left\{\begin{array}{c}{F}_1\left[H^{\prime }\left(\Delta {\lambda }_{qp}\right)\cos {\alpha }_{qp}\right]F_1\left({\xi }_{\cos }\right)+\\ F_1\left[H^{\prime }\left(\Delta {\lambda }_{qp}\right)\sin {\alpha }_{qp}\right]F_1\left({\eta }_{\cos }\right)\end{array}\right\}(7)$

where: p is the “fixed” point and q is the “dummy” or “running” point; ${\varphi }_q$ is the latitude of the parallel along which gravity anomalies are to be computed; ${\phi }_1$ and ${\phi }_2$ are the latitudes of the southernmost and northernmost parallels; $\text{Δ}\varphi$ and $\text{Δ}\lambda$ are the grid intervals in latitude and longitude; ${\lambda }_{qp}$ is the difference in longitude; and $F_1$ is the 1-D FFT. We introduce a kernel function $H^{\prime }$, which is defined as

$H^{\prime }=\frac{dH}{d{\psi }_{pq}}=-\frac{\cos \frac{{\psi }_{pq}}{2}}{2{\text{sin}}^2\frac{{\psi }_{pq}}{2}}+\frac{\cos \frac{{\psi }_{pq}}{2}\left(3+2\sin \frac{{\psi }_{pq}}{2}\right)}{2\sin \frac{{\psi }_{pq}}{2}\left(1+\sin \frac{{\psi }_{pq}}{2}\right)}(8)$

where ${\psi }_{pq}$ is the spherical distance between points p and q on the unit sphere, and this spherical distance can be found using

${\sin }^2\left(\frac{{\psi }_{pq}}{2}\right)={\sin }^2\left(\frac{\Delta {\phi }_{qp}}{2}\right)+{\sin }^2\left(\frac{\Delta {\lambda }_{qp}}{2}\right)\cos {\phi }_q\cos {\phi }_p(9)$

where $\text{Δ}{\phi }_{qp}={\phi }_q-{\phi }_p$ and $\text{Δ}{\lambda }_{qp}={\lambda }_q-{\lambda }_p$. The azimuth equation is then

$\tan {\alpha }_{qp}=\frac{-\cos {\phi }_p\sin \left(\Delta {\lambda }_{qp}\right)}{-\sin \left({\phi }_q-{\phi }_p\right)+2\sin {\phi }_q\cos {\phi }_p{\sin }^2\left(\frac{\Delta {\lambda }_{qp}}{2}\right)} (10)$

Initial Assessment of IS-2 Measurement Results

In this paper, we focus on verifying the ability of the IS-2 multibeam data to enhance the accuracy level of the directional component of DOV. However, we first need to verify the data performance of IS-2. Measurements from altimetry missions are typically validated on regional to global scales using a relative calibration method based on inter-mission as well as intra-mission statistical analysis (Zhang et al., 2018). In reality, however, the smaller variations in within-mission situations indicate better stability and internal consistency, and accuracy of the airborne instruments, while the crossover variations between multiple missions are more reliable for assessing the distance accuracy between altimetry measurements (Wang and Wang, 2001). Therefore, we plan to first evaluate the performance of IS-2 by analyzing cross-differences with another typical high-accuracy mission. Inter-mission cross-differences were also considered when evaluating the intra-mission accuracy (Wang et al., 2021).

We used Jason-2 pulsed radar altimetry satellite data with a repeated orbital period of 10 days for comparison with the IS-2 laser altimetry data. The repetitive orbital period of Jason-2 is an exact integer fraction of the 91-days orbital period of IS-2. Therefore, it is possible to compare the accuracy of pulsed radar altimetry satellites and laser altimetry satellites in calculating the ocean surface height.

In this study, the IS-2 SSH data were obtained directly from the ATL12 SSH data product, and the Jason-2 SSH data were acquired by adding different geophysical corrections including dry- and wet-troposphere path delays, ionospheric corrections, ocean state bias, ocean tides, solid earth tides, polar tides, high-frequency wind effects, and inverted barometer corrections. All of these corrections were provided separately for the Jason-2 SSH data, and no additional update procedures were applied. Furthermore, the incompletely constrained time-varying effects of the ocean surface inevitably affect the internal and intermittent cross-sectional differences. Therefore, cross-differences with and without time constraints need to be considered separately in the statistical process. To ensure the overlap of measurement times, the Jason-2 dataset, which has a subordinate relationship with the IS-2 time series, was selected as the interval validation data. The IS-2/Jason-2 crossover points were determined by fitting the ground trajectories of the sample data, and the crossover points were defined as the locations where each satellite intersected its ground position. At the same time, the intermittent intersection points were defined as the locations where IS-2 and Jason-2 crossed the same sea-surface position.

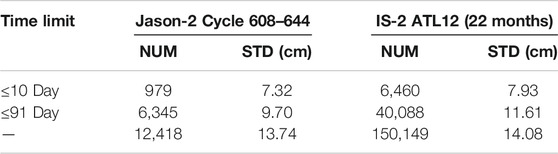
The minimum, maximum, average, number of crossover points (NUM), and standard deviation (STD) were obtained by calculating the crossover differences between the corresponding ascending and descending paths on the ocean surface with and without time limits, depending on the calculated positions of the crossover points. The specific results are presented in Tables 1, 2 and 3.

TABLE 1

TABLE 1. Statistical information of crossover differences under intra-mission situations.

TABLE 2

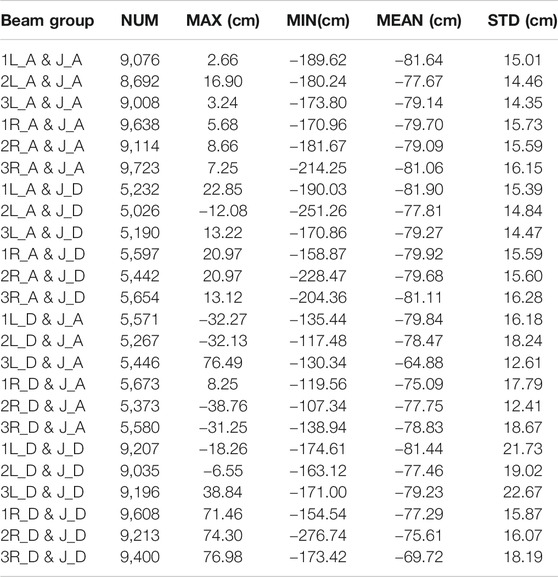
TABLE 2. Statistical information of crossover differences under intermission situation (“_A” and “_D” denote ascending and descending passes, J indicates Jason, and 1/2/3 and L/R represent the corresponding IS-2 beams).

TABLE 3

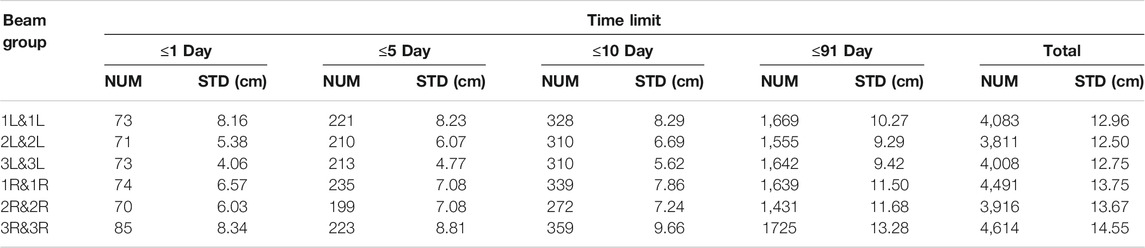
TABLE 3. Statistical information of crossover differences under the IS-2 six beams in the intra-mission situation (“L” and “R” denote the left and right beams, respectively).

Taking into account the effect of time-varying sea-surface topography, to verify the overall IS-2 SSH accuracy, see Table 1. The orbital periods of 10 and 91 days and the unrestricted time of the two satellites are chosen as the time interval of the intersection cross difference, respectively. We can conclude from Table 1 that: 1. IS-2 provides more information for the crossover point at the same time interval due to the synchronous observation of the six beams of IS-2. the discrepancy STD of the IS-2 SSH is somewhat larger, and this is because the wave effect, especially from wind-driven waves, is generally smoothed out at a footprint of about 2 km. For a 70-m along-track measurement (100 adjacent laser pulses), the wave effect is still significant.

The inter-mission crossover analysis was executed four times, and the resulting statistical information is listed in Table 2. According to the crossover analysis of the intra-mission or inter-mission situations, the IS-2 data is valid but has slightly worse performance than Jason-2. Also, the large fluctuations in the mean values of IS-2 and Jason-2 SSH are due to the different reference ellipsoids chosen by IS-2 and Jason-2 which are the WGS84 ellipsoid and T/P ellipsoid, and there is a vertical difference of about 0.7 m between the two.

We know that IS-2 completes one circle of the Earth in about 1.5 h, so there are many crossings of the same location on the ground in a single day. We assessed the accuracy of SSH measurements for each of the six beams based on the overall accuracy of the IS-2 data obtained in Table 1. The time intervals were chosen as 1 day, 5, 10, and 91 days, respectively. Among these intervals, the purpose of the 10-days interval was to compare the SSH measurement accuracy of Jason-2 with a repeated orbital period of 10 days. The results in Table 3 show that the accuracies of the SSH data from the six beams are similar.

The accuracy results we established to be reliable from the perspective of verifying the precision level of IS-2 in the horizontal and vertical directions of SSH by Smith et al. (2020) at Greenland Island. This validation initially implies that IS-2 is capable of investigating DOV due to its new data coverage and reliable range precision.

Numerical and Experimental DOV Direction Component

Along Trajectories DOV

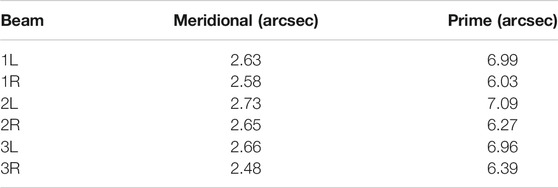
According to the solution formula for the DOV directional component given by (Hwang et al., 1998), we know that the ATDOV needs to be obtained first in the process of obtaining the DOV directional component using the SSH calculation. The validation results of the ATDOV calculations are shown in Table 4.

TABLE 4

TABLE 4. Statistical information of IS-2 ATVD.

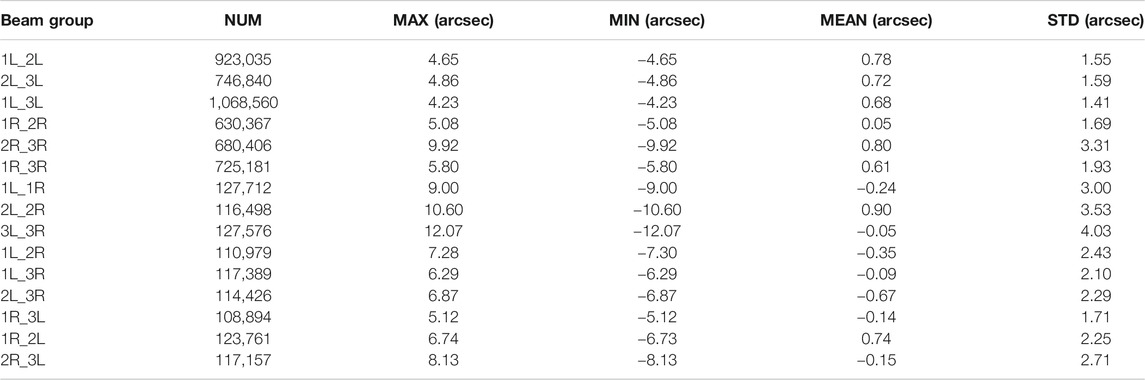
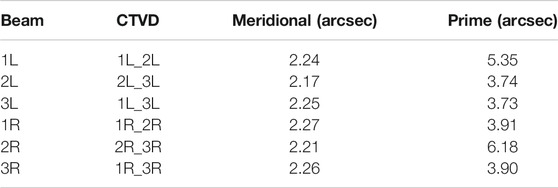
Figure 3 shows a diagram of the method used for calculating the CTDOV which includes the starting beam 1 and the calculated beam 2. The obtained CTDOV is a data point on the calculated beam 2 which will result in a large number of duplicate CTDOV points if a threshold range is not added. Therefore, in this paper, we used time and distance thresholds to limit the number of CTDOV points calculated. The CTDOV for the coupling between the 15 groups of six beams is shown in Table 5.

FIGURE 3

FIGURE 3. Calculation of the CTVD.

TABLE 5

TABLE 5. Statistical information of IS-2 CTVD.

Tables 4, 5 show the results of the calculations of ATDOV and CTDOV based on the IS-2 data. It can be seen that, during the accuracy verification of ATDOV with the XGM2019 model, the results from the middle pair are significantly better than those from the other two pairs, and the data from the other two pairs set tend to be smooth and without large fluctuations about 1.4″. For the calculation of CTDOV, to prevent a situation, in which two beams appear to be solved repeatedly, we obtained a two-by-two solution for the six beams according to the principle of calculating from left to right. From Table 5, we can see that the solving accuracy of the CTDOV obtained from the left and right beam solution is the worst. This is because, regardless of whether the IS-2 flight direction is forward (+x) or backward (−x), the left and right beams include strong and weak photons, and the along-track distance between these two beams far exceeds the theoretical value of 2.5 km due to the severe missing condition of the weak photons in the open sea (Morison et al., 2020). In addition, although we know that the IS-2 intermediate beam group data quality is superior, the minimum number of data points along the track has a large impact on the calculation of the CTDOV. Finally, we can draw conclusion that among the 15 sets of CTDOV data, there are six with similar accuracy to the ATDOV verification accuracy (1.4″), and most of these are values calculated from same-side beams. This confirms the reliability of the results of the CTDOV solution.

DOV Directional Component

GDOV Directional Component

In this study, the grid resolution of the GDOV is limited by the number of data points along the track and the study area. By analyzing the distance along-track of IS-2, the average along-track sampling interval of ATL12 is about 3–4 km by distance analysis, and the corresponding grid resolution is about 2 min. We, therefore, determined that the 2-min grid resolution data would be used as the comparison data for the ATDOV directional components from IS-2. Table 6 shows the validation accuracy of the GDOV directional components of the six beams with the XGM2019 model after removing the coarse difference data by the triple standard-deviation method.

TABLE 6

TABLE 6. Statistical information of 2-min GVD directional component.

The above two sets of data make it clear that the accuracy of the prime component of DOV is lower than that of the meridional component of DOV at the grid points calculated directly from ATDOV. This provides a basis for the DOV directional-component problem we proposed in the introduction.

ATDOV Directional Component

After verifying the accuracy of the ATDOV and CTDOV, we provide a basis for solving the ATDOV directional components. Combining the calculation method for the DOV directional component at the along-track points using the joint ATDOV and CTDOV given in Figure 2, we examined different combinations of the six beams to calculate the DOV directional components at the along-track points. The prime and meridional components were then checked against the XGM2019 model, as shown in Table 7.

TABLE 7

TABLE 7. Statistical information of ATVD directional component.

The comparison in Table 7 shows that the meridional component of the six IS-2 beams is similar to the accuracy of the meridional component at the grid points, and the accuracy of the prime component is greatly improved in the solution of the directional component of ATDOV. In addition, we found anomalies in the calculated ATDOV directional component values for the IS-2 1L beam combined with the cross-track 1L_2L, and the 2R beam combined with the cross-track 2R_3R. Therefore, the data from the 1L and 2R beams needed to be recalculated. Previously, we proposed that the left and right beam solutions reduce the computational accuracy, so we neglected the accuracy of the joint approach of Figures 2A,D in the process of solving the CTDOV. The approach is given in Figures 2B,C was used in the subsequent solution (see Table 8). The accuracy of the recalculated 2L and 3R beams is significantly improved, and the beams with superior accuracy in the CTDOV calculation were selected as the joint calculation data.

TABLE 8

TABLE 8. Statistical information of recalculation ATVD prime components.

Gravity Anomalies

In the previous section, we verified the accuracy of the GDOV directional components by using the ATDOV directional components and concluded that the accuracy of the latter component in the prime direction was improved substantially, but its meridional component was reduced. In this section, we adopt the inverse Vening Meinesz formula (1D-FFT) method introduced by Hwang et al. (1998) to calculate the gravity anomaly. Previously, we solved the gravity anomaly by using the Laplace equation method (Zhang et al., 2020), but the ICESat-2 slope data in the cross-track direction could not be reasonably applied to the calculation procedure. According to the inverse Vening Meinesz formula (1D-FFT) method, we first gridded the ATDOV directional components of the six beams into the GDOV directional component of 2 min. However, before that, it is necessary to check whether the distance-weighting method used to grid the ATDOV directional components is reliable, by matching with the XGM2019 model, to verify the GDOV directional component of 2 min, and the results are shown in Table 9.

TABLE 9

TABLE 9. Statistical information of ATVD directional component after gridding.

In Table 9, we can see that the accuracy of the GDOV directional components based on the distance-weighting method is similar to that in Table 6, which is better than the single-beam GDOV directional component. Then, we applied the WGS84 reference ellipsoid as the marine geodetic datum and used the remove–compute–restore technique to subtract the corresponding 2190-order EGM2008 model reference geoid relief and sea-surface topography from the MSSH obtained from the satellite altimetry data so as to obtain the remaining geoid relief values. The remaining feature relief values were used as input data for inversion of the SCS gravity anomaly according to Eqs. 1–7, and the results were verified by using the National Center for Environmental Information (NCEI) shipborne gravity measurements and the XGM2019 gravity field model. A comparison of the inverse gravity anomaly with the XGM2019 model gravity anomaly is shown in Figure 4. In addition, we preprocessed the NCEI shipborne gravity measurements by comparing them with the EGM2008 model gravity anomalies on a line-by-line basis for systematic bias correction, and subtracted about 3.17% of the coarse deviation observations according to the robust outlier detection algorithm (RODA).

FIGURE 4

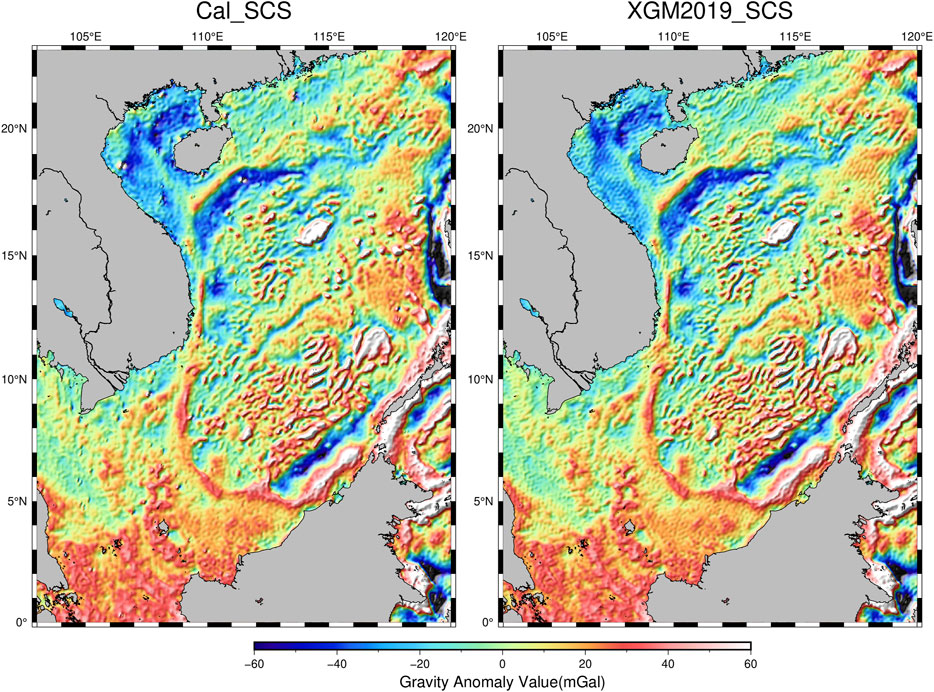
FIGURE 4. IS-2-derived gravity anomaly over the SCS with remove–compute–restore technique (left) and the corresponding XGM2019 model result (right).

In these statistics, the STD, of which values exceeding the mean errors by three times, were removed, accounting for 6.62 and 5.52%. The screening results are shown in Table 10, where the screening scales, the number of remaining data points, the maximum value, the minimum value, the mean value, and the standard deviation information are given. Furthermore, to verify the performance of the IS-2 nearshore, we analyzed the points with large differences inaccuracy from the shipborne gravity measurement verification. It can be seen that, to a large extent, the data with poor quality are located in the deep sea as well as in the nearshore regions, and the sea depth has a large impact on the data accuracy (Wan et al., 2020a), but the issue of water depth is not discussed further in this paper.

TABLE 10

TABLE 10. Statistical information of compared with shipborne data and XGM2019 gravity field mod.

The results in Table 10 show that the validation accuracies of the SCS gravity anomaly data based on the IS-2 single mission inversion with shipborne gravity measurements and the XGM2019 field model are 1.35 mGal and 2.47 mGal, respectively. IS-2 is expected to become an alternative data source for multi-mission fusion inversion of the ocean gravity field in the future.

Discussion and Conclusion

The IS-2 satellite has advantages in providing simultaneous multi-beam observations with an extremely high spatial sampling rate. We used a 22-months time series from the IS-2 ATL12 product and designed a four-step numerical experiment to construct a 4-min marine gravity grid in the SCS area. The main results were summarized as follows.

Firstly, we found that the ATLAS system carried by IS-2 could obtain reliable SSH observations. Inter- and intra-mission comparisons were used to obtain the crossover differences between data from IS-2 and the traditional pulse radar mission Jason-2. The verification results showed that their SSH measurements had approximately the same level of accuracy. In addition to this, the different reference ellipsoids of IS-2 and Jason-2 caused an average value of the inter-mission measurement height difference to be in the range of 64.88–81.90 cm. In addition, considering the influence of the time-varying sea surface terrain, we designed an inter-mission accuracy evaluation of SSH at the intersections of different time intervals for the six beams. The evaluation results showed that the shortest time interval has the highest accuracy, about 5 cm, which provides reliable support for calculating the CTDOV.

Secondly, we obtained valid results in calculating ATDOV and CTDOV while verifying them with the XGM2019 model. It can be seen from Tables 4, 5 that although the data point amplitudes are not of the same order of magnitude, the CTDOV accuracy obtained from six of the 15 sets of solutions are similar to beams’ ATDOV accuracy. The comparison indicates that CTDOV calculation between the six beams is mutually desirable in the cross-track direction. Also, we can conclude that the ATDOV accuracy of the middle pair is better than that of the other two pairs. Furthermore, the accuracy of the CTDOV obtained by using two beams on non-identical sides is worse.

Thirdly, based on the verification of the accuracy of the ATDOV calculations, we performed calculations of the ATDOV directional components by using the joint method shown in Figure 2. We first found that the accuracy of the CTDOV calculations has a significant impact on the accuracy of the ATDOV directional components. It is essential to verify the accuracy of CTDOV before carrying out the calculation of the directional component of ATDOV. Further, it was determined that the methods of joint calculation between different groups of beams (Figure 2B) and joint calculation between different groups and the same group of beams (Figure 2C) are the most reliable. By the comparison with the GDOV directional component accuracy, we conclude that the accuracy of the DOV prime directional component has been significantly improved.

Finally, we gridded the ATDOV directional components of the six beams into a 2′ × 2′ resolution GDOV directional component using a distance-weighting method, and the inverse Vening Meinesz formula (1D-FFT) was used to calculate the gravity anomalies over the SCS. It should be noted that after the six beams are uniformly gridded, the accuracy of the GDOV direction component is increased by about 8–22%, confirming the reliability of the gridding process using the distance-weighting method. The validation using NCEI shipborne gravity measurements and the XGM2019 gravity field model shows that the water depth has a large influence on the accuracy inversion of gravity anomaly, and the accuracy decreases in both coastal areas and deep waters. Meanwhile, the accuracy inversion of gravity anomaly data using IS-2 single-mission is 1.35 mGal and 2.47 mGal, respectively.

To conclude, IS-2, as a new type of laser altimetry satellite, has improved data collection capabilities. It can use a single mission to obtain gravity anomalies with good data accuracy over the SCS and can acquire high-precision DOV prime components with a single beam. However, it does not provide a significant improvement in the accuracy of the meridional component, which only increased by ∼15%. This is because, within a specified distance threshold, the amount of CTDOV data is far greater than the amount of ATDOV data, and the azimuth information is approximately horizontal. Therefore, we believe that with the increasing amount of IS-2 altimetry data and the joint solution between multiple tasks, a better determination of the DOV directional component can be expected and an accurate marine gravity field can be obtained.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author Contributions

DC and SZ designed the research and manuscript review. HL and BM performed the data analysis, prepared all figures and led the writing of the manuscript. All the authors discussed the results and commented on the manuscript.

Funding

This work was jointly supported by the National Natural Science Foundation of China (grant nos. 41871310 and 41804002), Fundamental Research Funds for the Central Universities (grant number N2124005).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We express our gratitude to hundreds of people at the NASA Goddard Space Flight Center and contracting partners that conceived, designed, and created the ICESat-2 Mission, the ICESat-2 Observatory, and the ATLAS instrument. We thank the NASA Earth Sciences Division, who produced the ATL12 ocean surface-height data. Meanwhile, We also thank NCEI for providing the shipborne gravity measurements and Zingerle et al. for providing the XGM2019 gravity field model.

References

Abdalati, W., Zwally, H. J., Bindschadler, R., Csatho, B., and Webb, C. (2010). The Icesat-2 Laser Altimetry Mission. IEEE Xplore 98 (5), 735–751. doi:10.1109/JPROC.2009.2034765

CrossRef Full Text | Google Scholar

Albayrak, M., Hirt, C., Guillaume, S., Halicioglu, K., Tevfik zlüdemir, M., and Shum, C. K. (2020). Quality Assessment of Global Gravity Field Models in Coastal Zones: A Case Study Using Astrogeodetic Vertical Deflections in Istanbul, Turkey. Stud. Geophys. Geod. 64, 306–329. doi:10.1007/s11200-019-0591-2

CrossRef Full Text

Andersen, O. B., Knudsen, P., Kenyon, S., and Holmes, S. (2014). Global and Arctic Marine Gravity Field from Recent Satellite Altimetry (Dtu13). doi:10.3997/2214-4609.20140897

CrossRef Full Text | Google Scholar

Chander, S., Chauhan, P., and Ajai, . (2012). Variability of Altimetric Range Correction Parameters over Indian Tropical Region Using Jason-1 & Jason-2 Radar Altimeters. J. Indian Soc. Remote Sensing 40 (3), 341–356. doi:10.1007/s12524-011-0171-6

CrossRef Full Text | Google Scholar

Friedl, M. A., Tan, B., Schneider, A., Ramankutty, N., Sibley, A., et al. (2010). Sulla-Menashe,Modis Collection 5 Global Land Cover: Algorithm Refinements and Characterization of New Datasets. Remote Sensing Environ. 114 (1), 168–182. doi:10.1016/j.rse.2009.08.016

CrossRef Full Text | Google Scholar

Fu, L-L., Christensen, E. J., Yamarone, C. A., Lefebvre, M., Ménard, Yves., Dorrer, M., et al. (1994). Topex/poseidon Mission Overview. J. Geophys. Res. Oceans 99 (C12). doi:10.1029/94JC01761

CrossRef Full Text | Google Scholar

Guo, J. Y., Shen, Y., Zhang, K., Liu, X., and Xie, F. (2016). Temporal-spatial Distribution of Oceanic Vertical Deflections Determined by Topex/poseidon and Jason-1/2 Missions. Earth Sci. Res. J. 20 (2), H1–H5. doi:10.15446/esrj.v20n2.54402

CrossRef Full Text | Google Scholar

Haagmans, R. (1993). Fast Evaluation of Convolution Integrals on the Sphere Using 1D FFT, and a Comparison with Existing Methods for Stokes?integral. Manuscripta Geodaetica 18, 227–241.

Google Scholar

Huang, M.-t., Zhai, G.-j., and Ouyang, Y.-z. (2006). Recovery of Marine Gravity Field Using Integrated Data from Multi-Satellite Missions. Sci. Surv. Mapp. 31 (6), 37–39. doi:10.1007/s11442-006-0415-5

CrossRef Full Text | Google Scholar

Hwang, C., Guo, J., Deng, X., Hsu, H. Y., and Liu, Y. (2006). Coastal gravity anomalies from retracked geosat/gm altimetry: improvement, limitation and the role of airborne gravity data. J. Geod. 80 (4), 204–216. doi:10.1007/s00190-006-0052-x

Hwang, C., Hsu, H. Y., and Jang, R. J. (2002). Global Mean Sea Surface and Marine Gravity Anomaly from Multi-Satellite Altimetry: Applications of Deflection-Geoid and Inverse Vening Meinesz Formulae. J. Geodesy 76 (8), 407–418. doi:10.1007/s00190-002-0265-6

CrossRef Full Text | Google Scholar

Hwang, C., and Hsu, H. Y. (2003). Marine Gravity Anomaly from Satellite Altimetry: a Comparison of Methods over Shallow Waters, Geophys. Oceanography, IAG symposiumProceedings of International Workshop on Satellite Altimetry for Geodesy, 126, 59–66. doi:10.1007/978-3-642-18861-9_7

CrossRef Full Text | Google Scholar

Hwang, C., Kao, E. C., and Parsons, B. (1998). Global Derivation of Marine Gravity Anomalies from Seasat, Geosat, Ers-1 and Topex/poseidon Altimeter Data. , 134(2), 449–459. doi:10.1111/j.1365-246x.1998.tb07139.x

CrossRef Full Text | Google Scholar

Jilan, S. (2004). Overview of the South china Sea Circulation and its Influence on the Coastal Physical Oceanography outside the Pearl River Estuary. Continental Shelf Res. 24 (16), 1745–1760. doi:10.1016/j.csr.2004.06.005

CrossRef Full Text | Google Scholar

Kwok, R., and Markus, T. (2017). Potential Basin-Scale Estimates of Arctic Snow Depth with Sea Ice Freeboards from Cryosat-2 and Icesat-2: an Exploratory Analysis. Adv. Space Res. 62 (6), 1243–1250. doi:10.1016/j.asr.2017.09.007

CrossRef Full Text | Google Scholar

Li, J., Ning, J., Chen, J., and Chao, D. (2001). Determination of Gravity Anomalies over the South China Sea by Combination of TOPEX/Poseidon,ERS2 and Geosat Altimeter Data. Acta Geodaetica et Cartographica Sinica 3, 197–202.

Google Scholar

Li, Z., Liu, X., Guo, J., Zhu, C., Yuan, J., Gao, J., et al. (2020). Performance of Jason-2/gm Altimeter in Deriving Marine Gravity with the Waveform Derivative Retracking Method: a Case Study in the South china Sea. Arabian J. Geosciences 13 (18), 1–13. doi:10.1007/s12517-020-05960-0

CrossRef Full Text | Google Scholar

Liu, S. W., Jun, L. J., Wan, J. H., and Yang, J. G. (2015). Calculation of gravity anomalies over China Sea and its vicinity based on multi-generation satellite altimetry data. Mar. Sci. 39 (12), 130–134.

Liu, Z., Yang, J., and Zhang, J. (2020). Jason-3 Global Statistical Assessment Based on Jason-2. Haiyang Xuebao 42 (03), 133–143. doi:10.3969/j.issn.0253−4193.2020.03.012

CrossRef Full Text | Google Scholar

Markus, T., Neumann, T., Martino, A., Abdalati, W., Brunt, K., Csatho, B., et al. (2017). The Ice, Cloud, and Land Elevation Satellite-2 (Icesat-2): Science Requirements, Concept, and Implementation. Remote Sensing Environ. 190, 260–273. doi:10.1016/j.rse.2016.12.029

CrossRef Full Text | Google Scholar

Morison, J. H., Hancock, D., Dickinson, S., Robbins, J., Roberts, L., Kwok, R., et al. (2020). ATLAS/IS-2 L3A Ocean Surface Height, Version 3. [Indicate Subset Used]. Boulder, Colorado USA. NASA National Snow and Ice Data Center Distributed Active Archive Center. the IS-2 Science Team. doi:10.5067/ATLAS/ATL12.003

CrossRef Full Text | Google Scholar

Moses, W., Bowles, J., and Corson, M. (2015). Expected Improvements in the Quantitative Remote Sensing of Optically Complex Waters with the Use of an Optically Fast Hyperspectral Spectrometer—A Modeling Study. Sensors 15 (3), 6152–6173. doi:10.3390/s150306152

PubMed Abstract | CrossRef Full Text | Google Scholar

National Snow and Ice Data Center (2019). Data-sets. Availableat: http://nsidc.org/data /IS-2/data-sets.

Google Scholar

Neuenschwander, A. L., Jelley, B., Pitts, K., Popescu, S. C., Nelson, R. F., Harding, D., et al. (2020a). ATLAS/ICESat-2 L3A Land and Vegetation Height, Version 2.NSIDC. Boulder, Colorado USA: National Snow and Ice Data Center. doi:10.5067/ATLAS/ATL08.002

CrossRef Full Text

Neuenschwander, A. L., Pitts, K. L., Jelley, B. P., Robbins, J., Klotz, B., Popescu, S. C., et al. (2020b). ATLAS/ICESat-2 L3A Land and Vegetation Height, Version 3. NASA National Snow and Ice Data Center Distributed Active Archive Center. Boulder, Colorado, USA. doi:10.5067/ATLAS/ATL08.003accessed April, 2020)

CrossRef Full Text

Neuenschwander, A., and Pitts, K. (2019). The ATL08 Land and Vegetation Product for the Icesat-2 Mission. Remote Sensing Environ. 221, 247–259.

CrossRef Full Text | Google Scholar

Neumann, T. A., Brenner, A. C., Hancock, D. W., Karbeck, K., Luthcke, S., Robbins, J., et al. (2018). Ice, Cloud, and Land Elevation Satellite-2 Project Algorithm Theoretical Basis Document for Global Geolocated Photons (ATL03). Available at: https://icesat-2.gsfc.nasa.gov/science/data-products.

Google Scholar

Neumann, T. A., Martino, A. J., Markus, T., Bae, S., Bock, M. R., Brenner, A. C., et al. (2019). The Ice, Cloud, and Land Elevation Satellite – 2 Mission: A Global Geolocated Photon Product Derived from the Advanced Topographic Laser Altimeter System. Remote Sensing Environ. 233. doi:10.1016/j.rse.2019.111325

PubMed Abstract | CrossRef Full Text | Google Scholar

Olgiati, A., Balmino, G., Sarrailh, M., and Green, C. M. (1995). Gravity Anomalies from Satellite Altimetry: Comparison between Computation via Geoid Heights and via Deflections of the Vertical. Bull. Géodésique 69 (4), 252–260. doi:10.1007/BF00806737

CrossRef Full Text | Google Scholar

Peng, Fuqing., and Xia, Zheren. (2004). Vertical Deflection Theorem of Satellite Altimetry. Hydroaphic Surv. Charting 2, 5–9.

Google Scholar

Sandwell, D. T. (1992). Antarctic Marine Gravity Field from High-Density Satellite Altimetry. Geophys. J. Int. 109 (2), 437–448. doi:10.1111/j.1365-246X.1992.tb00106.x

CrossRef Full Text | Google Scholar

Sandwell, D. T., and Smith, W. H. F. (1997). Marine Gravity Anomaly from Geosat and Ers 1 Satellite Altimetry. J. Geophys. Res. Solid Earth 102 (B5), 10039–10054. doi:10.1029/96JB03223

CrossRef Full Text | Google Scholar

Shaw, P. T., and Chao, S. Y. (1994). Surface Circulation in the South china Sea. Deep-sea Res. 41 (11-12), 1663–1683. doi:10.1016/0967-0637(94)90067-1

CrossRef Full Text | Google Scholar

Smith, B., Fricker, H. A., Gardner, A. S., Medley, B., and Zwally, H. J. (2020). Pervasive Ice Sheet Mass Loss Reflects Competing Ocean and Atmosphere Processes. Science 368 (6496), eaaz5845. doi:10.1126/science.aaz5845

CrossRef Full Text | Google Scholar

Smith, B., Fricker, H. A., Holschuh, N., Gardner, A. S., and Siegfried, M. R. (2019). Land Ice Height-Retrieval Algorithm for Nasa's Icesat-2 Photon-Counting Laser Altimeter. Remote Sensing Environ. 233, 111352. doi:10.1016/j.rse.2019.111352

CrossRef Full Text | Google Scholar

Sun, M., Guo, J., Yuan, J., Liu, X., Wang, H., and Li, C. (2021). Detecting Lake Level Change from 1992 to 2019 of Zhari Namco in Tibet Using Altimetry Data of TOPEX/Poseidon and Jason-1/2/3 Missions. Front. Earth Sci. doi:10.3389/feart.2021.640553

CrossRef Full Text | Google Scholar

Wan, X., Annan, R. F., Jin, S., and Gong, X. (2020a). Vertical Deflections and Gravity Disturbances Derived from Hy-2a Data. Remote Sensing 12 (14), 2287. doi:10.3390/rs12142287

CrossRef Full Text | Google Scholar

Wan, X., Jin, S., Liu, B., Tian, S., Kong, W., and Annan, R. F. (2020b). Effects of Interferometric Radar Altimeter Errors on Marine Gravity Field Inversion. Sensors (Basel, Switzerland) 20 (9). doi:10.3390/s20092465

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, H., and Wang, G (2001). Inversion of Gravity Anomalies from Along-Track Vertical Deflections with Satellite Altimeter Data and its Applications. Acta Geodaetica et Cartographica Sinica 1, 23–28. doi:10.3321/j.issn:1001-1595.2001.01.005

CrossRef Full Text | Google Scholar

Wang, H., and Lu, W. Y. (2008). High Precision Vertical Deflection over china Marginal Sea and Global Sea Derived from Multi-Satellite Altimeter, 11. Geomatics & Information Science of Wuhan University, 289–293. doi:10.1007/s11806-008-0122-8

CrossRef Full Text | Google Scholar

Wang, J., Xu, H., Yang, L., Song, Q., and Ma, C. (2021). Cross‐calibrations of the HY‐2B altimeter using Jason‐3 satellite during the period of 2019.4∼2020.9. Front. Earth Sci. doi:10.3389/feart.2021.647583

Yang, L., Zhou, X. H., Lin, M. S., Lei, N., Bo, M. U., and Zhu, L., (2016). Global Statistical Assessment of HY-2A Altimeter IGDR Data. Prog. Geophys. (Chinese) 31 (2), 0629–0636. doi:10.6038/pg20160216

CrossRef Full Text | Google Scholar

Zhang, S., Sandwell, D. T., Jin, T., and Li, D. (2017). Inversion of Marine Gravity Anomalies over Southeastern china Seas from Multi-Satellite Altimeter Vertical Deflections. J. Appl. Geophys. 137, 128–137. doi:10.1016/j.jappgeo.2016.12.014

CrossRef Full Text | Google Scholar

Zhang, S., Li, J., Jin, T., and Che, D. (2018). Hy-2a Altimeter Data Initial Assessment and Corresponding Two-Pass Waveform Retracker. Remote Sensing 10 (4), 507. doi:10.3390/rs10040507

CrossRef Full Text | Google Scholar

Zhang, S., Li, J., and Kong, X. (2020). Inversion of Global Marine Gravity Anomalies with Vertical Deflection Method Deduced from Laplace Equation. Acta Geodaetica et Cartographica Sinica 49 (4), 452–460. doi:10.11947/j.AGCS.2020.20190108

CrossRef Full Text | Google Scholar

Zhang, S. (2017). Research on Determination of Marine Gravity Anomalies from Multi-Satellite Altimeter Data. Acta Geodaetica et Cartographica Sinica. doi:10.11947/j.AGCS.2017.20170187

CrossRef Full Text | Google Scholar

Zhu, C., Guo, J., Gao, J., Liu, X., Hwang, C., Yu, S., et al. (2020). Marine Gravity Determined from Multi-Satellite Gm/erm Altimeter Data over the South china Sea: Scsga v1.0. J. Geodesy 94 (5). doi:10.1007/s00190-020-01378-4

CrossRef Full Text | Google Scholar

Zhu, C., Guo, J., Hwang, C., Gao, J., and Liu, X. (2019). How Hy-2a/gm Altimeter Performs in Marine Gravity Derivation: Assessment in the South china Sea. Geophys. J. Int. 219 (2), 1056–1064. doi:10.1093/gji/ggz330

CrossRef Full Text | Google Scholar

Zhu, C., Zhang, S., Xiao, F., Li, J., and Zhu, T. (2018). Threshold Determination for Local Instantaneous Sea Surface Height Derivation with Icebridge Data in Beaufort Sea. doi:10.5194/isprs-archives-XLII-3-2579-2018

CrossRef Full Text | Google Scholar

Zingerle, P., Pail, R., Gruber, T., and Oikonomidou, X. (2019). The experimental gravity field model XGM2019e. Potsdam: GFZ Data Services. doi:10.5880/ICGEM.2019.007

Zingerle, P., Pail, R., Gruber, T., and Oikonomidou, X. (2020). The combined global gravity field model xgm2019e. J. Geod. 94 (7). doi:10.1007/s00190-020-01398-0