Numerical Studies and Analyses on the Acidizing Process in Vug Carbonate Rocks

A vug porosity system, in addition to a matrix, is also the target rocks for the acidizing. In this work, the acidizing process in two typical core-scale separate-vug porosity systems is studied in detail. Numerous cases are conducted to discuss a parametric study on the acidizing process and hydraulic behavior. Results indicate that the presence of vug reduces the pore volume of acid solution consumed to achieve a breakthrough, which is consistent with experimental observations. Increasing the vug diameter and porosity decreases pore volume to breakthrough both for a vugular carbonate rock and isolated vug carbonate rock. In comparison, the acid mass does not change a lot. Typical dissolution patterns can also be observed in the acidizing process when a vug exists. Compared to matrix dissolution patterns, the presence of vug induces wormhole to pass through the vug region.

Introduction

Reactive flow in porous media plays an essential role in various physical, chemical, and biological processes in nature and has many applications (Fredd and Scott Fogler, 1998; Acharya et al., 2007; Li et al., 2008; Bijeljic et al., 2013; Nick et al., 2013; Menke et al., 2015; Li et al., 2018). This work is conducted to study the carbonate acidizing process in vug carbonate rocks.

Before, lots of studies have been conducted to study the carbonate matrix acidizing process. Both experimental (Bernadiner et al., 1992; Wang et al., 1993; Frick et al., 1994; Fredd and Fogler, 1999; Izgec et al., 2008; Furui et al., 2012a; Furui et al., 2012b; Dong, 2012; Aidagulov et al., 2018; Qiu et al., 2018) and numerical (Kanaka and Panga, 2003; Panga et al., 2005; Kalia and Balakotaiah, 2007; Kalia and Balakotaiah, 2009; Maheshwari et al., 2013; Maheshwari et al., 2016b; Liu et al., 2019) results show that an optimum acid injection rate widely exists, at which the minimum amount of acid solution is consumed to achieve a breakthrough (Jia et al., 2021). Meanwhile, different dissolution patterns (Hoefner and Fogler, 1989; Fredd and Fogler, 1998; Fredd and Fogler, 1999; Huang et al., 2000; Izgec et al., 2008; Aidagulov et al., 2018) can also be observed through visualization techniques at different acid injection velocities. Apart from the matrix, vug is also a widespread presence in carbonate rocks, which is a void space in the reservoir rock and provides the main storage space for reserves (Kossack and Gurpinar, 2001; Wang et al., 2016; Yue et al., 2018). According to the vug interconnection, a vuggy pore space can be divided into the separate-vug porosity system and toughing-vug porosity system (Nair et al., 2008). Because of complex porosity systems, a flow behavior is more complicated in vug carbonate rocks (Sadeghnejad and Gostick, 2020). In the toughing-vug porosity system, a vug is usually associated with fabric dissolution and karst process (Lucia, 2007), in which an interconnected pore system forms and has a much larger permeability (Zhang et al., 2005) of average 10³–10⁶ times more than that of the disconnected vug system (Kossack and Gurpinar, 2001). For a separate-vug porosity system, the addition of vug only increases the total porosity but has no significant contribution for the core permeability (Zhang et al., 2005). Such rocks are also the target reservoirs for the acidizing stimulation. However, a few studies have been performed to study the acidizing process in the separate-vug porosity system. For an experimental study, Izgec et al. (2008) have shown that the presence of vug does affect the acidizing process for calcite rocks. The pore volumes to breakthrough decreases with the increase of the vuggy fraction. Furthermore, Izgec et al. (2009) also developed a two-scale continuum model to simulate the acidizing process in the separate-vug porosity system, in which vuggy carbonates are divided into two distinct regions of the matrix region and the vuggy region. The Darcy equation is used in the matrix region, and the Stokes equation is used to account for the fluid flow in the vug (free flow) region. However, it is worth noting that when most of the matrix is dissolved, compared to the damping effect of porous media, the fluid phase viscous dissipation becomes dominant and cannot be ignored anymore. In such cases, the Darcy equation is not applicable any longer. Also, Izgec’s model neglects mass exchange between solid and liquid phases. Hence, a more accurate mathematical model is still needed to study the acidizing process in the separate-vug porosity system.

In this work, the Stokes–Darcy equation is used to describe the fluid flow instead of the Darcy equation, and a source term is added to the fluid mass conservation equation for considering the dissolution mass term from the solid phase to the fluid phase. A detailed explanation of the two-scale continuum model is given in the next section. In the third section, numerous cases are conducted to discuss a comprehensive parametric study on the acidizing process, including acid injection velocity, acid injection concentration, vug filling degrees, vug diameter, and matrix porosity heterogeneity.

Model Development

Reaction and Kinetics

In this study, a solid mineral is supposed to only containing calcite $\left(CaC{O}_3\right)$ (Alkhaldi et al., 2010; Maheshwari et al., 2016a; Mahrous et al., 2017). For simplicity, an overall chemical reaction equation is adapted to represent the acid consumption and calcite dissolution, which is given below:

$2HCl+CaC{O}_3\to CaC{l}_2+H_{2}C{O}_3.(1)$

Calcite $\left(CaC{O}_3\right)$ and hydrochloric acid $\left(HCl\right)$ react to form calcium chloride $\left(CaC{l}_2\right)$ and carbonic acid $\left(H_{2}C{O}_3\right)$. The surface reaction rate is dependent on the concentration by the power law expression:

$R_{HCl}=k_s{c}_{HCl,s}^n,(2)$

where $R_{HCl}$ is the acid reaction rate, $k_s$ is the acid reaction rate at the solid surface, $n$ is the reaction order, and $c_{HCl,s}$ is the surface acid concentration. The reaction rate of other components can be further determined according to Eq. 1.

Governing Equations

Modeling and numerical simulation of vuggy carbonate reservoirs is still challenging because of vug’s presence (Popov et al., 2009). The modeling of vuggy media is traditionally done based on the multiple-continuum concept model. In this model, the matrix and vug are assumed to have uniform and homogeneous properties, and the intercommunication flow between the matrix region and the vug region is at a pseudo-steady state (Kang et al., 2006; Wu et al., 2007). The continuum approaches behave pretty well in vug well-developed reservoirs, but the challenging part of this mode is that it is hard to determine accurate rock properties such as porosity and permeability (Yao et al., 2010). Another popular approach is based on the coupled Stokes and Darcy equations, in which the Darcy equation is only used in the porous region, and the Stokes equation is used in the free-flow region. Moreover, at the interface between the porous and free-flow regions, the additional boundary condition is employed to guarantee continuity of mass and momentum across the interface (Izgec et al., 2009; Yao et al., 2010). However, it is still very complicated and less practical to apply the coupled Darcy–Stokes approach to vuggy reservoirs. Because, on the one hand, the interface condition also introduces additional parameters such as material property, ${\alpha }_{BJ}$, in Beavers–Joseph–Saffman (BJS) condition (Beavers and Joseph, 1967; Saffman, 1971), which needs to be further determined numerically or experimentally. On the other hand, the Stokes equation used in the free-flow region can only handle the vug region free of any obstacles (Popov et al., 2009). The limitation of the coupled Darcy and Stokes approach can be overcome by using the Stokes–Brinkman equation, which uses a single equation rather than coupled equations to describe the fluid flow in entire vuggy reservoirs and avoids explicit modeling of the interface (Popov et al., 2009; De Oliveira et al., 2012; Fadlelmula F et al., 2016). In this work, a new two-scale continuum model is inspired by the Stokes–Brinkman equation. The Stokes–Darcy equation is employed to predict the momentum transport behavior of the fluid phase. The equation is given below:

$0=-\nabla p+\nabla \cdot \left(\mu \left(\nabla \frac{\mathbf{u}}{\varphi }+{\left(\nabla \frac{\mathbf{u}}{\varphi }\right)}^T\right)\right)-\frac{\mu }{k}\mathbf{u},(3)$

where $\varphi$ is the porosity, ${\rho }_{fluid}$ is the density of fluid phase, $\mathbf{u}={\left[\begin{array}{cc}u& v\end{array}\right]}^T$ is the superficial velocity, $k$ is the permeability, $\mu$ is the viscosity, and $p$ is the fluid pressure. The equation can represent all regions during the acidizing process. For example, in an undissolved matrix region with a low permeability, the damping effect of the solid structure is relatively significant, which is represented by the last term in Eq. 3. Moreover, in wormhole and vug regions, the influence of solid skeleton is gradually diminishing with a large permeability, and the viscous dissipation of fluid behaves dominantly, which can be considered by the viscous term in Eq. 3.

Then we continue to develop the mass conservation equations. According to Equation 1, the fluid phase consists of water $\left(H_{2}O\right)$, acid $\left(HCl\right)$, calcium chloride $\left(CaC{l}_2\right)$, and carbonic acid $\left(H_{2}C{O}_3\right)$. And the acid component $\left(HCl\right)$ is chosen as the main component. The matrix only contains calcite $\left(CaC{O}_3\right)$. Therefore, the governing equations for the fluid phase, acid solution, and calcite are independently developed by (Jia et al., 2021), which is as follows:

$\frac{\partial }{\partial t}\left(\varphi {\rho }_{fluid}\right)=-\nabla \cdot \left({\rho }_{fluid}\mathbf{u}\right)+s\left(\frac{M_{CaC{l}_2}}{2}+\frac{M_{H_{2}C{O}_3}}{2}-M_{HCL}\right)R_{HCl},(4)$

$\frac{\partial }{\partial t}\left(\varphi c_{HCl}\right)=-\nabla \cdot \left({\mathbf{D}}_{HCL}\cdot \nabla c_{HCl}+c_{HCl}\mathbf{u}\right)-s{R}_{HCl},(5)$

$\frac{\partial }{\partial t}\left(\left(1-\varphi \right){\rho }_{CaC{O}_3}\right)=-s\frac{M_{CaC{O}_3}}{2}{R}_{HCl}\left(c_{HCl,s}\right),(6)$

where $s$ stands for the specific surface area; $M_{HCL}$, $M_{CaC{l}_2}$, $M_{H_{2}C{O}_3}$, and $M_{CaC{O}_3}$ are the component for $HCl$, $CaC{l}_2$, $H_{2}C{O}_3$, and $CaC{O}_3$, respectively; $c_{HCl}$ is the acid concentration in the bulk phase; ${\mathbf{D}}_{HCL}$ is the acid diffusion coefficient, determined as ${\mathbf{D}}_{HCL}=\varphi D_m\mathbf{I}$; $\mathbf{I}$ is the unit tensor; $D_m$ is the molecular diffusion rate; and ${\rho }_{CaC{O}_3}$ is the matrix density. The main difference between the conventional two-scale continuum model (Panga et al., 2005; Kalia, 2008) and the model used in this study is reflected in the last term in Eq. 4, which represents a source term to the fluid mass conservation equation for considering the dissolution mass term from the solid phase to the fluid phase. Almost all of the previous numerical studies neglect it. The acid reaction rate $\left(R_{HCl}\right)$ is further determined as follows:

$R_{HCl}=k_s{c}_{HCl,s}^n=k_c\left(c_{HCl}-c_{HCl,s}\right),(7)$

where $k_c$ is the mass transfer rate, and it is quantified by a model derived by Balakotaiah (Balakotaiah and West, 2002)

$Sh=\frac{2k_{c}r}{D_m}=S{h}_{\infty }+0.7{\mathrm{Re}}_p^{\frac{1}{2}}S{c}^{\frac{1}{3}},(8)$

where $Sh$ is the Sherwood number, $S{h}_{\infty }$ is the asymptotic Sherwood number, the value used in this work is 3.66 for a circular pore structure, ${\mathrm{Re}}_p$ is defined as ${\mathrm{Re}}_p=2\left|\mathbf{u}\right|r/\nu$, $\nu$ is defined by $\nu =\mu /{\rho }_{liquid}$, and $Sc$ is the Schmidt number defined by $Sc=\nu /D_m$. The modified Carman–Kozeny equations are used to determine the changes of core parameters (Edery et al., 2011; Jia et al., 2021) which is given as follows:

$\frac{k}{k_0}={\left(\frac{\varphi }{{\varphi }_0}\right)}^{\gamma }{\left(\frac{\varphi \left(1-{\varphi }_0\right)}{{\varphi }_0\left(1-\varphi \right)}\right)}^{2\beta },(9)$

$\frac{r}{r_0}={\left(\frac{\varphi \left(1-{\varphi }_0\right)}{{\varphi }_0\left(1-\varphi \right)}\right)}^{\alpha },(10)$

$\frac{s}{s_0}=\left(\frac{\varphi }{{\varphi }_0}\right){\left(\frac{\varphi \left(1-{\varphi }_0\right)}{{\varphi }_0\left(1-\varphi \right)}\right)}^{-\alpha },(11)$

where $\gamma$, $\alpha$, and $\beta$ are the parameters describing pore connectivity and broadening structure, and ${\varphi }_0$, $k_0$, $r_0$, and $s_0$ are the initial porosity, permeability, pore diameter, and specific surface area, respectively.

Boundary and Initial Conditions

The calculation domain is selected as a 2D cross section of a cylindrical core with 4 cm diameter and 10 cm height. The boundary and initial conditions refer to the core flooding experiments (Izgec et al., 2008). Acid is injected at a constant velocity and concentration from one side of the core sample. The acid injection concentration is identical to the value, 15%, used in the experimental study. Constant pressure is held on the other core sample side. Because in the experiment process, the core sample is always surrounded by a high confining pressure to avoid the acid solution going through the gap between the core sample and the core holder plug. Initially, the core sample is saturated with water, and matrix porosity has a value of 0.15. Matrix permeability is assumed isotropic and has a value of 5 mD. Furthermore, a uniform distribution random function creates a heterogeneous distribution of porosity (Maheshwari et al., 2016a; Wei et al., 2017). Boundary and initial conditions are summarized below:

$-\mathbf{n}\cdot \mathbf{u}=u_0\mathrm{at}x=0,(12)$

$-\mathbf{n}\cdot \left(\mathbf{u}{c}_{HCl}+D_{HCl}\nabla c_{HCl}\right)=u_0{c}_0\mathrm{at}x=0,(13)$

$p=p_e\mathrm{at}x=L,(14)$

$\mathbf{n}\cdot D_{HCl}\nabla c_{HCl}=0\mathrm{at}x=L,(15)$

$\mathbf{n}\cdot \overline{\mathbf{v}}=0,\mathbf{n}\cdot \left(\mathbf{u}{c}_{HCl}+D_{HCl}\nabla c_{HCl}\right)=0\mathrm{on\; transverse\; boundaries,}(16)$

$c_{HCl}=0,\varphi ={\varphi }_0+\Delta {\varphi }_0\mathrm{at}t=0,(17)$

where $\mathbf{n}$ is the boundary unit direction vector, $u_0$ is the injection velocity, $c_0$ is the injection concentration, $p_e$ is the pressure at the core outside, and $\Delta {\varphi }_0$ is the initial heterogeneity magnitude of porosity.

Results and Discussions

The separate-vug porosity system covers a wide range of structures from millimeters to meters in the diameter (Arns et al., 2005; Sok et al., 2010; Mousavi et al., 2012; Sadeghnejad and Gostick, 2020). This study is concerned with two typical core-scale separate-vug porosity systems: the vugular carbonate rock and the isolated vug carbonate rock, as shown in Figure 1. For numerical studies, vug in vugular carbonate rock is supposed uniformly embedded in the matrix region, and each vug initially has a diameter of 3 mm (Casar-Gonzalez and Suro-Perez, 2000; Izgec et al., 2010). Moreover, for the isolated vug carbonate rock, vug has a centimeter diameter, 1.5 cm (Zhang et al., 2004; Casar-Gonzalez and Suro-Perez, 2000). For a separate-vug porosity system, the addition of vug only contributes to the increasing storage space. The acid breakthrough condition is still consistent with matrix acidizing, determined by a 100 times increase of the core average permeability (De Oliveira et al., 2012). The pore volume at a breakthrough condition is counted and normalized with the sample initial pore volume as an evaluation parameter cited as pore volume to breakthrough (PVBT) (Jia et al., 2021). Besides, acid breakthrough injection mass (AMBT) is also collected in this work because PVBT is simultaneously a function of porosity.

FIGURE 1

FIGURE 1. Two typical core-scale separate-vug porosity systems: (A) vugular carbonate rock and (B) isolated vug carbonate rock.

Model Comparison and Validation

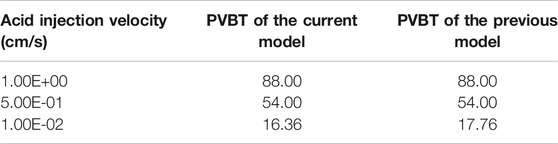
The two-scale continuum model is widely accepted and used to describe the core scale stimulation process (Kalia and Balakotaiah, 2007; Liu et al., 2017; Maheshwari et al., 2013). The Darcy equation is usually employed to determine the superficial velocity of the fluid phase. In this study, the Stokes–Darcy equation, as shown in Eq. 3, is employed to predict the fluid phase momentum transport behavior. When the acid solution acquires a very high injection rate, the core sample is uniformly dissolved by acid and still keeps the characteristic of porous media because of no existence of a wormhole. At this time, the Darcy equation can still be applicable. The acid breakthrough consumption volume calculated based on the Darcy equation has little difference from the value of PVBT calculated based on the Stokes–Darcy equation (Jia et al., 2021). Thus, the model can be validated by comparing PVBT values with the previous two-scale continuum model with high acid injection velocities. Table 1 shows the values of PVBT separately calculated by the current and previous two-scale continuum models with high acid injection velocities. The results show that the difference of PVBT values between the current and previous two-scale continuum model is not noticeable when acid acquires a very high injection rate. Figure 2 further compares dissolution images of current and previous two-scale continuum models with very high acid injection velocities. The current two-scale continuum model is well validated.

TABLE 1

TABLE 1. Comparison of PVBT values of different two-scale continuum models.

FIGURE 2

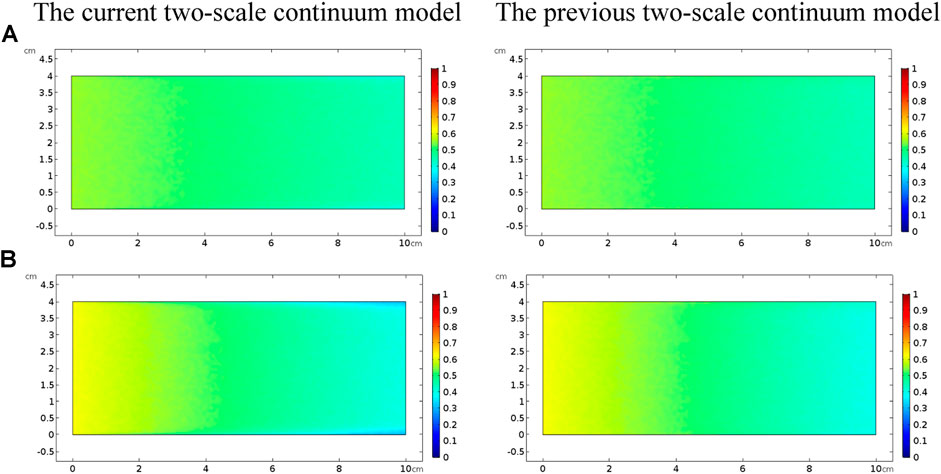
FIGURE 2. Comparison of dissolution images between the current and previous two-scale continuum model with high injection rates: (A) 1 cm/s and (B) 0.5 cm/s.

Effect of Acid Injection Velocity

This section studies the effect of the acid injection rate on the acidizing process of the vugular carbonate rock and the isolated vug carbonate rock. The porosity of the vug region is initially set as a high value of 0.99. The whole sample porosity is calculated as 0.3875 for vugular carbonate rock and 0.1871 for isolated vug carbonate rock. The whole sample mean permeability of the vugular carbonate rock and the isolated vug carbonate rock is measured as 10 and 6.6 mD, respectively. In comparison, the permeability of the matrix zone is 5 mD. The results show that the existence of vug in the vugular carbonate rock and the isolated vug carbonate rock does provide more storage space but has a little contribution to hydraulic conductivity for the matrix core sample.

Figure 3 shows the acidizing results of vugular carbonate rock. It can be observed from Figure 3A that the pore volume to breakthrough (PVBT) of vugular carbonate rock is less than the PVBT of matrix carbonate rock. The same change trend of the PVBT is also observed in the experimental study (Izgec et al., 2008). The acid mass to breakthrough (AMBT) change of the vugular carbonate rock and the matrix carbonate rock is not apparent compared to the change of the PVBT. The AMBT value of vugular carbonate rock is slightly lower than the AMBT value of matrix carbonate rock. However, in general, the AMBT values of the vugular carbonate rock and matrix carbonate rock are very close, as shown in Figure 3B. Figure 4 compares the dissolution patterns of the vugular carbonate rock and the matrix carbonate rock with different acid injection velocities. Typical dissolution patterns, including uniform, ramified wormhole, wormhole, and conical wormhole dissolution patterns (Jia et al., 2021), are also observed in the acidizing process of vugular carbonate rock. Compared to dissolution patterns of matrix carbonate rock, vug presence induces wormhole to pass through the vug region. Besides, more wormholes can be stimulated due to vug existence with a high acid injection rate, as shown in Figure 4B. Also, because of the existence of vug, less acid is used to dissolve the solid matrix. The apparent difference in pore volume to breakthrough is mainly caused by the vug increasing initial pore volume. Furthermore, according to the definition of PVBT, a higher initial pore volume leads to lower PVBT.

FIGURE 3

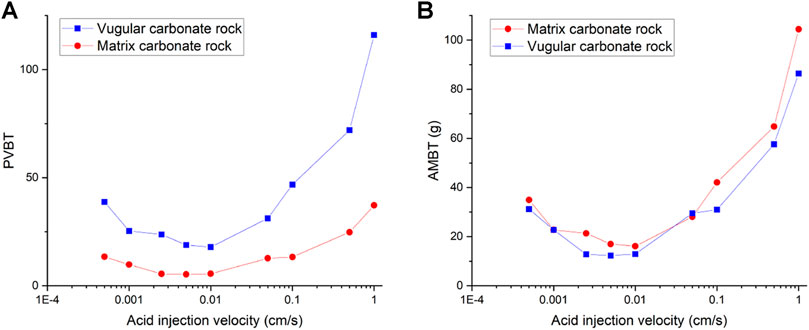
FIGURE 3. Effect of the acid injection rate on acidizing curves of the vugular carbonate rock: (A) PVBT and (B) AMBT.

FIGURE 4

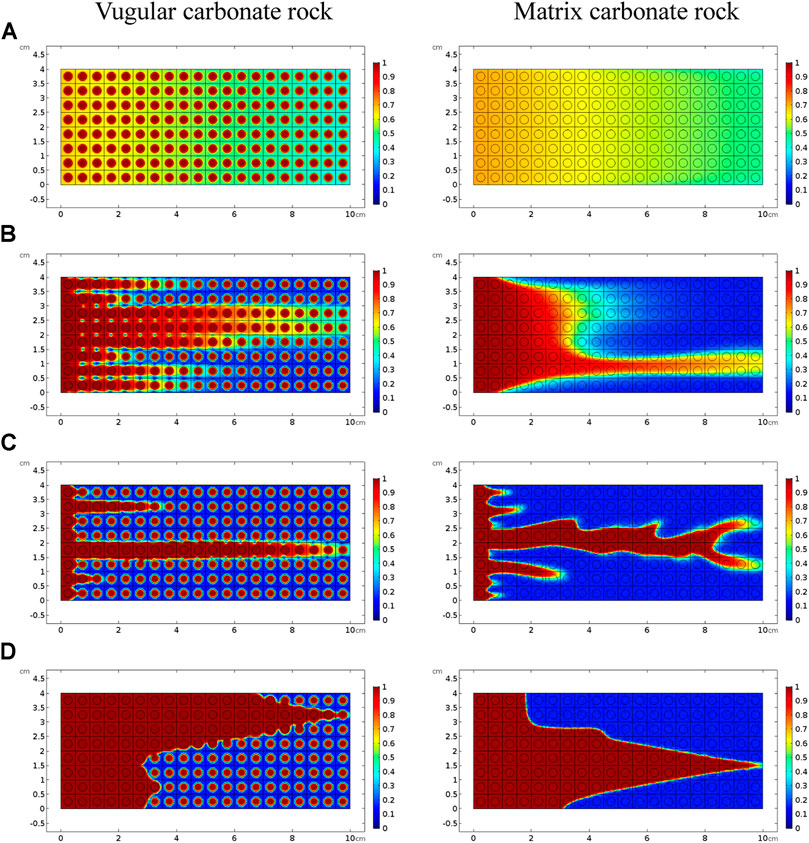
FIGURE 4. Comparison of dissolution patterns with different acid injection velocities: (A) 0.5 cm/s, (B) 0.05 cm/s, (C) 0.005 cm/s, and (D) 0.0005 cm/s.

Figure 5 and Figure 6 compare acidizing curves and dissolution patterns of the isolated vug carbonate rock and matrix carbonate rock, respectively. Similar conclusions can also be observed with the vugular carbonate rock. Because the presence of isolated vug is increasing the initial pore volume, the PVBT of isolated vug carbonate rock is higher than the PVBT of matrix carbonate rock, which is also consistent with the experimental observation (Izgec et al., 2008). Four typical dissolution patterns can also be observed in the acidizing process of the isolated vug carbonate rock, as shown in Figure 6. The induction effect of isolated vug on wormhole growth is more intuitive for the isolated vug carbonate rock. The main wormhole has a trend to close to and go through isolated vug. The main wormhole grows in a single direction for the matrix carbonate rock without any turning trend. The difference of the AMBT between the isolated vug carbonate rock and matrix carbonate rock is still not noticeable.

FIGURE 5

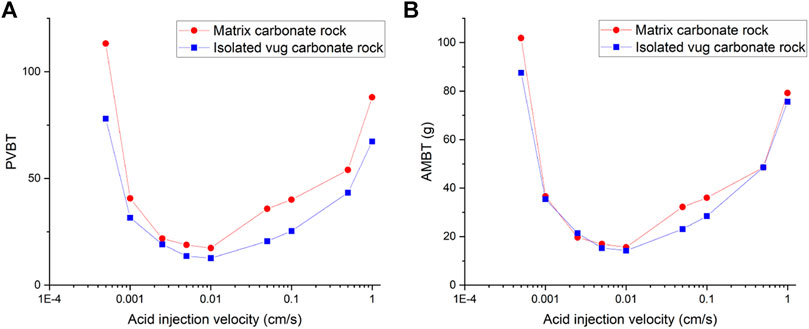
FIGURE 5. Effect of the acid injection rate on acidizing curves of the isolated vug carbonate rock: (A) PVBT and (B) AMBT.

FIGURE 6

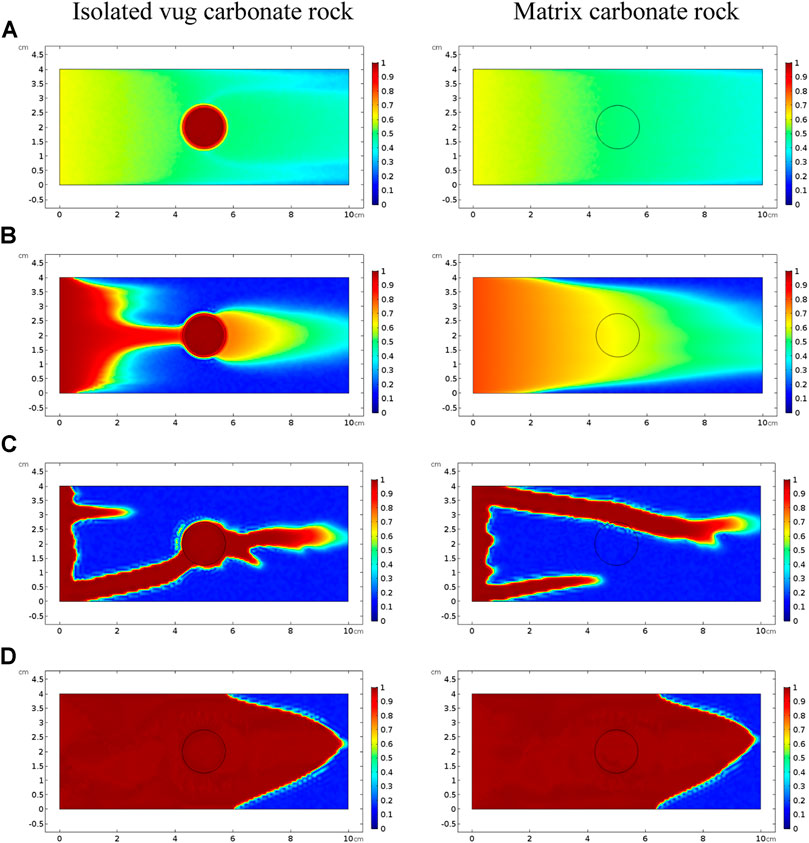
FIGURE 6. Comparison of dissolution patterns with different acid injection velocities: (A) 0.5 cm/s, (B) 0.05 cm/s, (C) 0.005 cm/s, and (D) 0.0005 cm/s.

Effect of Acid Injection Concentration

Acid injection concentration is also significant for the practical acidizing application. Initially, Fredd and Fogler (1999) adopted the concentration of 2% in core-flooding experiments. The concentration of 15% is widely used in the subsequent experimental studies (Furui et al., 2012a; Dong et al., 2014; Aidagulov et al., 2018; Kumar et al., 2020). Wang et al. (1993) ever used different concentrations such as 0.5, 3.4, and 15% to experimentally study the influence of acid injection concentration on the acidizing results. The results indicate that increasing acid injection concentration decreases the PVBT, while the optimum injection rate change is not apparent.

Figure 7 numerically calculates the acidizing curves with acid injection concentration changing from 5 to 25%. It can be found that when the acid injection concentration increases from 5 to 25%, PVBT values shows a pronounced decrease both for the vugular carbonate rock and isolated vug carbonate rock, which is consistent with experimental studies conducted by Wang et al. (1993) and numerical studies of matrix acidizing presented by Jia et al. (2020a). Besides, acid mass to breakthrough (AMBT) is also compared with different acid injection concentrations. Because it is very important to note that when we are studying the influence of acid injection concentration on acidizing results, the amount of acid solute and acid solvent are both changing. The change of PVTB reflects more information on the amount of acid solute (Fredd and Fogler, 1999; Panga et al., 2005). Few studies before noticed and discussed the change of acid solvent mass. Figure 7 shows that compared to the apparent change of PVBT, the amount of acid mass required to breakthrough does not change apparently with increasing acid injection concentration. Hence, the amount of solute in the acid system has an apparent relationship with the acid injection concentration, but the solvent required to achieve a breakthrough has a less obvious influence.

FIGURE 7

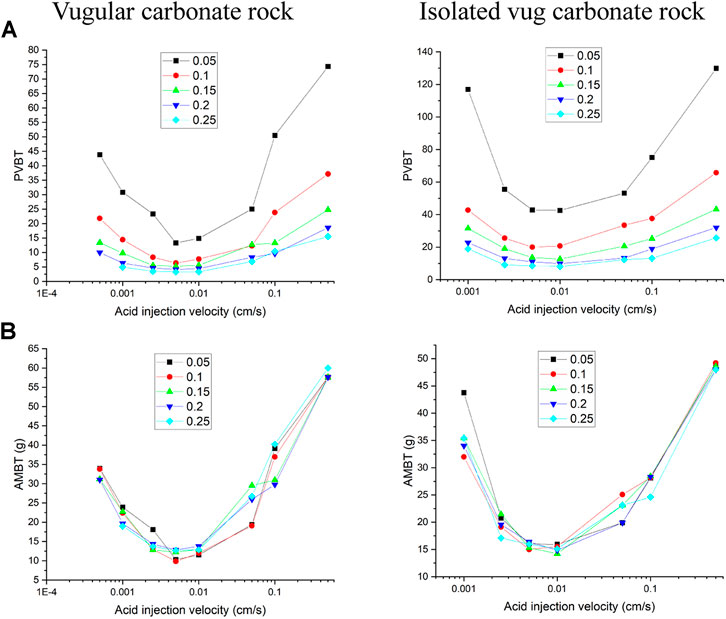
FIGURE 7. Effect of acid injection concentration on the acidizing results: (A) pore volume to breakthrough (PVBT) and (B) acid mass to breakthrough (AMBT).

Effect of Vug Porosity

The filling phenomenon is widespread in vug carbonate rocks. It is affected by multiple factors, such as mechanical deposition, collapsed deposition, chemical deposition, and so on, which eventually leads to the vug with different porosities (Li, 2017). This section studies the influence of vug porosity on the acidizing process of vugular carbonate rock and isolated vug carbonate rock. Figure 8 summarizes the change of core porosity and permeability, with the vug porosity varying from 15 to 99% considering different degrees of filling. The results show that both core porosity and permeability increase as the vug porosity increases. For the vugular carbonate rock, compared to the change of core porosity increasing from 15 to 40%, the change of core permeability is limited, increasing from 5 to 10 mD. The increase of core porosity and permeability in isolated vug carbonate rock is not apparent. Core porosity increases from 15 to 19%, and core permeability increases from 5 to 5.6 mD. Figure 9 further compares the acidizing results with different vug porosities from the low filling degree with vug porosity of 15% to the high filling degree with vug porosity of 99%. The results show that vug porosity mainly has a noticeable influence on the pore volume to breakthrough. Higher vug porosity results in a lower value of the PVBT. However, the difference of acid injection mass consumed to achieve breakthrough between different vug porosities is still not apparent.

FIGURE 8

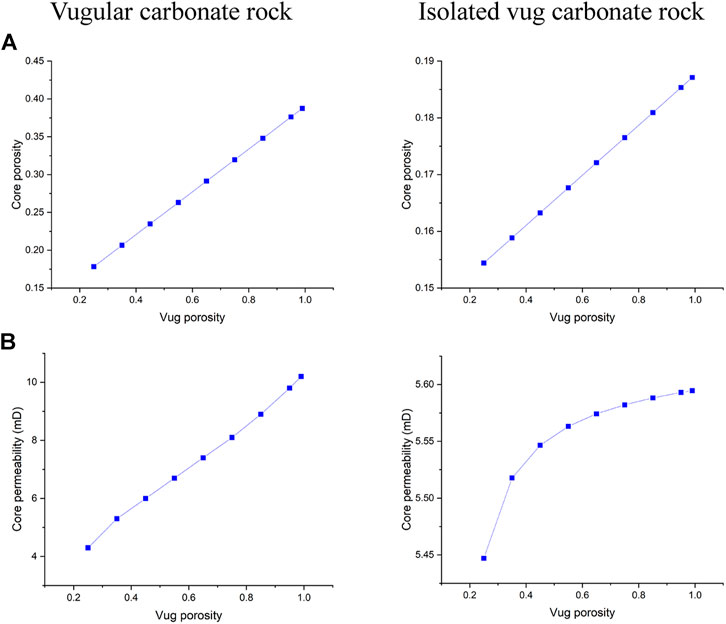
FIGURE 8. Effect of vug porosity on core physical parameters: (A) core porosity and (B) core permeability.

FIGURE 9

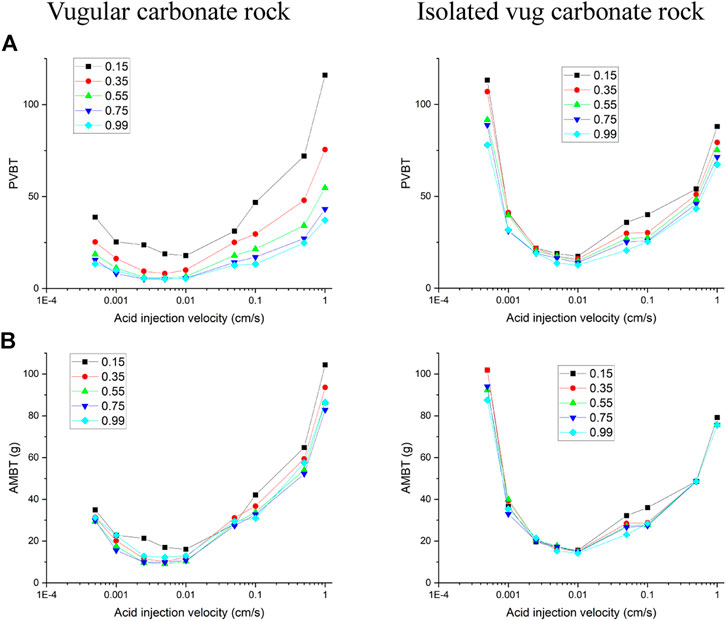
FIGURE 9. Effect of vug porosity on acidizing curves: (A) pore volume to breakthrough (PVBT) and (B) acid mass to breakthrough (AMBT).

Effect of Vug Diameter

This section studies the influence of vug diameter on the acidizing performance of vugular carbonate rock and isolated vug carbonate rock. Here, we suppose that for the vugular carbonate rock, the diameter of vug has the magnitude of a millimeter (Casar-Gonzalez and Suro-Perez, 2000; Ramakrishnan et al., 2001; Sok et al., 2010; Mousavi et al., 2012). Figure 10 shows core porosity and permeability with a vug diameter varying from 0.5 to 3.5 mm. It can be observed that when the vug diameter reaches 3.5 mm, core permeability is different from core permeability of other core samples with a vug diameter less than 3.5 mm. Besides, core porosity with a vug diameter of 3.5 mm reaches 47.33%. Hence, the final vug diameter below 3.5 mm is determined as the threshold diameter for the acidizing stimulation for the vugular carbonate rock. Then, we study the effect of isolated vug diameter on the acidizing process. The diameter of isolated vug on the core scale is supposed to have a centimeter magnitude (Casar-Gonzalez and Suro-Perez, 2000; Zhang et al., 2004; Arns et al., 2005). Unlike the vugular carbonate rock, the core porosity and permeability slowly increase with an increase of the isolated vug diameter. With the isolated vug diameter varying from 0.5 to 3 cm, the core porosity increases from 15.41 to 29.84% and core permeability increases from 5.1 to 6.9 mD.

FIGURE 10

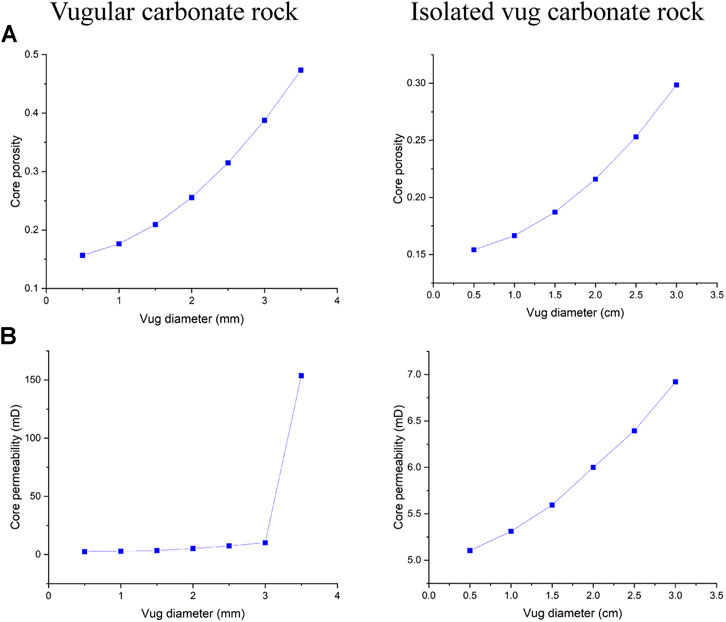
FIGURE 10. Effect of vug diameter on core physical parameters: (A) core porosity and (B) core permeability.

Finally, two varying vug diameters from 0.5 to 3 mm and 0.5 to 2.5 cm are separately chosen to study the influence of vug diameter on acidizing curves, as shown in Figure 11. The results indicate that the PVBT decreases as the vug diameter increases. The difference of the AMBT between different vug diameters is also not noticeable. For the isolated vug carbonate rock, the results indicate that the PVBT decreases as the isolated vug diameter increases. Acid mass does not change a lot with different isolated vug diameters. The noticeable difference of the AMBT in different isolated vug diameters is only shown when acid solution is pumped at an intermediate injection velocity of 0.05 cm/s. Compared to a core sample with a big isolated vug diameter, less acid is needed to achieve the breakthrough with a low isolated vug diameter. In acid solution with intermediated rates, a wormhole-shaped dissolution image is formed, as shown in Figure 12. The isolated vug with a higher diameter induces a wormhole to pass through the isolated vug, which leads to more acid consumption. Lower isolated vug diameter has little effect on the development of wormhole.

FIGURE 11

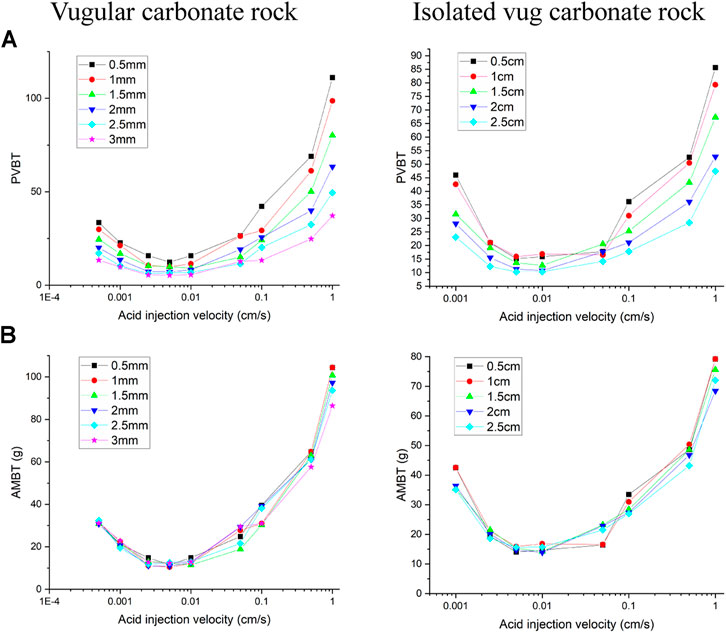
FIGURE 11. Effect of vug diameter on acidizing curves: (A) pore volume to breakthrough (PVBT) and (B) acid mass to breakthrough (AMBT).

FIGURE 12

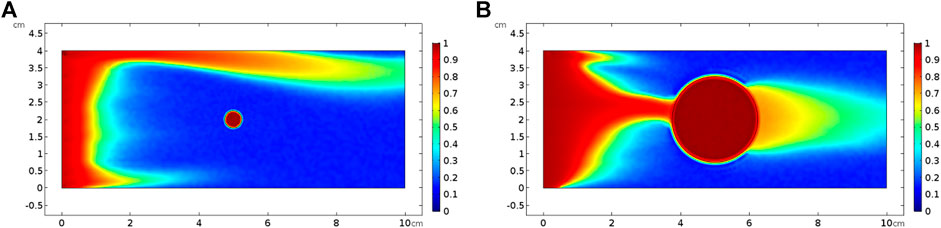
FIGURE 12. Effect of isolated vug porosity on dissolution pattern with an acid injection velocity of 0.05 cm/s: (A) isolated vug diameter of 0.5 cm and (B) isolated vug diameter of 2.5 cm.

Effect of Matrix Porosity

Unlike sandstones, the pore structure of carbonate rock is more complex due to complicated geology processes, which makes the carbonate rock with obvious porosity heterogeneity (Sok et al., 2010; Kim et al., 2011; Milad et al., 2020). This section studies the effect of matrix porosity on the acidizing process of vugular carbonate rock and isolated vug carbonate rock. In a recent work by Jia et al. (2020b), lots of rock sample porosity values measured by experiments are collected and compared. The results show that matrix acidizing target carbonate rock samples usually have rock porosity varying between 0.05 and 0.3.

Figure 13 first studies the effect of matrix porosity on carbonate core porosity. It can be founded that the matrix porosity has a more evident effect on the vugular carbonate rock porosity. The core porosity of vugular carbonate rock increases from 0.31 to 0.46, with an increase of the matrix porosity from 0.05 to 0.25. While for isolated vug carbonate rock, the core porosity only increases from 0.09 to 0.28. Figure 14 further compares the effect of matrix porosity on acidizing results. It can be observed from Figure 14 that matrix porosity mainly has an apparent influence on the stimulation process when acid is injected into the vugular carbonate rock and isolated vug carbonate rock core sample with high rates. Acid consumption mass increases as matrix porosity increases. Compared to the high acid injection rates, the acidizing curve difference becomes less obvious. It is because when the acid injection rate is high, the acid transportation process is more governed by the convection process, and acid is preferred to being uniformly transported into the core sample. Core samples with higher matrix porosity can provide more storage space, which results in more acid being stored in the solid matrix. When acid injection velocity is low, the PVBT slightly decreases as the matrix porosity increases.

FIGURE 13

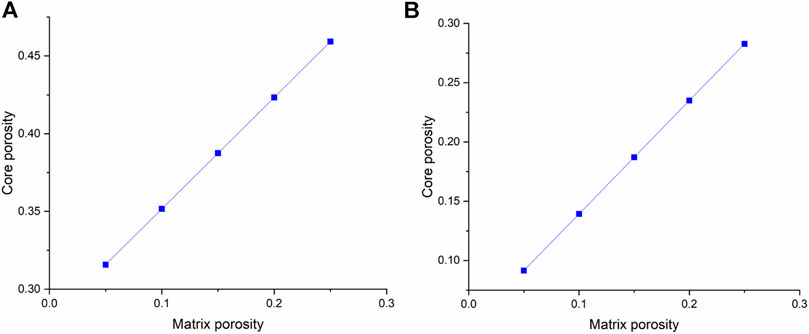
FIGURE 13. Effect of matrix porosity on core porosity: (A) vugular carbonate rock and (B) isolated vug carbonate rock.

FIGURE 14

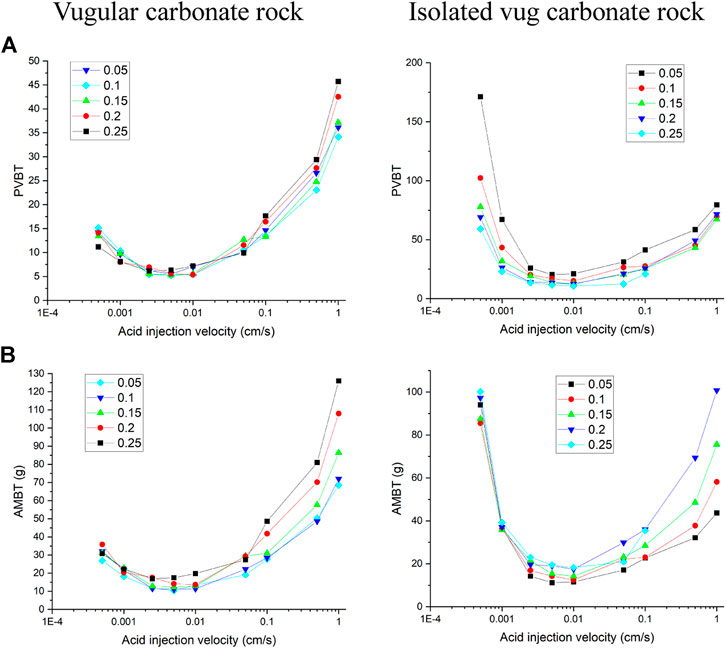
FIGURE 14. Effect of matrix porosity on the acidizing results: (A) pore volume to breakthrough (PVBT) and (B) acid mass to breakthrough (AMBT).

Conclusion

Apart from the matrix region, the presence of vug is very common in the carbonate rock, which provides the main storage space for reserves. In this work, the acidizing process in two typical core-scale separate-vug porosity systems, the vugular carbonate rock and the isolated vug carbonate rock, is studied in detail. The Stokes–Darcy equation is used to describe the fluid flow to avoid using different equations in the free-flow region and porous media region. Parameter sensitivity analysis is preformed to ascertain the effect of acid injection velocity, vug filling degrees, and vug diameter on acidizing results. The main conclusions are presented below:

1) Acid injection velocity and concentration have a noticeable influence on pore volume to breakthrough (PVBT) both for the vugular carbonate rock and isolated vug carbonate rock. The existence of vug reduces the PVBT values of both vugular carbonate rock and isolated vug carbonate rock, which is consistent with the experimental observations. In contrast, acid injection velocity has little influence on acid mass to breakthrough (AMBT).

2) Typical dissolution patterns, including uniform, ramified wormhole, wormhole, and conical wormhole dissolutions, can also be observed in the acidizing process when vug exists. Compared to dissolution patterns of matrix carbonate rock, the wormhole is induced to pass through the vug region.

3) The presence of vug in a separate-vug porosity system contributes to more storage space but has little contribution to hydraulic conductivity. Core porosity and permeability both increase as filling degrees of vug and vug diameter increase. However, the increasing core permeability is limited.

4) Increasing the vug diameter and vug porosity decreases the pore volume to breakthrough both for the vugular carbonate rock and isolated vug carbonate rock.

To sum up, this study provides a powerful two-scale continuum model for the 2D vug acidizing simulation. The improved two-scale continuum model can avoid to use different governing equations in the vug region and the matrix region. The fluid phase continuity equation is also modified to consider the solid matrix dissolution mass term into the fluid phase. Further, the 3D vug simulation will be performed in our following studies.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

CJ: conceptualization, methodology, and writing—original draft; KS: supervision, writing—review, and editing; HZ: software support; JY: supervision and funding acquisition.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We are here grateful for the financial support from the National Major Science and Technology Projects of China (No. 52034010), and China Scholarship Council (201906450038).

References

Acharya, R. C., Valocchi, A. J., Werth, C. J., and Willingham, T. W. (2007). Pore-scale Simulation of Dispersion and Reaction along a Transverse Mixing Zone in Two-Dimensional Porous media. Water Resour. Res. 43. doi:10.1029/2007wr005969

CrossRef Full Text | Google Scholar

Aidagulov, G., Qiu, X., Brady, D., Abbad, M., Onel, Y., and Ewert, U. (2018). New Insights into Carbonate Matrix Stimulation from High-Resolution 3D Images of Wormholes Obtained in Radial Acidizing Experiments in SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition, Dammam, Saudi Arabia (Richardson: Society of Petroleum Engineers), 19.

CrossRef Full Text | Google Scholar

Alkhaldi, M. H., Nasr-El-Din, H. A., and Sarma, H. K. (2010). Kinetics of the Reaction of Citric Acid with Calcite. SPE J. 15, 704–713. doi:10.2118/118724-pa

CrossRef Full Text | Google Scholar

Arns, C. H., Bauget, F., Limaye, A., Sakellariou, A., Senden, T., Sheppard, A., et al. (2005). Pore Scale Characterization of Carbonates Using X-Ray Microtomography. SPE J. 10, 475–484. doi:10.2118/90368-pa

CrossRef Full Text | Google Scholar

Balakotaiah, V., and West, D. H. (2002). Shape Normalization and Analysis of the Mass Transfer Controlled Regime in Catalytic Monoliths. Chem. Eng. Sci. 57, 1269–1286. doi:10.1016/s0009-2509(02)00059-3

CrossRef Full Text | Google Scholar

Beavers, G. S., and Joseph, D. D. (1967). Boundary Conditions at a Naturally Permeable wall. J. Fluid Mech. 30, 197–207. doi:10.1017/s0022112067001375

CrossRef Full Text | Google Scholar

Bernadiner, M. G., Thompson, K. E., and Fogler, H. S. (1992). Effect of Foams Used during Carbonate Acidizing. SPE Prod. Eng. 7, 350–356. doi:10.2118/21035-pa

CrossRef Full Text | Google Scholar

Bijeljic, B., Mostaghimi, P., and Blunt, M. J. (2013). Insights into Non-fickian Solute Transport in Carbonates. Water Resour. Res. 49, 2714–2728. doi:10.1002/wrcr.20238

PubMed Abstract | CrossRef Full Text | Google Scholar

Casar-Gonzalez, R., and Suro-Perez, V. (2000). “Stochastic Imaging of Vuggy Formations,” in SPE International Petroleum Conference and Exhibition in Mexico, Villahermosa, Mexico (Richardson: Society of Petroleum Engineers), 11.

CrossRef Full Text | Google Scholar

De Oliveira, T. J. L., De Melo, A. R., Oliveira, J. A. A., and Pereira, A. Z. I. (2012). Numerical Simulation of the Acidizing Process and PVBT Extraction Methodology Including Porosity/Permeability and Mineralogy Heterogeneity in SPE International Symposium and Exhibition on Formation Damage Control, Lafayette, Louisiana, USA (Richardson: Society of Petroleum Engineers), 9.

CrossRef Full Text | Google Scholar

Dong, K. (2012). Experimental Investigation for the Effect of the Core Length on the Optimum Acid Flux in Carbonate Acidizing. College Station: Texas A & M University.

Dong, K., Jin, X., Zhu, D., and Hill, A. D. (2014). The Effect of Core Dimensions on the Optimal Acid Flux in Carbonate Acidizing in SPE International Symposium and Exhibition on Formation Damage Control, Lafayette, Louisiana, USA (Richardson: Society of Petroleum Engineers), 10.

Google Scholar

Edery, Y., Scher, H., and Berkowitz, B. (2011). Dissolution and Precipitation Dynamics during Dedolomitization. Water Resour. Res. 47. doi:10.1029/2011wr010551

CrossRef Full Text | Google Scholar

Fadlelmula F, M. M., Qian, S., Wang, Y., Fraim, M., He, J., Gao, S., and Killough, J. E. (2016). Separable Multiple-Point Geostatistical Modeling of Three-Dimensional Discrete Fracture-Vug Networks in Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, UAE (Richardson: Society of Petroleum Engineers), 11.

CrossRef Full Text | Google Scholar

Fredd, C. N., and Fogler, H. S. (1998). Alternative Stimulation Fluids and Their Impact on Carbonate Acidizing. SPE J. - SPE J 3, 34–41. doi:10.2118/31074-pa

CrossRef Full Text | Google Scholar

Fredd, C. N., and Fogler, H. S. (1999). Optimum Conditions for Wormhole Formation in Carbonate Porous Media: Influence of Transport and Reaction. SPE J. 4, 196–205. doi:10.2118/56995-pa

CrossRef Full Text | Google Scholar

Fredd, C. N., and Scott Fogler, H. (1998). The Kinetics of Calcite Dissolution in Acetic Acid Solutions. Chem. Eng. Sci. 53, 3863–3874. doi:10.1016/s0009-2509(98)00192-4

CrossRef Full Text | Google Scholar

Frick, T. P., Mostofizadeh, B., and Economides, M. J. (1994). Analysis of Radial Core Experiments for Hydrochloric Acid Interaction with Limestones in SPE Formation Damage Control Symposium, Lafayette, Louisiana (Richardson: Society of Petroleum Engineers), 16.

CrossRef Full Text | Google Scholar

Furui, K., Burton, R. C. C., Burkhead, D. W. W., Abdelmalek, N. A. A., Hill, A. D. D., Zhu, D., et al. (2012a). A Comprehensive Model of High-Rate Matrix-Acid Stimulation for Long Horizontal Wells in Carbonate Reservoirs: Part I-Scaling up Core-Level Acid Wormholing to Field Treatments. SPE J. 17, 271–279. doi:10.2118/134265-pa

CrossRef Full Text | Google Scholar

Furui, K., Burton, R. C. C., Burkhead, D. W. W., Abdelmalek, N. A. A., Hill, A. D. D., Zhu, D., et al. (2012b). A Comprehensive Model of High-Rate Matrix-Acid Stimulation for Long Horizontal Wells in Carbonate Reservoirs: Part II-Wellbore/Reservoir Coupled-Flow Modeling and Field Application. SPE J. 17, 280–291. doi:10.2118/155497-pa

CrossRef Full Text | Google Scholar

Hoefner, M. L., and Fogler, H. S. (1989). Fluid-Velocity and Reaction-Rate Effects during Carbonate Acidizing: Application of Network Model. SPE Prod. Eng. 4, 56–62. doi:10.2118/15573-pa

CrossRef Full Text | Google Scholar

Huang, T., Ostensen, L., and Hill, A. D. (2000). Carbonate Matrix Acidizing with Acetic Acid in SPE International Symposium on Formation Damage Control, Lafayette, Louisiana (Richardson: Society of Petroleum Engineers), 6.

CrossRef Full Text | Google Scholar

Izgec, O., Keys, R. S., Zhu, D., and Hill, A. D. (2008). An Integrated Theoretical and Experimental Study on the Effects of Multiscale Heterogeneities in Matrix Acidizing of Carbonates in SPE Annual Technical Conference and Exhibition, Denver, Colorado, USA (Richardson: Society of Petroleum Engineers), 14.

CrossRef Full Text | Google Scholar

Izgec, O., Zhu, D., and Hill, A. D. (2009). Models and Methods for Understanding of Early Acid Breakthrough Observed in Acid Core-Floods of Vuggy Carbonates in 8th European Formation Damage Conference, Scheveningen, The Netherlands (Richardson: Society of Petroleum Engineers), 15.

CrossRef Full Text | Google Scholar

Izgec, O., Zhu, D., and Hill, A. D. (2010). Numerical and Experimental Investigation of Acid Wormholing during Acidization of Vuggy Carbonate Rocks. J. Pet. Sci. Eng. 74, 51–66. doi:10.1016/j.petrol.2010.08.006

CrossRef Full Text | Google Scholar

Jia, C., Huang, Z., Sepehrnoori, K., and Yao, J. (2020b). A New Mathematical Model and Numerical Studies for Carbonate Matrix Acidizing. SPE J. 197.

Google Scholar

Jia, C., Huang, Z., Sepehrnoori, K., and Yao, J. (2020a). Modification of Two-Scale Continuum Model and Numerical Studies for Carbonate Matrix Acidizing. J. Pet. Sci. Eng. 197, 107972.

Google Scholar

Jia, C., Huang, Z., Sepehrnoori, K., and Yao, J. (2021). Modification of Two-Scale Continuum Model and Numerical Studies for Carbonate Matrix Acidizing. J. Pet. Sci. Eng. 197, 107972. doi:10.1016/j.petrol.2020.107972

CrossRef Full Text | Google Scholar

Kalia, N., and Balakotaiah, V. (2009). Effect of Medium Heterogeneities on Reactive Dissolution of Carbonates. Chem. Eng. Sci. 64, 376–390. doi:10.1016/j.ces.2008.10.026

CrossRef Full Text | Google Scholar

Kalia, N., and Balakotaiah, V. (2007). Modeling and Analysis of Wormhole Formation in Reactive Dissolution of Carbonate Rocks. Chem. Eng. Sci. 62, 919–928. doi:10.1016/j.ces.2006.10.021

CrossRef Full Text | Google Scholar

Kalia, N. (2008). Modeling and Analysis of Reactive Dissolution of Carbonate Rocks. Houston: University of Houston.

Kanaka, M., and Panga, R. (2003). Multiscale Transport and Reaction: Two Case Studies. Richardson: University of Houston.

Kang, Z., Wu, Y.-S., Li, J., Wu, Y., Zhang, J., and Wang, G. (2006). Modeling Multiphase Flow in Naturally Fractured Vuggy Petroleum Reservoirs. SPE Annual Technical Conference and Exhibition. San Antonio, Texas, USA (Richardson: Society of Petroleum Engineers), 10.

CrossRef Full Text | Google Scholar

Kim, D., Peters, C. A., and Lindquist, W. B. (2011). Upscaling Geochemical Reaction Rates Accompanying Acidic CO2‐Saturated Brine Flow in Sandstone Aquifers. Water Resour. Res. 47 (1).

Kossack, C. A., and Gurpinar, O. (2001). A Methodology for Simulation of Vuggy and Fractured Reservoirs in SPE Reservoir Simulation Symposium, Houston, Texas (Richardson: Society of Petroleum Engineers), 12.

CrossRef Full Text | Google Scholar

Kumar, H. T., Muhemmed, S., and Nasr-El-Din, H. A. (2020). Impact of Oil Saturation, CO2 Evolution, and Rock Wettability on Acid Efficiencies during Carbonate Acidizing: A Three-phase Perspective in SPE International Conference and Exhibition on Formation Damage Control, Lafayette, Louisiana, USA (Richardson: Society of Petroleum Engineers), 20.

CrossRef Full Text | Google Scholar

Li, J., Ma, Y., Huang, K., Zhang, Y., Wang, W., Liu, J., et al. (2018). Quantitative Characterization of Organic Acid Generation, Decarboxylation, and Dissolution in a Shale Reservoir and the Corresponding Applications-A Case Study of the Bohai Bay Basin. Fuel 214, 538–545. doi:10.1016/j.fuel.2017.11.034

CrossRef Full Text | Google Scholar

Li, L., Steefel, C. I., and Yang, L. (2008). Scale Dependence of mineral Dissolution Rates within Single Pores and Fractures. Geochimica et Cosmochimica Acta 72, 360–377. doi:10.1016/j.gca.2007.10.027

CrossRef Full Text | Google Scholar

Li, Y. (2017). Development Theories and Methods of Fracture-Vug Carbonate Reservoirs. Academic Press.

Liu, P., Yan, X., Yao, J., and Sun, S. (2019). Modeling and Analysis of the Acidizing Process in Carbonate Rocks Using a Two-phase thermal-hydrologic-chemical Coupled Model. Chem. Eng. Sci. 207, 215–234. doi:10.1016/j.ces.2019.06.017

CrossRef Full Text | Google Scholar

Liu, P., Yao, J., Couples, G. D., Huang, Z., Sun, H., and Ma, J. (2017). Numerical Modelling and Analysis of Reactive Flow and Wormhole Formation in Fractured Carbonate Rocks. Chem. Eng. Sci. 172, 143–157. doi:10.1016/j.ces.2017.06.027

CrossRef Full Text | Google Scholar

Lucia, F. (2007). Carbonate Reservoir Characterization: An Integrated Approach. Springer-Verlag Berlin Heidelberg.

Maheshwari, P., Gharbi, O., Thirion, A., Ali, N. S. E. C., Peyrony, V., Aubry, E., Poitrenaud, H. M., and Benquet, J. C. (2016a). “Development of a Reactive Transport Simulator for Carbonates Acid Stimulation,” in SPE Annual Technical Conference and Exhibition, Dubai, UAE (Richardson: Society of Petroleum Engineers), 11.

Google Scholar

Maheshwari, P., Maxey, J., and Balakotaiah, V. (2016b). Reactive-Dissolution Modeling and Experimental Comparison of Wormhole Formation in Carbonates with Gelled and Emulsified Acids. SPE Prod. Operations 31, 103–119. doi:10.2118/171731-pa

CrossRef Full Text | Google Scholar

Maheshwari, P., Ratnakar, R. R., Kalia, N., and Balakotaiah, V. (2013). 3-D Simulation and Analysis of Reactive Dissolution and Wormhole Formation in Carbonate Rocks. Chem. Eng. Sci. 90, 258–274. doi:10.1016/j.ces.2012.12.032

CrossRef Full Text | Google Scholar

Mahrous, M., Sultan, A., and Sonnenthal, E. (2017). Towards Geochemically Accurate Modeling of Carbonate Acidizing with HCl Acid in SPE Annual Technical Conference and Exhibition, San Antonio, Texas, USA (Richardson: Society of Petroleum Engineers), 22.

CrossRef Full Text | Google Scholar

Menke, H. P., Bijeljic, B., Andrew, M. G., and Blunt, M. J. (2015). Dynamic Three-Dimensional Pore-Scale Imaging of Reaction in a Carbonate at Reservoir Conditions. Environ. Sci. Technol. 49, 4407–4414. doi:10.1021/es505789f

PubMed Abstract | CrossRef Full Text | Google Scholar

Milad, M., Shadizadeh, S. R., Manshad, A. K., and Mohammadi, A. H. (2020). Experimental Study of the Relationship between Porosity and Surface Area of Carbonate Reservoir Rocks. J. Pet. Explor. Prod. Technol. 1–18.

Mousavi, M., Prodanovic, M., and Jacobi, D. (2012). New Classification of Carbonate Rocks for Process-Based Pore-Scale Modeling. SPE J. 18, 243–263. doi:10.2118/163073-pa

CrossRef Full Text | Google Scholar

Nair, N. G., Bryant, S. L., and Jennings, J. W. (2008). Finding the Continuum Scale in Highly Heterogeneous Rocks: Example of a Large Touching Vug Carbonate in SPE Annual Technical Conference and Exhibition, Denver, Colorado, USA (Richardson: Society of Petroleum Engineers), 13.

CrossRef Full Text | Google Scholar

Nick, H. M., Raoof, A., Centler, F., Thullner, M., and Regnier, P. (2013). Reactive Dispersive Contaminant Transport in Coastal Aquifers: Numerical Simulation of a Reactive Henry Problem. J. Contaminant Hydrol. 145, 90–104. doi:10.1016/j.jconhyd.2012.12.005

CrossRef Full Text | Google Scholar

Panga, M. K. R., Ziauddin, M., and Balakotaiah, V. (2005). Two-scale Continuum Model for Simulation of Wormholes in Carbonate Acidization. Aiche J. 51, 3231–3248. doi:10.1002/aic.10574

CrossRef Full Text | Google Scholar

Popov, P., Qin, G., Bi, L., Efendiev, Y., Ewing, R. E., and Li, J. (2009). Multiphysics and Multiscale Methods for Modeling Fluid Flow through Naturally Fractured Carbonate Karst Reservoirs. SPE Reservoir Eval. Eng. 12, 218–231. doi:10.2118/105378-pa

CrossRef Full Text | Google Scholar

Qiu, X., Edelman, E., Aidagulov, G., Ghommem, M., Brady, D., and Abbad, M. (2018). Experimental Investigation of Radial and Linear Acid Injection into Carbonates for Well Stimulation Operations in SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition, Dammam, Saudi Arabia (Richardson: Society of Petroleum Engineers), 15.

Google Scholar

Ramakrishnan, T. S., Ramamoorthy, R., Fordham, E., Schwartz, L., Herron, M., Saito, N., and Rabaute, A. (2001). A Model-Based Interpretation Methodology for Evaluating Carbonate Reservoirs in SPE Annual Technical Conference and Exhibition, New Orleans, Louisiana (Richardson: Society of Petroleum Engineers), 15.

CrossRef Full Text | Google Scholar

Sadeghnejad, S., and Gostick, J. (2020). Multiscale Reconstruction of Vuggy Carbonates by Pore-Network Modeling and Image-Based Technique. SPE J. 25, 253–267. doi:10.2118/198902-pa

CrossRef Full Text | Google Scholar

Saffman, P. G. (1971). On the Boundary Condition at the Surface of a Porous Medium. Stud. Appl. Math. 50, 93–101. doi:10.1002/sapm197150293

CrossRef Full Text | Google Scholar

Sok, R. M., Knackstedt, M. A., Varslot, T., Ghous, A., Latham, S., and Sheppard, A. P. (2010). Pore Scale Characterization of Carbonates at Multiple Scales: Integration of Micro-CT, BSEM, and FIBSEM. Petrophysics 51, 9.

Google Scholar

Wang, D., Li, Y., Hu, Y., Li, B., Deng, X., and Liu, Z. (2016). Integrated Dynamic Evaluation of Depletion-Drive Performance in Naturally Fractured-Vuggy Carbonate Reservoirs Using DPSO-FCM Clustering. Fuel 181, 996–1010. doi:10.1016/j.fuel.2016.05.009

CrossRef Full Text | Google Scholar

Wang, Y., Hill, A. D., and Schechter, R. S. (1993). The Optimum Injection Rate for Matrix Acidizing of Carbonate Formations in SPE Annual Technical Conference and Exhibition, Houston, Texas (Richardson: Society of Petroleum Engineers), 13.

CrossRef Full Text | Google Scholar

Wei, W., Varavei, A., and Sepehrnoori, K. (2017). Modeling and Analysis on the Effect of Two-phase Flow on Wormhole Propagation in Carbonate Acidizing. SPE J. 22, 2067–2083. doi:10.2118/186111-pa

CrossRef Full Text | Google Scholar

Wu, Y.-S., Ehlig-Economides, C. A., Qin, G., Kang, Z., Zhang, W., Ajayi, B. T., and Tao, Q. (2007). A Triple-Continuum Pressure-Transient Model for a Naturally Fractured Vuggy Reservoir in SPE Annual Technical Conference and Exhibition (Anaheim, California, U.S.A.: Society of Petroleum Engineers), 10.

CrossRef Full Text | Google Scholar

Yao, J., Huang, Z., Li, Y., Wang, C., and Lv, X. (2010). Discrete Fracture-Vug Network Model for Modeling Fluid Flow in Fractured Vuggy Porous Media in International Oil and Gas Conference and Exhibition in China, Beijing, China (Richardson: Society of Petroleum Engineers), 14.

CrossRef Full Text | Google Scholar

Yue, P., Xie, Z., Huang, S., Liu, H., Liang, S., and Chen, X. (2018). The Application of N2 Huff and Puff for IOR in Fracture-Vuggy Carbonate Reservoir. Fuel 234, 1507–1517. doi:10.1016/j.fuel.2018.07.128

CrossRef Full Text | Google Scholar

Zhang, L., Bryant, S. L., Jennings, J. W., Arbogast, T. J., and Paruchuri, R. (2004). Multiscale Flow and Transport in Highly Heterogeneous Carbonates in SPE Annual Technical Conference and Exhibition, Houston, Texas (Richardson: Society of Petroleum Engineers), 9.

CrossRef Full Text | Google Scholar

Zhang, L., Nair, N. G., Jennings, J. W., and Bryant, S. L. (2005). Models and Methods for Determining Transport Properties of Touching-Vug Carbonates in SPE Annual Technical Conference and Exhibition, Dallas, Texas (Richardson: Society of Petroleum Engineers), 9.

CrossRef Full Text | Google Scholar