Relationship Between Altimetric Quality and Along-Track Spatial Resolution for iGNSS-R Sea Surface Altimetry: Example for the Airborne Experiment

The altimetric quality and the along-track spatial resolution are the critical parameters to characterize the performance of interferometric global navigation satellite systems reflectometry (iGNSS-R) sea surface altimetry, which is closely related to each other through signal processing time. Among them, the quality of sea surface height (SSH) measurement includes precision and accuracy. In order to obtain higher altimetric quality in the observation area, a longer signal processing time is needed, which will lead to the loss of spatial resolution along the track. In contrast, higher along-track spatial resolution requires more intensive sampling, leading to unsatisfactory altimetric quality. In this study, taking the airborne iGNSS-R observation data as an example, the relationship between the altimetric quality and the along-track spatial resolution is analyzed from the perspectives of precision and accuracy. The results indicate that the reduction in the along-track spatial resolution will improve the altimetric quality. The accuracy range is 0.28–0.73 m, and the precision range is 0.24–0.65 m. However, this change is not linear, and the degree of altimetric quality improvement will decrease as the along-track spatial resolution worsens. The research results in this paper can provide a scientific reference for the configuration of parameters for future spaceborne iGNSS-R altimetry missions.

Introduction

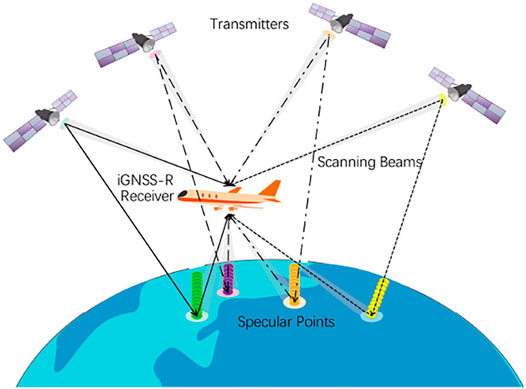
As an effective and innovative bistatic radar remote sensing technology, the global navigation satellite system reflectometry (GNSS-R) can measure a series of physical parameters of the earth’s surface by using GNSS reflected signals, including the sea surface wind speed (Garrison et al., 2002; Katzberg et al., 2006; Foti et al., 2015), the sea surface height (SSH) (Lowe et al., 2002; Rius et al., 2010; Cardellach et al., 2014; Gao et al., 2021) and the soil moisture (Masters et al., 2004; Rodriguez-Alvarez et al., 2009; Wu et al., 2021), etc. Among them, the height of the earth’s reflecting surface relative to the reference ellipsoid can be obtained by measuring the path delay between the direct signal and the reflected signal (Martin-Neira, 1993). Since Martin-Neira first proposed the concept of Passive Reflection and Interference System (PARIS) in 1993, this technology has been verified on various platforms such as ground (Martin-Neira et al., 2001; He et al., 2021), shipborne (Gao et al., 2020), airborne (Lowe et al., 2002; Ruffini et al., 2004; Cardellach et al., 2014), and satellite (Clarizia et al., 2016; Li et al., 2018; Cardellach et al., 2019). Compared with the traditional radar altimeter, GNSS-R altimetry has the advantages of low cost, multi-simultaneous observation, and high spatial coverage.

According to the signal processing method of obtaining path delay, cGNSS-R (conventional GNSS-R) and iGNSS-R (interferometric GNSS-R) are mainly used in GNSS-R sea surface altimetry at present. The cGNSS-R technology cross-correlates the locally generated replica of the transmission signal with the reflected signal for a certain time (typically 1 ms) after proper compensation of the Doppler frequency shift (Zavorotny et al., 2014). Therefore, cGNSS-R needs to use the GNSS signals with known structure, such as L1C, L2C, L5 of GPS, B1I, B1C, B2a of BDS-3 et al. However, the maximum bandwidth of the above signals can only reach 20.46 MHz, which limits the altimetric quality and the along-track spatial resolution (Cardellach et al., 2014). In order to overcome the bandwidth limitation, ESA proposed PARIS in-orbit demonstrator mission (PARIS IoD) in 2011 (Martin-Neira et al., 2010), which aimed to realize the signal interference processing originally proposed by Martin-Neira (Martin-Neira, 1993), i.e., iGNSS-R technology. The iGNSS-R technology makes complex cross-correlation between the direct signal and reflected signal, which can fully use the spectral components in the GNSS signal, and the bandwidth can reach 25 to 50 MHz. The sharper autocorrelation function can be obtained using the wider bandwidth, which will significantly improve the altimetric quality and the along-track spatial resolution (Li et al., 2016).

The altimetric quality and the along-track spatial resolution are the key indicators to characterize the iGNSS-R altimetry performance. It is worth noting that altimetric quality mainly includes precision and accuracy. Among them, the altimetric precision is mainly affected by zero-mean random error, and the altimetric accuracy is mainly determined by the total absolute measurement error affected by the additional random and deterministic errors (Li et al., 2019). The along-track spatial resolution represents the ability of spatial sampling along the orbit of iGNSS-R altimeter, which can be expressed as $R_{\text{a\_t}}=v_{\text{SP}}\cdot T_{\text{coh}}\cdot N_{\text{incoh}}$ ($v_{\text{SP}}$ is the speed of the specular point along the ground track, $T_{\text{coh}}$ is the coherent integration time and $T_{\text{incoh}}$ is the number of samples incoherently averaged) (Cardellach et al., 2014). The along-track spatial resolution can be improved by reducing signal integration time. However, the decrease in the number of independent waveform samples will increase the impact of speckle noise, resulting in a loss in the signal-to-noise ratio (SNR), which will increase the uncertainty of the waveform retracking and ultimately make the altimetric quality poor. Currently, there is no iGNSS-R altimetry satellite in orbit. In contrast, ESA has released several iGNSS-R altimetry mission plans in recent years, such as the PARIS IOD (Martin-Neira et al., 2010), the GNSS reflectometry, radio occultation, and scatterometry onboard the International Space Station (GEROS-ISS) (Wickert et al., 2016), the “Cookie” constellation (Martín-Neira et al., 2016) and the GNSS Transpolar Earth Reflectometry exploriNg system (G-TERN) (Cardellach et al., 2018). The airborne experiment (as shown in Figure 1) is usually used as a pre-research technology for satellite missions. At present, some experimental flight campaigns have been carried out, among which the more typical are the two missions carried out by the Institut d’Estudis Espacials de Catalunya (IEEC) in the Baltic Sea, which are called PIRA (Cardellach et al., 2014) and SPIR (Ribo et al., 2017). Based on this observation, a series of researches on the altimetric quality and the along-track spatial resolution of iGNSS-R were carried out. In 2014, Cardellach et al. used the PIRA observation data to analyze the altimetric precision of cGNSS-R and iGNSS-R under different signal processing times, and simulated the low-orbit iGNSS-R altimetry performance. The results showed that increasing the signal processing time will significantly improve the altimetric precision (Cardellach et al., 2014). In 2017, Ribo et al. first published the SNR results of the SPIR waveform under multi-GNSS (Ribo et al., 2017). In the same year, Li et al. studied the altimetric precision of the SPIR with the signal processing time in 1, 10, and 100 s (Li et al., 2017). In 2019, Fabra et al. analyzed the altimetric accuracy of the SPIR mission when the signal processing time was 10 s. The results show that the altimetric accuracy ranges from 0.09 to 0.66 m according to different signal sources and elevation angles (Fabra et al., 2019). Nevertheless, there has not been a comprehensive study on the relationship between the iGNSS-R altimetric quality (i.e., altimetric precision and accuracy) and the along-track spatial resolution.

FIGURE 1

FIGURE 1. Scheme of the airborne iGNSS-R altimeter theoretical method.

Different from previous studies, taking the experimental data of airborne interferometric GNSS-R provided by IEEC as an example, the altimetric precision and accuracy under different signal integration times are calculated in this paper. Then, through the relationship between the signal integration time and the along-track sampling, the relationship between the airborne iGNSS-R altimetric quality and the along-track spatial resolution is comprehensively analyzed from two aspects of the altimetric precision and accuracy. The purpose of this study is to provide a reference for the payload and orbit design of the future iGNSS-R altimetry satellites.

Data Sets

In this study, we used the iGNSS-R airborne observation data, the DTU15 global mean sea surface model and the DTU global tide model. Among them, we used the iGNSS-R airborne observation data to retrieve the SSH, and the DTU15 global mean sea surface model and the DTU10 global ocean tide model to construct the SSH validation model.

iGNSS-R Airborne Experiment Campaign

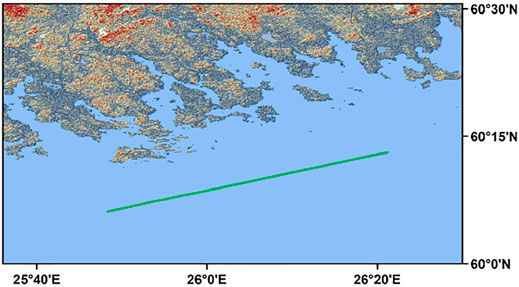
The iGNSS-R observation data used in this study come from the airborne experimental campaign carried out by IEEC on December 3, 2015. The mission location is in the Baltic Sea near Helsinki, Finland (as shown in Figure 2). The critical point of this mission is using the new-generation iGNSS-R receiver developed by IEEC for the first time, which can collect primitive and complex GNSS reflection signals from 16 front-ends at a sampling rate of 80 MHz. The operating frequency band includes all commonly used GNSS L1, L2, and L5 bands (Fabra et al., 2019).

FIGURE 2

FIGURE 2. Flight path of the experimental data over Baltic Sea used in this study.

In this study, we used the observation data of GPS PRN01 in the L1 band with a time of 40001-40600 (GPS SOD, i.e., GPS seconds of day) for a total of 10 min.

Sea Surface Height Validation Model

In order to obtain the altimetric accuracy, it is necessary to compare the SSH retrieved by iGNSS-R observation with the measured SSH data. However, we used the validation model in this study due to the lack of measured SSH data.

In this study, we used the DTU15 MSS model and the DTU10 global tide model to construct the SSH validation model:

$SS{H}_{\text{ref}}=DTU{15}_{\text{MSS}}+DTU{10}_{\text{Tide}}(1)$

The DTU15 mean sea surface (MSS) is a global high-spatial resolution (2 arc-min) mean sea surface model released by the Technical University of Denmark (DTU) in December 2015. Compared with the previous version, the most significant improvement of DTU15 model is the use of improved Cryosat-2 LRM, SAR, and SAR-In data (Skourup et al., 2017).

The DTU also releases the DTU10 global tide model. The DTU10 considered the influence of wavelength and water depth of diurnal and semidiurnal tidal components, and uses the dynamic difference method based on depth to interpolate the correction value into the FES 2004. The load tide uses the calculation results of the FES 2004. The grid resolution is 7.5′×7.5′ (Turner et al., 2013).

Signal Processing and Sea Surface Height Retrieval Methods

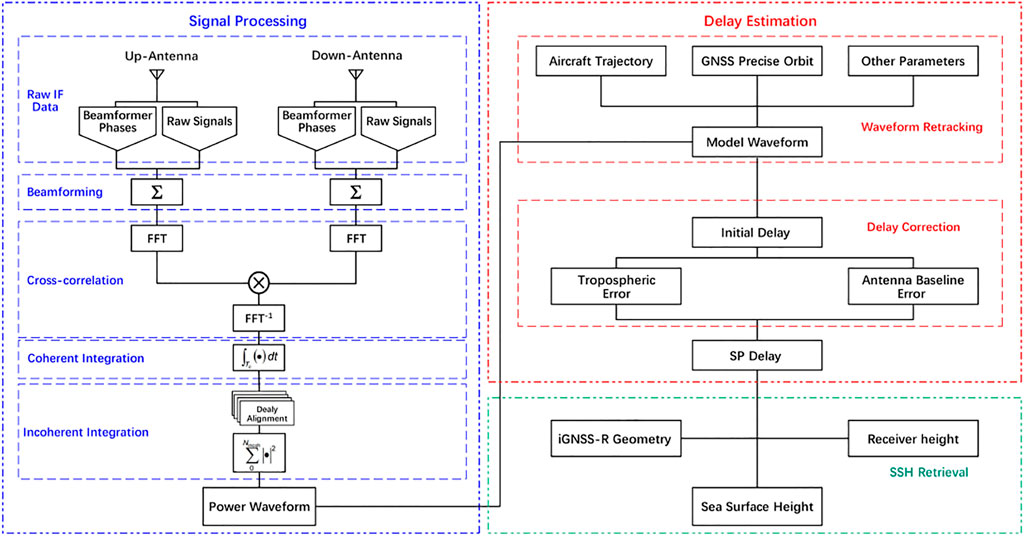
In this section, we illustrate the theoretical method of the SSH inversion from the raw IF data, including the signal processing, the delay estimation and the SSH retrieval. Figure 3 shows the whole process.

FIGURE 3

FIGURE 3. Schematic flow chart of the process followed by SSH inversion from raw IF signals.

Signal Processing

Raw Signal Processing

After receiving the raw IF data through the zenith and nadir antennas, it needs further processing to obtain the complex waveforms. This research adopts the original data processing method provided in Fabra et al. (2019). First of all, the direct and reflected signals are combined through beamforming. After that, the direct and reflected signals are cross-correlated in the frequency domain, and a total of $6\times {10}^5$ complex waveforms (1 ms) $c\left(t,\tau \right)$ are obtained. Compared with the signal processing method of cGNSS-R, the main difference of iGNSS-R is the need for beamforming and the use of the observed direct signal as the correlation input.

Coherent Integration and Incoherently Averaged

In order to reduce the influence of thermal and speckle noise, and improve the SNR of the power waveform, it is necessary to perform coherent integration ($T_{\text{coh}}$) and a large number of incoherent averages ($N_{\text{incoh}}$) on the complex waveform (1 ms) (Zavorotny et al., 2014):

$w\left(T_0+N_{\text{incoh}}\cdot T_{\text{coh}}/2,\tau \right)=\frac{1}{N_{\text{incoh}}}{\displaystyle \sum _{n=0}^{N_{\text{incoh}}-1}c\left(n{T}_{\text{coh}},\tau \right)}(2)$

where $T_0$ is the start time of the signal processing.

The corresponding power waveform is:

$W\left(T_0+N_{\text{incoh}}\cdot T_{\text{coh}}/2,\tau \right)={\left|w\left(T_0+N_{\text{incoh}}\cdot T_{\text{coh}}/2,\tau \right)\right|}^2(3)$

It is worth noting that waveform alignment is needed before the incoherent averages (Park et al., 2012). In this study, the coherent integration time is 1, 2, 5, and 10 ms, respectively, and the average number of incoherent is 1,000 (i.e., 1 s incoherent average time).

Delay Estimation

Accurate estimation of the delay at the specular point is the key to ensure the iGNSS-R altimetry quality. The initial delay can be obtained through waveform retracking. In addition, the correction of delay errors is needed, such as the tropospheric delay and the zenith-nadir antenna baseline delay.

Waveform Retracking

The reflected waveform retracking is based on comparing measured and modeled waveforms (Li et al., 2019). The modeled waveform corresponding to each measured waveform in this paper is obtained through the Z-V model implemented in the “wavpy” GNSS-R open-source software (Fabra et al., 2017). Currently, the waveform retracker mainly includes HALF (the point at a fraction of the peak power), DER (the point with the maximum of waveform’s first derivative), and FIT (fitting the waveform to its model) (Li et al., 2019). In this study, we used the DER to estimate the delay of the specular point along the waveform (Cardellach et al., 2014):

${\tau }_{\text{sp}}={\tau }_{\text{DER}}^{\text{obs}}+\left({\tau }_{\text{sp}}^{\text{model}}-{\tau }_{\text{DER}}^{\text{model}}\right)(4)$

where ${\tau }_{\text{DER}}^{\text{obs}}$ is the delay corresponding to the maximum derivative point calculated from the measured waveform, ${\tau }_{\text{sp}}^{\text{model}}$ and ${\tau }_{\text{DER}}^{\text{model}}$ represent the specular point delay and derivative maximum point delay of simulation waveform respectively.

Delay Correction

The troposphere goes generally from the ground to 15 km altitude. Due to the high humidity of the sea surface and the different transmission paths of direct and reflected signals, the deviation caused by the troposphere to the airborne iGNSS-R delay estimation cannot be ignored. In this study, we used the model provided in Jin et al. (2014) to estimate the tropospheric delay:

${\tau }_{\text{trop}}=2\frac{2.3}{\sin \theta }\left(1-e^{-H_{\text{R}}/H_{\text{trop}}}\right)(5)$

where $\theta$ is the elevation angle at the specular point, $H_{\text{R}}$ represents the height of the iGNSS-R receiver. The $H_{\text{trop}}$ is the height of the troposphere at the observation location (we take $H_{\text{trop}}$ = 8,621 m).

The zenith-nadir antenna baseline delay ${\tau }_{\text{antenna}}$ is obtained by the path difference between the zenith antenna and the nadir antenna relative to the specular point.

Sea Surface Height Retrieval

After correcting the delay error of the specular point, the ellipsoidal height of the sea surface above the WGS84 reference ellipsoid can be obtained by the geometric relationship of the airborne iGNSS-R (Li et al., 2019):

$SS{H}_{\text{iGNSS}-\text{R}}=\frac{{\tau }_{\text{sp}}-\left({\tau }_{\text{trop}}+{\tau }_{\text{antenna}}\right)}{2\sin \theta }-H_{\text{R}}(6)$

Altimetric Quality Standard

Altimetric Precision

The altimetric precision is affected by zero-mean random error, mainly due to the random nature of the received signals caused by thermal and speckle noise. The measured SSH sequence is subtracted from a fitted piecewise linear function to form zero mean, near white noise SSH residuals (Li et al., 2017). Therefore, we define the altimetric precision as:

${\sigma }_{\text{p}}=SS{H}_{\text{iGNSS}-\text{R}}-Fit\left(T_i\right)(7)$

where $Fit\left(\right)$ is the linear fitting equation based on the measured SSH, $T_i$ is the epoch.

We define the average altimetric precision of N specular points as:

${\overline{\sigma }}_{\text{p}}=\frac{{\displaystyle {\sum }_{i=1}^N\left|{\sigma }_{\text{p}}^i\right|}}{N}(8)$

Altimetric Accuracy

In this study, we define the altimetric accuracy as the difference between the measured SSH and the validation SSH:

${\sigma }_{\text{a}}=SS{H}_{\text{iGNSS}-\text{R}}-SS{H}_{\text{ref}}(9)$

We define the average altimetric accuracy of N specular points as:

${\overline{\sigma }}_{\text{a}}=\frac{{\displaystyle {\sum }_{i=1}^N\left|{\sigma }_{\text{a}}^i\right|}}{N}(10)$

Results and Discussion

Power Waveform

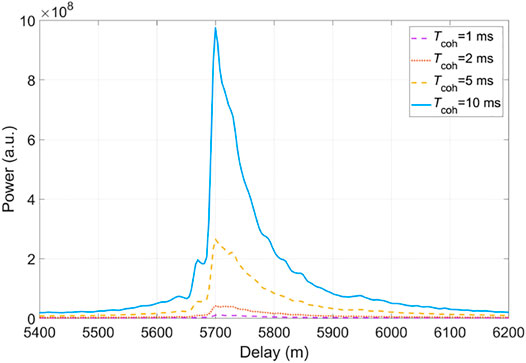
The power waveform is the database for obtaining the iGNSS-R altimetric quality. Among them, the altimetric precision is directly related to the SNR of the waveform, and the acquisition of the altimetric accuracy requires the power waveform retracking to calculate the delay of the specular points. In this study, the coherent integration time is set to 1, 2, 5, and 10 ms, and the number of the incoherent average is 1,000, so the signal processing time is 1, 2, 5, and 10 s, respectively. Since a total of 10 min of airborne iGNSS-R observations are used, the corresponding number of the power waveform is 600, 300, 120, and 60, respectively.

Figure 4 presents the iGNSS-R power waveform results at different signal processing times. Although the longer of signal processing time will generate the greater noise amplitude, it will increase the amplitude of the waveform power more significantly.

FIGURE 4

FIGURE 4. Power waveform of airborne iGNSS-R under different signal processing time.

In this study, we define the SNR of the waveform as (Lowe et al., 2002):

$SN{R}_{\text{wf}}=\frac{\max \left[W\left(\tau \right)\right]-A_{\text{noise}}}{{\sigma }_{\text{noise}}}(11)$

where $A_{\text{noise}}$ is the average noise amplitude of the waveform, ${\sigma }_{\text{noise}}$ is the standard deviation of noise amplitude. According to Equation (11), the corresponding SNR of 1, 2, 5, and 10 s power waveforms is 8.69, 11.09, 14.82, and 17.04 dB, respectively.

Relationship between Altimetric Precision and Along-Track Spatial Resolution.

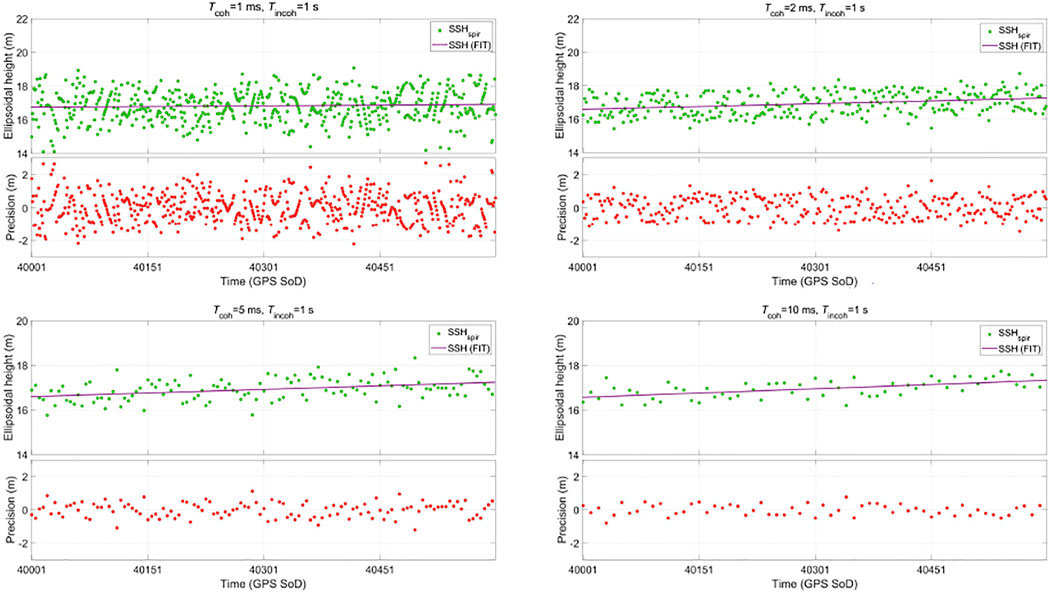
Based on the airborne iGNSS-R power waveform obtained by the signal processing, the altimetric precision corresponding to each specular point is calculated according to Equation (7). The results (Figure 5) show a clear stable distribution of the altimetric precision with the increase of signal processing time, suggesting a significant role played by the SNR. According to Equation (8), the average altimetric precision under different along-track spatial resolutions is calculated. The relationship between the average altimetric precision and along-track spatial resolution is intuitively presented in Table 1 and Figure 6.

FIGURE 5

FIGURE 5. Airborne iGNSS-R altimetric precision under different signal processing time.

TABLE 1

TABLE 1. The performance of the altimetric precision and the along-track spatial resolution.

FIGURE 6

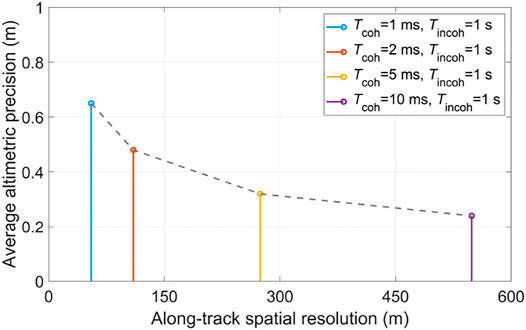
FIGURE 6. Altimetric precision as a function of along-track spatial resolution under airborne scene.

These results indicate that the altimetric precision of iGNSS-R gradually increases as the along-track spatial resolution decreases. However, this dependence is not linear. When the along-track spatial resolution changes in the range of 50 m–150 m, the altimetric precision changes sharply, and then the fluctuation of the altimetric precision becomes relatively weak with the increasing of the along-track spatial resolution, which is mainly due to the increase of signal processing time, and the SNR will tend to the stable state.

In order to estimate the performance of PARIS IOD, Martin-Neira et al. (2010) established a model of altimetric precision and SNR:

${\sigma }_{\text{p}}=\frac{c}{2\sin {\theta }_{\text{S}}\sqrt{N_{\text{incoh}}}}\cdot \frac{W\left(\text{0}\right)}{W{\left(\text{0}\right)}^{\prime }}\cdot \sqrt{{\left(1+\frac{1}{SNR}\right)}^2+{\left(\frac{1}{SNR}\right)}^2}(12)$

where $c$ is the speed of light in vacuum, $W\left(\text{0}\right)$ is the signal power at the specular point, $W{\left(\text{0}\right)}^{\prime }$ is the first derivative value at the specular point. Based on the SNR results in Section Power Waveform and Equation (12), the precision results under the model are calculated. The model precision results have an average deviation of 0.17 m from the results in Figure 6. We consider that the precision model does not take into account the correlation between power waveform and noise. The correlation between waveforms in the airborne scene is significantly stronger than that in the spaceborne scene (You et al., 2004), which leads to the precision estimation deviation using the model in the airborne scene.

Relationship Between Altimetric Accuracy and Along-Track Spatial Resolution

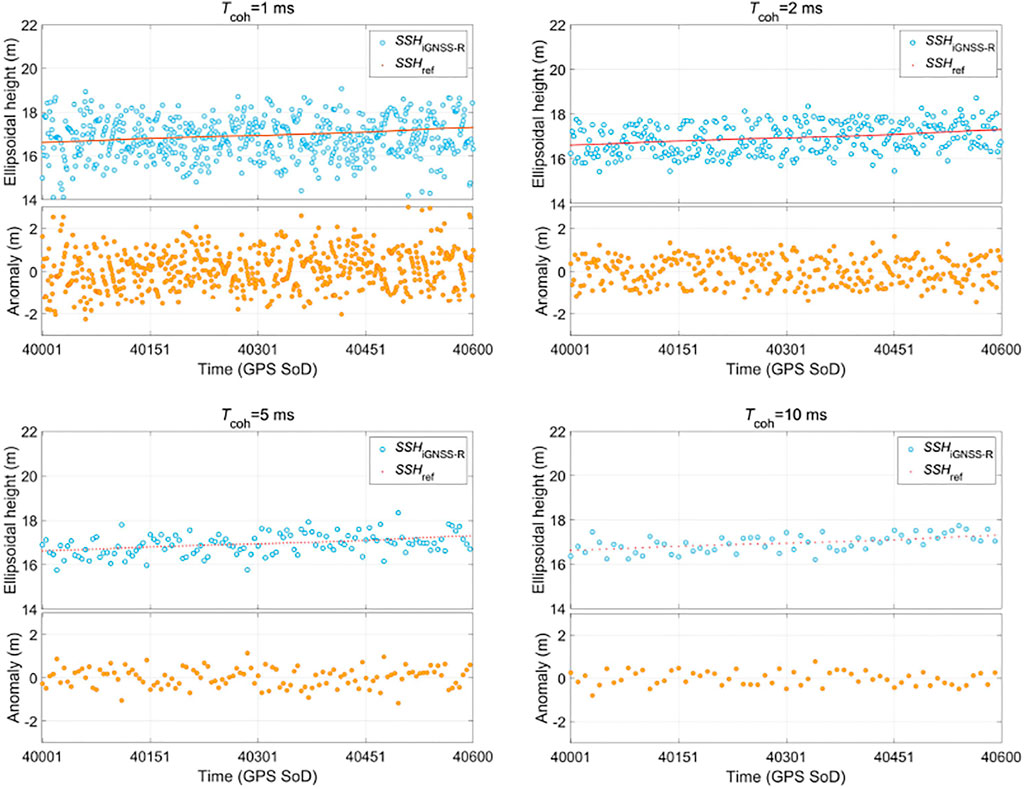
According to the iGNSS-R power waveform and the DER retracking algorithm, combined with Equation (6) and Equation (9), the SSH and the altimetric accuracy are calculated. The results (Figure 7) demonstrate that the SSH inversed from the airborne iGNSS-R observations is in good consistency with the validation model. As the coherent integration time increases, the deviation between SSH_iGNSS-R and SSH_ref gradually decreases. The main reasons for the deviation are as follows.

1) In this study, only the tropospheric delay and the zenith-nadir antenna baseline delay were considered in the altimetry retrieval, and other errors such as the aircraft positioning error and the flight altitude were not included in the SSH inversion.

2) The signal processing time ranges from 1 s to 10 s. Although the SNR of the reflected signal has been improved, there are still some speckle and thermal noise in the power waveform.

3) The validation model SSH_ref is obtained based on the inversion of observation from multiple remote sensing and gravity satellites for many years, which has good stability. However, the airborne experimental campaign only performed a single measurement at the observation area, and the results have certain randomness, which led to the deviations between the inversed SSH results and the validation model.

FIGURE 7

FIGURE 7. Airborne iGNSS-R altimetric accuracy under different signal processing time.

According to Equation (10), the average altimetric accuracy under different along-track spatial resolutions is calculated, and the results are given in Table 2 and Figure 8.

TABLE 2

TABLE 2. The performance of the altimetric accuracy and the along-track spatial resolution.

FIGURE 8

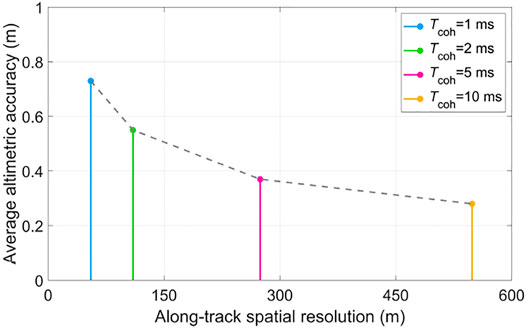
FIGURE 8. Altimetric accuracy as a function of along-track spatial resolution under the airborne scene.

The result of the altimetric accuracy changes with the along-track spatial resolution is similar to that in Section Relationship Between Altimetric Accuracy and Along-Track Spatial Resolution. The altimetric accuracy increases as the along-track spatial resolution decreases due to the steeper lead-edge of the power waveform, thus improving the accuracy of the specular point delay estimation.

Advices for Future Spaceborne iGNSS-R Altimetry Missions

Combined with the airborne experimental results, in order to give more accurate suggestions for future iGNSS-R altimetry satellite missions, the altimetric precision is simulated based on the NASNRM model (Liu et al., 2019), SNR model of direct signal (Jin et al., 2014) and the precision model (Martin-Neira et al., 2010). Simulation parameters are shown in Table 3. Combined with the simulation results of spaceborne iGNSS-R altimetric quality and along-track spatial resolution, the advices for future spaceborne iGNSS-R altimetry missions as follows.

1) The future iGNSS-R sea surface altimetry satellites require high-gain zenith and nadir antennas. The iGNSS-R altimetric precision increases as the along-track spatial resolution decreases, mainly due to the increase in signal processing time that improves the SNR of the waveform. The increase in the antenna gain can also increase the SNR of the waveform, which can reduce the signal processing time and thereby improve the along-track spatial resolution. The performance of spaceborne iGNSS-R altimetry under different gains when the elevation angle is 75 degrees is presented in Figure 9. The results show that the amplitude of accuracy varies with spatial resolution becomes gentle with the increase of antenna gain. When the antenna gain is greater than 20 dBi, the altimetric precision can be better than 1 m at the spatial resolution of 10 km. Of course, the increase in gain will also improve the quality of the antenna, which needs to be considered in the design of the satellite system.

2) The future spaceborne iGNSS-R receiver should be designed for all available GNSS satellites. Gao et al. (2019) studied the distribution of specular reflections under different GNSS systems. Compared with only the GPS as the illuminator, the number of specular reflection events is 3.75 times higher when the transmitter is four-system GNSS (i.e., GPS, BDS, GALILEO, and GLONASS), which indicates that the geometric relationship of iGNSS-R under four-system GNSS is better than only GPS, and reflection events with higher elevation angles can be obtained. The spaceborne iGNSS-R altimetry at different elevation angles is simulated when the antenna gain is 23 dBi. As shown in Figure 10, the influence of elevation angle on iGNSS-R altimetry performance is significant. When the spatial resolution is 10 km, the altimetric precision is 2.20 m when the height angle is 45 degrees and 0.25 m when the height angle is 85 degrees. Therefore, it can be predicted that the increase in the number of signal sources will significantly improve the iGNSS-R altimetry performance.

3) The future iGNSS-R altimetry satellites need to use wider bandwidth signals. The signal bandwidth is one of the main factors limiting the performance of GNSS-R altimetry. The iGNSS-R technology breaks through the limitation that cGNSS-R technology can only use signals with known structure. In the future iGNSS-R satellites can use signals with a wider bandwidth than GPS L1, such as Galileo E5 Full. The signal bandwidth of Galileo E5 Full can reach 51 MHz, so the spectral spatial resolution of Galileo E5 Full can be 1.43 times higher than that of GPS L1 Full. In addition, the altimetry sensitivity of Galileo E5 Full signal in the spaceborne scene can reach 0.19 m⁻¹, so the altimetric precision of Galileo E5 Full can be improved by 2.13 times compared with GPS L1 Full under the same SNR.

TABLE 3

TABLE 3. System and instrument parameters of the simulated spaceborne iGNSS-R altimeter.

FIGURE 9

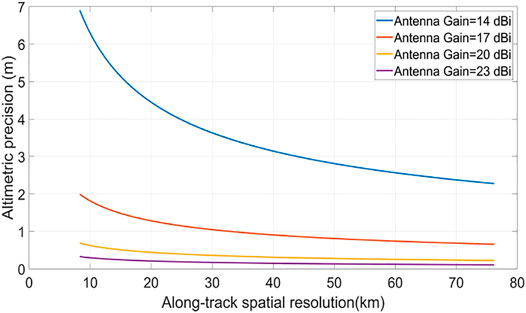
FIGURE 9. Relationship between precision and spatial resolution under different antenna gains at elevation angle of 75 degrees in the spaceborne scene.

FIGURE 10

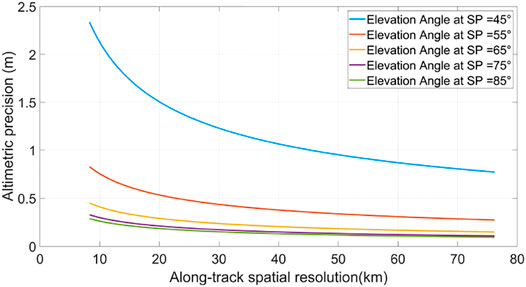
FIGURE 10. Relationship between precision and spatial resolution under different elevation angle at antenna gains of 23 dBi the spaceborne scene.

Conclusion

The altimetric quality and the along-track spatial resolution are critical parameters in the design of the spaceborne iGNSS-R altimetry missions. In order to reduce the error caused by the simulation, this research uses the airborne iGNSS-R altimetry experimental observation to analyze the relationship between the altimetric quality and the along-track spatial resolution from two perspectives precision and accuracy, in order to obtain more precise information of ocean activities under the condition of ensuring the altimetric quality. This study calculated the altimetric precision and accuracy under different along-track spatial resolutions by changing the signal processing time. The results indicate that the iGNSS-R altimetric quality increases with the decrease of the along-track spatial resolution. The range of altimetric precision is 0.24–0.65 m, and the altimetric accuracy is 0.28–0.73 m. However, this relationship is not linear, and the increase in altimetric quality gradually weakens as the along-track spatial resolution decreases, which is determined by the relationship between the power waveform characteristics and the signal processing time.

The estimated altimetry performance of spaceborne iGNSS-R altimeter is also discussed in this paper. The higher antenna gain and better GNSS observation geometry can obtain better altimetric quality with the same along-track spatial resolution. In addition, the GNSS signal under the new system will also bring available opportunities for the improvement of iGNSS-R altimetry. It is worth noting that we used the ideal instrument parameters in the simulation. Some errors generated in the practical application are not considered, such as the antenna efficiency, the power loss in the receiver channel, and phase error in beamforming. Of course, the increase of SNR can reduce the impact of the above errors on altimetry performance estimation.

This study verified the interdependence between the altimetric quality and the along-track spatial resolution, providing a theoretical reference for the balanced selection of the two parameters in the future spaceborne iGNSS-R altimetry missions.

In future research, due to the correlation between waveform and noise in signal processing, it is necessary to establish an optimization model of altimetric precision and effective coherent integration time to evaluate the optimal signal processing time.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

ZL: Conceived the experiments and wrote the paper. WZ and FW: Experiment design, project managment, review, and modification. GK: Provided suggestions for the experiments. XS and QW: Data collection. All authors contributed to the article and approved the submitted version. ZL, WZ, and FW contributed equally to this paper.

Funding

This work was supported by the National Natural Science Foundation of China under Grant (41774014, 41574014), the Liaoning Revitalization Talents Program under Grant (XLYC2002082), the Frontier Science and Technology Innovation Project and the Innovation Workstation Project of Science and Technology Commission of the Central Military Commission under Grant (085015), the Independent Research and Development Start-up Fund of Qian Xuesen Laboratory of Space Technology (Y-KC-WY-99-ZY-000-025), and the Outstanding Youth Fund of China Academy of Space Technology.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to thank Institute of Space Sciences (ICE, CSIC) and Institute for Space Studies of Catalonia (IEEC) for providing the raw data processing results of the air-borne experiment. We would also like to thank DTU for providing the DTU15 global mean sea surface model and the DTU10 global ocean tide model.

References

Cardellach, E., Flato, G., Fragner, H., Gabarro, C., Gommenginger, C., Haas, C., et al. (2018). GNSS Transpolar Earth Reflectometry exploriNg System (G-TERN): Mission Concept. IEEE Access 6, 13980–14018. doi:10.1109/ACCESS.2018.2814072

CrossRef Full Text | Google Scholar

Cardellach, E., Li, W., Rius, A., Semmling, M., Wickert, J., Zus, F., et al. (2020). First Precise Spaceborne Sea Surface Altimetry with GNSS Reflected Signals. IEEE J. Sel. Top. Appl. Earth Observations Remote Sensing 13, 102–112. doi:10.1109/JSTARS.2019.2952694

CrossRef Full Text | Google Scholar

Cardellach, E., Rius, A., Martin-Neira, M., FabraNogues-Correig, F. O., Nogues-Correig, O., Ribo, S., et al. (2014). Consolidating the Precision of Interferometric GNSS-R Ocean Altimetry Using Airborne Experimental Data. IEEE Trans. Geosci. Remote Sensing 52, 4992–5004. doi:10.1109/tgrs.2013.2286257

CrossRef Full Text | Google Scholar

Clarizia, M. P., Ruf, C., Cipollini, P., and Zuffada, C. (2016). First Spaceborne Observation of Sea Surface Height Using GPS‐Reflectometry. Geophys. Res. Lett. 43, 767–774. doi:10.1002/2015GL066624

CrossRef Full Text | Google Scholar

Fabra, F., Cardellach, E., Li, W., and Rius, A. (2017). “WAVPY: A GNSS-R Open Source Software Library for Data Analysis and Simulation,” in Proceeding of the . IEEE Int. Geosci. Remote Sens. Symp. (IGARSS), Fort Worth, TX, USA, July 2017 (IEEE), 4125–4128. doi:10.1109/IGARSS.2017.8127908

CrossRef Full Text | Google Scholar

Fabra, F., Cardellach, E., Ribó, S., Li, W., Rius, A., Arco-Fernández, J., et al. (2019). Is Accurate Synoptic Altimetry Achievable by Means of Interferometric GNSS-R? Remote Sensing 11, 5051–50519. doi:10.3390/rs11050505

CrossRef Full Text | Google Scholar

Foti, G., Gommenginger, C., Jales, P., Unwin, M., Shaw, A., Robertson, C., et al. (2015). Spaceborne GNSS Reflectometry for Ocean Winds: First Results from the UK TechDemoSat-1 Mission. Geophys. Res. Lett. 42, 5435–5441. doi:10.1002/2015GL064204

CrossRef Full Text | Google Scholar

Gao, F., Xu, T., Meng, X., Wang, N., He, Y., and Ning, B. (2021). A Coastal experiment for GNSS-R Code-Level Altimetry Using BDS-3 New Civil Signals. Remote Sensing 13 (7), 1378. doi:10.3390/rs13071378

CrossRef Full Text | Google Scholar

Gao, F., Xu, T., Wang, N., He, Y., and Luo, X. (2020). A Shipborne Experiment Using a Dual-Antenna Reflectometry System for GPS/BDS Code Delay Measurements. J. Geod 94, 88. doi:10.1007/s00190-020-01421-4

CrossRef Full Text | Google Scholar

Gao, F., Xu, T., Wang, N., Jiang, C., Du, Y., Nie, W., et al. (2018). Spatiotemporal Evaluation of GNSS-R Based on Future Fully Operational Global Multi-GNSS and Eight-LEO Constellations. Remote Sensing 10, 67. doi:10.3390/rs10010067

CrossRef Full Text | Google Scholar

Garrison, J. L., Komjathy, A., Zavorotny, V. U., and Katzberg, S. J. (2002). Wind Speed Measurement Using Forward Scattered GPS Signals. IEEE Trans. Geosci. Remote Sensing 40, 50–65. doi:10.1109/36.981349

CrossRef Full Text | Google Scholar

He, Y., Gao, F., Xu, T., Meng, X., and Wang, N. (2021). Coastal Altimetry Using Interferometric Phase from Geo Satellite in Quasi-Zenith Satellite System. IEEE Geosci. Remote Sensing Lett. 99, 1–5. doi:10.1109/LGRS.2021.3068376

CrossRef Full Text | Google Scholar

Huaizu You, H., Garrison, J. L., Heckler, G., and Zavorotny, V. U. (2004). Stochastic Voltage Model and Experimental Measurement of Ocean-Scattered GPS Signal Statistics. IEEE Trans. Geosci. Remote Sensing 42 (10), 2160–2169. doi:10.1109/TGRS.2004.834628

CrossRef Full Text | Google Scholar

Jin, S., Cardellach, E., and Xie, F. (2014). GNSS Remote Sensing: Theory, Methods and Applications; Remote Sensing and Digital Image Processing. Dutch, The Netherlands: Springer

Google Scholar

Katzberg, S. J., Torres, O., and Ganoe, G. (2006). Calibration of Reflected GPS for Tropical Storm Wind Speed Retrievals. Geophys. Res. Lett. 33, L18602-1–L18602-5. doi:10.1029/2006GL026825

CrossRef Full Text | Google Scholar

Li, W., Cardellach, E., Fabra, F., Ribo, S., and Rius, A. (2020). Assessment of Spaceborne GNSS-R Ocean Altimetry Performance Using CYGNSS mission Raw Data. IEEE Trans. Geosci. Remote Sensing 58, 238–250. doi:10.1109/tgrs.2019.2936108

CrossRef Full Text | Google Scholar

Li, W., Cardellach, E., Fabra, F., Ribó, S., and Rius, A. (2018). Lake Level and Surface Topography Measured with Spaceborne GNSS‐Reflectometry from CYGNSS Mission: Example for the Lake Qinghai. Geophys. Res. Lett. 45, 13332–13341. doi:10.1029/2018GL080976

CrossRef Full Text | Google Scholar

Li, W., Rius, A., Fabra, F., Cardellach, E., Ribo, S., and Martin-Neira, M. (2018). Revisiting the GNSS-R Waveform Statistics and its Impact on Altimetric Retrievals. IEEE Trans. Geosci. Remote Sensing 56, 2854–2871. doi:10.1109/tgrs.2017.2785343

CrossRef Full Text | Google Scholar

Li, W., Rius, A., Fabra, F., Martín-Neira, M., Cardellach, E., Ribó, S., et al. (2016). The Impact of Inter-Modulation Components on Interferometric GNSS-Reflectometry. Remote Sensing 8, 10131–101311. doi:10.3390/rs8121013

CrossRef Full Text | Google Scholar

Liu, Z. Q., Zheng, W., Wu, F., Kang, Q., Li, Z., Wang, Q., et al. (2019). Increasing the Number of Sea Surface Reflected Signals Received by GNSS-Reflectometry Altimetry Satellite Using the Nadir Antenna Observation Capability Optimization Method. Remote Sensing 11 (21), 2473. doi:10.3390/rs11212473

CrossRef Full Text | Google Scholar

Lowe, S. T., LaBrecque, J. L., Zuffada, C., Romans, L. J., Young, L. E., and Hajj, G. A. (2002). First Spaceborne Observation of an Earth-Reflected GPS Signal. Radio Sci. 37, 71–128. doi:10.1029/2000RS002539

CrossRef Full Text | Google Scholar

Lowe, S. T., Zuffada, C., Chao, Y., Kroger, P., Young, L. E., and LaBrecque, J. L. (2002). 5-cm-Precision Aircraft Ocean Altimetry Using GPS Reflections. Geophys. Res. Lett. 29, 1375. doi:10.1029/2002GL014759

CrossRef Full Text | Google Scholar

Martin-Neira, M. (1993). A Passive Reflectometry and Interferometry System (PARIS): Application to Ocean Altimetry. ESA J. 17, 331–355

Google Scholar

Martin-Neira, M., Caparrini, M., Font-Rossello, J., Lannelongue, S., and Vallmitjana, C. S. (2001). The PARIS Concept: an Experimental Demonstration of Sea Surface Altimetry Using GPS Reflected Signals. IEEE Trans. Geosci. Remote Sensing 39, 142–150. doi:10.1109/36.898676

CrossRef Full Text | Google Scholar

Martin-Neira, M., D'Addio, S., Buck, C., Floury, N., and Prieto-Cerdeira, R. (2011). The PARIS Ocean Altimeter In-Orbit Demonstrator. IEEE Trans. Geosci. Remote Sensing 49, 2209–2237. doi:10.1109/tgrs.2010.2092431

CrossRef Full Text | Google Scholar

Martín-Neira, M., Li, W., Andrés-Beivide, A., and Ballesteros-Sels, X. (2016). “Cookie”: A Satellite Concept for GNSS Remote Sensing Constellations. IEEE J. Sel. Top. Appl. Earth Observations Remote Sensing 9, 4593–4610. doi:10.1109/JSTARS.2016.2585620

CrossRef Full Text | Google Scholar

Masters, D., Axelrad, P., and Katzberg, S. (2004). Initial Results of Land-Reflected GPS Bistatic Radar Measurements in SMEX02. Remote Sensing Environ. 92, 507–520. doi:10.1016/j.rse.2004.05.016

CrossRef Full Text | Google Scholar

Park, H., Camps, A., Valencia, E., Rodriguez-Alvarez, N., Bosch-Lluis, X., Ramos-Perez, I., et al. (2012). Retracking Considerations in Spaceborne GNSS-R Altimetry. GPS Solut 16, 507–518. doi:10.1007/s10291-011-0251-7

CrossRef Full Text | Google Scholar

Ribó, S., Arco-Fernández, J., Cardellach, E., Fabra, F., Li, W., Nogués-Correig, O., et al. (2017). A Software-Defined GNSS Reflectometry Recording Receiver with Wide-Bandwidth, Multi-Band Capability and Digital Beam-Forming. Remote Sensing 9, 4501–45020. doi:10.3390/rs9050450

CrossRef Full Text | Google Scholar

Rius, A., Cardellach, E., and Martin-Neira, M. (2010). Altimetric Analysis of the Sea-Surface GPS-Reflected Signals. IEEE Trans. Geosci. Remote Sensing 48, 2119–2127. doi:10.1109/tgrs.2009.2036721

CrossRef Full Text | Google Scholar

Rodriguez-Alvarez, N., Bosch-Lluis, X., Camps, A., Vall-Llossera, M., Valencia, E., Marchan-Hernandez, J. F., et al. (2009). Soil Moisture Retrieval Using GNSS-R Techniques: Experimental Results Over a Bare Soil Field. IEEE Trans. Geosci. Remote Sensing 47, 3616–3624. doi:10.1109/TGRS.2009.2030672

CrossRef Full Text | Google Scholar

Ruffini, G., Soulat, F., Caparrini, M., Germain, O., and Martín-Neira, M. (2004). The Eddy Experiment: Accurate GNSS-R Ocean Altimetry from Low Altitude Aircraft. Geophys. Res. Lett. 31. doi:10.1029/2004GL019994

CrossRef Full Text | Google Scholar

Skourup, H., Farrell, S. L., Hendricks, S., Ricker, R., Armitage, T. W. K., Ridout, A., et al. (2017). An Assessment of State‐of‐the‐Art Mean Sea Surface and Geoid Models of the Arctic Ocean: Implications for Sea Ice Freeboard Retrieval. J. Geophys. Res. Oceans 122 (11), 8593–8613. doi:10.1002/2017JC013176

CrossRef Full Text | Google Scholar

Turner, J. F., Iliffe, J. C., Ziebart, M. K., and Jones, C. (2013). Global Ocean Tide Models: Assessment and Use within a Surface Model of Lowest Astronomical Tide. Mar. Geodesy 36, 123–137. doi:10.1080/01490419.2013.771717

CrossRef Full Text | Google Scholar

Wickert, J., Cardellach, E., Martin-Neira, M., Bandeiras, J., Bertino, L., Andersen, O. B., et al. (2016). GEROS-ISS: GNSS Reflectometry, Radio Occultation, and Scatterometry Onboard the International Space Station. IEEE J. Sel. Top. Appl. Earth Observations Remote Sensing 9, 4552–4581. doi:10.1109/JSTARS.2016.2614428

CrossRef Full Text | Google Scholar

Wu, X., Ma, W., Xia, J., Bai, W., Jin, S., and Calabia, A. (2021). Spaceborne GNSS-R Soil Moisture Retrieval: Status, Development Opportunities, and Challenges. Remote Sensing 13, 451–4521. doi:10.3390/rs13010045

CrossRef Full Text | Google Scholar

Zavorotny, V. U., Gleason, S., Cardellach, E., and Camps, A. (2014). Tutorial on Remote Sensing Using GNSS Bistatic Radar of Opportunity. IEEE Geosci. Remote Sens. Mag. 2, 8–45. doi:10.1109/mgrs.2014.2374220

CrossRef Full Text | Google Scholar