Application of multiple methods for reverse flow routing: A case study of Luxi river basin, China

Because of the lack of hydrological monitoring facilities and methods in many areas, basic hydrological elements cannot be obtained directly. In that case, the reverse flow routing method is frequently used, which allows for the simulation of hydraulic elements upstream using downstream data, and is of great significance for river and reservoir joint regulation, flood disaster management, flood control evaluation, and flood forecasting. The hydrological and hydrodynamic methods are the two main approaches to reverse flow routing. The hydrological method is mainly realized by constructing a distributed or lumped hydrological model based on rainfall, soil type, terrain slope, and other data. A distributed hydrological model focuses on the physical mechanism of runoff yield and flow concentration, the spatial variability of model input, and the hydraulic connection between different units. The solution of the hydrological method is relatively simple, but it requires a large amount of measured data, which limits the applicability of this method. The other method builds a hydrodynamic model by solving shallow water equations for reverse flow routing. This method has definite physical significance, higher accuracy, and obvious advantages of simple and fast calculations. It can not only simulate one-dimensional but also two-dimensional flood routing processes. In addition, the slope-area method is frequently used for flood reverse routing in many areas in China without relevant hydrological data, and can calculate the peak discharge, maximum water level, flood recurrence interval, and other information by the hydrodynamic formula, along with the cross-section and the measured flood mark water level. Due to the influence of extreme weather, a heavy rainstorm and flood occurred in the Luxi river basin in China on 16 August 2020, resulting in severe flood disasters in this area and causing significant economic losses. Moreover, due to the lack and damage of hydrological monitoring equipment, hydrological information such as flood hydrographs and peak discharges of this flood could not be recorded. To reduce the uncertainty of a single method for reverse flow routing, we integrated and applied the hydrodynamic, hydrological, and slope-area methods to reverse flow routing in the Luxi river basin on 16 August 2020. The simulation accuracy of the three methods was verified in terms of the measured flood mark water level, and the simulation results of the three methods were analyzed and compared. The results are as follows: 1) The hydrological method can better simulate flood hydrographs and durations, especially for flood hydrographs with multiple peaks, and is more applicable than the other two methods. However, the hydrodynamic and slope-area methods have better accuracy in the reverse simulation of flood peaks. Therefore, through the comprehensive comparative analysis of these three methods, flood elements such as flood hydrographs, peak discharges, and durations can be simulated more accurately, and the problem of large errors caused by a single method can be avoided; 2) The simulation results of the hydrodynamic and slope-area methods are similar, and the maximum error of the peak discharge calculated using the two methods is within 10%. According to the simulation results, the peak discharge reached 2,920 m³/s downstream of Luxi river basin, which is a flood having more than 100-year recurrence interval; 3) The simulation results of the hydrological method show that the flow hydrograph is a double-peak, and the two peaks occurred at 17:00 on August 16 and 6:00 on 17 August 2020, respectively.

1 Introduction

Rainstorm and flood disasters caused by extreme weather are becoming increasingly prominent and have been identified as one of the most common and destructive threats in recent years (Panthou et al., 2014). Rainstorms and floods are typically characterized by many rainstorm days, a long duration, a large process magnitude, wide coverage, heavy hourly rainfall, high river water levels, and heavy disaster losses (Chan et al., 2016; Bao et al., 2017; Busuioc et al., 2017). Because of the outburst and uncertainty of rainstorms and floods, the government and relevant departments must take measures to prevent and respond to flood disasters in advance, which makes flood assessment particularly important. However, sudden rainstorm and flood disasters usually lead to damage of hydrological monitoring equipment, thus causing loss of basic hydrological elements, which makes reverse flow routing become the main method for flood assessment. Reverse flow routing not only contributes to the construction and improvement of flood disaster prevention systems in a basin but also has important practical application value for measures to improve the flood control capacity of the basin.

At present, there are two main reverse flow routing methods: One is the hydrological method, which simulates the hydrological cycle process by establishing a lumped or distributed hydrological model (Lewis et al., 2018; Ehlers et al., 2019; Gichamo et al., 2020). The other is the hydrodynamic method, which simulates flood wave routing by building one-dimensional (1D), two-dimensional (2D) and even three-dimensional (3D) hydrodynamic models (Fleischmann et al., 2019; Wing et al., 2019; Haque et al., 2021). In recent years, many studies on coupling hydrological and hydrodynamic models for basin hydrological simulation have been conducted (Felder et al., 2017; Wu et al., 2017).

The hydrological method is an essential tool for research in hydrological processes and flood forecasting. This method is mainly realized by constructing a distributed or lumped hydrological model. Early hydrological models were mostly conceptual models based on the water balance theory (Behrangi et al., 2011; Essou et al., 2016). However, these conceptual models do not consider the spatial variability of a basin, and model parameters to calculate the runoff process are based on physical and empirical parameters, resulting in low accuracy of the calculation results. Thus, a conceptual hydrological model is difficult to meet the requirements of refined and optimized management and allocation of hydrological and water resources in a basin. Gradually, research on distributed hydrological models in a basin has become one of the main and hot research fields in hydrology. The research of Voisin et al. (2008) and Mazzoleni et al. (2019) shows that a distributed hydrological model can accurately simulate the river flow and can be used to evaluate the flow of medium and large river basins. Henriksen et al. (2003) used a distributed hydrological model based on physical processes to simulate the hydrological processes of groundwater and surface water in Denmark, and the accuracy of the model in spatial distributions was calibrated and verified. Siderius et al. (2018) used a hydrological model to simulate the hydrological process of medium-sized basins in East Africa, aiming to provide data support for basin management. Chernos et al. (2017) used a semi-distributed hydrological model to simulate watershed hydrology, established an international dataset, and proposed an effective workflow to establish a hydrological model for any catchment area.

Hydrodynamic models can be better used to simulate the runoff process in complex terrain than hydrological models, and this is because the effects of hydraulic structures such as gates, dikes, bridges, and weirs can be considered in hydrodynamic modeling (Vorogushyn et al., 2010; Dutta et al., 2013; Skubics et al., 2014). This also makes hydrodynamic models more reliable in extreme flood assessment (Felde et al., 2017). 1D or 2D hydrodynamic models have been widely used in practical engineering applications, such as flood event simulation (Quirogaa et al., 2016; Bellos and Tsakiris, 2016; Rashid et al., 2016), flood inundation mapping (Dimitriadis et al., 2016; Saksena et al., 2019; Tamiru and Dinka, 2021), dam break analysis (Wood and Wang, 2015; Bharath et al., 2021), the estimation of flood losses, and flood hazard vulnerability (Zischg et al., 2018). In addition, because hydrodynamic models rely on measured data as model input, many studies have attempted to integrate hydrodynamic models with other models to reduce the uncertainty caused by the measured data. Rahman et al. (2021) integrated a hydrodynamic model and machine learning algorithm to create flood inundation mapping in northeastern Bangladesh. Liu C et al. (2019) integrated hydrological and hydrodynamic models and used the coupled model to simulate urban storm floods to better analyze the flood inundation in cities. Wu et al. (2017) coupled hydrological and hydrodynamic modeling to study hydrodynamic characteristics such as the water exchange process. These studies contribute to the policy and management of water resources and provide strong support for flood prevention and response measures.

Moreover, many previous studies have applied different technologies to reverse flow routing research. D’Oria and Tanda, 2012 applied a Bayesian geostatistical approach to reverse flow routing in open channels, which could prevent instability and overfitting of other methods. Valeria Todaro et al. (2019) applied an ensemble smoother with multiple data assimilation, along with a given forward routing model, to solve the accuracy and speed of reverse flow routing. In addition to the above methods, there is another method commonly used for reverse flow routing, namely, the slope-area method, which has been effectively used in many areas in China without data. For example, Sun et al. (2012) applied the slope-area method to flood analysis in Xinjiang, China, which was mainly used to calculate the peak discharge, maximum water level, flood recurrence interval, and other information according to the Manning’s formula by measuring the cross-section and the flood mark water level.

In this study, due to the lack of hydrological monitoring facilities and basic data in our study area, it is necessary to analyze the flood magnitude, flood hydrograph, peak discharge, and other information through reverse flow routing. To reduce the uncertainty of a single method, this paper integrates the hydrological method, hydrodynamic method, and slope-area method to perform the reverse flow routing analysis of flood. The results of each method are compared and verified, and finally, flood elements such as peak discharge, recurrence interval, and the peak time during the flood are determined.

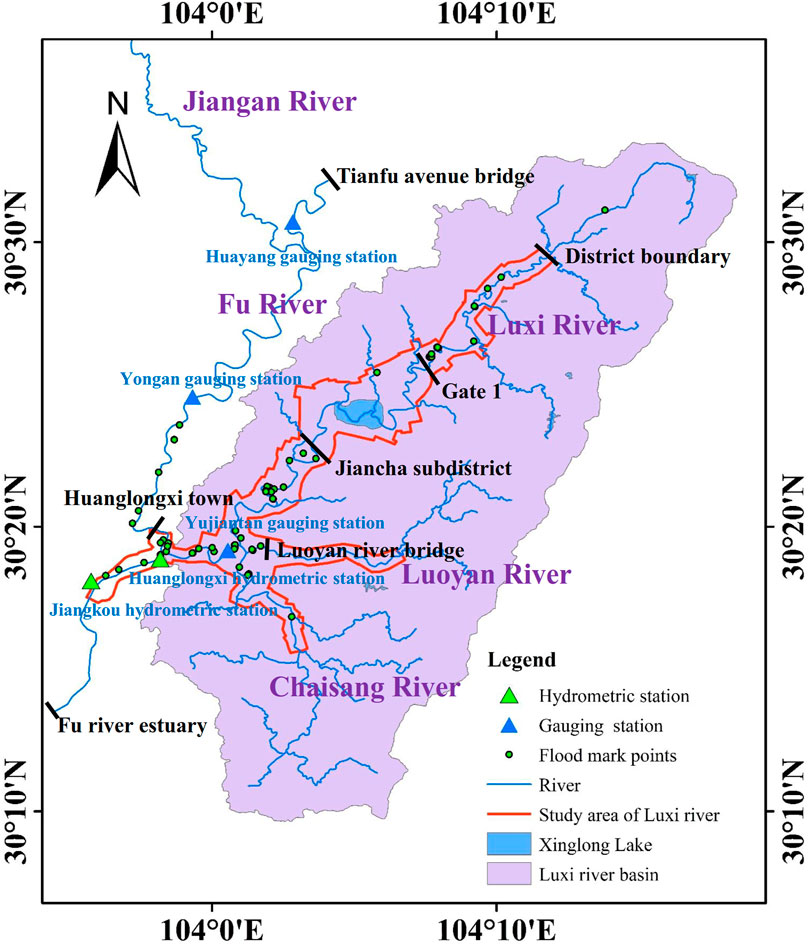
2 Study area

In August 2020, the monthly precipitation reached in Chengdu 695.1 mm, which is the highest rainfall in the same period in history (2.1 times more than that in the same period). In particular, the flood on 16 August 2020, in the Luxi river basin resulted in severe disaster losses to the Chengdu direct management area of Tianfu District. The flood affected approximately 32,000 people in the area, the flooded area of farmland was approximately 2,241.5 ha, and the direct economic loss was approximately 310 million yuan (incomplete statistics). Figure 1 shows the distribution of river network in the study area. During the flood period, the water level of the Luxi river, Luoyan river and Chaisang river rose significantly. Except for the Xinglong Lake reach (approximately 10.7 km), which has reached the flood control capacity of 100-year recurrence interval (RI =100 years), no overflow occurred, while other river reaches overflowed the embankments. Meanwhile, the water level downstream of the Luxi river exceeded the warning water level by 3.47 m. The flood washed away the only one gauging station (Yujiantan gauging station), and the peak and process data of this flood were not monitored. In addition, the stations with complete observation records on the Fu river include the Huayang gauging station, the Yongan gauging station upstream, and the Jiangkou hydrometric station downstream. However, the Huanglongxi hydrometric station at the estuary of the Luxi river did not observe the peak discharge because it exceeded the maximum observation flow range of the station design. Therefore, it is very necessary to conduct the reverse simulation analysis of the flood process in the Luxi river basin, which can provide theoretical support for flood control and disaster reduction system in the basin.

FIGURE 1

FIGURE 1. Schematic diagram of the study area.

The Luxi river is a first-class tributary of the Fu river. The length of the main stream is 74.6 km, and the drainage area is approximately 691 km², with an average gradient of 1.2‰. The main tributaries are the Luoyan river and the Chaisang river. As shown in Figure 1, in this study, the upstream starting point of the Fu river is Tianfu avenue bridge, and the downstream ending point is the junction of the Minjiang river and the Fu river. The starting point of the Luxi river is the junction of Tianfu district and Longquanyi district, and the downstream is the junction of the Luxi river and the Fu river.

3 Methods

The flood on 16 August 2020, in the Luxi river was simulated by the hydrodynamic method, the hydrological method, and the Manning formula method, respectively. The flood magnitude and process were comprehensively determined by combining the simulation results of the three methods.

3.1 Hydrodynamic method

3.1.1 Introduction of model software

The IFMS URBAN (referred to as IFMS) model is used to construct a 1D and 2D coupled hydrodynamic model of the Luxi river. IFMS model is composed of a 1D river network model, an urban pipe network model, a 2D hydrodynamic model and can realize the coupling simulation of 1D and 2D models (Ma et al., 2017), which has been successfully used in urban flood risk analysis, flood impact assessment, urban drainage simulation, design and evaluation of sponge cities, etc., (Yu et al., 2018).

3.1.2 Construction of the hydrodynamic model

The 1D model of the Luxi river basin considers 374 channel cross-sections. According to the segmentation of river channels, embankments, landforms, roads, and other ground objects within the research area, the 2D model grid of the Luxi river is divided, and the quadrilateral unstructured grid is used to discretize the simulation area. In the research area, a 30-m grid unit is used, the locations of key fields and towns are densified (the grid size is 10 m), and the total number of divided grids is approximately 172,000. Then, the 1D model and the 2D grid are coupled and constructed with the IFMS software.

3.1.3 Setting of model parameters and boundary conditions

The roughness of the upstream reach of the Fu river is 0.030, and the roughness of the downstream reach is between 0.035 and 0.043. The artificial flood discharge channel at the Xinglong Lake of the Luxi river has reached the flood control capacity of 100-year recurrence interval (RI =100 years). The roughness of the main trough of this reach of the river is set as 0.017, and the roughness of the beach is set as 0.025. The rest reaches of the Luxi river is a natural channel and overflows on both sides during a flood period, and the roughness is set to 0.045.

The upstream input flow boundary conditions and the flood mark water level are used to calculate the interval inflow. The model sets four flow boundary conditions, including the upper reaches of the Fu river, Luxi river, Chaisang river, and Luoyan river, and sets nine interval inflow boundaries, such as Huayang gauging station, Yongan gauging station, and Luxi river Gate 1, Jiancha street, etc. The water level boundary is set at the downstream outlet. The boundary condition of the water level, which is simulated from the measured data of the Pengshan hydrological station after the Fu river merges with the Minjiang river, is set at the outlet downstream of the Fu river.

3.1.4 Model calibration

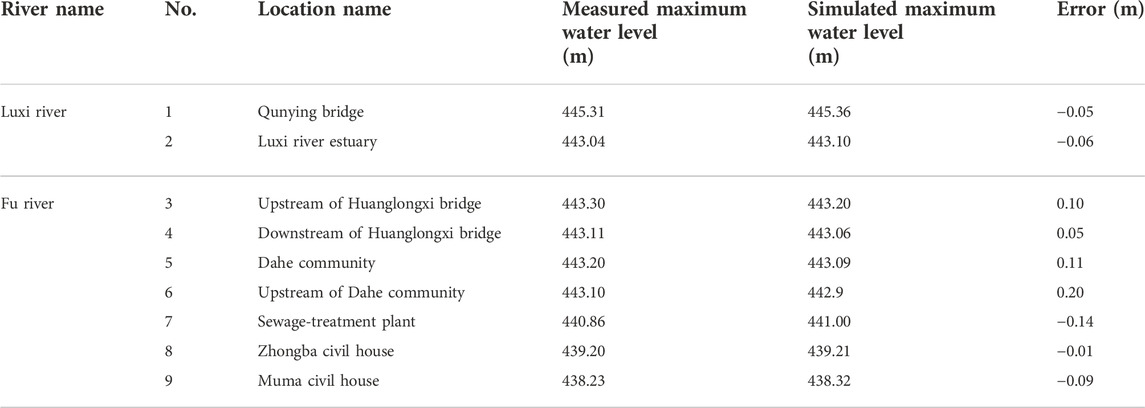
The early rainfall data and hydrological station data on 12 August 2020, were used to calibrate the model parameters. According to the stage-discharge curve and the measured water level of each gauging station, the discharge can be simulated. The results are used as input to the model. Finally, the model simulation shows that the peak discharge of the Luxi river is approximately 730 m³/s, that of the Fu river is approximately 960 m³/s, and that of the downstream Jiangkou hydrometric station is approximately 1,690 m³/s on 12 August 2020. The measured peak discharge of the Jiangkou hydrological station is 1,670 m³/s, and the relative error between the simulated and measured values is 1%. The error between the measured and simulated water levels of each gauging station is within 0.2 m (Table 1), showing that the parameters of the 1D and 2D coupled models are reasonable and have good accuracy, which can be used for subsequent simulation analysis.

TABLE 1

TABLE 1. Comparison of measured and simulated water levels.

3.1.5 Reverse simulation and analysis

3.1.5.1 Reverse simulation analysis of flood upstream of Fu river

During the flood period on 16 August 2020, the observed highest water levels of the Huayang and Yongan gauging stations (Figure 1) were 468.32 m and 452.28 m, respectively. According to the observed water level and flood mark points, the 1D model simulation results show that the peak discharge at Tianfu Avenue Bridge is approximately 650 m³/s, the peak discharge at the Jiangan river is 859 m³/s, the peak discharge at Yongan gauging station is approximately 895 m³/s, and the peak discharge at Huanglongxi town (before the Luxi river joins) is approximately 1,110 m³/s. The model simulations show that the water level of the Huayang gauging station is 468.25 m, and the water level of the Yongan gauging station is 452.16 m, which is close to the observed water level. From the 1D model results, the peak discharge upstream of the Fu river is approximately 1,110 m³/s before joining the Luxi river.

3.1.5.2 Reverse simulation analysis of flood downstream of Luxi river

During the flood period, the observed peak discharge at the Jiangkou hydrometric station was 3,620 m³/s, and the highest flood level was 437.75 m. The results in the previous section show that the peak discharge of the Fu river is approximately 1110 m³/s. Therefore, a 1D and 2D coupled model was used to estimate the peak discharge at the outlet downstream of the Luxi river, and the results are verified by comparison with the measured flood mark water level. The maximum permissible error of water level should be less than 20 cm in the Flood Risk Mapping Guidelines issued by the Ministry of Water Resources (China). Thus, we use the hydrodynamic model to simulate the peak discharge in the downstream of Luxi river, and verified by the measured flood mark water level. The simulation results show that when the inflow from the downstream of the Luxi river is 2,920 m³/s, the simulated water level at the Jiangkou hydrometric station is 437.87 m, which is only 0.12 m away from the observed water level (Table 2). It can be seen that the simulated water level is very close to the observed, which indicates that the peak flow input in Luxi river is accurate. As shown in Table 2, by comparing the simulated and measured flood marker water levels in the lower reaches of Luxi river, the water level error of all flood mark points is within 20 cm, which fully shows that the flood simulation results are reliable. That is, the peak discharge at the outlet of the Luxi river is 2,920 m³/s. However, as we have seen, the sum of the peak discharge of the Fu river (1,110 m³/s) and the Luxi river (2,920 m³/s) exceeded the observed peak discharge downstream the Jiangkou hydrometric station (3,620 m³/s) by approximately 410 m³/s. The first reason is that the two flood peaks are staggered, and the second reason is that the river overflowed during the flood period; therefore, the peak discharge monitored by the station was relatively small.

TABLE 2

TABLE 2. Comparison of simulated and measured water levels at flood mark points.

3.1.5.3 Reverse simulation results by the hydrodynamic model method

There are a total of 51 flood marks in the Luxi river, Chaisang river, and Luoyan river. The distribution map of flood marks is depicted in Figure 1. A 1D and 2D coupled model was used to analyze the flood discharge in the upper reaches of the Luxi river, and the routing flow is corrected, along with the measured water level of flood marks. The simulation results show that the flood distribution in the upper reaches of the Luxi river basin is as follows: The peak discharge at Gate 1 of Xinglong Lake was approximately 1,280 m³/s, the peak discharge at Jiancha subdistrict was approximately 1,680 m³/s, and the peak discharges at the Luoyan and Chaisang rivers were 595 m³/s and 705 m³/s, respectively. Comparing the simulated and measured water levels of 51 flood mark points, the results show that the error between the simulated water level and measured flood mark water level of 43 flood mark points is controlled within 20 cm, accounting for 84.3%. This shows that the simulation results are credible, and the comparison results of partial flood marks are shown in Table 3.

TABLE 3

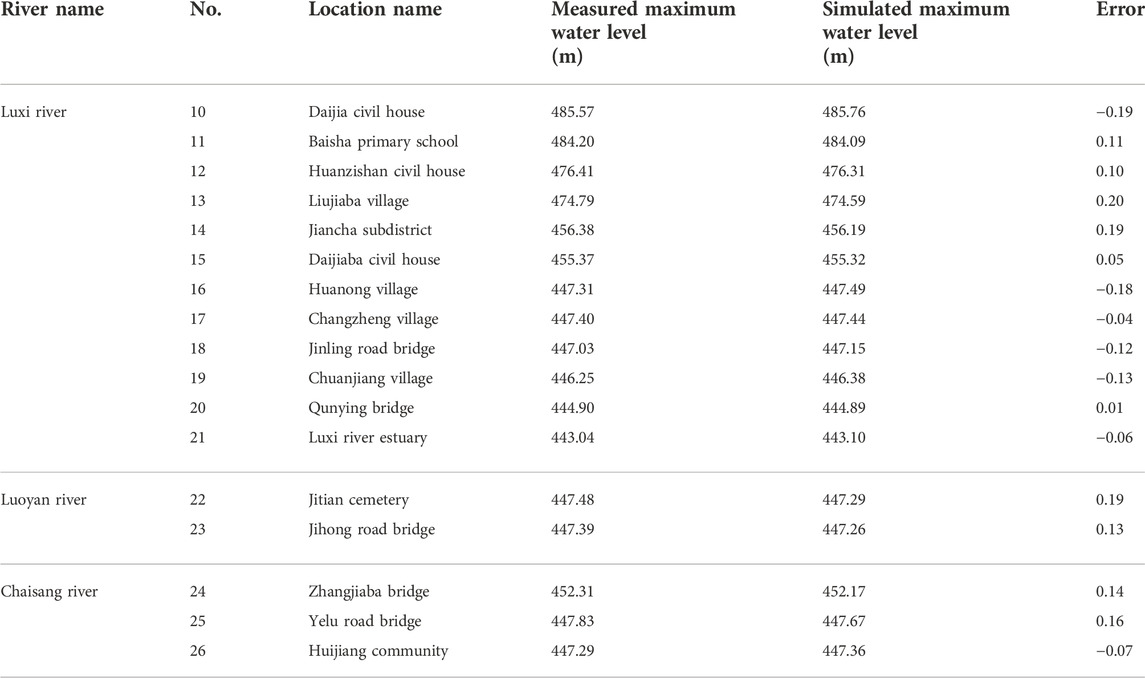
TABLE 3. Partial comparison of simulated and measured water level at flood mark points of Luxi river basin.

3.2 Slope-area method

3.2.1 Method introduction

First, the measured cross-sections shape data and flood marks water level are used to determine the area and river gradient of typical cross-sections, and then roughness is reasonably determined according to the river reach conditions (the same as Section 3.1). Finally, Manning’s formula, the most commonly used method in flood investigation, is used to calculate the peak discharge. The calculation formula is as follows:

$Q=\omega *C*\sqrt{RJ}$

where Q is the flow rate (m³/s); ω is the wetted cross-sectional area; R is the hydraulic radius; J is the hydraulic gradient; C is the Chezy coefficient.

3.2.2 Calculation of flood flow

3.2.2.1 Typical cross-section

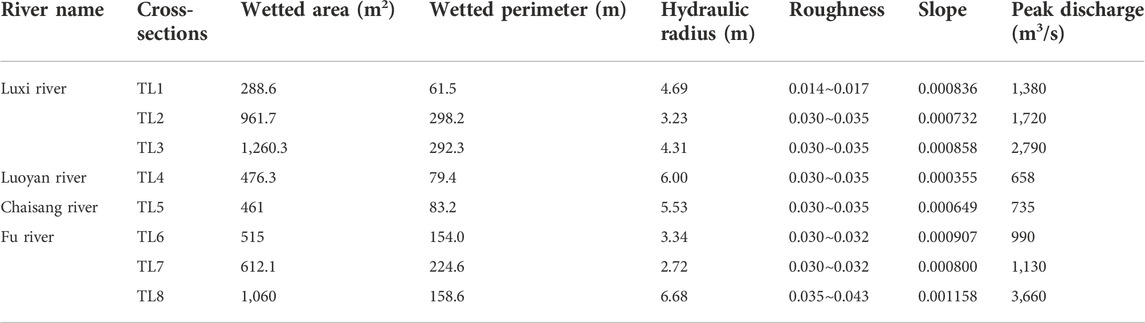
A total of eight typical cross-sections are selected in the main stream of the Luxi river, Luoyan river, Chaisang river and Fuhe river. The location and water level of each section are shown in Table 4. Among these, the TL1 typical cross-section is located on the artificial repair section of Xinglong Lake. The flood control capacity of this section is more than a 100-year recurrence interval (RI =100 years). During the flood on 16 August 2020, this section does not overflow the bank. The flood control capacity of TL2, 3, 4, and 5 sections is lower than the standard requirements of the river channel, and the bank overflows during the flood period. The TL6 typical cross-section is located in Yongan town downstream of Yongan gauging station, and the section is relatively regular. The flood level is approximately 0.9 m higher than the top elevation of the left bank, and the right bank is not overtopped during the flood period. The water level of TL7 typical cross-section is approximately 0.5 m higher than the top elevation of the left bank, and the right bank is not overtopped. The TL8 section is located near the Jiangkou hydrometric station downstream of the Fuhe river, and it does not overflow the bank during the flood period.

TABLE 4

TABLE 4. Water level of typical cross-sections.

3.2.2.2 Results of flood flow by the slope-area method

The results of flood flow by the slope-area method are shown in Table 5. From the table, the flood peak discharge at the TL8 section is approximately 3,660 m³/s, which is close to the observed peak discharge of 3,620 m³/s at the Jiangkou hydrometric station. The peak discharge of the Luxi river is approximately 2,920 m³/s (the TL3 section), and the peak discharge of the Fu river is approximately 1,130 m³/s (the TL7 section). The sum of the flood discharge of the Luxi river and the upstream of the Fuhe river is larger than the observed peak discharge at the Jiangkou hydrometric station after the confluence of the two rivers. This is due to the influence of transposition and attenuation of flood waves. Generally, the results of peak discharge by the slope-area method are reasonable and reliable.

TABLE 5

TABLE 5. Results of peak discharge by slope-area method.

3.3 Hydrological method

The peak discharge simulated by the hydrodynamic method and slope-area method can match well with the observed hydrological data of the monitoring station and the measured flood mark data; however, these two methods are difficult to simulate flood hydrographs. Conversely, the hydrological method can effectively simulate flood hydrographs.

3.3.1 Construction of hydrological model

In this section, a spatiotemporal variable source mixed runoff model (referred to as SVSMR) is used for simulation of hydrological processes. This model proposed by China Institute of Water Resources and Hydropower Research (IWHR), and has been successfully used in hydrologic simulation and fine simulation of flash flood in the basin (Hao et al., 2021; Liu et al., 2021; Ma et al., 2021). The SVSMR model is based on the water content and accumulated infiltration of the hydrological response unit in each period to calculate the area change of excess infiltration and full storage runoff, and at the same time to distinguish the relationship between rainfall intensity and the infiltration capacity of the underlying surface, so as to realize the space-time transformation of excess infiltration/full storage runoff in each geomorphological hydrological response unit (Liu J et al., 2019).

According to the analysis of basic geographic data, the main stream of the Luxi river is divided into 26 sub-watersheds, with a total area of 377.52 km². The tributary Luoyan river is divided into seven sub-watersheds, with a total area of 126.15 km². The tributary Chaisang river is divided into 15 sub-watersheds, with a total area of 187.59 km². The sub-watershed layer is imported into the hydrological model, and the parameters are set. In addition, there are 90 rainfall stations in the Luxi river basin, but only 42 of them keep continuous and complete observation records. The data of the 42 rainfall stations with complete observed records are used as the input of the model.

3.3.2 Model calibration and parameter setting

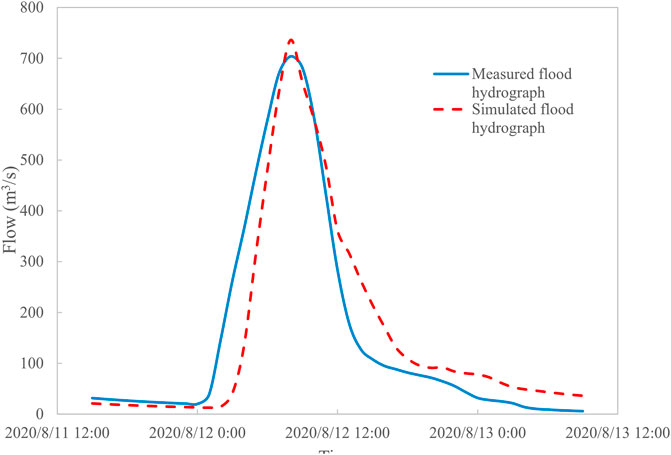
The hydrological model was calibrated using the early flood on 12 August 2020. First, according to the observed water level and the stage-discharge curve of the Yujiantan gauging station, the flow process on 12 August 2020, was simulated. Second, the process of runoff generation and concentration was simulated by inputting rainfall into the hydrological model, from which the flow process at the Yujiantan gauging station was calculated, and the results were compared with the former. As shown in Figure 2, the peak discharge obtained from the former is 704 m³/s, whereas that from the latter is 736 m³/s, the error is 4.3%. The flood process simulated by the hydrological model is consistent with the observed flood process, indicating that the calibrated hydrological model can be better used for subsequent flood process simulation.

FIGURE 2

FIGURE 2. Flood hydrograph of Yujiantan gauging station on 12 August 2020.

The parameters used in the hydrology model include evaporation coefficient, interception and filling coefficient, slope type coefficient, river channel parameters, soil texture parameters, etc. The main parameters are shown in Table 6.

TABLE 6

TABLE 6. The main parameters of hydrological model.

3.3.3 Reverse simulation results by the hydrological method

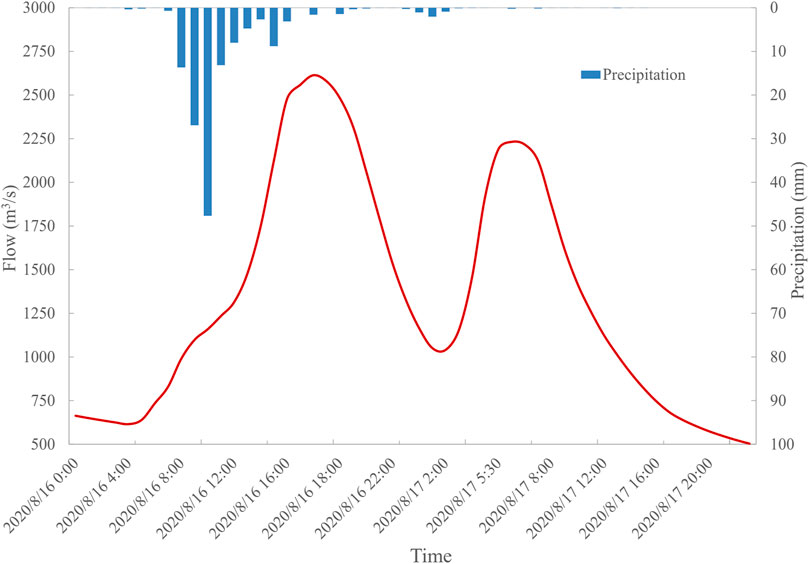
The hydrological model was used to simulate the flood process on 16 August 2020. The simulation time started from 0:00 on August 14 to 24:00 on August 18, and the results are shown in Figure 3. From the figure, the flood hydrograph of the Yujiantan gauging station is a double-peak process. The first flood peak occurred around 17:00 on August 16, with a peak discharge of 2,645 m³/s. After the first wave peak appeared, the flow began to decrease and rose again in the early morning of the 17th. The second peak appeared at 6:00 on August 17, with a peak discharge of 2,232 m³/s. As shown in Figure 4, the rainstorm center of this rainfall gradually moves from the upper reaches of the Luxi river to the middle reaches. Comparing the rainfall process, Figure 3 shows that the peak of rainfall occurs at 8:00 and 24:00 on August 16, respectively. After the confluence of overland flow and river networks, the flood peaks downstream are delayed for approximately 5 h. In addition, the flood fluctuation time is consistent with the simulation results according to the field investigation and inquiry of the local residents.

FIGURE 3

FIGURE 3. Flow hydrograph simulated by hydrological model on 16 August 2020.

FIGURE 4

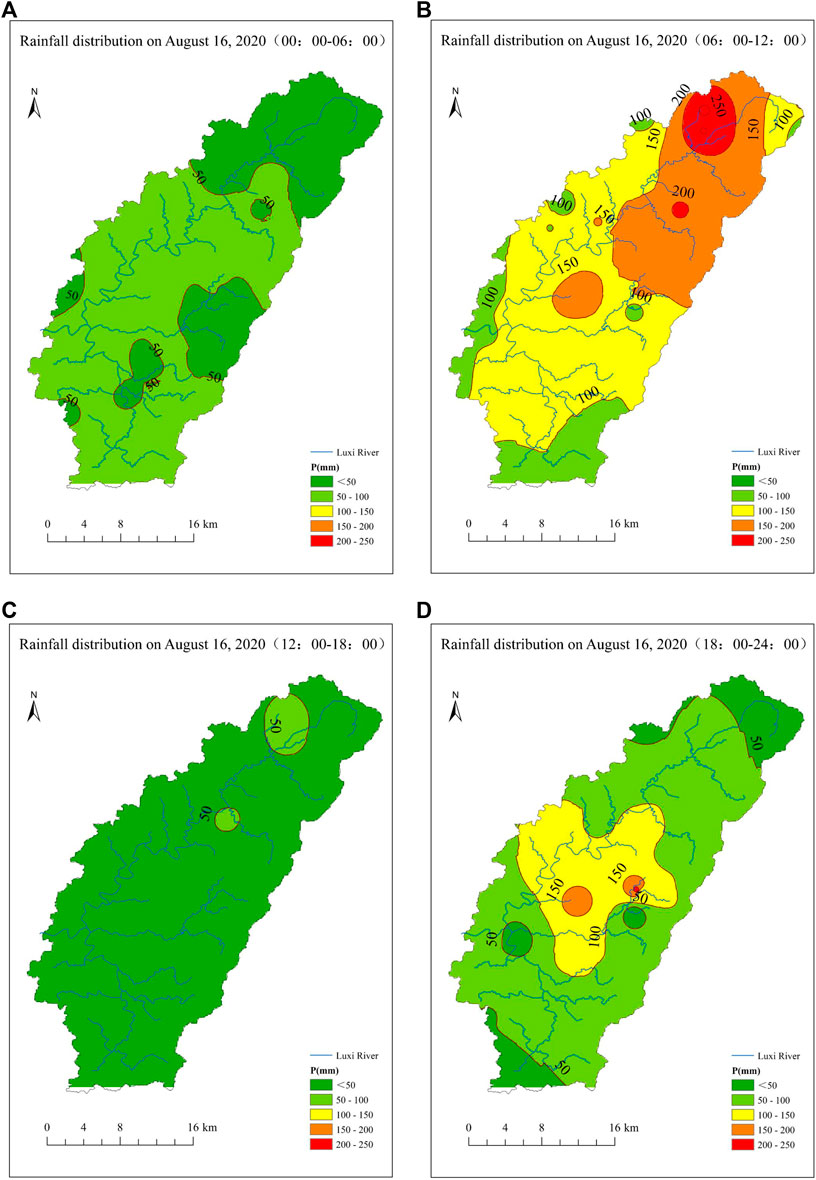
FIGURE 4. Rainfall distribution of Luxi river basin on 16 August 2020: (A)00:00–06:00, (B)06:00–12:00, (C)12:00–18:00, and (D)18:00–24:00.

4 Comparison of results

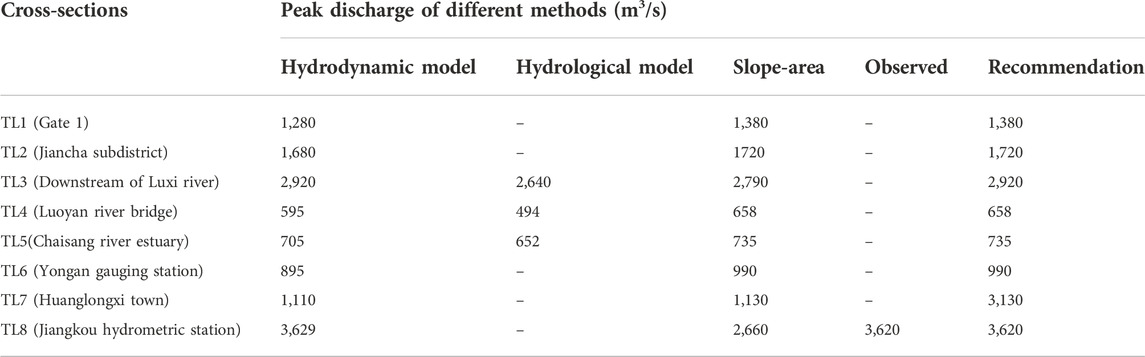
The reverse simulation results of the Luxi river on 16 August 2020, by the hydrodynamic, hydrological, and slope-area methods are shown in Table 7. The results of the hydrodynamic method and slope-area method are very close, the deviations do not exceed 130 m³/s, and the error is within 10%. At the Jiangkou hydrometric station, the peak discharges simulated by the hydrodynamic and slope-area methods are 3,629 m³/s and 3,660 m³/s, respectively, which are close to the observed peak discharge of 3,620 m³/s at the Jiangkou hydrometric station. The errors between the simulated peak discharge by the two methods and the observed peak discharge by the Jiangkou hydrometric station are 0.25% and 1.1% respectively, which shows that the reverse simulation results of the two methods can be well-matched with the observed peak discharge.

TABLE 7

TABLE 7. Comparison and recommendation of peak discharge results.

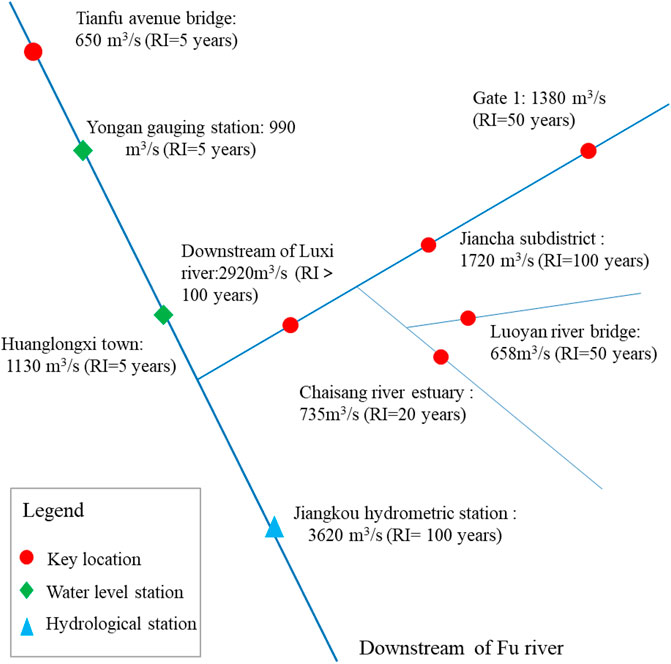
In contrast, the peak discharge simulated by the hydrological model is lower, but the maximum errors between the simulation results of the hydrological model and the other two methods are also within 20%, which also shows that the results of the three methods are mutually verified and reasonable. After comprehensive consideration, the larger peak discharge of the three methods are selected as the final peak discharge results of each typical cross-section, and the distributions of peak discharge results are shown in Figure 5. That is, the peak discharge of Gate 1 is 1,380 m³/s, which is a flood having 50-year recurrence interval (RI=50 years); the peak discharge of the Jiancha subdistrict is approximately 1720 m³/s (RI =100 years); the peak discharge of the Luoyan river bridge and Chaisang river estuary are 658 m³/s (RI =50 years) and 735 m³/s (RI =20 years), respectively; the peak discharge of downstream of Luxi river is 2,920 m³/s (RI > 100 years).

FIGURE 5

FIGURE 5. Distribution of peak discharge results.

5 Conclusion

(1) In this study, the hydrodynamic, hydrological, and slope-area methods are, respectively, used for reverse flow routing. Taking the rainstorm flood on 16 August 2020, in the Luxi river basin as an example, the reverse simulation accuracy of these three methods is verified and compared, which can ensure the accuracy of the simulation results and avoid the uncertainty caused by a single method. The simulation results can provide data support for flood control and prevention.

(2) The simulation results of the hydrodynamic and slope-area methods match well with the measured flood mark data, indicating that the two methods have good accuracy in peak discharge reverse simulation. However, these two methods are difficult to simulate the flood hydrograph. The hydrological model method can simulate the flood hydrograph, and the simulation results are consistent with the field investigation, which makes up for the shortcomings of the former two methods.

(3) The reverse simulation results of the hydrodynamic and slope-area methods show that the peak discharge downstream of the Luxi river is approximately 2,920 m³/s (RI > 100 years). The hydrological model method simulated that the rainstorm flood on 16 August 2020, in the Luxi river is a double-peak flood hydrograph, and the two peaks occurred at 17:00 on August 16 and 6:00 on 17 August 2020, respectively.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

XC and HY finished the manuscript. JM and WY collected the data and references. CL contributed to the result analysis. HY, XC, and JM modified the manuscript. All authors read this manuscript and agreed to submit to this journal.

Funding

The research is funded by the National Natural Science Foundation of China (51909272) and Beijing Natural Science Foundation (8181001).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bao, J., Sherwood, S. C., Alexander, L. V., and Evans, J. P. (2017). Future increases in extreme precipitation exceed observed scaling rates. Nat. Clim. Change 7, 128–132. doi:10.1038/nclimate3201

CrossRef Full Text | Google Scholar

Behrangi, A., Khakbaz, B., Jaw, T. C., AghaKouchak, A., Hsu, K., and Sorooshian, S. (2011). Hydrologic evaluation of satellite precipitation products over a mid-size basin. J. Hydrology 397 (3-4), 225–237. doi:10.1016/j.jhydrol.2010.11.043

CrossRef Full Text | Google Scholar

Bellos, V., and Tsakiris, G. (2016). A hybrid method for flood simulation in small catchments combining hydrodynamic and hydrological techniques. J. Hydrology 540, 331–339. doi:10.1016/j.jhydrol.2016.06.040

CrossRef Full Text | Google Scholar

Bharath, A., Shivapur, Anand V., Hiremath, C. G., and Maddamsetty, Ramesh (2021). Dam break analysis using HEC-RAS and HEC-GeoRAS: A case study of hidkal dam, Karnataka state, India. Environ. Challenges 5, 100401. doi:10.1016/j.envc.2021.100401

CrossRef Full Text | Google Scholar

Busuioc, A., Baciu, M., Breza, T., Dumitrescu, A., Stoica, C., and Baghina, N. (2017). Changes in intensity of high temporal resolution precipitation extremes in Romania: Implications for clausius-clapeyron scaling. Clim. Res. 72, 239–249. doi:10.3354/cr01469

CrossRef Full Text | Google Scholar

Chan, S. C., Kendon, E. J., Roberts, N. M., Fowler, H. J., and Blenkinsop, S. (2016). The characteristics of summer sub-hourly rainfall over the southern UK in a high-resolution convective permitting model. Environ. Res. Lett. 11, 094024. doi:10.1088/1748-9326/11/9/094024

CrossRef Full Text | Google Scholar

Chernos, M., MacDonald, R., and Craig, J. (2017). Efficient semi-distributed hydrological modelling workflow for simulating streamflow and characterizing hydrologic processes. Conflu. J. Watershed Sci. Manag. 1 (3). doi:10.22230/jwsm.2018v1n3a6

CrossRef Full Text | Google Scholar

Dimitriadis, P., Tegos, A., Oikonomou, A., Pagana, V., Koukouvinos, A., Mamassis, N., et al. (2016). Comparative evaluation of 1D and quasi-2D hydraulic models based on benchmark and real-world applications for uncertainty assessment in flood mapping. J. Hydrology 534, 478–492. doi:10.1016/j.jhydrol.2016.01.020

CrossRef Full Text | Google Scholar

D’Oria, M., and Tanda, M. G. (2012). Reverse flow routing in open channels: A bayesian geostatistical approach. J. Hydrology 460-461, 130–135. doi:10.1016/j.jhydrol.2012.06.055

CrossRef Full Text | Google Scholar

Dutta, D., Teng, J., Vaze, J., Lerat, J., Hughes, J., and Marvanek, S. (2013). Storage-based approaches to build floodplain inundation modelling capability in river system models for water resources planning and accounting. J. Hydrology 504, 12–28. doi:10.1016/j.jhydrol.2013.09.033

CrossRef Full Text | Google Scholar

Ehlers, L. B., Wani, O., Koch, J., Sonnenborg, T. O., and Refsgaard, J. C. (2019). Using a simple post-processor to predict residual uncertainty for multiple hydrological model outputs. Adv. Water Resour. 129, 16–30. doi:10.1016/j.advwatres.2019.05.003

CrossRef Full Text | Google Scholar

Essou, G. R. C., Arsenault, R., and Brissette, F. P. (2016). Comparison of climate datasets for lumped hydrological modeling over the continental United States. J. Hydrol. X. 537 (334-345), 334–345. doi:10.1016/j.jhydrol.2016.03.063

CrossRef Full Text | Google Scholar

Felder, G., Zischg, A., and Weingartner, R. (2017). The effect of coupling hydrologic and hydrodynamic models on probable maximum flood estimation. J. Hydrology 550, 157–165. doi:10.1016/j.jhydrol.2017.04.052

CrossRef Full Text | Google Scholar

Fleischmann, A., Paiva, R., and Collischonn, W. (2019). Can regional to continental river hydrodynamic models be locally relevant? A cross-scale comparison. J. Hydrology X X, 100027. doi:10.1016/j.hydroa.2019.100027

CrossRef Full Text | Google Scholar

Gichamo, T. Z., Sazib, N. S., Tarboton, D. G., and Dash, P. (2020). HydroDS: Data services in support of physically based, distributed hydrological models. Environ. Model. Softw. 125, 104623. doi:10.1016/j.envsoft.2020.104623

CrossRef Full Text | Google Scholar

Hao, S., Ma, Qiang, Zhai, Xiaoyan, Lv, Guomin, Fan, Suqi, Wang, Wenchuan, et al. (2021). A new machine learning approach for parameter regionalization of flash flood modelling in henan province, China. E3S Web Conf. 300, 02010. doi:10.1051/e3sconf/202130002010

CrossRef Full Text | Google Scholar

Henriksen, H. J., Troldborg, L., Nyegaard, P., Sonnenborg, T. O., Refsgaard, J. C., and Madsen, B. (2003). Methodology for construction, calibration and validation of a national hydrological model for Denmark. J. Hydrology 280 (1-4), 52–71. doi:10.1016/s0022-1694(03)00186-0

CrossRef Full Text | Google Scholar

Lewis, E., Birkinshaw, S., Kilsby, C., and Fowler, H. J. (2018). Development of a system for automated setup of a physically-based, spatially-distributed hydrological model for catchments in Great Britain. Environ. Model. Softw. 108, 102–110. doi:10.1016/j.envsoft.2018.07.006

CrossRef Full Text | Google Scholar

Liu, Changjun, Zhou, Jian, Wen, Lei, Ma, Qiang, Guo, Liang, Ding, Liuqian, et al. (2021). Research on spatio-temporal variable source mixed runoff generation model and parameter regionalization method for medium and small basins. J. China Acad. Water Resour. Hydropower Sci. 19 (01), 99–114. doi:10.13244/j.cnki.jiwhr.20200161

CrossRef Full Text | Google Scholar

Liu, C., Wen, Lei, Zhou, Jian, Zhao, Xuantao, Guo, Liang, and Yongqiang, Wei (2019). Comparison and analysis of hydrological models and hydrodynamic methods for flash flood in small watersheds. J. China Acad. Water Resour. Hydropower Res. 17 (04), 262–270+278. doi:10.13244/j.cnki.jiwhr.2019.04.003

CrossRef Full Text | Google Scholar

Liu, J., Shao, W., Xiang, C., Mei, C., and Li, Z. (2019). Uncertainties of urban flood modeling: Influence of parameters for different underlying surfaces. Environ. Res. 182, 108929. doi:10.1016/j.envres.2019.108929

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, Jianming, Yu, Haijun, and Zhang, Dawei (2017). Application of flood analysis software in flood risk map compilation. China Water Resour. 2017 (5), 17–20. doi:10.16867/j.issn.1673-9264.2018059

CrossRef Full Text | Google Scholar

Ma, Q., Guomin, L., and Hao, S. (2021). A new generation numerical modelling tool for hydrological simulation: Spatiotemporal-varied-source-mixed runoff model for small watershed. doi:10.1109/ICCEAI52939.2021.00029

CrossRef Full Text | Google Scholar

Mazzoleni, M., Brandimarte, L., and Amaranto, A. (2019). Evaluating precipitation datasets for large-scale distributed hydrological modelling. J. Hydrology 578, 124076. doi:10.1016/j.jhydrol.2019.124076

CrossRef Full Text | Google Scholar

Panthou, G., Vischel, T., and Lebel, T. (2014). Recent trends in the regime of extreme rainfall in the central sahel. Int. J. Climatol. 34, 3998–4006. doi:10.1002/joc.3984

CrossRef Full Text | Google Scholar

Quirogaa, V. M., Kurea, S., Udoa, K., and Manoa, A. (2016). Application of 2D numerical simulation for the analysis of the February 2014 Bolivian Amazonia flood: Application of the new HEC-RAS version 5. Ribagua 3 (1), 25–33. doi:10.1016/j.riba.2015.12.001

CrossRef Full Text | Google Scholar

Rahman, M., Chen, N., Islam, M. M., Mahmud, G. I., Pourghasemi, H. R., Alam, M., et al. (2021). Development of flood hazard map and emergency relief operation system using hydrodynamic modeling and machine learning algorithm. J. Clean. Prod. 311, 127594. doi:10.1016/j.jclepro.2021.127594

CrossRef Full Text | Google Scholar

Rashid, A. A., Liang, Q., Dawson, R. J., and Smith, L. S. (2016). Calibrating a high-performance hydrodynamic model for broad-scale flood simulation: Application to thames estuary, london, UK. Procedia Eng. 154. 967–974. doi:10.1016/j.proeng.2016.07.584

CrossRef Full Text | Google Scholar

Saksena, S., Merwade, V., and Singhofen, P. J. (2019). Flood inundation modeling and mapping by integrating surface and subsurface hydrology with river hydrodynamics. J. Hydrology 575, 1155–1177. doi:10.1016/j.jhydrol.2019.06.024

CrossRef Full Text | Google Scholar

Siderius, C., Biemans, H., Kashaigili, J. J., and Conway, D. (2018). Going local: Evaluating and regionalizing a global hydrological model’s simulation of river flows in a medium-sized East African basin. J. Hydrology Regional Stud. 19, 349–364. doi:10.1016/j.ejrh.2018.10.007

CrossRef Full Text | Google Scholar

Skublics, D., Seibert, S., and Ehret, U. (2014). Modelling flood retention with hydrological and hydrodynamic models under different boundary conditions – sensitivity analysis on the Danube reach from Neu-Ulm to Donauwörth. HyWa 58, 178–189. doi:10.5675/HyWa_2014

CrossRef Full Text | Google Scholar

Sun, Deshu, Wu, Huixiu, Li, Jie, Zhang, Zhongguo, and Du, Zhong (2012). Investigation and evaluation of flood in small and medium-sized rivers in areas without data -- taking Dasha River "20100821" rainstorm as an example. J. Liaodong Univ. Nat. Sci. Ed. 19 (03), 165–169. doi:10.14168/j.issn.1673-4939.2012.03.003

CrossRef Full Text | Google Scholar

Tamiru, H., and Dinka, M. O. (2021). Application of ANN and HEC-RAS model for flood inundation mapping in lower Baro Akobo River Basin, Ethiopia. J. Hydrology Regional Stud. 36, 100855. doi:10.1016/j.ejrh.2021.100855

CrossRef Full Text | Google Scholar

Todaro, V., D’Oria, M., Tanda, M. G., and Gómez-Hernández, J. J. (2019). Ensemble smoother with multiple data assimilation for reverse flow routing. Comput. Geosciences 131, 32–40. doi:10.1016/j.cageo.2019.06.002

CrossRef Full Text | Google Scholar

Voisin, N., Wood, A. W., and Lettenmaier, D. P. (2008). Evaluation of precipitation products for global hydrological prediction. J. Hydrometeorol. 9 (3), 388–407. doi:10.1175/2007jhm938.1

CrossRef Full Text | Google Scholar

Vorogushyn, S., Merz, B., Lindenschmidt, K.-E., and Apel, H. (2010). A new methodology for flood hazard assessment considering dike breaches. Water Resour. Res. 46 (8), W08541. doi:10.1029/2009WR008475

CrossRef Full Text | Google Scholar

Wing, O. E. J., Sampson, C. C., Bates, P. D., Quinn, N., Smith, A. M., and Neal, J. C. (2019). A flood inundation forecast of Hurricane Harvey using a continental-scale 2D hydrodynamic model. J. Hydrology X X, 100039. doi:10.1016/j.hydroa.2019.100039

CrossRef Full Text | Google Scholar

Wood, A., and Wang, K.-H. (2015). Modeling dam-break flows in channels with 90 degree bend using an alternating-direction implicit based curvilinear hydrodynamic solver. Comput. Fluids 114, 254–264. doi:10.1016/j.compfluid.2015.03.011

CrossRef Full Text | Google Scholar

Wu, B., Wang, G., Wang, Z., Liu, C., and Ma, J. (2017). Integrated hydrologic and hydrodynamic modeling to assess water exchange in a data-scarce reservoir. J. Hydrology 555, 15–30. doi:10.1016/j.jhydrol.2017.09.057

CrossRef Full Text | Google Scholar

Yu, Haijun, Ma, Jianming, and Zhang, Dawei (2018). Application of IFMS Urban software in the compilation of urban flood risk map. China Flood Control Drought Relief 28 (7), 13–17. doi:10.16867/j.issn.1673-9264.2018059

CrossRef Full Text | Google Scholar

Zischg, A. P., Felder, G., Mosimann, M., Röthlisberger, V., and Weingartner, R. (2018). Extending coupled hydrological-hydraulic model chains with a surrogate model for the estimation of flood losses. Environ. Model. Softw. 108, 174–185. doi:10.1016/j.envsoft.2018.08.009

CrossRef Full Text | Google Scholar