Simulation of hydraulic fracture initiation and propagation for glutenite formations based on discrete element method

The existence of gravels in the glutenite formations leads to the complex geometries of hydraulic fracturing propagation and difficult construction in fracturing engineering. To study the hydraulic fracturing propagation law of glutenite formations, this paper establishes a fracture propagation model for the heterogeneous glutenite formations based on discrete element method, and analyzes the effects of gravel content, particle size, distribution, horizontal stress difference, fracturing fluid viscosity and flow rate on hydraulic fracturing propagation behavior. Results show that the complex geometries of hydraulic fractures in glutenite formations can lead to the generation of branched fractures and fracture bifurcation. Small-sized gravels have little effect on the fracture propagation shape which leads to a single main fracture with a flat fracture surface, on the contrary, large-sized gravels may induce hydraulic fractures to deflect along the gravel interface and form branched fractures with distorted fracture surfaces. Hydraulic fractures can propagate around gravels under the condition of high stress difference, high viscosity and medium flow rate. Gravels can prevent the propagation of hydraulic fractures under low stress difference, low viscosity and small flow rate. Hydraulic fracture bifurcation can occur when encountering gravels under high stress difference and large displacement. Properly increasing the high viscosity of fracturing fluids can effectively promote the main hydraulic fracture propagation and reduce the fracture tortuosity, thereby avoiding sand up.

1 Introduction

Due to lithology change, low porosity, poor permeability and strong heterogeneity, fracturing design and parameters optimization of glutenite formations face great challenge (Jia et al., 2017; Wang et al., 2017). For the gravels in glutenite formation, fracture distortion and multi-fracture propagation are prone to occur in the hydraulic fracturing process, resulting in sand up and affecting hydraulic fracturing effects (Meng et al., 2010; Li et al., 2013; Feng et al., 2016; Ma et al., 2017). Therefore, studies of the fracture propagation law is of great significance for the stimulation and reconstruction in glutenite formation.

A large number of numerical simulations (Feng et al., 2017; Zhang et al., 2017; Zhang et al., 2018; Lu et al., 2020; Wang et al., 2021; Wei et al., 2021) and experimental investigations (Fan et al., 2014; Ma et al., 2017; Moghadasi et al., 2019; Tan et al., 2019; Xie et al., 2022) have been carried out for the hydraulic fractures propagation of different lithologies. Tan et al. (2017), Tan et al. (2020) summarized fracture morphology types in mid-depth and deep shale formation. For mid-depth shales, fracture geometries were characterized by simple fracture, fishbone-like fracture, fishbone-like fracture with fissure opening, and multilateral fishbone-like fracture network (2017). For deep shales, fracture geometries were characterized by horizontal hydraulic fracture, transverse fracture, step-shaped hydraulic fracture with fissure opening, and multilateral step-shaped hydraulic fracture network (2020). Wan et al. (2019); Tan et al. (2021) came up with the concept of “lithology transition zone” for coal measure strata and studied the fracture propagation and penetration behavior; Zhao et al. (2007) compared hydraulic fractures propagation law in different lithologies such as basalt, conglomerate, marl. For glutenite formations; Luo et al. (2013) considered that particle size, content of gravel and the properties of the interface are the internal reason for irregular hydraulic fractures and pressure fluctuations based on the numerical simulation results; Meng et al. (2010) analyzed the influence of gravel particle size and horizontal stress difference on fracture propagation morphology and pressure curve using artificial samples; Li et al. (2013) analyzed the effects of the in situ stress and gravels on fracture propagation with RFPA-Flow, and summed up four typical fracture propagation modes at the gravel, including fracture arrest, deflection, penetration and adsorption. Based on the three-dimensional reconstructed heterogeneous glutenite model; Ju et al. (2016) studied the initiation and propagation of hydraulic fractures under different horizontal stress differences by using the discrete element method, and compared with the physical simulation results. Although this research reveals the fracture propagation law of glutenite formation to some extent, there are still many issues worthy of further discussion. On the one hand, the glutenite formation is different from the sandstone reservoir which has fast phase transformation, large changes in lithology and permeability, and poor sandstone connectivity and strong heterogeneity. The brittle fracture morphology of the glutenite formation is obviously different from that of the normal sandstone reservoir especially when glutenite formation contains high gravel content and large gravel particles, the fracture surface is extremely irregular and prone to multiple fractures (Ma et al., 2017). Also, multiple fractures will increase the filtration of the fracturing fluid, thus affecting the fracture and sand carrying capacity, resulting in difficult large-scale fracturing treatment. At present, many studies has been carried out on the physical characteristics of glutenite formations, and these studies focus mainly on reservoir characteristics and flow problems in the development process (Zhang et al., 2019; Wang et al., 2020), However, the research on fracture propagation law in glutenite formation is relatively less. On the other hand, it is impossible to obtain directly theoretical solution of the fracture propagation law under the restriction of the factors such as the great lithology changes and the strong heterogeneity for glutenite formations. The laboratory experiment is one of the methods that can be tried, and some intuitive observations can be obtained through the laboratory experiments (Ma et al., 2017). However, due to the uncertainty of the content, size, properties and distribution characteristics of the gravels in the glutenite formations, the laboratory results are generally very discrete, and it is difficult to conclude a repeatable conclusion by a limited number of tests.

Based on the physical and mechanical parameters, the discrete element method is also an effective way to study the hydraulic fracturing propagation law under complex conditions (Zhang et al., 2017; Tan et al., 2018; Huang et al., 2019; Huang et al., 2023). Therefore, this paper uses 2D Particle Flow Code (PFC2D, 2006) to analyze the hydraulic fracturing propagation law in glutenite formations, in order to guide the fracturing design and construction for glutenite formations.

2 Model calibration and schemes

2.1 Model calibration

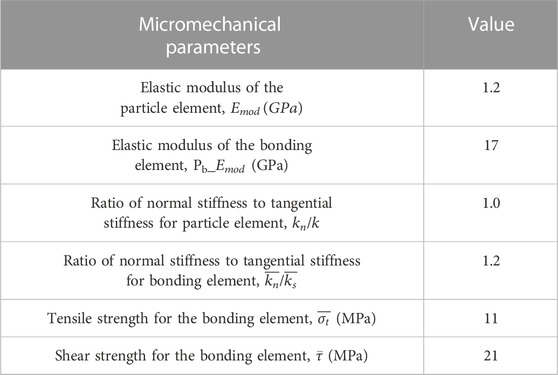
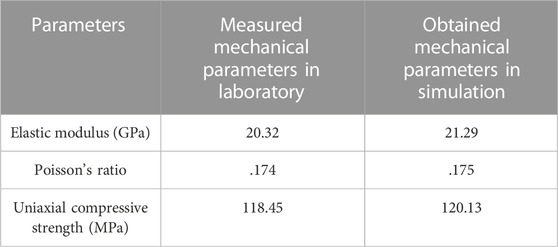
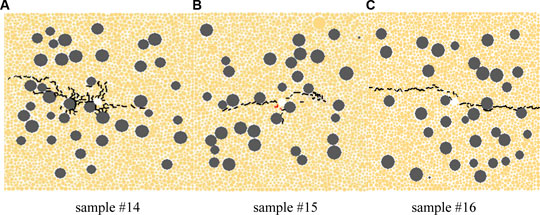
In order to illustrate the reliability of PFC2D, simulation of uniaxial compression is carried out, and the simulation results are compared with the laboratory results. The size of the model is 25 mm × 50 mm. The top and bottom surfaces are set as rigid walls with constant displacement. The left and right sides are set to the constant pressure wall controlled by servo to simulate the loading of confining pressure. The confining pressure is set to 0.1 MPa. Since the pressure is very small compared with the fracture pressure of the samples, thus it can be ignored and can be approximated to uniaxial loading. The micro parameters in the model are shown in Table 1. The samples in the laboratory were collected from sandstone cores of a block in Changqing Oilfield. The rock mechanics parameters obtained by numerical simulation are close to those obtained by laboratory experiment, as shown in Table 2. The hydraulic fracture geometries in the laboratory and simulation are similar which are shear fractures, as shown in Figure 1. Therefore, it proves the reliability of the PFC 2D method to reconstruct the rock structure and simulate the hydraulic fracturing process.

TABLE 1

TABLE 1. Calibrated micromechanical parameters.

TABLE 2

TABLE 2. Comparison of measured and simulated macro mechanical properties.

FIGURE 1

FIGURE 1. Comparison of the fracture geometry for the simulated result (A) and experimental result (B).

2.2 Hydraulic coupling model

In this paper, PFC2D software was utilized to establish the fluid solid coupling model of hydraulic fracturing. In the model, each particle contact is a flow channel to simulate the fluid flow, and that these channels contact up small “domains” that store some fluid pressure, as shown in Figure 2. The particles position can be changed by the change of contact force, and finally the change of channel pores is realized.

FIGURE 2

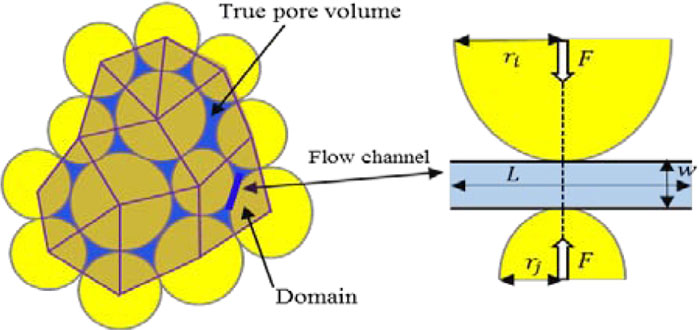
FIGURE 2. The model of domain and flow channel in PFC2D (Tan et al., 2018).

The flow rate of fluid exchange can be expressed by Hagen Poiseuille equation (Hiroyuki et al., 2011):

$Q=\frac{w^3\Delta P}{12\mu L}(1)$

Where, $\Delta P$ is the pressure difference between the two pore basins, $\mu$ is the fluid viscosity, $w$ is the aperture and $L$ is the length of the fluid channel.

Each channel has an aperture associated with it. The aperture is calculated by:

$w=\frac{w_0{F}_0}{F+F_0}(2)$

Where, $w_0$ is the residual aperture for particles that are just touching, $F$ is the normal stress at the contact and $F_0$ is the contact stress at which the aperture decreases to half of its initial aperture.

For each time increment, the change of fluid pressure $\Delta P$ is (Hiroyuki et al., 2011):

$\Delta P=\frac{K_f}{V_r}\left(\Sigma Q\Delta t-V_r\right)(3)$

Where, $\Sigma Q$ is the total flow rate of fluids, $\Delta t$ is the duration in one time step, $K_f$ is the compressive modulus of the fluid, $V_r$ is the “domain”, that is the pore volume and $\Delta V_r$ is the pore volume change.

2.3 Simulation scheme

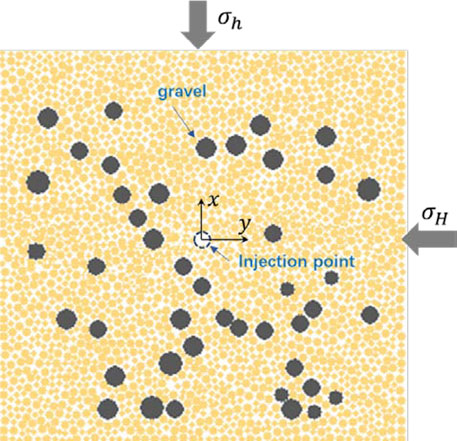
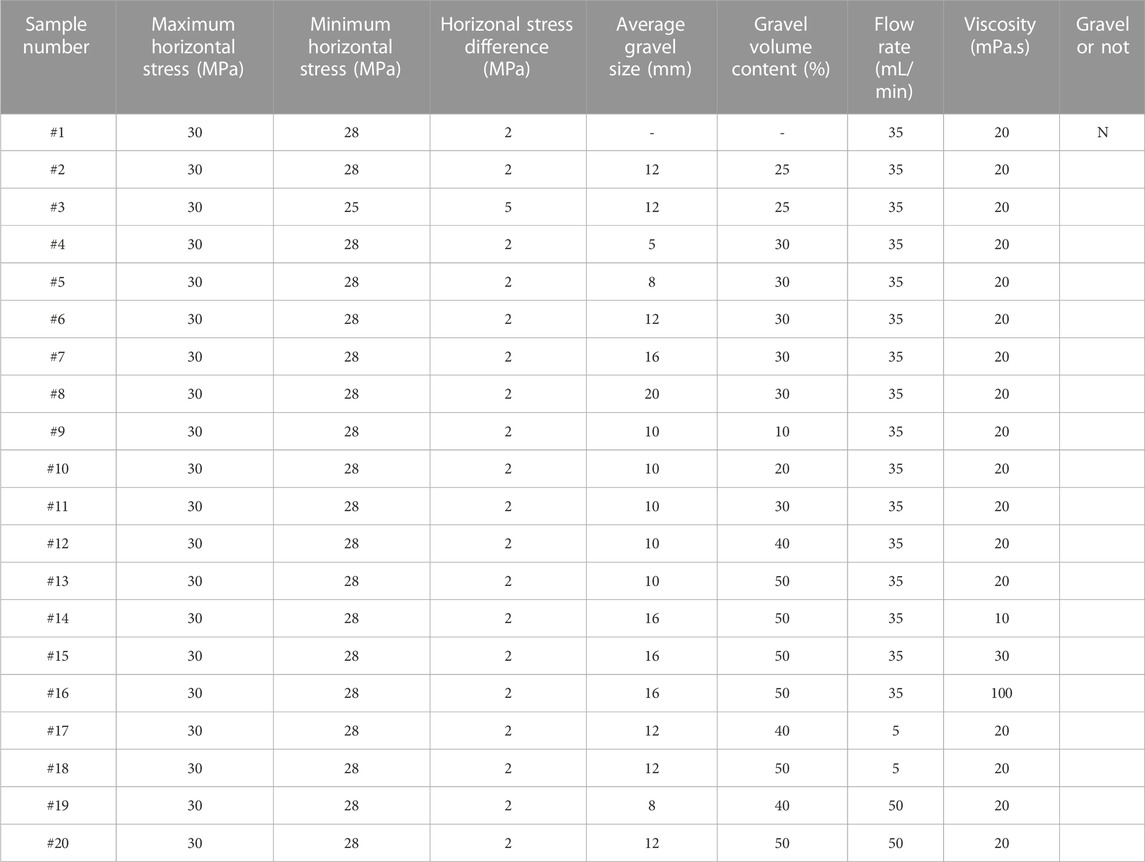
A two-dimensional plane model was established by using PFC2D, as shown in Figure 3. The size of the model is 50 cm × 50 cm, and the diameter of the composed spherical particles is set to 1 mm, with a total of 6,547 in particles. The diameter of the middle circular hole is 3 cm, which is utilized to simulate the injection hole. In Figure 3, the maximum horizontal in situ stress is applied along the X-axis direction, and the minimum horizontal in situ stress is applied along the Y-direction. The simulation parameters are shown in Table 3.

FIGURE 3

FIGURE 3. The geometric model.

TABLE 3

TABLE 3. Simulation parameters.

3 Results and discussion

3.1 Effects of geological factors

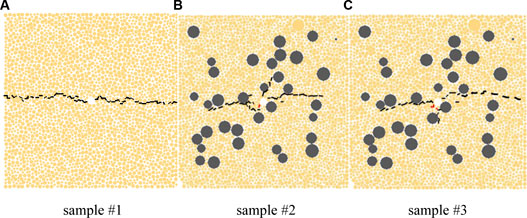
1) In-situ stress

Figure 4 shows the hydraulic fracture propagation patterns under different conditions of in situ stress differences for the two cases of whether there is gravel or not. The simulation results show that the presence of gravels increases the complexity of the hydraulic fracture propagation. When the horizontal stress difference is small, the fracture propagation is less restricted by the in situ stress, and radial fractures are easily formed along the wellbore direction. However, during the hydraulic fracture propagation, the branched fractures propagating in the direction of non-maximum in situ stress are prone to be arrested after encountering gravels, and the hydraulic fractures extending in the direction of maximum in situ stress become domination. When the horizontal stress difference is large, the hydraulic fractures tend to extend in the direction of the maximum horizontal stress, and there are few branched fractures. In this condition, the main hydraulic fracture will detour after encountering gravels during the propagation process.

2) Average gravel size

FIGURE 4

FIGURE 4. Fracture propagation geometry under different stress differences.

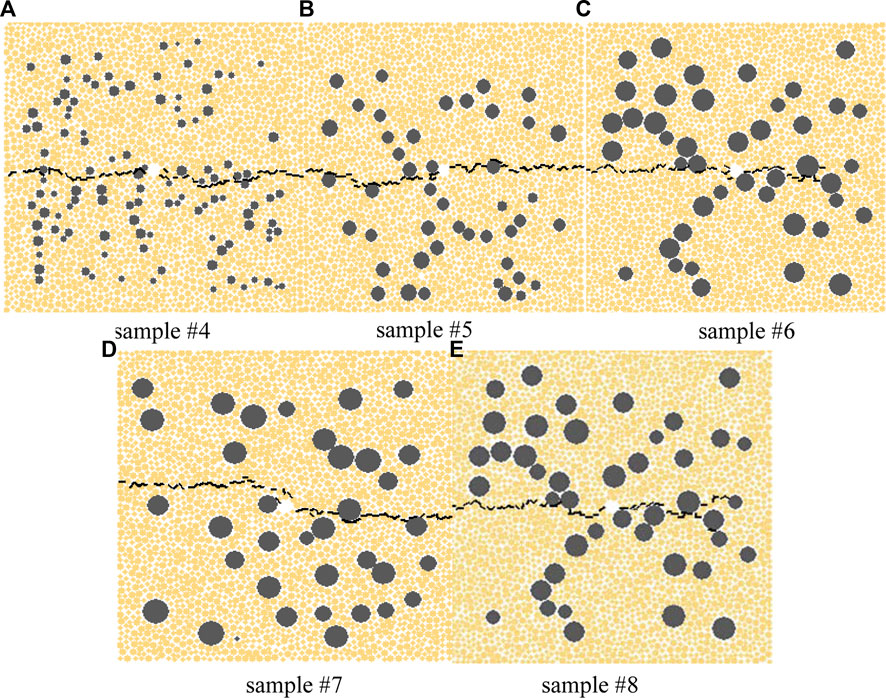
To study the influence of gravel particle size on hydraulic fracture propagation, five groups of calculation examples are designed. In each case, the principal stress difference is 2 MPa, and the gravel content is 30%. The simulation results are shown in Figure 5.

FIGURE 5

FIGURE 5. Fracture propagation geometry under different gravel sizes.

Simulation results show that, the distribution of gravels becomes more dispersed with the increase of the gravel size if the gravel content is same. The main fracture has enough spaces to propagate around the gravels, and the probability for encountering gravels decreases. However, under the control of the principal stresses, once the main fracture encounters the larger-sized gravel, more energy is required to bypass the gravel, and the hydraulic fracture will have a greater turning angle. When the particle size of the gravel is small, the number of the gravel increases, and the main fracture is more likely to encounter the gravels during propagation. However, the degree of stress concentration has been homogenized in the situation, and the hydraulic fracture can easily continue to propagate around the gravel. Hence, the inhibition and shielding effect of gravels on hydraulic fractures are relatively weak, and the fractures are relatively straight.

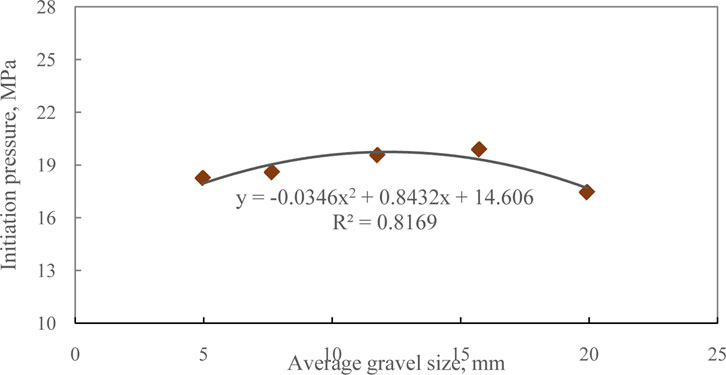
Figure 6 shows the relationship between different gravel sizes and fracture initiation pressure. Results show that under the same gravel content, the fracture initiation pressure increases at initial stage and then decreases with the increase of gravel size. At a certain volume content, the size of the gravel has a probabilistic effect on the fracture propagation. When the gravel particle size increases, the sensitivity and uncertainty of the system stability increases, and the probability characteristics are obvious. The decreases in the gravel particle size contribute to the generation of micro-fractures clusters between the gravel, matrix and matrix, which reduces the rock strength and the fracture initiation pressure. (Khristianovic, 1955; Li et al., 2013).

3) Gravel content

FIGURE 6

FIGURE 6. Initiation pressures under different gravel sizes.

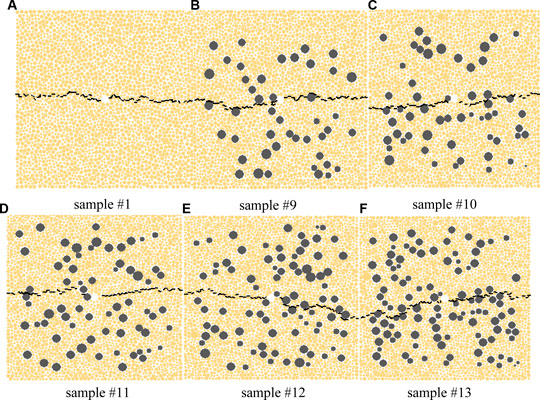
In this section, to simulate the hydraulic fractures propagation under different gravel contents, six groups of calculation examples are designed with gravel contents of 0%, 10%, 20%, 30%, 40% and 50%. The average gravel size is 10 mm. The simulation results are shown in Figure 7.

FIGURE 7

FIGURE 7. Fracture propagation geometry under different gravel volume contents.

Results show that the non-uniform distribution of gravels will lead to asymmetric hydraulic fracture propagation. With the increase of gravel content, micro-fractures at the end of the main fracture continue to initiate and propagate. The gravels distributed on the fracture propagation path will have an influence on the fracture propagation direction, which the gravels in other areas have little effect on the fracture propagation. With more gravel content on the propagation path, the fractures bypass and turn around the gravel to form S-shaped fractures.

3.2 Effects of engineering factors

1) Fracturing fluid viscosity

To study the influence of fracturing fluid viscosity on hydraulic fracture propagation, three groups of examples are designed in this section. The fracturing fluid viscosity is 10 $mPa·\mathrm{s}$, 30 $mPa·\mathrm{s}$ and 100 $mPa·\mathrm{s}$. The simulation results are shown in Figure 8.

FIGURE 8

FIGURE 8. Fracture propagation geometry under different fracturing fluid viscosity.

Results show that the lower the viscosity of the fracturing fluid is, the easier the fracturing fluid is to loss along the fracture to the matrix, resulting in the generation of multi-branched fractures. Due to the joint distribution of hydraulic energy by the multi-branched hydraulic fractures, the length of the main hydraulic fracture becomes shorter. As the viscosity of fracturing fluid increases, the possibility of infiltration in all directions is reduced, as a result, the hydraulic fracture morphology is relatively straight and the length of the main fracture increases. Therefore, the length of the main hydraulic fracture can be increased by increasing the viscosity of fracturing fluids during constructions.

2) Flow rate of fracturing fluid

To study the effect of flow rate on the fracture propagation, two sets of calculation examples are designed in this section, and the flow rates are 5 $ml/\mathit{min}$ and 50 $ml/\mathit{min}$. Under each flow rates, two kinds of gravel contents and gravel sizes were set respectively to simulate the hydraulic fracture propagation process. The simulation results are shown in Figure 9.

FIGURE 9

FIGURE 9. Fracture propagation geometry under different fluid flow rate.

The studies show that under small flow rate, the hydraulic fracture geometry is relatively simple, and the gravels can cause the arrest of the hydraulic fracture. Under large flow rate, after encountering gravels in the fracture propagation process, fluids in the fracture are likely to produce a “water hammer effect”, which leads to the fracture bifurcation and multiple fractures. Contrastively, for homogeneous reservoirs, high flow rate also does not cause fracture bifurcation (Stanchits et al., 2014).

4 Conclusion

1) The gravels in the glutenite formation will have a significant impact on the initiation and propagation of hydraulic fractures. Compared with homogeneous sandstone formations, the glutenite formations own complex hydraulic fracture geometries, which could easily lead to the generation of branched fractures and bifurcation fractures, making non-planar fracture type.

2) This study applied PFC to simulate the hydraulic fracturing propagation of glutenite formations, and there are three main behaviors for the hydraulic fracture as encountering gravels: bypass, stop and bifurcation. Under the high stress difference, high viscosity and moderate flow rate, hydraulic fractures can continue to propagate around the gravel. Under low in situ stress difference, lower viscosity and smaller flow rate, gravels can prevent the propagation of hydraulic fractures. Under the higher in situ stress difference and larger displacement, hydraulic fractures can bifurcate and continue to propagate.

3) The particle size and content of gravels have a certain influence on the fracture propagation. The larger gravel particle size makes it easier to cause the hydraulic fracture to stop or bypass at the gravel. Only the gravel distribution in the direction of hydraulic fracture propagation will cause the hydraulic fracture propagation changes, and the more gravels intensively distributes in the propagation direction, the more distorted the hydraulic fracture is, and which will result in a S-shaped fracture.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

PT: Conceptualization, Methodology, and Writing of the original draft. GC: Conceptualization, and Methodology. QW: Methodology, and Resources. QZ: Methodology, and Supervision. ZC: Methodology, and Supervision. DX: Conceptualization and Review. CX: Review and Editing. XF: Review and Editing. WZ: Methodology and Editing. ZY: Review and Editing. QS: Conceptualization and Review.

Funding

The authors gratefully acknowledge the support of CNPC science and technology project (2021DQ03-37, 2021DJ4706, 2021DJ4102), CPET science and technology project (CPET202105).

Conflict of interest

PT, GC, QW, QZ, ZC, DX, XF, WZ, and ZY was employed by CNPC Engineering Technology R and D Company Limited.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Fan, T. G., Zhang, G. Q., and Cui, J. B. (2014). The impact of cleats on hydraulic fracture initiation and propagation in coal seams. Petroleum Sci. 11, 532–539. doi:10.1007/s12182-014-0369-7

CrossRef Full Text | Google Scholar

Feng, Y. C., Jones, J. F., and Gray, K. E. (2016). A review on fracture-initiation and -propagation pressures for lost circulation and wellbore strengthening. SPE Drill. Complet. 31 (02), 134–144. doi:10.2118/181747-pa

CrossRef Full Text | Google Scholar

Feng, Y., Li, X. R., and Gray, K. E. (2017). Development of a 3D numerical model for quantifying fluid-driven interface debonding of an injector well. Int. J. Greenh. Gas Control 62, 76–90. doi:10.1016/j.ijggc.2017.04.008

CrossRef Full Text | Google Scholar

Hiroyuki, S. Z., Sumihiko, M., and Tsuyoshi, I. (2011). The distinct element analysis for hydraulic fracturing in hard rock considering fluid viscosity and particle size distribution. Int. J. Rock Mech. Min. Sci. 48 (5), 712–727. doi:10.1016/j.ijrmms.2011.04.013

CrossRef Full Text | Google Scholar

Huang, L. K., He, R., Yang, Z. Z., Tan, P., Chen, W., Li, X., et al. (2023). Exploring hydraulic fracture behavior in glutenite formation with strong heterogeneity and variable lithology based on DEM simulation. Eng. Fract. Mech. 278, 109020. doi:10.1016/j.engfracmech.2022.109020

CrossRef Full Text | Google Scholar

Huang, L. K., Liu, J. J., Zhang, F. S., Dontsov, E., and Damjanac, B. (2019). Exploring the influence of rock inherent heterogeneity and grain size on hydraulic fracturing using discrete element modeling. Int. J. Solids Struct. 176-177, 207–220. doi:10.1016/j.ijsolstr.2019.06.018

CrossRef Full Text | Google Scholar

Jia, H. B., Ji, H. C., Wang, L. S., Gao, Y., Li, X., and Zhou, H. (2017). Reservoir quality variations within a conglomeratic fan-delta system in the Mahu sag, northwestern Junggar Basin: Characteristics and controlling factors. J. Petroleum Sci. Eng. 152, 165–181. doi:10.1016/j.petrol.2017.03.002

CrossRef Full Text | Google Scholar

Ju, Y., Yang, Y. M., and Chen, J. L. (2016). 3D reconstruction of low permeability heterogeneous glutenites and numerical simulation of hydraulic fracturing behavior[J]. Chin. Sci. Bull. 61 (1), 82–93.

Google Scholar

Khristianovic, Z. A. (1955). “Formation of vertical fractures by means of highly viscous liquid,” in Paper presented at the 4th World Petroleum Congress, Rome, Italy, June 1955.

Google Scholar

Li, L. C., Li, G., Meng, Q. M., et al. (2013). Numerical simulation of propagation of hydraulic fractures in glutenite formation[J]. Rock Soil Mech. 34 (5), 1501–1507.

Google Scholar

Liu, H., Jiang, Z. X., Zhang, R. F., and Zhou, H. (2012). Gravels in the daxing conglomerate and their effect on reservoirs in the oligocene langgu depression of the bohai bay basin, north China. Mar. Petroleum Geol. 29 (1), 192–203. doi:10.1016/j.marpetgeo.2011.07.010

CrossRef Full Text | Google Scholar

Lu, M. J., Su, Y. L., Zhan, S. Y., and Almrabat, A. (2020). Modeling for reorientation and potential of enhanced oil recovery in refracturing. Adv. Geo-Energy Res. 4 (1), 20–28. doi:10.26804/ager.2020.01.03

CrossRef Full Text | Google Scholar

Luo, P., Li, Y. M., Jiang, Y. S., et al. (2013). Research on micro-morphology characteristics of hydraulic fractures for conglomerate reservoir[J]. Petroleum Geol. Recovery Effic. 20 (5), 103–106.

Google Scholar

Ma, X. F., Zou, Y. S., Li, N., Chen, M., Zhang, Y., and Liu, Z. (2017). Experimental study on the mechanism of hydraulic fracture growth in a glutenite reservoir. J. Struct. Geol. 97, 37–47. doi:10.1016/j.jsg.2017.02.012

CrossRef Full Text | Google Scholar

Meng, Q. M., Zhang, S. C., and Guo, X. M. (2010). A primary investigation on propagation mechanism for hydraulic fracture in glutenite formation[J]. J. Oil Gas Technol. 32 (4), 119–123.

Google Scholar

Moghadasi, R., Rostami, A., and Hemmati-Sarapardeh, A. (2019). Application of nanofluids for treating fines migration during hydraulic fracturing: Experimental study and mechanistic understanding. Adv. Geo-Energy Res. 3 (2), 198–206. doi:10.26804/ager.2019.02.09

CrossRef Full Text | Google Scholar

PFC2D (2006). User’s instruction manual version 3.1. Minneapolis, United States: Itasca Consulting Group Inc. Particle Flow Code in 2 Dimensions.

Google Scholar

Stanchits, S., Surdi, A., Gathogo, P., Edelman, E., and Suarez-Rivera, R. (2014). Onset of hydraulic fracture initiation monitored by acoustic emission and volumetric deformation measurements. Rock Mech. Rock Eng. 47, 1521–1532. doi:10.1007/s00603-014-0584-y

CrossRef Full Text | Google Scholar

Tan, P., Jin, Y., Han, K., Hou, B., Chen, M., Guo, X., et al. (2017). Analysis of hydraulic fracture initiation and vertical propagation behavior in laminated shale formation. Fuel 206, 482–493. doi:10.1016/j.fuel.2017.05.033

CrossRef Full Text | Google Scholar

Tan, P., Jin, Y., and Pang, H. W. (2021). Hydraulic fracture vertical propagation behavior in transversely isotropic layered shale formation with transition zone using XFEM-based CZM method. Eng. Fract. Mech. 248, 107707. doi:10.1016/j.engfracmech.2021.107707

CrossRef Full Text | Google Scholar

Tan, P., Jin, Y., Xiong, Z. Y., Mian, C., and Hou, B. (2018). Effect of interface property on hydraulic fracture vertical propagation behavior in layered formation based on discrete element modeling. J. Geophys. Eng. 15, 1542–1550. 9pp. doi:10.1088/1742-2140/aaa8ab

CrossRef Full Text | Google Scholar

Tan, P., Jin, Y., Yuan, L., Xiong, Z. Y., Hou, B., Chen, M., et al. (2019). Understanding hydraulic fracture propagation behavior in tight sandstone–coal interbedded formations: An experimental investigation. Petroleum Sci. 16 (1), 148–160. doi:10.1007/s12182-018-0297-z

CrossRef Full Text | Google Scholar

Tan, P., Pang, H. W., Zhang, R. X., Jin, Y., Zhou, Y., Kao, J., et al. (2020). Experimental investigation into hydraulic fracture geometry and proppant migration characteristics for southeastern Sichuan deep shale reservoirs. J. Petroleum Sci. Eng. 184, 106517. doi:10.1016/j.petrol.2019.106517

CrossRef Full Text | Google Scholar

Wan, L. M., Hou, B., Tan, P., Chang, Z., and Muhadasi, Y. (2019). Observing the effects of transition zone properties on fracture vertical propagation behavior for coal measure strata. J. Struct. Geol. 126, 69–82. doi:10.1016/j.jsg.2019.05.005

CrossRef Full Text | Google Scholar

Wang, J., Cao, Y. C., Liu, K. Y., Liu, J., and Kashif, M. (2017). Identification of sedimentary-diagenetic facies and reservoir porosity and permeability prediction: An example from the Eocene beach-bar sandstone in the Dongying Depression, China. Mar. Petroleum Geol. 82, 69–84. doi:10.1016/j.marpetgeo.2017.02.004

CrossRef Full Text | Google Scholar

Wang, X. H., Zhang, F. S., Tang, M. R., Du, X., and Tang, J. (2021). Effect of stress shadow caused by multistage fracturing from multiple well pads on fracture initiation and near-wellbore propagation from infill wells. SPE J. 27 (01), 204–225. doi:10.2118/208577-pa

CrossRef Full Text | Google Scholar

Wang, Z. Y., Lin, B. T., Yu, H. Y., et al. (2020). Characteristics of in⁃situ stress in sandy conglomerate reservoir of Badaowan formation in District No.7, Karamay oilfield[J]. Xinjiang Pet. Geol. 41 (3), 314–320.

Google Scholar

Wei, S. M., Kao, J. W., Jin, Y., Shi, C., Xia, Y., and Liu, S. (2021). A discontinuous discrete fracture model for coupled flow and geomechanics based on FEM. J. Petroleum Sci. Eng. 204, 108677. doi:10.1016/j.petrol.2021.108677

CrossRef Full Text | Google Scholar

Xie, H. P., Lu, J., Li, C., Li, M., and Gao, M. (2022). Experimental study on the mechanical and failure behaviors of deep rock subjected to true triaxial stress: A review. Int. J. Min. Sci. Technol. 32 (05), 915–950. doi:10.1016/j.ijmst.2022.05.006

CrossRef Full Text | Google Scholar

Zhang, F. S., Zhu, H. Y., Zhou, H. G., Guo, J., and Huang, B. (2017). Discrete-element-method/computational-fluid-dynamics coupling simulation of proppant embedment and fracture conductivity after hydraulic fracturing. SPE J. 22, 632–644. doi:10.2118/185172-pa

CrossRef Full Text | Google Scholar

Zhang, J. X., Xu, D. J., and Liao, R. Q. (2019). Prediction of the conductivity of the proppant in glutenite tight oil reservoir[J]. Petroleum Geol. Oilfield Dev. Daqing 38 (6), 149–154.

Google Scholar

Zhang, X., Wu, B. S., Connell, Luke, Han, Y., and Jeffrey, R. (2018). A model for hydraulic fracture growth across multiple elastic layers. J. Petroleum Sci. Eng. 167, 918–928. doi:10.1016/j.petrol.2018.04.071

CrossRef Full Text | Google Scholar

Zhao, Y. Z., Qu, L. Z., and Wang, X. Z. (2007). Simulation experiment on propagation law of hydraulic fracture for different lithologic formations[J]. J. China Univ. Petroleum Nat. Sci. 31 (3), 63–66.

Google Scholar