- 1Division of Artificial Intelligence, Pusan National University, Busan, South Korea
- 2School of Computer Science and Engineering, Pusan National University, Busan, South Korea
- 3Department of Industrial Engineering, Pusan National University, Busan, South Korea
- 4FACDAMM, Busan, South Korea
Developing seismic signal detection and phase picking is an essential step for an on-site early earthquake warning system. A few deep learning approaches have been developed to improve the accuracy of seismic signal detection and phase picking. To run the existing deep learning models, high-throughput computing resources are required. In addition, the deep learning architecture must be optimized for mounting the model in small devices using low-cost sensors for earthquake detection. In this study, we designed a lightweight deep neural network model that operates on a very small device. We reduced the size of the deep learning model using the deeper bottleneck, recursive structure, and depthwise separable convolution. We evaluated our lightweight deep learning model using the Stanford Earthquake Dataset and compared it with EQTransformer. While our model size is reduced by 87.68% compared to EQTransformer, the performance of our model is comparable to that of EQTransformer.
1 Introduction
Detection of seismic signals is essential for an on-site early earthquake warning system (EEWS). Major approaches for seismic signal detection, such as short-time average/long-time average (STA/LTA) (Allen, 1978), require an analysis of the ambient noise and structural vibration of sites in advance and the optimization of threshold values via multiple trials and errors for reducing false detection. Since the on-site EEWS needs multiple seismic sensors, data acquisition, and management systems, it is important that sensing systems are cost-effective, and detection is performed with no pre-analysis on on-site ambient noises.
Traditional approaches to detect P/S waves, such as STA/LTA and AIC (Maeda, 1985) techniques, process seismic signals using short-term and long-term averages for the amplitudes of continuous seismic waveforms. This process cannot be fully automated because various noises caused by the geographical locations and environments of the seismic monitoring equipment need to be removed. To overcome these issues, several studies have detected seismic signals using machine learning and deep learning (Ross et al., 2019; Zhu et al., 2019; Mousavi et al., 2020). Among these methods, EQTransformer is considered to perform the best (Mousavi et al., 2020). The EQTransformer structure consists of one encoder and three decoders that compress and restore data and is connected using long short-term memory (LSTM) and an attention mechanism. The EQTransformer model outputs probabilistic statistics for earthquakes and P/S waves Figure 1.
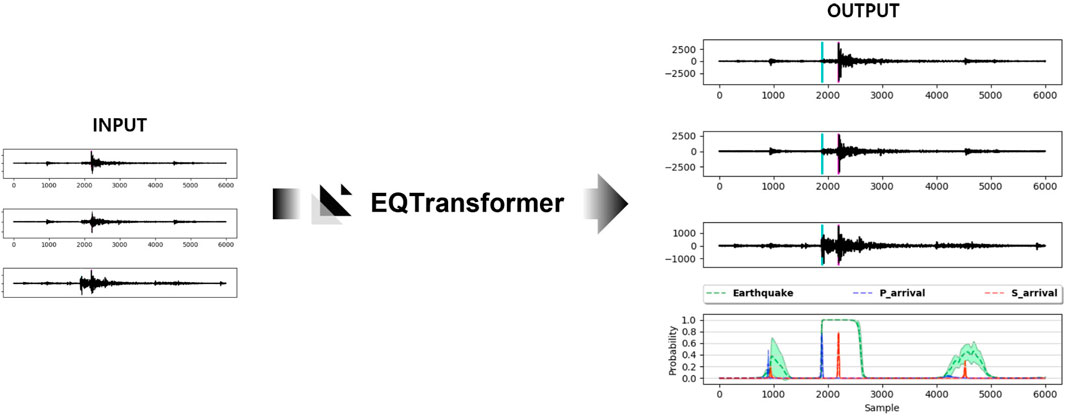
FIGURE 1. EQTransformer to input signals, detect earthquakes in earthquake waveforms, mark P/S wave arrivals, and output their probabilistic statistics. There are four plots in the output. Light blue lines indicate the earthquake locations in the three upper plots. In the last output plot, a green dotted line indicates the probability of an earthquake, a blue dotted line indicates the probability for the starting point of the P wave, and a red dotted line indicates the probability for the starting point of the S wave.
Although the EQTransformer model detects earthquakes and P/S phase pickings with high accuracy, it is almost impossible to mount the model on small IoT (Internet of Things) devices such as earthquake detection sensors that equip limited computing resources.
In this study, we proposed a lightweight seismic signal detection model called LEQNet to operate even in ultra-small devices. We applied various lightweight deep learning techniques, such as the recursive, deeper bottleneck, depthwise, and pointwise separable structures, to reduce the size of the deep learning model. We evaluated our lightweight deep learning system using STEAD datasets and compared them with EQTransformer. Compared to EQTransformer, our LEQNet reduced the number of parameters substantially, with no significant performance degradation (Mousavi et al., 2020). Our LEQNet model can be operated to detect seismic signals even in small devices. The source code of LEQNet is available at https://github.com/LEQNet/LEQNet.
2 Materials and Methods
2.1 Datasets and Preprocessing
STEAD (Mousavi et al., 2019), a high-quality, large-scale, global dataset was used in this experiment. STEAD consists of seismic waveforms with an epicenter of less than 350 km and noise waveforms without seismic signals. Regarding the configuration of the data, 120M data are provided, including 450K time series seismic data and noise data for 19,000 h.
One data include 6,000 data points, collected at 100 Hz for 1 min, and three channels, namely, E on the east–west axis, N on the north–south axis, and Z perpendicular to the ground. Based on the discussion of EQTransformer, in which the size of the training dataset did not significantly affect the performance, earthquake data and noise data were under-sampled by 50,000 each. The two classes were in equal ratio to resolve data imbalance and build a deep learning detection model. The ratio of training, validation, and test data set was divided into a general ratio of 8:1:1.
To add more diverse situations to the training data, we applied data aggregation techniques (Van Dyk and Meng, 2001). Augmented techniques include adding events, moving sequences in parallel, adding noise, deleting channels, and adding empty sequences with random probabilities.
2.2 Performance Evaluation
2.2.1 Confusion Matrix
The confusion matrix is typically used as an evaluation index in binary classification problems. When real seismic waves are detected as earthquakes, it is regarded as a true positive (TP). Conversely, if they are not detected, it is a false negative (FN). Noise data are true negative (TN) when predicted as noise and false positive (FP) when called earthquakes. For phase picking, it is counted as TP when the actual arrival time of P and S waves and time of the model are within 0.5 s. When actual P and S waves do not exist and our model does not call P and S arrivals, it is regarded as TN. We calculated precision and recall, as shown in Eqs 1 and 2. F1-score, that is, the harmonic average of precision and recall, was calculated as presented in Eq. 3.
2.2.2 Information Density
Information density is used to evaluate the lightweight technology. When the accuracy of the model is denoted as a(N), the number of parameters of the model as p(N) and the information density D(N) is calculated as shown in Eq. 4. This evaluation considers the number of parameters and accuracy.
2.2.3 Netscore
To consider the amount of computation and inference speed, we measured Netscore Ω(N), as proposed in Eq. 5. (Wong, 2019). The multiply-accumulate of the model is denoted by m(N). α, β, and γ are coefficients for controlling the influence of network accuracy, model complexity, and computational complexity, respectively. They are usually set to α = 2, β = 0.5, and γ = 0.5 (Wong, 2019). When the model became lighter, it had a smaller number of parameters and fewer operations. If the performance of the model remains unchanged, the Netscore increases. The higher the value of Netscore, the lighter is the model.
2.3 Baseline Model EQTransformer
Figure 2A illustrates the structure of EQTransformer that was designed with encoder, decoder, ResNet, and LSTM & transformer. The encoder consists of seven convolutional neural network (CNN) layers. This reduces STEAD seismic signal data into a lower dimension in terms of seismic signal length and allows to reduce the number of parameters in the model. The decoder consists of seven CNN layers. This decoder restores the extracted features to the original dimension. In the EQTransformer, there are three decoders for P, S, and earthquake detection. The ResNet part of the EQTransformer consists of five residual blocks. Each residual block outputs the addition of input and output in two linearly connected CNN layers. This allows to avoid performance degradation caused by a high number of layers. LSTM learns sequential features extracted by the encoder. The transformer carries the characteristics of the seismic signals to each decoder (for P, S, and earthquake detection). EQTransformer comprises several layers and learning parameters, which exceed 300k as it focuses on maximizing the predictive accuracy.
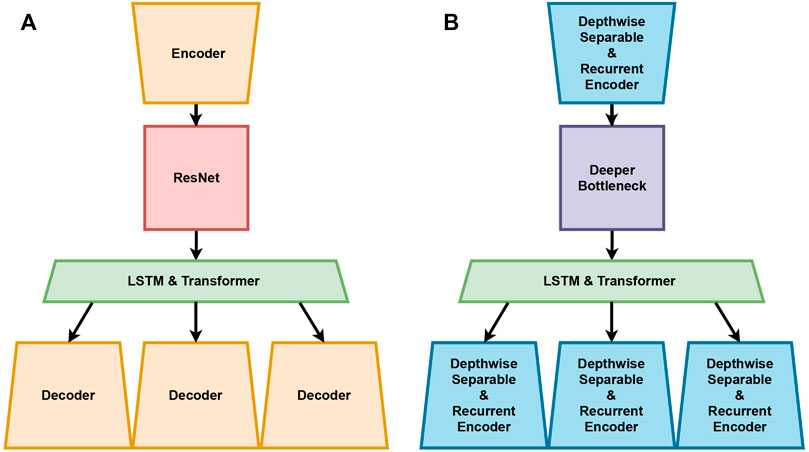
FIGURE 2. Structure of the EQTransformer. (A) EQTransformer is divided into four main parts: encoder, decoder, ResNet, and LSTM & transformer. (B) Structure of our LEQNet. LEQNet comprises four main parts: an encoder that uses the depthwise separable CNN with recurrent CNN, a decoder that uses the depthwise separable CNN with recurrent CNN, residual Bottleneck CNN, and LSTM & Transformer.
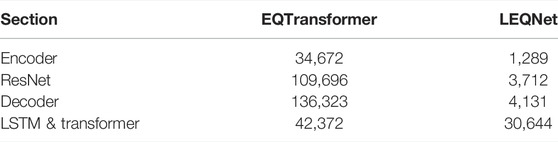
Figure 2A and Table 1 show the structure of EQTransformer that uses a total of 323,063 parameters. A total of 34,672 parameters were used for the encoder, 109,696 for ResNet, and 42,372 for LSTM & transformer. As EQTransformer uses separate decoders in earthquake, P-wave, and S-wave detections, 136,323 parameters are used. The ratio of the total number of parameters is 11% for the encoder, 34% for ResNet, 13% for LSTM & transformer, and 42% for the decoder. The layers with the most parameters in the structure include an encoder, a decoder, and ResNet composed of CNN layer-based structures, accounting for 87% of the total model parameters. The lightweight methods used in this study simplify the CNN-based layer structure with no significant performance degradation.
2.4 Model Lightweight Techniques
2.4.1 Depthwise Separable CNN
Depthwise separable convolution is a CNN that combines the depthwise and pointwise methods. It was first introduced in mobile net v1 (Howard et al., 2017) (Chollet, 2017). Depthwise convolution extracts channel features by performing a convolution operation per channel. Consequently, the input and output channels comprise the same number of channels. In addition, computations are exponentially reduced by skipping convolution between channels. Pointwise convolution compresses data at the same location inside each channel. It extracts the features between channels and controls the number of channels between the input and output. (Hua et al., 2018).
When convolution operations in the CNN perform redundantly among multiple channels, the depthwise separable convolution reduces the huge amount of computation required among the channels. (Paoletti et al., 2020).
2.4.2 Deeper Bottleneck Architecture
Deeper bottleneck architecture was proposed in ResNet to reduce training time (He et al., 2016). In this method, an additional convolution is performed before the convolution to reduce the size of the input channel. After convolution with input channels of reduced size, a convolution operation to restore the number of channels is executed. When one residual block consists of two layers in the EQTransformer, we changed it to three layers. While we have an additional layer, we used a kernel of size one in the first and last layers. This reduces the number of parameters substantially in the intermediate layer that performs the actual operation.
2.4.3 Recurrent CNN
Recurrent CNN is a concept that reuses the output of the CNN layer. To use the recurrent CNN, the number of channels in input and output needs to be equal with the same kernel shape. The layers also need to be continuous. We applied the recurrent CNN to the encoder and the decoder, respectively. This reduced the model size by reusing parameters.
The use of the recurrent CNN has an additional benefit of decreasing memory access costs needed for loading initial parameters, increasing nonlinearity, and updating gradients in multiple parts for learning the model (Köpüklü et al., 2019).
3 Results
We learned a detection model using 50,000 sets of earthquake data and noise data sampled from STEAD and repeated the learning process for 10 epochs. The threshold values were set for the probability of seismic detection and P- and S-phase pickings as detection = 0.5, p = 0.3, and S = 0.3, which were equal to EQTransformer.
3.1 LEQNet
Figure 2B illustrates the structure of LEQNet that was designed using the depthwise separable CNN, deeper bottleneck, and recurrent CNN. Depthwise separable CNN was applied to the encoder and decoder which were used in the feature compression and decompression steps. In addition, memory access time in the encoder and decoder was reduced using the recurrent CNN layers in LEQNet. These recurrent CNN layers also decreased the inference time and model size via the reuse of existing parameters.
Table 1 summarizes the reduction in the number of parameters. The number of parameters in the encoder was reduced from 34,672 to 1,289, and from 136,323 to 4,131 in the decoder. ResNet for central feature extraction in the EQTransformer was replaced by the deeper bottleneck CNN in our LEQNet. This reduced the number of parameters from 109,696 to 3,712. Although there was no structural change in LSTM & transformer, the decrease in the number of input parameters itself reduced the number of parameters from 42,372 to 30,644 in LSTM & transformer.
Figure 3 illustrates the LEQNet architecture. Each encoder and decoder of LEQNet consists of five layers, and the deeper bottleneck consists of four layers; however, EQTranformer has seven layers in each encoder and decoder and five layers for ResNet. The number of output channels in the encoder in the LEQNet has changed to 32, similar to the number of input channels, while the number of channels in the EQTransformer was 64.
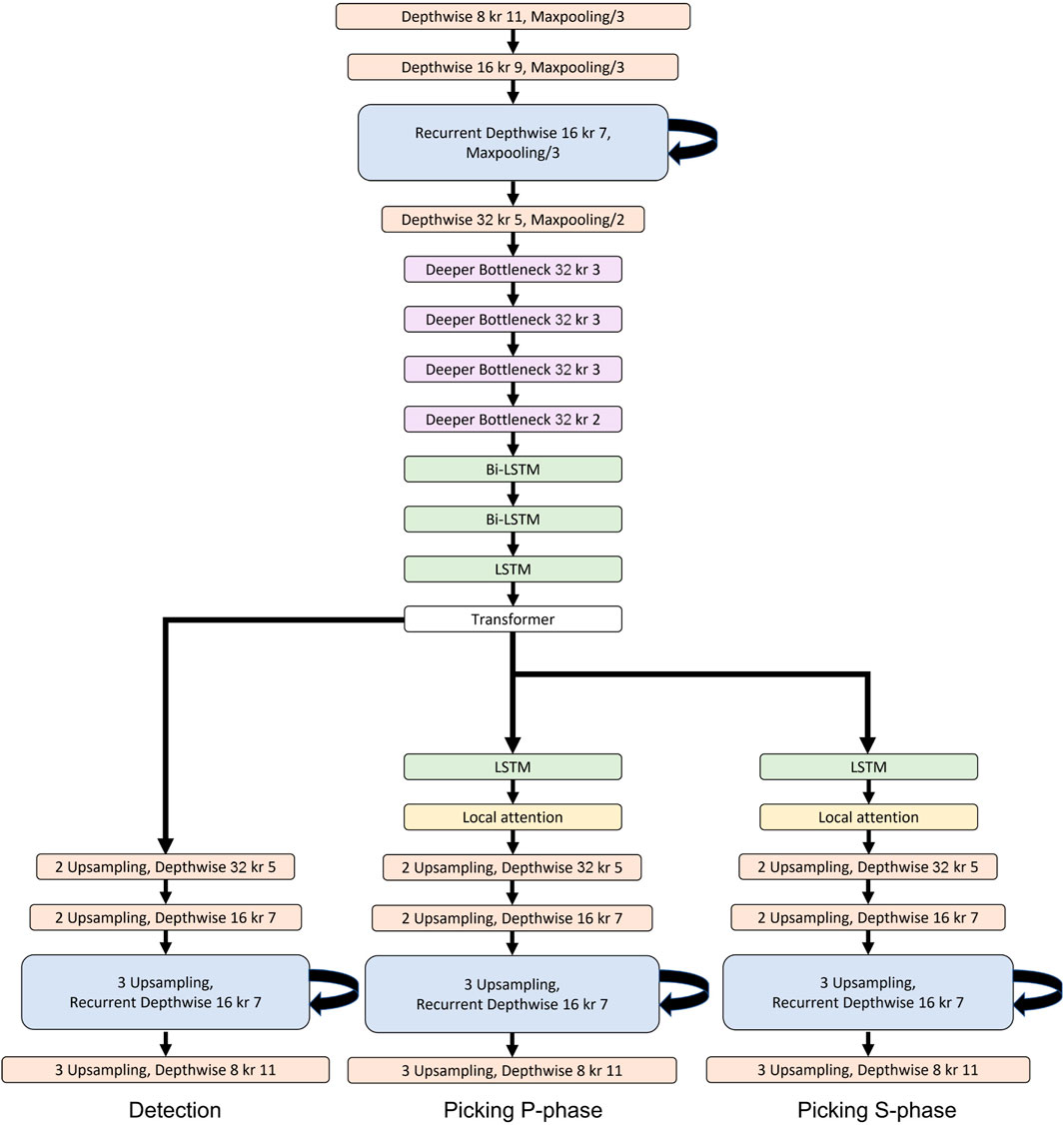
FIGURE 3. LEQNet model architecture. Depthwise separable CNN and recurrent CNN were applied to the encoder and decoder, respectively. The number of layers in the encoder was reduced to five, while the EQTransformer had seven layers in the encoder. Features can be extracted via four blocks using deeper bottleneck and via five blocks in the EQTransformer. Detailed description of each block is provided in the Methods section. The convolutional layers represent the number of kernels, and kr is the kernel size.
3.2 Model Size Reduction
LEQNet reduces the number of parameters and computation time substantially via the lightweight techniques (2 and Figure 4A). The number of parameters for the LEQNet in this study decreased by about 88% compared to the EQTransformer. The amount of computation floating-point operations (FLOPs) decreased from 79,687,040 to 5,271,488 (Table. 2). These results reduced the model size by about 79% compared to the EQTransformer (from 4.5MB to 0.94 MB). This suggests that our LEQNet model can operate in small devices with tiny memory.
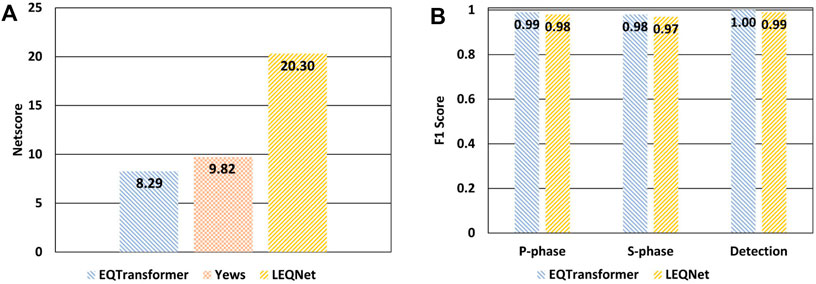
FIGURE 4. (A) Comparison of the Netscore, LEQNet, EQTransformer, and Yews. (B) Comparison of detection, S-phase, and P-phase scores between LEQNet and EQTransformer.
Table 2 shows the degree of model size reduction for the EQTransformer, Yews (Zhu et al., 2019) earthquake detection deep learning model, and LEQNet in terms of information density and Netscore. As the accuracy between these two models does not differ significantly, the information density score only depends on the number of parameters. LEQNet has improved the information density by about 8.09 times compared to EQTransformer.
Figure 4A shows Netscore, which measures the amount of computation according to FLOPs. When Netscore coefficients are usually set to α = 2, β = 0.5, and γ = 0.5, we changed γ to 0.1 because the Netscore was measured according to FLOPs in CNN layers. The theoretical maximum value of Netscore is 80, while EQTransformer showed 8.29 and Yews 9.82 in Netscore, LEQNet scored 20.30 (see Figure 4A), indicating that our LEQNet improves the Netscore by 2.44 times compared to the EQTransformer.
3.3 Detection Performance
We evaluated the detection performance of LEQNet and compared it with other existing methods, such as EQTransformer, PhaseNet (Ross et al., 2019), Yews, and STA/LTA (Table 3). F1-scores for earthquake detection, P-phase picking, and S-phase picking were also compared. EQTransformer showed F1-scores of 1.0, 0.99, and 0.98 in these three tasks. F1-scores (0.99, 0.98, and 0.97) of our LEQNet were almost similar to those of EQTransformer. Our F1-scores were higher than those of PhaseNet by 0.02 in P-phase picking and by 0.03 in S-phase picking, higher than those of Yews by 0.37 in P-phase picking and by 0.31 in S-phase picking, and by 0.14 in earthquake detection. Interestingly, FLOPs in our LEQNet was similar to those in Yews, although our LEQNet performed better than Yews in terms of the F1-score.
4 Discussion
EQTransformer and PhaseNet improved the performance of earthquake detection, P-phase picking, and S-phase picking substantially using deep neural networks. These models are difficult to operate on low-cost embedded devices for earthquake detection. The models should be processed in low-cost embedded devices using EEWS. Therefore, we aimed to construct a lightweight model while maintaining high performance.
Compared to existing deep neural network models, the size of our LEQNet model is reduced while maintaining high performance, as supported by the finding of this study. Remarkably, we reduced the number of parameters by 87.68% and FLOPs in CNN layers by 93.38%, compared to the EQTransformer. This model optimization was achieved by applying the depthwise separable CNN and recurrent CNN and by removing some layers in the encoder and decoder, which occupy 53% of the model. In addition, decreasing the number of output channels in the ResNet also contributed to reducing the number of parameters in our LEQNet. However, performance degradation was observed when some parameters were reduced in the encoder and decoder. To resolve this issue, we applied the deeper bottleneck architecture to our model, as in the EQTransformer. This increased the information density and Netscore of our LEQNet model: information density increased from 3.06e-4 to 24.76e-4, 8.09 times higher than that of EQTransformer, and Netscore increased from 8.29 to 20.30, 2.44 times higher than that of EQTransformer.
Although we reduced the model size substantially, there remains room for improvements. Our model needs to run on the traditional TensorFlow-like environments (Abadi et al., 2016), which may not be suitable for small devices. Therefore, we aimed to address this issue using TensorFlow Lite (Google, 2020) in future works.
5 Conclusion
A model for seismic signal detection for the EEWS needs to operate in low-cost sensors in an environment without the support of a server and interconnection with other management systems. As the EQTransformer has a model size of about 4.5 MB and needs a lot of computation, it is difficult to operate in limited environments such as low-power wireless communication devices and Arduino.
To resolve this issue, we developed LEQNet using lightweight deep learning techniques. LEQNet reduced the number of parameters of the detection model by 88% and the model size by 79% (from 4.5 MB to 0.94 MB), as compared to the EQTransformer, with no significant performance degradation. Our model can be mounted on IoT devices that include embedded RAM of less than 1 MB with no special external management systems.
Although this LEQNet model reduces the model size drastically compared to the EQTransformer, there remains room for improvement. Recently, tiny AI models, which can operate in smaller devices with memory less than 256 kB, are in high demand. Therefore, our model needs to be reduced more than the current model size to meet this requirement. Our LEQNet package is easy to install and is available for public use. We believe that this lightweight earthquake deep neural network can be a useful tool in a community burdened with geohazards and georisks.
Data Availability Statement
Publicly available datasets were analyzed in this study. These data can be found at: https://github.com/smousavi05/STEAD.
Author Contributions
JL, SJ, CJ, JG, and GS contributed to the conception and design of the study. JL, SJ, and CJ wrote the first draft of the manuscript. GS, JG, GJ, and JY wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.
Funding
This work was supported by the Institute of Information and Communications Technology Planning and Evaluation (IITP) grant funded by the Korean government (MSIT) (No. 2020-0-01450, Artificial Intelligence Convergence Research Center (Pusan National University)) to GS.
Conflict of Interest
Author JY was employed by FACDAMM.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abadi, M., Barham, P., Chen, J., Chen, Z., Davis, A., Dean, J., et al. (2016). “Tensorflow: A System for Large-Scale Machine Learning,” in 12th \{USENIX\} Symposium on Operating Systems Design and Implementation (\{OSDI\} 16), 265–283.
Allen, R. V. (1978). Automatic Earthquake Recognition and Timing from Single Traces. Bull. Seismol. Soc. Am. 68, 1521–1532. doi:10.1785/bssa0680051521
Chollet, F. (2017). “Xception: Deep Learning with Depthwise Separable Convolutions,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 1251–1258. doi:10.1109/cvpr.2017.195
Google, L. L. C. (2020). Tensorflow Lite. Available at: https://www.tensorflow.org/lite (Accessed Febuary 26, 2022).
He, K., Zhang, X., Ren, S., and Sun, J. (2016). “Deep Residual Learning for Image Recognition,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 770–778. doi:10.1109/cvpr.2016.90
Howard, A. G., Zhu, M., Chen, B., Kalenichenko, D., Wang, W., Weyand, T., et al. (2017). Mobilenets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv Prepr. arXiv:1704.04861.
Hua, B.-S., Tran, M.-K., and Yeung, S.-K. (2018). “Pointwise Convolutional Neural Networks,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 984–993. doi:10.1109/cvpr.2018.00109
Köpüklü, O., Babaee, M., Hörmann, S., and Rigoll, G. (2019). “Convolutional Neural Networks with Layer Reuse,” in 2019 IEEE International Conference on Image Processing (ICIP) (Piscataway, NJ, USA: IEEE), 345–349. doi:10.1109/icip.2019.8802998
Maeda, N. (1985). A Method for Reading and Checking Phase Time in Auto-Processing System of Seismic Wave Data. J. Seismol. Soc. Jpn. 38, 365–379. doi:10.4294/zisin1948.38.3_365
Mousavi, S. M., Ellsworth, W. L., Zhu, W., Chuang, L. Y., and Beroza, G. C. (2020). Earthquake Transformer-An Attentive Deep-Learning Model for Simultaneous Earthquake Detection and Phase Picking. Nat. Commun. 11, 3952. doi:10.1038/s41467-020-17591-w
[Dataset] Mousavi, S. M., Sheng, Y., Zhu, W., and Beroza, G. C. (2019). Stanford Earthquake Dataset (Stead): A Global Data Set of Seismic Signals for Ai. IEEE Access 7, 179464–179476. doi:10.1109/ACCESS.2019.2947848
Paoletti, M. E., Haut, J. M., Tao, X., Plaza, J., and Plaza, A. (2020). Flop-reduction through Memory Allocations within Cnn for Hyperspectral Image Classification. IEEE Trans. Geoscience Remote Sens. 59, 5938. doi:10.1109/TGRS.2020.3024730
Ross, Z. E., Yue, Y., Meier, M. A., Hauksson, E., and Heaton, T. H. (2019). Phaselink: A Deep Learning Approach to Seismic Phase Association. J. Geophys. Res. Solid Earth 124, 856–869. doi:10.1029/2018jb016674
Van Dyk, D. A., and Meng, X.-L. (2001). The Art of Data Augmentation. J. Comput. Graph. Statistics 10, 1–50. doi:10.1198/10618600152418584
Wong, A. (2019). “Netscore: Towards Universal Metrics for Large-Scale Performance Analysis of Deep Neural Networks for Practical On-Device Edge Usage,” in International Conference on Image Analysis and Recognition (Berlin, Germany: Springer), 15–26. doi:10.1007/978-3-030-27272-2_2
Zhou, Y., Yue, H., Kong, Q., and Zhou, S. (2019). Hybrid Event Detection and Phase‐Picking Algorithm Using Convolutional and Recurrent Neural Networks. Seismol. Res. Lett. 90, 1079–1087. doi:10.1785/0220180319
Keywords: seismic wave, earthquake detection, lightweight technology, deep learning, convolutional neural network
Citation: Lim J, Jung S, JeGal C, Jung G, Yoo JH, Gahm JK and Song G (2022) LEQNet: Light Earthquake Deep Neural Network for Earthquake Detection and Phase Picking. Front. Earth Sci. 10:848237. doi: 10.3389/feart.2022.848237
Received: 04 January 2022; Accepted: 17 May 2022;
Published: 04 July 2022.
Edited by:
Said Gaci, Algerian Petroleum Institute, AlgeriaReviewed by:
Stephen Wu, Institute of Statistical Mathematics, JapanChong Xu, Ministry of Emergency Management, China
Copyright © 2022 Lim, Jung, JeGal, Jung, Yoo, Gahm and Song. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jin Kyu Gahm, Z2FobWpAcHVzYW4uYWMua3I=; Giltae Song, Z3NvbmdAcHVzYW4uYWMua3I=
†These authors have contributed equally to this work and share first authorship
 Jongseong Lim1†
Jongseong Lim1† Jin Kyu Gahm
Jin Kyu Gahm Giltae Song
Giltae Song