- 1Department of Geology, University of Illinois at Urbana-Champaign, Urbana, IL, United States
- 2Earth and Planets Laboratory, Carnegie Institution for Science, Washington, DC, United States
Monitoring the activity of subglacial volcanoes along the Aleutian Arc in Alaska is important to the safety of local populations, as well as air traffic flying through the region. However, observations of volcanic unrest are limited by accessibility and resources, particularly at glacier-covered systems, making investigations of their stability challenging. Westdahl Peak, a subglacial volcano on Unimak Island in the Aleutian Arc has experienced significant unrest and uplift since its most recent VEI three eruption in 1991-1992. Given the magnitude of observed uplift, previous investigations suggested the potential for eruption by 2010, but no such event has occurred. One hypothesis to explain this prolonged unrest is that the 1-km thick glacier may increase the stability of the magma system. However, the impact of ice caps and glaciers on the short-term stability of volcanoes is not well understood. In this study, thermomechanical finite element models are used to evaluate how the stability of a glaciated volcano is impacted by variations in ice cap thickness, magma chamber depth, geometry, magma flux rate, and seasonal changes in ice cover thickness. Our numerical experiments indicate that the presence of an ice cap (1–3 km thick) increases the average repose interval for a magma system. Among models with different magma chamber geometries, depths, and flux rates, the greatest increases in repose interval are observed in prolate systems where the increase is up to 57% for a chamber located at 5 km-depth. Spherical and oblate also experience smaller, yet significant, increases in repose interval. Additionally, the percentage increase in repose interval is not impacted by variations in magma flux rate for a given ice cap thickness and magma chamber geometry. However, flux rates do influence the timing of eruptions when the system is experiencing seasonal variations in ice thickness. Our results show that systems with low flux rates are more likely to fail when the ice thickness is at its lowest. The numerical estimates further suggest that the ice cap on Westdahl Peak, which is ∼1 km, may slightly increase the stability of the magma system. In general, given flux rates and magma chamber geometries estimated for the Westdahl system, the repose interval can increase by ∼7 years due to the Westdahl glacier. This increase is small on a geologic scale but is significant on human time scales and the impact of glaciers must be considered in future forecasting efforts.
Introduction
Constraining the impact of glaciation on magma system stability is critical for evaluating potential hazards and the eruption potential of active volcanoes located in high latitudes. Previous studies have investigated the effects of deglaciation on magma systems through elastic axisymmetric models, and conclude that a decrease in surface load pressure may either enhance or inhibit conditions for dike initiation dependent upon magma chamber geometry and depth (Albino et al., 2010; Sigmundsson et al., 2010). In particular, these studies evaluate how decreasing surface loads impact both the pressure within the magma chamber and the threshold conditions for tensile failure and dike initiation in the host rock. Albino et al. (2010) apply their models to Grímsvötn and Katla Volcanoes in Iceland. Both applications conclude that surface load variations, such as jökulhlaups (large lake water discharge events) and annual snow cover melting, may enhance the potential for dike initiation and/or eruption when the magma chamber is already near failure. Additionally, recent numerical studies have shown that viscoelastic effects in the host rock impact the timing and conditions for failure of long-lived magma systems (Del Negro et al., 2009; Gregg et al., 2012; Cabaniss et al., 2018; Zhan and Gregg, 2019). However, the combined effects of both viscosity and ice cap loading have not yet been studied. It is therefore critical to investigate the roles that viscoelasticity and long-term stress accumulation play in glaciated systems.
In this study, we run a series of numerical simulations to investigate the impact of ice caps on the stability and eruption potential of long-lived magma systems. Viscoelastic, temperature-dependent models are developed to evaluate the overall effect of ice caps on magma systems. Particular care is taken to assess the effect of variables such as ice cap thickness, magma chamber size, geometry, and the flux of new material into the magma system. Finally, we apply our generic model to Westdahl Volcano, a caldera system on Unimak Island in the Aleutian Arc of Alaska (Figure 1). Westdahl is covered by ∼1 km of ice and has an active magma chamber at a depth of ∼7.2 km (Gong, 2015). Since its last eruption, in 1991-1992, Westdahl has experienced significant and ongoing inflation that previous studies interpreted as an indication of imminent eruption (Lu et al., 2004). However, no eruption has occurred despite continuing inflation well past the time scale considered in these studies. One potential explanation for this lack of eruption is that the mechanical loading of the ice cap is prolonging the magma reservoir’s stability. In applying our generic model, we investigate the contribution of Westdahl’s ice cap to the mechanical stress state of the volcano and the ongoing likelihood of eruption.
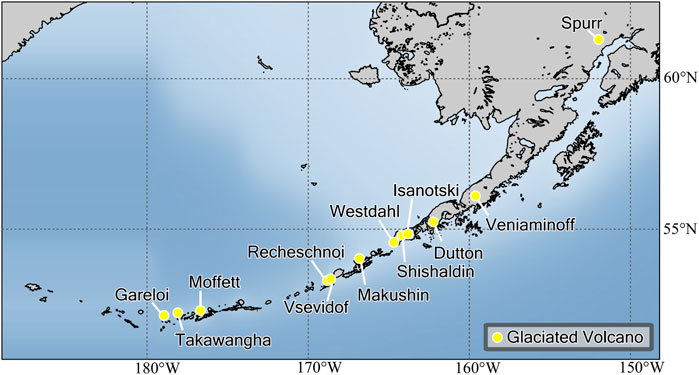
FIGURE 1. Map of Aleutian Arc, Alaska with glaciated volcanoes represented with yellow circles. Glaciated volcanoes from left to right are Gareloi, Takawangha, Moffett, Vsevidof, Recheschnoi, Makushin, Westdahl, Shishaldin, Isanotski, Dutton, Veniaminof, and Spurr.
Methods
Building upon previous models (Grosfils, 2007; Gregg et al., 2012; Albright et al., 2019), we use COMSOL Multiphysics 5.5 to create viscoelastic finite element models that incorporate temperature-dependent rheology (Figure 2). In these models, ice caps of various thicknesses are then implemented to simulate glaciated volcanoes. In a 50 by 25 km, two-dimensional model space, the magma reservoir is constructed as a pressurized elliptical void along a central axis of rotational symmetry. Roller boundaries are implemented on the right lateral and bottom walls. A layer with variable thickness is included to simulate an ice cap covering the volcano. The rock and ice domains are gravitationally loaded to impose an initial lithostatic stress.
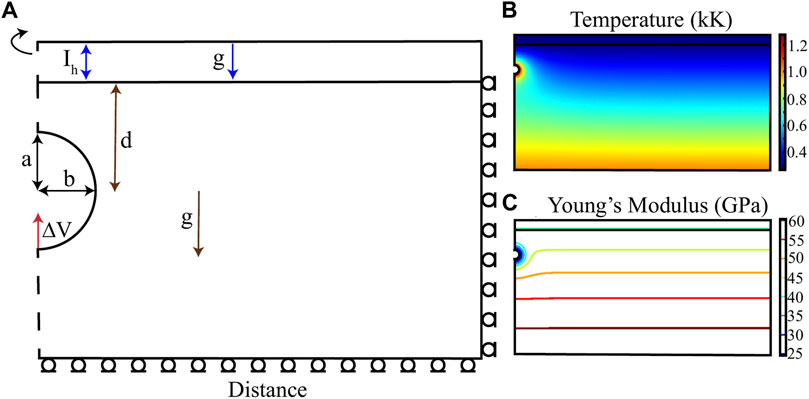
FIGURE 2. Finite element model setup. (A) Schematic diagram of model geometry and boundary conditions. The left boundary has rotational symmetry while roller conditions are implemented along the bottom and top boundaries. The model space is divided into a variable-thickness layer of ice on top of a 50 by 25 km domain representing the magmatic system host rock. The magma chamber is simulated as a pressurized elliptical void along the rotational boundary, while the labels indicate different parameter values used in this study and the gravitational loading incorporated into both model domains. Depth to center is indicated by “d”; however, some experiments use the depth to the crest of the magma chamber as indicated in the text. (B) Heat transfer module is incorporated in the model, and rock near the magma chamber (1,000°C) experiences higher temperatures. Temperature gradient of the Earth is also represented in the models as 30°C/km. (C) Temperature-dependent Young’s Modulus is defined in the models to make them viscoelastic, therefore temperature- and time-dependent.
In this study, we use a generalized Maxwell model to describe a viscoelastic rheology whose relaxation time,
In Eq (1), the shear modulus,
The COMSOL solid mechanics and heat transfer modules are used to implement both time- and temperature-dependence within the viscoelastic model space. Eq (2) represents the temperature-dependent host rock viscosity:
where
Throughout the modeling process, we measure the change in repose interval of the magma systems in response to changing parameters including different thicknesses of ice, magma chamber geometries, magma chamber depths, and magma flux rates. Repose interval is defined as the time period for the tensile stress along the reservoir wall to progress from a state of compression to tension. In this investigation, we focus on tensile failure along the reservoir boundary as a proxy for dike initiation and eruption, as opposed to shear failure in the surrounding host rock, which has also been shown to potentially catalyze eruptions (Gregg et al., 2012). Tensile rupture of the chamber and the onset of eruption is assumed to occur when tensile stress becomes positive:
Factors Controlling the Host Rock Stability in Ice-Covered Volcanoes
A series of numerical experiments are conducted to investigate the impact of ice cap loading on the stability of magma systems. In particular, we examine the relationship between the stability of a magma system replenished by a constant magma flux and the presence an ice cap. The repose interval is defined as the time from the start of new magma injection, which remains constant throughout the simulation, to when tensile failure is observed at the reservoir boundary, as described above. Specifically, repose intervals of magma systems with ice caps of 1–3 km are compared with repose intervals of otherwise identical magma systems without ice to calculate percent change in time to eruption due to the ice cap. We should note that the repose interval described here represents a minimum, and natural systems may have protracted periods with no new magma injection. Results, including both the absolute timescales as well as the percent change in repose for all of the experiments described below can be found in the Supplementary Material S1.
Ice Cap Thickness
In general, an additional load above a magma chamber, such as from ice, increases the confining stress along the reservoir wall, making it more difficult for the chamber to rupture (Grosfils, 2007). In all experiments, we found that ice cap thickness increases the repose interval, but different parameters of the magma system affect how much the repose interval is changed relative to an ice-free baseline. In the following sections, we investigate the effects of magma flux (3.2), depth to reservoir crest (3.3), and reservoir geometry (3.4).
Magma Flux
Magma flux is thought to be a primary driver of inflation and ultimately controls the timing of failure for magma systems (Cabaniss et al., 2018). As such, a wide range of fluxes is investigated from 0.0001 to 0.05 km3/yr (Wilson et al., 2006; Annen, 2009; Gelman et al., 2013). Model results indicate that the percent increase of repose interval due to glacial loading is independent of the flux rate (Figure 3). For instance, the repose interval of a spherical chamber at 5 km depth will increase by ∼4.8%, independent of varying the flux rate. Similarly, a prolate chamber located at a depth to center of 5 km underneath 3 km of ice, will see an increase in repose of ∼23%, regardless of the flux rate (Figure 3B). A similar response is observed for chambers with an oblate geometry (Figure 3C). Additionally, the timing of tensile failure in systems with identical depth, shape, and ice cap thickness occurs independent of flux rate for similar volumes of magma added. Although the modeled magma systems indicate an insensitivity to flux rate, their repose intervals are highly dependent on the total magnitude of volume change (Figure 4). For each simulation, tensile failure is produced for the same total volume of magma added, regardless of the rate of intrusion, for the flux rates investigated (0.0001–0.05 km3/yr). For example, tensile failure for a spherical magma chamber with a depth of 7 and 1 km of ice will occur when ∼0.24 km3 of magma is added to the chamber (Figure 4A).
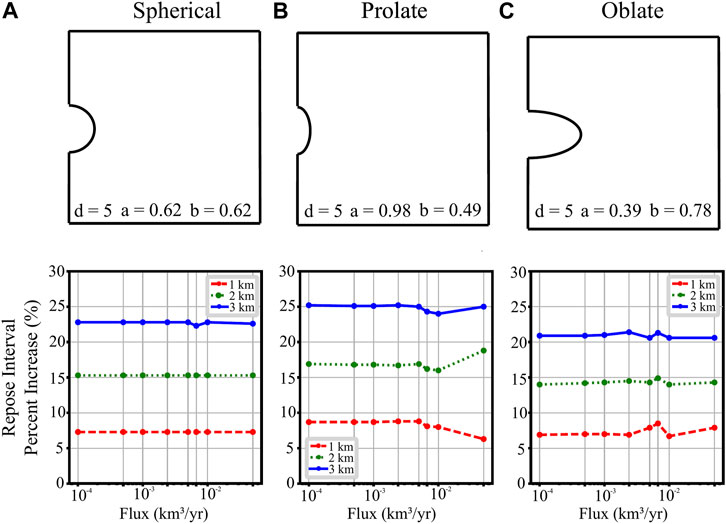
FIGURE 3. Flux rate versus percent change in the repose intervals of volcanic systems with spherical, prolate, and oblate magma chamber geometries. (A) In the spherical case, a magma chamber with radius ∼0.62 and 5 km depth to center is modeled. Flux rates range from 0.0001-0.05 km3/yr and percent changes due to an ice cap thickness of 1, 2, and 3 km are represented by the dashed red line, dotted green line, and solid blue line respectively. (B) A prolate chamber with depth of 5 km, horizontal radius of ∼0.49 km, and vertical radius of ∼0.98 km is modeled. (C) An oblate chamber with ∼0.78 km horizontal radius, ∼0.39 km vertical radius, and depth of 5 km is used.
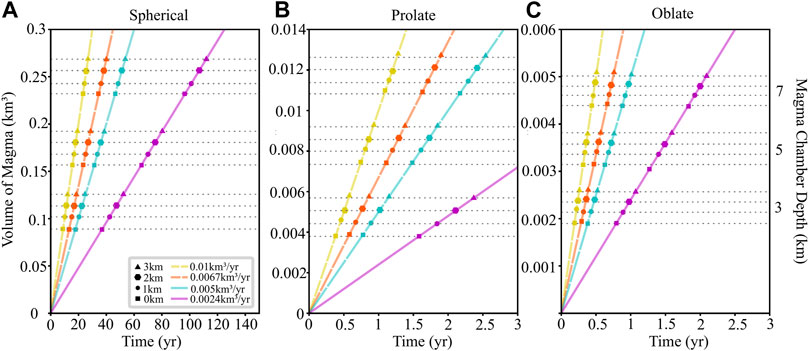
FIGURE 4. Volume of magma added into the chamber versus time with steady flux rates of 0.0024, 0.005, 0.0067 and 0.01 km3/yr for (A) spherical, (B) prolate, and (C) oblate chambers. The spherical chamber has a radius of ∼0.62 km. The prolate magma chamber has radii of ∼0.49 and 0.98 km, and oblate chamber radii are ∼0.39 and 0.78 km. Along each linear flux rate line, the times to failure of several different systems are indicated by points. Each magma chamber depth (3, 5 and 7 km) has four points representing the times to failure for each ice cap thickness (0, 1, 2 and 3 km). Tensile failure for systems with identical magma chamber depths and ice cap thicknesses occur at similar volumes, whose average approximations are represented by the horizontal dashed grey lines.
Magma Chamber Depth
Previous studies have interpreted magma chamber depth to be an influential factor on the stability of a magma system (Albino et al., 2010; Geyer and Bindeman, 2011; Satow et al., 2021). A suite of simulations is run to examine the impact of magma chamber depths to center, ranging from 2-9 km (e.g., Huber et al., 2019; Rasmussen et al., 2019; Kent et al., 2022). Results indicate that the ice cap has a decreased effect on the relative repose interval for deeper magma sources, as is expected given the overall contribution to the surface load. For instance, the repose interval of a system with a spherical chamber at a depth of 2 km will increase by ∼55% when loaded with a 3 km ice cap (Figure 5A). Identical loading conditions will increase the repose interval by only ∼11% for a system with a magma chamber at 9 km depth to center (Figure 5A). This effect is greater for non-spherical chambers, with prolate chambers being most sensitive to variations in magma chamber depth (Figure 5B). Specifically, a prolate chamber located at 2 km depth beneath 3 km of ice will experience an ∼86% increase in its repose interval. Whereas the same chamber at 9 km depth will have an increase in repose of ∼12% (Figure 5B).
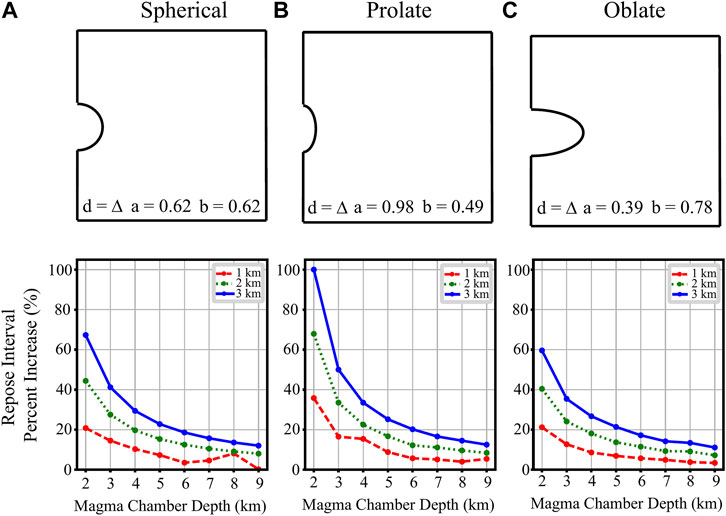
FIGURE 5. Depth versus percent change in the repose intervals of volcanic systems with spherical, prolate, and oblate magma chamber geometries. The flux remains constant at a rate of 0.0024 km3/yr. (A) Depth to the center of the magma chamber ranges from 2-9 km, and the spherical chamber radius of 0.62 km remains constant. Percent changes due to an ice cap thickness of 1, 2, and 3 km are represented by the dashed red line, dotted green line, and solid blue line respectively. As the depth of the magma chamber increases, the effect of the ice cap on the repose interval percent change generally decreases for each ice cap thickness. This pattern is also found for the magma systems with prolate and oblate magma chambers. (B) Depth of magma chamber center versus percent change in the repose interval of a prolate chamber. Depth varies from 2-9 km, but vertical radius and horizontal radius remain constant at ∼0.98 and 0.49 km respectively. (C) The percent change in repose interval as we vary depth and ice cap thickness is measured in a magma system with an oblate magma chamber. The horizontal radius is set at ∼0.78 km while the vertical radius is ∼0.39 km, and the depth to the center of the magma chamber ranges from 2-9 km.
Magma Chamber Geometry
The final parameter we investigate in this study is magma chamber geometry. In accordance with previous studies, we model three simplified magma chamber shapes: spherical, prolate, and oblate (Lisowski, 2007). Starting off, as the radius of a spherical chamber increases, we find glacial loading will ultimately have an increased effect on the repose interval. Our models show that the presence of a 3 km glacier increases the relative repose interval from 17.6% for a chamber with a 0.5 km radius to 34.6% for a chamber with a 4 km radius (Figure 6A). Oblate systems experience a similar, but amplified change in relative repose interval as the size of the horizontal radius is increased (Figure 6C). For example, a 3 km-thick ice cap will increase the repose interval from 22.3% for a 0.5 km horizontal radius to 103% for a 4 km horizontal radius (Figure 6C). Finally, as a prolate chamber becomes more prolate, there is not a significant change in the repose interval given a specific ice cap thickness.
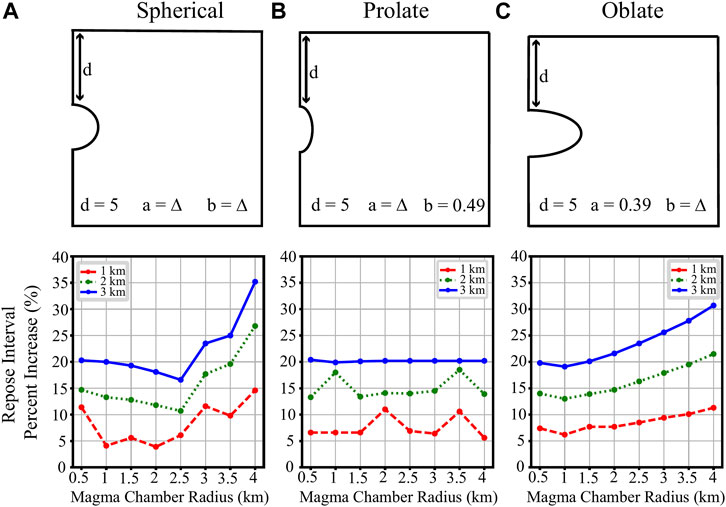
FIGURE 6. Magma chamber radius versus percent change in repose interval of volcanic systems with spherical, prolate, and oblate magma chamber geometries. In each case, a volcanic system with a depth of 5 km to the crest of the magma chamber and a 0.0024 km3/year flux rate is modeled. The magma chamber radii change for each of the spherical, prolate and oblate chamber systems. (A) In the spherical system, the horizontal and vertical radii are identical lengths and range from 0.5 to 4 km. The percent increase of repose interval from the presence of the glacier slightly decreases when the radius is increased from 0.5 to 2 km length and increases when the radius is increased from 2 to 4 km. (B) In the prolate system, the horizontal radius remains ∼0.49 km while the vertical radius ranges between 0.5 and 4 km. (C) The vertical radius for an oblate magma chamber system is held constant at ∼0.39 km while the horizontal radius ranges between 0.5 and 4 km. Repose interval percent change increases as the horizontal radius of an oblate magma chamber is increased in length.
Discussion
The Role of Glaciers in Maintaining Magma System Stability
Previous investigations have focused on the twofold impact of active regional ice cap withdrawal on both the flux of magma into the magma chamber (Sigmundsson et al., 2010) and the threshold conditions for driving tensile failure and dike initiation (Albino et al., 2010). In particular, the removal of ice caps may promote additional melt generation from the mantle source due to decompression, which may increase flux to the crustal magma system (Sigmundsson et al., 2010). Furthermore, the decreased load from the ice cap withdrawal will reduce confining pressure, promoting tensile failure and the likelihood of dike initiation if a magma system is near failure (Albino et al., 2010). In contrast, this investigation focuses purely on the static, long-term effects of the presence or absence of ice caps and does not consider the dynamic processes of their active removal. Motivated by high latitude, glacially covered systems such as Westdahl Volcano in Alaska, we seek to determine whether the presence of a large glacier or ice cap can account for unexpectedly long repose intervals (Lu et al., 2004).
Our numerical experiments indicate that glaciers modulate eruption timescales. In particular, the additional load from an ice cap increases the confining stress around the magma reservoir, which must subsequently be overcome to initiate tensile failure. For a given reservoir size and shape, this additional stress is dependent only on the thickness of the glacier, requiring a fixed volume change within the reservoir, and by extension time, to reach failure. In most cases, the delay due to ice loading is relatively small compared to the system’s baseline repose interval, which is predominantly controlled by the lithostatic stress. However, for shallow reservoirs (<5 km depth to center), an ice cap contributes a greater proportion of the overlying load, and as such has a larger relative impact on the potential repose interval. Regardless, even for deep systems where the relative change in repose interval due to the presence of ice is small, the impact is significant on human timescales and must be considered in future forecasting efforts. For example, a spherical chamber (radius of 0.62 km and flux of 0.0024 km3/yr) at 9 km depth will experience an increase in repose of ∼3 months–∼15 years with a 1 km or 3 km-thick ice cap respectively.
The Role of Flux
In many previous numerical modeling studies that use elastic rheology, the main driver of reservoir tensile failure has been the cumulative critical volume change or a critical change in overpressure of the magma reservoir (Grosfils, 2007; Gerbault et al., 2012; Gregg et al., 2012). This effect is somewhat modulated in viscoelastic rheology where the host rock can relax to dissipate some of the reservoir boundary stresses (Gregg et al., 2012; Gregg et al., 2013; Degruyter and Huber, 2014). In our results, however, the viscoelasticity does not appear to play a major role in system stability. If significant viscoelastic relaxation were present, we would expect to see a greater relative change in repose interval at lower fluxes. Specifically, in the time it takes to overcome the additional load of the ice cap, the system would have relaxed even further, requiring yet more volume change. In contrast, we observe a near constant relative change in repose interval, regardless of flux rate (Figure 3).
Our numerical results agree with previous studies, which indicate that volcanic unrest on year to decadal timescales mostly behaves in an elastic manner (Zhan and Gregg, 2019). With higher flux rates (>0.05 km3/yr), repose timescales will be even shorter, bringing the system even closer to the elastic endmember. Alternatively, at lower flux rates (<0.0001 km3/yr), the likelihood of solidification prior to eruption increases (Annen, 2009). Additionally, on longer timescales there is more time for viscoelastic relaxation to take effect, prolonging stable storage and inhibiting eruption even further.
The existence of an ice cap linearly increases the confining pressure around a magma reservoir, which must then be overcome by changing the volume of magma by a set amount,
For example, the total volume of magma required for the tensile failure of a volcanic system with a spherical magma chamber at 3 km depth will be ∼0.1 km3 of magma, independent of flux rate (Figure 4).
Seasonal Impacts on the Timing of Failure
In understanding the potential effects of loading on the stability of a magma system, previous studies have additionally investigated the effects of a seasonal surface load change. Annual unloading events, such as snow melt represented in numerical models, have suggested that a decrease in a load as thin as 6.5 m may trigger a dike initiation event, if the system is initially near failure conditions (Albino et al., 2010). This effect has been suggested in systems such as Katla Volcano, a subglacial system with annual snow cover, whose last nine major eruptions have been initiated between May and November when the yearly snow had melted (Larsen, 2000).
The results of our study suggest the presence of an annual snow cover increases the repose interval of the volcano, but the strength of this effect is strongly dependent on the thickness of the ice cover and parameters of the magma system. In particular, annual changes in snow and ice thickness at Katla and Westdahl volcanoes are on the order of 6.5 m (Albino et al., 2010; Littell et al., 2018), significantly less than the km-scale ice masses modeled here. Compared to the total overlying load that the magma chamber must overcome in order to reach tensile failure, small seasonal variations are unlikely to play a major role for most systems. However, seasonal ice loss may impact the timing of eruption for systems close to failure.
Using our modeling results above as well as additional simulations with 10 m of ice, we compare the impact of short-term ice thickness variations on the seasonal timing of magma system failure (Figure 7). Four end-member models are evaluated to determine the relative impacts of flux-rate and seasonal ice variability on when magma system failure is more likely to occur. In each case, the reservoir failure threshold is interpolated as a sinusoid that alternates yearly between the ice-free and the 1 km ice cap results. For lower seasonality, we assume a linear relationship between ice thickness and the reservoir failure threshold and proportionally reduce the amplitude of the sinusoid.
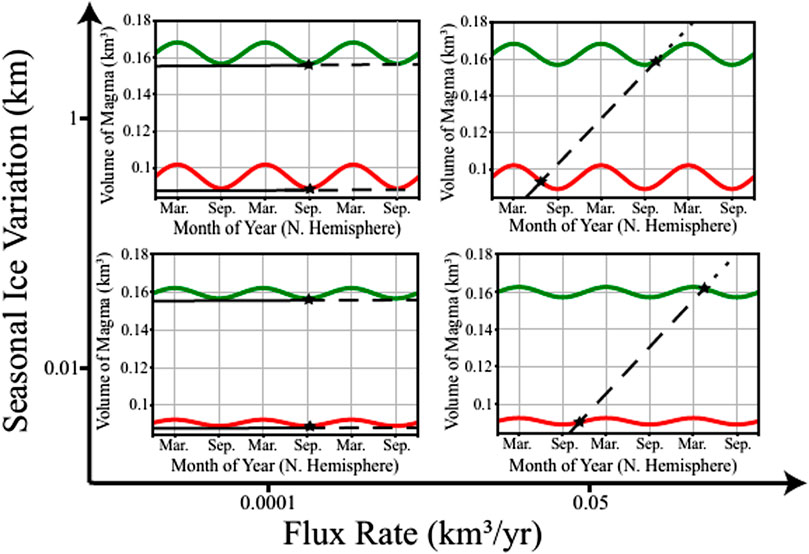
FIGURE 7. The relationship between flux rate and seasonality on the timing of reservoir tensile failure. Each subplot compares the seasonally varying tensile failure threshold of a 3 km deep (depth to center, red line) and 5 km deep (depth to center, green line) spherical reservoir (radius = 0.62 km) against the continuous volume flux into the magma system (black line). The subplots are arranged within a set of larger axes, determining the amount of seasonal ice variation (10 m vs. 1 km) and the flux rate (0.0001 km3/yr vs. 0.05 km3/yr) into the system. In each case, tensile failure occurs at the point where the volume in the magma reservoir first intersects the failure threshold (black stars). The solid, dashed, and dotted black lines indicate an example trajectory of the volume change before the initial rupture of the 3 km deep chamber, before the rupture of the 5 km chamber, and after the rupture of the 5 km chamber, respectively. When flux is low (left subplots), seasonal ice variations outpace the system’s long-term accumulation of magma volume, consistently causing failure when ice thickness reaches its minimum. On the other hand, high-flux systems (right subplots) can produce tensile failure in any season, although the distribution may be skewed depending on the magnitude of ice variation.
Our results indicate that low flux rate systems are much more likely to fail when the ice thickness is at its lowest, August - October in the northern hemisphere (Figure 7). In these systems ice mass variations impact the failure conditions more than increasing volume change in the magma reservoir. In contrast, for magma systems with high flux and low seasonal ice variability, the onset of failure is most sensitive to the accumulation of magma, rather than the timing of the lowest level of ice mass, and so can occur at any time of year. Finally, systems with both high magma flux and high-seasonal ice variability display a slight skew in the specific timing of reservoir failure; eruptions are possible at any time, but are more likely to occur during periods of low ice mass.
We should note, however, that our results are entirely based on the stresses within the host rock and do not take into account the pressure changes within the magma reservoirs during ice loss that may also affect the onset of eruptions, such as decompression melting in the magma reservoir (Mora and Tassara, 2019) or hydrologic effects from the influx of meltwater (Albino et al., 2010). Such effects would likely push eruptions to earlier in the warm season.
Is Westdahl’s Protracted Unrest due to Glacial Loading?
Previous investigations of the unrest of Westdahl have observed a prolonged period of surface inflation, but without an accompanying eruption (Lu and Dzurisin, 2014). To evaluate the effect Westdahl’s 1 km-thick ice cap has on this long-term stability, we apply our aforementioned numerical modeling approach to replicate conditions at this specific volcano. Based on previous geodetic inversions (Lu and Dzurisin, 2014; Gong, 2015), we simulate a 1.39 km-radius spherical reservoir centered 7.2 km below the ground surface with a flux of 0.0024 km3/yr, and then compare the system’s repose interval with and without an ice cover of 1 km (Figure 8).
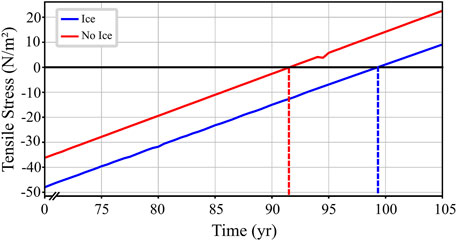
FIGURE 8. Westdahl tensile stress versus time with and without a 1 km glacier. The figure has been zoomed in to highlight the timing of failure. Failure condition is represented by the black horizontal line and repose intervals are represented by the dotted lines. Depth to reservoir center is 7.2 km, flux rate is 0.0024 km3/yr, and the radius of the magma chamber is 1.39 km (based on geodetic inversions conducted by Gong, 2015).
Based on our numerical results, we find that the presence of the glacier would at most delay the onset of eruption by ∼7 years as compared to models of Westdahl with no glacier (99 vs. 92 years from the start of constant inflation). This is significant on monitoring time scales, but relatively small compared to the modeled system’s repose interval of ∼100 years. However, the true system’s absolute repose times will vary as the system geometry and underlying flux rates evolve. Based on our more general results, Westdahl’s long-term stability is most likely controlled by the system’s relatively deep reservoir (Figure 5) and spherical geometry (Figure 6). Regardless, future models attempting to forecast Westdahl’s unrest need to consider all parameters that may significantly affect the onset of eruption on human time scales, including loading from the ice cap.
Westdahl’s 5–10 m seasonal ice variations (Littell et al., 2018) and recent inflation, which has an estimated flux of ∼0.0024 km3/yr (Lu and Dzurisin, 2014), place it as a moderately high flux rate system with low seasonal variability (Figure 7). As such, we would expect the timing of eruption from Westdahl to be only moderately sensitive to seasonal ice loss. However, we do not know how close to failure the system is currently, and recent geodetic data have not yet been investigated to update our estimates of the system’s flux rate. If the flux into Westdahl’s magma reservoir has slowed in recent years while the system remains close to failure, seasonality may ultimately play a larger role than would be expected from this study. Future investigations would benefit from comparing more up-to-date estimates of Westdahl’s unrest and its seasonal ice variations, as demonstrated here.
Conclusion
In this study, we investigate how the presence or absence of ice caps impacts the stability of volcanic systems on human timescales. Our numerical results indicate that large ice caps and glaciers with thicknesses of 1–3 km can appreciably delay the onset of eruptions on the order of years to decades. In particular, there is a linear relationship between the thickness of an ice cap and the additional reservoir volume change necessary to induce tensile failure. As such, the specific change in repose interval will depend on the underlying flux rate into the system for a given ice thickness. Therefore, when flux rates are low, seasonal variations in the overlying ice cap thickness may be adequate to trigger tensile failure once a system approaches the critical stress threshold. When we apply our findings to the recent unrest at Westdahl Volcano, Alaska, we find that for the previously modeled flux rate of 0.0024 km3/year, the ∼1 km ice cap would delay an eruption by ∼7 years. Although the ice cap may greatly increase stability of the volcano, it is unlikely to fully account for the volcano’s long periods of non-eruptive inflation. However, the numerical results presented assume constant flux, which may not capture the full dynamics of systems with long periods of quiescence or sudden spikes in flux rate. Moreover, we focus only on the stress conditions related to ice caps and not additional dynamic effects that may occur during their active emplacement or removal. This study establishes basic relationships between ice caps and volcanic reservoir stability, but future works should incorporate more realistic or dynamic parameters.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
LL led this work as part of her undergraduate research supervised primarily by JA with guidance from PG and YZ. All authors contributed to analyzing the numerical results, drafting figures, and writing the manuscript.
Funding
Numerical modeling to investigate magma system stability is funded U.S. National Science Foundation (NSF GRFP-Albright, EAR 2122745 and EAR 1752477–Gregg), NASA (80-NSSC19K-0357–Gregg), and the University of Illinois Department of Geology Summer Undergraduate Research Opportunity Program (Lucas).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors would like to thank C. Proistosescu, H. Cabaniss, R. Goldman, and M. Head for helpful conversations that enhanced this investigation.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.868569/full#supplementary-material
References
Albino, F., Pinel, V., and Sigmundsson, F. (2010). Influence of Surface Load Variations on Eruption Likelihood: Application to Two Icelandic Subglacial Volcanoes, Grímsvötn and Katla. Gr ´ ımsv otn, 1510–1524. doi:10.1111/j.1365-246X.2010.04603.x
Albright, J. A., Gregg, P. M., Lu, Z., and Freymueller, J. T. (2019). Hindcasting Magma Reservoir Stability Preceding the 2008 Eruption of Okmok, Alaska. Geophys. Res. Lett. 46, 8801–8808. doi:10.1029/2019GL083395
Annen, C. (2009). From Plutons to Magma Chambers: Thermal Constraints on the Accumulation of Eruptible Silicic Magma in the Upper Crust. Earth Planet. Sci. Lett. 284, 409–416. doi:10.1016/j.epsl.2009.05.006
Cabaniss, H. E., Gregg, P. M., and Grosfils, E. B. (2018). The Role of Tectonic Stress in Triggering Large Silicic Caldera Eruptions. Geophys. Res. Lett. 45, 3889–3895. doi:10.1029/2018GL077393
Degruyter, W., and Huber, C. (2014). A Model for Eruption Frequency of Upper Crustal Silicic Magma Chambers. Earth Planet. Sci. Lett. 403, 117–130. doi:10.1016/j.epsl.2014.06.047
Del Negro, C., Currenti, G., and Scandura, D. (2009). Temperature-dependent Viscoelastic Modeling of Ground Deformation: Application to Etna Volcano during the 1993-1997 Inflation Period. Phys. Earth Planet. Interiors 172, 299–309. doi:10.1016/j.pepi.2008.10.019
Gelman, S. E., Gutiérrez, F. J., and Bachmann, O. (2013). On the Longevity of Large Upper Crustal Silicic Magma Reservoirs. Geology 41, 759–762. doi:10.1130/G34241.1
Gerbault, M., Cappa, F., and Hassani, R. (2012). Elasto-plastic and Hydromechanical Models of Failure Around an Infinitely Long Magma Chamber. Geochem. Geophys. Geosyst. 13, a–n. doi:10.1029/2011GC003917
Geyer, A., and Bindeman, I. (2011). Glacial Influence on Caldera-Forming Eruptions. J. Volcanol. Geotherm. Res. 202, 127–142. doi:10.1016/j.jvolgeores.2011.02.001
Gong, W. (2015). Journal of Geophysical Research : Solid Earth. AGU J. Geophys. Res. Solid Earth 119, 3678–3699. doi:10.1002/2013JB010641.Received
Gregg, P. M., De Silva, S. L., Grosfils, E. B., and Parmigiani, J. P. (2012). Catastrophic Caldera-Forming Eruptions: Thermomechanics and Implications for Eruption Triggering and Maximum Caldera Dimensions on Earth. J. Volcanol. Geotherm. Res. 241-242, 1–12. –242. doi:10.1016/j.jvolgeores.2012.06.009
Gregg, P. M., de Silva, S. L., and Grosfils, E. B. (2013). Thermomechanics of Shallow Magma Chamber Pressurization: Implications for the Assessment of Ground Deformation Data at Active Volcanoes. Earth Planet. Sci. Lett. 384, 100–108. doi:10.1016/j.epsl.2013.09.040
Grosfils, E. B. (2007). Magma Reservoir Failure on the Terrestrial Planets: Assessing the Importance of Gravitational Loading in Simple Elastic Models. J. Volcanol. Geotherm. Res. 166, 47–75. doi:10.1016/j.jvolgeores.2007.06.007
Huber, C., Townsend, M., Degruyter, W., and Bachmann, O. (2019). Optimal Depth of Subvolcanic Magma Chamber Growth Controlled by Volatiles and Crust Rheology. Nat. Geosci. 12, 762–768. doi:10.1038/s41561-019-0415-6
Kent, A., Wieser, P. E., and Till, C. (2022). Geophysical and Geochemical Constraints on Magma Storage Depths along the Cascade Arc: Knowns and Unknowns. Goldschmidt.
Larsen, G. (2000). Holocene Eruptions within the Katla Volcanic System, South Iceland: Characteristics and Environmental Impact. Jökull 49, 1–28.
Littell, J., McAfee, S., and Hayward, G. (2018). Alaska Snowpack Response to Climate Change: Statewide Snowfall Equivalent and Snowpack Water Scenarios. Water 10, 668. doi:10.3390/w10050668
Lu, Z., and Dzurisin, D. (2014). InSAR Imaging of Aleutian Volcanoes: Monitoring a Volcanic Arc from Space.
Lu, Z., Rykhus, R., Masterlark, T., and Dean, K. G. (2004). Mapping Recent Lava Flows at Westdahl Volcano, Alaska, Using Radar and Optical Satellite Imagery. Remote Sens. Environ. 91, 345–353. doi:10.1016/j.rse.2004.03.015
Lisowski M., (Editor) (2007). Analytical Volcano Deformation Source Models (Bath, UK: Springer), 469. doi:10.1007/978-3-540-49302-0
Mora, D., and Tassara, A. (2019). Upper Crustal Decompression Due to Deglaciation-Induced Flexural Unbending and its Role on Post-glacial Volcanism at the Southern Andes. Geophys. J. Int. 216, 1549–1559. doi:10.1093/gji/ggy473
Rasmussen, D. J., Plank, T. A., and Roman, D. C. (2019). The Aleutian Arc through and through: Magmatic Water Content Controls Magma Storage Depth. New York, NY: Columbia University.
Satow, C., Gudmundsson, A., Gertisser, R., Ramsey, C. B., Bazargan, M., Pyle, D. M., et al. (2021). Eruptive Activity of the Santorini Volcano Controlled by Sea-Level Rise and Fall. Nat. Geosci. 14, 586–592. doi:10.1038/s41561-021-00783-4
Sigmundsson, F., Pinel, V., Lund, B., Albino, F., Pagli, C., Geirsson, H., et al. (2010). Climate Effects on Volcanism: Influence on Magmatic Systems of Loading and Unloading from Ice Mass Variations, with Examples from Iceland. Phil. Trans. R. Soc. A 368, 2519–2534. doi:10.1098/rsta.2010.0042
Wilson, C. J. N., Blake, S., Charlier, B. L. A., and Sutton, A. N. (2006). The 26·5 Ka Oruanui Eruption, Taupo Volcano, New Zealand: Development, Characteristics and Evacuation of a Large Rhyolitic Magma Body. J. Pet. 47, 35–69. doi:10.1093/petrology/egi066
Keywords: volcano, subglacial, flux rate, westdahl, seasonality, viscoelastic, finite element method
Citation: Lucas LC, Albright JA, Gregg PM and Zhan Y (2022) The Impact of Ice Caps on the Mechanical Stability of Magmatic Systems: Implications for Forecasting on Human Timescales. Front. Earth Sci. 10:868569. doi: 10.3389/feart.2022.868569
Received: 02 February 2022; Accepted: 13 April 2022;
Published: 29 April 2022.
Edited by:
Simona Petrosino, Istituto Nazionale di Geofisica e Vulcanologia, ItalyReviewed by:
Luis E. Lara, Servicio Nacional de Geología y Minería de Chile (SERNAGEOMIN), ChileLucia Capra, National Autonomous University of Mexico, Mexico
Copyright © 2022 Lucas, Albright, Gregg and Zhan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Patricia M. Gregg, cGdyZWdnQGlsbGlub2lzLmVkdQ==
 Lilian C. Lucas
Lilian C. Lucas John A. Albright
John A. Albright Patricia M. Gregg
Patricia M. Gregg Yan Zhan
Yan Zhan