Study on the Size and Occurrence Effects of Equivalent Elasticity Modulus of Orthogonal Random Jointed Rock Masses

Under the engineering background of a + 144-m mining platform on an open pit slope of Xinqiao Mining Corporation, the eigenvalue distribution function of joints was acquired based on the massive statistics of field joints. Next, an orthogonal random joint model was constructed using the Monte Carlo method based on the UDEC software platform. Subsequently, the representative elementary volume (REV) size and occurrence effects of the equivalent elasticity modulus of the orthogonal random jointed rock mass were explored through numerical experiments with lots of discrete elements. The results showed that the equivalent elasticity modulus of the orthogonal random jointed rock mass was of evident size effect, and the relationship between the mean equivalent elasticity modulus E_eq and the REV size of the rock mass followed the negative power function distribution. Before the model size reached the REV size, its E_eq was greatly discrete. Under different joint angles, both the standard deviation σ_f and coefficient of variation δ of the equivalent elasticity modulus of this model presented discrete distribution. As the model size reached the REV size, the mean equivalent elasticity modulus E_eq showed “two-high and one-low” morphological distribution. E_eq was small when the main joint angle was α$\in$[30°, 40°], but it was large when α = 0° or 90°. δ was taken as 10%, so the REV size of the corresponding E_eq was 10 m × 20 m. When the model size reaches the REV size, the occurrence effect of its equivalent elasticity modulus was no longer significant.

Introduction

Studies and engineering practices have shown that rock mass is a kind of complex geologic body (Sun, 1988), including slope engineering, tunneling, and deep underground chamber engineering, in which the reliability and accuracy of the mechanical parameter values of rock masses are specifically crucial for the engineering design, construction, and operation. The mechanical properties of rock masses are intricate due to the massive structural planes in them (Sun and Li, 1965; Gu, 1979). Usually constructed in jointed rock masses, rock mass engineering works are affected by the structural planes inside the rock masses of different sizes, so the mechanical parameters of engineering rock masses will unavoidably be characterized by heterogeneity or spatial variability. Representative elementary volume (REV) is the core content in the studies regarding the size effect of mechanical properties of rock masses (Bear, 1972; Bear, 1979), that is, the values of mechanical parameters should be determined in such studies. In practical geotechnical design, the mechanical parameters of REV, but not the mechanical parameters of intact rock specimens, should be used. Hence, the key to studying the real mechanical parameters of rock masses and the reliability design of rock mass engineering lies in figuring out the size effect of mechanical parameters of rock masses and determining the REV of rock masses. At present, the REV of rock masses is determined through the experimental method, analytical method, and numerical experimental method.

As for the experimental method, Wang et al. (2002) numerically estimated the REV of the coefficient of transmissivity based on the drilling data. Aubertin et al. (2000) studied the size effect of rock strength based on the MSDPu strength criterion and put forward the change relation of rock strength with the size. According to the laboratory test results, Zhang and Qiao. (2006a), Wang and Zuo. (1998) and Wang and Li. (2008) gave the expressions to the size effects of the corresponding mechanical parameters of rock masses. Fan et al. (2018) experimentally studied the crack propagation and evolution in shales with a material testing machine considering the bedding angle, loading rate, and specimen size. Du et al. (2021) developed a combined testing system for the size effect of the shear strength of structural planes in rock masses, thus providing a basic experimental support platform for studying key scientific problems such as the size effect of the shear strength of structural planes.

When it comes to the analytical method, Zhou and Xiong. (1996a) explored the relationships between the elastic parameters of random jointed rock masses with their volumetric change and permeability tensor, according to the principle of energy superposition, and then determined the REV of mechanical parameters of jointed rock masses. Zhang and Xu. (2008) simulated the 3D fracture network of jointed rock masses using a planar quadrangle and used this fracture network to study the indexes determining the REV size of rock masses. Chen S. J. et al. (2019) applied random numbers to the projective covering method, in an effort to improve triangulation when calculating the fractal dimensions of structural planes with the projective covering method.

The analytical methods adopted in the numerical experiments mainly include the finite element method, finite difference method, natural element method, and discrete element method. Kulatilake. (1985) and Pouya and Ghoreychi. (2001) simulated the structural planes in rock masses using Goodman joint elements in the finite element model and studied the REV of mechanical parameters of rock masses. Zhang et al. (2010), Zhou et al. (2004), Yan et al. (2009), and Zhu et al. (2009) explored the size effect of mechanical parameters of rock masses via FLAC3D finite difference software. Bhasin and Hoeg. (1998) and Min and Jing. (2003) studied the size effect of jointed rock masses through the UDEC software model. Lu et al. (2020) and Li et al. (2019) generated the plane network diagram of jointed rock masses based on fractal theory and the Monte Carlo method. Taking the center of the rock mass network diagram as the base point, the jointed rock mass simulation specimen was selected, and the numerical experiment of the compressive strength of jointed rock masses was performed via discrete element software UDEC. Ning et al. (2008) and Ni et al. (2015) introduced the Voronoi method into 3DEC discrete element software to probe the size effect of the deformation parameter of columnar basalt. Esmaileli et al. (2010) and Li et al. (2021) studied the REV size of mechanical parameters of jointed rock masses via PFC3D software. Wang et al. (2021) determined the REV of rock masses using the heterogeneity index (HI). Zhu et al. (2019) used FLUENT software to perform a 2D numerical analysis of seepage characteristics at nine differently sized crack intersections. Wang et al. (2018) established a rough discrete fracture network (RDFN) model and studied the mechanical properties of this RDFN model under direct shear conditions based on grain flow PFC2D. Chen Q. F. et al. (2019) built a multiscale three-dimensional fracture network model of rock mass with 35 combinations of ductility and spacing of different structural planes based on general block software. Using the proposed block degree correction theory, the geometric characteristic size rev of fractured rock mass is determined. Through the docking of correlation parameters of the general block-3dec model, a multiscale discrete fracture network model of the rock mass is constructed, the calculation results of geometric rev and mechanical Rev are compared, and the correlation between the geometric size effect and mechanical size effect of the rock mass is discussed.

To summarize, domestic (Chinese) and foreign scholars have investigated the size effect of mechanical parameters of rocks or rock masses through theoretical analysis, experimental study, and numerical simulation. Given the complexity of jointed rock masses, the randomness of joint distribution, experimental limitations, and the size effect of mechanical parameters of jointed rock masses remain to be further explored. In particular, the discreteness of small-size experimental results is considerably great, the number of numerical experimental times is partially small, and the statistical results are not reliable enough, all of which, to some extent, results in inconsistent research results and conclusions. The precondition for numerically studying the size effect of mechanical parameters of rock masses is to reflect the joint distribution laws in rock masses as truly as possible. Studies have shown that the geometric parameters such as joint length, joint distribution, and joint spacing are self-similarities, which can be calculated through a small-scale fracture network so as to derive the development characteristics of a large-scale fracture network. Such self-similarity is actually a fractal character. Given this, based on the statistical data of measured joints of rock masses on an engineering slope, a random fracture network model was established in this study according to the Monte Carlo principle. Next, the size effect of the equivalent elasticity modulus of orthogonal random jointed rock masses was analyzed via discrete element software UDEC. Subsequently, enough numerical experiments were conducted according to different experimental sizes so that the statistical results (such as the mean value and standard deviation) of sample parameters could be accurate and reliable, expecting to provide a theoretical support for the construction and safety operation of slope rock mass engineering.

Investigation and Statistics of Joints in Jointed Rock Masses

Engineering Background

Through decades of open-pit mining, a large-scale multi-metal sulfide ore deposit of the Xinqiao Mining Corporation is now about 148 m in the minimum elevation of the open pit and about + 320 m in the elevation of the slope crest, along with a bench slope angle of 50°, bench width of 12 m, and bench height of 25 m. With a + 144-m platform taken, for example, a group of orthogonal joints were developed on the slope through the site investigation, and it was obtained that the joint angles followed a normal distribution (Figure 1). The geometric parameters of the joints are listed in Table 1 he rock mass structure of the site slope is shown in Figures 1. The mechanical parameters of rocks and joint planes measured after field drilling are as seen in Table 2.

FIGURE 1

FIGURE 1. Open-pit slope of Xinqiao Mining Corporation.

TABLE 1

TABLE 1. Geometric parameters of joint fractures.

TABLE 2

TABLE 2. Mechanical parameters.

Generation of Orthogonal Random Joints

The joint fracture generating program was compiled through the FISH language in UDEC software. The uniformly distributed random numbers of central points of joints within the interval of [0,1] were generated using the Monte Carlo method, and then, random joint fractures were formed. The generated fracture network model of the slope on the + 144-m mining platform is shown in Figure 2.

FIGURE 2

FIGURE 2. Random fracture network model of the slope on the + 144-m platform.

Numerical Experimental Scheme of the Size Effect of Orthogonal Random Jointed Rock Masses

Reliability Analysis of Rock Parameters Solved via UDEC Software

The shear strength parameters—cohesion c and internal frictional angle φ—were acquired through the uniaxial and triaxial compression tests of rocks based on the Mohr–Coulomb strength criterion. In comparison, the reliability of the parameters obtained through the UDEC-aided uniaxial and triaxial numerical compression tests of rocks was verified. With an intact rock taken as the study object, the compressive strength values under different confining pressures were solved through triaxial numerical compression tests; the c and φ values were acquired using the Mohr–Coulomb strength theory and compared with the rock strength parameters obtained through laboratory tests, and the reliability of the solved equivalent strength parameters was verified.

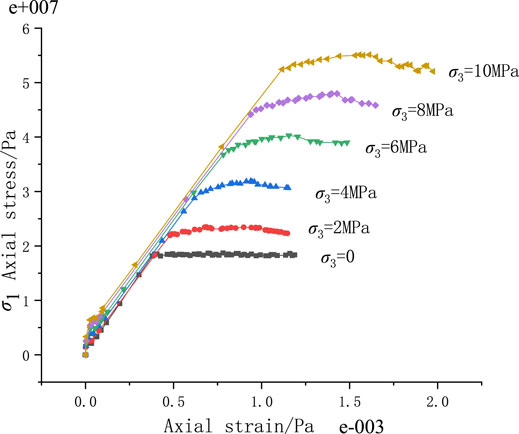
The dimensions of the numerical simulation test model were 1 m (width) * 2 m (height). The confining pressure was taken as 0–10 MPa at six levels with the interval of 2 MPa. The Mohr–Coulomb model was chosen as the constitutive model, and the rock parameters are listed in Table 2. The rock stress–strain curves under different confining pressures acquired through the numerical experiments are shown in Figure 3.

FIGURE 3

FIGURE 3. Axial stress–strain curves of the intact rock under different confining pressures.

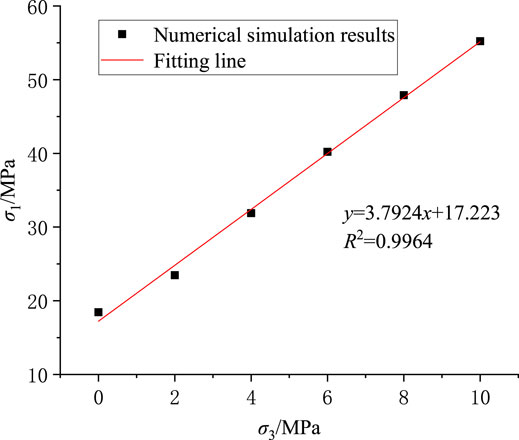
The numerical triaxial compression test results under different confining pressures were drawn within the σ₁-σ₃ plane. According to the Mohr–Coulomb strength failure criterion, σ₁-σ₃ followed a linear relation, so the σ₁-σ₃ data points were fitted using straight lines, as shown in Figure 4.

FIGURE 4

FIGURE 4. Relational graph of σ₁-σ₃.

The straight slope a and intercept b showed the following relations with the shear strength parameters c and φ:

$a=\frac{2c\cos \phi }{1-\sin \phi },(1)$

$b=\frac{1+\sin \phi }{1-\sin \phi }.(2)$

As solved through Eqs. 1,2, the internal frictional angle and cohesion of the intact rock were φ = 35.64 and c = 4.42, respectively, which were relatively approximate to the rock strength parameters acquired through the laboratory tests. Hence, it is reliable to perform the analog computation of equivalent rock strength parameters via UDEC software.

Numerical Experimental Scheme for the Representative Elementary Volume Size of Mechanical Parameters of Random Jointed Rock Masses

In order to determine the mechanical parameters representing the real mechanical properties of jointed rock masses, the rock structure model should accord with the physical situation as far as possible. When the structural plane network is simulated using the Monte Carlo method and since the random number generated each time is different under the same structural plane probability distribution model, the geometrical characteristics of structural planes generated each time, such as spatial position, trace length, and orientation, will be slightly different and so will the rock structure model, which is the error brought by the feature of this method. For the same structural plane probability distribution model, the mechanical parameters of different rock mass structure models generated by the Monte Carlo method may differ in the REV size. Min and Jing. (2003) generated 10 300 m × 300 m square rock mass structure models using the discrete fracture network (DFN) program and studied the REV size of equivalent deformation parameters by intercepting square rock specimens with different side lengths from the center of each model. Xiang (2005) compiled a random sampling program following probability distribution for the sake of Monte Carlo simulation, generated 8 10 m × 10 m fracture networks, and explored the REV size of rock strength parameters by intercepting squares with different side lengths from the center of each network. As deemed by Kulatilake (1985), such random errors can be eliminated only by experimenting on over ten rock specimens, so the rock mass of each size should be studied using multiple models when determining its mechanical parameters.

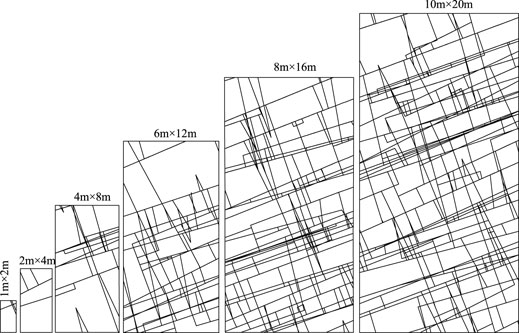
Therefore, a Monte Carlo method-based orthogonal random joint generation program was compiled using the FISH language of UDEC software to determine the REV size for the mechanical parameters of orthogonal random jointed rock masses. The model dimensions (width* height) were taken as 1 m × 2 m、2 m × 4 m, 4 m × 8 m, 6 m × 12 m, 8 m × 16 m, and 10 m × 20 m. To eliminate the random errors of rock joints simulated through the Monte Carlo method, a total of 11 rock joint models were generated for each model size. Given the anisotropic characteristics of mechanical parameters of rock masses, the main joint angle changed within [0°, 90°] at an interval of 10°. Taking the main joint angle of 20°, for example, the generated orthogonal random joint models with different sizes are presented in Figure 5.

FIGURE 5

FIGURE 5. Orthogonal random joint models with different sizes.

Representative Elementary Volume Size Effect Analysis of the Equivalent Elasticity Modulus E_eq of Orthogonal Random Jointed Rock Masses

Multiple rock joint models with the same size could reflect the random fluctuations of mechanical properties before the rock masses reached the REV size of their mechanical parameters, indicating that the size effect of their mechanical properties was not one sidedly understood as follows: the mechanical properties of rock masses declined with the increase in the rock size. Instead, the mechanical properties fluctuated now and then. Only when the rock size reached the REV size would the fluctuation range of their mechanical parameters be greatly reduced and tend to be constant. Therefore, the rock size-dependent change line of the coefficient of variation (CV) of each parameter could be obtained by calculating the CV of each equivalent mechanical parameter of multiple rock structure models with the same size. In addition, it was feasible to determine the REV size of each mechanical parameter according to the acceptance level of CV.

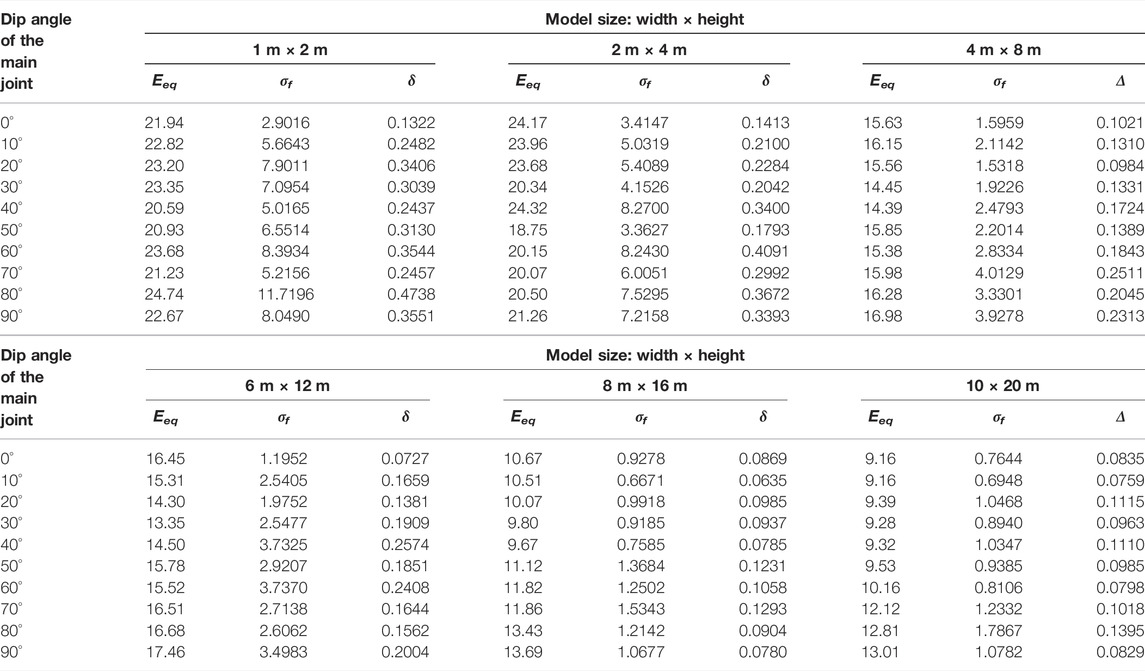
Without loss of generality, the elasticity moduli solved through the numerical experiments on different models under the same confining pressure were taken to analyze the rock size effect of orthogonal random joint models. E_eq, σ_f, and δ of orthogonal random joint masses acquired through the numerical experiments under σ₃ = 4 MPa are listed in Table 3. On this basis, the relationship between the equivalent elasticity modulus of orthogonal random jointed rock masses and the model size could be analyzed.

TABLE 3

TABLE 3. Mean elasticity moduli under different model sizes and joint angles (σ₃ = 4 MPa).

Relationship Between the Mean Equivalent Elasticity Modulus E_eq of Orthogonal Random Jointed Rock Masses and the Model Size

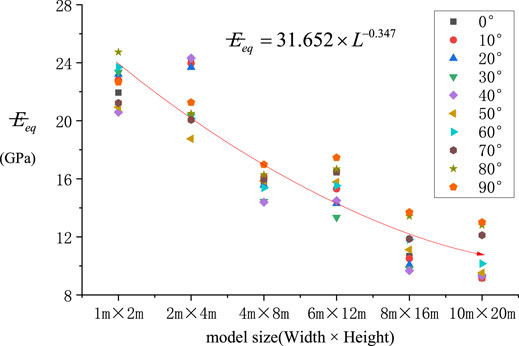
The relational graph between E_eq of orthogonal random joint models and the model size was drawn, as shown in Figure 6.

1) Regardless of the occurrence of the main model joint, E_eq of the random joint model was gradually reduced with the increase in the model size.

2) Under a small model size, the reduced amplitude of E_eq was large. As the model size was enlarged, the reduced amplitude of E_eq was gradually reduced. When the model size exceeded 8 m × 16 m, E_eq approached a stable value.

FIGURE 6

FIGURE 6. Relationship between the equivalent elasticity modulus and model size.

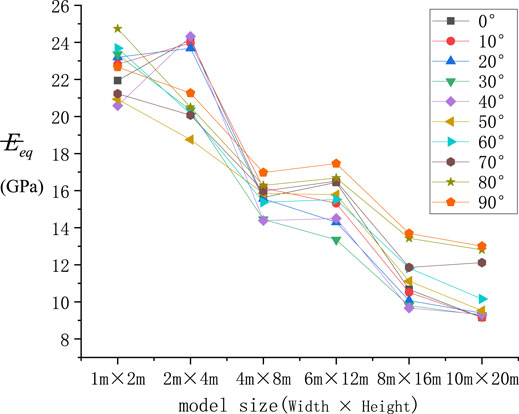
Relationship Between the Mean Equivalent Elasticity Modulus E_eq of Orthogonal Random Jointed Rock Masses and Main Joint Angle α

The relational graph between E_eq of orthogonal random joint models and the main joint angle was drawn, as shown in Figure 7.

1) Under different main joint angles α and a small model size, E_eq was discrete, with inapparent relational characteristic with the main joint angle α.

2) After the model size was enlarged to 4 m × 8 m, E_eq presented a “two-high and one-low” morphological distribution with the change in the main joint angle α. E_eq was small under α∈[30°, 40°] and large when α = 0° or 90°. Moreover, it reached the maximum value under α= 90°.

FIGURE 7

FIGURE 7. Relationship between the equivalent elasticity modulus and main joint angle α.

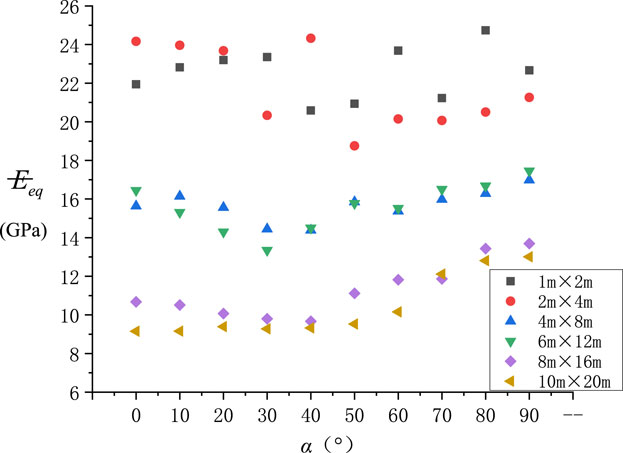
Relationship Between the Standard Deviation σ_f of the Equivalent Elasticity Modulus and Main Joint Angle α

For two or more groups of data with the same mean value, the dispersion degree of each group of data is different. For the mean value of the equivalent elastic modulus E_eq of the aforementioned jointed rock mass, the standard deviation can be used to reflect the difference of each group of data under the conditions of different sizes and joint dip angles.

The relational graph between σ_f of orthogonal random joint models and main joint angle α was drawn, as shown in Figure 8.

1) Under different main joint angles α and a small model size, σ_f of the equivalent elasticity modulus was discretely distributed without any obvious law. It shows that when the model size is small, the equivalent elastic modulus E_eq of each group of the jointed rock mass is greatly dispersed.

2) As the model size was enlarged, σ_f was gradually reduced. It shows that when the model size increases, the elastic modulus of any group of the randomly jointed rock mass can reflect the real value of the jointed rock mass under the strip of this size.

3) When the model size was enlarged to 8 m × 16 m, the standard deviation of the equivalent elastic modulus of different main joint dip models is very small, and the standard deviation is also very small. It shows that when the model size increases to a certain value, the difference in the elastic modulus of the jointed rock mass in the same group is very small. This size can be used as a reference for the selection of the equivalent elastic modulus REV scale of the jointed rock mass model.

FIGURE 8

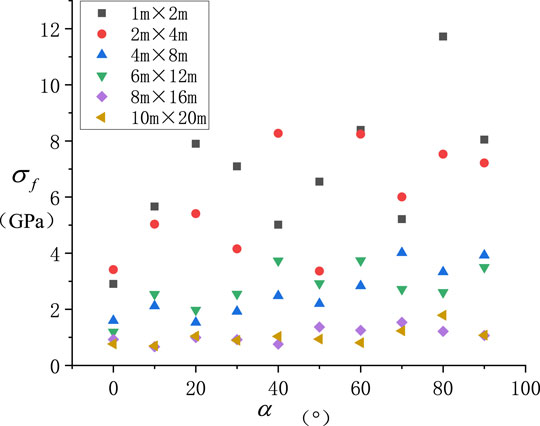
FIGURE 8. Relationship between the standard deviation σ_f of the equivalent elasticity modulus and main joint angle α; relationship between sample δ and main joint angle $\alpha$.

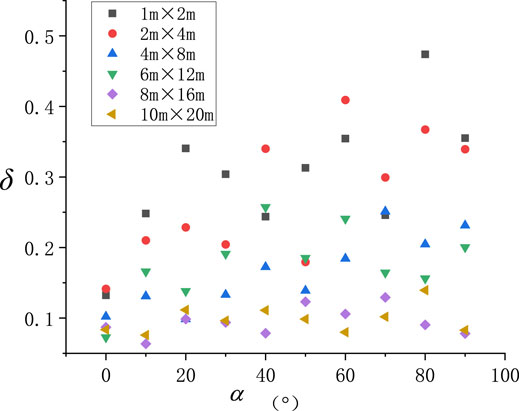
Relationship Between the Sample Coefficient of Variation δ and Main Joint Angle α

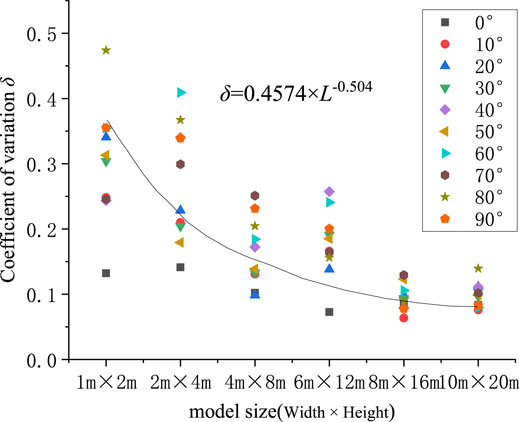
The sample coefficient of variation (δ) is the ratio of the standard deviation σ_f to E_eq, where δ is not restricted by the sample mean or standard deviation. The relational graph between δ of the equivalent elasticity modulus of orthogonal random joint models and the main joint angle α was drawn as shown in Figure 9.

1) The sample δ was greater than 10% under a small model size. A great difference was manifested between the models with different main joint angles in δ.

2) The sample δ was significantly reduced with the increase in the model size. After the model size was enlarged to 8 m × 16 m, the sample δ was about 10%. Under this circumstance, the occurrence effect of the equivalent elasticity modulus of the model was no longer significant. It can be inferred from this that there is a certain size value. When the size of the jointed rock mass model exceeds this value, the value of the variation coefficient of the sample equivalent elastic modulus will be less than a given value (e.g., 10%), which can be used as the scale of the equivalent elastic modulus REV of the jointed rock mass.

FIGURE 9

FIGURE 9. Relationship Between Sample δ and Main Joint Angle $\alpha$.

REV Scale of the Equivalent Elastic Modulus E_eq of Orthogonal Random Jointed Rock Mass Under Given Variation Conditions

The δ values of the equivalent elasticity modulus obtained through experimenting on the models with different sizes and main joint attitudes were drawn into a scatter diagram (Figure 10). Next, they were fitted using a power function to obtain the following relationship between δ of the equivalent elasticity modulus and model size:

$\delta \left(E_{eq}\right)=0.4574\cdot L^{-0.504}.(3)$

FIGURE 10

FIGURE 10. Relationship between the sample δ and model size.

The model size required under the given δ could be estimated according to Eq. 3, thus providing a reference for selecting the minimum model size needed in the numerical model tests.

$E_{eq}=31.652\cdot L^{-0.347}.(4)$

The equivalent elasticity moduli obtained by experimenting on the models with different sizes and main joint attitudes were drawn into a scatter diagram (Figure 11) and then fitted with a power function to acquire the relationship between the equivalent elasticity modulus and model size as follows:

FIGURE 11

FIGURE 11. Relationship between the equivalent elasticity modulus and model size.

Based on Eq. 3, the model size required under the given δ was acquired. The equivalent elasticity modulus under the corresponding model size could be solved through Eq. 4 so as to provide a reference for selecting the elasticity modulus value in the numerical model calculation.

Conclusion

Under the engineering background of the + 144-m mining platform on an open pit slope of the Xinqiao Mining Corporation, an orthogonal random joint model was constructed using the Monte Carlo method based on the UDEC software platform, followed by a lot of numerical discrete element experiments. In full consideration of the random distribution characteristic of orthogonal joints in the rock mass, the REV size effect characteristics of the equivalent elasticity modulus of orthogonal random jointed rock masses under the given confining pressure were acquired as follows:

1) As the model size is enlarged, E_eq of the random joint model is gradually reduced.

2) Under a small model size, E_eq is discrete, with inapparent relational characteristics with the main joint angle α. After the model size is enlarged to 4 m × 8 m, E_eq presents a “two-high and one-low” morphological distribution. It is small under α∈[30°,40°] and large when α = 0° or 90°.

3) When the model size is small, both σ_f and δ are discretely distributed. As the model size is enlarged to 8 m × 16 m, the models with different main joint angles differ little in σ_f and δ.

4) If δ is taken as 10%, the REV size of the corresponding E_eq is 10 m × 20 m. When the model reaches the REV size, the occurrence effect of its equivalent elasticity modulus is no longer significant.

5) The model size needed under the given δ can be solved according to the fitting formulas of δ, model size L, and E_eq, thus providing a reference for selecting a reasonable equivalent elasticity modulus value in the simulation analysis.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

CL designed the tests, provided funds, and experimental apparatus. TZ performed the tests and processed the data. NX performed the tests, wrote the manuscript, and also was responsible for contacting the journal editor. CS performed the laboratory tests.

Funding

This study was funded by the Anhui Natural Science Research Program of Universities and Colleges (No: KJ 2018A0073) and the Science and Technology Program of Key Major Safety Production Accident Prevention and Control Technology (No: anhui-0004-2017AQ).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors wish to acknowledge the support. The reviewers are gratefully acknowledged for their valuable comments on the manuscript.

References

Aubertin, M., Li, L., and Simon, R. (2000). A Multiaxial Stress Criterion for Short- and Long-Term Strength of Isotropic Rock media. Int. J. Rock Mech. Mining Sci. 37, 1169–1193. doi:10.1016/s1365-1609(00)00047-2

CrossRef Full Text | Google Scholar

Bear, J. (1972). Dynamics of Fluids in Porous media. New York: American Elsevier.

Google Scholar

Bear, J. (1979). Hydraulics of Groundwater. New York: McGraw-Hill.

Google Scholar

Bhasin, R., and Høeg, K. (1998). Numerical Modelling of Block Size Effects and Influence of Joint Properties in Multiply Jointed Rock. Tunnelling Underground Space Tech. 13 (2), 181–188. doi:10.1016/s0886-7798(98)00046-7

CrossRef Full Text | Google Scholar

Chen, Q. F., Zheng, W. S., and Niu, W. J. (2019b). Correlation of the Geometrical and Mechanical Size Effects of Fractured Rock Masses. Chin.J.Rock Mech.Eng. 38 (Suppl. 1), 2857–2870. doi:10.13722/j.cnki.jrme.2017.0988

CrossRef Full Text | Google Scholar

Chen, S. J., Yang, Z. D., and Wang, C. (2019a). Analysis of Size Effect of Structural Surface Roughness Based on Improved Projective Covering Method. Chin.J. Eng.Geol. 27 (6), 1244–1252. doi:10.13544./j.cnki.jeg.2018-451

CrossRef Full Text | Google Scholar

Chun, Z., Yuan, C., Xuebin, C., Fuqiang, R., and Xiaohu, Z. (2019). Study on the Size Effect of Fracture Intersections Based on the Fractal Theory. Geotech. Geol. Eng. 37, 2999–3006. doi:10.1007/s10706-019-00818-z

CrossRef Full Text | Google Scholar

Du, S. G., Lyu, Y. J., and Luo, Z. Y. (2021). Combined Test System for Size Effect of Rock Joint Shear Strength and its Primary Application Research. Chin.J.Rock Mech.Eng. 40 (7), 1337–1349. doi:10.13722/j.cnki.jrme.2020.1215

CrossRef Full Text | Google Scholar

Esmaieli, K., Hadjigeorgiou, J., and Grenon, M. (2010). Estimating Geometrical and Mechanical REV Based on Synthetic Rock Mass Models at Brunswick Mine. Int. J. Rock Mech. Mining Sci. 47 (6), 915–926. doi:10.1016/j.ijrmms.2010.05.010

CrossRef Full Text | Google Scholar

Fan, X. G., Guo, D. Y., and Zhang, Q. G. (2018). Experimental Study on the Crack Propagation Mechanism of Shale Considering the Effect of the Bedding Loading Rate and Sample Size. Chin.Sci. Tech. Eng. 18 (9), 63–71.

Google Scholar

Gu, D. Z. (1979). Fundamentals of Rock Engineering Geomechanics. Beijing: Science Press.

Google Scholar

Kulatilake, P. H. S. W. (1985). Estimating Elastic Constants and Strength of Discontinuous Rock. J. Geotechnical Eng. 111 (7), 847–864. doi:10.1061/(asce)0733-9410(1985)111:7(847)

CrossRef Full Text | Google Scholar

Li, D. P., Li, J., and Sun, R. R. (2019). Numerical Simulation on Compressive Strength Size Effect of Rock Mass Based on UDEC. Chin. J. Underground Space Eng. 15 (4), 1098–1105.

Google Scholar

Li, K. L., Song, X. K., and Zhang, C. S. (2021). Particle Flow Code Analysis Geometrical and Mechanical Representative Elementary Volumes Size of Fractured Rock Mass. J.Shandong Univ. Sci. Tech. (Natural Science) 40 (5), 59–68. doi:10.16452/j.cnki.sdkjzk.2021.05.007

CrossRef Full Text | Google Scholar

Lu, H. Y., Li, D. P., and Zhong, J. C. (2020). Numerical Study of Joint Rock Mass Compressive Strength Based on UDEC. J. Hebei Univ. Eng. ( Nat. Sci. Edition) 37 (3), 17–25. doi:10.3969/j.issn.1673-9469.2020.03.003

CrossRef Full Text | Google Scholar

Min, K.-B., and Jing, L. (2003). Numerical Determination of the Equivalent Elastic Compliance Tensor for Fractured Rock Masses Using the Distinct Element Method. Int. J. Rock Mech. Mining Sci. 40 (6), 795–816. doi:10.1016/S1365-1609(03)00038-8

CrossRef Full Text | Google Scholar

Ni, H. J., Xu, W. Y., Shi, A. C., Wang, W., Bo, L. U., Lifang, Z., et al. (2015). Scale Effect on Equivalent Continuum Elastic Modulus of Columnar Jointed Rock Masses by Distinct Element Method. Chin.Engineering Mech. 32 (3), 90–96. doi:10.6052/j.issn.1000-4750.2013.09.0849

CrossRef Full Text | Google Scholar

Ning, Y., Xu, W. Y., Zheng, W. T., Meng, G., Shi, A., Wu, G., et al. (2008). Study of Random Simulation of Columnar Jointed Rock Mass and its Representative Elementary Volume Scale. Chin.J.Rock Mech. Eng. 27 (6), 1202–1208.

Google Scholar

Pouya, A., and Ghoreychi, M. (2001). Determination of Rock Mass Strength Properties by Homogenization. Int. J. Numer. Anal. Meth. Geomech. 25 (13), 1285–1303. doi:10.1002/nag.176

CrossRef Full Text | Google Scholar

Sun, G. Z. (1988). Rock Mass Structure Mechanics. Beijing: Science Press.

Google Scholar

Sun, Y. K., and Li, J. G. (1965). Engineering Geological Study on Stability of Rock Slope. Chin.Geol.Sci. 04, 330–352.

Google Scholar

Wang, J. L., and Zuo, H. W. (1998). Study on Size Effect of Young’s Modulus for Rock. Chin.Rock Soil Mech. 19, 60–64.

Google Scholar

Wang, M., Kulatilake, P. H. S. W., Um, J., and Narvaiz, J. (2002). Estimation of REV Size and Three-Dimensional Hydraulic Conductivity Tensor for a Fractured Rock Mass through a Single Well Packer Test and Discrete Fracture Fluid Flow Modeling. Int. J. Rock Mech. Mining Sci. 39, 887–904. doi:10.1016/s1365-1609(02)00067-9

CrossRef Full Text | Google Scholar

Wang, P. T., Ren, F. H., and Cai, M. F. (2018). Mechanical Analysis and Size Effect of Rough Discrete Fractures Network Model under Direct Shear Tests Based on Particle Flow Code. Chin.J.China Coal Soc. 43 (4), 976–983. doi:10.13225/j.cnki.jccs.2017.1061

CrossRef Full Text | Google Scholar

Wang, Q. Y., and Li, Y. (2008). Experimental Study of Scale Effects in Strength and Deformation of Fractal-Joint Rock Masses. Chin.Rock Soil Mech. 29, 1325–1328. doi:10.1016/0148-9062(81)90262-X

CrossRef Full Text | Google Scholar

Wang, X. M., Du, Y. F., and Liang, X. L. (2021). Investigation of the Representative Elementary Volume of Fractured Rock Mass Using the Homogeneity index. Chin.Hydrogeology Eng. Geology. 48 (2), 55–60. doi:10.16030/j.cnki.issn.1000-3665.202007029

CrossRef Full Text | Google Scholar

Xiang, W. F. (2005). A Study on the Representative Elementary Volume of Fractured Rock Masses and the Size Effects of Mechanical Properties. China Wuhan: Wuhan University.

Google Scholar

Yan, C. G., Wu, F., Qi, S. W., Liu, T., and Masakasu, M. (2009). Deformation and Strength Parameters and Size Effect of Random Jointed Rock Mass by Numerical Simulation. Chin.J.Geotech.Eng. 31 (6), 879–885.

Google Scholar

Zhang, G. K., and Xu, W. Y. (2008). Analysis of Joint Network Simulation Method and REV Scale. Chin.Rock Soil Mech. 29 (6), 1675–1680. doi:10.16285/j.rsm.2008.06.052

CrossRef Full Text | Google Scholar

Zhang, Z. G., and Qiao, C. S. (2006b). Improved Empirical Determination of Strength Parameter for Jointed Rock Masses and its Application in Engineering. J. Beijing Jiaotong Univ. 30, 46–49.

Google Scholar

Zhang, Z. G., and Qiao, C. S. (2006a). Improved Empirical Method for Determination of Deformation Modulus of Jointed Rock Masses and its Application Engineering. Chia.J.Eng. Geol. 14, 233–238.

Google Scholar

Zhang, Z. R., Sheng, Q., Yang, Y. S., Zhu, Z. Q., Zhang, Y. M., and Wang, Z. W. (2010). Study of Size Effect of Rock Mass Deformation Modulus Based on Iin-Ssitu Test. Chin.Rock Soil Mech. 31 (9), 2875–2881. doi:10.16285/j.rsm.2010.09.032

CrossRef Full Text | Google Scholar

Zhou, C. B., and Xiong, W. L. (1996a). On Permeability Characteristics of Rock Mass. Chin.J. Eng. Geol. 4 (2), 69–74.

Google Scholar

Zhou, C. B., and Xiong, W. L. (1996b). Permeability Tensor for Jointed Rock Masses in Coupled Seepage and Stress Field. Chin.J.Rock Mech.Eng. 15 (4), 338–344.

Google Scholar

Zhou, H. M., Sheng, Q., and Chen, S. W. (2004). Numerical Simulation on Size-Effect in Deformation Test of Layer Composite Rockmass. Chin.J. Rock Mech. Eng. 23 (2), 289–292.

Google Scholar

Zhu, D. J., Yang, L. D., and Cai, Y. C. (2009). Research on Anisotropic Characteristics and Size Effect of Columnar Jointed Rock Mass. Chin.J.Rock Mech. Eng. 28 (7), 1405–1414.

Google Scholar