Seismogenic Patches in a Tectonic Fault Interface

Introduction

Earthquake source localization is one of the fundamental problems of seismology and continues to attract considerable attention. In 1910, H.F. Reid provided arguments that earthquakes are linked to faults in the Earth’s crust (Reid, 1910). The localization of earthquake hypocenters in fault zones and tectonic junctions manifests most evidently if the accuracy of their location is high enough (Waldhauser and Schaff, 2008). Earthquake epicenters trace tectonic faults, while the dynamics of seismicity allows judging about fault slip behavior (Valoroso et al., 2014; Vorobieva et al., 2016; Ross et al., 2020).

Earthquake rupture dynamics is controlled by the processes taking place in fault zones. Direct studies of exhumed faults are the main source of information about the fault zone structure. At all scales, fault planes are rough (Candella et al., 2012). Because of the roughness of fault edge surfaces, specific contact areas can be detected in fault interfaces, the so-called asperities, which concentrate tectonic stresses (Lay et al., 1982). Strong asperities form when granular mineral phases such as quartz, feldspar, pyroxene, olivine, calcite, and dolomite predominate. Their static strength is consistent with the Coulomb criterion under Byerlee’s friction law, 0.6 <μ < 0.85 (Collettini et al., 2019). To generate a dynamic rupture, the asperity must be velocity-weakening, which means that the resistance to shear decreases as the sliding velocity grows (Dieterich, 1978; Barbot, 2019). Thus, the asperity will be statically strong and dynamically weak. The area around an asperity is rather unloaded and with a high probability displays velocity strengthening (Scholz and Campos, 2012; Collettini et al., 2019), that is, frictional strength increases as the sliding velocity increases. The rheological heterogeneity of the fault interface can be traced at different scales (Fageneng, 2011; Collettini et al., 2019).

Sizes of asperities can be accessed via seismological methods by determining the slip distribution at the fault plane from the inversion of body waveforms. It is suggested that asperities correspond to the areas with maximum slip amplitude. The slip distribution may either have a single maximum or several slip maxima distributed over the fault plane (Zeng, Anderson, 2000; Yamanaka and Kikuchi, 2004). The slip distribution with several maxima may be interpreted as a complex rupture. In strong earthquakes, the co-seismic ruptures, starting at one of the asperities, can “pass” through the conditionally stable segment and trigger other asperities. The characteristic size of asperity is about 1.5–3 times less than the length of the co-seismic rupture (Kocharyan and Kishkina, 2021). The characteristic sizes of asperities become apparent in the spectra of emitted seismic waves as well (Gusev, 2013).

Geodetic measurements are one more source of information about the location and size of asperities. The degree of interseismic coupling (the ratio of the interseismic slip rate to the plate-convergence velocity (Ruff, Kanamori, 1983)) is determined by resting on the GPS data. Inside the asperity, when the fault is fully locked, the coupling is 1.0. Areas where the average coupling can reach values as low as 0.4 could, therefore, be associated with areas of velocity strengthening behavior—able to slow down or stop rupture propagation (Métois et al., 2016). At creeping segments, where no strong earthquakes occur, the coupling is small. High coupling (inside the asperity) occurs in zones subjected to high normal stresses with a switch to low coupling occurring abruptly as the normal stress decreases below a critical value (Scholz and Campos, 2012).

Probably, the structure of a fault interface remains invariable at least for several decades (Ide, 2019). As fault rupture starting at one of the asperities can “pass” through the conditionally stable segment and trigger other asperities, one cannot judge about the regularities of the emergence of different slip modes (fast dynamic rupture, slow slip event, and aseismic creep (Peng and Gomberg, 2010; Fageneng and Beall, 2021) without understanding the orderliness of asperities. Beyond all doubts, asperities have complex spatial structures. It is suggested that asperities have self-similar structures with the coefficient of self-similarity from 1.4 to 2.5 (Seno, 2003; Mykulyak, 2018; Kocharyan and Kishkina, 2021). But, both the slip distribution patterns obtained in the inversion of body waves and the seismic coupling distribution obtained in geodetic measurements cannot precisely trace the boundary between an asperity with velocity weakening and the surrounding relatively stable area with velocity strengthening. The high accuracy of a weak earthquake source location allows considering seismic catalogs as new sources of information about the structure of fault zones and about the asperity orderliness (Kocharyan and Ostapchuk, 2022). While a single seismic event points to a possible area of asperity localization, an ensemble of events allows judging about asperity orderliness.

Here, we concentrate on the spatial distribution of earthquakes over the fault interface. Before analyzing the seismicity over space, all dependent events, including the main shocks, were removed from the seismic catalog. We applied the method of topological filtering to obtain topologically dense clusters of seismic sources whose areas of localization were interpreted as seismogenic patches (SPs). SPs can be marked out in the fault interface. The structural features of SPs were investigated using Voronoi tessellation.

Seismic Data

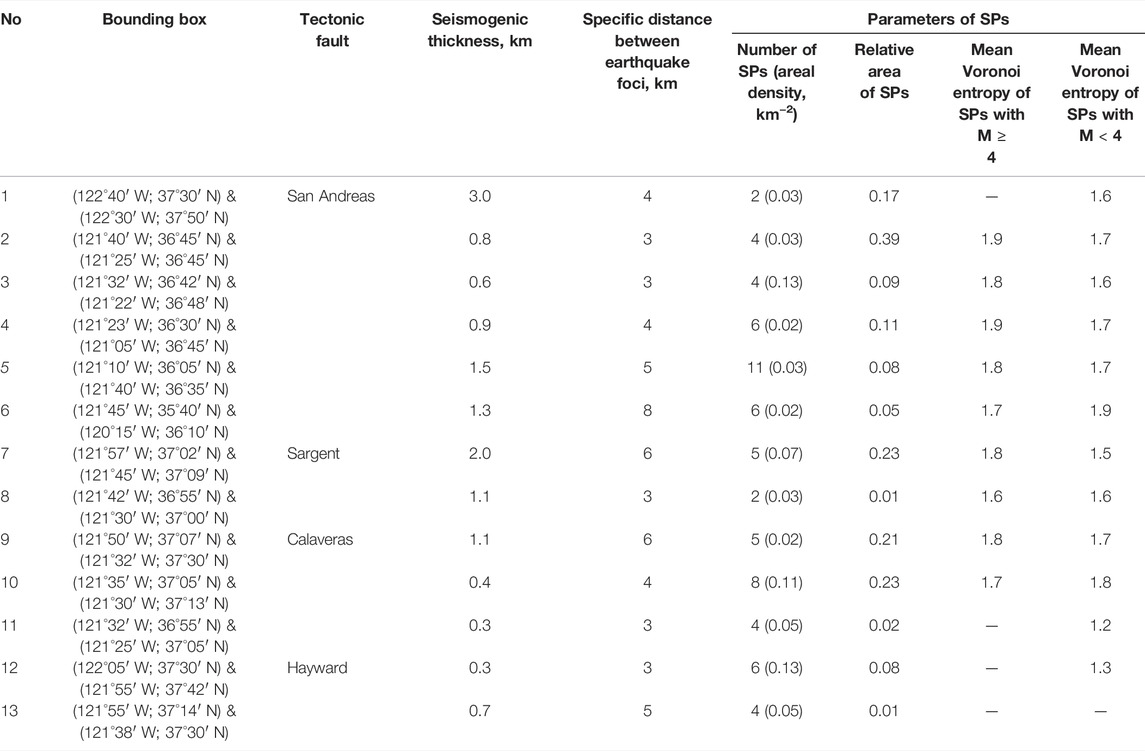
We examine spatial structuredness of the fault interface along the San Andreas fault system using the hypocenter information of Double-difference Earthquake Catalog for Northern California. The seismic catalog being analyzed includes 513,474 events from 1984 to 2011. The locations of earthquakes presented in the catalog are shown in Figure 1. The catalog is based on 1.7 billion CC differential time measurements with the correlation coefficients C_f > = 0.7 from all correlated pairs of events that are separated by less than 5 km (Schaff and Waldhauser, 2005). The accuracy of local earthquake locations over horizontal, and depth is less 40 m. The magnitude of completeness M_c is equal to 1.1 (Wiemer, 2001), and its Gutenberg–Richter distribution is as follows (Gutenberg and Richter, 1944):

$\log N\left[\mathbf{yea}{\mathbf{r}}^{-1}\mathbf{k}{\mathbf{m}}^{-2}\right] =0.25-0.96\cdot M.(1)$

FIGURE 1

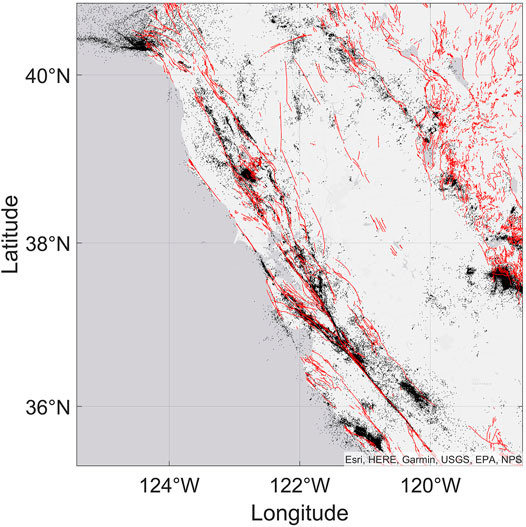
FIGURE 1. Map of seismicity and tectonic faults. Presented are earthquakes (dots) recorded by the Northern California Seismic System (NCSS) between January 1984 and December 2011. Red lines indicate the mapped surface fault traces.

Earthquake localization clearly traces the architecture of fault system. Eleven segments of the well-defined subvertical strike–slip faults were selected for detailed analysis (Table 1; Figure 1). Each selected segment comprises one zone of fault core (Fagereng and Sibson, 2010; McKay et al., 2021). The cumulative length of the selected segments is about 500 km, and 11 earthquakes with ML ≥ 5 belong to the selected segments from 1984 to 2011.

TABLE 1

TABLE 1. Characteristics of tectonic fault segments.

The hypocentral delineation shows that the main portion of earthquakes is concentrated in the vicinity of a single plane which should be interpreted as the fault plane (Figure 2). The layer including 95% of sources localized within 5 km from the fault plane was defined as the seismogenic thickness (Table 1).

FIGURE 2

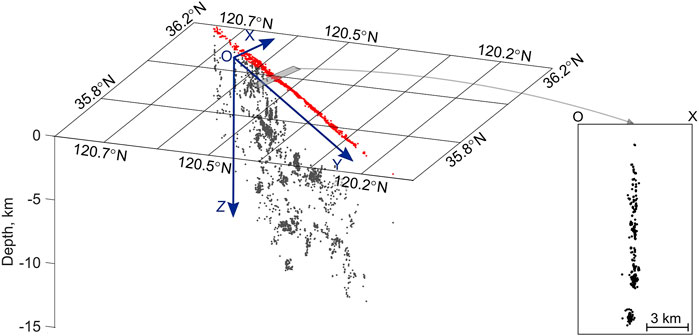
FIGURE 2. Localization of earthquake foci. 3D localization of earthquakes for segment no. 6 (Table 1). Red dots show localization of earthquake epicenters. The inset corresponds to the gray rectangle and shows the fault-normal 3D cross section 4 km long. oXYZ is the coordinate system linked to the fault: OY–direction of fault strike, OX–direction perpendicular to fault strike, and OZ–direction of fault dip.

Considering the segments with narrow seismogenic thickness, it seems reasonable further on to detect the structural properties of the interface in the coordinate system linked to the fault plane (Figure 2). OY is the distance along fault strike, OX is the distance perpendicular to fault strike, and OZ is the distance along fault dip. However, the difference of coordinates along the OX direction can be neglected because the seismogenic thickness is less (Table 1). Figure 3 presents localization of earthquake hypocenters over the fault plane for the segment no. 9. One can detect the areas of point concentration and areas with numerous scattered points. The spatial distribution tends the aggregated type. The distribution of distances between the earthquake foci shows the presence of a single maximum. The characteristic distances between the earthquake foci for all the segments are shown in Table 1.

FIGURE 3

FIGURE 3. Fault plane view of earthquake localizations for segment no. 9 (Table 1). (A) Projection of earthquake foci on the fault plane (yellow dots are the earthquakes with M_L ≥ 5 and red circle is the 1984 Morgan Hill earthquake M6.2); (B) Probability density function of the distance between each pair of earthquake foci on the fault plane. Single maximum of the distance distribution is observed, and the mode is 6 km.

Methods

Algorithm of Declustering the Earthquake Catalog

It is well known that foreshocks and aftershocks group in space and time. Declustering of the earthquake catalog (withdrawal of clustered events) is necessary for the analysis of timeless features of the fault structure. To identify the background and clustered populations of seismicity, we follow the method first proposed by Baiesi and Paczuski (2004). It is based on the calculation of nearest neighbor distance in time–space–magnitude domains. For each pair of earthquakes {i, j}, we compute the proximity function (Zaliapin et al., 2008):

${\mathbf{\eta }}_{\mathbf{i}\mathbf{j}}=\{\begin{array}{cc}{\mathbf{t}}_{\mathbf{i}\mathbf{j}}{\left({\mathbf{r}}_{\mathbf{i}\mathbf{j}}\right)}^{\mathbf{d}}{10}^{-\mathbf{b}{\mathbf{M}}_{\mathbf{i}}},& {\mathbf{t}}_{\mathbf{i}\mathbf{j}}>0\\ +\mathbf{\infty },& {\mathbf{t}}_{\mathbf{i}\mathbf{j}}\le 0\end{array},(2)$

where $t_{ij}=t_j-t_i$ is the event intercurrence time, $r_{ij}$ is the spatial distance between a pair of earthquakes in the fault plane, M_i is the magnitude of event i, d is the fractal dimension of the spatial earthquake distribution, and b is the slope of the Gutenberg–Richter distribution (Eq. 1). The nearest-neighbor distance for a given event j is the minimal distance among ${\eta }_{ij}$, where i goes over all the earlier events in the catalog. The event i which corresponds to the nearest-neighbor distance is called the nearest neighbor. Earthquakes of magnitude smaller than M were deselected, which are within a 0.02 × 10^0.5M km radius during the first 0.04 × 10^0.55M days after a magnitude M earthquake (Tsuboi, 1956; Shebalin and Narteau, 2017). The distribution of the nearest-neighbor function is shown in Figure 4. “Families” of the nearest neighbors were constructed using a threshold ${\eta }_0$ for the proximity function (2), which corresponds to 99% confidence interval for a stationary homogenous Poisson’s point process that a priori has no clustering (Zaliapin and Ben-Zion, 2013). Poisson’s point process is homogenous in d-dimensional space, stationary in time, and has magnitudes that follow the Gutenberg–Richter distribution. The dependent events are defined by the complementary condition ${\eta }_{ij}<{\eta }_0$, and event i is called the parent of event j. If ${\eta }_{ij}>{\eta }_0$, the events turn out to be independent. The population of independent events can be considered background seismicity, and the population of dependent events can be considered clustered seismicity. Figure 4 shows both the background and clustered modes of seismicity. One can see that the populations localize in the same areas.

FIGURE 4

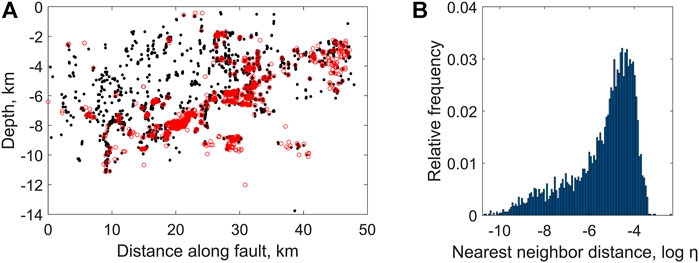
FIGURE 4. Two modes of seismicity (segment no. 9, Table 1). (A) Localizations of the background (dark) and clustered (red) modes of seismicity; (B) Relative frequency histogram of the nearest-neighbor distance η.

Algorithm of Seismic Source Topological Filtering

The spatial distribution of the background seismicity shows a severe inhomogeneity. Several areas of event grouping can be detected, where the stronger it manifests, the longer is the monitoring duration. The Discrete Perfect Sets (DPS) algorithm of topological filtering was applied to reveal dense clusters (Agayan et al., 2014; Dzeboev et al., 2021). The DPS is aimed at isolating subsets with a given density level α in a finite set of Euclidean space. The DPS cuts out isolated objects (subset H) and concatenates rest of the objects in dense clusters (subset B) from the set W of recognition objects of seismic sources:

$\mathbf{W}=\mathbf{B}\cup \mathbf{H},\mathbf{B}\cap \mathbf{H}=\mathbf{\varphi }.(3)$

The result of DPS algorithm is as follows:

$\mathbf{D}\mathbf{P}\mathbf{S}\left(\mathbf{q},\mathbf{\beta }\right):\mathbf{W}\to \left\{{\mathbf{B}}_1, \dots , {\mathbf{B}}_{\mathbf{n}}\right\},(4)$

where q and β are the free parameters of the algorithm.

The parameter q determines the localization radius r_q(W), which is calculated as the power mean of all nontrivial pairwise distances D(W) in a set of recognition objects W:

$\mathbf{r}={\left(\frac{{{\displaystyle \sum }}_{\mathbf{d}\in \mathbf{D}\left(\mathbf{W}\right)}{\mathbf{d}}^{\mathbf{q}}}{\left|\mathbf{D}\left(\mathbf{W}\right)\right|}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathbf{q}$}\right.}.(5)$

For a specified radius of location r, the density of an arbitrary subset $A \subseteq W$ in the point $w \in W$ is defined as the sum of the weights of points, localized in the r-neighborhood $B_A\left(w,r\right)$ of the point w:

${\mathbf{P}}_{\mathbf{A}}\left(\mathbf{w}\right)={\displaystyle \sum }_{\mathbf{g}\in {\mathbf{B}}_{\mathbf{A}}\left(\mathbf{w},\mathbf{r}\right)}\left(1-\frac{\mathbf{d}\left(\mathbf{w},\mathbf{g}\right)}{\mathbf{r}}\right).(6)$

The determination of density rests on a fuzzy comparison (Gvishiani et al., 2008). The measure of comparison of the densities P_W(W) of set W in all its points $w \in W$ and the density level α is defined as follows:

$n\left(P_W\left(W\right),\alpha \right)=\langle \frac{P_W\left(W\right)-\alpha }{\max \left(P_W\left(W\right),\alpha \right)}\rangle .(7)$

The parameter β in Eq. 4 defines the maximality of density and $\beta \in \left[-\mathrm{1,1}\right]$. If β is a necessary level of maximality of density P against the background of W, then the immediate level $\alpha =\alpha \left(\beta \right)$ because P is uniquely determined by β in the equation:

$\mathbf{n}\left({\mathbf{P}}_{\mathbf{W}}\left(\mathbf{W}\right),\mathbf{\alpha }\right)=\mathbf{\beta }.(8)$

It follows from Eq. 5 that $\alpha =\alpha \left(\beta ,q\right)$. At the same time, the set $W\left(\alpha \right)$ is the set of the required dense subsets:

$\mathbf{W}\left(\mathbf{\alpha }\right)=\left\{\mathbf{w}\in \mathbf{W}:{\mathbf{P}}_{\mathbf{W}\left(\mathbf{\alpha }\right)}\left(\mathbf{w}\right)\ge \mathbf{\alpha }\right\}=\left\{{\mathbf{B}}_1, \dots ,{\mathbf{B}}_{\mathbf{n}}\right\}.(9)$

The dense sets $\left\{B_1, \dots , B_n\right\}$ define the areas of SP localization. As the algorithm of topological filtration utilizes only the information about the locations of events, the repeating earthquakes and all the events located closer than 100 m from each other were withdrawn from the catalog. The withdrawal was performed by merging the events into a single point.

Detection of Seismogenic Patches

Detection of SPs was performed depending on the analysis of the catalog of background seismicity. We rely on the fact that SPs emerge in the zones of most intensive interaction of the fault edges; consequently, it should manifest in the background seismicity. After the DPS filtration of the declustered catalog, a dense set $\left\{B_1, \dots , B_n\right\}$ of seismic sources is formed. The areas of localization of each subset form separate SPs. The potential number of SPs depends strongly on the parameters q and β of the algorithm of topological filtration. By introducing two principal conditions, we can avoid ambiguity in defining the space location and number of SPs:

• Localization of earthquakes in the interface plane shows that along with a pronounced grouping of events, the specific distances between them can be detected (Figure 3). These specific distances are characteristic of all selected segments, and their values are given in Table 1. Condition I: if SPs form in an interface containing dense clusters of seismic sources, the specific distance between the clusters should correspond to the specific distance between all the sources that are localized in the fault segment under consideration.

• The number of SPs that could form in the fault plane, generally, should be defined by the geometry of fault edges, and particularly, by their long-wavelength roughness (Selvadurai and Glaser, 2017; Kocharyan et al., 2022). However, under high heterogeneity of the fault interface, some SPs can turn to be “invisible”, for example, due to velocity strengthening of the interface. Condition II: the SP configuration which best represents the current state of knowledge about the heterogeneity of the fault interface is the one with the largest number of SPs.

The two abovementioned conditions allow to unambiguously define the parameters q and β and, consequently, unambiguously detect the dense clusters of seismic sources $\left\{B_1, \dots , B_n\right\}$. The spatial boundaries of each subset $B_i$ should correspond to the boundaries of separate SPs. With some conditionality, the SP boundaries were designated as ellipses. The method of principal components was used to detect the directions of main ellipse axes (Jolliffe, 2002). The ellipse axis lengths were determined so that the ellipse area was minimal.

Results

Figure 5 presents the example for detecting SPs. SPs with areas from 0.03 to 56 km² are detected. Patch boundaries of an ellipse form and the most probable value of flattening is 0.6. Two to 11 SPs can be detected in a separate segment, and the areal density of SPs varies from 0.02 to 0.13 km⁻² (Table 1).

FIGURE 5

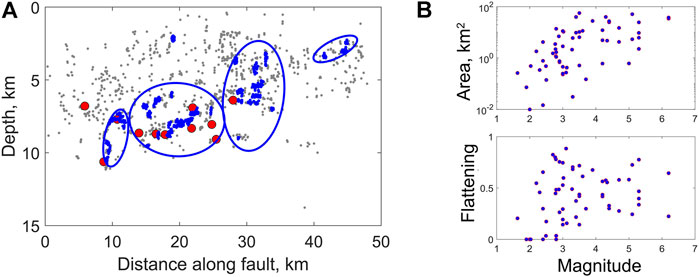
FIGURE 5. Seismogenic patches. (A) Localization of SPs in the interface of fault segment no. 9 (Table 1). Boundaries of SPs are represented by blue ellipses. Gray dots mark the background seismicity, blue dots correspond to dense clusters, and red dots represent earthquakes with ML ≥ 4. (B) Plots of SP area and SP flattening vs. magnitude of the largest earthquake localized inside or in the vicinity of the SP.

As SPs are detected over the declustered catalog, the question arises: «Do sources of earthquakes with ML ≥ 5 get into SPs?" Figure 6 shows the variation of distances from the earthquake sources to the boundary of the nearest SP. One can see that nine of 11 earthquakes with ML ≥ 5 are localized inside or in the vicinity [distance is less than one earthquake source radius (Brune, 1970)] of SPs. For earthquakes with ML ≥ 4, 60% of the events localize inside or in the vicinity of SPs.

FIGURE 6

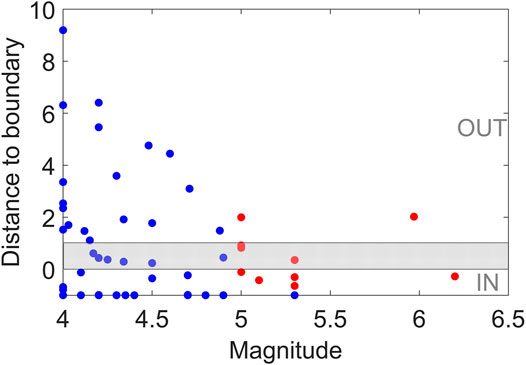
FIGURE 6. Attribution of earthquakes with M_L ≥ 4 to SPs. Distance from the earthquake focus to the SP boundary. Distance is normalized by earthquake radius. Distance “0” corresponds to the ellipse boundary. Gray area shows localization near the boundary.

Fault asperities are complex structured objects. Earthquakes are initiated by slippage in a distinct domain in the vicinity of velocity-weakening asperities (Collettini et al., 2019, Barbot, 2019; Kocharyan, 2021). Thus, the distribution of earthquake sources over an SP reveals localizations of some small-scale asperities inside this SP and allows judging about the structural peculiarities of the large-scale asperity [akin to building up a diffraction pattern from individual electrons by recording single one detection events diffracting through a double-slit (Bach et al., 2013)]. Voronoi tessellation is applied to characterize the distribution of background seismic sources from dense clusters $\left\{B_1, \dots , B_n\right\}$ (Voronoi, 1908; Schoenberg et al., 2009). The Voronoi tessellation divides the SPs into a space-filling, nonoverlapping convex polyhedral shown in Figure 7. To assess the validity of power-law distributions for areas of Voronoi cells, we use a likelihood-ratio test (Clauset et al., 2009; Phillips and Williams, 2021). This test compares the best fit probability density functions from each alternative distribution (P_alt) to the probability density function of the power-law fit (P_pow) (Phillips and Williams, 2021). We consider alternative log-normal and exponential distributions. A log-likelihood ratio is the sum of pointwise log-likelihood ratios for each cell area (x):

$R_{LR}={\displaystyle \sum _x\ln \left(\frac{P_{pow}\left(x\right)}{P_{alt}\left(x\right)}\right)}.(10)$

FIGURE 7

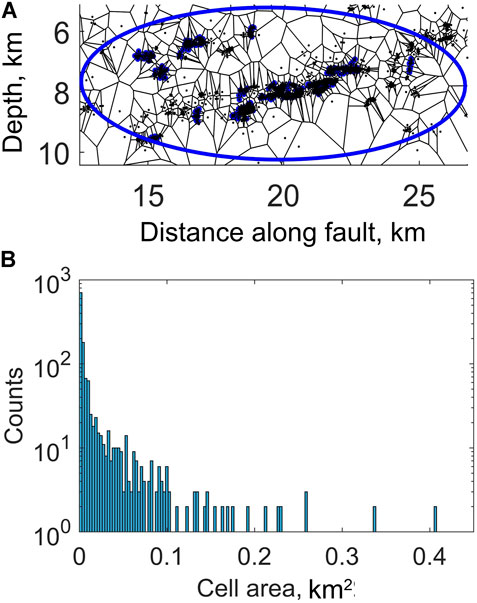
FIGURE 7. Example of Voronoi tessellation of SPs (segment no. 9, Table 1). Voronoi tessellation (A) and distribution of Voronoi cell areas (B) of SPs in the interface of a fault.

If R_LR is positive, then the power-law distribution is mathematically a better fit, while a negative value indicates that the alternative distribution is a better fit. We reveal that the log-normal distribution provides a statistically better fit for 75% of all the SPs of all the segments. The remaining SPs cannot be reliably statistically fitted by any of the three (power, log-normal, or exponential) distributions.

The Voronoi entropy is used to quantify the orderliness of the Voronoi tessellation (Bormashenko et al., 2018). The Voronoi entropy is defined as follows:

$S_{Vor}=-{\displaystyle \sum }_i{P}_i\log P_i,(11)$

where P_i is the fraction of cells with n sides for a given Voronoi tessellation. One can see that the entropy varies in a wide range from 1.2 to 1.9 (Table 1). There is no difference between the SPs with earthquakes ML ≥ 4 and SPs with earthquakes ML ≤ 4. The Voronoi entropy becomes zero for a perfectly ordered structure consisting of a single type of cells. For a fully random 2D distribution of points, the value of S_Vor is 1.71 (Bormashenko et al., 2018).

Discussion

Earthquake source localizations provide essential information about the crustal fault architecture (Kocharyan et al., 2010; Valoroso et al., 2014), while space distribution of dense earthquake clusters highlights the geometric features and rheological heterogeneity of the fault interface.

During a long-term evolution, asperities are subjected to crushing, cataclasis, and frictional wearing, which lead to asperity fragmentation. The log-normal distribution is characteristic of rock fragmentation in blasting and of particle-size distribution in cataclasis (Phillips and Williams, 2021). This can be explained by the fact that the probability of asperity fracturing is independent of asperity size and history (Epstein, 1947). Voronoi mosaic highlights the fragmentation of SPs. The areas of Voronoi cells are distributed according to the log-normal law; hence, the fragmentation of SPs should obey the log-normal law too.

While at the initial stages of fault evolution, an intensive crushing of asperities takes place, a frictional sliding along with flattened asperities goes on in mature faults (Yang et al., 2001). The seismogenic thickness of a mature fault corresponds to the effective thickness of the fractured zone, which is controlled by the waviness of the fault surface (Kocharyan et al., 2010). The inclination of a large-scale asperity at the edge of a mature fault is about $\text{θ }\sim 5÷7°$ (Kocharyan and Spivak, 2003).Thus, assuming that a fault core is rather narrow and comprises cataclastic rock, the asperity spacing (L) can be estimated via the seismogenic thickness of a fault (W) as

$W=2L\cdot \tan \theta \cong \left(0.18÷0.24\right)L.(12)$

Relation (12) can also link the specific distance between SPs and seismogenic thickness (Table 1). It means that the specific distance corresponds to the large-scale wavelength, and the localization of SPs is predetermined by the waviness of fault edges. SPs must be associated with the fault large-scale asperities. At the same time, fault roughness should control the orderliness at a lower scale. Since SPs are topologically dense clusters, areas of SP localization are characterized by relatively lower roughness.

Two conditions should be true for the slip instability to form. First, the fault segment should display velocity weakening, which means that the resistance to shear decreases as the sliding velocity increases (Dieterich, 1978). Second, the rheologic stiffness (k_c) of the fault segment should be higher than the stiffness of the host rock (K). The fault slip mode and earthquake radiation efficiency are governed by the ratio of k_c/K. The higher the ratio k_c/K is, the higher is the earthquake radiation efficiency (Leeman et al., 2016; Kocharyan et al., 2017). The stiffness of the host rock is (Scholz, 2002) as follows:

$K=\eta \frac{G}{L},(13)$

where G is the shear modulus of the enclosing massif, η ∼ 1 is the shape factor, and L is the characteristic fault size correlating with the earthquake magnitude. The rheologic stiffness (k_c) is determined as

$k_c=\frac{{\sigma }_n\left(b-a\right)}{D_c},(14)$

where (b–a) are the frictional rate parameters, ((b–a) > 0—the segment is velocity-weakening, (b–a) < 0—the segment is velocity-strengthening), σ_n is the normal stress, and D_c is the critical slip distance (Leeman et al., 2016). Spatial variations in the k_c/K ratio occur mainly due to changes in rheological stiffness.

The fault roughness controls the critical slip distance D_c (Dieterich, 1979). Laboratory studies have pointed out that D_c decreases with the decreasing fault roughness, and small D_c favors unstable slip. Since asperities are characterized by relatively lower roughness, the fault segments containing asperities are frictionally more unstable ones.

Single crustal fault, tens of kilometers long, can be characterized by both weak fault patches with velocity strengthening ((b–a) < 0) and strong fault patches with velocity weakening ((b–a) > 0) (Collettini et al., 2019). Formation of a frictionally heterogenous structure is determined by metasomatic processes that accompany the long-term evolution of a fault. In rather unloaded areas, an active fluid input occurs and crustal and mantle fluid exerts a chemical role, facilitating the replacement of strong with weak mineral phases (Collettini et al., 2019; Kocharyan, 2021). The frictional strength of the unloaded areas decreases, and the frictional parameter (b–a) decreases. In the stressed zones (in asperities), fluid-assisted reaction of softening is not efficient, and crustal deformation is achieved predominantly by fragmentation and grain-size reduction (Kocharyan, 2021). The frictional strength remains high and obeys the Byerlee’s law, while asperity remains velocity-weakening. As a rule, weak patches with velocity-strengthening show predominantly aseismic creep (Chen, Lapusta, 2009), while strong patches (asperities) determine the seismicity features of the fault segment.

Conclusion

We have presented a new approach to the analysis of seismicity clustering, revealing the structural features of fault interfaces. For the first time, the seismicity pattern is associated with the frictional heterogeneity of the fault interface. Spatial clustering of background seismicity is controlled by the geometric features and frictional heterogeneity of the fault interface. Topologically dense clusters (SPs) can be detected in the fault planes, which are associated with strong velocity-weakening asperities. It is in the vicinity of SPs that earthquakes of magnitudes greater than 5 are usually initiated.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://www.ldeo.columbia.edu/∼felixw/NCAeqDD/.

Author Contributions

AO was responsible for research conceptualization, organization of the work, and writing the first draft of the article. GK contributed to research conceptualization and problem statement. MP preprocessed the data, declustered the seismic catalog, and prepared figures. VP programed the algorithm and prepared figures. All authors were involved in editing the final version of the manuscript.

Funding

This work was partially supported by the Russian Science Foundation according to the research project No. 20-77-10087 for AO and MP. VP and GK acknowledge Program of IDG RAS No. 122032900178-7.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Agayan, S. M., Bogoutdinov, S. R., and Dobrovolsky, M. N. (2014). Discrete Perfect Sets and Their Application in Cluster Analysis. Cybern. Syst. Anal. 50, 176–190. doi:10.1007/s10559-014-9605-9

CrossRef Full Text | Google Scholar

Bach, R., Pope, D., Liou, S.-H., Batelaan, H., and Nebraska, U. (2013). Controlled Double-Slit Electron Diffraction. New J. Phys. 15 (3), 033018. doi:10.1088/1367-2630/15/3/033018

CrossRef Full Text | Google Scholar

Baiesi, M., and Paczuski, M. (2004). Scale-free Networks of Earthquakes and Aftershocks. Phys. Rev. E 69, 066106. doi:10.1103/PhysRevE.69.066106

PubMed Abstract | CrossRef Full Text | Google Scholar

Barbot, S. (2019). Slow-slip, Slow Earthquakes, Period-Two Cycles, Full and Partial Ruptures, and Deterministic Chaos in a Single Asperity Fault. Tectonophysics 768, 228171. doi:10.1016/j.tecto.2019.228171

CrossRef Full Text | Google Scholar

Bormashenko, E., Frenkel, M., Vilk, A., Legchenkova, I., Fedorets, A., Aktaev, N., et al. (2018). Characterization of Self-Assembled 2D Patterns with Voronoi Entropy. Entropy 20, 956. doi:10.3390/e20120956

PubMed Abstract | CrossRef Full Text | Google Scholar

Brune, J. N. (1970). Tectonic Stress and the Spectra of Seismic Shear Waves from Earthquakes. J. Geophys. Res. 75, 4997–5009. doi:10.1029/JB075i026p04997

CrossRef Full Text | Google Scholar

Candela, T., Renard, F., Klinger, Y., Mair, K., Schmittbuhl, J., and Brodsky, E. E. (2012). Roughness of Fault Surfaces over Nine Decades of Length Scales. J. Geophys. Res. 117, a–n. doi:10.1029/2011JB009041

CrossRef Full Text | Google Scholar

Chen, T., and Lapusta, N. (2009). Scaling of Small Repeating Earthquakes Explained by Interaction of Seismic and Aseismic Slip in a Rate and State Fault Model. J. Geophys. Res. 114, B01311. doi:10.1029/2008JB005749

CrossRef Full Text | Google Scholar

Clauset, A., Shalizi, C. R., and Newman, M. E. J. (2009). Power-law Distributions in Empirical Data. SIAM Rev. 51 (4), 661–703. doi:10.1137/070710111

CrossRef Full Text | Google Scholar

Collettini, C., Tesei, T., Scuderi, M. M., Carpenter, B. M., and Viti, C. (2019). Beyond Byerlee Friction, Weak Faults and Implications for Slip Behavior. Earth Planet. Sci. Lett. 519, 245–263. doi:10.1016/j.epsl.2019.05.011

CrossRef Full Text | Google Scholar

Dieterich, J. H. (1979). Modeling of Rock Friction: 1. Experimental Results and Constitutive Equations. J. Geophys. Res. 84, 2161–2168. doi:10.1029/jb084ib05p02161

CrossRef Full Text | Google Scholar

Dieterich, J. H. (1978). Time-dependent Friction and the Mechanics of Stick-Slip. PAGEOPH 116, 790–806. doi:10.1007/bf00876539

CrossRef Full Text | Google Scholar

Dzeboev, B. A., Gvishiani, A. D., Agayan, S. M., Belov, I. O., Karapetyan, J. K., Dzeranov, B. V., et al. (2021). System-Analytical Method of Earthquake-Prone Areas Recognition. Appl. Sci. 11, 7972. doi:10.3390/app11177972

CrossRef Full Text | Google Scholar

Epstein, B. (1947). The Mathematical Description of Certain Breakage Mechanisms Leading to the Logarithmico-Normal Distribution. J. Frankl. Inst. 244 (6), 471–477. doi:10.1016/0016-0032(47)90465-1

CrossRef Full Text | Google Scholar

Fagereng, Å., and Beall, A. (2021). Is Complex Fault Zone Behaviour a Reflection of Rheological Heterogeneity? Phil. Trans. R. Soc. A 379, 20190421. doi:10.1098/rsta.2019.0421

PubMed Abstract | CrossRef Full Text | Google Scholar

Fagereng, Å. (2011). Frequency-size Distribution of Competent Lenses in a Block-In-Matrix Mélange: Imposed Length Scales of Brittle Deformation? J. Geophys. Res. 116, B05302. doi:10.1029/2010JB007775

CrossRef Full Text | Google Scholar

Fagereng, Å., and Sibson, R. H. (2010). Mélange Rheology and Seismic Style. Geology 38 (8), 751–754. doi:10.1130/G30868.1

CrossRef Full Text | Google Scholar

Gusev, A. A. (2013). High-Frequency Radiation from an Earthquake Fault: A Review and a Hypothesis of Fractal Rupture Front Geometry. Pure Appl. Geophys. 170, 65–93. doi:10.1007/s00024-012-0455-y

CrossRef Full Text | Google Scholar

Gutenberg, R., and Richter, C. F. (1994). Frequency of Earthquakes in California. Bull. Seismol. Soc. Am. 34, 185

Google Scholar

Gvishiani, A. D., Agayan, S. M., Bogoutdinov, S. R., Zlotnicki, J., and Bonnin, J. (2008). Mathematical Methods of Geoinformatics. III. Fuzzy Comparisons and Recognition of Anomalies in Time Series. Cybern. Syst. Anal. 44 (3), 309–323. doi:10.1007/s10559-008-9009-9

CrossRef Full Text | Google Scholar

Ide, S. (2019). Frequent Observations of Identical Onsets of Large and Small Earthquakes. Nature 573, 112–116. doi:10.1038/s41586-019-1508-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Jolliffe, I. T. (2002). Principal Component Analysis. New York: Springer.

Google Scholar

Kocharyan, G. G., and Spivak, A. A. (2003). Dynamics of Rock Deformation. Moscow: Akademkniga. (in Russian).

Google Scholar

Kocharyan, G. G., Kishkina, S. B., and Ostapchuk, A. A. (2010). Seismic Picture of a Fault Zone. What Can Be Gained from the Analysis of Fine Patterns of Spatial Distribution of Weak Earthquake Centers? Geodyn. Tectonophys. 1 (4), 419–440. doi:10.5800/gt-2010-1-4-0027

CrossRef Full Text | Google Scholar

Kocharyan, G. G., and Kishkina, S. B. (2021). The Physical Mesomechanics of the Earthquake Source. Phys. Mesomech. 24, 343–356. doi:10.1134/s1029959921040019

CrossRef Full Text | Google Scholar

Kocharyan, G. G., Novikov, V. A., Ostapchuk, A. A., and Pavlov, D. V. (2017). A Study of Different Fault Slip Modes Governed by the Gouge Material Composition in Laboratory Experiments. Geophys. J. Int. 208 (1), 521–528. doi:10.1093/gji/ggw409

CrossRef Full Text | Google Scholar

Kocharyan, G. G. (2021). Nucleation and Evolution of Sliding in Continental Fault Zones under the Action of Natural and Man-Made Factors: A State-Of-The-Art Review. Izv. Phys. Solid Earth 57, 439–473. doi:10.1134/S1069351321040066

CrossRef Full Text | Google Scholar

Kocharyan, G., and Ostapchuk, A. (2022). The Mesostructure of the Slip Interface of a Tectonic Fault. Phys. Mesomech. 2022, 4

Google Scholar

Lay, T., Kanamori, H., and Ruff, L. (1982). The Asperity Model and the Nature of Large Subduction Zone Earthquakes. Earthq. Pred. Res. 1, 3

Google Scholar

Leeman, J. R., Saffer, D. M., Scuderi, M. M., and Marone, C. (2016). Laboratory Observations of Slow Earthquakes and the Spectrum of Tectonic Fault Slip Modes. Nat. Commun. 7, 11104. doi:10.1038/ncomms11104

PubMed Abstract | CrossRef Full Text | Google Scholar

McKay, L., Lunn, R. J., Shipton, Z. K., Pytharouli, S., and Roberts, J. J. (2021). Do intraplate and Plate Boundary Fault Systems Evolve in a Similar Way with Repeated Slip Events? Earth Planet. Sci. Lett. 559 (116), 116757. doi:10.1016/j.epsl.2021.116757

CrossRef Full Text | Google Scholar

Métois, M., Vigny, C., and Socquet, A. (2016). Interseismic Coupling, Megathrust Earthquakes and Seismic Swarms along the Chilean Subduction Zone (38°-18°S). Pure Appl. Geophys. 173, 1431–1449. doi:10.1007/s00024-016-1280-5

CrossRef Full Text | Google Scholar

Mykulyak, S. V. (2018). Hierarchical Block Model for Earthquakes. Phys. Rev. E 97, 062130. doi:10.1103/PhysRevE.97.062130

PubMed Abstract | CrossRef Full Text | Google Scholar

Peng, Z., and Gomberg, J. (2010). An Integrated Perspective of the Continuum between Earthquakes and Slow-Slip Phenomena. Nat. Geosci. 3, 599–607. doi:10.1038/ngeo940

CrossRef Full Text | Google Scholar

Phillips, N. J., and Williams, R. T. (2021). To D or Not to D? Re-evaluating Particle-Size Distributions in Natural and Experimental Fault Rocks. Earth Planet. Sci. Lett. 553, 116635. doi:10.1016/j.epsl.2020.116635

CrossRef Full Text | Google Scholar

Reid, H. F. (1910). The Mechanics of the Earthquake. The California Earthquake of April 18, 1906. Report of the State Investigation Commission. Washington, DC: Carnegie Institution of Washington.

Google Scholar

Ross, Z. E., Cochran, E. S., Trugman, D. T., and Smith, J. D. (2020). 3D Fault Architecture Controls the Dynamism of Earthquake Swarms. Science 368 (6497), 1357–1361. doi:10.1126/science.abb0779

PubMed Abstract | CrossRef Full Text | Google Scholar

Ruff, L., and Kanamori, H. (1983). Seismic Coupling and Uncoupling at Subduction Zones. Tectonophysics 99 (2–4), 99–117. doi:10.1016/0040-1951(83)90097-5

CrossRef Full Text | Google Scholar

Schaff, D. P., and Waldhauser, F. (2005). Waveform Cross-Correlation-Based Differential Travel-Time Measurements at the Northern California Seismic Network. Bull. Seismol. Soc. Am. 95, 2446–2461. doi:10.1785/0120040221

CrossRef Full Text | Google Scholar

Schoenberg, F. P., Barr, C., and Seo, J. (2009). The Distribution of Voronoi Cells Generated by Southern California Earthquake Epicenters. Environmetrics 20 (2), 159–171. doi:10.1002/env.917

CrossRef Full Text | Google Scholar

Scholz, C. H. (2002). The Mechanics of Earthquakes and Faulting. Cambridge: Cambridge University Press.

Google Scholar

Scholz, C. H., and Campos, J. (2012). The Seismic Coupling of Subduction Zones Revisited. J. Geophys. Res. 117, B05310. doi:10.1029/2011JB009003

CrossRef Full Text | Google Scholar

Selvadurai, P. A., and Glaser, S. D. (2017). Asperity Generation and its Relationship to Seismicity on a Planar Fault: a Laboratory Simulation. Geophys. J. Int. 208, 1009–1025. doi:10.1093/gji/ggw439

CrossRef Full Text | Google Scholar

Seno, T. (2003). Fractal Asperities, Invasion of Barriers, and Interplate Earthquakes. Earth Planet Sp. 55, 649–665. doi:10.1186/BF03352472

CrossRef Full Text | Google Scholar

Shebalin, P., and Narteau, C. (2017). Depth Dependent Stress Revealed by Aftershocks. Nat. Commun. 8, 1317. doi:10.1038/s41467-017-01446-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsuboi, C. (1956). Earthquake Energy, Earthquake Volume, Aftershock Area, and Strength of the Earth's Crust. J. Phys. Earth 4, 63–66. doi:10.4294/jpe1952.4.63

CrossRef Full Text | Google Scholar

Valoroso, L., Chiaraluce, L., and Collettini, C. (2014). Earthquakes and Fault Zone Structure. Geology 42 (4), 343–346. doi:10.1130/G35071.1

CrossRef Full Text | Google Scholar

Vorobieva, I., Shebalin, P., and Narteau, C. (2016). Break of Slope in Earthquake Size Distribution and Creep Rate along the San Andreas Fault System. Geophys. Res. Lett. 43, 6869–6875. doi:10.1002/2016GL069636

CrossRef Full Text | Google Scholar

Voronoi, G. (1908). Nouvelles applications des paramètres continus à la théorie des formes quadratiques Deuxième mémoire. Recherches sur les parallélloèdres primitifs. Reine Angew. Math. 1908, 198–287. doi:10.1515/crll.1908.134.198

CrossRef Full Text | Google Scholar

Waldhauser, F., and Schaff, D. P. (2008). Large-scale Relocation of Two Decades of Northern California Seismicity Using Cross-Correlation and Double-Difference Methods. J. Geophys. Res. 113, B08311. doi:10.1029/2007JB005479

CrossRef Full Text | Google Scholar

Wiemer, S. (2001). A Software Package to Analyze Seismicity: ZMAP. Seismol. Res. Lett. 72 (3), 373–382. doi:10.1785/gssrl.72.3.373

CrossRef Full Text | Google Scholar

Yamanaka, Y., and Kikuchi, M. (2004). Asperity Map along the Subduction Zone in Northeastern Japan Inferred from Regional Seismic Data. J. Geophys. Res. 109, B07307. doi:10.1029/2003JB002683

CrossRef Full Text | Google Scholar

Yang, Z. Y., Di, C. C., and Yen, K. C. (2001). The Effect of Asperity Order on the Roughness of Rock Joints. Int. J. Rock Mech. Min. Sci. 38, 745–752. doi:10.1016/S1365-1609(01)00032-6

CrossRef Full Text | Google Scholar

Zaliapin, I., and Ben-Zion, Y. (2013). Earthquake Clusters in Southern California I: Identification and Stability. J. Geophys. Res. Solid Earth 118, 2847–2864. doi:10.1002/jgrb.50179

CrossRef Full Text | Google Scholar

Zaliapin, I., Gabrielov, A., Keilis-Borok, V., and Wong, H. (2008). Clustering Analysis of Seismicity and Aftershock Identification. Phys. Rev. Lett. 101 (1), 018501. doi:10.1103/PhysRevLett.101.018501

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeng, Y., and Anderson, J. (2000). Evaluation of Numerical Procedures for Simulating Near‐fault Long‐period Ground Motions Using Zeng Method. Report 2000/01 to the PEER Utilities Program. UC Berkeley: PEER Center.

Google Scholar