Buried depth calculation of the slope of the unstable rock based on natural vibration frequency

The instability of the slope of the unstable rock poses a great threat to the safety of engineering and people’s lives and properties. The buried depth of an unstable rock is a key factor affecting its stability. It is difficult to directly measure the buried depth of the unstable rock. Therefore, it is of vital importance to indirectly and quickly identify the buried depth of the unstable rock. Assuming that the foundation soil is homogeneous and isotropic, the damping ratio is less than 1; it can be found that the deformation is linear elastic deformation within the amplitude range, and the unstable rock vibration model is simplified to a multi-degree-of-freedom vibration model. Through theoretical derivation, the quantitative relationship between the rock mass, foundation reaction force coefficient, rock burial depth, and the natural vibration frequency in the horizontal direction is established. The quantitative relationship was verified to be correct by laboratory tests. From the tests, the relationship is verified and shows that with the increasing buried depth of the unstable rock, its natural vibration frequency increases nonlinearly in the horizontal direction and also acts in a weakening growing trend; the mass of the unstable rock is a monotonically decreasing function of the natural vibration frequency, and it decreases by a one-half square with the increasing mass of the unstable rock. The research results can calculate the buried depth by measuring the vibration frequency of the unstable rock, which provides a new idea and theoretical basis for the stability evaluation of the slope of the unstable rock and the rapid identification and monitoring of the unstable rock.

Introduction

Unstable rocks on high and steep slopes are unstable due to natural or human factors such as rainfall, earthquakes, and vibrations, and the unstable rocks roll at high speed under the action of their gravity, which brings great threats to the safety of engineering and people’s lives and properties (Chen, 2014). In recent years, there have been frequent reports that the instability of unstable rocks on high and steep slopes has caused traffic jams and casualties. On 3 August 2014, an earthquake measuring 6.5 on the Richter scale occurred in Ludian, Yunnan Province, and a large number of super-large unstable rocks were accumulated on both sides of the main traffic road leading to the epicenter. After this earthquake, some of the unstable rocks rolled down the road, causing traffic jams (Yin et al., 2016). On 29 May 2012, an unstable rock disaster occurred after the rain on the slope of the Shimian-Luding Highway. The giant unstable rock hit the bus, causing the driver’s death. Therefore, it is of great significance to study the stability of unstable rocks. At present, scholars mainly focus on the research of Motion Characteristics Study (Cheng and Su, 2014; Xu et al., 2019), Impact Load Study (He et al., 2008; Wang et al., 2013), Dynamic Response Study (He et al., 2011), Risk Assessment Research (Zhang et al., 2005), and unstable rock protection research (Zhao and Liu, 2005; Yu et al., 2010), and the research results interpret the process of unstable rock movement, movement characteristics, existing risks, and possible hazards, which have important theoretical and guiding significance for the protection and management of unstable rocks. However, the impact energy of unstable rocks is relatively large, so the engineering measures of unstable rock protection and treatment require a lot of human and financial resources, so the passive protection and treatment of unstable rocks are expensive. This study can provide a certain theoretical basis to actively and quickly identify unstable rocks, evaluate their stability and monitor them.

The methods to evaluate unstable rock stability are divided into qualitative stability evaluation methods, quantitative numerical simulation methods, and limit equilibrium methods (Du et al., 2022). Fu et al. (2013) used the block theory to conduct quantitative statistics on the positioned block, the semi-positioned block, and the random block. Dong et al. (2012) according to the three first-level indexes like the hazard resource itself, the slope and the triggering factors, selected 9 second-level indexes corresponding to the first-level ones and 32 basic indexes and established an assessment system of the slope hazard source and degree. Yuan et al. (2011) analyzed and studied the development characteristics of the slope of unstable rocks in the Shuangjiangkou Hydropower Station, classified the stability, and put forward specific preventive measures in consideration of the topography, geology, construction, and other conditions. Yang et al. (2017) used the limit equilibrium method to quantitatively study the stability of the unstable rock of the unstable rock mass in the upper part of the Yufeng rock in the Wenchuan area of Sichuan Province, and the results show that the rainstorm condition mainly attributes to the instability of rolling rock in the unstable rock mass. (Liu et al., 2017) realized the quantitative evaluation of unstable rock stability through force points. (Zhang, 2017) monitored the blasting vibration frequency and the vibration speed of the slope of unstable rocks centroid near the tunnel, and evaluate the stability of the on-site unstable rocks. The results show that due to the differences in rock structure and joints in different directions, the vibration velocity peaks, K values, and α coefficients of the unstable rocks in the X, Y, and Z directions are also significantly different. Zhang et al. (2022) studied the fracture characteristics and anisotropic strength criterion of the structural plane of bedded sandstone through experiments. By using high-resolution computed tomographic scanning, Li et al. (2022) evaluated the damage of freeze-thaw granite. According to the results of (Huang and Liu, 2009), they found that the buried depth of unstable rocks has a particularly significant effect on the recovery coefficient of collision velocity, but there is no quantitative research on the impact of burial depth on the stability of unstable rocks. At present, most scholars assume that the burial depth of unstable rocks is zero, and the calculated safety factor is small. Therefore, it is of great significance to study the burial depth for calculating the stability of rolling stones.

The aforementioned qualitative research methods are difficult to quantitatively evaluate the stability of unstable rocks. The limit equilibrium method and numerical simulation method can realize the quantitative stability evaluation of unstable rocks, but the important factors affecting the stability of unstable rocks, buried depth of unstable rocks, are difficult to obtain directly. With the development of technology, a method for evaluating the stability of unstable rocks based on dynamic characteristic parameters has appeared in recent years. This method judges the stability of unstable rocks through the change of dynamic characteristic parameters. Japanese scholar Fujisawa (2007) studied the dynamic characteristics of the slip-type unstable rock and found that the particle trajectory and amplitude of the stable rock mass are much smaller than those of the unstable rock mass. Ma et al. (2012) further tested and concluded that the vibration frequency is closely related to the bonding state, and the bonding area is positively correlated with the vibration frequency. Ma et al. (2011) found that the vibration frequency of the unstable rock is closely related to the bonding area and quality. Du et al. (2016) further studied the slip-type unstable rock on the single-slip surface and realized their stability evaluation based on the vibration frequency. Yin et al. (2016) and Yao et al. (2015) established a stability evaluation model based on dynamic characteristic parameters for falling unstable rocks. Du et al. (2021) found that natural vibration frequency and other dynamics scientific indicators have obvious application advantages in the rock bridge damage analysis, rapid identification of dangerous rocks, and early warning of collapse. Du et al. (2022), Du et al. (2020), and Du et al. (2017) experimental study finds that the incompatible weakness of the structural plane is a necessary condition for the occurrence of rock burst, and the spatiotemporal difference of the structural plane strength is the main factor that determines the immediate or the time-delayed rock burst. Slow weakening of the structure causes time-delayed rock burst, whereas rapid weakening causes immediate rock burst. Jia et al. (2021), Jia, (2018), and Jia et al. (2017) obtained the fact that the dynamic characteristic parameters of unstable rock like fall type, topping type, and slip type, change with the laws of structural damage through experiments and theoretical analysis, and realized the quantitative stability assessment and monitoring and alarming of unstable rock of fall type, topping type, and slip type based on vibration frequency.

Although the stability evaluation method of unstable rocks based on dynamic characteristic parameters has the advantages of convenience, high efficiency, and accuracy, the current research mostly focuses on the dynamic characteristics of unstable rocks, and there are few reports on how to realize the stability evaluation of unstable rocks based on dynamic characteristic parameters. Taking the slope of unstable rocks as the research object, this study, through theoretical deduction, establishes the quantitative relationship between the unstable rock mass, the coefficient of subgrade reaction, the buried depth of unstable rocks, and the natural vibration frequency in the horizontal direction, and realizes the quick calculation of the buried depth based on the natural vibration frequency so as to verify the correctness of the theoretical model by laboratory experiments. This research study can provide new ideas and a theoretical basis to assess the slope of unstable rocks and quickly identify and monitor unstable rocks.

Slope of unstable rocks

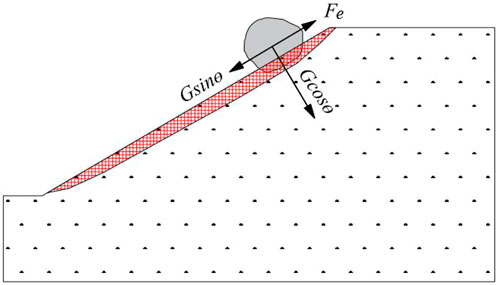
The unstable rock refer to the rock mass that is separated from the parent body, stays on the slope body, and moves downward directly or indirectly under the interference of factors such as rainfall, vibration, geological disasters, freeze-thaw cycles, wind action, animal activities, etc. Unstable rocks tend to have the characteristics of high-speed movement and high-impact energy. In addition to triggering factors, the occurrence of unstable rocks is also related to factors such as the slope conditions where unstable rocks are located, their properties of themselves, and their buried depth. Figure 1 is a schematic diagram of the force acting on the slope of unstable rocks, where G is the gravity, N; θ is the slope angle, °; Gsinθ is the downward component of the unstable rock gravity along the slope, N; Fe is other external forces, including friction, soil pressure, water pressure, etc.

FIGURE 1

FIGURE 1. Force acting on the slope of the unstable rock.

Dynamic characteristic model of the slope of unstable rocks

Under the interference of trigger factors, the unstable rock vibrates. Assuming that isotropic soil is homogeneous in all directions, the damping ratio is less than 1, and the deformation is linear elastic deformation within the amplitude range, the unstable rock vibration model can be simplified to a multi-degree-of-freedom vibration model. See Figure 2.

FIGURE 2

FIGURE 2. Dynamic characteristic model of the slope of the unstable rock.

According to the dynamics theory, when the unstable rock slope is disturbed by an external force, it vibrates along the slope. Assuming that the distance from the origin at a certain moment is x, the horizontal stiffness of the soil layer is $K_x$, and according to Newton’s second law, the mechanical balance Eqs 1, 2 of the horizontal direction of the unstable rock are obtained (Jia et al., 2017):

$\mathit{M}\ddot{\mathit{x}}=-{\mathit{K}}_{\mathit{x}}\mathit{x,}(1)$

${\mathit{p}}^{\mathbf{2}}={\mathit{K}}_{\mathit{x}}/\mathit{M}\mathit{.}(2)$

Then the undamped free vibration equation of the slope of unstable rocks in Eq. 3.

$\stackrel{\mathrm{..}}{\mathit{x}}+{\mathit{p}}^{\mathbf{2}}\mathit{x}=0.(3)$

The equation is solved as

$\mathit{x}={\mathit{e}}^{\mathit{xt}}.(4)$

Substitute the solution into Eq. 3 to obtain the equation roots and characteristic equations:

${\mathit{s}}_{\mathbf{12}}=\pm \mathit{ip,}(5)$

${\mathit{s}}^{\mathbf{2}}+{\mathit{p}}^{\mathbf{2}}=\mathbf{0.}(6)$

The general solution of the equation is further obtained as follows:

$\mathit{x}={\mathit{C}}_1{\mathit{e}}^{\mathit{ipt}}+{\mathit{C}}_2{\mathit{e}}^{-\mathit{ipt}}.(7)$

By applying Euler’s formula, the aforementioned formula can be rewritten as

$\mathit{x}=\mathit{C}\mathit{cos}\mathit{pt}+\mathit{D}\mathit{sin}\mathit{pt}\mathit{.}(8)$

C and D are integration constants whose magnitudes are determined by the initial conditions of the motion. When $t=0$ is set, substitute $x=x_0,\dot{x}={\dot{x}}_0$ into the aforementioned formula to get

$\mathit{C}={\mathit{x}}_0,\mathit{D}={\dot{\mathit{x}}}_0/\mathit{p},(9)$

$\mathit{x}={\mathit{x}}_{\mathit{p}}\mathit{cos}\mathit{pt}+\mathit{sin}\mathit{pt}\dot{\mathbf{x}}/\mathit{p}.(10)$

Through trigonometric transformation, the aforementioned formula can be rewritten as

$\mathit{x}=\mathit{A}\mathit{sin}\left(\mathit{pt}+\mathit{\alpha }\right),(11)$

where

$\mathit{A}=\sqrt{{\mathit{x}}_{\mathbf{0}}^{\mathbf{2}}+{\left(\frac{{\dot{\mathit{x}}}_{\mathbf{0}}}{\mathit{p}}\right)}^{\mathbf{2}}},\mathit{\alpha }=\mathit{t}{\mathit{g}}^{-1}\frac{\mathit{p}{\mathit{x}}_{\mathbf{0}}}{\stackrel{.}{{\mathit{x}}_{\mathbf{0}}}}.(12)$

The vibration period of the system is

$\mathit{T}=\mathbf{2}\mathit{\pi }/\mathit{p}=\mathbf{2}\mathit{\pi }\sqrt{\mathit{M}/{\mathit{K}}_{\mathit{x}}}.(13)$

The vibration frequency of the system is

$\mathit{f}=\mathbf{1}/\mathit{T}=\frac{\mathbf{1}}{\mathbf{2}\mathit{\pi }}\sqrt{\frac{{\mathit{K}}_{\mathit{x}}}{\mathit{M}}}.(14)$

The stiffness coefficient is a basic physical quantity used to describe the elastic deformation form of the material under the action of external force. The relationship between the stiffness coefficient $K_x$ and the coefficient of subgrade reaction $k$ is formula (15):

${\mathit{K}}_{\mathit{x}}=\mathit{khb}\mathit{.}(15)$

Combining Eqs 14, 15, the natural vibration frequency in the horizontal direction of the unstable rock is obtained as Eq. 16:

$\mathit{f}=\frac{\mathbf{1}}{\mathbf{2}\mathit{\pi }}\sqrt{\frac{\mathit{khb}}{\mathit{M}}}.(16)$

Considering the influence of the unstable rock height and the width ratio along the vibration direction on the natural vibration frequency of unstable rocks, and when there is weak damping, the unstable rock block on the slope overcomes the damping force to do work, the amplitude decreases with time, and the mechanical energy of the system is converted into thermal energy and dissipated until the system stops vibrating. Then formula (16) can be transformed into formula (17)

${\mathit{f}}_{\mathit{d}}=\frac{\sqrt{1-{\mathit{\xi }}^{\mathbf{2}}}}{2\mathit{\pi }}\sqrt{\frac{{\left(\frac{\mathit{a}}{{\mathit{H}}_{\mathit{s}}}\right)}^{\mathbf{2}}}{{\left(\frac{\mathit{a}}{{\mathit{H}}_{\mathit{s}}}\right)}^{\mathbf{2}}+\mathbf{1}}}\sqrt{\frac{\mathit{khb}}{\mathit{M}}},(17)$

where $f_d$ is the natural vibration frequency of the damped system ($Hz$); $\xi$ is the damping ratio of the system (unitless); $K_x$ is the stiffness coefficient of the foundation soil, $N/m$; $k$ is the coefficient of subgrade reaction of the foundation soil, $N/m^3$; $a$ is the length of the unstable rock along the vibration direction, $m$; $b$ is the unstable rock length in the vertical vibration direction, $m$; $M$ is the mass of the unstable rock, $kg$; $h$ is the buried depth of the unstable rock, $m$; $H$ is the height of the unstable rock, $m$; $H_s$ is the height of the unstable rock on the ground, $m$.

Model test

Test equipment

1) Vibrometer

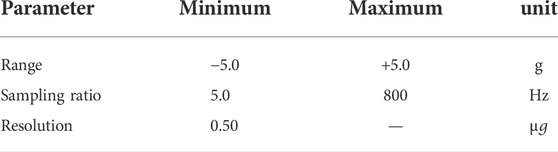
In the test, the wireless vibrometer of Beijing Beike Andi Technology Development Co., Ltd. - Microchip Cube was used. This vibrometer has the characteristics of a high sampling frequency, good signal-to-noise ratio, and wireless transmission, which can be used to measure the three-way vibration acceleration of the object through the fast Fourier transformation to obtain the three-way natural vibration frequency of the object. The specific parameters of the vibration meter are shown in Table 1.

2) Vibration measurement

TABLE 1

TABLE 1. Performance indexes of the microchip cube.

A vibration sensor is arranged on the top surface of the model, and epoxy resin is used to bond the fixed plate of the vibration sensor to the unstable rock block of the slope. After waiting for 72 h, when the epoxy resin is completely cured and the test model becomes a whole, then install the layout sensor. After excitation by the broadband hammer, the three-way acceleration/velocity of the measured object is triggered, that is, the time-domain diagram of the measured object and then the frequency domain diagram of the measured object is obtained through filter and Fourier transform, calculating the natural vibration frequency of the measured object according to the frequency diagram.

Experimental model

1) Test model

In the test, the unstable rock is simulated by cube concrete, and the size of model A is 0.3*0.3*0.4 m, with a mass of 84.3 kg; the size of model B is 0.3*0.3*0.3 m, with the mass 63.2 kg; the size of model C is 0.3*0.3*0.2 m, with the mass 42.5 kg; the unstable rock model in the test is shown in Figure 3.

2) Foundation soil

FIGURE 3

FIGURE 3. Unstable rock test models.

The soil on the Monkey Rock landslide mass of the Dadu River National Road slope was taken as the test foundation soil, and the conventional parameters of the soil obtained through the test are shown in Table 2.

TABLE 2

TABLE 2. Foundation soil parameters.

Test plan

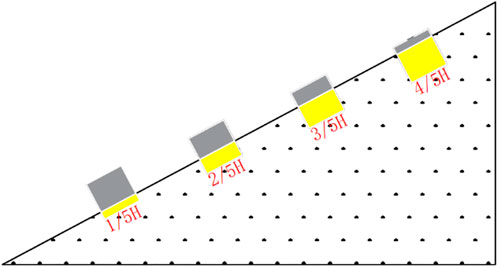
The unstable rock model is buried in the soil, and the buried depth is controlled at 1/5, 2/5, 3/5, and 4/5 of the unstable rock test model height. Then apply the broadband hammer to hit the unstable rock model so as to obtain its acceleration time-history curve by vibrometer. Filter the acceleration time-history curve in the horizontal direction of the unstable rock model, and perform Fourier transform on the filtered acceleration time-history curve to obtain the power spectrum of the unstable rock model. The test scheme is shown in Figure 4.

FIGURE 4

FIGURE 4. Test plan.

Test results

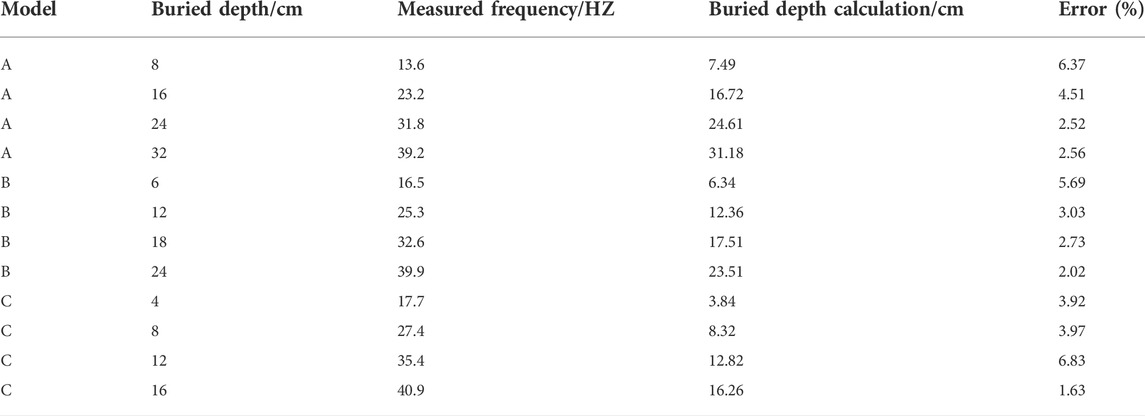
The horizontal natural vibration frequencies of unstable rock models with different buried depths are counted, and the statistical results are shown in Table 3.

TABLE 3

TABLE 3. Horizontal vibration frequencies of unstable rock models.

It can be seen from the test results that the maximum error of the inferred unstable rock buried depth is 6.83%, the minimum error is 1.63%, and the average error is 3.82%.

Discussion

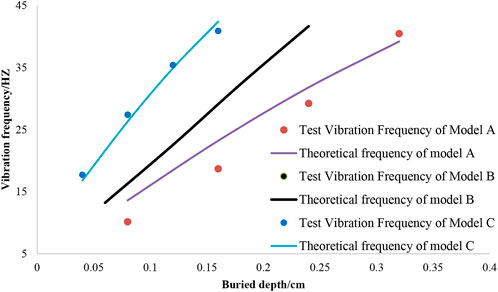
The test results are plotted in Figure 5.

FIGURE 5

FIGURE 5. Relationship between the natural vibration frequency and the buried depth.

Relationship between the unstable rock buried depth and natural vibration frequency

It can be seen from Figure 5 that, in Model A, Model B, and Model C, with the increase of the unstable-rock buried depth, the natural vibration frequency of unstable rock increases nonlinearly, and the natural vibration frequency increases with the growing buried depth.

According to formula (17), the relationship between the buried depth of the unstable rock and the natural vibration frequency is formula (18):

$\mathit{h}=\frac{\mathbf{4}{\mathit{\pi }}^{\mathbf{2}}\mathit{M}{\mathit{f}}_{\mathit{d}}^{\mathbf{2}}\left(\mathit{a}/{\mathit{H}}_{\mathit{s}}^{\mathbf{2}}+\mathbf{1}\right)}{\mathit{kb}\left(\mathbf{1}-{\mathit{\xi }}^{\mathbf{2}}\right){\left(\mathit{a}/{\mathit{H}}_{\mathit{s}}\right)}^{\mathbf{2}}}.(18)$

The burial depth $h$ of the unstable rock is a monotonically increasing function of the natural vibration frequency $f_d$. With the increase of the buried depth of the unstable rock, the natural vibration frequency of the unstable rock increases quadratically. In addition, the average error between the solid buried depth of the unstable rock calculated by the theoretical model 18) and the actual one is 3.82%, indicating that the theoretical model of the natural vibration frequency and the buried depth of the unstable rock is correct.

Relationship between the natural vibration frequency and the unstable rock mass

It can be seen from Figure 5 that when the natural vibration frequencies of Model A, Model B, and Model C are the same, the model with smaller mass has the smallest buried depth, and the model with larger mass has the largest buried depth: Model A buried depth > Model B buried depth > Model C buried depth; under the same buried depth, the natural vibration frequency of the unstable rock with large mass is lower than that of the small mass: Model C natural vibration frequency > Model B natural vibration frequency > Model A natural vibration frequency.

According to Eq. 17, the relationship between the mass of the unstable rock and the natural vibration frequency is Eq. 19:

$\mathit{M}=\frac{\text{kbh}\left(1-{\text{ξ}}^2\right){\left(\text{a}/H_s\right)}^2}{4{\text{π}}^2{\text{f}}_{\text{d}}^2((a/H_s{)}^2+1)}.(19)$

The experimental results of the relationship between the natural vibration frequency and the mass of the unstable rock are consistent with the model (19): the mass $M$ of the unstable rock is a monotonically decreasing function of the natural vibration frequency $f$. As the unstable rock mass increases, its natural vibration frequency decreases to the power of one-half.

Relationship between the natural vibration frequency and the unstable rock safety

The research of this study provides a simple and effective method to measure the buried depth of unstable rock. The deeper the buried depth of the unstable rock is, the higher the safety will be. Therefore, the safety of the unstable rock is positively correlated with the buried depth of the unstable rock, and the vibration frequency is also positively correlated with the buried depth. Therefore, the vibration frequency of unstable rock is positively correlated with its safety. The research results can provide certain new ideas and theoretical basis for the stability evaluation of the slope of the unstable rock and the rapid identification and monitoring of the unstable rock.

Conclusion

1) Based on the dynamic theory, the dynamic characteristic model of the unstable rock is established. Based on this dynamic characteristic model, the buried depth of the unstable rock can be measured by measuring the natural vibration frequency.

2) The test results show that with the increase of the buried depth of the unstable rock, the natural vibration frequency of the unstable rock increases nonlinearly in the horizontal direction, and the increase of the natural vibration frequency tends to weaken with the increase of the buried depth; the mass of the unstable rock is a monotonically decreasing function of the natural vibration frequency. As the mass increases, the natural vibration frequency of the rolling stone decreases to the power of one-half. The test results verify that the dynamic characteristic model of the unstable rock is correct.

3) The combination of the research results and the limit equilibrium model can realize the stability evaluation of the unstable rock based on the natural vibration frequency, and the safety factor can be monitored.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

YJ and TJ were responsible for the work concept or design; GS and GY were responsible for data collection; XP was responsible for drafting the manuscript; HL was responsible for making important revisions to the manuscript; YJ and XP were responsible for approving the final version of the manuscript for publication.

Funding

This research was supported by the National Natural Science Foundation of China (No. U1704243) and the Natural Science Foundation granted by the Department of Education, Anhui Province (No. KJ 2020A0235).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, G. J. (2014). Research on motion features and disaster prevention for rockfall disaster of highway slope (Fuzhou: Fuzhou :Fuzhou University). M.D. Thesis.

Cheng, Q., and Su, S. (2014). Movement characteristics of collapsed stones on slopes induced by Wenchuan earthquake. Rock Soil Mech. 35 (3), 772–776. doi:10.16285/j.rsm.2014.03.011

CrossRef Full Text | Google Scholar

Dong, J. X., Xu, G. L., Li, Z. P., and Zhang, S. (2012). Classification and risk rating assessment of hazard sources in surrounding slope of busigou hydropower project. J. Eng. Geol. 20 (5), 760–767. doi:10.3969/j.issn.1004-9665.2012.05.015

CrossRef Full Text | Google Scholar

Du, Y., Li, H., Chicas, S. D., and Huo, L. (2022). Progress and perspectives of geotechnical anchor bolts on slope engineering in China. Front. Environ. Sci. 10, 928064. doi:10.3389/fenvs.2022.928064

CrossRef Full Text | Google Scholar

Du, Y., Xie, M.-w., Jiang, Y.-j., Li, B., and Chicas, S. (2017). Experimental rock stability assessment using the frozen-thawing test. Rock Mech. Rock Eng. 50 (4), 1049–1053. doi:10.1007/s00603-016-1138-2

CrossRef Full Text | Google Scholar

Du, Y., and Xie, M. (2022). Indirect method for the quantitative identification of unstable rock. Nat. Hazards 112 (1), 1005–1012. doi:10.1007/s11069-021-05197-4

CrossRef Full Text | Google Scholar

Du, Y., Xie, M., and Jia, J. (2020). Stepped settlement: A possible mechanism for translational landslides. Catena 187, 104365. doi:10.1016/j.catena.2019.104365

CrossRef Full Text | Google Scholar

Du, Y., Xie, M. W., Jiang, Y. J., Chen, C., and Huo, L. C. (2021). Review on the formation mechanism and early warning of rock collapse. Metal. Mine 50 (01), 106–119. doi:10.19614/j.cnki.jsks.202101008

CrossRef Full Text | Google Scholar

Du, Y., Xie, M. W., Jiang, Y. J., Li, B., Gao, Y., and Liu, Q. Q. (2016). Safety monitoring experiment of unstable rock based on natural vibration frequency. Rock Soil Mech. 37 (10), 3035–3040. doi:10.16285/j.rsm.2016.10.039

CrossRef Full Text | Google Scholar

Fu, X. D., Sheng, Q., and Zhang, Y. H. (2013). Stepwise excavation process of underground caverns of hydropower station using DDA. Rock Soil Mech. 34 (2), 568–574. doi:10.16285/j.rsm.2013.02.035

CrossRef Full Text | Google Scholar

Fujisawa, K. (2007). Rock slope vibration measurement manual for extracting unstable rock block. Public Works Res. Inst. Mater. 40 (51), 42.

Google Scholar

He, S. M., Li, X. P., and Wu, Y. (2008). Research on yield property of soil under rock-fall impact. Chin. J. Rock Mech. Eng. 27 (Suppl. 1), 2973–2977.

Google Scholar

He, S. M., Shen, J., Luo, Y., and Wu, Y. (2011). Study on the characteristics of normal impact of post-earthquake rock-fall on slope. Eng. Mech. 28 (6), 118–124.

Google Scholar

Huang, R. Q., and Liu, W. H. (2009). In-situ test study of characteristics of rolling rock blocks based on orthogonal design. Chin. J. Rock Mech. Eng. 28 (5), 882–891. doi:10.3321/j.issn:1000-6915.2009.05.003

CrossRef Full Text | Google Scholar

Jia, Y. C., Jiang, T., and Liu, H. D. (2021). Stability evaluation model of toppling unstable rock based on natural vibration frequency. J. Appl. Sci. Eng. 24 (2), 177–184. doi:10.6180/jase.202104_24(2).0007

CrossRef Full Text | Google Scholar

Jia, Y. C. (2018). Study on stability model of slope dangerous rock mass based on dynamic characteristics (Beijing: University of Science and Technology Beijing). Ph.D. Thesis.

Jia, Y. C., Xie, M. W., Chang, S. X., and Fu-Xia, L. (2017). A model for evaluation of stability of sliding-and falling-type dangerous rock blocks based on natural vibration frequency. Rock Soil Mech. 38 (7), 2149–2156. doi:10.16285/j.rsm.2017.07.039

CrossRef Full Text | Google Scholar

Li, B., Zhang, G., Wang, G., and Qiao, J. (2022). Damage evolution of frozen-thawed granite based on high-resolution computed tomographic scanning. Front. Earth Sci. 10, 760. doi:10.3389/feart.2022.912356

CrossRef Full Text | Google Scholar

Liu, Z. J., Wang, X. N., and Mo, L. (2017). Classification of occurrence form of spheric weathered granite and stability analysis. J. Geol. Hazards Environ. Preserv. 29 (04), 40–44. doi:10.11113/jt.v72.4015

CrossRef Full Text | Google Scholar

Ma, G. C., Sawada, K., Saito, H., Uehan, F., and Yashima, A. (2012). Study on evaluating rock block stability by using a remotely positioned laser Doppler vibrometer. Geomate J. 2 (4), 247–252. doi:10.21660/2012.4.3j

CrossRef Full Text | Google Scholar

Ma, G. C., Sawada, K., Yashima, A., Uehan, F., Murata, O., and Saito, H. (2011). “Study of scale effect in rock block stability by remote vibration measurements and numerical experiments,” in Proceedings of the 40th symposium on rock Mechanics (Committee on Rock Mechanics), 339–344.

Google Scholar

Wang, D. P., He, S. M., Ouyang, C. J., Zhang, X. X., Xiang, B., and Wang, X. F. (2013). Study of dynamic response of shed reinforced concrete slab to impact load of rock-fall. Rock Soil Mech. 34 (3), 881–886. doi:10.16285/j.rsm.2013.03.006

CrossRef Full Text | Google Scholar

Xu, J. J., Tang, X. H., Liu, Q. S., and Feng, Y. F. (2019). Investigation on trajectory of rolling rock affected by rock fragmentation based on energy tracking method. Rock Soil Mech. 40 (S1), 541–548. doi:10.16285/j.rsm.2018.2334

CrossRef Full Text | Google Scholar

Yang, Z. X., Pei, X. J., and Yuan, J. K. (2017). Stability analysis of dangerous rock mass at high and steep slope. Subgr. Eng. (01), 25–29. doi:10.13379/j.issn.1003-8825.2017.01.06

CrossRef Full Text | Google Scholar

Yao, G. Z. (2015). Vibration characteristics of falling unstable rock under different stability states. Guizhou: Guizhou University. M.D. Thesis.

Google Scholar

Yao, G. Z., Yu, B., and Chen, J. (2015). Study on simulation test method for vibration characteristics of unstable rock. Railw. Eng. (12), 88–92. doi:10.3969/j.issn.1003-1995.2015.12.24

CrossRef Full Text | Google Scholar

Yin, Z. Q., Xu, Y. Q., Chen, H. Q., Sa, L., and Jiang, X. (2016). The development and distribution characteristics of geohazards induced by August 3, 2014 Ludian earthquake and comparison with Jinggu and Yingjiang earthquakes. Acta Geol. Sin. 90 (6), 1086–1097. doi:10.1007/s12583-014-0471-1

CrossRef Full Text | Google Scholar

Yu, H. C., Yu, H. M., Liu, H. D., and Lu, X. S. (2010). The calculation method for protective structure against rockfall based on orthogonal test and kinematics. J. China coal Soc. 35 (01), 55–60. doi:10.13225/j.cnki.jccs.2010.01.029

CrossRef Full Text | Google Scholar

Yuan, G. Q., Tan, R. Q., Zhang, M. S., and Chen, D. X. (2011). Study of slope stability of the Shuangjiangkou hydropower station. Acta Geol. Sichuan 31 (04), 435–437+445. doi:10.3969/j.issn.1006-0995.2011.04.014

CrossRef Full Text | Google Scholar

Zhang, K. S. (2017). Analysis of influence of blasting vibration at tunnel portal section on stability of slope rock. J. Highw. Transp. Res. Dev. (07), 323–325.

Google Scholar

Zhang, L., Niu, F., Liu, M., Ju, X., Wang, Z., Wang, J., et al. (2022). Fracture characteristics and anisotropic strength criterion of bedded sandstone. Front. Earth Sci. 10, 451. doi:10.3389/feart.2022.879332

CrossRef Full Text | Google Scholar

Zhang, L. Q., Yang, Z. F., and Zhang, Y. J. (2005). Risk analysis of encountering rockfalls on highway and method study. Chin. J. Rock Mech. Eng. 24 (21), 5543–5548. doi:10.2116/analsci.20.717

CrossRef Full Text | Google Scholar

Zhao, X., and Liu, H. D. (2005). Research on protective structures for high slopes rockfall around a hydropower station. Chin. J. Rock Mech. Eng. 24 (20), 3742–3748. doi:10.1007/s11769-005-0030-x

CrossRef Full Text | Google Scholar