A multi-scale dense-connection denoising network for DAS-VSP records

Due to high spatial resolution, low cost, and wide bandwidth, distributed optical fiber acoustic sensing (DAS) is regarded as a potential tool for data acquisition in vertical seismic profile (VSP) surveys. However, in real DAS-VSP records, desired signals are often seriously plagued by various noise, which does not appear in the conventional seismic data received by electronic geophones. Exploring a high-performing attenuation method for the background noise can significantly improve the quality of DAS-VSP records and has essential impacts on the following imaging and interpretation. Deep-learning-based methods, especially convolutional neural network (CNN), have shown remarkable performance in seismic data denoising. However, the conventional CNN-based methods may degrade when dealing with DAS-VSP records in low signal-to-noise ratio. In this study, we propose a novel multi-scale dense-connection denoising network (MDD-Net) to achieve high-accuracy processing of the complex DAS background noise. Unlike conventional multi-scale networks, MDD-Net utilizes widen convolution block to capture the multi-scale features of the analyzed data. On this basis, dense connection operations are employed to fuse the features and improve the network efficiency. Meanwhile, an enhanced spatial attention (ESA) block is designed to reinforce the features, which are helpful for noise suppression and weak signal recovery. Both synthetic and field DAS-VSP records are processed to verify the effectiveness of MDD-Net. Meanwhile, we also compare the denoising results with other competing methods. The experimental results demonstrate that MDD-Net can significantly attenuate the complex DAS background noise and restore the desired signals, even for the weak upgoing signals.

1 Introduction

Distributed optical fiber acoustic sensing (DAS) is a novel acquisition method that uses the phase information of the scattered signals to receive the deformation induced by the seismic wave field (Spikes et al., 2019; Dong and Li, 2020). Compared with traditional geophones, DAS is superior in terms of recording resolution and acquisition cost, such as easy arrangement and high-observation density (Bellefleur et al., 2020; Feng and Li, 2022). Due to its advantages, DAS has begun to apply in seismic surveillance and seismic exploration. Moreover, some successful applications are reported in vertical seismic profile (VSP) data acquisition (Yu et al., 2016). Nonetheless, the weak scatter optical signals tend to be contaminated by the DAS background noise, resulting in a low signal-to-noise ratio (SNR) for field DAS data (Binder et al., 2020). In addition, rare studies focus on analyzing the properties of DAS noise, which has become one of the obstacles to designing effective attenuation methods. To our knowledge, DAS noise is mainly composed of instrument noise and coupled interferences, representing differently from the noise in the geophones-acquired seismic records (Dong et al., 2020; Tian et al., 2022). Notably, some types of background noise, such as time-frequency variant noise and horizontal noise, uniquely exist in DAS records (Zhong et al., 2022a). Thus, we can deduce that it is challenging for the available denoising methods to deal with the DAS background noise. Attenuating the seismic background noise is significant for the following process, such as seismic inversion and interpretation. Therefore, research on effective approaches to suppress the DAS background noise has attracted increasing attention in the seismic data processing.

To suppress the DAS background noise, some attempts are put into practice to improve the data quality. However, due to the short development time of DAS technology, only some simple denoising methods, such as weighted-mean stack (Kobayashi et al., 2020) and linear filtering techniques (Soto et al., 2016), are applied to the issue of background noise suppression. In addition, the denoising performance for these methods may degenerate when confronted with complex DAS data. Although the denoising issues for DAS data have not been extensively studied, we still can get references from similar research in conventional seismic data processing. The conventional denoising methods can be roughly divided into five categories according to the denoising principles, including classical methods, time-frequency-based methods, decomposition methods, sparse transform methods, and diffusion filtering. Here, the classical methods refer to the methods derived from Applied Mathematics and Physics, such as Wiener filtering (Mendel, 1977), median filtering (Huang et al., 2017), band-pass filtering (Stein and Bartley, 1983), and f-x deconvolution (Canales, 1984). All these methods attempt to utilize the differences between the signals and interferences in physical properties, such as propagation velocity and frequency components. To simplify the problem, these methods also make some prior assumptions, such as the noise should be stationary (Zhong et al., 2015). It means that these methods will suffer from degraded performance if the assumptions are not tally with the actual noise properties. Thus, the classical methods fall short of expectations when dealing with complex seismic data, although they are still widely used in the exploration industry due to their stableness and efficiency. Inspired by the classical methods, the denoising methods, which utilized the features of time-frequency plate, have been employed to cope with the seismic noise. The time-frequency-based attenuation methods, such as S-transform (Stockwell et al., 1996), short-time-Fourier-transform and time-frequency peak filtering (TFPF) (Xiong et al., 2014; Zhuang et al., 2015), outperform the classical methods in denoising capability. The good performances of these methods are built on good separation ability and appropriate threshold setting. However, the reflection signals always overlap with the background noise in the frequency domain, and these methods have very limited effects on the spectral aliasing noise (Wu et al., 2014). Similar to time-frequency-based methods, the noisy seismic data can also be sparse decomposed, thereby reconstructing the desired signals by leveraging the decomposition results. Typical decomposition methods, such as wavelet transform (WT) (Chakraborty and Okaya, 1995), empirical mode decomposition (EMD) (Bekara and van der Baan, 2009), and ensemble empirical mode decomposition (EEMD) (Gaci, 2016), can separate the effective signals and unwanted noise into different intrinsic modes or decomposition coefficients, then the noise-dominated components are discarded to recover the desired signals. Nonetheless, it is challenging to determine the optimal reconstruction strategy for the seismic records in low-SNR conditions, resulting in severe residual noise and signal amplitude loss (Dong et al., 2020). Besides, sparse transform methods, including but not limited to curvelet transform (Herrmann et al., 2008), shearlet (Liu et al., 2019), seislet (Liu et al., 2015), and dictionary learning method (Chen et al., 2016), are proposed to suppress the complex seismic noise. The basic principle for these methods is to take advantage of the differences within the sparse properties to recover reflection signals from the field noisy records. However, the huge computational cost becomes an obstacle to the widespread use of the corresponding methods, especially for the massive exploration data processing. Moreover, due to the parameter selection dilemma, some untrue information, such as false events, may be restored and mistaken for effective signals, bringing negative impacts on the subsequent processing of the seismic records (Zhong et al., 2020). To further improve the denoising capability, the diffusion filtering methods, such as fractal conservation law (Meng et al., 2015), fractional anisotropic diffusion (Zhou et al., 2016), and deep complex reaction-diffusion model (Zhang et al., 2022), are gradually applied in the complex seismic data processing. As we know, the denoising process has similarities to the thermal diffusion phenomenon, and the diffusion process can be modified by a given partial differential equation (PDE). Notably, we can control the noise attenuation and signal preservation ability by amending the diffusion term and anti-diffusion term of the PDE. Like time-frequency-based methods, diffusion filtering always shows its downside when attenuating spectral aliasing noise (Zhong et al., 2022b). Other denoising methods, including singular value decomposition (Oropeza and Sacchi, 2011), robust principal component analysis (RPCA) (Cheng et al., 2015), and local-feature-based methods (Bonar and Sacchi, 2012), are also introduced to suppress the complex seismic noise, however, their applications in DAS data processing are rarely reported. Overall, although the conventional denoising methods can improve seismic data quality to a certain extent, it still has an urgency to design powerful denoising methods to meet the requirements of DAS data processing.

In recent years, convolutional neural networks (CNN) have achieved significant breakthroughs with the development of hardware and optimal algorithms (Sun et al., 2018). In addition, some CNN-based denoising methods, such as generative adversarial network (GAN) (Wang et al., 2020) and feedforward denoising CNNs (DnCNNs) (Zhao et al., 2019), are also introduced to cope with the complex seismic noise. Inspired by these researches, deep learning networks are also utilized to achieve the DAS noise attenuation (van den Ende et al., 2021). On this basis, a series of important findings are obtained (Zhu et al., 2019). These denoising networks aim to establish a non-linear high-dimensional mapping relationship between desired signals and noisy records. Meanwhile, we can use training data to strengthen the learned mapping, and the final denoising models are obtained after the training process. Notably, unlike conventional methods, the denoising network can be considered a “data-driven” approach to adaptively accomplish complex seismic noise suppression without parameter fine-tuning (Dong et al., 2022). It is always true that CNN-based networks have advantages over conventional methods if appropriate training data can feed into the networks. Although CNN-based methods can provide excellent results, the denoising performance can be further improved since most networks only utilize single-scale information. Taking DnCNN as an instance, it only uses a simple architecture with unitary convolutional layers to extract the potential features of the analyzed data, leading to the degeneration of trained models for the seismic data with a low SNR (Ma et al., 2020). Another important factor that hinders the improvement in denoising capability is the generalization and authenticity of the training dataset (Zhong et al., 2022c). It is known that we cannot separate the clean signals from the real seismic records. Thus, finding an appropriate way to construct the training dataset is challenging, having critical effects on the attenuation results.

To break through the predicament in DAS data processing, we propose a multi-scale dense-connection denoising network (MDD-Net) in this paper. Here, the multi-scale strategy for MDD-Net is accomplished by applying the widen convolution block. Compared with conventional convolution, widen convolution block utilizes the convolution layers with different kernel sizes to capture the multi-scale features of the analyzed seismic data. It means that the features neglected by the conventional networks, such as DnCNN, could be extracted and used by MDD-Net, thereby improving the representability of the effective features. On this basis, we employ dense connections to guide feature extraction and promote feature fusion. Meanwhile, we design an enhanced spatial attention (ESA) block to improve denoising performance by reinforcing discriminatory features. Furthermore, we combine the synthetic data and field DAS noise records to construct a high-quality training dataset to meet the network training requirements. For investigating the denoising capability, a detailed comparison with other popular methods is made, both for synthetic and field data processing. The experimental results indicate that MDD-Net can tell the desired signals from the complex DAS noise, even for the weak upgoing signals.

2 Network architecture and training process

2.1 Architecture for MDD-Net

Recently, multi-scale networks have achieved attention in signal processing due to their excellent performance. However, the feature interactions between different scales are time-consuming, resulting in the low efficiency of the corresponding networks. Here, a novel multi-scale strategy, combing widen convolution block with dense connection operations, is utilized in MDD-Net to ensure processing accuracy and improve network efficiency. Figure 1A shows the network architecture. Specifically, the widen convolution block can significantly reinforce the feature extraction ability and effectively reduce the elapsed time in the interaction process. On this basis, the dense connection operations are established to fuse the potential features. The feature extraction capability for MDD-Net can be strengthened by changing the connection fashion rather than stacking convolutional layers. We can use fewer convolutional layers to obtain excellent performance by applying dense connections, further reducing the network size. Besides, the ESA block is also applied to refine and enhance the effective features, minimizing the impact of negative samples and secondary features. The descriptions for the network components are shown below:

FIGURE 1

FIGURE 1. The Architecture for MDD-Net: (A) the architecture, (B) widen convolution block, and (C) ESA block.

2.1.1 Widen convolution block

As shown in Figure 1B, the widen convolution block is composed of three convolutional layers with kernel sizes of 1×1, 3×3, and 5×5. Therefore, widen convolution block can use different receptive fields to extract the multi-scale features. Unlike conventional multi-scale networks, we use novel convolutional layers to exact multi-scale features, not through multi-scale network architectures. Here, the output of the widen convolution block $o_i$ can be expressed as:

$o_i={\displaystyle \sum }_{k=\mathrm{1,3,5}}{w}_k{x}_i+{\displaystyle \sum }_{k=\mathrm{1,3,5}}{b}_k(1)$

where x_i is the input data, while ω_k and b_k are the weight and bias parameters.

2.1.2 Dense connection block

The shallow features will have limited contribution on the deep features with the increase of the network depth, resulting in the loss of the features. To make full use of the features, the dense connection operations have been applied in MDD-Net. Specifically, the input of each module is also connected to the subsequent modules, serving as the guide information, achieving great feature fusion results and enhancing the accuracy of the captured features. In addition, a 1×1 convolutional layer, right after the widen convolution block, is applied to maintain the channel number to a proper size, thus further reducing the model complexity.

2.1.3.Enhanced spatial attention block

In this study, an ESA block is designed to refine the extracted features and improve the denoising performance, while the detailed architecture is depicted in Figure 1C. To minimize the computational cost, a 1×1 convolutional layer is utilized to reduce the channel number. On this basis, we use down-sampling and up-sampling blocks to modify the feature map size, and then the detailed features are captured by two 3×3 convolutional layers. Here, we use a sigmoid function to obtain the probability distributions for different features. Therefore, the attention mechanism is accomplished by multiplying the input features with the probability distributions, thereby enhancing the effective features. On the whole, the effects of the ESA block can be denoted as follows:

$\begin{array}{l}{A}_E\left(F^I\right)=\sigma \left(W_1\left(F_{avg}^I\left(W_3\left(F_{up}^I\left(W_3\left(W_1\right)\right)\right)\right)\right)+1\right)\\ F^o=A_E\left(F^I\right)\otimes F^I\end{array}(2)$

where F^I and F^O are the input and output of the ESA block. In addition, W₁ and W₃ denote the 1×1 and 3×3 convolutional layers, while σ represents the sigmoid function.

2.1.4 Denoising principle

In seismic data processing, we also assume that the noisy data y can be regarded as the combination of effective signals x and unwanted noise n, denoted as y=x+n (Zhong et al., 2022a). After the training process, a non-linear mapping R is established between the noisy record and desired signals, and the estimated signals x_est are represented as:

$x_{est}=R\left(y,\theta \right)(3)$

where network parameter θ={ω, b}is composed of weight ω and bias b, respectively. For optimizing the learning process, a loss function based on l₂ norm is utilized, as shown below:

$l\left(\theta \right)=\frac{1}{2M}{\displaystyle \sum }_{i=1}^M\Vert R\left(y_i,\theta \right)-x_i\Vert (4)$

where $\Vert ·\Vert$ is the Frobenius norm, while x_i and y_i represent the signal and noisy data patches in the training dataset. The optimal parameters θ_opt can be obtained by minimizing the loss function. On this basis, we can reconstruct the desired signal x_opt.

$x_{opt}=R\left(y,{\theta }_{opt}\right)(5)$

2.2 Training process

2.2.1 Construction of the training dataset

As we know, the supervised network can derive the potential features from the training dataset. Thus, the quality of training data has a significant impact on the denoising performance of the trained models (Dong et al., 2022). In MDD-Net, we need to construct two training datasets, a signal set and a noise set, to support the network training process. Meanwhile, it is unable to separate pure signals from the field DAS records. To solve the problem of clean signal scarcity, the synthetic data, generated by forward modeling methods, is utilized to constitute the signal set. Specifically, we generate 60 geological models, considering the pre-acquired profile records. It can ensure that the geological models conform to the actual characteristics and guarantee the rationality of the generated synthetic data. By utilizing the elastic wave equation, the corresponding forward models are excited by the seismic wavelets with different dominant frequencies. On this basis, a series of synthetic records are obtained. Table 1 lists the detailed parameters for the forward models. Figure 2 gives a typical forward model and the generated clean signal records. We can observe that the synthetic record has similar properties to the field DAS data. Finally, the clean signal records are intercepted, and 17004 64×64 signal patches are randomly selected to compose the signal set. Similarly, we extract 19003 64×64 noise patches from the field DAS background noise records to compose the noise set. Then, both signal patches and noise patches are fed into the network, and the signal patches are taken as the label data.

TABLE 1

TABLE 1. Physical parameters for the forward models.

FIGURE 2

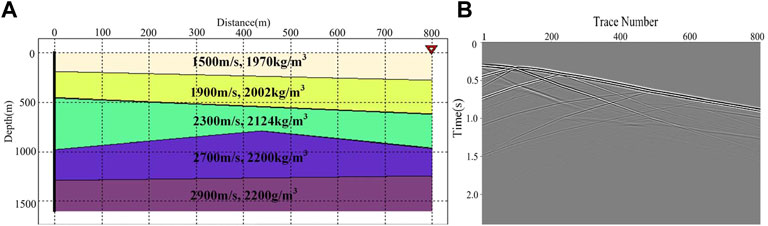
FIGURE 2. The forward model and corresponding synthetic DAS record: (A) the forward model, and (B) the synthetic DAS data.

2.2.2 Training process and experimental environment

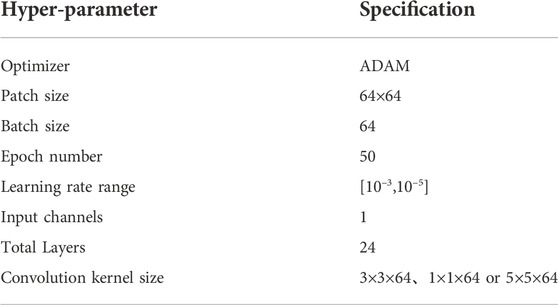
The excellent performance of CNN-based methods mainly relies on the hardware condition and computational efficiency. In this study, the configuration of the experimental environment can be concluded as follows: a CPU (Intel i9-9990K, 3.6 Hz), an NVidia GeForce GTX 1080Ti, and a RAM (16 GB). All the experiments are conducted in Matlab 2016b, and the CNN-based methods use the same training dataset. In general, the batch size and the initial learning rate of the network are set to 32 and [10^–3, 10^–5], respectively. Here, we use ADAM algorithm to optimize the training process, and the training process is composed of 50 epochs. Table 2 lists the network parameters for MDD-Net.

TABLE 2

TABLE 2. Network parameters of MDD-Net.

3 Processing results for synthetic data and field DAS-VSP records

3.1 Synthetic data analysis

For investigating the denoising performance, a synthetic record, shown in Figure 3B, is generated based on the forward model in Figure 3A. The forward model contains four formations with different geometric features. Notably, for a fair comparison, the forward model and the synthetic record are not included in the training dataset. On this basis, we add the field DAS noise data (Figure 3C) to the clean synthetic record, then the noisy record with an SNR of -5 dB (Figure 3D) is obtained. By observing the figures, the effective signals are seriously contaminated by the complex DAS noise. Thus, it is challenging to recover effective signals, especially for the weak events buried in the intense interferences.

FIGURE 3

FIGURE 3. The generation of the noisy DAS data: (A) the forward model, (B) the clean synthetic record, (C) the added field DAS background noise, and (D) the noisy synthetic record.

3.1.1 Comparisons of denoising results

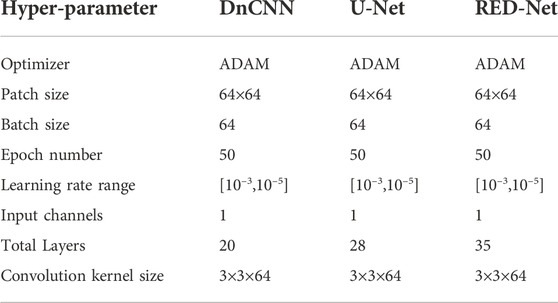
For getting compelling results, we choose some conventional methods and classical denoising networks as the competing methods to verify the effectiveness of MDD-Net. Here, the conventional methods mainly include BPF, TFPF, and RPCA. By analyzing the energy distribution of DAS data, the pass-band for BPF is set to [30–70 Hz], and the window length for TFPF is selected to 11. In addition, for RPCA, we set the weight on sparse error term in loss function to 0.025. Besides, the classical denoising network, including DnCNN, Residual Encoder-Decoder Networks (RED-Net), and U-Net, are also taken as the competing methods. Table 3 lists the corresponding network parameters. To facilitate comparison, we train the competing denoising networks with the same dataset, as MDD-Net used.

TABLE 3

TABLE 3. Network parameters of DnCNN, U-Net and RED-Net.

We use the aforementioned methods to process the noisy record shown in Figure 3D, and the denoising results are displayed in Figure 4. As shown in Figure 4B, TFPF fails to attenuate the DAS noise and only suppress some high-frequency components. Although BPF and RPCA, depicted in Figures 4C,D, can achieve better results, the recovered signals of BPF are disordered, and plenty of residual interferences still severely influence the recognition of the effective signals for RPCA results. On the contrary, the CNN-based methods outperform the conventional methods both in noise attenuation and signal preservation, such as the recovery of the weak upgoing signals. Overall, MDD-Net (Figure 4H) has the best performance in complex DAS noise suppression, compared with the results of competing CNN-based networks represented in Figures 4E–G. On this basis, we also enlarge the area marked by the yellow block for detailed comparisons. Notably, the effective signals are seriously contaminated by the time-variant noise, and no reflection events can be clearly observed in the area of interest. By observing the results shown in Figure 5, MDD-Net can recover the signals with great continuity and smoothness.

FIGURE 4

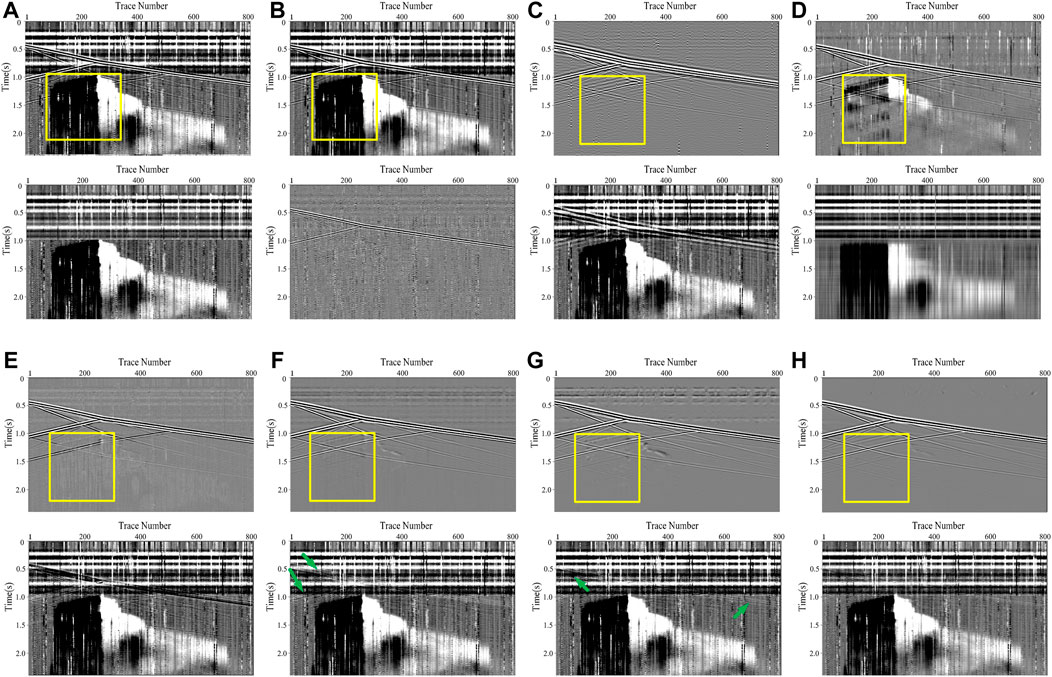
FIGURE 4. The processing results for different methods: (A) the clean data and the added DAS noise, and (B–H) represent the processing results of TFPF, BPF, RPCA, DnCNN, U-Net, RED-Net and MDD-Net, respectively.

FIGURE 5

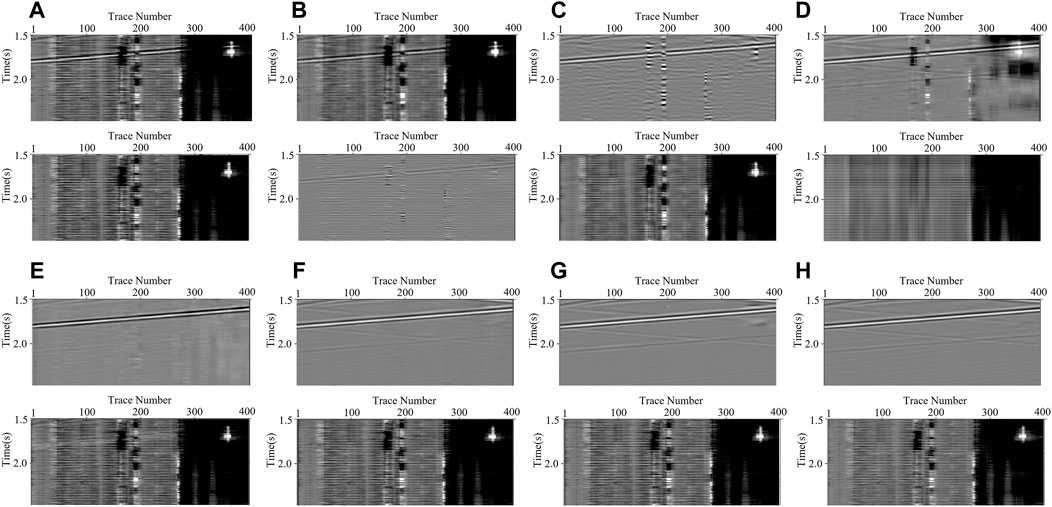
FIGURE 5. The enlargements for the results shown in the yellow blocks in Figure 4: (A) the enlargements for the clean data and the added DAS noise, and (B–H) represent the enlarged processing results of TFPF, BPF, RPCA, DnCNN, U-Net, RED-Net, and MDD-Net, respectively.

3.1.2 Quantitative comparison and computational cost analysis

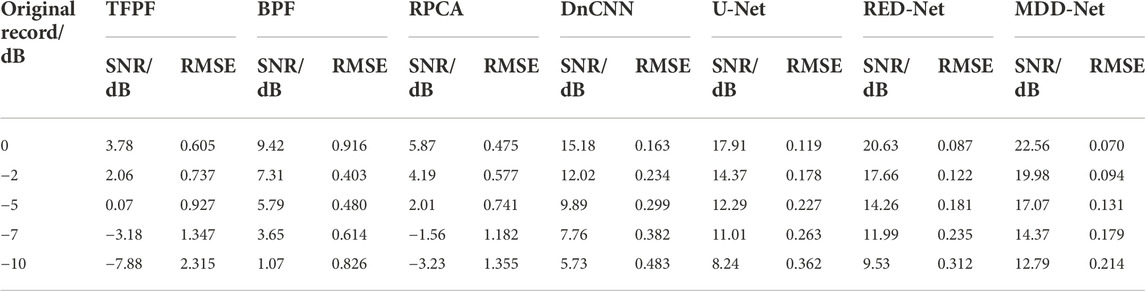
In this study, we use SNR and root-mean-square error (RMSE) to quantitatively evaluate the denoising results for different methods (Zhao et al., 2019). In general, SNR is the energy ratio of clean signals and residual noise, and RMSE is the estimated errors between the clean signals and recovered results. Thus, SNR can reflect the noise attenuation capability, while small RMSE demonstrates that the corresponding method performs well in signal amplitude preservation. The definition equations for SNR and RMSE are shown below:

$SNR\left(dB\right)=10{\log }_{10}\left(\frac{{\sum }_{i=1}^N{\sum }_{j=1}^{M}u{\left(i,j\right)}^2}{{\sum }_{i=1}^N{\sum }_{j=1}^M{\left[u\left(i,j\right)-v\left(i,j\right)\right]}^2}\right)(6)$

$RMSE=\sqrt{\frac{1}{MN}{\sum }_{i=1}^N{\sum }_{j=1}^M{\left[u\left(i,j\right)-v\left(i,j\right)\right]}^2}(7)$

where the $v\left(i,j\right)$ and $u\left(i,j\right)$ are the clean record and recovered signals. Meanwhile, M and N represent the time samples and the trace index, respectively. Here, we use the aforementioned methods to process the noisy synthetic records with different SNR. Table 4 shows the improved SNR and RMSE. By observing the results, we can obtain that the CNN-based networks precede the conventional methods in denoising capability since the improved SNR for the denoising networks surpass the conventional methods. Among these denoising methods, MDD-Net can obtain the most significant improvement in SNR, such as over 22 dB increment for the noisy DAS data. Thus, we can conclude that MDD-Net is effective in DAS noise attenuation and desired signal recovery. In addition, the computational cost for different methods is also analyzed, as listed in Table 5. Compared with conventional methods, the training process for CNN-based methods is time-consuming, such as that for U-Net is over 12 h. Among these denoising networks, MDD-Net has a similar backbone and number of convolutional layers with DnCNN. Avoiding the sampling operating in U-Net, their training costs are relatively small, such as those for DnCNN and MDD-Net are 6.10 and 6.56 h. Although the training time cannot be neglected, the processing time for these networks is competitive by comparing with conventional methods. Taking MDD-Net as an example, the average processing time is only 0.171 s, only inferior to BPF. Notably, CNN-based networks always have generalization ability. The trained models can be applied to plenty of DAS records with similar properties to the training datasets. From this view, the high computational cost is acceptable, and the situation will be relieved with the development of hardware and optimization algorithms.

TABLE 4

TABLE 4. The comparisons of SNR and RMSE for different attenuation methods.

TABLE 5

TABLE 5. The computational cost for different attenuation methods.

3.2 Field data processing results

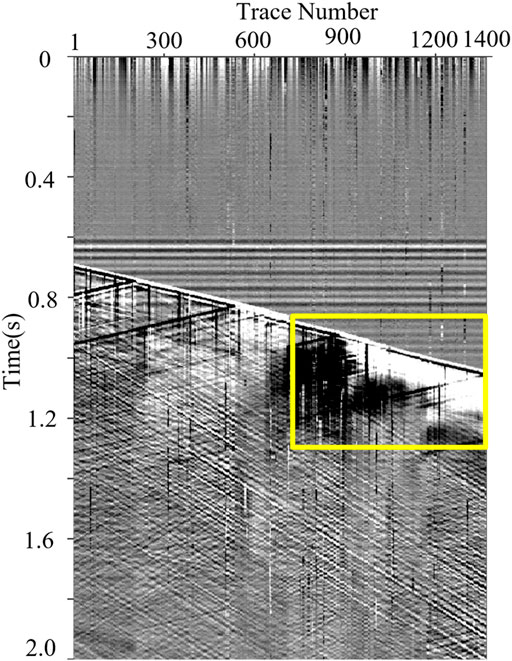
In this subsection, we process some field DAS-VSP records to verify the effectiveness of our proposed method. Figure 6 represents a field DAS-VSP record that contained 1400 trace records with a sampling frequency of 2500 Hz. It is shown that the field DAS data are affected by various types of interferences, resulting the challenges in detecting the weak upgoing signals. We apply the aforementioned methods to process the DAS record, and the corresponding results are shown in Figure 7. Here, for the CNN-based methods, we utilize the denoised models, having the best performance in synthetic data processing, to tell the desired signals from the unwanted noise. As shown in Figures 7A,B, TFPF and BPF cannot offer satisfactory denoising results. TFPF can only eliminate a small quantity of noise, and the obvious horizontal noise leakage (marked by the red arrows) remains in the denoising results of BPF. Meanwhile, although RPCA (Figure 7C) can attenuate the complex noise to some extent, the residual noise still influences signal recognition and negatively impacts the DAS data processing. Consistent with the synthetic data results, CNN-based networks, shown in Figures 7D–G, can separate the weak events from the intense interferences, representing better performance by comparing them with conventional methods. Notably, only MDD-Net can effectively suppress the horizontal noise owing to its efficient multi-scale strategy. On this basis, a comparison for the area of interest (the yellow block in Figure 6) is also conducted, and the corresponding results are plotted in Figure 8. It is shown that the conventional methods all have limitations in DAS background noise attenuation, while the denoising results, as shown in Figures 8A–C, suffer from the apparent residual noise. In contrast, CNN-based methods, plotted in Figures 8D–G, can almost eliminate the noise impacts and recover the signals. Compared with other CNN-based methods, MDD-Net has the best performance with the smooth recovered signals and a clean background.

FIGURE 6

FIGURE 6. The field DAS-VSP record.

FIGURE 7

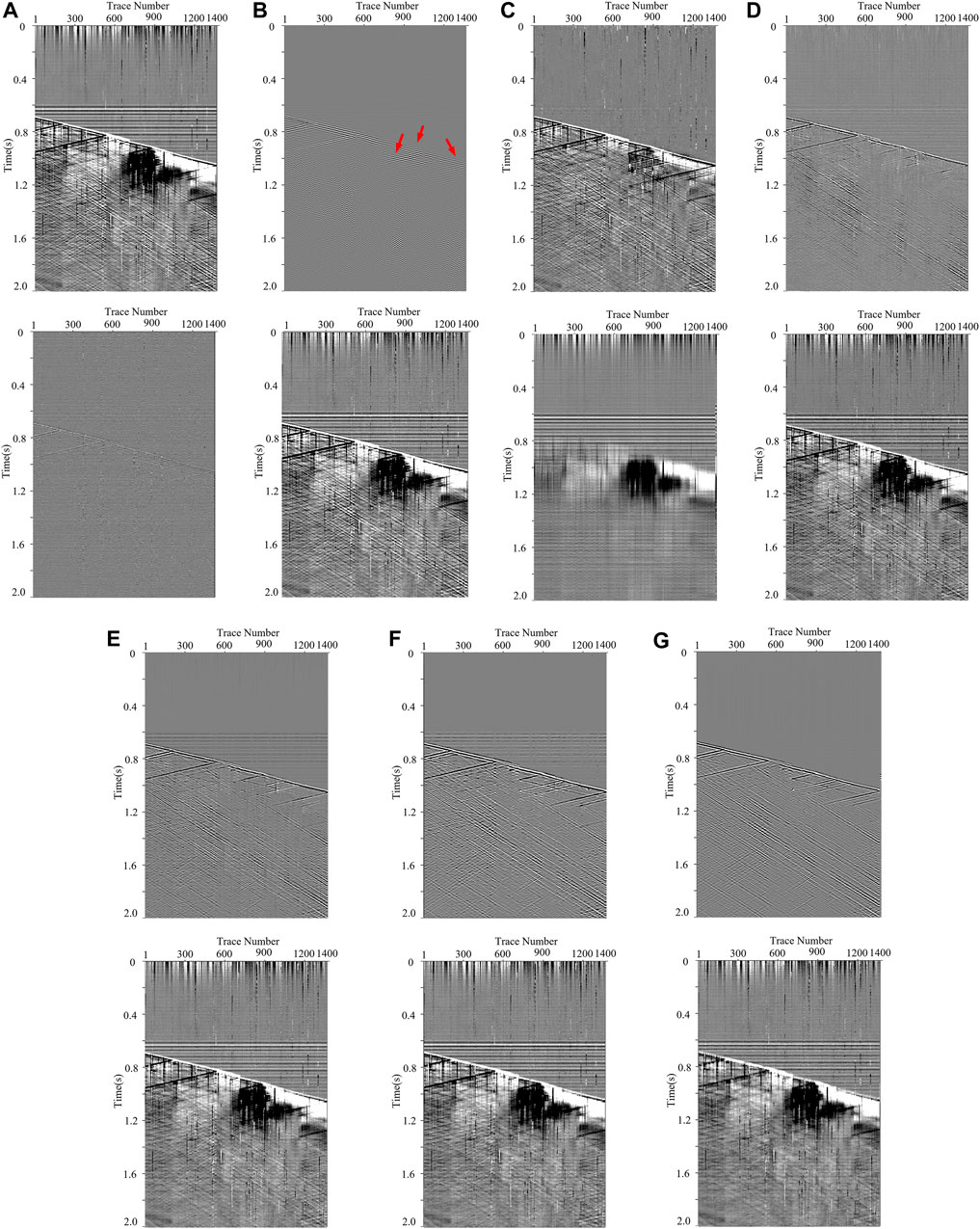
FIGURE 7. The processing results for the field DAS data in Figure 6: (A–G) are the denoising results (top subfigures) and filtered noise (bottom subfigures) obtained by TFPF, BPF, RPCA, DnCNN, U-Net, RED-Net and MDD-Net.

FIGURE 8

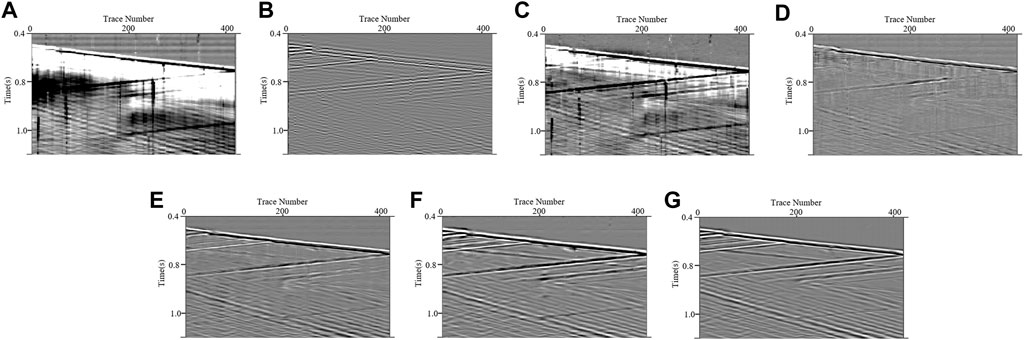
FIGURE 8. The enlargements for the results shown in Figure 7: (A–G) represent the enlarged denoising results obtained by TFPF, BPF, RPCA, DnCNN, U-Net, RED-Net and MDD-Net.

Meanwhile, another field DAS-VSP record (Figure 9A) is processed to further investigate the generalization and denoising capability of MDD-Net. Notably, the effective signals in the DAS data are different from those in Figure 7. On this basis, the DAS data is processed by MDD-Net and other competing methods. Figures 9B–H give the denoising results. It is demonstrated that TFPF and BPF fail to provide acceptable attenuation results, similar to the finding reflected in Figure 7. Moreover, RPCA still cannot eliminate time-variant noise, and the noise leakage impedes the detection of weak events. Furthermore, although the CNN-based methods can effectively suppress the DAS background noise, the performances of the competing networks also need further improvement in attenuating the horizontal noise. By observing the results, MDD-Net (Figure 9H) outperforms the other denoising networks, while no conspicuous residual noise or signal leakage can be observed. In summary, all the corresponding results demonstrate that MDD-Net is a competent method to cope with complex DAS background noise.

FIGURE 9

FIGURE 9. The denoising results for another field DAS-VSP record: (A) is the field DAS data, and (B–H) are the attenuation results after TFPF, BPF, RPCA, DnCNN, U-Net, RED-Net and MDD-Net, respectively.

4 Conclusion

In this study, a novel denoising network, called MDD-Net, is proposed for DAS-VSP data processing. In general, MDD-Net use the multi-scale strategy, combined widen convolution with dense connections, to accurately extract the potential features in seismic data. At the same time, an ESA block is also applied to fuse the features and enhance those beneficial to the denoising task. To guarantee the denoising performance, we generate high-quality training data according to DAS data properties. On this basis, synthetic and field DAS-VSP records are processed. We compare the denoising results with other popular denoising methods. It is shown that MDD-Net can achieve the best denoising performance with an SNR increment over 22dB, reflecting the superiority over the competing methods in complex DAS noise attenuation. Overall, the experimental results prove the effectiveness of the proposed methods, especially for the recovery of the desired signals seriously contaminated by the intense interferences. It means that the MDD-Net can significantly improve the quality of seismic data, bringing convenience for the following procedure of seismic data processing, such as imaging and inversion. However, the denoising ability of MDD-Net is related to the quality of the training data. The performance may degenerate if the seismic data has different properties from the training dataset.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

XD was responsible for data curation, methodology and writing original draft preparation. JL contributed to the conceptualization and supervision. SL carried out the software, visualization, and validation. TZ carried out the methodology and reviewing and editing of the manuscript. YL helped with the visualization and supervision.

Funding

This work was financially supported by Key Project of Guangdong Province for Promoting High-quality Economic Development (Marine Economic Development) in 2022: Research and development of key technology and equipment for Marine vibroseis system Grants GDNRC[2022]29, National Natural Science Foundation of China under Grants 42204114 and 42074123, China Postdoctoral Science Foundation Grants 2021M701378, Natural Science Foundation of Jilin Province Grants 20220101190JC, and Research Project of Jilin Province Education Department under Grants JJKH20210094KJ.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bekara, M., and van der Baan, M. (2009). Random and coherent noise attenuation by empirical mode decomposition. Geophysics 74 (5), V89–V98. doi:10.1190/1.3157244

CrossRef Full Text | Google Scholar

Bellefleur, G., Schetselaar, E., Wade, D., White, D., Enkin, R., and Schmitt, D. R. (2020). Vertical seismic profiling using distributed acoustic sensing with scatter-enhanced fibre-optic cable at the Cu-Au new afton porphyry deposit, British columbia, Canada. Geophys. Prospect. 68 (1), 313–333. doi:10.1111/1365-2478.12828

CrossRef Full Text | Google Scholar

Binder, G., Titov, A., Liu, Y., Simmons, J., Monk, D., Byerley, G., et al. (2020). Modeling the seismic response of individual hydraulic fracturing stages observed in a time-lapse distributed acoustic sensing vertical seismic profiling survey. Geophysics 85 (4), T225–T235. doi:10.1190/GEO2019-0819.1

CrossRef Full Text | Google Scholar

Bonar, D., and Sacchi, M. D. (2012). Denoising seismic data using the nonlocal means algorithm. Geophysics 77 (1), A5–A8. doi:10.1190/GEO2011-0235.1

CrossRef Full Text | Google Scholar

Canales, L. L. (1984). “Random noise reduction,” in 54th annual international meeting, SEG., 525–527. doi:10.1190/1.1894168

CrossRef Full Text | Google Scholar

Chakraborty, A., and Okaya, D. (1995). Frequency-time decomposition of seismic data using wavelet-based methods. Geophisics 60 (6), 1906–1916. doi:10.1190/1.1443922

CrossRef Full Text | Google Scholar

Chen, Y. K., Ma, J. W., and Fomel, S. (2016). Double-sparsity dictionary for seismic noise attenuation. Geophysics 81 (2), V103–V116. doi:10.1190/GEO2014-0525.1

CrossRef Full Text | Google Scholar

Cheng, J., Chen, K., and Sacchi, M. D. (2015). Application of robust principal component analysis (RPCA) to suppress erratic noise in seismic records. Seg. Tech. Program Expand. Abstr. 34, 4646–4651. doi:10.1190/segam2015-5869427.1

CrossRef Full Text | Google Scholar

Dong, X., and Li, Y. (2020). Denoising the optical fiber seismic data by using convolutional adversarial network based on loss balance. IEEE Trans. Geosci. Remote Sens. 59 (12), 10544–10554. doi:10.1109/TGRS.2020.3036065

CrossRef Full Text | Google Scholar

Dong, X., Lin, J., Lu, S. P., Huang, X. G., Wang, H. Z., and Li, Y. (2022). Seismic shot gather denoising by using a supervised-deep-learning method with weak dependence on real noise data: A solution to the lack of real noise data. Surv. Geophys. 43, 1363–1394. doi:10.1007/s10712-022-09702-7

CrossRef Full Text | Google Scholar

Dong, X., Zhong, T., and Li, Y. (2020). New suppression technology for low-frequency noise in desert region: The improved robust principal component analysis based on prediction of neural network. IEEE Trans. Geosci. Remote Sens. 58 (7), 4680–4690. doi:10.1109/TGRS.2020.2966054

CrossRef Full Text | Google Scholar

Feng, Q., and Li, Y. (2022). Denoising deep learning network based on singular spectrum analysis—DAS seismic data denoising with multichannel SVDDCNN. IEEE Trans. Geosci. Remote Sens. 60, 1–11. doi:10.1109/TGRS.2021.3071189

CrossRef Full Text | Google Scholar

Gaci, S. (2016). A new ensemble empirical mode decomposition (EEMD) denoising method for seismic signals. Energy Procedia 97, 84–91. doi:10.1016/j.egypro.2016.10.026

CrossRef Full Text | Google Scholar

Herrmann, F. J., Wang, D., Hennenfent, G., and Moghaddam, P. (2008). Curvelet-based seismic data processing: A multiscale and nonlinear approach. Geophysics 73 (1), A1–A5. doi:10.1190/1.2799517

CrossRef Full Text | Google Scholar

Huang, W., Wang, R., Gong, X., and Chen, Y. K. (2017). Iterative deblending of simultaneous-source seismic data with structuring median constraint. IEEE Geosci. Remote Sens. Lett. 15 (1), 58–62. doi:10.1109/LGRS.2017.2772857

CrossRef Full Text | Google Scholar

Kobayashi, Y., Uematsu, Y., Mochiji, S., and Xue, Z. (2020). A field experiment of walkaway distributed acoustic sensing vertical seismic profile in A deep and deviated onshore well in Japan using A fibre optic cable deployed inside coiled tubing. Geophys. Prospect. 68 (2), 501–520. doi:10.1111/1365-2478.12863

CrossRef Full Text | Google Scholar

Liu, J., Gu, Y., Chou, Y., and Gu, J. F. (2019). Seismic random noise reduction using adaptive threshold combined scale and directional characteristics of shearlet transform. IEEE Geosci. Remote Sens. Lett. 17 (9), 1637–1641. doi:10.1109/LGRS.2019.2949806

CrossRef Full Text | Google Scholar

Liu, Y., Fomel, S., and Liu, C. (2015). Signal and noise separation in prestack seismic data using velocity-dependent seislet transform. Geophysics 80 (6), WD117–WD128. doi:10.1190/GEO2014-0234.1

CrossRef Full Text | Google Scholar

Ma, H., Yao, H., Li, Y., and Wang, H. (2020). Deep residual encoder-decoder networks for desert seismic noise suppression. IEEE Geosci. Remote Sens. Lett. 17 (3), 529–533. doi:10.1109/LGRS.2019.2925062

CrossRef Full Text | Google Scholar

Mendel, J. (1977). White-noise estimators for seismic data processing in oil exploration. IEEE Trans. Autom. Contr. 22 (5), 694–706. doi:10.1109/TAC.1977.1101597

CrossRef Full Text | Google Scholar

Meng, F., Li, Y., Wu, N., Tian, Y., and Lin, H. (2015). A fractal conservation law for simultaneous denoising and enhancement of seismic data. IEEE Geosci. Remote Sens. Lett. 12 (2), 374–378. doi:10.1109/LGRS.2014.2342731

CrossRef Full Text | Google Scholar

Oropeza, V., and Sacchi, M. D. (2011). Simultaneous seismic data denoising and reconstruction via multichannel singular spectrum analysis. Geophysics 76 (3), V25–V32. doi:10.1190/1.3552706

CrossRef Full Text | Google Scholar

Soto, M. A., Ramírez, J., and Thévenaz, A. L. (2016). Intensifying the response of distributed optical fibre sensors using 2D and 3D image restoration. Nat. Commun. 7, 10870. doi:10.1038/ncomms10870

PubMed Abstract | CrossRef Full Text | Google Scholar

Spikes, K. T., Tisato, N., Hess, T. E., and Holt, J. W. (2019). Comparison of geophone and surface-deployed distributed acoustic sensing seismic data. Geophysics 84 (2), A25–A29. doi:10.1190/geo2018-0528.1

CrossRef Full Text | Google Scholar

Stein, R. A., and Bartley, N. R. (1983). Continuously time-variable recursive digital band-pass filters for seismic signal processing. Geophysics 48 (6), 702–712. doi:10.1190/1.1441500

CrossRef Full Text | Google Scholar

Stockwell, R. G., Mansinha, L., and Lowe, R. P. (1996). Localization of the complex spectrum: The S transform. IEEE Trans. Signal Process. 44 (4), 998–1001. doi:10.1109/78.492555

CrossRef Full Text | Google Scholar

Sun, X., Kottayil, N. K., Mukherjee, S., and Cheng, I. (2018). “Adversarial training for dual-stage image denoising enhanced with feature matching,” in International conference on smart multimedia. Springer, 357–366. doi:10.1007/978-3-030-04375-9_30

CrossRef Full Text | Google Scholar

Tian, Y., Sui, J., Li, Y., Wu, N., and Shao, D. (2022). A novel iterative PA-MRNET: Multiple noise suppression and weak signals recovery for downhole DAS data. IEEE Trans. Geosci. Remote Sens. 60, 1–14. doi:10.1109/TGRS.2022.3170635

CrossRef Full Text | Google Scholar

van den Ende, M., Lior, I., Ampuero, J. P., Sladen, A., Ferrari, A., and Richard, C. (2021). A self-supervised deep learning approach for blind denoising and waveform coherence enhancement in distributed acoustic sensing data. IEEE Trans. Neural Netw. Learn. Syst., 1–14. doi:10.1109/TNNLS.2021.3132832

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, H., Li, Y., and Dong, X. (2020). Generative adversarial network for desert seismic data denoising. IEEE Trans. Geosci. Remote Sens. 59 (8), 7062–7075. doi:10.1109/TGRS.2020.3030692

CrossRef Full Text | Google Scholar

Wu, N., Li, Y., Ma, H. T., and Xu, X. C. (2014). Intermediate-frequency seismic record discrimination by radial trace time–frequency filtering. IEEE Geosci. Remote Sens. Lett. 11 (7), 1280–1284. doi:10.1109/LGRS.2013.2292114

CrossRef Full Text | Google Scholar

Xiong, M., Li, Y., and Ni, W. (2014). Random-noise attenuation for seismic data by local parallel radial-trace TFPF. IEEE Trans. Geosci. Remote Sens. 52 (7), 4025–4031. doi:10.1109/TGRS.2013.2278981

CrossRef Full Text | Google Scholar

Yu, G., Cai, Z. D., Chen, Y. Z., Wang, X. M., Zhang, Q. H., Li, Y. P., et al. (2016). Borehole seismic survey using multimode optical fibers in A hybrid wireline. Measurement 125, 694–703. doi:10.1016/j.measurement.2018.04.058

CrossRef Full Text | Google Scholar

Zhang, Y., Lin, H., Li, Y., Ma, H., and Yao, G. (2022). Low-frequency seismic noise reduction based on deep complex reaction–diffusion model. IEEE Trans. Geosci. Remote Sens. 60, 1–14. doi:10.1109/TGRS.2021.3086317

CrossRef Full Text | Google Scholar

Zhao, Y., Li, Y., Dong, X., and Yang, B. (2019). Low-frequency noise suppression method based on improved DNCNN in desert seismic data. IEEE Geosci. Remote Sens. Lett. 16 (5), 811–815. doi:10.1109/LGRS.2018.2882058

CrossRef Full Text | Google Scholar

Zhong, T., Cheng, M., Dong, X., and Li, Y. (2020). Seismic random noise suppression by using adaptive fractal conservation law method based on stationarity testing. IEEE Trans. Geosci. Remote Sens. 59 (4), 3588–3600. doi:10.1109/TGRS.2020.3016922

CrossRef Full Text | Google Scholar

Zhong, T., Cheng, M., Dong, X., Li, Y., and Wu, N. (2022a). Seismic random noise suppression by using deep residual U-net. J. Petroleum Sci. Eng. 209, 109901. doi:10.1016/j.petrol.2021.109901

CrossRef Full Text | Google Scholar

Zhong, T., Cheng, M., Dong, X. T., and Wu, N. (2022b). Seismic random noise attenuation by applying multiscale denoising convolutional neural network. IEEE Trans. Geosci. Remote Sens. 60, 1–13. doi:10.1109/TGRS.2021.3095922

CrossRef Full Text | Google Scholar

Zhong, T., Cheng, M., Lu, S., Dong, X., and Li, Y. (2022c). Rcen: A deep-learning-based background noise suppression method for DAS-VSP records. IEEE Geosci. Remote Sens. Lett. 19, 1–5. doi:10.1109/LGRS.2021.3127637

CrossRef Full Text | Google Scholar

Zhong, T., Li, Y., Wu, N., Nie, P., and Yang, B. (2015). A study on the stationarity and gaussianity of the background noise in land seismic prospecting. Geophysics 80 (4), V67–V82. doi:10.1190/GEO2014-0153.1

CrossRef Full Text | Google Scholar

Zhou, Q., Gao, J., Wang, Z., and Li, K. (2016). Adaptive variable time fractional anisotropic diffusion filtering for seismic data noise attenuation. IEEE Trans. Geosci. Remote Sens. 54 (4), 1905–1917. doi:10.1109/TGRS.2015.2490158

CrossRef Full Text | Google Scholar

Zhu, W., Mousavi, S. M., and Beroza, G. C. (2019). Seismic signal denoising and decomposition using deep neural networks. IEEE Trans. Geosci. Remote Sens. 57 (11), 9476–9488. doi:10.1109/TGRS.2019.2926772

CrossRef Full Text | Google Scholar

Zhuang, G., Li, Y., Wu, N., and Tian, Y. (2015). Curvature-varying hyperbolic trace TFPF for seismic random noise attenuation. IEEE Geosci. Remote Sens. Lett. 12 (11), 2252–2256. doi:10.1109/LGRS.2015.2464233

CrossRef Full Text | Google Scholar