- 1School of Mechanics and Engineering, Liaoning Technical University, Fuxin, China
- 2School of Safety Science and Engineering, Liaoning Technical University, Fuxin, China
A mechanical model of a circular section of a tunnel roadway considering damage is established to improve the impact protection performance of the “roadway rock-support” system and provide a theoretical basis for designing coal mine impact ground pressure roadway support. The formula of the critical rock burst load of a circular roadway is derived according to the instability theory of rock burst disturbance response. The influence of mechanical properties of surrounding rock and roadway support strength on the critical rock burst load of a roadway rock-support system is studied using the control variable method. The research shows that 1) under the support condition of a roadway, with the increase of uniaxial compressive strength, softening modulus, and internal friction angle of surrounding rock, the critical rock burst load of a roadway has an increasing trend; the critical rock burst load of roadway decreases with the increase of the elastic modulus of the surrounding rock. 2) Under the condition of no support, with the increase of uniaxial compressive strength, elastic modulus, and internal friction angle of surrounding rock, the critical rock burst load of roadway tends to increase. With the decrease of the surrounding rock’s softening modulus, the critical rock burst load of the roadway decreases. When the aforementioned four kinds of surrounding rock influence factors are the same, the critical load of rock burst under the supporting condition is much larger than that under the non-supporting condition. 3) A new impact tendency index K is defined as the ratio of the softening modulus and the elastic modulus. 4) The critical load of rock burst increases approximately linearly with the increase of support stress. The critical load of a rock burst is about 400 times as large as the supporting stress. Increasing roadway support strength can greatly improve the stability of the supporting and roadway surrounding rock system, and the stability of the supporting and roadway surrounding rock system can be improved by reasonably changing the mechanical properties of the surrounding rock.
1 Introduction
Control of the rock surrounding a deep roadway is one of the theoretical bottlenecks and key problems in deep mining. Roadway support is a core issue in coal mining, and it is also the key issue in rock burst prevention (Kang et al., 2015; Li and Wu, 2019). The load corresponding to the unstable equilibrium point of the roadway system is called the critical rock burst load on the tunnel. The critical rock burst load of the tunnel is one of the most important indexes to characterize the problem of a rock burst when the roadway is disturbed in a specific stress environment. It is also the theoretical basis of stress control theory in rock burst prevention theory.
Scholars have studied and advanced the understanding of the critical load of rock bursts in roadways (Pan, 1999; Pan et al., 2014). Li et al. examined the rock burst instability theory and concluded that the modulus ratio was an important parameter affecting the critical load of a rock burst (Li et al., 2018). Ma et al. used the roof shear beam model to deduce that the critical load decreased with an increase in the width-height ratio of a rectangular section roadway but increased with the increase of roof thickness. The critical load decreased with an increase in the stiffness ratio of the coal seam to the roof but increased with the increase in the modulus ratio (Ma et al., 2011). Several studies found that the internal friction angle had a relatively strong influence on the damage radius, stress, and displacement of the surrounding rock, while the influence of cohesion is small (Pan and Wang, 2004a; Pan and Wang, 2004b; Pan et al., 2006; Pan et al., 2007). Guo et al. proposed that the rock burst occurrence conditions were related to the ratio of the ascending and descending modulus of rock mass and the development degree of rock fracture (Guo et al., 2011). Chen et al. conducted a theoretical analysis on the critical rock burst of a circular section of a roadway and concluded that the critical rock burst increases with the increase of unified strength theoretical parameters, supporting force, modulus ratio, and internal friction angle and decreases with the increase of dilatancy parameters (Chen et al., 2019; Chen et al., 2020). Meng et al. concluded that part of the input energy in the surrounding rock of a deep circular roadway is released in the form of work conducted by surrounding rock pressure and is used to resist support pressure. When there is no support, this part of the energy is converted into surrounding rock kinetic energy (Meng et al., 2014). Several studies proposed the shape method of the airfoil arch section roadway to improve the bearing capacity and optimize the support parameters (Xiao et al., 2016; Xiao et al., 2017; Ding et al., 2020). Wang et al. used the theory of elastic-plastic mechanics, defined the ratio of pre-peak plastic strain to elastic strain as the pre-peak damage coefficient (K), and established the constitutive relationship of coal and rock based on the Scott model. The results show that the smaller the K value is, the greater the impact tendency is (Wang et al., 2019). Yin et al. found that the lateral pressure coefficient, roadway radius, and mechanical parameters of surrounding rock (cohesion and internal friction angle) were the main factors affecting the shape and size of the plastic zone in a circular roadway (Yin et al., 2018a; Yin et al., 2018b). Huang and Gao proposed that the critical condition of a roadway rock burst was closely related to changes in the surrounding rock support mode, initial strength parameters, and strength parameters of the plastic zone. When the critical plastic zone depth and critical load are small, the rock burst occurs easily, the occurrence frequency is high, and the damage is small. When the critical plastic zone depth and critical load are large, a rock burst does not occur easily, and its occurrence frequency is low. Once it occurs, its strength is destructive (Huang and Gao, 2001). Liu et al. analyzed the airfoil tension crack at the pre-existing crack tip in the roadway coal wall, determined the critical stress of rock burst, and analyzed its influencing factors (Liu et al., 2018; Liu et al., 2019; Liu et al., 2020; Liu et al., 2021). Several studies used acoustic emission and infrared monitoring to conduct experimental research on rock failures, which was of great significance in detecting rock mass failure on the engineering scale (Dong et al., 2019; Dong et al., 2020a; Dong et al., 2020b; Dong et al., 2021; Dong and Luo, 2022).
Due to the initial stress state of the surrounding rock before roadway excavation, the stress redistribution after excavation reaches the secondary stress state. Therefore, the surrounding rock is not only the main load source but also an important part of the bearing structure. An analytical solution is the most powerful means to analyze such roadway engineering problems. Li et al. believed that once the stress in a certain area of the surrounding rock exceeds the strength of the rock mass, the surrounding rock in this part will enter the plastic or failure state. The elastic solutions of a circular tunnel under a nonaxisymmetric external load and radial and shear internal load were derived. Using these solutions, the new elastic–plastic solution and plastic zone radius equation of a circular tunnel under non-axisymmetric external load and radial internal load were derived (Li et al., 2022). Guo et al. thought that the form of a plastic zone of roadway surrounding rock determines its failure form and degree. Based on the implicit equation of a plastic zone boundary, the variation law of the general form of the plastic zone of rock surrounding a circular roadway was comprehensively studied (Guo et al., 2016; Guo et al., 2018).
In conclusion, the critical load of roadway rock burst is one of the main research topics of tunnel anti-shock support design, but the influence trend of the properties of the surrounding rock on the critical load of a rock burst is not clear. This article considers the small disturbance and three-dimensional equivalent strain caused by the external load of the surrounding rock system in the equilibrium state and adopts the bilinear constitutive relationship. In other words, the overall stress is characterized by a linear climb before the peak and a rapid decline after the peak, which is mainly reflected in the elastic stage and the softening stage after the peak. Based on the Coulomb yield criterion and the rock burst initiation criterion, the critical load formulas with and without support are obtained. According to the analytical solution of the critical rock burst load of a circular roadway, the influence of surrounding rock properties such as uniaxial compressive strength, softening modulus, elastic modulus, and internal friction angle on the critical rock burst load of a roadway was studied by controlling single and double variables. FLAC3D software was used for numerical simulation, and the theoretical and numerical solutions were compared and analyzed to provide a theoretical basis for analyzing roadway anti-impact engineering problems.
2 Formula derivation of the critical rock burst load of the circular roadway
Assuming that the coal–rock mass system is subjected to external force
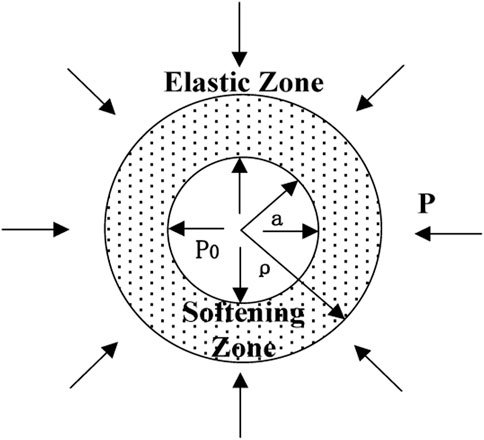
Assuming that the roadway is a circular cavity with radius a (m), under the action of hydrostatic pressure
In Eq. 2 (Pan, 1999),
The coal rock at the junction of softening zone and the elastic zone has just entered the yield state, so the damage variable
In Eq. 4,
According to the deformation geometry equation,
In Eq. 5, B is the integral constant, u(m) is radial displacement,
The von Mises yield criterion indicates that under certain deformation conditions when the equivalent effect force at a point within a stressed object reaches a certain value, that point begins to enter a plastic state. The equivalent effect variation is a physical quantity used to determine the location of the yield surface of a material after strengthening and is calculated using the same formula as the fourth strength theory formula for calculating the equivalent effect force, except that the stress is changed to a strain. For coal and rock materials, it is considered that the strain
In Eq. 7,
In the area where the elastic zone and the failure damage zone intersect, the coal rock reaches peak strength and peak strain. Based on the plastic mechanics theory, the uniaxial strain is transformed into the triaxial strain, and the equivalent strain
In Eq. 8,
Without considering the volume force, the equilibrium equation in the softening zone is
Based on the equilibrium equation and the yield condition, the stress partial differential equation of the damage zone is
In Eq. 10,
By solving this equation, the stress is
In Eq. 11, Q is the integral constant.
Boundary conditions on the roadway surface are as follows:
In the area where the elastic zone and the failure damage zone intersect, the continuous condition of radial stress is
According to Eq. 11, combined with boundary conditions (Chen et al., 2019; Chen et al., 2020),
By solving the aforementioned formula
In Eq. 15,
When support stress is not considered:
Corresponding to Eq. (15), it is deduced that the critical load
When support stress is not considered:
3 Analysis of factors that influence the critical rock burst load in a circular roadway
According to Eq. (18), the critical rock burst load of a circular roadway is related to the mechanical properties of the surrounding rock, including uniaxial compressive strength σc, softening modulus λ, elastic modulus E, internal friction angle φ, and support stress P0. According to the Mining Engineering Design Manual (Zhang, 2003), the rock grades of the surrounding rock are soft, medium-hard, and hard. The rock mass test parameters are as follows: the uniaxial compressive strength is 95.6 MPa, the softening modulus is 25 GPa, the elastic modulus is 24 GPa, and the internal friction angle is 30°. The mechanical properties of surrounding rock, such as uniaxial compressive strength, softening modulus, elastic modulus, internal friction angle, and the influence of support stress on the critical load of roadway rock burst, were studied by the control variable method. The control variable method means that when a physical quantity is affected and restricted by multiple factors at the same time, the multi-factor problem is transformed into multiple single-factor problems. When studying the relationship between this physical quantity and one of the factors, only one factor is allowed to change, and the other factors are controlled to remain unchanged to determine the relationship between the relevant physical quantities.
3.1 Effect of the uniaxial compressive strength on the critical load
The roadway surrounding rock softening modulus is 25 GPa, the elastic modulus is 24.9 GPa, the internal friction angle is 30°, the uniaxial compressive strength is 36.7–231.7 MPa, and roadway support stress is 5 MPa. These parameters are used in Eqs. 17 and 18. Figure 2A shows the relationship curve between uniaxial compressive strength and critical load under supporting conditions; Figure 2B represents the relationship curve between uniaxial compressive strength and critical load under supporting conditions.
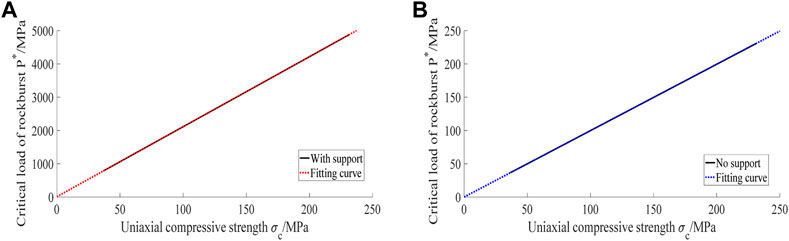
FIGURE 2. Uniaxial compressive strength–critical load curve. (A) Uniaxial compressive strength–critical load (with support). (B) Uniaxial compressive strength–critical load (no support).
It can be seen from Figure 2 that when the support stress is 5 MPa and the uniaxial compressive strength is 36.7 and 231.7 MPa, the critical loads of rock burst are 782.1 and 4884 Mpa, respectively (Kang et al., 2015). The critical load of rock burst increases with increasing uniaxial compressive strength. The fitting curve equation is
3.2 Effect of the softening modulus on the critical load
The uniaxial compressive strength of the surrounding rock is 95.6 MPa, the elastic modulus is 24.9 GPa, the internal friction angle is 30°, the softening modulus is 10–40 GPa, and the roadway support stress is 5 MPa. When these parameters are used in Eqs. 17 and 18, Figure 3A represents the relationship curve between the softening modulus and the critical load under supporting conditions, and Figure 3B represents the relationship curve between the softening modulus and the critical load without supporting conditions.
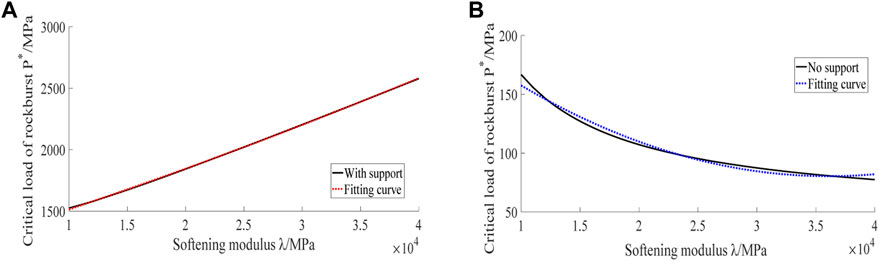
FIGURE 3. Softening modulus–critical load curve. (A) Softening modulus–critical load (with support). (B) Softening modulus–critical load (no support).
It can be seen from Figure 3 that when the support stress is 5 MPa and the softening modulus is 10 and 40 GPa, the critical loads of rock burst are 1524 and 2577 MPa, respectively (Kang et al., 2015). The critical load of rock burst increases with the increase of softening modulus. The fitting curve equation is
3.3 Effect of the elastic modulus on the critical load
The uniaxial compressive strength of the roadway surrounding rock is 95.6 MPa, the softening modulus is 25 GPa, the internal friction angle is 30°, the elastic modulus is 5.2–79.8 GPa, and the roadway support stress is 5 MPa. When these parameters are used in Eqs. 17 and 18, Figure 4A represents the relationship curve between the elastic modulus and the critical load under supporting conditions, and Figure 4B represents the relationship curve between the elastic modulus and the critical load without supporting conditions.
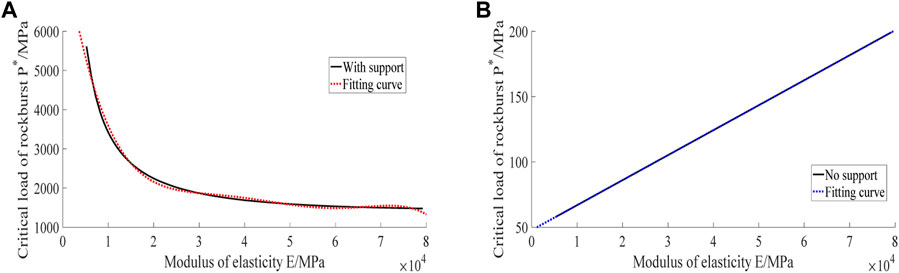
FIGURE 4. Modulus of the elasticity–critical load curve. (A) Modulus of elasticity–critical load (with support). (B) Modulus of elasticity–critical load (no support).
It can be seen from Figure 4 that under the condition of 5 MPa support stress, with the increase of elastic modulus, the critical rock burst load has experienced three stages of rapid decrease, slow decrease, and basic stability (Kang et al., 2015). The elastic modulus is in the stage of rapid decrease of the critical load from 5 to 10 GPa, and the slope of the curve is −0.5. The elastic modulus is in the stage of a slow decrease of the critical load from 10 to 50 GPa, and the slope of the curve is −0.0375. The elastic modulus of 50–79.8 GPa is the stable stage of the critical load. The fitting curve equation is
3.4 Effect of the internal friction angle on the critical load
The uniaxial compressive strength of the roadway surrounding rock is 95.6 MPa, the softening modulus is 25 GPa, the elastic modulus is 24.9 GPa, the internal friction angle is 20°–40°, and the roadway support stress is 5 MPa. When these parameters are used in Eqs. 17 and 18, Figure 5A represents the relationship curve between the internal friction angle and the critical load under supporting conditions, and Figure 5B represents the relationship curve between the internal friction angle and the critical load without supporting conditions.
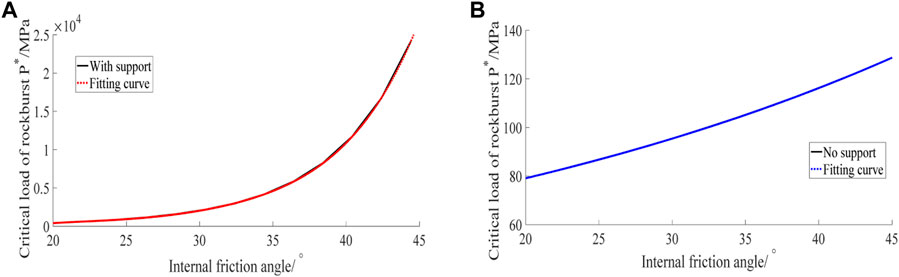
FIGURE 5. Internal friction angle–critical load curve. (A) Internal friction angle–critical load (with support). (B) Internal friction angle–critical load (no support).
It can be seen from Figure 5 that under the condition of support stress of 5 MPa, the critical load of rock burst increases with the internal friction angle, and it has experienced three different change trend stages of 20°–30°, 30°–35°, and 35°–40° (Kang et al., 2015). In particular, when the internal friction angle is greater than 35°, the critical load of rock burst increases rapidly with the increase of the internal friction angle (Li and Wu, 2019). Without support, when the internal friction angles are 20° and 40°, the critical rock burst loads are 79.66 and 131.4 MPa. This indicates that the critical load of rock burst increases with the increase of the internal friction angle.
3.5 Effect of the support stress on the critical load
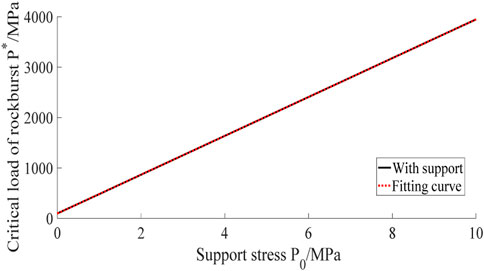
The uniaxial compressive strength of the roadway surrounding rock is 95.6 MPa, the softening modulus is 25 GPa, the elastic modulus is 24.9 GPa, the internal friction angle is 30°, and the roadway support stress is 0–10 MPa. When these parameters are used in Eq. 17, the relationship curve between the roadway support stress and the critical rock burst load of a circular roadway is obtained, as shown in Figure 6.
According to Figure 6, when the support stress is 0 and 10 MPa, the critical loads of the rock burst are 95.41 and 3947 Mpa, respectively. The critical load of a rock burst increases with the increase of support stress, the slope of the curve is 3.9 × 102, approximately, and the critical load of a rock burst is about 400 times higher than the support stress. The fitting curve equation is
3.6 Effect of K on the critical load
According to the analysis provided in Sections 3.1–3.5, under the condition of support, the critical load of a roadway rock burst increases with the increase of the uniaxial compressive strength, softening modulus, and internal friction angle of the surrounding rock and decreases with the increase of elastic modulus of the surrounding rock. Under the condition of no support, the critical rock burst load of the roadway increases with the increase of uniaxial compressive strength, elastic modulus, and internal friction angle of the surrounding rock, and decreases with the decrease of the surrounding rock softening modulus. Under the conditions of support and non-support, the softening modulus and elastic modulus have opposite effects on the critical rock burst load of the roadway. Therefore, to better obtain the influence law of the softening modulus and elastic modulus on the critical load of a roadway rock burst, we define a new index K of rock burst tendency as the ratio of the softening modulus and the elastic modulus:
The uniaxial compressive strength of the roadway surrounding rock is 95.6 MPa, the internal friction angle is 30°, the roadway support stress is 5 MPa, and K is 0.1–10. When these parameters are used in Eqs. 17 and 18, Figure 7A represents the relationship curve between the new index K of impact tendency and the critical load under supporting conditions, and Figure 7B represents the relationship curve between the new index K of impact tendency and the critical load without supporting conditions.
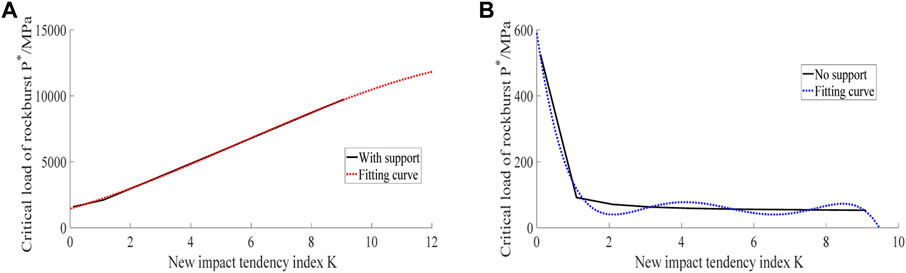
FIGURE 7. K–critical load curve. (A) K–ctical load (with support). (B) K–critical load (no support).
It can be seen from Figure 7 that 1) when the support stress of the roadway is 5 MPa, and the new indexes of impact tendency K are 0.1 and 10, the critical loads of a rock burst are 1627 and 87000 MPa, indicating that the critical load of a rock burst increases with the increase of the new index of impact tendency K. The fitting curve equation is
3.7 Effect of double variables on the critical load of the rock burst
To study the influence of double variables on the critical load P*, consider the conditions when the uniaxial compressive strength σc is 95.6 MPa, the softening modulus λ is 25 GPa, the elastic modulus E is 24.9 GPa, and the internal friction angle φ is 30°. The support stress P0 is 5 MPa. According to Figure 8A, when the softening modulus and uniaxial compressive strength change, and other parameters remain unchanged, the critical load increases with the increase of softening modulus and uniaxial compressive strength. According to Figure 8B, when the elastic modulus and uniaxial compressive strength change, and other parameters remain unchanged, the critical load increases with the decrease of elastic modulus and the increase of uniaxial compressive strength. According to Figure 8C, when the support stress and uniaxial compressive strength change, and other parameters remain unchanged, the critical load increases with the increase of support stress and uniaxial compressive strength. Figure 8D shows that when the elastic modulus and softening modulus change, and other parameters remain unchanged, the critical load increases with the decrease of elastic modulus and the increase of softening modulus. It can be seen from Figure 8E that when the support stress and softening modulus change, and other parameters remain unchanged, the critical load increases with the increase of support stress and softening modulus. According to Figure 8F, when the elastic modulus and internal friction angle change, and other parameters remain unchanged, the critical load increases with the decrease of elastic modulus and the increase of internal friction angle.
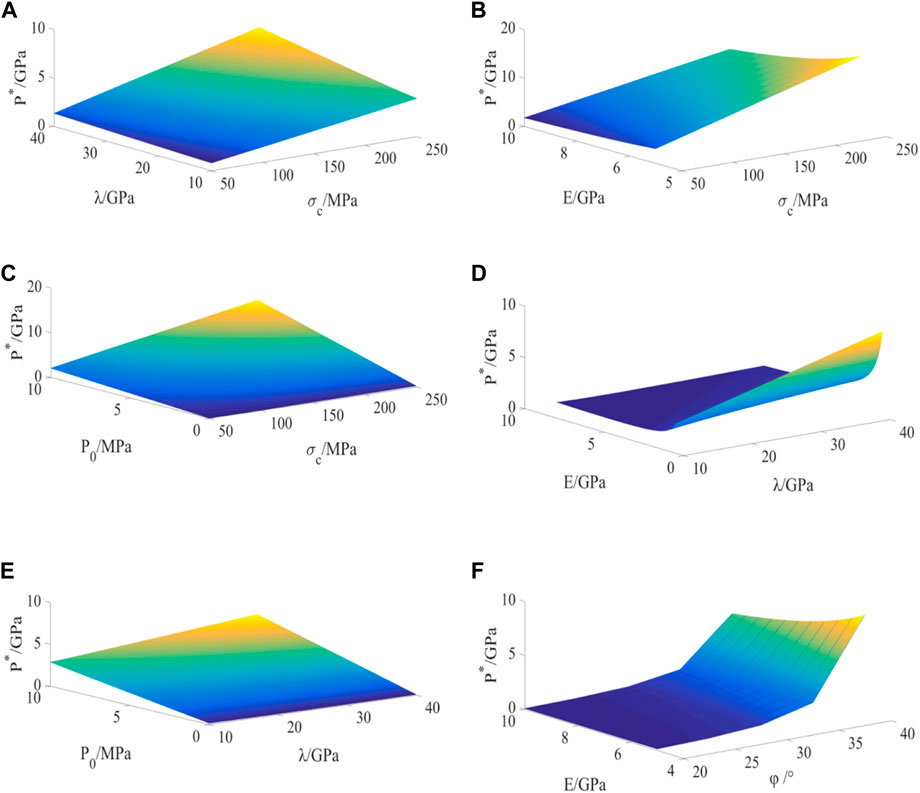
FIGURE 8. Double variables–critical load curves. (A) Uniaxial compressive strength–softening modulus–critical load curve. (B) Uniaxial compressive strength–modulus of elasticity–critical load curve. (C) Uniaxial compressive strength–support stress–critical load curve. (D) Softening modulus–modulus of elasticity–critical load curve. (E) Softening modulus–support stress–critical load curve. (F) Internal friction angle–modulus of elasticity–critical load curve.
4 Numerical solution of the uniaxial compressive strength, elastic modulus, and internal friction angle
According to the results of the analysis of the factors affecting the critical load of the rock burst in Section 3, the uniaxial compressive strength, elastic modulus, and internal friction angle are selected for numerical simulation. Using Flac3D software, a circular roadway model is established that is 400 m underground, 12 m long, and has a radius of 3 m, as shown in Figure 9.
The constitutive model adopts the Mohr–Coulomb model, which requires six parameters: bulk modulus, shear modulus, internal friction angle, dilatancy angle, cohesion, and tensile strength. The bulk modulus and shear modulus are obtained from the elastic modulus and Poisson’s ratio, as shown in Eq. 19.
In the formula, K* is the bulk modulus, G is the shear modulus, and v is Poisson’s ratio.
According to the Griffith strength criterion, the tensile strength of rock is generally one-tenth of the compressive strength. For soil or rock, the dilatancy angle ranges from 0° to 20°. In the Flac3D model, the default value is 0°. The outside of the circular roadway is homogeneous surrounding rock. The rock mass test parameters are as follows: volume weight = 25 KN/M3, cohesion = 0.8 Mpa, internal friction angle = 30°, Poisson’s ratio = 0.3, and elastic modulus = 24.9 GPa.
4.1 Numerical solution of the uniaxial compressive strength
When the uniaxial compressive strength changes and other parameters remain unchanged, Figure 10 is obtained. Figure 10A represents the vertical displacement curve of a circular roadway when the uniaxial compressive strength is 36.7 MPa, and (B) represents the vertical displacement curve of a circular roadway when the uniaxial compressive strength is 231.7 MPa. It can be concluded that the vertical displacement increases with the increase of the load step. When the load step is the same, the vertical displacement value is small when the uniaxial compressive strength is large.
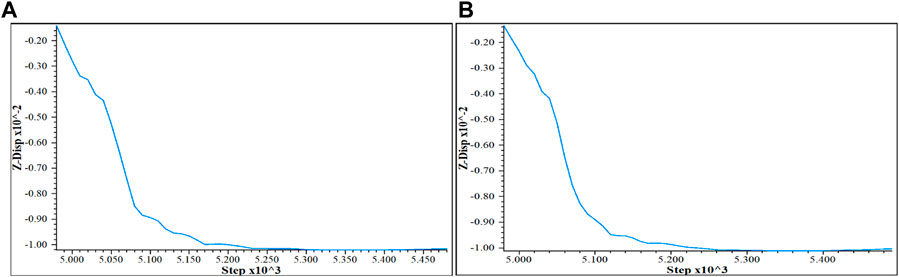
FIGURE 10. Vertical displacement curve when the uniaxial compressive strength changes. (A) Vertical displacement curve when the uniaxial compressive strength is 36.7 MPa (with support) (B) Vertical displacement curve when the uniaxial compressive strength is 231.7 MPa (with support).
4.2 Numerical solution of the elastic modulus
When the elastic modulus changes and other parameters remain unchanged, Figure 11 is obtained. Figure 11A represents the vertical displacement curve of the circular roadway when the elastic modulus is 5.2 GPa, and (B) represents the vertical displacement curve of the circular roadway when the elastic modulus is 79.8 GPa. It can be concluded that the vertical displacement increases with the increase of the load step. When the load step is the same, the vertical displacement value is small when the elastic modulus is small.
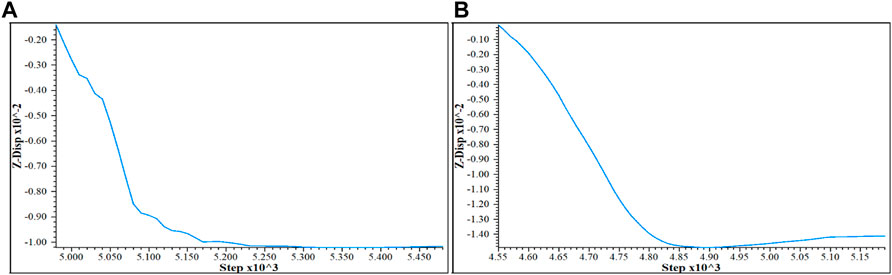
FIGURE 11. Vertical displacement curve when the elastic modulus changes. (A) Vertical displacement curve when the elastic modulus is 5.2 GPa (with support). (B) Vertical displacement curve when the elastic modulus is 79.8 GPa (with support).
4.3 Numerical solution of the internal friction angle
When the internal friction angle changes and other parameters remain unchanged, Figure 12 is obtained. Figure 12A represents the vertical displacement curve of the circular roadway when the internal friction angle is 20°, and (B) represents the vertical displacement curve of the circular roadway when the internal friction angle is 40°. It can be concluded that when the vertical displacement is the same, the load step is less when the internal friction angle is small, indicating that the displacement changes faster when the internal friction angle is small.
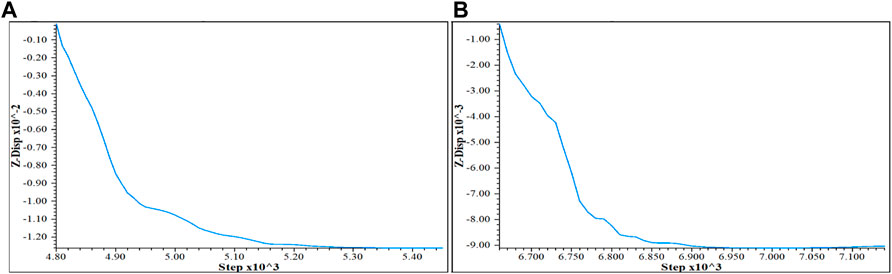
FIGURE 12. Vertical displacement curve when the internal friction angle changes. (A) Vertical displacement curve when the internal friction angle is 20° (with support). (B) Vertical displacement curve when the internal friction angle is 40° (with support).
5 Conclusion
(1) A mechanical model of a circular “roadway rock-support” system considering damage is established. The critical load formula of the rock burst in the roadway with and without supporting conditions is derived according to the instability theory of rock burst disturbance response.
(2) Under the conditions of support and no support, the critical rock burst load of the roadway increases with the increase of uniaxial compressive strength. When the uniaxial compressive strength is the same, the critical load of the rock burst with support is 20 times larger than that without support. The critical load of rock burst increases with the increase of support stress, which is about 400 times larger than the support stress. The stability of the support and the roadway surrounding the rock system can be greatly improved by increasing the support strength.
(3) Under the condition of support, the critical load of rock burst increases with the internal friction angle. In particular, when the internal friction angle is greater than 35°, the critical load of rock burst increases rapidly with the increase of the internal friction angle. When the internal friction angle is the same, the critical load of the rock burst with support is much larger than that without support, and the difference is nearly three orders of magnitude.
(4) Under the support condition of the roadway, the critical load of rock burst increases with the increase of the softening modulus. The critical load of rock burst experienced three stages of rapid decrease, slow decrease, and basic stability with the increased elastic modulus. When the values of the softening modulus and the elastic modulus are the same, the critical load with support is much larger than that without support.
(5) A new index of impact tendency K is defined as the ratio of the softening modulus to the elastic modulus. When the new index K of impact tendency is the same, the critical load of the rock burst with support is much larger than that without support. The conclusions have certain limitations due to the complex rock burst mechanism. The assumption of strain equivalence, isotropic, and homogeneity should be continuously reexamined in subsequent research into establishing a circular section roadway model.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors without undue reservation.
Author contributions
Conceptualization, ZT and WZ. Methodology, ZT. Software, WZ and XC. Validation, KG. Formal analysis, WZ. Investigation, KG. Resources, KG. Data curation, XC. Writing—original draft preparation, WZ. Writing—review and editing, ZT. Visualization, XC. Supervision, ZT. Project administration, ZT. Funding acquisition, ZT.
Funding
This study was supported by the National Natural Science Foundation of China (51804152, 52174116), the Liaoning Revitalization Talents Program (XLYC1907168), and the Discipline Innovation Team of Liaoning Technical University (LNTU20TD08).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Chen, H. X., Wang, M. Y., and Li, J. (2019). Characteristic energy factor of deformation and failure of deep rock mass and its application. Explos. Shock 39 (08), 41–51.
Chen, H. X., Wang, M. Y., Qi, C. Z., and Li, J. (2020). Energy adjustment mechanism and balance relationship of surrounding rock in deep circular roadway. Chin. J. Geotechnical Eng. 42 (10), 1849–1857.
Ding, X., Xiao, X. C., Pan, Y. S., Lu, X. F., and Wu, D. (2020). Mechanical analysis of constitutive relationship and impact tendency index of coal. J. Undergr. Space Eng. 16 (05), 1371–1382.
Dong, L. J., Chen, Y. C., Sun, D. Y., and Zhang, Y. H. (2021). Implications for rock instability precursors and principal stress direction from rock acoustic experiments. Int. J. Min. Sci. Technol. 31 (5), 789–798. doi:10.1016/j.ijmst.2021.06.006
Dong, L. J., Hu, Q. C., Tong, X. J., and Liu, Y. F. (2020). Velocity-free MS/AE source location method for three-dimensional hole-containing structures. Engineering 6 (7), 827–834. doi:10.1016/j.eng.2019.12.016
Dong, L. J., and Luo, Q. M. (2022). Investigations and new insights on earthquake mechanics from fault slip experiments. Earth-Science Rev. 228, 104019. doi:10.1016/j.earscirev.2022.104019
Dong, L. J., Tong, X. J., and Ma, J. (2020). Quantitative investigation of tomographic effects in abnormal regions of complex structures. Engineering 7 (7), 1011–1022. doi:10.1016/j.eng.2020.06.021
Dong, L. J., Zou, W., Li, X. B., Shu, W. W., and Wang, Z. W. (2019). Collaborative localization method using analytical and iterative solutions for microseismic/acoustic emission sources in the rockmass structure for underground mining. Eng. Fract. Mech. 210, 95–112. doi:10.1016/j.engfracmech.2018.01.032
Guo, X. F., Ma, N. J., and Zhao, X. D. (2016). General shapes and criterion for surrounding rock mass plastic zone of round roadway. J. China Coal Soc. 41 (8), 1871–1877.
Guo, X. F., Zhao, Z. Q., Gao, X., Wu, X. Y., and Ma, N. J. (2018). Analytical solutions for characteristic radii of circular roadway surrounding rock plastic zone and their application. Int. J. Min. Sci. Technol. 29, 263–272. doi:10.1016/j.ijmst.2018.10.002
Guo, Y. H., Jiang, F. X., and Zhang, C. G. (2011). Analytical solution of critical rockburst in circular roadway under high geostress. Eng. Mech. 28 (02), 118–122.
Huang, Q. X., and Gao, Z. N. (2001). Damage and fracture mechanics model of rock burst in roadway. J. Coal Sci. (02), 156–159.
Kang, H. P., Fan, M. J., and Gao, F. Q. (2015). Deformation and support of rock roadway at depth more than 1000 meters. Chin. J. Rock Mech. Eng. 34 (11), 2227–2241.
Li, G., Li, N., Bai, Y., and Yang, M. (2022). An new elastic–plastic analytical solution of circular tunnel under non-axisymmetric conditions. Sci. Rep. 12, 4367. doi:10.1038/s41598-022-08353-3
Li, P., and Wu, P. P. (2019). Optimization of support parameters for deep roadway surrounding rock control. Coal Technol. 38 (02), 40–42.
Li, Z. H., Bao, S. Y., and Liang, Y. (2018). Study on influencing factors of rock burst in rectangular roadway. Coal Sci. Technol. 46 (10), 51–57.
Liu, X., Liang, Z., Zhang, Y., Liang, P., and Tian, B. (2018). Experimental study on the monitoring of rockburst in tunnels under dry and saturated conditions using AE and infrared monitoring. Tunn. Undergr. Space Technol. 82 (12), 517–528. doi:10.1016/j.tust.2018.08.011
Liu, X., Wu, L., Zhang, Y., Liang, Z., Yao, X., and Liang, P. (2019). Frequency properties of acoustic emissions from the dry and saturated rock. Environ. Earth Sci. 8 (3), 67. doi:10.1007/s12665-019-8058-x
Liu, X., Wu, L., Zhang, Y., and Mao, W. (2021). Localized enhancement of infrared radiation temperature of rock compressively sheared to fracturing sliding: Features and significance. Front. earth Sci. 9, 756369. doi:10.3389/feart.2021.756369
Liu, X., Wu, L., Zhang, Y., Wang, S., and Wu, X. (2020). The characteristics of crack existence and development during rock shear fracturing evolution. Bull. Eng. Geol. Environ. 80 (2), 1671–1682. doi:10.1007/s10064-020-01997-3
Ma, Q., Zhao, J. H., Wei, X. Y., and Zhu, Q. (2011). Stress field analysis of surrounding rock of circular tunnel based on damage theory. J. Build. Sci. Eng. 28 (02), 84–94.
Meng, Q. B., Han, L. J., Qiao, W. G., Lin, D. G., and Fan, J. D. (2014). Support technology for mine roadways in extreme weakly cemented strata and its application. Int. J. Min. Sci. Technol. 24 (02), 157–164. doi:10.1016/j.ijmst.2014.01.003
Pan, Y. S., and Dai, L. P. (2021). Theoretical formula of rock burst in coal mines. J. China Coal Soc. 46 (3), 789–799.
Pan, Y. S. (1999). Study on the occurrence and failure process of rock burst. Beijing, China: Tsinghua University.
Pan, Y. s., and Wang, Z. Q. (2004). Research method of work and energy increment-catastrophe theory for dynamic instability of rock mas. J. Rock Mech. Eng. (09), 1433–1438.
Pan, Y. s., and Wang, Z. Q. (2004). Study on load-displacement relationship of surrounding rock of circular chamber with nonlinear strain softening. Rock Soil Mech. (10), 1515–1521.
Pan, Y. s., Wang, Z. Q., and Wu, M. Y. (2007). Analysis and calculation of energy release and deviatoric stress-strain energy generation of surrounding rock during roadway excavation. Rock Soil Mech. (04), 663–669.
Pan, Y. S., Xiao, Y. H., and Li, Z. H. (2014). Research and application of rock-burst mine roadway support theory. J. Coal Sci. 39 (2), 222–228.
Pan, Y. s., Zhang, Y., and Yu, G. M. (2006). Analysis of rockburst mechanism and catastrophe theory of circular chamber. Appl. Math. Mech. (06), 741–749.
Wang, Z. Q., Wu, C., Shi, L., Su, Z. H., Wang, P., and Huang, X. (2019). Analysis of stress and plastic zone of surrounding rock of circular roadway under biaxial unequal pressure based on complex variable theory. J. Coal Sci. 44 (S2), 419–429.
Xiao, X. C., Jin, C., Pan, Y. S., Ding, X., Zhao, X., and Xu, J. (2016). Experimental study on acoustic emission characteristics and burst proneness of combined coal and rock. Chin. J. Saf. Sci. 26 (04), 102–107.
Xiao, X. C., Jin, C., and Zhao, X. (2017). Experimental study on the charge criterion of coal-rock bodies burst tendency[J]. Rock Soil Mech. 38 (6), 1620–1628.
Yin, W. L., Pan, Y. S., and Li, Z. H. (2018). Study on critical condition of rockburst in circular roadway considering deterioration of strength parameters in plastic zone. J. Coal Sci. 43 (02), 348–355. doi:10.13225/J.CNKI.Jccs.2017.4159
Yin, W. L., Pan, Y. S., and Li, Z. H. (2018). Study on the mechanism of rock burst in rectangular section roadway. Chin. J. Geotechnical Eng. 40 (06), 1135–1142.
Keywords: “roadway rock-support” system, anti-impact performance, roadway support strength, rock burst, theoretical research
Citation: Tang Z, Zuo W, Gao K and Cai X (2023) Factors influencing the anti-impact performance of a “roadway rock support” system. Front. Earth Sci. 11:1117140. doi: 10.3389/feart.2023.1117140
Received: 06 December 2022; Accepted: 17 February 2023;
Published: 02 March 2023.
Edited by:
Chao Liu, China University of Mining and Technology, ChinaReviewed by:
Liu Zhongzhong, China University of Mining and Technology, ChinaBeichen Yu, Chongqing University, China
Copyright © 2023 Tang, Zuo, Gao and Cai. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhi Tang, dGFuZ3poaTAxMjdAMTYzLmNvbQ==
 Zhi Tang1*
Zhi Tang1* Wenbo Zuo
Wenbo Zuo