Study on rock-breaking efficiency evaluation of TBM disc cutters based on Rostami prediction equations

As the main cutting tool of Tunnel Boring Machine (TBM) for rock-breaking, the rock-breaking efficiency of TBM disc cutters directly affects the TBM’s boring speed, which in turn affects the overall progress of the tunnelling project. Therefore, a simple and accurate evaluation method of the rock-breaking efficiency of TBM disc cutters is an essential prerequisite to improve the rock-breaking performance of TBM. In this paper, the classical force prediction equations of disc cutters were summarized and the applicability of each equation for the constant cross-section disc cutters was analyzed. The calculation equation of the specific energy per ring of TBM rock-breaking was derived based on the Rostami prediction equations and the specific energy theory for disc cutter rock-breaking. The specific energy per ring equation was verified through a practical engineering case. The results show that the maximum relative error of the effective thrust force and the effective torque of the cutter head based on the Rostami force prediction equations is 9.8%. The relative error of the specific energy per ring is 8.0%, which indicates that the prediction of the specific energy per ring equation can accurately reflect the rock-breaking efficiency of disc cutters. The derived equation of the specific energy per ring can not only simplify the rock-breaking efficiency evaluation of TBM disc cutters, but also serve as a valuable reference for practical engineering projects.

1 Introduction

With the expansion of the scale of urban subway construction, the shield Tunnel Boring Machine (TBM) tunnelling method has become the primary construction method for urban underground railway tunnels, owing to its good adaptability, low environmental interference, high efficiency and safety (Lu et al., 2004; Yagiz, 2008). For TBM, the disc cutter is the main cutting tool for rock breaking. The working principle of the disc cutter involves the combined effect of the hydraulic propulsion and rotary system on the excavation surface to break the rock (Hu et al., 2022). Previous studies have shown that the load and impact are directly applied on the disc cutter and the tunneling efficiency and reliability of TBM is closely related to its rock-breaking condition (Zhang et al., 2021; Li et al., 2022). Therefore, the mechanical condition of the disc cutter is the critical factor for the design and manufacture of TBM. However, due to the large impact and the harsh working environment that act on the disc cutter, abnormal failures such as partial grinding and breaking frequently appear and the cutting tools need to be constantly replaced during tunnel construction, leading to low overall boring efficiency and high construction costs for TBM tunnelling (Sun et al., 2019). Hence, it is of great significance to understand the rock-breaking mechanism of disc cutters, develop the accurate load prediction model, and make the rock-breaking efficiency evaluation of disc cutters simple and efficient.

Since the 1960s, as rapid development of TBM technology, a lot of research work has been carried out about the rock-breaking theory of disc cutters. At the present stage, the mainstream theories can be summarized into three categories: the shear rock-breaking theory, the tension rock-breaking theory, and the comprehensive rock-breaking theory (Zhang et al., 2022). The Colorado School of Mines (CSM) proposed the shear rock-breaking theory in 1977–1979 (Ozdemir and Wang, 1979). The CSM rock-breaking model was summarized based on the linear grooving test of the V-shaped disc cutter. In the 1980s, through theoretical analysis and experimental research on the rock-breaking model of disc cutters, the rock-breaking laboratory of the Northeast University of Technology put forward the tension rock-breaking theory (Jin, 1981; Jin et al., 1981). With new advances in research, some researchers have proposed that the rock-breaking process by disc cutters is a complex process with multiple forms of damage. Zhang et al. (Zhang et al., 1996; Zhang, 2008) carried out laboratory tests using disc cutters and proposed that the rock-breaking process of disc cutters is mainly subjected to shear load combined with extrusion and tension. Through observing the friction marks on the cross-section of the slag sample of rock-breaking test, Mao et al. (Mao and Liu, 1988) pointed out that the cracks caused by the rock-breaking process of disc cutter are the result of the combined effect of extrusion, tension, and shear load. At present, although many researchers have conducted in-depth studies on the rock-breaking mechanism and the force prediction model of disc cutters, the assumptions and applicability of the prediction models are quite different. Therefore, for the varying of actual engineering situations, it is still necessary to compare and analyze the applicability of these models.

In this paper, the existing classical force prediction models of disc cutters were summarized. The applicability of the Rostami force prediction equations for the constant cross-section disc cutters was then analyzed. Based on the Rostami force prediction equations, the calculation equation of the specific energy per ring of TBM rock-breaking was derived which quantifies the specific energy required for one ring excavation distance. The derived equation offers a simplified approach to evaluate the rock-breaking efficiency of TBM disc cutters. This approach eliminates the need to consider rock slag volume and the effect of surrounding cracks on rock-breaking energy. Instead, the rock-breaking volume per ring and the rock-breaking energy consumption per ring was used to calculate the rock-breaking specific energy of TBM, thus making the rock-breaking efficiency evaluation more simple and more efficient. Finally, the applicability and accuracy of the specific energy per ring equation were evaluated and verified based on the actual TBM tunneling parameters of a construction section of the Qingdao metro, which can provide theoretical support and reference for related projects.

2 TBM disc cutters

The rolling cutter is the main cutting tool for TBM rock-breaking. According to the appearance forms of the rolling cutter, it can be classified into disc cutter and toothed cutter. According to the cutter ring structure, the disc cutter can be classified into conventional disc cutter and inserted tooth disc cutter. The toothed cutter is often used in soft rock, as shown in Figures 1B, D. According to the number of blades of the disc cutter, it can be classified into single-blade disc cutter, double-blade disc cutter, and multi-blade disc cutter, as shown in Figures 1A, B, D. Single-blade disc cutter and double-blade disc cutter are commonly used in tunnel construction in Qingdao.

FIGURE 1

FIGURE 1. Common types of the TBM rolling cutter (A) single-blade disc cutter (B) inserted tooth disc cutter (C) double-blade disc cutter (D) toothed cutter (E) multi-blade disc cutter.

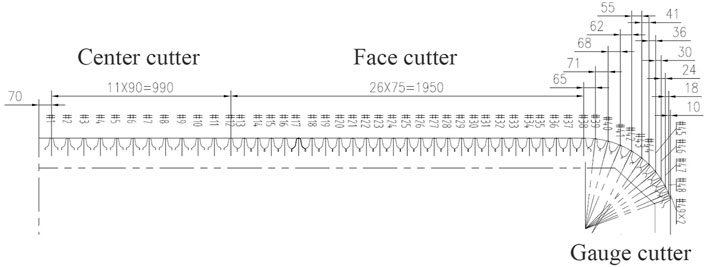
According to the installation position, disc cutter can be classified into center cutter, face cutter, and gauge cutter, as shown in Figure 2. In general, the center cutter of TBM mostly adopts double-blade cutter, which has relatively small radius of rotation and complex force state. The face cutter mostly adopts the single-blade cutter, which is the main cutting tool for TBM tunneling. The gauge cutter adopts the single-blade cutter with increasing installation angle from the inside to the outside to produce rounding arc transition. The outermost edge cutters ensure the excavation diameter of the tunnel.

FIGURE 2

FIGURE 2. Schematic diagram of installation positions of disc cutters.

3 Force prediction theory for disc cutter rock-breaking

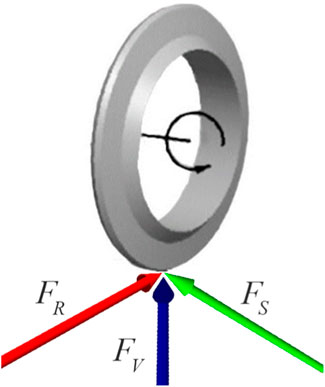
In the process of rock-breaking, the disc cutter ring intrudes into the rock, producing a normal destructive effect on the rock. The disc cutter rotates around the cutter shaft and revolves around the center of the cutter head, producing a tangential destructive effect on the rock. The destruction of the disc cutter to the rock is the interaction between the disc cutter ring and the rock mass of tunnel face. As the disc cutter is constantly loaded by the thrust cylinder as well as the main drive system, its resultant motion includes constant intrusion, revolution, and rotation motion. The rock mass of the tunnel face is constantly deformed and destroyed under the load of the disc cutter, which eventually leads to the failure and detachment of the rock mass from the tunnel face. As shown in Figure 3, the disc cutter is mainly subjected to a vertical force ($F_V$), a tangential force ($F_R$), and a lateral force ($F_S$) during the rock-breaking process.

FIGURE 3

FIGURE 3. Force diagram of the disc cutter during rock-breaking process.

3.1 Rock-breaking mechanism of disc cutters

The rock-breaking process of the disc cutter is influenced by many factors, such as the tunneling parameters of the TBM, the geometric parameters and arrangement of the cutter, as well as the macro-mechanical parameters and stress state of the rock mass at the tunnel face and the occurrence state of the joint fissure, etc. Due to the complexity of the rock-breaking process, there is no explicit and unified theory for rock-breaking process of the disc cutter. However, after years of exploration, three classical theories have been developed: shear rock-breaking theory, tension rock-breaking theory, and comprehensive rock-breaking theory.

The theory of shear rock-breaking assumes that the rock mass at the blade position of the disc cutter undergoes a stress concentration under the influence of vertical forces. Once the stress concentration reaches its limit, the rock mass is pulverized into fine particles, forming a compacted core subject to volumetric compression. This core, also called a dense core, plays a significant role in rock fragmentation during tunnel boring machine excavation.

According to the shear rock-breaking theory, a dense core is created when the rock mass at the blade of disc cutter is loaded by the vertical force. Owing to the inclined angle of the cutter edge, the rock mass on both sides of the dense core is broken as a result of shear failure under the cutter lateral force. The tension rock-breaking theory holds that the rock mass on both sides of the dense core is broken due to tensile failure when the disc cutter intrudes into the rock. The comprehensive rock-breaking theory argues that the dense core is subjected to a combination of extrusion, tension, and shear force. The cracks developed around the dense core are mainly from tension failure and the rest are from shear failure. The rock slag is generated by the combined effect of these two failure modes.

3.2 Rock-breaking theories of disc cutters

As shown in Figures 4A, B, C, the cross-sectional form of the disc cutter ring mainly includes V-shaped section, wedge section, and constant cross-section. Compared to other cross-section disc cutters which tend to become dull and less efficient due to wear and tear, the constant cross-section disc cutters can maintain their dimensions consistently despite wear and tear. Therefore, the constant cross-section disc cutters are generally preferred for rock-breaking and widely used in practical tunnel construction. The geometric parameters of the disc cutter are mainly the diameter ($R$) or radius ($r$), the half-angle of the cutter edge ($\alpha$), the radius of the cutter nose ($\gamma$), etc. A series of force prediction equations of disc cutter have been proposed based on theoretical analysis, field tests, laboratory tests, etc. The classical force prediction equations of disc cutter for rock-breaking are summarized below.

FIGURE 4

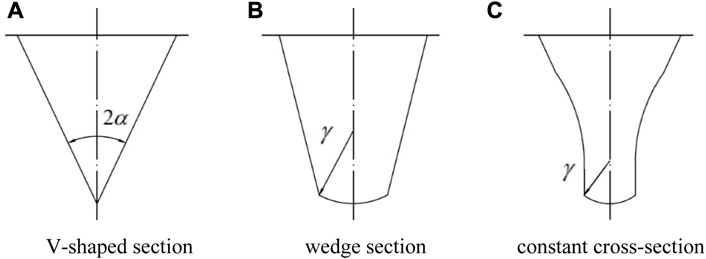
FIGURE 4. The cross-sectional forms of the disc cutter ring (A) V-shaped section (B) wedge section (C) constant cross-section.

Evans prediction equation: Through theoretical studies, Evans (Evans and Pomeroy, 1966) analyzed the vertical force loaded on the disc cutter in the rock-breaking process. Under a certain degree of penetration, it is considered that the vertical thrust of the disc cutter is proportional to the uniaxial compressive rock strength (${\sigma }_{\mathrm{c}}$) and the projected area ($A_p$) between the cutter ring and the rock surface. The projected area is the half of the area enclosed by two parabolas. However, it has been proved by experiments that the vertical thrust calculated by the Evans prediction equation is smaller than the actual vertical thrust of rock-breaking.

$F_V={\sigma }_c{A}_p=\frac{4}{3}{\sigma }_{c}p\sqrt{r^2-{\left(r-p\right)}^2}\tan \alpha (1)$

Where: $r$ = Radius of cutter

$p$ = Penetration per revolution

$\alpha$ = Half-angle of the cutting edge

(2) Tosaburo Akiyama prediction equations: Tosaburo Akiyama (Akiyama, 1970) developed the Evans prediction equation and proposed two equations for calculating the lateral force of the disc cutter:

  ① Based on the extrusion rock-breaking theory:

$F_S=\frac{{\sigma }_c}{2}{R}^2\left(\varphi -\sin \varphi \cos \varphi \right)(2)$

  ② Based on the shear rock-breaking theory:

$F_S=R\varphi \delta S{\sigma }_c(3)$

Where: $S$ = Cutter space

$\delta$ = Rock-breaking coefficient ($\tau /{\sigma }_c$)

$\tau$ = Unconfined shear strength of rock

$\varphi$ = Relative Angle of Hob and Rock ($\sqrt{\left(3\sigma S/R\right)}$)

(3) Roxborough prediction equations: Roxborough and Phillips (1975) improved the calculation method of the projected area between the cutter ring and the rock surface in the Evans prediction equation. They regarded the contact surface between the cutter and the rock as a rectangle, and deduced the calculation equations of the vertical force, the tangential force and the lateral force of the V-shaped disc cutter:

$F_V=4{\alpha }_{c}p\tan \alpha \sqrt{2r{p}^3-p^4}(4)$

$F_R=4{\sigma }_c{p}^2\tan \alpha (5)$

$F_S=\frac{F_V}{2}\cot \alpha (6)$

CSM prediction equations: Based on the shear rock-breaking theory and the tension rock-breaking theory, Ozdemir et al. [8] from Colorado School of Mines (CSM) conducted indentation experiments on different types of rocks by disc cutter. They regarded the contact surface between the disc cutter and the rock as a triangle, and derived the calculation equations of the vertical force and the tangential force of the V-shaped disc cutter:

$F_V=\sqrt{2r}{p}^{1.5}\left[\frac{4}{3}{\sigma }_c+2\tau \left(\frac{S}{p}-2\tan \alpha \right)\right]\tan \alpha (7)$

$F_R=\left[{\sigma }_c+p^2+\frac{4\tau \varphi \left(S-2p\tan \alpha \right)}{r\left(\varphi -\sin \varphi ·\cos \varphi \right)}\right]\tan \alpha (8)$

Where: $\varphi$ = Contact angle between cutter and rock ($\arccos \left(r-p/r\right)$)

$\tau$ = Shear strength of rock

Rostami prediction equations: Rostami and Ozdemir (1993) from Colorado School of Mines (CSM) developed the CSM model for the constant cross-section disc cutter, and deduced the calculation equation of the resultant force of the disc cutter in the rock-breaking process:

$F=\frac{P\varphi TR}{1+\psi }(9)$

Where: $P$ = Compressive stress in the breaking zone

$\psi$ = Pressure distribution coefficient of the cutter edge

$P=K{\left(\frac{S{\sigma }_c^2{\sigma }_t}{\varphi \sqrt{rT}}\right)}^{\left(1/3\right)}(10)$

Where: $K$ = A constant, approximately equal to 2.12

$T$ = Edge width of the disc cutter

The calculation equations of the vertical force and the tangential force can be obtained by decomposing Eq.10:

$F_V=K\frac{r\varphi T}{1+\psi }{\left(\frac{S{\sigma }_c^2{\sigma }_t}{\varphi \sqrt{rT}}\right)}^{\left(1/3\right)}\cos \frac{\varphi }{2}(11)$

$F_R=K\frac{r\varphi T}{1+\psi }{\left(\frac{S{\sigma }_c^2{\sigma }_t}{\varphi \sqrt{rT}}\right)}^{\left(1/3\right)}\sin \frac{\varphi }{2}(12)$

(6) Prediction equations of the Northeast University of Technology: Based on the Evans prediction equation, Jin et al. [9] from the Northeast University of Technology proposed a powder nucleus-splitting model for calculating the rock-breaking force of disc cutters. They regarded that the vertical force of disc cutter rock-breaking is not constant, and there is a leap phenomenon:

$F_v=\frac{4}{3}{k}_d{\sigma }_c+2p\tan \alpha \sqrt{4rp-p^2}(13)$

$F_R=\epsilon k_d{\sigma }_c{p}^2\tan \alpha (14)$

Where: $k_d$ = Rolling coefficient, normally 0.4–0.7

$\epsilon$ = Reduction coefficient, 2.0–2.5 for smooth rocks, 0.8 for rough rocks.

3.3 Evaluation of disc cutter force prediction theories

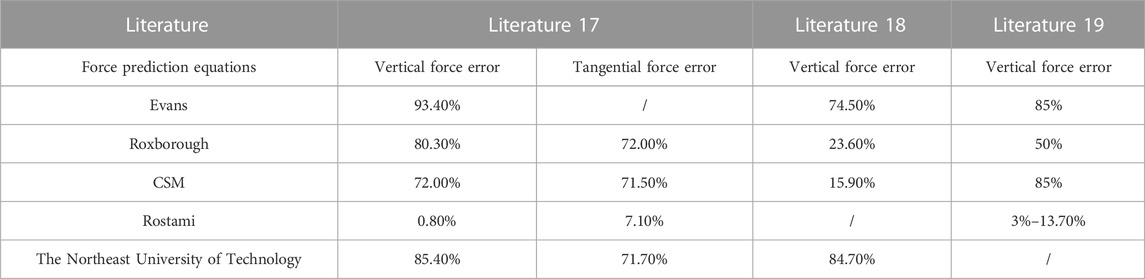
Since the above force prediction theories of disc cutter (summarized in Section 3.2) were based on different experimental and theoretical methods, a comparative evaluation of their predicted values is required. Cao et al. (2018), Wu et al. (2010), and Liu, (2015) analyzed the predicted force values of the constant cross-section disc cutter based on the actual TBM tunneling parameters. The relative errors between the calculated and the measured values are listed in Table 1.

TABLE 1

TABLE 1. The relative error of the disc cutter force prediction equations.

As shown in Table 1, the relative errors of rock-breaking force calculated by the Rostami prediction equations are between 0.8% and 13.7%, which are the minimal among all summarized equations. Therefore, in this study, we choose the Rostami prediction equations to calculate the force of the constant cross-section disc cutters.

4 Derivation of the rock-breaking specific energy per ring equation

In the process of TBM tunneling, breaking the largest volume of rock with the minimal energy consumption, i.e., improving the rock-breaking efficiency of TBM is an important goal of designing cutter head and cutting tool. In 1936, Teale, (1965) proposed the concept of rock-breaking specific energy ($SE$), which is defined as the energy consumed by disc cutters to break rock per unit volume and can be used to evaluate the rock-breaking efficiency of cutters. The smaller the rock-breaking specific energy of the disc cutter is, the higher the rock-breaking efficiency is. The equation of $SE$ is:

$SE=\frac{E}{V}=\frac{E_V+E_R}{V}=\frac{\sum F_V\cdot p+\sum F_{R}l}{V}(15)$

Where: $E$ = Total energies of rock-breaking

$V$ = Total volume of rock-breaking

$E_V$ = Vertical rock-breaking energy

$E_R$ = Tangential rock-breaking energy

p = Vertical cutting stroke of the disc cutter

$l$ = Tangential cutting stroke of the disc cutter

How to calculate reasonably the volume of rock-breaking is a major difficulty in the application of the above rock-breaking specific energy equation. The main reason is that the rock slag generated in the rock-breaking process is irregular. It is worth noting that as the rock slag is generated during rock-breaking, there will be initiation of lateral cracks and vertical cracks in the rock which will also consume the rock-breaking energy. Therefore, considering only the volume of rock slag is not enough to reflect the effect of the rock-breaking energy on the rock. The cracks developed in the rock mass during rock-breaking are shown in Figure 5.

FIGURE 5

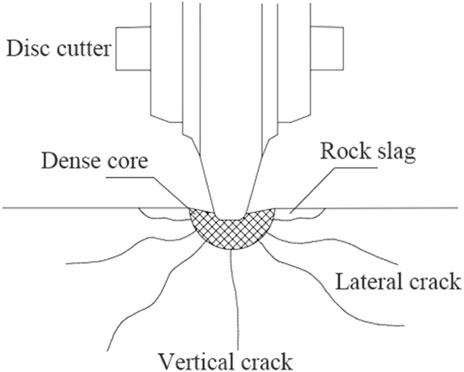
FIGURE 5. Schematic diagram of cracks developed in the rock mass during the rock-breaking process of disc cutter.

According to the actual TBM operation condition, the stiffness of the cutter is very large and its deformation is negligible. The normal displacement of each disc cutter after one rotation is equal, so there is no influence of the arc-shaped arrangement of the gauge cutters on the rock-breaking volume per ring of the TBM. In addition, since the abrasion loss of the gauge cutters is very small for one ring excavation distance, the excavation diameter of the TBM remains constant and the rock-breaking volume per ring can be assumed unchanged.

If the TBM tunneling parameters and the physical and mechanical properties of the rock remain constant, the crack distribution per ring of the tunnel face can be regarded as unchanged. Therefore, the energy consumed by the cracks is the same for each tunnelling ring. In this case, the rock-breaking volume per ring and the rock-breaking energy consumption per ring can be used to calculate the rock-breaking specific energy of TBM. Under these assumptions, the specific energy per ring can be derived which quantifies the specific energy required for one ring excavation distance. In addition, the specific energy per ring can be regarded as a critical indicator that reflects the overall energy consumption and the associated costs of the excavation process.

According to the rock-breaking specific energy equation of the disc cutter (Eq. 15), as long as the vertical force and tangential force of the disc cutter are known, the vertical energy consumption and tangential energy consumption of TBM rock-breaking can be obtained. Suppose the effective rock-breaking thrust is F, the total torque is M, the penetration is p, the length of each tunnel ring is L, and the rotation number of disc cutter per tunneling ring is L/h. The vertical energy consumption EV and the tangential energy consumption EV of the disc cutter per ring can be obtained:

$E_V={\displaystyle \sum _{i=1}^n}{F}_{Vi}L=FL(16)$

$E_R=\frac{L}{p}{\displaystyle \sum _{i=1}^n}2\pi R_i{F}_{Ti}=2\pi \frac{L}{p}{\displaystyle \sum _{i=1}^n}{R}_i{F}_{Ti}=\frac{2\pi LM}{p}(17)$

It has been evaluated in Section 2.3 that the Rostami prediction equations have the minimal relative error to calculate the rock-breaking force of constant cross-section disc cutters. Therefore, combining the Rostami prediction equations with the rock-breaking specific energy equation, the rock-breaking specific energy per ring equation can be derived. Substituting the calculation results of the vertical force and tangential force of each disc cutter ($F_{Vi}$, $F_{Ti}$) from the Rostami prediction equations into Eq. 16 and Eq. 17, the prediction equation of the specific energy per ring can be obtained:

$V=L\pi R_{\max }^2(18)$

$S{E}_{ring}=\frac{E_V+E_R}{V}=\frac{FL+2\pi LM{p}^{-1}}{V}=\frac{F+2\pi M{p}^{-1}}{\pi R_{\max }^2}(19)$

According to the structure of Eq. 18 and Eq. 19, it can be seen that the rock-breaking specific energy prediction per ring equation can also be used to calculate the actual rock-breaking specific energy of TBM.

5 Validation of rock-breaking specific energy per ring equation

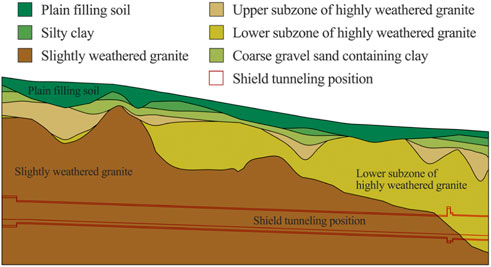
The Shanwu tunnel section of the Qingdao Metro is located in the Shinan District of Qingdao. The tunnel passes under Shandong Road which is a main road of Qingdao. Since there are many high-rise buildings and ultra-high buildings around the tunnel, the environmental risk of the tunnel is high. The tunnel body mainly passes through the slightly weathered granite stratum. The buried depth of the tunnel is 25–35 m, the inner diameter of the tunnel is 6 m, the outer diameter of the segment is 6.7 m, and the excavation diameter of TBM is 6.98 m. The length of each tunnel ring is 1.5 m. The groundwater type is mainly quaternary pore phreatic water and bedrock fissure water. The geological profile of the Shanwu tunnel section is shown in Figure 6.

FIGURE 6

FIGURE 6. Geological profile of the Shanwu tunnel section of the Qingdao Metro.

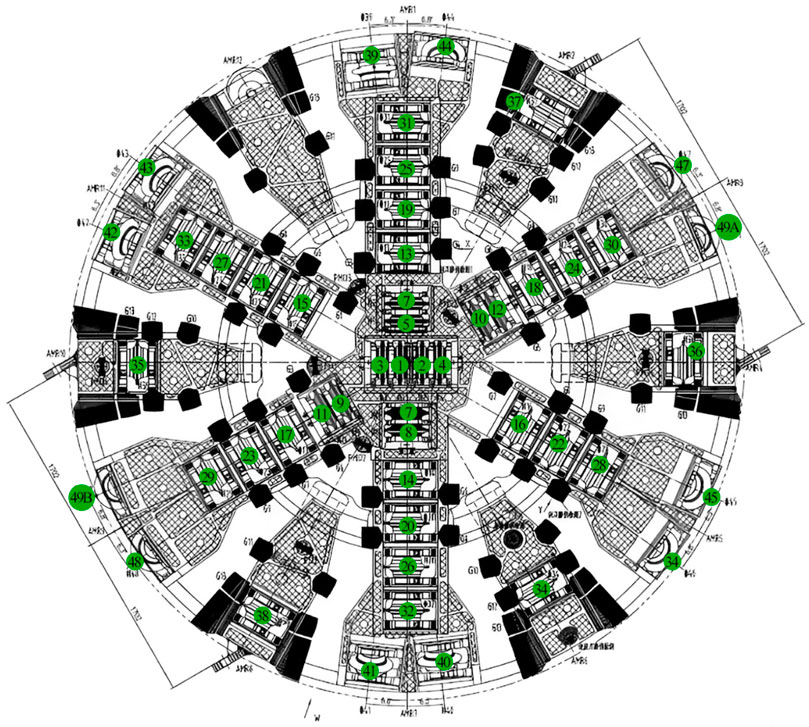
Two dual-mode TBMs were used for tunnel excavation in this section. The dual-mode TMB was produced by the China Railway Engineering Equipment Group Co., Ltd. (CREG), which can be converted between shield mode and single shield TBM mode. The TBM utilizes a composite cutterhead and eighteen-inch disc cutters. The disc cutters mainly include six central cutters, twenty-six face cutters, twelve gauge cutters, and two edge cutters. And the central cutters adopt the double-blade cutter. The schematic diagram of disc cutters arrangement is shown in Figure 7.

FIGURE 7

FIGURE 7. Schematic diagram of disc cutters arrangement.

The cutters of the TBM utilized in this study are all constant cross-section disc cutters. The cutter diameter is 457.22 mm, the edge width is 22 mm, the edge angle is 9.5°, the nose angle is 140°, and the rated load is 250 kN.

5.1 Acquisition of actual TBM tunneling parameters

In the Shanwu tunnel section, the right line tunnel face of the 205th ring is complete, and the joints are less exposed. The photograph of the tunnel face is shown in Figure 8.

FIGURE 8

FIGURE 8. Tunnel surface of the 205th ring in the Shanwu tunnel section.

The M8Z2-TAW-41 exploration hole is located on the right side of the 205th ring. The rock mechanical parameters at the M8Z2-TAW-41 exploration hole were obtained by consulting the geological survey report of the rock mass (as shown in Table 2).

TABLE 2

TABLE 2. Rock mechanical parameters at the M8Z2-TAW-41 exploration hole.

To verify the prediction equations of the cutter force and the specific energy per ring, the gross thrust, penetration, and cutter head torque of TBM from the 201st ring to the 207th ring were collected from the shield construction management information system of the Qingdao Metro. The variations of these three tunneling parameters are shown in Figure 9. It is obtained that the average gross thrust is 9564.7 kN, the average penetration is 6.5 mm/r, and the average cutter head torque is 1598 kNm from the 201st ring to the 207th ring.

FIGURE 9

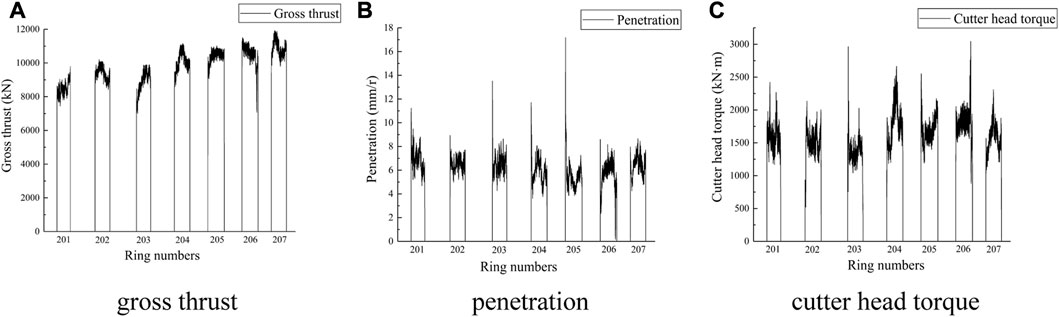
FIGURE 9. The variations of the tunneling parameters from the 201st ring to the 207th ring. (A) gross thrust (B) penetration (C) cutter head torque.

The gross thrust of TBM is mainly composed of the effective rock-breaking thrust ($F_1$), the shield sliding friction ($F_2$), the traction resistance of rear supporting facilities ($F_3$), the component of TBM gravity caused by the tunnel slope ($F_4$), and the friction between the shield tail and the segment ($F_5$) (Guan et al., 2013).

$F_{sum}=F_1+F_2+F_3+F_4+F_5(20)$

The gross thrust during the TBM exit process is not affected by the effective rock-breaking thrust, the slopes of the tunnel are identical, and the gravitational component $F_4$ can be regarded as a constant. By querying the gross thrust data during the TBM exit process, it is obtained that $F_2+F_3+F_4+F_5$ = 2560 kN, so the effective rock-breaking thrust ($F_1$) is calculated to be 7004.7 kN. Substituting the effective rock-breaking thrust and the average cutter head torque into the specific energy per ring equation, the actual specific energy per ring is obtained to be 40.55 MJ/m³.

5.2 Prediction of TBM tunneling parameters

The obtained TBM tunneling data were substituted into the Rostami prediction equations and the specific energy per ring equation. The installation angle of the gauge cutters was ignored in the calculation. To ensure the excavation diameter of the tunnel, two edge cutters with the same radius are set on the outermost side of the cutter head. In the calculation, the penetration value of the edge cutter is set to be half of the average penetration.

Obtained by the Rostami prediction equations, the effective thrust is 7574.5 kN and the cutter head torque is 1726.0 kNm. Substituting the calculated data into the specific energy per ring equation, the specific energy per ring is obtained to be 43.80 MJ/m³.

5.3 Comparation between actual and predicted results

The comparation between actual and predicted results based on the Rostami prediction equations is presented in Table 3. The table shows that the maximum relative error of the effective thrust and the cutter head torque is 9.8%. The relative error of the specific energy per ring is 8.0%. The predicted errors are all less than 10%, so the predicted results can provide a certain reference value for practical engineering projects.

TABLE 3

TABLE 3. Comparation between actual and predicted results.

6 Conclusion

1) In this study, the existing classical force prediction equations for disc cutters and their applicability to constant cross-section disc cutters were analyzed. The Rostami prediction equations were found to be the most suitable force prediction theory due to its minimal relative errors among all summarized equations. Furthermore, based on the Rostami prediction equations and the theory of rock-breaking specific energy, a specific energy per ring equation for TBM was proposed to calculate TBM’s actual and predicted rock-breaking specific energy. This equation simplifies the calculation of rock-breaking volume, as it eliminates the need to consider rock slag volume and the effect of surrounding cracks on rock-breaking energy.

2) The applicability of the specific energy per ring equation was verified based on the actual TBM tunneling parameters in the Shanwu tunnel section of the Qingdao Metro. The verification results show that the maximum relative error of the effective thrust and the cutter head torque calculated by the Rostami prediction equations is 9.8%, and the relative error of the specific energy per ring equation is 8.0%. The predicted errors are all less than 10%, so the proposed specific energy per ring equation can provide a certain reference value for practical engineering projects.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

Conceptualization, GZ, ML, and XW; methodology, GZ and ML; field test, GZ, ZH, and WW; data curation, GZ, ZH, and WW; data analysis, GZ, ZH, and WW; writing—original draft preparation, GZ and ML; writing—review and editing, XW and DW; supervision, XW and DW; project administration, XW and DW; funding acquisition, XW and DW All authors have read and agreed to the published version of the manuscript.

Funding

This research was financially supported by the National Natural Science Foundation of China (grant no: 52108371 and grant no: 52204115), and the Shield/TBM Construction Risk Consultation Project in Qingdao Metro. The research was supported by the Foundation of Research Institute for Deep Underground Science and Engineering (Grant No. XD2021022).

Acknowledgments

Thanks are due to Guangzhao Zhang (Qingdao University of Technology, Qingdao) and Zelin Lu (Qingdao University of Technology, Qingdao) for valuable advice.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akiyama, Tosaburo (1970). A theory of the rock-breaking function of the disc cutter. Komatsu Technol. 16 (3), 56–61. (In Japanese).

Google Scholar

Cao, Jianfeng, Zhang, Na, and Liang, Guohui, (2018). Analysis of thrust and torque prediction method for TBM cutter head. Constr. Mech. 39 (05), 51–54. (In Chinese). doi:10.13311/j.cnki.conmec.2018.05.015

CrossRef Full Text | Google Scholar

Evans, I., and Pomeroy, C. D. (1966). Wedge penetration into coal. Amsterdam, Netherlands: Science Direct. doi:10.1016/B978-1-4831-9633-6.50014-1

CrossRef Full Text | Google Scholar

Guan, Huisheng, Yang, Yandong, and Guo, Lichang, (2013). Calculation on thrust force of dual-mode shield machine used in colliery inclined shaft. Min. Process. Equip. 41 (07), 123–127. (In Chinese). doi:10.16816/j.cnki.ksjx.2013.07.032

CrossRef Full Text | Google Scholar

Hu, Mengmeng, Zhang, Bo, Li, Biao, Liu, B., Cao, W., and Xu, B. (2022). TBM-cutter rock-breaking effect and mechanism considering different cutting sequences. Bull. Eng. Geol. Environ. 81 (3), 102–121. doi:10.1007/s10064-022-02576-4

CrossRef Full Text | Google Scholar

Jin, Guodong (1981). Analysis of rock breaking mechanism of disc cutter of full face rock tunnel boring machine (II). Power Gener. Technol. 102 (04), 21–27. CNKI: SUN: SLJX.0.1981-04-003 (In Chinese).

Google Scholar

Jin, Guodong, Huang, Shifang, and Yu, Heji, (1981). Analysis of rock breaking mechanism of disc cutter of full face rock tunnel boring machine (I). Power Gener. Technol. 102 (03), 1–9. CNKI: SUN: SLJX.0.1981-03-000 (In Chinese).

Google Scholar

Li, Xiaojing, Zhang, Huaken, Bai, Yifan, and Zhang, X. y. (2022). Factor analysis and numerical simulation of rock breaking efficiency of TBM deep rock mass based on orthogonal design. J. Central South Univ. 29 (4), 1345–1362. doi:10.1007/s11771-022-4994-9

CrossRef Full Text | Google Scholar

Liu, Haijian (2015). Numerical simulation study of rock fragmentation mechanism and effect by TBM disc cutter. Beijing, China: China University of Geosciences. (In Chinese). doi:10.27493/d.cnki.gzdzy.2015.000006

CrossRef Full Text | Google Scholar

Lu, Yang, Ma, Jiming, Xu, Qianjun, and Han, M. N. (2004). TBM in the future of China. Mar. Georesources Geotechnol. 22 (3), 185–193. doi:10.1080/10641190490467116

CrossRef Full Text | Google Scholar

Mao, Chengjue, and Liu, Chunlin (1988). Indentation test analysis of disc rolling cutter in drifter. Constr. Mach. Equip. 04, 9–14+56. CNKI: SUN: GCJA.0.1988-04-002 (In Chinese).

Google Scholar

Ozdemir, L., and Wang, F. D. (1979). Mechanical tunnel boring prediction and machine design. Nasa Sti/Recon Tech. Rep. N. 80, 16239. doi:10.1016/0148-9062(78)91060-4

CrossRef Full Text | Google Scholar

Rostami, J., and Ozdemir, L. (1993). “New model for performance production of hard rock TBMs,” in Proceedings of the Rapid Excavation and Tunneling Conference, Boston, MA, USA, January 1993, 793–809. doi:10.4236/jbbs.2013.32020

CrossRef Full Text | Google Scholar

Roxborough, F. F., and Phillips, H. R. (1975). Rock excavation by disc cutter. Int. J. Rock Mech. Min. Sci. Geomechanics Abstr. 12 (12), 361–366. doi:10.1016/0148-9062(75)90547-1

CrossRef Full Text | Google Scholar

Sun, Zhenchuan, Zhao, Hailei, Hong, Kairong, Chen, K., and Zhou, J., (2019). A practical TBM cutter wear prediction model for disc cutter life and rock wear ability. Tunn. Undergr. space Technol. 85, 92–99. doi:10.1016/j.tust.2018.12.010

CrossRef Full Text | Google Scholar

Teale, R. (1965). The concept of specific energy in rock drilling. Int. J. Rock Mech. Min. Sci. Geomechanics Abstr. 2 (2), 57–73. doi:10.1016/0148-9062(65)90022-7

CrossRef Full Text | Google Scholar

Wu, Qixing, Huang, Weiran, and Ma, Hongwei (2010). Research on methods of calculating normal rock breaking force by means of disc cutter of composite TBM. Min. Process. Equip. 38 (24), 58–63. (In Chinese). doi:10.16816/j.cnki.ksjx.2010.24.016

CrossRef Full Text | Google Scholar

Yagiz, Saffet (2008). Utilizing rock mass properties for predicting TBM performance in hard rock condition. Tunn. Undergr. Space Technol. 23 (3), 326–339. doi:10.1016/j.tust.2007.04.011

CrossRef Full Text | Google Scholar

Zhang, Qinglong, Zhu, Yanwen, Du, Canxun, Du, S., Shao, K., and Jin, Z. (2022). Dynamic rock-breaking process of TBM disc cutters and response mechanism of rock mass based on discrete element. Adv. Civ. Eng. 2022, 1–10. doi:10.1155/2022/1917836

CrossRef Full Text | Google Scholar

Zhang, Xu, Wang, Juan, and Meng, Qingguo, (2021). Coal rock breaking simulation and cutting performance analysis of disc cutters. Teh. Vjesn. 28 (5), 1755–1761. doi:10.17559/TV-20210423115559

CrossRef Full Text | Google Scholar

Zhang, Zhaohuang, Mao, Chengjue, and Liu, Chunlin (1996). Statistical analysis of disc cutter pressing mark results about full face rock tunnel boring machine. Mod. Electr. Power 23 (01), 63–68. (In Chinese). doi:10.19725/j.cnki.1007-2322.1996.01.011

CrossRef Full Text | Google Scholar

Zhang, Zhaohuang (2008). The research on theory and techniques of service life management of TBM disc cutters. Beijing, China: North China Electric Power University. CNKI: CDMD: 1.2009.090407 (In Chinese).

Google Scholar