- 1School of Civil Engineering, Xi’an University of Architecture and Technology, Xi’an, China
- 2Key Laboratory of Geotechnical and Underground Space Engineering, Xi’an University of Architecture and Technology, Xi’an, China
- 3School of Civil Engineering, Hunan University, Changsha, Hunan, China
- 4China Railway 20th Bureau Group Limited, Xi’an, China
Deep excavation construction safety has become a challenging and crucial aspect of modern infrastructure engineering, and its risk assessment is frequently carried out using the Fuzzy Analytic Hierarchy Process (FAHP). However, when using FAHP to evaluate the risks of deep excavation construction, the results of the weightings obtained through subjective weighting are heavily influenced by the subjective factors of the evaluators. In addition, using linear operators to calculate the risk level can easily cause a weakening effect on the influence of prominent risk factors, resulting in poor rationality of the evaluation results. To address these problems, this paper constructs a deep excavation construction risk evaluation model based on combined weighting and nonlinear FAHP. The WBS-RBS method is used to guide the construction of the risk evaluation index system for deep excavation construction. The combined weighting values of subjective and objective weightings are calculated through the game theory combined weighting method. The fuzzy relation matrix is constructed using the membership degree vector obtained from the expert evaluation method. Nonlinear operators are introduced for comprehensive calculation. According to the maximum membership degree principle, the final risk level of the excavation construction is obtained. The newly constructed model is applied to the risk analysis of the deep excavation construction of the Rongmin Science and Innovation Park project in Xi’an. The evaluation result for the excavation construction risk is N= [0.3125, 0.3229, 0.1939, 0.0854, 0.0854], and according to the maximum membership degree principle, the risk level of the excavation is classified as Level 2, which is a relatively low risk. Based on the deep excavation construction of the Rongmin Science and Innovation Park project, this paper discusses the differences between the new model and the traditional FAHP evaluation method, further verifies the reliability of the new model, optimizes the construction plan based on the evaluation results, avoids risks, and determines its guiding significance.
1 Introduction
With the continuous increase of high-rise buildings, the vigorous development of municipal construction and the utilization of space, a large number of deep excavations have been created, and their construction safety issues have become a hotspot and difficulty in current foundation engineering (Fan et al., 2021). The demand for deep excavations in engineering is developing towards greater excavation depth, wider excavation area, and higher technical level. In relatively narrow urban spaces, improper operation during excavation of deep excavations can have serious effects on surrounding structures. The construction phase of deep excavation engineering is of utmost importance in engineering management, and risk assessment of deep excavation construction is even more critical.
Currently, some domestic and foreign experts and scholars have conducted related research and made certain achievements. WANG (2005) and Huchzermeier (2001) proposed to establish risk analysis-based management for excavation engineering. Zhou Hongbo et al. (2022) coupled the evaluation indicators of excavations using the WBS-RBS method, and analyzed the excavation of subway excavations using fault tree analysis. Feng et al. (2021) proposed an innovative method that combines analytic hierarchy process (AHP) with finite element method (FEM) to assess the potential impact risk of uncertain factors on the surrounding environment of the bridge excavation. Issa et al. (2022) introduced and applied an approach to support decision makers in construction projects by distinguishing among different deep excavation supporting systems. Meng et al. (2020) analyzed risk from two aspects—severity of consequences and probability of occurrence. They divided the severity of consequences into five indexes, calculated risk using AHP, and established expert weight index to obtain an objective calculation result from subjective expert scoring. Zhang G. H. et al. (2020) proposed a comprehensive methodology for dynamic risk analysis of foundation pit collapse during construction based on fuzzy Bayesian network (FBN) and fuzzy analytical hierarchy process (FAHP).
In conclusion, scholars and experts commonly use the Fuzzy Analytic Hierarchy Process (FAHP) for evaluating the risks of deep excavation construction, which effectively addresses the fuzziness and randomness of the evaluation. FAHP often employs the AHP method for weighting, and there have been abundant research advancements on AHP in recent years. For instance, Rabin et al. (2018) modeled and mapped groundwater potential zones using AHP and GIS technology. Sadhan et al. (2018) utilized AHP, Knowledge Driven, Fuzzy Logic, and Logistic Regression Four models to predict flood-prone areas. Xu et al. (2020) proposed a cloud model-based FAHP for risk assessment of tunnels. Moreover, Alireza et al. (2021), Shahab et al. (2020), Indrajit et al. (2020), Guo et al. (2022), Zhao et al. (2021), Song et al. (2021)and other researchers combined methods such as machine learning, Numerical simulation, and the N-K model with FAHP approach to broaden its application scope.
However, there are various problems with existing risk evaluation models for deep excavations, so it is necessary to establish a scientific and reasonable risk evaluation model for deep excavations. AHP is subject to subjective weighting, and the weighting results are heavily influenced by the evaluators’ subjective factors. To address the limitations of using a single weighting method to calculate indicator weights, this paper employs the Analytic Hierarchy Process (AHP) and Entropy Weight Method to calculate the subjective and objective weights of the risk evaluation indicators for deep excavation construction. The combination weights of the evaluation indicators are obtained by using the Game Theory method to combine the subjective and objective weights. In order to establish a scientific and rational risk evaluation indicator system for deep excavation construction, the Work Breakdown Structure- Risk Breakdown Structure (WBS-RBS) method is adopted to identify and construct the risk evaluation indicator system. However, the Fuzzy Analytic Hierarchy Process (FAHP) using the linear operator to calculate risk levels cannot address the non-linear problems in deep excavation construction risk evaluation, which reduces the accuracy of the final risk evaluation results. To address this issue, this paper introduces a non-linear operator into the traditional FAHP for risk evaluation of deep excavation construction. Finally, the newly developed risk evaluation model based on the combination weighting and non-linear FAHP is applied to the deep excavation construction of the Rongmin Science and Technology Innovation Park project on Gaoxin Second Road in Xi’an City to verify the scientific and accurate nature of the new model.
2 Construction of risk assessment indicators for deep excavation construction based on the WBS-RBS method
The construction of a reasonable and effective risk assessment indicator system is the first step in analyzing the risk of deep excavation construction. The Work Breakdown Structure (WBS) refers to the overall hierarchical structure of the deep excavation construction project. The Risk Breakdown Structure (RBS) refers to the decomposition of possible risk sources into smaller risk factors, until the risk factors can be ignored (Yang, 2006). Hillson et al. (2006) were the first to combine WBS and RBS methods by coupling them to establish an engineering project WBS-RBS risk identification coupling matrix, highlighting risk factors and establishing a risk assessment indicator system.
2.1 Developing a work breakdown structure for the construction of deep excavations
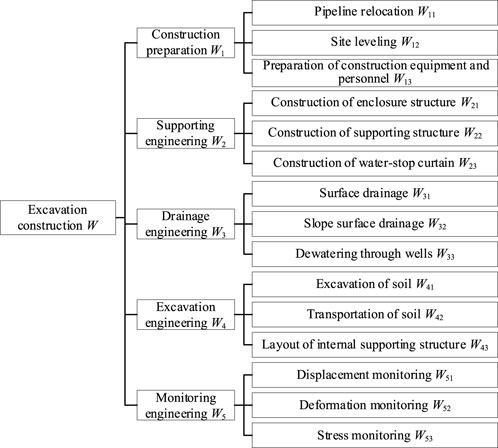
To ensure that the risk assessment indicators for deep excavation construction are appropriately detailed, expert opinions were consulted and the construction work was decomposed into a two-level structure. Based on the construction process of deep excavations, the first level is divided into five stages, including preparation for deep excavation construction (W1), enclosure engineering (W2), drainage engineering (W3), excavation engineering (W4), and monitoring engineering (W5).
Through an analysis of the characteristics of each stage of deep excavation construction work, some work procedures that are not significant enough have been combined and eliminated, resulting in a breakdown of the first-level structure. The second-level structure has 15 units. Figure 1 shows the constructed work breakdown structure for deep excavation construction.
2.2 Developing a structure for the breakdown of risk sources in the construction of deep excavations
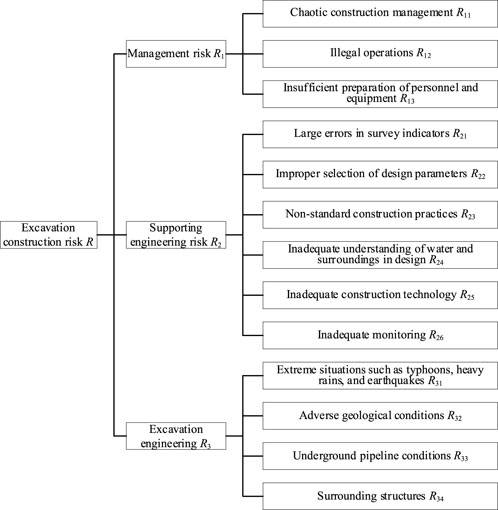
The risk sources were also broken down into a two-level structure, with the first level of risk breakdown including management risks (R1), technical risks (R2), and surrounding environmental and geological risks (R3). Based on this, factors such as extreme weather and personnel safety were considered, and the first-level structure was further decomposed to establish a second-level risk factor structure, with 13 units. Figure 2 shows the constructed risk breakdown structure for deep excavation construction.
2.3 Developing a risk identification coupling matrix for the construction of deep excavations
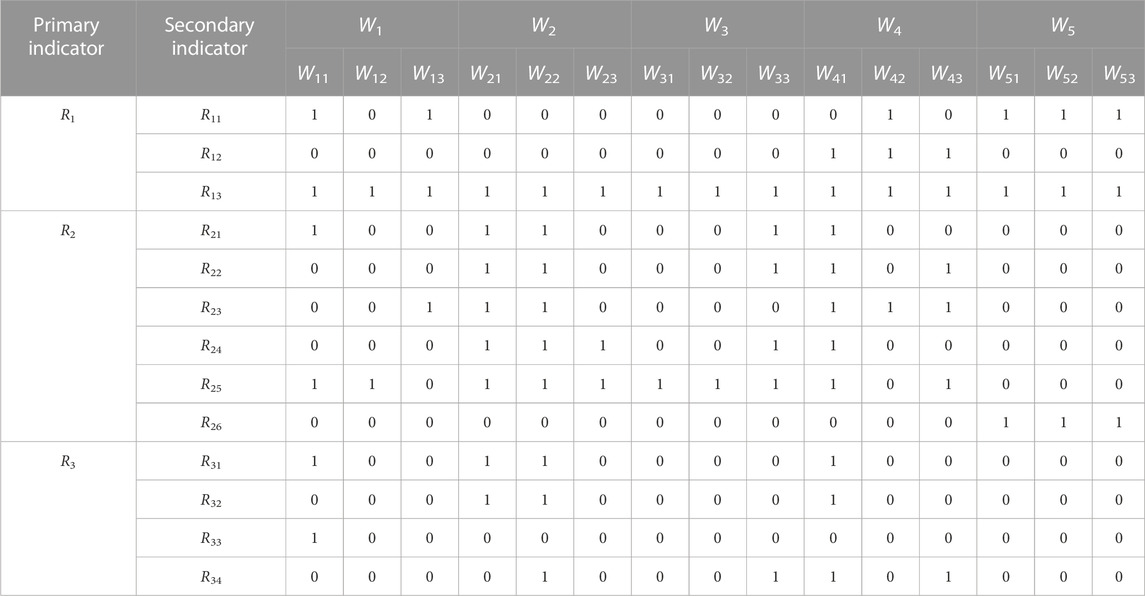
Based on the work breakdown structure and risk breakdown structure of deep excavation construction, the second-level units of both structures were coupled to obtain a coupling matrix for identifying risks in deep excavation construction (Huang et al., 2004). The coupling matrix for risk identification in deep excavation construction is shown in Table 1, where “1”indicates a risk resulting from the coupling of the two structures, and “0”indicates no risk. The risks identified in the coupling matrix for risk identification in deep excavation construction are as follows.
1) The risk of W11R11, W11R21, W11R25, W11R31, W11R33 is the leakage or fracture of underground pipelines; 2) The risk of W11R13, W12R13, W21R13, W22R13, W23R13, W31R13, W33R13, W41R13, W42R13, W43R13 is personnel safety accidents; 3) The risk of W12R25, W21R25, W22R25, W23R25, W31R25, W32R25, W33R25 is construction quality defects; 4) The risk of W13R11, W13R13, W13R23 is construction machinery failure; 5) The risk of W21R21, W21R22,W21R23, W21R24, W21R31 is failure of retaining structure; 6) The risk of W23R24 is water seepage in excavation; 7) The risk of W33R21, W33R22, W33R24 is blowout sand flow caused by excessive or inadequate precipitation-induced dewatering; 8) The risk of W22R34, W33R34, W41R24, W41R34, W43R34 is cracking and tilting of surrounding buildings; 9) The risk of W41R12, W41R21, W41R25, W41R31 is collapse and sliding of deep excavation; 10) The risk of W41R22 is upheaval of soil in deep excavation; 11)The risk of W41R23 is over-excavation of deep excavation; 12)The risk of W42R11, W42R12, W42R23 is excessive foundation load; 13)The risk of W22R21, W22R22, W22R23, W22R24, W22R31, W43R12, W43R22, W43R23, W43R25 is failure of support structure; 14)The risk of W51R11, W51R13, W51R26, W52R11, W52R13, W52R26, W53R11, W53R13, W53R26 is Inadequate monitoring leading to failure to handle accidents in a timely manner; 15)The risk of W21R32, W22R32, W41R32 is geological difficulties hindering construction.
2.4 Developing a system of risk evaluation indicators for the construction of deep excavations
Based on the opinions of technical personnel and experts at the construction site, referring to the coupling matrix for risk identification in deep excavation construction, an evaluation index system for the risks in deep excavation construction was established as shown in Figure 3.
3 Risk assessment for the construction of deep excavations
3.1 Developing a fuzzy relation matrix
3.1.1 Developing a set of risk factors
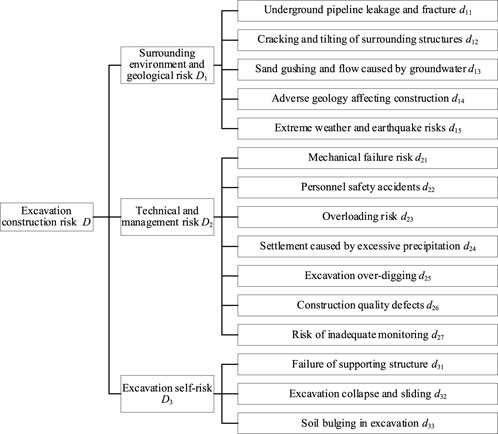
The risk factor set of the deep excavation construction risk assessment index system established through the WBS-RBS method includes two levels. The first-level indicator layer risk factor set is D = {D1,D2,D3}, and the second-level factor layer risk factor set includes D1 = {d11,d12,d13,d14,d15}, D2 = {d21,d22,d23,d24,d25,d26,d27}, and D3 = {d31,d32,d33}.
3.1.2 Developing a set of risk assessment comments
The risk evaluation comment set for deep excavation construction is established based on the “The code of construction project management” (GB/T 50326-2006). The risk evaluation comment set for deep excavation construction is divided into five levels from low to high: V = {v1,v2,v3,v4,v5} = {low risk, relatively low risk, moderate risk, relatively high risk, high risk}.
3.1.3 Building a fuzzy relation matrix using membership degree vectors
A membership degree vector is constructed for risk assessment in deep excavation construction using the expert evaluation method (Xie et al., 2005). A group of experts form an evaluation team and score each evaluation index in the risk factor set based on the five levels in the risk evaluation comment set. The membership degree vector is then organized. The fuzzy relationship matrix S between the risk evaluation comment set and the risk factor set is constructed using this vector.
In the equation, S is the fuzzy relationship matrix between the risk evaluation comment set and the risk factor set, where 0≤sij≤1, and sij represents the membership degree of the ith deep excavation construction risk factor to the jth level risk rating.
3.2 Determination of weight vectors
There are mainly two methods for determining index weights: subjective weighting and objective weighting. Subjective weighting relies on the subjective experience of decision-makers or experts to determine the weight of risk evaluation indicators. However, this method can be influenced by various factors such as the decision-maker’s knowledge structure, work experience, and preferences, which may not fully reflect the importance of risk evaluation indicators.
Objective weighting determines the weight of risk evaluation indicators based on the amount of discerning information provided by the indicators and the relationships between them. However, this method may ignore the rich experience of experts and scholars, and the results may not always match the actual situation, with a strong dependence on the samples.
Compared to subjective and objective weighting, combination weighting can comprehensively integrate the subjective and objective weights of each evaluation indicator and reflect the objective information of the indicators and the subjective judgment of the evaluators, so it can correctly reflect the actual weight of each indicator. This paper uses the Analytic Hierarchy Process (AHP) and entropy method to calculate the subjective and objective weights of deep excavation construction risk evaluation indicators respectively. Then, using game theory, the subjective and objective weights are combined to obtain the composite weights of deep excavation construction risk evaluation indicators, which can incorporate the theoretical and empirical knowledge of experienced experts and judge the importance of each indicator while avoiding the shortcomings of these two methods (Shan et al., 2012).
3.2.1 Calculation of subjective weight using analytic hierarchy process
AHP weighting is a method of determining the relative importance of different factors by comparing them. AHP provides pair-wise comparison matrix, through which the criterions are structured according to their hierarchical order (Das et al., 2020).
Step 1. Constructing the judgment matrix:
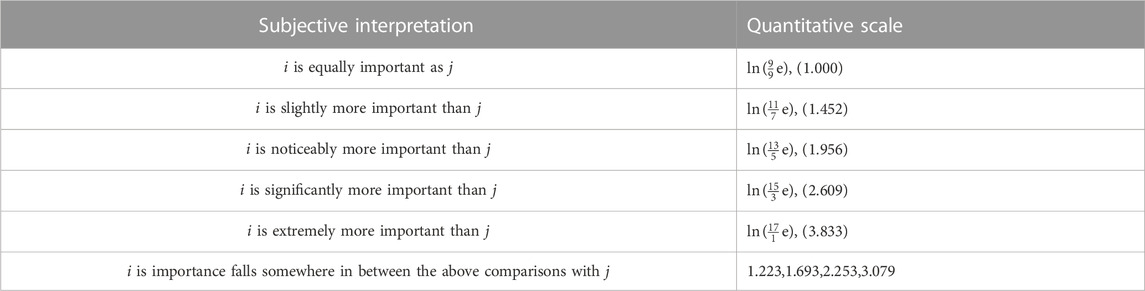
ln (9e/9)∼ln (17e/1) was chosen as the scale for constructing the judgment matrix of risk evaluation indicators for deep excavation construction due to its improved stability, rationality, and effectiveness. This method involves comparing each indicator with all other indicators at the same level, including itself, to convert abstract subjective understanding into quantitative data. The specific evaluation criteria for ln (9e/9)∼ln (17e/1) as the scale of the judgment matrix are listed in Table 2.
Based on a constructed judgment matrix, the maximum eigenvalue and corresponding eigenvector can be determined by solving for the matrix’s eigenvectors and eigenvalues. This provides the maximum eigenvalue λmax and the eigenvector associated with it.
Step 2. Consistency check.
To check the consistency of the constructed judgment matrix, a consistency ratio (CR) test is performed. If CR<0.10, it indicates that the constructed judgment matrix has good consistency.
In the equation, n represents the order of the judgment matrix, and RI is the average random consistency index (Wang et al., 1990), with specific values shown in Table 3.
Step 3. Calculation of weight vector.
The eigenvector associated with the maximum eigenvalue λmax is normalized to obtain the subjective weight vector Uk1 passing the consistency test of the judgment matrix.
3.2.2 Calculation of objective weight using Entropy Weight Method
Entropy was proposed by R Xlausis as a measure of the uniformity of the distribution of an ability in space. The entropy method can be used to calculate the objective weights of various indicators, providing a basis for multi-index comprehensive evaluation (Zhang et al., 2017). Compared with subjective weighting methods, the entropy method has higher accuracy and stronger objectivity, which can better explain the results obtained (Zhu et al., 2015). The steps are as follows:
Step 1. Constructing the entropy method judgment matrix:
The original data matrix
Step 2. Standardization:
Extreme value entropy method was used for normalization. First, the extreme value method was applied to transform the original data into dimensionless values, which then underwent standardization to obtain the judgment matrix R:
In the formula, rij represents an element of the standardized judgment matrix R, and min{xij} and max{xij}, represent the minimum and maximum values, respectively.
Step 3. Handling of zeros in the matrix.
To ensure meaningful logarithmic operations, the standardized matrix is processed to eliminate zeros by shifting all elements to the right by a constant value, usually 0.001. The resulting matrix is
Step 4. Determination of entropy value
In the formula,
Step 5. Calculation of entropy weighting Wj
After obtaining the entropy weights Wj, they are assembled into an entropy weight vector Uk2.
3.2.3 Calculation of combined weight using game theory method
The combined weighting vector for risk evaluation indicators in deep excavation construction is obtained by integrating subjective and objective weights using the game theory method. The game theory approach takes into account inherent information among various risk evaluation indicators, which ensures consistency and harmony among subjective, objective, and combined weights, minimizes deviations between different weights, and reduces the impact of subjectivity on risk evaluation results. The process for determining the combined weight using the game theory method is as follows (Zhou et al., 2022):
Step 1. Construct the set of basic weight vectors Uk = {Uk1,Uk2,
In the formula, U represents the combined weight vector; αk is the linear combination coefficient,
Step 2. Optimize the weight coefficients αk to minimize the deviation between the combined weight vector U and the basic weight vectors Uk, that is:
In the formula, Uk is the set of basic weight vectors, and
Step 3. Normalize the weight coefficients
Step 4. The final weight vector M for the combination of various evaluation indicators is obtained as follows:
The symbol M represents the final combination weight vector obtained after weighting and combining, where M=[
3.3 Nonlinear fuzzy comprehensive evaluation
FAHP method is employed for multi-criteria decision problems (Das et al., 2019). Traditional AHP method was modified by Van Laarhoven in 1983 to develop the hierarchical analysis more accurately by employing fuzzy ratios in place of exact ratios (Van et al., 1983).
However, the traditional AHP method employs a linear operator to calculate risk levels, which may weaken the importance of certain indicators. Moreover, the construction process of deep excavations is full of ambiguity and uncertainty due to various factors, and extreme situations are inevitable. Linear operators cannot reflect the actual situation on site. Therefore, a nonlinear fuzzy comprehensive evaluation method is adopted. The nonlinear fuzzy matrix synthesis operator used for risk assessment is (Zhang et al., 2005):
The symbols used in the equation are:
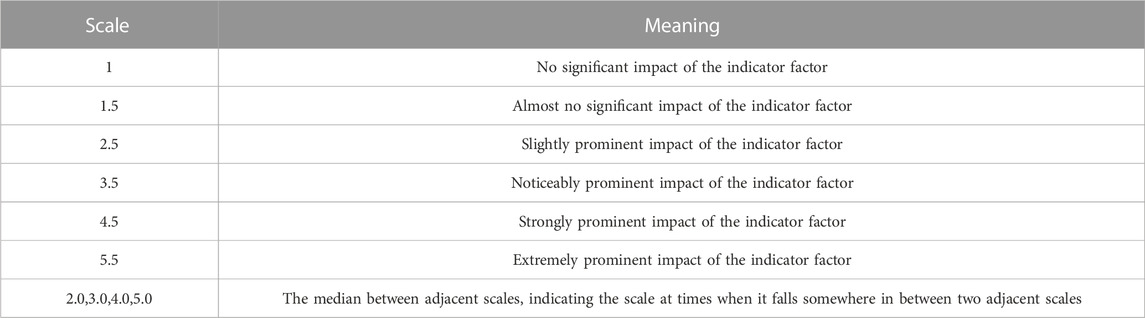
The criteria for the values of salient influence coefficients are shown in Table 4.
After obtaining the salient influence coefficients at each level, the fuzzy judgment matrix is processed to meet the requirements for using nonlinear operators to synthesize fuzzy matrices. Since si≥1 in the nonlinear fuzzy evaluation matrix, but the membership degree values are between [0,1], it is necessary to convert the original fuzzy judgment matrix. The conversion is shown below:
The symbol sij’ represents the value of the transformed nonlinear fuzzy evaluation matrix, whereas the symbol sij represents the value of the original fuzzy judgment matrix.
3.4 A new model for risk assessment in the construction of deep excavations
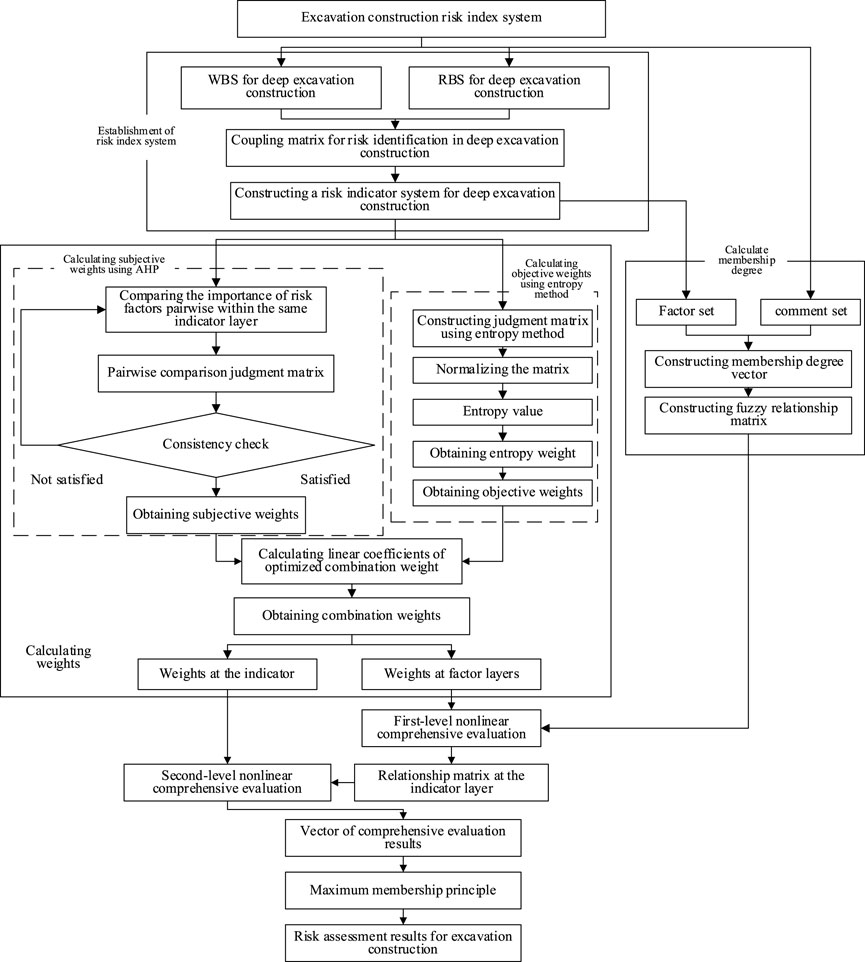
The deep excavation construction risk evaluation model based on combination weighting and nonlinear FAHP is established through the above steps. The specific evaluation process is shown in Figure 4.
4 Case study analysis
4.1 Overview of the case project
The construction risk assessment model for deep excavations based on the combined weighting-nonlinear FAHP method was applied to verify the deep excavation construction of the Rongmin Science and Technology Innovation Park project on High-tech Second Road in the High-tech Zone of Xi’an City. The strata involved in the project are divided into 14 layers, including fill soil, loess-like fine-grained clay, loess, ancient soil, and 10 different types of fine-grained clay from top to bottom. The construction site belongs to Category II, and liquefaction of sandy soil can be disregarded based on geological data. The safety level of the excavation wall is Level I, the support safety level is Level I, and the safety level of the deep excavation is also Level I. The excavation depth is between 7.30 and 12.97 m, which is considered a deep excavation.
4.2 Weight calculation
4.2.1 Calculation of subjective weight
The subjective weight is determined by using the scale of ln (9e/9)∼ln (17e/1) as the judgment matrix. The importance of the judgment criteria is compared through expert evaluation to construct the judgment matrix. Taking the weight of the index layer as an example, the specific calculation process is as follows:
Step 1. Construct the judgment matrix A for establishing the evaluation indicators of deep excavation construction risk
Calculate the maximum eigenvalue
Step 2. Perform consistency check, and the matrix A passes the test.
Step 3. Normalize the eigenvector to obtain the subjective weight of the index layer.
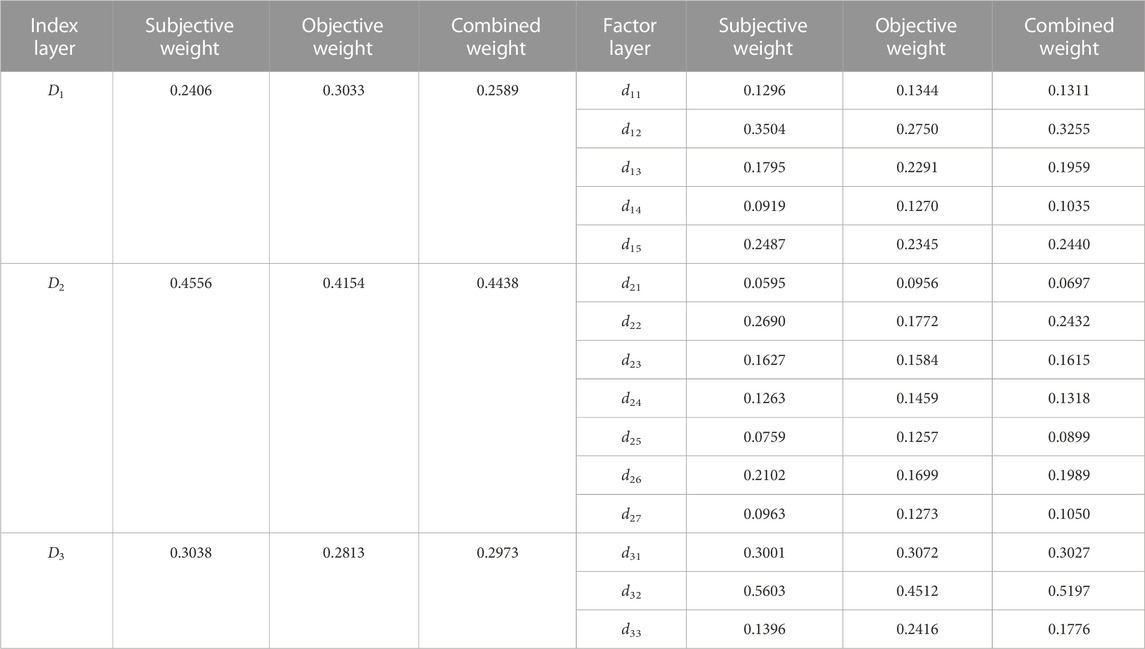
Similarly, the subjective weight corresponding to each indicator in the deep excavation construction risk evaluation project is obtained. The specific subjective weights are shown in Table 5.
4.2.2 Calculation of objective weight
The entropy weight data matrix was obtained from a questionnaire survey of 11 experts and referred to the research of Chowdhuri et al. (2019). The 15 factor-level indicators and 3 criterion-level indicators were scored using a percentage-based scale. Taking objective weighting calculation at the criterion level as an example:
Step 1. After standardization, the entropy judgment matrix B with zeros processed values is:
Step 2. Calculate the determined entropy value ej according to Eq. 4:
Step 5. Calculate the entropy weight corresponding to each determined entropy value, and organize them into an entropy weight vector
Similarly, the entropy weight vector for other indicators can be obtained and is shown in Table 5.
4.2.3 Calculation of combination weight using game theory
Calculating the combination weight using game theory first requires determining the basic weight vector. Taking the combination of index layer weights as an example, the calculation process is as follows:
Step 1. Determine the basic weight vectors that need to be combined:
Step 2. Optimize the linear coefficients of the combination weight using Eq. 8 to obtain:
After normalization, the result is:
Step 3. Calculate the combination weight M of the index layer for deep excavation construction risk evaluation by using Eq. 9 to combine the linear coefficients with subjective and objective weights. The combination weights obtained based on game theory are shown in Table 5.
The overall weight vector is:
Similarly, the weight vector for the factor layer can be obtained:
Based on the calculated weights, it can be seen that technical and management risks are the biggest risks in the construction of deep excavations for this project. This is because the geological conditions of the project are relatively good, and if the construction technology and management level are in place, risks can be avoided.
4.3 Membership degree calculation
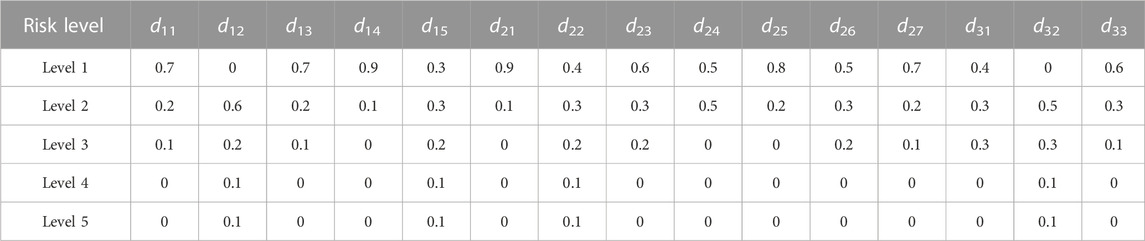
Based on the actual construction situation of the deep excavation of the Rongmin Science and Technology Innovation Park project on High-tech Second Road in the High-tech Zone of Xi’an City, the fuzzy judgment matrix for the risk assessment of the deep excavation construction was obtained using the expert evaluation method. Experts rated the secondary risk projects established in the risk assessment indicator system through a questionnaire survey. The membership degree values were obtained after processing the questionnaire data, as shown in Table 6.
The given text describes the construction of a single-factor evaluation matrix for the risk factors associated with the deep excavation construction of the Rongmin Science and Technology Innovation Park project on High-tech Second Road, according to Table 6. To perform nonlinear fuzzy comprehensive evaluation, the matrix is processed using Eq. 11 to obtain evaluation matrices S1∼S3 that can be used for nonlinear fuzzy comprehensive calculation.
4.4 Determination of prominent impact factors for risk indicators
According to Table 4 and expert opinions, combined with the actual situation of the deep excavation construction of Rongmin Science and Technology Innovation Park on High-tech Second Road, the prominent impact coefficients of the first-level risk factors and second-level risk factors are obtained, as shown in Table 7.
The prominent impact coefficient vectors corresponding to S1∼S3 can be obtained from Table 7 as follows:
And the prominent impact coefficient vectors of the indicator layer
4.5 First-level nonlinear fuzzy comprehensive evaluation
The factor layer weight vector M1∼M3, the nonlinear fuzzy evaluation judgment matrices S1∼S3, and the level-2 risk factor salient influence coefficient vectors Λ1∼Λ3 are inputted into Eq. 10 for nonlinear fuzzy comprehensive evaluation to obtain the evaluation results N1∼N3 for level-2 risk factors. Taking N1 as an example, the calculation process is as follows:
The calculated N1 is normalized to obtain the result vector of first-level nonlinear fuzzy comprehensive evaluation for the construction risk assessment of deep excavations in the Rongmin Science and Innovation Park project on High-tech Second Road, as follows:
Similarly, the evaluation results for the other level-2 risk factors in the construction risk assessment of deep excavations in the Rongmin Science and Innovation Park project on High-tech Second Road are as follows:
4.6 Second-level nonlinear fuzzy comprehensive evaluation
The N1∼N3 are used as new factors to construct a second-level nonlinear fuzzy comprehensive evaluation matrix
From Table 7, it can be obtained that the salient influence coefficient vector Λ=[4.5,5.5,5] corresponds to level-1 risk factors in the construction risk assessment of deep excavations in the Rongmin Science and Innovation Park project on High-tech Second Road, and the weight vector M = [0.2589,0.4438,0.2973] corresponds to level-1 risk factors.
By substituting the above results into Eq. 10 for nonlinear fuzzy comprehensive evaluation, the determined second-level nonlinear fuzzy comprehensive evaluation result vector N is obtained:
The result vector N is normalized to obtain the second-level nonlinear fuzzy comprehensive evaluation result vector for the construction risk assessment of deep excavations in the Rongmin Science and Innovation Park project on High-tech Second Road:
This vector is the comprehensive evaluation vector of total risk. Using the maximum membership principle, an overall evaluation of the construction risk of deep excavations in the Rongmin Science and Innovation Park project on High-tech Second Road in Xi’an High-tech Zone is conducted. According to the fuzzy comprehensive evaluation vector, the risk level of this project is level-2, with a comment of low risk. The overall risk of deep excavation construction is relatively small, as long as the construction quality is qualified and the site management is orderly, the construction risk of deep excavations for this project can be controlled. The evaluation result is consistent with the actual situation, indicating the accuracy of the model.
5 Discussion
To verify the effect of the non-linear operator in the risk evaluation process of the new model, a traditional FAHP is used to conduct a risk assessment of the deep excavation construction of the case project, with reference to Zhang G. et al. (2020) The values of the prominent influence coefficients are all 1, that is,
Using the linear FAHP method based on the combination weighting method for comprehensive evaluation, the risk level of the deep excavation construction is level 1, which is considered low risk. The introduction of the nonlinear fuzzy comprehensive evaluation method results in a risk assessment level of level 2, indicating a lower risk. The comparison between the result vector
In response to the risk assessment results, the following improvements will be made.
(1) The design usage time for deep excavation support will be extended to 12 months, and the design value for the top load of the deep excavation will be increased to 20 kPa.
(2) The deep excavation support system will be enhanced with the use of pumped piles, prestressed anchor cables, and soil nails.
(3) Construction personnel will undergo additional technical training to enhance their skills.
(4) Construction management will be strengthened to ensure construction quality and eliminate safety and quality hazards during the construction process.
(5) Drainage ditches will be constructed outside the pit, and drainage ditches and sump pumps will be installed inside the pit to facilitate timely pumping.
(6) Regular monitoring will be carried out, and monitoring information will be communicated to all units, with appropriate measures taken as necessary.
After making the improvements to the plan, there were no accidents during the construction of the deep excavation in Rongmin Science and Technology Innovation Park on High-tech Second Road in Xi’an High-tech Zone. This indicates that the improvements made based on the risk assessment model using a combination weighting method and nonlinear FAHP were effective, further demonstrating the rationality and effectiveness of the model.
Currently, this paper has made a innovative attempt to establish a risk evaluation model for deep excavation construction based on the combination weighting and non-linear FAHP. The main limitations of this study are that expert judgments and on-site data are required for a relatively accurate risk assessment, and the calculation process is relatively complex and has not yet been developed into an executable program. In constructing the judgment matrix, subjective evaluations are required from experts, which may introduce subjectivity and errors. Looking ahead, this risk evaluation model can be further expanded by integrating with Geographical Information System and machine learning to broaden its application scope Hong-bo et al., 2009; Malik et al., 2020.
6 Conclusion
(1) The WBS-RBS method is used to identify and construct an evaluation index system for the construction risks of deep excavations to ensure that no important factors are overlooked during the risk identification process and to obtain a scientifically reasonable risk evaluation index system.
(2) A combination of subjective weights calculated by fuzzy analytic hierarchy process (AHP) and objective weights calculated by entropy method using game theory is used to obtain more reasonable combined weights, avoiding the limitations of both subjective and objective weighting methods.
(3) Nonlinear operators are used to avoid weakening the influence of prominent risk factors in the calculation of risk levels using linear operators in fuzzy AHP, which can lead to reduced accuracy of the final evaluation results. This helps to make the results more reasonable.
(4) The new model is applied to the risk assessment of deep excavation construction in the Rongmin Science and Innovation Park project on High-tech Second Road in Xi’an. Based on the evaluation results, the construction plan for the excavation is optimized. After improving the plan, no accidents occurred during the construction process of deep excavations for this project, further demonstrating the instructiveness of the new model in risk analysis for actual construction of deep excavations.
(5) A novel risk evaluation model for deep excavation construction based on the combination weighting and non-linear FAHP has been established, and its feasibility has been verified through engineering examples. This model can provide reference and guidance for safety management of deep excavation construction in other countries around the world.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
Under the guidance of ZS, DG, and SL wrote this article. During the writing process, YZ, TZ, JX, and YS provided practical engineering information and assisted SL in conducting the questionnaire survey. All authors contributed to the article and approved the submitted version.
Funding
Shaanxi Province Hanjiang-to weihe river valley water diversion Joint Fund (2021JLM-52), Science and Technology Innovation Team of Shaanxi Innovation Capability Support Plan (No. 2020TD005), The Provincial Natural Science Foundation of Shaanxi (No. 2021JM-373).
Acknowledgments
The authors would like to express their sincere gratitude for the contribution of Hanjing-to weihe river valley water diversion project construction Co., Ltd.
Conflict of interest
YS and JX were employed by China Railway 20th Bureau Group Limited.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Arabameri, A., Pal, S. C., Rezaie, F., Chakrabortty, R., Ngo, P., Blaschke, T., et al. (2021). Comparison of multi-criteria and artificial intelligence models for land-subsidence susceptibility zonation. J. Environ. Manag. 284 (2), 112067. doi:10.1016/j.jenvman.2021.112067
Band, S. S., Janizadeh, S., Pal, S. C., Saha, A., Mosavi, A., Melesse, A. M., et al. (2020). Flash flood susceptibility modeling using new approaches of hybrid and ensemble tree-based machine learning algorithms. Remote Sens. 12 (3568), 3568. doi:10.3390/rs12213568
Chowdhuri, I., Pal, S. C., Arabameri, A., Ngo, P. T. T., Roy, P., Malik, S., et al. (2020). Ensemble approach to develop landslide susceptibility map in landslide dominated Sikkim himalayan region, India. Environ. Earth Sci. 79 (20), 476. doi:10.1007/s12665-020-09227-5
Chowdhuri, I., Pal, S. C., and Chakrabortty, R. (2019). Flood susceptibility mapping by ensemble evidential belief function and binomial logistic regression model on river basin of eastern India. Adv. Space Res. 65 (5), 1466–1489. doi:10.1016/j.asr.2019.12.003
Das, B., and Pal, S. C. (2020). Assessment of groundwater vulnerability to over-exploitation using mcda, ahp, fuzzy logic and novel ensemble models: A case study of goghat-i and ii blocks of West Bengal, India. Environ. Earth Sci. 79 (5), 104. doi:10.1007/s12665-020-8843-6
Das, B., and Pal, S. C. (2019). Combination of gis and fuzzy-ahp for delineating groundwater recharge potential zones in the critical goghat-ii block of West Bengal, India. HydroResearch 2, 21–30. doi:10.1016/j.hydres.2019.10.001
Fan, S., Song, Z., Xu, T., Wang, K., and Zhang, Y. (2021). Tunnel deformation and stress response under the bilateral foundation pit construction: A case study. Archives Civ. Mech. Eng. 21, 109. doi:10.1007/s43452-021-00259-7
Feng, S. X., Lei, H. Y., Wan, Y. F., Jin, H. Y., and Han, J. (2021). Influencing factors and control measures of excavation on adjacent bridge foundation based on analytic hierarchy process and finite element method. Front. Struct. Civ. Eng. 15 (2), 461–477. doi:10.1007/s11709-021-0705-0
Guo, D. S., Song, Z. P., Xu, T., Zhang, Y. W., and Ding, L. B. (2022). Coupling analysis of tunnel construction risk in complex geology and construction factors. J. Constr. Eng. Manag. 148 (9), 13. doi:10.1061/(asce)co.1943-7862.0002360
Hillson, D., Grimaldi, S., and Rafele, C. (2006). Managing project risks using a cross risk breakdown matrix. Risk Manag. 8 (1), 61–76. doi:10.1057/palgrave.rm.8250004
Hong-bo, Z. H. O. U., Gao, W.-J., Cai, L.-B., and Zhang, H. (2009). Risk identification and analysis of subway foundation pit by using fault tree analysis method based on WBS-RBS. Rock Soil Mech. (09), 2703–2707+2726. doi:10.16285/j.rsm.2009.09.012
Huang, Y., and Jianxin, H. (2004). Risk pre-diagnosis in urban rail transit engineering using the WBS-RBS method. Urban rapid transit. Urban Express Rail Transit 13 (04), 9–12. doi:10.3390/su132011507
Huchzermeier, A., and Loch, C. H. (2001). Project management under risk: Using the real options approach to evaluate flexibility in R.D. Manag. Sci. 47 (1), 85–101. doi:10.1287/mnsc.47.1.85.10661
Issa, U., Saeed, F., Miky, Y., Alqurashi, M., and Osman, E. (2022). Hybrid AHP-fuzzy TOPSIS approach for selecting deep excavation support system. Buildings 12 (3), 295. doi:10.3390/buildings12030295
Laarhoven, P. M. J. V., and Pedrycz, W. (1983). A fuzzy extension of saaty's priority theory. Fuzzy Sets Syst. 11 (13), 199–227. doi:10.1016/S0165-0114(83)80082-7
Malik, S., Pal, S. C., Chowdhuri, I., Chakrabortty, R., and Das, B. (2020). Prediction of highly flood prone areas by gis based heuristic and statistical model in a monsoon dominated region of bengal basin. Remote Sens. Appl. Soc. Environ. 19, 100343. doi:10.1016/j.rsase.2020.100343
Meng, G. W., Huang, J. S., Wu, B., Zhu, Y. P., Xu, S. X., and Hao, J. H. (2020). Risk assessment of deep foundation pit construction based on analytic hierarchy process and fuzzy mathematics. Adv. Civ. Eng. 2020, 1–12. doi:10.1155/2020/8840043
Rabin, C., Chandra, P. S., Sadhan, M., and Biswajit, D. (2018). Modeling and mapping of groundwater potentiality zones using ahp and gis technique: A case study of raniganj block, paschim bardhaman, West Bengal. Model. Earth Syst. Environ. 4, 1–26. doi:10.1007/s40808-018-0471-8
Shan, C., Dong, Z., Fan, K., Yang, J., Chen, L. .I. .U., and Fang, Q.1 (2012). Application of combined weighting method in the calculation of river health evaluation weights. J. River Sea Univ. Nat. Sci. Ed. (06), 622–628. doi:10.3876/j.issn.1000-1980.2012.06.005
Song, Z., Su, W., Tian, X., Zhang, Y., and Zhou, G. (2021). Risk analysis of tunnel construction scheme change based on field monitoring and numerical analysis. Adv. Civ. Eng. 2021, 1–15. doi:10.1155/2021/8888886
Wang, J., Hou, W., Wang, X., and Riqing, X. U. (2005). “Analysis of accident and risk sources factors for deep foundation pit,” in Paper presented at the Asia Pacific Symposium on Safety; 20051102-04; Shaoxing(CN), Shaoxing, China, November 2005.
Wang, L.F., and Xu, S. (1990). Introduction to hierarchical analysis. Beijing, China: People's University of China Press.
Xie, J., and Liu, C. (2005). Fuzzy mathematical methods and their applications. Huazhong, China: Huazhong University of Technology Press.
Xu, T., Song, Z., Guo, D., and Song, Y. (2020). A cloud model-based risk assessment methodology for tunneling-induced damage to existing tunnel. Adv. Civ. Eng. 2020 (14), 1–11. doi:10.1155/2020/8898362
Yang, Y. (2006). “Work breakdown structures of construction project and its applications in engineering,”. Doctoral dissertation (Tianjin, China: Tianjin University).
Zhang, A.-L., Zhang, X.-Y., Xu, Y.-J., and yang, C. (2017). Study on modified AHP-entropy method-based fuzzy comprehensive evaluation of urban utility tunnel construction schedule risk. Archit. Technol. (09), 922–926. doi:10.13731/j.issn.1000-4726.2017.09.006
Zhang, G. H., Wang, C. T., Jiao, Y. Y., Wang, H., Qin, W. M., Chen, W., et al. (2020a). Collapse risk analysis of deep foundation pits in metro stations using a fuzzy bayesian network and a fuzzy AHP. Math. Problems Eng. 2020, 1–18. doi:10.1155/2020/4214379
Zhang, G., Wang, C., Jiao, Y., Wang, H., Qin, W., Chen, W., et al. (2020b). Collapse risk analysis of deep foundation pits in metro stations using a fuzzy bayesian network and a fuzzy ahp. London, United Kingdom: Hindawi Limited.
Zhang, X., and Feng, Y. (2005). A nonlinear fuzzy comprehensive assessment model. J. Syst. Eng. Electron. (10), 54–59. doi:10.1007/978-3-642-14880-4_53
Zhao, M., Cheng, Y., Song, Z., Wang, T., Zhang, Y., Gong, Y., et al. (2021). Stability analysis of TBM tunnel undercrossing existing high-speed railway tunnel: A case study from yangtaishan tunnel of shenzhen metro line 6. Adv. Civ. Eng. 2021, 1–18. doi:10.1155/2021/6674862
Zhou, Y., Wang, W., Lu, X., and Wang, K. (2022). Combination weighting prediction modeland application of rock burst disaster based on game theory. China Saf. Sci. J. (07), 105–112. doi:10.16265/j.cnki.issn1003-3033.2022.07.0620
Keywords: deep excavation, nonlinearity, risk assessment, FAHP, game theory method, WBS-RBS
Citation: Liu S, Song Z, Zhang Y, Guo D, Sun Y, Zeng T and Xie J (2023) Risk assessment of deep excavation construction based on combined weighting and nonlinear FAHP. Front. Earth Sci. 11:1204721. doi: 10.3389/feart.2023.1204721
Received: 12 April 2023; Accepted: 16 May 2023;
Published: 30 May 2023.
Edited by:
Sandipan Das, Symbiosis International University, IndiaReviewed by:
Rabin Chakrabortty, University of Burdwan, IndiaSubodh Chandra Pal, University of Burdwan, India
Copyright © 2023 Liu, Song, Zhang, Guo, Sun, Zeng and Xie. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhanping Song, c29uZ3pocHl0QHhhdWF0LmVkdS5jbg==
 Shihao Liu1
Shihao Liu1 Zhanping Song
Zhanping Song Desai Guo
Desai Guo