Numerical calculation of phase change heat conduction in freezing soil by lattice Boltzmann method based on enthalpy method

In the freezing process, the soil is accompanied by heat conduction, heat release for ice-water phase change, phase change interface movement, and a change in thermal diffusion coefficient, which is a complex nonlinear problem and is hard to solve. This study uses the enthalpy method to establish a unified control equation for heat conduction in the entire calculation region (including the solid-phase zone, liquid-phase zone, and phase change interface). It solves the equation numerically, relying on the D2Q4 model of the lattice Boltzmann method, and determines the evolution of the temperature field and solid-liquid phase change interface position with time. The trends in the soil’s temperature field evolution and freezing front movement under unilateral and bilateral cold sources are discussed using an example from an artificial freezing project. The results show that when −10°C is taken as the limit for freezing wall temperature, the freezing wall thickness developed at 5, 10, 20, 30, and 40 days under the unilateral cold source is 0.24, 0.33, 0.47, 0.57, and 0.66 m, respectively. The overall temperature in the soil drops below −13.6°C and −26.4°C at 35 days and 45 days under the bilateral cold sources. These values can provide a basis for engineering design.

1 Introduction

In building underground projects, the heat conduction problem accompanied by phase change frequently occurs, such as in tunnelling projects in cold areas (Hunag et al., 1986), constructing underground projects, including subways (Van Dorst, 2013), artificial freezing reinforcement of soil during shaft sinking at mine (Levin et al., 2021), treatment of underground repositories of permanently isolated radioactive waste (Jing et al., 1995), and others. If the development mechanism of the temperature field of the geotechnical materials in the freezing process cannot be comprehended in engineering practice, it will seriously affect the project’s safety and directly or indirectly cause significant economic losses. For example, a shaft submergence accident occurred in an auxiliary shaft of Huainan Xieqiao Mining Area due to the freezing tube fracture, resulting in direct economic losses of over 10 million yuan. Repeated water-bursting accidents happened during excavation in a concealed excavation tunnel in Shenzhen because of a frozen wall connection failure. Due to the water gushing at the frozen wall in the intermediate wind well in the tunnel of Shanghai Metro Line 4, a severe surface collapse occurred, and the entire tunnel was destroyed by Huangpu River water gushing, resulting in an economic loss of nearly 150 million yuan. Therefore, a systematic and in-depth study of the development trends of the solid-liquid phase change interface, and the evolution of the temperature field during the soil freezing process, can provide a valuable technical foundation for projects associated with soil freezing. This has significant value for theoretical research and offers broad engineering application prospects.

When soil water condenses into ice and forms a solid-liquid phase change interface, heat will be released at the interface, and the interface will move continuously with time during freezing. Thus, the heat conduction problem with phase change is highly nonlinear. Due to the nonlinear nature of the phase change system at its moving interfaces, it is difficult to predict its behaviour, and no rigorous theory can be developed (Rabin and Korin, 1993; Costa et al., 1998). A large number of practical engineering problems are often solved with the assistance of numerical algorithms. In dealing with phase change boundaries, current computational methods include the heat capacity (Rabin and Korin, 1993; Alva et al., 2006), Kirchhoff transformation (Voller et al., 1990), and enthalpy methods (Costa et al., 1998; Jiaung et al., 2001; Miller and Succi, 2002; Eshraghi and Felicelli, 2012). In dealing with phase change interfaces, the enthalpy approach has been widely used because of its advantages, such as clear physical meaning, no need to trace the interface, and ease of numerical calculation. The lattice Boltzmann method is a mesoscopic numerical calculation technique that can establish the relation between macroscopic and microscopic computations in numerical simulation of heat conduction. The method core is to establish a bridge between the microscopic and macroscopic scales. It does not need to consider the motion law of individual particles but instead considers the motion of all particles as a whole and describes their overall macroscopic motion characteristics using the distribution function. Due to its clear physical concepts, ease in dealing with complex boundaries, simple implementation of procedures, and suitability for parallel computation, it has gained increasing attention for phase change heat conduction problems. Jiaung et al. (Jiaung et al., 2001) improved the lattice Boltzmann model using the enthalpy method to simulate the heat conduction problem associated with solid-liquid phase changes. Miller and Succi (Miller and Succi, 2002) simulated two-dimensional crystal solidification and dendrite growth by introducing a time-dependent phase change fraction. Eshraghi and Felicelli (Eshraghi and Felicelli, 2012) developed an implicit lattice Boltzmann model for phase change heat conduction using the D2Q9 model and considering different boundary conditions.

By combining the enthalpy method and the lattice Boltzmann method, the strengths of both approaches can be leveraged, enhancing the accuracy and reliability of heat conduction studies in soil. Both the enthalpy method and the lattice Boltzmann method are capable of dealing with intricate geometries and boundary conditions. This enables more precise simulations of heat conduction in soil with complex structures and spatial heterogeneity. The lattice Boltzmann method inherently lends itself to parallel computing. When combined with the enthalpy method, the parallel computing advantage can be further exploited, accelerating the computational speed of heat conduction simulations and improving efficiency. The enthalpy and lattice Boltzmann methods allow for modeling at different scales. Their combination enables multiscale heat conduction simulations, encompassing various scales from micro to macro, facilitating a comprehensive understanding of heat transfer behavior in soil.

This study uses the lattice Boltzmann model relying on the enthalpy method to transform the heat conduction problem solved by partitioning it into a nonlinear heat conduction problem with a phase change over the entire region. The enthalpy method establishes a unified control equation for the entire computational region (solid-phase zone, liquid-phase zone, and solid-liquid phase change interface). The heat conduction equation with phase change is solved numerically in the discrete calculation region utilizing the lattice Boltzmann method. The temperature field and the solid-liquid phase change interface’s position are derived as a time function based on the relationship between enthalpy and temperature. The calculation method validity is verified by combining the Neumann solution of the semi-infinite space solid-liquid phase change heat conduction problem. Finally, trends of temperature field evolution and freezing front movement in the soil under unilateral and bilateral cold sources are discussed using an example from an artificial freezing project.

2 Materials and methods

2.1 Physical model of soil freezing

In order to study the temperature field evolution in the soil during freezing and the movement trend of the freezing front, a schematic diagram of the freezing model for the soil’s solid-liquid phase in a semi-infinite region is established (Figure 1), where the X-axis direction represents the soil’s freezing direction; $L$ is the length of the freezing influence range; the adiabatic boundary is located at $y=L$; $T_0$ is the constant cold source temperature; $T_f$ is the soil’s freezing temperature; $T_i$ is the soil’s initial temperature; $s\left(t\right)$ is the location of the interface for the solid-liquid phase change in the soil.

FIGURE 1

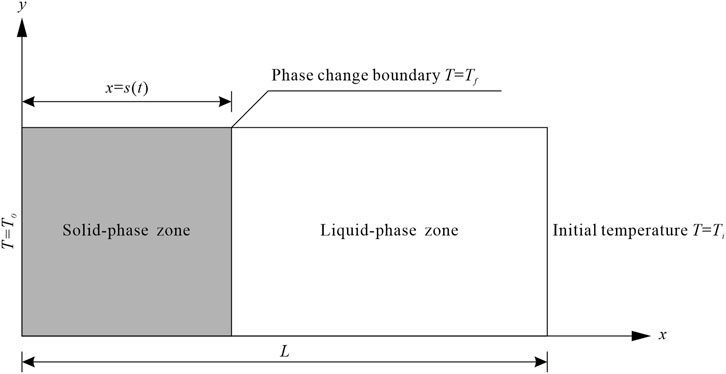
FIGURE 1. Schematic diagram of the soil’s solid-liquid phase freezing model in a semi-infinite region.

2.1.1 Basic assumptions

In order to numerically solve the heat conduction equation while considering the phase change, the following basic assumptions were made: 1) The soil was considered a homogeneous isotropic continuous medium, which was divided into solid and liquid phase zones according to the physical state of the internal moisture. The thermophysical parameters of each phase zone were fixed at constant values and were made independent of the temperature; 2) The effects of moisture migration, soil frost heaving, and stress field change were ignored. Whereas the heat conduction effect during the freezing process was only considered; 3) The heat conduction and the movement of the phase change interface during the soil’s freezing process are along a single direction; 4) The effect of the solid-liquid phase change interface’s thickness in the soil body is not considered; 5) The soil’s freezing temperature is constant. Besides, the freezing process was completed instantaneously, ignoring its physical evolution process.

2.1.2 Mathematical equations

The mathematical equation for the temperature field evolution can be simplified according to the temperature-induced change in the physical state of water in the soil, which is divided into the solid-phase zone and liquid-phase zones (Ozisik, 1993) as follows:

Solid-phase zone:

$\begin{array}{c}\frac{\partial T_s\left(x,t\right)}{\partial t}={\alpha }_s\frac{{\partial }^2{T}_s\left(x,t\right)}{\partial x^2}\left(0<x<s\left(t\right)\right)\end{array}(1)$

Liquid-phase zone:

$\begin{array}{c}\frac{\partial T_l\left(x,t\right)}{\partial t}={\alpha }_l\frac{{\partial }^2{T}_l\left(x,t\right)}{\partial x^2}\left(s\left(t\right)<x<L\right)\end{array}(2)$

where $T_s$ and $T_l$ are the soil’s temperatures in the solid-phase zone and liquid-phase zone, respectively; ${\alpha }_s$ and ${\alpha }_l$ are the thermal diffusion coefficients of the soil in the solid-phase zone and liquid-phase zone, respectively, in which $\alpha =k/\left(\rho C_p\right)$, where $\rho$ is the density, $C_p$ is the specific heat capacity, and $k$ is the thermal conductivity that can be obtained from the volume fraction of water (or ice), soil particles, and air in the soil and their respective thermophysical parameters (Radoslwa et al., 2006); $t$ is the freezing time.

2.1.3 The enthalpy method model

In order to study the movement process for the phase change interface during soil freezing, the enthalpy parameter was introduced into the heat conduction equation according to the enthalpy model proposed by Shamsundar and Sparrow (Shamsundar and Sparrow, 1975) as follows:

$\begin{array}{c}\rho \frac{\partial H}{\partial t}=k\frac{{\partial }^{2}T}{\partial x^2}\end{array}(3)$

where $H$ is the enthalpy; $C_p$ is the soil’s specific heat capacity, which is assumed to not change with temperature; $H$ can be expressed as:

$\begin{array}{c}H=C_{p}T+\phi L_a\end{array}(4)$

where $\phi$ is the liquid-phase fraction, in which $\phi =1$ in the liquid phase and $\phi =0$ in the solid phase.

Substituting Eq. 4 into Eq. 5 yields the following:

$\begin{array}{c}\frac{\partial T}{\partial t}=\alpha \frac{{\partial }^{2}T}{\partial x^2}-\frac{L_a}{C_p}\frac{\partial \phi }{\partial t}\end{array}(5)$

Comparing Eq. 5 to the heat conduction in Eqs. 1, 2, it can be seen that Eq. 5 adds a source term related to the latent heat of the phase change $L_a$ in the heat conduction equation.

When the soil’s freezing temperature is a constant value $T_f$, the relationship between the liquid-phase fraction and the enthalpy can be defined as follows:

$\begin{array}{c}\phi =\left\{\begin{array}{c}0H<C_p{T}_f\\ \frac{H-C_p{T}_f}{L_a}{C}_p{T}_f\le H\le C_p{T}_f+L_a\\ 1H>C_p{T}_f+L_a\end{array}\right.\end{array}(6)$

2.1.4 Boundary conditions

The temperature of the soil’s cold source can be defined as follows:

$\begin{array}{c}T\left(0,t\right)=T_0\end{array}(7)$

The soil body has a constant initial temperature that is defined as follows:

$\begin{array}{c}T\left(x,0\right)=T_i\end{array}(8)$

At the solid-liquid phase change interface $y=s\left(t\right)$:

$\begin{array}{c}{T}_s\left(x,t\right)=T_l\left(x,t\right)=T_f\end{array}(9)$

$\begin{array}{c}{k}_s\frac{\partial T_s\left(x,t\right)}{\partial x}-k_l\frac{\partial T_l\left(x,t\right)}{\partial x}={\rho }_s{L}_a\frac{ds\left(t\right)}{dt}\end{array}(10)$

2.1.5 Dimensionless processing

In order to simplify the calculation, the soil’s heat conduction equation and the corresponding boundary conditions are normalized as follows:

$\begin{array}{c}\left\{\begin{array}{c}X=\frac{x}{L}\\ S=\frac{s}{L}\\ F_0=\frac{{\alpha }_{s}t}{L^2}\\ \theta =\frac{T-T_0}{T_i-T_0}\end{array}\right.\end{array}(11)$

where $X$ is the dimensionless length; $S$ is the dimensionless solid-liquid phase change position; $F_0$ is the dimensionless time; $\theta$ is the dimensionless temperature.

Substituting Eq. 11 into Eqs. 1, 2 yields the following:

Solid-phase zone:

$\begin{array}{c}\frac{\partial {\theta }_s\left(X,F_0\right)}{\partial F_0}=\frac{{\partial }^2{\theta }_s\left(X,F_0\right)}{\partial X^2}\left(0<X<S\left(F_0\right)\right)\end{array}(12)$

Liquid-phase zone:

$\begin{array}{c}\frac{\partial {\theta }_l\left(X,F_0\right)}{\partial F_0}=\frac{{\alpha }_s}{{\alpha }_l}\frac{{\partial }^2{\theta }_l\left(X,F_0\right)}{\partial X^2}\left(S\left(F_0\right)<X<1\right)\end{array}(13)$

The corresponding boundary condition transformations are cold source temperature ${\theta }_s\left(0,F_0\right)=0$ and initial temperature ${\theta }_l\left(X,0\right)=1$.

The following equations are valid at the solid-liquid phase change interface $X=S\left(F_0\right)$:

$\begin{array}{c}{\theta }_s\left(X,F_0\right)={\theta }_l\left(X,F_0\right)=\frac{T_f-T_i}{T_0-T_i}\end{array}(14)$

$\begin{array}{c}\frac{\partial {\theta }_s\left(X,F_0\right)}{\partial X}-\frac{k_l}{k_s}\frac{\partial {\theta }_l\left(X,F_0\right)}{\partial X}=\frac{\frac{T_f-T_i}{T_0-T_i}}{Ste}\frac{dS\left(F_0\right)}{d{F}_0}\end{array}(15)$

where $Ste$ is the Stephen number, a dimensionless quantity that is related to the phase change process, $Ste=\frac{C_p\left(T_f-T_0\right)}{L_a}$.

2.2 Lattice Boltzmann model based on the enthalpy method

2.2.1 Lattice Boltzmann model

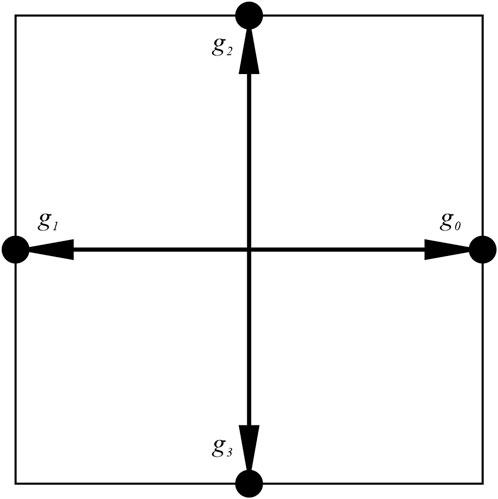
In this study, the temperature in the macroscopic heat conduction equation is taken as a scalar, and the D2Q4 model proposed by Qian et al. (Qian et al., 1992) is used for the soil’s temperature field evolution process during freezing (Figure 2). The time evolution of the particle temperature distribution function $g_i\left(r,t\right)$ can be expressed by the discrete lattice Boltzmann equation in the form of BGK (Bhatnagar, Gross, and Krook) as:

$\begin{array}{c}{g}_i\left(r+{\mathbf{e}}_{\mathbf{i}}{\delta }_t,t+{\delta }_t\right)-g_i\left(r,t\right)=-\frac{g_i\left(r,t\right)-g_i^{eq}\left(r,t\right)}{\tau }+S{r}_i{\delta }_t\left(i=0,1,2,3\right)\end{array}(16)$

where $g_i\left(r,t\right)$ is the particle temperature distribution function along direction $i$ at lattice point $r$ and moment $t$; $e_i$ is the discrete velocity, which consists of a set of velocity vectors in four directions defined as follows:

$\begin{array}{c}\mathbf{e}=c\left[\left(\mathrm{1,0}\right),\left(-\mathrm{1,0}\right),\left(\mathrm{0,1}\right),\left(0,-1\right)\right]\end{array}(17)$

where $c$ is the lattice velocity, $c=\frac{{\delta }_x}{{\delta }_t}$; ${\delta }_x$ and ${\delta }_t$ are the discrete lattice step and time step, respectively; $\tau$ is the dimensionless relaxation time, in which a stable solution is usually obtained for $\tau =1.0$ (Sukop and Thorne, 2006); $g_i^{eq}\left(r,t\right)$ is the equilibrium state distribution function. Since the convection effect was not considered in the soil freezing process, the D2Q4 model $g_i^{eq}\left(r,t\right)$ can be expressed by the following equation:

$\begin{array}{c}{g}_i^{eq}\left(r,t\right)={\omega }_{i}T\left(r,t\right)\end{array}(18)$

where ${\omega }_i$ is the weight factor, ${\omega }_0={\omega }_1={\omega }_2={\omega }_3=\frac{1}{4}$.

FIGURE 2

FIGURE 2. Schematic showing the 4 discrete velocity directions in the D2Q4 model.

The discrete source term $S{r}_i$ in Eq. 16 is defined as:

$\begin{array}{c}S{r}_i={\omega }_{i}Sr\end{array}(19)$

where $Sr$ can be obtained from Eq. 5 as:

$\begin{array}{c}Sr=\frac{L_a}{C_p}\frac{\partial \phi }{\partial t}\end{array}(20)$

Substituting Eqs. 18, 19, and 20 into Eq. 16, the final discrete lattice Boltzmann equation for the freezing process of the soil is obtained as follows:

$\begin{array}{c}{g}_i\left(r+e_i{\delta }_t,t+{\delta }_t\right)-g_i\left(r,t\right)\\ =-\frac{g_i\left(r,t\right)-g_i^{eq}\left(r,t\right)}{\tau }+{\omega }_i\frac{L_a}{C_p}\left[\phi \left(t+{\delta }_t\right)-\phi \left(t\right)\right]\left(i=0,1,2,3\right)\end{array}(21)$

In this study, Eq. 21 was implemented in two steps for the convenience of the programming calculations. These steps are as follows:

(1) Collision

$\begin{array}{c}{g}_i\left(r,t+{\delta }_t\right)-g_i\left(r,t\right)\\ =-\frac{g_i\left(r,t\right)-g_i^{eq}\left(r,t\right)}{\tau }+{\omega }_i\frac{L_a}{C_p}\left[\phi \left(t+{\delta }_t\right)-\phi \left(t\right)\right]\left(i=0,1,2,3\right)\end{array}(22)$

(2) Migration

$\begin{array}{c}{g}_i\left(r+e_i{\delta }_t,t+{\delta }_t\right)=g_i\left(r,t+{\delta }_t\right)\left(i=0,1,2,3\right)\end{array}(23)$

Based on the Chapman-Enskog multiscale expansion method, the lattice Boltzmann Eq. 21 can be reduced to Eq. 5 that contains the phase change by considering the relationship between the macroscopic temperature $T$ and the particle temperature distribution function (i.e., $T={\displaystyle \sum _{i=0}^3}{g}_i\left(r,t\right)$). The expression for the thermal diffusion coefficient $\alpha$ was obtained (Mohamad, 2011) as follows:

$\begin{array}{c}\alpha =c_s^2\left(\tau -\frac{1}{2}\right){\delta }_t\end{array}(24)$

where $c_s$ is the lattice speed of sound. For the D2Q4 model, $c_s^2=\frac{1}{2}{c}^2$.

Since the soil’s thermal diffusion coefficients in the liquid and solid phase zones during freezing soil differ, the relaxation times also vary. In this paper, the variation of the variable relaxation time with the liquid-phase fraction was considered and set according to the thermal diffusion coefficients of different phases as follows:

$\begin{array}{c}\tau =\frac{\phi {\alpha }_l+\left(1-\phi \right){\alpha }_s}{{\delta }_t{c}_s^2}+\frac{1}{2}\end{array}(25)$

The soil’s thermal diffusion coefficient is found according to the percentage of the liquid phase fraction among different phases. Consequently, a unified equation can solve the thermal diffusion coefficient of different phases according to the changes in liquid phase fraction. During the numerical calculation, the relaxation time is obtained from Eq. 25, which is then brought into Eq. 16 for the evolution of the temperature field.

2.2.2 Boundary conditions

Accurate simulation of the boundary conditions is an important part of the numerical calculation that significantly influences accuracy, efficiency, and stability. The following determines the corresponding particle temperature distribution functions according to the macroscopic boundary conditions:

(1) Initial conditions

Assuming that the temperature of the soil body at the initial moment is constant $T_i$, and the particle temperature distribution function at each grid point is in equilibrium, then:

$\begin{array}{c}{g}_i\left(x,0\right)={\omega }_i{T}_i\left(i=\mathrm{0,1,2,3}\right)\end{array}(26)$

(2) Boundary conditions

The non-equilibrium state extrapolation format proposed by Guo et al. (Guo et al., 2002) was used to handle the seepage field boundary of the soil. For the temperature field boundary, there is no essential difference between the two in terms of application (Yong et al., 2009; Gao et al., 2014). This method produces the distribution function with overall second-order accuracy. The basic idea is that the particle temperature distribution function $g_i\left(B,t\right)$ on the boundary lattice point $B$ can be decomposed into two parts: the equilibrium state $g_i^{eq}\left(B,t\right)$ and the non-equilibrium state $g_i^{neq}\left(B,t\right)$, that is:

$\begin{array}{c}{g}_i\left(B,t\right)=g_i^{eq}\left(B,t\right)+g_i^{neq}\left(B,t\right)\end{array}(27)$

For the equilibrium part $g_i^{eq}\left(B,t\right)$, the cold source constant temperature boundary (temperature is always $T_0$) can be obtained from Eq. 18. The adiabatic boundary can be taken as $g_i^{eq}\left(O,t\right)$ with its neighbouring grid point $O$. The solution of the non-equilibrium part $g_i^{neq}\left(B,t\right)$ is complicated. However, the calculation can be simplified by approximating $g_i^{neq}\left(O,t\right)$ of the adjacent lattice points in the temperature field as follows:

$\begin{array}{c}{g}_i\left(B,t\right)=g_i^{eq}\left(B,t\right)+\left[g_i\left(O,t\right)-g_i^{eq}\left(O,t\right)\right]\end{array}(28)$

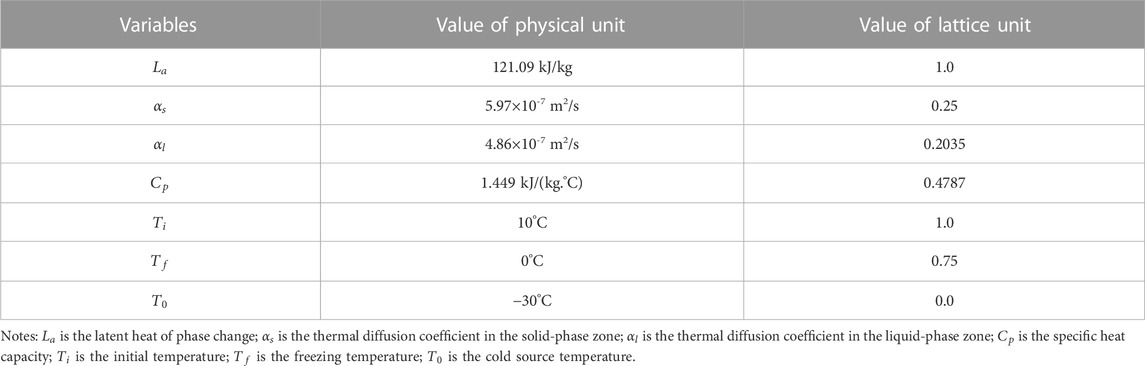
2.2.3 Unit conversions

The program’s parameters are typically taken in lattice units during the numerical calculation of the lattice Boltzmann method. In contrast, physical problems are usually taken in physical units. Hence, a conversion relationship between physical and lattice units must be established. For this purpose, all physical and lattice units involved in the calculation must be dimensionless separately to ensure that the heat conduction criterion before and after dimensionless processing remains the same. Accordingly, a dimensionless parameter was used as a connection bridge to realize the unit conversion between the physical and lattice units.

Based on the dimensionless time, the relationship between the physical time t and the lattice time step can be established as follows:

$\begin{array}{c}{F}_0=\frac{{\alpha }_p{t}_p}{L_p^2}=\frac{{\alpha }_L{t}_L}{L_L^2}\end{array}(29)$

where ${\alpha }_p$ and ${\alpha }_L$ are the thermal diffusion coefficients of the physical and lattice units, respectively; $t_p$ and $t_L$ are the times of the physical and lattice units, respectively ($t_L=N{\delta }_t$, where $N$ is the number of calculation time steps); $L_P$ and $L_L$ are the reference lengths of physical and lattice units, respectively.

If $L_P$ is the length of the whole calculation domain, then $L_L=n\delta x$, where $n$ is the number of lattices in the calculation domain.

The correspondence between the physical unit phase change parameters (latent heat of phase change $L_{\alpha }$, specific heat capacity $C_p$ and the lattice unit can be established by combining the dimensionless temperature based on the dimensionless $Ste$ number as follows:

$\begin{array}{c}Ste=\frac{C_{pp}\left(T_{fp}-T_{0p}\right)}{L_{ap}}=\frac{C_{pL}\left(T_{fL}-T_{0L}\right)}{L_{aL}}\end{array}(30)$

where $C_{pp}$ and $C_{pL}$ are the specific heat capacities of the physical and lattice units, respectively; $L_{ap}$ and $L_{aL}$ are the latent heats of phase change in the physical and lattice units, respectively; $T_{fp}$ and $T_{fL}$ are the phase change temperatures of the physical and lattice units, respectively; $T_{0p}$ and $T_{0L}$ are the cold source temperatures of the physical and lattice units, respectively.

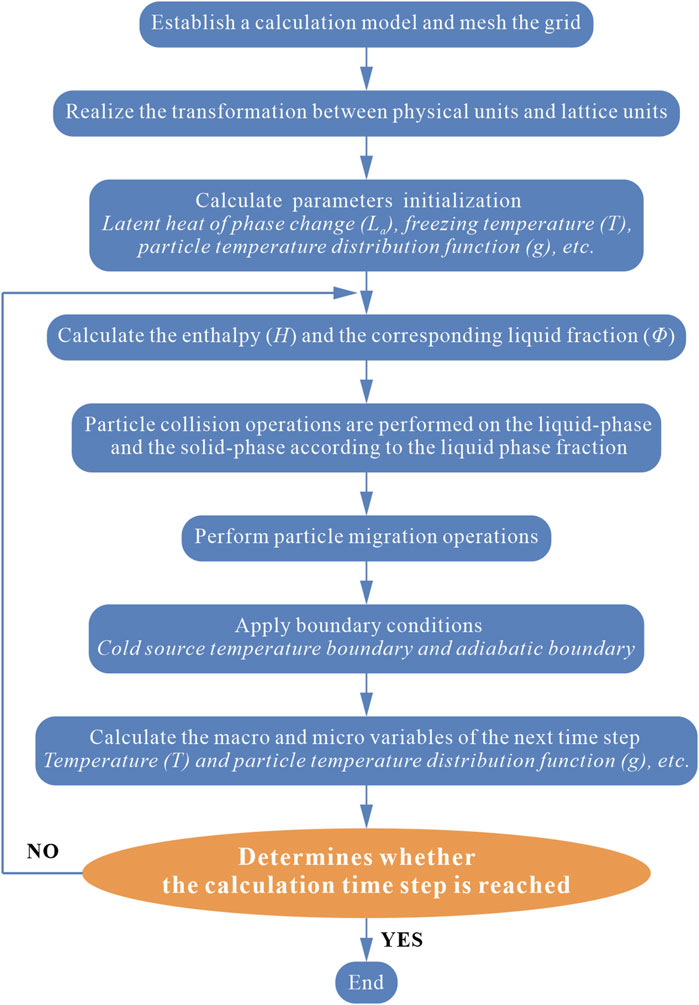
2.2.4 Flow chart of the calculation procedure

In this study, a lattice Boltzmann model based on the enthalpy method is established, and the corresponding calculation procedure is prepared by considering the effects of heat conduction, latent heat release from solid-liquid phase change, and phase change interface movement in the soil’s freezing process. The adopted flowchart is shown in Figure 3.

FIGURE 3

FIGURE 3. Flowchart of the program for investigating soil freezing.

3 Results

3.1 Algorithm validation

In order to verify the accuracy and rationality of this numerical calculation method, the Neumann solution of the unidirectional solid-liquid phase change heat conduction process in a semi-infinite region was solved based on Eqs. 31, 32, 33, and 34 (Ozisik, 1993).

$\begin{array}{c}\frac{e^{-{\lambda }^2}}{\mathit{erf}\left(\lambda \right)}+\frac{k_l}{k_s}{\left(\frac{{\alpha }_s}{{\alpha }_l}\right)}^{1/2}\frac{T_f-T_i}{T_f-T_0}\frac{e^{-\lambda \left({\alpha }_s/{\alpha }_l\right)}}{erfc\left[\lambda {\left({\alpha }_s/{\alpha }_l\right)}^{1/2}\right]}=\frac{\lambda L\sqrt{\pi }}{C_{ps}\left(T_f-T_0\right)}\end{array}(31)$

$\begin{array}{c}\frac{T_s\left(x,t\right)-T_0}{T_f-T_0}=\frac{\mathit{erf}\left[x/2{\left({\alpha }_{s}t\right)}^{1/2}\right]}{\mathit{erf}\left(\lambda \right)}\end{array}(32)$

$\begin{array}{c}\frac{T_l\left(x,t\right)-T_0}{T_f-T_0}=\frac{erfc\left[x/2{\left({\alpha }_{s}t\right)}^{1/2}\right]}{erfc\left[\lambda {\left({\alpha }_s/{\alpha }_l\right)}^{1/2}\right]}\end{array}(33)$

$\begin{array}{c}s\left(t\right)=2\mathrm{\lambda }{\left({\alpha }_{s}t\right)}^{1/2}\end{array}(34)$

The calculation area was set into a $200\times 10$ grid. The calculation model is shown in Figure 1. The macroscopic calculation parameters were all based on the dimensionless parameters. The initial temperature of the calculation region is $T_i=2$, the cold source temperature on the left side of the model is $T_0=0$, the freezing temperature of the solid-liquid phase change is $T_f=1$, the latent heat of the phase change is $L_{\alpha }=0.5$, the specific heat capacity is $C_p=1.0$, and the thermal diffusion coefficient of the solid-phase is ${\alpha }_s=0.25$. The position of the liquid-phase fraction $\phi =0.5$ was set to the solid-liquid phase change interface. The boundary conditions were set to the non-equilibrium extrapolation format at the microscopic level. For the lattice Boltzmann model, the parameters were taken as follows: the time step is ${\delta }_t=1.0$, the transverse and longitudinal are equal to the lattice steps ${\delta }_x={\delta }_y=1.0$, lattice velocity is $c=1.0$, and lattice sound velocity is $c=1/\sqrt{2}$.

Figure 4 shows the solid-liquid phase change interface variation with time when ${\alpha }_s/{\alpha }_l=1,2,and5$, respectively. It can be seen that the numerical solution of the lattice Boltzmann method in this paper matches well with the analytical solution. The error gradually increases with the decrease in the thermal diffusion coefficient of the liquid phase. The maximum relative errors are 1.16%, 1.69%, and 6.17% when $\frac{{\alpha }_s}{{\alpha }_l}$ =1, 2, and 5, respectively. This is mainly because the relaxation time gradually decreases as the thermal diffusion coefficient of the liquid phase decreases at a fixed lattice step and time step, which affects the accuracy of the numerical calculation (Gao, 2001). Based on the soil freezing problem calculated numerically herein, it can be seen that the calculation accuracy can meet the needs of engineering construction, given that the difference between the thermal diffusion coefficients of the soil before and after freezing is not significant.

FIGURE 4

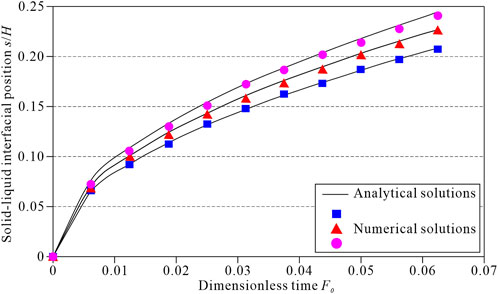
FIGURE 4. Comparison between the numerical and analytical solutions. The top black curve represents ${\alpha }_s/{\alpha }_l=5$, the middle black curve represents ${\alpha }_s/{\alpha }_l=2$, and the bottom black curve represents ${\alpha }_s/{\alpha }_l=1$. The blue square represents ${\alpha }_s/{\alpha }_l=1$, the red triangle represents ${\alpha }_s/{\alpha }_l=2$, and the pink circle represents ${\alpha }_s/{\alpha }_l=5$.

Figure 5 shows a comparison between the numerical calculation results and the analytical solutions for the temperature field at a dimensionless time of $F_0=0.0625$ (the calculated time step is 10,000) and ${\alpha }_s/{\alpha }_l=1,2,and5$, respectively. It can be seen that the numerical and analytical solutions of the lattice Boltzmann method are consistent. In contrast, the error increases with the decrease in the thermal diffusion coefficient of the liquid phase. The maximum relative errors are 0.42%, 0.84%, and 2.58% when ${\alpha }_s/{\alpha }_l=1,2,and5$, respectively. The maximum error occurs at the solid-liquid phase change interface, and the farther the distance from the interface, the smaller the error.

FIGURE 5

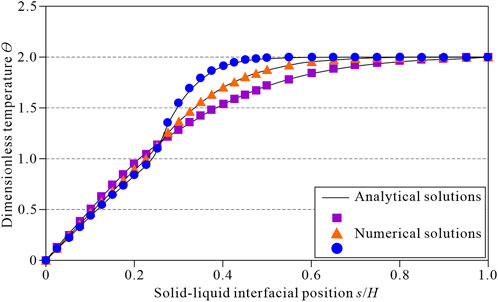
FIGURE 5. Comparison between the numerical and analytical solutions when $F_0=0.0625$ (the calculated time step is 10,000). The top black curve represents ${\alpha }_s/{\alpha }_l=5$, the middle black curve represents ${\alpha }_s/{\alpha }_l=2$, and the bottom black curve represents ${\alpha }_s/{\alpha }_l=1$. The purple square represents ${\alpha }_s/{\alpha }_l=1$, the orange triangle represents ${\alpha }_s/{\alpha }_l=2$, and the blue circle represents ${\alpha }_s/{\alpha }_l=5$.

3.2 An example of the temperature field evolution

As many researchers have done, all the methods should be verified by examples (Wang et al., 2019; Lei et al., 2022; Wang et al., 2023; Zhao et al., 2023). We have chosen an engineering example in Shanghai to validate the lattice Boltzmann model based on the enthalpy method. The foundation soil of an artificial freezing project in Shanghai is straw-yellow sandy silt. The thermophysical parameters were measured according to the physical property tests of samples in the normal state and the frozen state as follows: the thermal diffusion coefficient of the formation is ${\alpha }_s=5.97\times {10}^{-7}{m}^2/s$ in the solid-phase zone and ${\alpha }_l=4.86\times {10}^{-7}{m}^2/s$ in the liquid-phase zone; the latent heat of phase change is $L_{\alpha }=121.09kJ/kg$; the specific heat capacity is $C_p=1.449kJ/\left(kg\bullet ℃\right)$. The soil’s initial measured temperature is $T_i=10℃$, the freezing temperature is $T_f=0℃$, and the cold source temperature is $T_0=-30℃$. For the convenience of calculation, the length of the calculation area was assumed as $L=2m$. Besides, the same settings for the basic parameters and boundary conditions of the lattice Boltzmann model were made as in the validation example. At the same time, the length of the calculation range was taken as $L=2000$. Moreover, a unit transformation was carried out to correspond to the soil’s freezing parameters and obtain the calculation parameters of the corresponding lattice Boltzmann model, as shown in Table 1.

TABLE 1

TABLE 1. Parameter values used in the simulation.

3.2.1 Evolution of temperature field in the soil under unilateral cold source

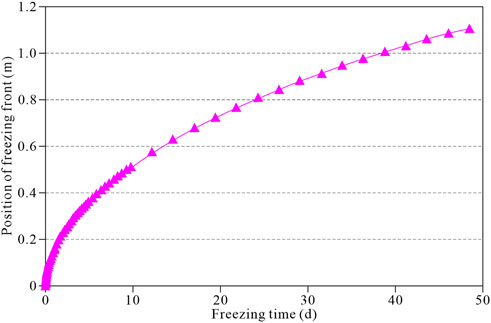
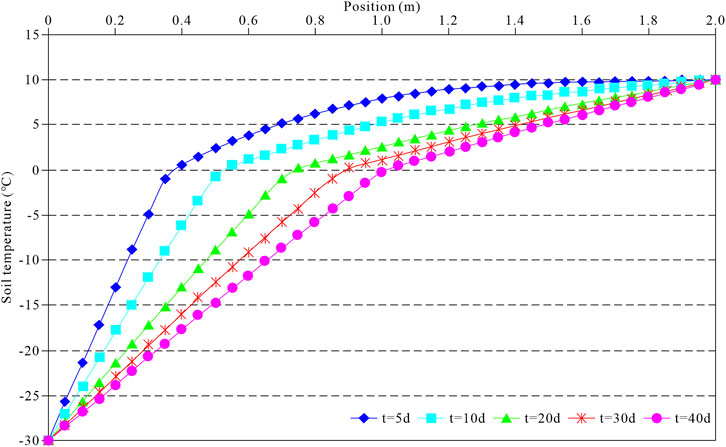
Under a unilateral cold source, the temperature of the soil body decreases rapidly, leading to the freezing front’s formation by condensing internal water into ice. Figure 6 shows the evolution of the freezing front in the soil body with time. The figure shows that at the early stage of freezing, the freezing front in the soil body moves faster, and the evolution rate slows down with time. Besides, the frozen front moved 0.37, 0.52, 0.74, 0.89, and 1.02 m at 5, 10, 20, 30, and 40 days, respectively.

FIGURE 6

FIGURE 6. Position of freezing front plotted against freezing time.

Figure 7 shows the development of the soil’s temperature field under the unilateral cold source. The soil temperature decreases rapidly at the early stage of freezing because the cold source temperature is $-30℃$, much lower than the initial temperature of $10℃$. Thereafter, over time, the temperature field decreases because the temperature difference in the soil gradually becomes smaller. Considering the freezing front as the boundary, the two sides present a significant difference in the trend of the temperature field due to the influence of heat release from the solid-liquid phase change and different thermal diffusion coefficients. The soil temperature in the solid-phase zone develops faster and is approximately linear; in the liquid-phase zone, the soil develops slowly and gradually converges to the initial temperature of the soil. According to the code (DG/T J08-902, 2016), when the soil excavation depth is 12–30 m, the design reference value of the average temperature in the freezing wall must be taken as $-8\sim -10℃$. Therefore, when $-10℃$ is taken as the limit for freezing wall temperature, the thickness of the freezing wall developed at 5, 10, 20, 30, and 40 days under the unilateral cold source is 0.24, 0.33, 0.47, 0.57, and 0.66 m, respectively.

FIGURE 7

FIGURE 7. Distribution of soil temperature field when time $t$ is different.

3.2.2 Evolution of temperature field in the soil under the action of bilateral cold sources

In artificial freezing works, multiple tubes are usually used to form the soil’s freezing curtain. Therefore, the interaction between two or more cold sources must be studied. For this purpose, the temperature of the cold source was applied on both sides of the soil within 2.0 m width to study the variation of the temperature field in the soil. Figure 8 shows the trend in the variation of the liquid-phase fraction in the soil for 5, 10, 20, and 30 days. It can be seen that the position of the freezing front moves 0.37, 0.54, 0.78, and 0.98 m under the action of the bilateral cold sources for the time periods of 5, 10, 20, and 30 days. Compared to the unilateral cold source, the freezing front’s movement has moved faster with time.

FIGURE 8

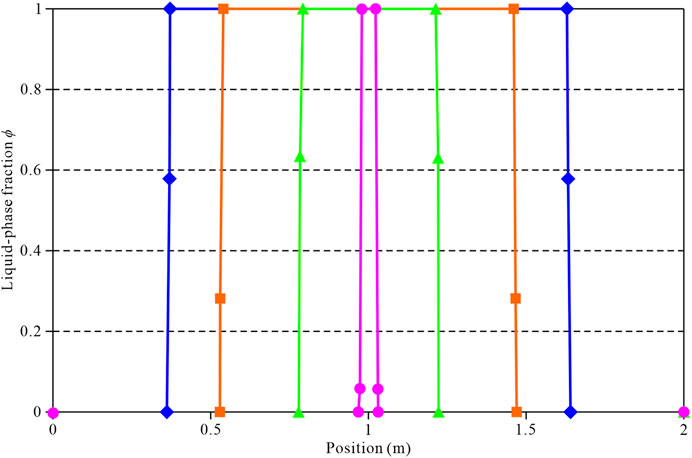
FIGURE 8. Distribution of the liquid-phase fraction $\phi$ when time $t$ is different under the bilateral cold source. The blue rhombus represents $t=5d$, the orange square represents $t=10d$, the green triangle represents $t=20d$, and the pink circle represents $t=30d$ .

Figure 9 shows that due to the bilateral cold sources, the temperature in the soil gradually decreases from both sides to the middle. The overall temperature in the soil drops below $0℃$ in about 30 days, and all the water condenses into ice. The temperature in the soil decreases rapidly after that, and at 35 days and 45 days, the overall temperature in the soil drops below $-13.6℃$ and $-26.4℃$, which are less than the average temperature of the frozen wall design’s reference value. Hence, the excavation work of underground works can be carried out.

FIGURE 9

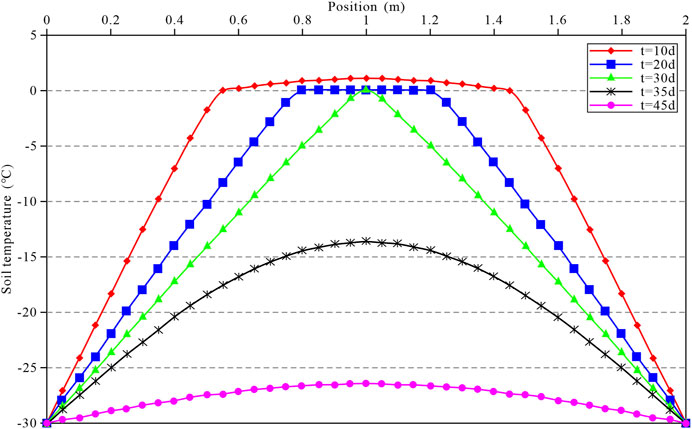
FIGURE 9. Variation in the soil temperature field when time $t$ is different under the bilateral cold source.

4 Conclusion and discussion

This study considers the effects of heat conduction, heat release from solid-liquid phase change, phase change interface movement, and heat diffusion coefficient changes during soil freezing to establish a unified evolution equation in the entire calculation region (solid-phase zone, liquid-phase zone, and phase change interface) using the enthalpy method. It numerically solves the D2Q4 model based on the lattice Boltzmann method for the heat conduction equation accompanied by the phase change. Combined with an engineering example of an artificial freezing method in Shanghai, the temperature field in the soil, the development trend of the freezing front with time, and the formation time of the freezing wall under the influence of unilateral and bilateral cold sources (considering the interaction between the cold sources) are determined, and the following conclusions are drawn:

(1) The numerical calculation results are analysed based on the lattice Boltzmann method and compared to the Neumann solution of the solid-liquid phase change heat conduction problem in semi-infinite space, which verifies the accuracy of the present numerical calculation method.

(2) According to the code (DG/T J08-902, 2016), when $-10℃$ is taken as the limit for freezing wall temperature, the thickness of the freezing wall developed at 5, 10, 20, 30, and 40 days under the unilateral cold source is 0.24, 0.33, 0.47, 0.57, and 0.66 m, respectively. These values can provide a basis for engineering design.

(3) Compared to the unilateral cold source, the freezing front’s movement moves faster under the bilateral cold sources. The position of the freezing front moves 0.37, 0.54, 0.78, and 0.98 m for the time periods of 5, 10, 20, and 30 days. The overall temperature in the soil drops below $-13.6℃$ and $-26.4℃$ at 35 days and 45 days, which are less than the average temperature of the frozen wall design’s reference value. Hence, the excavation work of underground works can be carried out.

(4) The lattice Boltzmann model based on the enthalpy method established in this paper can be used to deal with the heat conduction problem accompanied by phase change in underground engineering. However, the effect of moisture migration during the freezing process of soil and the resulting freezing deformation are not considered. The next step is to study the coupled heat transfer mechanism between the moisture field and soil particles using the double distribution function. Besides, a numerical model for simulating the freezing process of soil at the pore scale needs to be established by considering the freezing phase change of the moisture field and the influence of moisture migration heat conduction.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

LT, and LS contributed to conception and methodology of the study. JL organized the database. ZW performed the statistical analysis. LT and LS wrote the first draft of the manuscript. LT, LS, ZW, and JL wrote sections of the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (Grant Numbers 11962008, 42167022, and 42067043).

Acknowledgments

The authors thank Chao Yang and Qiming Zhou for their invaluable assistance in plotting figures.

Conflict of interest

Author JL was employed by Power China Kunming Engineering Corporation Limited, Kunming, China.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alva, L. H., González, J. E., and Dukhan, N. (2006). Initial analysis of PCM integrated solar collectors. J. Sol. Energy Eng. 128, 173–177. doi:10.1115/1.2188532

CrossRef Full Text | Google Scholar

Costa, M., Buddhi, D., and Oliva, A. (1998). Numerical simulation of a latent heat thermal energy storage system with enhanced heat conduction. Energy Convers. manage. 39, 319–330. doi:10.1016/S0196-8904(96)00193-8

CrossRef Full Text | Google Scholar

DG/T J08 902 (2016). Technical code for crosspassage freezing method. Shanghai, China: Shanghai Municipal Commission of Housing and Urban-Rural Development.

Google Scholar

Eshraghi, M., and Felicelli, S. D. (2012). An implicit lattice Boltzmann model for heat conduction with phase change. Int. J. Heat. Mass Transf. 55, 2420–2428. doi:10.1016/j.ijheatmasstransfer.2012.01.018

CrossRef Full Text | Google Scholar

Gao, D. Y., Chen, Z. Q., and Chen, L. H. (2014). A thermal lattice Boltzmann model for natural convection in porous media under local thermal non-equilibrium conditions. Int. J. Heat. Mass Transf. 70, 979–989. doi:10.1016/j.ijheatmasstransfer.2013.11.050

CrossRef Full Text | Google Scholar

Gao, D. Y. (2001). Study on solid-liquid phase change heat transfer in metal foams based on lattice Boltzmann method. Doctor Thesis. Nanjing: Southeast University.

Google Scholar

Guo, Z. L., Zheng, C. G., and Shi, B. C. (2002). Non-equilibrium extrapolation method for velocity and pressure boundary conditions in the lattice Boltzmann method. Chin. Phys. 11, 366–374. doi:10.1088/1009-1963/11/4/310

CrossRef Full Text | Google Scholar

Huang, S. L., Aughenbaugh, N. B., and Wu, M. C. (1986). Stability study of CRREL permafrost tunnel. J. Geotech. Eng. 112, 777–790. doi:10.1061/(ASCE)0733-9410(1986)112:8(777)

CrossRef Full Text | Google Scholar

Jiaung, W. H., Ho, J. R., and Kuo, C. P. (2001). Lattice Boltzmann method for the heat conduction problem with phase change. Numer. Heat. Transf. Part B 39, 167–187. doi:10.1080/10407790150503495

CrossRef Full Text | Google Scholar

Jing, L., Tsang, C. F., and Stephansson, O. (1995). DECOVALEX—An international co-operative research project on mathematical models of coupled THM processes for safety analysis of radioactive waste repositories. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 32, 389–398. doi:10.1016/0148-9062(95)00031-B

CrossRef Full Text | Google Scholar

Lei, Z. D., Wu, B. S., Wu, S. S., Nie, Y. X., Cheng, S. Y., and Zhang, C. (2022). A material point-finite element (MPM-FEM) model for simulating three-dimensional soil-structure interactions with the hybrid contact method. Comput. Geotechnics 152, 105009. doi:10.1016/j.compgeo.2022.105009

CrossRef Full Text | Google Scholar

Levin, L., Golovatyi, I., Zaitsev, A., Pugin, A., and Seminet, M. (2021). Thermal monitoring of frozen wall thawing after artificial ground freezing: Case study of Petrikov Potash Mine. Tunn. Undergr. Space Technol. 107, 103685. doi:10.1016/j.tust.2020.103685

CrossRef Full Text | Google Scholar

Miller, W., and Succi, S. (2002). A lattice Boltzmann model for anisotropic crystal growth from melt. J. Stat. Phys. 107, 173–186. doi:10.1023/A:1014510704701

CrossRef Full Text | Google Scholar

Mohamad, A. A. (2011). Lattice Boltzmann method: Fundamentals and engineering applications with computer codes. London: Springer-Verlag. doi:10.1007/978-0-85729-455-5

CrossRef Full Text | Google Scholar

Ozisik, M. (1993). Heat conduction. New York: John Wiley and Sons.

Google Scholar

Qian, Y. H., D’Humières, D. D., and Lallemand, P. (1992). Lattice BGK models for Navier-Stokes equation. Europhys. Lett. 17, 479–484. doi:10.1209/0295-5075/17/6/001

CrossRef Full Text | Google Scholar

Rabin, Y., and Korin, E. (1993). An efficient numerical solution for the multidimensional solidification (or melting) problem using a microcomputer. Int. J. Heat. Mass Transf. 36, 673–683. doi:10.1016/0017-9310(93)80043-T

CrossRef Full Text | Google Scholar

Radoslwa, L., Michaloeski, E., and Zhu, M. (2006). “Freezing and ice growth in frost-susceptible soils,” in Geotechnical symposium in roma, soil stress-strain behavior: Measurement, modeling and analysis (Roma, Italy: Spinger). doi:10.1007/978-1-4020-6146-2_25

CrossRef Full Text | Google Scholar

Shamsundar, N., and Sparrow, E. M. (1975). Analysis of multidimensional conduction phase change via the enthalpy model. J. Heat. Transf. 97, 333–340. doi:10.1115/1.3450375

CrossRef Full Text | Google Scholar

Sukop, M. C., and Thorne, D. T. (2006). Lattice Boltzmann Modeling: An introduction for geoscientists and engineers. Berlin: Springer-Verlag. doi:10.1007/978-3-540-27982-2

CrossRef Full Text | Google Scholar

Van Dorst, A. A. E. (2013). Artificial ground freezing as a construction method for underground spaces in densely built up areas. Master thesis. Delft: Delft University of Technology.

Google Scholar

Voller, V. R., Swaminathan, C. R., and Thomas, B. G. (1990). Fixed grid techniques for phase change problems: A review. Int. J. Numer. Meth. Engng. 30, 875–898. doi:10.1002/nme.1620300419

CrossRef Full Text | Google Scholar

Wang, G. J., Tian, S., Hu, B., Xu, Z. F., Chen, J., and Kong, X. Y. (2019). Evolution pattern of tailings flow from dam failure and the buffering effect of debris blocking dams. Water 11, 2388. doi:10.3390/w11112388

CrossRef Full Text | Google Scholar

Wang, G. J., Zhao, B., Wu, B. S., Zhang, C., and Liu, W. L. (2023). Intelligent prediction of slope stability based on visual exploratory data analysis of 77 in situ cases. Int. J. Min. Sci. Technol. 33, 47–59. doi:10.1016/j.ijmst.2022.07.002

CrossRef Full Text | Google Scholar

Yong, Y. M., Yang, C., and Mao, Z. S. (2009). Numerical simulation of thermal convection in triangular enclosure using lattice Boltzmann method. Chin. J. Process Eng. 9, 841–847. doi:10.3321/j.issn:1009-606X.2009.05.002

CrossRef Full Text | Google Scholar

Zhao, B., Wang, G. J., Wu, B. S., and Kong, X. Y. (2023). A study on mechanical properties and permeability of steam-cured mortar with iron-copper tailings. Constr. Build. Mat. 383, 131372. doi:10.1016/j.conbuildmat.2023.131372

CrossRef Full Text | Google Scholar