Earthquake recurrence probability assessment using integrated multi-fault paleoseismic data: application to the East Kunlun Fault Zone

Reliable earthquake recurrence probability assessment is crucial for seismic hazard mitigation but remains challenging due to sparse paleoseismic data on individual faults. We present an enhanced integrated multi-fault approach that addresses critical limitations in existing methods by incorporating both local and regional paleoseismic data through Monte Carlo simulation. Our method: (1) includes local fault variability data rather than relying solely on non-local sources, (2) restricts analysis to tectonically similar fault zones, and (3) explicitly accounts for epistemic uncertainties in mean recurrence intervals. We applied Brownian Passage Time (BPT) models to seven segments of the East Kunlun Fault Zone in China. Our analysis reveals that mean recurrence intervals are systematically higher than simple arithmetic averages. When dating uncertainties are not considered, coefficients of variation range from 0.48 to 0.60. However, when dating uncertainties are incorporated, coefficients of variation increase substantially to 0.59–0.81. Fifty-year earthquake probabilities vary significantly among segments, with Dongxidatan (0.115), Maqu (0.054), Maqin (0.040), and Tazang (0.026) showing highest probabilities. These results highlight the crucial role of chronological uncertainty in hazard assessment. This methodology provides a robust framework for seismic hazard assessment in data-sparse regions, offering improved reliability for earthquake risk evaluation and disaster preparedness.

1 Introduction

Based on Reid’s elastic rebound theory (Reid, 1910), large earthquake occurrence on a given fault exhibits temporal memory characteristics. According to this hypothesis, following a large earthquake, the fault requires a prolonged period to accumulate sufficient energy for the next large earthquake, characterizing the process as quasi-periodic (McCann et al., 1979; Shimazaki and Nakata, 1980). Building upon Reid’s elastic rebound theory as the foundational physical assumption, Schwartz and Coppersmith introduced the concept of “characteristic earthquakes” based on analysis of repeated large earthquake data on the San Andreas Fault (Schwartz and Coppersmith, 1984). A “characteristic earthquake” describes repeated ruptures along specific fault segments that share similar rupture lengths, displacements, magnitudes, and quasi-periodic recurrence intervals.

To describe the recurrence times between characteristic events in this time-dependent model, researchers proposed various probability distributions, including the biexponential distribution (Utsu, 1972), Gaussian distribution (Rikitake, 1974), lognormal distribution (Nishenko and Buland, 1987), Weibull distribution, gamma distribution (Utsu, 1984), and BPT distribution (Ellsworth et al., 1999; Matthews, 2002). However, defining reliable probability density functions (PDFs) for recurrence intervals remains challenging.

Considering limited data availability on individual faults, particularly where only one or two data points exist, Nishenko and Buland assumed that characteristic earthquake recurrence intervals across multiple faults exhibit universal variability (Nishenko and Buland, 1987). They employed a normalization function $\frac{T}{T_{ave}}$ to integrate recurrence interval data from multiple faults for statistical analysis, obtaining a universal distribution pattern and coefficient of variation. Here, $T_{ave}$ represents the mean of limited recurrence interval samples on each fault, and T represents individual recurrence intervals. This method assumes that $T_{ave}$ for each fault represents the true mean recurrence interval (μ), linking multiple faults through $T_{ave}$. However, using $\frac{T}{T_{ave}}$ has a critical limitation: the observed sample mean ($T_{ave}$) of recurrence intervals on each fault does not necessarily represent the true mean recurrence interval (μ) for that fault. Assuming that different fault $T_{ave}$ values represent actual mean recurrence intervals ignores this deviation, potentially leading to biased statistical results by overlooking epistemic uncertainty in mean recurrence intervals.

Considering the uncertainty and variability of actual mean recurrence intervals (μ) in short earthquake series, Guo et al. proposed a method to calculate large earthquake recurrence probabilities using normalized recurrence intervals from multiple short earthquake series (Guo et al., 2018). Unlike Nishenko and Buland’s normalization method (Nishenko and Buland, 1987), Guo et al. linked local and non-local recurrence interval data through random pairing, eliminating the need for normalization functions ($\frac{T}{T_{ave}}$) (Guo et al., 2018). Any given local recurrence interval can occupy the same position as a non-local recurrence interval within the probability density distribution function, thereby linking the variability of local and non-local earthquake series. Through extensive random pairing of local and non-local recurrence intervals, numerous synthetic local potential recurrence intervals are generated, enabling statistical analysis of their distribution. However, Guo et al.'s method relies entirely on non-local data from the database to extract variability data, meaning that all the obtained variability information originates from non-local sources. Local data are only randomly sampled to reflect epistemic uncertainty in local mean recurrence intervals. While statistical results consider epistemic uncertainty regarding mean recurrence intervals based on local recurrence interval data quantity, they do not utilize variability data from local faults.

Building upon Guo et al.'s methodology, we propose an enhanced integrated multi-fault paleoseismic data approach for earthquake recurrence probability assessment. While maintaining original advantages, our method includes local fault earthquake series in the established database, better utilizing local earthquake variability data.

Additionally, Guo et al.'s methodology utilized a fault database containing data from 40 faults across mainland China (Guo et al., 2018). Although the dataset is substantial, it spans different regions and fault zones with potentially significant differences in tectonic settings. Therefore, we propose restricting the regional scope to a single seismic tectonic zone or earthquake fault zone.

This approach yields smaller variability datasets with less smooth distribution curves, necessitating fitting procedures for large earthquake recurrence probability assessment. For example, we employ the commonly used BPT distribution for fitting.

Finally, we apply our proposed integrated multi-fault paleoseismic data approach to assess large earthquake recurrence probabilities for seven fault segments in the East Kunlun Fault Zone, western China.

2 Methods

For a given fault, if sufficiently long earthquake sequences (including paleoseismic and historical records) are available, probability density functions (PDFs) for large earthquake recurrence can be accurately derived through statistical analysis. However, fault sequences typically contain limited seismic event records, and paleoseismic datasets often contain fewer than 10 recurrence intervals, which is insufficient for reliable probability density function (PDF) determination (Ellsworth et al., 1999; Parsons, 2008).

Nishenko and Buland used normalization function $\frac{T}{T_{ave}}$ to integrate recurrence interval data from multiple faults for statistical analysis, obtaining universal distribution patterns and coefficients of variation (Nishenko and Buland, 1987). This method expands local datasets but assumes that $T_{ave}$ on each fault represents the true mean recurrence interval, thereby linking normalized recurrence interval data $\frac{T}{T_{ave}}$ from different faults. However, observed sample means ($T_{ave}$) of recurrence intervals on each fault do not represent actual mean recurrence intervals for given faults. This statistical approach ignores epistemic uncertainty in mean recurrence intervals, potentially leading to biased statistical results. Using $T_{ave}$ to link local and non-local data, while simple, loses uncertainty considerations. For instance, as long as two faults have identical $T_{ave}$ values, the quantity of local recurrence data has no impact on distribution patterns.

Considering epistemic uncertainty regarding mean recurrence intervals in short earthquake sequences, Guo et al. proposed linking local and non-local recurrence interval data through random pairing rather than assuming $T_{ave}$ represents actual mean recurrence intervals (Guo et al., 2018). This approach acknowledges that mean recurrence intervals on each fault are unknown and that positions of individual recurrence interval data within actual PDFs are also unknown. This approach assumes that any local recurrence interval data and any non-local recurrence interval data may occupy identical positions within the recurrence probability density functions (PDFs). Furthermore, based on the principle of indifference (Laplace’s principle), it assumes that any pairwise combination between local and non-local recurrence interval datasets exhibits equal probability.

Through extensive random pairing, each pairing achieved through equiprobable random selection can link local and non-local recurrence interval data while reflecting epistemic uncertainty regarding mean recurrence intervals.

Through extensive random pairing of local and non-local recurrence intervals, numerous synthetic local potential recurrence intervals are generated, enabling statistical analysis of their distributions. However, Guo et al.'s method, while establishing connections between local and non-local faults and utilizing non-local fault data, derives all variability data entirely from non-local faults in the database, failing to incorporate local data—representing a significant data gap (Guo et al., 2018).

Additionally, Guo et al.'s methodology utilized a fault database containing data from 40 faults across mainland China, distributed across different regions and fault zones with potentially significant tectonic setting differences and varying recurrence patterns, making joint statistical analysis inappropriate (Guo et al., 2018).

To address these issues, building upon Guo et al.'s research foundation, we implement several improvements and propose an integrated multi-fault paleoseismic data approach for earthquake recurrence probability assessment.

2.1 Stochastic pairing method for utilizing integrated multi-fault paleoseismic data

Paleoseismic data from a single fault are typically insufficient to establish reliable probability density distributions for earthquake recurrence. To address this limitation, Guo et al. (2018) proposed a random pairing approach that integrates local and non-local paleoseismic datasets, utilizing paleoseismic data from multiple remote faults to estimate large earthquake recurrence probabilities on the local fault. Using the Monte Carlo framework from Guo et al. (2018) as a foundation, we develop an improved method for integrating multi-fault paleoseismic data that addresses key limitations while retaining the benefits of random pairing for uncertainty handling.

Our proposed methodology incorporates the following fundamental assumptions and settings:

1. Given the limited paleoseismic data available for individual faults, we assume that all faults within a single fault zone exhibit consistent variability and probability density distribution patterns, thereby enabling the utilization of paleoseismic data from other regional faults. While Guo et al. (2018) incorporated paleoseismic data from different fault zones across mainland China, we constrain our regional scope to multiple faults within a single seismic fault zone. This refinement is based on the premise that faults within the same fault zone share similar tectonic environments, comparable fault characteristics, and consistent geological backgrounds.

2. We establish a comprehensive database encompassing paleoseismic sequences from multiple faults within the defined region. Recognizing the critical importance of local paleoseismic sequences in predicting local recurrence probabilities, our database explicitly includes local paleoseismic data—a significant departure from the Guo et al. (2018)’s methodology.

3. Our method maintains Guo et al. (2018)’s fundamental assumption that for limited recurrence interval data on individual faults, the actual mean recurrence interval remains unknown, and the percentile positions of each recurrence interval datum within actual probability density distributions are uncertain.

4. For multiple faults within the database, any recurrence interval T from the local fault can be paired with any recurrence interval T′ from other faults in the database, meaning that T and T′ occupy equivalent percentile positions within their respective recurrence interval distribution patterns. This approach establishes a relationship between local recurrence intervals and non-local recurrence interval data. Applying Laplace’s principle of equal likelihood, any local recurrence interval and any recurrence interval from other faults have an equal probability of being paired together.

5. Monte Carlo simulation methods effectively model this random pairing process, enabling the utilization of variability data from other faults. Moreover, with sufficient simulation iterations, this approach can adequately represent the positional uncertainty of recurrence interval data within their respective probability density functions (PDFs).

Based on these fundamental principles, our specific methodology follows:

First, in each simulation, we randomly select one recurrence interval interval T (the reference interval for the target fault) from local recurrence interval dataset. Subsequently, connections with non-local data can be established through this reference interval T. From faults other than the target fault in the regional paleoseismic database, we respectively randomly select one recurrence interval datum T′ as the associated reference interval. We assume this datum pair (T-T′) occupies the same percentile position within the recurrence interval probability distribution function, thereby providing each fault with a reference interval. In this random association process, the local earthquake sequence in the database does not require random selection, and T is directly used as the reference interval.

Second, with each fault having a reference interval, ratios between other recurrence interval data on the fault and the reference interval become relative variability data, reflecting potential variation relative to reference data. For a fault with k recurrence interval data points (where k ≥ 2), we can obtain k-1 relative variability data points. For this database, if N faults in the study region collectively contain x total recurrence intervals, we can obtain x-N relative variability data points, each simulation we equiprobably randomly selects one from the x-N relative variability data points. Multiplying this by reference datum T from local fault yields one potential recurrence interval datum from one simulation.

Finally, through extensive simulation, we obtain sample distributions of numerous potential recurrence intervals, enabling estimation of large earthquake recurrence probability distribution patterns on target faults.

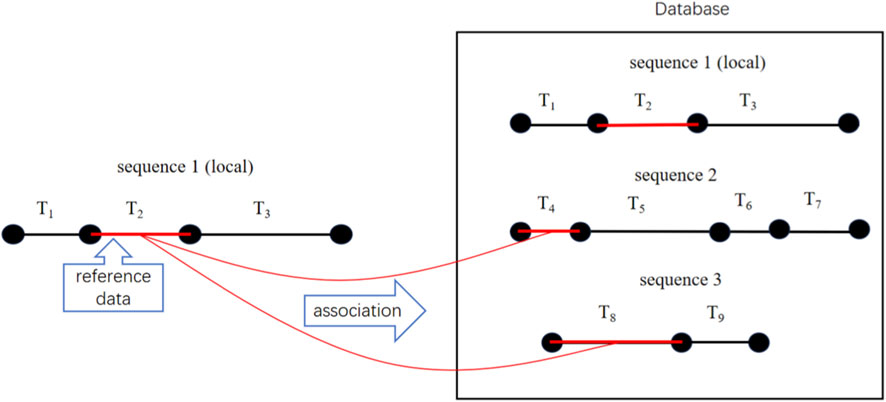
For clarity, we provide a simple example of our method (See Figure 1), where, three faults are contained within a fault zone with consistent tectonic settings, and a database is established based on the earthquake sequences from these three faults. To estimate large earthquake recurrence probability distributions on the first fault using our proposed integrated multi-fault paleoseismic data approach for earthquake recurrence probability assessment:

Figure 1

Figure 1. Schematic illustration of a single simulation process.

First, randomly select one from recurrence interval samples on Fault 1 as reference data, for example: the reference datum selected this time is T₂.

Then, select one recurrence interval datum each from Faults 2 and 3 as associated reference data. For example: associated reference data selected from Faults 2 and 3 are T₄ and T₈, respectively.

Through correspondence relationships between reference data and associated reference data, we establish connections between local and non-local faults. By dividing the recurrence intervals (excluding the reference data) of the three faults in the database by their respective reference recurrence intervals, we can obtained 6 relative variability values. Multiplying these relative variability values by the local reference recurrence interval $T_2$ yields 6 potential recurrence interval data. Consequently, sequence 1 contains 2 recurrence data T₁ and T₃, sequence 2 contains 3 recurrence data $\frac{T_5{T}_2}{T_4}$, $\frac{T_6{T}_2}{T_4}$ and$\frac{T_7{T}_2}{T_4}$, and sequence 3 contains 1 recurrence datum $\frac{T_9{T}_2}{T_8}$.

In this simulation, to obtain a recurrence datum, we equiprobably randomly select 1 from the 6 potential interval data. This value represents one simulation result and one potential recurrence interval datum.

Through extensive simulation, we obtain sample distributions of numerous potential recurrence intervals on Fault 1, enabling estimation of large earthquake recurrence probability distributions on Fault 1.

2.2 Improvements from previous methods

First, in Guo et al.'s method, the database contains entirely non-local data, meaning all obtained variability data originates entirely from non-local sources (Guo et al., 2018). Local data random sampling only reflects epistemic uncertainty in local mean recurrence intervals.

The database serves as the source of relative variability data. Our method effectively combines local and non-local data. In each simulation, after establishing connections with local faults, local relative variability data and other fault relative variability data have equal weights. Through equiprobable selection, we randomly obtain one from relative variability data.

Additionally, since associated reference data on other faults require additional random selection in each simulation while local reference data do not require further random selection, local variability data appear more frequently in results and are less likely to be diluted.

Second, following Nishenko and Buland’s approach, this study assumes generic variability in earthquake recurrence across regions with similar tectonic settings (Nishenko and Buland, 1987). However, regions should not be excessively large, preferably within the same fault zone. When Ellsworth et al. proposed the BPT model (Ellsworth et al., 1999), they suggested α = 0.5 as a universal coefficient of variation. Field et al. employed uniform coefficients of variation for California in the UCERF3 model (Field et al., 2015). Zöller believes that variability within small regions is consistent and related to b-values (Zöller, 2018). Therefore, we propose limiting regional scope to single seismic tectonic zone or earthquake fault zone.

Third, Guo et al.'s methodology utilized fault databases containing data from 40 faults across mainland China (Guo et al., 2018). Although substantial, these data span different regions and fault zones with potentially significant tectonic setting differences. Since we propose limiting regional scope to single seismic tectonic zones or earthquake fault zone, obtained variability data quantities are smaller with less smooth distribution curves, necessitating fitting for large earthquake recurrence probability assessment. For example, we select the commonly used BPT distribution for fitting. Time-dependent seismic hazard studies generally employ BPT distributions to describe large earthquake recurrence characteristics (Field et al., 2015). BPT distributions, also called inverse Gaussian distributions, can be expressed as Equation 1:

$\mathit{f}\left(\mathit{T}\right)=\sqrt{\frac{\mathit{\mu }}{2\mathit{\pi }{\mathit{\alpha }}^2{\mathit{T}}^3}}{\mathit{e}}^{-\frac{{\left(\mathit{T}-\mathit{\mu }\right)}^2}{2\mathit{\mu }{\mathit{\alpha }}^2\mathit{T}}}(1)$

where μ represents mean recurrence intervals and α represents coefficients of variation.

Alternatively, we can employ other distributions such as lognormal, Weibull, or normal distributions for fitting.

2.3 Implementation steps

The simulation and implementation procedures for the proposed Integrated Multi-fault Paleoseismic Data-based Earthquake Recurrence Probability Assessment Method are outlined as follows:

1. In each simulation, based on paleoseismic data from the target fault, we randomly select one recurrence interval from several local recurrence interval samples with equal probability as the local reference interval for this simulation.

2. In each simulation, from the regional multi-fault paleoseismic databases, for each fault except the local fault, we randomly select one recurrence interval from limited recurrence interval samples with equal probability as a reference interval to be associated with the local reference interval, assuming that the reference recurrence intervals on each fault (including local and non-local faults in the database) occupy identical percentile positions in their respective probability density functions (PDFs), thus establishing the connection between local and non-local faults.

3. After completing the associations, by dividing each recurrence interval by the reference data on the corresponding fault, for a fault with k recurrence interval data in the database, we can obtain k-1 relative variability data points. If N faults in the database contain x total recurrence interval data, we can obtain x-N relative variability data points. From these x-N relative variability data points, we randomly select one with equal probability and multiply it by the local reference data to obtain a potential recurrence interval datum T, thereby completing one simulation.

4. Through extensive repeated simulations (e.g., 100,000 iterations), we generate numerous potential local recurrence interval T data. Under the assumption that large earthquake recurrence intervals conform to the widely adopted BPT distribution model, we can applied statistical fitting techniques to identify the optimal BPT distribution and estimate its associated parameters.

5. Finally, we can calculate conditional probabilities for large earthquake occurrence within future time periods using Equation 2 (Wesnousky, 1986).

$\mathit{P}\left({\mathit{T}}_{\mathit{e}},\Delta \mathit{T}\right)=\frac{{\displaystyle {\int }_{{\mathit{T}}_{\mathit{e}}}^{\mathit{T}+\Delta \mathit{T}}}\mathit{f}\left(\mathit{T}\right)\mathit{d}\mathit{T}}{{\displaystyle {\int }_{\mathit{T}}^{\mathit{\infty }}}\mathit{f}\left(\mathit{T}\right)\mathit{d}\mathit{T}}(2)$

Where $T_e$ is the elapsed time since the last earthquake, and $\Delta T$ is the future time window for calculating recurrence probability.

2.4 Uncertainties in paleoseismic dating

A fundamental challenge in paleoseismic data analysis is the inherent chronological uncertainty associated with event age determination. Geological investigations generally yield temporal windows rather than precise dates for earthquake occurrences, which significantly complicate accurate recurrence interval calculations. To address this limitation, Ellsworth et al. developed a bootstrap resampling approach based on probability density functions (PDFs) of radiocarbon dating, followed by maximum likelihood estimation to constrain seismic recurrence distribution parameters. When chronological uncertainties are neglected, the median values of time windows can be directly utilized.

For the methodology employed in this study, two approaches can be implemented regarding paleoseismic age determination uncertainties in the procedures outlined in Section 2.3. When uncertainties are not considered, the median value of each paleoseismic event’s chronological uncertainty range serves as the occurrence time for all simulations, whether for the local fault or other regional faults. In this case, the paleoseismic event ages and recurrence interval data remain constant across all simulations for each fault.

Conversely, when paleoseismic age determination uncertainties are considered, the implementation procedures in Section 2.3 involve randomly sampling a value with equal probability from each paleoseismic event’s chronological uncertainty range as the occurrence time in each simulation, regardless of whether it concerns the local fault or other regional faults. Consequently, the paleoseismic event ages and recurrence interval data vary across simulations for each fault. Through numerous iterative simulations, this approach effectively captures and reflects the uncertainties inherent in paleoseismic chronological determinations.

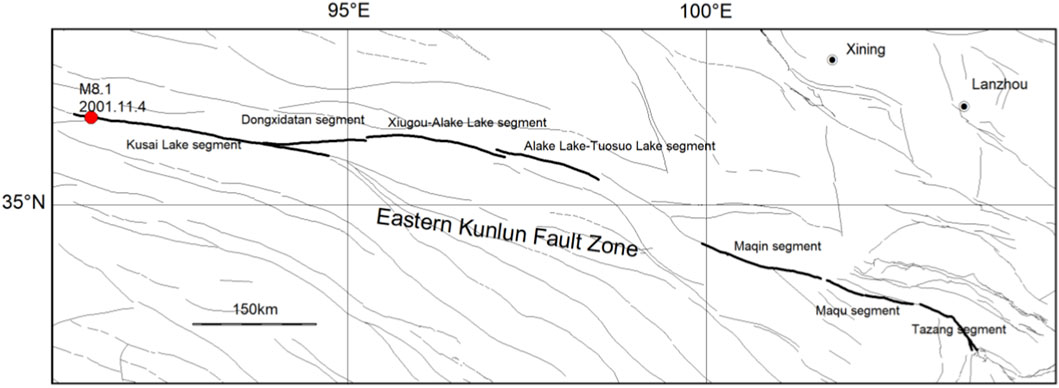
3 Application to the East Kunlun Fault Zone

The East Kunlun Fault Zone is selected as the study area to demonstrate the application of the proposed integrated paleoseismic recurrence probability assessment method (see Figure 2). This fault zone represents an ideal natural laboratory for testing the methodology due to its well-documented paleoseismic records across multiple segments and relatively consistent seismotectonic characteristics.

Figure 2

Figure 2. Distribution of fault segmentation along the East Kunlun Fault Zone in western China.

According to the Seismological Bureau of Qinghai Province and the Institute of Crustal Deformation, China Seismological Bureau (1999), The East Kunlun Fault Zone is a major active fault system in the northeastern Tibetan Plateau, characterized by sinistral strike-slip motion and formed during Indian-Eurasian plate convergence. Extending approximately 2,000 km with a WNW strike orientation, it constitutes the northern boundary of the Bayan Har Block and comprises eight en échelon fault segments separated by extensional basins or compressional uplifts. Notable segments include Kusai Lake, Dongxidatan, Xiugou-Alake Lake, Tuosuo Lake-Anyemaqen Mountain, Maqin, Maqu, and the easternmost Tazang section. The Kusai Lake segment experienced an M8.1 earthquake in 2001. Recent investigations of different segments within the East Kunlun Fault Zone have yielded substantial paleoseismic sequence data, providing favorable conditions for seismic hazard assessment (Cai and Zhang, 2018; Li et al., 2012; Hu et al., 2007; Hu et al., 2006; Li, 2009). The availability of multiple paleoseismic datasets from different segments, combined with the coherent tectonic framework of the fault zone, makes it particularly suitable for demonstrating the effectiveness of integrated multi-segment recurrence probability assessment. This study focuses on seven fault segments with relatively abundant and reliable paleoseismic data for comprehensive recurrence probability evaluation.

3.1 Data

The seven fault segments within the East Kunlun Fault Zone (Table 1) possess relatively abundant paleoseismic data. However, the completeness of paleoseismic data varies significantly among different fault segments. Therefore, establishing screening criteria for paleoseismic data selection is essential for major earthquake recurrence probability assessment.

Table 1

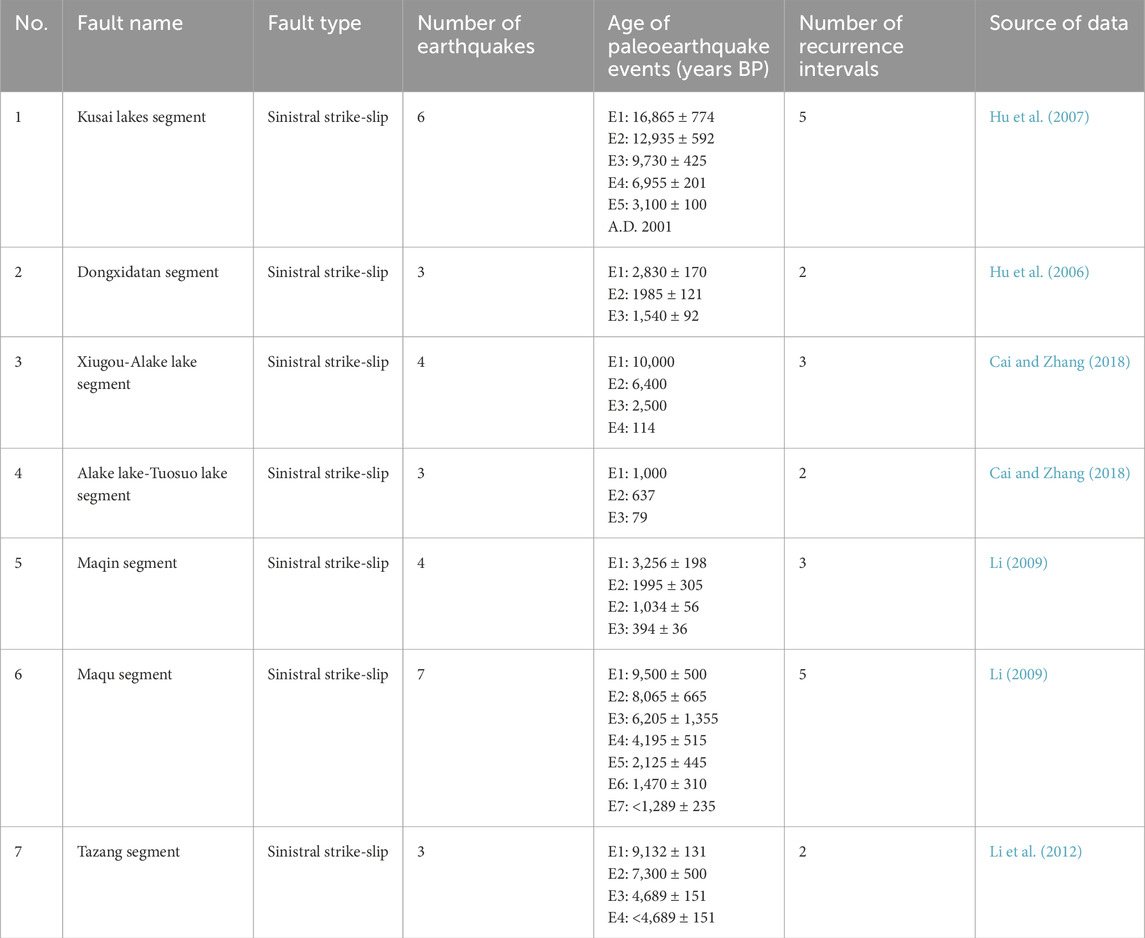
Table 1. Paleoseismic data compilation for fault segments in the East Kunlun Fault Zone, western China.

The paleoseismic data selection in this study adheres to the following criteria: (1) Priority is given to the most recently published and authoritative paleoseismic investigations; (2) Events lacking upper or lower age constraints exhibit excessive uncertainty and are excluded from recurrence interval calculations. For instance, the most recent seismic events on the Maqu and Tazang segments lack lower age limits and are therefore excluded from recurrence probability calculations; (3) Considering the substantial uncertainties associated with extremely ancient data, this database exclusively incorporates paleoseismic data from the past 20,000 years; (4) Complete paleoseismic sequences are employed, datasets with obvious gaps are excluded, such as those from the Maqin and Dongxidatan segments. Historical records can be divided into two clusters, each displaying quasi-periodic behavior, likely indicating missing events. Even without apparent gaps, data from the most recent cluster should be utilized to avoid overestimating recurrence intervals and underestimating risk; (5) Only seismic events with similar magnitudes, rupture dimensions, and coseismic displacements conform to the quasi-periodic characteristic earthquake model. Considering the existence of hierarchical rupturing, secondary ruptures or moderate earthquakes on fault segments are not considered.

3.2 Results and analysis

For the recurrence probability assessment of seven fault segments within the East Kunlun Fault Zone, considerable uncertainties exist in age determination within the paleoseismic sequences of multiple fault segments, including the Kusai Lakes segment, Dongxidatan segment, Maqin segment, Maqu segment, and Tazang segment. Therefore, this study employs a comparative analytical approach when utilizing joint multi-fault paleoseismic data to calculate the major earthquake recurrence probability for the East Kunlun Fault Zone. Specifically, we conduct calculations under two scenarios: (1) without considering uncertainties in paleoseismic age determination, and (2) incorporating these uncertainties, thereby enabling a comprehensive evaluation of how age determination uncertainties influence the calculated results.

Through extensive Monte Carlo simulations conducted 100,000 times, we obtained the probability density distributions of major earthquake recurrence intervals and fitted Brownian Passage Time (BPT) distributions for seven fault segments along the East Kunlun Fault Zone. Figure 3 presents the distribution patterns excluding dating uncertainty, while Figure 4 illustrates the distributions incorporating dating uncertainty.

Figure 3

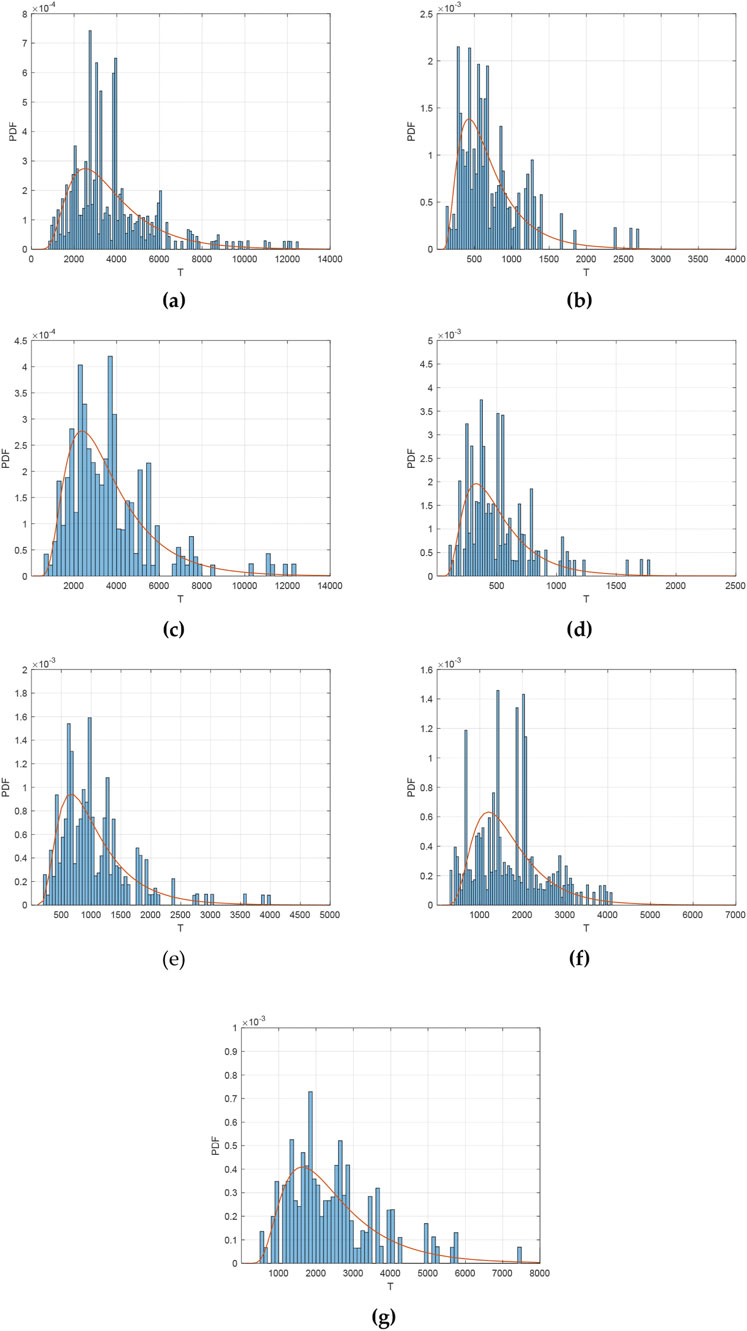
Figure 3. Probability density distributions of major earthquake recurrence intervals and fitted BPT distributions for seven fault segments along the East Kunlun Fault Zone (excluding dating uncertainty). The panels show: (a) Kusai Lake segment; (b) Dongxidatan segment; (c) Xiugou-Alake Lake segment; (d) Alake Lake-Tuosuo Lake segment; (e) Maqin segment; (f) Maqu segment; (g) Tazang segment.

Figure 4

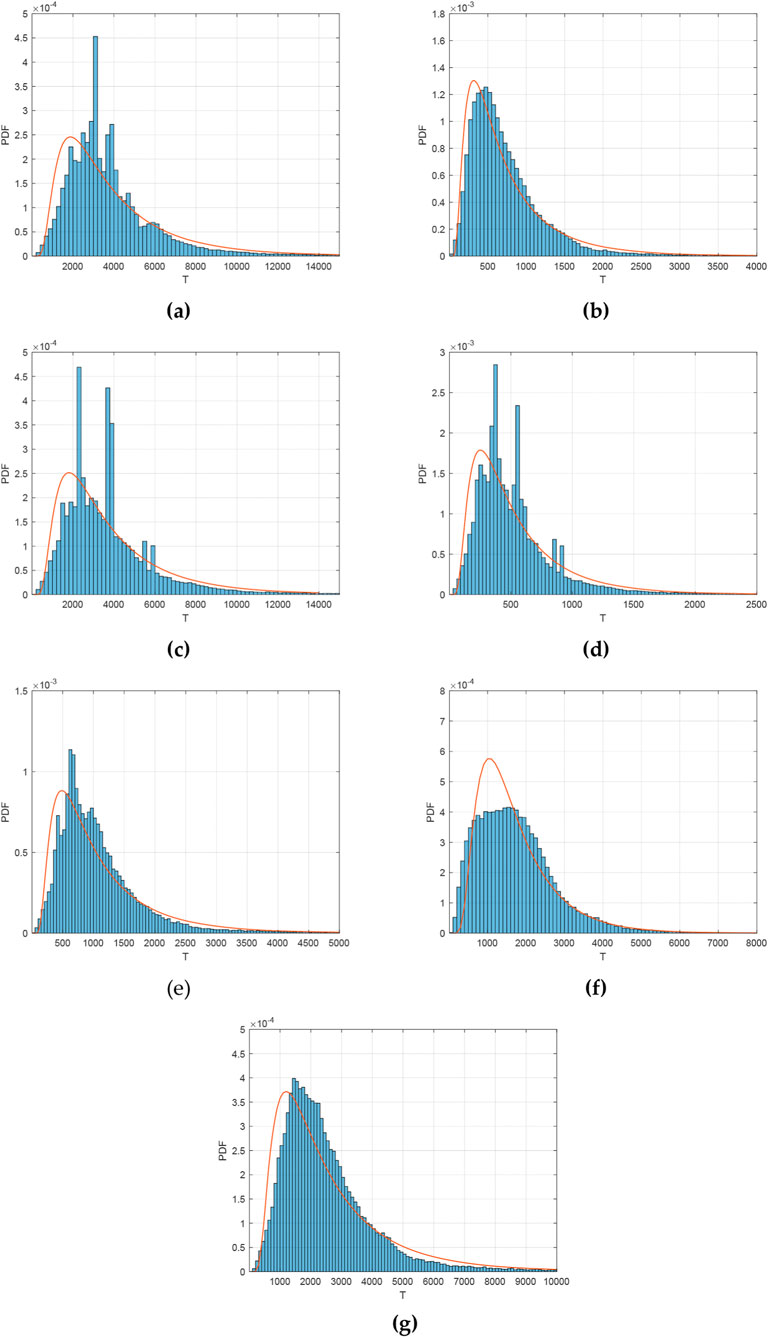
Figure 4. Probability density distributions of major earthquake recurrence intervals and fitted BPT distributions for seven fault segments along the East Kunlun Fault Zone (incorporating dating uncertainty). The panels show: (a) Kusai Lake segment; (b) Dongxidatan segment; (c) Xiugou-Alake Lake segment; (d) Alake Lake-Tuosuo Lake segment; (e) Maqin segment; (f) Maqu segment; (g) Tazang segment.

The recurrence interval distributions reveal that despite expanding sample sizes through multiple fault segments, the sample sizes remain limited, resulting in non-smooth distributions (see Figure 3). In comparison, by incorporating the uncertainties in paleoseismic dating, we can obtain a greater number of possible recurrence interval data values, which leads to more stable distribution patterns, However, the distributions remain insufficiently smooth (see Figure 4). Therefore, distribution fitting is necessary for recurrence probability calculations.

Statistical analysis yielded the BPT distribution parameters μ and α, as shown in Table 2, which also presents the μ and α values derived from local finite sample statistics. Comparison reveals that after considering the uncertainties in paleoseismic dating, both μ and α values increase significantly. Particularly, the α values calculated incorporating paleoseismic dating uncertainties are markedly larger than those computed without considering such uncertainties. This phenomenon can be attributed to the fact that when dating uncertainties are incorporated, random sampling within paleoseismic age windows generates a broader range of recurrence interval values, including both smaller and larger extremes, thereby widening the overall distribution and increasing the coefficient of variation.

Table 2

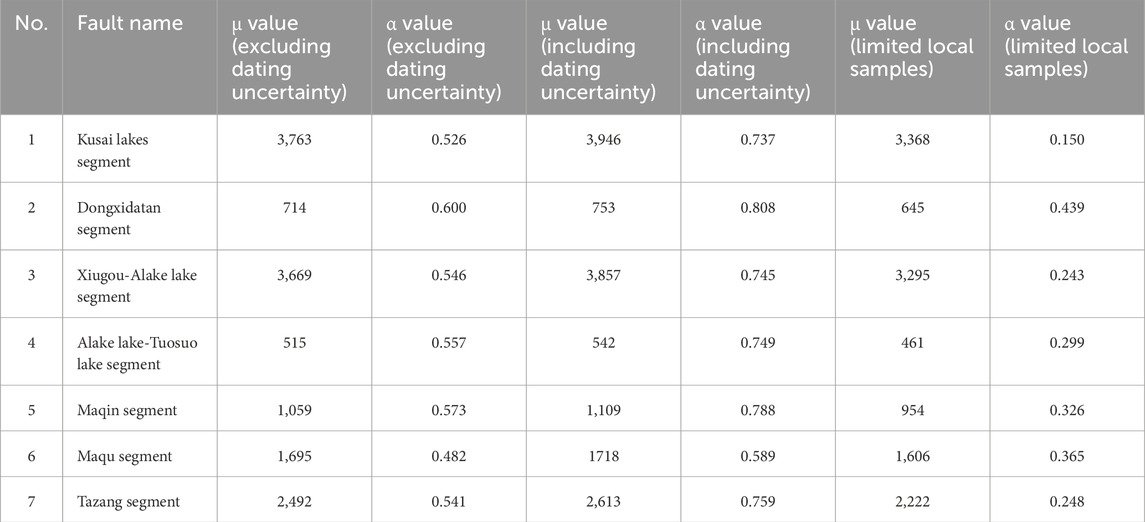
Table 2. Mean (μ) and coefficient of variation (α) values for recurrence interval distributions across seven faults in the East Kunlun Fault Zone.

Furthermore, the μ parameters obtained through our method are consistently larger than the mean values ($T_{ave}$) derived from limited recurrence interval samples. This finding aligns with results reported by Parsons (2008). Direct application of observed recurrence interval sample means not only fails to consider parameter uncertainties but also leads to underestimation of μ values, resulting in overestimated seismic probabilities.

The α value derived directly from the local limited sample is smaller and neglects all epistemic uncertainties. In contrast, our approach produces a systematically increased coefficient of variation (α), which is due to the inclusion of epistemic uncertainties related to the mean recurrence interval as well as those associated with the paleoseismic age determinations. It is important to note that the α we derived does not represent the actual coefficient of variation of the recurrence interval. Rather than determining a single maximum likelihood distribution, our approach considers the distribution of recurrence intervals after accounting for multiple epistemic uncertainties. The statistical significance of the α value outweighs its physical significance.

Figure 5 simultaneously presents the 50-year major earthquake occurrence probabilities across East Kunlun Fault Zone segments both with and without considering paleoseismic dating uncertainties. Comparison of the two curves reveals that when the elapsed time since the last earthquake is less than approximately 0.6μ, the calculations incorporating uncertainties yield higher probabilities; conversely, when the elapsed time exceeds approximately 0.6μ, the calculations excluding uncertainties produce higher values. This indicates that incorporating paleoseismic dating uncertainties results in substantially elevated recurrence probabilities for shorter elapsed time periods.

Figure 5

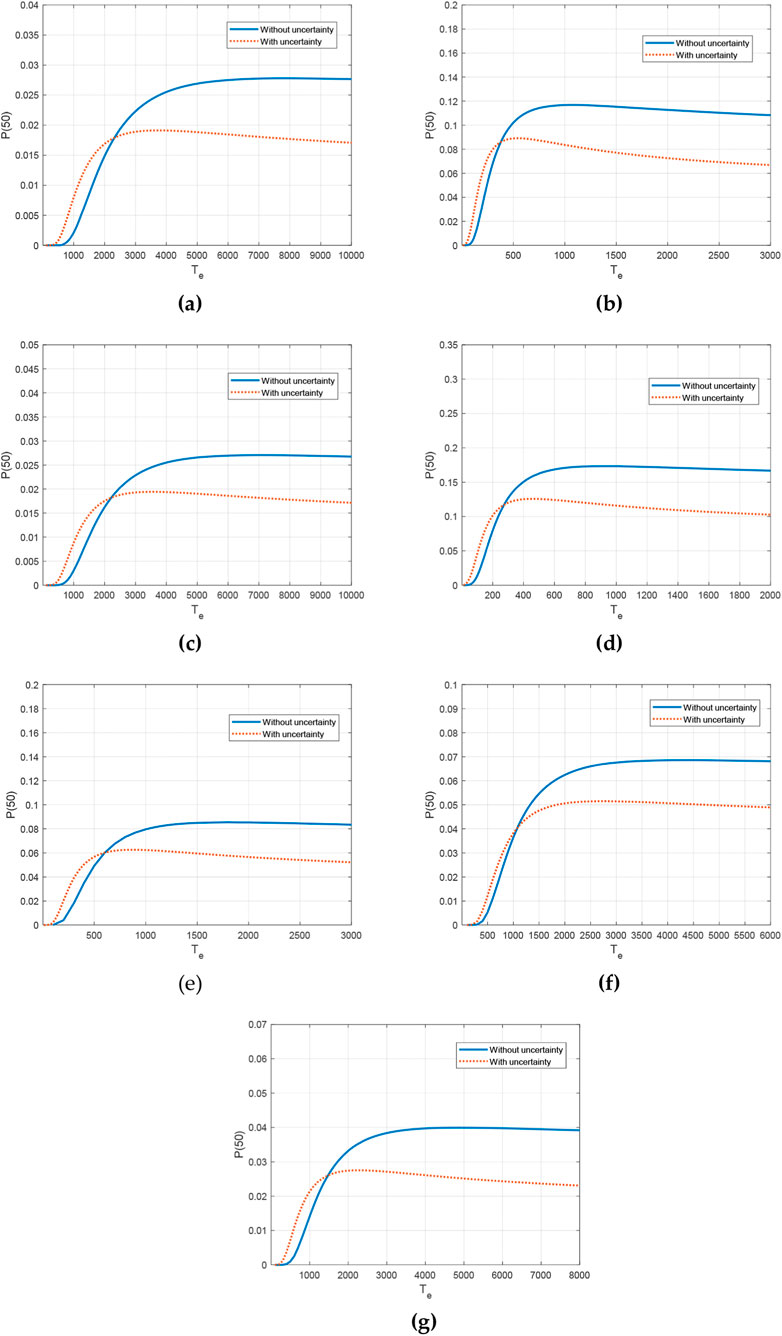
Figure 5. Occurrence probability curves for seven fault segments along the East Kunlun Fault Zone in the next 50 years, where $T_e$ represents the elapsed time since the last earthquake. Solid lines denote results excluding dating uncertainties, and dashed lines denote results including dating uncertainties. The panels show: (a) Kusai Lake segment; (b) Dongxidatan segment; (c) Xiugou-Alake Lake segment; (d) Alake Lake-Tuosuo Lake segment; (e) Maqin segment; (f) Maqu segment; (g) Tazang segment.

Based on elapsed times since the last major earthquake ($T_e$), Figure 5 demonstrates the following findings: When paleoseismic dating uncertainties are not considered, the Dongxidatan segment exhibits a 50-year earthquake probability of 0.115, the Maqin segment shows a probability of 0.040, while the Kusai Lake, Xiugou-Alake Lake, and Alake Lake-Tuosuo Lake segments all display 50-year seismic probabilities below 0.001. However, when paleoseismic dating uncertainties are incorporated, the Dongxidatan segment exhibits a reduced 50-year earthquake probability of 0.077, the Maqin segment shows an increased probability of 0.051, while the Kusai Lake, Xiugou-Alake Lake, and Alake Lake-Tuosuo Lake segments maintain 50-year seismic probabilities still below 0.001.

For the Tazang and Maqu segments, accurate 50-year occurrence probability estimates cannot be directly obtained from the figure due to uncertain major earthquake elapsed times.

Previous research has addressed calculations for segments lacking precise major earthquake elapsed times, providing Bayesian estimation-based recurrence probability assessment methods (Guo et al., 2018; Field and Jordan, 2015). We propose a Monte Carlo simulation-based recurrence probability assessment method for cases with uncertain last earthquake timing. Based on known recurrence interval distributions (BPT or other distributions), earthquake sequences are simulated to statistically determine 50-year recurrence probabilities through specific event frequency analysis.

Example: Consider the following scenario: the time elapsed since the penultimate major earthquake is T_s; one additional earthquake event occurred within this timespan T_s, though its exact timing remains uncertain; earthquake recurrence intervals follow a BPT (Brownian Passage Time) distribution characterized by mean recurrence interval μ and coefficient of variation α.

Through the Monte Carlo method, we take T_s as our initial reference point and probabilistically generate two consecutive recurrence intervals T₁ and T₂ according to the established BPT distribution. We define two events:

Event B occurs when: T₁ < T_s and T₁ + T₂ ≥ T_s and T₁ + T₂ < T_s + 50 years.

Event A occurs when: T₁ < T_s and T₁ + T₂ ≥ T_s years.

Through 100,000 simulation iterations, we tabulate the frequencies: n (occurrences of event A) and N (occurrences of event B).

The 50-year earthquake probability is subsequently calculated as P = $\frac{n}{N}$.

Using the proposed Monte Carlo method, the 50-year occurrence probabilities for the Maqu and Tazang segments are calculated as 0.054 and 0.026, respectively, when paleoseismic dating uncertainties are not considered; when paleoseismic dating uncertainties are incorporated, the 50-year occurrence probabilities for the Maqu and Tazang segments are calculated as 0.042 and 0.022, respectively.

Results indicate significant variation in 50-year major earthquake occurrence probabilities among the seven East Kunlun Fault Zone segments. The Dongxidatan, Maqin, Maqu, and Tazang segments exhibit relatively higher probabilities, with notable differences in calculated seismic probabilities when considering versus not considering paleoseismic dating uncertainties. In contrast, the Kusai Lake, Xiugou-Alake Lake, and Alake Lake-Tuosuo Lake segments show relatively lower probabilities. Following the elastic rebound theory (Reid, 1910), the elapsed time since the last major earthquakes on these fault segments may be insufficient for the accumulation of adequate strain energy required for subsequent major events.

4 Discussion

4.1 Methodological framework and improvements

The proposed integrated multi-fault paleoseismic data approach addresses critical limitations of existing methods while maintaining statistical rigor. Traditional approaches, such as those by Nishenko and Buland, assume that observed sample means represent the true mean recurrence interval (μ). This assumption can lead to unrealistic results, as it implies that faults with identical sample means yield identical probabilities regardless of the quality of the data (Nishenko and Buland, 1987). Guo et al. addressed this issue by incorporating epistemic uncertainties through Monte Carlo simulation but relied exclusively on non-local data for variability information (Guo et al., 2018).

Our enhanced methodology retains Guo et al.'s Monte Carlo framework while introducing three key improvements: (1) direct incorporation of local paleoseismic data into the variability database, ensuring local fault behavior contributes to probability assessments; (2) restriction of analysis to tectonically coherent fault zone rather than diverse continental datasets, improving geological consistency; and (3) explicit BPT distribution fitting to handle smaller, regionally-constrained datasets with less smooth distribution curves.

4.2 Limitations and future research directions

While our proposed methodology represents a significant advancement in earthquake recurrence probability assessment, several important limitations require careful consideration for comprehensive scientific evaluation.

1. The current paleoseismic database lacks sufficient volume for refined categorical analyses based on fault characteristics such as slip rates, maximum magnitudes, or fault types—factors that may significantly influence recurrence variability patterns across different tectonic environments. Building upon this limitation, regional database size constraints represent a fundamental challenge, as smaller fault zone-specific datasets inherently reduce statistical power compared to continental-scale analyses, potentially affecting parameter estimation reliability and confidence intervals.

2. Given that time-dependent seismic hazard analyses predominantly employ the Brownian Passage Time (BPT) distribution (Field et al., 2015), this study adopts the BPT distribution for fitting procedures. However, paleoseismic datasets exhibit considerable variability across individual fault systems, with correspondingly different levels of epistemic uncertainty. Regardless of whether BPT, lognormal, or Weibull distributions are selected, a single fixed distribution model often cannot adequately capture the complexity of the data. Therefore, comparative analyses among different distribution models and exploration of more flexible distribution frameworks are warranted for future investigations.

3. In addition to these statistical considerations, methodological constraints emerge when applying this approach across diverse geological settings. Specifically, the assumption of uniform recurrence variability within fault zones may not hold universally across different tectonic regimes, such as extensional versus compressional environments, or varying crustal rheologies.

4. Another critical limitation concerns the uncertainty in paleoseismic age determination, which significantly affects computational results. However, assuming a uniform distribution within a temporal window for age determination may not necessarily represent the optimal approach. Recent literature demonstrates that incorporating each event’s age probability density function (PDF) from radiocarbon dating or varve chronology can shift 50–100 years forecasts by approximately 10% while simultaneously narrowing uncertainty bounds (e.g., Acuña et al., 2022).

Looking toward future research directions, several priority areas emerge to address these limitations. Primarily, future investigations should prioritize the expansion of paleoseismic databases to enable comprehensive fault characteristic classifications, coupled with the implementation of advanced chronological uncertainty quantification methods that incorporate event-specific probability density functions derived from radiocarbon dating analyses. Furthermore, investigating and exploring optimal distribution fitting approaches remains essential to accommodate distributional variations arising from epistemic uncertainty differences across diverse fault systems. Ultimately, comparative validation studies across multiple fault systems would further enhance methodological robustness and broaden applicability to diverse seismotectonic environments globally.

5 Conclusion

This study successfully develops and applies an enhanced integrated multi-fault paleoseismic data approach for earthquake recurrence probability assessment in the East Kunlun Fault Zone, addressing critical limitations in existing methodologies while maintaining statistical rigor. Through comprehensive application to seven fault segments within this tectonically coherent strike-slip system, through comprehensive application to seven fault segments within this tectonically coherent strike-slip system, we demonstrate the method’s effectiveness in complex continental fault environments under both scenarios with and without considering paleoseismic dating uncertainties.

Our quantitative analysis reveals that mean recurrence intervals (μ) are systematically higher than simple arithmetic averages across all seven fault segments. When paleoseismic dating uncertainties are not considered, coefficients of variation consistently approximate 0.5 (ranging 0.482–0.600), demonstrating excellent agreement with established seismic hazard models. However, when dating uncertainties are incorporated, both μ and α values increase significantly, with α values reaching 0.589–0.808, reflecting the substantial impact of chronological uncertainties on recurrence interval distributions. This validates our methodological approach while highlighting the importance of explicitly accounting for paleoseismic dating uncertainties in hazard assessments.

The calculated fifty-year earthquake probabilities exhibit significant spatial variation across the fault zone and notable sensitivity to dating uncertainty treatment. When dating uncertainties are excluded, the Dongxidatan (0.115), Maqu (0.054), Maqin (0.040), and Tazang (0.026) segments show elevated probabilities. When dating uncertainties are incorporated, probability estimates shift accordingly, with the Maqin segment showing an increased probability of 0.051, while the other fault segments exhibit a decrease in probability. Considering the inherent challenges in quantifying paleoseismic dating uncertainties, we recommend using the conservative probability estimates (excluding dating uncertainties) as baseline values for current seismic hazard assessment in the East Kunlun Fault Zone, while acknowledging that future refinements in uncertainty quantification may provide additional insights.

The developed approach effectively integrates local and regional paleoseismic data while maintaining tectonic coherence and explicitly quantifies epistemic uncertainties through Monte Carlo simulation. The framework proves particularly well-suited for regions with multiple fault segments containing adequate paleoseismic records within tectonically coherent zones, though it requires substantial paleoseismic databases and currently cannot incorporate detailed fault characteristic classifications due to data constraints.

This framework offers a novel approach for evaluating the recurrence probability of major earthquakes on individual faults characterized by limited paleoseismic records. Future developments will focus on three key areas to enhance the methodology’s reliability and applicability: (1) continuous expansion of paleoseismic databases, (2) refinement of approaches for quantifying and propagating chronological uncertainties in paleoseismic data, and (3) systematic validation through applications across diverse tectonic settings, particularly on faults with extensive paleoseismic records. These advances will significantly improve our understanding of seismic hazards associated with complex fault systems worldwide, thereby contributing to more robust seismic risk assessments.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

XG: Conceptualization, Data curation, Formal Analysis, Methodology, Software, Writing – original draft, Writing – review and editing. JL: Funding acquisition, Project administration, Resources, Supervision, Validation, Writing – review and editing.

Funding

The authors declare that financial support was received for the research and/or publication of this article. This study was funded by National Key R&D Program of China (2022YFC3003502).

Acknowledgements

We thank Meng Zhang for his contributions to the methodology and software aspects of this work.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Acuña, F., Montalva, G. A., and Melnick, D. (2022). How good is a paleoseismic record of megathrust earthquakes for probabilistic forecasting? Seismol. Soc. Am. 93 (2A), 739–748. doi:10.1785/0220210044

CrossRef Full Text | Google Scholar

Cai, Y. Y., and Zhang, J. L. (2018). Repeating intervals and potentials of earthquakes in the east Kunlun fault zone. Earthquake 38, 58–65. doi:10.3969/j.issn.1000-3274.2018.03.006

CrossRef Full Text | Google Scholar

Ellsworth, W. L., Matthews, M. V., Nadeau, R. M., Nishenko, S. P., Reasenberg, P. A., and Simpson, R. W. (1999). A physically based earthquake recurrence model for estimation of long-term earthquake probabilities. U.S. Geol. Surv. Open-File Rep., 99–522. doi:10.3133/ofr99522

CrossRef Full Text | Google Scholar

Field, E. H., and Jordan, T. H. (2015). Time-dependent renewal-model probabilities when date of last earthquake is unknown. Bull. Seismol. Soc. Am. 105, 459–463. doi:10.1785/0120140096

CrossRef Full Text | Google Scholar

Field, E. H., Biasi, G. P., Bird, P., Dawson, T. E., Felzer, K. R., Jackson, D. D., et al. (2015). Long-term time-dependent probabilities for the third uniform California earthquake rupture forecast (UCERF3). Bull. Seismol. Soc. Am. 105, 511–543. doi:10.1785/0120140093

CrossRef Full Text | Google Scholar

Guo, X., Pan, H., Li, J., and Hou, C. (2018). A method for computing the recurrence probability of large earthquakes based on empirical distribution. Acta Seismol. Sin. 40, 506–518. doi:10.11939/jass.20170167

CrossRef Full Text | Google Scholar

Hu, D. G., Ye, P. S., Wu, Z. H., Cao, Z. Q., Wang, A. G., Chen, H., et al. (2006). Research on Holocene paleoearthquakes on the Xidatan segment of the east kunlun fault zone in northern Tibet. Quat. Sci. 26, 1012–1020. doi:10.3321/j.issn:1001-7410.2006.06.018

CrossRef Full Text | Google Scholar

Hu, D. G., Wu, Z. H., Wu, Z. H., Cao, Z. Q., Wang, A. G., Yao, H. J., et al. (2007). Late quaternary paleoseismic history on the Kusai lake segment of East Kunlun fault zone in northern Tibet. Quat. Sci. 27, 27–34. doi:10.3321/j.issn:1001-7410.2007.01.004

CrossRef Full Text | Google Scholar

Li, C. X. (2009). The long-term faulting behavior of the eastern segment (Maqin-Maqu) of the East Kunlun fault since the late Quaternary. Beijing: Institute of Geology, China Earthquake Administration.

Google Scholar

Li, Z. F., Zhou, B. G., and Ran, H. L. (2012). Strong earthquake risk assessment of eastern segment on the East Kunlun fault in the next 100 years based on paleo-earthquake data. Chin. J. Geophys. 55, 3051–3065. doi:10.6038/j.issn.0001-5733.2012.09.023

CrossRef Full Text | Google Scholar

Matthews, M. V. (2002). A Brownian model for recurrent earthquakes. Bull. Seismol. Soc. Am. 92, 2233–2250. doi:10.1785/0120010267

CrossRef Full Text | Google Scholar

McCann, W. R., Nishenko, S. P., Sykes, L. R., and Krause, J. (1979). Seismic gaps and plate tectonics: seismic potential for major boundaries. Pure Appl. Geophys. 117, 1082–1147. doi:10.1007/bf00876211

CrossRef Full Text | Google Scholar

Nishenko, S. P., and Buland, R. A. (1987). A generic recurrence interval distribution for earthquake forecasting. Bull. Seismol. Soc. Am. 77, 1382–1399.

Google Scholar

Parsons, T. (2008). Monte Carlo method for determining earthquake recurrence parameters from short paleoseismic catalogs: example calculations for California. J. Geophys. Res. Solid Earth 113, B3. doi:10.1029/2007JB004998

CrossRef Full Text | Google Scholar

Reid, H. F. (1910). “The mechanics of the earthquake,” in The California earthquake Washington: State Earthquake investigation commission (Carnegie Institution of Washington), 43–47.

Google Scholar

Rikitake, T. (1974). Probability of earthquake occurrence as estimated from crustal strain. Tectonophysics 23, 299–312. doi:10.1016/0040-1951(74)90029-8

CrossRef Full Text | Google Scholar

Schwartz, D. P., and Coppersmith, K. J. (1984). Fault behavior and characteristic earthquakes: examples from the wasatch and San Andreas fault zones. J. Geophys. Res. 89, 5681–5698. doi:10.1029/jb089ib07p05681

CrossRef Full Text | Google Scholar

Seismological Bureau of Qinghai Province, and Institute of Crustal Deformation, China Seismological Bureau (1999). East Kunlun active fault zone. Beijing: Seismological Press.

Google Scholar

Shimazaki, K., and Nakata, T. (1980). Time-predictable recurrence model for large earthquakes. Geophys. Res. Lett. 7, 279–282. doi:10.1029/GL007i004p00279

CrossRef Full Text | Google Scholar

Utsu, T. (1972). Large earthquakes near Hokkaido and the expectancy of the occurrence of a large earthquake of nemuro. Rep. Coord. Comm. Earthq. Predict. 7, 1–13.

Google Scholar

Utsu, T. (1984). Estimation of parameters for recurrence models of earthquakes. Bull. Earthq. Res. Inst. Univ. Tokyo 59, 53–66.

Google Scholar

Wesnousky, S. G. (1986). Earthquakes, Quaternary faults, and seismic hazard in California. J. Geophys. Res. 91, 12587–12631. doi:10.1029/jb091ib12p12587

CrossRef Full Text | Google Scholar

Zöller, G. (2018). A statistical model for earthquake recurrence based on the assimilation of paleoseismicity, historic seismicity, and instrumental seismicity. J. Geophys. Res. Solid Earth 123, 4906–4921. doi:10.1029/2017jb015099

CrossRef Full Text | Google Scholar