Infiltration and stability analysis of gravelly soil slopes under rainfall with the improved green-ampt model

Rainfall infiltration is a key cause of slope instability, especially in complex soil-rock mixture slopes with preferential flow paths. The classic Green-Ampt model, widely used in infiltration studies, has limitations in handling air pressure variations near the surface of such slopes, causing errors. This study proposes an improved Green-Ampt model that incorporates atmospheric pressure boundary conditions and adjusts the permeability parameter for soil-rock mixtures. The refined model can analyze wetting front depth under various conditions, including constant pressure with/without ponding and atmospheric pressure effects. Finite element simulations of slopes with different stone contents show that block content significantly controls preferential flow and saturation patterns in heterogeneous media, influencing slope stability. Comparisons between theoretical predictions and numerical results confirm the model’s effectiveness in calculating wetting front variations. This study provides a theoretical method for calculating wetting front depth during infiltration in soil-rock mixture slopes, considering atmospheric pressure variations.

1 Introduction

Slope stability stands as a critically important research topic in geological engineering, directly relating to the safety of infrastructure, the protection of the natural environment, and the sustainable development of the social economy (Al-Homoud and Masanat, 1998; He et al., 2025; Hong, 2005; Ries, 2011; Wu et al., 2023). Globally, slope instability events induced by rainfall occur frequently, not only resulting in significant casualties but also causing severe property losses and environmental damage. Particularly in regions with variable climates and concentrated rainfall, the impact of rainfall infiltration on slope stability is especially pronounced, becoming one of the primary factors triggering geological hazards such as landslides and debris flows (Ahuja, Sharpley, and Lehman, 1982; Fang et al., 2008; Friedel, Thielen, and Springman, 2006; Rahardjo et al., 2005). Therefore, delving deeply into the slope stability mechanisms under rainfall infiltration conditions and developing scientific and rational analytical models and predictive methods are of great significance for effectively preventing and mitigating the risks of geological hazards.

The stability of slopes is jointly influenced by multiple factors, including geological structures, the mechanical properties of soil and rock masses, hydrogeological conditions, climate change, and human engineering activities (Biscontin and Pestana, 2006; Gonzalez, Schaefer, and Rollins, 2021; Shafer, Ajmera, and Upadhaya, 2024; Technology and Beijing 2006; Wang, Saha, and Hawlader, 2015; Xiao-Li and Feng, 2006; Zhang et al., 2024). During rainfall, water infiltrates into the interior of slopes through channels such as surface cracks and pores, altering the physical and mechanical properties of rock and soil masses. For instance, it increases pore water pressure, reduces effective stress, and softens the rock and soil, thereby weakening the anti-sliding capacity of slopes and increasing the risk of instability. Especially in soil-rock mixture slopes, due to their characteristics of high porosity and permeability heterogeneity, the rainfall infiltration process is more complex, and its impact on slope stability is more significant (Huang et al., 2017; Junhua, 2017; Shao and Ji, 2014). Soil-rock mixture slopes are widely distributed in mountainous and hilly regions, as well as along infrastructure such as highways and railways. Their stability directly relates to the safe operation of transportation routes and the life and property safety of surrounding residents. However, due to the complexity and uncertainty of the internal structure of soil-rock mixture slopes, traditional slope stability analysis methods often struggle to accurately describe the rainfall infiltration process and the changing patterns of slope stability (Chongshi et al., 2009; Dongmei et al., 2015; Huang, Xiong, and Liu, 2010; Liu et al., 2015; Zhou et al., 2025).

In the analysis of rainfall infiltration and slope stability, the Green-Ampt model, as a classic unsteady - state infiltration model, has been widely applied due to its clear physical significance and simple calculation. Based on a series of assumptions, such as a uniform initial soil moisture content, a distinct wetting front during the infiltration process, and an infiltration flux driven by both gravitational potential and matric suction, this model can effectively describe the infiltration process of homogeneous soil under ponded conditions (Chu, Onstad, and Rawls, 1986; Davidson, 1984; Liu, Zhang, and Feng, 2008; Ma et al., 2010; Quanjiu, Jianbing, and Yi, 2002; Swartzendruber, 2000). In practical applications, the Green-Ampt model has also revealed some limitations. It is mainly suitable for infiltration analysis under ponded conditions and provides an inaccurate description of the infiltration process with air pressure variations under non - ponded conditions. During actual rainfall events, it is difficult to form a distinct ponded layer on the slope surface, and the air pressure in the surface soil of the slope differs from the standard atmospheric pressure. The surface ponding depth parameter H in the model cannot accurately reflect the real - world situation (Langhans et al., 2014; Li et al., 2024; Shukla et al., 2006; Tsihrintzis and Hamid, 2015). At the initial stage of rainfall, the surface soil of the slope may experience rapid infiltration, compressing the pore air and forming a positive pressure zone, which hinders further water infiltration. During rainfall breaks or dry seasons, the surface soil of the slope may develop a negative pressure zone due to evaporation, promoting water uptake (Kirchhoff et al., 1996; Nadal-Romero et al., 2008). The Green-Ampt model fails to account for these air pressure effects, leading to its limitations in practical applications. Moreover, for soil-rock mixture slopes, given the complexity and uncertainty of their internal structure, the assumption of homogeneous soil in the Green-Ampt model is clearly not applicable. Factors such as the block stone content, particle size distribution, and spatial arrangement in soil-rock mixture slopes significantly affect their permeability and infiltration process, making it difficult for the traditional Green-Ampt model to accurately describe their rainfall infiltration characteristics.

This study aims to enhance the applicability of the Green-Ampt model for describing the rainfall infiltration process in soil-rock mixture slopes considering atmospheric pressure variations through methods such as model improvement and numerical simulation. By introducing atmospheric pressure boundary conditions, the infiltration processes under three scenarios: non - ponded and atmospheric pressure conditions, ponded conditions, and conditions influenced by atmospheric pressure are comprehensively considered. This approach expands the application scope of the Green-Ampt model and improves its descriptive accuracy under actual rainfall conditions. A permeability coefficient calculation formula suitable for soil-rock mixtures is established based on their physical characteristics. Through the constructed finite element model of slopes, the applicability and accuracy of the improved Green-Ampt model in real slope problems are verified. This contributes to a deeper understanding of the seepage mechanism in soil-rock mixture slopes under rainfall infiltration conditions.

2 Theoretical model

The classical Green-Ampt model is employed to describe the unsteady state infiltration process. Its primary assumptions are as follows: 1) The initial soil moisture content is uniform; 2) During the infiltration process, the wetting front is distinct, and the soil ahead of it still maintains the initial moisture content; 3) The infiltration flux is jointly driven by gravitational potential and matric suction. Its fundamental form is presented in Equation 1. This model assumes that the ground is horizontal. However, the slope surface is an inclined plane, and the soil above the wetting front is not fully saturated. According to survey data, the initial soil moisture content does not distribute uniformly with depth. Under natural conditions, the basic pattern of soil moisture content in slope soil exhibits a gradual increase from the slope surface to the groundwater table.

$f\left(t\right)=K_s\left(1+\frac{S_f+H}{F\left(t\right)}\right)(1)$

Where f(t) is the instantaneous infiltration rate, K_s is the saturated permeability, S_f is the suction head at the wetting front, H is the depth of ponding water on the surface, F (t) is the depth of the wetting front.

When rainfall does not result in significant ponding, but the air pressure at the soil surface differs from the standard atmospheric pressure, an air-pressure head Δh_a = Δp_a/γ_w (where the air - pressure difference is converted into an equivalent water head), can be introduced. Its expression is given by Equation 2. In this way, three scenarios can be comprehensively considered: non-ponding under normal atmospheric pressure; ponding; and the influence of atmospheric pressure.

$f\left(t\right)=K_s\left(1+\frac{S_f+\Delta h_a+H}{F\left(t\right)}\right)(2)$

Where Δp_a is the difference between the current air pressure and the standard atmospheric pressure, γ_w is the unit weight of water.

It is crucial to note that the pore structure of soil-rock mixtures is relatively complex. Although the permeability coefficients of their soil masses or test blocks can be readily measured in the laboratory, obtaining an accurate value for the overall permeability coefficient is challenging due to factors such as experimental conditions and the distribution of rock block content. Zhou et al. (2016) explored the calculation methods for the permeability of soil-rock mixtures. The permeability in his modified model is derived from three models: the ordered - arrangement model (assuming that soil and crushed rock particles are arranged in series along the seepage path, as shown in Equation 3), the parallel - arrangement model (assuming that soil and crushed rock particles are arranged in parallel along the seepage path, as shown in Equation 4), and the composite model (which incorporates the characteristics of both the ordered and parallel models by introducing a seepage structure factor, as shown in Equation 5).

$K_{S-R\left(S\right)}=\frac{K_S{K}_R}{C_S{K}_R+C_R{K}_S}(3)$

$K_{S-R\left(P\right)}=C_S{K}_S+C_R{K}_R(4)$

$K_{S-R\left(SP\right)}=0.5\left(\frac{K_S{K}_R}{C_S{K}_R+C_R{K}_S}+C_S{K}_S+C_R{K}_R\right)(5)$

Where K_S-R(S) is permeability coefficient of the soil and rocks, K_S-R(P) is the permeability coefficient of the soil and broken rocks formed in parallel, K_S-R(SP) is the permeability coefficient of the soil and broken rocks mixtures in series and in parallel.

Taking into account the impacts of porosity and particle diameter on permeability within the Kozeny-Carman model, the porosities of soil (n_S) and crushed rock (n_R) prior to mixing were measured, while also considering the influence of soil particle filling in the pores of crushed rock. A modified formula for calculating the permeability coefficient of soil-rock mixtures was derived by revising the composite series - parallel model, as shown in Equation 6.

$K_{S-RM\left(SP\right)}=\frac{n_{S-RM}^3{\left(1-n_{S-R}\right)}^2}{n_{S-R}^3{\left(1-n_{S-RM}\right)}^2}{K}_{S-R\left(SP\right)}(6)$

Wher K_S is the soil permeability, K_R is the permeability of crushed rock, C_S and C_R are the volume percentages of soil and crushed rock, n_S-R is the weighted - average porosity of soil and crushed rock before mixing, which can be calculated using the formula n_S-R = C_S⋅n_S + C_R⋅n_R

Soil-rock mixture slopes are characterized by high porosity, elevated permeability coefficients, and rapid infiltration processes. Rainfall can readily penetrate into deep layers due to the excellent connectivity of macropores, which makes it difficult for pore gases to become trapped. However, localized air pressure blockages may still form. The interaction between infiltration and air pressure exerts a significant influence on slope stability. Rapid infiltration leads to an increase in pore water pressure, subsequently reducing effective stress and potentially causing instability. Van Genuchten (1980) proposed an expression for the soil-water characteristic curve that describes the relationship between matric suction and water content, as shown in Equation 7. Furthermore, expressions for the suction head at the wetting front can be derived using the Brooks-Corey model (Brooks et al., 1964), the Van Genuchten and Neuman method (Neuman, 1976) (Equations 8–11), as presented in Equation 12.

$\theta ={\theta }_r+\frac{{\theta }_s-{\theta }_r}{{\left[1+{\left(\alpha h\right)}^n\right]}^m}(7)$

Where θ is the volumetric water content, h is the positive value of the soil suction head, θ_s and θ_r are the saturated water content and residual water content, α、m、n are model parameters (where, m = 1–1/n)

$k_r=k\left(h\right)/k_s(8)$

${\lambda }^2=3^2+\frac{2}{\mu }(9)$

$\mu =-\frac{d\left(\mathit{ln}\frac{\theta -{\theta }_r}{{\theta }_s-{\theta }_r}\right)}{d\left(\mathit{ln}h\right)}(10)$

$S_f={\int }_0^{h_d}{k}_r\mathrm{d}h(11)$

Where h_d is the initial soil suction head (cm), k_r is the relative permeability, k(h) is the unsaturated permeability, μ is the pore-size distribution index, λ is a related parameter concerning the pore-size distribution index μ

$S_f={\int }_0^{\frac{\left[{\left(\frac{{\theta }_d-{\theta }_r}{{\theta }_s-{\theta }_r}\right)}^{-1/m_{-1}}\right]1/n}{\alpha }}{\left(1+\left|\alpha \right.h{|}^n\right)}^{-m\lambda }dh(12)$

Substituting Equations 6, 12 into Equation 2 allows for the determination of the wetting front position during the infiltration process. Through the aforementioned improvements, the infiltration characteristics of soil-rock mixtures can be more accurately described, particularly in terms of their dynamic responses when accounting for pore heterogeneity, air pore pressure, and ponding effects. These modifications contribute to enhancing the accuracy of the model and hold practical significance, especially for slope seepage and stability analysis.

3 Materials and model

A certain soil-rock mixture slope in the Jiangxi region was selected as the research object. Soil and stone samples were collected from the area where the slope is located. The natural moisture content of the soil is 12.5%, the particle size range of the block stones is between 5 and 20 cm, with a stone content of 36.2%. Based on the results of particle analysis and stone particle size analysis, it is determined that the undisturbed soil-rock mixture in this area belongs to a gravel (stone)-bearing clayey mixture. Through laboratory infiltration tests, the infiltration coefficients of soil and gravel were measured, the soil permeability K_S is 1.23 × 10⁻⁹ m/s, and the block stone permeability K_R is 1.46 × 10⁻¹³ m/s. The volume percentages of soil and crushed rock, C_S and C_R, are 0.8 and 0.2, respectively. The porosity of the soil is 36.5%, and the porosity of the block stones is 2.3%. To conduct an in-depth study of the characteristics of this soil-rock mixture slope using a finite element model and to validate relevant theoretical methods, targeted simulation settings were implemented. The mechanical parameters of the model are presented in Table 1. The cohesion and internal friction are determined through triaxial shear tests. Three repeated tests are conducted and the average value is taken as the result.

Table 1

Table 1. Mechanical parameter indicators of model materials.

In the construction of the finite element model, the length of the slope model was set at 65.0 m, with a 20.0 m reservation at the slope crest and a 10.0 m reservation at the slope toe. The slope height was defined as 20 m, and the slope angle as 33.5°, to accurately simulate the geometric configuration of the actual slope. In this study, the boundary and initial conditions are precisely defined: the bottom boundary is set as an impermeable boundary, the lateral boundaries are designated as zero-flux boundaries to represent no lateral water flow exchange, at the surface boundary, an infiltration rate of 250 mm/24 h (In China’s standard for rainfall classification, “Classification of Precipitation Amount” (GB/T 28,592-2012), a “super heavy rain” is defined as a rainfall amount ≥250 mm/24 h), along with an atmospheric pressure difference of 1.2 atm (With a difference of Δp = +0.2 atm from the standard atmospheric pressure (1 atm, 101.3 kPa) was considered to simulate the non-standard atmospheric pressure conditions on the slope under extreme weather conditions. This difference was based on meteorological observation data and reflects the abnormal atmospheric pressure that may occur under specific climatic conditions). For mechanical boundary conditions, the bottom is constrained vertically and the lateral boundaries are constrained horizontally to reflect a stable lateral environment, and the initial stress field is assumed to be self-weight stresses. To simulate the soil-rock mixture structure within the slope in the finite element model, the characteristics of the soil-rock mixture were represented by randomly distributing stones of different particle sizes in the model, as Figure 1. Based on the previously determined proportion of block stones, stones were randomly arranged in the model to mimic the state of mixing stones with soil, aiming to closely approximate the actual situation and provide more realistic conditions for simulating the slope’s response under rainfall, thereby enhancing the understanding of its seepage characteristics.

Figure 1

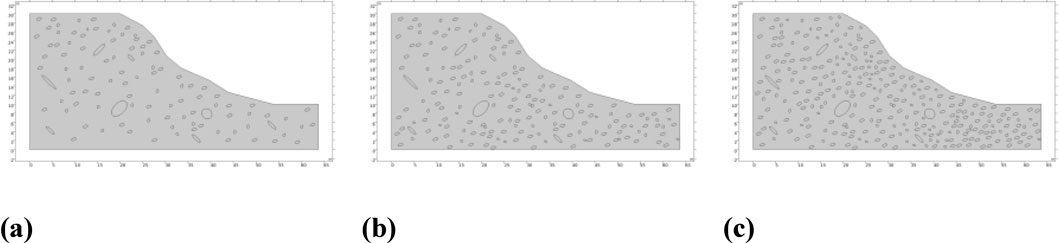
Figure 1. Schematic diagram of the finite element model. (a) Stone content: 20%, (b) Stone content: 40%, (c) Stone content: 60%.

The Richards model is employed to describe the rainfall infiltration process. The soil-water characteristic curve and unsaturated permeability coefficient involved in the model are fitted using the Van Genuchten formula. To depict the deformation characteristics of the slope, the elastic deformation is determined by the generalized Hooke’s law, while the plastic deformation is matched with the Mohr-Coulomb criterion using the DP (Drucker-Prager) criterion. The equation expressions are shown in Equation 13. By adjusting the grid density and the time step size, using the preset regular grid size in the software, and when the time step is less than 0.1 days, the simulation results tend to stabilize.

$\left\{\begin{array}{l}d{\epsilon }^p=\lambda \frac{\mathrm{\partial }Q}{\mathrm{\partial }S},\lambda \ge 0\\ F\left(\sigma ,{\sigma }_{ys}\right)\le 0,\lambda F=0\\ F_{cone}=\sqrt{J_2}+\alpha I_1-k\\ \alpha =\frac{\tan \phi }{\sqrt{9+12{\tan }^2\phi }},k=\frac{3c}{\sqrt{9+12{\tan }^2\phi }}\end{array}\right.(13)$

4 Results and discussion

4.1 Comparison of infiltration behaviors

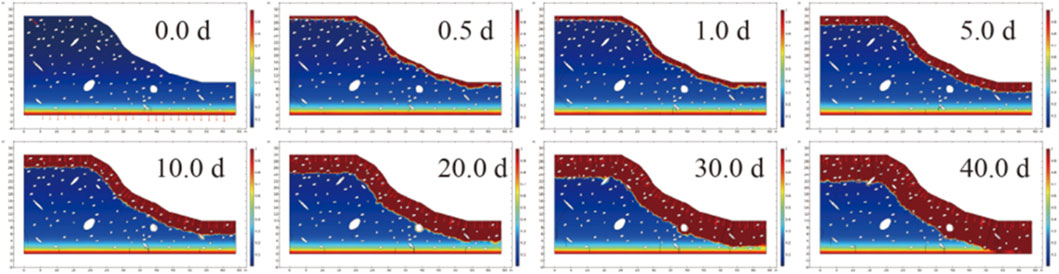
Under rainfall conditions, the moisture infiltration process in soil-rock mixture slopes exhibits complex and dynamic spatio-temporal evolution characteristics. As shown in Figure 2, from the saturation distribution across a series of time series (ranging from 0.0 days to 40.0 days), it can be observed that in the initial stage (0.0 days), the saturation at the slope surface is extremely low, with moisture only sporadically distributed. As rainfall continues, during the period from 0.5 days to 1.0 days, moisture starts to significantly infiltrate into the surface soil. The slope surface and shallow soil are the first to be affected by moisture penetration, showing a noticeable downward movement of the wetting front. Moisture gradually migrates towards the interior of the slope, and the saturated area gradually expands. This process is influenced by the spatial distribution of stones in the soil-rock mixture, as the voids around the stones serve as preferential channels for moisture infiltration. By the time period of 5.0 days–10.0 days, the saturated area further extends into the deep and interior parts of the slope. The guiding effect of stones on the moisture infiltration path becomes increasingly evident, forming localized areas of high saturation. Over the relatively long period from 20.0 days to 40.0 days, the saturated area continues to move downward and approaches the bottom of the slope, demonstrating the continuous infiltration characteristics of moisture under the combined action of multiple factors such as gravity and capillary forces.

Figure 2

Figure 2. Rainfall infiltration process of the slope (with a stone content of 20%).

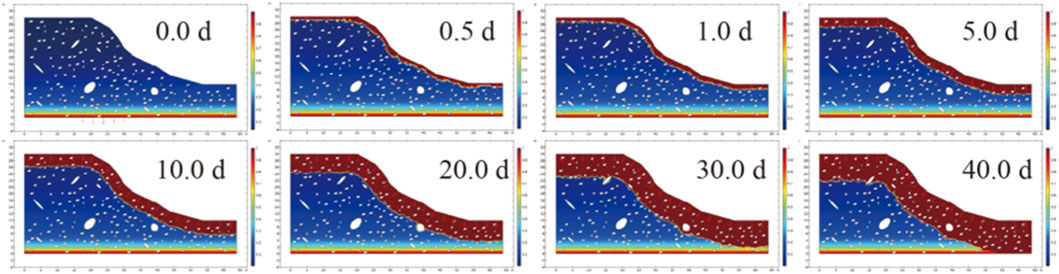
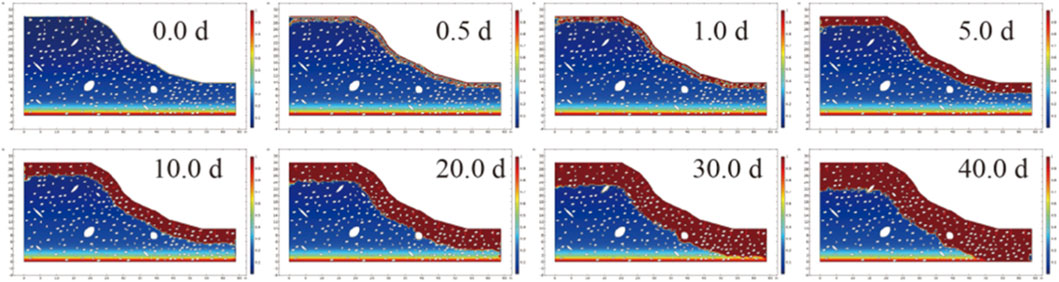
From Figures 2–4, by comparing soil-rock mixture slopes with different stone contents, significant differences are observed in their infiltration processes. There are variations in both the infiltration rate and the advancement of the wetting front. Under the condition of a low stone content (20%), the overall porosity of the soil mass is relatively small. The infiltration process is controlled by matric suction, and the advancement of the wetting front is relatively slow. In contrast, under the condition of a high stone content (40%), the crushed stones form numerous connected macropores or preferential pathways. This accelerates the radial infiltration of rainfall, and the advancement speed of the wetting front is significantly increased.

Figure 3

Figure 3. Rainfall Infiltration Process on Slope (with 40% stone content).

Figure 4

Figure 4. Rainfall Infiltration Process on Slope (with 60% stone content).

There are also differences in the spatial distribution characteristics of the wetting zone. For slopes with a stone content of 10%, after 20.0 days, the wetting zone is mainly concentrated at the slope toe and in the shallow layer, and the moisture migration is manifested as a gradual and uniform infiltration. In comparison, for slopes with a stone content of 40%, a large - scale continuous wetting zone has already formed at the same stage, and the deep soil mass is affected by moisture earlier. This indicates that when the crushed stone content is high, moisture is more likely to form non - uniform seepage channels within the slope, resulting in the wetting zone showing striped and irregular distribution characteristics. The wetting expansion process of slopes with a low stone content is relatively uniform, and the instability mode may be manifested as progressive softening and overall strength degradation. On the other hand, due to the preferential pathway effect, slopes with a high stone content are prone to forming local high - water - content zones and concentrated infiltration areas, which can induce local failure and accelerate the development of shear zones.

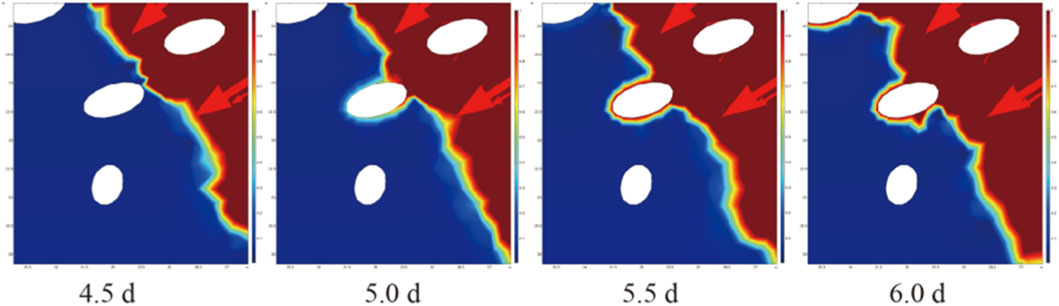
4.2 Seepage process at the soil - Rock interface

An analysis of the local seepage process reveals that in soil-rock mixture slopes, the presence of stones significantly alters the internal seepage characteristics of the slope, giving rise to the phenomenon of seepage around stones and the distribution pattern of saturated zones. As shown in Figure 5, the simulation results indicate that when water flow encounters stones, it bypasses the stones to form preferential seepage paths. This phenomenon stems from the stones’ alteration of the water flow direction, causing moisture to be more inclined to infiltrate through the soil surrounding the stones rather than directly passing through them. The formation of these preferential seepage paths not only accelerates moisture migration in local areas but also leads to an uneven distribution of moisture within the slope. Particularly behind the stones, due to the bypassing of water flow, local saturated zones are prone to form. The saturation levels in these zones are significantly higher than those in the surrounding soil. Further analysis shows that the local saturated zones resulting from seepage around stones have a significant impact on slope stability. As rainfall continues, the extent of these local saturated zones gradually expands, and the saturation levels continuously rise, thereby reducing the soil’s shear strength. In the lower part of the slope, because of the lower terrain and the dense distribution of stones, moisture tends to accumulate here, forming large - scale continuous saturated zones. The expansion of these saturated zones further weakens the slope stability and increases the risk of slope instability. It is noteworthy that the stone content and arrangement pattern have a significant influence on seepage around stones and the distribution of saturated zones. In slopes with a high stone content, the connected macro-pores or preferential channels formed by crushed stones accelerate moisture infiltration, speeding up the advancement of the wetting front and the more rapid expansion of saturated zones. In contrast, in slopes with a low stone content, due to the relatively small overall porosity of the soil, the infiltration process is controlled by matric suction. The advancement of the wetting front is slow, and the distribution of saturated zones is relatively uniform.

Figure 5

Figure 5. Local seepage process (with 20% stone content).

Figure 6 illustrates the variation of saturation over time at measurement points within soil-rock mixture slopes with different stone contents (20%, 40%, and 60%). In the case of a 20% stone content (Figure 6a), the saturation remains relatively stable during the initial stage and then rapidly increases and approaches a stable value near 1 day. This indicates that in slopes with a low stone content, where soil particles dominate, the infiltration process is relatively slow and uniform. The increase in saturation is gradual until it reaches a relatively stable state. When the stone content is 40% (Figure 6b), the variation of saturation exhibits different characteristics. During the period from 3.3 days to 3.55 days, the saturation rises slowly, followed by a distinct rapid increase phase, and stabilizes around 3.55 days. This suggests that as the stone content increases, the seepage paths within the slope become more complex. The presence of stones forms preferential seepage channels, causing the saturation to increase rapidly within a specific time period. For slopes with a 60% stone content (Figure 6c), the variation of saturation is even more dramatic. Starting from 2.2 days, the saturation gradually rises and rapidly reaches a stable state around 2.8 days. A high stone content makes the pore structure within the slope more heterogeneous. The connected macropores or preferential channels significantly accelerate moisture infiltration, enabling the saturation to increase rapidly and reach a stable state within a relatively short time. Overall, an increase in stone content clearly accelerates the rate of saturation increase at measurement points within the slope and shortens the time required to reach a stable state.

Figure 6

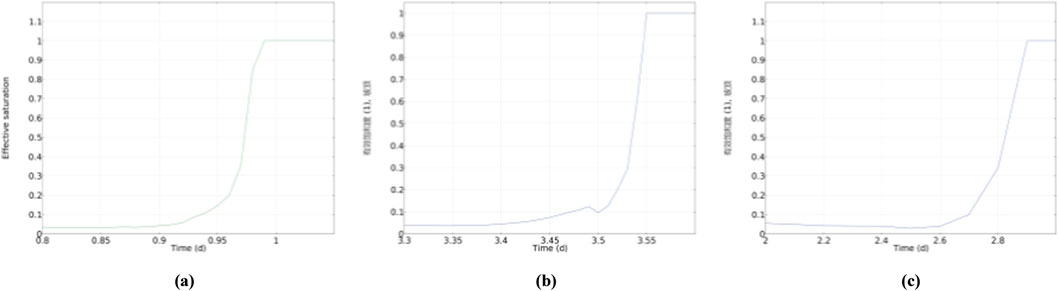
Figure 6. Changes in saturation at the in-situ points within the slope. (a) Stone content 20% (b) Stone content 40% (c) Stone content 60%.

4.3 Model validation

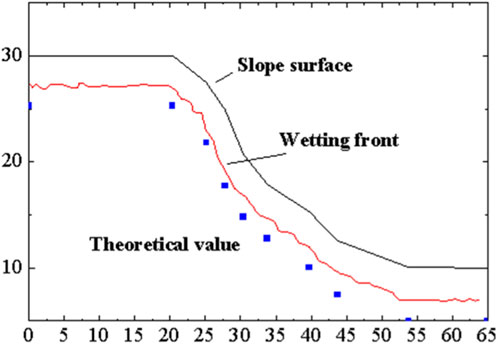
The calculated parameters for the Van Genuchten model are presented in Table 2. By comparing the calculation results with an infiltration time of 5 days, as shown in Figure 7, it can be observed that the calculated results of the improved Green-Ampt model (the red curve) exhibit a relatively high overall agreement with the actual values obtained from finite - element simulation (the blue dots). This indicates that the improved model can effectively reflect the infiltration characteristics of soil-rock mixture slopes under rainfall conditions. It is noteworthy that, in most stages, the theoretical calculated values are slightly larger than the numerical simulation values. This discrepancy mainly stems from the following two aspects: (1) Although the improved Green-Ampt model incorporates the atmospheric pressure boundary condition and a modified permeability coefficient formula, it is still based on the assumptions of a well - defined wetting front and uniform infiltration paths. Consequently, it fails to fully capture the complex heterogeneous structure within the soil-rock mixture. In actual numerical simulations, the irregular distribution of stones can delay the infiltration process in some areas, thereby relatively slowing down the overall advancement rate of the wetting front. (2) The numerical model takes into account the slope geometry, heterogeneous pore distribution, and soil - rock interface effects. Under the combined influence of these factors, the retention and bypass of pore gases lead to a local reduction in infiltration efficiency, further widening the gap between the theoretical and simulated values. Overall, the theoretical prediction results of the improved model are relatively consistent with the numerical simulation values in terms of trends. This demonstrates the applicability and reliability of the improved Green-Ampt model proposed in this paper, which can provide effective support for seepage analysis and stability evaluation of soil-rock mixture slopes.

Table 2

Table 2. Parameters of the Van Genuchten model for soil-rock mixtures.

Figure 7

Figure 7. Comparison of theoretical values and actual values.

5 Conclusion

This study investigated the rainfall infiltration of soil-rock mixture slopes and evaluated the reliability of the improved infiltration model through theoretical modification and finite - element verification. The main conclusions are as follows:

1. By introducing the atmospheric pressure boundary condition and a modified permeability formula for soil-rock mixtures, the improved Green-Ampt model can effectively account for the influences of non-ponded infiltration, ponded conditions, and air pressure. As a result, it significantly enhances the prediction accuracy.

2. An increase in rock block content accelerates the advancement of the wetting front by forming preferential flow channels and heterogeneous saturated zones. These characteristics promote the concentration of local pore pressure and the development of shear bands, thereby increasing the likelihood of progressive instability.

3. The presence of rock blocks in soil-rock mixture slopes significantly alters the internal seepage characteristics of the slopes, resulting in the local formation of preferential seepage around rocks and abnormal distribution patterns of saturated zones.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

XX: Funding acquisition, Writing – review and editing, Writing – original draft. WW: Conceptualization, Writing – review and editing, Investigation. JC: Methodology, Writing – review and editing, Supervision. LG: Project administration, Formal Analysis, Data curation, Writing – review and editing. ZC: Resources, Validation, Writing – review and editing.

Funding

The authors declare that no financial support was received for the research and/or publication of this article.

Acknowledgements

The authors are grateful to the reviewers for their helpful comments on the manuscript.

Conflict of interest

Author XX was employed by Jiangxi Nuclear Industry Engineering Geology Investigation Institute Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahuja, L. R., Sharpley, A. N., and Lehman, O. R. (1982). Effect of soil slope and rainfall characteristics on phosphorus in runoff. J. Environ. Qual. 11 (1), 9–13. doi:10.2134/jeq1982.00472425001100010003x

CrossRef Full Text | Google Scholar

Al-Homoud, A. S., and Masanat, Y. (1998). A classification system for the assessment of slope stability of terrains along highway routes in Jordan. Environ. Geol. 34 (1), 59–69. doi:10.1007/s002540050256

CrossRef Full Text | Google Scholar

Biscontin, G., and Pestana, J. M. (2006). Factors affecting seismic response of submarine slopes. Nat. Hazards and Earth Syst. Sci. 6 (1), 97–107. doi:10.5194/nhess-6-97-2006

CrossRef Full Text | Google Scholar

Chongshi, G. U., Haizhen, W. U., and Huaizhi, S. U. (2009). Research on stability of the accumulated rock-soil body of reservoir bank under rainfall condition. Chin. Sci. Tech. Sci. Engl. Ed. (9), 8. doi:10.1007/s11431-009-0250-x

CrossRef Full Text | Google Scholar

Chu, S. T., Onstad, C. A., and Rawls, W. J. (1986). Field evaluation of layered green-ampt model for transient crust conditions. Trans. Asae 29 (5), 1268–1272. doi:10.13031/2013.30307

CrossRef Full Text | Google Scholar

Davidson, M. R. (1984). A green-Ampt Model of infiltration in a cracked soil. Water Resour. Res. 20 (11), 1685–1690. doi:10.1029/WR020i011p01685

CrossRef Full Text | Google Scholar

Dongmei, S., Jiang, G., Peng, X., Wang, S., Li, Y, and Jiang, P. (2015). Runoff erosion process on slope of engineering accumulation with different soil-rock ratio. Trans. Chin. Soc. Agric. Eng. doi:10.11975/j.issn.1002-6819.2015.17.020

CrossRef Full Text | Google Scholar

Fang, H. Y., Cai, Q. G., Chen, H., and Li, Q. Y. (2008). Effect of rainfall regime and slope on runoff in a gullied loess Region on the Loess Plateau in China. Environ. Manag. 42 (3), 402–411. doi:10.1007/s00267-008-9122-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Friedel, S., Thielen, A., and Springman, S. M. (2006). Investigation of a slope endangered by rainfall-induced landslides using 3D resistivity tomography and geotechnical testing. J. Appl. Geophys. 60 (2), 100–114. doi:10.1016/j.jappgeo.2006.01.001

CrossRef Full Text | Google Scholar

Gonzalez, Y. T., Schaefer, V. R., and Rollins, D. K. (2021). Assessing diagnostic error of factors of safety of slopes applying bayesian inference. Int. J. Geomechanics 21 (11), 4021203.1–4021203.10. doi:10.1061/(ASCE)GM.1943-5622.0002173

CrossRef Full Text | Google Scholar

He, X., Liu, X., Liu, Z., and Wang, W. (2025). The deformation and stability of excavation in multi-aquifer-aquitard system. Int. Conf. Mineral Resour. Geotechnol. Geol. Explor., 212–223. doi:10.1007/978-3-031-78690-7_22

CrossRef Full Text | Google Scholar

Hong, L. (2005). A systematic research on the deformation and stability of high embankment of jiuzhai-huanglong airport, sichuan China. Earth and Environ. 33 (B10), 133–135. doi:10.3969/j.issn.1672-9250.2005.z1.029

CrossRef Full Text | Google Scholar

Huang, X. L., Xiong, J., Liu, J. J., Guo, L., Joseph, D. D., Matsumoto, Y., et al. (2010). Two-phase seepage analysis in unsaturated rock and soil slope during rainfall. AIP Conf. Proc. 1207 (1), 507–512. doi:10.1063/1.3366418

CrossRef Full Text | Google Scholar

Huang, Da, Ren, F., and Cen, D. (2017). Shear deformation and strength of the interphase between the soil-rock mixture and the benched bedrock slope surface. Acta Geotechnica Int. J. Geoengin. 12, 391–413. doi:10.1007/s11440-016-0468-2

CrossRef Full Text | Google Scholar

Junhua, D. (2017). Stability analysis of rock-soil mixture slope based on finite element local strength reduction method and excavation unloading. Pearl River. doi:10.1088/1755-1315/638/1/012099

CrossRef Full Text | Google Scholar

Kirchhoff, V. W. J. H., Alves, J. R., Da Silva, F. R., and Fishman, J. (1996). Observations of ozone concentrations in the Brazilian cerrado during the trace a field expedition. J. Geophys. Res. Atmos. 101 (D19), 24029–24042. doi:10.1029/95JD03030

CrossRef Full Text | Google Scholar

Langhans, C., Govers, G., Diels, J., Stone, J. J., and Nearing, M. A. (2014). Modeling scale-dependent runoff generation in a small semi-arid watershed accounting for rainfall intensity and water depth. Adv. Water Resour. 69, 65–78. doi:10.1016/j.advwatres.2014.03.005

CrossRef Full Text | Google Scholar

Li, Li, Lin, H., Qiang, Y., Zhang, Yi, Liang, S., Hu, S., et al. (2024). Stability analysis of rainfall-induced landslide considering air resistance delay effect and lateral seepage. Sci. Rep. 14 (1), 8377. doi:10.1038/s41598-024-59121-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, H., Hu, R., Tan, R., Wang, Y., and Zeng, R. (2006). Endogenic and exogenic geological factors causing deformation and failure of bank slopes on tiger-leaping gorge reach of jinsha river. J. Eng. Geol. 14 (4), 488–495. doi:10.1016/S1872-2040(06)60004-2

CrossRef Full Text | Google Scholar

Liu, J., Zhang, J., and Feng, J. (2008). Green-Ampt model for layered soils with nonuniform initial water content under unsteady infiltration. Soil Sci. Soc. Am. J. 72 (4), 1041–1047. doi:10.2136/sssaj2007.0119

CrossRef Full Text | Google Scholar

Liu, S., Yang, Lu, Weng, L., and Bai, F. (2015). Field study of treatment for expansive soil/rock channel slope with soilbags. Geotext. and Geomembranes 43 (4), 283–292. doi:10.1016/j.geotexmem.2015.04.004

CrossRef Full Text | Google Scholar

Ma, Y., Feng, S., Su, D., Gao, G., and Huo, Z. (2010). Modeling water infiltration in a large layered soil column with a modified Green-Ampt model and HYDRUS-1D. Comput. and Electron. Agric. 71 (Suppl. S1), S40–S47. doi:10.1016/j.compag.2009.07.006

CrossRef Full Text | Google Scholar

Nadal-Romero, E., Latron, J., Marti-Bono, C., and Reguees, D. (2008). Temporal distribution of suspended sediment transport in a humid mediterranean badland area: the Araguás catchment, Central pyrenees. Geomorphology 97 (3-4), 601–616. doi:10.1016/j.geomorph.2007.09.009

CrossRef Full Text | Google Scholar

Quanjiu, W., Lai, J., and Yi, Li (2002). Comparison of green-ampt model with Philip Infiltration model. Trans. Chin. Soc. Agric. Eng. doi:10.1007/s11769-002-0038-4

CrossRef Full Text | Google Scholar

Rahardjo, H., Lee, T. T., Leong, E. C., and Rezaur, R. B. (2005). Response of a residual soil slope to rainfall. Can. Geotechnical J. 42 (2), 340–351. doi:10.1139/t06-085

CrossRef Full Text | Google Scholar

Ries, A. (2011). Characterization of banks and slope failures along the shoreline of Lake sakakawea. USA: Geological Society of America.

Google Scholar

Shafer, B., Ajmera, B., Raj, D. U., and Aaron, L. M. (2024). Assessment of factors leading to the failure of slopes in North Dakota. Landslides 21 (5), 1109–1128. doi:10.1007/s10346-024-02211-1

CrossRef Full Text | Google Scholar

Shao, S., and Ji, S. Y. (2014). Effects of rock spatial distributions on stability of rock-soil-mixture slope. Eng. Mech. doi:10.6052/j.issn.1000-4750.2012.04.0248

CrossRef Full Text | Google Scholar

Shukla, M. K., Lal, R., Ebinger, M., and Meyer, C. (2006). Physical and chemical properties of soils under some piñon-juniper-oak canopies in a semi-arid ecosystem in New Mexico. J. Arid Environ. 66 (4), 673–685. doi:10.1016/j.jaridenv.2005.12.002

CrossRef Full Text | Google Scholar

Swartzendruber (2000). Derivation of a two-term infiltration equation from the green-Ampt model. J. Hydrology 236, 247–251. doi:10.1016/S0022-1694(00)00297-3

CrossRef Full Text | Google Scholar

Tsihrintzis, V. A., and Hamid, R. (2015). Runoff quality prediction from small urban catchments using SWMM. Hydrol. Process. 12 (2), 311–329. doi:10.1002/(sici)1099-1085(199802)12:2<311::aid-hyp579>3.0.co;2-r

CrossRef Full Text | Google Scholar

Wang, C., Saha, B., and Hawlader, B. (2015). “Some factors affecting retrogressive failure of sensitive clay slopes using large deformation finite element modeling,” in The 68th Canadian geotechnical conference and 7th Canadian permafrost conference.

Google Scholar

Wu, Q., Liu, Y., Tang, H., Kang, J., Wang, L., Li, C., et al. (2023). Experimental study of the influence of wetting and drying cycles on the strength of intact rock samples from a red stratum in the Three gorges reservoir area. Eng. Geol. 314, 107013. doi:10.1016/j.enggeo.2023.107013

CrossRef Full Text | Google Scholar

Xiao-Li, Y., and Jin-Feng, Z. (2006). Stability factors for rock slopes subjected to pore water pressure based on the hoek-Brown failure criterion. Int. J. Rock Mech. Min. Sci. 43, 1146–1152. doi:10.1016/j.ijrmms.2006.03.010

CrossRef Full Text | Google Scholar

Zhang, B., Tang, H., Ning, Y., Fang, K., and Xia, D. (2024). Weight analysis of impact factors of interbedded anti-inclined slopes block-flexure toppling based on support vector regression. J. Earth Sci. Engl. Ed. 35 (35), 568–582. doi:10.1007/s12583-023-1835-1

CrossRef Full Text | Google Scholar

Zhou, Z., Yang, H., Wang, X., and Liu, B. (2016). Model development and experimental verification for permeability coefficient of soil–rock mixture. Int. J. Geomechanics 17, 04016106. doi:10.1061/(asce)gm.1943-5622.0000768

CrossRef Full Text | Google Scholar

Zhou, F., Wu, H., Qiang, Y., Liu, G., Zhang, Z., Zhang, Yi, et al. (2025). Investigating the coupling effects of rainfall intensity and slope inclination on soil-rock mixture slope stability and failure modes. PLoS ONE 20 (2), e0314752. doi:10.1371/journal.pone.0314752

PubMed Abstract | CrossRef Full Text | Google Scholar