Detecting Multidimensional Differential Item Functioning with the Multiple Indicators Multiple Causes Model, the Item Response Theory Likelihood Ratio Test, and Logistic Regression

Educational and psychological assessments are typically designed to have a simple structure in which items are associated with a single latent trait (Thurstone, 1947; Revelle and Rocklin, 1979; Finch, 2012). In the absence of a simple structure, one or more items may be associated with multiple latent traits within a more complex structure, which is often called either a circumplex (Guttman, 1954; Acton and Revelle, 2004) or a non-simple structure (Tate, 2003). When item bias is investigated in an assessment with a non-simple structure, there is a need for a differential item functioning (DIF) procedure that can take two or more latent traits into account. DIF, first defined by Holland and Thayer (1988), refers to a conditional dependency between group membership of examinees (e.g., male vs. female) and item performance (i.e., the probability of answering the item correctly) after controlling for latent traits. As a result of DIF, a biased item provides either a constant advantage for a particular group (i.e., uniform DIF) or an advantage varying in magnitude and/or in direction across the latent trait continuum (i.e., non-uniform DIF). Although uniform DIF is more frequently observed than non-uniform DIF in practice, several studies indicated that non-uniform DIF can also be present in real data sets from educational and psychological assessments (e.g., Mazor et al., 1994; De Beer, 2004; Le, 2006; Woods and Grimm, 2011; Teresi and Fleishman, 2017). Therefore, when conducting DIF analyses, the type of DIF (i.e., uniform or non-uniform) is crucial because different DIF methods can be more appropriate for each type of DIF (Penfield and Camilli, 2007).

To investigate DIF in a multidimensional test with a non-simple structure, DIF detection procedures designed for tests that measure a single latent trait—such as the Mantel–Haenszel method (Mantel and Haenszel, 1959), simultaneous item bias test (SIBTEST; Shealy and Stout, 1993), and Lord’s chi-square method (Lord, 1980)—may not be appropriate. When the DIF detection procedure is not appropriate for the test structure, it may lead to unintended consequences, such as misidentification of DIF due to different conditional distributions of latent traits for different examinee subgroups (Clauser et al., 1996; Mazor et al., 1998; Tate, 2003). Therefore, it is essential to find a DIF detection approach that would match examinees on the joint distribution of the latent traits so that examinees can be comparable on all primary latent traits (Clauser et al., 1996; Mazor et al., 1998).

To date, several DIF detection approaches have been proposed for investigating DIF in multidimensional assessments that intentionally measure two or more latent traits. These approaches are typically multidimensional extensions of conventional DIF detection approaches designed for unidimensional tests, such as multidimensional SIBTEST (Stout et al., 1997), differential functioning of items and tests (Oshima et al., 1997), logistic regression (Mazor et al., 1998), item response theory likelihood ratio (IRT-LR) test (Suh and Cho, 2014), and multiple indicators multiple causes (MIMIC) model (Lee et al., 2016). Among these approaches, MIMIC, IRT-LR, and logistic regression are widely used and readily available for detecting DIF in dichotomously and polytomously scored items because of their ease of use and their connection with IRT models. Previous studies compared the unidimensional forms of MIMIC, IRT-LR, and logistic regression with each other as well as with other DIF detection methods (e.g., Finch, 2005; Woods, 2009a; Atar and Kamata, 2011; Woods and Grimm, 2011; Kan and Bulut, 2014). However, the relative performances of these approaches are still unknown in the context of multidimensional tests. Therefore, this study aims to extend the comparison of the MIMIC, IRT-LR, and logistic regression approaches to multidimensional item response data in which items are associated with one or multiple latent traits. The performances of the three DIF approaches were systematically compared in a simulation study with regard to Type I error and rejection rates in detecting uniform and non-uniform DIF in a non-simple and multidimensional test structure. Although each of the three methods can be extended to deal with two or more latent traits, the simplest case (two latent traits) was considered in this study.

Theoretical Background

DIF Detection with MIMIC

Jöreskog and Goldberger (1975) introduced the MIMIC model as a special case of the full structural equation model where the latent variables are regressed on observed covariates and there are no regressions among the latent variables. Early forms of the MIMIC model were only used for examining uniform DIF for dichotomously or polytomously scored item responses (e.g., Finch, 2005, 2012; Shih and Wang, 2009; Woods et al., 2009). To examine uniform and non-uniform DIF simultaneously, Woods and Grimm (2011) introduced the MIMIC-interaction model, which is similar to restricted factor analysis models with an interaction term (Ferrando and Lorenzo-Seva, 2000; Barendse et al., 2010). The MIMIC-interaction model can be written as follows:

$y_i{}^{\ast }={\lambda }_{\text{i}}\eta +{\mathrm{\beta }}_{\text{i}}z+{\omega }_{\text{i}}\eta z+{\epsilon }_i,$ (1)

where $y_i{}^{\ast }$ is the continuous latent response underlying the observed item response for item i, λ_i is the factor loading for item i, which is analogous to the item discrimination parameter in IRT models (Takane and De Leeuw, 1987; McDonald, 1997), η is the latent variable that follows a normal distribution, η ~ N(0,1)¹, z is a categorical covariate (i.e., grouping variable), β_i is the uniform DIF effect, ω_i is the non-uniform DIF effect for item i, and ε_i is the random error for item i.

In Eq. 1, if β_i = 0, then item i is homogenous over the grouping variable z, suggesting that there is no DIF observed in the item (Shih and Wang, 2009). If, however, β_i ≠ 0, then the item is considered as having uniform DIF due to the direct effect of the grouping variable z. The interaction term (ηz) between the latent trait and the grouping variable allows the MIMIC-interaction model to examine non-uniform DIF (i.e., if ω_i ≠ 0). ηz can be estimated using the latent moderated structural equations (LMS) method (Klein and Moosbrugger, 2000) in Mplus (Muthén and Muthén, 1998). The LMS method relies on a full-information maximum-likelihood estimation that gives an important efficiency and power advantage in analyzing non-normally distributed interaction effects between latent variables and observed variables [for more details on the LMS method, see Klein and Moosbrugger (2000)]. The major assumptions of the MIMIC-interaction model are independent observations and groups, locally independent items, equal latent variable variance among groups, and anchor (i.e., DIF-free) items (Woods and Grimm, 2011).

MIMIC for Multidimensional Data

Lee et al. (2016) recently introduced a multidimensional extension of the MIMIC-interaction model that can handle two or more latent traits. Assuming dichotomously scored items measure two latent traits (η₁ and η₂), then the MIMIC-interaction model in Eq. 1 can be extended as follows:

$y_i{}^{\ast }={\lambda }_{1i}{\eta }_1+{\lambda }_{2i}{\eta }_2+{\beta }_{i}z+{\omega }_{1i}{\eta }_{1}z+{\omega }_{2i}{\eta }_{2}z+{\epsilon }_i,$ (2)

where λ_1i and λ_2i are factor loadings of item i on latent trait 1 (η₁) and latent trait 2 (η₂), respectively, β_i is the uniform DIF effect of the grouping variable (z) on item i (when β_i ≠ 0), ω_1i and ω_2i are non-uniform DIF effects (when ω_1i ≠ 0 and/or ω_2i ≠ 0) on item i due to the interaction between the grouping variable and the two latent traits, and ε_i is the error term. To ensure model identification in the multidimensional MIMIC-interaction model, the two latent variables are assumed to have a bivariate normal distribution with means of 0 and variances of 1. However, factor loadings do not have to be fixed to 0 for the items and latent traits are allowed to the correlated.

DIF Detection with IRT-LR

The IRT-LR test depends on the comparison of two nested IRT models with a series of likelihood ratio (LR) tests. In general, the procedure begins with an omnibus test that examines whether any item parameter for a given item (e.g., item difficulty, item discrimination, or both in a two-parameter logistic model) differs between the reference and focal groups. The steps for conducting an omnibus test are as follows: First, a compact (C) model, where all item parameters are constrained to be equal across the reference and focal groups, is estimated. Second, an augmented (A) model, where all parameters of the item are allowed to vary across the two groups, is estimated. To test whether the item exhibits DIF, the LR test statistic, which is −2 times the difference in log likelihoods from the compact and augmented models, is computed as follows:

$\text{LR}=-2\text{ln\hspace{0.17em}}{L}_C-\left(-2\text{ln\hspace{0.17em}}{L}_A\right),$ (3)

where L_C is the log likelihood of the compact model and L_A is the log likelihoods of the augmented model. The LR statistic is approximately distributed as a chi-square (χ²) distribution with degrees of freedom (df) equal to the difference in the number of parameter estimates between the two models.

If the LR statistic from the omnibus test is significant, then follow-up tests should be performed to identify the type of DIF (Woods, 2009b). In the subsequent analyses, the discrimination parameter of the item is constrained to be equal but the difficulty parameter of the item is estimated for the two groups separately. This process results in a second compact model that can be compared against the same augmented model from the omnibus test. A significant LR statistic from this comparison indicates that the item should be flagged for non-uniform DIF. If this LR statistic is not significant, then the item should be tested for uniform DIF. For this test, the second compact model should be compared with the first compact model from the omnibus test. A significant LR statistic from this comparison indicates that the item should be flagged for uniform DIF.

IRT-LR for Multidimensional Data

Suh and Cho (2014) extended the IRT-LR test for multidimensional IRT (MIRT) models. Similar to the IRT-LR test for unidimensional IRT models, the IRT-LR test for MIRT models depends on the evaluation of model fit by comparing nested models (Suh and Cho, 2014). The IRT-LR test for MIRT models requires additional assumptions. To ensure metric indeterminacy across multiple latent traits in their application, the means and variances of two latent traits are fixed at 0 and 1 s, respectively, in both groups. Also, the correlation between the two latent traits is fixed at 0 in the augmented model with freely estimated item parameters across the two groups. In addition, the discrimination parameter for the first item is fixed at 0 on the second latent trait for both groups to satisfy the model identification when the test has a non-simple structure. Details on actual IRT-LR tests used in this study are provided later.

DIF Detection with Logistic Regression

Logistic regression, introduced by Swaminathan and Rogers (1990) as a DIF approach, aims to predict the probability of answering an item correctly as a function of total test score (either raw or latent scores), group membership, and the interaction between total test score and group membership. Depending on the statistical significance of the group effect and the interaction between total test score and group membership, one can determine whether an item exhibits uniform or non-uniform DIF. The logistic regression model can be written as follows:

$P\left(u=1\right)=\frac{e^z}{1+e^z},$ (4)

where

$z={\beta }_0+{\beta }_{1}X+{\beta }_{2}G\text{\hspace{0.17em}for\hspace{0.17em}detecting\hspace{0.17em}uniform\hspace{0.17em}DIF},\text{\hspace{0.17em}or}$ (5)

$z={\beta }_0+{\beta }_{1}X+{\beta }_{2}G+{\beta }_3\mathrm{XG}\text{\hspace{0.17em}for\hspace{0.17em}detecting\hspace{0.17em}nonuniform\hspace{0.17em}DIF}.$ (6)

In Eqs 4–6, P(u = 1) is the probability of responding to a given item correctly, X is the total test score on the test, and G indicates the group membership (G = 1 for the focal group; G = 0 for the reference group). If there is a significant group effect (i.e., β₂ ≠ 0), the item is flagged as uniform DIF. If there is a significant group and total score interaction (i.e., β₃ ≠ 0), the item is flagged as non-uniform DIF, regardless of the significance status of β₂.

Logistic Regression for Multidimensional Data

Mazor et al. (1998) used the logistic regression procedure to accommodate multiple traits as matching variables. Assuming the item is associated with two traits (X₁ and X₂), Mazor et al. (1998) expanded the logistic regression model in Eq. 5 for two traits as follows:

$z={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_{3}G.$ (7)

Although Mazor et al. (1998) only considered uniform DIF in their study, the logistic regression approach can also be used for detecting non-uniform DIF in the presence of multiple traits. Following the logistic regression model in Eq. 6, non-uniform DIF for an item associated with two traits (X₁ and X₂) can be evaluated as follows:

$z={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_{3}G+{\beta }_4{X}_{1}G+{\beta }_5{X}_{2}G.$ (8)

Uniform and non-uniform DIF can be identified using the same null hypotheses from the unidimensional form of logistic regression. If there is a significant group effect (i.e., β₃ ≠ 0 in Eq. 7), the item is flagged as uniform DIF; if there is a significant group and total score interaction (i.e., β₄ ≠ 0 and/or β₅ ≠ 0 in Eq. 8), then the item is flagged as non-uniform DIF, regardless of whether β₃ is significant.

This Study

As mentioned earlier, each of the three DIF detection approaches has a unique procedure to evaluate uniform and non-uniform DIF in multidimensional tests. Previous studies focused on the performances of these DIF detection methods under various conditions (e.g., test length, sample size, and DIF magnitude). However, the relative performances of these approaches are still unknown in the context of multidimensional tests. To address this gap, this study aims to compare the relative performances of the IRT-LR test, the multidimensional MIMIC-interaction model, and logistic regression in detecting DIF for multidimensional tests with a non-simple structure. The objectives of this study are threefold: (a) to compare the rejection rates of the three DIF detection approaches in detecting uniform and non-uniform DIF in multidimensional tests; (b) to compare the false positive rates (i.e., Type I error) of the three DIF detection approaches in evaluating DIF in multidimensional tests; and (c) to examine the impact of different factors (test length, DIF magnitude, sample size, correlation between latent traits, and latent mean differences between the focal and reference groups) on the performances of the three DIF detection approaches.

Method

Simulation Conditions

The simulation study consisted of six factors: (a) DIF types (non-DIF, uniform DIF, or non-uniform DIF); (b) test lengths (12-item test with 10 anchor items and 2 DIF items, or 22-item test with 20 anchor items and 2 DIF items); (c) the magnitude of DIF (low or medium)¹; (d) sample sizes for the reference (R) and focal (F) groups (R500/F100, R1,000/F200, R1,500/F500, or R1,000/F1,000); (e) correlations between the latent traits (ρ = 0, ρ = 0.3, or ρ = 0.5 for both groups); and (f) latent mean differences between the reference and focal groups (${\text{μ}}_{{\text{θ}}_1}$ = 0 and ${\text{μ}}_{{\text{θ}}_2}$ = 0 for both groups; or ${\text{μ}}_{{\text{θ}}_1}$ = 0 and ${\text{μ}}_{{\text{θ}}_2}$ = 0 for the reference group and ${\text{μ}}_{{\text{θ}}_1}$ = − 0.5 and ${\text{μ}}_{{\text{θ}}_2}$ = − 0.5 for the focal group). Except the non-DIF condition in the first factor, DIF type, the first five factors were fully crossed. The latent mean difference condition (${\text{μ}}_{{\text{θ}}_1}$ and ${\text{μ}}_{{\text{θ}}_2}$ = 0 for the reference group and ${\text{μ}}_{{\text{θ}}_1}$ and ${\text{μ}}_{{\text{θ}}_2}$ = − 0.5 for the focal group) was only crossed with two types of sample size (R1,500/F500 or R1,000/F1,000) and two types of correlations among the latent traits (ρ = 0 or ρ = 0.5 for both groups) for each DIF type. For each crossed condition, 100 replications were implemented.

The two test lengths (12 and 22 items) were chosen to resemble the values observed in earlier DIF studies using the DIF detection methods (either unidimensional or multidimensional applications) that we considered in this study (e.g., Woods, 2009b; Woods and Grimm, 2011; Lee et al., 2016). Also, in the multidimensional application of the logistic regression by Mazor et al. (1998), a fairly long test (64 items) was considered in their simulation study. Therefore, having relatively shorter tests would be worthwhile to be studied in this study. Given the same number of DIF items (i.e., two items) simulated for the two test lengths, the results of our simulation study can also indicate the effect of increasing the number of anchor items twice. In this study, the proportion of DIF items was 20% for the 12-item test condition and 10% for the 22-item test condition.

The four sample sizes were common values used across many DIF studies (e.g., Woods, 2009a,b; Suh and Cho, 2014). Also, the first three conditions (R500/F100, R1,000/F200, and R1,500/F500) were chosen because the focal group is typically smaller than the reference group in real testing programs, whereas the last condition (R1,000/F1,000) was selected because it has been frequently used in DIF simulation studies to obtain stable parameter estimates especially when complex models such as MIRT models were used.

According to Oshima et al. (1997), a distributional difference can arise from the correlation of latent traits and/or the location of latent means in the context of multidimensional DIF studies. Thus, to investigate the effect of having the mean difference between the two groups, two conditions were considered for the F group: (a) a bivariate normal distribution, with each dimension with a mean of 0 and a variance of 1, and (b) a bivariate normal distribution, with each dimension with a mean of −0.5 and a variance of 1. For the correlation between the two dimensions under each distributional condition, three levels, ρ = 0.0, ρ = 0.3, and ρ = 0.5, were simulated to signify three different correlational levels. For the R group, two latent traits were generated from a bivariate normal distribution, with each dimension with a mean of 0 and a variance of 1.

Data Generation

A two-dimensional test structure was used for generating dichotomous item response data. The multidimensional two-parameter logistic model (M2PL; Reckase, 1985) was chosen as the studied MIRT model to generate item response data. Based on the M2PL model, the probability of responding to item i (i = 1, …, K) correctly for person j (j = 1, …, J) with the latent traits θ_j = {θ_1j, θ_2j} in a two-dimensional test can be written as follows:

$P_{ji}=P\left(x_{ji}=1\text{|}{\mathbf{\theta }}_j,a_i,b_i\right)=\frac{e^{a_i^T{\theta }_j-b_i}}{1+e^{a_i^T{\theta }_j-b_i}},$ (9)

where θ _j is a vector of latent abilities of person j, ${\mathbf{a}}_i^T$ is a transposed vector of discrimination parameters of item i (a _i = {a_1i, a_2i}), and b_i is the intercept parameter related to difficulty level of item i.

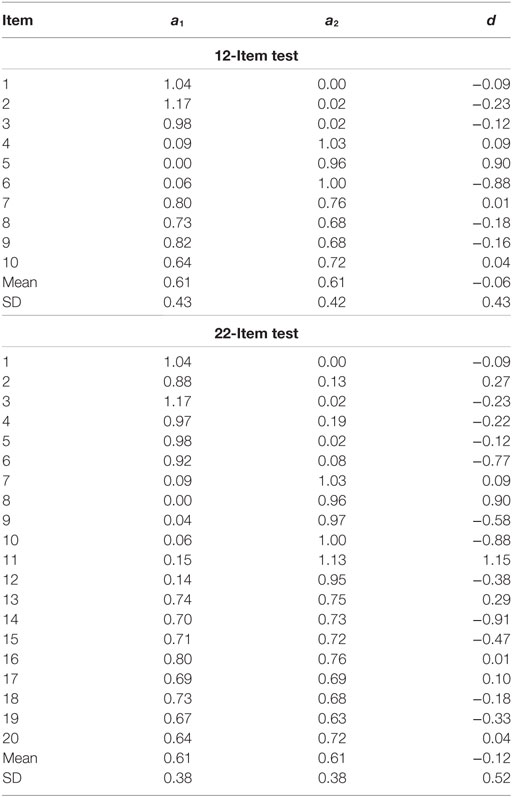
Table 1 presents item parameters for DIF items in 12-item and 22-item tests (i.e., two DIF items for each test). The same anchor item parameters (see Appendix) were used for reference and focal groups to generate DIF-free anchor items. These anchor item parameters were the same as the values reported in a previous study (Lee et al., 2016). DIF items were introduced in the last two items for both tests. Using the anchor items and DIF items, three types of data sets were generated: (a) non-DIF condition, (b) uniform DIF condition, and (c) non-uniform DIF condition. Data for the non-DIF condition were generated using the parameters of the reference group in Table 1 for both groups. Data sets with uniform and non-uniform DIF were generated by modifying item parameters for the last two items for the focal group depending on the condition of DIF. The item parameters and magnitude of DIF between the focal and the reference groups in Table 1 were similar to previous multidimensional DIF studies (e.g., Oshima et al., 1997; Suh and Cho, 2014; Lee et al., 2016).

TABLE 1

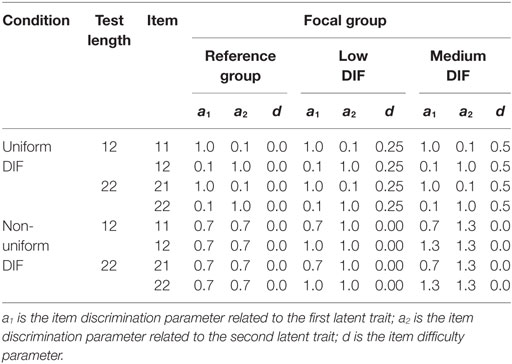
Table 1. Item parameters used for generating differential item functioning (DIF) conditions in the last two items.

Data Analysis Procedures

For each simulated data set, (a) the LR statistic for the IRT-LR test was obtained from a full-information maximum-likelihood estimation of the M2PL model using the mirt package (Chalmers et al., 2015) in R (R Core Team, 2016); (b) the multidimensional MIMIC-interaction model was estimated using the maximum-likelihood estimation and the LMS method in Mplus 7 (Muthén and Muthén, 1998); and (c) logistic regression models were run using the glm function in the R stats package (R Core Team, 2016). Similar to the study of Mazor et al. (1998), two logistic regression models were used: the first one with raw scores as total scores and the second one with latent trait (theta) scores as total scores. To reflect the multidimensionality from the two dimensions, two raw scores were computed by summing up individual item scores (binary responses) related to the first latent trait and second latent trait,² based on the factor loading (discrimination) patterns used for data generation (see Appendix). Two latent trait scores were estimated using the MIRT model in Eq. 9 (i.e., M2PL model).³ DIF was tested only for items 11 and 12 in the 12-item test and items 21 and 22 in the 22-item test, assuming that these items were initially determined as suspicious items for exhibiting uniform or non-uniform DIF.

Evaluation Criteria

Type I error rates from non-DIF conditions and rejection rates from uniform and non-uniform DIF conditions were evaluated to compare the three DIF detection approaches. Type I error rates for the IRT-LR test were computed as the proportion of significant LR test statistics out of 100 replications in the non-DIF conditions. To make the three DIF detection procedures as comparable as possible, this study did not consider the result of the omnibus DIF test from the IRT-LR approach. Instead, the process of detecting DIF started with a partially augmented model in which item parameters for all items, except for suspicious items (i.e., items 11 and 12 in the 12-item test; items 21 and 22 in the 22-item test), were constrained to be equal across the reference and focal groups. Then, the augmented model was compared with a series of augmented models in which item difficulty parameter (b in Table 1) and item discrimination parameters (a₁ and a₂ in Table 1) for each suspicious item were constrained (to be equal across the two groups) one at a time. If at least one of these comparisons (IRT-LR tests) was significant, it was considered as false identification of DIF. Type I error rates for the MIMIC-interaction model were determined based on the proportion of significant DIF parameter estimates (β₁ for uniform DIF; ω_1i or ω_2i for non-uniform DIF in Eq. 2). Items flagged for exhibiting either uniform or non-uniform DIF were considered as false identification of DIF. Type I error rates for logistic regression were computed based on the proportion of significant regression coefficients (β₃ for uniform DIF; β₄ or β₅ for non-uniform DIF in Eqs 7 and 8). Two logistic regression analyses were conducted using raw and latent trait scores, as explained earlier. Similar to the IRT-LR test and the MIMIC-interaction model, items that were falsely identified as either uniform or non-uniform DIF represented Type I errors.

All of the three DIF detection approaches were evaluated at the nominal level α = 0.05. Therefore, we would expect that 5 of the 100 replications would be false positives for each DIF detection approach. To investigate the inflation of Type I error rates, Bradley’s (Bradley, 1978) liberal robustness criterion was used.⁴ If Type I error rates for each DIF approach fell in the range of 0.025–0.075, then Type I error rate was considered well-controlled (Bradley, 1978). Rejection rates for uniform and non-uniform DIF conditions were calculated in the same manner using the data sets generated with uniform and non-uniform DIF conditions.

Finally, a repeated-measures multivariate analysis of variance (MANOVA) was used to test the effects of simulation factors [DIF type (i.e., uniform or non-uniform), DIF magnitude (low or medium), test length (12 or 22 items), sample size (R500/F100, R1,000/F200, R1,500/F500, or R1,000/F1,000), and correlation between latent traits (i.e., 0, 0.3, or 0.5)] as between-factor variables and the type of DIF method (IRT-LR, MIMIC, logistic regression with raw scores, and logistic regression with latent trait scores) as a within-factor variable on rejection rates. For each factor, partial eta squared (η²) was computed as a measure of effect size. For the within-subject factors, η² was computed based on the method described by Tabachnick and Fidell (2007) as follows:

${\eta }^2=1-\sqrt{\mathrm{\Lambda }},$ (10)

where Λ is Wilk’s lambda in MANOVA. For the between-subject factors, η² was the ratio of the sum of squares of the main effect of the factor (SS_effect) to the sum of squares of the total variance (SS_effect + SS_error).

Results

Type I Error Rates

Figure 1 shows Type I error rates under the non-DIF condition based on the average of the two DIF items (i.e., items 11 and 12 in the 12-item test; items 21 and 22 in the 22-item test). In the 12-item test, Type I error rates for logistic regression analyses based on raw scores (LR-R) and latent trait scores (LR-T) were consistently higher than Type I error rates from the IRT-LR test and the MIMIC-interaction model across all simulation conditions. The two logistic regression results (LR-R and LR-T) show similar patterns. Furthermore, Type I error rates for logistic regression analyses were consistently outside of Bradley’s liberal robustness criteria (i.e., 0.025 < Type I error < 0.075), except for logistic regression with raw scores under R1,000/F1,000 and ρ = 0.3.

FIGURE 1

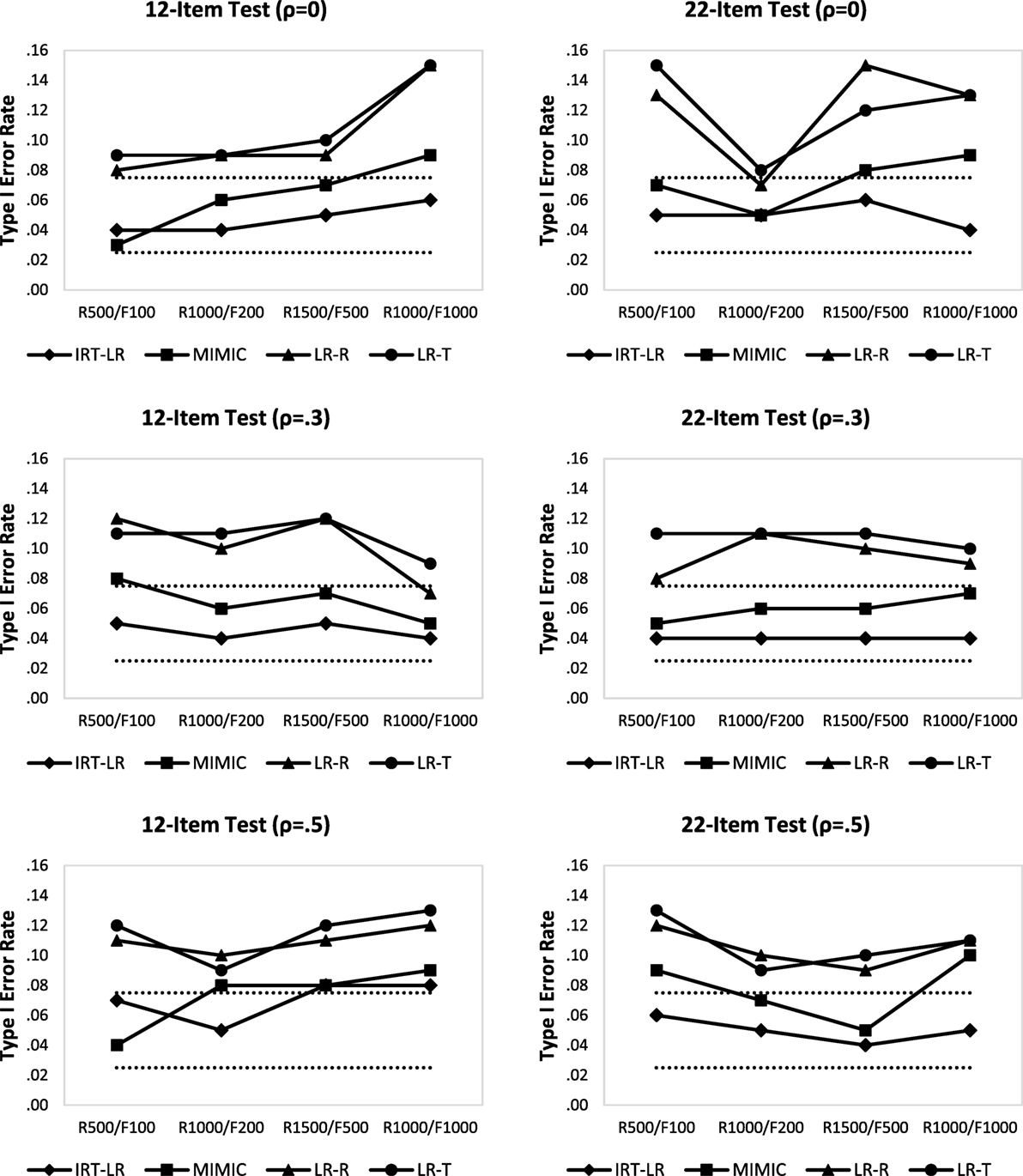
Figure 1. Type I error rates in the 12-item and 22-item tests (note: dotted lines indicate Bradley’s liberal robustness criteria; LR-R is logistic regression with raw scores; and LR-T is logistic regression with latent trait scores).

The MIMIC-interaction model had higher Type I error rates than the IRT-LR test across all conditions in the 12-item test, except for the small sample size condition (i.e., R500/F100) with ρ = 0 and ρ = 0.5. Type I error rates for the IRT-LR test were slightly outside of Bradley’s liberal robustness criteria only when latent traits were moderately correlated (ρ = 0.5) and the sample size was large (i.e., R1,500/F500 or R1,000/F1,000). There was no consistent pattern related to different correlations and sample sizes. It appears that the error rates increased as the sample size increased in ρ = 0 condition, but that was not observed in other correlation conditions.

In the 22-item test, Type I error rates from logistic regression based on raw and latent trait scores were again consistently higher than the other two DIF detection methods. Type I error rates for logistic regression analyses were within Bradley’s liberal robustness criteria only when the correlation between latent traits was ρ = 0 and the sample size condition was R1,000/F200. Type I error rates of the MIMIC-interaction model were consistently higher than the IRT-LR test across all conditions, especially for the R1,000/F1,000 condition. Unlike in the 12-item test where no obvious pattern was observed, increasing the correlation between latent traits in the 22-item test tended to produce smaller Type I error rates for logistic regression, not for the other methods. Type I error rates from the IRT-LR test remained within Bradley’s liberal robustness criteria, whereas the MIMIC model had Type I error rates higher than 0.075, especially when sample size was large.

Overall, Type I error rates were well controlled for the IRT-LR test and relatively for the MIMIC-interaction model, whereas Type I error rates for logistic regression were almost always outside of the robustness criteria. The logistic regression with raw scores performed slightly better than the logistic regression with latent trait scores on average. The effects seemed to be confounded by different levels of each factor and different methods.

Rejection Rates

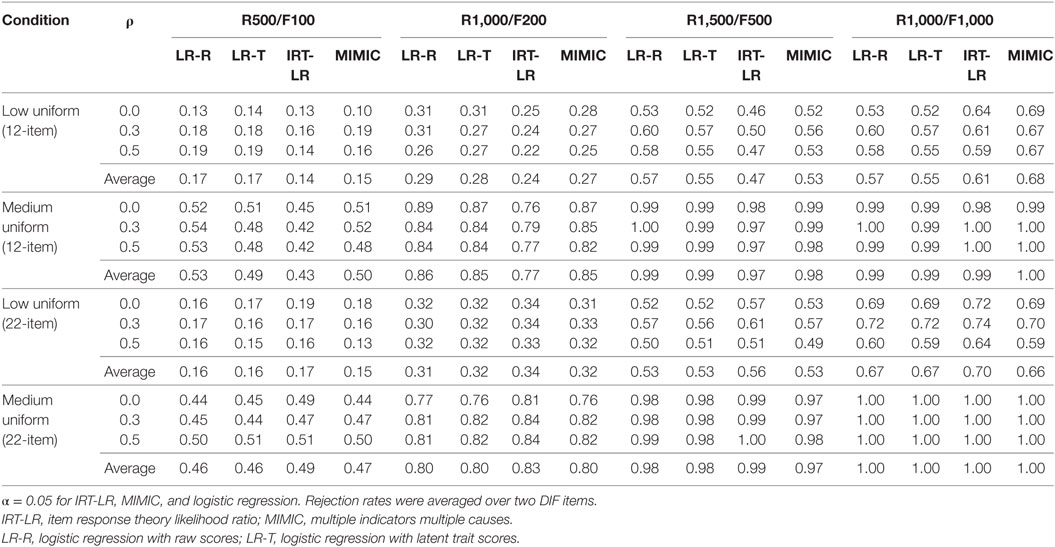
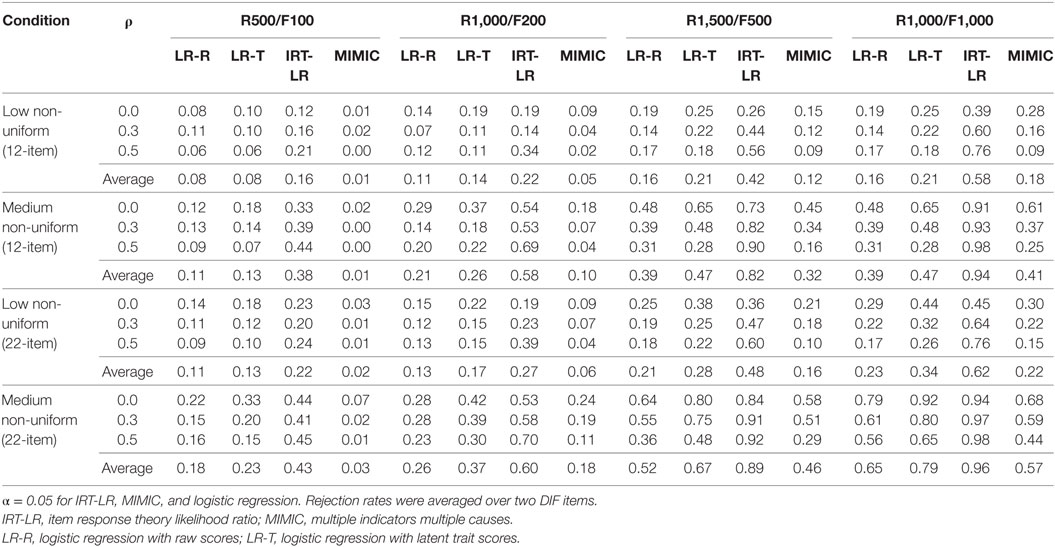
Tables 2 and 3 show rejection rates (i.e., correct identification of DIF) of the two logistic regression analyses (LR-R and LR-T), IRT-LR test, and MIMIC-interaction model in detecting uniform and non-uniform DIF, respectively, in the 12-item and 22-item tests. Rejection rates from the two DIF items in the 12-item (items 11 and 12) and 22-item tests (items 21 and 22) were averaged to facilitate the interpretation of the findings.

TABLE 2

Table 2. Rejection rates in detecting uniform differential item functioning (DIF).

TABLE 3

Table 3. Rejection rates in detecting non-uniform differential item functioning (DIF).

Uniform DIF

In detecting uniform DIF in the 12-item test, the two logistic regression analyses performed comparable to or better than the MIMIC-interaction model except for the R1,000/F1,000 condition in which the MIMIC-interaction model performed the best among the four DIF detection methods. The MIMIC-interaction model outperformed the IRT-LR test across all conditions. However, it should be noted that rejection rates for low uniform DIF were substantially small for all four methods, when the sample sizes were relatively small (i.e., R500/F100 and R1,000/F200). When the uniform DIF amount increased from low to medium, the rejection rates markedly improved for all of the DIF detection methods. The lowest rejection rate was observed with the IRT-LR test in the R500/100 condition on average, the highest rejection rate was found with the MIMIC-interaction model in the R1,000/F1,000 condition. When the uniform DIF effect was medium, the IRT-LR performed slightly worse than the other three methods in the two small sample size conditions; however, all three methods performed very similarly in the two large sample size conditions. Like in the low uniform DIF condition, the MIMIC-interaction model worked the best in the R1,000/F1,000 condition on average.

In the 22-item test, the IRT-LR test performed the best, and the other DIF detection methods performed similarly across all conditions when detecting uniform DIF. As a result of increasing the number of DIF-free items from 10 to 20, rejection rates from the IRT-LR test substantially improved, whereas rejection rates from the other three methods either remained the same or slightly decreased/increased depending on sample sizes and DIF magnitudes. Rejection rates for low uniform DIF in the smallest sample size condition were again very low. Like in the 12-item test, rejection rates increased as the magnitude of DIF increased from low to medium in the 22-item test. The rejection rates tended to increase as the sample size increased in both test lengths, and within the two large sample sizes, the balanced design (R1,000/F1,000) produced slightly higher rates than the unbalanced design (R1,500/F500) on average, especially under the low uniform DIF condition with the IRT-LR test and the MIMIC-interaction model. There was no obvious pattern associated with the correlation factor in both test length conditions.

Non-Uniform DIF

Based on the results in Table 3, the IRT-LR test outperformed the other three methods in detecting non-uniform DIF across all simulation conditions. The MIMIC-interaction model performed the worst on average, and the logistic regression with latent trait scores produced slightly higher rejection rates than the logistic regression with raw scores. Rejection rates for low non-uniform DIF were fairly small except for the IRT-LR test in the two large sample sizes. The rejection rates improved when the magnitude of non-uniform DIF increased from low to medium. There was a substantial improvement in the performance of the IRT-LR test, whereas the improvement was less noticeable with the other three methods, especially when the sample size was small.

As for uniform DIF, the rejection rates for non-uniform DIF increased as the sample size increased in both test length conditions, and within the two large sample sizes, the balanced design (R1,000/F1,000) produced slightly higher rates than the unbalanced design (R1,500/F500) on average. All four DIF detection methods reached their highest rejection rates when the sample size was large and balanced. There was no obvious pattern associated with the correlation factor in both test length conditions. Unlike the uniform DIF condition in which rejection rates with the IRT-LR test only improved as the number of DIF-free items increased (from 10 to 20), the rejection rates in the non-uniform DIF conditions increased regardless of which DIF detection method was used. In general, the non-uniform DIF conditions yielded smaller rejection rates than the uniform DIF conditions, particularly with the MIMIC-interaction model and the two logistic regression methods.

Latent Mean Difference

Figures 2 and 3 show rejection rates for detecting uniform and non-uniform DIF, respectively, when there are latent mean differences between the focal and reference groups (i.e., ${\text{μ}}_{{\text{θ}}_1}$ = 0 and ${\text{μ}}_{{\text{θ}}_2}$ = 0 for the reference group; ${\text{μ}}_{{\text{θ}}_1}$ = − 0.5 and ${\text{μ}}_{{\text{θ}}_2}$ = − 0.5 for the focal group) and when the means are the same between the two groups in the 22-item test.⁵ The dashed lines show the rejection rates in the unequal latent mean condition, whereas the solid lines show the rejection rates from the equal latent mean condition presented in Tables 2 and 3.

FIGURE 2

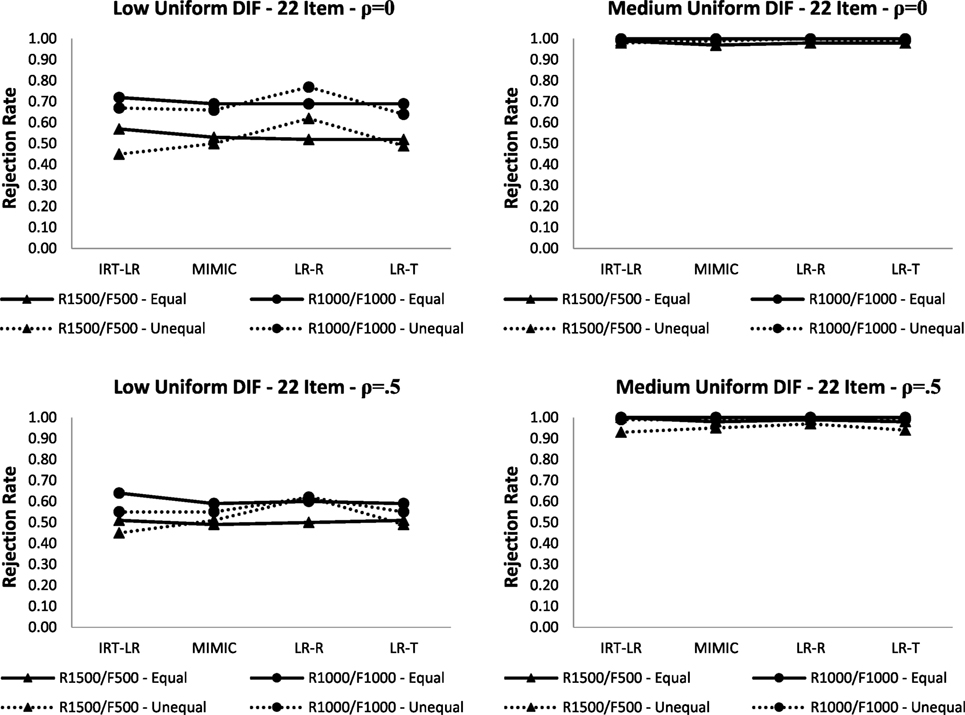
Figure 2. Rejection rates for uniform differential item functioning (DIF) with equal and unequal latent means between focal and reference groups in the 22-item test (note: LR-R is logistic regression with raw scores; LR-T is logistic regression with latent trait scores).

FIGURE 3

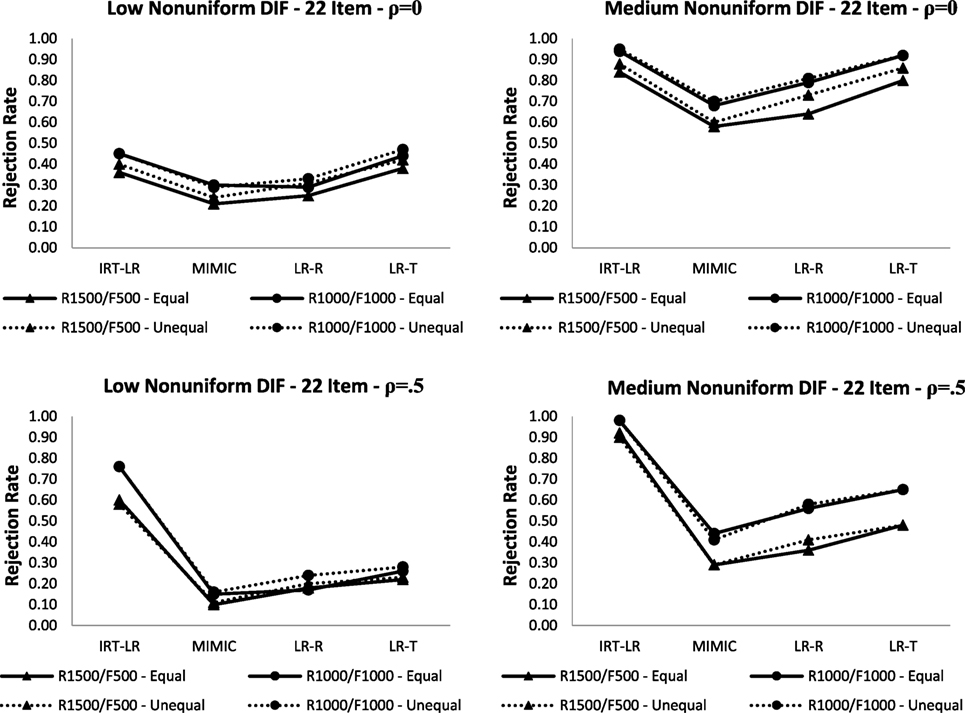
Figure 3. Rejection rates for non-uniform differential item functioning (DIF) with equal and unequal latent means between focal and reference groups in the 22-item test (note: LR-R is logistic regression with raw scores; LR-T is logistic regression with latent trait scores).

Figure 2 indicated that all four DIF detection methods were robust against latent mean differences between the focal and reference groups in detecting medium uniform DIF. Increasing the correlation between latent traits from ρ = 0 to ρ = 0.5 slightly reduced the rejection rates in the R1,500/F500 condition with the unequal latent mean condition. Unlike for medium uniform DIF, the rejection rates for low uniform DIF appeared to be affected by latent mean differences. The rejection rates for the logistic regression with latent trait scores, the MIMIC-interaction model, and the IRT-LR test tended to decrease, whereas the rejection rates for the logistic regression with raw scores either remained the same or increased slightly depending on the correlation between latent traits. When detecting non-uniform DIF (see Figure 3), the presence of latent mean differences between reference and focal groups did not appear to have a substantial impact on the rejection rates. The rejection rates from the unequal latent means conditions were slightly higher only when the DIF magnitude was medium and the correlation between latent traits was set to ρ = 0.

Effects of Simulation Factors

Table 4 shows the findings from MANOVA regarding the effects of simulation factors on rejection rates. Two DIF types, two DIF magnitudes, two test lengths, four sample sizes, and three correlations between latent traits were used as between-factor variables, and the four DIF detection methods were considered as a within-factor variable. For each factor, partial eta squared (η²) was computed as a measure of effect size. The results indicated that there was a statistically significant difference among the four DIF detection methods in terms of their rejection rates, F(3, 549) = 188.801, p < 0.001, η² = 0.517, and DIF method indicated a significant interaction with DIF type (i.e., uniform or non-uniform), F(3, 549) = 219.584, p < 0.001, η² = 0.523. Furthermore, DIF type had statistically significant interactions with DIF magnitude (low or medium), sample size (R500/F100, R1,000/F200, R1,500/F500, or R1,000/F1,000), and the correlation between latent traits (0, 0.3, or 0.5). Effect sizes for these interactions were relatively smaller than the effect size for the DIF method–DIF type interaction. There was no significant interaction between DIF method and test length (12 items or 22 items). As between-subject factors, all simulation conditions were statistically significant, except for the correlation factor. The effect sizes indicated that DIF type, DIF magnitude, and sample size were highly influential on rejection rates, whereas test length did not seem to have a strong impact on rejection rates. These results of MANOVA were consistent with the patterns of the rejection rates presented in Tables 2 and 3.

TABLE 4

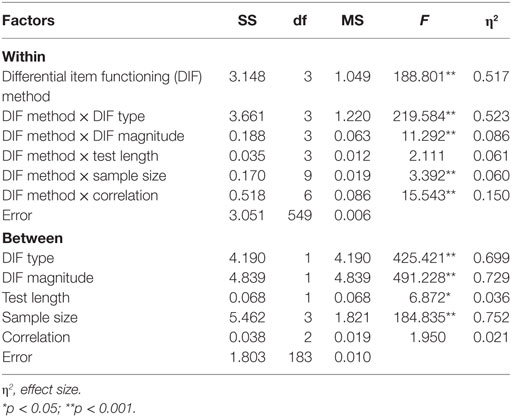
Table 4. Multivariate analysis of variance results for examining the effects of the simulation factors on rejection rates.

Discussion

There have been several methods proposed for the detection of DIF in multidimensional item response data (e.g., Stout et al., 1997; Mazor et al., 1998; Fukuhara and Kamata, 2011; Suh and Cho, 2014; Lee et al., 2016). Among these methods, the logistic regression, the MIMIC-interaction model, and the IRT-LR test are the most readily available for detecting DIF in dichotomously and polytomously scored items because of their ease of use. Earlier simulation studies compared the performances of the MIMIC model and IRT-LR test in detecting uniform and non-uniform DIF (e.g., Finch, 2005; Woods and Grimm, 2011). However, these studies have been limited to simple test structures in which items are expected to measure a single latent trait. Considering the increasing complexity of today’s assessments, the purpose of this study was to compare the logistic regression, the MIMIC-interaction model, and IRT-LR approaches in studying uniform and non-uniform DIF under non-simple test structures in which items can be associated with multiple latent traits. The performances of the three approaches were evaluated in terms of Type I error rate and rejection rates using a simulation study.

Type I error rates of the IRT-LR test were better controlled than those of the MIMIC-interaction model under most conditions. Type I error rates for the two logistic regression analyses were consistently outside of the range of Bradley’s liberal robustness criteria (i.e., 0.025 and 0.075) except for logistic regression with raw scores under two conditions: R1,000/F1,000 and ρ = 0.3 in the 12-item test and R1,000/F200 and ρ = 0 in the 22-item test. Type I error rates of the IRT-LR test were slightly outside Bradley’s liberal robustness criteria only under the two large sample sizes (R1,500/F500 and R1,000/F1,000) and ρ = 0.5 in the 12-item test. The error rates in the 22-item test were all within the range of Bradley’s liberal robustness criteria. The MIMIC-interaction model showed fairly controlled Type I error rates with a few exceptions. Specifically, when both focal and reference groups have large sample sizes (e.g., 1,000 per group) and the correlation between latent traits is either 0 or around 0.5, the MIMIC-interaction model falsely identifies DIF above the upper limit of Bradley’s liberal robustness criteria (i.e., 0.075). These findings appear to be consistent with previous studies that compared the MIMIC-interaction model and IRT-LR test (Finch, 2005; Woods and Grimm, 2011). The effects of different sample sizes and correlations on Type I error rates appeared to be inconsistent across the four DIF detection approaches.

The rejection rates of the two logistic regression approaches were similar to or slightly better than those of the MIMIC-interaction model, which were always higher than the IRT-LR test at detecting uniform DIF, when the anchor test length is was short (i.e., 10 anchor items in the 12-item test). It should be also noted that the MIMIC-interaction model showed the highest rejection rates when the sample size was large and balanced (R1,000/F1,000), regardless of the correlation levels. However, when the anchor test length increased to 20 items (i.e., the number of anchor items was doubled), the IRT-LR performed the best, and the other three approaches performed similarly. When the two large sample sizes were used and the DIF magnitude was medium, the four DIF detection approaches showed nearly identical rejection rates. In particular, the rejection rates of the four approaches were all equal to 1.0 under the large and balanced sample size condition (R1,000/F1,000) with medium DIF.

Differential item functioning magnitude and sample size highly and positively influenced the rejection rates in detecting both uniform and non-uniform DIF. As the number of anchor items increased, only the IRT-LR produced improved rejection rates in the uniform DIF conditions, whereas all four DIF detection approaches yielded increased rejection rates in the non-uniform DIF conditions. The observed rejection rates were smaller in the non-uniform DIF conditions than in the uniform DIF conditions. No consistent pattern was found in relation to the effects of correlations. There was no obvious pattern associated with the level of the correlation factor in both test length conditions. All four DIF detection approaches were robust against latent mean differences in detecting uniform and non-uniform DIF. Latent mean differences were influential only when the DIF magnitude was low and the DIF type was uniform. The rejection rates were slightly lower in the presence of latent mean differences, except for the logistic regression with raw scores.

Based on both Type I error and rejection rates, the IRT-LR appeared to be preferable over the other three approaches in detecting uniform and non-uniform DIF. However, when the anchor test length was short (i.e., 10 items), the MIMIC model might be a viable option in detecting uniform DIF, but the Type I error needed to be considered because the error rate was inflated depending on sample size and the correlation between latent traits. In summary, the IRT-LR test seems to be a more balanced and powerful approach than the MIMIC-interaction model and the logistic regression (with raw scores or latent trait scores) in detecting DIF in multidimensional tests with a non-simple structure.

Limitations and Future Research

The scope of this study has been limited in some aspects. First, this study focused on the detection of DIF based on statistical significance of the MIMIC-interaction model, IRT-LR test, and logistic regression. Further research should consider using and/or developing effect size measures for these approaches to facilitate practical interpretations of significant DIF results in multidimensional test structures. Also, it should be noted that the identification of DIF items may not imply a significant bias in the items. Therefore, the sources of DIF should be identified to ensure that DIF items do not lead to unfairness (e.g., Gierl and Khaliq, 2001; Stark et al., 2004; Chernyshenko et al., 2007). If the presence of DIF is related to unintended content or property in the item, then the item can be considered unfair (Penfield and Camilli, 2007).

Second, this study examined group differences in either item difficulty (uniform DIF) or item discrimination (non-uniform DIF). However, the difference might occur in both item difficulty and discrimination when non-uniform DIF exists. Also, the latent mean difference was considered assuming normal distributions with the variance equal to 1 for both groups although latent trait distributions with different variability are also likely especially when the focal group is small. Therefore, considering various DIF patterns as well as the conditions due to different variances and means in the distributions of latent traits would be valuable.

Third, this study focused on the M2PL model, ignoring the guessing parameter. Future studies may need to evaluate the performances of the logistic regression, the MIMIC model, and the IRT-LR when guessing is present in multidimensional test structures. In addition, DIF can occur in the guessing parameter (e.g., there can be a systematic difference in guessing patterns between two groups). Hence, it would be worthwhile to examine the effect of guessing patterns on DIF detection results.

Finally, this study assumed that anchor items (DIF-free items) were known as a priori to prevent any contamination effect of the anchor items on the DIF test results. However, a carefully designed purification procedure needs to be the first step for identifying potential DIF items when conducting DIF analyses with real data. In the literature, different anchor purification methods have been suggested to select DIF-free items for different DIF detection approaches (e.g., French and Maller, 2007; Wang et al., 2009; Woods, 2009b; Gonzalez-Betanzos and Abad, 2012). Depending on the selection of DIF-free items (i.e., purification), the DIF detection methods may provide different results regarding the number and type of detected DIF items.

Author Contributions

OB developed the multidimensional MIMIC modeling framework, designed and conducted the simulation study, and played the lead role in the manuscript writing process. YS contributed to the theoretical framework of the multidimensional MIMIC model, the design of the simulation study, and the manuscript writing process.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^“Low” and “medium” do not represent an absolute size of DIF (e.g., small effect size of DIF magnitude). Therefore, low and medium DIF in this study should be interpreted relatively, not absolutely.
2. ^In the 12-item test, raw score 1 is the sum of items 1, 2, 3, 7, 8, 9, 10, and 11; raw score 2 is the sum of items 4, 5, 6, 7, 8, 9, 10, and 12. In the 22-item test, raw score 1 is the sum of items 1 through 6 and items 13 through 21; raw score 2 is the sum of items 7 through 20 and item 22.
3. ^Latent trait scores were estimated as expected a posteriori (EAP) scores using the mirt package (Chalmers et al., 2015). In the same vein as raw scores, items were associated with either the first latent trait or the second latent trait, or both.
4. ^There are other methods for controlling for Type I error rates, such as the Benjamini–Hochberg procedure (BH; Benjamini & Hochberg, 1995). For more details of the BH procedure in the context of latent variable modeling, see Raykov et al. (2013).
5. ^The results from the 12-item test were similar to those from the 22-item test length. Therefore, they were not included in the manuscript. These results can be obtained from the corresponding author of this study.

References

Acton, G. S., and Revelle, W. (2004). Evaluation of ten psychometric criteria for circumplex structure. Methods Psychol. Res. 9, 1–27.

Google Scholar

Atar, B., and Kamata, A. (2011). Comparison of IRT likelihood ratio test and logistic regression DIF detection procedures. Hacettepe Univ. J. Educ. 41, 36–47.

Google Scholar

Barendse, M. T., Oort, F., and Garst, G. J. A. (2010). Using restricted factor analysis with latent moderated structures to detect uniform and nonuniform measurement bias: a simulation study. Adv. Stat. Anal. 94, 117–127. doi: 10.1007/s10182-010-0126-1

CrossRef Full Text | Google Scholar

Benjamini, Y., and Hochberg, Y. (1995). Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. B 57, 289–300.

Google Scholar

Bradley, J. V. (1978). Robustness? Br. J. Math. Stat. Psychol. 31, 144–152. doi:10.1111/j.2044-8317.1978.tb00581.x

CrossRef Full Text | Google Scholar

Chalmers, R. P., Pritikin, J., Robitzsch, A., and Zoltak, M. (2015). mirt: Multidimensional Item Response Theory [Computer Software]. Available from http://CRAN.R-project.org/package=mirt

Google Scholar

Chernyshenko, O. S., Stark, S., and Guenole, N. (2007). Can the discretionary nature of certain criteria lead to differential prediction across cultural groups? Int. J. Select. Assess. 15, 175–184. doi:10.1111/j.1468-2389.2007.00379.x

CrossRef Full Text | Google Scholar

Clauser, B. E., Nungester, R. J., Mazor, K., and Ripkey, D. (1996). A comparison of alternative matching strategies for DIF detection in tests that are multidimensional. J. Educ. Measure. 33, 202–214. doi:10.1111/j.1745-3984.1996.tb00489.x

CrossRef Full Text | Google Scholar

De Beer, M. (2004). Use of differential item functioning (DIF) analysis for bias analysis in test construction. SA J. Indus. Psychol. 30, 52–58. doi:10.4102/sajip.v30i4.175

CrossRef Full Text | Google Scholar

Ferrando, P. J., and Lorenzo-Seva, U. (2000). Unrestricted versus restricted factor analysis of multidimensional test items: some aspects of the problem and some suggestions. Psicológica 21, 301–323.

Google Scholar

Finch, H. (2005). The MIMIC model as a method for detecting DIF: comparison with Mantel-Haenszel, SIBTEST, and the IRT likelihood ratio. Appl. Psychol. Measure. 29, 278–295. doi:10.1177/0146621605275728

CrossRef Full Text | Google Scholar

Finch, H. (2012). The MIMIC model as a tool for differential bundle functioning detection. Appl. Psychol. Measure. 36, 40–59. doi:10.1177/0146621611432863

CrossRef Full Text | Google Scholar

French, B. F., and Maller, S. J. (2007). Iterative purification and effect size use with logistic regression for differential item functioning detection. Educ. Psychol. Meas. 67, 373–393. doi:10.1177/0013164406294781

CrossRef Full Text | Google Scholar

Fukuhara, H., and Kamata, A. (2011). A bi-factor multidimensional item response theory model for differential item functioning analysis on testlet-based items. Appl. Psychol. Measure. 35, 604–622. doi:10.1177/0146621611428447

CrossRef Full Text | Google Scholar

Gierl, M. J., and Khaliq, S. N. (2001). Identifying sources of differential item and bundle functioning on translated achievement tests: a confirmatory analysis. J. Educ. Measure. 38, 164–187. doi:10.1111/j.1745-3984.2001.tb01121.x

CrossRef Full Text | Google Scholar

Gonzalez-Betanzos, F., and Abad, F. J. (2012). The effects of purification and the evaluation of differential item functioning with the likelihood ratio test. Methodology 8, 134–145. doi:10.1027/1614-2241/a000046

CrossRef Full Text | Google Scholar

Guttman, L. (1954). “A new approach to factor analysis: the radex,” in Mathematical Thinking in the Social Sciences, ed. P. F. Lazarsfeld (Glencoe, IL: Free Press), 258–348.

Google Scholar

Holland, P. W., and Thayer, D. T. (1988). “Differential item performance and the Mantel–Haenszel procedure,” in Test Validity, eds H. Wainer and H. I. Braun (Hillsdale, NJ: Erlbaum), 129–145.

Google Scholar

Jöreskog, K. G., and Goldberger, A. S. (1975). Estimation of a model with multiple indicators and multiple causes of a single latent variable. J. Am. Stat. Assoc. 70, 631–639. doi:10.1080/01621459.1975.10482485

CrossRef Full Text | Google Scholar

Kan, A., and Bulut, O. (2014). Examining the relationship between gender DIF and language complexity in mathematics assessments. Int. J. Test. 14, 245–264. doi:10.1080/15305058.2013.877911

CrossRef Full Text | Google Scholar

Klein, A., and Moosbrugger, H. (2000). Maximum likelihood estimation of latent interaction effects with the LMS method. Psychometrika 65, 457–474. doi:10.1007/BF02296338

CrossRef Full Text | Google Scholar

Le, L. T. (2006). Investigating gender differential item functioning across countries and test languages for PISA science items. Paper Presented at the International Test Commission Conference, Brussels, Belgium.

Google Scholar

Lee, S., Bulut, O., and Suh, Y. (2016). Multidimensional extension of multiple indicators multiple causes models to detect DIF. Educ. Psychol. Measure. doi:10.1177/0013164416651116

CrossRef Full Text | Google Scholar

Lord, F. M. (1980). Applications of Item Response Theory to Practical Testing Problems. Hillsdale, NJ: Erlbaum.

Google Scholar

Mantel, N., and Haenszel, W. (1959). Statistical aspects of the analysis of data from retrospective studies of disease. J. Natl. Cancer Inst. 22, 719–740.

Google Scholar

Mazor, K. M., Clauser, B. E., and Hambleton, R. K. (1994). Identification of nonuniform differential item functioning using a variation of the Mantel-Haenszel procedure. Educ. Psychol. Meas. 54, 284–291. doi:10.1177/0013164494054002003

CrossRef Full Text | Google Scholar

Mazor, K. M., Hambleton, R. K., and Clauser, B. E. (1998). Multidimensional DIF analyses: the effects of matching on unidimensional subtest scores. Appl. Psychol. Measure. 22, 357–367. doi:10.1177/014662169802200404

CrossRef Full Text | Google Scholar

McDonald, R. P. (1997). “Normal-ogive multidimensional model,” in Handbook of Modern Item Response Theory, eds W. J. van der Linden and R. K. Hambleton (New York, NY: Springer), 257–269.

Google Scholar

Muthén, L. K., and Muthén, B. O. (1998). Mplus: Statistical Analysis with Latent Variables User’s Guide. Los Angeles, CA: Muthén & Muthén.

Google Scholar

Oshima, T. C., Raju, N. S., and Flowers, C. P. (1997). Development and demonstration of multidimensional IRT-based internal measures of differential functioning of items and tests. J. Educ. Measure. 34, 253–272. doi:10.1111/j.1745-3984.1997.tb00518.x

CrossRef Full Text | Google Scholar

Penfield, R. D., and Camilli, G. (2007). “Differential item functioning and item bias,” in Handbook of Statistics: Psychometrics, eds C. R. Rao and S. Sinharay (Amsterdam, The Netherlands: Elsevier), 125–167.

Google Scholar

R Core Team. (2016). R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing.

Google Scholar

Raykov, T., Marcoulides, G. A., Lee, C.-L., and Chang, C. (2013). Studying differential item functioning via latent variable modeling: a note on a multiple-testing procedure. Educ. Psychol. Meas. 73, 898–908. doi:10.1177/0013164413478165

CrossRef Full Text | Google Scholar

Reckase, M. D. (1985). The difficulty of items that measure more than one ability. Appl. Psychol. Measure. 9, 401–412. doi:10.1177/014662168500900409

CrossRef Full Text | Google Scholar

Revelle, W., and Rocklin, T. (1979). Very simple structure: an alternative procedure for estimating the optimal number of interpretable factors. Multivariate Behav. Res. 14, 403–414. doi:10.1207/s15327906mbr1404_2

PubMed Abstract | CrossRef Full Text | Google Scholar

Shealy, R., and Stout, W. (1993). A model-based standardization approach that separates true bias/DIF from group ability differences and detects test bias/DIF as well as item bias/DTF. Psychometrika 58, 159–194. doi:10.1007/BF02294572

CrossRef Full Text | Google Scholar

Shih, C.-L., and Wang, W.-C. (2009). Differential item functioning detection using the multiple indicators, multiple causes method with a pure short anchor. Appl. Psychol. Measure. 33, 184–199. doi:10.1177/0146621608321758

CrossRef Full Text | Google Scholar

Stark, S., Chernyshenko, O. S., and Drasgow, F. (2004). Examining the effects of differential item (functioning and differential) test functioning on selection decisions: when are statistically significant effects practically important? J. Appl. Psychol. 89, 497–508. doi:10.1037/0021-9010.89.3.497

PubMed Abstract | CrossRef Full Text | Google Scholar

Stout, W., Li, H., Nandakumar, R., and Bolt, D. (1997). MULTISIB – a procedure to investigate DIF when a test is intentionally multidimensional. Appl. Psychol. Measure. 21, 195–213. doi:10.1177/01466216970213001

CrossRef Full Text | Google Scholar

Suh, Y., and Cho, S.-J. (2014). Chi-square difference tests for detecting functioning in a multidimensional IRT model: a Monte Carlo study. Appl. Psychol. Measure. 38, 359–375. doi:10.1177/0146621614523116

CrossRef Full Text | Google Scholar

Swaminathan, H., and Rogers, H. J. (1990). Detecting item bias using logistic regression procedures. J. Educ. Measure. 27, 361–370. doi:10.1111/j.1745-3984.1990.tb00754.x

CrossRef Full Text | Google Scholar

Tabachnick, B. G., and Fidell, L. S. (2007). Using Multivariate Statistics, 5th Edn. Boston: Allyn and Bacon.

Google Scholar

Takane, Y., and De Leeuw, J. (1987). On the relationship between item response theory and factor analysis of discretized variables. Psychometrika 52, 393–408. doi:10.1007/BF02294363

CrossRef Full Text | Google Scholar

Tate, R. (2003). A comparison of selected empirical methods for assessing the structure of responses to test items. Appl. Psychol. Measure. 27, 159–203. doi:10.1177/0146621603027003001

CrossRef Full Text | Google Scholar

Teresi, J. A., and Fleishman, J. A. (2017). Differential item functioning and health assessment. Qual. Life Res. 16, 33–42. doi:10.1007/s11136-007-9184-6

CrossRef Full Text | Google Scholar

Thurstone, L. L. (1947). Multiple-Factor Analysis: A Development and Expansion of the Vectors of Mind. Chicago, IL, US: University of Chicago Press.

Google Scholar

Wang, W.-C., Shih, C.-L., and Yang, C.-C. (2009). The MIMIC method with scale purification for detecting differential item functioning. Educ. Psychol. Meas. 69, 713–731. doi:10.1177/0013164409332228

CrossRef Full Text | Google Scholar

Woods, C. M. (2009a). Evaluation of MIMIC-model methods for DIF testing with comparison to two-group analysis. Multivariate Behav. Res. 44, 1–27. doi:10.1080/00273170802620121

CrossRef Full Text | Google Scholar

Woods, C. M. (2009b). Empirical selection of anchors for tests of differential item functioning. Appl. Psychol. Measure. 33, 42–57. doi:10.1177/0146621607314044

CrossRef Full Text | Google Scholar

Woods, C. M., and Grimm, K. J. (2011). Testing for nonuniform differential item functioning with multiple indicator multiple cause models. Appl. Psychol. Measure. 35, 339–361. doi:10.1177/0146621611405984

CrossRef Full Text | Google Scholar

Woods, C. M., Oltmanns, T. F., and Turkheimer, E. (2009). Illustration of MIMIC-model DIF resting with the schedule for nonadaptive and adaptive personality. J. Psychopathol. Behav. Assess. 31, 320–330. doi:10.1007/s10862-008-9118-9

CrossRef Full Text | Google Scholar

Appendix

TABLE A1

Table A1. The anchor item parameters in the two-dimensional M2PL model.