The Role of “Opportunity to Learn” in the Geometry Curriculum: A Multilevel Comparison of Six Countries

Bokhove, Christian; Miyazaki, Mikio; Komatsu, Kotaro; Chino, Kimiho; Leung, Allen; Mok, Ida Ah Chee

doi:10.3389/feduc.2019.00063

ORIGINAL RESEARCH article

Front. Educ., 03 July 2019

Sec. STEM Education

Volume 4 - 2019 | https://doi.org/10.3389/feduc.2019.00063

The Role of “Opportunity to Learn” in the Geometry Curriculum: A Multilevel Comparison of Six Countries

$\nChristian Bokhove$ Christian Bokhove¹^*

¹Southampton Education School, University of Southampton, Southampton, United Kingdom
²Institute of Education, Shinshu University, Nagano, Japan
³Department of Education Studies, Hong Kong Baptist University, Kowloon Tong, Hong Kong
⁴Faculty of Education, The University of Hong Kong, Pokfulam, Hong Kong

In international comparisons for mathematics in PISA and TIMSS, Asia outperforms England considerably at secondary level. For geometry this difference is even greater. With a new maths curriculum having come into play in England in 2014, and hence the need to explore the impact of the curriculum on student achievement, this article focuses on how differences in achievement might be attributed to differences in “opportunity to learn” within a country's curriculum. The aims of this paper are two-fold. Firstly, we want to provide an integrated conceptual framework that combines elements from educational effectiveness, a curriculum model and “opportunity to learn” for analyzing curriculum effects, which we call the Dynamic Opportunities in the Curriculum (DOC) framework. Secondly, using multilevel models, we empirically investigate with TIMSS 2011 data whether the “opportunity to learn” in the curriculum is associated with achievement in geometry education in six countries, thus validating that model. The results show that our conceptualization of “opportunity to learn” can be useful in analyzing curriculum effects.

Introduction

The mathematics and science performance of students in a comparative perspective has long been scrutinized. Several large-scale assessments like the Trend in International Mathematics and Science Study (TIMSS) and the Programme for International Student Assessment (PISA) give rise to discussions about the relative performance of countries for mathematics, science and literacy and often end in heated debates, celebrations and criticism about “going up the rankings” or “going down the rankings” (Coughlan, 2016). One thing which has recently sparked a lot of debate is the good performance of Asian countries vs. countries in the west. For many years it has been clear that there are distinct differences in mathematics education in the east and in the west (Leung, 2001; Shimizu and Williams, 2013). Recently this became apparent again when the PISA 2015 results, based on the achievement of 15 year olds, were released (Organisation for Economic Co-operation Development, 2016). Like previous years, Asian countries like Japan, Taiwan, and parts of China scored higher on mathematics than England. A similar pattern can be seen in year 8 TIMSS studies ranging from 2007 to 2015 (Mullis et al., 2008, 2012, 2016a). Especially for some topics, like geometry, the differences seem vast, as can be seen in Table 1.

TABLE 1

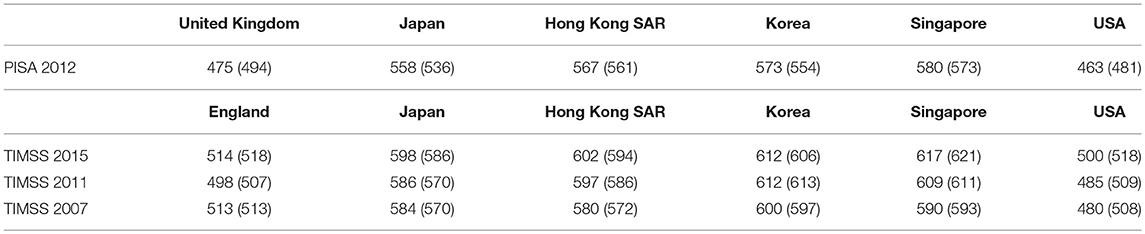
Table 1. Geometry scores (overall mathematics score between brackets) for PISA 2012 (‘space and shapes') and TIMSS grade 8 2007, 2011, and 2015.

We wondered what the particular role of curriculum differences was in relation to differing performance in geometry at secondary school level in these countries. In the “enGasia project”¹ we sought to explore these curricular differences between three of these countries: England on the one hand, and two Asian jurisdictions on the other hand, Japan and Hong Kong, as the differences seemed even more pronounced there with regard to the gap between “East and West.” As can be seen in Table 1 England and the USA scored on or under the international mean of around 500, with Japan, Hong Kong SAR, Korea and Singapore scoring at least 558 or higher. We felt it was relevant to investigate these differences in geometry achievement, especially with a new curriculum for mathematics in place for England. Content-wise the changes seem to have gone from very specific to quite general. As a case in point we can look at the way a topic like congruence is described. In the previous curriculum document (Department for Education Employment, 1999, p. 38) for Key Stage 3 (11–13 year olds) there is specific mention that pupils should be taught to “understand, from their experience of constructing them, that triangles satisfying SSS, SAS, ASA, and RHS are unique, but SSA triangles are not”². In the new curriculum (Department for Education, 2013, p.8), however, there are no specific congruence cases: “use the standard conventions for labeling the sides and angles of triangle ABC and know and use the criteria for congruence of triangles.” In our view, this begs the question whether national changes to the geometry curriculum are related to national changes in geometry achievement. The purpose of this study, then, is to understand the role of curricular elements in mathematics achievement, with a particular emphasis on geometry education, at lower secondary level within and across selected countries in the East and West. We will adopt a particular “lens” that adopts a “curriculum view” and takes into account multiple actors within education through use of a dynamic model. The aims of this paper are two-fold. Firstly we want to provide an integrated conceptual framework that combines elements from educational effectiveness, a curriculum model and “opportunity to learn.” Secondly, we want to empirically investigate with TIMSS 2011 data whether our “opportunity to learn” conceptualization of the curriculum is associated with achievement in geometry education. To this end, the article is divided in two distinct parts. Firstly, a part where we briefly review literature on the dynamic model of educational effectiveness and “opportunity to learn” (OTL) within the curriculum, which leads to a conceptual multilevel framework for studying the OTL component in the curriculum with large-scale data. We have called this the Dynamic Opportunities in the Curriculum (DOC) framework. Secondly, we explore the usefulness of that model by applying it to TIMSS 2011 data for six countries, through the construction of statistical multilevel models.

Conceptualizing “Opportunity to Learn” in the Curriculum

In this section, we carefully want to build an argument for our approach in this study:

(i) From the perspective of the dynamic model of educational effectiveness we need to take into account the multilevel nature of education: students in classrooms in schools in countries.

(ii) The curriculum is a key variable that influences this at every level.

(iii) At all these levels so-called “Opportunity to Learn” and “Academic Learning Time” is closely related to these curricular influences. However, we will have to take into account Socio-Economic status, as this interacts with this.

We briefly review some of the background literature, as to support our study. It is not meant as a complete review of the literature base, for that we refer to the underpinning articles. As the complete study has quite a complex interlocking framework, we state take-away points from the literature at the end of each section.

The Dynamic Model of Educational Effectiveness

Reynolds et al. (2014) in a review of Educational Effectiveness Research (EER) recommended that more international work should analyse complex data from multiple levels of the educational system. One challenge described by Reynolds et al. (2014) is the lack of focus on classrooms and teachers. As teacher effects exceed school effects over time (Scheerens and Bosker, 1997; Teddlie and Reynolds, 2000; Muijs and Reynolds, 2011) they argue that the teacher and classroom level should receive more attention. This recommendation coincides with elements from the so-called dynamic model of educational effectiveness, as developed by Creemers and Kyriakides (2008). This model attempts to define the dynamic relations between multiple factors found to be associated with effectiveness. Influences on student achievement in this model are multilevel in nature, with students, classrooms, schools, and the educational system all playing a role. School and context level have both direct and indirect effects on student achievement since they are able to not only influence student achievement directly but also to influence teaching and learning situations. For example, the presence of school facilities like a library might directly influence student achievement, as it allows them to find a quiet place to study. However, school factors are also expected to indirectly influence classroom-level factors, which can partly be explained by what teachers do in the classroom (e.g., Creemers and Kyriakides, 2011). For example, good technological facilities might help teachers better prepare their lessons which in turn, it is hypothesized, can contribute to student achievement.

The first implication for our theoretical lens is that we will adopt a multilevel approach in our study.

Opportunity to Learn

One particular element within this multilevel lens we wanted to focus on is the role of the curriculum. This manifests itself in different ways, but certainly one important way is in the form of educational content exposure (e.g., Schmidt and McKnight, 2012; Schmidt et al., 2015). The conception of so-called “opportunity to learn”(OTL) is based on work by Carroll (1963) and rests on the assumption that students' ability to learn a subject depends on how long they are exposed to it in school. The idea of OTL as a measure of schooling has a long history, going back to the 1960s, with Carroll (1963) being among the first to include time explicitly in his model of school learning. In Carroll's model (Carroll, 1963) student learning depended on both student factors (aptitude, ability, and perseverance) and factors controlled by teachers (time allocated for learning, OTL and quality of instruction).

Carroll's model (Carroll, 1963) included six variables:

1. Academic Achievement is the output variable (as measured by various sorts of standard achievement tests).

2. Aptitude is the main explanatory variable defined as the “the amount of time a student needs to learn a given task, unit of instruction, or curriculum to an acceptable criterion of mastery under optimal conditions of instruction and student motivation” (Carroll, 1989, p. 26). This definition of aptitude resembles the principles behind mastery learning, popularized by Bloom (1974). “High aptitude is indicated when a student needs a relatively small amount of time to learn, low aptitude is indicated when a student needs much more than average time to learn” (Carroll, 1989, p. 26).

3. Opportunity to learn is the amount of time available for learning both in class and within homework. Carroll (1989) notes that “frequently, opportunity to learn is less than required in view of the students aptitude.” (p. 26).

4. Ability to understand instruction, which relates to learning skills, information needed to understand, and language comprehension.

5. Quality of instruction, which includes good instructional design. If quality of instruction is bad, time needed will increase.

6. Perseverance: the amount of time a student is willing to spend on a given task or unit of instruction. This is an operational and measurable definition for motivation for learning.

The most important question the Carroll model (and numerous follow-up studies) raised, was what the appropriate time needed to learn (TTL) was. Carroll's model differs from Bloom's by seeking equality of “opportunity”, not necessarily equality of attainment. Recent work defined OTL in terms of specific content covered in classrooms and the amount of time spent covering these topics (Schmidt et al., 2001). Specifically for mathematics, Schmidt et al. (2001), Schmidt et al. (2011), Fuchs and Woessman (2007), and Dumay and Dupriez (2007) concluded that a greater OTL in mathematics was related to higher student achievement in mathematics. In other words, more opportunities for the student to learn, were associated with higher student achievement. OTL can also be defined broader, for example including teacher quality, resources and peers, which have been found to also be related to outcomes and Socio-Economic Status (SES, e.g., Levin, 2007). Schmidt and McKnight (2012) argued the existence of inequalities in OTL and asserted that part of the SES role was caused by systematically weaker content offered to lower-income students: rather than dampening SES effects, schools were increasing the inequality gap. SES can be said to mediate content coverage. The interaction between OTL with SES was also confirmed in other studies (Schmidt et al., 2012, 2015; Bokhove, 2016), again indicating that socio-economic status not only was strongly associated with student achievement but also indirectly via the content that was covered in the classroom.

We propose that we focus on variables regarding “opportunity to learn” (OTL) in our study. In doing so we should include controls for SES and indicators for quality of instruction.

Curriculum Model—TIMSS

From the previous sections we concluded that adopting a multilevel approach for variables concerning “opportunity to learn” could be a good way to explore the influence of the curriculum on mathematics achievement. However, this first requires further insight into what role the curriculum plays in existing large-scale assessments. In our view, an international, comparative perspective on mathematics education in secondary schools can start by looking at existing secondary datasets for this, for example by looking at two major providers of international large-scale assessments for secondary mathematics, PISA and TIMSS. PISA is the Programme for International Student Assessment, a worldwide study administered by the Organization for Economic Co-operation and Development (OECD) on achievement of 15-year-olds in mathematics, science, and reading. TIMSS stands for Trends in International Mathematics and Science Study and is administered by the International Association for the Evaluation of Educational Achievement (IEA) in grades 4 and 8. In line with what both the OECD and IEA say about their assessments, Rindermann and Baumeister (2015), confirmed that for solving PISA tasks, thinking/reasoning ability and general intelligence were rated as being more important, while in TIMSS tasks were seen as more curriculum-related and requiring more school knowledge than PISA tasks. It is this curriculum focus that makes us choose TIMSS over PISA for this study. The larger curriculum focus also is apparent in the TIMSS curriculum model, which reflects the importance of analyzing relationships between opportunities to learn and educational outcomes (Mullis et al., 2009)³. The TIMSS curriculum model has three aspects: the intended curriculum, the implemented curriculum, and the attained curriculum, as depicted in Figure 1.

FIGURE 1

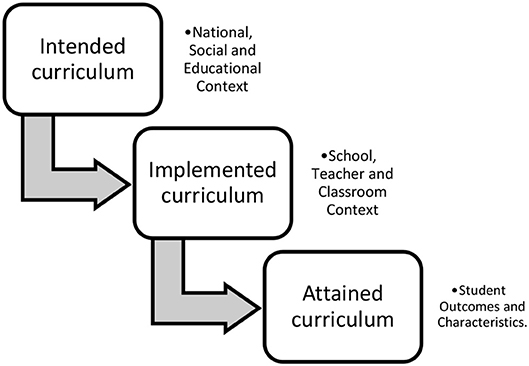
Figure 1. TIMSS curriculum framework (adapted from Mullis and Martin, 2013).

These represent, respectively, the mathematics and science that students are expected to learn as defined in countries' curriculum policies and publications and how the educational system should be organized to facilitate this learning; what is actually taught in classrooms, the characteristics of those teaching it, and how it is taught; and, finally, what it is that students have learned and what they think about learning these subjects. The framework for TIMSS in grade 8 explicitly includes four content domains: number, algebra, geometry and data. For the focus of the enGasia project, geometry entails being able to analyse the properties and characteristics of a variety of two- and three-dimensional figures and be competent in geometric measurement (perimeters, areas, and volumes). In addition, students should be able to solve problems and provide explanations based on geometric relationships (Grønmo et al., 2013). In the results section we will highlight particular curricular differences between the six countries in this study.

We use TIMSS 2011 data in this study because of its curriculum focus.

Linking the Dynamic Model, OTL and TIMSS' Curriculum Model

This study brings together the three elements described, as shown in Table 2. The dynamic model of educational effectiveness argues that effectiveness studies conducted in several countries have shown that the influences on student achievement are multilevel in nature; educational outcomes are influenced by variables at the student level, the classroom level, the school level and national/regional level (Creemers and Kyriakides, 2008). In the dynamic model, OTL is seen as part of “management of time” at the teacher/classroom level and is considered a significant factor of effectiveness.

TABLE 2

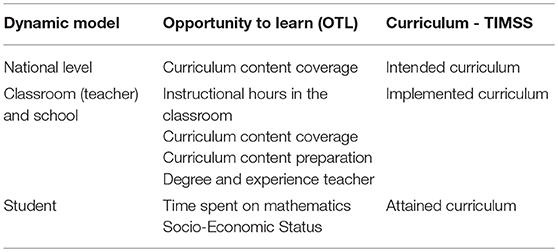
Table 2. The multilevel dynamic opportunities in the curriculum (DOC) framework: linking the dynamic model, opportunity to learn and the TIMSS curriculum model.

What is intended as curriculum is often the actual content prescribed in national curriculum documents. At the national level we therefore can be interested in the amount of space and time devoted to the curriculum content of interest, for example “year 8 geometry.” This formal curriculum is then implemented by mathematics teachers in the classroom. From the perspective of OTL we argue that the actual time devoted to teaching the curriculum content, here geometry, is what provides the “opportunity to learn.” In other words, OTL can be conceptualized as the interplay of how much time is spent on mathematics content (instructional hours) and then what proportion of that time is spent on a specific topic (curriculum content coverage). As the extent in which the curriculum content is transferred from teacher to student is not just a matter of “quantity” (i.e., time), we also want to take into account “quality” of instruction. As “indicators” or “proxies” for teaching quality we can look at the degree and experience of the teacher, and the extent in which the teacher feels prepared for teaching a specific topic (curriculum content preparation). Finally, after the teacher has taught the topic, the person who then has to demonstrate the attained curriculum is the student. A student needs to invest time, for example in doing homework. As we have described, SES plays a role in this as well. Table 2 describes an integrated conceptual framework that combines elements from educational effectiveness, a curriculum model and “opportunity to learn,” which we will call the Dynamic Opportunities in the Curriculum (DOC) framework. We propose that such a framework can provide a useful and important contribution to the way we look at the role the curriculum plays in education systems. Note that the model only incorporates two key elements from Carroll's (1963) original model, namely OTL and proxies for quality of instruction. Toward the end of the paper we will return to the framework and critically discuss some of the limitations of focusing on these aspects.

The empirical part of the paper, then, aims to see if this conceptualization of the DOC framework can inform us about the specific focus of the enGasia project, geometry education in grade 8 in six countries from “the West” and “the East”. Our assumption is that, if we can successfully apply the framework to the specific sub-domain of geometry, we might use the framework for other mathematical content and cognitive domains as well. We apply the framework to our geometry context by taking the specific elements from the framework, as described in Table 2, and using them to inform our data analysis methods. In line with the framework, we use a multilevel approach with multiple variables regarding “opportunity to learn” geometry in the TIMSS 2011 dataset. We posit that using the framework will allow us to answer the following specific questions:

(1) How much of the variance in grade eight student achievement in geometry is explained by student- and classroom-level OTL curriculum factors within and across England, Japan, Hong Kong SAR, Korea, Singapore, and the USA?

(2) How much are these OTL curriculum factors, controlled for SES, related to geometry achievement at grade eight in England, Japan, Hong Kong SAR, Korea, Singapore, and the USA?

We are interested in the former question because it would indicate whether there actually are meaningful differences at student- and classroom-level within and across countries. The latter question then focuses on possible OTL predictors.

Methodology

Dataset

We make use of the TIMSS 2011 grade eight dataset (Mullis et al., 2012). Three elements of the data are used: (i) achievement and background data of students, (ii) classroom level data from the teacher questionnaire, and (iii) curriculum data at the country level. Sample sizes and descriptives are presented in the results section, as well as their position on the ranking for geometry. England, Japan, and Hong Kong are relevant from the enGasia project's perspective. Three other countries, Korea, Singapore, and the USA are a convenience sample, as these countries seem to have a large influence on international mathematics education policy and relate to the distinction between “West” and “East” as set out in the introduction. Ethical approval for secondary data analysis was granted by the first author's institution.

Analytical Approach

Given the multilevel nature of our framework and the TIMSS 2011 data, namely students in classrooms in countries, we utilize multilevel modeling. Multilevel modeling is an adaptation of the general linear model for hierarchical datasets, which partitions the variance in the dependent variable across the relevant levels (Snijders and Bosker, 2012). Model building is done by creating four models: a null model, a model with SES variables, a model with OTL variables and a model with both SES and OTL variables. Several OTL variables are used as described in the “variables” section. All models have two levels (students in classrooms) and are created with IEA's IDB Analyzer software⁴ and multilevel software HLM 6.08, published by Scientific Software International⁵ As we only included a limited number of six countries, it was not deemed appropriate to make the country level a separate level in a three-level multilevel model (e.g., based on Maas and Hox, 2005). Therefore, we created six separate two-level multilevel models, one for each country. This meant that we did not use variables for the national level of the DOC framework in this study. However, we do return to this issue toward the end of the paper. As missing data for the variables generally was between 0 and 10%, it is imputed with an Expectation-Maximization algorithm in SPSS, finally resulting in a dataset for six countries. As we are dealing with the complex sampling design of the TIMSS 2011 study, we take into account three aspects to make sure we made correct inferences (Rutkowski et al., 2010), namely sampling weights, proficiency estimation and variance estimation. To cater for different probabilities of units being selected (classrooms, students) sampling weights are used. Sampling weights ensure that the choice of sampling design does not have an undesired effect on the analyses of data. In this case weights are used at the student and classroom level. As TIMSS 2011 uses an incomplete and rotated-booklet design for testing children on the major outcome variables, five plausible values are used. Correct analyses would combine the five plausible values for grade eight geometry achievement into a single set of point estimates and standard errors using Rubin's rules (Rubin, 1987). A final aspect concerns the variance estimation. As standard variance estimation formulas are not appropriate for data obtained with a complex sample design (Rutkowski et al., 2010), the multilevel structure caters for this. For the multilevel models, independent variables were group-centered at the student level and grand-mean centered at the classroom level. Full maximum likelihood was used for the models.

Variables

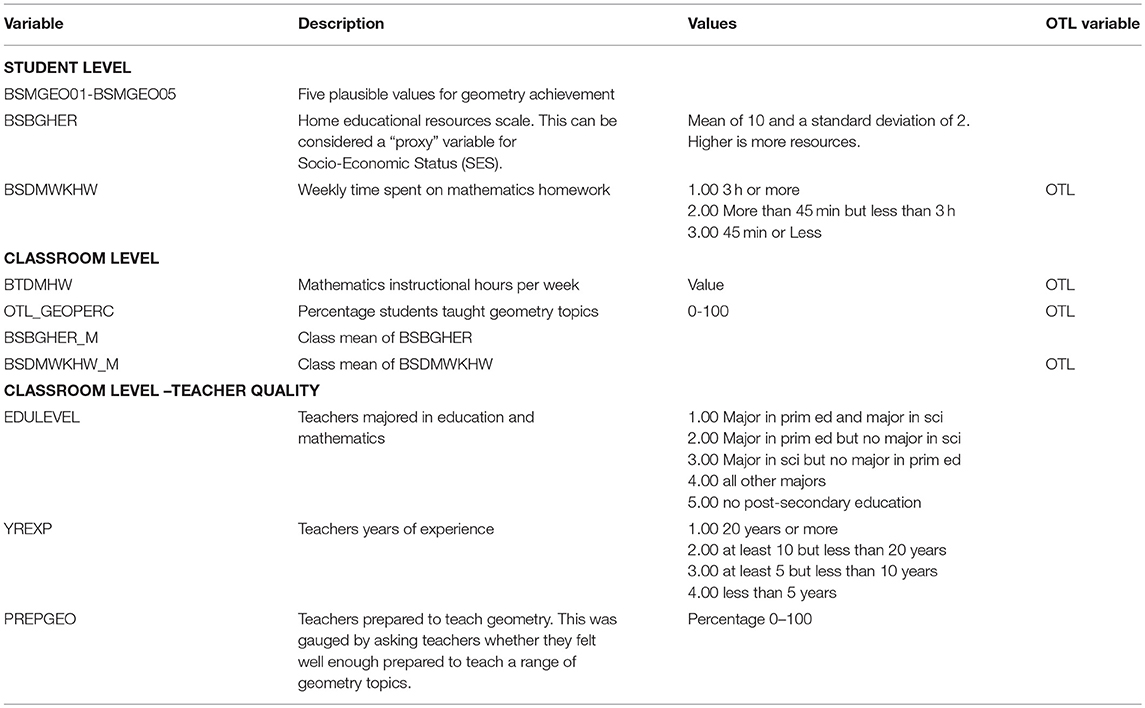
An overview of all variables is provided in Table 3. As the focus of this paper is on geometry education, we isolate all the variables that pertain to geometry. As dependent variable(s) we use the five plausible values for geometry achievement: BSMGEO01, BSMGEO02, BSMGEO03, BSMGEO04, and BSMGEO05 are combined in the HLM 6.08 software.

TABLE 3

Table 3. Variables included in the models.

Student Level Variables

As independent variable at the student level the TIMSS “Home Economic Resources” scale (BSBGHER) is used. This scale combines three measures of availability of home resources and can be used as a proxy for SES. The scale contains items on the number of books at home, the highest level of education of both parents and the number of home study support. The scale is constructed with IRT scaling methods, specifically the Rasch partial credit model (Masters and Wright, 1997). The scale has been standardized by a linear transformation to have a mean of 10 and a standard deviation of 2. Time for homework is also added as indicator for Table 2's “time spent on mathematics,” but only as ordinal variable, with 1 = 3 hours or more, 2 = between 45 min and 3 hours, 3 = 45 min or less. This variable indicates the self-reported weekly time students spend on assigned mathematics homework and is constructed by the IEA from answers to two questions on the frequency and time for homework (Foy et al., 2013, p. 38).

Classroom Level Variables

The independent variables at the classroom level are the mean SES for all students in a class, and some further measures we propose are essential to operationalise the “Opportunity to Learn Geometry.” The first measure takes the derived variables from question 23⁶ of the TIMSS teacher questionnaire with mean “percentage students taught” geometry. This percentage between 0 and 100 can be seen as a measure of teachers' perceptions of geometry content coverage. This variable is referred to as OTL_GEOPERC. A second measure represents mathematics instructional hours per week, adopting the assumption “having heard of a topic more often is assumed to reflect a higher degree of opportunity to learn.” (Organisation for Economic Co-operation Development, 2014, p. 146). Both measures are standardized. In addition, we use the classroom mean for homework time and SES. Finally, a set of variables that serve as proxies for teaching quality characteristics, namely education level (in the dataset a lower value indicates a higher education level), years of teaching experience (in the dataset a lower value indicates more experience) and whether teachers feel prepared for geometry (a higher percentage indicates a higher self-reported level of preparedness).

Results

This section reports on the results. Table 4 provides the descriptives for all the included variables.

TABLE 4

Table 4. Mean and Standard Deviation (SD) of the 14 variables for the six countries.

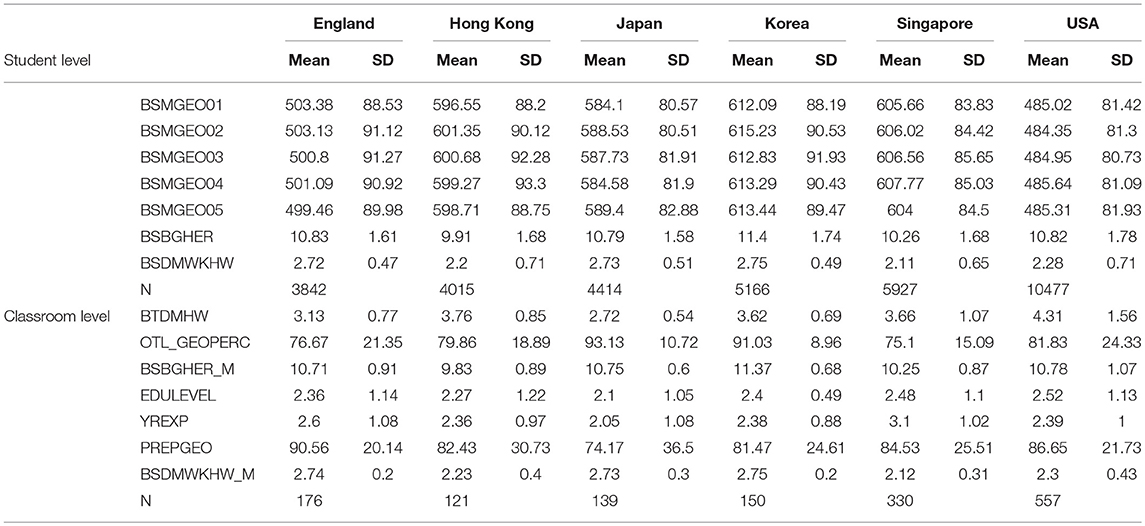
The achievement scores (BSMGE001 to 005) are in line with previous observations, with Korea scoring highest, then Singapore, Hong Kong and Japan. There is quite a big gap to England then, with the USA scoring well below that. England, Japan and the USA have comparable SES levels (BSBGHER). Hong Kong and Singapore are slightly lower. Korea has by far the highest SES level. English, Japanese and Korean students spend less time on homework (BSDMWKHW) than Hong Kong, Singaporean and American students. Japan has the lowest number of mathematics instruction hours (BTDMHW), and then England. The USA has the highest number of instruction hours. The percentage of students taught geometry (OTL_GEOPERC) is highest for Japan and Korea, and lowest for England and Singapore. Regarding teachers' education (EDULEVEL), levels are comparable, but it is notable that teachers often miss either an education or science degree. Singaporean teachers have the least experience (YREXP); Japanese have the most, with the rest in-between. Finally, English teachers feel most prepared (PREPGEO) to teach geometry and Japanese teachers least.

This feeling of being prepared might be related to the aforementioned percentage of geometry taught. Based on the descriptives we can already hypothesize that curriculum seems to matter, as there are distinct differences between the countries. We will now check this by scrutinizing the multilevel models, as described in the methodology. The final models are presented in Table 5. We can see that there are big differences in variance explained for the different countries. Variance explained is very different as well within Japan and Korea with almost all variance at the individual student level, indicating that classrooms between them are relatively homogeneous. At a practical level such high variance at the individual level means the differences between students (within-classrooms) far exceed the differences between classrooms (between-classrooms). In the other countries the difference is almost 50–50. At the individual level in four countries individual SES is a predictor for achievement. For example, the value of 7.56 for England would indicate that a 1-point increase in the BSBGHER variable would predict a 7.56 point increase in the achievement score. Given the homogeneity of Hong Kong and Singapore it is not surprising that SES does not significantly predict outcome at the student level. At the classroom level, the models show that class mean SES is a predictor for mathematics achievement in all countries. In four out of six countries the class mean of weekly time spent on homework the coefficient is significantly negative, which seems to imply that less time spent on homework predicts lower achievement. Only in Korea do years of teacher's experience significantly predict outcome, with more experience predicting a higher outcome (note the direction of the variables). All other teacher-related variables are no significant predictor. In Japan mathematics instructional hours per week positively predict the higher geometry outcomes, but this is not the case for the other countries.

TABLE 5

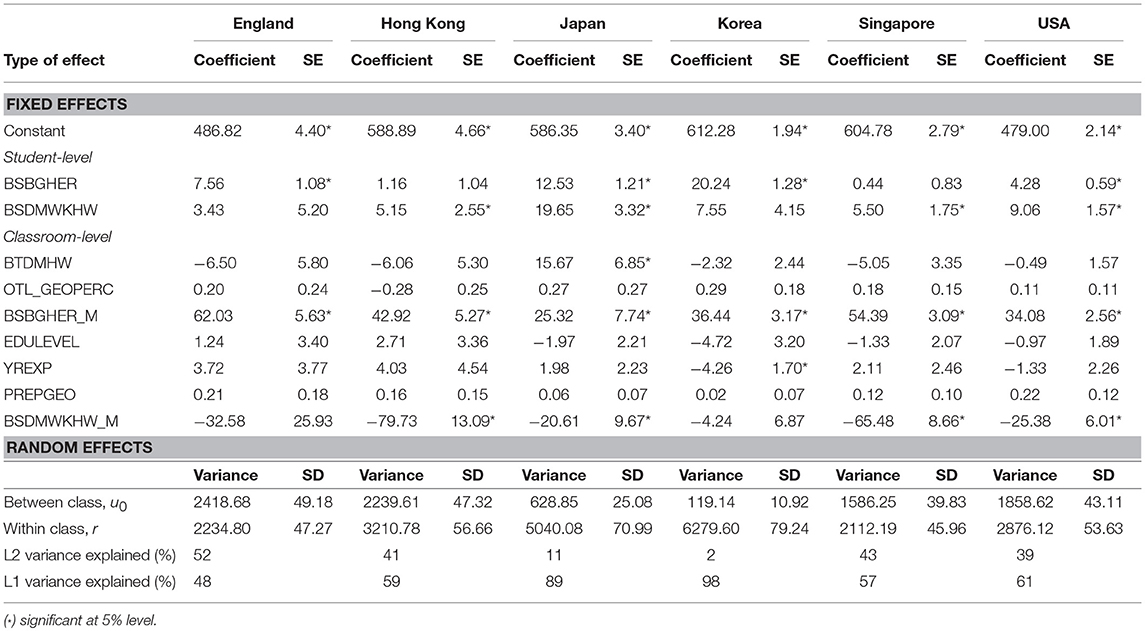
Table 5. Final multilevel models; other models of the model building process are included in the Supplementary Materials.

Conclusion and Discussion

This article set out to link theories about educational effectiveness (the dynamic model) to a conceptual framework involving curriculum and “opportunity to learn,” to see if such a “joined-up” framework could provide a useful lens for analyzing TIMSS 2011 data on mathematics education achievement, by applying it to a geometry achievement context. Table 2 describes such an integrated conceptual framework, the DOC framework. To check the utility of the framework, we then sought to use this framework to answer the following questions:

(1) How much of the variance in grade eight student achievement is explained by student- and classroom-level OTL curriculum factors within and across England, Japan, Hong Kong SAR, Korea, Singapore, and the USA?

(2) How much are these OTL-related factors, controlled for SES, related to geometry achievement at grade eight in England, Japan, Hong Kong SAR, Korea, Singapore and the USA?

The first question aimed to see whether the framework could highlight meaningful distinctions at student- and classroom level within and across countries by looking at the variance at student- and classroom-level. There were meaningful differences within and between the six countries. We saw that Japan and Korea had almost all variance at the individual level, while the other four countries had a more equal distribution over individual and classroom levels. This result seems to indicate that classrooms in Japan and Korea are quite homogenous compared to the other four countries. In other words, classrooms were much less different than in the other countries. The second question then turned to the role of OTL variables in all of this. Results showed that SES was an important predictor in the classroom for all six countries, with the homogeneity of smaller countries Hong Kong and Singapore making SES less predictive at the individual level. This is in line with findings by Schmidt et al. (2015) and gives weight to the conclusion that the issue of equality of opportunity to learn could be major policy issue in most countries. However, although the predictive nature of SES is still considerable, based on the difference in coefficient between the second model (with just SES) and the final model (with SES and OTL) we could not confirm that the inclusion of the OTL variable has dampened the influence of SES. Based on the literature mentioned in the beginning of the article, this was unexpected; we had expected that the magnitude of the SES coefficient would have been reduced by taking into account OTL.

The two geometry content related variables, denoting the percentage students were taught geometry topics and teachers' preparedness, did not show a significant difference. Teacher variables barely played a role except in Korea where less years of experience had a negative effect. Two time-related variables had a differential effect. Firstly, the variable for “weekly time spent on mathematics homework”: at the individual level in Hong Kong, Japan, Singapore and the USA the models indicate that less time is associated with more positive outcomes. However, for the same countries, at the classroom level this effect is exactly the opposite and as expected: a higher average weekly time spent on mathematics homework in a classroom is positively associated with higher geometry achievement. This emphasizes the strength of multilevel models, as this seems to indicate a form of Simpson's paradox, in which a trend appears in several different groups of data but disappears or reverses when these groups are combined (Simpson, 1951). The advise to use multilevels models is in line with prior work by Dettmers et al. (2009) on homework as well. Their work with PISA 2003 data showed that a positive association between homework time and achievement decreased considerably after controlling for SES (Dettmers et al., 2009). They also concluded there was no clear-cut relationship between homework time and achievement at the student level. However, there was a positive relationship at the school level. Both statements correspond with this study. Interestingly, their analyses included three of the six countries included in this study and the relative levels in their study, USA more homework than Japan and Korea, also correspond with the findings in this study (USA 2.8, Japan 2.0, Korea 1.7). However, in all this we need to keep in mind that these are associations and therefore cannot explain causal relations. As (Leung, 2014, p. 602) already noted students may have higher achievement because they do more homework, but students may also need to do more homework because they have low achievement. According to Gustafson (2012) such causal relations can be explored with TIMSS data, using different data analysis techniques, and these should result in a positive effect of homework on student achievement. Perhaps SES has reduced it until below significance; this claim, however, would need further research.

A second difference holds for Japan and “mathematics instructional hours per week”: more hours are positively associated with higher geometry achievement. However, for two reasons this must not be seen as a trivial finding. Firstly, Table 4 already showed that Japan has the lowest average number of instructional hours of all six countries. Nevertheless, this was positively associated with high performance. We carefully speculate this might be related to the way geometry is embedded in the curriculum. Secondly, the coefficients for the other five countries show a rather counter-intuitive result: although they are non-significant the direction is rather the other way, namely more hours—lower results. We do not have a sensible explanation for this but do in general conclude that these differences with OTL variables make it worthwhile to study achievement through the lens we have constructed.

There are several lines of discussion that can follow from this. Firstly, we want to posit that OTL and the curriculum perhaps might be more amenable than economic or social characteristics. In that respect the interplay of SES and OTL could provide an incentive for emphasizing that changes to the curriculum can also work emancipatory. This view could be seen to be in line with E.D. Hirsch's stance that the curriculum can ensure equal opportunities for students of all backgrounds (Hirsch, 2016). However, given the very large SES effects, this should not be used as “excuse” to disregard the other factors of course. Carnap's (1950) Total Evidence Rule, which might result in an error of induction known as the “fallacy of the neglected aspect” (Castell, 1935, pp. 32–33), still applies. In other words, it's useful to focus on the curriculum, but we should not ignore other, sometimes even more predictive, variables in the mix.

Secondly, we could also be critical about Carroll's model itself. Fisher et al. (1978) used Carroll's ideas to observe hundreds of hours in the “Beginning Teacher Evaluation Study” of classrooms and concluded that Carroll's model was too unrefined for practical use. They reconfigured Carroll's ideas in a revised model called “Academic Learning Time,” which occurs when three conditions apply simultaneously: when time is allocated to the task, the student is engaged in the task, and the student has a high rate of success (Fisher et al., 1978). Subsequent studies showed that overall perhaps a relatively low percentage of variance in student outcomes could be explained through “time,” but that for struggling students, time was much more important (e.g., Rossmiller, 1986). Berliner (1990) also was convinced of the crucial nature of “time” in educational processes: “The fact is that instructional time has the same scientific status as the concept of homeostasis in biology, reinforcement in psychology, or gravity in physics. That is, like those more admired concepts, instructional time allows for understanding, prediction, and control, thus making it a concept worthy of a great deal more attention than it is usually given in education and in educational research” (p. 3), and incorporated this in his own, so-called ALT-model (Academic Learning Time). Compared to the Carroll model, ALT attempts to provide a time metric for all variables and therefore makes it more suitable for empirical investigation. Over time, many other operationalisations of the time aspect have been implemented. For example, Karweit and Slavin (1981) define time-on-task as the time actually spent on learning activities rather than general measures of curriculum time, and Walkup et al. (2009) talk about academic engagement time. Other factors related to OTL, like school funding, teacher quality and student motivation could be included. We included experience and degree level of teachers but these can be seen as proxies for actual teacher quality: they do not tell the whole story. In other words, the ways in which we account for opportunities to learn and time devoted to learning, can vastly differ. Different models and assumptions might give different outcomes. Although, we looked at only one of those operationalisations, we think the underpinning lens is strong and solid.

A third point to mention, is that this study only looked at geometry performance because upfront it was suspected that differences in performance might be related to the differences in curriculum. The same analyses could be conducted for different content domains like algebra and data and chance. Perhaps there also are differential effects for cognitive domains, like “knowing,” “applying” and “reasoning” about mathematics. As these content and cognitive domains form part of the “standard” data collection in TIMSS, and the data is collected over numerous countries and at scale, it provides a readily available source for studying these aspects. Of course, to be able to genuinely study causal effects of curriculum features on student achievement, we would need to have relevant data, collected over time. However, TIMSS data are cross-sectional which prevents strong causal assertions. Longitudinal research is needed, because OTL effects might compound over time, especially for an hierarchical subject like mathematics. For some studies like TIMSS, an added bonus could be that an encyclopedia (Mullis et al., 2016b) is published, which provides curriculum details at the country level.

This brings us to the fourth and final point, which relates to the way in which we can actually include details about the curriculum into our analyses. After all, is a curriculum in essence not qualitative in nature: it is a set of themes and topics to address over the span of several years. Or is it more than that? And what about the national level diversity in the way curriculums are being made and enforced? Some countries do not have a national curriculum but organize the curriculum at regional levels. For example, the US “Common Core State Standards Initiative” was created exactly with the idea in mind that there would be more harmonization in what states think students should know in English and Mathematics at the end of each grade. These complexities make comparisons between countries even more challenging. We can see this challenge in the statistical models we constructed here and also in previous work of the first author (Bokhove, 2016). In this article we have argued that inclusion of variables at country level with only six countries was not appropriate for multilevel modeling. But as Bokhove (2016) showed, even when they are included factors such as OTL and the associated curriculum are reduced to categorical variables or percentages of teaching time and are therefore necessarily reductive. The complexity of a curriculum is summarized in one number. Complex statistical models are then applied to the set of variables. There is a focus on what researchers can measure, rather than on what is important. As Labaree (2011, p. 625) puts it: “methodologically sophisticated at exploring educational issues that do not matter.” On this tendency to quantify Labaree (2011) further reports on his own research where he concluded, after some years, that in his quantitative studies, the most interesting questions in the study emerged from qualitative data, exclaiming: “When you are holding a hammer, everything looks like a nail.” (p. 628). It is at this point we would stress the complementary nature of quantitative and qualitative approaches; depending on the research question one or the other can provide unique insights. The model described in the first part of this paper does not conflict with such a complementary approach. At a national level curriculum content can be studied, as to find plausible explanations for differential achievement. In previous studies differences in curriculum content have been raised as important criticism about the extent in which the TIMSS tests match with the different countries' curricula (Leung, 2014, p. 603). To explore this further for the data we used, we had a closer look at the TIMSS 2011 Test-Curriculum Matching Analysis (Mullis et al., 2012 p. 465). The Test-Curriculum Matching Analysis (TCMA) is conducted to investigate the extent to which the TIMSS 2011 mathematics assessment is relevant to each country's curriculum. The TCMA also investigates the impact on a country's performance of including only achievement items that were judged to be relevant to its own curriculum. In the 2011 TCMA for grade 8, out of a total of 230 score points for the curriculum Japan covered the least (205 points, ≈89%) and England the most (222 points, ≈97%). It therefore seems that the TCMA results provide evidence that the TIMSS 2011 mathematics assessment provides a reasonable basis for comparing achievement of the participating countries and benchmarking entities. The performance on similar test items across countries (percentage correct) did not fluctuate more than three percentage points, seemingly indicating that possible curriculum differences did not notably influence TIMSS 2011 performance (Mullis et al., 2012 p. 468). However, the TCMA looked at all content domains, and therefore further research on differences in topics would be appropriate. Anecdotally, for example, in the enGasia project we found out that one reasoning question on geometric shapes Japan scored particularly low. After discussion in the research team it turned out that it typically was only covered in grade 9, one year later. A look at the finer details of the different (geometry) curriculums would be useful. In sum, we think the framework provides a useful view, as a starting point, on the curriculum, but to get a fuller picture multiple methods should be utilized.

Apart from these curriculum elements, there also are other factors that then come into play when it comes to quality (geometry) education. If we say the aforementioned curriculum aspect concerns the national level, the intended curriculum in Table 2, we can also say that at the other levels there are factors we have not taken into account. There are qualitative characteristics of the curriculum, and OTL in particular, that provide concrete insights into the relationship between the curriculum, OTL and student achievement. For example, the quality of mathematics textbook, if used, plays an important role, and also the actual teaching strategies used by teachers in the classroom. And also the role of tutoring outside of classrooms, so-called shadow education, will have an impact on “opportunities to learn” (e.g., see Bray, 2014).

Some commentators have argued that such rich contexts can perhaps only be “caught” by thick and rich descriptions of the curriculum experience. However, if we only go for the qualitative data, it will be virtually impossible to study the range and number of countries, classrooms and students in the largescale datasets. Our view is that, using the lens from Table 2, we can construct multilevel models at a scale that is simply not possible in more qualitative ways. These models point us toward a direction; they might highlight points to follow-up, as indeed has happened in our models. These then can be followed-up with a more in-depth analysis of the situation.

In sum, this paper showed that our integrated conceptual framework that combines elements from educational effectiveness, a curriculum model and “opportunity to learn” (the DOC framework) can be usefully applied to data from international largescale assessments, in this case TIMSS. It also showed that elements of “Opportunity to Learn” could then be analyzed through multilevel models in TIMSS 2011's grade 8 assessment data, providing comparative international insight in the role the (geometry) curriculum can play in (geometry) education. Further research might be able to further unpick this relationship.

Author Contributions

All authors designed the ideas in the paper. CB drafted the first manuscript. MM, KK, KC, AL, and IM contributed substantially to further iterations.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank the British Academy for funding the first author under their International Partnership and Mobility Scheme, IPM 2014 - PM130271.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2019.00063/full#supplementary-material

Footnotes

1. ^http://engasia.soton.ac.uk/

2. ^SSS, SAS, ASA, RHS, and SSA refer to congruence types, for example SSS to Side-Side-Side where three known sides uniquely define a triangle. A refers to Angle. RHS to Right Angle-Hypothenuse-Side.

3. ^Other authors have highlighted similar distinctions but with different emphases. For example, in the context of a workplace curriculum, Billett (2007) talked about the intended, enacted and experienced curriculum. Remillard and Heck (2014) distinguish between curricular elements that are officially sanctioned (the official curriculum) and those that are operationalized through practice (the operational curriculum), with the latter including the teacher-intended curriculum, the curriculum that is actually enacted with students, and student outcomes.

4. ^https://www.iea.nl/data

5. ^http://www.ssicentral.com/

6. ^This question tabulates mathematics content items, for example for geometry “Points on the Cartesian plane” and “Congruent figures and similar triangles” and asks teachers to self-report whether the topics were “mostly taught before this year,” “mostly taught this year” or “not yet taught or just introduced” (for more information see Foy et al., 2013, p. 50).

References

Berliner, D. C. (1990). “What's all the fuss about instructional time?,” in The Nature of Time in Schools: Theoretical Concepts, Practitioner Perceptions, eds M. Ben-Peretz and R. Bromme (NewYork, NY: Teachers College Press),3–35.