Research Methods for Education With Technology: Four Concerns, Examples, and Recommendations

Wright, Daniel B.

doi:10.3389/feduc.2019.00147

POLICY AND PRACTICE REVIEWS article

Front. Educ., 10 December 2019
Sec. Digital Education
Volume 4 - 2019 | https://doi.org/10.3389/feduc.2019.00147

Research Methods for Education With Technology: Four Concerns, Examples, and Recommendations

Daniel B. Wright^*

Department of Education Psychology and Higher Education, University of Nevada, Las Vegas, Las Vegas, NV, United States

The success of education with technology research is in part because the field draws upon theories and methods from multiple disciplines. However, drawing upon multiple disciplines has drawbacks because sometimes the methodological expertise of each discipline is not applied when researchers conduct studies outside of their research training. The focus here is on research using methods drawn largely from psychology, for example, evaluating the impact of different systems on how students perform. The methodological concerns discussed are: low power; not using multilevel modeling; dichotomization; and inaccurate reporting of the numeric statistics. Examples are drawn from a recent set of proceedings. Recommendations, which are applicable throughout the social sciences, are made for each of these.

Spending on EdTech is around 19 billion dollars per year (Koba, 2015). Research on using computer technology within education began soon after microcomputers began appearing in universities (e.g., Suppes, 1966). Given the amount of accumulated wisdom in the field and the amount of investment, it is a concern that the current EdTech landscape has been likened to the Wild West (Reingold, 2015), with schools buying systems without convincing evidence of their efficacy. There are many issues that researchers in the field can address to better serve schools (Wright, 2018). One issue is what to call the field. I have been using the phrase Education with Technology (EwT) for research on education and educational outcomes when using technology. I use EdTech to refer to the technology companies that sell technology aimed specifically at the education market.

There is some excellent research examining the effectiveness of technology for learning. For example, decades of high-quality research by Anderson and colleagues (e.g., Anderson et al., 1985; Ritter et al., 2007) on the Cognitive Tutor has shown the successful application of cognitive science to education software (see https://www.carnegielearning.com/). Two important aspects of this success story are: (1) the applications developed alongside the theory (ACT-R) that Anderson had developed for cognition, and (2) the successful application to the classroom took decades of rigorous research. The focus of this paper is to improve the quality of existing research in order to allow more progress to occur.

Four concerns of research methods were chosen. These were picked both because examples were found where there are concerns and recommendations exist for improvement that can be easily accommodated. Many other topics, covering different design and analytic methods (e.g., robust methods, visualizations), could also have been included, but having four seems a good number so that each receives sufficient attention. The four concerns are:

1. Power analysis (the sample size can be too low to have an adequate likelihood of producing meaningful results);

2. Multilevel modeling (the units are not independent, which is assumed for traditional statistical tests, and this usually means that the p-values are lower than they should be);

3. Dichotomizing (continuous variables are turned into dichotomous variables at arbitrary points, like the median, thereby losing information);

4. Inaccurate statistical reporting (sometimes because of typos, sometimes because of reading the wrong output, the reported statistics are incorrect).

Choosing Examples

The field of EwT was chosen for three reasons. First, it offers valuable potential for education, though the impact has failed to live up to the potential/hype (see Cuban, 2001; Reingold, 2015). There are several possible reasons for this (e.g., Wright, 2018), one of which is that the methods and statistical procedures used in empirical studies leave room for improvement. Second, it is an area in which I have been working. Third, as a multidisciplinary field, different researchers bring different expertise. It may be that a research team does not have someone trained in psychology and social science research methods (e.g., Breakwell et al., 2020). As someone who is trained in these procedures, I hope to bring my skills to this field.

Some examples will be used both to show that these issues arise and to illustrate the problems. It is important to stress that in any field it is possible to find illustrations of different concerns. Papers from the 2017 Artificial Intelligence in Education (AIED) conference in Wuhan, China, were examined. This conference is a showcase for mostly academic researchers developing and evaluating new procedures and technologies. The papers are published in five categories: papers, posters, doctoral, industry, and tutorials. Only the papers and posters are examined here: the doctoral papers often sought advice on how to conduct the planned research; the industry papers often described a product or were a case study using a product; and the tutorials gave accounts of what their audiences would learn.

According to their website¹, only 36 of the 121 papers submitted for oral presentations were accepted as oral presentations. Thirty-seven of these were accepted as posters (and 7 of 17 papers submitted for posters were accepted). Of the 138 total submissions, 80 were accepted as a paper or a poster (58% acceptance rate). There were 36 papers and 37 posters in the proceedings, so not all accepted posters appeared in the proceedings. The main difference between oral presentations and posters for the proceedings is that authors of oral presentations were allowed 12 pages of text for their papers and authors of posters were allowed only four pages of text. In many cases it was difficult to know what methods and statistical techniques were used, particularly for the posters, presumably because the authors had to make difficult choices of what to include because of the length restrictions.

Reflecting the multidisciplinarity of the field, the papers differed in their approaches. Some papers were primarily focused on statistical procedures to classify student responses and behaviors. Others were demonstrations of software. The focus here is on research that used methods common to what Cronbach (1957) called the experimental and correlational psychologies. Of the 63 full papers and posters, 43 (68%) involved collecting new data from participants/students not simply to show the software could be used. Some of these were described as “user studies” and some as “pilot studies.” It is important to stress that while examples will be shown to illustrate concerns, some aspects of these studies were good and overall the conference papers are high-quality. For example, those evaluating the effectiveness of an intervention tended to use pre- and post-intervention measures and compare those in the intervention condition with a control condition.

The methods—both the design of the study and the statistical procedures—were examined for concerns that a reviewer might raise. Four concerns are discussed here and recommendations are made. These were chosen both by how much they may affect the conclusions and how easily they can be addressed. While these comments are critical, the purpose of the paper is to be constructive for the field. Only a couple of examples are shown for each concern. These were picked because of how well they illustrate the concern. Before doing this, some background on hypothesis testing is worth providing. Some statistical knowledge about this procedure is assumed in this discussion. At the end of each section specific readings are recommended.

Crisis in Science and Hypothesis Testing

Educational with Technology research is not done in isolation. While the theme of this paper is to look at how EwT researchers deal with some issues, there is a crisis within the sciences more broadly that requires discussion. The crisis is due to the realization that a substantial proportion (perhaps most) of the published research does not replicate (Ioannidis, 2005; Open Science Collaboration, 2015). This occurs even in the top scientific journals (Camerer et al., 2018). This has led to many suggestions for changing how science is done (e.g., Munafò et al., 2017). For discussion see papers in Lilienfeld and Waldman (2017) and a recent report by Randall and Welser (2018). Unfortunately using traditional methods, which have been shown to produce results that are less likely to be replicated, are ones that can make the researchers' CVs look better (Smaldino and McElreath, 2016).

One aspect that many are critical of is the use and often mis-use of hypothesis testing. It is worth briefly describing what this is. In broad terms, a scientist has a set of data, assumes some model H for the data, and calculates the distribution of different characteristics for plausible samples assuming this model is true. Suppose some characteristics of the observed data are far away from the distribution of plausible samples. This would be very rare if your assumed model were correct. “It follows that if the hypothesis H be true, what we actually observed would be a miracle. We don't believe in miracles nowadays and therefore we do not believe in H being true” (Neyman, 1952, p. 43). There are some problems with this approach. If we only react when the data would require a miracle to have occurred if H is true, scientific findings would accumulate too slowly. Instead, for most research situations a threshold below miracle is needed to allow evidence to accumulate, but then it is necessary to accept that sometimes errors occur because of this lower threshold. Neyman (1952, p. 55) called this “an error of the first kind” (emphasis in original). What is important here is that the possibility of error is not only recognized, but quantified.

Hypothesis testing is usually done by testing what is called the null hypothesis. This is usually a point hypothesis and that there is no effect of the independent variable, no difference between groups, or no association. It is often denoted as H₀. As a single point, it can never be true. This creates a conceptual problem: the procedure assumes a hypothesis that is always false (Cohen, 1994).

The conditional probability is usually called the p-value or sometimes just p. Calculating the p-value for different problems can be complex. Traditionally most researchers have accepted a 5% chance of making a Type 1 error when the null hypothesis is true. This is called the α (alpha) level and if the observed conditional probability is less than this, researchers have adopted the unfortunate tradition of saying it is “significant.” Unfortunate because finding p < 5% does not mean the effect is “significant” in the English sense of the word. If comparing the scores for two groups of students, finding a “significant” effect in a sample only provides information that the direction of the true effect in the population is likely the same as observed in the sample. Recently there has been a move to use different α levels. In some branches of physics it is set much lower (see Lyons, 2013) for discoveries because the cost of falsely announcing a discovery is so high that it is worth waiting to claim one only when the data would have had to arise by almost a “miracle” if the null hypothesis were true. Some social scientists think it is appropriate to have a lower threshold than this (Benjamin et al., 2018), but others have pointed out problems with this proposal (e.g., Amrhein and Greenland, 2018; McShane et al., 2019). For current purposes 5% will be assumed because it remains the most used threshold.

There are other problems with the hypothesis testing approach and scientific practices in general. Alternatives have been put forward (e.g., more visualization, pre-registering research, Bayesian models), but each alternative has limitations and can be mis-used. The remainder of this paper will not address these broader issues.

Background Reading

The report by the Open Science Collaboration (2015), while focusing on psychology research, discusses topics relevant to those applicable to the EwT studies considered. Cohen (1994) presents a good discussion of what null hypothesis significance testing is and is not.

Concern #1: Power Analysis and Small Samples

The hypothesis testing framework explicitly recognizes the possibility of errantly rejecting the null hypothesis. This has been the focus of much discussion because this can lead to publications that are accepted in journals, but do not replicate. Another problem is when research fails to detect an effect when the true effect is large enough to be of interest. This is a problem because this often limits further investigations. This is called a Type 2 error: “failure to reject H₀ when, in fact, it is incorrect, is called the error of the second kind” (Neyman, 1942, p. 303). As with Type 1 errors, the conditional probability of a Type 2 error is usually reported. Researchers specify the Minimum Effect that they design their study to Detect (MED). The conditional probability of a Type 2 error is usually reported as the probability of failing to find a significant effect conditional on this MED and is often denoted with the Greek letter β (beta). The statistical concept power is 1–β and convention is that it should usually be at least 80%. However, if it is relatively inexpensive to recruit participants or if your PhD/job prospects require that you detect an effect if it is as large as the MED, it would be wise to set your power higher, for example 95% (this is the default for the popular power package G^*Power, Faul et al., 2007, 2009).

Over the past 50 years several surveys of different literatures have shown that many studies have too few participants to be able to detect the effects of interest with a high likelihood (e.g., Sedlmeier and Gigerenzer, 1989). The problem of having too few participants exists in many fields. Button et al. (2013), for example, found about 30% of the neuroscience studies they examined had power <11%. This means that these studies had only about a one-in-nine chance of observing a significant effect for an effect size of interest. It is important to re-enforce the fact that low power is a problem in many disciplines, not just EwT.

Conventional power analysis allows researchers to calculate a rough guide to how many participants to have in their study to give them a good chance of having meaningful results. Many journals and grant awarding bodies encourage (some require) power analysis to be reported. The specifics of power analysis are tightly associated with hypothesis testing, which is controversial as noted above, but the general notion that the planned sample size should be sufficient to have a high likelihood of yielding meaningful information is undisputed. If researchers stop using hypothesis testing, they will still need something like power analysis in order to plan their studies and to determine a rule for when to stop collecting data.

Tables (e.g., Cohen, 1992) and computer packages (e.g., Faul et al., 2007, 2009) are available to estimate the sample size needed to have adequate power for many common designs. Simulation methods can be used for more complex designs not covered by the tables and packages (e.g., Browne et al., 2009; Green and MacLeod, 2016).

Deciding the minimum effect size for your study to detect (MED) is difficult. For many education examples a small improvement in student performance, if applied throughout their schooling, can have great consequences. For example, Chetty et al. (2011) estimated that a shift upwards of 1 percentile in test scores during kindergarten is associated with approximately an extra $130 per annum income when the student is 25–27 years old. When multiplied across a lifetime this becomes a substantial amount. Researchers would like to detect the most miniscule of effects, but that would require enormous samples. The cost would not be justified in most situations. It is worth contrasting this message with the so-called “two sigma problem.” Bloom (1984) discussed how good one-on-one tutoring could improve student performance a large amount: two sigma (two standard deviations) or from the 50th percentile to the 98th percentile. He urged researchers to look for interventions or sets of interventions that could produce shifts of this magnitude. Many in the EwT arena talk about this as a goal, but for product development to progress research must be able to identify much smaller shifts.

The choice of MED is sometimes influenced by the observed effects from similar studies. If you expect the effect to be X, and use this in your power calculations, then if your power is 80% this means that you have about a 4 in 5 chance of detecting the effect if your estimate of the expected effect is fairly accurate. However, if you are confident that your true effect size is X, then there is no reason for the study. It is usually better to describe the MED in relation to what you want to be able to detect rather than in relation to the expected effect.

To allow shared understanding when people discuss effect sizes, many people adopt Cohen's (1992) descriptions of small, medium, and large effects. While people have argued against using these without considering the research context (Lipsey et al., 2012), given their widespread use they allow people to converse about effect sizes across designs and areas.

Two Examples

Two examples were chosen to show the importance of considering how many participants are likely to complete the study. The studies show the importance of considering what the minimum effect size to detect (MED) should be. Overall, across all 43 studies, the sample sizes ranged from <10 to 100.

Arroyo et al. (2017) compared collaboration and no collaboration groups. They collected pre and post-intervention scores and the plan was to compare some measure of improvement between the groups. Originally there were 52 students in the collaboration group and 57 in the no collaboration group. If they were using G^*Power (Faul et al., 2007, 2009) and wanted a significance level of 5% and power of 80%, it appears the MED that they were trying to detect was d = 0.54sd. This MED is approximately the value Cohen describes as a medium effect. This value might be reasonable depending on their goals. Only 47 students completed the post-test. Assuming 24 and 23 of these students were in the two groups, respectively, the power is now only 44%. They were more likely to fail to detect an effect of this size than to detect one.

Another example where the sample size decreased was Al-Shanfari's et al. (2017) study of self-regulated learning. They compared three groups that varied depending on the visualizations used within the software (their Table 1). One hundred and ten students were asked to participate. This is approximately the sample size G^*Power suggests for a one-way Anova with α = 5%, power of 80%, and a MED of f = 0.3, which is between Cohen's medium and large effects. The problem is some students did not agree to participate and others did not complete the tasks. This left few students: “9 students remained in the baseline group, 9 students in the combined group and 7 in the expandable model group” (p. 20). Assuming the same α and MED, the power is now about 22%. Even if the authors had found a significant effect, with power this low, the likelihood is fairly high that the direction of the effect could be wrong (Gelman and Carlin, 2014).

Were these MEDs reasonable? The choice will vary by research project and this choice can be difficult. As noted above, in educational research, any manipulation that raises student outcomes, even a minute amount, if applied over multiple years of school, can produce large outcomes. Further, a lot of research compares an existing system to one with some slight adaptation so the expected effect is likely to be small. If the adaptation is shown to have even a slight advantage it may be worth implementing. If Arroyo et al. (2017) and Al-Shanfari et al. (2017) planned to design their studies to detect what Cohen (1992) calls small effects (d = 0.2 and f = 0.1), the suggested samples sizes would have been n = 788 and n = 969. To yield 80% power to detect a 1 percentile shift, which Chetty et al. (2011) noted could be of great value, would require more than 10,000 students in each group.

Recommendations

1a. Report how you choose your sample size (as well as other characteristics of your sample). This often means reporting a power analysis. Try to have at least the number of participants suggested by the power analysis and justify the MED you used. The expected drop out rate should be factored into these calculations.

1b. If it is not feasible to get the suggested number of participants,

- Do not just do the study anyway. The power analysis shows that there is a low likelihood to find meaningful results so your time and your participants' time could be better spent. And do not just change the MED to fit your power analysis.

- Use more reliable measurements or a more powerful design (e.g., using covariates can increase power, but be careful, see for example, Meehl, 1970; Wright, 2019).

- Combine your efforts with other researchers. This is one of Munafò et al.'s (2017) recommendations and they give the example of The Many Lab (https://osf.io/89vqh/). In some areas (e.g., high-energy particle physics) there are often dozens of authors on a paper. The “authors” are often differentiated by listing a few as co-speakers for the paper, and/or having some listed as “contributors” rather than “authors.”

- Change your research question. Often this means focusing your attention on one aspect of a broad topic.

- Apply for a grant that allows a large study to be conducted.

Caveat: Power analyses are not always appropriate. Power analysis is used to suggest a sample size. If you are just trying to show that your software can be used, then you do not need a large sample.

Background Reading

Cohen (1992) provides a brief primer for doing power analysis for many common research designs. Baguley (1994) and Lenth (2001) provide more critical perspectives of how power analysis is used.

Concern #2. Multilevel Modeling

Two common situations where multilevel modeling is used in education research are when the students are nested within classrooms and when each student has data for several measurements. For the first situation, the data for the students are said to be nested within the classrooms and for the second the measurements nested within the students. The problem for traditional statistical methods is that the data within the same higher level unit tend to be more similar with each other than with those in other units. The data are not independent: an assumption of most traditional statistical procedures. Educational statisticians and educational datasets have been instrumental in the development of ways to analyze data in these situations (e.g., Aitken et al., 1981; Aitkin and Longford, 1986; Goldstein, 2011). The approach is also popular in other fields, for example within ecology (e.g., Bolker et al., 2009), geography (e.g., Jones, 1991), medicine (e.g., Goldstein et al., 2002), psychology (e.g., Wright, 1998), and elsewhere. The statistical models have several names that can convey subtle differences (e.g., mixed models, hierarchical models, random coefficient models). Here the phrase “multilevel models” is used.

Suppose you are interested in predicting reading scores for a 1,000 students in a school district equally divided among 10 schools from hours spent on educational reading software. Both reading scores and hours spent likely vary among schools. If you ran the traditional regression:

\begin{array}{l} r e a d i n g_{i} = β_{0} + β_{1} h o u r s_{i} + e_{i} & (1) \end{array}

It is assumed that the e_i are independent of each other, but they are not. There are a few approaches to this; the multilevel approach assumes each of the 10 schools has a different intercept centered around a grand intercept, β₀ in Equation (1). The method assumes these are normally distributed and estimates the mean and standard deviation of this distribution. Letting the schools be indexed by j, the multilevel equation is:

\begin{array}{l} r e a d i n g_{i j} = β_{0} + β_{1} h o u r s_{i j} + u_{j} + e_{i j} & (2) \end{array}

where u_j denotes the variation around the intercept. Most of the main statistical packages have multilevel procedures.

The R statistics environment (R Core Team, 2019) will be used for this, and subsequent, examples². It was chosen because of functionality (there are over ten thousand packages written for R) and because it is free, and therefore available to all readers. It can be downloaded from: https://cran.r-project.org/. Here the package lme4 (Bates et al., 2015) will be used. To fit the model in Equation (2) with a multilevel linear model you enter:

lmer(reading ~ hours + (1|school))

Two Examples

The two examples were picked to illustrate the two main ways that education data are often multilevel. The first is when the students are nested within classrooms and this is one of the first applications of multilevel modeling to education data (e.g., Aitkin and Longford, 1986). The second is where the students have several measurements. The measurements can be conceptualized as nested within the individual. These are often called repeated measures or longitudinal designs.

The textbook education example for multilevel modeling is where students are nested within a class. Li et al. (2017) used this design with 293 students nested within 18 classrooms. They compared student performance on inquiry and estimation skills using a linear regression. Inference from this statistic assumes that the data are independent from each other. It may be that the students in the different classrooms behave differently on these skills and that the teachers in these classrooms teach these skills differently. In fact, these are both highly likely. Not taking into account this variation is more likely to produce significant results than if appropriate analyses were done. Therefore, readers should be cautious with any reported p-values and the reported precision of any estimates.

Another common application of multilevel modeling is where each student provides multiple data points, as with Price et al. (2017) study of why students ask for a hint and how they use hints. Their data set had 68 students requesting 642 hints. Hints are nested within students. Students were also nested within classes and hints within assignments (and hints were sometimes clustered together), but the focus here is just hints being nested within students. The authors state that “the number of hints requested by student varied widely” (p. 316) so they were aware that there was student-level variation in hint frequency. There likely was also variation among students for why they requested hints and how they used the hints. One interest was whether the student did what the hint suggested: a binary variable. A generalized linear multilevel model could be used to predict which students and in which situations hints are likely to be followed. Instead Price et al. rely mostly on descriptive statistics plus a couple of inferential statistics using hints as the unit of study, thereby ignoring the non-independence of their data. Thus, their standard errors and p-values should not be trusted. For example, they examined whether how much time was spent looking at a hint predicted whether the hint was followed without considering that this will likely vary by student. Following a hint is a binary variable, and often a logistic regression is used for this. The lme4 package has a function for generalized linear multilevel regressions called glmer. Here is a model that they could have considered.

glmer(followHint ~ time + (1|student), family = "binomial")

While treating time as either a linear predictor of the probability of following a hint, or linear with the logit of the probability, is probably unwise, a curved relationship (e.g., a b-spline) could be estimated and plotted within the multilevel modeling framework. In R there is a function, bs, for b-splines:

glmer(follow ~ bs(time) + (1|student), family = "binomial")

Recommendations

2a. When the data are clustered in some way so that information about one item in a cluster provides information about others in the cluster, the data are not independent. This is an assumption of traditional statistical tests. The resulting p-values will usually be too low, but sometimes they will be too high, and sometimes the effects will be in the opposite direction. Alternatives should be considered. If the non-independence is ignored there should be justification and readers should be cautious about the uncertainty estimates (including p-values) of the results.

2b. There are alternatives to multilevel modeling. Some latent variable (including item response theory [IRT]) and Bayesian approaches can take into account individual variation and are sometimes nearly equivalent. In some disciplines it is common to estimate separate values for each school or student, what is sometimes called the fixed effect approach. There are arguments against this approach (e.g., Bell and Jones, 2015), but sometimes estimation problems with multilevel models mean the fixed effect is preferred (Wright, 2017).

2c. When the data have a multilevel structure, multilevel modeling (or some other way to take into account the non-independence of the data) should be used. There are many resources available at http://www.bristol.ac.uk/cmm/learning/ to learn more about these procedures. Several multilevel packages are reviewed at http://www.bristol.ac.uk/cmm/learning/mmsoftware/. Many free packages are available in R and these are discussed at: http://bbolker.github.io/mixedmodels-misc/MixedModels.html.

Background Reading

Goldstein (2011) provides detailed mathematical coverage of multilevel modeling. Hox (2010) provides a detailed textbook that is less mathematical. Field and Wright (2011) is an applied introduction.

Concern #3. Dichotomizing

Numerous authors have criticized researchers for splitting continuous measures into a small number of categories at arbitrary cut-points (e.g., Cohen, 1983; MacCallum et al., 2002). Sometimes the cut-scores are chosen at particular points for good reasons (e.g., the boiling and freezing points for water, the passing score on a teenager's driving test to predict parent anxiety), but even in these situations some information is lost and these particular breakpoints could be accounted for by allowing discontinuities in the models used for the data.

Consider the following example. Figure 1A shows the proportions of positive ratings for rigor and collaboration for New York City schools in 2014–2015³. The two variables are not dichotomized and there is a clear positive relationship. Other aspects of the data are also apparent, like the increased variance for lower values (proportions tend to have larger variance near 50% than at the extremes) and also the non-linearity related to 1.0 being the highest possible proportion. Non-linearity is important to examine. Figures 1B–D shows that information is lost when dichotomizing either variable. In Figure 1B the x-variable (rigorous) has been dichotomized by splitting the variable at the median, a procedure called a median split. The median is 0.86. Therefore, this procedure treats 0.70 and 0.85 as the same, and 0.87 and 0.99 as the same, but assumes there is some leap in rigor between 0.85 and 0.87. In Figure 1C the y-variable, collaboration, has been dichotomized. Here information about how collaborative a school is—beyond just whether they are in the top 50% of schools or not—is lost. In Figure 1D both variables have been dichotomized. The researcher might conduct a 2 × 2 χ², but would not be able to detect any additional interesting patterns in the data.

FIGURE 1

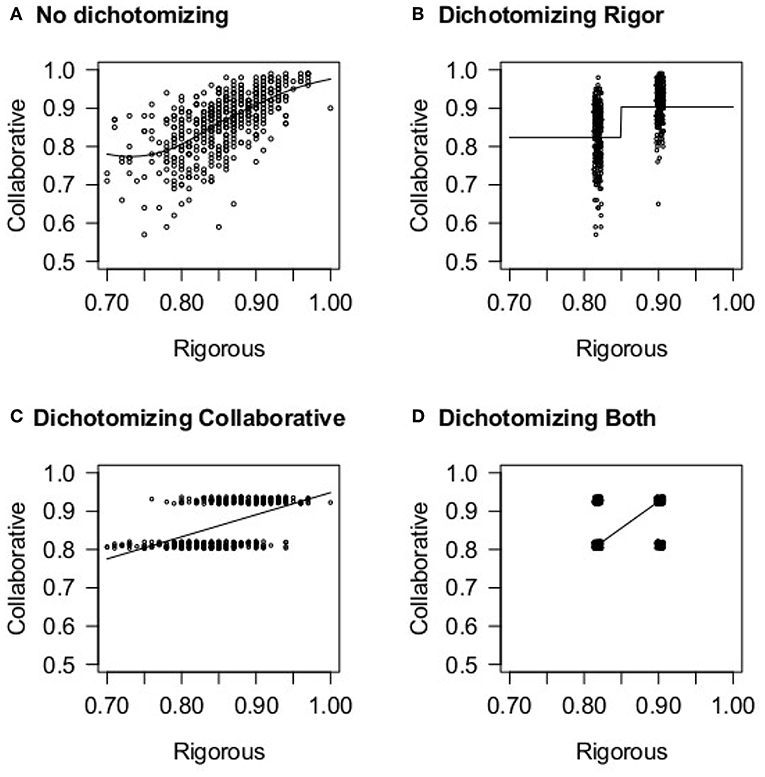
Figure 1. Data from New York City schools on the relationship between collaborative and rigorous ratings. (A) Shows the original variables. (B–D) Dichotomize the variables thereby presenting less information. A slight random “jitter” has been added to the values of dichotomized variables so that it can be seen when multiple schools have similar values.

Two Examples

The examples were chosen to illustrate two issues with dichotomization. The first was chosen because it uses a common, but much criticized, procedure called a median split. The choice of the example was also based on the authors providing enough data so that samples could be created that are consistent with the dichotomized data but lead to different conclusions if not dichotomized. The second example involves the authors using a complex method to dichotomize the data. This was chosen to stress that using a complex procedure does not prevent the loss of information.

Perez et al. (2017) allocated students either to a guided or to an unguided learning condition, and then focused on those 74 students who performed less well on a pre-test. They transformed the post-test score using a median split (they do not say how values at the median are classified, but here it is assumed the “high” group is at or above the median). Table 1 shows the results. Using a 2 × 2 χ² with Yates' correction the result is $χ_{(1)}^{2}$ = 0.21, p = 0.65, with an odds ratio of 1.37 (the null is 1.00) with a 95% confidence interval from 0.50 to 3.81 (found using the odds.ratio function in the questionr package, Barnier et al., 2017). While the condition variable is a truly dichotomous variable—participants were either in the guided condition or not—the post-test scores vary. Dichotomizing the variable loses information about how much above or below the median the scores were.

TABLE 1

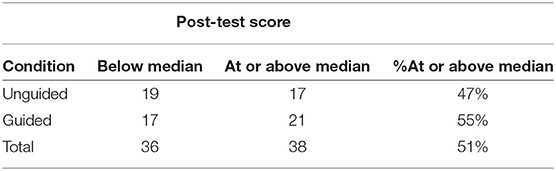
Table 1. The cross-tabulation table for (Perez et al., 2017) data.

It is likely that Perez et al. (2017) were interested in whether their manipulation affected post-test scores. If they had analyzed their data taking into account information lost by dichotomizing, they might have detected a statistically significant difference. Suppose their post-scores were based on responses to 10 items. The data in Sample 1 in Table 2 are consistent with the dichotomized values in Table 1. Perez et al. might have conducted a Wilcoxon rank sum test, calculated here using the defaults of R's function wilcox.test. A t-test leads to similar results, but readers might question the distribution assumptions of the t-test for these data. The result for Sample 1 is W = 472.5, a p-value of 0.02, with the guided condition performing better. The researchers could have concluded an advantage for this approach.

TABLE 2

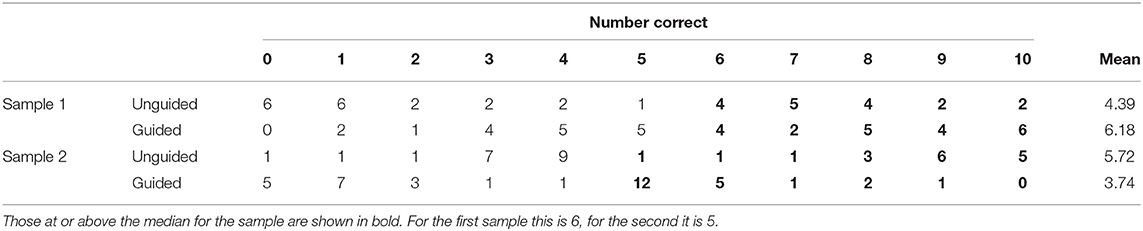
Table 2. Possible datasets for the data in Table 1.

However, Sample 2 of Table 2 is also consisted with the dichotomized values. It has W = 893.5, p = 0.02, but this finding is in the opposite direction with the guided condition doing worse. Perez et al.'s (2017) data might be like Sample 1, Sample 2, or neither of these.

The study by Li et al. (2017, their Table 2) was mentioned earlier because multilevel modeling could have been used, but their use of dichtomization is also noteworthy. They recorded the number of inquiry skills and explanation skills each student used, and conducted some preliminary statistics. They dichotomize both variables (like Figure 1D). Rather than using a median split on the total scores, they ran a K = 2 means cluster analysis on the individual items. The authors label the clusters high and low. If evidence were presented that people really were in two relatively homogeneous groups (using for example, taxometric methods, Waller and Meehl, 1998) then this could have been appropriate but if the constructs are dimensions information is lost. They then test the association that these dichotomized variables are associated and found the Pearson $χ_{(1)}^{2}$ = 6.18, p = 0.01. Interestingly, they also calculated Pearson's correlation using the continuous measures (r = 0.53, p < 0.001). It is unclear why both were done and, in relation to significance testing, it is inappropriate to test the same hypothesis multiple times even if one is inappropriate.

Recommendations

There are reasons to dichotomize. If the continuous variable results in a dichotomy, and that dichotomy is of interest, then dichotomizing can be useful. Sometimes it is useful to include a dummy variable for whether a person partakes in some behavior (e.g., having a computer at home; being an illegal drug user) and the amount of that behavior (e.g., hours at home using the computer; frequency of drug use). The concern here is when dichotomization (or splitting into more than two categories) is done without any substantive reason and where the cut-off points are not based on substantive reasons. Sometimes continuous variables are split into categories so that particular plots (e.g., barplots) and types of analyses (e.g., Anova, χ² tests) can be used as opposed to scatter plots and regression.

3a. If you believe a continuous variable or set of continuous variables may be based on a small number of categorical constructs, use appropriate methods (e.g., taxometric methods, Waller and Meehl, 1998) to justify this.

3b. Consider non-linear and dis-continuous models. Dummy variables can be included, along with quantitative variables, in regression models if you believe there are certain discontinuities in relationships.

3c. Do not dichotomize a variable just to allow you to use a statistical or graphical procedure if there are appropriate and available procedures for the non-dichotomized variables.

Background Reading

(MacCallum et al., 2002) provides a detailed and readable discussion about why dichotomization should usually be avoided.

Concern #4. Errors in Numbers

Humans, including myself, make typing mistakes.

There are several reasons why people distrust scientific results. The easiest of these to address is errors in the numbers reported in tables and statistical reports. These types of errors will always be part of any literature, but it is important to lessen their likelihoods. Some examples were chosen to show different types of errors.

Some Examples

Pezzullo et al. (2017, p. 306) report the following F statistics:

F_{(1, 115)} = 2.4579, p = 0.0375 “significant main effect”

F_{(1, 115)} = 2.9512, p = 0.0154 “significant interaction”

The p-values associated with these F statistics should be 0.12 and 0.09, respectively. The authors have turned non-significant findings into significant ones. There is no reason to think that this was a deliberate fabrication. If the authors had wanted to create significant effects where there was none, and they wanted to conceal this act, they could have changed the F-values too.

Some errors can be found with software like the freeware statcheck (Nuijten et al., 2016). It reads statistical text and tries to determine if the statistic and p-value match. If in R (with the statcheck package loaded) you write:

statcheck("F(1,115) = 2.4579, p = .0375")

it tells you that there may be some errors in the expression. The software has been created to allow entire text to be analyzed, parsing out the statistical material. Nuijten and colleagues used this to analyze data from several American Psychological Association (APA) journals. They found that about 10% of p-values reported were incorrect. The package does not catch all errors so should not be the only thing relied upon to check a manuscript before submission (an analogy would be just using a spellchecker rather than proofreading).

Another example is from Talandron et al. (2017, p. 377). They were interested in the incubation effect where waiting to solve a problem after failure can help to produce the correct response. One of their key findings was “the average number of attempts prior to post-incubation of all IE-True (M = 32, SD = 21) was significantly lower than those of IE-False (M = 46, SD = 22) [t₍₁₆₉₎ = 1.97, two-tailed p < 0.01].” The true p-value for t₍₁₆₉₎ = 1.97 is 0.05.

The errors by Pezzullo et al. and Talandron et al. were relatively easy to identify. Other errors can be more difficult to notice. Sjödén et al. (2017, p. 353) analyzed data of 163 students playing 3,983 games. They compared the number of games played by each student with the student's average goodness rating and found “Pearson r = 0.146; p = 0.000.” The p associated with r = 0.146 with n = 163 is, two-tailed, 0.06. The likely source of the error is that the wrong n has been used either when looking up the p-value manually or these student-level variables were repeated for each game the student played in the data file and the authors took the numbers from the statistics package without noticing this problem.

It is important to check the degrees of freedom carefully, because errant degrees of freedom may mean the wrong statistic is being reported. For example, Kumar (2017, p. 531) compared student performance before and after some changes were made to the software that he was examining. He reports no significant main effect between these two groups. He then repeated the analyses including a covariate: number of puzzles solved during the task. He reports that the main effect is now significant: F_(2,169) = 3.19, p = 0.044. The 2 in the numerator of the degrees of freedom is odd. There are only two groups so there should only be 1 degree of freedom for the numerator if this is a test of the difference between the model with the covariate and the model with the covariate plus the single grouping variable that distinguishes the two groups. If it is a typo and it is 1 then the F and/or the p is wrong. From the description it appears that the covariate also has only one degree of freedom. Because some statistics software produces the F value for the entire model as well as its components, it could be that Kumar took the statistic from the wrong part of the output. He argues that the covariate should have been associated with the outcome, so it would not be surprising that the covariate plus the group difference were statistically significant.

Recommendations

4a. While packages like statcheck (Nuijten et al., 2016) can catch some errors, they will not catch all errors. As the software evolves, more (but not all) errors will be caught. This might have the negative affect of people relying on it too much (like not learning to spell because of the ubiquity of spellcheckers). Given that only some errors will be caught it is important not to treat this as if it is checking all numeric output. There will always be the chance of some typographical errors, but it is worth using modern technology to catch some errors.

4b. Procedures exist to include the statistical code in your word processing document that reads the data and creates the numeric output (and plots) directly. An example is the package knitr (Xie, 2015). It allows you to write your paper in LaTeX and have chunks of R (and many other statistical packages), typing

names(knitr::knit_engines$get())

in R currently (Nov. 20, 2019) shows 41 languages, including STATA, SAS, Java Script, and Python) embedded within it. An author could write “The p-value was \Sexpr{t.test(DV~IV)$p.value}” in LaTeX and the p-value would appear in the document. This has the additional advantage that if an error in the data file is discovered and fixed, then the tables, plots, and any statistics embedded in the text can be automatically corrected.

4c. While the responsibility for checking numbers and words is primarily the authors, the reviewing process for conferences and journals could identify some of these errors and allow the authors to correct them. Some journals already do this. For example the Association of Psychological Science (APS) uses statcheck both before manuscripts are sent for review and it is required that authors submit a statcheck report with their final submission (https://www.psychologicalscience.org/publications/psychological_science/ps-submissions#STATCHK). It may be worthwhile to have statistical and methods reviews of submissions as is done in some medical journals. Some of the issues are discussed in Altman (1998). If there are not enough statistics reviewers, other reviewers could be given guidelines for when to direct a submission to a statistics/methods reviewer. Example guidelines are in Greenwood and Freeman (2015).

Background Reading

The statcheck webpage (https://mbnuijten.com/statcheck/) has links to sources showing show to use it. The web page for knitr (https://yihui.name/knitr/) will also provide more up-to-date information about at least that package than print sources. For advice to journal and conference referees and editors, see Greenwood and Freeman (2015).

Summary

The crisis in behavioral science has led to several guidelines for how to avoid some of the pitfalls (e.g., Munafò et al., 2017). These include teaching more fundamentals and ethical issues in statistics and methods courses, pre-registering research design/analytic methods, using alternatives to hypothesis testing, and more transparent methods for disseminating research findings. These are issues within the current crisis in science. Stark and Saltelli (2018) discuss an under-lying cause of why bad science abounds: Cargo Cult Statistics. This is a phrase taken from Feynman's (1974) famous commencement address “Cargo Cult Science,” which itself is taken from Worsley (1957). Stark and Saltelli define the statistical variety as “the ritualistic miming of statistics rather than conscientious practice” (Stark and Saltelli, 2018, p. 40). They describe how this miming is often the most effective way to get papers published (have it superficially look like other published papers) and having many publications is necessary for career development in modern academia. It is important to focus on both the broad issues like how research organizations reward output and on the specific issues that have created cargo cult statistics. The focus here is on how to address the more specific issues.

The area examined was the field of Education with Technology (EwT) and studies that might fit content-wise within applied psychology. EwT was chosen because of its importance for society. Its inter-disciplinarity means many of those conducting research had their formal research training outside that of those disciplines that tend to conducted studies on human participants. The hope is that this paper provides some helpful guidance.

Four issues were chosen in part because they can be addressed by researchers relatively easily: power analysis, multilevel modeling, dichotomization, and errors when reporting numeric statistics. Other issues could have been included (e.g., using better visualizations, using more robust methods), and with all of these issues, studies from many fields also show these (and other) concerns.

A small number of underlying themes relate both to the issues raised in this paper for EwT and to the crisis in science more generally.

1. Don't get excited by a p-value.

2. Don't think that because a paper is published that it is replicable and certainly not that it is the end of the story. The evidence reported in papers contributes to the story.

3. Empirical science, done well, is difficult and time-consuming. Time taken planning research is usually well spent.

4. The goals of science are different than the goals of many scientists and are not perfectly aligned with the structures put in place to reward scientists.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

DW is the Dunn Family Foundation Endowed Chair of Educational Assessment, and as such receives part of his salary from the foundation.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^http://www.springer.com/cda/content/document/cda_downloaddocument/9783319614243-p1.pdf?SGWID=0-0-45-1609692-p180928554 (accessed May 5, 2018).

2. ^Power analyses (Concern #1) can also be conducted in R. There are function in the base R package including power.t.test and specialized packages for more involved designs including PoweR (Lafaye de Micheaux and Tran, 2016) and pwr (Champely, 2018).

3. ^From https://data.cityofnewyork.us/Education/2014-2015-School-Quality-Reports-Results-For-High-/vrfr-9k4d.

References

Aitken, M., Anderson, D. A., and Hinde, J. P. (1981). Statistical modelling of data on teaching styles (with discussion). J. R. Stat. Soc. Ser. A 144, 419–461. doi: 10.2307/2981826

POLICY AND PRACTICE REVIEWS article

Research Methods for Education With Technology: Four Concerns, Examples, and Recommendations

Choosing Examples

Crisis in Science and Hypothesis Testing

Background Reading

Concern #1: Power Analysis and Small Samples

Two Examples

Recommendations

Background Reading

Concern #2. Multilevel Modeling

Two Examples

Recommendations

Background Reading

Concern #3. Dichotomizing

Two Examples

Recommendations

Background Reading

Concern #4. Errors in Numbers

Some Examples

Recommendations

Background Reading

Summary

Author Contributions

Funding

Conflict of Interest

Footnotes

References

People also looked at